Simultaneously estimating the task-related and stimulus-evoked components of hemodynamic imaging measurements

Abstract.

Task-related hemodynamic responses contribute prominently to functional magnetic resonance imaging (fMRI) recordings. They reflect behaviorally important brain states, such as arousal and attention, and can dominate stimulus-evoked responses, yet they remain poorly understood. To help characterize these responses, we present a method for parametrically estimating both stimulus-evoked and task-related components of hemodynamic responses from subjects engaged in temporally predictable tasks. The stimulus-evoked component is modeled by convolving a hemodynamic response function (HRF) kernel with spiking. The task-related component is modeled by convolving a Fourier-series task-related function (TRF) kernel with task timing. We fit this model with simultaneous electrode recordings and intrinsic-signal optical imaging from the primary visual cortex of alert, task-engaged monkeys. With high $R^2$, the model returns HRFs that are consistent across experiments and recording sites for a given animal and TRFs that entrain to task timing independent of stimulation or local spiking. When the task schedule conflicts with that of stimulation, the TRF remains locked to the task emphasizing its behavioral origins. The current approach is strikingly more robust to fluctuations than earlier ones and gives consistently, if modestly, better fits. This approach could help parse the distinct components of fMRI recordings made in the context of a task.

1. Introduction

Functional magnetic resonance imaging (fMRI) measurements, both blood oxygen-level dependent (BOLD) and cerebral blood volume (CBV), show prominent task-related endogenous hemodynamic responses. These reflect behaviorally important brain states, such as attention, vigilance, and anticipation (reviewed, e.g., in Refs. ^1–3). The neural mechanisms underlying these endogenous responses are still poorly understood because of the relative paucity of studies combining imaging with electrophysiology in alert task-engaged subjects. However, a growing number of studies are starting to fill this gap.^4–7

This paper concerns a particular task-related hemodynamic response that we first measured in the alert macaque primary visual cortex (V1).⁸ With the animals engaged in a periodic task, the task-related response was entrained to task timing independent of visual stimulation^8,9 (also see Ref. 10). Although it correlated with task performance,⁹ this response was not visuotopically specific and, thus, likely distinct from spatial attention (also see Refs. ¹¹ and ¹²). Concurrent electrode recordings showed it to be unpredicted by local spiking or local field potential (LFP; also see Refs. ^13–15). In the presence of visual stimuli, this task-related response added linearly to the stimulus-evoked component of the response, which, by contrast, was very well predicted by local spiking^16,17 (also see Refs. ¹⁸ and ¹⁹). We measured these brain hemodynamic responses from monkey V1 using intrinsic-signal optical imaging (ISOI), an optical analog of fMRI that deduces changes in local blood volume and oxygenation from changes in light reflection off the brain surface (Refs. ^20–22; see acknowledgment for a more detailed discussion of ISOI). However, similar task-related hemodynamic responses were also reported in human subjects by at least two groups using BOLD fMRI.^23–25 Having the animal model, thus, offers an important avenue to investigate the neural basis of task-related endogenous components of fMRI measurements.

Here, we describe a parametric method for simultaneously fitting the task-related and stimulus-evoked components of measured hemodynamics, which improves considerably on our earlier technique for calculating these components. Our earlier approach was a hybrid one; we fit a hemodynamic response function (HRF) to the responses evoked by the controlled visual stimuli alone, which we estimated by subtracting the mean blank-trial response (i.e., with no stimulus) from all other responses. This subtraction was intended to remove the task-related component along with responses to uncontrolled visual stimulation. The task-related component itself was not fitted but rather defined as the residual that could not be regressed away using the fitted HRF.^16,17 This approach (labeled “blank-subtracted” in this paper) was adequate in the earlier work where we tried to keep the task and thus, presumably, the task-related hemodynamic component stereotyped throughout an experiment. However, we find that changing behavioral parameters (reward size²⁶ and task performance⁹) strongly modulate the task-related component. To investigate the effect of the behavioral state on the task-related component, it is helpful to develop a parametric model. Therefore, for our approach, we parametrize the task-related component as a “task-related function (TRF)” kernel, modeled as a Fourier series, which we convolve with delta functions aligned to trial onsets. The resultant estimate of the task-related component is summed linearly with the stimulus-evoked component—still modeled as an HRF kernel convolved with spiking—to predict the measured hemodynamics. The parameters of the full model (labeled “HRF+TRF” here) are obtained by fitting the net prediction to the observed hemodynamics. We find that the HRF+TRF fits are markedly more robust to error than our original blank-subtracted ones. These fits are also consistently, albeit modestly, better (giving higher $R^2$). In addition, the new HRF+TRF fits confirm our earlier finding that the stimulus-evoked component of hemodynamics is better predicted by concurrent spiking than by LFP.¹⁷

2. Materials and Methods

This paper presents a reanalysis of earlier data¹⁷ (65 sites combining electrode recordings and imaging, from four hemispheres in two monkeys comprised the main body of data used to compare the HRF+TRF model to alternate models; nine additional sites in one monkey were used to test this model for cases where the task and the visual stimulation had conflicting timing). Earlier publications^8,16,17 contain detailed descriptions of the experimental approach and recording techniques, which are summarized briefly here while we focus on the current analytical approach. All procedures were performed in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and were approved by the Institutional Animal Care and Use Committees of Columbia University and the New York State Psychiatric Institute.

2.1. Overall Experimental Setup

Our original experiments were designed to rigorously test the linear separability of task-related and stimulus-evoked hemodynamic responses over a wide dynamic range of combinations of the two. We chose a task, comprising periodic fixation, for juice reward, that evokes strong task-related responses⁸ in V1. Each trial was behaviorally identical. It started with a fixation cue changing color (e.g., from equiluminent red to green), the signal for the animal to hold fixation until the color changed back again; the animal received a juice reward for holding fixation, but no time out or other punishment if not. Fixations lasted from 3 to 4 s; net trial periods ranged from 10 to 20 s in different experiments but were fixed and predictable within an experiment. While the animal fixated, he was presented passively with visual stimuli chosen to elicit a wide dynamic range of stimulus-evoked responses. They consisted of drifting sinusoidal gratings ranging in contrast (one per trial) from near-background to 100% in contrast-doubled steps (e.g., 3.125%, 6.25%, 12.5%, 25%, 50%, 100%, and a “blank,” i.e., 0% contrast; some experiments were run with fewer contrasts, in the interest of speed). Contrasts were presented in “blocks” of one full (randomized) set per block and were repeated within a block until the animal had correctly completed one trial per contrast. This was intended to have equal numbers of correct trials per contrast in an experiment, distributed roughly uniformly across long-term changes in the behavioral state (alert/drowsy).

2.2. Optical Imaging and Electrophysiology

ISOI (Dalsa 1M30P camera, $15\text{frames}/\mathrm{s}$; software modified from that in Ref. 27) was carried out through a surgically implanted glass-windowed stainless steel recording chamber with a clear silicone artificial dura.²⁸ The imaging wavelength (green: 530 nm; high-intensity LED, Agilent Technologies and Purdy Electronics) is absorbed equally by oxy- and deoxyhemoglobin thus measuring changes in total hemoglobin, analogous to local CBV.¹⁶ Concurrent electrode recordings [Plexon (RRID:nif-0000-10382)] were mostly, but not exclusively, confined to upper cortical layers, roughly matching the $\sim 500\text{-}\mu \mathrm{m}$ sampling depth of the ISOI measurement. The electrode measurement was split into spiking (250 Hz to 8 kHz bandpass) and LFP (0.7 to 170 Hz) using standard Plexon settings. All spiking was multiunit activity (MUA), defined by the spiking signal crossing a threshold. (See Refs. ^{8, 16}, and ¹⁷ for details on recording setup). Gamma LFP was defined as the 30- to 90-Hz bandpass-limited LFP spectral power (multitaper spectral analysis using the Chronux MATLAB^® toolbox).

The analysis only considered trials where the monkey correctly held fixation.⁹ Trials with transients greater than $35\times$ of the baseline standard deviation on the electrophysiological signal were rejected; the accepted trial pairs (hemodynamics and electrophysiology) were converted into $z$-scores for fitting after removing slow baseline drifts ($>30\mathrm{s}$) and heart rate artifacts (filter $\sim 2$ to 3 Hz) from the hemodynamic response (using the “runline” command in the Chronux MATLAB^® toolbox).

2.3. HRF+TRF Model Relating Hemodynamics to Electrophysiology and Task Timing

The measured hemodynamics $H(t)$ was modeled as the sum of two components: a stimulus-evoked component comprising an HRF kernel convolved with the concurrently measured spiking $S(t)$, and the task-related component comprising a TRF kernel convolved with the set of delta functions at trial onsets, $\mathrm{Trl}(t)$. The symbol * denotes convolution over time

$$H(t)=\mathrm{HRF}*S(t)+\mathrm{TRF}*\mathrm{Trl}(t).$$ (1)

The HRF kernel was parametrized, as in Refs. ^{8, 16}, and ¹⁷, as a gamma-variate function of time $t$

$$\mathrm{HRF}(t,\tau ,W,A)=A{\left(\frac{t}{\tau }\right)}^{\alpha }\exp (-\alpha \frac{t-\tau }{\tau }).$$ (2)

The HRF parameters fitted during optimization are the amplitude $A$, time to peak $\tau$, and full width at half maximum $W$.^8,29,30 The factor $\alpha =8.0\times \log (2.0)\times {(\frac{\tau }{W})}^2$.

The TRF kernel was parametrized as the finite sum of a Fourier time series

$$\mathrm{TRF}(t,a,b,P,N)=\sum _{n=1}^N\left[a_n\cos \right(n\frac{2\pi }{PT}t)+b_n\sin (n\frac{2\pi }{PT}t\left)\right].$$ (3)

Although the Fourier series were based on the trial period $T$, the fundamental Fourier period was allowed to vary as a fraction $P$ of the trial period and optimized in the fit. The parameters, $a_n$ and $b_n$ (with $n$ ranging from 1 to the total number of terms in the Fourier series, $N$), are the pairs of cosine and sine coefficients, respectively, for the $n$’th Fourier term, and are also optimized in the fit along with the parameter $P$ and the three parameters for the HRF.

In Sec. 3.6, the measured spiking $S(t)$ was replaced by the concurrently measured gamma LFP.

2.4. Earlier Approach: Blank-Subtracted Fit

The earlier blank-subtracted fit was repeated for comparison with the current results. We used the model

$$H_{\text{Blanksubtracted}}(t)=\mathrm{HRF}*S_{\text{Blanksubtracted}}(t),$$ (4)

where the subscript Blanksubtracted indicates that mean blank-trial responses were subtracted from the measured hemodynamics and spiking (see Ref. 16). The HRF was modeled as a gamma-variate function as above [Eq. (2)].

2.5. Control: Gamma Prime HRF Convolved with Spiking

We wanted to control for the possibility that the model did not need any term independent of spiking; that simply using a more complex HRF with more terms was adequate. We tested by fitting with a multicomponent “gamma prime HRF” kernel but with no additional task-related terms or blank-subtraction

$$H(t)={\mathrm{HRF}}_{\text{Gammaprime}}*S(t).$$ (5)

The ${\mathrm{HRF}}_{\text{Gammaprime}}$ was modeled as a gamma-variate function and its first time derivative^31,32

$$\begin{gathered} {\mathrm{HRF}}_{\text{Gammaprime}}(t,\tau ,W,A,K)=A{\left(\frac{t}{\tau }\right)}^{\alpha }\exp (-\alpha \frac{t-\tau }{\tau }) \\ +K\left[\alpha A{\left(\frac{t}{\tau }\right)}^{\alpha -1}\exp \right(-\alpha \frac{t-\tau }{\tau })-\frac{\alpha }{\tau }A{\left(\frac{t}{\tau }\right)}^{\alpha }\exp (-\alpha \frac{t-\tau }{\tau }\left)\right]. \end{gathered}$$ (6)

All terms shared with the gamma-variate HRF [see Eq. (2)] are defined as for the HRF. $K$ is an additional amplitude parameter multiplying the time derivative. The prediction for this model consisted of the convolution of this ${\mathrm{HRF}}_{\text{Gammaprime}}$ with the full measured spiking.

2.6. Fitting the Models

All relevant models were fitted independently for each experiment ($N=65+9$) by matching the predicted to the measured hemodynamics. The error was defined as the normalized sum squared error $\left(\frac{S{S}_{\text{error}}}{S{S}_{\text{total}}}\right)$ calculated separately per contrast and then averaged over all contrasts, including the blank. This was intended to give equal weight to the fractional error at each stimulus contrast. The error was minimized by varying the fitted parameters using a downhill simplex algorithm (“fminsearch,” MATLAB^® methods as in Ref. 17). For the HRF+TRF model, we optimized HRF parameters, $A$, $\tau$, and $W$, and TRF parameters, $a_{1,}{b}_{1,},\dots a_{N,},b_{N,}$, and $P$; for other models, we optimized the smaller sets of relevant model parameters. To reduce the chances of getting caught in a local minimum, we started with large sets of initial parameter values, independently covering more than an order of magnitude for each fitted parameter. The fits were robust and converged to the same optimal parameters from multiple starting values, giving us confidence that we had reached global and not local minima.

It is important to emphasize that the fitting procedure was formally identical for each of the models tested. Specifically, we constructed concatenated sequences of the average response per contrast, randomized per contrast (same random sequence for hemo and spiking or LFP depending on the fit), and over multiple blocks (an arbitrarily large number 52, about $100\times$ larger than a single HRF kernel convolution length; to minimize edge effects, we only matched traces two convolution lengths in from the edge). For the blank-subtracted model, the blank trial responses consisted of flat lines and all other responses were blank subtracted; for all other models, we used the mean measured responses. These sequences of hemo and spiking or LFP traces were then fitted against each other for the model being tested, as described in the above paragraph. Thus, differences in the robustness of the fitted parameters (see below) or in the goodness of fit result from differences in the model rather than in the fitting process.

The goodness of fit $R^2$ for the optimal prediction was defined as the coefficient of determination $(1-\frac{S{S}_{\text{error}}}{S{S}_{\text{total}}})$ calculated separately per contrast and averaged across contrasts. This, again, was intended to give equal weight to errors at each contrast. When comparing fits across models, it is also important to note that the denominators $(S{S}_{\text{total}})$ in these calculations of $R^2$ were identical for all models fitted to a given experiment. Thus, differences in $R^2$ reflected the differences in the residual errors $(S{S}_{\text{error}})$ for the models being compared.

For the HRF+TRF fit, the optimal number of Fourier terms $N$ for the TRF kernel ($N=1$: fundamental alone, $N=2$: fundamental and first harmonic, etc.) was deduced by comparing the cross-validated goodness of fit obtained using models with progressively increasing $N$ (see Sec. 3.2).

2.7. Comparing Robustness across Models: Bootstrap

We used a bootstrap procedure to assess the robustness of our models to variability in the measured responses, simulating fluctuations in the data with bootstrapped sample sets of spiking and hemodynamic response pairs. Sets were generated for each stimulus contrast separately, choosing randomly with replacement from the recorded trials for that stimulus while preserving the number of trials. Selections were block randomized, as with the cross-validation test sets. Each such sample set was then separately fitted using HRF+TRF and blank-subtracted approaches.

We then used two measures of robustness to compare the two fitting approaches.

• 1.The robustness of the optimal HRF: We first calculated, for each bootstrapped sample, and separately for the two fitting approaches, the mismatch of the bootstrap HRF to the original HRF. This mismatch was quantified as the sum squared difference normalized by the sum of squares of the original HRF. The standard deviation of this mismatch over the population of bootstrap samples was taken as a measure of robustness: the lower the standard deviation, the more robust the fit.
• 2.The robustness of the $R^2$ measurements: We similarly calculated the standard deviation of the $R^2$ over the population of bootstrap samples, separately for each fitting approach. Again, the lower the standard deviation, the more robust the fit. For both measures, we quantified the statistical significance of the comparison at two levels: within each experiment and pairwise across all experiments. Within each experiment, we tested that the dispersion (a generalization of variance or standard deviation for nonnormal data) across the bootstrapped blank-subtracted fits was higher than that across the HRF+TRF fits, rejecting the null hypothesis that they are equal. Since the distributions of the fits were nonnormal, we used a single-tailed Ansari–Bradley test on the distributions centered around their respective medians (“ansaribradley” in MATLAB^®); this test is a nonparametric analog of the 2-sample $F$ test (testing that two normal distributions have the same variance). For the pairwise tests across all experiments, we used the Wilcoxon signed-rank test to calculate $p$ values comparing blank-subtracted versus HRF+TRF fits.

2.8. Comparing Goodness of Fit $R^2$ across Models: Cross Validation

$R^2$ was compared pairwise across models using 50–50 cross validation. For each experiment, we first generated a “master set” of 1000 (or, in the interest of speed, 500) training and test data pairs using random 50–50 splits. Using standard cross-validation methods, we fit this master set with each model separately, getting sets of test $R^2$ using parameters fit to corresponding training sets. To compare a pair of models “A” and “B,” we obtained the distribution of cross-validated [$R^2$ (model A) – $R^2$ (model B)], as pairwise differences per data split for an experiment. We tested for the hypothesis that [$R^2$ (model A) > $R^2$ (model B)] by estimating the one-sided $p$ value of the null [$R^2$ (model A) – $R^2$ (model B) = 0]. This defined our $p$ value per model comparison, per experiment.

Since our stimuli were presented block randomized, the trial splitting for the initial master set was also done blockwise (i.e., randomly selecting entire blocks of trials for the model or test half), to avoid problems due to slow changes in brain state during the experiment. This constraint still allowed a large sample space. For an experiment of 30 blocks, each with its full set of stimuli, this gives $30!/(15!\times 15!)$ or $1.5\times {10}^8$ possible splits.

3. Results

3.1. HRF+TRF Model

The HRF+TRF model fits our measured data with generally high $R^2$. The resulting optimal HRFs were consistent across experiments and recording sites for a given animal; accompanying TRFs were tightly entrained to the fixation task schedule. Notably, when the task schedule differed from that of visual stimulation, the TRF remained locked to the task schedule, suggesting its basis in behavioral versus stimulus-evoked brain activity. Comparisons with the blank-subtracted approach showed that the current fits are markedly more robust. Their $R^2$ values are also consistently, if modestly higher.

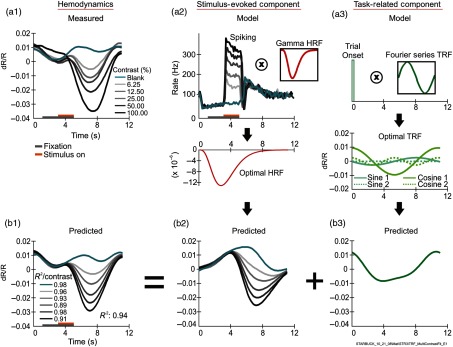
The HRF+TRF approach to fitting [see Eqs. (1)–(3)] and the resultant optimal predictions are illustrated in Fig. 1 for the same example data set as used in our earlier work (see Figs. 1 and 2 of Ref. 16). The recordings were made in V1 of an alert monkey whose task was to hold fixation periodically for a juice reward (4-s fixations, 11.2-s trials. We found earlier that this task evokes strong task-related responses).^8,16 While fixating, the monkey was passively shown grating stimuli ranging in contrast from near background to 100% in contrast-doubled steps, along with a blank stimulus. These stimuli evoked a wide dynamic range of responses as evident in the recorded hemodynamic [Fig. 1(a1)] and concurrent spiking traces [Fig. 1(a2), main panel]. As in our earlier work, the hemodynamic response is proposed to be the sum of a stimulus-evoked and a task-related component. In our current approach, both the stimulus-evoked and task-related components are fitted parametrically. The stimulus-evoked component is modeled as the convolution of measured spiking with a gamma-variate HRF kernel [Fig. 1(a2); HRF shown as inset; also see Eq. (2)]. The task-related component is modeled as the convolution of delta functions at trial onsets, of unit amplitude independent of visual stimulation, with a Fourier-series TRF kernel [Fig. 1(a3); also see Eq. (3)]. To get optimal fitted HRF and TRF, the kernels are varied parametrically to get the best match between the sum of these two modeled components and the measured hemodynamic response (see Sec. 2.6).

Fig. 1.

HRF+TRF model and optimal predictions compared with measured hemodynamics. (a1)–(a3) Measured responses and schematic of the model. (a1) The measured hemodynamic response (shown for an experiment with five stimulus contrasts and a blank) is proposed to be the sum of two components. The first component, the stimulus-evoked one (a2), is modeled as the measured spiking response per contrast [(a2), main panel], convolved ($\otimes$) with a gamma-variate HRF kernel [(a2), inset]. The optimal HRF kernel after fitting is shown below (a2), with the corresponding prediction in (b2). The second component, the task-related one (b3), is modeled as the convolution of unit-amplitude delta functions at trial onsets [(b3), main panel] convolved with a Fourier series kernel [TRF: (a3) inset: illustrated here with just the fundamental sine term]. The optimal fitted TRF for a Fourier series model that includes the fundamental and the first harmonic is shown below (a3). It sums to the predicted task-related component shown in (b3). Note that although the period of the fundamental appears to match that of the trial, the model does not assume a match. Rather, it lets the fundamental be a variable fraction $P$ of the trial period. Thus, for this model, the set of optimized parameters comprises $P$ and the two pairs of cosine and sine Fourier coefficients $a_n$ and $b_n$ for the TRF, and the three parameters amplitude, time to peak, and peak width for the HRF [see Eqs. (1)–(3) in Sec. 2.3]. Also note, parenthetically, that the task-related component cannot simply be equated to the no-stimulus (blank-trial) response. All trials, including the blank, have a prominent trial-locked spiking response: reduced spiking as the animal fixates on the gray screen, increasing with a rebound at the end of fixation [(a2); also see supplementary Fig. 1 in Ref. 16). This trial-locked spiking would evoke trial-locked hemodynamics that is impossible to disambiguate from the trial-locked task-related component without a model such as the one here. (b1)–(b3) Optimal predictions. (b1) Optimal predicted hemodynamics. This is the sum of the optimal predicted stimulus-evoked component (b2) and the optimal predicted task-related component (b3). The $R^2$ of the prediction compared to the measured hemodynamics, contrast by contrast, and the mean $R^2$ averaged across contrasts are shown in (b1). Contrast is color coded, as shown in the key in (a1. Note: For this and all other figures, please see online version for color coding; print version only uses grayscale). All hemodynamic responses both measured and predicted are shown in units of fractional change in light reflected off the cortical surface ($\mathrm{d}R/R$); this is proportional to local change in blood volume, with downward excursions indicating increased absorption of light and thus increased blood volume. All traces other than inset kernels are on a common time scale. (a1) and (a2) show the trial structure, i.e., the fixation and stimulus presentation periods on the time axis, color coded as in the key in (a1). The label below (b3) (“STARBUCK_…”) identifies the experiment. Similar labels are used in all figures to identify data sets.

The resulting optimal predictions are shown in Figs. 1(b1)–1(b3). For this fit, the TRF kernel was modeled as a Fourier series consisting of the fundamental frequency and its first harmonic (see Sec. 3.2 regarding the optimal number of TRF Fourier terms). The two resulting pairs of cosine and sine components, scaled by the optimal fitted Fourier coefficients, are plotted in Fig. 1(a3) with their sum, the optimal predicted task-related component in Fig. 1(b3). The fitted fundamental frequency came to 0.092 Hz, i.e., $1.026\times$ the task trial frequency of 0.089 Hz (corresponding to the trial period of 11.2 sec). The optimal HRF from the same fit, shown below 1(a2), predicts the stimulus-evoked components shown in 1(b2). Note the apparent upward shift in the stimulus-evoked component relative to the measured hemodynamics at each contrast, which is corrected by summing with the predicted task-related component [1(b3)]. The final predictions [1(b1)] match measured values well, as evident in the high $R^2$ values per contrast shown alongside the predictions. The overall goodness of fit ($R^2=0.94$) defined as the mean of these $R^2$ values per contrast (see Sec. 2.6) is comparable to that obtained earlier with blank-subtracted fits [$R^2=0.93$; fit not shown. See Fig. 2(c) of Ref. 16].

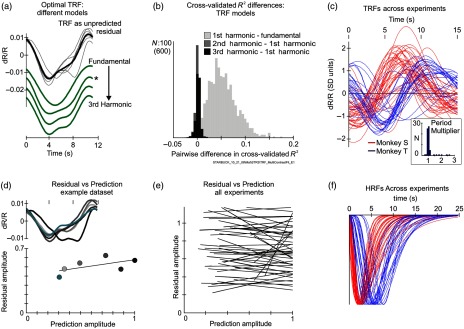
3.2. Optimal Number of TRF Fourier Terms

The question that remained unanswered was: how many terms should be used in the Fourier series defining the TRF kernel (Fig. 2)? In principle, more Fourier terms lead to more high-frequency structure in the TRF kernel [Fig. 2(a)] and better fits, but the improvements could be due to overfitting. We determined the optimal number of Fourier terms using cross validation (see Sec. 2.8). We compared four nested HRF+TRF models with increasing numbers of TRF Fourier terms, from the fundamental alone up to the third harmonic (i.e., the fundamental frequency, along with harmonics $2\times$, $3\times$, and $4\times$ the fundamental), using the same dataset as in Fig. 1. The tests showed that models where the TRF Fourier series included the first harmonic with the fundamental gave significantly better fits (higher $R^2$) than ones with the fundamental alone [Fig. 2(b)]. However, increasing the number of TRF Fourier terms to the second and third harmonics led to no further significant improvement. We thus used TRF Fourier series with the fundamental and first harmonic as the standard for fitting all experiments [optimal TRFs across experiments are shown in Fig. 2(c)]. These TRFs largely tracked the task period [see inset, Fig. 2(c)] and were dominated in amplitude by the fundamental (amplitude of first harmonic relative to the fundamental: ($\text{median}=0.34$ [0.20; 0.82, $-/+$ 34th percentile (1 SD), $N=65$]). Notably, both the TRFs [Fig. 2(c)] and corresponding HRFs [Fig. 2(f)] appear to have distinct distributions of time courses for the two animals, suggesting that both kernels carry physiologically significant information about neurovascular coupling that varies among individuals.

Fig. 2.

Optimal TRFs and HRFs. (a) Comparison of optimal TRFs for different models fitted to the same data set as in Fig. 1. Top “TRF as unpredicted residual” shows TRF estimated for the blank-subtracted fit, as the residual after regressing away all spiking-related components from the measured hemodynamics. Gray lines: individual contrasts; black: average across contrasts. The four traces below (green, in online version) show optimal TRFs from HRF+TRF fits, for models using progressively more Fourier terms from the fundamental alone up to the third harmonic; (traces are shifted vertically downward for visibility). Asterisk marks the fundamental + first harmonic, the same TRF as in Fig. 1(b3). Note the increasing high-frequency structure with increasing numbers of Fourier terms. (b) Using cross validation to test if increasing the number of TRF Fourier terms increases $R^2$ and improves the fit (1000 samples, 50–50 splits; each sample fitted with all four models). Histograms of pairwise differences in cross-validated $R^2$ for three pairs of models (see color coding; labels refer to the maximum number of harmonics in the Fourier series). We tested each pairwise difference of $R^2$ for an improvement in $R^2$ on adding more Fourier terms, against the null hypothesis that the two $R^2$ values are equal to each other (see Sec. 2.8). The $R^2$ for the fundamental + first harmonic was significantly higher than that for the fundamental alone ($p<0.017$ for the null hypothesis; see histogram for “first harmonic – fundamental”). However, there was no further improvement on adding the second ($p=0.44$) or the third harmonic ($p=0.30$; note that the corresponding histograms are largely centered on 0). Histogram bin size = 0.005. $Y$ Scale bar: $N=100$ counts for first harmonic – fundamental, and 600 counts for the other two. (c) Optimal TRFs across experiments (fundamental + first harmonic Fourier model), shown per monkey “S” ($N=40$) and “T” ($N=25$). Traces scaled by the amplitude (standard deviation) of the hemodynamic response for the experiment. Inset shows the histogram of the fitted optimal factors $P$ expressing the TRF Fourier fundamental period as a fraction of the trial period. The values are very close to 1 (median = 0.99 [0.95; 1.1], $N=65$, where the numbers in square brackets [..] mark the $-/+$ 34th percentile limits flanking the median, equivalent to $-/+1$ SD, Gaussian). (d): Top panel: residual unpredicted by spiking, same data set as Fig. 1, using the same optimal HRF. Same horizontal (time) and vertical scale as the TRF traces in (a). Color coded for stimulus contrast as in Fig. 1. Lower panel: amplitudes of the residuals, plotted against the amplitudes of predictions from spiking, color-coded for contrast. Amplitudes were quantified as the standard deviation over a trial, normalized to the prediction from spiking at the highest contrast. Line shows the linear regression. (e) Regressions between residual and spiking prediction calculated as in (d), shown for the full set of experiments. (f) Optimal HRFs, also separated by animal [same color coding as in (c)], shown normalized to the peak to help distinguish time courses. Note the distinct HRF time courses per monkey, consistent across experiments and recording sites (monkey S: $\tau =2.5$ [2.0 3.2]; $W=2.9$ [1.6 5.4]; monkey T: $\tau =5.6$ [3.1 8.0]; $W=4.0$ [2.7 6.0], where $\tau$: time to peak, $W$: peak full width at half maximum, and data are expressed as “median [min max]”).

Even though the model fits the measured data well overall, we wondered if our forcing the fitted TRF to have a fixed amplitude independent of stimulus strength or spiking might obscure a real interaction between the task-related component and visual stimulation. We checked by testing the residual left unpredicted by spiking: after getting the optimal HRF+TRF, we tested the difference between measured hemodynamics [Fig. 1(a1)] and the optimal prediction from spiking alone [Fig. 1(b2)]. If there were some interactions, this residual [Fig. 2(d), upper panel] would scale with the measured spiking and, by extension, with the prediction from spiking since the prediction scales linearly with spiking [see Eq. (1)]. While a regression fit appears to show some scaling for this particular experiment [Fig. 2(d), lower panel], similar analyses over the full set of experiments fail to show any systematic relation between the unpredicted residual and spiking. This result supports our basic premise that the TRF reflects a mechanism of hemodynamic control independent of local visually stimulated spiking.

3.3. Optimal TRF Tracks the Fixation Schedule When Stimulation and Fixation Timing Are in Conflict

We wanted to test the utility of our model in cases where the fixation task and the stimulation had different schedules, with the stimulus being presented at one period while the animal fixated at a different period (e.g., a faster multiple of stimulation). The typical response is illustrated in Fig. 3. For both sets of trials, the monkey received identical visual stimulation [gratings, with contrasts of 0% (blank), 12.5% and 100% in block-randomized order, presented every 30 s]. However, in one case the animal’s task consisted of 15-s fixation trials, resulting in doublets of these shorter trials per stimulation cycle [Figs. 3(a1)–3(a3)]; in the other, the animal had triplets of 10-s fixation trials per stimulation cycle [Figs. 3(b1)–3(b3)] (the animal saw a blank screen for the unstimulated fixations). The spiking responses largely follow the 30-s stimulation schedule, as expected [Figs. 3(a1) and 3(b1)]. By contrast, the hemodynamics shows prominent fluctuations at the faster 15- or 10-s fixation period [Figs. 3(a2) and 3(b2)]. Similar disjunctions between timing of hemodynamic and spiking responses were seen in all such experiments ($N=9$ experiments in monkey T. Analyzing sequences of correct trials only. These data were analyzed earlier using the blank-subtracted approach; see Fig. 5 of Ref. 16).

Fig. 3.

The TRF follows behavioral rather than stimulus-linked timing when the two are in conflict. (a1)–(a3) Results from experiment where stimulus was presented every 30 s while the animal engaged in 15-s fixation trials. (a1) Measured spiking per stimulus contrast. It has the expected 30-s period albeit with a weak modulation at the fixation period: note the dip at 15 s as the animal fixates on a gray screen. (a2) Corresponding hemodynamics. Note the prominent modulation at the 15-s fixation period in the measured response (main panel); this is well reproduced in the optimal prediction (inset, “Pred”), leading to a good fit ($R^2=0.97$) and a small residual (“Residual” below main panel). (a3) Optimal fitted TRF ($\text{fundamental period}=15.7\mathrm{s}$) and HRF ($\tau =4.3\mathrm{s}$, $W=3.9\mathrm{s}$). (b1)–(b3) Same, for an experiment with 10-s fixation trials ($R^2=0.96$; TRF $\text{fundamental period}=10.7\mathrm{s}$; HRF: $\tau =5.3\mathrm{s}$, $W=4.4\mathrm{s}$; Note: since the animal is allowed an 800-ms grace period to achieve fixation after cue onset, per fixation, the actual overall period is $\sim 31.6\mathrm{s}$ for (a), 32.5 s for (b), slightly longer than the 30-s cued; all behavioral times scale accordingly).

We based the HRF+TRF model on the distinct time courses of the spiking and hemodynamic responses. For the spiking, we used a standard gamma-variate HRF and 30 s for the overall period. However, the TRF Fourier fundamental was initialized at the shorter (15 or 10 s) fixation period for the fit, giving a doublet or triplet of TRF fundamentals, respectively, for each stimulation cycle. These models fit the measured results well, with high $R^2$ and small residuals [Figs. 3(a2) and 3(b2)]. The optimal HRFs [Figs. 3(a3), 3(b3), lower panels] had time courses well in the range for monkey T [compare $\tau$, $W$ with the range over experiments, Fig. 2(f)]. Strikingly, the optimal TRFs followed the fixation period closely, with high amplitude that dominated the overall hemodynamic response [Figs. 3(a3), 3(b3), lower panels]. This observation again underscores our basic contention that the TRF reflects a behaviorally driven, as opposed to a stimulus-evoked, mechanism of brain hemodynamic control.

3.4. HRF+TRF Fit is More Robust to Fluctuations than Blank-Subtracted

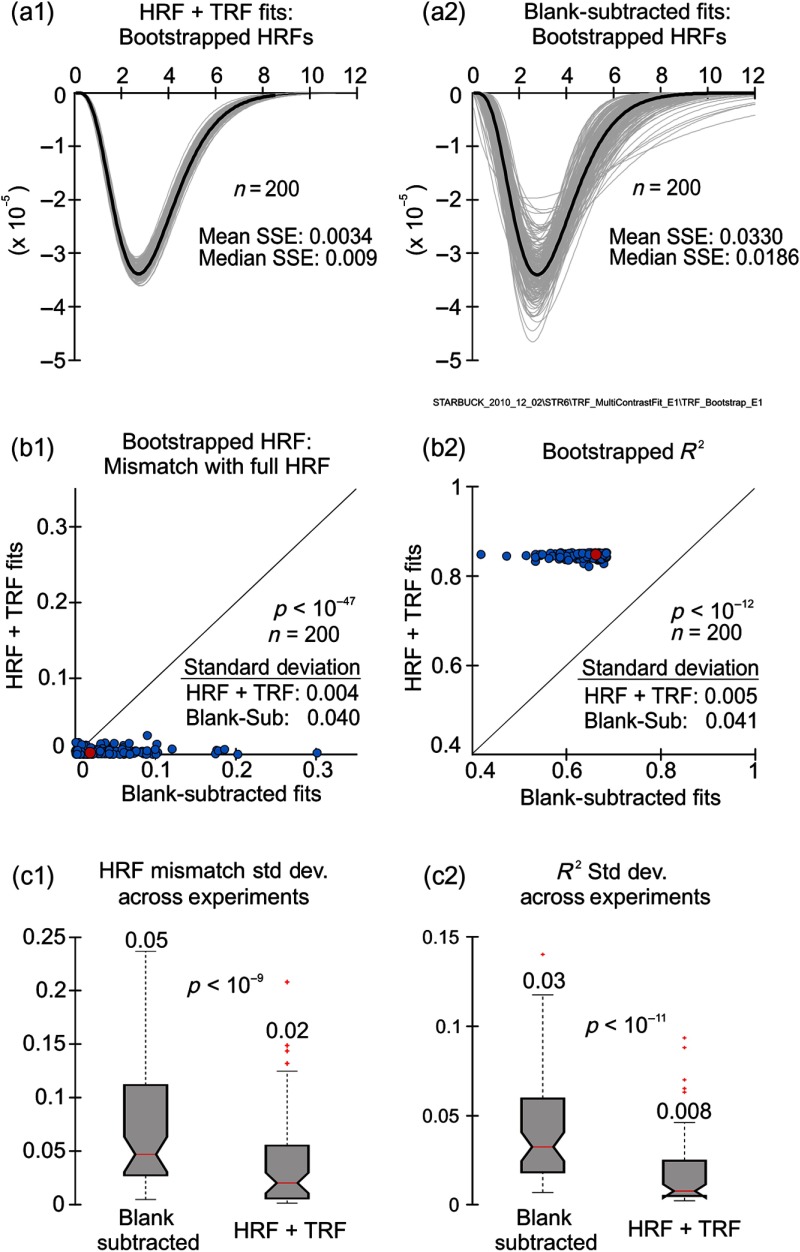
We wanted to evaluate the strengths of our current approach relative to the earlier blank-subtracted one. An important issue was: how robust are the fitted model parameters to input fluctuations? This issue is particularly relevant when fitting to brain hemodynamic responses given their large trial-by-trial variability. We surmised that the HRF+TRF fit would be more robust since the blank-subtraction step in the earlier approach unavoidably added any fluctuations in the blank response to those in all other trials. To test robustness, we simulated fluctuations in the input data using a bootstrap procedure to generate 200 sample data sets per experiment (see Sec. 2.7); we then fit each sample using both HRF+TRF and blank-subtracted approaches. To quantify and compare the robustness of the two fitting approaches, we considered two measures: (1) how variable is the fitted optimal HRF over the population of bootstrap samples? and (2) how variable is the $R^2$, over the same population? For both measures, the less variable the result, the more robust the fit.

With both measures, the HRF+TRF fits were significantly less variable and, thus, more robust than blank-subtracted (Fig. 4). This is illustrated with a representative data set in the upper four panels of Fig. 4. The two approaches to fitting gave essentially identical HRFs with the full data set [dark black traces in Figs. 4(a1), 4(a2)]. On the other hand, HRFs for the sample data sets (gray lines) were considerably less variable for the HRF+TRF fits. This led to a $10\times$ lower standard deviation in the distribution of HRF mismatch values (normalized sum squared error, see Sec. 2.7) over the population of bootstrap samples [Fig. 4(b1)] suggesting that these fitted HRFs are $10\times$ more robust to input fluctuations. Similarly, the $R^2$ from HRF+TRF fits were $8\times$ more robust [Fig. 4(b2)]. We quantified the statistical significance of this improved robustness as the probability of the null hypothesis, that the two fits had the same dispersion, against the alternate hypothesis that the blank-subtracted fits had a higher dispersion. The corresponding $p$ values were $p<{10}^{-47}$; (HRF) and $p<{10}^{-12}$ ($R^2$), (single-tailed Ansari–Bradley test, $N=200$; see Sec. 2.7).

Fig. 4.

HRF+TRF fits are more robust than blank-subtracted fits to fluctuations in the input data. (a) and (b) Comparing variability of HRF+TRF versus blank-subtracted fits over bootstrapped samples ($N=200$) for one example data set. (a1) Optimal fitted HRFs obtained with HRF+TRF fits. Black: full data set; gray: individual bootstrapped samples. (b2) Optimal HRFs from blank-subtracted fits to the same data as in (a1), using the same color convention. Note the much greater variability in bootstrapped HRF profiles compared to (a1). (b1) Quantifying the variability in bootstrapped HRFs for each fitting method by comparing distributions of mismatch values (defined as normalized sum squared error of bootstrapped HRF relative to the full HRF; see Sec. 2.7). Each data point corresponds to one bootstrapped sample, fitted separately using both approaches. Note the larger values and much higher variability in HRF mismatches for the blank-subtracted fits. This variability, quantified as the standard deviation over the bootstrap samples ($N=200$), is indicated in the figure. Red circle: median values (blank-subtracted: 0.0186, HRF+TRF: 0.0019; $N=200$). (b2) Comparing variability in $R^2$ for the fits to the same bootstrap samples, plotted pairwise for the two fitting methods. Note, again, the much higher variability (standard deviation) for blank-subtracted fits. In both (b1) and (b2), $p$ values indicate the significance of the blank-subtracted fits having higher dispersion, against the null hypothesis that the dispersion equaled that of the HRF+TRF fits (one-tailed Ansari–Bradley test, $N=200$). Red circle: median values (blank-subtracted: 0.66, HRF+TRF: 0.85; $N=200$). (c1) Box plots showing distributions of HRF variability [standard deviation of the mismatch, as in (b1)] across experiments, for the two fitting approaches. Median values across experiments are represented by horizontal red bars and indicated above each distribution’s upper edge. The bottom and top edges of each box represent the 25th and 75th percentiles, respectively. Values lying within the whiskers extending to the most extreme are not considered outliers. Outliers (crosses: in red, online figure) exceed 1.5 times the interquartile range. $p$ values for equality of the distributions are indicated in the figures [Wilcoxon signed rank test, for pairwise comparisons across experiments ($N=65$)]. Some outlier data points are not shown for ease of visualization: blank-subtracted has five outliers, HRF+TRF has six. All data were included in the analysis. (c2) Box plots showing distributions of $R^2$ variability [standard deviation as in (b2)] across experiments. Conventions as in (c1), note, again that not all outliers are shown for ease of visualization. Blank-subtracted has two outliers, and HRF+TRF has five.

Similar results were obtained over the body of experiments. Optimal HRFs were significantly more robust (at $p<0.05$, single-tailed Ansari–Bradley test) for the HRF+TRF as versus blank-subtracted fits, for 86% of the experiments (56 of 65). For the $R^2$, the corresponding fraction came to 89% of the experiments (58 of 65). This improved robustness was underscored by pairwise comparisons of the two fits per experiment, over the full body. This showed a $2.5\times$ greater robustness in HRF overall when fitted using HRF+TRF [Fig. 4(c1)] and a $4.2\times$ greater robustness in $R^2$ [Fig. 4(c2)], significant to $p<{10}^{-9}$ (HRF) and $p<{10}^{-11}$ ($R^2$) as estimated with a Wilcoxon signed rank test, $N=65$.

3.5. HRF+TRF Model Fits the Data Best

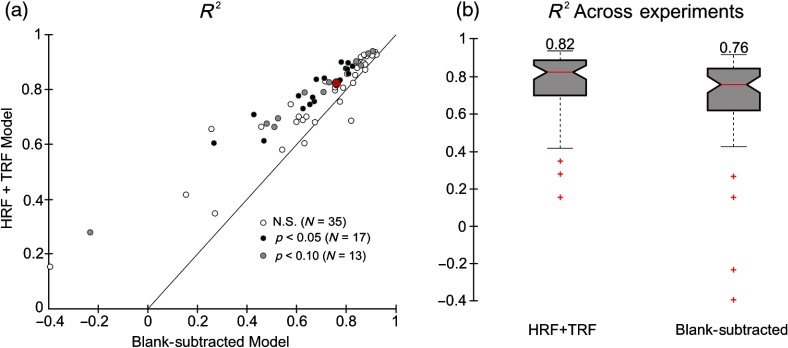
We wondered if, in addition to being more robust, the HRF+TRF model also give better fits, i.e., with higher ($R^2$) compared to those using our earlier blank-subtracted approach. Making this comparison is not straightforward because the two models have different numbers of parameters. One standard approach is to compare not $R^2$ but rather the “adjusted $R^2$”, which discounts the improvement that could result due to one model having more parameters.³³ However, calculating the adjustment factor involves the total number of sample points that are assumed to be independent. Our sample points (camera frames) are not independent because of the slow time course of the hemodynamic response (scale of seconds) relative to the camera frame rate ($15\text{frames}/\mathrm{s}$) and a standard adjusted $R^2$ could be misleading. A useful alternative approach for model selection when parametric statistical tests are difficult is to use cross validation (e.g., see Ref. 34). Since cross validation automatically discounts for overfitting, it also discounts for any improvement in $R^2$ purely due to an increased number of parameters while maintaining improvements due to model parameters that are informative. Thus, for comparing $R^2$, we used 50–50 cross validation. We defined the $R^2$ for a given model and experiment as the median of the corresponding cross-validated sample $R^2$. The significance of a model comparison, per experiment, was quantified as the probability “$p$” that the pairwise difference in corresponding sample $R^2$ is indistinguishable from the null (see Sec. 2.8).

The comparison as defined above showed that the HRF+TRF model fits consistently better than blank-subtracted, with higher $R^2$ overall [Fig. 5(a)]. In individual pairwise comparisons, one quarter of the datasets (17 of 65) fits with significantly higher $R^2$ in the current approach ($p<0.05$); for another 20% (13 of 65), $p$ lies between 0.05 and $<0.1$ [Fig. 5(a)]. Overall, for 67% ($44/65$) the $p<0.2$. The consistently higher $R^2$ for HRF+TRF was also reflected in the significance of a pairwise comparison per dataset across experiments [Fig. 5(a). $p<{10}^{-10}$ Wilcoxon signed rank test].

Fig. 5.

The HRF+TRF model fits measured hemodynamics better than blank-subtracted. (a) $R^2$ values for HRF+TRF fits compared with blank-subtracted fits. $R^2$ data points shown are the medians of the distributions of cross-validated sample $R^2$ for the model and experiment; significance ($p$ value) is quantified as the probability of the null hypothesis that the cross-validated $R^2$ (HRF+TRF) – $R^2$ (blank-subtracted) = 0 (see Sec. 2.8). Each point corresponds to one experiment; the red circle is the median $R^2$ across experiments (blank-subtracted: 0.76, HRF+TRF: 0.82; $N=65$). Data points are color-coded by significance of this improved fit per experiment (see key in figure panel for $p$ values). Pairwise comparison per experiment ($N=65$) using a Wilcoxon signed rank test further confirms that the HRF+TRF fit is better than blank-subtracted (the null hypothesis that they are equal has $p<{10}^{-10}$. (b) Box plots showing the same distributions of $R^2$. Conventions for box plot as in Figs. 4(c1) and 4(c2).

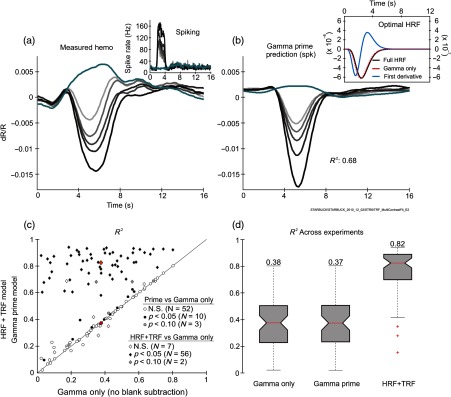
We wanted to test how important it was for the model to have terms (e.g., TRF) independent of spiking in addition to those operating linearly on spiking (HRF). As a control, we checked if we could get good fits with no TRF but with more complex HRF kernels, including components beyond the gamma-variate core [Eq. (5) in Sec. 2.5; compare with Eq. (1); Fig. 6]. In particular, we considered a standard multicomponent ${\mathrm{HRF}}_{\text{Gammaprime}}$ comprising a gamma-variate function and its first time derivative^31,32 [see Eq. (6) in Sec. 2.5 and Fig. 6(b)]. This was compared to a single-component “gamma only” HRF [gamma-variate only; no TRF, and no blank-subtraction, Figs. 6(c) and 6(d)]. The additional first-derivative term in the ${\mathrm{HRF}}_{\text{Gammaprime}}$ was found to confer essentially no advantage relative to gamma only. By contrast, HRF+TRF fits showed a dramatic improvement relative to gamma only [Figs. 6(c), 6(d)]. While this considers only one particular extension of the HRF and cannot exhaustively cover all possible variants, the comparison provides compelling evidence that the model needs a spiking-independent component such as the TRF term in our HRF+TRF model; more complex HRFs acting on the local electrophysiology alone, with no accompanying TRF, are unlikely to be adequate.

Fig. 6.

Gamma prime HRF gives poor fits, with little improvement due to the additional first-derivative term in ${\mathrm{HRF}}_{\text{Gammaprime}}$. (a) Measured hemodynamics. Inset shows concurrent spiking. (b) Optimal prediction from spiking using gamma prime HRF. Inset shows the optimal HRF: both as separate “gamma only” and “first derivative only” components, and added to give the full optimal ${\mathrm{HRF}}_{\text{Gammaprime}}$. Note two different $Y$-axis scales: for the full HRF and the gamma only on the left, and for first derivative only on the right. The amplitude of the first derivative only term is an order of magnitude smaller than that of gamma only, making a correspondingly smaller contribution to the prediction. (c) Two sets of pairwise comparisons over the body of experiments to gamma only $R^2$ (i.e., gamma-variate HRF with no TRF and no blank-subtraction). Fits to gamma prime (circles) shows little improvement due to the additional first derivative term in the HRF [Wilcoxon signed rank test: $p=0.0025$; red circle: median across experiments (gamma prime: 0.37; gamma only: 0.38, $N=65$)]. By contrast, fits to HRF+TRF (diamonds) show a striking improvement due to the spike-independent TRF term (Wilcoxon signed rank test: $p<{10}^{-11}$; red diamond: median across experiments: HRF+TRF: 0.82; gamma only: 0.38; $N=65$). $R^2$ and their significance ($p$ values) per experiment calculated using cross validation as in Fig. 5. $p$ values color coded as shown in panel key. (d) Box plots showing the same distributions of $R^2$. Conventions for box plot same as Figs. 4(c1) and 4(c2).

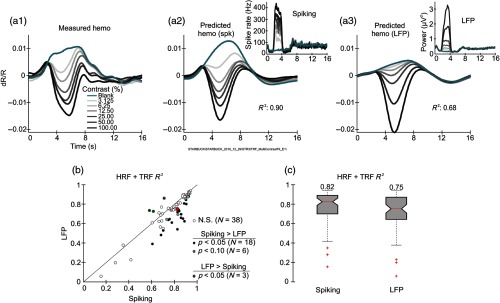
3.6. Fit to LFP is Poorer than to Spiking

We showed earlier that the stimulus-evoked hemodynamic response is predicted more accurately by concurrently measured spiking than by LFP.¹⁷ This reflected the close match between the contrast tuning of the hemodynamic and spiking responses, versus that of the LFP. We checked if our current approach still gives a better fit to spiking than to LFP, specifically gamma LFP (30 to 90 Hz) since that was the most informative LFP measure in our earlier study. The HRF+TRF model was fitted using the measured LFP in a manner exactly like the fits to spiking illustrated in Fig. 1. The results show that as in our earlier study the HRF+TRF fit to gamma LFP was poorer than to spiking (Fig. 7). The example data set suggests, as before, that the poorer fit reflects the poorer match in contrast tuning. The spiking response [Fig. 7(a2), inset] increases in roughly equal steps for each doubling of the stimulus contrast, matching that of hemodynamics [Fig. 7(a1)]; gamma LFP has smaller steps at low contrast and larger steps at high contrast [Fig. 7(a3), inset; the contrast tuning is not plotted here; see our earlier results¹⁷]. These mismatches in contrast tuning are reflected in the corresponding predictions and lead to worse fits for this example [Figs. 7(a2), 7(a3), each compared with Fig. 7(a1)] and across experiments [Figs. 7(b) and 7(c)].

Fig. 7.

Spiking predicts hemodynamics better than gamma LFP. (a1)–(a3) Example dataset. (a1) Measured hemodynamics compared to predictions using spiking (a2) versus gamma LFP (a3) as regressor. The regressors are shown as insets in the top right of each panel. Corresponding $R^2$ values are shown for each fit. (b) Comparing $R^2$ for HRF+TRF fits using the LFP, versus spiking, across experiments. Each point corresponds to one experiment. While three data points showed significantly better fits to LFP (“LFP > spiking”), the much larger majority were better fit to spiking, or trended in that direction, leading to substantially better fits to spiking overall ($p<{10}^{-6}$, Wilcoxon signed rank test). Red circle: median values (spiking: 0.82, LFP’: 0.75; $N=65$). (c) Box plot shows the $R^2$ values shown in (b). $R^2$ and $p$ values based on cross validation as in Fig. 5.

4. Discussion

We describe a method for parametrically estimating both stimulus-evoked and task-related components of brain hemodynamic responses (specifically, CBV) recorded while subjects are engaged in a temporally predictable task. The stimulus-evoked component is modeled as the convolution of concurrent local spiking with a gamma-variate HRF kernel. The task-related component is modeled as a TRF Fourier series kernel—optimally comprising the first two frequencies, i.e., the fundamental and the first harmonic—convolved with delta functions aligned to trial onsets. This HRF+TRF model contrasts with our earlier blank-subtracted approach where we parametrically estimated only the stimulus-evoked component and defined the task-related portion as the unpredicted residual.^16,17 We evaluated the current model by fitting it to earlier published data and compared the fits to ones using the blank-subtracted approach, as well as to fits using three alternate models. All fits employed identical procedures for fitting and for assessing goodness of fit ($R^2$).

The HRF+TRF fits were uniformly good, with high $R^2$ and small residuals. The task-related component that emerged from our fits showed no residual relationship to stimulus-evoked spiking or hemodynamics, over a comprehensive dynamic range of stimulated responses [Figs. 2(d), 2(e)]. This lack of interaction supports our premise that the TRF is not predicted by local spiking and reinforces our decision to model the TRF as a trial-aligned term of fixed amplitude independent of stimulus intensity [Eq. (3)]. Intriguingly, the optimal TRF, while consistent for a given animal in this particular task, had distinctly different time courses for the two animals. Understanding this difference likely involves a comprehensive study of the behavioral significance of the TRF. Such a study is outside the scope of the current paper, but we discuss it in the last paragraph in the context of future directions. In contrast to the good HRF+TRF fits, attempts to predict hemodynamics from spiking without using a TRF gave uniformly poor fits. There was relatively little difference in $R^2$ whether fitting with a single gamma-variate HRF (gamma only) or a more complex HRF with additional terms [gamma prime; Figs. 6(c) and 6(d)] underscoring the important contribution of the TRF to the prediction. Additional evidence of the distinct, behavioral origins of the TRF came from experiments where the behavioral schedule of the task conflicted with the schedule of visual stimulation. In such cases, the optimal TRF closely matched behavioral rather than stimulation timing. These results suggest that the TRF reflects a neural mechanism of brain hemodynamic control (neuromodulatory? feedback?) distinct from solely stimulation-linked mechanisms and related spiking.

Comparison with the earlier blank-subtracted approach shows that HRF+TRF fits are significantly more robust to fluctuations and are better (give higher $R^2$) than our earlier values. The HRF+TRF model thus provides a better approach for analyzing hemodynamic recordings made in a task context. As a corollary, we obtained better fits when using spiking rather than LFP as the regressor for the stimulus-evoked component of the HRF+TRF fit, corroborating an analogous finding with our earlier approach.¹⁷

The specifics of the current work suggest ways to further develop and refine the HRF+TRF model. We wanted to start here with the simplest functional links between stimulus-evoked and task-related responses. We thus controlled the levels of spiking and evoked hemodynamics using large, uniform gratings where only the contrast was varied. This was intended to change activity monotonically over a more-or-less homogeneous mix of active neurons. Ongoing work in the lab uses more complex spatially inhomogeneous stimuli: small point stimuli, center-surround stimuli with varying centers and surrounds, etc. These are intended to test our model with more complex local variations in excitation, inhibition, and lateral interactions. The stimuli in the work presented here are also strictly periodic and use a blank (0% contrast) in the stimulus set. The blank is not crucial although it helps extend the dynamic range of stimulation strengths; as long as responses can be combined linearly, our model can be used over any range of stimulus strengths [note, in passing, that our blank already includes a large fixation-related spiking and hemodynamic response Fig. 1(a2)]. Having periodic stimuli make the model simple, and they are a good model for block-design tasks. However, initial work in our lab shows that randomly cued trials of variable length also evoke large, reproducible task-related responses. After some binning by time ranges, these could also be analyzed using our approach. Thus, this approach has the potential for being extended over a much broader range of tasks and visual stimuli, and the current work is intended to just provide a base.

Analysis tools, such as the one we use here, are likely to become more important in brain imaging with the increasing recognition that task-related and other endogenous hemodynamic responses contribute significantly to measured hemodynamics. Such responses, while long noted,³⁵ were considered a global signal “of no experimental value”³⁶ that added uninformative variance³⁷ and needed to be removed.^4,38 More recent results suggest otherwise. Regressing these components away can change the functional relationships and even the sign of the nominal signal.³⁹ Task-related components are also behaviorally relevant. They entrain to task timing,^9,23,24,40 correlate with gauges of brain state such as pupil dilation,⁵ and carry diagnostic information about neuropsychiatric disorders such as schizophrenia.⁴¹ Preliminary results from our lab show that our measured TRF is strongly modulated by anticipation, reward size, and task performance.^9,26 It also appears to change its shape and timing considerably over the course of training that the animal receives (unpublished data; note, in this context, that the two animals used in this paper were at very different stages of training; one had just started while the other had worked for over four years on visual tasks). Tools, such as the one here, should help the field to better parametrize behavioral correlates of endogenous task-related responses and, thus, focus even more sharply on understanding their significance. We developed this tool for use with spiking data, which restricts its application primarily to animals. But it can be extended to human fMRI using realistic models of the spiking response to the stimulus under consideration.^36,42 We hope that such efforts would lead to greater insights in our overall understanding of fMRI measurements and brain activity.

Biographies

Max Herman is a neuroscientist with an interest in sensory systems and the microbiological environments of said systems. He is attending medical school at Rutgers Robert Wood Johnson where he hopes to pursue a career in neurodegenerative diseases as a researching physician.

Mariana M. B. Cardoso did her undergraduate and master’s work at Instituto Superior Técnico, University of Lisbon, in physics engineering. Her graduate work was in Aniruddha Das’s lab at Columbia University. She holds a PhD in neuroscience from New Univeristy of Lisbon in partnership with the Champalimaud Neuroscience Programme. Currently, she is part of Dr. Philip Sabes’s lab at UCSF, collaborating in a project on brain machine interfaces.

Bruss Lima obtained his bachelor’s degree in biology at the University of Brasilia, Brazil in 1998, master degree in biophysics at the Federal University of Rio de Janeiro, Brazil in 2002, and PhD in natural sciences (biology) at the Max-Planck Institute, Frankfurt, Germany in 2010. After completing postdoctoral training at Columbia University, he is currently an assistant professor at the Federal University of Rio de Janeiro, working on behavior and visual processing in primates.

Yevgeniy B. Sirotin holds a PhD in neurobiology and behavior from Columbia University. His academic work focused on understanding neural circuit function using optical imaging, electrophysiology, and behavioral testing in a variety of animal models. After transitioning to industry, he now applies experimental and analytical techniques to design and evaluate systems involving the interaction between humans and technology. Much of that work is now focused on identity and biometric systems.

Aniruddha Das received his initial training in physics, including undergraduate from Indian Institute of Technology,-Kanpur, India and PhD in Berkeley, California. But then he saw the light and decided to pursue a long-standing interest in visual perception, starting with postdoctoral training with Charles Gilbert at Rockefeller University. He has been at Columbia since 2002, trying, broadly, to understand the stages of processing early in the cortical visual pathway.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.