Improved HIV-1 Viral Load Monitoring Capacity using Pooled Testing with Marker-Assisted Deconvolution

Abstract

Objective

Improve pooled viral load (VL) testing to increase HIV treatment monitoring capacity, particularly relevant for resource-limited settings.

Design

We developed mMPA (marker-assisted mini-pooling with algorithm), a new VL pooling deconvolution strategy that utilizes information from low-cost, routinely-collected clinical markers to determine an efficient order of sequential individual VL testing and dictates when the sequential testing can be stopped.

Methods

We simulated the use of pooled testing to ascertain virological failure status on 918 participants from three studies conducted at the Academic Model Providing Access to Healthcare (AMPATH) in Eldoret, Kenya, and estimated the number of assays needed when using mMPA and other pooling methods. We also evaluated the impact of practical factors such as specific markers used, prevalence of virological failure, pool size, VL measurement error, and assay detection cutoffs on mMPA, other pooling methods, and single testing.

Results

Using CD4 count as a marker to assist deconvolution, mMPA significantly reduces the number of VL assays by 52% (CI=48–57%), 40% (CI=38–42%), and 19% (CI=15–22%) compared with individual testing, simple mini-pooling, and mini-pooling with algorithm (MPA), respectively. mMPA has higher sensitivity and negative/positive predictive values than MPA, and comparable high specificity. Further improvement is achieved with additional clinical markers such as age and time on therapy, with or without CD4 values. mMPA performance depends on prevalence of virological failure and pool size but is insensitive to VL measurement-error and VL assay detection cutoffs.

Conclusions

mMPA can substantially increase the capacity of VL monitoring.

Introduction

Monitoring and maintaining VL suppression in HIV-infected individuals on antiretroviral therapy (ART) is crucial to control the spread of HIV and to reduce HIV-related morbidity and mortality^1–5. In resource-limited settings (RLS), diagnoses of ART failure based on clinical and CD4 count criteria result in high misclassification rates^6–12, leading to World Health Organization (WHO) recommendation of routine VL testing for ART monitoring where available¹³. Despite this recommendation, VL testing in many RLS is still constrained by cost, technology and capacity, and the feasibility of routine VL testing varies widely^14,15. Although it is expected that more HIV care programs will establish or increase capacity for VL monitoring with time, and point of care VL testing and associated price reductions are emerging¹⁶, VL testing will most likely remain limited and expensive in RLS for years to come, particularly with the expected continued global increase in ART access¹⁷. Thus, improved VL testing capacity combining efficiency, diagnostic accuracy and high clinical utility is important to increase access to this clinically essential diagnostic test.

In settings where VL monitoring is limited, the VL test is typically used as confirmation for treatment failure based on CD4 or clinical criteria¹⁸. We have developed methods for targeted triage of VL testing¹⁹, which was subsequently applied in a South African cohort²⁰. Another approach to optimizing utilization of limited VL assays is pooled testing, which has long been applied to qualitative assays that yield binary results (e.g. positive versus negative) for ascertaining individual disease status or estimating disease prevalence^21–26, including HIV infection^27–29. Pooled testing also can be used on quantitative assays such as VL that yield a measured value. The simplest pooling strategy involves a single test on a pooled sample that combines equal amounts of samples from several subjects, which determines whether further testing of all individual samples (i.e. deconvolution of the pool) is needed. This basic approach is often referred to as mini-pooling (MP), to distinguish it from more complex pooling strategies such as hierarchical^22,30 and matrix pooling^31,32. May et al³³ improved the MP strategy by testing the individual samples sequentially at the deconvolution stage using an algorithm to decide when sequential testing can be stopped. This method is referred to as “mini-pooling with algorithm” (MPA)^{14,31,34–38}.

If the rank ordering of VL values in a pool was known, the number of VL tests needed to resolve that pool would be minimized. We hypothesize that information on low-cost, routinely-collected clinical markers (RCMs) that are correlated with VL, such as CD4 count, CD4%, ART adherence, treatment history, and time on ART, can be used to rank samples in a pool, and thereby reduce the number of assays needed for deconvolution. For VL testing, which uses quantitative assays, we develop a pooling strategy called ‘marker assisted mini-pooling with algorithm’ (mMPA) that uses a predicted VL based on RCMs to rank order individual samples. By testing samples with a higher risk of virological failure first, we show that mMPA requires, on average, fewer VL assays for deconvolution than MPA, without sacrificing diagnostic accuracy. Applied broadly, this approach has potential to substantially increase the capacity of comprehensive VL monitoring. The proposed algorithm is a method of informative retesting, first proposed by Bilder and colleagues for qualitative assays^22,23,39. Use of a quantitative assay introduces a modification of the deconvolution algorithm as well as issues such as assay measurement error and lower limit of detection (LLD), which must be incorporated into assessments of algorithm performance.

Methods

Definitions of Virological Failure and Pool Positivity

At the individual level, virological failure is defined as VL exceeding a threshold value C. In RLS, the WHO recommends using C = 1,000 copies/mL (for brevity, units are omitted henceforth). When K samples are combined for a pooled test, pool positivity is defined using a threshold of

$$C_{\mathit{pool}}=C/K$$

to account for the dilution effect. For example, for a pool of size K = 3, C_pool = 1000/3 = 333. If the pool VL is ≤ 333, one can deduce that no individual sample can have VL > 1000, and no further tests are needed. However if a pool has VL > 333, one or more individuals may have VL > 1000, prompting the need for individual tests. See May et al ³³ for more examples.

mMPA Procedure

The mMPA strategy uses information from RCMs that are correlated with individual VL to develop a risk score S for rank ordering individual samples. The score is expressed as an explicit function of the RCMs. Two examples include the value of a single marker such as concurrent CD4 count; and predicted VL derived from a statistical model using multiple markers as inputs. The latter can be developed by fitting a prediction model on a representative sample of individuals where both the RCMs and VL have been measured.

Given the risk scores, if sequential individual testing is indicated based on the pool VL, then mMPA assays the individual samples sequentially in the decreasing rank order of their estimated risks. Thus, samples with higher risk of virological failure are tested first. Though ordering by S cannot guarantee that the individual sample with the highest VL is tested first, correlation between S and VL makes this more likely, and higher correlations imply higher likelihood of correct ordering. A schematic overview of mMPA is given by a numerical example in Figure 1. In general, after testing each individual sample, the average VL value among the remaining samples can be deduced. The remaining (say K′) samples can be regarded as a “sub-pool”. Thus, if the sub-pool VL is less than C/K′, the sub-pool is negative and no more individual tests are needed; otherwise we continue testing the next individual sample. So intuitively by rank ordering and testing high-risk individuals first, the virological status of each individual can be quickly ascertained.

Figure 1. Schematic overview of MP, MPA, and mMPA using a numerical example of pooling K = 3 individual samples with VLs of 300, 2500, and 50 copies/mL respectively.

The figure provides an example of VL pooling of samples from K = 3 patients, with individual VLs of 300, 2500 and 50. With a threshold of C = 1000, only the subject with VL=2500 has virologic failure. Deconvolution is based on the three methods used in this paper: (a) mini pool (MP); (b) mini-pool + algorithm (MPA); and (c) marker-assisted mini-pool + algorithm (mMPA). Each method incorporates two stages, the first incorporating VL testing of the pooled sample and the second incorporating deconvolution, outlined by text boxes. In the first stage, common for all three methods, the pool is “positive” because its VL of 950 is greater than the pool threshold (C/K) = 333, prompting the second stage. Using MP (a), all three individuals are then tested, for a total of 4 VL assays. Using MPA (b), sequential random testing of individual samples and a deconvolution algorithm determine the need for additional testing. In this example a total of 3 VL assays are needed. Using mMPA (c), with a risk score indicates that the second subject has the highest likelihood of VL failure and is thus tested first, only two VL assays are needed. { } denotes testing on the pool, and [ ] testing on an individual sample.

Data Sources

Our empirical comparison of mMPA with other testing strategies is based on simulating the application of each VL testing strategy in a combined cohort of patients enrolled in three studies at the Academic Model Providing Access to Healthcare (AMPATH) in Eldoret, Kenya: The “Crisis” study (n=191)⁴⁰, conducted in 2009–2011 to investigate the impact of the 2007–2008 post-election violence in Kenya on ART failure and drug resistance; the “2^nd-line” study (n=394)⁴¹, conducted in 2011–2012 to investigate ART failure and drug resistance among patients on 2^nd-line ART; and the “TDF” (tenofovir) study (n=333)⁴², conducted in 2012–2013 to investigate the impact of WHO guidelines changes to recommend TDF-based 1^st-line ART, on ART failure and drug resistance (see Supplementary Material for further details). The individual studies and this combined analysis were reviewed by the Lifespan and AMPATH ethics review committees.

In each study, demographic, clinical, laboratory and VL data were collected for all participants. We use these data to calculate four candidate risk scores: (1) concurrent CD4 count; (2) predicted VL value generated by fitting a generalized additive model (GAM)⁴³ of log-10 VL to gender, age, CD4 count, CD4%, time on current ART, and WHO staging; (3) predicted VL from fitting a GAM to the same predictors as in (2), but without CD4 count and CD4%; and (4) predicted VL generated from a random forests model (RF)⁴⁴ using the same predictors as (2). Scenario (3) is relevant for settings where CD4 counts are limited or not routinely collected⁴⁵, which is the case for some programs that have adopted yearly monitoring of VL.

Simulation Study to Compare Testing Strategies

For each HIV testing strategy, we calculate the average number of tests required (ATR) to establish individual-level virological failure status per 100 individuals. The ATR for direct individual VL testing is 100; pooling methods will generally have ATR < 100, with lower values indicating greater efficiency. Generally, the number of VL tests needed for a fixed sample depends on the order in which individuals are placed into pools. Therefore, to obtain ATR for a single sample, we implement the pooling algorithm on 200 random permutations of the sample, and calculated the average number of VL tests needed over the 200 permutations. Using permutations, we also calculate the sensitivity, specificity, and negative and positive predictive values (NPV and PPV) associated with each VL testing strategy.

For each pool formed by K individuals, the pool VL is simulated using the average value of the individual VLs. For individuals with undetectable VL (n=584), we impute values as follows: for those with VL<40 (n=557), we impute a uniform random value between 0 and 40; next, for those with VL<400 (n=27), we sample a random VL value from among those with VL<400 (to avoid dependence on distributional assumptions).

To study robustness of each monitoring method, our evaluation further assesses the impact of the following factors on ATR and diagnostic accuracy: choice of risk score used by mMPA, prevalence of virological failure, pool size, assay measurement error, and assay LLD.

Impact of risk score on ATR

Risk scores having a higher correlation with VL are expected to lead to higher testing efficiency for mMPA. Efficiency gain depends on the markers used to calculate the risk score and the method used to translate marker information into a score. The composite risk scores (2)–(4) (as described above) are generated using two types of models: generalized additive model⁴³, which allows nonlinear predictive effects of continuous markers; and random forests⁴⁴, a tree-based approach machine learning method that allows interactions and nonlinear predictor effects.

Having the actual VL measurements also allows us to calculate the theoretical best possible ATR for mMPA by using ranks of true VL values as a risk score. This “oracle” risk score is also included in our comparisons to provide a benchmark for the deconvolution algorithms.

Because mMPA uses risk scores to rank-order individual samples for sequential testing, we use rank (Spearman) correlation to quantify the relative strength of each risk score.

Impact of virological failure prevalence on ATR

Testing efficiency of mMPA depends on the prevalence of virological failure in the population. Higher prevalence implies higher proportion of positive pools, which generally reduces the advantage of all pooling strategies (including mMPA). In addition to using the WHO-recommended threshold C = 1000, which corresponds to 16% failure prevalence in our sample, we further consider thresholds of C = 500, 1500, and 3000, yielding prevalences of 18%, 14%, and 11%, respectively.

Impact of pool size on ATR

Pool size is another important parameter because larger pool sizes are technically more difficult to resolve and potentially more susceptible to measurement errors³³. Moreover, pool size is a parameter for defining pool positivity (i.e. C/K). In our study, we consider pool sizes ranging from K = 3 to 10.

Impact of measurement error

Individual VL assays can be subject to measurement error, reducing diagnostic accuracy. To study its impact, we add random deviations to individual and pool VL values on the log scale. Deviations are generated using log-normal distributions with mean zero and standard deviation σ. Three scenarios are considered: (1) σ = 0, or no measurement error; (2) σ = 0.12, applicable to commonly-used assays³³; and (3) σ = 0.20, likely representing an upper bound³³. The impact of measurement error on the VL testing methods is quantified in terms of sensitivity, specificity, PPV, and NPV.

Impact of lower limit of detection of VL assays

VL assays used for treatment monitoring typically have LLD between 20 and 400 ^13,46. The LLD impacts pooled testing in two ways. First, for a given virological failure threshold C, LLD dictates the maximum allowable pool size because of the definition of C_pool; e.g., if C = 1000 and LLD = 100, then the allowable pool size is K = 10. Second, LLD impacts the second-stage pool deconvolution, because the deconvolution algorithm of mMPA involves a sequence of subtractions of individual VLs from K times the pool VL to determine whether tests of remaining samples are needed (Figure 1). When an individual sample has a VL < LLD, the true VL is only known to be between 0 and LLD. In this case, it can be shown (see Supplementary Material) that a conservative approach is to treat individuals below LLD as having VL = 0 and continue individual testing. Using this approach, assays with higher LLD will, on average, increase the number of tests needed by MPA and mMPA.

Results

Participant Characteristics

Data were available from 918 participants, whose characteristics are summarized in Table 1. Overall, the demographic, clinical and laboratory characteristics were similar between the three studies, with the exceptions of types of ART and prevalence of VL > 1000. Table 2 summarizes the average number of tests required (ATR) for individual testing, MP, MPA and mMPA for pool size K = 5, assuming LLD=0 and no measurement error (scenarios using other values of LLD and measurement error are addressed below). We implemented mMPA using each of the four versions of the risk score as described in Methods.

Table 1.

Characteristics of participants according to study^a.

	Crisis (n = 191)	2nd Line (n = 394)	TDF (n = 333)	Total (n = 918)
Age (yr)	42 [36, 50]	42 [36, 49]	41 [36, 48]	42 [36, 49]
Gender
Female	62%	60%	55%	59%
Male	38%	40%	45%	41%
Viral Load (VL)	44 [<40, <400]	<40 [<40, 430]	<40 [<40, <40]	<40 [<40, 192]
VL > 1000	15%	21%	10%	16%
CD4 Count (NA=19)	361 [249, 503]	282 [182, 419]	336 [226, 470]	314 [210, 453]
CD4% (NA=19)	23 [17, 28]	17 [12, 23]	21 [15, 28]	19 [14, 26]
Most Recent CD4	376 [262, 553]	273 [165, 409]	321 [210, 467]	311 [201, 458]
Most Recent CD4%	20 [16, 26]	16 [11, 21]	2 [15, 27]	18 [13, 25]
Chg of CD4/yr b	−14.3 [−121, 94]	0.5 [−75, 170]	0.0 [−63, 112]	0.0 [−85, 127]
Chg of CD4%/yr b	2.2 [.0, 5.3]	2.0 [.0, 6.9]	.9 [−1.3, 6.5]	1.7 [.0, 6.5]
Yrs on Current ART	2.7 [2.1, 4.4]	1.1 [.6, 3.3]	1.7 [1.2, 2.2]	1.8 [.9, 2.7]
Yrs on ART	4.3 [3.6, 5.1]	5.9 [4.4, 7.4]	2.1 [1.4, 4.6]	4.5 [2.6, 6.2]
ART adherence c
Most	0.0%	0.8%	0.3%	0.4%
Some	1.6%	5.1%	1.8%	3.2%
None	98.4%	94.1%	97.9%	96.4%
WHO Stage (NA=4)
Stage 1	18%	14%	24%	19%
Stage 2	18%	16%	16%	17%
Stage 3	46%	48%	43%	45%
Stage 4	18%	22%	17%	19%
ART
1st line	100%	0%	100%	57%
2nd line	0%	100%	0%	43%

^aContinuous variables are summarized by median and interquartile range (IQR), and categorical variables by percentages. Numbers inside [ ] are IQR;

^bChange = (value at enrollment - most recent before enrollment)/(time between the two visits);

^cART adherence of last week by the self-report percentage: Most (>50%), Some (<50%), None (0%).

ART = antiretroviral therapy; chg = change; NA = not available; TDF = tenofovir; WHO = World Health Organization; yr = year.

Table 2.

Efficiency comparison among pooling deconvolution methods^a.

Method	Risk score	Spearman correlation b	Average # of VL assays required per 100 subjects	Relative reduction (%) in the number of assays required
				REF = IND	REF = MP	REF = MPA
IND			100	REF
MP			80 (73, 86)	−20 (−27, −14)	REF
MPA			59 (54, 63)	−41 (−46, −37)	−26 (−28, −24)	REF
mMPA	CD4	0.24	48 (43, 52)	−52 (−57, −48)	−40 (−42, −38)	−19 (−22, −15)
	GAM	0.34	46 (41, 50)	−54 (−59, −50)	−43 (−45, −41)	−23 (−25, −19)
	GAM*	0.25	50 (46, 54)	−50 (−54, −46)	−37 (−39, −35)	−14 (−19, −10)
	RF	0.27	47 (43, 52)	−53 (−57, −48)	−41 (−43, −38)	−20 (−23, −16)
	ORS	1.00	37 (34, 39)	−63 (−66, −61)	−54 (−55, −53)	−38 (−39, −36)

^aPool size K = 5; numbers in parentheses are 95% confidence intervals obtained using the bootstrap method (with 500 resamples) where the intervals are the 2.5 and 97.5 percentiles of bootstrap distributions;

^bSpearman (rank) correlation between risk score and VL;

REF = reference method; GAM = generalized additive model; GAM* = GAM without CD4 markers as predictor; RF = random forest model; ORS = oracle rank score.

Deconvolution of VL Pooling with mMPA and Risk Score Impact

When applied to this combined cohort, mMPA requires between 46 and 50 assays to diagnose 100 individuals, depending on the risk score being used (Table 2). The most efficient risk score is derived using GAM with gender, age, CD4 count, CD4%, time on current ART, and WHO staging as predictors (ATR=46, 95% CI 41 to 50); however, a GAM-based score without CD4 count still yields ATR=50 (95% CI 46 to 54). Compared to other pooling methods, mMPA reduces the ATR relatively by 19% (95% CI 15 to 22%) compared to MPA, and by 40% (95% CI 38 to 42%) compared to MP; all reductions are statistically significant as evidenced by the 95% confidence intervals excluding zero. Moreover, ATR for mMPA is relatively close to the best possible ATR of 37 based on the oracle risk score where correct ranks are known. The superior performance of mMPA has similar patterns when applied individually to the three studies (Supplementary Table 1).

In the next sections, for simplicity, we used CD4 count as the risk score for mMPA.

Impact of Virological Failure Prevalence and Pool Size

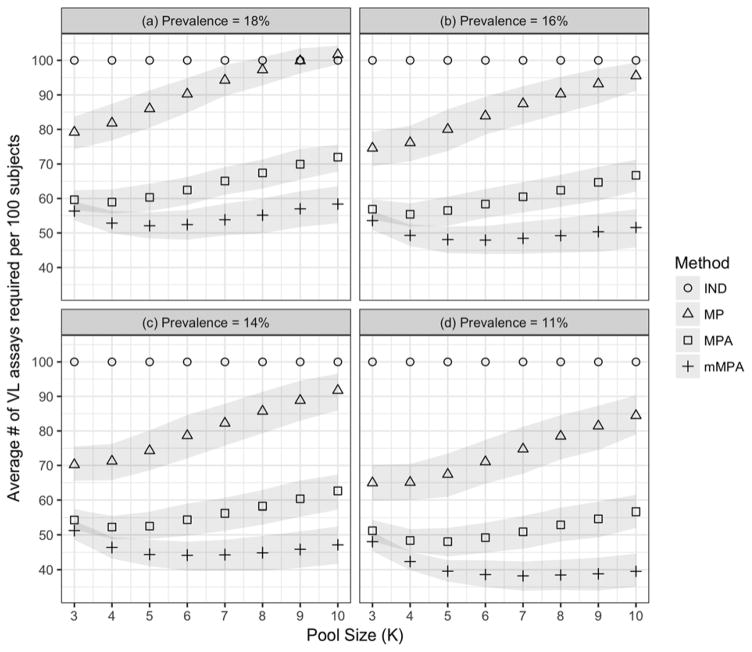
The prevalence of virological failure in the combined cohort was 16% based on the WHO recommended VL > 1000 threshold. To study the effect of prevalence on ATR, we applied threshold values of 500, 1500 and 3000, yielding prevalences 11%, 14% and 18%, respectively. We also varied the pool size from 3 to 10. Figure 2 depicts testing efficiency of mMPA with individual testing (IND), MP and MPA in terms of ATR under various failure prevalences and pool sizes, demonstrating the advantage of using mMPA in terms of ATR. Both mMPA and MPA have lower ATR than IND and MP, especially when virological failure prevalence is low. MP may need more VL tests than IND when the prevalence is high and a large pool size is used (Figure 2a). In general, mMPA is most advantageous when prevalence is low; for our data, when using a pool size of 5 or larger, mMPA has significant lowest ATR among all VL testing strategies.

Figure 2. Impact of virological failure prevalence and pool size on pooling deconvolution methods.

The figure demonstrates the impact of pool sizes K (X axis; from 3–10) and viral failure prevalence ((a)=18%; (b)=16%; (c)=14%; and (d)=11%) on the ATR (y axis) according to individual testing (IND; circles), MP (squares), MPA (plus signs) and mMPA (triangles). CD4 is used as a risk score for mMPA. The gray bounds indicate point-wise 95% confidence intervals obtained using the bootstrap method (with 500 resamples) where the intervals are the 2.5 and 97.5 percentiles of the bootstrap distributions.

Figure 2 also shows that the impact of pool size on pooled testing efficiency is non-linear, and the optimal pool size that achieves the lowest ATR depends on the prevalence of virological failure. In general, pooling methods can achieve the best testing efficiency with a larger pool size when the prevalence is lower. This nonlinear pattern and low prevalence preferences are consistent with findings of other pooled testing procedures^26,33. For this combined cohort, the optimal pool size for mMPA is 5 when the prevalence is 18%, 6 when the prevalence is 14–16%, and 7 when the prevalence is 11%. mMPA maintains its superior performance for all pool sizes considered here.

Impact of VL Assay Measurement Error

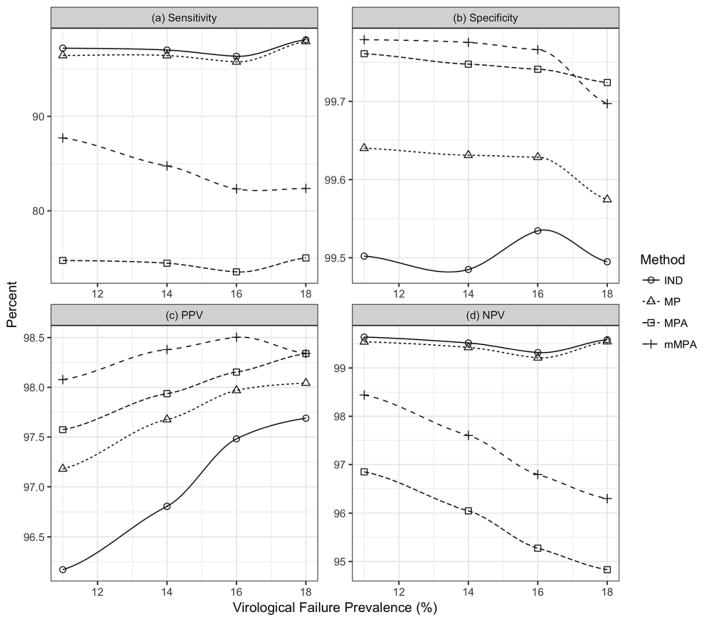
Figure 3 shows diagnostic accuracy as a function of virological failure prevalence for each testing method for assay-level measurement errors SD = .12 on the log-10 scale. All methods have high specificity (>99%). Sensitivity of mMPA ranges between 80–90%, lower than IND and MP, but greater than MPA (<80%). NPV for mMPA exceeds 95% for all prevalences considered, better than MPA and only slightly lower than IND and MP. Moreover, mMPA has the highest PPV among all methods (though all are over 95%). mMPA outperforms MPA on all four accuracy measures because it requires fewer VL assays than MPA, which implies fewer subtractions during deconvolution and therefore fewer opportunities for measurement error to affect diagnostic decisions. Similar patterns in diagnostic accuracy are observed when the assay-level measurement error has a standard deviation of 0.20 (log-10 scale) (Supplementary Figure 1).

Figure 3. Impact of VL assay measurement error on diagnostic accuracy of pooling deconvolution methods.

The figure demonstrates the impact of VL assay measurement errors on individual testing (IND; circles), MP (triangles), MPA (squares) and mMPA (plus signs). CD4 is used as a risk score for mMPA. The impact of measurement error on pooling deconvolution is quantified in terms of (a) sensitivity, (b) specificity, (c) PPV, and (d) NPV. The measurement error is assumed to have a log normal distribution with a zero mean and a standard deviation of 0.12 on the log10 scale. PPV = positive predictive value. NPV = negative predictive value.

Impact of LLD

Theoretically a high LLD increases ATR for MPA and mMPA. In our data, the impact is negligible (Supplementary Figure 2) because the majority (557/918=61%) had VL<40. Thus treating those with VL below the LLD as VL=0 had little impact on the deconvolution process and subsequent individual-level diagnoses resulting from pooled testing.

Discussions

mMPA is an informative retesting strategy to improve deconvolution of pooled HIV VL assays for ART monitoring. It uses an algorithm that relies on information from routinely-collected clinical information to rank-order samples contributing to the pool, resulting in faster and more efficient deconvolution and fewer VL tests than other approaches. The efficiency gains realized by mMPA persist across variations in virological failure prevalence, pool size, assay measurement error, and LLD.

Bilder and colleagues ^22,23,39 developed single- and multi-stage informative retesting algorithms for pooled testing using qualitative assays, and provided a comprehensive evaluation of their operating characteristics. The mMPA proposed here is designed for quantitative assays; the algorithm itself is similar to “informative Sterrett” (IS) algorithm⁴⁷ for qualitative assays, in which positive pools lead to an ordered sequence of tests on individual samples and on pools formed from remaining samples (quantitative assays do not require this latter step). There are important differences such as a modified deconvolution algorithm using sequential subtractions, assay measurement error, and assay limit of detection that are related to the implementation of mMPA.

In light of expanding VL monitoring in RLS, pooled VL testing methods, and MPA in particular, have demonstrated high potential to increase capacity of individual-level monitoring^{31,33,34,36–38,48}. Our study demonstrates that by incorporating sequential ranked deconvolution, mMPA can further improve the efficiency of pooled VL testing. Analysis of data from western Kenya demonstrates reductions of 52% relative to individual testing and by 19% relative to MPA. In terms of laboratory capacity and frequency of individual-level monitoring in programs with comparable characteristics, mMPA could double the number of virological failure ascertainments (a 108% increase in capacity) relative to individual testing; or increase by 23% the capacity relative to MPA. Moreover, mMPA has greater sensitivity, PPV, and NPV than MPA, and equally high specificity. Consequently, programmatic incorporation of mMPA would allow patients to get more, and perhaps more frequent (e.g. twice yearly rather than the recommended annual) VL monitoring. Such improvement in treatment monitoring capacity would provide more reliable guidance to physicians in clinical care and reduce the risk of maintaining patients on ineffective ART.

mMPA incorporates an estimated risk score using routinely-collected clinical markers. Though we show the advantage of using composite risk scores from multiple markers, including one which does not use CD4 values, the majority of our analyses focused on CD4 count as the risk score for its simplicity. We show that CD4 count alone, although inadequate to determine virological status, still contains valuable information that could significantly improve the efficiency of pooled VL testing. Developing risk scores for risk assessment and prediction has been an important topic in areas such as statistics and machine learning. We are exploring the use of methods such as generalized boosting⁴⁹, classification and regression trees⁵⁰, and ensemble techniques such as super learner⁵¹ to develop risk scores with even better diagnostic properties.

Some limitations of this study point to future research directions. First, our analysis relies on a simulated application of the methods to patients participating in three separate research studies, as VL data from routine clinical care in RLS are still limited. This data aggregation provides a large sample size and heterogeneous 1st- and 2nd-line ART exposure for evaluating different testing strategies (our focus), but the combined cohort is not necessarily a representative sample of all patients in care. Degree of improved capacity depends on correlation between risk score and VL, which could differ in a randomly-selected patient population. Second, variables such as time, cost and practical constraints associated with mMPA testing, deconvolution and implementation, are not considered in this simulation study, yet are important in assessing the feasibility and benefit of this approach, particularly in resource limited settings. These limitations have motivated a comparative evaluation of mMPA performance using actual patient samples, currently ongoing.

Despite some limitations, this study demonstrates the potential for mMPA to substantially improve capacity for VL monitoring relative to individual testing and other VL pooling strategies, a particularly important issue in light of urgent demand for expanding virological monitoring in RLS. To enable its application to specific settings, we have developed a software package called ‘mMPA’ using R⁵². The package allows HIV care facilities to evaluate the capacity of ART monitoring for their patients when using pooled testing to meet their context (e.g. virological failure prevalence, available clinical markers, pool size, and detection cutoff). More information about the package is provided in Supplemental Material.