Sigmoidal mixed models for longitudinal data

Abstract

Linear mixed models are widely used to analyze longitudinal cognitive data. Often, however, the trajectory of cognitive function is nonlinear. For example, some participants may experience cognitive decline that accelerates as death approaches. Polynomial regression and piecewise linear models are common approaches used to characterize nonlinear trajectories, although both have assumptions that may not correspond with the actual trajectories. An alternative is to use a flexible sigmoidal mixed model based on the logistic family of curves. We describe a general class of such a model, which has up to five parameters, representing (1) final level, (2) rate of decline, (3) midpoint of decline, (4) initial level before decline, and (5) asymmetry. Focusing on a 4-parameter symmetric sub-class of the model, with random effects on two of the parameters, we demonstrate that a likelihood approach to fitting this model produces accurate estimates of mean levels across time, even in the case of model misspecification. We also illustrate the method on deceased participants who had completed at least 5 years of annual cognitive testing and annual assessment of body mass. We show that departures from a stable body can modify the trajectory curves and anticipate cognitive decline.

1 Introduction

With the aging of the population in developed countries, there is great interest in understanding how complex human behaviors change in old age. Longitudinal studies with repeated behavioral assessment over time have documented age-related changes in diverse domains, including cognitive function ¹, motor function ², sensory function ³, and well being ⁴. However, trajectories of change are not always linear ⁵. In particular, common neurodegenerative conditions ⁵ and impending death ⁴ are associated with acceleration in rates of behavioral change.

Researchers have tried different approaches to model nonlinear trajectories of behavioral change. Piecewise models ⁴ or mixed-effects change point models^6–9 are informative strategies and may provide a good model fit in some cases, but they are unlikely to capture the true trajectory. Mixed-effects change point models are often fitted in a Bayesian framework using Markov chain Monte Carlo methods that can be slow to converge, especially with several risk factors and multiple change points^{10, 11}. Smoothing splines are another approach, but they yield many parameters that may be difficult to interpret ¹². Polynomials can approximate nonlinear models but, with several parameters, providing a biologically based interpretation can be challenging ¹³. Nonlinear mixed effect models are not typically used to analyze late-life changes in behavior with rare exceptions ¹⁴. Without multiple covariates¹⁵ or random effects, and with more control over the experimental time, these models are more commonly applied to studies in areas such as microbiology, pharmacokinetics ¹⁶ and agriculture ¹³. Here, we demonstrate a very useful nonlinear mixed model, the sigmoidal model that allows the inclusion of covariates that are related to parametric quantities such as the rate of decline and half decline(the decline midpoint), as well as early levels, final levels. In contrast to piecewise linear models, the model can potentially provide better year by year fit due to its smoothness and flexibility.

In this paper, we study late life change in cognitive function using sigmoid mixed model structures based on logistic curves. We first describe a class of models with five main parameters, each of which may be a function of covariates and two of which have random effects. Focusing on a four parameter subclass of the model in a single-group setting, we then use simulations to explore the statistical properties of our estimation technique over a variety of situations in which it might be used such as variable number of follow-ups, non-smooth trajectories, and with normal and non-normal random errors. The technique is illustrated using data from two longitudinal cohort studies on deceased participants with at least 5 years of annual observations.

2 Sigmoid mixed model for longitudinal data

Let i=1, …, N denote subjects and j=1, …, n_i denote repeated observations per subject. Let t_ij denote the negative time between the j^th observation and the terminal event (death). For example, if a subject has observations every other year, starting 9 years before death, then j=1, 2, 3, 4, 5, and t_ij=−9, −7, −5, −3, −1. Suppose that Y is a continuous normal outcome whose mean changes over time as a nonlinear function of, for simplicity, a single covariate X. Generally, a nonlinear mixed model ¹⁷ can be written in terms of a known nonlinear function g given by

$$y_{ij}=g(t_{ij},{\delta }_i,\phi )+e_{ij},$$ (1)

where the random errors e_ij~N(0,σ²), δ_i is a vector of person-specific parameters and φ is a vector of fixed parameters. Suppose that δ_i = (θ_1i, θ_4i), φ = (θ₂, θ₃, θ₅), and we let the nonlinear trajectory of Y follow a five-parameter logistic structure¹², such that,

$$g\left(t_{ij},{\delta }_i,\phi \right)={\theta }_{4i}-({\theta }_{4i}-{\theta }_{1i})\frac{1}{{(1+{(t_{ij}/{\theta }_2)}^{{\theta }_3})}^{{\theta }_5}}.$$ (2)

The parameter θ_1i represents the random intercept at t_ij=0. The parameter θ_4i represents the limiting random response before the onset of decline, since $\underset{t_{ij}\to -\infty }{lim}{y}_{ij}$ equals θ_4i. Since time starts negative and progress to zero at the final event (e.g. death), θ_1i is the final level and θ_4i is the initial level before decline for person i. We can allow θ_1i to accommodate a fixed covariate and random effects by representing it by

$${\theta }_{1i}={\alpha }_1+{\beta }_{1}x+u_i,$$ (3)

where u_i~ N(0,σ_u²). Hence, in the cognitive decline example, if there is no covariate, α₁ represents the mean level of cognitive function proximate to death. Similarly, θ_4i can be represented by

$${\theta }_{4i}={\alpha }_4+{\beta }_{4}x+v_i,$$ (4)

where v_i~N(0,σ_v²). Again, in the cognitive decline example, if there is no covariate, α₄ represents the mean level of cognitive function in early adulthood.

Note that the equation 2 has two parts. The first part of the equation is the initial level θ_4i. The second part of the equation is the total decline (θ_4i–θ_1i ) multiplied by a proportion (p) that is a nonlinear function of time, $\left(\mathrm{p}=\frac{1}{{(1+{({\mathrm{t}}_{\text{ij}}/{\mathrm{\theta }}_2)}^{{\mathrm{\theta }}_3})}^{{\mathrm{\theta }}_5}}\right)$. The interpretation of θ₂ and θ₃ are influenced by θ₅. The model can be simplified. If θ₅ is always one, we will have a four-parameter logistic. If, in addition, θ_4i is set to zero, we will have a three-parameter logistic. We now provide interpretation of θ₂ and θ₃ for the four and three parameters logistic models represented by the special case where θ₅ equals $1\left(\mathrm{p}=\frac{1}{1+{({\mathrm{t}}_{\text{ij}}/{\mathrm{\theta }}_2)}^{{\mathrm{\theta }}_3}}\right)$. Later we discuss the more complex cases where θ₅ does not equal 1.

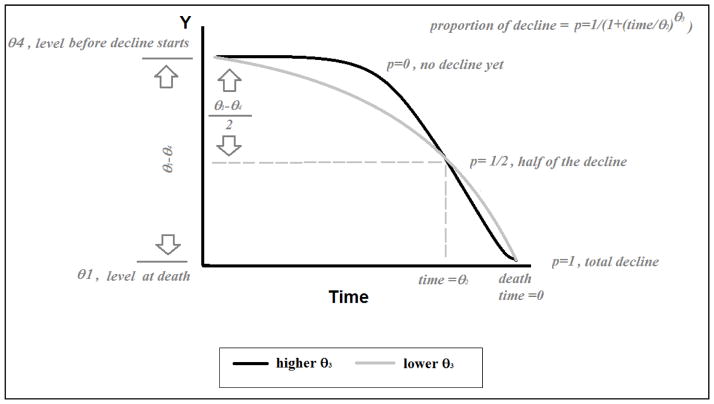
Figure 1 illustrates the interpretation of the model based on four parameters. At each point in time a nonlinear proportion p of the total decline θ_4i–θ_1i will be reduced from the initial level θ_4i until final level θ_1i was reached. The parameter θ₂ represents the point in time where half of the total decline occurred, i.e., the midpoint of decline. That is, when time equals θ₂ , then t_ij/ θ₂ equals one and p equal 0.5. It can accommodate a fixed covariate effect by representing it by

Figure 1.

Interpretation of the sigmoidal model based on the 4-parameters logistic

$${\theta }_2={\alpha }_2+{\beta }_{2}x$$ (5)

The parameter space of θ₂ must be negative to allow t_ij/θ₂ to be positive, since t_ij starts at a negative number and increases towards zero.

The parameter θ₃ represents the variations of rate of decline around the time θ₂. If t_ij/ θ₂ is above 1 (time before the half decline), high values of θ₃ will decrease p. For example, if t_ij/ θ₂ = 1.25, then a θ₃ of 1 will yield a p of 1/(1+1.25), while a θ₃ of 2 will yield a smaller p of 1/(1+1.25²). Conversely,if t_ij/ θ₂ is less than 1 (time after the half decline, closer to death), high values of θ₃ will increase p. For example, if t_ij/ θ₂ = 0.25, then a θ₃ of 1 will yield a p of 1/(1+0.25), while a θ₃ of 2 will yield a larger p of 1/(1+0.25²). The parameter θ₃ represents the variations of rate of decline. It can be represented by

$${\theta }_3={\alpha }_3+{\beta }_{3}x$$ (6)

The rate of decline θ₃ is a scale modification over time of the person specific curves, and influences the nonlinearity, or the steepness, of the curve. A positive effect on the rate of decline represents a decline that starts earlier versus a curve that starts flat and declines later. For three parameters logistic models where θ_4i is always zero the interpretation of the parameters θ_1i, θ₂ and θ₃ is the same as described above. Note that these three shape/scale parameters represented by θ₂and θ₃ do not have random effects. Conceptually, random effects for scale parameters could be added to the model, but estimation may be impractical.

An additional rate/scale parameter can be added to allow for further flexibility. The parameter θ₅ can be represented by

$${\theta }_5={\alpha }_5+{\beta }_{5}x$$ (7)

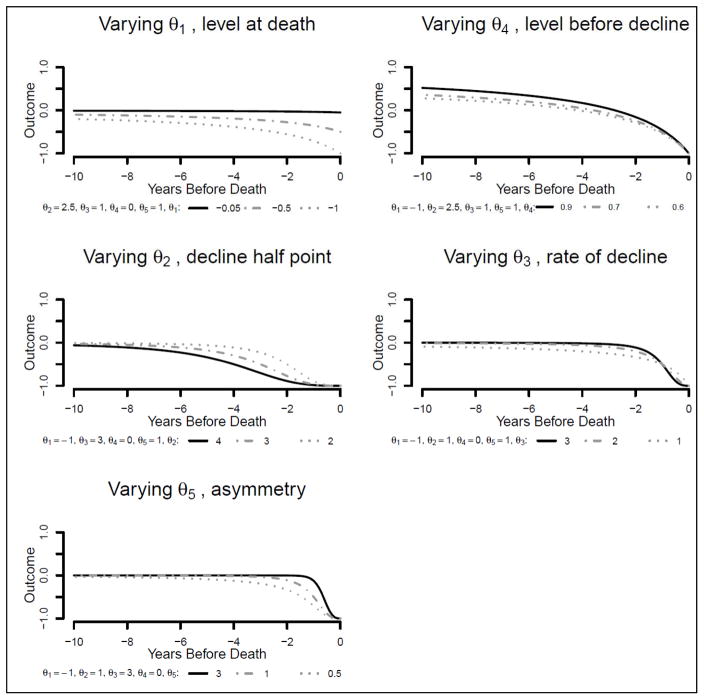
To understand θ₅ , let’s revisit the proportion p that now has the general form $\frac{1}{{(1+{({\mathrm{t}}_{\text{ij}}/{\theta }_2)}^{{\theta }_3})}^{{\theta }_5}}$. The parameter θ₅, termed in the literature an “asymmetry” parameter, will modify the curve given by the combination of θ₂ and θ₃, so that high values of the asymmetry θ₅ will postpone decline (including the half decline). The curve will look more asymmetric with a sharper decline close to death. While in the three and four parameters logistic θ₂ represents the half decline, in the five parameters model that is no longer the case. When time equal θ₂, p will be $\frac{1}{2^{\theta }5}$. For example, at time equals θ₂, for a θ₅ equals 1 p will be ½, while for a θ₅ equals 2 p will still be only ¼. Figure 2 illustrates how changes in each parameter may change the trajectory.

Figure 2.

Theoretical illustration of possible trajectories of the sigmoidal model for 3 choices of each parameter

In many cases, four parameters may provide adequate parsimony, fit and interpretation. A likelihood ratio test can be used to assess the need of the additional parameter in the five-parameter structure. Due to preliminary results from our dataset, we focus this work on the four-parameter logistic model. As described above, we assume that the between person random effects (u_i and v_i), as well as the within-person residuals (e_ij), follow normal distributions, where u_i and v_i may be correlated with each other but are assumed to be independent of the e_ij.

The model can be fit using SAS PROC NLMIXED. The model is fit by finding the maximum likelihood integrated over the random effects using adaptive Gaussian quadrature and Quasi-Newton Optimization. The initial parameter values required for the PROC NLMIXED can be obtained by examining the data trajectories. For example, an initial value for θ₁ can be the average of the observations close to death. Because we are describing a declining process, the initial for θ₄ should be smaller than the initial of θ₁. The linear slope close to death (i.e. from death to 3 years before death) versus the earlier linear slope (i.e. more than 3 years before death) can help define θ₂ and θ₃. If the ratio of the slopes is close to 1, we should use higher initials of θ₂ and θ₃. In our experience, it is helpful to start with the empty model before adding risk factors. We provide a sample code on how to find the initial values for the empty model in the supplementary material, Appendix A. In Appendix A, we also provide a sample code for fitting sigmoidal models with risk factors. The estimates of the empty model can be used for the model with risk factors.

3 Simulations

The models are often used in laboratory work where the curves are smooth and the number of observations is controlled. Epidemiological studies often have a varying number of follow-ups and trajectories are not necessarily smooth. The properties of the four-parameter longitudinal sigmoidal model were assessed via simulation over a range of situations. Parameters were selected based on preliminary data from studies described in section 4. A total of 1,000 datasets were randomly generated with different seeds and with a sample of 100 participants and 20 observations per participant. We generated data assuming smooth nonlinear trajectories, linear trajectories, and non-smooth trajectories with abrupt changes (piecewise linear trajectories). In addition, for a more challenging “wrong model” simulation, we generated data assuming a non-smooth trajectory with non-normal random effects.

Data were first generated using the four-parameter logistic with parameter values selected to reproduce what was observed during application of the method to real data. We use two sets of parameters: data of type A were generated from β₁= −0.6111, β ₂ = −1.8259, β₃ = 0.7418, β₄ = 0.5293; data of type B were generated from β₁= −1.06544, β₂=−1.9992, β₃= 1.10456, β₄= 0.82006. Data A and B assume error variance 0.068 (σ=0.2610), variance of u equal 3.018 (σ_u =1.7374), variance of v equal 0.035 (σ_v =0.1870), and a correlation of zero between random effects.

To access robustness, we simulated modeling under misspecification. Given that the four-parameter logistic characterizes curves that are nonlinear and smooth, we considered declines that are linear as well as declines that are not smooth. First, we considered an underlying linear decline (data generated assuming a linear trajectory). Data of type C were generated from one linear slope of −0.15 and intercept at death of −1.8. Second, we considered one or multiple abrupt changes to the underlying linear decline. Data of type D were generated from an underlying one-change-point linear decline: a pre-terminal slope of −0.1, one change point at −4 years from death, a terminal slope of −0.4, and intercept at death of −1.8. Data E were generated from an underlying two-change-point linear decline: an early slope of −0.005 (slope 1), an early change point at −8 years from death (point of transition from slope 1 to slope 2), a pre-terminal slope of −0.1 (slope 2), a terminal change point at −4 years from death (point of transition between slope 2 and 3), a terminal slope of −0.4 (slope 3), and intercept at death of −1.8.

Robustness under non-normal random effects was also evaluated. For an additional challenge, we assumed a non-smooth decline. Data F were generated similarly to data E but assuming a departure from normality for the random effects. This was done by generating random errors following a gamma distribution with a shape parameter of 9 and a scale parameter of 0.5, and centering the distribution at its median. This introduced skewness in the random error distribution of about 0.7.

Using the data generated with an underlying four-parameter logistic we studied the effect of the number of observations per participant on the characterization of the curve using the sigmoidal mixed model. To be able to include the period of accelerated decline that occurs around 3 years before death (known as terminal decline), data of type A were also generated with a period of 5, 7 and 10 years before death to death (or 5, 7 and 10 annual observations per participants). The sigmoidal mixed model was fit with the SAS PROC NLMIXED, with 1,000 repeats. Parameter bias and accuracy were evaluated. In addition for data of types A and B, the linear mixed model with a quadratic term for time before death was fit with the SAS PROC MIXED. Bias and accuracy of the estimated longitudinal mean were evaluated year by year, as these simulations were performed under misspecification (that is the true parameters used for data generation are not estimated).

Using the data generated from underlying linear or change-point linear declines (data C, D and E), we assessed the sigmoidal mixed model robustness under misspecification. The sigmoidal mixed model was fit with the SAS PROC NLMIXED as described above. Bias and accuracy of the estimated longitudinal mean were evaluated year by year, as these simulations were performed under misspecification.

Parameters from the sigmoidal mixed model were adequately estimated using as few as five observations per participants (Supplementary Material Appendix B). All simulated parameters had coverage of above 93% and very low bias. The mean square error of the estimated parameters remained less than 0.035 with the decreasing number of observations.

Table 1 shows the results from simulations of sigmoidal mixed modeling and linear mixed modeling with a quadratic term using data A and B. Estimated longitudinal annual means had more than 10 times higher bias and mean square errors using linear models with a quadratic term compared to the sigmoidal mixed models.

Table 1.

Simulation results of sigmoidal mixed modeling and linear mixed modeling with quadratic term

Time from death	μ†	Simulation data A*				μ†	Simulation data B**
		Sigmoidal model		Linear with quadratic term			Sigmoidal model		Linear with quadratic term
		Bias	MSE	Bias	MSE		Bias	MSE	Bias	MSE
0	−0.61	−0.00	0.03	0.31	0.11	−1.07	−0.00	0.03	0.45	0.22
−1	−0.17	−0.00	0.01	−0.05	0.02	−0.47	−0.00	0.01	0.03	0.01
−2	−0.02	−0.00	0.01	−0.10	0.02	−0.12	−0.00	0.01	−0.13	0.03
−3	0.06	−0.00	0.01	−0.10	0.02	0.09	−0.00	0.01	−0.16	0.03
−4	0.12	−0.00	0.00	−0.06	0.01	0.22	−0.00	0.00	−0.11	0.02
−5	0.16	−0.00	0.00	−0.01	0.00	0.32	−0.00	0.00	−0.03	0.00
−6	0.20	−0.00	0.00	0.04	0.00	0.39	−0.00	0.00	0.08	0.01
−7	0.22	−0.00	0.00	0.11	0.01	0.44	−0.00	0.00	0.21	0.04
−8	0.24	−0.00	0.00	0.18	0.03	0.48	−0.00	0.00	0.35	0.12
−9	0.26	−0.00	0.00	0.25	0.06	0.52	−0.00	0.00	0.49	0.25
−10	0.28	−0.00	0.00	0.32	0.11	0.55	−0.00	0.00	0.65	0.42
−11	0.29	−0.00	0.00	0.40	0.16	0.57	−0.00	0.00	0.81	0.65
−12	0.30	−0.00	0.00	0.48	0.23	0.59	−0.00	0.00	0.97	0.94
−13	0.31	−0.00	0.00	0.56	0.32	0.61	−0.00	0.00	1.13	1.29
−14	0.32	−0.00	0.00	0.64	0.42	0.62	−0.00	0.00	1.30	1.70
−15	0.33	−0.00	0.00	0.72	0.53	0.64	−0.00	0.00	1.47	2.16
−16	0.34	−0.00	0.00	0.81	0.66	0.65	−0.00	0.00	1.64	2.70
−17	0.35	−0.00	0.00	0.89	0.81	0.66	−0.00	0.00	1.81	3.29
−18	0.35	−0.00	0.00	0.97	0.97	0.67	−0.00	0.00	1.98	3.95
−19	0.36	−0.00	0.00	1.06	1.14	0.68	−0.00	0.00	2.15	4.67
−20	0.36	−0.00	0.00	1.14	1.33	0.68	−0.00	0.00	2.33	5.46

^*β₁= −0.6111, β ₄= 0.5293, β ₃= 0.7418, β ₂=−1.8259, σ_uv =0, σ=0.2610, σ_u =1.7374, σ_v =0.1870

^**β ₁= −1.06544, β ₄= 0.82006, β ₃= 1.10456, β ₂=−1.9992, σ_uv =0, σ=0.2610, σ_u =1.7374, σ_v =0.1870.

^†μ= true mean.

Table 2 shows the analysis of robustness under misspecification. Underlying linear decline (data type C) generated a very large estimated decline midpoint, θ₂. Overall, the longitudinal mean estimated year by year using the sigmoidal mixed model was close to the true underlying longitudinal mean. Bias was low overall but relatively higher in estimations close to death.

Table 2.

Simulation results of sigmoidal model for misspecification underlying processes

Years before death	Linear Data C				Non-smooth piecewise linear data
					Data D*				Data E**				Data F†
	True mean	Predicted	Bias	MSE	True mean	Predicted	Bias	MSE	True mean	Predicted	Bias	MSE	True mean	Predicted	Bias	MSE
0	−1.80	−1.60	0.20	0.15	−1.80	−1.24	0.55	0.31	−1.80	−1.49	0.31	0.10	−1.80	−1.46	0.34	0.11
−1	−1.65	−1.45	0.20	0.14	−1.40	−0.91	0.49	0.24	−1.40	−0.97	0.43	0.18	−1.40	−0.94	0.46	0.21
−2	−1.50	−1.30	0.20	0.13	−1.00	−0.64	0.35	0.12	−1.00	−0.54	0.45	0.21	−1.00	−0.51	0.49	0.24
−3	−1.35	−1.16	0.19	0.12	−0.60	−0.43	0.17	0.03	−0.60	−0.27	0.33	0.11	−0.60	−0.23	0.37	0.14
−4	−1.20	−1.01	0.19	0.11	−0.20	−0.24	−0.04	0.00	−0.20	−0.10	0.10	0.01	−0.20	−0.05	0.15	0.02
−5	−1.05	−0.86	0.19	0.10	−0.10	−0.07	0.03	0.00	−0.10	0.01	0.11	0.01	−0.10	0.06	0.16	0.03
−6	−0.90	−0.72	0.18	0.09	0.00	0.08	0.08	0.01	0.00	0.08	0.08	0.01	0.00	0.14	0.14	0.02
−7	−0.75	−0.57	0.18	0.08	0.10	0.22	0.12	0.01	0.10	0.13	0.03	0.00	0.10	0.19	0.09	0.01
−8	−0.60	−0.42	0.17	0.08	0.20	0.34	0.14	0.02	0.20	0.16	−0.04	0.00	0.20	0.23	0.03	0.00
−9	−0.45	−0.28	0.17	0.07	0.30	0.46	0.16	0.03	0.21	0.19	−0.02	0.00	0.21	0.26	0.05	0.00
−10	−0.30	−0.13	0.16	0.06	0.40	0.57	0.17	0.03	0.21	0.21	0.00	0.00	0.21	0.28	0.07	0.01
−11	−0.15	0.01	0.16	0.06	0.50	0.67	0.17	0.03	0.22	0.22	0.01	0.00	0.22	0.30	0.08	0.01
−12	0.00	0.15	0.15	0.06	0.60	0.77	0.16	0.03	0.22	0.23	0.01	0.00	0.22	0.31	0.09	0.01
−13	0.15	0.30	0.15	0.05	0.70	0.85	0.15	0.02	0.23	0.24	0.02	0.00	0.23	0.32	0.09	0.01
−14	0.30	0.44	0.14	0.05	0.80	0.94	0.14	0.02	0.23	0.25	0.02	0.00	0.23	0.33	0.10	0.01
−15	0.45	0.58	0.13	0.05	0.90	1.02	0.12	0.01	0.24	0.26	0.02	0.00	0.24	0.33	0.10	0.01
−16	0.60	0.72	0.12	0.05	1.00	1.10	0.09	0.01	0.24	0.26	0.02	0.00	0.24	0.34	0.10	0.01
−17	0.75	0.86	0.11	0.05	1.10	1.17	0.07	0.01	0.25	0.27	0.02	0.00	0.25	0.35	0.10	0.01
−18	0.90	1.00	0.10	0.06	1.20	1.24	0.04	0.00	0.25	0.27	0.02	0.00	0.25	0.35	0.10	0.01
−19	1.05	1.14	0.09	0.06	1.30	1.30	0.00	0.00	0.26	0.27	0.02	0.00	0.26	0.35	0.10	0.01
−20	1.20	1.28	0.08	0.07	1.40	1.37	−0.03	0.00	0.26	0.27	0.01	0.00	0.26	0.36	0.10	0.01

^*piecewise linear with one point change and normal random effects,

^**piecewise linear with two points of change and normal random effects,

^† piecewise linear with two points of change and non-normal random effects

Using a sigmoidal model was also relatively robust to data with non-smooth declines and with non-normal random effects. Overall, the longitudinal means estimated year by year using the sigmoidal mixed model were still close to the true underlying longitudinal mean. However, there was a noticeable increase in bias close to death and in the earlier years. We also observed a small increase in the mean square error with moderate departures from normality of the random effects (data F versus data E).

4 Analyses of late-life body mass index and cognitive decline

Analyses of body mass index (BMI) and late-life cognitive decline showed mixed results. Some studies show that low or decreasing BMI is associated with cognitive decline, but others show no association ^18–20. Few of these studies, however, followed both cognition and BMI for many years until death. Annual assessment of cognition, weight, and height from the Rush Religious Order Study and the Rush Memory and Aging Project were used to model change in global cognition and BMI. These analyses indicate that departures from stable body mass are associated with earlier cognitive decline.

The Religious Orders Study began in 1994. Participants are older Catholic nuns, priests, and monks recruited from more than 40 groups across the United States ²¹. The Rush Memory and Aging Project began in 1997. It involves older lay persons recruited from retirement communities, subsidized housing facilities, churches, and social service agencies in the Chicago metropolitan area ²² . Studies were approved by the institutional review board of Rush University Medical Center. Details on the individual tests and the derivation of the composite measure of global cognition have been previously published ^{6, 23, 24}. Years of formal education is obtained at baseline. For each individual, BMI was calculated as weight at visit in kilograms over personspecific median height in meters squared (kg/m²). Range of person-specific BMI was calculated as the average of the two largest values minus the average of the two lowest values

Data from 512 deceased participants with 5 to 20 years of annual cognitive testing (4,982 observations) were included in the analyses. Among these individuals, 436 had BMI information close to death, obtained in the same visit of the last cognitive evaluation or visit before that. A random sample of person-specific observed BMI and global cognition is available as Supplementary Material (Appendix C). These 436 participants had a mean of 78.6 years of age at baseline (sd = 6.5), 88.4 years of age at death (sd = 6.2), and 16.7 years of formal education (sd = 3.6). They had a mean BMI of 27 at baseline and 25 at death. The median range of person-specific BMI was 3.1 (min=0 and max=14.8).

In the preliminary analyses, we compared the sigmoidal model with a more established method, the mixedeffects change point model¹⁰ . The change point model is a piecewise linear model such that

$$y_{ij}=\{\begin{array}{ll}{b}_{1i}+b_{2i}{t}_{ij}+e_{ij}\hfill & if{t}_{ij}\le b_{3i}\hfill \\ b_{1i}+b_{2i}{b}_{3i}+b_{4i}(t_{ij}-b_{3i})+e_{ij}\hfill & if{t}_{ij}>b_{3i}\hfill \end{array},$$ (8)

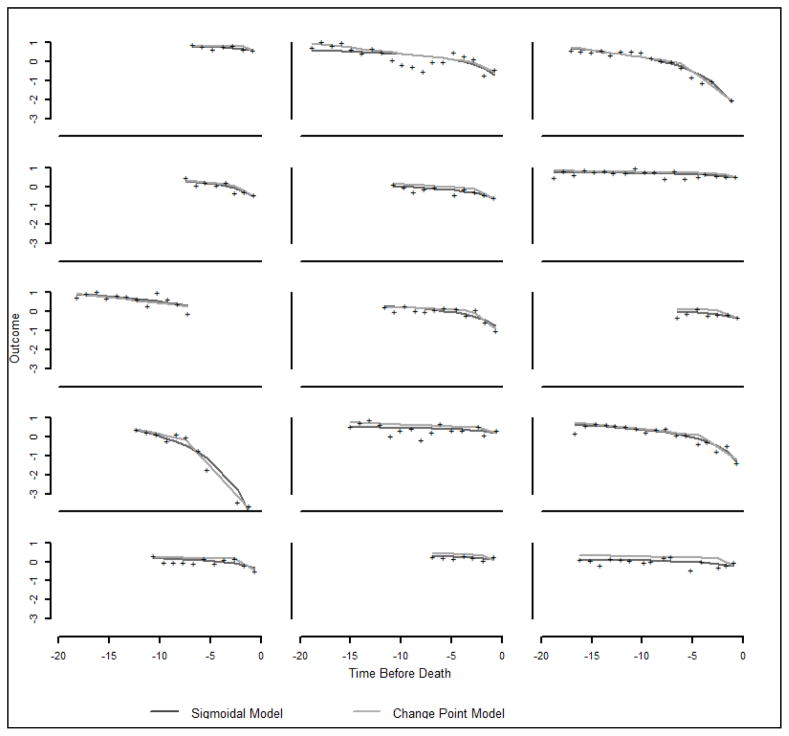
where i=1, …, N subjects, j=1, …, n_i repeated observations per subject and t_ij time between the j^th observation and the terminal event (death). The random effects for cognition at death (b_1i), terminal slope (b_2i), change point (b_3i), and preterminal slope (b_4i) are assumed follow a normal distribution. We modeled the nonlinear trajectory of global cognition as a function of education only (data not shown). To fit the mixed-effects change point model, we used a Bayesian Monte Carlo Markov Chain Approach^{11, 25} . Modeling was performed in Openbugs ²⁶ using 10,000 iterations, 3,000 burn-ins and 100 as a thinning parameter. Figure 2, which shows person-specific observed and predicted trajectories for a random sample of 15 cases, suggests good agreement between the two modeling approaches.

In the main analyses, we modeled the nonlinear trajectory of global cognition as a function of age, BMI and education. Age and education were centered close to their means to improve interpretation of results. It is important to adjust for the fact that participants that enter the study at earlier age should have higher initial cognition, as well as participants that die younger may end up with a higher cognition. For this reason, we entered a term for age at baseline for early levels of cognition(θ4) and a term for age at death for level of cognition at death(θ1). The initial level of global cognition(θ₄) also included terms for education and BMI at baseline. Conversely, the level of global cognition at death(θ₁) also included terms for education and the last BMI available before death. The decline midpoint(θ₂) and the rate of decline(θ₃) included terms for education, age at baseline and death, and range of person-specific BMI. Modeling was performed in SAS using the PROC NLMIXED.

Table 3 presents results from the main model. Consider a typical person with 17 years of formal education that, 79 years of age at baseline and 89 years of age at death, and constant BMI of 26. Initial(α₄) and final(α₁) level of cognition were estimated to be 0.59 and −0.90, respectively. Half of the decline in global cognition(α₂) was estimated to occur 1.4 years before death. That is, half of the decline was estimated to occur during the years before the last 1.4 years of life, and half of the decline was estimated to occur the last 1.4 years of life. That is because the nonlinear curve is much steeper proximate to death. Education was only related to the initial(θ₄) global cognitive score, with each additional year of formal education increasing initial(θ₄) global cognitive score by 0.018. Age at baseline was related to initial(θ₄) but not final(θ₁) level of cognition. Age at death was related to final(θ₁) but not initial level(θ₄) of cognition. Participants who were younger at baseline had a higher initial(θ₄) level of global cognition. Participants who were younger at death had a higher final(θ₁) level of global cognition. The effect of age at death in the midpoint of decline(θ₂) was larger than the effect of age at baseline.

Table 3.

Results from sigmoidal modeling on global cognition

Parameters	Estimate	Standard Error	Pr > |t|
Initial level
α4	0.587	0.057	<.0001
Education	0.018	0.009	0.045
Age at baseline	−0.016	0.005	0.000
BMI at baseline	0.002	0.005	0.725
Decline midpoint
α 2	−1.402	0.172	<.0001
Education	0.001	0.027	0.981
Age at baseline	0.169	0.029	<.0001
Age at death	−0.216	0.025	<.0001
Range of BMI	−0.265	0.048	<.0001
Rate of decline
α 3	0.830	0.091	<.0001
Education	0.027	0.009	0.003
Age at baseline	−0.033	0.009	0.001
Age at death	0.067	0.010	<.0001
Range of BMI	0.037	0.014	0.009
Level at death
α 1	−0.902	0.092	<.0001
Education	0.016	0.022	0.465
Age at death	−0.037	0.012	0.003
Last BMI before death	−0.016	0.014	0.237
Variance and covariance
Error	0.246	0.003	<.0001
u	2.120	0.227	<.0001
v	0.174	0.034	<.0001
u,v	−0.284	0.100	0.005

Education represents years of formal education centered at 17 years. Age at baseline and at death is centered respectively at 79 and 89 years. BMI at baseline and the last before death were centered at 26.

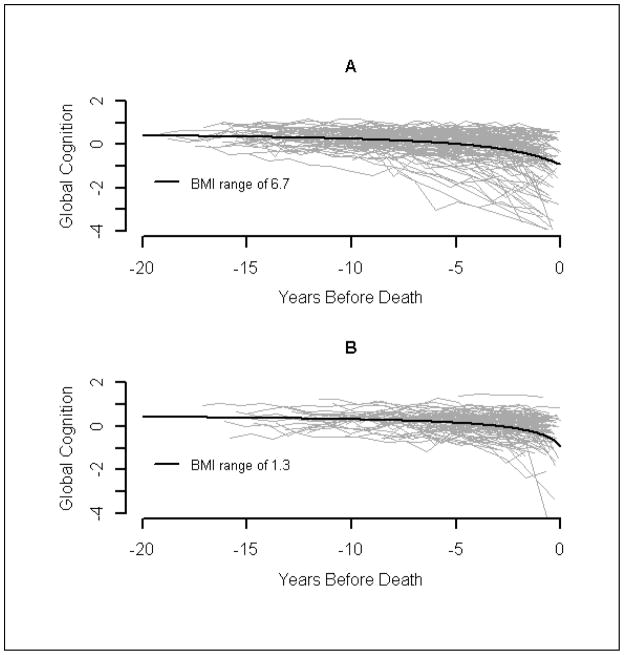
Range of person-specific BMI over time was significantly related to cognitive decline. BMI at baseline and the last BMI available before death did not have a significant effect on either initial(θ₄) or final(θ₁) level of global cognition. However, for every additional 4 points of range of person-specific BMI, the midpoint of decline(θ₂) occurred about 1 year earlier (or −0.265 years for an increment of 1 in the range of BMI). That is, half of the decline in global cognition(θ₂) was estimated to occur 2.4 years before death for a typical person if range of person-specific BMI equalled 4. Figure 3 shows the predicted curves for a person with a range of person-specific BMI of 1.3 versus 6.7.

Figure 3.

A random sample of person-specific observed and predicted global cognition

In secondary analyses, we estimated two additional models. In one model, the term for the last BMI before death was replaced by a term for range of person-specific BMI; in a second model, the terms for range of person-specific BMI and BMI proximate to death were replaced by terms for BMI at baseline. These analyses did not present additional significant terms (data not shown).

5 Discussion

Sigmoidal models based on the logistic family can accommodate longitudinal decline that includes a variety of monotone trajectories. For example, depending on risk and protective factors, some participants may never decline or decline only shortly before death, while others may begin to decline early but decline at a gradual rate, and others may decline more precipitously but differ in when decline accelerates.

With the sigmoidal model we were able to identify risk/protective factors for initial levels of cognition and risk/protective factors for final levels of cognition. The model offers a theoretical possibility of including some correlation between u and v that is demonstrated in the example presented in this paper. Results from the example are consistent with previous research on education and terminal decline ^{7, 9}. Person-specific BMI range is included as one of the covariates in the analysis. We could detect whether changes in BMI can modify the trajectory curves and anticipate decline. Here we test change in body mass that is not necessarily a trend. Although decline in BMI is observed in general among the elderly, BMI range also captures drops in BMI even when followed by complete recovery. Most of the contribution of BMI range is on the midpoint of decline. In general the effects on rate of decline θ3, although significant, were small.

The model showed adequate fit to the data. Comparing the person-specific predicted trajectories obtained with the sigmoidal model to the change-point model was, therefore, an important exercise. Although both models were informative and person-specific fit was in general very close, fitting the sigmoidal model took less time. While convergence with change-point models can take hours to days, depending on the complexity of the model, the sigmoidal model often takes minutes. We observed that the trajectories predicted by the sigmoidal model are sometimes less influenced by “bad days” represented by drops outside the pattern as shown in the person-specific plots. The models share a limitation that inference only reflects the observed period. For example, we cannot ascertain a change point or fully characterize a non-linear curve when the period that precedes the terminal acceleration was not observed.

Model adequacy aside, formulating hypotheses for certain research questions using a change point model can be difficult. While the sigmoidal model with four parameters allows for risk factors to modify initial and/or final level, the change point model has only one parameter directly determining level (intercept). For example we show that education is important for the initial level but not for the final level of global cognition. In addition multiple change points would be necessary for certain trajectories (e.g. Figure 1, lower θ₃).

Hypotheses concerning the location of the half decline will be more mathematically tractable than hypotheses concerning a single change point.

Based on results from the simulations, we used 5 or more years of follow-up to characterize the non-linear curve. In future work, it would be of interest to determine whether including very brief periods of follow-up for some individuals would improve or degrade the estimation. Another limitation is that the alignment of person-specific trajectories is fundamental. For example, in this work, all curves are aligned at death. Alignment at the diagnoses of dementia has being used in other studies that employed change-point methods¹⁰. Regardless of the biological event used, a misalignment of trajectories may create a false idea that some are declining before others.

In addition to the simulations presented herein, we explored other situations. For example, we re-generated data A with a covariance between u and v of −0.2 instead of assuming no covariance. Coverage above 90% for all four parameters was obtained with five observations per participant and a sample of 500. The covariance of u and v has an impact on the coverage of θ₂ and θ₃, being these two parameters related with dispersion. We also regenerated data A with increasing standard deviation σ_u of 3 and σ_v of 0.2 (variance of 9 and 0.04). Simulation was repeated using five observations per participant. The estimated parameters had coverage above 93%, bias below 0.02, the mean square error of 0.08 or below.

Simulations indicated that the sigmoidal model was robust under misspecification. The bias and mean square error were relatively low even for data with non-smooth trajectories and moderate departure from normality of random effects. The model could fit linear trajectories but underlying linear declines tend to be translated into high θ₂. That is, if θ₂ is, it is important to consider whether trajectories are linear.

A linear mixed model with a fixed quadratic term for time is a common approach for non-linear trajectories. However, these models are more adequate for trajectories with a peak or a valley. Simulations showed much lower bias of the sigmoidal model compared to the linear mixed model with a fixed quadratic term for time. That is not surprising given that data was simulated following an underlying sigmoidal curve. However, if bias was close, there would be no justification for the additional complexity of the sigmoidal model.

We believe that these innovative yet practical models will help researchers in a wide array of fields where longitudinal trajectories are nonlinear. In particular, neurodegenerative diseases have a chronic course that involves very gradual changes in behavior over time, eventually resulting in rapid change in the last years of life. The current clinical understanding of the most common neurodegenerative disease, Alzheimer’s disease, describes such phases over a period of many years, so that longitudinal studies with 5 to 10 annual evaluations may include people with multiple observation points in each phase ²⁷ . Since the neurodegenerative changes progress over time, it is thought that the influences of environmental, genetic, and behavioral factors may differ across the time-course of the disease. Statistical models that accurately capture variation are valuable tools to identify factors that are more important early and others that are more important only later. Understanding how environmental and genetic factors influence these nonlinear trajectories may, therefore, be enhanced by using sigmoidal mixed models.

Supplementary Material

Appendix

Appendix A. Sample code to fit the four parameters sigmoidal model

Appendix B. Simulation results of sigmoid mixed modeling of 1000 randomly generated

Appendix C. A random sample of person-specific observed global cognition (outcome variable, in black) and observed BMI (in red), and predicted global cognition (in grey) from the sigmoidal model of the main analyses

Figure 4.

Spaghetti plot of global cognition among participants with upper quartile of range of person-specific BMI over time (plot A, BMI range ≥4.7) and lower quartile of range of person-specific BMI over time (plot B, BMI range ≤1.9), and predicted line based on sigmoidal model for a specific range of person-specific BMI (plot A, BMI range = 6.7; plot B, BMI range = 1.3)