A geometric atlas to predict lung tumor shrinkage for radiotherapy treatment planning

Abstract

Purpose

To develop a geometric atlas that can predict tumor shrinkage and guide treatment planning for non-small-cell lung cancer. To evaluate the impact of the shrinkage atlas on the ability of tumor dose escalation.

Method

The creation of a geometric atlas included twelve patients with lung cancer who underwent both planning CT and weekly CBCT for radiotherapy planning and delivery. The shrinkage pattern from the original pretreatment to the residual posttreatment tumor was modeled using a principal component analysis, and used for predicting the spatial distribution of the residual tumor. A predictive map was generated by unifying predictions from each individual patient in the atlas, followed by correction for the tumor’s surrounding tissue distribution. Sensitivity, specificity, and accuracy of the predictive model for classifying voxels inside the original gross tumor volume (GTV) were evaluated. In addition, a retrospective study of predictive treatment planning (PTP) escalated dose to the predicted residual tumor while maintaining the same level of predicted complication rates for a clinical plan delivering uniform dose to the entire tumor. The effect of uncertainty on the predictive model’s ability to escalate dose was also evaluated.

Result

The sensitivity, specificity and accuracy of the predictive model were 0.73, 0.76, and 0.74, respectively. The area under the ROC curve for voxel classification was 0.87. The Dice coefficient and mean surface distance between the predicted and actual residual tumor averaged 0.75, and 1.6mm, respectively. The PTP approach allowed elevation of PTV D95 and mean dose to the actual residual tumor by 6.5Gy and 10.4Gy, respectively, relative to the clinical uniform dose approach.

Conclusion

A geometric atlas can provide useful information on the distribution of resistant tumors and effectively guide dose escalation to the tumor without compromising the OAR complications. The atlas can be further refined by using more patient data sets.

I. INTRODUCTION

Lung cancer is the leading cause of cancer death in the United States (Siegel 2016). Definitive radiotherapy with or without chemotherapy is the standard of care for the treatment of inoperable locally advanced non-small cell lung cancer (NSCLC) following the National Comprehensive Cancer Network (NCCN) guidelines. However, long-term locoregional control rates are disappointing, ranging from 30–40% (Machtay 2012). Previous studies have shown an improvement in locoregional control with dose escalation (Rosenzweig 2005). However, dose escalation using a uniform dose to the entire tumor is frequently limited by large tumor volumes that are unavoidably associated with high radiation doses to adjacent organs at risk (OAR), especially spinal cord, heart, esophagus, and normal lung. In fact, recent attempts to uniformly escalate the radiation dose to the entire tumor volume from 60 Gy to 74 Gy in a large randomized trial failed to show a survival benefit due to severe toxicities (Bradley 2015). Thus the need for novel, safe and effective dose escalation paradigms that only aim at the resistant portion of the tumor is particularly urgent. In response to radiation, the tumor often regresses during the course of radiotherapy (Kupelian 2005, Woodford 2007, Gillham 2008, Fox 2009, Feng 2009, Bral 2009, Sonke 2010). The residual tumor at the end of radiotherapy is an ideal target for dose escalation if it can be accurately predicted and appropriately accounted for at the stage of treatment planning.

We have developed a novel treatment paradigm called predictive treatment planning (PTP) to guide nonuniform dose escalation (Zhang 2014). This utilized a predictive model of tumor regression during radiotherapy by examining patients’ longitudinal imaging studies. Tumor regression patterns were extracted from geometrical affine transformation models that correlated the spatial distributions of original tumor volumes drawn on pretreatment planning CT with the residual (resistant) tumor volumes on the cone-beam CT (CBCT) scans acquired in the last week of radiotherapy. We then incorporated the predictive model into the optimization of a personalized radiotherapy plan, which progressively escalated dose to the predicted residual portion of the tumor. In a retrospective planning study, we were able to demonstrate that PTP was able to raise the mean dose to the actual resistant tumor observed on the last week CBCT an average of 10 Gy compared to the conventional uniform dose approach, and 6 Gy compared to a midcourse replanning approach, with negligible difference in radiation dose to the OARs.

The predictive model used in the PTP prototype has several limitations, however. It suffers mainly from the small number of patients included in the original study. It is focused on the shrinkage patterns of parenchymal tumors, and ignores shrinkage of centralized tumors attached to the mediastinum, which are often larger and have a more complicated shape, thus presenting challenges for dose escalation. In this report we address the deficiencies of the earlier model with regard to variability in patient and tumor geometry by expanding the database of the geometric atlas and analyzing data from patients recruited on recent IRB-approved clinical protocols that include longitudinal imaging studies. We expect that these data will allow us to better understand the dependence of shrinkage patterns on tumor location, improve the accuracy of the predictive model, and evaluate the effect of uncertainty on the predictive model’s ability to escalate dose via PTP.

II. METHOD AND MATERIALS

2.1 Longitudinal imaging study of NSCLC

For this retrospective study, we identified twelve patients with locally advanced NSCLC who underwent treatment planning CT and consecutive weekly CBCT scans for their conventional radiotherapy (2Gy/fraction, 30–35 fractions). The image sets were restored from our institutional picture archive and communications system (PACS) and imported into a commercial treatment planning system (Eclipse v13, Varian Medical Systems, Palo Alto, CA). A radiation oncologist and medical physicist segmented gross tumor volume (GTV) on the planning CT and last-week CBCT using a lung or abdominal window, and transferred tumor contours to the planning CT via rigid 3-dimensional image registration that aligned the spinal cord and outer lung. The volume of these tumors ranged from 4cc to 401cc. All tumors had moderate shrinkage: the residual gross tumor volume (GTV_resd) observed on the last-week CBCT was on average 57% of the original GTV (GTV_ori), observed on the planning CT, with a range of 41% to 74%, and a standard deviation of 9%. The average tumor shrinkage rate was 1%/day, which fell in the range of 0.6–2.4%/day as reported by Sonke and Belderbos (2010).

2.2 Geometrical shrinkage Atlas

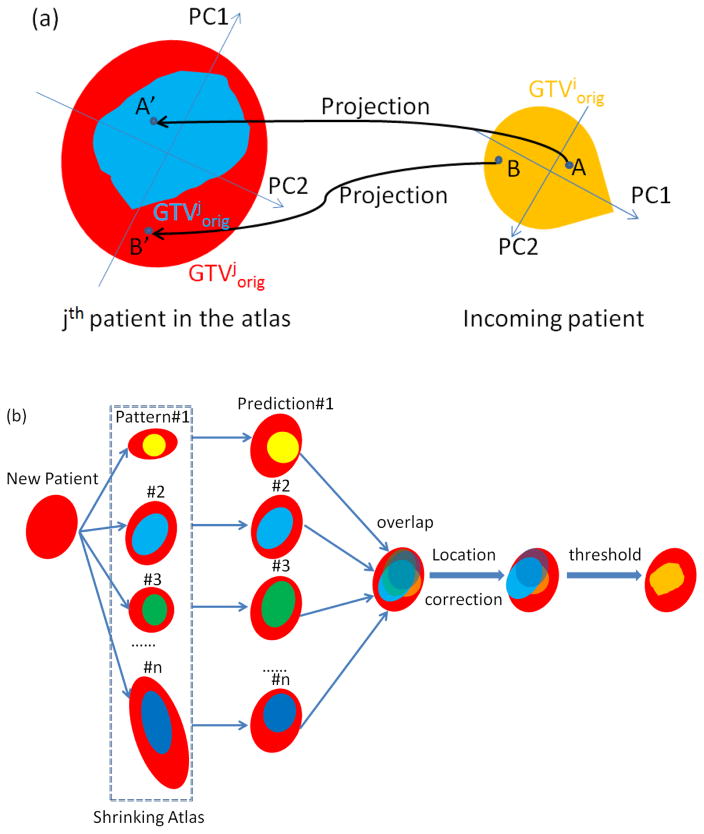
We hypothesize that there are patterns in the way that locally advanced NSCLC tumors shrink during conventional radiotherapy, consisting of a tumoricidal dose delivered at approximately 2Gy/fraction. As the dose to a lung tumor accumulates and takes effect, the periphery of the tumor may erode, or the center of the tumor may collapse and peripheral tissue may fill in. We have observed that a common feature of the tumor shrinkage pattern is that the residual tumor tends to distribute heavily toward the center of the original tumor, but each varies in its own unique way at the periphery. Similar patterns were observed and reported (Sonke 2010). We attempt to capture these patterns with a population-based model (atlas) that includes as many shrinkage patterns as we can reliably find in our clinic, and then predict tumor regression patterns for each individual incoming patient using their treatment planning CT. The key components of building such a geometric shrinkage atlas include: a description of the geometric distribution of the predicted residual GTV_resd inside the original GTV_ori for each patient, a method to project the shrinkage pattern from one patient to the other, a way to synthesize the predictions from all patients in the atlas, and a correction for its surrounding anatomy for an incoming patient. The flowchart of the algorithm is shown in Figure 1.

Figure 1.

Flowchart of the prediction algorithm: (a) original GTVⁱ_orig of the incoming patient is scaled and aligned with GTV^j_orig of the j^th patient from the atlas by matching the principle components. A voxel inside GTVⁱ_orig is projected onto GTV^j_orig using its normalized principle component score. If the projection falls into the residual GTV^j_resd of j^th patient, it is classified as a residual voxel following the j^th pattern (voxel A); otherwise classified as a disappearing voxel (voxel B). (b) Accumulation of predictions from all atlas patients is corrected for anatomical location and forms a binary map of prediction.

2.2.1 Formation of a predictive probability map

We utilized principal component analysis (PCA) to describe the geometric representation of GTV_resd inside GTV_ori for each individual patient. We first extracted the Cartesian coordinates of all voxels inside GTV_ori to form a points cloud (PC_ori; voxel resolution is the same 1x1x2.5mm as the planning CT):

$${PC}_{\mathit{ori}}=\{{(\mathrm{x},\mathrm{y},\mathrm{z})}_{\mathrm{n}}\},\forall \mathrm{n}\in {\mathit{GTV}}_{\mathit{ori}}$$ Eq. 1

We then performed PCA on PC_ori:

$$[\mathit{coeff},\mathit{Score}]=\mathit{pca}({PC}_{\mathit{ori}})$$ Eq. 2

and recorded the principal component coefficients (coeff), as well as principal component scores (Score). The three coefficients give the 3-D orientation of the three principal axes of the point cloud, and the score of each point simply indicates the projection of the Cartesian coordinate on these axes. To correlate the geometries of the GTV_ori from one patient to another, we projected the principal component scores assuming shrinkage patterns are independent of tumor size. For the n^th point inside the GTV_ori of incoming patient i, its k^th (k=1,2,3) principal component score ${\mathit{Score}}_n^i(k)$ was normalized to its k^th maximal principal component score, MaxScoreⁱ(k), scaled to the k^th maximal principal component score of atlas patient j, MaxScore^j(k), and projected as ${\mathit{Score}}_n^{ij}(k)$:

$${\mathit{Score}}_n^{ij}(k)={\mathit{Score}}_n^i(k)\times \frac{{\mathit{MaxScore}}^j(k)}{{\mathit{MaxScore}}^i(k)}$$ Eq. 3

Therefore, the position of the n^th point inside GTV_ori of patient i was projected onto patient j as:

$${(x,y,z)}_n^{ij}={\mathit{Score}}_n^{ij}\times {\mathit{coeff}}^j$$ Eq. 4

In other words, the above procedure in effect aligns the centroids and principal axes of the original GTV of the incoming patient with that of the j^th atlas patient, and adjusts the incoming patient’s tumor size to match that of the atlas patient. The matching of the two tumors using the principle axes eliminates the orientation difference existing in the native Cartesian coordinates. If the projected position ${(x,y,z)}_n^{ij}$ was inside GTV_resd of patient j, this point was labeled as predicted residual tumor following the shrinkage pattern of patient j; otherwise it is classified as a disappearing voxel. The shrinkage pattern of patient j is fully duplicated onto the incoming patient i after all the points inside its original GTV are transformed and inspected. Note that multiple separate tumors, parenchymal or mediastinal, may exist in the same patient. We treated each separate tumor as a separate pattern in our atlas.

After obtaining the predicted residual tumor distributions following the shrinkage patterns from all patients in the atlas, we superimposed these individual predictions, counted the number of overlaps per voxel, and normalized each voxel against the maximal number of overlapping incidences (number of patterns in the atlas), and formed a predictive probability map of residual tumor.

2.2.2 Consideration of tumor center of mass shift

An important complicating factor is that clinical visual observations at our institution showed that tumors attached to mediastinum or chest wall tend to shrink toward the fixed anatomies, whereas purely parenchymal tumors tend to shrink towards their center. Since the prediction was generated as an overlap among predictions from all patterns in the atlas, the high probability region was in general positioned in the middle of the tumor, and thus would introduce errors when dealing with mediastinal tumors. Therefore a correcting step was introduced to correct the probability map for location and tissue density in the neighborhood around the tumor, in order to accommodate both mediastinum and parenchymal tumors. To do this, we first expanded GTV_ori of the incoming patient with a three dimensional 2cm margin, and formed a 2cm thick shell around the tumor. We calculated the center of mass (COM) of the shell using the voxel CT numbers, and formed a vector (v_r) between the geometric center of the shell and its COM. For a parenchymal tumor surrounded by homogeneous low density lung tissue, COM and the geometric center almost coincide. In contrast, v_r shows a significant shift for tumors attached to a mass of tissue such as chest wall or mediastinum. Next, we formed a vector (v_t) between the geometric center of GTV_ori and GTV_resd for each atlas patient. Subsequently we correlated the two vectors for all patients in the atlas, and formed a linear empirical equation to estimate the shift of the tumor center, $\stackrel{\sim }{v_t}$, with respect to v_r:

$$\stackrel{\sim }{v_t}=a{v}_r+v_0$$ Eq. 5

where a=[0.13 0.28 0.14], and v₀=[0.67 0.96 0.34] are the resulting linear fitting coefficients, and r² of the fit is 0.62. We rounded the shift along each direction to the nearest mm since the image resolution is 1 mm, and used the shift to translate the center of the predictive probability map inside GTV_ori to obtain a revised probability map. The absolute shift along each direction ranged from 0 mm to 2 mm with a median of 1 mm for parenchymal tumors, and ranged from 3 mm to 8 mm with a median of 6 mm for a tumor attached to the mediastinum.

2.2.3 A binary prediction

Finally we applied a threshold to convert the probability map into a binary prediction map. This threshold was optimized across the patients in the atlas using a leave-one-out scheme to maximize the accuracy of the predictive model, defined as the ratio of the summed volume of true positive and true negative voxels to the total volume.

2.3 Retrospective treatment planning

The resultant binary prediction of residual tumor, GTV_pred, was converted to a set of contours using the helper functions provided in Computational Environment for Radiotherapy Research (CERR, Deasy 2003). In the case of multiple isolated islands on the binary prediction, CERR treated each island as a separate segment, and exported all islands as a single RT structure to a file in the format of digital imaging and communications in medicine (DICOM). Subsequently the DICOM file was imported into Eclipse for treatment planning. Uncertainties of respiratory motion and setup caused inaccuracy in matching the planning CT and last-week-CBCT, and further affecting the spatial accuracy of the prediction model. The impact was estimated at 2 mm in our previous study (Zhang 2014). To account for all uncertainties in lung radiotherapy we added 1 cm margin to expand both GTV_ori and GTV_pred and form planning target volumes PTV_ori and PTV_pred for the purpose of plan optimization. We employed a selective dose escalation strategy, PTP, to maximize the therapeutic ratio given such a personalized tumor resistance map. We escalated the radiation dose to 95% of the predicted residual tumor voxels (PTV_pred) as high as possible using a simultaneous integrated boost while maintaining the dose prescribed in the original clinical plan (ranging from 2Gy x 30 fractions to 2Gy x 35 fractions) to the disappearing tumor (PTV_dsp=PTV_ori-PTV_pred), and respecting our in-house OAR dosimetric constraints including the mean normal lung (normal lung excluding GTV_orig) dose less than 20 Gy, and a maximal dose to the spinal cord below 50 Gy. This robust scheme was effective for dose escalation because it safely deposited dose to the most resistant portion of the tumor without underdosing the original tumor or overdosing OARs. In addition, we produced an idealized PTP plan that escalated dose to only the true residual tumor, thereby simulating the scenario of a perfect prediction, and investigated the potential upper limit of PTP. All PTP plans were optimized inside Eclipse and consisted of seven IMRT beams with 6MV photons. Applying the thorax imaging protocol, the weekly CBCT dose has been reported as at the level of 1–2 cGy at the center portion of the phantom for the Varian on-board-imager used in our clinic (Gardner 2014). The dose from the 6–7 weekly CBCT is less than 1% compared to the 60–70Gy prescription dose, thus not included in the optimization process.

2.4 Model evaluation

We first evaluated the accuracy and uncertainty of the predictive model in the spatial domain. We correlated the spatial distribution of the predicted target (GTV_pred) with the true residual tumor (GTV_resd) contoured on the last weekly CBCT scan, and calculated the Dice coefficient and mean surface distance between the two to evaluate the spatial uncertainty of the model. We also calculated the sensitivity, specificity, and accuracy of the model, and constructed the receiver operating characteristic (ROC) curve by varying the binary-map threshold of the model. In addition, we compared the ROC curves of the model with and without the GTV_pred positional correction to demonstrate the advantage of anatomical correction. Furthermore we evaluated the prediction uncertainty in respect to using different assemblies of patients in the atlas. Given a total number of 12 patients included in the study, under the leave-one-out rule, we formed 10 assemblies, each containing 10 patients, to construct the predictive probability map for a particular patient. We calculated the standard deviations of the accuracy, Dice coefficient, and average surface distance among the 10 predictions from the 10 assemblies, and used them as the quantifications of prediction uncertainties.

To evaluate the performance of the predictive model as well as the PTP approach in the dose domain, we tabulated dosimetric characteristics of the PTP plans including the PTV_resd D95 (dose to 95% of the actual residual PTV), PTV_dsp D95, PTV_pred D95, PTV_resd Dmean, PTV_dsp Dmean, PTV_pred Dmean, lung mean dose, and spinal cord maximal dose. We compared the characteristics of PTP with the counterparts of the standard clinical plan in which a uniform dose was delivered to the entire tumor in 2Gy/fx. We also calculated the margin on PTV_pred necessary to cover 95% of PTV_resd in the PTP plans. This margin is a measure of the dosimetric uncertainty in the PTV_resd caused by the shortcomings of the prediction model.

III. RESULTS

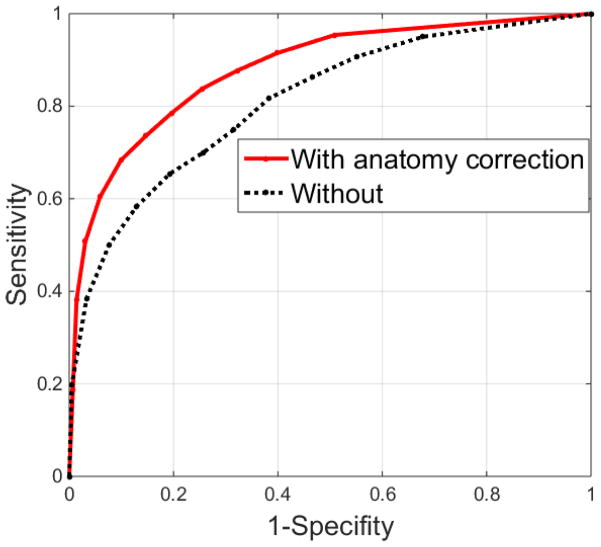
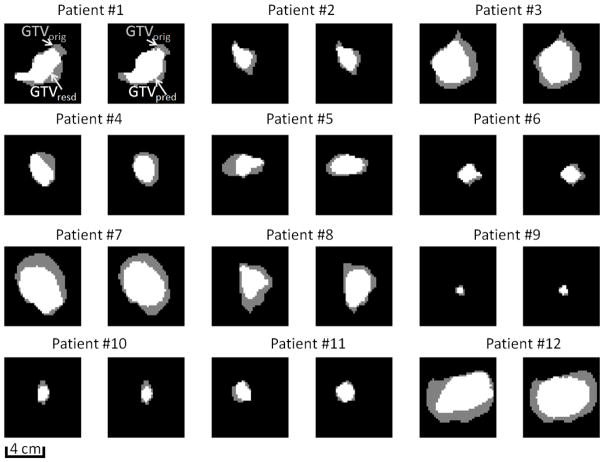
The error in predicting the tumor shrinkage rate averaged 6%±13% (mean ± standard deviation) compared to the true shrinkage rate. Figure 2 shows the ROC curve constructed based on different binary-map thresholds used in prediction. At each threshold, sensitivity and specificity were computed on a voxel-by-voxel basis according to the actual physician-drawn residual tumor. The area under of the ROC curve (AUC) with estimated GTV_pred shift was 0.87. A threshold of 0.45 (close to simple majority) maximized the accuracy of the prediction model across the atlas, and therefore was used for individual predictions. Under this condition, the sensitivity, specificity, and accuracy of the prediction model were 0.73, 0.76, and 0.74, respectively. When the prediction was applied to each individual patient, the resultant accuracy was independent of the original tumor volume (p value=0.36), or actual tumor shrinkage rate (p value=0.52), indicating that the predictive model is independent and robust with respect to a broad spectrum of initial and final tumor sizes. The Dice coefficient and mean surface distance between predicted and actual residual tumor averaged 0.75±0.04, and 1.6±0.8mm, respectively. If the correction based on tumor neighborhood was omitted in the prediction process, the loss of the sensitivity, specificity, and accuracy was 0.02, 0.05, and 0.03, respectively, and the ROC curve suffered a reduction of 0.06 in AUC, which demonstrated the advantage of including such an anatomical correction step. Figure 3 shows a specific example of transversal, sagittal, and frontal views of a neighborhood-corrected prediction (orange) situated within the original tumor (yellow, transferred from the planning CT via registration), and the actual residual tumor (red) are shown on the last weekly CBCT. Note that the mediastinum, to which the original tumor is attached laterally, triggered a correction in which the original prediction (green) shifted 8mm medially and formed a more accurate prediction (orange). Figure 4 shows the representative tumor shrinkage patterns of the twelve patients in the atlas through the transverse cut from the center of gravity of GTV_orig. For each patient, the spatial distribution of GTV_resd inside GTV_orig, and GTV_preds inside GTV_orig are shown in the first and second cell, respectively. The standard deviation of the accuracy, Dice coefficient, and average surface distance in the predictions resulting from using different assemblies in the atlas is 0.006, 0.005, and 1.0 mm, respectively, which can be used to assess the prediction uncertainties due to the composite of the atlas.

Figure 2.

ROC curve of the prediction model with or without an anatomy correction.

Figure 3.

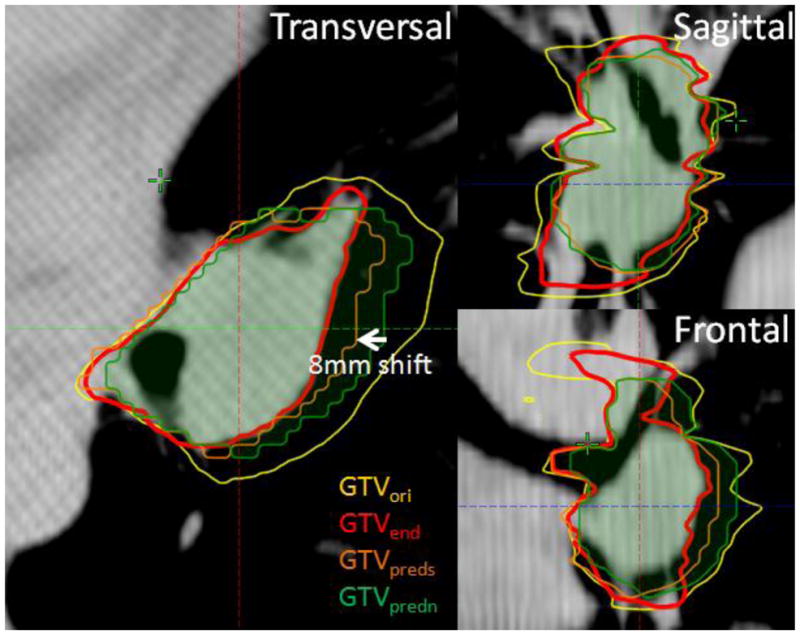
An example of predicted residual tumor (with corrected shift, GTV_preds, orange) with respect to the original tumor (yellow), actual residual tumor (red), and prediction without corrected shift (green) shown on the latest weekly CBCT.

Figure 4.

Representative tumor shrinkage patterns of the twelve patients in the atlas through the transverse cut from the center of gravity of GTV_orig. For each patient, the spatial distribution of GTV_resd inside GTV_orig, and GTV_pred inside GTV_orig are shown in the first and second cell, respectively. Note that for patient #9, the parenchymal GTV, not the patient’s bigger mediastinal GTV, is selected to show the shrinkage pattern of a small tumor.

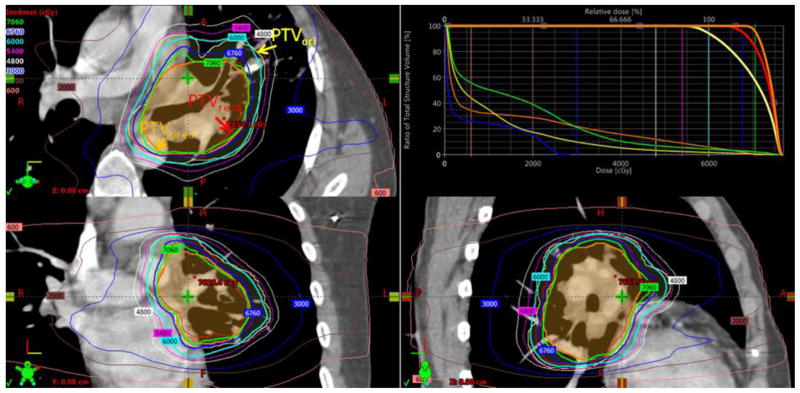
Compared to the clinical plans in which a uniform dose to PTV_ori was delivered, the PTP plans were able to maintain the same OAR (cord, lung, heart, and esophagus) dosimetric characteristics, but yielded an increased PTV_resd D95 and PTV_resd Dmean to the actual residual tumor of 6.5±1.8Gy and 10.4±2.9Gy, respectively. The relatively smaller volume of the predicted resistant PTV compared to the original PTV (average PTV_pred/PTV_ori ratio was 0.51) enabled alignment of hotspots in the dose distribution with the resistant subvolume of the tumor, while keeping a similar toxicity level. An example of a PTP plan is illustrated in Figure 5, where the 60Gy and 70.6Gy isodose lines were optimized to cover 95% of PTV_ori (yellow) and PTP_pred (orange), respectively. Since PTV_pred did not exactly predict PTV_resd (red), 95% of the latter volume was enclosed by a lower (67.6Gy) isodose line. The average distance between the isodose surface covering PTV_pred and that of PTV_resd, d_iso, is 3mm. Since the volume of PTV_resd was similar to PTV_pred (154 cc vs 128cc) in this case, targeting PTV_resd in the PTP plan would result in a PTV_resd D95 of 70.5Gy, indicating that PTP could potentially escalate dose an additional 2.9Gy if perfect prediction were achieved. The degradation between the dose optimized to escalate dose to PTV_pred and the actual dose to PTV_resd reflected the propagation of errors from the prediction model to the dosimetric domain. Across the 12 patients in the retrospective planning study, the degradations were 2.9±1.6Gy and 0.9±0.5Gy, for PTVD95 and PTVDmean, respectively; d_iso measured 2.7±1.0mm. Note that d_iso was slightly larger than the mean surface distance between predicted and actual tumor, indicating the inaccuracy of the prediction model was magnified from the spatial to the dosimetric domain due to the process of dose optimization. Nevertheless, knowing the limitations of the prediction within both the spatial and dosimetric domain can help us set a realistic goal and margin in PTP planning, and eventually achieve an optimal therapeutic ratio.

Figure 5.

A PTP plan was designed to deliver 60Gy to the original PTV_ori (yellow), and 70.6Gy to predicted PTV_pred (orange). As a result, the actual residual PTV_resd (red) received a dose escalation of 67.6Gy compared to the standard 60Gy uniform dosing scheme.

IV. DISCUSSION

The main focus of this paper is to build a diversified geometric atlas that can be used to accurately predict tumor shrinkage at the end of a course of conventional radiotherapy. In our previous attempt we simply modeled both original and residual tumor as ellipsoids, and calculated the affine transformation matrix between the apexes of the two ellipsoids as the prior for pattern prediction (Zhang 2014). As a result, detailed geometric features inside the ellipsoids such as the concave shape were lost in the modeling procedure. Our current approach relied on principal component analysis of the original and residual tumors to predict the shrinkage pattern, thereby becoming less sensitive to the contouring noises, and preserving the complicated shape of the shrinkage pattern compared to our previous approach. Furthermore the positional correction of the residual prediction based on an analysis of the tumor neighborhood also broadened the scope of the predictive model and accommodated both mediastinal and parenchymal tumors. Finally, expansion of the atlas by increasing the patient sample size allowed a determination of an optimal threshold to use in the prediction procedure, and maximized the accuracy of the prediction. Furthermore, the revised atlas yielded an average Dice coefficient of 0.75, compared to 0.68 in the previous approach. By means of the new atlas, we were able to show robust escalation of dose to the residual tumors while maintaining the standard prescription dose inside the original tumor for all twelve patients, thus potentially achieving a higher tumor control probability compared to the standard 60Gy approach.

By constraining the PTP plans to the same level of toxicity as the standard uniform dose plans, the dose escalation ability of PTP is limited by the ratio of predicted residual (target of escalation) and original target volumes. The larger the ratio becomes, the lower the dose can be escalated without inducing unnecessary complications. An ultra-high sensitivity, that correctly identify most of the actual residual tumor but unavoidably associates with a low specificity in a predictive model, would not be able to differentiate the escalating target from the rest of the tumor, and would lose its ability to guide a meaningful dose escalation. Thus accuracy, and not sensitivity, was chosen as the dosimetrically relevant objective when optimizing the parameters of the predictive model.

Many researchers have been engaged in predicting the failure patterns of radiotherapy based on patients’ demographic parameters, tumor characteristics, imaging features, treatment fraction schemes, and pretreatment medications (Tan 2012, Zhang 2014, Kohutek, 2015, Zhou 2016, Toma-Dasu, 2016). The prediction of potential failure of response can be utilized to stratify patients into different radiotherapy schemes, such as dose escalation vs standard 60Gy treatment, during the treatment planning phase, in order to maximize tumor control and avoid radiation-related toxicities on a population basis. However, a false prediction of response would exclude a patient from necessary dose escalation, and potentially result in a loss of local tumor control. In contrast, the PTP approach does not stratify patients, but rather always assumes some degree of shrinkage, quantified according to the atlas, and integrates a meaningful dose escalation into the initial treatment plan. Note that because all OAR tolerance limits are respected, patients who respond well to radiation (with greater shrinkage than predicted) would not be harmed by PTP and might even benefit by increased dose to microscopic residual disease. Therefore PTP is more sensitive and aggressive than patient stratification in dealing with the presence of resistant tumor.

We are making a continuous effort to systemically recruit patients into this longitudinal imaging study, and accumulate more shrinkage patterns. As the number of patients in the atlas increases, we expect the prediction will have more power, leading to improved prediction accuracy, increased Dice coefficient, and, more relevant to radiotherapy, better agreement between the radiation dose to the predicted and actual residual tumor. However, we do expect this improvement to eventually reach a plateau, which will complete the recruitment. When there are more patients in the atlas, in a followup study we may be able to further divide the atlas into subcategories with respect to parenchymal and mediastinal tumors. The prediction model may also be improved by additional tools such as the incorporation of texture analysis of the tumor.

V. Conclusion

A geometric atlas utilizing our proposed algorithm can provide useful information on the distribution of resistant NSCLC tumor that remain following radiotherapy and effectively guide a dose escalation to the tumor without compromising the OAR complications. The atlas can be further refined by using more patient data sets.

Table 1.

Tumor (corresponding to Figure 4) dosimetric characteristics resulting from predictive treatment planning. For mediastinal tumors, the D95 and mean dose difference between PTV_pred and PTV_resd averaged 3.4 Gy and 1.1 Gy, slightly higher compared to that of 2.9 Gy and 0.9 Gy for parenchymal tumors.

	PTVori D95 Gy	PTVpred D95 Gy	PTVresd D95 Gy	PTVpred Dmean Gy	PTVresd Dmean Gy
mediastinal tumors
1	59.5	70.6	67.7	73.9	73.1
2	70.9	79.5	76.6	84.2	83.0
3	70.7	79.3	76.1	81.4	80.4
4	60.0	70.3	65.5	73.0	71.7
5	61.0	69.6	66.4	73.4	72.2
6	61.5	70.4	66.7	73.9	72.9
parenchymal tumors
7	70.0	76.2	74.4	78.5	78.0
8	60.3	67.8	67.8	71.8	71.8
9	57.0	64.3	63.3	65.6	65.4
10	70.3	87.5	81.6	91.4	89.7
11	61.5	70.5	68.9	74.4	73.8
12	70.0	78.5	75.5	82.5	81.4