Abstract
One of the long standing debates in actinide chemistry is the level of localization and participation of the actinide 5f valence orbitals in covalent bonds across the actinide series. Here we illuminate the role of the 5f valence orbitals of uranium, neptunium and plutonium in chemical bonding using advanced spectroscopies: actinide M4,5 HR-XANES and 3d4f RIXS. Results reveal that the 5f orbitals are active in the chemical bonding for uranium and neptunium, shown by significant variations in the level of their localization evidenced in the spectra. In contrast, the 5f orbitals of plutonium appear localized and surprisingly insensitive to different bonding environments. We envisage that this report of using relative energy differences between the 5fδ/ϕ and 5fπ*/5fσ* orbitals as a qualitative measure of overlap-driven actinyl bond covalency will spark activity, and extend to numerous applications of RIXS and HR-XANES to gain new insights into the electronic structures of the actinide elements.
Understanding the chemistry of heavy radioactive elements is crucial to harnessing them for fuel and medicine. Here, the authors combine advanced X-ray spectroscopy and modelling to the study the chemical bonding of the 5f valence orbitals of uranium, neptunium and plutonium.
One of the long lasting controversial debates in actinide chemistry is the level of localization and participation of the actinide (An) 5f valence orbitals in covalent bonds across the actinide series1,2. The 5f orbitals of the lighter An elements can be very active up to Am; thereafter, they strongly contract and are considered as core-orbitals similar to their 4f counterparts, the lanthanides (Ln). Advanced spectroscopy methods can provide new insights into the electronic structure of the An elements and thereby help resolve this controversy, as well as promote development and optimization of theoretical approaches to predicting their chemical and physical properties. Progress in modern theory now permits precise electronic structure calculations of large An systems in an excited state relevant to advanced spectroscopy, where not only valence but also core-electrons are removed from the atom2,3,4. Marriage of advanced spectroscopy and theoretical modelling delivers mechanistic understanding of the electronic structure of An radioelements crucial to a number of applications. Those include the improved understanding of An interaction with the constituents of the geo and ecosphere on a molecular scale being highly relevant for the reliable assessment of their behaviour in the environment5,6,7,8,9. Understanding the electronic structure of An bondings is also of crucial importance for the design and optimization of selective and stable ligands for highly efficient separation processes for closed nuclear fuel cycle concepts and the potential application of actinides in nuclear medicine10,11,12.
We are applying An M4,5 absorption edge high-energy resolution XANES (HR-XANES; XANES=X-ray absorption near edge structure) and 3d4f resonant inelastic X-ray scattering (3d4f RIXS) as bulk sensitive techniques, which can be applied in-situ and under extreme conditions (for example, high/low temperatures or pressures) for investigations of matter in any state13,14,15,16,17,18,19. Particularly 3d4f RIXS is a novel experimental tool for comparison of the level of localization of unoccupied 5f orbitals across the An series and their participation in chemical bonding. In this report, we investigate uranium (U)/neptunium (Np)/plutonium (Pu) in different oxidation states in several materials in solid/liquid state. One focus is on U, Np and Pu in their hexavalent oxidation states U(VI), Np(VI) and Pu(VI) in aqueous 1 M perchloric acid (HClO4), where they form strong covalent trans dioxo linear bonds, also often referred to as actinyl (AnO2 2+) bonding, with short axial oxygen, An-Oax, bonds. Five loosely bound equatorial water (H2O) molecules are located in the equatorial plane of the actinyl cation. Under oxidizing and aerobic conditions AnO2 2+ can be quite stable where UO2 2+ clearly has the highest stability and NpO2 2+ might only be of relevance under hyperalkaline conditions. UO2 2+ is frequently found in the environment as a constituent of mineral phases but also as a highly mobile aqueous species or in colloidal form7,8,20.
Experimental results are compared to and interpreted using theoretically calculated data. Pu(VI) M5 absorption edge HR-XANES is calculated with multiplet calculations using the DIRAC programme system21 and with the finite difference method (FDMNES code22). The object of these calculations is to verify if the An M4,5 absorption edge HR-XANES spectra are sensitive to the ligand field and if they closely describe the ground state 5f partial density of states (5f-DOS) of the An.
As well as the orbital model, other one-electron effects, in particular spin–orbit splittings, and many-body effects, in particular multiplet splittings, contribute in a major way to the XANES spectra. Furthermore, the relative importance of the ligand-field splittings and the spin–orbit splittings may need to be considered. These other effects and their contributions to the XANES spectra are discussed.
Here we provide insight into one of the most controversial questions in actinide chemistry: What is the role of the 5f valence orbitals in the covalency of the chemical bonding of the actinide elements? HR-XANES and RIXS at the M4,5 absorption edges of the early actinide elements (U, Np, Pu) probe the 5f unoccupied density of states of the actinides with superior energy resolution. These advanced spectroscopy tools allow to distinguish between increase of covalency due to building up of electronic charge between the atoms, classical overlap of orbitals, and due to better energy match between metal and ligand valence orbitals as illustrated for U(VI)O2 2+, Np(VI)O2 2+ and Pu(VI)O2 2+. It is demonstrated that the 5f orbitals are more localized for Pu compared with U and Np, and their energies are not influenced by changes in bonding environments. A broad set of data obtained from different actinide compounds are compared—including spectra for aqueous and solid state species as well as highly radioactive materials like spent nuclear fuel. Spectroscopic results are corroborated by state of the art quantum-chemical calculations.
Results
Molecular orbital scheme of actinyl
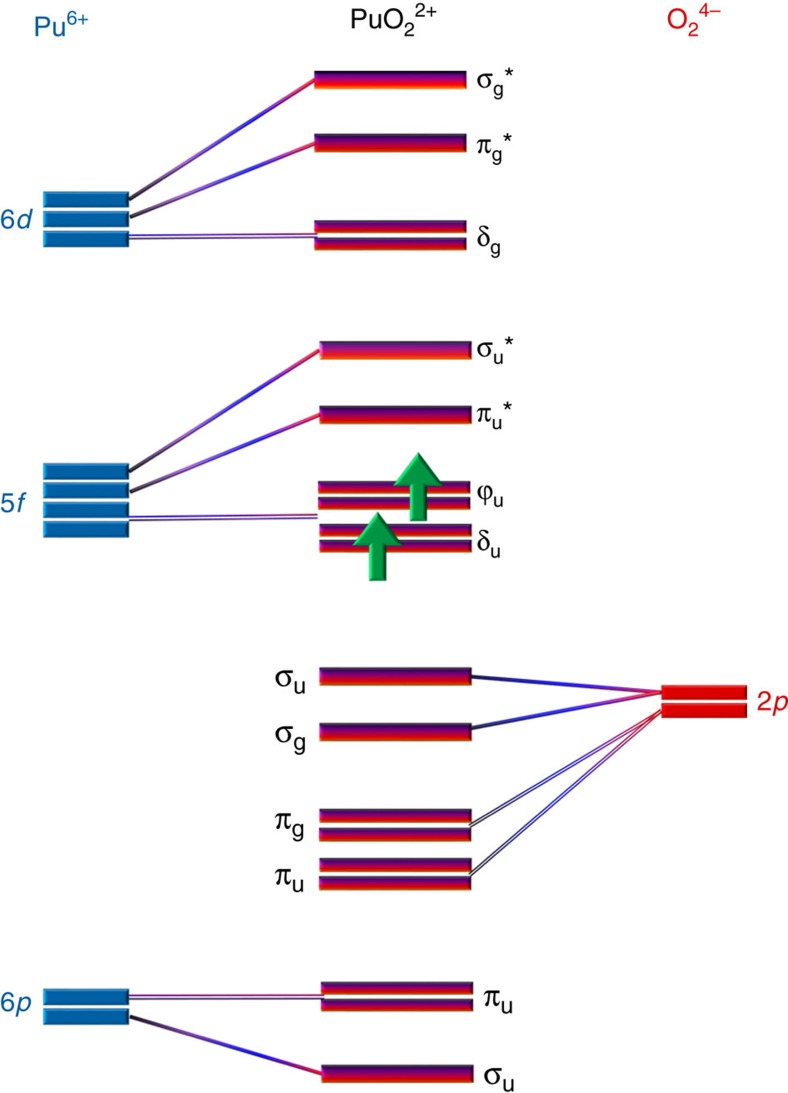
The An oxidation states and their electronic structures are interconnected2,3,4,23; a qualitative molecular orbital scheme of PuO2 2+ is depicted in Fig. 1 (refs 23, 24). Note that in Fig. 1 the spin–orbit splitting of the 5f levels is not shown, An estimate of these splittings can be obtained from the data for UO2 in Fig. 1 of ref. 25, where the 5fπ3/2 to 5fπ1/2 splitting is shown to be ∼1.2 eV. This splitting is significant for the broadening of features in the HR-XANES as discussed later. The linear structure of the AnO2 2+ molecule (Supplementary Fig. 1) leads to the An valence orbitals being most usefully described in terms of their σ, π, δ and ϕ character with respect to rotation about the axial An-Oax z axis (D∞h point group symmetry). The σ and π are anti-bonding with the O 2p orbitals and are denoted σ* and π*, while the δ and ϕ are non-bonding for a gas phase molecule. The δ and ϕ might become π* and, σ* and π* with respect to weakly bound equatorial ligands. For simplicity, we use only the assignments σ, π, δ and ϕ, for the D∞h symmetry of linear AnO2 2+. An M4,5 absorption edge HR-XANES and 3d4f RIXS directly measure the relative energies of the unoccupied 5fδ/ϕ, 5fπ* and 5fσ* orbitals of the An in the same spectrum, thus avoiding experimental artifacts introducing uncertainties due to different sample preparation protocols or variable measurement conditions17. Especially, the 5fσ* orbital can be evaluated with high precision. The relative energies of these lowest lying unoccupied orbitals of the An with mainly 5f-based character can also be measured with optical (5fδ, 5fϕ, 5fπ*) and X-ray absorption/emission spectroscopy (5fπ*, 5fσ*), yielding excited state data that deviate <0.5 eV compared with the theoretically calculated ground state values3. However, these two methods have limitations, including low temperature requirement for precise optical spectroscopy measurements and ultra-high vacuum for, for example, O K absorption edge XANES3.
Figure 1. Molecular orbital scheme.
A qualitative molecular orbital scheme of PuO2 2+ adapted from (refs 23, 24). Only frontier electrons are indicated.
Actinide 3d4f RIXS maps
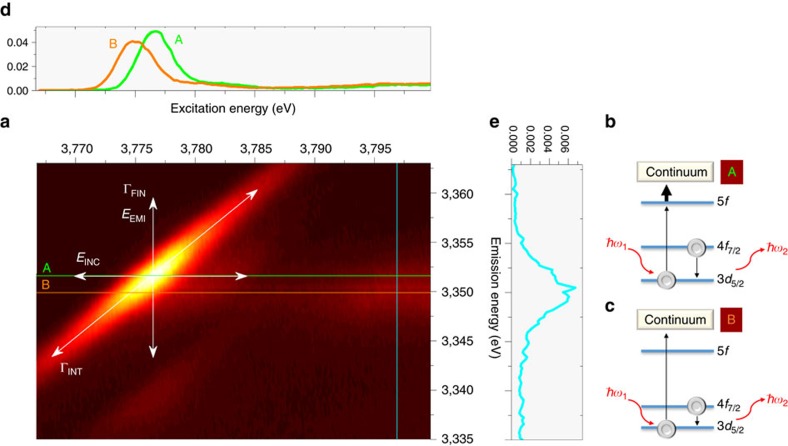
A RIXS map depicts a 2D representation of X-ray fluorescence emission measured as a function of the excitation X-ray energy scanned across an absorption edge (Fig. 2a)13,26,27,28,29. If the excited electron (for example, 3d5/2 of Pu, 3d5/2→5f Pu M5 absorption edge) and the electron filling the created core-hole (for example, 4f7/2 of Pu, 4f7/2→3d5/2 Pu Mα emission) are close to the nucleus, that is, core-electrons, the map is denoted as a 3d4f core-to-core RIXS map (3d4f CC-RIXS). For simplicity, we will refer to the 3d4f CC-RIXS maps recorded at the U M4 (3d3/2→5f excitation, 4f5/2→3d3/2 U Mβ emission) and Pu/Np M5 absorption edges as RIXS. The RIXS map of PuO2 and a simplified one-electron scheme describing the emission process are shown in Fig. 2. The 3d5/2 electrons are mainly excited to the unoccupied states with substantial 5f character (3d5/2→5f); the orbital angular momentum quantum number l changes ±1, according to the dipole selection rule, Δl=±1.
Figure 2. RIXS map of PuO2 and schematics of the emission process.
(a) 3d4f RIXS map of PuO2. (b) One-electron scheme of the emission process for excitation energies of about 3,776.5 eV and (c) above 3,785 eV. The intense resonant structures at about 3,351.6 eV emission energy in the 3d4f RIXS map correspond to 4f7/2→3d5/2 Pu Mα emission, whereas the peaks with weaker intensity at about 3,340 eV emission energy describe 4f5/2→3d5/2 Pu Mα emission. The energy positions of the most intense resonance (3,351.6 eV) and the normal emission line (3,350 eV) for the 3d5/2→5f Pu M5 absorption edge and 4f7/2→3d5/2 Pu Mα emission, are marked with lines A and B, respectively; (d) the HR-XANES extracted for lines A and B; (e) the emission line measured at 3,797 eV excitation energy. The experimental broadening depending on the specifications of the beamline (EINC), and the spectrometer (EEMI), as well as the core-hole lifetime broadening effects in the intermediate (ΓEMI) 3d95fN+1 (N=number of electrons in the An 3d105fN ground state) and final (ΓFIN) 4f135fN+1 states, are indicated.
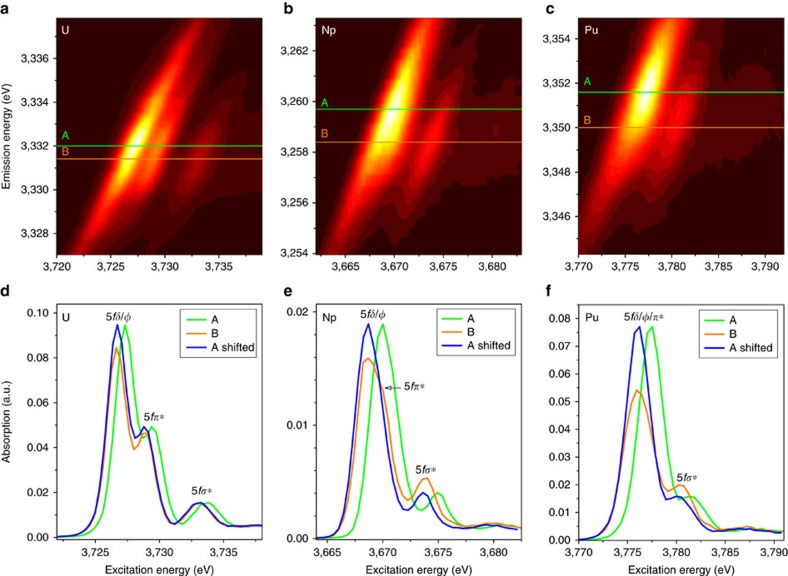
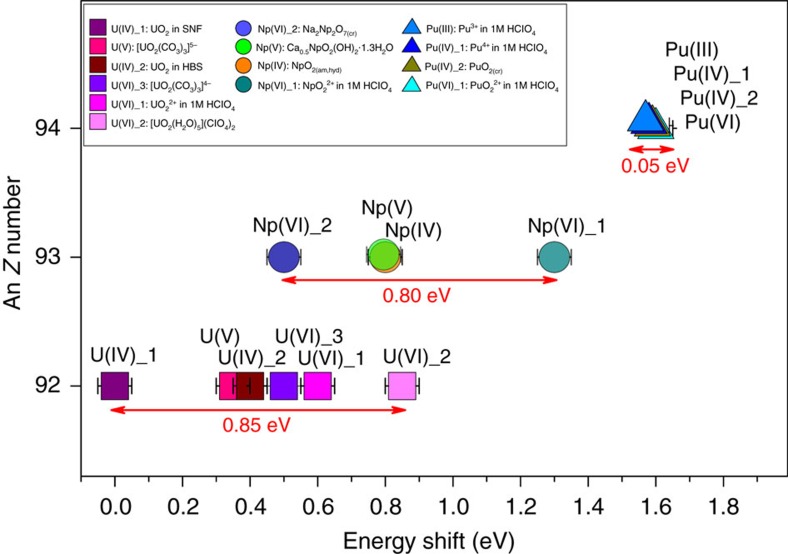
The RIXS map can be divided into a resonant emission and a non-resonant (normal) emission, where the electron is excited to bound unoccupied states (<3,785 eV excitation energy) and to the continuum (>3,785 eV excitation energy), respectively, both with subsequent 4f7/2→3d5/2 Pu Mα emission. Simplified schemes of these two processes are depicted in Fig. 2b,c. The RIXS maps of UO2 2+, NpO2 2+ and PuO2 2+ are shown in Fig. 3a–c. Typically when recording a HR-XANES spectrum, the analyzer crystals of an X-ray emission spectrometer are positioned at the energy position of the maximum of the normal emission line and the energy of the incident beam is scanned across the absorption edge27,28,30. Then the HR-XANES spectrum corresponds to a cross section across the RIXS map marked with line B in Figs 2 and 3. The broadening of the spectral peaks depends on experimental and core-hole broadening effects. The beamline (EINC) and the spectrometer (EEMI) experimental broadening contribute along the x and y axis of the RIXS map, respectively (Fig. 2). The smaller core-hole lifetime broadening31,32 in the final state (ΓFIN) mainly contributes to the HR-XANES spectrum (Fig. 2; Supplementary Table 1)28,33; in our case, ΓFIN equals 4f135fN+1, where N is the number of electrons in the ground state 3d105fN of the An (0, 1 and 2 for UO2 2+, NpO2 2+ and PuO2 2+). The HR-XANES spectrum can exhibit different features compared with the conventional XANES spectrum when the core-hole potential in the intermediate (3d95fN+1) state is significantly different than that for the final state (4f135fN+1)34,35,36,37,38. This effect is well visible in Figs 2a and 3a–c, where line B marking the normal emission maximum is shifted with respect to the most intense resonant peak, line A. The HR-XANES spectra extracted at emission energy marked with line A are also shown in Figs 2d and 3d–f. Three peaks at about 3,726.7, 3,728.8 and 3,732.9 eV are resolved in the UO2 2+ RIXS map, which are also visible in the HR-XANES spectra (Fig. 3d). We have previously been able to assign these to transitions of 3d electrons to 5fδ/ϕ, 5fπ* and 5fσ* orbitals, respectively17. The first two peaks 5fδ/ϕ and 5fπ* are not resolved in the NpO2 2+ and PuO2 2+ RIXS maps/HR-XANES, but a peak shoulder (indicated with an arrow and 5fπ*) and asymmetry are evident for NpO2 2+ (Fig. 3d,e). To better compare spectra, we removed the energy shift between A and B spectra so they appear overlaid. In the overlaid spectra, features have similar energy positions but the main peak intensities for the A spectra are much higher than the B (normal emission) spectra. Note that the shoulder observed on the main peak in the NpO2 2+ B spectrum is not visible in the A spectrum. When the entire emission intensity is integrated symmetrically with respect to the normal emission line (line B), the resulting XANES spectrum corresponds to a conventional fluorescence mode measurement (Supplementary Fig. 2b). The conventional spectrum is dominated by one broad absorption feature, without a shoulder, but with a maximum shifted to higher energies than the B HR-XANES spectrum due to the contribution of the lower energy intense resonance marked with line A (Fig. 3a–c). The energy difference or shift between lines A and B is 0.6, 1.3 and 1.6 eV for UO2 2+, NpO2 2+ and PuO2 2+ in 1 M HClO4, respectively. These values are compared with those measured for other materials in Fig. 4. The size of this shift varies between 0–0.85 eV (U) and 0.5–1.3 eV (Np) for the various materials, whereas it remains the same for Pu(III)/Pu(IV)/PuO22+ in 1 M HClO4 and PuO2. Emission energy shift of the resonant peaks with respect to the normal emission was previously reported for 3d36 and 4f34,35,37,38 elements and was attributed to the strong interaction between the excited electron in the lowest unoccupied bound electronic states and the created core-hole, which differs from the ionized case, that is, excitation into continuum. The energy shift between lines A and B, therefore, probes the localization of those lowest unoccupied 5f states on the absorbing atom. Schematics of the effect are shown in Fig. 2b,c. The experimentally observed increase in energy shift going from U to Pu in our actinyl system shows that the 5f orbitals undergo stronger localization in this order, that is, from UO2 2+ to NpO2 2+ than from NpO2 2+ to PuO2 2+. Note that the shift can be slightly different for the U M5 absorption edge RIXS due to associated variations in the core–electron interaction. Observed invariance of the Pu energy shift indicates that the localization of the Pu 5f orbitals is not influenced by changes in oxidation state and appears to be the same for molecular and solid state species. This is not true for U and Np, as significant variations are observed for these elements. An important observation is also that the main resonance peak (line A) is shifted to higher energies with respect to the normal emission (line B), a trend opposite to pre-edge peaks in K edge RIXS measurements for transition metals36. This effect might be related to the relativistic nature of the core-electrons of the An elements, yielding strong contraction of the electronic orbitals for the ionized atoms.
Figure 3. RIXS maps and extracted HR-XANES spectra.
(a–c) 3d4f RIXS maps (3d3/2→5f U M4 absorption edge, 4f5/2→3d3/2 U Mβ emission; 3d5/2→5f Np/Pu M5 absorption edge, 4f7/2→3d5/2 Np/Pu Mα emission) and (d,e) U M4 and Np/Pu M5 absorption edge HR-XANES spectra extracted along lines A and B for (d) UO2 2+, (e) NpO2 2+ and (f) PuO2 2+.
Figure 4. Energy shifts obtained from RIXS maps.
Energy shift of the main resonance peak (line A in Figs 2 and 3) compared to the energy position of the normal emission line (line B in Figs 2 and 3) for different U, Np and Pu materials measured at the U M4 (filled squares) and Np/Pu M5 absorption edge (Np: filled circles and Pu: triangle). Spent nuclear fuel and high-burn up structure are abbreviated with SNF and HBS, respectively. Information about the samples in given in SI (cf. Supplementary Table 1; Supplementary Note 1).
Actinide M4,5 absorption edge HR-XANES
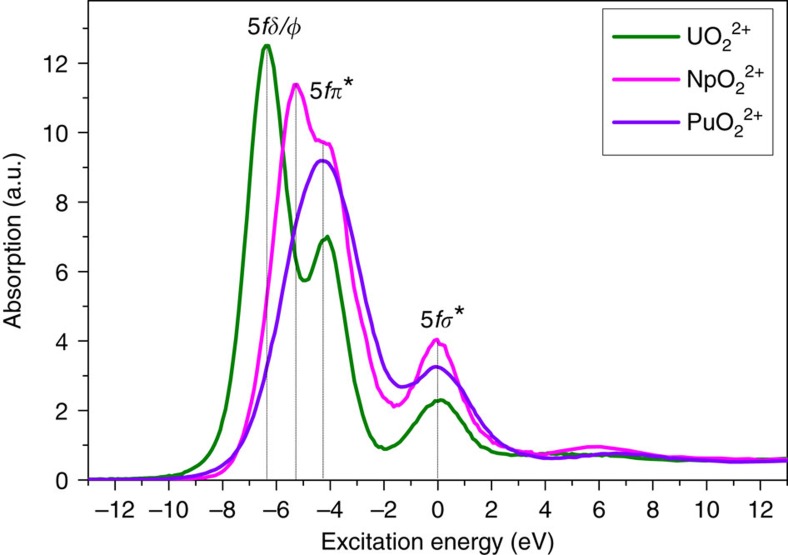
In Fig. 5 the HR-XANES spectra of UO2 2+, NpO2 2+ and PuO2 2+ are aligned so that the 5fσ* peak is at 0 eV. Comparison of the HR-XANES reveals differences in intensity and energy position of resonant features. The main 5fδ/ϕ peak intensity changes drastically going from U to Pu, since the non-bonding orbitals are free for U but have 5fδ1 and 5fδ15fϕ1 configurations for Np and Pu, respectively. In addition, changes in the intensity can be linked to the increasing energy shift between the most intense emission resonance (line A) and the normal emission (line B). For many of the An materials the first 5fδ/ϕ peak in the HR-XANES is associated with a cross section of the tail of the emission spectrum and not the maximum of the resonance peak of the RIXS spectra (cf. B spectra in Figs 2 and 3). The multiplet splittings with highest importance for Pu(VI) also introduce broadening, yielding decreased peak heights (cf. calculations of Pu(VI) M5 HR-XANES spectra below). As the An(VI) samples are in aqueous solutions and their concentrations are the same, we rule out self-absorption effects as playing any substantial role in damping of intensities of spectral features.
Figure 5. Experimental HR-XANES spectra.
U M4 and Np/Pu M5 absorption edge HR-XANES spectra of UO2 2+, NpO2 2+ and PuO2 2+.
The energy difference between features hints at differences between bonding covalencies. The seven empty or partially occupied 5f orbitals of the AnO2 2+ cation (Fig. 1) are split by spin–orbit coupling and the ligand field of the axial and equatorial ligands (ax. field and eq. field). When there is more than one electron in the 5f shell, Coulomb repulsions between the electrons become important and affect the covalent mixing39. The spin–orbit splitting of the 5f electrons is ∼1 eV while their ligand-field splitting can be as large as 7 eV for actinyls. Matsika et al.40 pointed out that the influence of these effects can be ordered as follows: ax. field (5fσ*, 5fπ*)>spin–orbit>ax. field (5fδ, 5fϕ)+eq. field. The ax. field exerts the strongest effect caused by the strong covalent nature of the An-Oax bond. As a result, the 5fσ* and 5fπ* states are shifted with respect to the 5fδ and the 5fϕ orbitals (5fδ≈5fϕ<5fπ*<<5fσ*). The shift is stronger for the 5fσ* than the 5fπ* states due to interaction of the filled An-O συ orbital and the semi-core 6pz orbital with the same συ symmetry (‘pushing from below’)1,41,42,43,44. It is the formation of a συ hybrid orbital from An 5f and pseudocore 6p, mixed with Oax 2p valence orbitals, that is the source of high covalency of the U-Oax bond. The mixing coefficient (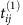 ) of a metal (
) of a metal (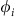 ) with ligand (
) with ligand (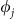 ) orbitals is associated with the covalency of the bond; it can be large due to their strong overlap or near degeneracy as described to the first order by perturbation theory:
) orbitals is associated with the covalency of the bond; it can be large due to their strong overlap or near degeneracy as described to the first order by perturbation theory: 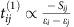 , where
, where 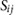 and
and 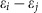 are the overlap and energy difference of the orbitals, respectively2,12. The change of these two parameters,
are the overlap and energy difference of the orbitals, respectively2,12. The change of these two parameters, 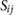 and
and 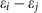 , can lead to increase of
, can lead to increase of 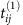 and thereby to increase of overlap or energy-driven covalency2,45. Denning3 pointed out that the strong overlap of the 6p with 2p orbitals plays a substantial role for the covalency of the UO2 2+ bond. Changes in this overlap lead to variations in the filled-filled interaction and is manifested in the HR-XANES spectra as the observed changing peak energy differences, most substantially between the 5fδ/ϕ and 5fσ* peaks. In Fig. 5, the energy difference between the main 5fδ/ϕ peak and the 5fπ*/5fσ* peaks for Np is significantly smaller (Δ5fδ/ϕ−5fπ*=1.6 eV, Δ5fδ/ϕ−5fσ*=5.4 eV) compared to that for U (Δ5fδ/ϕ−5fπ*=2.3 eV, Δ5fδ/ϕ−5fσ*=6.4 eV) (Supplementary Fig. 3; Supplementary Table 3). The trend is preserved for Pu but difficult to quantify since the 5fδ/ϕ and 5fπ* peaks are not resolved in the HR-XANES spectrum. Note that the Np 5fσ* state lies 1 eV nearer to the 5fδ/ϕ orbital than for U, whereas the 5fπ* is 0.7 eV nearer. Since the 5fπ* orbital is closer to the nucleus the effect cannot be explained with mere contraction of the 5f orbitals. In an in-situ experiment, we electrochemically reduced [U(VI)O2(CO3)3]4− to [U(V)O2(CO3)3]5− and observed the same qualitative result; energy differences are much smaller for U(V) (Δ5fδ/ϕ−5fπ*=1 eV, Δ5fδ/ϕ−5fσ*=3.4 eV) compared to those for U(VI) (Δ5fδ/ϕ−5fπ*=1.6 eV, Δ5fδ/ϕ−5fσ*=5.1 eV). The additional electron in the U(V) system lowers the covalent character of the U-Oax bond, which is expressed in the smaller energy difference between the 5fδ/ϕ and the 5fπ*/5fσ* peaks. The same effect is observed by comparison of the U M4 HR-XANES spectra of UO3·1–2(H2O) (metaschoepite) (Δ5fδ/ϕ−5fπ*=2.1 eV, Δ5fδ/ϕ−5fσ*=5.6 eV) and CaU2O7 (Δ5fδ/ϕ−5fπ*=1.7 eV, Δ5fδ/ϕ−5fσ*=4.2 eV). The U-Oax bond length is elongated (ΔR=+0.16 Å) in the latter, which is also associated with decreased covalency of the bond18,42. We propose to use the relative energy difference between the 5fδ/ϕ and the 5fπ*/5fσ* HR-XANES spectral peaks as a qualitative measure of relative changes in the overlap-driven covalency of the actinyl bond2.
and thereby to increase of overlap or energy-driven covalency2,45. Denning3 pointed out that the strong overlap of the 6p with 2p orbitals plays a substantial role for the covalency of the UO2 2+ bond. Changes in this overlap lead to variations in the filled-filled interaction and is manifested in the HR-XANES spectra as the observed changing peak energy differences, most substantially between the 5fδ/ϕ and 5fσ* peaks. In Fig. 5, the energy difference between the main 5fδ/ϕ peak and the 5fπ*/5fσ* peaks for Np is significantly smaller (Δ5fδ/ϕ−5fπ*=1.6 eV, Δ5fδ/ϕ−5fσ*=5.4 eV) compared to that for U (Δ5fδ/ϕ−5fπ*=2.3 eV, Δ5fδ/ϕ−5fσ*=6.4 eV) (Supplementary Fig. 3; Supplementary Table 3). The trend is preserved for Pu but difficult to quantify since the 5fδ/ϕ and 5fπ* peaks are not resolved in the HR-XANES spectrum. Note that the Np 5fσ* state lies 1 eV nearer to the 5fδ/ϕ orbital than for U, whereas the 5fπ* is 0.7 eV nearer. Since the 5fπ* orbital is closer to the nucleus the effect cannot be explained with mere contraction of the 5f orbitals. In an in-situ experiment, we electrochemically reduced [U(VI)O2(CO3)3]4− to [U(V)O2(CO3)3]5− and observed the same qualitative result; energy differences are much smaller for U(V) (Δ5fδ/ϕ−5fπ*=1 eV, Δ5fδ/ϕ−5fσ*=3.4 eV) compared to those for U(VI) (Δ5fδ/ϕ−5fπ*=1.6 eV, Δ5fδ/ϕ−5fσ*=5.1 eV). The additional electron in the U(V) system lowers the covalent character of the U-Oax bond, which is expressed in the smaller energy difference between the 5fδ/ϕ and the 5fπ*/5fσ* peaks. The same effect is observed by comparison of the U M4 HR-XANES spectra of UO3·1–2(H2O) (metaschoepite) (Δ5fδ/ϕ−5fπ*=2.1 eV, Δ5fδ/ϕ−5fσ*=5.6 eV) and CaU2O7 (Δ5fδ/ϕ−5fπ*=1.7 eV, Δ5fδ/ϕ−5fσ*=4.2 eV). The U-Oax bond length is elongated (ΔR=+0.16 Å) in the latter, which is also associated with decreased covalency of the bond18,42. We propose to use the relative energy difference between the 5fδ/ϕ and the 5fπ*/5fσ* HR-XANES spectral peaks as a qualitative measure of relative changes in the overlap-driven covalency of the actinyl bond2.
Extended X-ray absorption fine structure (EXAFS) and calculations with density functional theory (DFT) using relativistic effective core potentials (RECPs) were performed previously for the AnO2 2+ system23. Going from UO2(H2O)52+ to PuO2(H2O)52+ the An-Oax bond distance slightly decreases (RU-Oax=1.76 Å46/1.78 Å47, RNp-Oax=1.75 Å48, RPu-Oax=1.74 Å49), suggesting strengthening of the chemical bond and more electronic density on the An atom. This has been theoretically studied and the net overlap population of the U 5f with the O valence orbitals was found to decrease by about 10% going from U to Pu, explained with the contraction of the 5f orbitals across the An series23,40. More recent experiments and calculations for AnO2+/2+ support the concept that the covalency of the An increases with the An Z number across the actinide series45,50,51. One strong argument is the less favourable oxo-exchange of AnO2+/2+ with methanol and water going from U to Pu51. The theoretical results are inconclusive but prevails the notion that this is an energy-driven covalency. This hypothesis is underpinned by the observed trends for the 5f orbitals in our RIXS maps. The stronger localization of the 5f orbitals likely leads to a better energy match with the O 2p orbitals for Pu, a less optimal energy match for U.
Calculations of Pu(VI) M5 absorption edge HR-XANES spectra
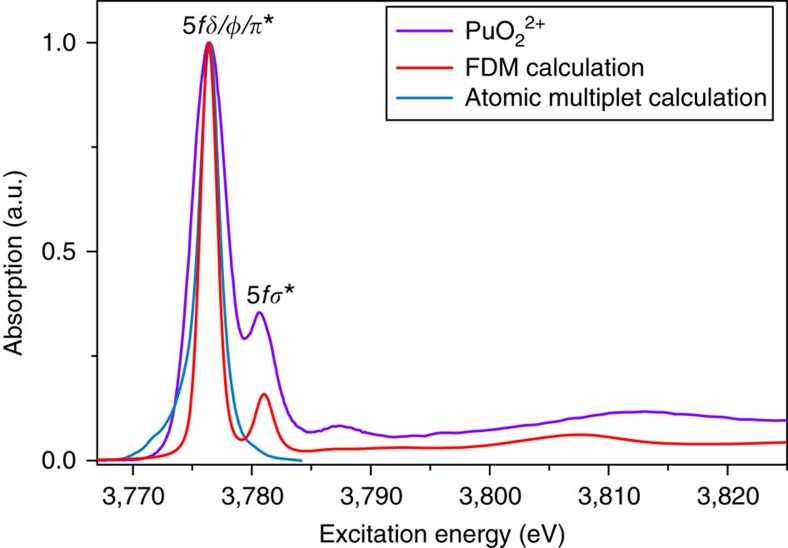
To answer the question if the An M4,5 absorption edge HR-XANES spectra are a good approximation of the ground state partial An 5f density of state, we have explicitly considered the role of multiplets in the Pu M4,5 absorption edge HR-XANES spectrum. The multiplets arise from the angular momentum coupling of the open-shell electrons, both for the core-hole as well as the open 5f shell where the excited state occupation of the 5f shell must be used. The energy spacing of these multiplets may be reasonably large and this splitting will cause the XANES spectra to differ from a ground state partial density of states (DOS). It is well known that these multiplet effects dominate in Ln M edge spectra52. An example of the different importance of multiplets in the XANES of closed shell systems depending on the spin–orbit splitting in the excited core-level is given by Bagus et al.25. U(VI) does not have 5f electrons in the ground state, and we showed previously that the spectrum can be well-described with ground state DFT electronic structure calculations17; the deviations between calculated and measured relative energies are <0.6 eV. Hay et al. compared splitting of the virtual orbitals for 5f1 and 5f2 configurations for PuO23+ and PuO2 2+, and found a significant spread of orbital energies23,53. Electron–electron interactions become important in the ground state when a second electron is added (5f2). Clearly the broadening and the strong overlap of the 5fδ/ϕ and the 5fπ* orbitals in the PuO2 2+ M5 HR-XANES spectrum is partially caused by such multiplet effects.
We performed atomic multiplet calculations to examine the effect of multiplet splittings and to compare excited state calculated spectra with our HR-XANES measurement on hydrated PuO2 2+ (Supplementary Note 2). The results are depicted in Fig. 6. Only the main peak is reproduced for calculations taking only the atomic multiplets into account. Furthermore, the width of the main peak for the atomic multiplet XANES is significantly narrower than the width measured in the HR-XANES. The theoretical width is obtained with a broadening for resolution and lifetime as determined for the HR-XANES (Supplementary Note 2; Supplementary Fig. 4). The smaller width of the atomic multiplet calculation is an evidence for the presence of unresolved multiplets arising from the ligand-field splittings. This is a clear sign that the ligand field is important for correct theoretical description of the Pu spectrum; similar evidence has been also recently shown for ThO2 (ref. 54). For the FDMNES calculation of PuO2(H2O5)(ClO4)2 spectra based on a single-electron approximation, the satellite features of the main peak are present, although this method does not take electron–electron correlation effects into account (Fig. 6). The best agreement between the calculated FDMNES spectrum and the experiment was achieved for the ground state calculations, that is, no inclusion of screening of the core-hole, approximating electron–hole interactions. The calculated spectrum (Fig. 6) and the partial 5f-DOS (Supplementary Note 2; Supplementary Fig. 5) closely resemble the experimental PuO2 2+ M5 edge HR-XANES up to 3,790 eV. The post edge features in the theoretical spectrum are shifted to lower energies compared to experiment. That no core-hole screening was needed for reproducing the experimental spectra also substantiates the strong localization of the 5f states on the Pu atom. There are substantial differences in screening of the core-hole when the electron is in the bound states and when it is in the continuum. We observed these differences manifested in the RIXS map. The calculated intensities somewhat deviate from the experimental spectrum.
Figure 6. Calculated and experimental Pu M5 HR-XANES spectra.
Pu M5 absorption edge HR-XANES experimental and calculated spectra of PuO2 2+ in 1 M HClO4, The atomic multiplets are from a full relativistic treatment of initial and final states with the DIRAC code21; the FDM calculations are performed with the FDMNES code22.
Discussion
We illustrate the unique utility that An 3d4f RIXS offers in characterizing actinide electronic structures; it allows direct determination and comparison of the level of 5f orbital localization and these orbitals’ participation in the chemical bonding for any type of materials, under static or dynamic conditions, not possible with other methods. We have applied this technique to U, Np and Pu in the actinide series and find that the localization of the U and Np 5f orbitals varies for different materials, but does not change for Pu, although studied in several different oxidation states (III, IV, VI) and states of matter (solid, solution). This result indicates that the 5f states in Pu are less active in the chemical bonding, compared to U and Np, and contrasts the general notion that the 5f orbitals are widely responsible for the ability of Pu to co-exist in several different oxidation states24. Investigations of additional An materials and quantum-chemical calculations of An 3d4f RIXS maps will be very beneficial for verification of these conclusions. Covalent mixing between the An 6d and the O 2p orbitals exists too and it might play an important role55,56. Further, changes in the relative energy differences between the 5fδ/ϕ and the 5fπ*/5fσ* orbitals, determined from their RIXS and HR-XANES, provide a direct qualitative measure for the level of overlap-driven covalency in the actinyl bond. The observed trends in these energy differences indicate that U(VI)-Oax is more covalent compared to the Np(VI)-Oax and Pu(VI)-Oax bonds due to stronger orbital overlap of U 5f/6p and O 2p orbitals. The An M4,5 absorption edge HR-XANES and 3d4f RIXS can help to distinguish between the classical notion of overlap-driven covalency and energy-driven covalency. Apparently the overlap-driven covalent character of the An-O binding in the actinyl cations decrease within the U-Pu series, while the energy-driven covalent character increases without increasing the electron density of the binding. Taking into account, the results on oxygen isotope exchange of Lucena et al.51 and the computational results of Kaltsoyannis12, the energy-driven covalency might have a higher impact on chemical binding stability/strength than the overlap-driven covalency.
The An M4,5 absorption edge HR-XANES spectra qualitatively resemble the partial 5f-DOS of the An (Supplementary Note 2; Supplementary Fig. 5). It was shown that electron–electron interactions lead to broadening but are not the dominant effect in the An M4,5 absorption edge HR-XANES spectra. The axial ligand field plays the most important role and therefore it needs to be considered in calculations.
Methods
Preparation of the samples
All preparation procedures of the UO2 2+, NpO2 2+ and PuO2 2+ samples were performed in Ar glove boxes. The UO2 2+ and NpO2 2+ solutions were prepared by dissolving calculated amounts of Na2U2O7(cr) and Na2Np2O7(cr) in 1 M HClO4 aqueous solution. The PuO2 2+ was prepared starting from aqueous Pu4+ in an electrochemical cell equipped with Pt-mesh working, Pt-wire counter and Ag/AgCl reference electrodes. Each sample contained ∼0.06 M U/Np/Pu. The U(VI) and Pu(VI) samples were 100% pure; whereas ultraviolet-vis-NIR spectroscopy performed after the HR-XANES experiments indicated the Np(VI) sample to contain <25 % Np(V). Overall, 135 μl aliquot of each sample was measured in specially designed liquid cells made of polyether ether ketone (PEEK) equipped with 10 μm thick Kapton windows. These cells comprised the first containment and were placed in a second containment inert gas cell prior transportation to the beamline, mounting and measurement (Supplementary Note 1; Supplementary Table 2).
Experiments
The U M4 (3,728 eV), Np M5 (3,664 eV) and Pu M5 (3,775 eV) edge57 HR-XANES/RIXS spectra of UO2 2+, NpO2 2+ and PuO2 2+ were measured using the Johann type X-ray emission spectrometer installed at the INE-Beamline for actinide research at the ANKA synchrotron radiation facility, Karlsruhe, Germany14,58. The incident energy was monochromatized by a Si(111) double crystal monochromator (DCM). Sample, five analyzer crystals and a single diode VITUS silicon drift detector (VITUS SDD KETEK) were arranged in a vertical Rowland geometry59; A box encompassing the spectrometer and maintaining constant He flow was installed to avoid intensity losses due to scattering and absorption of photons. The HR-XANES spectra were obtained by recording the maximum intensity of the Mα/Mβ emission lines (U Mβ, Np Mα, Pu Mα) diffracted by the five spherically bent Si(220) crystal analyzers (SAINT-GOBAIN) with 1 m bending radius and focused onto a single diode VITUS SDD (Supplementary Table 4). The crystals were aligned at 75.17° (U), 83.42° (Np) or 75.22° (Pu) Bragg angles. The RIXS maps of the UO2 2+, spent nuclear fuel (SNF, UO2), high-burn up structure of SNF (HBS, UO2)60,61,62, [UO2(CO3)3]5−, [UO2(CO3)3]4−, (ref. 63) [UO2(H2O)5](ClO4)2(cr), NpO2(am,hyd), Ca0.5NpO2(OH)2·1.3H2O, Na2Np2O7(cr) (refs 64, 65), NpO2 2+, PuO2(cr) (ref. 66), Pu(III) (ref. 67), Pu(IV) and PuO2 2+ were recorded by measuring HR-XANES spectra across a Mα/Mβ normal emission line. The DCM was calibrated by assigning 3,725.2 and 3,775 eV to the maxima of the WLs of the U/Pu M4/M5 edge HR-XANES spectra of a UO2 and a PuO2 samples, respectively. The experimental energy resolution was 1.2 eV (U/Pu) or 1 eV (Np), estimated by measuring the full width at half maximum of the elastically scattered incident beam (Supplementary Tables 1 and 4).
Multiplet calculations
An isolated Pu6+ cation served as a model for our fully relativistic calculations of the wavefunctions for the analysis of the Pu M5 HR-XANES.
Wavefunctions (WFs) were determined with a Dirac–Hartree–Fock calculation of four-component spinors followed by a complete open-shell configuration interaction, COSCI, to treat the angular momentum coupling of the open-shell electrons. The Dirac–Coulomb Hamiltonian without Breit and higher order interactions was used; furthermore an approximation for a class of two-electron integrals involving the small components was also used. These approximations have been tested and found to lead to only small changes. These WFs treat scalar relativistic effects, spin–orbit splittings, and the angular momentum coupling of the open-shell electrons on an equal footing.
The approach is completely non-empirical and no parameters in the calculation of the WFs are adjusted to fit experiment. The application of these methods to core-level ionizations, X-ray photoemission spectroscopy or XPS, has been reviewed in ref. 55 and references therein. Calculations of the WFs were performed with the DIRAC programme21 and calculations of the Irel were performed with the CLIPS programme68. Large flexible basis sets were used to expand the orbitals. For Pu, the basis set was taken from the Dyall basis sets distributed with DIRAC21 and for O, the same basis set was used as in our earlier work on heavy metal oxides (Supplementary Note 2)55,69.
FDMNES calculations
FDMNES22 is an ab initio code simulating the spectroscopies related to the X-ray absorption process. It contains a time-dependent DFT extension, but this study was performed using the standard DFT approach. The electronic structure can be calculated using the multiple scattering theory under the muffin-tin approximation on the potential shape, but in the present study better results are obtained in its more precise scheme using the finite difference method70, which allows a free-shape potential. To get the absorption cross section, FDMNES first solves the electronic structure in the cluster probed by the photoelectron around the absorbing atom, giving thus the projected DOS in the atoms. This calculation can be, on demand, self-consistent or not, relativistic, with or without spin–orbit. In this last case, we follow Wood and Boring71 solving explicitly only the large component orbital instead of the four determined in the Dirac–Slater calculations. This reformulation gives a couple of Schrödinger-like equations closely akin but improved to the Pauli equation. Different imperfect schemes can be used to improve the excited state description by the taking into account of the core-hole with different model of screening. Nevertheless, we found here that the best choice was the simulation in the ground state. The code benefited from recent improvements by Guda et al.72 in the numerical process, allowing simulations on PC, here with a 3.5 Å radius cluster containing 18 atoms, without any symmetry, but identity, and with spin–orbit. The calculations shown in Fig. 6 and Supplementary Fig. 5 are self-consistent, relativistic and include spin–orbit coupling (Supplementary Note 2).
Data availability
The data can be provided by the authors on request.
Additional information
How to cite this article: Vitova, T. et al. The role of the 5f valence orbitals of early actinides in chemical bonding. Nat. Commun. 8, 16053 doi: 10.1038/ncomms16053 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Material
Acknowledgments
We acknowledge the Helmholtz Association of German Research Centers for the VH-NG-734 grant, and the synchrotron light source ANKA for provision of instrumentation and beamtime. We acknowledge support by Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of Karlsruhe Institute of Technology. P.S.B. acknowledges support from the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Chemical Sciences, Geosciences, and Biosciences (CSGB) Division through the Geosciences programme at Pacific Northwest National Laboratory. We thank P. Lindqvist-Reis, J. Gaona Martinez and D. Prieur for provision of samples as well as E. Bohnert, K. Dardenne and V. Krepper for the technical support.
Footnotes
The authors declare no competing financial interests.
Author contributions T.V. designed and built the experimental set-up, designed the study, performed the experiments, analysed the data and wrote the manuscript; I.P. prepared the samples, designed the cells, performed the experiments and analysed the data; D.F. prepared the samples; P.S.B. performed the multiplet calculations and wrote the manuscript; Y.J. performed the FDMNES calculations and wrote the manuscript; T.P. designed and built the experimental set-up; performed the experiments; S.B. built the experimental set-up; performed the experiments; E.G.-R. prepared the samples; J.R. designed and built the experimental set-up and wrote the manuscript; M.A. wrote the manuscript; M.A.D. designed the experimental set-up and wrote the manuscript; H.G. wrote the manuscript.
References
- Pepper M. & Bursten B. E. The electronic-structure of actinide-containing molecules—a challenge to applied quantum-chemistry. Chem. Rev. 91, 719–741 (1991). [Google Scholar]
- Neidig M. L., Clark D. L. & Martin R. L. Covalency in f-element complexes. Coord. Chem. Rev. 257, 394–406 (2013). [Google Scholar]
- Denning R. G. Electronic structure and bonding in actinyl ions and their analogs. J. Phys. Chem. A 111, 4125–4143 (2007). [DOI] [PubMed] [Google Scholar]
- Kovacs A., Konings R. J. M., Gibson J. K., Infante I. & Gagliardi L. Quantum chemical calculations and experimental investigations of molecular actinide oxides. Chem. Rev. 115, 1725–1759 (2015). [DOI] [PubMed] [Google Scholar]
- Kersting A. B. et al. Migration of plutonium in ground water at the Nevada Test Site. Nature 397, 56–59 (1999). [Google Scholar]
- Novikov A. P. et al. Colloid transport of plutonium in the far-field of the Mayak Production Association, Russia. Science 314, 638–641 (2006). [DOI] [PubMed] [Google Scholar]
- Altmaier M., Gaona X. & Fanghanel T. Recent advances in aqueous actinide chemistry and thermodynamics. Chem. Rev. 113, 901–943 (2013). [DOI] [PubMed] [Google Scholar]
- Geckeis H., Lutzenkirchen J., Polly R., Rabung T. & Schmidt M. Mineral-Water interface reactions of actinides. Chem. Rev. 113, 1016–1062 (2013). [DOI] [PubMed] [Google Scholar]
- Ewing R. C. Long-term storage of spent nuclear fuel. Nat. Mater. 14, 252–257 (2015). [DOI] [PubMed] [Google Scholar]
- Morgenstern A. et al. Cross-sections of the reaction Th-232(p,3n)Pa-230 for reaction of U-230 production for targeted alpha therapy. Appl. Radiat. Isot 66, 1275–1280 (2008). [DOI] [PubMed] [Google Scholar]
- Panak P. J. & Geist A. Complexation and extraction of trivalent actinides and lanthanides by triazinylpyridine N-donor ligands. Chem. Rev. 113, 1199–1236 (2013). [DOI] [PubMed] [Google Scholar]
- Kaltsoyannis N. Does covalency increase or decrease across the actinide series? implications for minor actinide partitioning. Inorg. Chem. 52, 3407–3413 (2013). [DOI] [PubMed] [Google Scholar]
- Butorin S. M. et al. Resonant X-ray fluorescence spectroscopy of correlated systems: a probe of charge-transfer excitations. Phys. Rev. Lett. 77, 574–577 (1996). [DOI] [PubMed] [Google Scholar]
- Rothe J. et al. The INE-beamline for actinide science at ANKA. Rev. Sci. Instrum. 83, 043105 (2012). [DOI] [PubMed] [Google Scholar]
- Vitova T. et al. Actinide and lanthanide speciation with high-energy resolution X-ray techniques. J. Phys. 430, 012117 (2013). [Google Scholar]
- Kvashnina K. O., Butorin S. M., Martin P. & Glatzel P. Chemical state of complex uranium oxides. Phys. Rev. Lett. 111, 2253002 (2013). [DOI] [PubMed] [Google Scholar]
- Vitova T. et al. Polarization dependent high energy resolution X-ray absorption study of dicesium uranyl tetrachloride. Inorg. Chem. 54, 174–182 (2015). [DOI] [PubMed] [Google Scholar]
- Podkovyrina Y. et al. Probing covalency in the UO3 polymorphs by U M4 edge HR-XANES. J. Phys. 712, 012092 (2016). [Google Scholar]
- Pidchenko I. et al. Uranium redox transformations after U(VI) coprecipitation with magnetite nanoparticles. Environ. Sci. Technol. 51, 2217–2225 (2017). [DOI] [PubMed] [Google Scholar]
- Walther C. & Denecke M. A. Actinide colloids and particles of environmental concern. Chem. Rev. 113, 995–1015 (2013). [DOI] [PubMed] [Google Scholar]
- DIRAC. a relativistic ab initio electronic Structure Program, Release DIRAC08 written by L. Visscher, H. J. Aa. Jensen, and T. Saue, with new contributions from R. Bast, S. Dubillard, K. G. Dyall, U. Ekström, E. Eliav, T. Fleig, A. S. P. Gomes, T. U. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, P. Norman, J. Olsen, M. Pernpointner, K. Ruud, P. Sałek, and J. Sikkem, Available at http://dirac.chem.sdu.dk (2008).
- Bunau O. & Joly Y. Self-consistent aspects of X-ray absorption calculations. J. Phys. Condens. Matter 21, 345501 (2009). [DOI] [PubMed] [Google Scholar]
- Hay P. J., Martin R. L. & Schreckenbach G. Theoretical studies of the properties and solution chemistry of AnO2 2+ and AnO2 + aquo complexes for An=U, Np, and Pu. J. Phys. Chem. A 104, 6259–6270 (2000). [Google Scholar]
- Clark D. L., Hecker S. S., Jarvinen G. D. & Neu M. P. in The Chemistry of the Actinide and Transactinide Elements (eds Morss, L. R., et al.) 813–1264 (Springer, 2006).
- Bagus P. S., Freund H., Kuhlenbeck H. & Ilton E. S. A new analysis of X-ray adsorption branching ratios: use of Russell–Saunders coupling. Chem. Phys. Lett. 455, 331–334 (2008). [Google Scholar]
- Kotani A. & Shin S. Resonant inelastic X-ray scattering spectra for electrons in solids. Rev. Mod. Phys. 73, 203–246 (2001). [Google Scholar]
- Glatzel P. & Bergmann U. High resolution 1s core hole X-ray spectroscopy in 3d transition metal complexes—electronic and structural information. Coord. Chem. Rev. 249, 65–95 (2005). [Google Scholar]
- Glatzel P. et al. Reflections on hard X-ray photon-in/photon-out spectroscopy for electronic structure studies. J. Electron Spectrosc. Relat. Phenom. 188, 17–25 (2013). [Google Scholar]
- Rueff J. P. & Shukla A. Inelastic X-ray scattering by electronic excitations under high pressure. Rev. Mod. Phys. 82, 847–896 (2010). [Google Scholar]
- Hämäläinen K., Siddons D. P., Hastings J. B. & Berman L. E. Elimination of the inner-shell lifetime broadening in X-ray-absorption spectroscopy. Phys. Rev. Lett. 67, 2850–2853 (1991). [DOI] [PubMed] [Google Scholar]
- Raboud P. A., Dousse J. C., Hoszowska J. & Savoy I. L1 to N5 atomic level widths of thorium and uranium as inferred from measurements of L and M X-ray spectra. Phys. Rev. A. 61, 012507 (1999). [Google Scholar]
- Fuggle J. C. & Alvarado S. F. Core-level lifetimes as determined by X-ray photoelectron spectroscopy measurements. Phys. Rev. A 22, 1615–1624 (1980). [Google Scholar]
- de Groot F. M. F., Krisch M. H. & Vogel J. Spectral sharpening of the Pt L edges by high-resolution X-ray emission. Phys. Rev. B 66, 195112 (2002). [Google Scholar]
- Carra P., Fabrizio M. & Thole B. T. High-resolution X-ray resonant raman-scattering. Phys. Rev. Lett. 74, 3700–3703 (1995). [DOI] [PubMed] [Google Scholar]
- Kotani A., Kvashnina K. O., Butorin S. M. & Glatzel P. A new method of directly determining the core-hole effect in the Ce L-3 XAS of mixed valence Ce compounds-An application of resonant X-ray emission spectroscopy. J. Electron Spectrosc. Relat. Phenom. 184, 210–215 (2011). [Google Scholar]
- Kas J. J., Rehr J. J., Soininen J. A. & Glatzel P. Real-space Green's function approach to resonant inelastic X-ray scattering. Phys. Rev. B 83, 235114 (2011). [Google Scholar]
- Kvashnina K. O., Butorin S. M. & Glatzel P. Direct study of the f-electron configuration in lanthanide systems. J. Analyt. Atom. Spectrom. 26, 1265–1272 (2011). [Google Scholar]
- Kotani A., Kvashnina K. O., Glatzel P., Parlebas J. C. & Schmerber G. Single impurity anderson model versus density functional theory for describing Ce L-3 X-ray absorption spectra of CeFe2: resolution of a recent controversy. Phys. Rev. Lett. 108, 036403 (2012). [DOI] [PubMed] [Google Scholar]
- Bagus P. S., Nelin C. J., Hrovat D. A. & Ilton E. S. Covalent bonding in heavy metal oxides. J. Chem. Phys. 146, 134706 (2017). [DOI] [PubMed] [Google Scholar]
- Matsika S. et al. Electronic structure and spectra of actinyl ions. J. Phys. Chem. A 105, 3825–3828 (2001). [Google Scholar]
- Tatsumi K. & Hoffmann R. Bent cis d0 MoO2 2+ vs linear trans d0f0 UO2 2+: a significant role for non-valence 6p orbitals in uranyl. Inorg. Chem. 19, 2656–2658 (1980). [Google Scholar]
- Dyall K. G. Bonding and bending in the actinyls. Mol. Phys. 96, 511–518 (1999). [Google Scholar]
- Kaltsoyannis N. Computational study of analogues of the uranyl ion containing the –N=U=N– unit: density functional theory calculations on UO2 2+, UON+, UN2, UO(NPH3)3+, U(NPH3)2 4+, [UCl4{NPR3}2] (R=H, Me), and [UOCl4{NP(C6H5)3}]−. Inorg. Chem. 39, 6009–6017 (2000). [DOI] [PubMed] [Google Scholar]
- Denning R. G. et al. Covalency in the uranyl ion: a polarized X-ray spectroscopic study. J. Chem. Phys. 117, 8008–8020 (2002). [Google Scholar]
- Kaltsoyannis N. Covalency hinders AnO2(H2O)+→AnO(OH)2+ isomerisation (An=Pa–Pu). Dalton Trans. 45, 3158–3162 (2016). [DOI] [PubMed] [Google Scholar]
- Allen P. G., Bucher J. J., Shuh D. K., Edelstein N. M. & Reich T. Investigation of aquo and chloro complexes of UO2 2+, NpO2 +, Np4+, and Pu3+ by X-ray absorption fine structure spectroscopy. Inorg. Chem. 36, 4676–4683 (1997). [DOI] [PubMed] [Google Scholar]
- Wahlgren U. et al. Structure of uranium(VI) in strong alkaline solutions. A combined theoretical and experimental investigation. J. Phys. Chem. A 103, 8257–8264 (1999). [Google Scholar]
- Tait C. D. et al. Bond length correlations with vibrational spectra of the trans dioxo unit for actinide complexes. Abstr. Pap. Am. Chem. Soc. 217, U54–U55 (1999). [Google Scholar]
- Conradson S. D. Application of X-ray absorption fine structure spectroscopy to materials and environmental science. Appl. Spectrosc. 52, 252a–279a (1998). [Google Scholar]
- Rios D., Micheini M. D., Lucena A. F., Marcalo J. & Gibson J. K. On the origins of faster oxo exchange for uranyl(V) versus plutonyl(V). J. Am. Chem. Soc. 134, 15488–15496 (2012). [DOI] [PubMed] [Google Scholar]
- Lucena A. F. et al. Oxo-exchange of gas-phase uranyl, neptunyl, and plutonyl with water and methanol. Inorg. Chem. 53, 2163–2170 (2014). [DOI] [PubMed] [Google Scholar]
- Groot F. Multiplet effects in X-ray spectroscopy. Coord. Chem. Rev. 249, 31–63 (2005). [Google Scholar]
- Infante I. et al. A Fock space coupled cluster study on the electronic structure of the UO2, UO2+, U4+, and U5+ species. J. Chem. Phys. 127, 124308 (2007). [DOI] [PubMed] [Google Scholar]
- Butorin S. M., Kvashnina K. O., Vegelius J. R., Meyer D. & Shuh D. K. High-resolution X-ray absorption spectroscopy as a probe of crystal-field and covalency effects in actinide compounds. Proc. Natl Acad. Sci. USA 113, 8093–8097 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagus P. S., Ilton E. S. & Nelin C. J. The interpretation of XPS spectra: insights into materials properties. Surf. Sci. Rep. 68, 273 (2013). [Google Scholar]
- Bagus P. S. & Nelin C. J. Covalent interactions in oxides. J. Electron Spectrosc. Relat. Phenom. 194, 37 (2014). [Google Scholar]
- Elam W. T., Ravel B. D. & Sieber J. R. A new atomic database for X-ray spectroscopic calculations. Radiat. Phys. Chem. 63, 121–128 (2002). [Google Scholar]
- Walshe A., Prussmann T., Vitova T. & Baker R. J. An EXAFS and HR-XANES study of the uranyl peroxides [UO2(h2-O2)(H2O)2]· nH2O (n=0, 2) and uranyl (oxy)hydroxide [(UO2)4O(OH)6)]·6H2O. Dalton Trans. 43, 4400–4407 (2014). [DOI] [PubMed] [Google Scholar]
- Kleymenov E. et al. Five-element Johann-type X-ray emission spectrometer with a single-photon-counting pixel detector. Rev. Sci. Instrum. 82, 065107 (2011). [DOI] [PubMed] [Google Scholar]
- González-Robles E. et al. Physico-chemical characterization of a spent UO2 fuel with respect to its stability under final disposal conditions. MRS Proc. 1665, 283–289 (2014). [Google Scholar]
- González-Robles E. et al. Determination of fission gas release of spent nuclear fuel in puncturing test and in leaching experiments under anoxic conditions. J. Nucl. Mater. 479, 67–75 (2016). [Google Scholar]
- Rondinella V. V. & Wiss T. The high burn-up structure in nuclear fuel. Mater. Today 13, 24–32 (2010). [Google Scholar]
- Ikeda A. et al. Comparative study of uranyl(VI) and -(V) carbonato complexes in an aqueous solution. Inorg. Chem. 46, 4212–4219 (2007). [DOI] [PubMed] [Google Scholar]
- Fellhauer D., Neck V., Altmaier M., Lützenkirchen J. & Fanghänel T. Solubility of tetravalent actinides in alkaline CaCl2 solutions and formation of Ca4 [An (OH)8]4+ complexes: a study of Np (IV) and Pu (IV) under reducing conditions and the systematic trend in the An (IV) series. Radiochim. Acta Int. J. Chem. Aspects Nucl. Sci. Technol. 98, 541–548 (2010). [Google Scholar]
- Fellhauer D. et al. Np (V) solubility, speciation and solid phase formation in alkaline CaCl2 solutions. Part I: experimental results. Radiochim. Acta 104, 355–379 (2016). [Google Scholar]
- Prieur D., Carvajal-Nunez U., Vitova T. & Somers J. Local and Electronic structure of americium-bearing PuO2. Eur. J. Inorg. Chem. 2013, 1518–1524 (2013). [DOI] [PubMed] [Google Scholar]
- Kirsch R. et al. Oxidation state and local structure of plutonium reacted with magnetite, mackinawite, and chukanovite. Environ. Sci. Technol. 45, 7267–7274 (2011). [DOI] [PubMed] [Google Scholar]
- Scrimgeour J. et al. Three-dimensional optical lithography for photonic microstructures. Adv. Mater. 18, 1557 (2006). [Google Scholar]
- Nelin C. J., Bagus P. S. & Ilton E. S. Theoretical analysis of the U L3-edge NEXAFS in U oxides. RSC Adv. 4, 7148–7153 (2014). [Google Scholar]
- Joly Y. X-ray absorption near-edge structure calculations beyond the muffin-tin approximation. Phys. Rev. B 63, 125120 (2001). [Google Scholar]
- Wood J. H. & Boring A. M. Improved Pauli Hamiltonian for local-potential problems. Phys. Rev. B 18, 2701–2711 (1978). [Google Scholar]
- Guda S. A. et al. Optimized finite difference method for the full-potential XANES simulations: application to molecular adsorption geometries in MOFs and metal-ligand intersystem crossing transients. J. Chem. Theory. Comput. 11, 4512–4521 (2015). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data can be provided by the authors on request.