Design and application of ‘J-shaped’ stress-strain behavior in stretchable electronics: a review

Abstract

A variety of natural biological tissues (e.g., skin, ligaments, spider silk, blood vessel) exhibit ‘J-shaped’ stress-strain behavior, thereby combining soft, compliant mechanics and large levels of stretchability, with a natural ‘strain-limiting’ mechanism to prevent damage from excessive strain. Synthetic materials with similar stress-strain behaviors have potential utility in many promising applications, such as tissue engineering (to reproduce the nonlinear mechanical properties of real biological tissues) and biomedical devices (to enable natural, comfortable integration of stretchable electronics with biological tissues/organs). Recent advances in this field encompass developments of novel material/structure concepts, fabrication approaches, and unique device applications. This review highlights five representative strategies, including designs that involve open network, wavy and wrinkled morphoologies, helical layouts, kirigami and origami constructs, and textile formats. Discussions focus on the underlying ideas, the fabrication/assembly routes, and the microstructure-property relationships that are essential for optimization of the desired ‘J-shaped’ stress-strain responses. Demonstration applications provide examples of the use of these designs in deformable electronics and biomedical devices that offer soft, compliant mechanics but with inherent robustness against damage from excessive deformation. We conclude with some perspectives on challenges and opportunities for future research.

Graphical abstract

The Review highlights representative material/structure strategies to achieve ‘J-shaped’ stress-strain responses, and introduces their applications in strerchable electronics.

1. Introduction

Significant progress in the development of stretchable electronics^1-8 based on inorganic materials enables systems that combine extremely deformable mechanics and high-performance electrical properties. These unconventional technologies have significant commercial potential in biomedicine, either to replace the function of biological tissues/organs (e.g. skin-like prosthesis^9-13, biomimetic robots^14-17, etc.), or to integrate with biological tissues/organs (such as epidermal electronics^18-24, flexible implantable medical instruments^25-28, etc.).

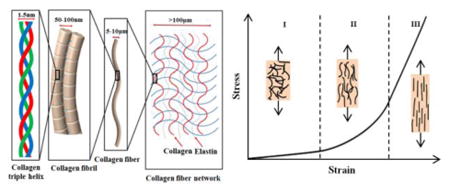
Many biological tissues, such as skin^{29, 30}, ligaments³¹, spider silk^{32, 33}, blood vessel^{34, 35}, etc., exhibit ‘J-shaped’ stress–strain behaviors³⁶ as depicted in Figure 1a²⁹, as a result of their curved and chained microstructures (e.g., collagen triple helix, collagen fibril, collagen fiber in Figure 1a). This type of stress-strain response is typically characterized by three different stages. In Stage I (Figure 1a), wavy and crimped collagen fibers begin to unfurl by bending and twisting, thereby resulting in a negligible stiffness and compliant mechanics (linear). As the applied strain increases (Stage II), the collagen fibers uncoil, leading to an increase of tangent modulus. After the collagen fibers straighten (Stage III), the stress-strain behavior is dominated by stretching of the fibers, thereby offering relative linear response and high tangent modulus. A goal in the development of engineering materials as substrates or superstrates in stretchable electronics focuses on the development of design that can precisely reproduce the ‘J-shaped’ stress-strain behavior of the real biological tissues.

Figure 1. Microstructures of biological tissues and five representative strategies to enable ‘J-shaped’ stress-strain behavior.

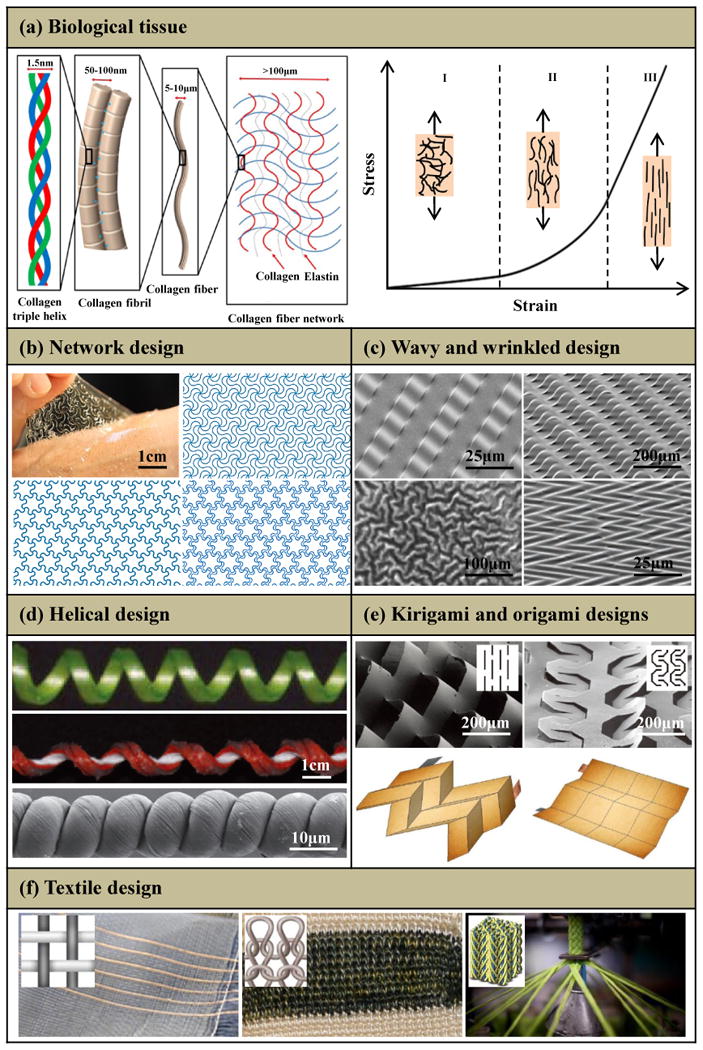
(a) Hierarchical structure of a representative biological tissue spanning the nanoscale dimensions of collagen triple helices to microscale networks of collagen and elastin fibers, and its representative ‘J-shaped’ stress-strain behavior. (b) Network design: optical image (left-top) of a 2D network [triangular (right-top), honeycomb (left-bottom) and Kagome (right-bottom)] embedded in an ultralow-modulus matrix on skin. (c) Wavy and wrinkled design: stiff filamentary ribbons wrinkle on a unidirectionally pre-strained compliant substrate with uniform (left-top) and patterned (right-top) bonding, and stiff films wrinkle on an equi-biaxially (left-bottom) and nonequi-biaxially (right-bottom) pre-strained compliant substrate. (d) Helical design: coiled tendril, silicone fabric ribbon and helical carbon fiber. (e) Kirigami and origami designs: two microscale kirigami patterns in GO-PVA nanocomposites after photolithography (top) and quadrilateral mesh models and two representative Miura origami patterns (bottom). (f) Textile design: weaving (left), knitting (middle) and braiding (right). Panel (a) is adapted with permission from Ref. [29] (Copyright 2015, Nature Publishing Group). Panel (b) is adapted with permission from Ref. [49] (Copyright 2015, Nature Publishing Group). Panel (c) is adapted with permission from Ref. [50] (Copyright 2006, the American Association for the Advancement of Science), Ref. [51] (Copyright 2006, Nature Publishing Group), Ref. [52] (Copyright 2015, John Wiley and Sons) and Ref. [53] (Copyright 2007, American Chemical Society). Panel (d) is adapted with permission from Ref. [54] (Copyright 2012, the American Association for the Advancement of Science) and Ref. [55] (Copyright 2015, Nature Publishing Group). Panel (e) is adapted with permission from Ref. [56] (Copyright 2015, Nature Publishing Group) and Ref. [57] (Copyright 2014, Nature Publishing Group). Panel (f) is adapted with permission from Ref. [58] (Copyright 2017, the American Association for the Advancement of Science) and Ref. [59] (Copyright 2014, MDPI).

To enable natural, comfortable integration of stretchable electronics with biological tissues/organs, an important design consideration is to reduce the stresses induced on the skin by the presence of the devices to within thresholds for somatosensory perception. Specifically, the electronics must be sufficiently compliant to accommodate deformations of soft biological tissues^{37, 38}, typically within several to tens of percent. Materials with ‘J-shaped’ stress-strain behavior are well-matched to this requirement due to their low elastic modulus at small strains³⁹.

In the aforementioned applications, another challenge is in the development of materials/structures strategies to minimize the possibility of mechanically induced device failure^40-42. Several design concepts allow stretchable, integrated systems of hard, functional, inorganic components and soft, elastomeric substrate^43-48. Here, an emerging design strategy involves the use of a layer with ‘J-shaped’ stress-strain behavior placed between the electronics and the biological tissue. This embedded layer has a high elastic modulus at large strain, to shield the electronics from the potential for large deformations^{39, 49}, thereby providing a so-called “strain-limiting” function.

Figures 1b-f summarize five structural designs that can offer ‘J-shaped’ stress–strain behavior: (i) Network designs⁴⁹ that adopt wavy, horseshoe microstructures patterned in periodic lattices (e.g., triangular, right-top; honeycomb, left-bottom; Kagome, right-bottom; Fig. 1b); (ii) wavy and wrinkled designs^50-53 induced using a pre-strain [unidirectional (top) or bidirectional (bottom) in Fig. 1c] strategy; (iii) helical designs either with natural (e.g., coiled tendril⁵⁴, in the top of Fig. 1d) or synthetic (e.g, silicone fabric ribbon⁵⁴ and helical carbon⁵⁵, in the middle and bottom of Fig. 1d) constructions; (iv) kirigami (in the top of Fig. 1e)⁵⁶ and origami (in the bottom of Fig. 1e)⁵⁷ designs that exploiting pre-defined patterns of cuts and creases; (v) textile designs manufactured by weaving (in the left of Fig. 1f)⁵⁸, knitting (in the middle of Fig, 1f)⁵⁸ or braiding (in the right of Fig. 1f)⁵⁹ to yield fabrics. Sections 2-6 summarize each design strategy, highlighting the fundamental principles as well as the key parameters that govern the ‘J-shaped’ stress–strain behavior. A brief discussion of the challenges and prospects for the further study is presented in Section 7.

2. Network design

Curved and chained microstructures in biological tissues (e.g., collagen fiber network in Figure 1a) consist of cross-linked fiber networks with random distributions^60-62 that can be reproduced, at some level, in synthetic materials by various approaches (e.g., ionic liquid grinding^{63, 64}, two-step shearing⁶⁵, plasma-induced modification⁶⁶ and two-step polymerization⁶⁷). Ban et al.⁶⁸ adopted a numerical approach to study the effect of fiber crimp on the stiffness of random fiber networks. To simulate the crimp, a fraction f of the total fibers are assumed to have a sinusoidal form with wavelength 2l and amplitude cl [i.e., x₂ = cl sin(πx₁/l), as shown in Figure 2a]. The other fibers are straight with length l. Figure 2b shows that the normalized modulus stiffness [E_elastic/E₀, where E_elastic (f,c) is the elastic modulus at infinitesimal strain. E₀ = E_elastic (f,0)] decreases as f and c increase, indicating that the crimper fibers lead to a reduction of modulus. As the applied stress (σ) increases, the tangent modulus increases (Figure 2c), due to the transition of deformations in the fibers from bending to stretching dominated mode. Jungebluth et al.⁶⁹ used electrospun synthetic fibers as an artificial scaffolds, and then introduced cells to produce an tissue-engineered rat trachea (Figure 2e) with microstructures and mechanical properties similar to those of native tissues (Figure 2d). The percolation networks based on metal nanowire^{70, 71}, graphene flakes^72-74 and carbon nanotubes^{75, 76} have high conductivity, transmittance and magnetic response, and also can achieve the ‘J-shaped’ stress-strain behavior. The low modulus stages of such percolation networks due to the ‘J-shaped’ stress-strain behavior, together with their own physical characteristics are well-matched with the demands of bio-integrated electronics.

Figure 2. Random network design.

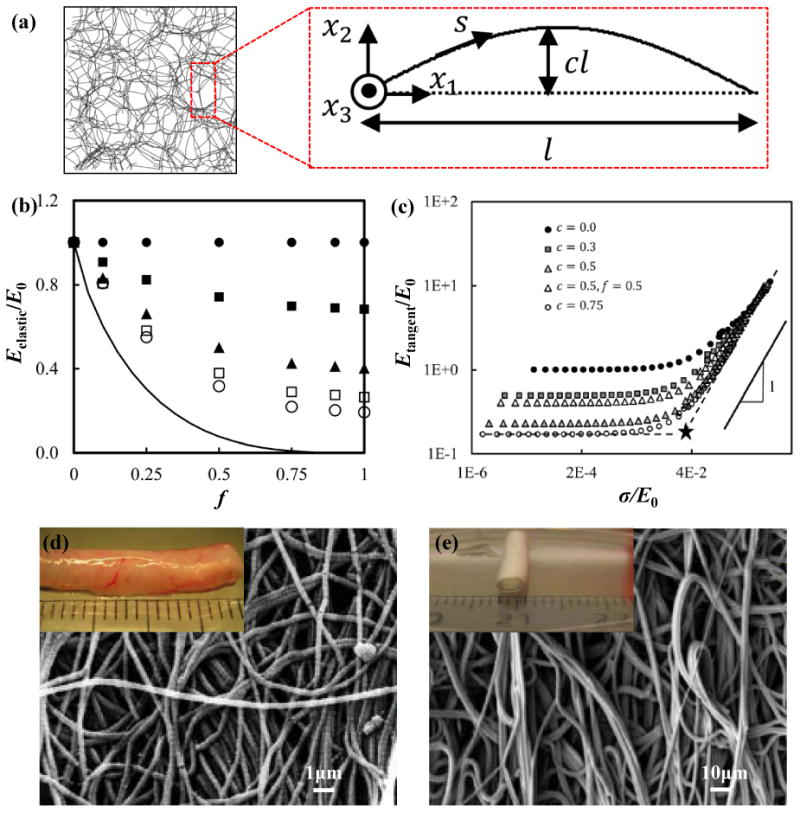
(a) Snapshot of an undeformed random network (f=1 and c=0.2) and schematic diagram of an individual crimped fiber. (b) Normalized network stiffness versus fraction of crimped fibers (f) with c=0 (filled circles), 0.25 (filled squares), 0.5 (triangles), 0.66 (open squares), and 1 (open circles). The solid curve represents the lower bound of the normalized modulus stiffness (E_elastic/E₀). (c) Normalized tangent stiffness versus normalized true stress with f=1 for all cases, except for that indicated in the legend. (d, e) SEM images of (d) native rat trachea and (e) electrospun artificial trachea (macroscopic view shown in inset figure). Panels (a), (b) and (c) are adapted with permission from Ref. [68] (Copyright 2016, ASME). Panels (d) and (e) are adapted with permission from Ref. [69] (Copyright 2014, Nature Publishing Group).

Recent work establishes deterministic and bio-inspired design principles based on a two-dimensional (2D) wavy filamentary network embedded in an ultralow-modulus matrix. Here, the ‘J-shaped’ stress-strain behavior can be controlled, through careful choices in geometry, to precisely match those of human skin, as supported by finite element analyses (FEA) and experiment. Specifically, filamentary networks adopt a hierarchical construction of lattice topologies^77-83 with horseshoe microstructures^{46, 84-88}, as shown in Figure 1b⁴⁹. These microscale features can be formed in a variety of materials (e.g, photodefinable polymers, metals and semiconductors) using lithographic approaches. Ma et al.⁸⁹ introduced a finite deformation model for the horseshoe microstructures (inset, Figure 3a) to predict the nonlinear stress-strain responses. Figures 3a and b⁸⁹ show normalized stresses (σ/E_material) as a function of applied strain, where σ is the effective stress of the horseshoe microstructure, and E_material is the elastic modulus of the solid material. The resulting ‘J-shaped’ stress–strain behavior depends on two normalized parameters, the normalized width (w̄ = w/R₀) and the arc angle (θ₀). As the normalized width (w̄) decreases, the transition of the ‘J-shaped’ stress-strain behavior becomes sharper, as shown in Figure 3a. The critical strain for the transition between low and high modulus regimes is approximately ε_cr = θ₀/[2 sin (θ₀/2)]−1, as marked by the dashed line in Figures 3a and b. A large arc angle (θ₀) gives a large critical strain, consistent with the results in Figure 3b. As shown in Figures 3c and d, the triangular lattice network (inset, Figure 3c) maintains the ‘J-shaped’ stress-strain behavior of the horseshoe microstructures⁸⁹. Four key parameters, the elastic modulus, transition strain, peak tangent modulus and peak strain, characterize the ‘J-shaped’ stress-strain curves of the lattice network. Quantitative mechanics models offer accurate predictions of these parameters as well as the deformed configurations⁸⁹. Fractal designs⁹⁰ provide routes to strain-limiting materials with improved stretchabilities and multiple transition points during stretching. Figure 3e shows the normalized stresses (in logarithmic scale) versus applied strain for first-, second- and third-order fractal horseshoe microstructures, respectively, with fixed arc angle (θ₀=240°), normalized width (w̄=0.2) and 8 unit cells for each order. In addition, the high-order (e.g., > 2) fractal horseshoe microstructures have a substantially reduced elastic modulus, as compared to traditional, first-order horseshoe designs. This result is advantageous for strain-limiting materials in bio-integrated applications, due to reduced levels of induced stresses.

Figure 3. Deterministic network design.

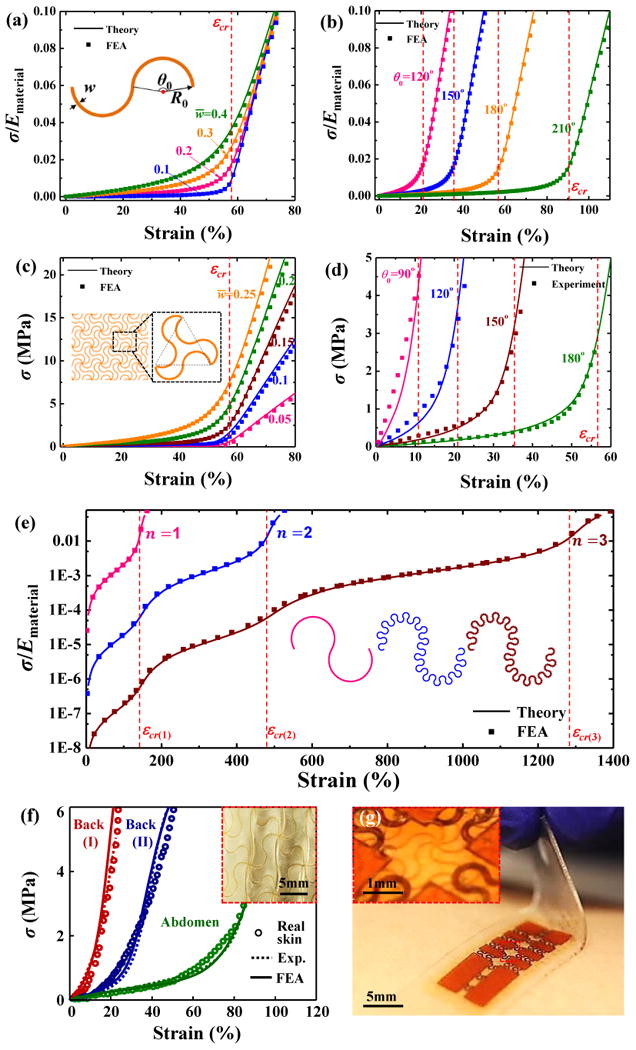
Normalized stress-strain relation for a horseshoe microstructure with (a) fixed arc angle (θ₀=180°) and several normalized width (w̄), and (b) fixed normalized width (w̄=0.2) & several arc angle (θ₀). Stress-strain relation for a network design based on hierarchical triangular lattice consisting of horseshoe microstructures with (c) fixed arc angle (θ₀=180°) & several normalized width (w̄), and (d) fixed normalized width (w̄=0.15) & several arc angle (θ₀). (e) Stress-strain relation for the first-, second- and third-order fractal horseshoe microstructures, respectively, with the fixed arc angle (θ₀=240°), normalized width (w̄=0.2) and 8 unit cells for each order. (f) Stress–strain responses of human skin and artificial skin for various locations on different individuals (inset figure: optical images of artificial skin). (g) Optical image of a core/shell structure with electronics that includes a strain-limiting layer in the form of a wave filamentary network of polyimide. Panels (a), (b), (c) and (d) are adapted with permission from Ref. [89] (Copyright 2016, Elsevier). Panel (e) is adapted with permission from Ref. [90] (Copyright 2016, ASME). Panel (f) is adapted with permission from Ref. [49] (Copyright 2015, Nature Publishing Group). Panel (g) is adapted with permission from Ref. [37] (Copyright 2015, John Wiley and Sons).

The network design can be implemented in a sandwich construction (Silbione/filamentary network/ Silbione) to match precisely the non-linear stress-strain responses of human skin at different regions (e.g., back and abdomen), as shown in Figure 3f ⁴⁹. Here, a copper layer was deposited on a glass slide to serve as a sacrificial layer, followed by spin casting of a PI layer onto the top of the copper layer.³⁷ Photolithographic patterning of this PI layer enables formation of a deterministic network that was then transfer printed onto the surface of the elastomer, and uniformly coated with another elastomer layer. Transfer printing of the stretchable electronics onto this composite, strain-limiting structure finishes the integration of the entire device system. The strain-limiting effect of such network design can be also utilized to protect the electronics from levels of stretching that could lead to fracture of the electronic materials³⁷, as shown in Figure 3g.

3. Wavy and wrinkled design

For a stiff thin film bonded to a compliant substrate, differences in strain (either by thermally induced mismatch⁹¹ or mechanical pre-strain^92-95) between the film and substrate can lead to wrinkling of the film into a sinusoidal form (Figure 1c). Figure 4a presents a schematic illustration of a process for fabricating wavy films of PI bonded on to a low modulus silicone substrate (Silbione) ³⁹. At small applied strain, the wrinkled PI film has a negligible stiffness and does not contribute to the tensile stiffness of the system⁹⁶. The result is a low elastic modulus (Stage I in Figure 4b), with a value that is almost the same as the intrinsic value of the substrate. As the applied strain increases, the wrinkled PI film becomes flat and therefore contributes to the stiffness of the system, yielding a high tangent modulus (Stage II in Figure 4b). As a result, the wrinkled film/substrate structure has a bilinear stress-strain behavior with an extremely sharp transition point, and an exceptionally high ratio of tangent to elastic modulus, which is particularly valuable as a strategy for constructing strain-limiting materials.

Figure 4. Wavy and wrinkled design.

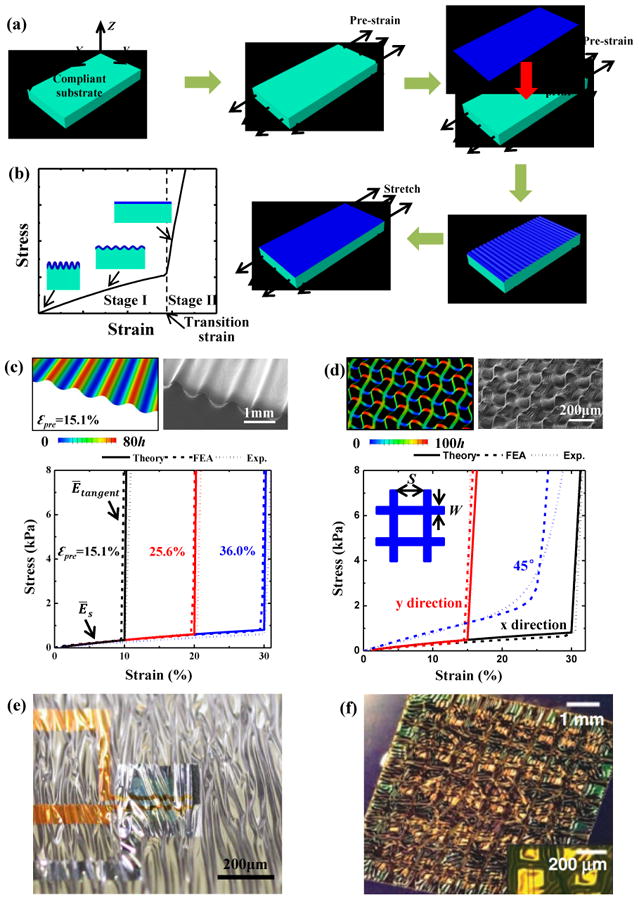
(a) Schematic illustration of the process for fabricating wavy/wrinkled strain-limiting structures. (b) Bilinear stress–strain behavior of the strain-limiting structure. (c) Bilinear stress–strain curves of 1 μm-thick PI film on 1 mm-thick Silbione substrate subjected to various pre-strains, along with its optical morphology and out-of-plane displacement subjected to 15.1% pre-strain. (d) Stress-strain curves for x-, y-, and 45°-stretching of 1 μm-thick PI mesh (width W=0.1mm and spacing S=0.4mm) on 1 mm-thick Silbione substrate subjected to pre-strains of ${\varepsilon }_{\mathit{\text{pre}}}^x$=30.8% and ${\varepsilon }_{\mathit{\text{pre}}}^y$=15.7%, along with its optical morphology and out-of-plane displacement. (e, f) Optical images of wrinkling electronic films when substrate shrinks caused by (e) pre-strain releasing and (f) temperature change. Panels (a), (b), (c) and (d) are adapted with permission from Ref. [39] (Copyright 2016, John Wiley and Sons). Panel (e) is adapted with permission from Ref. [97] (Copyright 2013, Nature Publishing Group). Panel (f) is adapted with permission from Ref. [98] (Copyright 2008, the American Association for the Advancement of Science).

Release of the pre-strain in the substrate leads to the bending of the system with a curvature κH = 6[9Ē_fh³/(Ē_sH³)]^1/3, when no additional constraints are involved⁹⁶. If such bending is noticeable, it can be eliminated by adopting additional constraints, e.g., through use of fixture to minimize the rotations of the system at two ends during the release of the pre-strain. When such strain-limiting system sticks onto the target body (e.g., skin), the bending also can be eliminated by applying constraints to the bottom surface of the system.

Substrates with finite thickness no longer recover to their initial length upon release of the pre-strain. The result is a transition strain (ε_transition, as shown in Figure 4b) that is not equal to the pre-strain (ε_pre). Ma et al.³⁹ gives a relation between the transition strain (ε_transition) and the pre-strain (ε_pre) as

$${\varepsilon }_{\mathit{\text{transition}}}=\frac{{\varepsilon }_{\mathit{\text{pre}}}-\frac{1}{4}{\left(\frac{9{\overline{E}}_f{h}^3}{{\overline{E}}_s{H}^3}\right)}^{1/3}}{1+\frac{1}{4}{\left(\frac{9{\overline{E}}_f{h}^3}{{\overline{E}}_s{H}^3}\right)}^{1/3}}$$ (1)

where H and h are the thickness of the substrate and film. ${\overline{E}}_s=E_s/\left(1-v_s^2\right)$ and ${\overline{E}}_f=E_f/\left(1-v_f^2\right)$ are the plane-strain modulus of the substrate and film, respectively, and E_s, E_f, v_s and v_f are the corresponding elastic modulus and Poisson's ratios. In addition to the transition strain, the ratio of the tangent to the elastic modulus also represents an important property, given by Ē_tangent/Ē_elastic ≈ 1 + h Ē_f/HĒ_s)³⁹. Figure 3c shows bilinear stress-strain curves for a 1 μm-thick PI film on a 1 mm-thick Silbione substrate with three different levels of pre-strain³⁹. The transition strains are 10%, 20% and 30%, respectively.

Figure 4d shows a wavy, wrinkled design created by biaxial stretching. The thin film is replaced by a thin mesh (width W and spacing S, Figure 4d) on a biaxially pre-strained ( ${\varepsilon }_{\mathit{\text{pre}}}^x$ and ${\varepsilon }_{\mathit{\text{pre}}}^y$), compliant substrate. The transition strain and ratio of tangent to elastic modulus are given by³⁹

$${\varepsilon }_{\mathit{\text{transition}}}^i=\frac{{\varepsilon }_{\mathit{\text{pre}}}^i-\frac{W}{6\left(W+S\right)}{\left(\frac{9{\overline{E}}_f{h}^3}{{\overline{E}}_s{H}^3}\right)}^{1/3}}{1+\frac{W}{6\left(W+S\right)}{\left(\frac{9{\overline{E}}_f{h}^3}{{\overline{E}}_s{H}^3}\right)}^{1/3}},\frac{{\overline{E}}_{\mathit{\text{tangent}}}}{{\overline{E}}_{\mathit{\text{elastic}}}}\approx 1+\left[W/\left(W+S\right)\right]\frac{{\overline{E}}_{f}h}{H{\overline{E}}_s}$$ (2)

where the superscript i denotes either x or y. Figure 4d shows the stress-strain curves for x-, y- and 45°-stretching of a 1 μm-thick PI mesh on a 1 mm-thick Silbione substrate subjected to the pre-strains ${\varepsilon }_{\mathit{\text{pre}}}^x=30.8\%$ and ${\varepsilon }_{\mathit{\text{pre}}}^y=15.7\%$ (Ref. 39). The resulting transition strains ${\varepsilon }_{\mathit{\text{transition}}}^x$ and ${\varepsilon }_{\mathit{\text{transition}}}^y$ are 30% and 15%, respectively.

In addition to ‘J-shaped’ stress–strain behavior, the wavy and wrinkled design also provides a route to stretchability in electronic materials, representing a strategy that has been widely used in many stretchable electronic devices. For example, Kaltenbrunner et al.⁹⁷ printed an ultrathin electronic polymer foil onto a pre-strained elastomer (Figure 4e), which forms a wrinkled configuration that can accommodate relative large tensile strains. Kim et al.⁹⁸ fabricated biaxially wavy CMOS (complementary metal–oxide–semiconductor) circuits on a thin polymer film (Figure 4f), through use of biaxial thermal strain in the elastomeric substrate. Both of these examples^{97, 98} give compliant response at small strain, due to the low elastic modulus. The polymer film becomes stiff when it is stretched flat again, which shields the electronics from high strains.

4. Helical design

Helical microstructures⁹⁹ also possess the ‘J-shaped’ stress–strain behavior^100-104. For a helical ribbon, as shown in Figure 5a, Pham et al.¹⁰⁵ gave an analytical expression that captures the non-linear mechanics response under the conditions that the ratio of t/w ≪ 1 and L/w ≪ 1, i.e.,

Figure 5. Helical design.

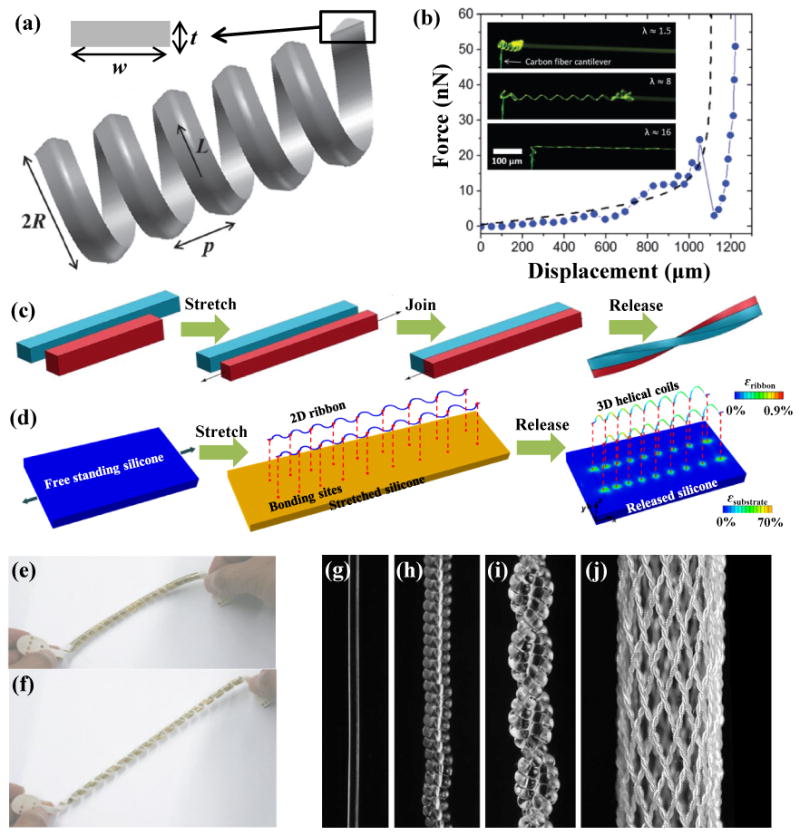
(a) Geometrical illustration of the helical microstructure. (b) Optical image of the stretching process for a helical carbon fiber and its ‘J-shaped’ stress-strain behavior. (c, d) Two alternative approaches to assembly of the 3D helix from 2D structures. (e, f) A thin-film transistor array helix (e) before and (f) after 50% stretching. (g) A 300-mm-diameter nylon 6,6 fiber; (h) a coil fiber; (i) a two-ply fiber formed from (h); (j) a braid formed from 32 two-ply fiber (i). Panels (a) and (b) are adapted with permission from Ref. [105] (Copyright 2014, Royal Society of Chemistry). Panel (c) is adapted with permission from Ref. [110] (Copyright 2014, Public Library of Science). Panel (d) is adapted with permission from Ref. [112] (Copyright 2015, the American Association for the Advancement of Science). Panels (e) and (f) are adapted with permission from Ref. [117] (Copyright 2010, Nature Publishing Group). Panels (g-j) are adapted with permission from Ref. [120] (Copyright 2014, the American Association for the Advancement of Science).

$$F=\frac{E{\pi }^{2}w{t}^{3}p}{3l^3}\left[\frac{\sqrt{1-{\left(p_0/l\right)}^2}}{\sqrt{1-{\left(p/l\right)}^2}}+\frac{1-v}{1+v}\right],$$ (3)

where the geometry is described by the contour length (L = Nl, with l denoting the contour length of a single turn, and N the number of helical turns), pitch (p), radius $(R=\sqrt{l^2-p^2}/2\pi )$, width (w) and thickness (t), as illustrated in Figure. 5a. p₀ and R₀ are the initial pitch and radius. E and v are the elastic modulus and Poisson's ratio of the material, respectively. To verify this analytical solution, Pham et al.¹⁰⁵ also carried out experiments on a helical carbon fiber (R₀=15μm, L=1190μm, N=12.5, w=5.9μm, t=122nm, E=1.3GPa and v=0.3). The measured force-displacement curves agree well with the analytical solution (Eq. 3), as shown in Figure 5b.

Three-dimensional (3D) printing⁹⁹ (e.g., fused deposition modeling¹⁰⁶, UV-assisted 3D printing¹⁰⁷ and solvent-cast 3D printing¹⁰⁸) represents one straightforward approach to helical microstructures, but with limited choices in materials. Figure 5c summarizes an alternative strategy that uses mechanical assembly. Specifically, two strips of different lengths are adhered together side-by-side, after stretching the short strip to a length that matches that of the long one. Upon release of the stretch, this bi-strip twists and bends either into a helix or a hemihelix^109-111. Recently, Xu et al.¹¹² reported a mechanically-guided approach for assembly of complex, 3D architectures in a diversity of high-performance materials, including semiconductors (e.g, silicon), metals (e.g., Au, Cu, Ni), polymers (e.g., PI, SU8), and their heterogeneous integration. Here, filamentary serpentine ribbons serve as 2D precursors that are bonded to a pre-stretched silicone elastomer at selected points (red dots in Figure 5d). 3D helical microstructures form spontaneously upon release of the pre-strain. This type of 2D-3D geometric transformation follows from a process of compressive buckling that can be analyzed quantitatively using a finite-deformation model¹¹³. Similar processes can form coiled nanowires^114-116.

By exploiting the compliant nature of the helical structure under small tensile strain, Sekitani et al.¹¹⁷ fabricated a thin-film transistor array on a shape-memory polymer film that was transformed into a helical configuration to shield the electronics from high strains. Figures 5e and f show this helical thin-film transistor array before and after 50% stretching. To mimic the ‘J-shaped’ stress–strain behavior of the muscle^{118, 119}, Haines et al.¹²⁰ proposed a type of artificial muscle by using the nylon 6,6 coil fibers show in Figures 5g-j.

5. Kirigami and origami designs

Kirigami^{56, 121-124} is an ancient art of paper cutting and folding to form 3D sculptures. Figure 6a shows a kirigami model in Kent paper (thickness of 0.2-0.3mm and modulus of 2.45-3.27GPa) with regularly arranged cuts (w≃10-30mm and d≃1-5mm), and its force-displacement curve is presented in Figure 6b¹²⁵. In the initial regime (small applied strain), the elementary plates in Kent paper deform mainly via in-plane buckling, which leads to a linear force-displacement curve as shown in the inset. As the applied strain increases (second regime), out-of-plane buckling occurs, resulting in force reduction of the paper. In the final regime, the elementary plates in Kent paper are straightened, which induces an increase in the stiffness again. In this design, a small thickness¹²⁶ promotes out-of-plane buckling, and thereby shortens the initial regime. Bahamon et al.^{127, 128} used molecular dynamics (MD) to calculate the stress-strain curve of kirigami structures in graphene, in which the initial stiff regime almost disappears entirely.

Figure 6. Kirigami and origami designs.

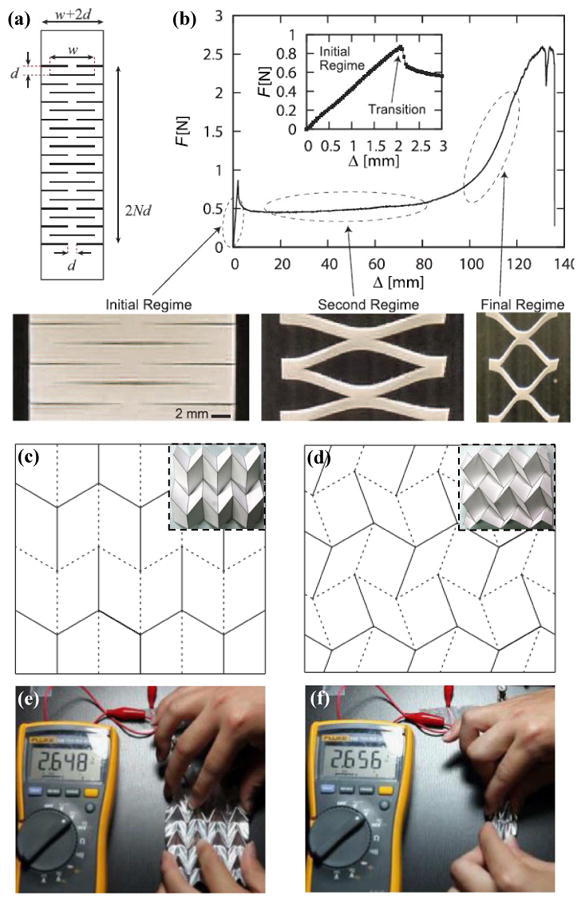
(a) Kirigami pattern in a Kent paper and (b) its force-displacement curve with initial (inset), second and final regimes. Crease mesh and folding morphology for (c) Miura and (d) double corrugation origami. (e) Folding and (f) unfolding status of an origami lithium-ion batteries while it was connected to a voltmeter. Panels (a) and (b) are adapted with permission from Ref. [125] (Copyright 2016, Nature Publishing Group). Panels (c) and (d) are adapted with permission from Ref. [134] (Copyright 2016, The Royal Society). Panels (e) and (f) are adapted with permission from Ref. [57] (Copyright 2014, Nature Publishing Group).

Origami^129-133 is an ancient art of paper folding, in which the key is to form pre-defined crease patterns. Figures 6c and d¹³⁴ show two quadrilateral mesh creases. Folding these ‘mountain’ (solid line) and ‘valley’ (dotted line) creases forms Miura and double corrugation origami (Figures 6c and d, inset). These origami designs possess similar mechanics properties as those of the wavy and wrinkled structures. At a small applied strain, the parallelogram faces experience almost zero strains except at the creases, and the entire system has a very low stiffness. As the applied strain increases, the folding creases straightened, and the parallelogram faces dominate the stretching such that the structure becomes stiff. These deformation mechanisms result in ‘J-shaped’ stress-strain behavior¹³⁵. Recently, Yan et al.¹³⁶ proposed a strategy to produce engineered folding creases for microscale origami structures in polymer films, with ‘J-shaped’ stress-strain behaviors. Song et al.⁵⁷ exploited an origami design with 45° Miura folding for applications in a lithium-ion battery that is highly deformable at different modes (e.g., stretching, folding, bending and twisting). Figures 6e and f show folded and unfolded origami lithium-ion batteries where the output voltages remain almost unchanged (2.65 V) during the deformations.

6. Textile design

Textiles are flexible materials that consist of networks of natural or artificial yarns as shown in Figure 1f. Weaving and knitting⁵⁸ are the most widely used methods for manufacturing textiles. In the weaving process (Figure 1f, left), perpendicular and individual yarns (warp and weft yarns) interlace together to form the fabric. In the knitting process (Figure 1f, middle), the yarns adopt wavy, looped configurations, with the potential to offer large stretchabilities. Figure 7a gives a schematic diagram of stress-strain responses for a single yarn, a weaved fabric, and a knitted fabric⁵⁸. The single yarn has a relative linear stress–strain behavior and a large initial modulus. The ‘J-shaped’ stress–strain behavior of the knitted fabric is more significant than that of the weaved fabric, while they both approach the stiffness of the single yarn at high strain. Figure 7b shows the load-displacement curves for samples of cotton knitted fabrics cut at different angles¹³⁷, displaying a significant anisotropy. The sample cut at 90° direction has the lowest initial stiffness and largest transition strain between low and high stiffness, followed by the 45° and 0° directions. For 3D textile fabrics, braiding (Figure 1f, right) is a widely used method, which forms the textile by inter-plaiting yarns along three orthogonal directions, also with capabilities in offering ‘J-shaped’ stress–strain behavior¹³⁸. Figure 7c shows stress-strain responses and optical images of a fabric integrated with electronics under stretching¹³⁹. As for the other cases mentioned previously, the ‘J-shaped’ stress–strain behavior of the fabric maintains compliance of stretchable electronics at small strain, and also eliminates the possibility of failure at large strain¹⁴⁰.

Figure 7. Textile design.

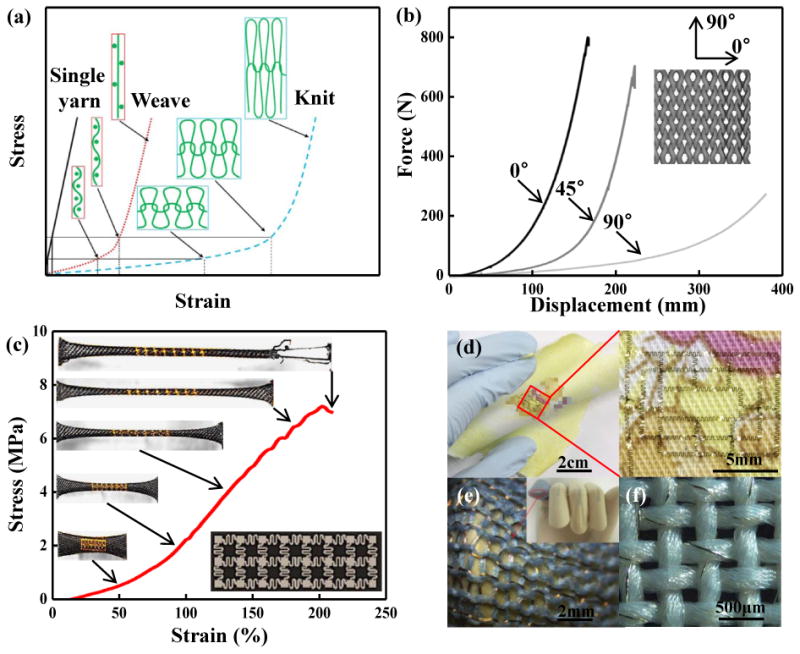
(a) Stress-strain responses of a single yarn, a weaved fabric, and a knitted fabric. (b) Anisotropy of a knitted fabric cut under different angles. (c) Stress-strain response of a fabric integrated with stretchable electronics. (d) An ultrathin IGZO-based 7-stage ring oscillator transferred on a handkerchief. (e) A knitted fabric circuit board on a human finger. (f) Copper wires embedded in yarns to realize a textile circuit. Panel (a) is adapted with permission from Ref. [58] (Copyright 2017, the American Association for the Advancement of Science). Panel (b) is adapted with permission from Ref. [137] (Estonian Academy Publishers). Panel (c) is adapted with permission from Ref. [139] (Copyright 2014, Nature Publishing Group). Panel (d) is adapted with permission from Ref. [141] (Copyright 2016, Nature Publishing Group). Panel (e) is adapted with permission from Ref. [142] (Copyright 2014, The Royal Society). Panel (f) is adapted with permission from Ref. [59] (Copyright 2014, MDPI).

The rough textures of the fabric can create challenges in the transfer of stretchable electronics onto its surface. Yoon et al.¹⁴¹ introduced an artificial cilia structure at the periphery regions of stretchable electronic platforms as adhesive elements to facilitate transfer printing. Using this strategy, an ultrathin layer of indium gallium zinc oxide as the basis of a 7-stage ring oscillator was successfully transferred onto a handkerchief, as shown in Figure 7d. Figures 7e and f show two alternatives approaches for integrating stretchable electronics with fabric: (1) replacing parts of fabric yarns by metal wire (Figure 7e)¹⁴²; (2) embedding metal wire into fabric yarns (Figure 7f)⁵⁹.

7. Concluding remarks

Collectively, the advances in materials and mechanics described here provide several promising engineering approaches to materials with ‘J-shaped’ stress–strain behaviors, with potential for applications in tissue engineering and biomedical devices. Table 1 summarizes the characteristic dimensions, fabrication methods and featured performances of these approaches described in this review paper. Nevertheless, there are many opportunities for further work. For example, previous studies on artificial tissues mainly focus on matching the ‘J-shaped’ stress–strain responses of biological tissues in 1D (e.g., muscle fiber and ligament), 2D (e.g., skin) or very simple 3D (e.g., trachea and blood vessel) configurations. Reproduction of nonlinear, multi-axial, mechanical behaviors in complex 3D organs/tissues remains a challenge. Many biological tissues (e.g., ligament) have intrinsic anisotropic mechanical properties and different tension-compression moduli, also representing design challenges in the tissue engineering. In addition to mechanical compatibility with biological tissues, the biocompatibility to avoid the immune response in the tissue engineering is important to consider, which limits the material selections for the artificial tissues. The strain-limiting structures introduced in this paper offer only a capacity to shield stretchable electronics from in-plane tension. Development of structural designs with strain-limiting properties under in-plane compression or out-of-plane pressure by exploiting 3D designs represents an important direction for future research. Furthermore, the thickness and stiffness of the stretchable electronics increase after integration with the strain-limiting structures, which may increase the foreign body sensation of the biological tissues when wearing such stretchable electronics. Optimization of the structural designs to enable reduced thickness and stiffness of the entire integrated device system is an important consideration for future bio-integrated applications. In conclusion, the above opportunities provide strong motivation for continued and expanded efforts in the fields of biomedical devices and stretchable electronics.

Table 1.

Minimum microstructure dimensions, fabrication methods and featured performances of various structural designs to achieve ‘J-shaped’ stress–strain behaviors.

Design	Minimum microstructure dimension	Fabrication	Featured performance
Random network design	∼10nm	Ionic liquid grinding63,64, two-step shearing65, plasma-induced modification66, and two-step polymerization67	Small dimension (Nano scale)
Deterministic network design	∼100μm	Lithographic approach49	High degree of design flexibility
Wavy and wrinkled design	∼100μm	Thermally induced mismatch91, pre-strain92-95	Sharp transition point, and high ratio of tangent to elastic modulus
Helical design	∼10μm	3D printing99, mechanically-guided approach112	Strain limiting feature only along the axial direction of helices
Kirigami and origami designs	∼10μm	Lithographic approach56, laser cutting122, mechanically-guided approach136	Transformable between 2D and 3D configurations
Textile design	∼1mm	Weaving58, knitting58, and braiding59	Mature technology for commercial application

Biographies

John A. Rogers is the Louis Simpson and Kimberly Querrey Professor of Materials Science and Engineering, Biomedical Engineering, Mechanical Engineering, Electrical Engineering and Computer Science, Chemistry and Neurological Surgery at Northwestern University where he also serves as Director of the Center on Bio-Integrated Electronics. Rogers' research focuses on unusual electronic and photonic devices, with an emphasis on bio-integrated and bio-inspired systems. He has published nearly 600 papers and is a member of the National Academy of Engineering, the National Academy of Sciences and the American Academy of Arts and Sciences.

Xue Feng is a Professor of Engineering Mechanics at Tsinghua University. His research interests include flexible electronics, solid mechanics and experimental mechanics in extreme environments. He is an associate editor of “Journal of Applied Mechanics” (ASME Transactions), and serves on the editorial board of “npj Flexible Electronics” and “Flexible and Printed Electronics”.

Yihui Zhang is an Associate Professor of Engineering Mechanics at Tsinghua University. Before joining Tsinghua, he was a Research Assistant Professor at Northwestern University. His research interests include mechanically guided 3D assembly, bioinspired soft materials, and stretchable electronics. His recent honors and awards include ASME Journal of Applied Mechanics Award (2017), MIT Technology Review's 35 Innovators Under 35 (2016), Qiu Shi Outstanding Young Scholar Award (2016). He is an associate editor of Journal of Applied Mechanics (ASME Transactions), and serves on the editorial board of Proceedings of the Royal Society A, npj Flexible Electronics and Acta Mechanica Solida Sinica.

Yinji Ma is a postdoctoral fellow at the Northwestern University of USA. He received his PhD degree from Tsinghua University of China. His research interests include experimental mechanics, solid mechanics and flexible electronics.

Yonggang Huang is the Walter P. Murphy Professor of Mechanical Engineering, Civil and Environmental Engineering, and Materials Science and Engineering at Northwestern University. He is interested in mechanics of stretchable and flexible electronics, and mechanically guided deterministic 3D assembly. He is a member of the US National Academy of Engineering. His recent research awards (since 2013) include the Drucker Medal in 2013 and Nadai Medal in 2016 from American Society of Mechanical Engineers, and Prager Medal in 2017 from the Society of Engineering Sciences; and Highly Cited Researcher.