Differential item functioning magnitude and impact measures from item response theory models

Abstract

Measures of magnitude and impact of differential item functioning (DIF) at the item and scale level, respectively are presented and reviewed in this paper. Most measures are based on item response theory models. Magnitude refers to item level effect sizes, whereas impact refers to differences between groups at the scale score level. Reviewed are magnitude measures based on group differences in the expected item scores and impact measures based on differences in the expected scale scores. The similarities among these indices are demonstrated. Various software packages are described that provide magnitude and impact measures, and new software presented that computes all of the available statistics conveniently in one program with explanations of their relationships to one another.

This paper describes magnitude and impact measures of item and scale level effects of differential item functioning (DIF) that are derived from item response theory (IRT) models, and specialized parameterizations of structural equation models (SEM).

The magnitude of DIF relates to item level effect sizes and refers to the degree of difference in item performance between or among groups, conditional on the trait assessed, denoted theta (θ). Magnitude has been defined as the weighted (by the trait distribution) group differences in the probability of an affirmative item response (Wainer, 1993). Magnitude measures are an essential component of examining DIF because reliance upon significance tests alone may result in identification of items with inconsequential DIF (Gómez-Benito, Dolores-Hidalgo, & Zumbo, 2013; Hambleton, 2006).

Impact refers to the influence of DIF on the scale score at the aggregate and individual level. In the context of IRT, aggregate DIF is evidenced by constructing and plotting differences in “test” response functions (Lord, 1980; Lord & Novick, 1968), also referred to as test characteristic curves (TCC) or expected scale score functions. Similar approaches are used in the context of SEM in which unadjusted and DIF adjusted means are compared. Individual-level impact is examined by comparing DIF adjusted and unadjusted trait (theta) estimates for individual respondents. These measures are described in more detail below.

True scores and expected scores

IRT-derived magnitude and impact measures described here are based on the notion of IRT true scores (Lord, Novick, & Birnbaum, 1968). The item true score function (also called the expected item score function or item characteristic curve) describes the relationship between the trait level and the person’s expected value of the item score. A person’s true score is his or her expected score, expressed in terms of probabilities for binary items and weighted probabilities for polytomous items. The test characteristic curve (expected scale score function) relates true scores (average expected scores) to theta.

DIF and expected scores

The use of expected scores to examine DIF magnitude for binary items was proposed by Wainer (1993), and expanded for polytomous items by Kim (see Kim, Cohen, Alagoz, & Kim, 2007). Raju, van der Linden and Fleer (1995) proposed a similar methodology to examine magnitude of DIF. These measures and/or related graphics are contained in several software packages described below: Differential Functioning of Items and Tests (DFIT; Oshima, Kushubar, Scott, & Raju, 2009; Raju et al., 2009); Item Response Theory for Patient Reported Outcomes (IRTPRO; Cai, duToit, & Thissen, 2009), logistic ordinal regression differential item functioning (lordif; Choi, Gibbons, & Crane, 2011), and a software package introduced here (MAGNITS). Additionally, Woods (2011) introduced the average unsigned difference (AUD), which is contained in two of the packages.

Effect size estimates and expected score calculation

Each respondent is posited to have two true (expected) scores, one as a member of the focal (studied) group and one as a member of the reference group. For each person in the focal group, the estimated theta is calculated so that the comparison groups are on the same scale (i.e., equated). Given the estimated theta for each person, his or her estimated true score on item i if a member of the reference group (P_R(θ)) is calculated, and also the estimated true score if a member of the focal group (P_F(θ)). For binary items, expected (true) scores equal the probability of item endorsement, conditional on trait (θ) level: P_i(θ_s). For example, for a binary item, P_iF(θ_s) is the expected score for individual s as a member of the focal (studied) group, reflecting the probability of a correct response to a test item.

Graded response model

For a polytomous item i, with K categories taking a graded response form, $P_{iK}^{\ast }(\theta )={\{1+\exp [-{\alpha }_i(\theta -{\beta }_{iK})]\}}^{-1}$, the true score can be expressed as:

$$T_i\left(\theta \right)={\displaystyle \sum _{k=1}^{K_i}{y}_{ik}{P}_{ik}\left(\theta \right)}.$$

The expected score is thus the sum of the weighted probabilities of scoring in each of the possible categories for the item. For an item with 5 response categories, coded 0 to 4, for example, this sum would be: $0\ast \left[{\mathrm{P}}_{\mathrm{i}0}\left({\theta }_{\mathrm{s}}\right)\right]+1\ast {\mathrm{P}}_{\mathrm{i}1}\left({\theta }_{\mathrm{s}}\right)+2\ast {\mathrm{P}}_{\mathrm{i}2}\left({\theta }_{\mathrm{s}}\right)+3\ast {\mathrm{P}}_{\mathrm{i}3}\left({\theta }_{\mathrm{s}}\right)+4\ast {\mathrm{P}}_{\mathrm{i}4}\left({\theta }_{\mathrm{s}}\right)$. For a detailed explication, see Collins, Raju, and Edwards (2000); Teresi et al. (2007).

Most of the effect size measures described here are based on examination of the differences in the expected item scores for two or more groups, as illustrated in Figure 1, panel B. For example, for item i, calculated is the average (expected value) of the squared difference between expected item scores for individuals as a member of the focal group and as a member of the reference group (see also Morales, Flowers, Gutierrez, Kleinman, & Teresi, 2006).

Figure 1.

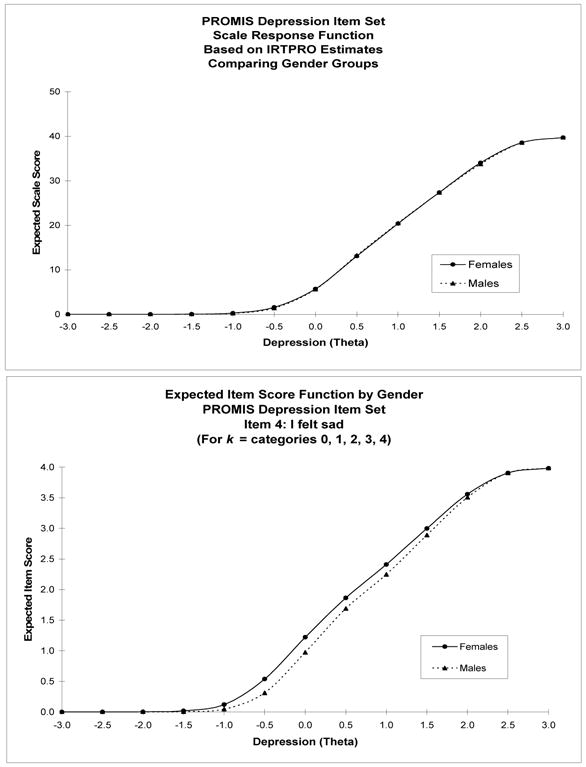
Patient Reported Outcomes Measurement Information System^® (PROMIS^®) depression short form item set: Expected scale and item scores for gender subgroups from which differential item functioning magnitude and impact measures can be constructed

The precursors to these measures were various area and probability difference measures. The exact area methods compare the areas between the item characteristic functions estimated in different groups. Although a detailed explication of these measures is beyond the scope of this article, they are related to those described here (see also Raju, 1988; 1990; Teresi, Kleinman, & Ocepek-Welikson, 2000).

The signed and unsigned area differences for binary items are defined as follows (see Raju, 1990):

$$\begin{array}{l}\mathrm{SA}\left(\text{signed area}\right)={\widehat{b}}_2-{\widehat{b}}_1;\\ \mathrm{UA}(\text{unsigned}\text{area})=\left|\left[2\left({\widehat{a}}_2-{\widehat{a}}_1\right)/D{\widehat{a}}_1{\widehat{a}}_2\right]\left[\ln \left\{1+\exp [D{\widehat{a}}_1{\widehat{a}}_2\left({\widehat{b}}_2-{\widehat{b}}_1\right)/\left({\widehat{a}}_2-{\widehat{a}}_1\right)\right\}\right]-\left({\widehat{b}}_2-{\widehat{b}}_1\right)\right|\end{array}$$

The variance for the signed area is: ${\sigma }^2\left(\mathrm{SA}\right)={\sigma }^2\left({\widehat{b}}_2\right)+{\sigma }^2\left({\widehat{b}}_1\right)$;

where, ${\sigma }^2\left({\widehat{b}}_i\right)=I{\widehat{a}}_i/\left(I{\widehat{a}}_{i}I{\widehat{b}}_i-I^2{\widehat{a}}_i{\widehat{b}}_i\right)$ and I is the information matrix.

The variance for the unsigned area is:

$${\sigma }^2\left(\mathrm{UA}\right)=B_1^2{\sigma }^2\left({\widehat{b}}_1\right)+B_2^2{\sigma }^2\left({\widehat{b}}_2\right)+A_1^2{\sigma }^2\left({\widehat{a}}_1\right)+A_2^2{\sigma }^2\left({\widehat{a}}_2\right)+2B_1{A}_1\sigma \left({\widehat{b}}_1,{\widehat{a}}_1\right)+2B_2{A}_2\sigma \left({\widehat{b}}_2,{\widehat{a}}_2\right),$$

where B₁ = 1 – 2 exp(Y) / (1 + exp(Y)) and B₂ = −B₁

$$\begin{array}{l}{A}_1=2/{\widehat{a}}_1^2\left\{{\widehat{a}}_1{\widehat{a}}_2\left({\widehat{b}}_2-{\widehat{b}}_1\right)/\left({\widehat{a}}_2-{\widehat{a}}_1\right)\left(\exp \left(Y\right)/(1+\exp \left(Y\right)\right)-\ln \left[1+\exp \left(Y\right)\right]/D\right\};\\ A_2=(-{\widehat{a}}_1^2/{\widehat{a}}_2^2)/A_1\end{array}$$

and $Y=D{\widehat{a}}_1{\widehat{a}}_2\left({\widehat{b}}_2-{\widehat{b}}_1\right)/\left({\widehat{a}}_2-{\widehat{a}}_1\right)$. D is a scaling constant equal to 1.7 that places values of the logistic function to within 0.01 of those of the normal distribution function.

Wainer (1993) points out several problems with using area statistics to assess DIF. When ability distributions differ between reference and studied groups, area statistics may show large differences but affect very few subjects. Conversely, a small area difference may affect a relatively large number of people in the studied group. The area statistics do not take into account the distribution of the ability parameter within the focal group. Also, in a 3-parameter model the area differences cannot be computed precisely if the c (guessing) parameter differs in the two groups.

Wainer effect size estimates

Wainer (1993) proposed several effect size measures for binary items, denoted T (1) to T (4). T (2), shown below is thus the sum of the differences $({\displaystyle \sum _{i=1}^N\left[P_R\left(\theta \right)-P_F\left(\theta \right)\right]})$ across all members of the focal group.

Based on the estimated theta for each member of the focal group, for any given item, the true score for a subject is calculated based on the estimated parameters for the reference group (T_R(θ)) and the true score is also calculated based on the estimated parameters for the focal group (T_F(θ)). Let N_F denote the number of subjects in the focal group.

$$\begin{array}{l}T\left(2\right)={\displaystyle \sum _{i=1}^N\left[T_R\left(\theta \right)-T_F\left(\theta \right)\right]}\\ T\left(1\right)=T\left(2\right)/N_F\end{array}$$

(In DFIT, this is called “Mean of D”. This can be either positive favoring the reference group or negative favoring the focal group.)

$$\mathrm{AUD}={\displaystyle \sum _{i=1}^N\left|\left[T_R\left(\theta \right)-T_F\left(\theta \right)\right]\right|}/N_F$$

(The AUD described below is the same as T (1) except that the absolute value of the difference is taken). This is also a graphic available in lordif (see Figure 2, lower right panel.)

$$\begin{array}{l}T\left(4\right)={\displaystyle \sum _{i=1}^N{\left[T_R\left(\theta \right)-T_F\left(\theta \right)\right]}^2}\\ T\left(3\right)=T\left(4\right)/N_F\end{array}$$

(This is the same as non-compensatory DIF (NCDIF) index (Raju et al., 1995) described below). This is the sum of the unsigned (squared) differences weighted by the theta distribution for the focal group.

T (4) is the sum of the differences squared, resulting in an unsigned difference such that any difference, regardless of the direction is significant. Because T (4) is the sum of the squared differences and T (3) is the average squared difference, these indices capture the magnitude of non-uniform DIF, whereas T (1) and T (2) do not. Non-uniform DIF occurs when the probability of response is in a different direction for the reference and focal groups, at different levels of the latent ability (θ). For example, Black older persons may have a lower probability than White older persons of endorsing a depression item at low levels of the depression trait and higher probabilities of endorsement than White older persons at higher levels.

NCDIF

A method for quantification of the difference in the average expected item scores is the NCDIF index (Raju et al, 1995) used in DFIT (Oshima, et al., 2009; Raju et al., 2009). NCDIF is the average squared difference between the expected item scores for comparison groups, based on the actual distribution of thetas in the focal group. This is the same as Wainer’s T (3) provided that one uses the actual distribution of estimated thetas in computing Wainer’s statistics. These measures can be used with both binary and polytomous items and are thus appropriate for both Rasch (Rasch, 1980) and graded response (Samejima, 1969) models.

Prior to computations, it is necessary to equate the item parameters so that they are on the same scale for comparison groups. This is usually accomplished with a linear transformation of the item parameters for the focal (studied or targeted) group; however, see Chalmers, Counsell, and Flora (2016) for an alternative to linking. Scaling constants are defined and the linking constants are often computed using the test characteristic curve method (Stocking & Lord, 1983). Baker’s Equate (Baker, 1995) program has typically been used for this procedure. (This procedure is explicated in more detail in the section on software below.) It is noted that just like other methods, it is necessary to provide iterative purification of the equating constants, after removing items with DIF (Huggins, 2014; Seybert & Stark, 2012).

NCDIF for item (i) is defined as the average squared difference between the true or expected scores for an individual (s) as a member of the focal group (F) and as a member of the reference group (R). For each subject in the focal group, two estimated scores are computed. One is based on the subject’s ability estimate and the estimated item parameters for the focal group and the other based on the ability estimate and the estimated item parameters for the reference group. Each subject’s difference score (d) is squared and summed for all subjects (j = 1, N_F) to obtain NCDIF.

${\mathrm{NCDIF}}_{\mathrm{i}}=\left[{{\displaystyle \sum _{j=1}^{N_F}\left({\mathrm{ES}}_{\mathrm{siF}}-{\mathrm{ES}}_{\mathrm{siR}}\right)}}^2\right]/{\mathrm{N}}_{\mathrm{F}}$, which can also be expressed as T (4) / N_F, given above.

While chi-square tests of significance are available for NCDIF, these were found to be too stringent, over identifying DIF when sample sizes are larger. Cutoff values established based on simulations (Fleer, 1993; Flowers, Oshima, & Raju, 1999) can be used in the estimation of the magnitude of item-level DIF. For example, the cutoff values recommended by Raju are 0.006 for binary items, and 0.024, 0.054 and 0.096 for polytomous items with three, four and five response options (Raju, 1999). Because NCDIF is expressed as the average squared difference in expected scores for individuals as members of the focal group and as members of the reference group, the square root of NCDIF provides an effect size in terms of the original metric. Thus, for a polytomous item with three response categories, the recommended cutoff of 0.024 would correspond to an average absolute difference greater than 0.155 (about 0.16 of a point) on a three point scale (see Raju, 1999; Meade, Lautenschlager, & Johnson, 2007).

Because of the sensitivity of cutoff thresholds to the distribution of parameter estimates, simulations to derive cutoffs based on empirical distributions have been incorporated into the latest versions of software such as DFIT (Raju et al., 2005) and ordinal logistic regression (Choi et al., 2011). Recently tables have been developed for use in determining moderate and large DIF for the NCDIF statistic; however, they apply only to dichotomous items (Wright & Oshima, 2015). Simulations by Meade et al. (2007) resulted in the recommendation to use empirically derived DIF cutoff values. Seybert and Stark (2012) examined item parameter replication (IPR) methods used in the newer software with testwide cutoffs developed by Flowers et al. (1999) based on simulations. It was found that it is critical to perform iterative linking involving purification of the equating constants in order to maintain a balance between power and type 1 error (excess DIF detection). The findings were that test-wide critical values were more powerful than IPR in detecting DIF, but at the expense of inflated type 1 error. However, under iterative linking procedures, the test-wide critical values given above appear to work sufficiently well to continue their use.

AUD

The average unsigned difference is the absolute value of the difference between the expected item response functions, weighted by the focal (studied) group distribution. The differences can be evaluated at various quadrature (theta) points (Woods, 2011). However, in many instances, evaluating the differences at theta points that reflect the observed densities in the current sample may provide a more accurate reflection of the magnitude of DIF for the data investigated.

For the AUD the absolute value of the difference between the expected item scores is calculated.

$\mathrm{AUD}={\displaystyle \sum _{i=1}^N\left|\left[T_R\left(\theta \right)-T_F\left(\theta \right)\right]\right|/N_F}.$

The AUD is the same as T (1) except that it is the absolute value of the differences across subjects that is summed, and divided by N. When the AUD is close to the value of T (1), this is an indication of uniform DIF; that is, the probability of response is consistently higher for either the reference or focal group across all levels of the latent ability θ. For this reason it is helpful to report both T (1) and AUD in order to investigate instances of non-uniform DIF, in which case, T (1) and AUD could differ substantially.

Wainer’s T (2) is the sum of the differences (both positive and negative), so that positive and negative differences can potentially cancel each other out. Thus it is possible to have a fairly large value for AUD, while T (2) could be close to zero in the case of nonuniform DIF. The AUD always takes a positive value, whereas T (2) and T (1) can be negative. Kim (2000) suggests that when the absolute value of T (1) is greater than .10, the item requires ‘close examination’, but the basis for this claim is unclear. Based on empirical data shown in the examples in this series of articles, this cutoff may be overly conservative.

Impact measures

IRT severity parameters are on the same (usually) z-score metric, as the latent construct, so that a severity or location (b) parameter difference of 0.50 represents one half standard deviation on the trait estimate (θ). Thus, effect sizes at the item level have a relationship to impact measures at the scale level (Steinberg & Thissen, 2006). Several impact measures based on IRT examine the group differences in the area between the expected scale score functions (see Figure 1, panel B and Figure 3).

The Differential Test Functioning (DTF) index (Raju et al., 1995) is a summary measure of these differences in expected scale (total test) scores that incorporates a weight, and reflects the aggregated net impact. The DTF is the sum of the item-level compensatory DIF indices, and as such reflects the results of DIF cancellation. Stark, Chernyshenko, and Drasgow (2004) describe a similar effect size measure, Differential Test Functioning R (DTFR), a total test score statistic. DTFR measures the difference between groups in the relationship of θ to the expected observed scores.

Defining θ as the estimated theta for a given subject in the focal group, TCC_EF(θ) is that subject’s expected total test score based on the equated focal (EF) group parameter estimates of a’s and b’s for all items in the test. Similarly, TCC_R (θ) represents the same subject’s expected total test score based on the reference group parameter estimates of a’s and b’s. Then the DTFR value in raw score points can be obtained by integration, as shown in Stark et al. (2004, pg. 499):

DTFR = ∫[TCC_R (θ)−TCC_EF (θ)] f_F (θ) d(θ), where f_F(θ) is the ability density for the focal group, which is assumed to be normally distributed, and TCC_EF is the expected total test score for the focal group based on focal group equated item parameters. TCC_R is the expected total test score based on reference group parameters.

The proposed calculation of DTFR described below is not based on the assumption that the ability density for the focal group is normally distributed; instead statistics are based on the actual distribution of estimated thetas in the focal group (after equating). This measure assesses the expected impact of DIF on scores in absolute group differences between item true-score functions and density-weighted differences between groups. The latter, shown below, adjusts for the actual distribution of individuals; if few respondents are located at the point where the differences are greatest, the weighted impact will be less.

For each member of the focal group, the expected total test score is calculated based on estimated parameters for the reference group and then based on estimated parameters for the focal group.

Then, $\mathrm{DTFR}={\displaystyle \sum _{i=1}^N\left[TC{C}_R\left(\theta \right)-TC{C}_{EF}\left(\theta \right)\right]/N_F}$, where N_F = the number of subjects in the focal group.

A positive value for DTFR is indicative of DIF impact against the focal group, and a negative value in favor of the focal group. A DTFR value represents the number of raw score points that are due to scale level DIF.

To obtain a measure of magnitude of effect for DTFR, one can divide DTFR by the standard deviation for the focal group’s observed scores or alternatively, the standard deviation of the expected scale scores. The MAGNITS program described below computes the standard deviation of the expected scale scores because DTFR is based on the difference in expected scale scores. Because this method yields a slightly smaller standard deviation, the effect size (d) would be slightly larger (Stark et al., 2004).

$$d_{\mathit{DTF}}=\mathit{DTFR}/S{D}_F$$

This statistic is closely related to DTF (Raju et al., 1995). Instead of the above,

$$\mathrm{DTF}={\displaystyle \sum _{i=1}^N{\left[TC{C}_R\left(\theta \right)-TC{C}_{EF}\left(\theta \right)\right]}^2/N_F}.$$

Because each difference is squared, the positive and negative values of the differences do not cancel each other out, which can happen with the DTFR statistic described above in the case of non-uniform DIF. It is because of this difference between DTFR and Raju’s DTF that in the case of DTFR, individual items may show DIF but at the scale level DTFR may be quite small. Egberink, Meijer and Tendeiro (2015) point out that if the total test score is the main concern, a test statistic such as DTFR will only be large if many items in the scale exhibit uniform DIF in the same direction; that is, favoring either the reference or the studied group.

Individual impact

The impact measures just described are all at the aggregate or group level rather than the individual level. The impact on specific individuals rather than on the group as a whole can also be examined. Individual impact can be assessed through an examination of changes in theta estimates with and without adjustment for DIF. The unadjusted thetas are produced from a model with all item parameters set equal for the two groups. The adjusted thetas are produced from a model with parameters that showed DIF based on the IRT results estimated separately (freed) for the groups. The capacity to fix and free parameters based on DIF, and compare theta estimates is incorporated into software packages such as IRTPRO (Cai et al., 2009). This method permits comparisons of trait measure estimates that are DIF free (adjusted) to those with parameters estimated without DIF adjustment. This methodology has been used by several authors to examine the individual impact of DIF (e.g., Kim, Pilkonis, Frank, Thase, & Reynolds, 2002; Teresi et al., 2009).

Crane and colleagues (2007) used a similar method in calculating the difference between naïve scores that ignore DIF and scores that account for DIF to examine cumulative impact of DIF on individual participants. The distribution of these difference scores is then examined; for individual-level DIF impact, a box-and-whiskers plot of the difference scores is constructed. The differences due to DIF are plotted against the median standard error of measurement (SEM). Differences larger than that value are termed salient individual-level DIF impact (see Figure 4).

Software

DFIT

The DFIT methodology (Flowers et al., 1999; Raju, 1999; Oshima, & Morris, 2008; Raju, et al., 1995; Raju et al., 2009) permits examination of the magnitude of the gap between the ICCs (in this case boundary response functions) for two or more groups, such as illustrated in Figure 1. Non-Compensatory DIF (NCDIF) is an effect size measure that is weighted by the focal group density such that more weight is given to differences in the region of the trait with the highest frequency in the targeted group. As reviewed above, because simulation studies found over-identification of DIF with the use of Chi-square tests, cutoff values are used instead to identify DIF (see Morales, et al., 2006). DFIT yields both magnitude and impact measures.

lordif

Psychometric software is available in R (Rizopoulus, 2006, 2009). The R package lordif (Choi et al., 2011), similar to DFIT is based on the notion of true (expected) scores, from which various DIF magnitude and impact measures are derived. lordif uses mirt in R (Chalmers, 2012; see also https://cran.r-project.org/web/packages/mirt/index.html) to obtain IRT item parameter estimates for the Graded Response Model (Samejima, 1969) or the Generalized Partial Credit Model (Muraki, 1992), and the Design package for OLR. The R-Project website is https://www.r-project.org/. The link is: http://watson.nci.nih.gov/cran_mirror/.lordif is free software and can be found under “Packages” at the following link: https://cran.r-project.org/web/packages/lordif/index.html. Figures 2–4 provide illustrations from lordif.

DIF magnitude measures

One measure shown in the lower right panel of Figure 2 is similar to the non-compensatory DIF test of Wainer (1993). However, the metric in this panel (shown for a range of theta values) is summed, and is the AUD described by Woods (2011) as the unsigned difference between the true scores for the comparison groups weighted by the studied (focal) group density. The unweighted unsigned differences appear in the upper right panel of Figure 2. As shown in Figure 2, the expected item scores (upper left panel) and category response functions (lower left panel) are also presented.

Figure 2.

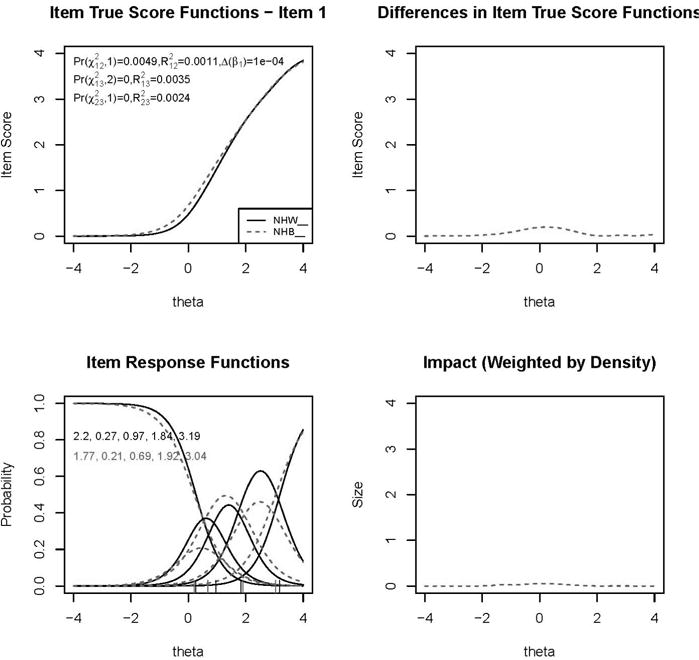
Example graphics depicting magnitude of differential item functioning (from lordif) comparing non-Hispanic Blacks (NHB) and non-Hispanic Whites (NHW)

Expected item scores; category response functions; differences in expected scores and density weighted differences.

(The latter are similar to Wainer’s (1993) magnitude measures and are unsigned differences weighted by the theta distributions of the focal group) (lordif depression NHB vs NHW)

DIF aggregate impact measures

lordif also shows the graphic of the expected item and test score functions for groups, including differences for items with DIF. Expected test score plots show the expected total (sum scores) for groups for different theta levels (See Figure 3.)

Figure 3.

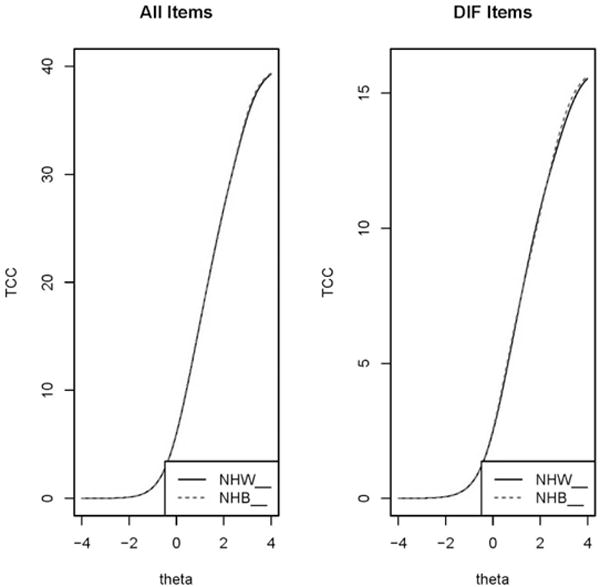
Graph depicting differential item functioning impact with all items included and with only items with DIF included (from lordif) comparing non-Hispanic Blacks (NHB) and non-Hispanic Whites (NHW)

Aggregate DIF Impact:

Expected Scale Scores for groups at each theta level (Test Characteristic Curves) (lordif depression NHB vs NHW)

DIF individual impact

Individual theta scores are calculated after fixing and freeing parameters for items without and with DIF respectively. Graphics are displayed (see Figure 4). Theta estimates by group before and after accounting for DIF and median differences before and after DIF adjustment (fixing and freeing parameters based on DIF) are plotted. A dotted line shows the mean difference between the initial and DIF-adjusted theta estimates.

Figure 4.

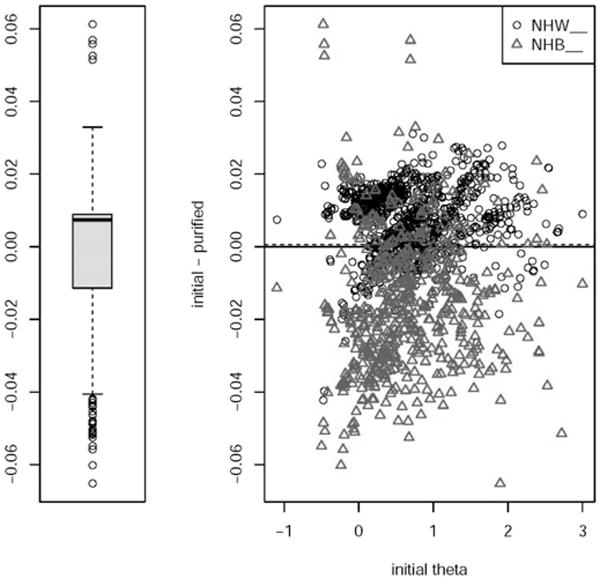
Graphs depicting individual-level differential item functioning impact (from lordif) comparing non-Hispanic Blacks (NHB) and non-Hispanic Whites (NHW)

Individual Impact (Theta estimates by group before and after accounting for DIF and median differences before and after DIF adjustment (fixing and freeing parameters based on DIF)

*Dotted line is the mean difference between the initial and DIF-adjusted theta estimates (lordif depression NHB vs NHW)

Just as with most such software, the Stocking-Lord (1983) equating procedure identifies the equating constants to place the IRT item parameters for groups on the same metric. The items without DIF are used as anchors (see below). The software package, lordif also allows the user to designate a specific subset of items s an anchor set.

MAGNITS

This program (available upon request from the authors) computes item-level magnitude and scale level impact measures of DIF (see Figure 5). The magnitude measures are as follows: T (1) through T (4) (Wainer, 1993); NCDIF (Raju et al., 1995) and AUD (Woods, 2011). The magnitude measures are all closely related to each other. Impact measures are DTF (Raju et al) and DTFR from Stark et al. (2004).

Figure 5.

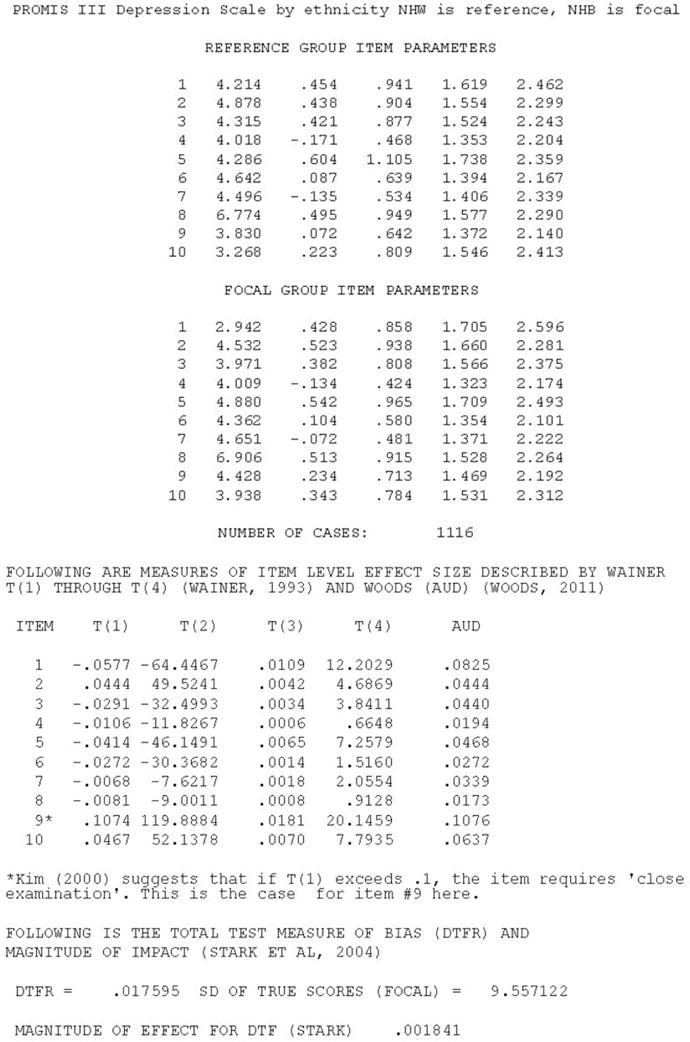
Output from MAGNITS showing magnitude and impact indices

As discussed above, prior to running this program, it is necessary to equate parameters and theta estimates for the focal group so that they are on the same metric scale as the reference group. There are several methods for doing so. Baker’s EQUATE (Baker, 1995) software, which employs the test characteristic curve method of Stocking and Lord (1983) is the most popular method of equating, and is used in Magnits; lordif also uses the Stocking and Lord (1983) procedure, which is explicated as follows, based on Teresi et al. (2000; pg 1663–1664).

In order to compare the a_i ’s (denoted a’s) and the b_i ’s (denoted b’s) of one group with those of another on the same set of items, a linear transformation of the a’s and b’s for the second group (usually the focal group) is performed so that the parameters for both groups are on the same scale. Two scaling constants, α and β, are defined : $b_i^{\ast }=\alpha b_i+\beta$, where b_i is the b for the item in the second group and $b_i^{\ast }$ is the equated b and $a_i^{\ast }=a_i∕\alpha$, where a_i is the a value for item i in the second group and $a_i^{\ast }$ is the equated a value.

More than two groups can be compared by equating each group to the reference group, determining the constants α and β for each of the two or more groups. The constants α and β then can be used to place the ability values of the subjects in group 2 on the same scale as the ability values for group 1. Equated θ ’s for group 2 are calculated in a fashion similar to that used for the b’s: ${\theta }_j^{\ast }=\alpha {\theta }_j+\beta$, where θ_j is the original θ, and ${\theta }_j^{\ast }$ is the equated θ for individual j.

The linking constants α and β are computed using the characteristic curve method (Stocking & Lord, 1983). If t_1i is the estimated true score of individual i of estimated ability level θ_i in group 1, and t_2i is the estimated true score of the same individual i if a member of group 2, then α and β are chosen to minimize the difference between t_1i and t_2i for all members of group 1. The function to be minimized is $f=1/N{\displaystyle \sum _{i=1}^N{\left(t_{1i}-t_{2i}\right)}^2}$, where N is the number of subjects in group 1.

It is noted that such linking algorithms may result in some error in estimation as contrasted with simultaneous linking in which parameter estimation and DIF testing is conducted holding constant the latent scale across groups (Woods, Cai, & Wang, 2013). As presented above, many magnitude measures such as those in this program and lordif rely on equating algorithms to link the groups on a common latent trait metric. DIF in the equating anchor set could compromise this process (Dorans, 2004). Recent simulations showed that directional DIF favoring one group over the other had a greater impact on equating (Huggins, 2014). While the Stocking and Lord equating method used in MAGNITS and lordif was more robust to the effects of DIF than an alternative method, in general and particularly under conditions of group differences in the mean trait level, as often occurs in health and mental health-related applications, DIF in the anchor set can affect equating (Huggins, 2014). Thus, purification of equating constants and careful selection of anchor items for each subgroup comparison is important. Such purification can be conducted using most software reviewed here.

Summary and conclusions

This paper is meant to orient the reader to magnitude and impact measures associated with IRT-based methods for DIF detection. Magnitude measures are an essential part of DIF detection because of the need to avoid false positives (Seybert & Stark, 2012), particularly in an environment in which items have been studied carefully and subjected to qualitative and quantitative analyses prior to DIF detection. It is desirable to identify and flag only items with salient DIF. Impact is essential at the aggregate level to determine if items identified with DIF have an appreciable impact at the scale level. However, also important is an examination of DIF at the level of the person.

Individual-level DIF impact may be important to clinicians who wish to know how different an unadjusted score might be from a score that accounted for DIF for a particular person. An example of this is shown, using the Patient Reported Outcomes Measurement Information System^® (PROMIS^®) anxiety item bank data (Choi et al., 2011), and in the depression item bank (Teresi, et al., 2009). Additional examples, using depression, anxiety and cognitive measures are found in the articles in this two-part series.

DIF magnitude and impact analyses are conducted to help answer the question of what difference is meaningful and makes a practical difference. Recent work on effect sizes in the context of DIF is presented in Stark et al. (2004); Steinberg and Thissen (2006); and Kim et al. (2007); and Seybert and Stark (2012). More work is needed in order to determine optimal cutoff values. For example, an effect size measure for NCDIF has been proposed recently (Wright & Oshima, 2015); however, only binary item response models were included. Most recently, Chalmers et al. (2016) have developed differential test functioning statistics for both polytomous and binary data that consider sampling variation and are not reliant upon cutoff scores. Empirically derived thresholds based on Monte Carlo simulations to detect optimal cutoffs for the sample investigated were embedded into lordif for various chi-square tests associated with ordinal logistic regression, based on a latent conditioning variable. Most software does not permit such calculations. In the context of DFIT, test-wide thresholds such as those developed by Flowers et al., (1999) may be sufficiently accurate (Seybert & Stark, 2012). Further work is needed to compare their performance with that of other methods of threshold derivation.