Estimates and Standard Errors for Ratios of Normalizing Constants from Multiple Markov Chains via Regeneration

Abstract

In the classical biased sampling problem, we have k densities π₁(·), …, π_k(·), each known up to a normalizing constant, i.e. for l = 1, …, k, π_l(·) = ν_l(·)/m_l, where ν_l(·) is a known function and m_l is an unknown constant. For each l, we have an iid sample from π_l,·and the problem is to estimate the ratios m_l/m_s for all l and all s. This problem arises frequently in several situations in both frequentist and Bayesian inference. An estimate of the ratios was developed and studied by Vardi and his co-workers over two decades ago, and there has been much subsequent work on this problem from many different perspectives. In spite of this, there are no rigorous results in the literature on how to estimate the standard error of the estimate. We present a class of estimates of the ratios of normalizing constants that are appropriate for the case where the samples from the π_l’s are not necessarily iid sequences, but are Markov chains. We also develop an approach based on regenerative simulation for obtaining standard errors for the estimates of ratios of normalizing constants. These standard error estimates are valid for both the iid case and the Markov chain case.

1 Introduction

The problem of estimating ratios of normalizing constants of unnormalized densities arises frequently in statistical inference. Here we mention three instances of this problem. In missing data (or latent variable) models, suppose that the data is X_obs, and the likelihood of the data is difficult to write down but X_obs can be augmented with a part X_mis in such a way that the likelihood for (X_mis, X_obs) is easy to write. In this case (using generic notation) we have p_θ(X_mis | X_obs) = p_θ(X_mis, X_obs)/p_θ(X_obs). The denominator, i.e. the likelihood of the observed data at parameter value θ, is precisely a normalizing constant. For the purpose of carrying out likelihood inference, if θ₁ is some reference value, knowledge of $\log \left(p_{\theta }(X_{\text{obs}})/p_{{\theta }_1}(X_{\text{obs}})\right)$ is equivalent to knowledge of log(p_θ(X_obs)): for these two functions the maximum occurs at the same point, and the negative second derivative at the maximum (i.e. the observed Fisher information) is the same.

A second example arises when the likelihood has the form p_θ(x) = g_θ(x)/z_θ, where g_θ is a known function. This situation arises in exponential family problems, and except for the usual textbook examples, the normalizing constant is analytically intractable. If for some arbitrary point θ₁ we know the ratio $z_{\theta }/z_{{\theta }_1}$, then we would know p_θ(x) up to a multiplicative constant and, as before, this would be equivalent to knowing p_θ(x) itself. A third example arises in certain hyperparameter selection problems in Bayesian analysis. Suppose that we wish to choose a prior from the family $\left\{{\pi }_h,h\in \mathscr{H}\right\}$, where the π_h’s are densities with respect to a dominating measure μ. For any h ∈ $\mathscr{H}$, the marginal likelihood of the data X when the prior is π_h is given by m_h(X) = ∫ p_θ(X)π_h(θ) μ(dθ), i.e. it is the normalizing constant in the statement “the posterior is proportional to the likelihood times the prior.” The empirical Bayes choice of h is by definition argmax_h m_h(X). Suppose that h₁ is some arbitrary point in $\mathscr{H}$. As in the previous two examples, for the purpose of finding the empirical Bayes choice of h, knowing $m_h(X)/m_{h_1}(X)$ is equivalent to knowing m_h(X). (One may also be interested in the closely related problem of estimating the posterior expectation of a function f(θ) when the hyperparameter is h, which is given by E_h(f(θ) | X) = (∫ f(θ)p_θ(X)π_h(θ) μ(dθ))/m_h(X). Estimating E_h(f(θ) | X) as h varies is relevant in Bayesian sensitivity analysis. The scheme for doing this used in Buta and Doss (2011) does not involve estimating m_h(X) itself and requires only estimating $m_h(X)/m_{h_1}(X)$ for some fixed $h_1\in \mathscr{H}$.)

Now, estimation of a normalizing constant is generally a difficult problem; for example, the so-called harmonic mean estimator proposed by Newton and Raftery (1994) typically converges at a rate that is much slower than $\sqrt{n}$ (Wolpert and Schmidler, 2011). On the other hand, estimating a ratio of normalizing constants typically can be done with a $\sqrt{n}$-consistent estimator. To illustrate this fact, consider the second of the problems described above, and let μ be the measure with respect to which the p_θ’s are densities. Suppose that X₁, X₂, … are a “sample” from $p_{{\theta }_1}$ (iid sample or ergodic Markov chain output). For the simple and well-known estimator $(1/n){\displaystyle {\sum }_{i=1}^n{g}_{\theta }(X_i)/g_{{\theta }_1}(X_i)}$ we have

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{g_{\theta }(X_i)}{g_{{\theta }_1}(X_i)}}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\displaystyle \int \frac{g_{\theta }(x)}{g_{{\theta }_1}(x)}{p}_{{\theta }_1}(x)\mu (dx)}=\frac{z_{\theta }}{z_{{\theta }_1}},$$ (1.1)

and under certain moment conditions on the ratio $g_{\theta }(X_i)/g_{{\theta }_1}(X_i)$ and mixing conditions on the chain, the estimate on the left of (1.1) also satisfies a central limit theorem (CLT). In fact, in all the problems mentioned above, it is not necessary to estimate the normalizing constants themselves, and it is sufficient to estimate ratios of normalizing constants.

If θ is not close to θ₁, or more precisely, if g_θ and $g_{{\theta }_1}$ are not close over the region where the X_i’s are likely to be, the ratio $g_{\theta }(X_i)/g_{{\theta }_1}(X_i)$ has high variance, so the estimator above does not work well. It is better to choose θ₁, …, θ_k appropriately spread out in the parameter space Θ, and on the left side of (1.1) replace $g_{{\theta }_1}$ with ${\displaystyle {\sum }_{s=1}^k{w}_s{g}_{{\theta }_s}}$, where w_s > 0, s = 1, …, k. The hope is that g_θ will be close to at least one of the $g_{{\theta }_s}$’s, and so preclude having large variances. To implement this, suppose we know all the ratios $z_{{\theta }_s}/z_{{\theta }_t}$, s, t ∈ {1, …, k}, or equivalently, we know $z_{{\theta }_1}/z_{{\theta }_s}$, s ∈ {1, …, k}. In this case, if for each l = 1, …, k there is available a sample $X_1^{(l)}$, …, $X_{n_l}^{(l)}$ from $g_{{\theta }_l}/z_{{\theta }_l}$, then letting $n={\displaystyle {\sum }_{l=1}^k{n}_l}$ and a_l = n_l/n, we have

$$\begin{array}{l}{\displaystyle \sum _{l=1}^k\frac{1}{n_l}}{\displaystyle \sum _{i=1}^{n_l}\frac{a_l{g}_{\theta }\left(X_i^{(l)}\right)}{{\displaystyle {\sum }_{s=1}^k{a}_s{g}_{{\theta }_s}}\left(X_i^{(l)}\right)\left(z_{{\theta }_1}/z_{{\theta }_s}\right)}}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\displaystyle \sum _{l=1}^k{\displaystyle \int \frac{a_l{g}_{\theta }(x)}{{\displaystyle {\sum }_{s=1}^k{a}_s{g}_{{\theta }_s}(x)\left(z_{{\theta }_1}/z_{{\theta }_s}\right)}}\frac{g_{{\theta }_l}(x)}{z_{{\theta }_l}}}\mu (dx)}\\ ={\displaystyle \int {\displaystyle \sum _{l=1}^k\frac{a_l{g}_{{\theta }_l}(x)/z_{{\theta }_l}}{{\displaystyle {\sum }_{s=1}^k{a}_s{g}_{{\theta }_s}(x)\left(z_{{\theta }_1}/z_{{\theta }_s}\right)}}{g}_{\theta }(x)\mu (dx)=\frac{z_{\theta }}{z_{{\theta }_1}}}.}\end{array}$$ (1.2)

When compared with the estimate on the left side of (1.1), the estimate on the left side of (1.2) is accurate over a much bigger range of θ’s. But to use it, it is necessary to be able to estimate the ratios $z_{{\theta }_1}/z_{{\theta }_s}$, s ∈ {1, …, k}, and it is this problem that is the focus of this paper.

We now state explicitly the version of this problem that we will deal with here, and we change to the notation that we will use for the rest of the paper. We have k densities π₁, …, π_k with respect to the measure μ, which are known except for normalizing constants, i.e. we have π_l = ν_l/m_l, where the ν_l’s are known functions and the m_l’s are unknown constants. For each l we have a Markov chain ${\mathrm{\Phi }}_l=\left\{X_1^{(l)},\dots ,X_{n_l}^{(l)}\right\}$ with invariant density π_l, the k chains are independent, and the objective is to estimate all possible ratios m_i/m_j, i ≠ j or, equivalently, the vector

$$\mathit{d}=\left(m_2/m_1,\dots ,m_k/m_1\right).$$

When the samples are iid sequences, this is the biased sampling problem introduced by Vardi (1985), which contains examples that differ in character quite a bit from those considered here.

Suppose we are in the iid case, and consider the pooled sample $S=\left\{X_i^{(l)},i=1,n_l,l=1,\dots ,k\right\}$. Let x ∈ S, and suppose that x came from the l^th sample. If we pretend that the only thing we know about x is its value, then the probability that x came from the l^th sample is

$$\frac{n_l{\pi }_l(x)}{{\displaystyle {\sum }_{s=1}^k{n}_s{\pi }_s(x)}}=\frac{a_l{\nu }_l(x)/m_l}{{\displaystyle {\sum }_{s=1}^k{a}_s{\nu }_s(x)}/m_s}:={\lambda }_l(x,\mathit{m}),$$ (1.3)

where m = (m₁, …, m_k). Geyer (1994) proposed to treat the vector m as an unknown parameter and to estimate it by maximizing the quasi-likelihood function

$$L_n(\mathit{m})={\displaystyle \prod _{l=1}^k{\displaystyle \prod _{i=1}^{n_l}{\lambda }_l\left(X_i^{(l)},\mathit{m}\right)}}$$ (1.4)

with respect to m. Actually, there is a non-identifiability issue regarding L_n: for any constant c > 0, L_n(m) and L_n(cm) are the same. So we can estimate m only up to an overall multiplicative constant, i.e. we can estimate only d. Accordingly, Geyer (1994) proposed to estimate d by maximizing L_n(m) subject to the constraint m₁ = 1. (A more detailed discussion of the quasi-likelihood function (1.4) is given in Section 3.) In fact, the resulting estimate, $\widehat{\mathit{d}}$, was originally proposed by Vardi (1985), and studied further by Gill, Vardi and Wellner (1988), who showed that it is consistent and asymptotically normal, and established its optimality properties, all under the assumption that for each l = 1, …, k, $X_1^{(l)}$, …, $X_{n_l}^{(l)}$ is an iid sequence. Geyer (1994) extended the consistency and asymptotic normality result to the case where the k sequences $X_1^{(l)}$, …, $X_{n_l}^{(l)}$ are Markov chains satisfying certain mixing conditions. The estimate was rederived in Meng and Wong (1996), Kong et al. (2003), and Tan (2004) from completely different perspectives, all under the iid assumption.

As mentioned earlier, for the kinds of problems we have in mind the distributions π_l are analytically intractable, and the estimate on the left side of (1.1) or (1.2) are applicable to a much larger class of problems if we are willing to use Markov chain samples instead of iid samples. The variances of these estimates have a complex form which is difficult to estimate consistently. The variance matrix of $\widehat{\mathit{d}}$ is much harder to estimate since $\widehat{\mathit{d}}$ is not given in closed form, but is given only implicitly as the solution to a constrained optimization problem.

The present paper deals with two issues. First, none of the authors cited above give consistent estimators of the variance matrix of $\widehat{\mathit{d}}$, even in the iid case. (For the iid case, Kong et al. (2003) give an estimate that involves the inverse of a certain Fisher information matrix, but this formal calculation does not establish consistency of the estimate, or even the necessary CLT, nor do the authors make such claims.) As mentioned earlier, the problem of estimating the variance is far more challenging when the samples are Markov chains as opposed to iid sequences. In this paper we give a CLT for the vector $\widehat{\mathit{d}}$ based on regenerative simulation. The main benefit of this result is that it gives, essentially as a free by-product, a simple consistent estimate of the variance matrix in the Markov chain setting. Second, the estimate of d obtained by the afore-mentioned authors is optimal in the case where the samples are iid. When the samples are Markov chains, the estimate is no longer optimal. We present a method for forming estimators which are suitable in the Markov chain setting. The regeneration-based CLT and estimate of the variance matrix both apply to the class of estimators that we propose.

The rest of this paper is organized as follows. In Section 2 we extend the quasi-likelihood function used by Geyer (1994) to a class of quasi-likelihood functions, each of which gives rise to an estimator of d. The main theoretical developments of this paper are in Section 3, where we use ideas from regenerative simulation to develop CLTs for any of these estimators, and we show that variance estimates emerge as by-products. There are two reasons why we need to be able to estimate the variance of an estimate of d. One is the standard rule that a point estimate should always be accompanied by a measure of uncertainty, an important rule that applies to any context. The other is that when the samples are Markov chains, as opposed to iid samples, the quasi-likelihood function (1.4) gives rise to a non-optimal estimator. So in Section 4 we consider the other quasi-likelihood functions presented in Section 2 and we develop a method for choosing the one which gives rise to the estimator with the smallest variance. It is precisely our ability to estimate the variance that makes this possible. In Section 5 we present a small study that illustrates the gains obtained from using an estimate of d designed for Markov chains, and we illustrate our methodology by showing how it can be used to estimate certain quantities of interest in the Ising model of statistical mechanics. The Appendix provides proofs of the three assertions made by the theorem in Section 3, namely strong consistency of our estimates of d, the CLT for the estimates, and strong consistency of the estimates of the variance matrix.

2 Estimation of the Ratios of Normalizing Constants in the Markov Chain Setting

We begin by considering more carefully the quasi-likelihood function for m given by (1.4), and for the technical development it is much more convenient to work on the log scale. So define the vector ζ by

$${\zeta }_l=-\log (m_l)+\log (a_l),\text{for }l=1,\dots ,k,$$ (2.1)

and rewrite (1.3) as

$$p_l(x,\mathit{\zeta })=\frac{{\nu }_l(x)e^{{\zeta }_l}}{{\displaystyle {\sum }_{s=1}^k{\nu }_s(x)e^{{\zeta }_s}}},\text{for }l=1,\dots ,k.$$ (2.2)

Clearly, ζ determines and is determined by (m₁, …, m_k), and the log quasi-likelihood function for ζ is

$$l_n(\mathit{\zeta })={\displaystyle \sum _{l=1}^k{\displaystyle \sum _{i=1}^{n_j}\log \left(p_l\left(X_i^{(l)},\mathit{\zeta }\right)\right)}}.$$ (2.3)

In (2.1), (m₁, …, m_k) is an arbitrary vector with strictly positive components, i.e. m_l need not correspond to the normalizing constant for ν_l. We will use ζ_(t) to denote the true value of ζ, i.e. the value it takes when the m_l’s are the normalizing constants for the ν_l’s. The non-identifiability issue now is that for any constant c ∈ ℝ, l_n(ζ) and l_n(ζ +c1_k) are the same (here, 1_k is the vector of k 1’s), so we can estimate ζ_(t) only up to an additive constant. Accordingly, with ζ₀ ∈ ℝ^k defined by ${\left[{\mathit{\zeta }}_0\right]}_l={\left[{\zeta }_{(t)}\right]}_l-\left({\displaystyle {\sum }_{s=1}^k{\left[{\zeta }_{(t)}\right]}_s}\right)/k$, Geyer (1994) proposed to estimate ζ₀ by $\widehat{\mathit{\zeta }}$, the maximizer of l_n subject to the linear constraint ζ^⊤1_k = 0, and thus obtain an estimate of d.

The term p_l(x, ζ) in (2.2) has the appearance of a likelihood ratio, and for the denominator, in the term ${\nu }_s\left(x\right)e^{{\zeta }_s}=a_s\left({\nu }_s(x)/m_s\right)$, the probability measure ν_s/m_s is given weight proportional to the length of the chain Φ_s. Now Gill et al’s. (1988) optimality result does not apply to the Markov chain case, in which, among other things, the chains Φ₁, …, Φ_k mix at possibly different rates, and the a_s’s should in some sense reflect the vague notion of “effective sample sizes” of the different chains. The optimal choice of the vector a = (a₁, …, a_k) is very difficult to determine theoretically, and in Section 4 we describe an empirical method for choosing a. Accordingly in (2.1) and henceforth, a will not necessarily be given by a_l = n_l/n, but will be an arbitrary probability vector satisfying the condition that a_l > 0 for l = 1, …, k.

A Quasi-Likelihood Function Designed for the Markov Chain Setting

As mentioned earlier, Geyer (1994) showed that when we take a_j = n_j/n, the maximizer of the log quasi-likelihood function defined by (2.3) (subject to the constraint ζ^⊤1_k = 0) is a consistent estimate of the true value ζ₀, and also satisfies a CLT, even when the k sequences ${\left\{X_i^{(l)}\right\}}_{i=1}^{n_l}$, l = 1, …, k are Markov chains. But when the k sequences are Markov chains, the choice a_j = n_j/n is no longer optimal, and for other choices of a, the (constrained) maximizer of (2.3) is not necessarily even consistent. We will present a new log quasi-likelihood function which does yield consistent asymptotically normal estimates, and before doing this, we give a brief motivating argument.

Suppose that we are in the simple case where we have a parametric family {p_θ, θ ∈ Θ} and we observe data Y₁, …, $Y_n\stackrel{\text{iid}}{~}{p}_{{\theta }_0}$, for some θ₀ ∈ Θ. Let l_y(θ) = log(p_θ(y)), and let $Q(\theta )=E_{{\theta }_0}\left(l_Y(\theta )\right)$. The fact that argmax_θ Q(θ) = θ₀ is well known (and easy to see via a short argument involving Jensen’s inequality). The log likelihood function based on Y₁, …, Y_n is ${\displaystyle {\sum }_{i=1}^n{l}_{Y_i}}(\theta )$. By the strong law of large numbers,

$$n^{-1}{\displaystyle {\sum }_{i=1}^n{l}_{Y_i}}(\theta )\stackrel{\mathrm{a}.\mathrm{s}.}{\to }Q(\theta )\text{for all }\theta \in \mathrm{\Theta },$$ (2.4)

and assuming sufficient regularity conditions, ${\mathrm{argmax}}_{\theta }{n}^{-1}{\displaystyle {\sum }_{i=1}^n{l}_{Y_i}}(\theta )\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\mathrm{argmax}}_{\theta }Q(\theta )={\theta }_0$, i.e. the maximum likelihood estimator is consistent.

We now return to the present situation, in which for l = 1, …, k, ${\left\{X_i^{(l)}\right\}}_{i=1}^{n_l}$ is a Markov chain with invariant density π_l. Suppose we use l_n(ζ) given by (2.3), with a an arbitrary probability vector (i.e. a is not necessarily given by a_j = n_j/n), and let $Q(\mathit{\zeta })=E_{{\mathit{\zeta }}_0}(l_n(\mathit{\zeta }))$. The key condition

$$\underset{\mathit{\zeta }}{\mathrm{argmax}}Q(\mathit{\zeta })={\mathit{\zeta }}_0$$ (2.5)

need not hold, and the constrained maximizer of l_n(ζ) may converge, but not to the true value.

With this in mind, suppose that a is an arbitrary probability vector with non-zero entries and define w ∈ ℝ^k by

$$w_l=a_l\frac{n}{n_l},l=1,\dots ,k.$$ (2.6)

The log quasi-likelihood function we will use is

$${\ell }_n(\mathit{\zeta })={\displaystyle \sum _{l=1}^k{w}_l}{\displaystyle \sum _{i=1}^{n_l}\log \left(p_l\left(X_i^{(l)},\mathit{\zeta }\right)\right)}$$ (2.7)

instead of l_n given by (2.3) [note the slight change of notation from l to ℓ]. As will emerge in our proofs of consistency and asymptotic normality of the constrained maximizer of ℓ_n(ζ), for this log quasi-likelihood function, the stochastic process (in ζ) n⁻¹ ℓ_n(ζ) converges almost surely to a function of ζ which is maximized at ζ₀, a condition that plays the role of (2.4) and (2.5). Note that if a_l = n_l/n, then w_l = 1 and (2.7) reduces to (2.3).

3 A Regeneration-Based CLT and Estimate of the Variance Matrix

Here we discuss estimation of the variance matrix of the estimator $\widehat{\mathit{\zeta }}$ developed in Section 2. Estimation of the variance matrix is complicated by the fact that $\widehat{\mathit{\zeta }}$ is based on several Markov chains and that it is given only implicitly as the solution of a constrained maximization problem. Before describing our approach for estimating the variance matrix of $\widehat{\mathit{\zeta }}$, we first review what is available in a much simpler setting.

3.1 Estimation of the Variance of the Sample Mean in the Single Markov Chain Setting

Suppose we have a single Markov chain X₁, X₂, … on the measurable space $(\mathrm{X},ℬ)$, with invariant distribution π, f : X → ℝ is a function whose expectation μ = E_π(f(X)) we estimate via $\widehat{\mu }={\overline{f}}_n:=n^{-1}{\displaystyle {\sum }_{i=1}^{n}f(X_i)}$, and we are interested in estimating the variance of $\widehat{\mu }$. Here we describe the commonly used approaches for the simple case, namely those based on batching, regeneration, and spectral methods. We explain how regeneration may be used for the case of the statistic $\widehat{\mathit{\zeta }}$ in Section 3.2 (see also the Appendix), and in Section 6 we explain how batching and spectral methods can be implemented for the case of the statistic $\widehat{\mathit{\zeta }}$ using the theoretical development in Section 3. We then compare and contrast the three methods of estimating the variance matrix and argue that, when it can be carried out, regeneration is the method of choice, but point out that unfortunately regeneration-based methods are not always feasible.

Batching

This method involves breaking up ${\left\{X_i\right\}}_{i=1}^n$ into M non-overlapping segments of equal length called batches. For m = 1, …, M, batch m is used to produce an estimate ${\widehat{\mu }}^{[m]}$ in the obvious way. If we have a CLT that states $n^{1/2}(\widehat{\mu }-\mu )\stackrel{d}{\to }\mathcal{N}(0,{\kappa }^2)$, then we can conclude that for fixed M, ${\left(n/M\right)}^{1/2}({\widehat{\mu }}^{[m]}-\mu )\stackrel{d}{\to }\mathcal{N}(0,{\kappa }^2)$ for each m. If the batch length is large enough relative to the “mixing time” of the chain, then these estimators are approximately independent. If the independence assumption was exactly true rather than approximately true, then the sample variance of the ${\widehat{\mu }}^{[m]}’\mathrm{s}$ would be a valid estimator of (M/n)κ². The batch means estimate of κ² is simply n/M times this sample variance. Under regularity conditions that include M → ∞ at a certain rate, the batch means estimate of κ² is strongly consistent; see Jones et al. (2006), and also Flegal, Haran and Jones (2008). The method of batching has the advantage that it is trivial to program, although some authors caution that it can be outperformed by spectral methods in terms of mean squared error; see, e.g., Geyer (1992).

Regenerative Simulation

A regeneration is a random time at which a stochastic process probabilistically restarts itself. The “tours” made by the chain in between such random times are iid, and this fact makes it much easier to analyze the asymptotic behavior of averages, and of statistics which are functions of several averages. In the discrete state space setting, if x ∈ X is any point to which the chain returns infinitely often, then the times of return to x form a sequence of regenerations. For most of the Markov chains used in MCMC algorithms, the state space is continuous, and there is no point to which the chain returns infinitely often with probability one. Even when the state space is discrete, regenerations based on returns to a point x, as described above, are often not useful, because if x has very small probability under the stationary distribution, then on average it will take a very long time to return to x. Fortunately, Mykland, Tierney and Yu (1995) provided a general technique for identifying a sequence of regeneration times 1 = τ₀ < τ₁ < τ₂ < ⋯ that is based on the construction of a minorization condition. This construction will be reviewed shortly, but we now briefly sketch how having a regeneration sequence ${\left\{{\tau }_t\right\}}_{t=0}^{\infty }$ enables us to construct a simple estimate of the standard error of $\overline{f}$. Define

$$Y_t={\displaystyle \sum _{i={\tau }_{t-1}}^{{\tau }_t-1}f(X_i)}\text{and}{T}_t={\displaystyle \sum _{i={\tau }_{t-1}}^{{\tau }_t-1}1={\tau }_t-{\tau }_{t-1}},t=1,2,\dots ,$$

and note that the pairs (Y_t, T_t) form an iid sequence. If we run the chain for ρ regenerations, then the total number of cycles, starting at τ₀, is given by $n={\displaystyle {\sum }_{t=1}^{\rho }{T}_t}$. We may write $\overline{f}$ as

$$\frac{{\displaystyle {\sum }_{i=1}^{n}f(X_i)}}{n}=\frac{{\displaystyle {\sum }_{t=1}^{\rho }{Y}_t}}{{\displaystyle {\sum }_{t=1}^{\rho }{T}_t}}=\frac{\left({\displaystyle {\sum }_{t=1}^{\rho }{Y}_t}\right)/\rho }{\left({\displaystyle {\sum }_{t=1}^{\rho }{T}_t}\right)/\rho }.$$ (3.1)

Equation (3.1) expresses $\overline{f}$ as a ratio of two averages of iid quantities, and this representation enables us to use the delta method to obtain both a CLT for $\overline{f}$ and a simple standard error estimate for $\overline{f}$.

An outline of the argument is as follows. From (3.1) we see that as ρ → ∞ (which implies that n → ∞) we have

$$E_{\pi }(f(X))\stackrel{\mathrm{a}.\mathrm{s}.}{\leftarrow }\frac{{\displaystyle {\sum }_{i=1}^{n}f(X_i)}}{n}=\frac{\left({\displaystyle {\sum }_{t=1}^{\rho }{Y}_t}\right)/\rho }{\left({\displaystyle {\sum }_{t=1}^{\rho }{T}_t}\right)/\rho }\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\frac{E(Y_1)}{E(T_1)},$$ (3.2)

where the convergence statement on the left follows from the ergodic theorem, and the convergence statement on the right follows from two applications of the strong law of large numbers. (In (3.2) the subscript π to the expectation indicates that X ∼ π.) From (3.2) we obtain E(Y₁) = E_π(f(X))E(T₁). Now the bivariate CLT gives

$${\rho }^{1/2}\left(\begin{array}{c}\overline{Y}-E_{\pi }(f(X))E(T_1)\\ \overline{T}-E(T_1)\end{array}\right)\stackrel{d}{\to }\mathcal{N}(0,{\sum }_f),$$ (3.3)

where Σ_f = Cov ((Y₁, T₁)^⊤). The delta method applied to the function h(y, t) = y/t gives the CLT

$${\rho }^{1/2}(\overline{Y}/\overline{T}-E_{\pi }(f(X)))\stackrel{d}{\to }\mathcal{N}(0,{\sigma }_f^2)$$

where ${\sigma }_f^2={\left(\nabla h\right)}^{\top }{\sum }_f\nabla h$ (and ∇h is evaluated at the vector of means in (3.3)). Moreover, it is straightforward to check that for the variance estimator

$${\widehat{\sigma }}_f^2=\frac{{\displaystyle {\sum }_{t=1}^{\rho }{\left(Y_t-\overline{f}{T}_t\right)}^2}}{\rho {\overline{T}}^2},$$ (3.4)

we have ${\widehat{\sigma }}_f^2\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\sigma }_f^2$. The regularity conditions needed to make this argument rigorous are spelled out when we discuss the case of the more complicated estimator $\widehat{\mathit{\zeta }}$ (Section 3.2 and the Appendix).

The argument above hinges on being able to arrive at a sequence of regeneration times, and whether these are useful depends on whether the sequence has the property that the length of the tours between regenerations is not very large. We now describe the minorization condition that can sometimes be used to construct useful regeneration sequences. Let K_x(A) be the Markov transition function. The construction described in Mykland et al. (1995) requires the existence of a function s: X → [0, 1), whose expectation with respect to π is strictly positive, and a probability measure Q, such that K satisfies

$$K_x(A)\ge s(x)Q(A)\text{for all }x\in \text{X and }A\in ℬ.$$ (3.5)

This is called a minorization condition and, as we describe below, it can be used to introduce regenerations into the Markov chain driven by K. Define the Markov transition function R by

$$R_x(A)=\frac{K_x(A)-s(x)Q(A)}{1-s(x)}.$$

Note that for fixed x ∈ X, R_x is a probability measure. We may therefore write

$$K_x=s(x)Q+(1-s(x))R_x,$$

which gives a representation of K_x as a mixture of two probability measures, Q and R_x. This provides an alternative method of simulating from K. Suppose that the current state of the chain is X_n. We generate δ_n ∼ Bernoulli(s(X_n)). If δ_n = 1, we draw X_n+1 ~ Q; otherwise, we draw $X_{n+1}~R_{X_n}$. Note that if δ_n = 1, the next state of the chain is drawn from Q, which does not depend on the current state. Hence the chain “forgets” the current state and we have a regeneration. To be more specific, suppose we start the Markov chain with

$$X_1~Q$$ (3.6)

and then use the method described above to simulate the chain. Each time δ_n = 1, we have X_n+1 ∼ Q and the process stochastically restarts itself; that is, the process regenerates.

In practice, simulating from R can be extremely difficult. Fortunately, Mykland et al. (1995), following Nummelin (1984, p. 62), noticed a clever way of circumventing the need to draw from R. Instead of making a draw from the conditional distribution of δ_n given x_n and then generating x_n+1 given (δ_n, x_n), which would result in a draw from the joint distribution of (δ_n, x_n+1) given x_n, we simply draw from the conditional distribution of x_n+1 given x_n in the usual way (i.e. using K), and then draw δ_n given (x_n, x_n+1). This alternative sampling mechanism yields a draw from the same joint distribution, but avoids having to draw from R. Moreover, given (x_n, x_n+1), δ_n has a Bernoulli distribution with success probability given simply by

$$P\left({\delta }_n=1|x_n=x^{\prime },x_{n+1}=x\right)=\left[\frac{d(s(x^{\prime })Q)}{d{K}_{x^{\prime }}}\right](x),$$

where $[d(s(x^{\prime })Q)/d{K}_{x^{\prime }}]$ is the Radon-Nikodym derivative of s(x′)Q with respect to K_x′, whose existence is implied by (3.5).

We note that both batching and regenerative simulation involve breaking up the Markov chain into segments. In batching, the segments are only approximately independent, but they are of equal lengths; in regenerative simulation, the segments are exactly independent, but they are not of equal lengths, and in fact the lengths are random.

Spectral Methods

The asymptotic variance, σ², of $(1/n){\displaystyle {\sum }_{i=1}^{n}f(X_i)}$ (when it exists) is the infinite series

$${\sigma }^2={\gamma }_0+2{\displaystyle {\sum }_{j=1}^{\infty }{\gamma }_j},$$

where γ_j = Cov(f(X₁), f(X_1+j)) is calculated under the assumption that X₁ has the stationary distribution. Spectral methods involve truncating the series after M_n terms and estimating the truncated series. In more detail, we consider the sum ${\displaystyle {\sum }_{j=1}^{M_n}{w}_n(j/n)}{\gamma }_j$, where w_n is a decreasing function on [0, 1] satisfying w_n(0) = 1 and w_n(1) = 0, and is called the lag window. We estimate σ² via ${\widehat{\sigma }}^2={\widehat{\gamma }}_0+2{\displaystyle {\sum }_{j=1}^{M_n}{w}_n(j/n){\widehat{\gamma }}_j}$, where ${\widehat{\gamma }}_j$ are estimates of γ_j. To ensure consistency, we must have M_{n →} ∞, but M_n must increase slowly with n; precise conditions on the truncation point M_n and the window w_n are given in Flegal and Jones (2010).

3.2 A CLT for the Estimate of d Designed for Markov Chains

We assume that for l = 1, …, k, chain l has Markov transition function $K_x^{(l)}(A)$ which satisfies the minorization condition

$$K_x^{(l)}(A)\ge s_l(x)Q_l(A)\text{for all }x\in \mathrm{X},A\in ℬ$$ (3.7)

for some probability measure Q_l and function s_l : X → [0, 1) with $E_{{\pi }_l}\left(s_l\left(X\right)\right)>0$, and that the chain has been run for ρ_l regenerations. Let $1={\tau }_0^{(l)}<{\tau }_1^{(l)}<\cdots <{\tau }_{{\rho }_l}^{(l)}$ denote the regeneration times of the l^th chain, and let $T_t^{(l)}={\tau }_t^{(l)}-{\tau }_{t-1}^{(l)}$ be the length of the t^th tour of the l^th chain. So the length of the l^th chain, $n_l=T_1^{(l)}+\cdots +T_{{\rho }_l}^{(l)}$, is random. We will assume that ρ₁, …, ρ_k → ∞ in such a way that ρ_l/ρ₁ → c_l ∈ (0, ∞), for l = 1, …, k. We will allow the vector a to depend on ρ = (ρ₁, …, ρ_k), i.e. a = a^(ρ) (although we will suppress this dependence in the notation except when this dependence matters), and we will make the minimal assumption that a^(ρ) → α as ρ₁, …, ρ_k → ∞, where α is a probability vector with strictly positive entries. The extra generality is needed if we wish to choose a in a data-driven way (cf. Remark 3 of Section 4). The definitions of ζ and p_l(x, ζ) given by (2.1) and (2.2), respectively, are still in force, ζ₀ is still the centered version of the true value of ζ, but now $\widehat{\mathit{\zeta }}$ is the constrained maximizer of the new log quasi-likelihood function (2.7). We will show that $\widehat{\mathit{\zeta }}$ is a consistent asymptotically normal estimate of ζ₀, and since ζ₀ determines and is determined by d, this will produce a corresponding estimate $\widehat{\mathit{d}}$ of d. Before proceeding, we mention the fact that difficulties arise if the supports of the distributions π₁, …, π_k differ (the difficulties are pervasive: for the case where we have a continuum of distributions {π_θ, θ ∈ Θ}, the simple estimate (1.1) is not even defined if π_θ is not absolutely continuous with respect to ${\pi }_{{\theta }_1}$). So for the rest of this paper, we will assume that the k distributions π₁, …, π_k are mutually absolutely continuous. We do not really need to make an assumption this strong, but the assumption is satisfied for all the classes of problems we are considering, and making it eliminates some technical issues.

In order to state our CLT for the vector ${\rho }_1^{1/2}(\widehat{\mathit{d}}-\mathit{d})$, we need to define the quantities that go into the expression for the asymptotic variance matrix. We first consider the vector ${\rho }_1^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)$, whose variance matrix is singular (since this vector sums to 0). The asymptotic distribution of ${\rho }_1^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)$ involves the matrices B and Ω defined below. Let ζ_α be the vector whose components are [ζ_α]_l = −log(m_l) + log(α_l), and let B be the k × k matrix given by

$$\begin{array}{l}{B}_{rr}={\displaystyle \sum _{j=1}^k{\alpha }_j{E}_{{\pi }_j}(p_r(X,{\mathit{\zeta }}_{\mathit{\alpha }})[1-p_r(X,{\mathit{\zeta }}_{\mathit{\alpha }})])},r=1,\dots ,k,\\ B_{rs}=-{\displaystyle \sum _{j=1}^k{\alpha }_j{E}_{{\pi }_j}(p_r(X,{\mathit{\zeta }}_{\mathit{\alpha }})p_s(X,{\mathit{\zeta }}_{\mathit{\alpha }})),}r,s=1,\dots ,k,r\ne s.\end{array}$$ (3.8)

We will be using the natural estimate defined by

$$\begin{array}{l}{\widehat{B}}_{rr}={\displaystyle \sum _{l=1}^k{\alpha }_l\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r(X_i^{(l)},\widehat{\mathit{\zeta }})[1-p_r(X_i^{(l)},\widehat{\mathit{\zeta }})]}\right)},r=1,\dots ,k,\\ {\widehat{B}}_{rs}=-{\displaystyle \sum _{l=1}^k{\alpha }_l\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r(X_i^{(l)},\widehat{\mathit{\zeta }})p_s(X_i^{(l)},\widehat{\mathit{\zeta }})}\right)},r,s=1,\dots ,k,r\ne s.\end{array}$$ (3.9)

Let

$$\begin{array}{l}{y}_i^{(r,l)}(\mathit{a})=p_r(X_i^{(l)},{\mathit{\zeta }}_0)-E_{{\pi }_l}(p_r(X,{\mathit{\zeta }}_0)),i=1,\dots ,n_l,\\ y_i^{(r,l)}(\mathit{\alpha })=p_r(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }})-E_{{\pi }_l}(p_r(X,{\mathit{\zeta }}_{\mathit{\alpha }})),i=1,\dots ,n_l,\end{array}$$ (3.10)

and note that both $y_i^{(r,l)}\left(\mathit{a}\right)$ and $y_i^{(r,l)}\left(\mathit{\alpha }\right)$ have mean 0. Define

$$\begin{array}{c}{Y}_t^{(r,l)}(\mathit{a})={\displaystyle \sum _{i={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}{y}_i^{(r,l)}(\mathit{a}),}{\overline{Y}}^{(r,l)}(\mathit{a})=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}{Y}_t^{(r,l)}(\mathit{a})},\\ Y_t^{(r,l)}(\mathit{\alpha })={\displaystyle \sum _{i={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}{y}_i^{(r,l)}(\mathit{\alpha }),}{\overline{Y}}^{(r,l)}(\mathit{\alpha })=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}{Y}_t^{(r,l)}(\mathit{\alpha })},\text{and}{\overline{T}}^{(l)}=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}{T}_t^{(l)}}.\end{array}$$ (3.11)

Let Ω be the k × k matrix defined by

$${\mathrm{\Omega }}_{rs}={\displaystyle \sum _{l=1}^k\frac{{\alpha }_l^2}{C_l}\frac{E(Y_1^{(r,l)}(\mathit{\alpha })Y_1^{(s,l)}(\mathit{\alpha }))}{{(E(T_1^{(l)}))}^2}},r,s=1,\dots ,k,$$ (3.12)

To obtain an estimate $\widehat{\mathrm{\Omega }}$, we let

$$Z_t^{(r,l)}={\displaystyle \sum _{i={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}{p}_r(X_i^{(l)},\widehat{\mathit{\zeta }})}\text{and}{\widehat{\mu }}_r^{(l)}=\frac{{\displaystyle {\sum }_{i=1}^{n_l}{p}_r(X_i^{(l)},\widehat{\mathit{\zeta }})}}{n_l},$$

and define $\widehat{\mathrm{\Omega }}$ by

$${\widehat{\mathrm{\Omega }}}_{rs}={\displaystyle \sum _{l=1}^k\frac{a_l^2}{c_l}\frac{1}{{({\overline{T}}^{(l)})}^2}\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}(Z_t^{(r,l)}-T_t^{(l)}{\widehat{\mu }}_r^{(l)})(Z_t^{(s,l)}-T_t^{(l)}{\widehat{\mu }}_r^{(l)})}},r,s=1,\dots ,k.$$ (3.13)

The function g : ℝ^k → ℝ^k−1 that maps ζ₀ into d is

$$g(\mathit{\zeta })=\left(\begin{array}{c}{e}^{{\zeta }_1-{\zeta }_2}{a}_2/a_1\\ e^{{\zeta }_1-{\zeta }_3}{a}_3/a_1\\ ⋮\\ e^{{\zeta }_1-{\zeta }_k}{a}_k/a_1\end{array}\right),$$ (3.14)

and its gradient at ζ₀ (in terms of d) is

$$D=\left(\begin{array}{cccc}{d}_2& d_3& \dots & d_k\\ -d_2& 0& \dots & 0\\ 0& -d_3& \dots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & -d_k\end{array}\right).$$ (3.15)

We have d = g(ζ₀), and by definition $\widehat{\mathit{d}}=g(\widehat{\mathit{\zeta }})$.

The theorem below has three parts, pertaining to the strong consistency of $\widehat{\mathit{d}}$, asymptotic normality of $\widehat{\mathit{d}}$, and a consistent estimate of the asymptotic variance matrix of $\widehat{\mathit{d}}$. For consistency we need only minimal assumptions on the Markov chains Φ₁, …, Φ_k, namely the so-called basic regularity conditions (irreducibility, aperiodicity and Harris recurrence) that are needed for the ergodic theorem (Meyn and Tweedie, 1993, Chapter 17). CLTs and associated results always require a stronger condition, and the one that is most commonly used is geometric ergodicity. The theorem refers to the following conditions, which pertain to each l = 1, …, k.

• A1 The Markov chain $\{X_1^{(l)},X_2^{(l)},\dots \}$ satisfies the basic regularity conditions.

• A2 The Markov chain $\{X_1^{(l)},X_2^{(l)},\dots \}$ is geometrically ergodic.

• A3 The Markov transition function K^(l) satisfies the minorization condition (3.7).

For a square matrix C, C^† will denote the Moore-Penrose inverse of C.

Theorem 1

Suppose that for each l = 1, …, k, the Markov chain $\{X_1^{(l)},X_2^{(l)},\dots \}$ has invariant distribution π_l.

1. Under A1, the log quasi-likelihood function (2.7) has a unique maximizer subject to the constraint ζ^⊤1_k = 0. Let $\widehat{\mathit{\zeta }}$ denote this maximizer, and let $\widehat{\mathit{d}}=g(\widehat{\mathit{\zeta }})$. Then as ρ₁ → ∞, $\widehat{\mathit{d}}\stackrel{a.s.}{\to }\mathit{d}$.

2. Under A1 and A2, as ρ1 → ∞,

   $${\rho }_1^{1/2}(\widehat{\mathit{d}}-\mathit{d})\stackrel{d}{\to }\mathcal{N}(0,W)\mathit{where}W=D^{\top }{B}^{†}\mathrm{\Omega }{B}^{†}D.$$ (3.16)

3. Assume A1–A3. Let $\widehat{D}$ be the matrix D in (3.15) with $\widehat{\mathit{d}}$ in place of d, and let $\widehat{B}$ and $\widehat{\mathrm{\Omega }}$ be defined by (3.9) and (3.13), respectively. Then, $\widehat{W}:={\widehat{D}}^{\top }{\widehat{B}}^{†}\widehat{\mathrm{\Omega }}{\widehat{B}}^{†}\widehat{D}$ is a strongly consistent estimator of W.

4 Choice of the Vector a

As mentioned earlier, the log quasi-likelihood that has been proposed and studied in the literature involves the functions p_l(x, ζ) given by (2.2), which have the form

$$\frac{\frac{n_l}{n}{\nu }_l\left(x\right)/m_l}{{\displaystyle {\sum }_{s=1}^k\frac{n_s}{n}{\nu }_s\left(x\right)/m_s}},$$ (4.1)

where in the denominator of (4.1), the probability density ν_s(x)/m_s is given weight proportional to the length of the s^th chain. Intuitively, one would want to replace n_s with the “effective sample size” for chain s, so that if chain s mixes slowly, the weight that is given to ν_s(x)/m_s is small. Unfortunately, there is really no such thing as an effective sample size because the effect of slow mixing varies quite a bit with the function whose mean is being estimated. Therefore, it is better to take a direct approach that involves replacing the vector (n₁/n, …, n_k/n) by a probability vector a, and choose a to minimize the variance of the resulting estimator. (It should be emphasized that the estimator is a complicated function of k chains.)

In more detail, we do the following. Let ${\mathcal{S}}_k=\{\mathit{a}\in {ℝ}^k:a_1,\dots ,a_k\ge 0\text{and}{\displaystyle {\sum }_{s=1}^k{a}_s=1}\}$ be the k-dimensional simplex. For each a ∈ ${\mathcal{S}}_k$, in (4.1) replace n_s/n by a_s and form the corresponding log quasi-likelihood function (see equation (2.7)), call it ${\ell }_n^{(\mathit{a})}(\mathit{\zeta })$. We let ${\widehat{\mathit{\zeta }}}_{\mathit{a}}$ be the constrained maximizer of ${\ell }_n^{(\mathit{a})}(\mathit{\zeta })$, and let ${\widehat{\mathit{d}}}_{\mathit{a}}$ be the corresponding estimate of d. Let W_a be the variance matrix of ${\widehat{\mathit{d}}}_{\mathit{a}}$ given by Part 2 of Theorem 1, and let ${\widehat{W}}_{\mathit{a}}$ be its estimate. We choose a to minimize $\text{trace}({\widehat{W}}_{\mathit{a}})$ (this corresponds to the classical “A-optimal design”). It should be noted that we are able to carry out this optimization scheme precisely because Theorem 1 enables us to estimate W_a.

Remarks

1. It is natural to ask whether in the Markov chain case our procedure gives rise to an optimal estimate of d, and we now address this question. To keep the discussion as simple as possible, we consider the case k = 2. Let $ℬ$ be the set of all “bridge functions” β : X → ℝ satisfying the conditions that 0 < | ∫ β(x)π₁(x)π₂(x) μ(dx)| < ∞ and β(x) = 0 when either π₁(x) = 0 or π₂(x) = 0. It is easy to see that when the two sequences $X_1^{(l)},\dots ,X_{n_l}^{(l)}$, l = 1, 2 are each iid, for any β ∈ $ℬ$, the estimate

   $${\widehat{d}}_2=\frac{n_1^{-1}{\displaystyle {\sum }_{i=1}^{n_1}\beta (X_i^{(1)}){\nu }_2(X_i^{(1)})}}{n_2^{-1}{\displaystyle {\sum }_{i=1}^{n_2}\beta (X_i^{(2)}){\nu }_1(X_i^{(2)})}}$$

   is a consistent and asymptotically normal estimate of d₂. Meng and Wong (1996) show that within $ℬ$, the function for which the asymptotic variance is minimized is

   $${\beta }_{\text{opt},\text{iid}}\left(x\right)={\left[s_1{\nu }_1\left(x\right)+s_2{\nu }_2\left(x\right)/d_2\right]}^{-1},$$

   where s_j = n_j/n, j = 1, 2. Because this function involves the unknown d₂, Meng and Wong (1996) propose an iterative scheme in which we start with, say, ${\widehat{d}}_2^{(0)}=1$, and at stage m, we from

   $${\widehat{d}}_2^{(m+1)}=\frac{\frac{1}{n_1}{\displaystyle \sum _{i=1}^{n_1}\frac{{\nu }_2(X_i^{(1)})}{s_1{\nu }_1(X_i^{(1)})+s_2{\nu }_2(X_i^{(1)})/{\widehat{d}}_2^{(m)}}}}{\frac{1}{n_2}{\displaystyle \sum _{i=1}^{n_2}\frac{{\nu }_1(X_i^{(2)})}{s_1{\nu }_1(X_i^{(2)})+s_2{\nu }_2(X_i^{(2)})/{\widehat{d}}_2^{(m)}}}}.$$

   They show that ${\lim }_{m\to \infty }{\widehat{d}}_2^{(m)}$ exists and is exactly equal to the estimate considered by Geyer (1994), and so established an equivalence between the iterative bridge estimator and the estimate based on maximization of the log quasi-likelihood function.
   When the sequences $X_1^{(l)},\dots ,X_{n_l}^{(l)}$, l = 1, 2 are Markov chains, the optimal bridge function has the form β_opt,mcmc(x) = β_∗(x)β_opt,iid(x), where the correction factor, β_∗(x), is the solution to a complicated Fredholm integral equation (Romero, 2003) and reflects the dependence structure of the two chains. In particular, for the case of Markov chains, the optimal bridge function need not have the form

   $$\beta \left(x\right)={\left[t_1{\nu }_1\left(x\right)+t_2{\nu }_2\left(x\right)\right]}^{-1},$$ (4.2)

   for any t₁, t₂. Unfortunately, β_∗ is very hard to identify, let alone estimate. To conclude, since our procedure is, effectively, searching within the class (4.2), it will not yield an optimal estimate in general, and instead should be viewed as a method for yielding estimates which are practically useful, even if not optimal.

2. A crude way to find ${\widehat{\mathit{a}}}_{\text{opt}}:={\mathrm{argmin}}_{\mathit{a}}\text{trace}({\widehat{W}}_{\mathit{a}})$ is to calculate $\text{trace}({\widehat{W}}_{\mathit{a}})$ as a varies over a grid in ${\mathcal{S}}_k$ and then find the minimizing a. This is inefficient and unnecessary, as there exist efficient algorithms for minimizing real-valued functions of several variables; see, e.g., Robert and Casella (2004, Chapter 5).

3. The vector ${\widehat{\mathit{a}}}_{\text{opt}}$ can be calculated from a small pilot experiment, after which new chains are run and used to form the log quasi-likelihood function ${\ell }_n^{({\widehat{\mathit{a}}}_{\text{opt}})}\left(\mathit{\zeta }\right)$, from which we obtain $\widehat{\mathit{\zeta }}$ (and hence $\widehat{\mathit{d}}$).

4. If for each l, $X_1^{(l)},\dots ,X_{n_l}^{(l)}$ is an iid sequence, then a regeneration occurs at each step. In this case, there is no need to estimate a, since the optimal value is known to be a_j = n_l/n (Meng and Wong, 1996). The w_l’s in (2.6) reduce to 1, and the log quasi-likelihood function (2.7) reduces to exactly the log quasi-likelihood function used by Geyer (1994), so our estimate is exactly the estimate introduced by Vardi (1985), who worked in the iid setting.

5 Illustrations

Here we have two goals. In Section 5.1 we provide a simulation study to show the gains in efficiency that are possible if we use the method for choosing the weight vector a described in Section 4. Our illustration involves toy problems. The purpose of Section 5.2 is to demonstrate the applicability of our methodology, and we return to the second of the three classes of problems we discussed in Section 1, where we have a family of probability densities of the form p_θ(x) =g_θ(x)/z_θ, which are intractable because the normalizing constant z_θ cannot be computed in closed form. Our focus here is a bit different, in that we are not interested in estimating the family z_θ, θ ∈ Θ; rather, we are now interested in estimating a family of expectations of the form E_θ(U(X)), θ ∈ Θ, where U is a function, as well as estimating functions of these expectations. Our illustration is in the context of the Ising model of statistical physics, and we show how to estimate the internal energy and specific heat of the system as a function of temperature.

5.1 Gains in Efficiency When Using the Optimal Weight Vector a

Recall that ${\widehat{\mathit{a}}}_{\mathrm{opt}}={\text{argmin}}_{\mathit{a}}\text{trace}\left(\widehat{W_{\mathit{a}}}\right)$ is calculated from a small pilot experiment. Let ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ be the corresponding estimate of d. Also, let ${\widehat{\mathit{d}}}_{\text{conv}}$ denote the estimate of d obtained when we use the conventional choice a_j = n_j/n. In this section we demonstrate through a simulation study that significant gains in efficiency are possible if we use ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$instead of ${\widehat{\mathit{d}}}_{\text{conv}}$ in situations where the Markov chains mix at different rates. We consider a very simple situation where k = 2, so that d is just d₂. We take π₁ and π₂ to be two t distributions, specifically π₁ = t_5,1 and π₂ = t_5,0, where t_r,μ denotes the t distribution with r degrees of freedom, centered at μ. The representation π_l = ν_l/m_l is taken to be trivial: ν_l = π_l and m_l = 1 for l = 1, 2. So d₂ = m₂/m₁ is known to be 1, but we proceed to estimate it as if we didn’t know that fact.

In our simulations, chain 1 is an iid sequence from π₁. Chain 2 is an independence Metropolis-Hastings (IMH) chain with proposal density t_5,μ. That is, if the current state of the chain is x, a proposal Y ~ t_5,μ is generated; the chain moves to Y with acceptance probability min {[t_5,0(Y)t₅,_μ (x)]/[t_5,0(x)t_5,μ(Y)], 1} and stays at x with the remaining probability. We will let μ range over a fine grid in (−3, 3). Note that when μ = 0, the proposal is always accepted, and the chain is an iid sequence from t_5,0, but as μ moves away from 0 in either direction, proposals are less likely to be accepted, and the mixing rate of the chain is slower. It is simple to check that inf_x (t_5,μ(x)/t_5,0(x)) > 0, which implies that the IMH algorithm is uniformly ergodic (Mengersen and Tweedie, 1996, Theorem 2.1) and hence geometrically ergodic. Moreover, Mykland et al. (1995, Section 4.1) have shown that for IMH chains there is always a scheme for producing minorization conditions and regeneration sequences, and here we use the scheme they described.

Our simulation study is carried out as follows. For each value of μ, we conduct a pilot study to calculate ${\widehat{\mathit{a}}}_{\text{opt}}$, using the method described in Section 4. The pilot study is based on 1000 iid draws from π₁ and a number of regenerations of the IMH Markov chain for π₂ that gives a sample of approximately the same size. Then we run the main study, in which we form ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ (where ${\widehat{\mathit{a}}}_{\text{opt}}$ is obtained in the pilot study), and also form ${\widehat{\mathit{d}}}_{\text{conv}}$. The main study is 10 times as large as the pilot study. For each μ, the above is replicated 1000 times, and from these replicates we calculate the average squared distance between the ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ ’s and 1, the average squared distance between the ${\widehat{\mathit{d}}}_{\text{conv}}$’s and 1, and form the ratio, which we take as a measure of the efficiency of ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ vs. ${\widehat{\mathit{d}}}_{\text{conv}}$.

Figure 1 gives a plot of the ratio of these estimated mean squared errors as μ varies over (−3, 3), along with 95% confidence bands, valid pointwise (the bands are constructed via the delta method applied to the function f(o, c) = o/c). From the figure we see that, as expected, the efficiency is about 1 when μ is near 0. But it grows rapidly as μ moves away from 0 in either direction, reaching about 15 when μ is 3 or −3, and it is reasonable to believe that the efficiency is unbounded as μ → ∞ or μ→ −∞. Figure 2 provides a graphical description of the explanation. The figure gives a plot of ${\left[{\widehat{\mathit{a}}}_{\text{opt}}\right]}_1$, the first component of ${\widehat{\mathit{a}}}_{\text{opt}}$, as μ varies over (−3, 3). When μ = 0, the two chains are each iid sequences, and ${\widehat{\mathit{a}}}_{\text{opt}}\dot{=}(.5,.5)$, so that ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}\dot{=}{\widehat{\mathit{d}}}_{\text{conv}}$. But when μ moves away from 0 in either direction, chain 2 mixes more slowly, and ${\left[{\widehat{\mathit{a}}}_{\text{opt}}\right]}_1$ increases towards 1, so that in the term (2.2) in our quasi-likelihood function, less weight is given to chain 2, which is why ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ is more efficient than is ${\widehat{\mathit{d}}}_{\text{conv}}$.

Figure 1.

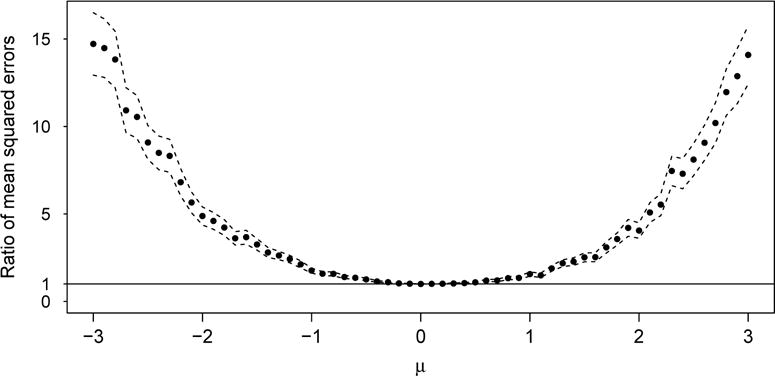
Estimated relative efficiency of ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ vs. ${\widehat{\mathit{d}}}_{\text{conv}}$, together with 95% confidence bands. As μ moves away from 0, the mixing rate of chain 2 slows, and the efficiency of ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ vs. ${\widehat{\mathit{d}}}_{\text{conv}}$ increases. The horizontal line at height 1 serves a reference line.

Figure 2.

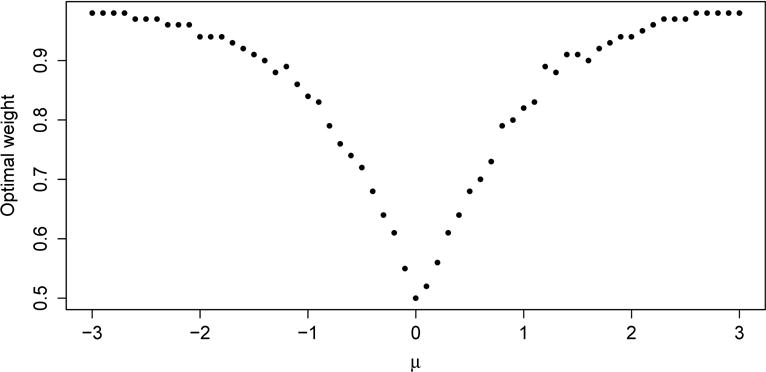
The points are the medians of the first component of ${\widehat{\mathit{a}}}_{\text{opt}}$, i.e. the weight assigned to sample 1 in the term (2.2) in our quasi-likelihood function, over the 1000 replications at each μ. As μ moves away from 0, the weight given to the second (slower mixing) chain decreases to 0.

Of course, because the calculation of ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ requires a pilot study, the comparison above could be viewed as unfair. However, for ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ to perform well all that is required, both in theory and in practice, is that ${\widehat{\mathit{a}}}_{\text{opt}}$ consistently estimate ${\mathrm{argmin}}_{\mathit{a}}\text{Var}({\widehat{\mathit{d}}}_{\mathit{a}})$, and for this to occur all that is required is that the size of the pilot study increase to infinity. That is, the size of the pilot study can increase to infinity arbitrarily slowly when compared to the size of the main study so, asymptotically, the amount of time required to compute ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ and ${\widehat{\mathit{d}}}_{\text{conv}}$ is the same.

Since ultimately our estimates ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ and the standard error estimates given by Theorem 1 are to be used to produce confidence intervals for d₂ (more generally confidence regions for d), we checked the coverage probability of these intervals. Figure 3 gives a graphical display of the observed coverage rates of the nominal 95% confidence intervals over the 1000 repetitions, as μ ranges from −3 to 3. The figure shows that these hover neatly around .95, with no systematic deviation from .95, and no deviation from .95 that is not accounted for in an experiment involving only 1000 repetitions.

Figure 3.

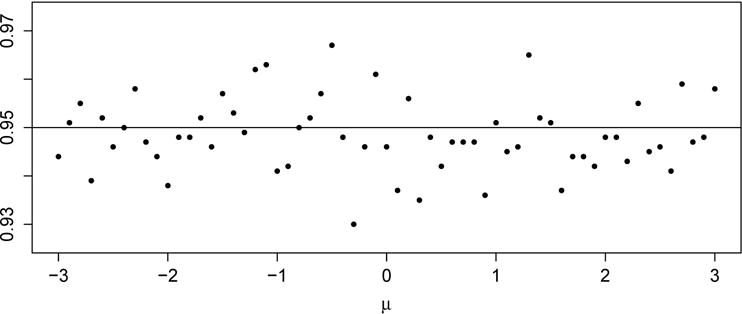
Observed coverage rate of confidence intervals based on ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ and the standard error estimates given by Theorem 1.

5.2 Estimation of the Internal Energy and Specific Heat as Functions of Temperature in the Ising Model

We consider the Ising model on a c × c square lattice with periodic boundary conditions. That is, we have a graph (V, E) where V denotes the set of c² vertices of the lattice, and E denotes the set of 2c² edges that connect nearest neighbors on the lattice. Vertices in the first and last rows are also considered neighbors, as are vertices in the first and last columns, so the graph resides on the torus. For each vertex i ∈ V, we have a random variable X_i taking on the values 1 and −1. The random vector X = {X_i, I ∈ V} gives the state of the system, and the state space S contains $2^{c^2}$ states. For x ∈ S, let $H(x)=-{\displaystyle {\sum }_{i~j}{x}_i{x}_j}$, where the notation i ~ j signifies that i and j are nearest neighbors. For each θ ∈ Θ := [0, ∞), define a probability distribution p_θ on S by

$$p_{\theta }\left(x\right)=z_{\theta }^{-1}\exp \left[-\theta H\left(x\right)\right],x\in S,$$

where $z_{\theta }={\displaystyle {\sum }_{x\in S}\exp \left[-\theta H\left(x\right)\right]}$ is the normalizing constant, called the partition function in the physics literature, and θ = 1/(κT), where T is the temperature and κ is the Boltzmann constant. See, e.g., Newman and Barkema (1999, sec. 1.2) for an overview.

Important to physicists are the internal energy of the system, defined by

$$I_{\theta }=E_{p_{\theta }}\left[H\left(X\right)\right],\theta \in \mathrm{\Theta },$$

and the specific heat, which is the derivative of the internal energy with respect to temperature, or equivalently,

$$C_{\theta }=-\kappa {\theta }^2\frac{\partial I_{\theta }}{\partial \theta }=\kappa {\theta }^2\{E_{p_{\theta }}[H^2(X)]-{(E_{p_{\theta }}[H(X)])}^2\},\theta \in \mathrm{\Theta },$$

and interest is focused on how these quantities vary with θ. Because the size of the state space increases very rapidly as c increases, except for the case c ≤ 5, the quantities above cannot be evaluated, and MCMC must be used. It is simple to implement a Metropolis-Hastings algorithm that randomly chooses a site, proposes to flip its spin, and accepts this proposal with the Metropolis-Hastings probability; however this algorithm converges very slowly. Swendsen and Wang (1987) proposed a data augmentation algorithm in which bond variables are introduced: if i and j are nearest neighbors and X_i = X_j, then with probability 1 − exp(−θ) an edge is placed between vertices i and j. This partitions the state space into connected components, and entire components are flipped. This algorithm converges far more rapidly than the single-site updating algorithm, and it is the algorithm we use here. Mykland et al. (1995, sec. 5.3) developed a simple minorization condition for the Swendsen-Wang algorithm, and we use it here to produce the regenerative chains that are needed to estimate the families {I_θ, θ ∈ Θ} and {C_θ, θ ∈ Θ} via the methods of this paper.

We now consider the problem of estimating the families {I_θ, θ ∈ Θ} and {C_θ, θ ∈ Θ}, and as we will see, the issue of obtaining standard errors for our estimates is quite important. We are in the framework of the second of the three classes of problems mentioned in Section 1, and the two-step procedure given there, described in the present context, is as follows:

• Step 1 We choose points θ₁, …, θ_k appropriately spread out in the region of Θ of interest, and for l = 1, …, k, we run a Swendsen-Wang chain with invariant distribution $p_{{\theta }_l}$ for ρ_l regenerations. Using these k chains, we form $\widehat{\mathit{d}}$, the estimate of the vector d, where $d_l=z_{{\theta }_l}/z_{{\theta }_1}$, l = 2, …, k.

• Step 2 For each l = 1, …, k, we generate a new Swendsen-Wang chain with invariant distribution $p_{{\theta }_l}$ for R_l regenerations, and we use these new chains, together with the estimate $\widehat{\mathit{d}}$ produced in Step 1, to estimate I_θ and C_θ.

We now describe the details involved in Step 2. Denote the l^th sample (in Step 2) by $\{X_i^{(l)},i=1,\dots ,n_l\}$. For each θ ∈ Θ, define g_θ(x) = exp[−θH(x)] for x ∈ S. Let

$$u\left(x\right)=\frac{g_{\theta }\left(x\right)}{{\displaystyle {\sum }_{s=1}^k{g}_{{\theta }_s}\left(x\right)}},v\left(x\right)=H\left(x\right)u\left(x\right),\text{and}z\left(x\right)=H^2\left(x\right)u\left(x\right),$$

and let

$${\widehat{u}}_n={\displaystyle \sum _{l=1}^k\frac{{\widehat{d}}_l}{n_l}{\displaystyle \sum _{i=1}^{n_l}u(X_i^{(l)})}},{\widehat{v}}_n={\displaystyle \sum _{l=1}^k\frac{{\widehat{d}}_l}{n_l}{\displaystyle \sum _{i=1}^{n_l}v(X_i^{(l)})}},\text{and}{\widehat{z}}_n={\displaystyle \sum _{l=1}^k\frac{{\widehat{d}}_l}{n_l}{\displaystyle \sum _{i=1}^{n_l}z(X_i^{(l)})}}.$$

(These quantities depend on θ, but this dependence is temporarily suppressed in the notation.) Using E_l to denote expectation with respect to $p_{{\theta }_l}$, we have

$${\widehat{I}}_{\theta }:=\frac{{\widehat{v}}_n}{{\widehat{u}}_n}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\frac{{\displaystyle {\sum }_{l=1}^k{d}_l{E}_l(v(X))}}{{\displaystyle {\sum }_{l=1}^k{d}_l{E}_l(u(X))}}=\frac{\left(z_{\theta }/z_{{\theta }_1}\right){\displaystyle {\sum }_{x\in S}H\left(x\right)p_{\theta }\left(x\right)}}{\left(z_{\theta }/z_{{\theta }_1}\right){\displaystyle {\sum }_{x\in S}{p}_{\theta }\left(x\right)}}=I_{\theta }$$

as ρ_l → ∞ and R_l → ∞ for l = 1, …, k, where the convergence statement follows from ergodicity of the Swendsen-Wang chains and the fact that $\widehat{\mathit{d}}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathit{d}$_. Similarly, we have

$${\widehat{C}}_{\theta }:=\kappa {\theta }^2\left(\frac{{\widehat{z}}_n}{{\widehat{u}}_n}-{\left(\frac{{\widehat{v}}_n}{{\widehat{u}}_n}\right)}^2\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{C}_{\theta }.$$

Furthermore, Theorem 2 of Tan, Doss and Hobert (2012) deals precisely with the asymptotic distribution of estimates of the form ${\widehat{I}}_{\theta }$ and ${\widehat{C}}_{\theta }$, in the framework of regenerative Markov chains. This theorem, which relies on Theorem 1 of the present paper, states that if (i) both Stage 1 and Stage 2 chains satisfy A1–A3 of the present paper, (ii) for l = 1, …, k, R_l/R₁ and ρ_l/ρ₁ converge to positive finite constants, and (iii) R₁/ρ₁ converges to a nonnegative finite constant, then $R_1^{1/2}({\widehat{I}}_{\theta }-I_{\theta })$ and $R_1^{1/2}({\widehat{C}}_{\theta }-C_{\theta })$ have asymptotically normal distributions, and the theorem also provides regeneration-based consistent estimates of the asymptotic variances. These are the estimates we use in this section.

We will apply the approach described above in two situations. The first involves the Ising model on a square lattice small enough so that exact calculations can be done. This enables us to check the performance of our estimators and confidence intervals. The second involves the Ising model on a larger lattice, where calculations can be done only through Monte Carlo methods.

We first consider the Ising model on a 5 × 5 lattice, and we focus on the problem of estimating C_θ, the specific heat. Figure 4 was created using our methods. The left panel gives a plot of ${\widehat{C}}_{\theta }$, together with 95% confidence bands (valid pointwise), and a plot of the exact values. The right panel gives the standard error estimates for ${\widehat{C}}_{\theta }$.To create the figure, we used the approach described above, with k = 5 and (θ₁, …, θ₅) = (.3, .4, .5, .6, .7). For each l = 1, …, 5, regenerative Swendsen-Wang chains of (approximate) length 10,000 were run for θ_l, based on which $\widehat{\mathit{d}}$and $\widehat{W}$ from Theorem 1 were calculated. We then ran independent chains for the same five θ values, for as many iterations, to form estimates ${\widehat{C}}_{\theta }$ on a fine grid of θ values that range from .2 to 1 in increments of .01. The plot in the right panel was obtained from the formula in Theorem 2 of Tan et al. (2012) and the exact values of C_θ were obtained using closed-form expressions from the physics literature.

Figure 4.

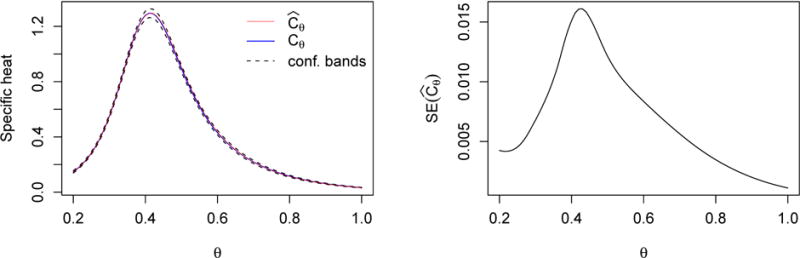
Estimation of the specific heat for the Ising model on a 5 × 5 lattice. Left panel gives a plot of the point estimates and a plot of the exact values, as θ varies. The two plots are visually indistinguishable. Also provided are 95% confidence bands. Right panel gives standard errors for ${\widehat{C}}_{\theta }$.

We mention that Newman and Barkema (1999, sec. 3.7) also considered the problem of estimating the specific heat for the Ising model on a 5 × 5 lattice. They have a plot very similar to ours, but they produced it by running a separate Swendsen-Wang chain for each θ value on a fine grid, and each chain is used solely for the θ value under which it was generated. In contrast, our method requires only k Swendsen-Wang chains, where k is fairly small, and all chains are used to estimate C_θ for every θ. Here, we have considered a simple instance of the Ising model, the so-called one-parameter case. It is common to also consider the situation where there is an external magnetic field, in which case θ has dimension 2, and $p_{\theta }\left(x\right)\propto \exp \left({\theta }_1{\displaystyle {\sum }_{i~j}{x}_i{x}_j+{\theta }_2{\displaystyle {\sum }_{i\in V}{x}_i}}\right)$. Running a separate Swendsen-Wang chain for each θ in a fine subgrid in dimension 2 becomes extremely time consuming, whereas our approach is easily still workable.

In our second example, we consider the Ising model on a 30 × 30 lattice, for which exact calculations of physical quantities are prohibitively expensive, and our interest is now on estimating the internal energy. The left panel of Figure 5 shows a plot of ${\widehat{I}}_{\theta }$ vs. θ as θ ranges from .35 to 1.5 in increments of .01. To form the plot we carried out the two-step procedure discussed earlier, with k = 5 and reference points (θ₁, …, θ₅) = (.65, .75, .85, .95, 1.05), and a sample size of 100,000 for each chain in both steps. The left panel also shows 95% bands, valid pointwise, and the right panel shows the estimated standard errors. From the plot, we can see that the standard errors are much larger when θ < θ₁ = .65 than they are when θ ≥ θ₁. The importance sampling estimates are not stable when we try to extrapolate below the lowest reference θ value, but we can go well above the highest reference value and still get accurate estimates. It is our ability to estimate SE’s through regeneration that makes it possible for us to determine the range of θ’s for which we have reliable estimates. In fact, this range depends in a complicated way on the reference points and the sample sizes, and even for the relatively simple case where k = 1, the range is not simply an interval centered at θ₁.

Figure 5.

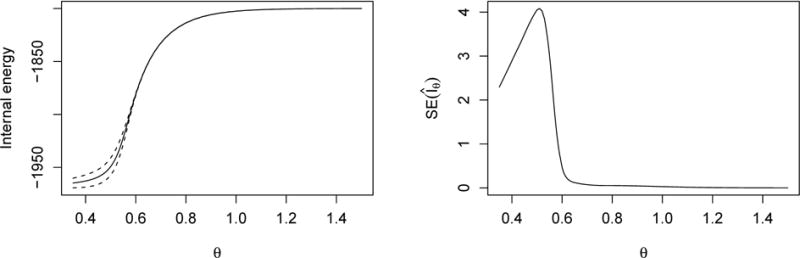
Estimation of the internal energy for the Ising model on a 30 × 30 lattice. Left panel gives estimated values, together with 95% confidence bands. Right panel gives the corresponding standard error estimates.

6 Discussion

The main contributions of this paper are the development of estimators of the vector d which are appropriate for the Markov chain setting, and of consistent standard errors for these estimators. Although we have discussed only estimating variances via regenerative simulation, both batching and spectral methods can also be used (and we believe that a rigorous asymptotic theory can be developed for each of these two methods, although we do not attempt to do so here).

There are two ways to do batching. One is trivial, and is described as follows. Suppose we have some method for estimating d, and let $\widehat{\mathit{d}}$ be the estimate produced by this method when we use the sequences ${\left\{X_i^{(1)}\right\}}_{i=1}^{n_1},\dots ,{\left\{X_i^{(k)}\right\}}_{i=1}^{n_k}$. We break up each of the k chains into M non-overlapping segments of equal length, and we let ${\widehat{\mathit{d}}}^{[1]}$ be the estimate produced from the first segment of each chain, i.e. ${\widehat{\mathit{d}}}^{[1]}$ is produced from the sequences ${\left\{X_i^{(1)}\right\}}_{i=1}^{n_1/M},\dots ,{\left\{X_i^{(k)}\right\}}_{i=1}^{n_k/M}$ (we ignore the problem that the n_j’s may not be divisible by M). Similarly define ${\widehat{\mathit{d}}}^{[2]},\dots {\widehat{\mathit{d}}}^{[M]}$. Assuming we have established that $n^{1/2}(\widehat{\mathit{d}}-\mathit{d})\stackrel{d}{\to }\mathcal{N}(0,V)$, we have, for m = 1, …, M, the corresponding result ${(n/M)}^{1/2}({\widehat{\mathit{d}}}^{[m]}-\mathit{d})\stackrel{d}{\to }\mathcal{N}(0,V)$. Denoting the average $M^{-1}{\displaystyle {\sum }_{m=1}^M{\widehat{\mathit{d}}}^{[m]}}$ by ${\widehat{\mathit{d}}}^{[\cdot ]}$, we may estimate the variance matrix V by $(n/M){\displaystyle {\sum }_{m=1}^M{({\widehat{\mathit{d}}}^{[m]}-{\widehat{\mathit{d}}}^{[\cdot ]})}^2/(M-1)}$, or what is slightly better, $(n/M){\displaystyle {\sum }_{m=1}^M{({\widehat{\mathit{d}}}^{[m]}-\widehat{\mathit{d}})}^2/(M-1)}$ This method requires essentially no programming effort and gives ball-park estimates of the variance matrix.

The crude estimates obtained by the method above are badly outperformed by the regeneration-based estimates developed in this paper (this is illustrated by Figure 6 below, which we will discuss shortly). To obtain better batching-based variance estimates, we must make use of the structure of the problem. We now outline the approach for doing this. Notably, the approach applies equally well to spectral methods. As mentioned earlier, $\widehat{\mathit{d}}=g(\widehat{\mathit{\zeta }})$ and d = g(ζ₀), where g is given by (3.14). So asymptotic normality of ${\rho }_1^{1/2}(\widehat{\mathit{d}}-\mathit{d})$ follows from asymptotic normality of ${\rho }_1^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)$ by the delta method. As we will see in the Appendix, the proof of asymptotic normality of ${\rho }_1^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)$, or that of $n^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)$, is based on representing each component of this vector as a linear combination of standardized averages of functions of the k Markov chains, plus a vanishingly small term. This will be made clear in Appendix A.2; see in particular (A.16) and (A.9). We express this generically as

$${[n^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)]}_r={\displaystyle \sum _{j=1}^k{c}_{rj}\frac{1}{n_j^{1/2}}{\displaystyle \sum _{i=1}^{n_j}{f}_{rj}(X_i^{(j)})+o_p(1)}}\text{for }r=1,\dots ,k,$$

where f_r1, …, f_rk are real-valued functions for which $E\left(f_{rj}(X_i^{(j)})\right)=0$, and c_r1, …, c_rk are constants. For each r and j, the variance of $n_j^{-1/2}{\displaystyle {\sum }_{i=1}^{n_j}{f}_{rj}(X_i^{(j)})}$ can be estimated by batching in the usual way, or via spectral methods, and since the k Markov chains are independent, this leads to an estimate of the variance of ${[n^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)]}_r$, r = 1, …, k. The covariances $\text{Cov}({[n^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)]}_r,{[n^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)]}_s)$, r, s = 1, …, k, are handled in a similar way.

Figure 6.

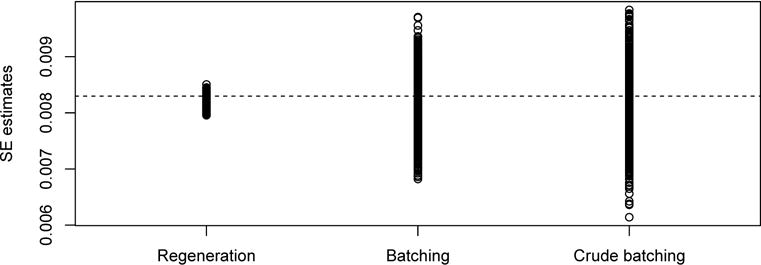
Dotplots of 1000 estimates of standard error of ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ in the setting of Section 5.1 with μ = 1, for three methods: regenerative simulation, structure-based batching, and crude batching. The height of the horizontal dotted line is the true value of the standard error.

Figure 6 compares the distributions of the estimates of standard deviation of the statistic ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ based on regeneration, structure-based batching, and the crude method of batching, for the toy example of Section 5.1 with μ = 1. The length of the chains is n = 10,000 (approximately) and the number of batches is b_n ≈ n^1/2, as recommended in Flegal and Jones (2010). Here we do not know the true value of the standard deviation of ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$, so we estimate this quantity via the sample standard deviation based on 1000 independent replications. The horizontal dotted line is positioned at this empirical estimate. The figure gives a dotplot of the 1000 values for each of the three methods. It shows that structure-based batching outperforms crude batching, and both are outperformed by the regeneration-based method developed in this paper, at least in this particular scenario. When we change the parameter values the ordering is maintained, although the magnitude of the differences varies. (We do not display results for the spectral-based estimate because its performance varies quite a bit with the choice of of window and truncation point; however we can say that in almost all cases it is outperformed by the regeneration-based methods.)

Flegal and Jones (2010) provide a thorough analysis and comparison of confidence intervals produced by regeneration, batching, and spectral methods, for the case where the statistic is an average, They studied confidence intervals of the form ${\overline{f}}_n\pm 1.96{\widehat{\sigma }}_n/n^{1/2}$, and they report that when tuning parameters are chosen in a suitable manner all three methods produce acceptable results. The significant differences in performance we report above are not inconsistent with the results in Flegal and Jones (2010)—all that is needed for confidence intervals to be asymptotically valid is convergence of ${\widehat{\sigma }}_n$ to σ in probability.

We now mention some of the advantages of regenerative simulation for our problem.

1. Batching is generally acknowledged to be outperformed in terms of accuracy by spectral methods (Geyer, 1992), but estimation by spectral methods is computationally expensive. Typically, the truncation point M_n is of the order n^η for some η ∈ (0, 1), and for each j estimation of γ_j requires O(n) operations, so the number of operations needed to estimate the variance by spectral methods is O(n^1+η). By contrast, the number of operations needed to calculate the variance estimate (3.4) is of the order O(n). Consider now the estimate ${\widehat{\mathit{d}}}_{{\widehat{\mathit{a}}}_{\text{opt}}}$ constructed in Section 4, whose calculation requires us to repeatedly compute trace $({\widehat{W}}_{\mathit{a}})$ for a in ${\mathcal{S}}_k$, in order to obtain ${\widehat{\mathit{a}}}_{\text{opt}}:={\mathrm{argmin}}_{\mathit{a}}\text{trace}({\widehat{W}}_{\mathit{a}})$. Once we have constructed the k regeneration sequences ${\tau }_0^{(l)}<{\tau }_1^{(l)}<\cdots {\tau }_{{\rho }_l}^{(l)}$, l = 1, …, k, these same sequences may be used in the computation of ${\widehat{W}}_{\mathit{a}}$ for all a ∈ $\mathcal{S}$. But the analogous minimization procedure applied to spectral methods would come at a significantly greater computational cost.

2. Regeneration does not require us to specify tuning parameters such as the batch size for the case of batching or the truncation point and window for the case of spectral methods.

3. By (3.6) we start each chain at a regeneration point. Therefore, the issue of burn-in does not even exist.

We now discuss the general applicability of the three methods. Regeneration has been applied successfully to a number of problems in recent years; see for example Mykland et al. (1995), Sahu and Zhigljavsky (2003), Roy and Hobert (2007), Tan and Hobert (2009), and Flegal, Jones and Neath (2012). We believe that, when feasible, regenerative simulation is the method of choice. Unfortunately, its successful implementation is problem-specific, i.e. it cannot be routinely applied (the general-purpose method developed by Mykland et al. (1995) applies only to independence Metropolis-Hastings chains). To use regenerative simulation, one must come up with a minorization condition which gives rise to regeneration times that are not too long, and there does not exist a generic procedure for doing this. In most of the published examples, the successful minorization condition is obtained only after some trial and error.

Appendix: Proof of Theorem 1

A.1 Proof of Consistency of $\widehat{\mathit{d}}$

We first work in the ζ domain, and at the very end switch to the d domain. As mentioned earlier, in the standard textbook situation in which we have X₁, …, $X_n\stackrel{\text{iid}}{~}{p}_{{\theta }_0}$ where θ₀ ∈ Θ, l_n(θ) is the log likelihood and $Q(\theta )=E_{{\theta }_0}(l_1(\theta ))$, the classical proof of consistency (Wald, 1949) is based on the observation that Q(θ) is maximized at θ = θ₀, and that for each fixed θ, $l_n(\theta )\stackrel{\mathrm{a}.\mathrm{s}.}{\to }Q(\theta )$. The, convergence may be non-uniform, and care needs to be exercised in showing that the maximizer of l_n(θ) converges to the maximizer of Q(θ). The present situation is simpler in that the log likelihood and its expected value are twice differentiable and concave, but is more complicated in that we have multiple sequences, they are not iid, and we have a non-identifiability issue, so that maximization is carried out subject to a constraint.

We will write ℓ_ρ instead of ℓ_n to remind ourselves that the ρ_l’s are given and the n_l’s are determined by these ρ_l’s. Also, we will write ℓ_ρ(X, ζ) instead of ℓ_ρ(ζ) when we need to note the dependence of ℓ_ρ(ζ) on X, where $\mathit{X}=\left(X_1^{(1)},\dots ,X_{n_1}^{(1)},\dots ,X_1^{(k)},\dots ,X_{n_k}^{(k)}\right)$. We define the (scaled) expected log quasi-likelihood by

$$\lambda (\mathit{\zeta })={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}(\log [p_l(X,\mathit{\zeta })]).}$$

As ρ_l → ∞, we have n_l → ∞, so $n_l^{-1}{\displaystyle {\sum }_{i=1}^{n_l}\log \left(p_l\left(X_i^{(l)},\mathit{\zeta }\right)\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }}{E}_{{\pi }_1}\left(\log [p_l(X,\mathit{\zeta })]\right)$, and so

$$n^{-1}{\ell }_{\rho }(\mathit{X},\mathit{\zeta })\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\lambda (\mathit{\zeta })\text{for all }\mathit{\zeta }.$$

The structure of our proof is similar to that of Theorem 1 of Geyer (1994), and the outline of our proof is as follows. First, define S = {ζ : ζ^⊤1_k = 0}, and recall that $\widehat{\mathit{\zeta }}$ is defined to be a maximizer of ℓ_ρ(X, ζ) satisfying $\widehat{\mathit{\zeta }}\in S$.

1. We will show that for every X, ℓ_ρ(X, ζ) is everywhere twice differentiable and concave in ζ.

2. We will show that λ(ζ) is finite, everywhere twice differentiable, and concave. We further show that its Hessian matrix is semi-negative definite, and that its only null eigenvector is 1_k.

3. We will show that ∇λ(ζ₀) = 0.

4. We will note that the two steps above imply that ζ₀ is the unique maximizer of λ subject to the condition ζ₀ ∈ S.

5. We will argue that with probability one, for every ζ, ∇²ℓ_ρ(X, ζ) is semi-negative definite, and 1_k is its only null eigenvector. This will show that $\widehat{\mathit{\zeta }}$ is the unique maximizer of ℓ_ρ(X, ζ) subject to $\widehat{\mathit{\zeta }}\in S$.

6. We will conclude that the convergence of ℓ_ρ(X, ζ) to λ(ζ) implies convergence of their maximizers that reside in S, that is, $\widehat{\mathit{\zeta }}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\mathit{\zeta }}_0$.

We now provide the details.

1. The differentiability is immediate from the definition of ℓ_ρ (see (2.7)). To show concavity, it is sufficient to show that for every x, log(p_l(x, ζ)) is concave in ζ. Now

   $$\frac{{\partial }^2\log (p_l(x,\mathit{\zeta }))}{\partial {\mathit{\zeta }}^2}=-(\text{diag}(\mathit{p})-\mathit{p}{\mathit{p}}^{\top }),$$ (A.1)

   where p = (p₁(x, ζ), …, p_k(x, ζ))^⊤. The matrix inside the parentheses on the right side of (A.1) is the variance matrix for the multinomial distribution with parameter p, so this matrix is positive semi-definite.
2. First, λ(ζ) is finite because λ(ζ) ≤ 0, and

   $$\begin{array}{l}-\lambda (\mathit{\zeta })={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}}\left[\log \left(\frac{1}{p_l(X,\mathit{\zeta })}\right)\right]\\ ={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}}\left[\log \left(1+{\displaystyle \sum _{s\ne l}\frac{{\nu }_s(X)}{{\nu }_l(X)}{e}^{{\zeta }_s-{\zeta }_l}}\right)\right]\\ \le {\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}}\left({\displaystyle \sum _{s\ne l}\frac{{\nu }_s(X)}{{\nu }_l(X)}{e}^{{\zeta }_s-{\zeta }_l}}\right)(\log (1+a)<a\text{for}a>0)\\ \le {\displaystyle \sum _{l=1}^k{a}_l}{\displaystyle \sum _{s\ne l}{e}^{{\zeta }_s-{\zeta }_l}}{\displaystyle \int \frac{{\nu }_s(x)}{{\nu }_l(x)}{\pi }_l(x)}\mu (dx)\\ ={\displaystyle \sum _{l=1}^k{a}_l}{\displaystyle \sum _{s\ne l}{e}^{{\zeta }_s-{\zeta }_l}}\frac{m_s}{m_l}{\displaystyle \int \frac{{\pi }_s(x)}{{\pi }_l(x)}{\pi }_l}(x)\mu (dx)<\infty .\end{array}$$

   We now obtain the first and second derivatives of λ. By a standard argument involving the dominated convergence theorem, we can interchange the order of differentiation and integration. (If v is the vector of length k with a 1 in the r^th position and 0’s everywhere else, then for any x, any ζ, and any l ∈ {1, …, k}, [log(p_l(x, ζ + υ/m)) − log(p_l(x, ζ))]m = ∂ log(p_l(x, ζ_∗))/∂ζ_r, where ζ_∗ is between ζ + υ/m and ζ, and this partial derivative is uniformly bounded between −1 and 1.) So for r = 1, …, k, we have

   $$\frac{\partial \lambda (\mathit{\zeta })}{\partial {\zeta }_r}={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}}\left(\frac{\partial \log \left(p_l(X,\mathit{\zeta })\right)}{\partial {\zeta }_r}\right)=a_r-{\displaystyle \sum _{l=1}^k{a}_l}{E}_{{\pi }_l}\left(p_r(X,\mathit{\zeta })\right).$$ (A.2)

   Consider the integrand on the right side of (A.2), i.e. p_r(X, ζ). Its gradient is given by $\partial p_r/\partial {\zeta }_r=p_r-p_r^2$ and ∂p_r/∂ζ_l = −p_rp_l for l ≠ r, and these derivatives are uniformly bounded in absolute value by 1. Hence again by the dominated convergence theorem, we can interchange the order of differentiation and integration, and doing this gives

   $$\begin{array}{l}-\frac{{\partial }^2\lambda (\mathit{\zeta })}{\partial {\zeta }_r^2}={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}}\left(\frac{\partial p_r(X,\mathit{\zeta })}{\partial {\zeta }_r}\right)={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}[p_r(X,\mathit{\zeta })-p_r^2(X,\mathit{\zeta })]}\\ -\frac{{\partial }^2\lambda (\mathit{\zeta })}{\partial {\zeta }_s\partial {\zeta }_r}={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}}\left(\frac{\partial p_r(X,\mathit{\zeta })}{\partial {\zeta }_s}\right)={\displaystyle \sum _{l=1}^k{a}_l{E}_{{\pi }_l}[-p_r(X,\mathit{\zeta })p_s(X,\mathit{\zeta })]}\text{for }s\ne r.\end{array}$$ (A.3)

   Define the expectation operator $E_P={\displaystyle {\sum }_{l=1}^k{a}_l{E}_l}$. From (A.3) we have −∇²λ(ζ) = E_P(J), where J = diag(p) − pp^⊤, and as before p = (p₁(X, ζ), …, p_k(X, ζ))^⊤. As before, J is the covariance of the multinomial, so is positive semi-definite, and therefore so is E_P (J).
   We now determine the null eigenvectors of ∇²λ(ζ) (which is −E_P (J)). If ∇²λ(ζ)u = 0, then u^⊤[∇²λ(ζ)]u = 0, so E_P(u^⊤Ju) = 0. Since J is positive semi-definite, it has a square root, J^1/2. Hence E_P (‖J^1/2u‖²) = 0, which implies Ju = 0 [P]-a.e. The condition Ju = 0 [P]-a.e. is expressed as

   $$p_r(X,\mathit{\zeta })\left({\displaystyle {\sum }_{l=1}^k{p}_l(X,\mathit{\zeta })u_l-u_r}\right)=0[P]-\mathrm{a}.\mathrm{e}.\text{for }r=1,\dots ,k,$$ (A.4)

   and under our assumption that ν₁, …, ν_k are mutually absolutely continuous, (A.4) implies that $u_r={\displaystyle {\sum }_{l=1}^k{p}_l(X,\mathit{\zeta })}{u}_l$ for r = 1, …, k. So u₁ = ⋯ = u_k, i.e. u ∝ 1_k.
3. To show that ∇λ(ζ₀) = 0, we write

   $$\begin{array}{l}{\frac{\partial \lambda (\mathit{\zeta })}{\partial {\zeta }_r}|}_{{\mathit{\zeta }}_0}=a_r-{\displaystyle \sum _{l=1}^k{a}_l}{\displaystyle \int \frac{{\nu }_r(x)a_r/m_r}{{\displaystyle {\sum }_{s=1}^k{\nu }_s(x)a_s}/m_s}}{\pi }_l(x)\mu (dx)\\ =a_r-{\displaystyle \int \frac{{\displaystyle {\sum }_{l=1}^k{a}_l{\pi }_l}(x)}{{\displaystyle {\sum }_{s=1}^k{a}_s{\nu }_s(x)}/m_s}}{\nu }_r(x)a_r/m_r\mu (dx)\\ =a_r-a_r{\displaystyle \int {\pi }_r(x)\mu (dx)}=0.\end{array}$$
4. For any ζ satisfying ζ^⊤1_k = 0, we may write

   $$\begin{array}{l}\lambda (\mathit{\zeta })=\lambda ({\mathit{\zeta }}_0)+{\left(\mathit{\zeta }-{\mathit{\zeta }}_0\right)}^{\top }\nabla \lambda ({\mathit{\zeta }}_0)+\frac{1}{2}{\left(\mathit{\zeta }-{\mathit{\zeta }}_0\right)}^{\top }{\nabla }^2\lambda \left({\mathit{\zeta }}_{\ast }\right)\left(\mathit{\zeta }-{\mathit{\zeta }}_0\right)\\ =\lambda ({\mathit{\zeta }}_0)+\frac{1}{2}{\left(\mathit{\zeta }-{\mathit{\zeta }}_0\right)}^{\top }{\nabla }^2\lambda \left({\mathit{\zeta }}_{\ast }\right)\left(\mathit{\zeta }-{\mathit{\zeta }}_0\right),\end{array}$$

   where ζ_∗ is between ζ and ζ₀. If ζ ≠ ζ₀, i.e. ζ − ζ₀ ≠ 0, then since (ζ − ζ₀)^⊤ 1_k = 0, ζ − ζ₀ cannot be a scalar multiple of 1_k. Hence by Step 2, (ζ − ζ₀)^⊤∇²λ(ζ_∗)(ζ − ζ₀) < 0.

5. Clearly $\nabla {\ell }_{\rho }\left(\mathit{X},\widehat{\mathit{\zeta }}\right)$. The proof that (i) ∇²ℓ_ρ(X, ζ) is semi-negative definite, (ii) the only null eigenvector of ∇²ℓ_ρ(X, ζ) is 1_k, and (iii) $\widehat{\mathit{\zeta }}$ is the unique maximizer of ℓ_ρ(X, ζ) subject to the constraint ζ ∈ S, is essentially identical to the proof of these assertions for λ(ζ).

6. Since $n^{-1}{\ell }_{\rho }\left(\mathit{X},\mathit{\zeta }\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\lambda (\mathit{\zeta })$ for each ζ, a.s. convergence occurs on a dense subset of S. Also, the functions involved are all concave in the entire space of ζ’s, hence are concave in S. Therefore, we have a.s. uniform convergence of $n^{-1}{\ell }_{\rho }\left(\mathit{X},\mathit{\zeta }\right)$ to λ(ζ) on compact subsets of S. Under concavity, this is enough to imply ${\mathrm{argmax}}_{\mathit{\zeta }\in S}{\ell }_{\rho }\left(\mathit{X},\mathit{\zeta }\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\mathrm{argmax}}_{\mathit{\zeta }\in S}\lambda (\mathit{\zeta })$, i.e. $\widehat{\mathit{\zeta }}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\mathit{\zeta }}_0$.

Finally, to see that $\widehat{\mathit{d}}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathit{d}$, we write $\widehat{\mathit{d}}-\mathit{d}=g\left(\widehat{\mathit{\zeta }}\right)-g\left({\mathit{\zeta }}_0\right)=\nabla g{\left({\mathit{\zeta }}_{\ast }\right)}^{\top }\left(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\right)$, where ζ_∗ is between $\widehat{\mathit{\zeta }}$ and ζ₀. The function g actually depends on a^(ρ), so depends on ρ, but the gradient ∇g(ζ_∗) is bounded for large ρ because $\widehat{\mathit{\zeta }}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\mathit{\zeta }}_0$ and α^(ρ) → α. Therefore $\widehat{\mathit{d}}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathit{d}$.

A.2 Proof of Regeneration-Based CLT for $\widehat{\mathit{d}}$

We begin by considering ${\rho }_1^{1/2}\left(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\right)$. As in the classical proof of asymptotic normality of maximum likelihood estimators, we expand ∇ℓ_ρ at $\widehat{\mathit{\zeta }}$ around ζ₀, and using the appropriate scaling factor, we get

$$-\frac{{\rho }_1^{1/2}}{n}\left(\nabla {\ell }_{\rho }(\widehat{\mathit{\zeta }})-\nabla {\ell }_{\rho }({\mathit{\zeta }}_0)\right)=-\frac{1}{n}{\nabla }^2{\ell }_{\rho }({\mathit{\zeta }}_{\ast }){\rho }_1^{1/2}\left(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\right),$$ (A.5)

where ζ_∗ is between $\widehat{\mathit{\zeta }}$ and ζ₀. Consider the left side of (A.5), which is just ${\rho }_1^{1/2}{n}^{-1}\nabla {\ell }_{\rho }\left({\mathit{\zeta }}_0\right)$, since $\nabla {\ell }_{\rho }(\widehat{\mathit{\zeta }})=0$. There are several nontrivial components to the proof, so we first give an outline.

1. We show that each element of the vector n⁻¹∇ℓ_ρ(ζ₀) can be represented as a linear combination of mean 0 averages of functions of the k chains plus a vanishingly small term.

2. Using Step 1 above, we obtain a regeneration-based CLT for the scaled score vector, via a considerably more involved version of the method we used in Section 3.1: we show that ${\rho }_1^{1/2}{n}^{-1}\nabla {\ell }_{\rho }({\mathit{\zeta }}_0)\stackrel{d}{\to }\mathcal{N}(0,\mathrm{\Omega })$, where Ω is given by (3.12).

3. We argue that $-n^{-1}{\nabla }^2{\ell }_{\rho }({\mathit{\zeta }}_{\ast })\stackrel{\mathrm{a}.\mathrm{s}.}{\to }B$ and that ${\left(-n^{-1}{\nabla }^2{\ell }_{\rho }({\mathit{\zeta }}_{\ast })\right)}^{†}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{B}^{†}$, where B is defined in (3.8), using ideas in Geyer (1994).

4. We conclude that ${\rho }_1^{1/2}\left(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\right)\stackrel{d}{\to }\mathcal{N}(0,B^{†}\mathrm{\Omega }{B}^{†})$.

5. We note the relationships d = g(ζ₀) and $\widehat{\mathit{d}}=g(\widehat{\mathit{\zeta }})$, where g was define by (3.14), and apply the delta method to obtain the desired result.

We now provide the details.

1. We start by considering n⁻¹∇ℓ_ρ(ζ₀). For r = 1, …, k, we have

   $$\begin{array}{l}\frac{\partial {\ell }_{\rho }({\mathit{\zeta }}_0)}{\partial {\zeta }_r}=w_r{\displaystyle \sum _{i=1}^{n_r}\left(1-p_r(X_i^{(r)},{\mathit{\zeta }}_0)\right)-{\displaystyle \sum _{\begin{array}{l}l=1\\ l\ne r\end{array}}^k{w}_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_0\right)}}\\ =w_r{\displaystyle \sum _{i=1}^{n_r}\left(1-p_r\left(X_i^{(r)},{\mathit{\zeta }}_0\right)-\left[1-E_{{\pi }_r}(p_r(X,{\mathit{\zeta }}_0))\right]\right)}\\ -{\displaystyle \sum _{\begin{array}{l}l=1\\ l\ne r\end{array}}^k{w}_l}{\displaystyle \sum _{i=1}^{n_l}\left[p_r\left(X_i^{(l)},{\mathit{\zeta }}_0\right)-E_{{\pi }_l}\left(p_r(X,{\mathit{\zeta }}_0)\right)\right]+e,}\end{array}$$ (A.6)

   where

   $$e=w_r{\displaystyle \sum _{i=1}^{n_r}[1-E_{{\pi }_r}\left(p_r(X,{\mathit{\zeta }}_0)\right)]-{\displaystyle \sum _{\begin{array}{l}l=1\\ l\ne r\end{array}}^k{w}_l}{\displaystyle \sum _{i=1}^{n_l}{E}_{{\pi }_l}}\left(p_r(X,{\mathit{\zeta }}_0)\right).}$$ (A.7)
   We claim that e = 0. To see this, note that from (A.7) we have

   $$e=w_r{n}_r-{\displaystyle \sum _{l=1}^k{w}_l{n}_l{E}_{{\pi }_l}\left(p_r(X,{\mathit{\zeta }}_0)\right)=w_r{n}_r-{\displaystyle \sum _{l=1}^k{w}_l{n}_l}\frac{a_r}{a_l}{E}_{{\pi }_r}\left(p_l(X,{\mathit{\zeta }}_0)\right).}$$ (A.8)
   The last equality in (A.8) holds because

   $$\begin{array}{l}{E}_{{\pi }_l}\left(p_r(X,{\mathit{\zeta }}_0)\right)={\displaystyle \int \frac{{\nu }_r(x)e^{{[{\zeta }_0]}_r}}{{\displaystyle {\sum }_{s=1}^k{\nu }_s(x)e^{{[{\zeta }_0]}_s}}}{\pi }_l\left(x\right)\mu (dx)={\displaystyle \int \frac{{\nu }_r(x)a_r/m_r}{{\displaystyle {\sum }_{s=1}^k{\nu }_s(x)a_s/m_s}}{\pi }_l(x)\mu (dx)}}\\ ={\displaystyle \int \frac{{\nu }_l(x)a_r/m_l}{{\displaystyle {\sum }_{s=1}^k{\nu }_s(x)a_s/m_s}}{\pi }_r(x)\mu (dx)=\frac{a_r}{a_l}{E}_{{\pi }_r}\left(p_l(X,{\mathit{\zeta }}_0)\right).}\end{array}$$
   Therefore, using the fact that w_ln_la_r/a_l = w_rn_r, we get

   $$e=w_r{n}_r-w_r{n}_r{\displaystyle {\sum }_{l=1}^k{E}_{{\pi }_r}\left(p_l(X,{\mathit{\zeta }}_0)\right)=w_r{n}_r-w_r{n}_r{E}_{{\pi }_r}\left({\displaystyle {\sum }_{l=1}^k{p}_l(X,{\mathit{\zeta }}_0)}\right)=0.}$$
   We summarize: Because e = 0, (A.6) can be used to view n⁻¹∂ℓ_ρ(ζ₀)/∂ζ_r as a linear combination of mean 0 averages of functions of the k chains. To express these averages in terms of iid quantities, we first recall the definitions of $y_i^{(r,l)}(\mathit{a})$, $Y_t^{(r,l)}(\mathit{a})$, ${\overline{Y}}^{(r,l)}(\mathit{a})$, and ${\overline{T}}^{(l)}$ given in (3.10) and (3.11), and multiplying by the scaling factor ${\rho }_1^{1/2}{n}^{-1}$, we rewrite (A.6) as

   $$\frac{{\rho }_1^{1/2}}{n}\frac{\partial {\ell }_{\rho }({\mathit{\zeta }}_0)}{\partial {\zeta }_r}=-\frac{{\rho }_1^{1/2}}{n}{\displaystyle \sum _{l=1}^k{w}_l}{\displaystyle \sum _{i=1}^{n_l}\left[p_r\left(X_i^{(l)},{\mathit{\zeta }}_0\right)-E_{{\pi }_l}\left(p_r(X,{\mathit{\zeta }}_0)\right)\right]}$$ (A.9a)

   $$=-{\displaystyle \sum _{l=1}^k\frac{{\rho }_1^{1/2}{n}_l}{n}{w}_l\frac{1}{n_l}{\displaystyle \sum _{t=1}^{{\rho }_l}{Y}_t^{(r,l)}(a)}}$$ (A.9b)

   $$=-{\displaystyle \sum _{l=1}^k\frac{{\rho }_1^{1/2}{n}_l}{n}{w}_l\frac{{\displaystyle {\sum }_{t=1}^{{\rho }_l}{Y}_t^{(r,l)}(a)}}{{\displaystyle {\sum }_{t=1}^{{\rho }_l}{T}_t^{(l)}}}}$$ (A.9c)

   $$=-{\displaystyle \sum _{l=1}^k\left[{\left(\frac{{\rho }_1}{{\rho }_l}\right)}^{1/2}\frac{n_l}{n}{w}_l\right]\left[{\rho }_l^{1/2}\frac{{\overline{Y}}^{(r,l)}(a)}{{\overline{T}}^{(l)}}\right]}$$ (A.9d)

   $$=-{\displaystyle \sum _{l=1}^k\left[{\left(\frac{{\rho }_1}{{\rho }_l}\right)}^{1/2}{a}_l\right]\left[{\rho }_l^{1/2}\frac{{\overline{Y}}^{(r,l)}(a)}{{\overline{T}}^{(l)}}\right].}$$ (A.9e)

2. We now apply a more complex and more rigorous version of the argument we used in Section 3.1. We note the following: (i) the k chains are geometrically ergodic by Assumption A2; (ii) since p_r(x, ζ) ∈ (0, 1) for all x and all ζ, $E_{{\pi }_l}\left({\left|y_1^{(r,l)}(\mathit{a})\right|}^{2+\epsilon }\right)<\infty$ for some ε > 0 (in fact for any ε > 0); and (iii) by (3.10) the mean of $Y_t^{(r,l)}(\mathit{a})$ is 0. The usual CLT for iid sequences does not apply to the sequence $Y_1^{(r,l)}(\mathit{a})$, …, $Y_{{\rho }_l}^{(r,l)}(\mathit{a})$ because a = a^(ρ) is allowed to change with ρ, so the distribution of $Y_t^{(r,l)}(\mathit{a})$ changes with ρ. Since r and l are now fixed and play no important role, while the dependence of a on ρ now needs to be noted we will write y_i(a^(ρ)) instead of $y_i^{(r,l)}(\mathit{a})$, Y_t(a^(ρ)) instead of $Y_t^{(r,l)}(\mathit{a})$, etc. We really have a triangular array of random variables, and we will apply the Lindeberg-Feller version of the CLT.

   We first need to show that $E\left({\left[Y_t\left({\mathit{a}}^{(\rho )}\right)\right]}^2\right)<\infty$. (This condition is nontrivial because Y_t(a^(ρ)) is the sum of a random number of terms.) Note that since p_r(x, ζ) ∈ (0, 1), |y_i(a^(ρ))| ≤ 1, and therefore,

   $$\left|Y_t(a^{(\rho )})\right|\le T_t^{(l)}.$$ (A.10)
   Theorem 2 of Hobert, Jones, Presnell and Rosenthal (2002) states that $E\left[{\left(T_t^{(l)}\right)}^2\right]<\infty$ under geometric ergodicity. So E([Y_t(a^(ρ))]²) < ∞, and we may form the triangular array whose ${\rho }_l^{\text{th}}$ row consists of the variables U₁(a^(ρ)), …, $U_{{\rho }_l}({\mathit{a}}^{(\rho )})$ where

   $$U_t(a^{(\rho )})=\frac{Y_t(a^{(\rho )})}{{\left({\displaystyle {\sum }_{s=1}^{{\rho }_l}\text{Var}\left[Y_s(a^{(\rho )})\right]}\right)}^{1/2}}.$$

   Clearly, E[U_t(a^(ρ))] = 0 and ${\displaystyle {\sum }_{t=1}^{{\rho }_l}\text{Var}}\left[U_t({\mathit{a}}^{(\rho )})\right]=1$.

   The Lindeberg Condition is that for every η > 0,

   $${\displaystyle \sum _{t=1}^{{\rho }_l}E\left({\left[U_t(a^{(\rho )})\right]}^{2}I\left(\left|U_t(a^{(\rho )})\right|>\eta \right)\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }}0\text{as}{\rho }_l\to \infty ,$$

   and this is equivalent to the condition

   $$E\left[\frac{{\left[Y_1(a^{(\rho )})\right]}^2}{\text{Var}\left[Y_1(a^{(\rho )})\right]}I\left(\frac{\left|Y_1(a^{(\rho )})\right|}{{\left({\rho }_l\text{Var}[Y_1(a^{(\rho )})]\right)}^{1/2}}>\eta \right)\right]\to 0\text{as}{\rho }_l\to \infty .$$ (A.11)
   To see (A.11) note that as ρ_l → ∞, by the assumption that a^(ρ) → α where all the components of α are strictly positive and dominated convergence, we have

   $$Y_1(a^{(\rho )})\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{Y}_1(\mathit{\alpha }).$$

   By (A.10), we have ${\left[Y_t({\mathit{a}}^{(\rho )})\right]}^2\le {\left(T_t^{(l)}\right)}^2$, and $E\left[{\left(T_t^{(l)}\right)}^2\right]<\infty$ by Theorem 2 of Hobert et al. (2002). Therefore, E([Y_t(a^(ρ))]²) → E([Yt(α)]²) by (A.10) and dominated convergence, and we also have E[Y_t(a^(ρ))] → E[Y_t(α)], so that Var[Y_t(a^(ρ))] → Var[Y_t(α)]. Since I[|Y₁(a^(ρ))| > (ρ_l Var[Y₁(a^(ρ))])^1/2η] = 0 for large ρ, (A.11) follows by dominated convergence.

   The Lindeberg-Feller theorem (together with the fact that ${\overline{T}}^{(l)}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }E\left(T_1^{(l)}\right)$)) now states that the term in the second set of brackets in (A.9e) has an asymptotic normal distribution, with mean 0, and variance $E\left({\left[Y_1^{(r,l)}(\mathit{\alpha })\right]}^2\right)/{\left(E\left(T_1^{(l)}\right)\right)}^2$. The term in the first set of brackets converges to ${\alpha }_l{c}_l^{-1/2}.$ Since the k chains are independent, we conclude that

   $$\frac{{\rho }_1^{1/2}}{n}\frac{\partial {\ell }_{\rho }({\mathit{\zeta }}_0)}{\partial {\zeta }_r}\stackrel{d}{\to }\mathcal{N}(0,{\mathrm{\Omega }}_{rr})\mathrm{as}{\rho }_1\to \infty ,$$

   where Ω was defined in (3.12). But by the Cramér-Wold Theorem, we obtain the more general statement involving the asymptotic distribution of the entire gradient vector. The argument is standard and gives

   $$\frac{{\rho }_1^{1/2}}{n}\nabla {\ell }_{\rho }({\mathit{\zeta }}_0)\stackrel{d}{\to }N(0,\mathrm{\Omega })\text{as }{\rho }_1\to \infty .$$
3. Now, referring to (A.5), denote the matrix −n⁻¹∇²ℓ_ρ(ζ_∗) by B_ρ. We have

   $$\begin{array}{l}{[B_{\rho }]}_{rr}={\displaystyle \sum _{l=1}^k{a}_l}\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_{\ast }\right)}\left[1-p_r\left(X_i^{(l)},{\mathit{\zeta }}_{\ast }\right)\right]\right),r=1,\dots ,k,\\ {[B_{\rho }]}_{rs}=-{\displaystyle \sum _{l=1}^k{a}_l\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_{\ast }\right)p_s\left(X_i^{(l)},{\mathit{\zeta }}_{\ast }\right)}\right),r,s=1,\dots ,k,r\ne s,}\end{array}$$ (A.12)

   and for later use also define $B_{\rho }^{(\mathit{\alpha })}$ by

   $$\begin{array}{l}{\left[B_{\rho }^{(\mathit{\alpha })}\right]}_{rr}={\displaystyle \sum _{l=1}^k{a}_l}\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)}\left[1-p_r\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)\right]\right),r=1,\dots ,k,\\ {\left[B_{\rho }^{(\mathit{\alpha })}\right]}_{rs}=-{\displaystyle \sum _{l=1}^k{a}_l\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)p_s\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)}\right),r,s=1,\dots ,k,r\ne s.}\end{array}$$ (A.13)
   From (A.12) we can check that

   $$B_{\rho }{1}_k=0,$$ (A.14)

   and because $1_k^{\top }\widehat{\mathit{\zeta }}=0$ and $1_k^{\top }{\mathit{\zeta }}_0=0$, we have

   $$\left(\begin{array}{l}{B}_{\rho }\\ \frac{1_k^{\top }}{\sqrt{k}}\end{array}\right){\rho }_1^{1/2}\left(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\right)=\left(\begin{array}{c}\frac{{\rho }_1^{1/2}}{n}\nabla {\ell }_{\rho }({\mathit{\zeta }}_0)\\ 0\end{array}\right).$$
   Hence

   $$\left(B_{\rho }^{†},\frac{1_k}{\sqrt{k}}\right)\left(\begin{array}{l}{B}_{\rho }\\ \frac{1_k^{\top }}{\sqrt{k}}\end{array}\right){\rho }_1^{1/2}\left(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\right)=\left(B_{\rho }^{†},\frac{1_k}{\sqrt{k}}\right)\left(\begin{array}{c}\frac{{\rho }_1^{1/2}}{n}\nabla {\ell }_{\rho }({\mathit{\zeta }}_0)\\ 0\end{array}\right).$$ (A.15)
   Now from (A.14) and the spectral decomposition of the symmetric matrix B_ρ, we have $B_{\rho }^{†}{B}_{\rho }=I_k-1_k{1}_k^{\top }/k$, so (A.15) becomes

   $${\rho }_1^{1/2}\left(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\right)=B_{\rho }^{†}\frac{{\rho }_1^{1/2}}{n}\nabla {\ell }_{\rho }({\mathit{\zeta }}_0).$$ (A.16)
   We now study the asymptotic behavior of $B_{\rho }^{†}$. From (A.13), the fact that w_l = a_ln/n_l by definition, and ergodicity, we have

   $$\begin{array}{l}{\left[B_{\rho }^{(\mathit{\alpha })}\right]}_{rr}={\displaystyle \sum _{l=1}^k{a}_l}\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_0\right)\left[1-p_r\left(X_i^{(l)},{\mathit{\zeta }}_0\right)\right]}\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{B}_{rr},\\ {\left[B_{\rho }^{(\mathit{\alpha })}\right]}_{rs}=-{\displaystyle \sum _{l=1}^k{a}_l}\left(\frac{1}{n_l}{\displaystyle \sum _{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_0\right)p_s\left(X_i^{(l)},{\mathit{\zeta }}_0\right)}\right)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{B}_{rs},r\ne s.\end{array}$$
   The first part of Theorem 1 states that $\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$ as ρ₁ → ∞. Now since partial derivatives (with respect to ζ) of terms of the form p_r(x, ζ) (1 − p_r(x, ζ)) or p_r(x, ζ)p_s(x, ζ) are uniformly bounded by 1 in absolute value, we see that ${[B_{\rho }]}_{rs}-{[B_{\rho }^{(\mathit{\alpha })}]}_{rs}=O({\Vert {\mathit{\zeta }}_{\ast }-{\mathit{\zeta }}_{\mathit{\alpha }}\Vert }_1)$ a.s. for all r and s, and conclude that $B_{\rho }\stackrel{\mathrm{a}.\mathrm{s}.}{\to }B$. (Here, ‖υ‖₁ denotes the L₁ norm of a vector $\upsilon \in {ℝ}^k$.) Similarly, ${[\widehat{B}]}_{rs}-{[B_{\rho }^{(\mathit{\alpha })}]}_{rs}=O({\Vert \widehat{\mathit{\zeta }}-{\mathit{\zeta }}_{\mathit{\alpha }}\Vert }_1)$ a.s. for all r and s, so $\widehat{B}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }B$. Furthermore, the spectral decomposition of B_ρ and B, and the fact that B_ρ1_k = 0 and B1_k = 0, we have

   $$B_{\rho }^{†}={\left(B_{\rho }+\frac{1}{k}{1}_k{1}_k^{\top }\right)}^{-1}-\frac{1}{k}{1}_k{1}_k^{\top }\text{and}{B}^{†}={\left(B+\frac{1}{k}{1}_k{1}_k^{\top }\right)}^{-1}-\frac{1}{k}{1}_k{1}_k^{\top },$$ (A.17)

   showing that $B_{\rho }^{†}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{B}^{†}$.

4. The convergence statement ${\rho }_1^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)\stackrel{d}{\to }\mathcal{N}(0,B^{†}\mathrm{\Omega }{B}^{†})$ now follows immediately.

5. Finally, we write ${\rho }_1^{1/2}\left(\widehat{\mathit{d}}-\mathit{d}\right)={\rho }_1^{1/2}(g(\widehat{\mathit{\zeta }})-g({\mathit{\zeta }}_0))=\nabla g{\left({\mathit{\zeta }}_{\ast }\right)}^{\top }{\rho }_1^{1/2}(\widehat{\mathit{\zeta }}-{\mathit{\zeta }}_0)$, where ζ_∗ is between $\widehat{\mathit{\zeta }}$ and ζ₀. Since $\nabla g{\left({\mathit{\zeta }}_{\ast }\right)}^{\top }\stackrel{\mathrm{a}.\mathrm{s}.}{\to }D$, the desired result (3.16) now follows.

A.3 Proof of Consistency of the Estimate of the Asymptotic Variance Matrix

In the proof of the first part of Theorem 1, we showed that $\widehat{\mathit{\zeta }}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\mathit{\zeta }}_0$ and $\widehat{\mathit{d}}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathit{d}$. Hence, $\widehat{D}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }D$. In the proof of the second part of Theorem 1 we showed that $\widehat{B}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }B$. Using the spectral representation of $\widehat{B}$ and of B (see (A.17)), we see that this entails ${\widehat{B}}^{†}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{B}^{†}$.

To complete the proof, we need to show that $\widehat{\mathrm{\Omega }}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathrm{\Omega }$. Consider the expressions for Ω and $\widehat{\mathrm{\Omega }}$ given by (3.12) and (3.13), respectively. Since a → α and ${\overline{T}}^{(l)}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }E\left(T_1^{(l)}\right)$, to show that $\widehat{\mathrm{\Omega }}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathrm{\Omega }$, we need only show that

$$\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}\left(Z_t^{(r,l)}-{\widehat{\mu }}_r^{(l)}{T}_t^{(l)}\right)\left(Z_t^{(s,l)}-{\widehat{\mu }}_r^{(l)}{T}_t^{(l)}\right)}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }E\left(Y_1^{(r,l)}(\mathit{\alpha })Y_1^{(s,l)}(\mathit{\alpha })\right).$$ (A.18)

Now, the left side of (A.18) is an average of quantities that involve $Z_t^{(r,l)}$ and ${\widehat{\mu }}_r^{(l)}$, which themselves are a sum and an average, respectively, of a function that involves the random quantity $\widehat{\mathit{\zeta }}$. At the risk of making the notation more cumbersome, we will now write $Z_t^{(r,l)}\left(\widehat{\mathit{\zeta }}\right)$ instead of $Z_t^{(r,l)}$ and ${\widehat{\mu }}_r^{(l)}\left(\widehat{\mathit{\zeta }}\right)$ instead of ${\widehat{\mu }}_r^{(l)}$. Our plan is to introduce ${\mathrm{\Omega }}_{\rho }^{(\mathit{\alpha })}$, a version of $\widehat{\mathrm{\Omega }}$ in which $\widehat{\mathit{\zeta }}$ is replaced by the non-random quantity ζ_α, and show that (i) ${\mathrm{\Omega }}_{\rho }^{(\mathit{\alpha })}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathrm{\Omega }$ and (ii) $\widehat{\mathrm{\Omega }}-{\mathrm{\Omega }}_{\rho }^{(\mathit{\alpha })}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$. To this end, let

$$Z_t^{(r,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)={\displaystyle \sum _{i={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}{p}_r}\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)\text{and}{\widehat{\mu }}_r^{(l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)=\frac{{\displaystyle {\sum }_{i=1}^{n_l}{p}_r\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)}}{n_l},$$

and note that by definition

$$Z_t^{(r,l)}\left(\widehat{\mathit{\zeta }}\right)={\displaystyle \sum _{i={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}{p}_r}\left(X_i^{(l)},\widehat{\mathit{\zeta }}\right)\text{and}{\widehat{\mu }}_r^{(l)}\left(\widehat{\mathit{\zeta }}\right)=\frac{{\displaystyle {\sum }_{i=1}^{n_l}{p}_r\left(X_i^{(1)},\widehat{\mathit{\zeta }}\right)}}{n_l}.$$

Define the k × k matrices Ψ, $\widehat{\mathrm{\Psi }}$, and ${\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}$ by

$$\begin{array}{c}{\mathrm{\Psi }}_{rs}=E\left[\left\{Z_1^{(r,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)-T_1^{(l)}{E}_{{\pi }_l}\left[p_r(X,{\mathit{\zeta }}_{\mathit{\alpha }})\right]\right\}\left\{Z_1^{(s,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)-T_1^{(l)}{E}_{{\pi }_l}\left[p_s(X,{\mathit{\zeta }}_{\mathit{\alpha }})\right]\right\}\right],\\ {\widehat{\mathrm{\Psi }}}_{rs}=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}\left(Z_t^{(r,l)}\left(\widehat{\mathit{\zeta }}\right)-T_t^{(l)}{\widehat{\mu }}_r^{(l)}(\widehat{\mathit{\zeta }})\right)}\left(Z_t^{(s,l)}\left(\widehat{\mathit{\zeta }}\right)-T_t^{(l)}{\widehat{\mu }}_s^{(l)}\left(\widehat{\mathit{\zeta }}\right)\right),\\ {\left[{\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}\right]}_{rs}=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}\left(Z_t^{(r,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)-T_t^{(1)}{\widehat{\mu }}_r^{(l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)\right)\left(Z_t^{(s,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)-T_t^{(1)}{\widehat{\mu }}_s^{(l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)\right)}.\end{array}$$

Note that Ψ_rs is simply the right side of (A.18). Here, Ψ_rs is the population-level quantity (which we wish to estimate), ${\widehat{\mathrm{\Psi }}}_{rs}$ is the empirical estimate of this quantity, and ${\left[{\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}\right]}_{rs}$ is an “intermediate” or bridging quantity, used only in our proof. We will show that (i) ${\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathrm{\Psi }$ and (ii) ${\widehat{\mathrm{\Psi }}}_{\rho }^{(\mathit{\alpha })}-{\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$.

To show that ${\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathrm{\Psi }$, we first express ${\widehat{\mathrm{\Psi }}}_{rs}$ as a sum of four averages. That the four averages converge to their respective population counterparts follows from the ergodic theorem, together with the fact that $E\left[{\left(T_1^{(l)}\right)}^2\right]<\infty$.

To show that ${\widehat{\mathrm{\Psi }}}_{rs}-{\left[{\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}\right]}_{rs}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$, we express ${\widehat{\mathrm{\Psi }}}_{rs}-{\left[{\mathrm{\Psi }}_{\rho }^{(\mathit{\alpha })}\right]}_{rs}$ as the sum of four differences of averages, and show that each of these converges almost surely to 0. Consider the first difference, which is

$$D_1:=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}\left[Z_t^{(r,l)}\left(\widehat{\mathit{\zeta }}\right)Z_t^{(s,l)}\left(\widehat{\mathit{\zeta }}\right)-Z_t^{(r,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)Z_t^{(s,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)\right]}.$$ (A.19)

The expression inside the brackets in (A.19) is equal to

$$D_{1t}:={\displaystyle \sum _{i={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}{\displaystyle \sum _{j={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}\left[p_r\left(X_i^{(l)},\widehat{\mathit{\zeta }}\right)p_s\left(X_j^{(1)},\widehat{\mathit{\zeta }}\right)-p_r\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)p_s\left(X_j^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)\right]}}$$ (A.20)

and because all partial derivatives with respect to ζ of functions of the form p_r(x, ζ)p_s(y, ζ) are uniformly bounded by 1 in absolute value, the expression inside the brackets in (A.20) is bounded by ${\Vert \widehat{\mathit{\zeta }}-{\mathit{\zeta }}_{\mathit{\alpha }}\Vert }_1$. Since there are ${\left(T_t^{(l)}\right)}^2$ summands in the double sum in (A.20), $\left|D_{1t}\right|<{\left(T_t^{(l)}\right)}^2{\Vert \widehat{\mathit{\zeta }}-{\mathit{\zeta }}_{\mathit{\alpha }}\Vert }_1$, and from the fact that $E\left[{\left(T_1^{(l)}\right)}^2\right]<\infty$ we now see that $D_1\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$.

The second difference is

$$D_2:=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}\left[Z_t^{(r,l)}\left(\widehat{\mathit{\zeta }}\right)T_t^{(l)}{\widehat{\mu }}_s^{(l)}\left(\widehat{\mathit{\zeta }}\right)-Z_t^{(r,l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)T_t^{(l)}{\widehat{\mu }}_s^{(l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)\right]}.$$ (A.21)

The expression inside the brackets in (A.21)

$$D_{2t}:=T_t^{(l)}\frac{1}{n_l}{\displaystyle \sum _{i={\tau }_{t-1}^{(l)}}^{{\tau }_t^{(l)}-1}{\displaystyle \sum _{j=1}^{n_l}\left[p_r\left(X_i^{(l)},\widehat{\mathit{\zeta }}\right)p_s\left(X_j^{(l)},\widehat{\mathit{\zeta }}\right)-p_r\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)p_s\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)\right]}},$$

and reasoning as we did for the case of the first difference, we have $\left|D_{2t}\right|<T_t^{(l)}\cdot T_t^{(l)}{\Vert \widehat{\mathit{\zeta }}-{\mathit{\zeta }}_{\mathit{\alpha }}\Vert }_1$, which implies that $D_2\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$. The third difference is handled in a similar way.

The fourth difference

$$D_4:=\frac{1}{{\rho }_l}{\displaystyle \sum _{t=1}^{{\rho }_l}\left[{\left(T_t^{(l)}\right)}^2{\widehat{\mu }}_r^{(l)}\left(\widehat{\mathit{\zeta }}\right){\widehat{\mu }}_s^{(l)}\left(\widehat{\mathit{\zeta }}\right)-{\left(T_t^{(l)}\right)}^2{\widehat{\mu }}_r^{(l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right){\widehat{\mu }}_s^{(l)}\left({\mathit{\zeta }}_{\mathit{\alpha }}\right)\right]}.$$ (A.22)

The expression inside the brackets in (A.22) is

$$D_{4t}:={\left(T_t^{(l)}\right)}^2\frac{1}{n_l^2}{\displaystyle \sum _{i=1}^{n_l}{\displaystyle \sum _{j=1}^{n_l}\left[p_r\left(X_i^{(l)},\widehat{\mathit{\zeta }}\right)p_s\left(X_j^{(l)},\widehat{\mathit{\zeta }}\right)-p_r\left(X_i^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)p_s\left(X_j^{(l)},{\mathit{\zeta }}_{\mathit{\alpha }}\right)\right]}},$$

and we have $\left|D_{4t}\right|<{\left(T_t^{(l)}\right)}^2{\Vert \widehat{\mathit{\zeta }}-{\mathit{\zeta }}_{\mathit{\alpha }}\Vert }_1$, from which we conclude that $D_4\stackrel{\mathrm{a}.\mathrm{s}.}{\to }0$.