Dynamic prediction of motor diagnosis in Huntington’s disease using a joint modeling approach

Abstract

BACKGROUND

Prediction of motor diagnosis in Huntington’s disease (HD) can be improved by incorporating other phenotypic and biological clinical measures in addition to cytosine-adenine-guanine (CAG) repeat length and age.

OBJECTIVE

The objective was to compare various clinical and biomarker trajectories for tracking HD progression and predicting motor conversion.

METHODS

Participants were from the PREDICT-HD study. We constructed a mixed-effect model to describe the change of measures while jointly modeling the process with time to HD diagnosis. The model was then used for subject-specific prediction. We employed the time-dependent receiver operating characteristic (ROC) method to assess the discriminating capability of the measures to identify high and low risk patients. The strongest predictor was used to illustrate the dynamic prediction of the disease risk and future trajectories of biomarkers for three hypothetical patients.

RESULTS

1078 individuals were included in this analysis. Five longitudinal clinical and imaging measures were compared. The putamen volume had the best discrimination performance with area under the curve (AUC) ranging from 0.74 to 0.82 over time. The total motor score showed a comparable discriminative ability with AUC ranging from 0.69 to 0.78 over time. The model showed that decreasing putamen volume was a significant predictor of motor conversion. A web-based calculator was developed for implementing the methods.

CONCLUSIONS

By jointly modeling longitudinal data with time-to-event outcomes, it is possible to construct an individualized dynamic event prediction model that renews over time with accumulating evidence. If validated, this could be a valuable tool to guide the clinician in predicting age of onset and potentially rate of progression.

1. Introduction

Huntington’s disease (HD) is an inherited neurodegenerative disease caused by a cytosine-adenine-guanine (CAG) repeat expansion in the Huntingtin (HTT) gene [1] and is characterized by motor, cognitive and psychiatric symptoms. The identification of this gene almost two decades ago has allowed clinicians to determine whether an individual will develop HD. However, the ability to tell an individual when they will manifest symptoms remains elusive. It has long been recognized that the mean age of disease onset is strongly correlated to age and the length of the CAG mutation [2]. Thus, CAG, age and their interaction are generally used as progression indexes to predict time of motor onset [3,4]. However, prediction based on CAG and age needs improvement.

Paulsen et al. [5] used the Neurobiological Predictors of Huntington’s Disease (PREDICT-HD) study database to assess the ability of various longitudinal markers to predict motor diagnosis (a rating of 4 on the diagnostic confidence level of the Unified Huntington’s Disease Rating Scale) in addition to CAG repeat length, age and their interaction. They jointly modeled the trajectories of markers and time to HD diagnosis and identified several significant phenotypic and biological predictors. In addition, such a model framework allows an individualized dynamic prediction approach, whereby a patient’s estimated future risk, as well as longitudinal markers, are updated as each new observation value is obtained [6]. The overarching goal of this study was to compare the predictive ability of various markers to determine, with improved accuracy, the timing of symptom onset, and illustrate a way to make individualized dynamic prediction on the rate of disease progression for an individual with a CAG expansion compatible with HD. Such dynamic predictions on Huntington’s disease diagnosis and rate of progression have not been attempted in previous studies, and have potential future value in counseling patients regarding prognosis, improved clinical trial design, and most importantly allowing for earlier intervention when and if a disease modifying agent becomes available.

2. Materials and Methods

2.1 Study design and participants

Data used in this analysis were obtained from PREDICT-HD study, which was a prospective longitudinal study assessing predictors of the development of HD. The study followed 1078 participants who had mutation consistent with HD (greater than 35 HTT CAG repeats), but did not yet have a motor diagnosis at study entry. These individuals were studied annually from 2002 to 2014. Detailed information on PREDICT-HD study procedures, including participant inclusion/exclusion criteria have been published previously [7,8] and will not be covered in this paper. The research protocol was approved by each site’s respective institutional review board and ethics committee, and all participants gave written informed consent and were treated in accordance with ethical standards.

The PREDICT-HD study collected a broad range of clinical and biological data from participants. We focused on examining the five strongest predictors identified in Paulsen et al. [5]: total motor score, putamen volume, Stroop word score, Frontal Systems Behavioral Scale (FrSBe) - executive subscale, and total functional capacity. The motor examination [9] in the Unified Huntington Disease Rating Scale (UHDRS) consisted of oculomotor, dysarthria, chorea, dystonia, gait and postural stability with a total motor score ranging from 0 to 124, with a higher score indicating more impaired motor functioning. Brain images were measured on 1.5T MRI scanners, and subsequently on 3T scanners (in most sites) as advancing technology occurred. All structural imaging measures were expressed as a ratio of reginal volume to intracranial volume. Stroop word test [10] examined the effects of interference on reading ability, and scores were generated using the number of items correctly completed. A higher Stroop word score reflected better performance on ability to read out loud. The FrSBe - executive subscale assessed the behavior associated with damage to the dorsolateral prefrontal region, with a higher rating score indicating more severe impairment. The UHDRS total functional capacity is a 5-item clinician rating scale used to measure the capacity of function in HD. The five items were summed to yield a total score, which ranges from 0 to 13 with greater scores indicating a higher or more independent level of functioning. We defined the motor diagnosis of Huntington’s disease as a rating of 4 on the diagnostic confidence level (DCL) on the UHDRS during the follow-up period. The DCL was administered by a movement disorder specialist after the 15-item standardized motor assessment [5].

2.2 Statistical Analysis

The aforementioned measures in this analysis were collected on the participants at multiple time points during the follow-up period and were hypothesized to be related to HD progression, the event of interest. When the value of a covariate (e.g., biomarkers) at a time point can be affected by an event occurring at an earlier time point (e.g., HD conversion), the covariate is an endogenous (internal) time-dependent covariate. Suppose that a particular patient has HD conversion 2 years from the study onset. It is directly evident that at a future time point, say 2.5 years, the level of the biomarkers will be affected by the fact that this patient had HD conversion. The Cox model and its extensions cannot properly handle this endogenous time-varying covariates [11]. Joint modeling of longitudinal and survival data is a popular framework to analyze data sets when repeated measurements and time-to-event outcomes are strongly correlated. It can handle endogenous time-dependent covariates properly and is able to give more accurate parameter estimation and smaller standard errors which in turn yield greater statistical power. We refer the readers to Ibrahim et al. [12] for an introductory overview on joint modeling and the comparison with Cox model.

We considered the joint longitudinal-survival modeling framework and focused on the assessment of the predictive ability of the future risk of HD diagnosis. Specifically, it was of interest to predict HD progression for a new participant who has available a set of aforementioned measures and baseline characteristics, using the fitted joint model results. The regular joint models can only analyze one longitudinal measure at a time, and thus each of the aforementioned longitudinal measures was analyzed in a separate joint model and the prediction of the future risk was made based on one longitudinal measure and other baseline characteristics. The survival time (in years) was defined from study entry to HD diagnosis or censoring. Although certain participants were followed after the event of interest in the original study, we excluded the visits and measurements after HD diagnosis from this analysis. The survival sub-model took the form of a Cox proportional hazards model with CAG-Age Product (CAP; [age in years at baseline] X [CAG-33.66]) [4] as baseline covariates, and one of the five longitudinal measures as a time-dependent covariate. The longitudinal sub-model allowed us to describe the evolution of the repeat measures over time with the main effects from variables time (in years), age at baseline, CAG, and CAP. Random effects were used to capture the between subject variation. As some of the patients in the dataset showed nonlinear evolutions in their longitudinal measures, we expanded the time effect in longitudinal sub-model into a spline basis matrix to capture the nonlinear subject-specific evolution.

Suppose y_i(t_ij) were the observations of one of the longitudinal measures for the ith person (i = 1, …,N) at the jth time point (j = 1, …,n_i), t_ij. The joint model was represented as

$$y_i(t_{ij})=m_i(t_{ij})+{\epsilon }_i(t_{ij}),\text{where}$$ (1)

$$m_i(t_{ij})=({\beta }_{\mathit{0}}+b_{\mathit{0}i})+({\beta }_{\mathit{1}}+b_{\mathit{1}i})B_n(t,{\lambda }_{\mathit{1}})+({\beta }_{\mathit{2}}+b_{\mathit{2}i})B_n(t,{\lambda }_{\mathit{2}})+({\beta }_{\mathit{3}}+b_{\mathit{3}i})B_n(t,{\lambda }_{\mathit{3}})+{\beta }_{\mathit{4}}{\mathit{baselineAge}}_i+{\beta }_{\mathit{5}}{\mathit{CAG}}_i+{\beta }_{\mathit{6}}{\mathit{CAP}}_i,\text{and}$$ (2)

$$h_i(t)=h_{\mathit{0}}(t)\mathit{exp}\{{\gamma }_{\mathit{1}}{\mathit{CAP}}_i+\alpha m_i(t)\}.$$ (3)

The hazard function was denoted as h(t), and h₀(t) was the baseline hazard function. The matrix {B_n(t_ij,λ_k); k = 1,2,3} denoted a spline basis matrix for a natural cubic spline of time with two internal knots (three degree of freedom) placed at the 33.3% and 66.7% percentiles of the follow-up times. The parameter b_0i was the random intercept, {b_1k; k = 1, 2, 3} were the random slopes indicated subject-specific change rate of the measure, and ε_i(t_ij) was measurement error term. An association parameter α linked the two component sub-models, assuming the hazard at time t was dependent on the true longitudinal trajectory, m_i(t), through its value at time t. A significant α indicated a strong association between the longitudinal measures and time to motor diagnosis of HD. When α = 0, the model was reduced to separate models of longitudinal and survival outcomes, and the advantage of joint model disappeared. The quantity exp(α) was the hazard ratio (HR; inverse hazard ratio HR⁻¹ was used when the α estimate was negative) for a one-unit increase in the trajectory m_i(t), at time t. Specifically, a one-unit increase in trajectory increased the hazard by exp(α) times. For Stroop word score, depression (Beck Depression Inventory) was added as a covariate to Model (2) to account for mood changes because evidence suggested that mood affected cognitive performance [5]. For putamen volume, field strength (binary variable with 1.5T as reference group) was added as a covariate to Model (2) because some sites updated their scanners from 1.5T MRI to 3T MRI during the study. To facilitate the comparison of the association parameter among measures, each measure was scaled to zero mean and unit variance using the mean and standard deviation (SD) among all the participants and all the time points. The proportional hazards assumption was evaluated by examining the plots of Schoenfeld residuals for each covariate based on the Cox model with baseline data. The residual plots did not show extreme nonlinearity or other irregularities, which indicated that the proportional hazards assumption was reasonable for the analysis.

We adopted a Bayesian approach for model inference and for making predictions. The key step in prediction for a new subject was to obtain samples of subject’s random effects from the posterior distribution given the estimated parameters and previous longitudinal observations (at least one measure). The samples were then used to calculate the predictions for the markers’ future trajectories and risk of HD diagnosis. More details of the prediction method can be found in Rizopoulos [13]. We assessed how well each longitudinal measure can discriminate between patients who had an HD diagnosis from patients who did not. We calculated time-dependent areas under receiver-operating characteristics (ROC) curves (AUCs) to assess the performance of the longitudinal marker at different time points over the follow-up period. We also calculated dynamic discrimination index (DDI) proposed by Rizopoulos [14], which summarized the discrimination power of the measure over the whole follow-up period, using a weighted average of AUCs. In general, higher AUCs and higher DDI indicate higher discrimination of the models. We predicted the probabilities of HD diagnosis occurring in the time frame (t, t+Δt], using all measures collected till time t. Then the AUCs were calculated to assess how well the longitudinal marker distinguished the status of patients at time t+Δt. Since the participants were reassessed approximately every year, we selected t at 2^nd, 4^th, and 6^th year, and Δt as 1 and 2 years. To avoid overestimation of the predictive performance of the markers [15], we conducted a k-fold cross validation. Specifically, the total sample of participants was randomly split into k subgroups of equal size. The analysis was repeated k times with one subgroup being left out as the test set and the other subgroups being used as the training set. Parameter estimates of the joint model were derived from the training set and applied to the test set. Predictive accuracies were then computed by averaging the k separate analyses. We let k be 10 to have about 970 subjects in the training set and 108 subjects in the test set, which was a balance of estimation power and a reasonable size of test set. For comparison, we also fitted proportional hazards models (Cox model) with baseline measures. We then assessed the predictive performance of these models using time-dependent AUCs.

In addition, we applied the resulting joint models to predict the future marker trajectories and risk of HD diagnosis for new participants. We selected three target patients with low, medium and high risks of HD diagnosis, and demonstrated how individualized dynamic prediction was updated over time as new clinical information became available. All the analyses were performed using R (version 3·2·1). Proportionality testing was conducted using the R survival package. The joint model fitting and predictions were achieved using the R JMbayes package [13]. To facilitate the use of the methods in practice, an interactive web-based calculator with friendly interface was developed for the implementation of the proposed models.

3. Results

1078 participants were followed up for a mean of 4.78 years (SD 3.3; range 0.0–11.3). The average age at baseline was 39.8 (SD 10; range 18.1–75.9), 64% were women and a 14.5 years average education length (SD 2.6; range 8–20). Participants had an average of 42.49 CAG repeats (SD 2.69; range 36–62). Among the 1078 participants with genetic risk, 225 (21%) of participants were diagnosed with Huntington’s disease during a mean follow-up period of 5.2 years (SD 2.6, range 1.0–11.0), 853 participants remained in the premanifest phase, of which 373 were censored before 3 years of follow-up, 118 (11%) participants had data for only one visit. All the 1078 participants were included in our analyses.

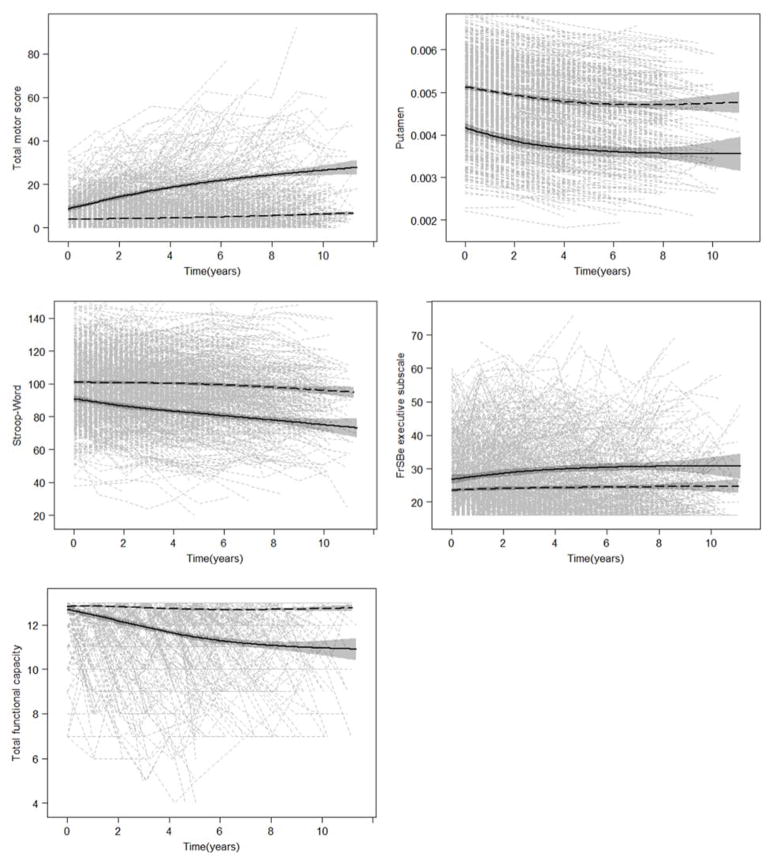
Figure 1 showed the trajectories for participants diagnosed and not diagnosed HD, for total motor score, putamen intracranial-corrected volume (ICV), Stroop word score, FrSBe - executive subscale, and total functional capacity. The figures suggested that participants with or without HD diagnosis during the study could be clearly distinguished by each of these measures.

Figure 1. Trajectories of total motor score, putamen intracranial-corrected volume (ICV), Stroop word score, FrSBe - executive subscale, and total functional capacity for all participants.

Gray dashed lines are individual empirical data. The black solid and dashed lines are natural cubic spline curves with three degree of freedom (shading shows 95% CIs) obtained from the participants diagnosed with HD during the study and from those not diagnosed with HD during the study, respectively. 0 denotes year of entry the study. FrSBe = Frontal Systems Behavioral Scale.

Table 1 showed the estimated association parameter (α) in the model (3) for each measures. Based on the results of the joint models, all the measures were significant predictors of the hazard of HD progression. Specifically, an increase of one SD in trajectory of total motor score (mean: 7.81; SD: 9.47) increased the hazard of HD diagnosis by 1.90 times (95% CI 1.72–2.11), a reduction of one SD in trajectory of putamen ICV (mean: 0.0047; SD: 0.0010) increased hazard by 1.97 times (95% CI 1.52–2.57), a reduction of one SD in trajectory of Stroop word score (mean: 96.07; SD: 19.12) increased hazard by 1.74 times (95% CI 1.47–2.04), an increasing of one SD in trajectory of FrSBe - executive subscale (mean: 25.48; SD: 10.20) increased hazard by 1.40 times (95% CI 1.22–1.62), and a reduction of one SD in total functional capacity (mean: 12.53; SD: 1.20) increased hazard by 1.48 times (95% CI 1.35–1.61). The full parameter estimation for the joint models were presented in supplementary Table 1. Table 2 compared the discriminative capability of the five predictors of interest by calculating the time-dependent AUCs at 2^nd, 4^th and 6^th year using longitudinal measures. The values in the first row in Table 2 evaluated the performance of using all previous observations of the remaining premanifest individuals (not progressed to HD) at 2^nd year (sample size n = 531), to predict their disease status between 2^nd and 3^rd year. The DDIs summarized the discrimination power of the marker to predict patients’ disease status in the next year. The results in Table 2 suggested that all five measures had a moderate discriminative capability. The putamen ICV had the best discrimination performance with AUC ranging from 0.74 to 0.82 for all combinations of t, Δt and DDI being 0.77 and 0.76 for Δt = 1 and 2, respectively. The total motor score showed a comparable discriminative ability with AUC ranging from 0.69 to 0.78 for all combinations of t, Δt and DDI being 0.75 and 0.72 for Δt = 1 and 2, respectively. In comparison, Stroop word score, FrSBe - executive subscale, and total functional capacity had lower discriminative capability.

Table 1.

Prediction of risk of HD diagnosis: estimated association parameter α in joint models.

Variables	α	SE	HR* or HR−1 (95% CI)
Total motor score	0.64	0.05	1.90 (1.72–2.11)
Putamen ICV	−0.68	0.13	1.97 (1.53–2.57)
Stroop word score	−0.56	0.08	1.74 (1.47–2.04)
FrSBE-executive subscale	0.34	0.07	1.40 (1.22–1.62)
Total functional capacity	−0.39	0.05	1.48 (1.35–1.61)

^*Hazard ratio (HR) or inverse hazard ratio (HR⁻¹) show the hazard for HD diagnosis associated with a difference of one SD in each measure.

Table 2.

Areas under the ROC curve and estimated dynamic discrimination index for the five predictors: longitudinal prediction

		Longitudinal prediction (Joint Model)
Δt (year)	t (n) (year)	Total motor score		Putamen ICV		Stroop word score		FrSBE-executive subscale		Total functional capacity
		AUC	DDI	AUC	DDI	AUC	DDI	AUC	DDI	AUC	DDI
1	2 (n = 531)	0.78	0.75	0.82	0.77	0.8	0.68	0.78	0.69	0.74	0.70
	4 (n = 276)	0.76		0.77		0.66		0.70		0.69
	6 (n = 144)	0.77		0.75		0.62		0.63		0.72
2	2 (n = 531)	0.77	0.72	0.76	0.76	0.77	0.66	0.74	0.67	0.72	0.70
	4 (n = 276)	0.78		0.75		0.65		0.72		0.71
	6 (n = 144)	0.69		0.74		0.65		0.62		0.61

t is follow-up time, corresponding to different amounts of available longitudinal information. n is the remaining premanifest HD patients at time t. Predictive utility is evaluated based on the longitudinal measure of these n patients observed before time t. Δt is relevant time window, corresponding to different prediction intervals. AUC is areas under the ROC curve and DDI is dynamic discrimination index. Higher value indicates higher discrimination capability. FrSBe = Frontal Systems Behavioral Scale.

Table 3 showed the discriminative capability at different time points of Cox models using the baseline measures of the five strongest predictors. The values in the first row in Table 3 evaluated the performance of the baseline measures in predicting the disease status of the 531 participants between 2^nd and 3^rd year. All the AUC values predicted by total motor score and putamen ICV in Table 3 were smaller than their counterparts in Table 2, suggesting that prediction of HD progression based on both baseline measures and longitudinal changes of these two markers was generally better than the prediction based only on baseline measures. The longitudinal measures of Stroop word score, FrSBe - executive subscale, and total functional capacity only showed a notable enhancement in predictive performance at two years of follow-up. This may indicate that their predictive values decline as time closer to the motor diagnosis.

Table 3.

Areas under the ROC curve for the five predictors: cross-sectional prediction

		Cross-sectional prediction (Cox Model)
Δt (year)	t (n) (year)	Total motor score	Putamen ICV	Stroop word score	FrSBE-executive subscale	Total functional capacity
		AUC	AUC	AUC	AUC	AUC
1	2 (n = 531)	0.71	0.73	0.70	0.71	0.69
	4 (n = 276)	0.68	0.72	0.68	0.68	0.68
	6 (n = 144)	0.65	0.70	0.65	0.66	0.66
2	2 (n = 531)	0.70	0.73	0.70	0.70	0.69
	4 (n = 276)	0.67	0.72	0.67	0.68	0.67
	6 (n = 144)	0.64	0.69	0.65	0.65	0.65

n is the remaining premanifest HD patients at time t. Predictive utility is evaluated based on the baseline measure of these n patients. Δt is relevant time window, corresponding to different prediction intervals.

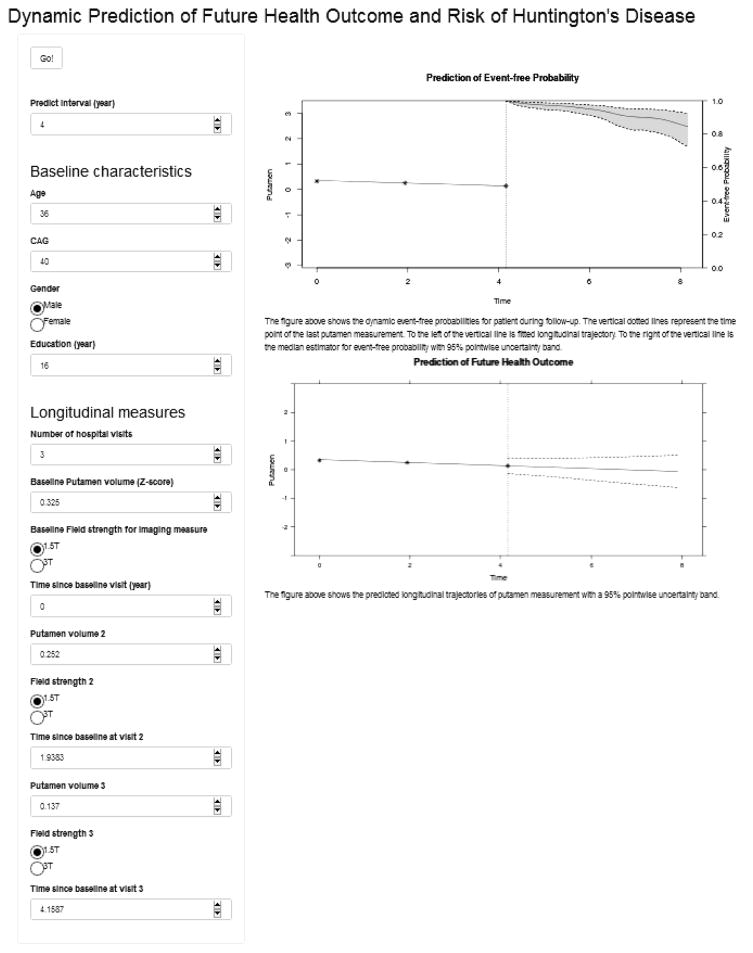
We developed a web-based calculator that predicts future marker trajectories and risk of HD diagnosis for new participants based on our proposed models. The web-based calculator is available at https://kanli.shinyapps.io/HD_prediction/. This web-based calculator requires the input of a patient’s baseline characteristics, such as age, number of CAG repeats, and his/her longitudinal sequence of putamen ICV or other markers. It projects the predictions of future putamen ICV as well as the estimates of the probability of event-free up to two years (default) ahead via plots. For illustration purposes, we did not plot a longer time frame for prediction because the patient were reassessed at least every two years, at which point the calculation can be updated. However, a longer-term prediction based on the available data can be calculated by setting the prediction time frame to an appropriate range. Figure 2 showed a screenshot of the web-based calculator predicting the event free probability and future trajectory of putamen for a hypothetic patient with three putamen measures.

Figure 2.

A screenshot of the web-based calculator for prediction.

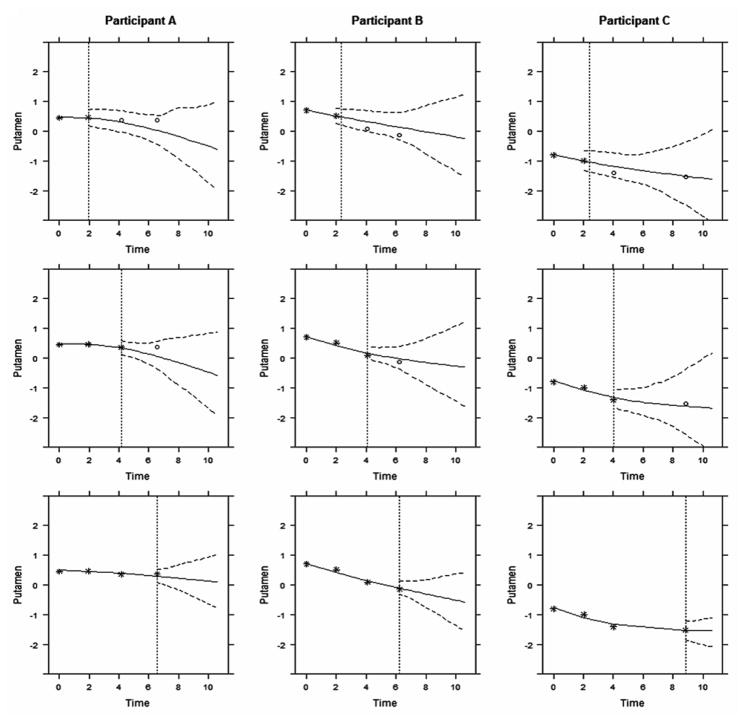
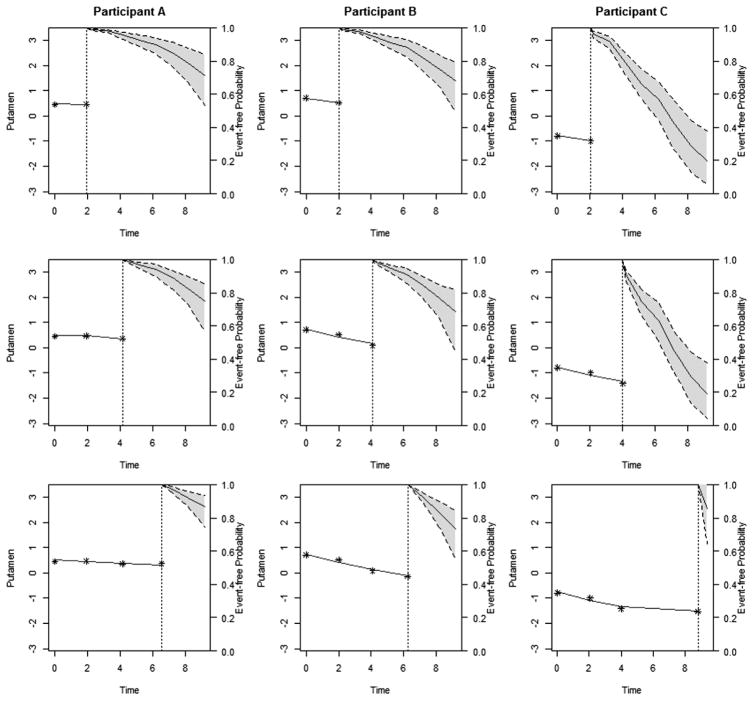
For illustration, we used the proposed models to make dynamic predictions for three new participants with low, medium and high risks of the disease, based on their putamen ICV measurements. The observations of these three participants were excluded from the whole dataset that was used for model estimation. To better assess the evolving longitudinal markers in making dynamic predictions, we hypothetically assigned the three participants with same baseline age (36 years) and CAG length (41). Figure 3 displayed the predicted standardized putamen volume for these three participants. From top to bottom on Figure 3, by using more follow-up data (stars), predictions (solid curve) were closer to the true future observed values (circles) and the 95% uncertainty band narrowed. Participant A’s predicted putamen volume after 6.5 years was relatively stable because his/her observed putamen volume was relatively stable. In comparison, Participants B and C’s predicted putamen volume deteriorated more rapidly, indicating a higher risk of HD diagnosis in the near future. Figure 4 displayed the predicted probability of being free of HD diagnosis. For Participant A, the event-free probability curve did not show large changes because Participant A’s putamen measures were relatively high and stable. However, because participants B and C had a faster rate of atrophy in the putamen within 2 years period as compared to A, they had considerable decline in the event-free probability, suggesting that they were at increased risk of HD diagnosis and should be monitored frequently.

Figure 3. The predicted longitudinal trajectories of putamen ICV measurement with a 95% pointwise uncertainty band.

The vertical dotted lines represent the time point of the last putamen measurement. Each column represent one participants. From top to bottom, predictions were calculated accounting for all putamen ICV that measured previously and were updated when new measure became available. Stars denote observed measures, and circles denote future observations.

Figure 4. The dynamic event-free probabilities for patient during follow-up.

The vertical dotted lines represent the time point of the last putamen measurement. To the left of the vertical line is fitted longitudinal trajectory. To the right of the vertical line is the median estimator for event-free probability with 95% pointwise uncertainty band. Each column represent one participants. From top to bottom, predictions were calculated accounting for all putamen volumes that measured previously and were updated when new measure became available.

4. Discussion

In this paper, we compared the discrimination power of five strong predictors using time-dependent areas under receiver-operating characteristics curves (AUCs) and dynamic discrimination indexes (DDIs) specifically adapted to joint models. Putamen volume and total motor score were demonstrated to be the best predictors of HD diagnosis in prodromal HD patients. A number of variables showed poor prediction, such as total functional capacity and FrSBe - executive subscale. These findings were consistent with previous studies [16,17]. Although the imaging measures have slightly better predictive values than the total motor score, the latter may serve as a better measure for everyday use in clinical practice, considering its superiority in expense and time required.

We also illustrated the use of joint models of longitudinal and time-to-evet data for individualized dynamic event prediction. Based on the longitudinal measures such as putamen volume or total motor score, the risk of HD diagnosis and trajectory were calculated and updated when more measurements became available. This approach can guide the personalized assessment frequency and facilitate earlier diagnoses, and thus enhance prognostication and improve the timing to intervention with a disease modifying agent once available. In addition, the best predictors identified in this paper, along with the dynamic prediction model may further help design preventive clinical trials. The web-based calculator we developed could be an easily accessible tool for physicians to make prognostic predictions for patients in the premanifest phase and facilitate the medical decision-making process.

There are several limitations in our study. First, recent research has examined the prediction of motor diagnosis in HD using multiple baseline measures [17,18]. In comparison, the joint model adopted in this present analysis can only handle a single longitudinal measure. In the future work we will extend the model to incorporate multiple longitudinal measures using multivariate joint modeling as proposed in He, et al. [19]. The general idea is to introduce a continuous latent variable to represent patients’ underlying disease severity. The observed longitudinal markers can be modeled as measurements of the latent variable using a multilevel latent trait sub-model and the time-to-event data are modeled using a Cox proportional hazard sub-model. Because all outcomes share the same latent variable, the dimensionality of the data can be reduced and fewer parameters are needed. Wang, et al. [20] proposed a prediction framework for multiple longitudinal measures and event time data based on the method. Simultaneous modeling of multiple longitudinal outcomes in joint models may substantially enhance the predictive ability of a joint model and help to identify the optimal combination of measures in determining the risk of motor conversion among prodromal HD patients. Second, the cross-validation used in the analysis was an internal validation, and external validation with an independent dataset, e.g., TRACK-HD, Enroll-HD, etc., is needed to verify the present results and improve the web-based calculator. Finally, there may be factors that are not included in the proposed models and may influence prediction and decision making. To this end, the proposed methods and tools can be supportive in clinical decision-making, but will not replace clinical expertise. In addition, given the complexity of the methodology, additional instructions of the web-calculator are needed to guide clinicians to properly use the tools.