Design of 3-D Printed Concentric Tube Robots

Abstract

Concentric tube surgical robots are minimally invasive devices with the advantages of snake-like reconfigurability, long and thin form factor, and placement of actuation outside the patient’s body. These robots can also be designed and manufactured to acquire targets in specific patients for treating specific diseases in a manner that minimizes invasiveness. We propose that concentric tube robots can be manufactured using 3-D printing technology on a patient- and procedure-specific basis. In this paper, we define the design requirements and manufacturing constraints for 3-D printed concentric tube robots and experimentally demonstrate the capabilities of these robots. While numerous 3-D printing technologies and materials can be used to create such robots, one successful example uses selective laser sintering to make an outer tube with a polyether block amide and uses stereolithography to make an inner tube with a polypropylene-like material. This enables a tube pair with precurvatures of 0.0775 and 0.0455 mm⁻¹, which can withstand strains of 20% and 5.5% for the outer and inner tubes, respectively.

I. Introduction

Robot-assisted minimally invasive surgical (RMIS) systems offer enhanced dexterity, vision, and control compared with traditional open surgery. Numerous procedures are now being performed using RMIS systems due to the potential to decrease pain, shorten recovery time, and reduce patient scarring. Although there exist some examples of systems capable of accessing remote places within the body, e.g., [1], [2], the current commercial systems are limited by their large size, high cost, and inability to move in highly curved paths. In addition, commercial RMIS systems are often used to accommodate a wide range of procedures and patients, resulting in a system that is not necessarily optimal for any specific case. An alternative approach is to design procedure- and patient-specific (i.e., personalized) robots, which would allow for optimization of operations. The need for personalized surgical robots is particularly apparent when considering specialized groups of patients, such as pediatric or obese patients, whose anatomical differences may prove current template systems to be inadequate. We propose the use of flexible 3-D printed concentric tube robots designed for patient- and procedure-specific cases (see Fig. 1).

Fig. 1.

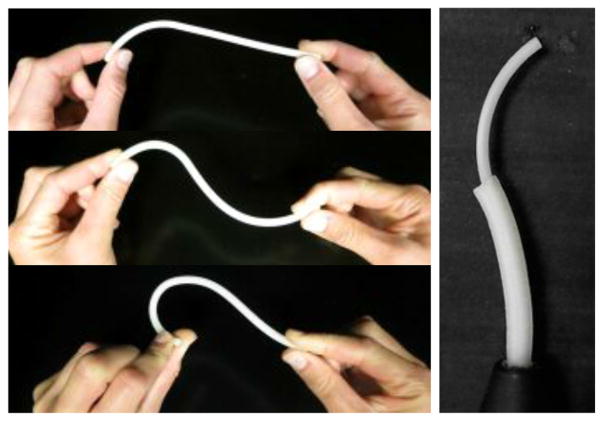
(Left) Example of a highly flexible 3-D printed concentric tube. It was printed out of PEBA 2301 using selective laser sintering (SLS). (Right) Overhead view of a concentric tube robot consisting of two tubes, each 3-D printed with a different plastic.

One specific application example is accessing and removing kidney stones in pediatric patients [3]. The formation of kidney stones, also called urolithiasis, occurs when urine contains high levels of crystal-forming substances, such as calcium or uric acid, and causes severe lower-back and abdominal pain. Approximately 2–3% of pediatric patients are affected each year [4]. Although access to the kidney via needle puncture of the skin is relatively straightforward in adults, the procedure is more difficult in pediatric patients. Because of the small body surface area of children, accessing the diseased sites with a straight needle and catheter risks damaging nearby tissue, in particular puncturing the pleural cavity. The design of a tool that can safely navigate through the compact anatomy of a pediatric patient in order to access hard-to-reach stones could improve outcomes in this specialized patient group.

A. Background

1) Concentric Tube Robots

In order to design personalized surgical robots, researchers have proposed to use a class of dexterous continuum robots known as concentric tubes [5], [6]. They consist of a set of hollow precurved elastic tubes that fit concentrically, each one inside the next. As the tubes are rotated and inserted relative to each other, their curvatures interact to change the robot’s overall shape as well as its tip position. Because this elastic interaction inherently results in bending of the tubes, there is no reliance on external wires or tissue forces. This allows the design of robots that are smaller and more dexterous than traditional surgical tools. Previous work has proposed their use as tools in transendoscopic [5], [7]–[9], transvascular [10]–[12], natural orifice [13], and percutaneous [6], [14]–[16] surgical procedures.

2) Materials for Concentric Tube Robots

The primary material for concentric tube robots to date is Nitinol, a nickel and titanium alloy that possesses both shape memory and superelastic properties. Concentric tube designs take advantage of the latter. Nitinol has been reported to sustain recoverable strains of around 8–11% [17], making it a highly elastic material. In order to make concentric tube robots, straight Nitinol tubing must be formed into the desired shape. To do so, a fixture to hold the tube at the desired precurvature must be made, and the Nitinol must go through a series of heating and cooling cycles until it is set in that desired shape. This heat treatment process requires refinement to optimize the temperatures and time periods necessary for shape-setting. It is also a lengthy process, and even after the precurved tube is formed, the material often relaxes when it is removed from the fixture [18]. It is, therefore, difficult to achieve the exact design that was planned. One other group has presented preliminary studies on the use of thermoplastic materials [19]. Challenges in creating concentric tubes with the necessary geometry and material properties motivate our work on 3-D printed concentric tubes.

3) 3-D Printed Personalized Medical Robots

The applications of 3-D printing beyond rapid prototyping has been quickly expanding, even entering into the medical device sector [20]. Because 3-D printing enables the generation of a physical model from a digital model that can easily be changed to fit a specific need, its use in making personalized parts is natural. 3-D printing is now being used for various personalized medical robots and interventions. One such example is the Eksosuit [21] developed by Ekso Bionics and 3D Systems. A 3-D scan of a patient was used to create a personalized digital model, from which customized parts were printed and a fully functional patient-specific device built. Similarly, a project called #CAST [22] scans patients’ arms to create personalized casts that are more comfortable and durable. Beyond the use of 3-D printing to increase fit and comfort, several groups have described how 3-D printing patient-specific physical models could be a useful modality for understanding anatomical nuances of a particular patient while planning procedures [23]–[25]. Two-dimensional images are often insufficient for visualizing complex anatomical structures, and the use of a physical model can help with this visualization as well as with the subsequent planning and preparation. Additionally, 3-D printed models have been used for surgical simulation and training [26], [27], allowing surgeons to practice on an anatomically accurate model and educating less experienced surgeons without risk of patient complications. Finally, several groups are developing methods for manufacturing patient-specific implants, mainly for bone repair or replacement [20].

B. Contributions

Our contributions are as follows. 1) We present a method for selecting appropriate materials for 3-D printing concentric tube robots. We start with an analysis of the strain during bending of hollow precurved tubes for the general case. The resulting equations are used to calculate a lower limit on the recoverable strain necessary for a specific design, therefore aiding in the selection of an appropriate material. Although previous groups have developed approximations of this limit, our proposal for a new manufacturing technique for concentric tube robots drives the need for more careful modeling. 2) This work presents the most thorough analysis of 3-D printing concentric tube robots. Previous work has used Nitinol and heat treating processes in order to manufacture precurved tubes, and one work presents preliminary studies on three thermoplastics [19]. We present results from novel experimental evaluation of various 3-D printed tubes, such as those in Fig. 1, and show that there are certain materials whose interaction with other tubes closely matches previously developed in-plane beam mechanics models for concentric tube robots. These results lay the groundwork for future research on the design of a surgeon control/teleoperation interface. We envision that this surgeon interface will remain the same, even though the sets of concentric tubes will be specific for each patient and procedure.

II. Design Requirements

For any given set of concentric tubes, the initial curvatures of the individual tubes and the final combined curvature are critical design parameters. These curvatures are limited by the yield strain of the material. Ideally, the chosen material would be flexible enough to withstand high strains during bending without yielding or breaking, such that the initial radius of curvature could be small. This would allow the overall robot to be more dexterous.

Previous literature on concentric tube robot design has analyzed the limits on the initial precurvature of a given tube, such that it can be fully straightened without plastic deformation [5], [17]. However, there are often cases when a given tube does not need to be fully straightened, and instead only needs to be capable of unbending enough to reach a desired equilibrium curvature. Although Sears and Dupont [6], [28] looked at an approximation of this strain due to bending from an initial to final curvature, we present here a derivation for the general case to be used for any tube geometry. The model presented here for calculating the lower limit on the recoverable strain of a material for a given set of concentric tubes enables the selection of an appropriate material for the implementation of a specific concentric tube robot design (e.g., for a specific patient and specific procedure).

A. Derivation of Strain During General Bending of Precurved Tubes

The equations describing the deformations that occur when a straight prismatic beam is subjected to in-plane bending are well known. However, the more general equations describing the deformations of an initially curved beam subjected to in-plane bending require new analysis for application to concentric tube robots. We show here a derivation similar to the derivation by Hibbeler [29] for the strain of a straight beam in bending, except we consider curved beams. The variables used in the derivation are listed in Table I.

TABLE I.

Nomenclature

Δx	Length of segment on neutral axis
Δs	Length of segment located distance
	y from neutral axis before bending
Δs′	Length of segment located distance
	y from neutral axis after bending
Δθi	Initial angle
Δθf	Final angle
rni	Initial radius of curvature to neutral surface
rnf	Final radius of curvature to neutral surface
y	Distance to segment of interest from neutral surface
ε	Strain
A	Area of cross section
Am	${\int }_A\frac{dA}{r}$
Ri	Initial radius of curvature
Rf	Final radius of curvature
R	Radius to point of interest
Ic	Area moment of inertia of the cross section

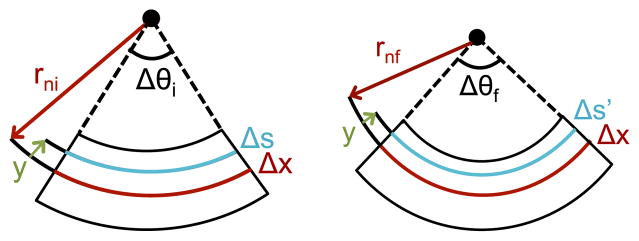
As in the case of an initially straight beam, the neutral surface is the surface in which the material experiences no change in length during bending. Fig. 2 shows an isolated differential element of the beam. The length of a segment located on the neutral surface is

Fig. 2.

Differential element (a) before and (b) after bending. Δx is the length of a segment located on the neutral axis, Δs is the length of a segment located a distance y from the neutral surface before bending and Δs′ is the length of that same segment after bending, r_ni is the radius of curvature to the neutral surface before bending, r_nf is the radius of curvature to the neutral surface after bending, and Δθ_i and Δθ_f are the angles before and after bending, respectively.

$$\mathrm{\Delta }x=r_{ni}\mathrm{\Delta }{\theta }_i.$$ (1)

The length of a segment located a distance y from the neutral surface is

$$\mathrm{\Delta }s=(r_{ni}-y)\mathrm{\Delta }{\theta }_i$$ (2)

where r_ni and Δθ_i are the initial radius of curvature to the neutral surface and the initial angle, respectively. Assuming that there is no change in length of segments located on the neutral surface, the length after bending is

$$\mathrm{\Delta }x=r_{nf}\mathrm{\Delta }{\theta }_f=r_{ni}\mathrm{\Delta }{\theta }_i$$ (3)

where r_nf and Δθ_f are the final radius of curvature to the neutral surface and the final angle, respectively. Due to bending, the length of the segment located a distance y from the neutral surface changes in length from Δs to

$$\mathrm{\Delta }{s}^{\prime }=(r_{nf}-y)\mathrm{\Delta }{\theta }_f.$$ (4)

The normal strain along Δs is

$$\epsilon =\underset{\mathrm{\Delta }s\to 0}{lim}\frac{\mathrm{\Delta }{s}^{\prime }-\mathrm{\Delta }s}{\mathrm{\Delta }s}.$$ (5)

Rearranging and substituting (1)–(4)

$$\epsilon =\underset{\mathrm{\Delta }{\theta }_f\to 0}{lim}\frac{(r_{nf}-y)\mathrm{\Delta }{\theta }_f-(1-\frac{y}{r_{ni}})r_{nf}\mathrm{\Delta }{\theta }_f}{(1-\frac{y}{r_{ni}})r_{nf}\mathrm{\Delta }{\theta }_f}$$ (6)

$$\epsilon =\frac{y(r_{nf}-r_{ni})}{r_{nf}(r_{ni}-y)}.$$ (7)

Equation (7) is the strain during bending of a tube with any given initial precurvature bending to any final curvature. Previous concentric tube literature has examined an approximation to this result [28], $\epsilon \approx \frac{\text{OD}}{2}(\frac{1}{R_i}-\frac{1}{R_f})$, as well as special cases of this general result. Webster et al. [5] showed the special case of bending an initially straight tube. Using r_ni = ∞, r_nf = r, and $y=\frac{-\text{OD}}{2}$ in (7) and rearranging gives the same result $r=\frac{\text{OD}}{2\epsilon }$ as in [5]. Similarly, Webster et al. [5] showed that for the case of fully straightening an initially precurved tube, the minimum radius of curvature, r, that can be achieved without plastic deformation is given by $r=\frac{\text{OD}}{2\epsilon }+\frac{\text{OD}}{2}$. This is a special case of (7), where r_ni = r, r_nf = ∞, and $y=\frac{\text{OD}}{2}$. With the general result derived here, we can analyze cases that may not begin or end with a fully straight tube.

The equations above depend on both r_ni and r_nf, which, in the case of an initially straight beam, are the same as the initial and final radii of curvature. However, the neutral axis of an initially curved beam may or may not pass through its centroid. The exact location of the neutral axis depends on the ratio of the radius of curvature to the height of the cross section, or $\frac{R}{\text{OD}}$, since the height of the cross section is simply the outer diameter in this case. Depending on the value of $\frac{R}{\text{OD}}$, the beam will fall into one of three possible cases [30], described below. Using the appropriate parameters, r_n can be calculated for both the initial and final configurations (r_ni and r_nf).

Case 1

$0.6<\frac{R}{\text{OD}}<8$. When large diameter beams have a small radius of curvature, the radius of curvature to the neutral axis does not pass through the centroid and is

$$r_n=\frac{A}{{\int }_A\frac{dA}{r}}=\frac{A}{A_m}$$ (8)

where r is the radius to the point of interest, and A_m for a hollow tube is

$$A_m=2\pi \left(\sqrt{r^2-{\left(\frac{\text{ID}}{2}\right)}^2}-\sqrt{r^2-{\left(\frac{\text{OD}}{2}\right)}^2}\right).$$ (9)

Although using the straight-beam formulas results in insignificant stress errors when $\frac{R}{OD}$ is below this range, stress errors are around 4–5% [31] when $\frac{R}{OD}$ falls within this range.

Case 2

$\frac{R}{\text{OD}}>8$. Calculating the distance of neutral axis shift from the centroidal axis can be largely affected by round-off errors when $\frac{R}{\text{OD}}>8$ [30]. The radius of curvature to the neutral axis should instead be approximated as

$$r_n\approx R-\frac{I_c}{RA}$$ (10)

where I_c is the area moment of inertia of the cross section about the centroidal axis.

Case 3

$\frac{R}{\text{OD}}\gg 8$. The radius of curvature to the neutral axis is approximately equal to the radius of curvature of the beam

$$r_n\approx R.$$ (11)

B. Lower Limit of Recoverable Strain of a Material for a Specific Concentric Tube Design

The discussion so far has been for any generic tube with some initial and final curvature. In order to develop a model that enables the selection of an appropriate material for the implementation of a specific concentric tube robot design, we will now focus on applying these general equations to the interaction of two concentric tubes. Our analysis focuses on the 2-D bending problem for this first case of development of concentric tube robots made from 3-D printed materials. In addition, it should be noted that this modeling assumes frictional effects to be negligible. Friction has been largely neglected in concentric tube models to date; the only literature addressing friction modeling limits its analysis to the effects of friction during tube rotation [32]. Because the experiments in Section IV only involve the relative insertion of tubes, we believe this is a reasonable assumption.

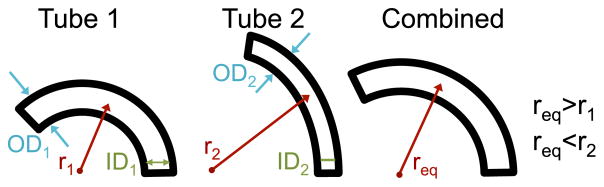
As shown in Fig. 3, there are several parameters that define any given tube, j, where in the two tube case, j = 1, 2 refers to the outer and inner tubes, respectively. Each tube can be characterized by its outer diameter (OD_j), inner diameter (ID_j), and curvature (κ_j), where ${\kappa }_j=\frac{1}{r_j}$ and is assumed to be constant. Each set of tubes also has a combined (equilibrium) curvature (κ_eq) that describes its curvature in regions where both tubes overlap. In the planar case, this equilibrium curvature is related to the individual tube’s precurvatures by

Fig. 3.

Parameters defining any given tube, j, include the outer diameter (OD_j), inner diameter (ID_j), and constant radius of curvature (r_j). The point where strain will be the largest for tube j during bending depends on whether the final radius of curvature is greater than or less than the initial radius of curvature. In this case, the final radius of curvature is equivalent to the combined (equilibrium) radius of curvature (r_eq).

$${\kappa }_{eq}=\frac{E_1{I}_1{\kappa }_1+E_2{I}_2{\kappa }_2}{E_1{I}_1+E_2{I}_2}$$ (12)

where I_j and E_j are the cross-sectional moment of inertia of tube j and Young’s modulus of tube j, respectively [5], [17].

The range of acceptable values for the parameters outlined above (OD_j, ID_j, κ_j, κ_eq, I_j, E_j) will be defined by constraints imposed by the specific surgical procedure, tools, patient geometry, and 3-D printing process. Explanations of these constraints, as well as ranges for the associated parameters, are given in Table II. Once these constraints and ranges have been identified for a given application, a lower limit on recoverable strain can be calculated, enabling the selection of a material that can withstand the necessary bending.

TABLE II.

Constraints and Parameter Ranges

Model Parameter	Constraint	Range dependencies
OD1	Maximum: patient size	—
ID1 and OD2	Gap needed between inner and outer tubes for smooth relative insertion/rotation	Printer resolution, wall thickness
ID2	Minimum: tool size	—
κeq	Dependent on the individual tube materials and strain at yield	Allowable workspace, desired path to follow, patient anatomy
κj	Maximum: strain at yield of material	Patient anatomy, procedure

To begin, the size of the patient will put a limit on the maximum size of the overall set of concentric tubes, thus putting an upper limit on OD₁. Second, the size of the tool to be passed through will determine the minimum possible ID₂. The minimum wall thickness of the tubes may depend on the 3-D printing process, therefore putting a limit on the possible range of dimensions of ID₁ and OD₂. The equilibrium curvature often depends on the allowable workspace or desired path to be followed, and tube precurvatures typically depend on a combination of the patient anatomy and specific medical procedure. Although the arc length of each tube is not explicitly a parameter used here, it is indirectly used when determining the desired path for a given workspace. The value of Young’s modulus will vary widely depending on the class of material (thermoplastic, nylon, etc.) chosen.

To calculate the lower limit of the recoverable strain of a material for a specific concentric tube robot design, we must identify the point where strain will be the largest during bending. As shown in Fig. 3, there are two possible cases—the final radius of curvature of a tube is greater than its initial radius of curvature, or the final radius of curvature is less than its initial radius of curvature. When the final radius of curvature is greater, the inner surface, initially shorter than the outer surface, reaches its strain limit first. The point of interest will, therefore, be on this inner surface. For the case when the final radius of curvature is less than the initial radius of curvature (i.e., the tube is bending further), the outer surface will reach its strain limit first, and the point of interest will be on this outer surface. In some cases, the maximum strain is expected to occur when the curved segments are bending against one another. The only difference between this case and the case where both tubes are bending in the same direction is that the signs of the curvature of the two tubes are opposite.

The strain can now be calculated using (7), the appropriate equations (8)–(11) depending on the value of $\frac{R}{\text{OD}}$, and the following parameters, specific to concentric tube robots. The initial radius of curvature is $R_i=\frac{1}{{\kappa }_j}$, and the final radius of curvature is $R_f=\frac{1}{{\kappa }_{eq}}$. The radius to the point of interest is

$$r=-\left(\pm \frac{\text{OD}}{2}-R\right)$$ (13)

where R is either R_i or R_f. The distance to the point of interest from the neutral surface is

$$y=r_{ni}-R_i\pm \frac{\text{OD}}{2}$$ (14)

where $+\frac{\text{OD}}{2}$ gives values for calculating strain at a point on the inner surface, and $-\frac{\text{OD}}{2}$ gives values for calculating strain at a point on the outer surface. The calculated strain is the maximum a material would need to be able to withstand in order to go from initial curvature, κ_j, to final equilibrium curvature, κ_eq without yielding, thus defining the lower limit for the material’s strain at yield. A material can then be selected for the given design based on the criteria that the maximum strain at yield is greater than the strain value calculated above. The material of choice for concentric tube robots in previous work has been Nitinol, which typically has a maximum strain at yield of 8%. In subsequent sections, we explore the use of alternative materials and manufacturing processes.

III. 3-D Printing Materials for Concentric Tubes

3-D printing is an additive manufacturing process, in which 3-D physical objects are created from a digital file. The process involves computer-controlled building of parts, typically layer-by-layer. The range of materials that can be 3-D printed has been rapidly expanding beyond the traditional plastics such as acrylonitrile butadiene styrene (ABS) and polylactic acid (PLA). Much of this expansion is due to the variety of different 3-D printing processes now available. We experimented with parts printed using several different processes [33], [34], described below, as well as several different materials, shown in Table V (at the end of the paper).

TABLE V.

3-D Printing Processes and Materials Tested

Process	Material Type	Material Name	Tensile/Flexural Strength [MPa]	Tensile/Flexural Modulus [MPa]	Min wall [mm]	Max length* [mm]	Build Orientation	Available surface finishes	Pros/Cons and Notes
SLA	Polypropylene-like/ABS-like	Accura 25 (photopolymer liquid resin)	38/55	1590–1660/1380	0.381 (0.5 recommended)	550	Vertical	Sanded and primed (smooth, low-friction surface)	Smooth finish compared to SLS parts, but seems limited in how much it can bend before the walls crack
	Polypropylene-like/ABS-like	VisiJet SL Flex	38/57	1620/1420	0.381 (0.5 recommended)	250	Vertical	Same as above	Used interchangeably with Accura 25
DLP	photosensitive resin (photo polymer)	DL 360 (DWS)	30/76	1340/1670	0.5	100	Horizontal (with supports along bottom)	Ground and polished	Too stiff. DL 350 should be more flexible but hard to find a provider
	photosensitive resin (photo polymer)	PIC100 (Envisiontech)	16.8/23	20.3 (as measured by Zabti thesis)/404	0.05	100	Vertical (curved side down)	Sanded	The amount of UV curing time makes a difference in the stiffness, and our samples were too flimsy (not stiff enough)
SLS	Nylon 12	PA2200	48/58	1700/1500	0.7	650	Horizontal	—	Very brittle and lots of support material stuck inside
	Nylon 11	Nylon D80	35.85/Not given	1392/868.7	1.0	355	Vertical	CA coating (similar to dipping in super-glue)	Parts were printed as far away from the laser as possible to limit direct heat, but powder was still stuck inside and hard to remove
	Nylon 11	PA860	48/Not given	1475/1310	0.8	650 (if horizontal) and 530 (if vertical) but 130 recommended	Unknown	Vibratory finish (tumbled) and sanded	Powder stuck inside and hard to remove
	Thermoplastic polyurethane	TPU 92A	27/Not given	Not given/9	0.8	650	Unknown	Unknown	Very flexible, but actually too flimsy (not stiff enough)
	PEBA (polyether block amide)	EOS PrimePart ST (PEBA 2301)	7–8/Not given	75–80/Not given	0.8	700	Unknown	Sanded	Good flexibility as well as stiffness, but some powder stuck inside. Hard to find provider
	Thermoplastic elastomer	DuraForm Flex	1.8/Not given	7/5.9	0.8	550	Unknown	Infiltration for strengthening and sealing	Good flexibility, but slightly flimsy and some powder stuck inside
FDM	Modified ABS	Bendlay	Not given/33	1400/1500	1.0	280	Horizontal	—	Fragile between layers (easily splits) and very brittle, plus difficult to determine settings to successfully print
MJP	UV cured resin	VisiJet M3 Crystal	42.4/49	1463/1590	0.381 (0.5 recommended)	200	Horizontal	Sanded	Snapped a piece pretty easily when bending by hand

^*Based on available print bed size.

A. 3-D Printing Technologies for Concentric Tube Robots

1) Fused Deposition Modeling

Currently, the majority of materials available for fused deposition modeling (FDM) are stiff plastics that cannot withstand the high strain necessary for concentric tube robots. The materials that we tested were problematic due to material properties as well as the limitations of the FDM process. The layer thickness depends on the size of the extrusion nozzle and generally results in thicker layers compared with other processes. This makes it difficult to build parts with small features and thin walls. And although our particular builds did not require support material to anchor the parts, this would be a problem for removing small thin-walled tubes from the build platform without any damage.

2) Digital Light Processing

Although digital light processing (DLP) produces high-quality smooth parts, the materials available are limited, and the current DLP printers are small, therefore restricting the maximum length of printable concentric tube robots. For these reasons, we did not test DLP parts in our experiments described in Section IV; however, due to the rapidly changing nature of the 3-D printing industry, there may be larger printers and a wider range of material options available in the near future.

3) Selective Laser Sintering

A benefit of selective laser sintering (SLS) is that there is no need for support material beyond the unsintered powder that surrounds the part during the build. However, some of this excess powder can get stuck on the inside of printed concentric tubes, which must be hollow and clean, therefore making postprocessing quite labor intensive. SLS parts can have a rough powdery surface, and the excess powder needs to be sanded off in order to get a smooth finish. Although the post-processing of parts manufactured with SLS can be time consuming, there are numerous material options, ranging from nylons to thermoplastics, as well as printers capable of building parts of various sizes, making it an attractive option.

4) Stereolithography

Although the material options for stereolithography (SLA) are limited to various photoreactive resins, because the layers tend to blend together and not form ridges, the final part is typically smooth compared with processes that use a plastic filament. SLA parts can also be printed with very low tolerances, resulting in precise consistent cross sections and smooth parts. There are also a large number of existing SLA printers, enabling the production of parts with a range of sizes and resolutions.

5) Multijet Printing

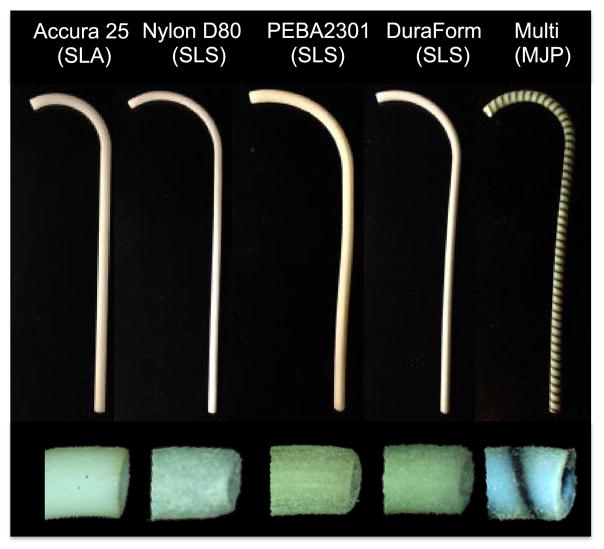
Multijet printing (MJP) allows for the possibility of printing a single part using different materials and combinations of materials. As shown in Fig. 4, we used MJP to make a concentric tube comprised of two different materials for a final part with properties in between those of either material individually. Selection of appropriate material combinations and proportions, along with optimization of the design of multimaterial parts, is left for future work.

Fig. 4.

Examples of 3-D printed concentric tubes. The Accura 25 tube is printed with SLA. The Nylon D80, PEBA 2301, and DuraForm Flex parts are printed with SLS. The multimaterial part is printed with MJP.

B. Selection of 3-D Printed Materials for Concentric Tubes

Due to the geometric and material constraints of concentric tube robots, the 3-D printing technology plays a large role in the success of the parts. Taking into consideration the advantages and disadvantages of each of the technologies outlined above, along with the results of initial test parts as outlined in Table V, we chose to print parts for performing the experiments in Section IV using SLA and SLS. Although biocompatibility was not a main focus of this work, these processes are common in the medical device sector [20]; they have been used for applications including surgical aid tools [35] and tissue scaffolds [36]. The exact materials and tubes printed for these experiments are given in Table III, and examples are shown in Fig. 4.

TABLE III.

Tube Parameters

Material	OD* [mm]	ID* [mm]	E† [MPa]	κ1∓ [mm−1]	Predicted κeq [mm−1]
Accura 25	4.05 ± 0.05	3.1 ± 0.1	1625 ± 35	0.0208 ± 0.0001	0.0181 ± 0.00045
Accura 25	4.1 ± 0.1	3.0 ± 0.1	1625 ± 35	0.0321 ± 0.00025	0.0284 ± 0.0009
Nylon D80	4.15 ± 0.15	2.5 ± 0.1	1392	0.0205 ± 0.0001	0.0183 ± 0.00045
Nylon D80	4.15 ± 0.15	2.5 ± 0.1	1392	0.0316 ± 0.0001	0.0282 ± 0.00065
PEBA2301	4.6 ± 0.1	2.55 ± 0.1	77.5 ± 2.5	0.0192 ± 0.00035	0.0084 ± 0.00075
PEBA2301	4.675 ± 0.075	2.65 ± 0.1	77.5 ± 2.5	0.0261 ± 0.0005	0.0112 ± 0.0011
DuraForm Flex	4.2 ± 0.1	2.6 ± 0.05	7.4	0.0167 ± 0.0002	0.0007 ± 0.0001
DuraForm Flex	4.15 ± 0.05	2.65 ± 0.05	7.4	0.0255 ± 0.00075	0.0011 ± 0.00015

^*Based on physical measurements,

^†As given by the manufacturer,

^∓Based on image processing.

Table III shows the tube diameters physically measured and the curvatures determined based on the image processing described in Section IV. Both the diameters and curvatures of the actual tubes vary slightly from the original CAD files that they were built from. The amount of variation depends on the printing process, material, and company hired to manufacture the parts, and sometimes even varies slightly within the same part. The variability is part of the manufacturing process that should be taken into consideration during the design. The values of Young’s modulus shown in the fourth column are those given by the manufacturer. The final column shows the curvature predicted using (12) when the same inner tube is inserted into each of the 3-D printed tubes. The inner tube is made of stainless steel 304 and is initially straight, with OD = 0.686 mm, ID = 0 mm, and E = 190 GPa.

IV. Experimental Evaluation of 3-D Printed Concentric Tubes

We experimentally evaluated the performance of the 3-D printed concentric tubes described in Section III by inserting an inner stainless steel tube and analyzing the resulting equilibrium curvature. Our aim was to measure the equilibrium curvature of overlapping tubes and compare the experimental result to the curvature predicted by (12). We also analyzed the nonoverlapping precurved region to evaluate whether it maintained its initial precurvature value. All tests were performed for both insertion and retraction of an inner tube. Four different tube materials were tested, and as shown in Table III, there were two curvatures tested for each. These first experiments with 3-D printed concentric tube robots focus on the planar case, because we can obtain clearer experimental results in 2-D than 3-D.

A. Experimental Setup

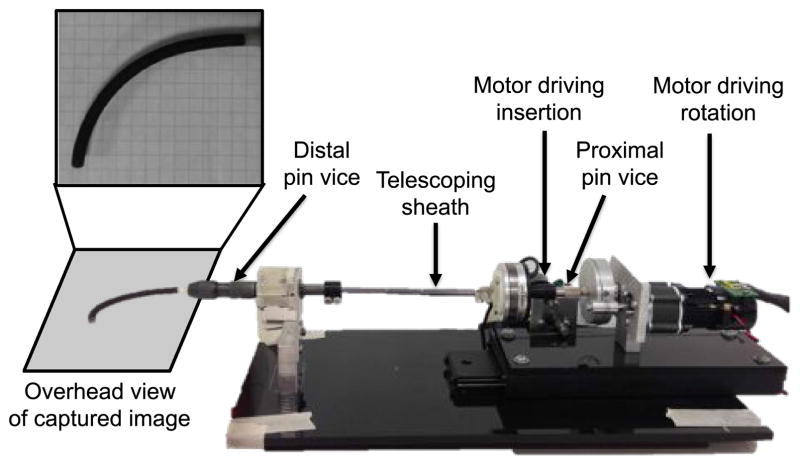
The experimental apparatus used to drive the insertion and rotation of the concentric tubes is similar to the actuation units in [7] and [13] and is shown in Fig. 5. Two pin vices clamp and hold tubes of various sizes in place. The distal pin vice holding the outer tube is stationary, while the proximal pin vice holding the inner tube can both insert and rotate. The entire actuation system is attached to a linear slide, which moves via a capstan drive transmission mechanism [37]. This linear insertion/retraction has a range of 95 mm. The rotational degree of freedom also uses a capstan drive, and has a range of 325°. Both degrees of freedom are actuated using Faulhaber 2342L012CR DC motors with a 64:1 gear ratio and an optical encoder. Although the device is capable of insertion and rotation, only insertion was used in these experiments. A telescoping sheath, made by disassembling and modifying a telescoping antenna similar to that in [38], is placed between the distal and proximal pin vices in order to guide the inner tube during these insertions. All movements are controlled via a MATLAB interface that communicates serially with an Arduino Uno which in turn drives the motors.

Fig. 5.

Experimental apparatus includes two pin vices, distal and proximal, to hold the outer and inner tubes respectively. Two DC motors actuate the rotational and translational degrees of freedom using capstan drive. A telescoping sheath is placed between the distal and proximal pin vices in order to guide the inner tube.

A webcam mounted above the distal end of the device captures an overhead view of the entire curved region of the outer tube throughout the experiments. In order to calibrate the images, a 5.71-mm grid is laid below this curved region.

B. Experimental Procedure

To test the tubes listed in Table III, each tube, in turn, was clamped in the pin vice located at the distal end of the device, and the stainless steel inner tube described above was clamped in the proximal vice. The inner tube was then automatically inserted in 15-mm increments, pausing after each insertion for image capture. The inner tube was inserted a total of 45 mm into the higher curvature samples and 60 mm into the lower curvature samples. It was then retracted in the same manner. Each tube was tested in one of these insertion–retraction cycles a total of five times.

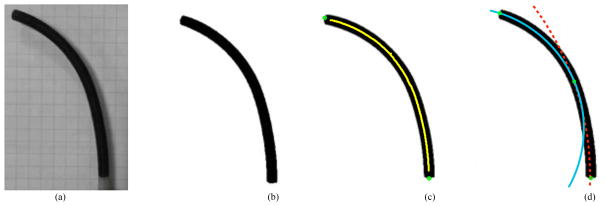
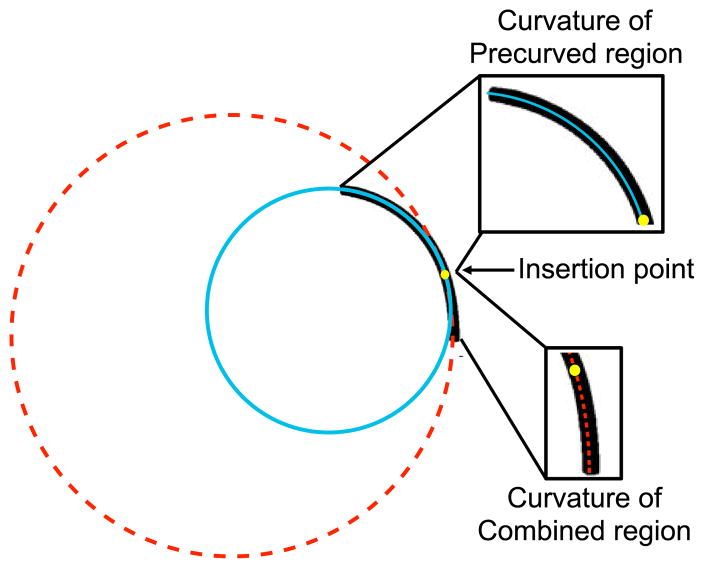
To determine the curvature of each set of tubes, the video data were analyzed and still frame images at each insertion point were collected. The process for analyzing each image is shown in Fig. 6, starting with the initial still frame. The still frame image was then converted to a binary image, and the center line of the tube, along with the base and tip positions, was identified. Assuming constant curvature, two circles were fit to the centerline. One (solid blue) circle was fit to the precurvature region, which lies between the tip and the insertion point, and the other (dashed red)was fit to the combined region, which lies between the insertion point and the base. Fig. 7 illustrates these two different regions along with their associated circle fits.

Fig. 6.

Image analysis process starting with (a) the original still frame image which was converted to (b) a binary image. The center line, base position, and tip position (c) were then found. Finally, two circles were fit to the center line (d). The solid blue circle was fit to the precurvature region, between the tip and the insertion point, and the dashed red circle was fit to the combined region, between the insertion point and the base.

Fig. 7.

Example tube with two different regions and circle fits. The precurved region (solid blue) is the section with only the outer 3-D printed tube and goes from the tip to the insertion point. The combined region (dashed red) is the section where both tubes overlap and goes from the insertion point to the base.

C. Results

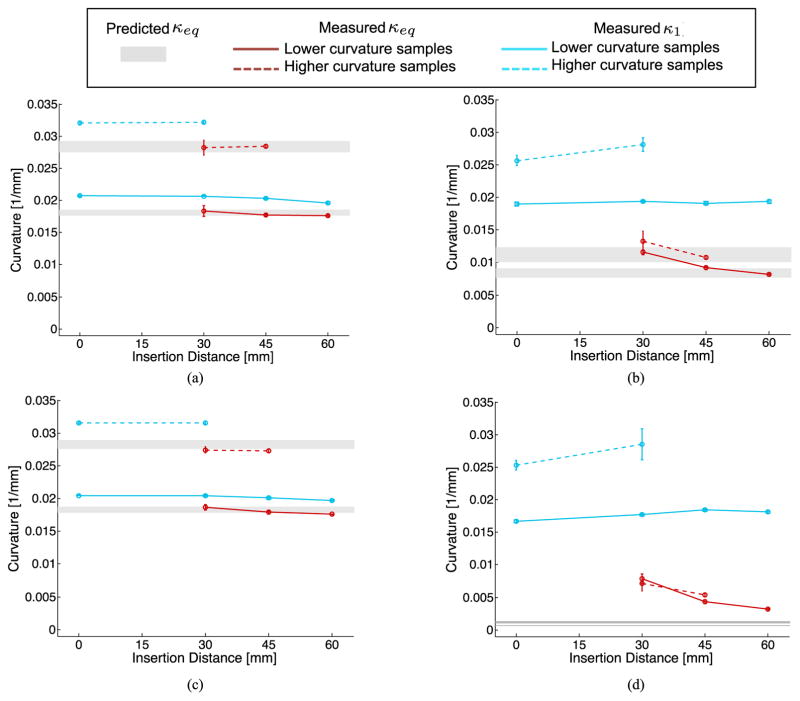
Based on in-plane beam mechanics models developed in [5] and [17], the proximal regions where the two tubes overlap should have an equilibrium curvature predicted by (12) and the distal regions should maintain the initial precurvature of the outer (3-D printed) tube. Fig. 8 shows the results of the experiments described above for each of the samples listed in Table III. The experimentally determined curvature of the combined region is shown in red, and the experimentally determined distal precurvature region is shown in blue for different insertion distances. The corresponding predictions for the curvature for the combined tubes are given in Table III and shown in gray in Fig. 8. Because the parameters used to calculate the combined curvature are only known within some range of values, the predicted combined curvature is also a range of values, as depicted by the gray region, rather than a line.

Fig. 8.

Measured and predicted curvatures for (a) Accura 25, (b) PEBA 2301, (c) Nylon D80, and (d) DuraForm Flex. The predicted equilibrium curvature is shown in gray, the measured equilibrium curvature (κ_eq) in red, and the measured curvature of tube 1 (κ₁) in blue. The solid lines represent the lower curvature samples for a given material, and the dashed lines represent the higher curvature samples.

Fig. 8(a) shows the results for both the higher and lower curvature samples made with Accura 25. For both cases, the pre-curved regions remain relatively constant throughout insertion, and on average, the curvature of the combined region falls within the range of predicted values. Similarly, the samples made with D80 and shown in Fig. 8(c) demonstrate relatively constant pre-curved regions throughout insertion and equilibrium curvature values close to those predicted. Although the tubes made with D80 and Accura 25 behave as expected, the change in curvature from the precurved to equilibrium value is relatively limited due to the somewhat low yield strain of the materials.

Fig. 8(b) and (d) shows the results for the PEBA2301 and DuraForm Flex samples, respectively. The precurved regions for both cases show a slight increase in curvature with increasing insertion distance, while the combined region shows a slight decrease in curvature. The experimentally determined equilibrium curvature of the PEBA2301 sample is close to that predicted, while the experimentally determined equilibrium curvature of the DuraForm Flex sample is greater than that predicted, likely due to discrepancies between the material’s actual value of Young’s Modulus and that provided by the manufacturer. We identify three possible explanations for the trend of decreasing equilibrium curvature with increasing insertion distance, as follows.

1) Inaccuracies of Fitting a Small Section to a Large Circle

The first explanation is that the length of the section of the tube being fit is only a very small proportion of the overall circumference of the fitted circle. This ratio between the length of the section being fit and the circumference of the circle becomes even smaller when the tube is more flexible and the combined curvature becomes smaller, i.e., the radius of the circles becomes larger. Consequently, this trend of decreasing curvature with increasing insertion distance becomes more apparent for the more flexible materials, such as PEBA2301 and DuraForm Flex.

2) Nonconstant Curvature

The second explanation is that the region of overlapping tubes may have a nonconstant curvature. Therefore, depending on which section of the tube is being fit, the resulting curvature calculated will vary. One of the main assumptions of the mechanics-based models for concentric tube robots is that they have piecewise constant curvature. However, this may not hold. For 3-D printed tubes, in particular, the physical properties, including outer and inner diameter, and Young’s modulus, may not be consistent throughout the entire length. This inhomogeneity may partially account for the varying curvature at different insertion distances.

3) Commanded Versus Actual Insertion Distance

The third explanation is that the actual insertion distance may not have been as far as the commanded distance during experiments when the outer tube applies a force against the insertion. Although encoders were used to measure the motor position, the cables used in the capstan drive mechanism can stretch. Thus, the exact location of the tip of the inner tube may be slightly different than expected, even when the motor is in the correct position.

V. Obstacle Avoidance and Target Acquisition With a 3-D Printed Concentric Tube Robot

We demonstrate here a concentric tube robot consisting of two 3-D printed tubes. Through a series of insertions and rotations, we show its capability to reach targets and avoid obstacles.

A. Task Objective and Tube Design

The objective was to design a concentric tube robot using two of the previously tested 3-D printing materials that could successfully avoid obstacles and reach final targets. Although not based on a specific anatomical region within the body, the test environment was designed to simulate a scenario in which the surgeon punctures the skin at as close to a 90° angle as possible and must then maneuver around multiple obstacles. These obstacles could be various organs or tissues that should not be punctured on the way to reaching the planned targets. The test environment is meant to represent a sagittal view, where the skin is along the bottom edge of the images shown in Fig. 9.

Fig. 9.

Still frame images captured (a) after insertion of the two tubes through the outer sheath, (b) during insertion of the inner tube, (c) when the inner tube tries to hit Target 1, (d) during rotation of the inner tube, and (e) when the inner tube tries to hit Target 2.

Once the test environment was determined, the next step was to design a set of tubes that could successfully navigate through it to reach the targets. Based on the size of the distal pin vice and the minimum layer thickness for typical 3-D printing processes, initial values were selected for OD₁ and ID₁. This determined the maximum value for OD₂ based on our previous tests on the minimum gap between the two tubes needed for insertion. And similarly, the maximum value for ID₂ was determined based on the minimum wall thickness requirement for 3-D printing. With the goals of inserting perpendicular to the “skin” and avoiding both obstacles, an initial curved path was selected. From this path, κ_eq, κ₂, and the lengths of both curved sections were measured.

The final necessary parameters were κ₁, E₁, and E₂. We selected an initial combination of materials from the ones tested, and calculated κ₁ using (12) and the previously determined parameters. The relevant equations from Section II were then used to calculate the maximum strain the material would need to withstand in order to make this specific set of concentric tubes. We considered the different combinations of previously tested materials and found a combination that could withstand the maximum strain the tubes would undergo. For Tube 1, the maximum strain will occur when it is inserted through the stiff outer sheath (the pin vice) and must fully straighten. Using (7), the maximum strain was found to be 20%; therefore, PEBA 2301 was selected. For Tube 2, the precurved region will undergo the maximum strain when being inserted through the outer sheath, and the straight region will undergo the maximum strain when inserted through the curved region of Tube 1. Again using (7), the maximum strain was calculated to be 5.5% and 2.95% for the two cases, respectively, and Accura 25 was selected. The final selection of desired tube parameters is shown in the first row of Table IV.

TABLE IV.

Tube Parameters

	OD1 [mm]	ID1 [mm]	OD2 [mm]	ID2 [mm]
Desired	4.3	3.0	2.3	1.3
Ordered	4.05	3.35	2.3	1.3
Measured	4.36 ± 0.22	2.985 ± 0.155	2.265 ± 0.035	1.24 ± 0.02

The final step in the design process was to adjust the inner and outer diameters of the tubes in order to account for the specific materials and 3-D printing processes selected. From previous tests, we found that the designed and actual printed diameters varied slightly, and the amount by which they varied depended on the material. In particular, the parts made with PEBA 2301 swelled from the designed diameters. Past samples were measured, and it was found that there was an increase of 0.15–0.35 mm between the designed and actual outer diameters, and a decrease of 0.25–0.55 mm between the designed and actual inner diameters. In order to obtain the desired inner and outer diameters, the dimensions of the tubes were modified to account for this variability, and the second row of Table IV shows these ordered dimensions. The inner tube, made with Accura 25, was ordered to be the same dimensions as the desired ones, since previous samples printed using SLA had proved to have very tight tolerances. The curvatures were 0.0775 and 0.0455 mm⁻¹ for Tube 1 and Tube 2, respectively.

B. Implementation and Results

The physical measurements of the tubes are shown in the last row of Table IV. Several measurements of the outer diameter were taken at various points along the length of the tube. In addition, several measurements of the inner diameter were taken at different orientations within the openings at the top and bottom of each tube. As shown in Fig. 9(a), the two overlapping tubes were inserted through the pin vice, avoiding Obstacle 1. The inner tube was then automatically inserted through the outer tube as shown in Fig. 9(b). Once the inner tube had been inserted 30 mm, the calculations predicted that it would hit Target 1. However, as shown in Fig. 9(c), the tip of the concentric tube robot is approximately 4.5 mm off of the center of the target. The inner tube was then automatically rotated as shown in Fig. 9(d). After the tube rotated 180°, Fig. 9(e) shows that the tip of the robot is approximately 2.5 mm from hitting the center of Target 2.

This demonstration illuminates several challenges that arise as a result of using 3-D printed concentric tubes in comparison to Nitinol tubes. As explained previously, each 3-D printed process and material has given uncertainty that must be taken into consideration during the design process. There is also some variability in the actual printed cross section, which seems to correlate with the print orientation. Both of these sources of variability depend greatly on the particular process and material.

We did an initial study of error propagation to examine how uncertainty in the tube parameters affects the equilibrium curvature and, therefore, the kinematics. We evaluated the standard formula for the variation in a function y of several toleranced variables x_i given by

$$\delta y\approx \sqrt{{\left(\frac{\delta y}{\delta x_1}\delta x_1\right)}^2+{\left(\frac{\delta y}{\delta x_2}\delta x_2\right)}^2+\cdots +{\left(\frac{\delta y}{\delta x_n}\delta x_n\right)}^2}$$ (15)

where y is the equilibrium curvature as given in (12), and δy gives the variation in the equilibrium curvature due to δx_i, the errors in each variable. Using (12), the equilibrium curvature based on the designed parameters was calculated to be 0.0257 mm⁻¹ (when the curved section of the outer tube and the straight section of the inner tube overlap). Using parameters OD_i, ID_i, E_i, κ_i, and parameter errors as measured during the demonstration in Section V-A, (15) predicts that the variation based on printing uncertainties was 0.0059 mm⁻¹. This means that with the current tolerances, it is reasonable that the actual equilibrium curvature be anywhere between 0.0198 and 0.0316 mm⁻¹. If the equilibrium curvature was indeed on the lower end of this range, then the overlapping portion of the concentric tube robot would be slightly straighter than predicted, which could result in what is shown in Fig. 9(c) and (e).

In addition, the required size difference between the outer diameter of tube 2 and the inner diameter of tube 1, as evidenced in Fig. 9, is larger than that of a standard Nitinol concentric tube pair. Two factors can help explain this wider gap. First, the slight variability in the inner diameter of tube 1 makes it such that the largest diameter tube that can fit inside it may not “fillup” the entire width. Overhead images, such as those in Fig. 9, can highlight this inconsistency when taken from certain viewpoints. Second, high forces are required for smooth insertion and rotation when there is a minimal gap between a concentric tube pair, due to the large coefficients of friction of the 3-D printed tubes. The issue of higher levels of friction can be addressed by exploring the various finishing options available for each of the 3-D printed materials. Another option is to use ultrathin heat shrink polytetrafluoroethylene (PTFE) tubing similar to that used in [39].

VI. Discussion

Prior to implementation as a clinically viable approach for robot-assisted surgery, there remain several challenges. The first challenge is to ensure the biocompatibility and sterilizability of the 3-D printed materials. The aim of the current work was to demonstrate the potential of 3-D printing as a manufacturing method for concentric tube robots, and the questions of biocompatibility and sterilizability were not a main focus. There are, however, already numerous biocompatible 3-D printing materials that have been used for applications including tissue grafts and patient-specific implants [20]; this number is increasing as 3-D printing becomes more prominent in the medical field. There has also been initial research on the sterilizability of 3-D printed materials, where four of the main methods for removing microorganisms were tested [40]. Further investigation of these methods is left for future work. The second challenge is to investigate the effect of plastic deformation on the performance of concentric tube robots. Although the materials presented here may exhibit higher levels of plastic deformation than Nitinol tubes, a proposed use of 3-D printed concentric tube robots is in a patient- and procedure-specific context, which facilitates the production of single-use designs.

The results of this work expand the potential for concentric tube robots to be used in patient- and procedure-specific applications. The new manufacturing process also creates the possibility of nontraditional concentric tube designs. One such possibility includes making multi-material tubes in order to obtain ideal material properties or to increase torsional stiffness relative to bending stiffness. The latter could help solve the bifurcation problem as described in [8] and [17]. Some researchers created grooved patterns on Nitinol tubes as a possible solution [39], but this lengthens an already time-intensive complex Nitinol tube manufacturing process. Multimaterial tubes or tubes with grooved designs can be 3-D printed to help address this issue. In addition, 3-D printing enables the creation of nonannular profiled tubes in order to prevent torsional deformation. By creating a polygonal cross section [41], the tubes would be “keyed” together, constraining their rotational motion with respect to each other.

Biographies

Tania K. Morimoto (S’16) received the B.S. degree in engineering from the Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA, in 2012 and the M.S. degree in mechanical engineering in 2015 from Stanford University, Stanford, CA, USA, where she is currently working toward the Ph.D. degree in mechanical engineering.

Her research interests include robotics, haptics, and medical devices.

Allison M. Okamura (F’11) received the B.S. degree from the University of California, Berkeley, CA, USA, in 1994, and the M.S. and Ph.D. degrees from Stanford University, Stanford, CA, in 1996 and 2000, respectively, all in mechanical engineering.

She is currently a Professor of mechanical engineering with Stanford University. Her research interests include haptics, teleoperation, medical robotics, virtual environments and simulation, neuromechanics and rehabilitation, prosthetics, and engineering education.