A microfluidic platform to study the effects of vascular architecture and oxygen gradients on sickle blood flow

Abstract

Objective

Our goal was to develop a model of the microvasculature that would allow us to quantify changes in the rheology of sickle blood as it traverses the varying vessel sizes and oxygen tensions in the microcirculation.

Methods

We designed and implemented a microfluidic model of the microcirculation that comprises a branching microvascular network and physiologic oxygen gradients. We used computational modeling to determine the parameters necessary to generate stable, linear gradients in our devices. Sickle blood from 6 unique patients was perfused through the microvascular network and subjected to varying oxygen gradients while we observed and quantified blood flow.

Results

We found that all sickle blood samples fully occluded the microvascular network when deoxygenated, and we observed that sickle blood could cause vaso-occlusions under physiologic oxygen gradients during the microvascular transit time. The number of occlusions observed under 5 unique oxygen gradients varied among the patient samples, but we generally observed that the number of occlusions decreased with increasing inlet oxygen tension.

Conclusions

The model system we have developed is a valuable tool to address fundamental questions about where in the circulation sickle cell vaso-occlusions are most likely to occur and to test new therapies.

Introduction

Sickle cell disease (SCD) is a pleomorphic, genetic disorder that affects nearly 100,000 people in the United States and over 13 million people worldwide^1,2. In the United States alone, healthcare costs for SCD patients exceed $1 billion each year³. The origin of the disease is a variant hemoglobin (sickle hemoglobin or HbS) that polymerizes under hypoxic conditions. Polymerization of HbS in sickle erythrocytes leads to increasing cell stiffness, dramatic increases in blood viscosity, and even occlusion of the vasculature^4–8. Clinically, the disease manifests in vaso-occlusive crisis (VOC), where occlusion of the microvasculature leads to tissue infarction, pain, long term organ damage, and significantly shortened life expectancy^9,10. In addition to the biophysical mechanisms of erythrocyte stiffening, increased adhesion of sickle erythrocytes to vascular endothelium and immune interactions also contribute to vaso-occlusion in vivo. Although fundamental questions remain about both the biological and biophysical mechanisms of the disease, a significant and unanswered question on the biophysical side is how sickle blood flow changes as it traverses the varying vessel sizes and oxygen tensions in the microcirculation^11–14. An improved understanding of this process would allow us to understand where in the microcirculation vaso-occlusions are most likely to occur, under which conditions patients may be at the highest risk for VOC, and when therapies are most likely to be effective.

What we know about sickle blood flow under physiologic conditions comes primarily from transgenic mouse models, from in vitro studies, and from a limited number of intravital imaging studies in humans^5,15–16. Imaging in humans and mice has revealed important qualitative information about the behavior of sickle blood in vivo, but these studies are typically limited to parts of the vasculature that can be easily accessed for imaging and thus do not represent the wide range of conditions in vivo^17,18. Moreover, in vivo studies do not allow us to easily differentiate between biological (adhesion, immune, etc.) and biophysical mechanisms of occlusion and impaired flow. In vitro model systems, by contrast, allow for control over a wide range of physiologically relevant parameters⁵. Classic in vitro studies of sickle cell biophysics either quantified the mechanics of individual sickle erythrocytes or performed rheology measurements in bulk rheometers, but these studies did not capture the integrated rheologic effects of a population of sickle erythrocytes as it transits the range of physiologic conditions in the microvasculature^5,8,19–20. We previously developed a microfluidic platform that permitted quantification of blood effective viscosity in arteriole or venule-sized microchannels under specific conditions of pressure bias and oxygen tension, and experiments in this device have led to several new observations about the rheological changes that may occur in vivo^21–23. However, this device did not attempt to replicate the branching architecture, the oxygen gradients, or the transit times within the microvasculature. Work by Tsai et al. demonstrated that the branching architecture in the vasculature was critical to understand the role of endothelial adhesion in VOC²⁴. Similarly, to understand the changes in sickle blood flow that occur in humans, we need an in vitro model system that captures these critical elements and allows quantification of blood flow in samples from human patients.

To study the changes in sickle blood flow as it transits the microvasculature, we have developed a novel in vitro model of the microvasculature that comprises two critical components: 1) a hierarchal, bifurcating vascular network that mimics in vivo vascular architecture, and 2) an oxygen gradient along the vascular network. Here, we report the development and characterization of this new model system, and we report findings from studies with sickle blood. We show, for the first time in an in vitro system, that occlusions can occur in the microvasculature under physiologic oxygen gradients due solely to biophysical changes in erythrocytes.

Materials and Methods

Blood sample collection

Whole sickle cell blood samples were collected from patients with homozygous SS disease from the University of Minnesota Medical Center, Massachusetts General Hospital, and Brigham and Women’s Hospital under protocols authorized by Institutional Review Boards at the University of Minnesota and Partners Healthcare. The blood samples were collected in 5mL EDTA vacutainers and stored at 4°C for between a few hours and up to 5 days. Previous studies have found that these storage, temperature, and anticoagulation settings did not cause significant changes in the rheological properties of blood^25,26. A Sysmex XE-500 automated analyzer (Sysmex, Kobe, Japan) and high performance liquid chromatography using a Tosoh G7 column (Tosoh Bioscience, San Francisco, California) were used to measure the hematocrit and hemoglobin fractions of the blood samples shown in table 1. Hematocrit and hemoglobin fractions were not measured for blood samples shown in Figure 5.

Table 1.

Blood sample hemoglobin fractions and hematologic parameters.

Sample #	Blood Sample Indices						WBC	Storage
	HbS	HbF	HbA	HCT	MCV	MCHC
	%	%	%	%	fl/cell	g/dL	x1000/mm3	# days
1	81.4	6.8	4.3	26.9	79.8	34.2	10.34	3
2	42.5	5.5	47.7	24.9	84.4	32.5	13.1	5
3	73.8	19.6	3	28.5	94.4	35.4	11.73	3
4	81.4	6.8	4.3	25.1	79.7	33.1	14	4
5	81.5	11.3	2.9	21.7	96	34.6	9.06	1
6	72.8	15	12.2	26.9	68.6	33.8	9.92	0
HbAA Control	0	0.8	96.3	53.3	88.4	34.5	5.03	0

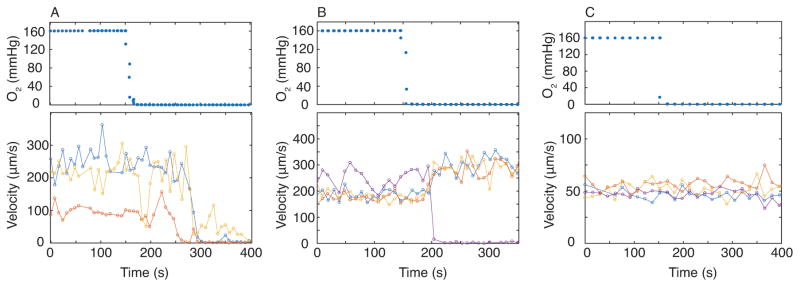
Figure 5.

Sickle blood velocity response is patient specific. We tracked blood velocity in three to four capillary channels each represented by a different color (lower panel, blue, yellow, red, and purple dots) in response to changing oxygen tension (upper panel) and found variation between patient samples. (A) Sickle patient blood occludes in all tracked channels when oxygen tension is set to 0 mmHg. Blood sample was not recently transfused with healthy, non-sickle cell blood. (B) Sickle patient blood sample occludes in only some of the channels, and only one of the channels that we tracked showed occlusion. Blood sample was not recently transfused with healthy, non-sickle cell blood. (C) Sickle patient blood sample shows no response to oxygen tension in all channels we tracked. Blood sample was transfused recently (HbS: 46.4%, HbA: 44.1%).

Microfluidic device design

A multi-layered polydimethylsiloxane (PDMS) based microfluidic device lies at the heart of our microvascular platform. The device consists of three layers: 1) a 15μm tall blood microchannel layer, 2) a 100μm tall hydration layer, and 3) a 150μm tall oxygen gas tension control layer (Fig. 1). This multi-layered approach allows us to diffusively couple the oxygen control layer with the blood microchannel layer to control the oxygen tension directly in the blood microchannels^22,23. Each of the layers is separated by a 100μm thick PDMS membrane. The blood microchannel layer, located at the base of the device, is an adapted and modified design from Tsai, et al, and mimics the branching capillary tree vascular architecture²⁴. Above the blood microchannel layer is a hydration layer that is necessary to prevent dehydration²⁷. The oxygen gas control layer consists of five separate channels running perpendicular to the blood flow in the blood microchannel layer, which allows for the generation of oxygen gas tension gradients across the blood microchannel layer²⁸.

Figure 1.

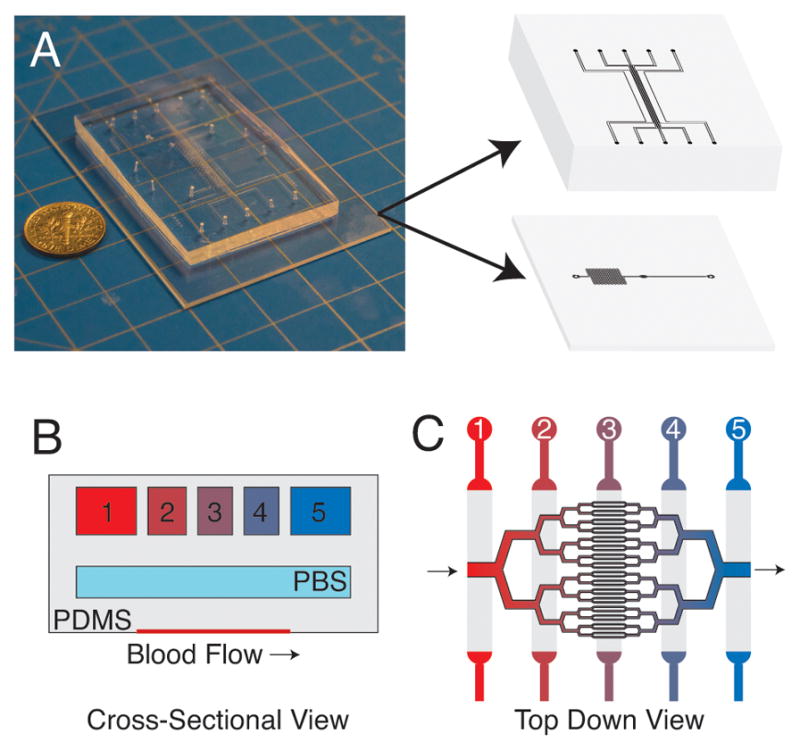
Schematic of the microfluidic device. (A) Photograph of microfluidic device with 3D illustration depicting the oxygen gas channel and blood microchannel layers. The device comprises multiple PDMS layers that are bonded using oxygen plasma activation. This multi-layered approach allows for the precise control of oxygen gas tension in the blood microchannel layer. (B) Cross-section view of the device showing the three layers of the device (illustration is not to scale). (C) Top down view of the microvascular portion of device with illustrated oxygen channels above. Gas with varying oxygen tension are perfused through each of the oxygen gas channels (B,C) to generate linear oxygen gradients in the microvascular layer.

Microfluidic device fabrication

To fabricate the multilayered PDMS device, we employed soft-photolithography to first create three separate master molds for each of the three layers as described previously²². To assemble the device, we first cast 10:1 elastomer/curing agent ratio PDMS onto the oxygen gas layer mold at a 5mm height. Compression molding was then utilized to create individual PDMS layers of specified thickness for the blood microchannel and hydration layer molds as described previously²³. After creating each of the PDMS layers, each of the layers were plasma bonded together and to a glass microscope slide at a power of 100 W, an oxygen flow rate of 100 cc/minute, and an exposure time of 30 seconds.

CFD and luminescent oxygen tension gradients

To assess our platform’s ability to generate oxygen tension gradients across the blood microchannel, we utilized computational simulations. A two-dimensional cross section of the microfluidic device was modeled in COMSOL (COMSOL Multiphysics, Stockholm, Sweden) with diffusion coefficients taken from literature²⁹.

We then utilized the luminescent dye Tris(2,2′-bipyridyl)dichlororuthenium(II) hexahydrate (Ru(BPY)₃) to experimentally validate our model platform’s ability to generate oxygen tension gradients. Ru(BPY)₃ luminescence intensity scales inversely with oxygen tension and allows us to quantitatively analyze oxygen tension within our microfluidic device. Ru(BPY)3 was diluted to 1mM in deionized water and perfused through the blood microvascular channels of the device in the absence of blood. Luminescent intensity was measured using epi illumination on a wide field inverted microscope. Images were analyzed using ImageJ (ImageJ, Bethesda, MD). Known oxygen concentrations were used to calibrate luminescent intensity for conversion into oxygen tension in subsequent experiments.

Blood flow experimental setup

For blood flow experiments, the microfluidic device was mounted to a temperature-regulated (37°C) Axio Vert.A1 (Carl Zeiss, Jena, Germany) with an xiQ CMOS camera (Ximea, Germany). An electronic pressure regulator (PCD-15PSIG, Alicat Scientific, Tucson Arizona) was used to drive whole sickle cell blood flow through the blood microchannel layer at a constant pressure of 0.5 PSI. To prevent dehydration of the blood, a syringe pump (NE-500, New Era Pump Systems, Farmingdale, New York) was used to push phosphate buffered saline (PBS) through the hydration layer of the device. To create oxygen gradients, we adapted a previously described system based on cycling 160mmHg oxygen gas (21% O₂, 5% CO₂, balance N₂) and 0mmHg oxygen gas (5% CO₂, balance N₂) using a solenoid valve system²⁸. Oxygen gas mixing was monitored using a fiber optic oxygen sensor connected to the gas channel outlet ports (NeoFox-Gt, Ocean Optics, Dunedin, Florida). As sickle blood perfused through the microfluidic device, we captured 30fps videos of the blood flow at fully oxygenated and deoxygenated conditions, and at a series of oxygen tension gradients starting with a 91mmHg to 0mmHg (12% to 0%) and incrementally stepping the high end of the oxygen tension by 15mmHg (2%) increments until a significant number of occlusions were seen. Each oxygen gradient cycle was held for a minimum of 8 minutes prior to video capture to allow the system to reach steady state. A few samples were also computationally velocity tracked by capturing 300fps burst videos and tracking the blood velocity using a morphologic criterion as described previously³⁰.

Results

Development of a microfluidic microvasculature model with physiologic oxygen gradients

As shown in Figure 1, we have developed a novel microfluidic model for sickle vaso-occlusion that combines a branching vascular network on which we impose a steady gradient of oxygen to approximate conditions in vivo. The device, which is fabricated in PDMS using soft lithography, comprises three layers: a layer with the microvascular network, a hydration layer, and a layer to generate the oxygen gradients. The microvascular layer branches 5 times from a single 250 μm inlet to form 32 capillaries that are each 10 μm in width and then converges back symmetrically to a single 250 μm outlet. Lengths for each branched channel vary from 85μm to 200μm, and all channels in the microvascular network are 15μm tall. Channel widths and lengths are well within the range observed in the microvasculature in vivo^31,32. The oxygen gradient layer comprises five separate channels running perpendicular to the microvascular network. Through each channel, we flow a gas mixture with a unique concentration of oxygen, which is generated using an off-chip gas mixer. The oxygen diffuses through the PDMS layers and into the blood, and in so doing, the sharp oxygen concentration boundaries are smeared out to form a smooth oxygen gradient. The hydration layer is a large reservoir of water that is used to prevent dehydration of the blood by flowing gases in the oxygen layer.

To test the device, we perfused whole, anticoagulated sickle (genotype HbSS) and healthy (genotype HbAA) blood through the microvascular network under steady pressure bias and at atmospheric oxygen tension. We quantified mean blood transit times through the entire microvascular network to be 10.29 (+/− 2.9 [SD]) seconds and a capillary mean transit time to be 3.56 (+/− 1.1 [SD]) seconds, which is in the range of what is observed in vivo^33–35. Additionally, we determined blood velocities of these samples to range from 133μm/s to 273μm/s across the various parts of the microvascular network. Figure 2 shows blood velocity distributions across the microvascular network for 6 unique patient samples. We found that blood velocities were higher in larger channel widths (arteriole and venule sized) and slowest in the capillary sized channels, similar to what is observed in vivo^33,35. Both transit times and blood velocities varied between patient samples, which may be attributable to differences in hematologic parameters between samples (Table 1) or other patient specific differences.

Figure 2.

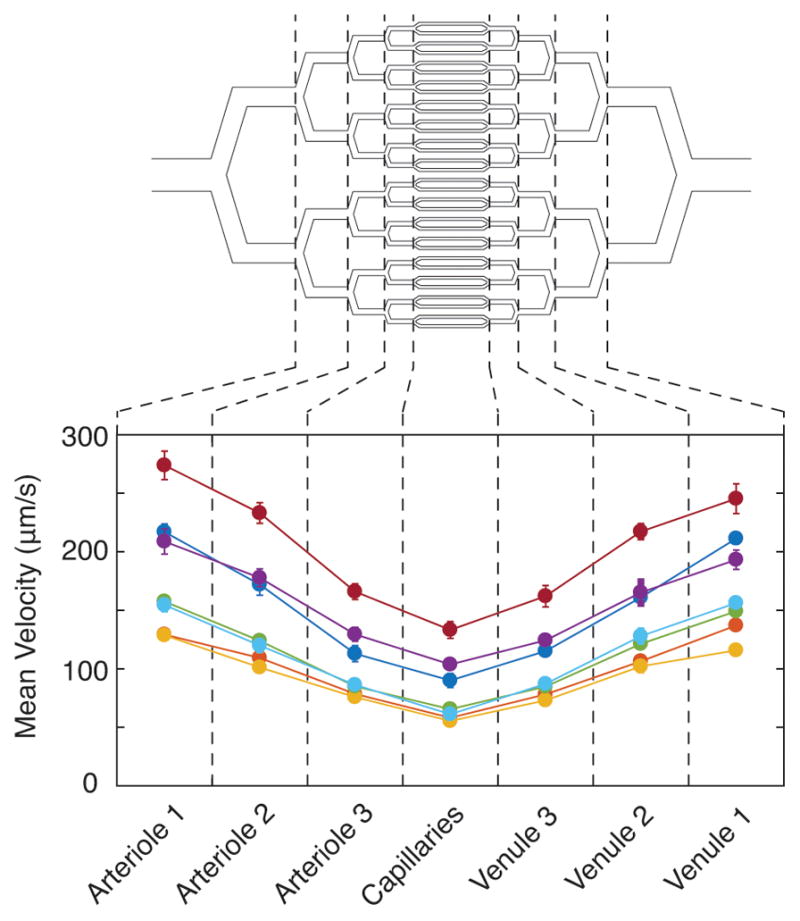
Sickle cell blood velocity across the microvasculature. We measured blood velocity for both sickle (yellow, orange, green, dark blue, light blue, and purple) and healthy (red) patient blood samples in each section of our microvascular channels at atmospheric oxygen tension. Blood velocity for all samples is highest in the largest channels and lowest in the capillaries.

Modelling and characterization of oxygen gradients in the microvasculature model

A computational simulation was used to assist in the design of the oxygen gradient generator. A 2D cross section of the device was modeled using finite element analysis (COMSOL, Burlington, MA). Simulations were conducted over a range of parameters including the number of gas channels (3 to 8), gas channel widths (60μm to 150μm), pitch between oxygen channels (50μm to 450μm), and vertical distances from the blood layer (200μm to 500μm). As expected, we found that having more channels, smaller gap lengths, and longer vertical distances leads to smoother, more linear oxygen tension gradients, and we found that an increasing distance between the gas channels and the blood layer increases the time necessary to reach steady state. We found that the optimum design with the least number of gas channels to produce a smooth oxygen gradient within 30 seconds included 5 oxygen gas channels, channel widths of 150μm, gas channel pitch of 110μm, and a vertical distance from the blood layer of 300μm. Figure 3 shows the COMSOL simulations of this device design with two different imposed oxygen gradients, which reveal that in both scenarios, steady linear oxygen gradients are achieved within 30 seconds of changing the conditions in the gas channel from 160 mmHg oxygen in all channels.

Figure 3.

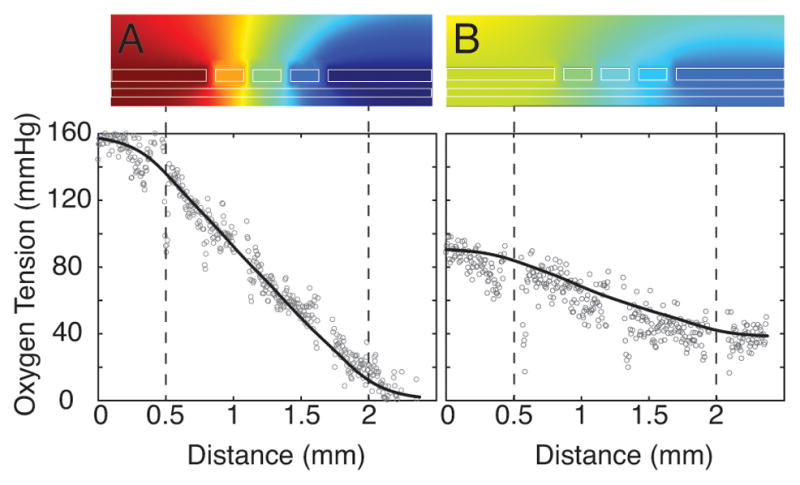
Theoretical and experimental oxygen gradients in our microfluidic device. 2D COMSOL simulations (top) of an oxygen gradient spanning (A) 160 mmHg to 0 mmHg or (B) 91 mmHg to 38 mmHg. Plots (bottom) show theoretical (COMSOL simulation, solid line) compared to experimental (Ru(BPY)₃, open circles) oxygen gradients over the length of the microvascular blood channel. Small gaps in experimental Ru(BPY)₃ data denote the location of gas channel vertical walls, which produce optical artifacts but do not affect oxygen tension. Blood microvascular network is located in between the dashed lines.

To validate the device design, we used the oxygen sensitive luminescent dye Ru(BPY)₃ to directly quantify oxygen tensions within the microvascular layer (Supplemental Figure 1). First, we determined the luminescent intensities at fully oxygenated and fully deoxygenated conditions and used these values to calibrate the luminescence intensity values using Beer’s Law³⁶. We then imposed a linear oxygen gradient by flowing 160, 114, 76, 38, 0 mmHg oxygen in the five gas channels, respectively, and we measured the luminescent intensity across the length of the microvascular network. We repeated this for an oxygen tension gradient that spanned from 91mmHg to 38mmHg and again measured the luminescent intensity. As seen by the open dots in Figure 3, luminescent intensities show that for both oxygen tension gradients tested, a steady, linear oxygen gradient, that matched our computational simulations, was observed in the microfluidic device.

Rheological changes and occlusion of human sickle blood in the microvasculature model

Using our microvascular model, we observed the flow of whole anti-coagulated blood from six unique sickle patients (genotype HbSS) and 1 healthy donor (genotype HbAA) under five unique oxygen gradients. Figures 4A and 4D show sickle blood flowing through the microfluidic device under a constant oxygen tension of 160mmHg. As expected, healthy blood shows no response to any of the oxygen conditions tested, and fully oxygenated sickle blood flow is similar to that observed for healthy blood. By contrast, when sickle blood is perfused under fully deoxygenated conditions (all gas channels at 0 mmHg oxygen), Figures 4B and 4E, nearly all channels are occluded for all sickle blood samples. Oxygen gradients produced a more varied response between sickle blood samples. Figures 4C and 4F show a representative blood flowing mostly occlusion-free with an oxygen gradient of 91mmHg to 0mmHg (12% to 0%). Flow variations can be seen in Supplemental Movie 1. However, as seen in Table 2 (complete blood indices found in Table 1), one out of the six samples demonstrated occlusion or slowing of flow even when the inlet oxygen tension was supra-physiologic. When we decreased inlet oxygen tension to 76 mmHg, samples that began to show occlusive behavior under a 0–91 mmHg oxygen gradient showed higher fractions of the channels occluded. Further decreasing the inlet oxygen to 61 mmHg and beyond, we observed a continued increase in occlusion percentage, eventually culminating in the highest occlusion percentages for inlet oxygen tensions of 31 mmHg. We also identified the locations of occlusions by looking for regions in the microchannels filled with plasma but no blood cells, indicating an occlusion upstream of that region (Fig. 4B). We found that occlusions did not always occur downstream of the capillaries. When all gas channels were fully deoxygenated, occlusions frequently occurred upstream of the capillaries. As we increased the inlet oxygen tension, we observed no distinct location for the occlusion, suggesting it was happening downstream of the capillaries.

Figure 4.

Sickle cell blood flow in the microvasculature is dependent on oxygen tension. Representative sickle blood in our microvasculature mimic at 10X magnification (A–C) and at 40X magnification (D–F) shows differences in flow velocity depending on oxygen tension. At constant, high oxygen gas tensions (160mmHg) blood flow is fast flowing and similar to healthy, non-sickle patient blood samples (A,D). At constant, low oxygen gas tensions (0mmHg) blood flow becomes impaired and nearly completely occludes (B,E). Here, many of the channels appear to occlude upstream of the capillaries. When an oxygen gas tension gradient is imposed, 91mmHg to 0mmHg in this case, sickle blood velocity again becomes impaired, but is highly sensitive to patient and sample variation (C,F). In all images, a Soret band filter was utilized to show relative hemoglobin saturation. Lighter intensities indicate higher oxygen saturation and darker intensities represent low oxygen saturation. Scale bars are 200μm in (A–C) and 50μm in (D–F).

Table 2.

Occlusion percentage as a function of imposed oxygen gradient.

Oxygen Gradients (mmHg)	92 to 0	76 to 0	61 to 0	46 to 0	31 to 0	Constant 0
Sample #	%	%	%	%	%	%
1	0	0	0	68	68	72
2	0	0	5	9	52	35
3	4	8	15	69	100	96
4	0	0	0	8	58	77
5	0	0	54	50	100	100
6	0	52	52	86	100	100
HbAA Control	0	0	0	0	0	0

We also computationally tracked and quantified sickle blood velocities within the capillaries for 3 additional samples (not listed in table 1). Under fully oxygenated conditions, velocities ranged between 50 μm/s to 300 μm/s depending on the sample, while under fully deoxygenated conditions, velocities dropped to 0 μm/s across all samples. As with occlusion frequency, velocity changes were sample specific. Figure 5 compares the blood velocities of three different samples in response to 0–160 mmHg oxygen gradients. Two of the samples, from patients who had not been transfused immediately prior to sample collection (Figure 5A,B), showed velocity reductions in some channels when subjected to low oxygen tension throughout. The sample shown in Fig. 5C shows little response to oxygen gradients, which is likely because this patient was heavily transfused with HbAA blood immediately prior to sample collection, and thus the blood contains a large fraction of normal erythrocytes. We also observed that as individual capillary channels became occluded in our system, blood velocity in nearby un-occluded channels increased as seen in Supplemental Figure 2. This observation provided another means to indirectly quantify occlusions in the microvascular network (Supplemental Figure 3).

Discussion

Despite decades of work in SCD, we still lack a clear and quantitative picture of the rheological changes that occur as sickle blood transits the wide range of vessel sizes, pressures, and oxygen tensions in the microcirculation⁵. Many in vitro systems have been used to study various aspects of sickle cell disease, including systems to quantify single cell biomechanics, bulk rheometers to quantify effective viscosity, and microfluidic systems to mimic some aspects of blood flow in vivo, but none of these experimental platforms account for the dynamics of a whole population of erythrocytes as it transits the microvasculature^5,20. In this study, we have developed a model of sickle cell vaso-occlusion that incorporates a branched vascular network that mimics both in vivo transit times and vessel sizes and imposes oxygen gradients that more closely approximate in vivo oxygenation conditions than existing models. Because this model captures a more integrated picture of rheological changes in the microcirculation than other in vitro systems, we believe that it is a valuable tool to address fundamental questions about where in the circulation and under which conditions occlusions are most likely to occur and to test new therapies that work by modulating these biophysical interactions such as therapies that increase hemoglobin oxygen binding affinity^40–42.

We have previously shown that deoxygenation of sickle blood was sufficient to occlude small microchannels even in the absence of endothelial interactions, but a lingering question was whether these effects would be sufficient to occlude the blood vessels during microvascular transit^19,20,43. Here we provide evidence that it is possible to observe biophysical occlusions within the microvasculature on the time scale of microvascular transit. As expected, we observe that occlusion frequency decreases with increasing inlet oxygen concentration in our devices, but our limited sample size limits our ability to draw broad quantitative conclusions about occlusion probabilities. Nevertheless, these results suggest that this model system should be useful in identifying under which conditions in the vasculature and possibly in which patient occlusions are most likely to occur, and it should allow us to quantify the potential benefit of new therapies.

Another interesting observation is that under certain conditions, we observe occlusions upstream of the capillaries in our microvascular network. Most studies in transgenic mice have focused on occlusions in the post-capillary venules^37–39, and this study supports the idea that occlusions likely do occur downstream of the capillaries (or the post-capillary venules) but not exclusively. Our previous work suggested that sickle blood rheology becomes impaired even at arterial oxygen tensions, leading us to speculate that when adhesive events are integrated, occlusions may occur upstream of the venous circulation²³. Here we show that occlusions occur upstream of the capillaries in our platform due solely to biophysical mechanisms, especially when the inlet oxygen tension drops below 46 mmHg. While this low oxygen tension is more representative of venous oxygen tensions in vivo for healthy individuals, oxygen tensions in this range have been observed in the arterial circulation of sickle patients⁴⁴. Due to limitations in the number of patient samples measured, more work would be necessary to isolate the most likely location of occlusions in the microcirculation, but we believe this platform is an important tool in addressing this critical question.

We note several aspects of our model that could be modified in future studies depending on the specific questions and applications. First, we note that most of the samples measured here were stored for more than 24 hours, and we recognize that many properties of the blood do change with storage such as the functional status of platelets and white blood cells and that blood biophysical properties may change with improper storage^45–47. Despite these concerns, we have observed little effect of storage on rheological properties in previous studies^21–23. Moreover, in this study, we measured a fresh blood sample (measured within 5 hours of collection), which showed qualitatively similar results to the stored samples. More samples would have to be tested to rigorously characterize the effects of storage, but our emphasis here is on the development of a new platform rather than a systematic study of blood rheological properties.

We also recognize that our microvascular network does not include all features of the microvasculature in vivo such as flow recirculation, varying branching angles, asymmetric arterial and venous circulation, adaptive vasoconstriction and dilation, among others. Additionally, our smallest channels are only 15μm by 10μm in cross section, which is generally larger than most capillaries found in vivo. Other groups have developed microvascular networks that include some of these features^48–50, and the addition of these features to our model could help probe some unanswered questions: Are sickle cells more likely to aggregate at bifurcations within a specific range of branching angles? Does the asymmetry in the arterial and venous circulation affect the likelihood of occlusion? However, similar to the work by Tsai et al, we believe the model presented here captures the most salient features of the microcirculation for some important questions of sickle blood flow, and inclusion of more physiologic architecture or smaller capillaries would likely magnify the effects observed here but would not change the qualitative findings²⁴. Also missing from this model are important biological influences like endothelial adhesion and immune interactions, but even without these critical influences we still find that sickle blood flow can become impaired and occluded solely from oxygen-dependent rheological changes triggered by the oxygen gradients. Combining our model with biological influences of SCD would allow a more integrated picture of how sickle blood flow changes in the microcirculation²⁴.

Perspectives

We present a microfluidic model of sickle cell vaso-occlusion that captures some of the rheological changes that occur as sickle blood transits the wide range of vessel sizes, shear rates, and oxygen tensions in the microcirculation. We believe that this platform is a valuable tool to address fundamental questions about where in the circulation and under which conditions vaso-occlusions are most likely to occur and to test new therapies that work by modulating biophysical processes such as therapies that increase hemoglobin oxygen binding affinity.

List of Abbreviations

SCD

Sickle cell disease

HbS

Sickle cell hemoglobin

VOC

Vaso-occlusive crisis

PDMS

Polydimethylsiloxane

Ru(BPY)₃

Tris(2,2′-bipyridyl)dichlororuthenium(II) hexahydrate

PBS

Phosphate buffered saline

HbA

Normal, adult hemoglobin

HbF

Fetal hemoglobin

HCT

Hematocrit

MCV

Mean corpuscular volume

MCHC

Mean corpuscular hemoglobin concentration

WBC

White blood cell