Measuring the Kinetic and Mechanical Properties of Non-Processive Myosins using Optical Tweezers

Abstract

The myosin superfamily of molecular motors utilizes energy from ATP hydrolysis to generate force and motility along actin filaments in a diverse array of cellular processes. These motors are structurally, kinetically, and mechanically tuned to their specific molecular roles in the cell. Optical trapping techniques have played a central role in elucidating the mechanisms by which myosins generate force and in exposing the remarkable diversity of myosin functions. Here, we present thorough methods for measuring and analyzing interactions between actin and non-processive myosins using optical trapping techniques.

1. Introduction

Myosins are cytoskeletal motors that use the energy from ATP hydrolysis to generate force and movement along actin filaments. Humans express thirty-eight myosin motor proteins (1) with diverse biochemical and mechanical properties that enable them to function in a wide-array of cellular processes, including muscle contraction, cell migration, mechanosensing, intracellular transport, generating membrane dynamics, and cellular signaling (2–4). Mutations in myosin genes can result in cardiomyopathies, hearing loss, blindness, cancer, and developmental defects (5).

Despite their diverse functions, all characterized myosins follow a similar ATPase and mechanochemical cycles (4). The rate and equilibrium constants that define the ATPase pathway vary substantially across the myosin family, resulting in differences in the steady-state populations and lifetimes of intermediates that confer diverse mechanical functions to the motors. It has been a substantial challenge to the field to determine how the biochemical intermediates on the myosin ATPase pathway are linked to structural changes that ultimately lead to force generation. Additionally, it has been a challenge to determine how divergent biochemical properties lead to mechanical differences among different myosins isoforms, how mechanical loads affect myosin power output, and how myosin mutations affect motor function in disease.

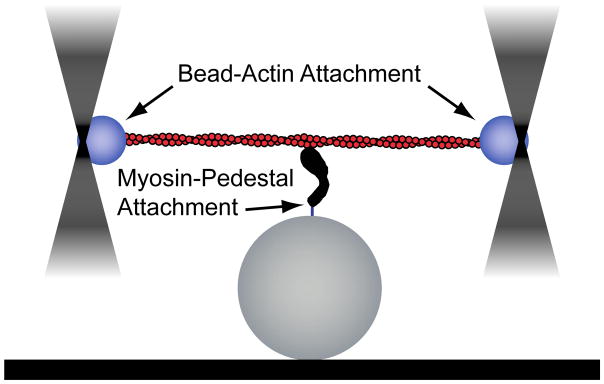
Single-molecule techniques, in conjunction with biochemical, spectroscopic, and structural studies, have been incredibly powerful in their ability to elucidate the molecular mechanisms of molecular motors (6, 7). Notably, optical tweezers have served as an indispensable tool for discovering the mechanisms of myosin function. Pioneering work by the laboratory of Dr. James Spudich led to the development of an assay to probe the properties of non-processive myosin motors (i.e., motors that only take a single step on actin before detaching), dubbed the three-bead assay (8). In this assay, an actin filament is suspended between two optically trapped beads, tensed, and then lowered onto a pedestal bead that is sparsely coated with myosin (Fig. 1). The myosin motor can then bind to the actin, displacing the beads. From these displacements, it is possible to extract information about the myosin working stroke, attachment lifetime, and magnitude of force generation. The three-bead assay has also been used to probe the kinetics and mechanics of processive myosins (9, 10). It is worth noting that other geometries have also been employed to study single non-processive motors (11–13).

Figure 1.

Cartoon of the three-bead geometry. A dual-beam optical trap is used to form a bead-actin-bead dumbbell. This dumbbell is then lowered over a surface-bound bead that is sparsely coated with myosin and single-molecule interactions between myosin and actin can be detected.

To conduct the three-bead assay, one must (1) couple beads to actin, (2) prepare flow cells with pedestal beads, (3) attach myosins to the pedestal, and (4) identify single-molecule interactions between myosin and actin. In this chapter, we describe the procedures for performing this assay along with techniques for measuring myosin’s force-dependent kinetics and stiffness. We also describe techniques for data analysis. Our optical trapping setup is briefly described in Subheading 3.9 below. For detailed instructions on building a dual-beam optical trap for the three-bead assay, the reader is directed to an excellent chapter by the Spudich laboratory (14). For single-bead assays, the reader is referred to experiments in Chaps. 5, 17, and 18.

2. Materials

2.1 Preparation of Acetone Powder for Actin Purification

1. Appropriate muscle tissue (see ^{Note 1}).

2. Myosin extraction solution (0.5 M KCl, 0.1 M K₂HPO₄ cooled to 4°C).

3. Cold distilled water (chilled to 4°C).

4. 1 M sodium carbonate.

5. Cold reagent grade acetone (chilled to 4°C).

6. Chloroform

7. Meat grinder

8. Cheesecloth

9. Blender or Omni Mixer.

2.2 Preparation of Actin from Acetone Powder

1. Buffer A (2 mM Tris, pH 8.0 at 25°C, 0.2 mM ATP, 0.5 mM DTT, 1 mM sodium azide, 0.1 mM CaCl₂) (see ^{Note 2}).

2. 2 M KCl

3. 1 M MgCl₂

4. Cheesecloth

5. Dounce homogenizer (see ^{Note 3}).

2.3 Bead-Actin Linkages: Preparation of N-Ethylmaleimide Modified Myosin Beads

1. High Salt Buffer (HSB) (500 mM KCl, 4 mM MgCl₂, 1 mM EGTA, 20 mM KH₂PO₄, pH 7.2).

2. KMg25 buffer (25 mM KCl, 60 mM MOPS pH 7.0, 1 mM EGTA, 1 mM MgCl₂, 1 mM DTT), (see ^{Note 4}).

3. 1 mL of 1 M Dithiothreitol (DTT), (see ^{Note 5})

4. 50 mM N-ethylmaleimide (Sigma 04259-5G) in water prepared fresh (see ^{Note 6}).

5. Skeletal muscle myosin in glycerol (see ^{Note 7}).

6. Glycerol (Sigma G7893).

7. Polystyrene beads (1.1 μm diameter, 10% solids, Sigma LB-11).

8. Bovine serum albumin (BSA, Fisher 50-230-3400).

2.4 Bead-Actin Linkages: Preparation of Neutravidin-Coated Beads

1. KMg25 buffer (25 mM KCl, 60 mM MOPS pH 7.0, 1 mM EGTA, 1 mM MgCl₂, 1 mM DTT), (see ^{Note 4}).

2. Polystyrene beads (1.1 μm diameter, 10% solids, Sigma LB-11)

3. Neutravidin (Fisher 31000) can be diluted to 0.1 mg/mL in water and frozen at -20°C.

4. Biotinylated actin (see ^{Note 8}).

5. 50 μM TRITC-labeled phalloidin (Sigma P1951) in methanol (see ^{Note 9}).

2.5 Bead-Actin Linkages: Purification of HaloTagged, Actin-Binding Domain of α-Actinin (HT-ABD)

1. Lysis buffer (25 mM Tris, pH 7.5, 20 mM Imidazole, 300 mM NaCl, 0.5 mM EGTA, 0.5% Igepal, 1 mM beta-mercaptoethanol, 1 mM PMSF, 0.01 mg/mL aprotinin and leupeptin) (see ^{Note 10}).

2. Wash buffer (same as lysis buffer minus Igepal).

3. Elution buffer (12 mM imidazole, 300 mM NaCl, 25 mM Tris, pH 7.5, 1 mM EGTA, 1 mM DTT).

4. FPLC buffer A (10 mM Tris, pH 7.5, 50 mM KCl, 1 mM DTT, 1 mM EGTA).

5. FPLC buffer B (same as buffer A except 1 M KCl).

6. KMg25 buffer (25 mM KCl, 60 mM MOPS, pH 7.0, 1 mM EGTA, 1 mM MgCl₂, 1 mM DTT).

2.6 Bead-Actin Linkages: Coupling HT-ABD to Beads

1. 1 μm diameter Polybead amino microspheres (Polysciences 17010-5).

2. Bovine serum albumin (BSA, Fisher 50-230-3400).

3. HaloTag succinimidyl-ester (O2) ligand (Promega P1691) (see ^{Note 11}).

4. Phosphate buffered saline (PBS; Fisher 14190-136).

5. KMg25 buffer (25 mM KCl, 60 mM MOPS, pH 7.0, 1 mM EGTA, 1 mM MgCl₂, 1 mM DTT).

2.7 Preparation of Flow Cells for Optical Trapping

1. Amyl acetate (Electron Microscopy Sciences 10815).

2. 2% nitrocellulose in amyl acetate (Electron Microscopy Sciences 1262030).

3. Dry silica beads, 2.5-μm diameter (Bangs Laboratories SS05N).

4. Borosilicate cover glass (Fisher 12-544B).

5. Double-sided tape (Scotch 391775).

6. Silicon vacuum grease (Fisher 146355D).

7. Razor cutting tool (single-edged razor or X-ACTO knife).

2.8 Filling Flow Cells for Optical Trapping

1. Myosin (see Subheading 3).

2. Actin (see Subheadings 3.1–3.2)

3. 10 mL KMg25 buffer (25 mM KCl, 60 mM MOPS, pH 7.0, 1 mM EGTA, 1 mM MgCl₂, 1 mM DTT) (see ^{Note 4}).

4. 0.1 mg/mL streptavidin (Sigma S0677-5MG) in water (250 μL stock, stored at -80°C) (see ^{Note 12}).

5. 10 mg/mL bovine serum albumin (1 mL, 10x stock) (BSA, Fisher 50-230-3400) in KMg25 made fresh.

6. 1 mL of 1 mg/mL bovine serum albumin in KMg25 (from the 10x stock).

7. ATP (Sigma A2383-25G) dissolved in water, pH 7.0 (see ^{Note 13}).

8. 250 mg/mL glucose (Sigma G8270) in water (see ^{Note 14}).

9. 50 μL192 U/mL glucose oxidase (Sigma G2133) in KMg25 prepared fresh.

10. Catalase from bovine liver (Sigma C3155).

11. 100x GOC mixture (prepared fresh). Add 2 μL catalase to 20 μL glucose oxidase solutions. Centrifuge at 15,000 x g for 1 minute and save the supernatant.

12. 50 μM TRITC-labeled phalloidin (Sigma P1951) in methanol (see ^{Note 15} ).

13. 100 μL 2 μM TRITC-labeled phalloidin stabilized actin in KMg25. Add 1.1 molar excess TRITC-labeled phalloidin to actin in KMg25. Let sit overnight on ice or 30 minutes at room temperature.

14. 1 M MgCl₂

15. Calmodulin (see ^{Note 16}).

16. 5–10 nM myosin in KMg25 (see ^{Note 17}).

17. Coated beads for trapping (see Subheadings 3.3 to 6)

18. Activation buffer (1 mg/mL BSA, 1 μL 100x glucose, 1 μL GOC, 0.2 nM TRITC-labeled phalloidin stabilized actin, MgATP), (see ^{Notes 16} and ¹⁸).

3. Methods

In the three-bead geometry, an actin filament is stretched between two optically trapped beads and then lowered on to a pedestal bead that is sparsely coated with myosin (Fig. 1). Therefore, before starting, one must: (1) purify actin and myosin, (2) functionalize beads so that they can stick to actin, and (3) assemble and load flow cells with the necessary components. Here, we provide protocols for each of these procedures.

Optical trapping assays require purified actin and myosin. The purification of myosin will depend on the specific myosin construct being used. Myosin can be tissue purified or produced recombinantly using an appropriate eukaryotic expression system (15–19).

3.1 Preparation of Acetone Powder for Actin Purification

While various systems are used to prepare myosin, actin can be prepared in large quantities from rabbit back muscle (20). In the first part of this preparation, muscle is ground and washed with both aqueous and organic solvents to form an “acetone powder”. This powder can be stored for long periods at −20 °C and can be used for a simple actin-extraction preparation (Subheading 3.2 and ^{Note 19}). The procedure for generating acetone powder is the following:

1. If whole muscle tissue is used, cut into 1 in. pieces and grind 2x in a meat grinder. Place on plastic wrap and weigh. A typical adult rabbit yields ~300 g muscle.

2. Extract the myosin for exactly 10 minutes using 3 mL of myosin extracting solution per gram of starting tissue while stirring in the cold room. Longer incubation times prematurely extract the actin.

3. Centrifuge for 15 minutes at 4,000 x g and save the pellet. Discard the myosin-containing supernatant.

4. Add 3 mL of cold distilled water per gram of starting tissue. Stir in the cold room and adjust the pH to 8.2–8.5 with 1 M sodium carbonate.

5. Centrifuge at 4,000 x g at 4°C and save the pellet. Mark the volume of the pellet with a pen directly on the centrifuge tube.

6. Discard the supernatant and repeat steps 4 and 5 up to 4 times. As soon as the pellet begins to swell, continue to the next step, regardless of the number of washes.

7. Add 2–3 volumes of cold acetone to the muscle residue and stir 20 minutes vigorously in a fume hood. Acetone is flammable, so take appropriate precautions.

8. Filter the muscle residue through cheesecloth and save the insoluble material.

9. Repeat steps 7 and 8. At this stage, the insoluble material should be mostly white.

10. Spread the insoluble material on a large piece of filter paper in a fume hood and allow it to dry overnight at room temperature (see ^{Note 20}).

11. The next day, wash the muscle residue twice with enough chloroform to cover the residue. Filter the muscle residue with cheesecloth and save the insoluble material.

12. When dry, very briefly disperse the acetone powder in a blender or Omni Mixer to break up chunks.

13. Store the acetone powder desiccated at −20°C. A typical yield is 10% of the starting muscle weight.

3.2 Preparation of Actin from Acetone Powder

The procedure for purifying actin from acetone powder is the following:

1. Add 20 ml Buffer A per gram of muscle acetone powder and stir on ice for 30 minutes (see ^{Note 21}).

2. Centrifuge for 30 minutes at 4,000 x g at 4° C.

3. Filter through cheesecloth and save the actin-containing supernatant.

4. Resuspend pellets in original volume of Buffer A and repeat steps 2 and 3 .

5. Measure the volume of the actin-containing supernatant. Add KCl to 50 mM and MgCl₂ to 2 mM to polymerize the actin. Cover and stir slowly for 1 hour at room temperature. The solution will become viscous and air bubbles will remain suspended in solution due to the viscosity of the filamentous actin.

6. Add solid KCl to the solution to a final concentration of 800 mM while stirring in the cold room for 30 mins to dissociate contaminating tropomyosin from the actin filaments.

7. Centrifuge the actin for 5 minutes at 4,000 x g to remove remaining acetone powder. Save the actin-containing supernatant.

8. Ultracentrifuge the actin for 2 hours at 142,000 x g to pellet the filamentous actin.

9. Discard the supernatant and gently wash the pellets with 3 mL of Buffer A per gram of starting material. Scrape the pellets off the side of the centrifuge tube with a stainless steel spatula. Homogonize the pellets using a Dounce homogonizer. Dialyze in Buffer A with 3 buffer changes over 2 days to depolymerize the actin filaments.

10. Clarify the depolymerized actin solution by ultracentrifugation at 142,000 x g for 2 hr. Save the supernatant containing actin monomers on ice for up to 1 month (see ^{Note 22}).

11. Measure the concentration of actin by absorbance at 290 nm. The extinction coefficient is 26,600 M⁻¹ cm⁻¹.

3.3 Bead-Actin Linkages: Preparation of N-Ethyl Maleimide (NEM) Modified Myosin Beads

Building a stable and well-defined bead-actin-bead dumbbell is crucial for measuring single-molecule attachment events. The dumbbell consists of two optically-trapped beads and a single actin filament, and the actin filament must remain stably associated with the beads (i.e., it must not dissociate or slip) in the presence of mechanical tension. Several methods have been developed to couple actin filaments to polystyrene beads. Here, we will describe three different reagents for creating actin-bead attachments: N-ethylmaleimide modified myosin, neutravidin-biotin, and a HaloTagged, actin-binding domain from α-actinin (HT-ABD).

N-ethylmaleimide (NEM) modifies reactive sulfhydryl residues in myosin, resulting in a non-enzymatically active motor domain that binds strongly to actin. NEM-myosin bound to beads has been shown to be highly effective for creating stable dumbbells for experiments performed at low ATP concentrations. However, at ATP concentrations > 100 μM, we find that the linkages between the actin and the NEM-myosin slip when the dumbbell is placed under tension. Perform the following steps:

1. Dilute 0.8 mg of rabbit skeletal myosin to ~1 mg/mL in water to a final volume of 0.8 mL. Myosin will start to form filaments once the salt is lowered below 200 mM KCl (21) and the final salt concentration should be less than 25 mM after dilution in water. If the initial stock concentration of myosin is dilute, then dilute 0.8 mg of myosin into a solution than contains less than 25 mM salt, concentrate, and proceed as described below.

2. Centrifuge at 15,000 x g at 4^°C for 30 minutes in a benchtop centrifuge. Discard the supernatant and save the myosin pellet.

3. Resuspend the pellet in 110 μL HSB. The high salt depolymerizes the myosin.

4. Add 12 μL of 50 mM NEM to the myosin. Let incubate 90 minutes at room temperature (see ^{Note 23}).

5. Add 1 mL of water and DTT to 20 mM to quench the reaction and polymerize the myosin.

6. Centrifuge at 15,000 x g at 4°C for 30 minutes using benchtop centrifuge. Discard the supernatant and save the myosin pellet.

7. Resuspend the pellet in 200 μL HSB and add 200 μL glycerol. Add DTT to 10 mM. NEM-modified myosin can be stored up to 1 month at −20°C.

8. Wash 2 μL of polystyrene beads 2 times with 250 μL Milli-Q H₂O to remove surfactants. Centrifuge at 15,000 x g at 4°C for 2 minutes using benchtop centrifuge. Remove the supernatant. If a well-formed pellet is not formed, remove some supernatant and centrifuge again.

9. Resuspend the beads in ~15 μL Milli-Q H₂O in a bath sonicator for 30 s.

10. Add 80 μL of NEM-modified myosin to the beads and let sit for 2 hours at 4°C or overnight on ice.

11. Prepare BSA-coated 1.5 mL microcentrifuge tubes during the incubation above. Prepare two tubes with 1 mL HSB containing 1 mg/mL BSA and two tubes with 1 mL KMg25 containing 1 mg/mL BSA. Let sit at room temperature for at least 30 minutes (see ^{Note 24}).

12. After 2 hours, add 1 mL of HSB to the beads and then centrifuge in the BSA coated tubes at 10,000 x g for 8 minutes using the benchtop centrifuge. Repeat wash.

13. Wash beads 1 time in 1 mL KMg25. Centrifuge in a BSA coated tube at 10,000 x g for 8 minutes using the benchtop centrifuge.

14. Resuspend the pellet in 200 μL KMg25 (without BSA) and transfer to the last BSA-coated tube (after removing the BSA solution from the tube).

15. Store NEM-myosin coated beads at 4°C for up to 10 days.

3.4 Bead-Actin Linkages: Preparation of Neutravidin-Coated Beads

Biotinylated-actin binding to neutravidin- (or streptavidin-) coated beads is an easily implemented, high-affinity linkage that is very stable to applied tension, tolerant of a wide-range of solution conditions, and insensitive to physiological MgATP concentrations. The disadvantages of the linkage are that it requires covalent modification of actin, and that it cannot be used if myosin is adhered to pedestals using a biotin-neutravitin/streptavidin attachment strategy. Biotinylated actin can be prepared by the experimenter or purchased from commercial sources (see ^{Note 8}). Perform the following steps:

1. Add 1 μL of beads to 50 μL of neutravidin and incubate at room temperature overnight.

2. Wash beads 3 times in KMg25 buffer. Centrifuge at 10,000 x g for 8 minutes in the benchtop centrifuge after each wash to pellet the beads.

3. When conducting the experiment, copolymerize 25% biotinylated actin with unlabeled actin. Add 1.1 molar excess TRITC phalloidin to actin in KMg25. Let sit overnight on ice or 30 minutes at room temperature. Use this stock for all trapping experiments (see ^{Note 25}).

3.5 Bead-actin Linkages: Purification of HaloTagged, Actin-Binding Domain of α-Actinin (HT-ABD)

Recently, our lab attached beads to the actin-binding domain of α-actinin fused to a HaloTag (22). This strategy generates an ATP-insensitive bead-to-actin linkage that does not interfere with other biotin-streptavidin linkages in solution. The preparation is more complicated than the methods described above, and it requires bacterial expression and purification of a recombinant protein. The sequence details of the HT-ABD construct containing a hexa-histadine tag for purification is described in detail elsewhere (22). The procedure is the following:

1. Express HT-ABD using the pLT36 plasmid available from the Ostap Lab in Rosetta2(DE3) pLysS cells using standard techniques. Expression is induced with 0.1 mM IPTG after cells reach a density of 0.6 – 0.8 OD and then the cells are grown for 3 hrs. The cell pellet can be stored at -80°C.

2. For each liter of cells, resuspend in 50 mL lysis buffer on ice using a homogenizer.

3. Sonicate cells 5 times for 15 s using a probe-tip sonicator.

4. Centrifuge at 25,000 x g for 30 minutes at 4°C. Save the supernatant.

5. Load the supernatant onto a 2 mL nickel-NTA column at 1 mL/min using a peristaltic pump.

6. Wash the column 5 times with 3 mL of wash buffer.

7. Add 5 mL of elution buffer to the column. Let sit for 30 min.

8. Elute the protein and then repeat step 7.

9. Dialyze the elutant versus FPLC buffer A overnight at 4 °C.

10. Use FPLC with a MonoQ column to purify the protein with a gradient of FPLC buffers A and B.

11. Concentrate protein using centrifugal filter units (Millipore UFC901024), dialyze versus 1 L KMg25 overnight, and then freeze and store in liquid nitrogen in 50 μL aliquots.

3.6 Bead-Actin Linkages: Coupling of HT-ABD to Beads

The HT-ABD construct is linked to beads to create an ATP-insensitive actin-linkage. Amino-functionalized beads are linked via a succinimidyl ester to a chloroalkane group. The chloroalkane covalently links to the HaloTag gene-product fused to the α-actinin actin-binding-domain. Perform the following steps:

1. Use a bath sonicator to disperse 50 μL of amino microspheres in 1 mL of water.

2. Wash beads three times in 1 mL water. Centrifuge at 10,000 x g for 8 minutes in the benchtop centrifuge after each wash to pellet the beads.

3. Resuspend the beads in 200 μL of phosphate buffered saline. Split this volume into 40 μL aliquots and sonicate the beads using a bath sonicator for 20 minutes.

4. Add 2 μL of 100 mM succinimidyl ester ligand to each aliquot. Sonicate beads for 30 minutes in a bath sonicator. Let the beads sit at room temperature for 30 minutes. During the incubation, the succinimidyl ester becomes covalently linked to the amino-groups on the beads.

5. Prepare BSA-coated 1.5 mL Eppendorf tubes while you wait. Prepare two tubes of 1 mL KMg25 + 1 mg/mL BSA. Let sit at room temperature for at least 30 minutes.

6. Combine all of the bead aliquots in a BSA-coated tube and then wash beads 3 times with 1 mL PBS. Centrifuge at 10,000 x g for 8 minutes in the benchtop centrifuge after each wash.

7. Resuspend the beads in 200 μL of PBS. Split this volume into 40 μL aliquots and sonicate the beads using a bath sonicator for 20 minutes with added ice to prevent the temperature from rising.

8. Add 50 μL of HT-ABD to each aliquot. Let sit in a water bath at 37°C for 1 hr.

9. Combine all of the bead aliquots in a BSA-coated tube and then wash beads 3 times with 1 mL PBS. Centrifuge at 10,000 x g for 8 minutes in the benchtop centrifuge after each wash.

10. After the final wash, resuspend the beads in 1 mL of KMg25. Aliquot the beads into 20 μL aliquots, snap freeze in liquid nitrogen, and store in liquid nitrogen or in a −80°C freezer.

3.7 Preparation of Bead-Coated Slides

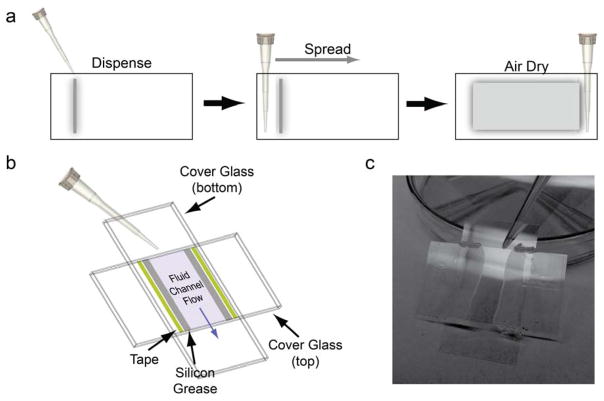
In the three-bead geometry, silica beads are adhered to the surface of the cover glass to act as myosin-binding pedestals. Pedestal beads are coated with nitrocellulose to aid with protein binding to the flow cell surface and to adhere the beads to the cover glass. Here, we describe the assembly of flow cells for the three-bead assay (Fig. 2):

Figure 2.

Preparation of flow chambers for optical trapping. (a) Beads in nitrocellulose are first added to one side of a clean cover glass in a straight line. A pipet tip is then used to spread the beads across the surface of the glass. Bead-coated cover glasses are dried, wet side up, in petri dishes. Pipet tips are used to elevate the cover glass (visible in 2c). (b) Fully assembled chambers are formed using double-stick tape and vacuum grease. (c) Flow chambers are filled by adding liquids to chambers that are raised on petri dishes. Liquid that has flowed through the chamber can be collected using cotton-tipped applicators or filter paper.

1. Suspend silica beads in amyl acetate by vigorous pipetting and vortexing. The beads should be suspended at a concentration of 200 mg/mL to give a 100x solution. This solution can be stored at 4°C (see ^{Note 26}).

2. Prepare a fresh solution of beads in 0.1% nitrocellulose by adding 1 μL of 100x bead solution to 94 μL amyl acetate and 5 μL 2% nitrocellulose. Pipet vigorously.

3. Spread 4 μL of the diluted bead solution across the end of the short axis of a pre-cleaned cover glass in a straight line (Fig. 2a).

4. Use the plastic pipet tip to spread the solution evenly over the surface of the cover glass in one continuous motion (see ^{Note 27}).

5. Let the coated cover glass dry for at least 30 minutes in a covered petri dish. Cover glasses should be stored covered and used within 48 hours of coating (see ^{Note 28}).

6. Take a clean (non-coated) cover glass and place it on a cutting mat with the long axis of the glass parallel to the cutting mat.

7. Place pieces of double stick tape perpendicular to the long axis of the cover glass on both sides of the glass (only on the face up side). Press down the tape with a razor.

8. Use a razor to cut off the extra tape so that it is even with the long axis of the cover glass.

9. Apply vacuum grease on the glass next to the sides of the tape using a syringe. Ensure that the lines of grease are continuous.

10. Place a bead-coated cover glass orthogonal to the taped and greased glass. Ensure that the bead-coated side faces the interior of the chamber (Fig. 2b).

11. Carefully squeeze the two pieces of glass together using a razor blade.

12. Apply a thin layer of vacuum grease at the tape-glass interface so that liquids cannot go under the tape.

13. The flow chamber is now ready to be filled.

3.8 Filling Flow Cells for Optical Trapping

Place the flow cell at a ~30° angle by resting its the top on an elevated surface (we use the petri dish that was used for storing the cover glass after drying, Fig. 2c). Add solutions to the top of the flow cell and ensure that all liquid flows through the flow cell. If necessary, use absorbent filter paper or cotton-tipped applicators to wick the solutions at the bottom of the flow chamber while being careful not to over draw the solution through the chamber. Perform the following steps:

1. If the myosin will be attached to the surface via biotin-streptavidin linkages, add 50 μL of the streptavidin to the flow cell surface and incubate for 5 minutes. If myosin will be adsorbed to the surface directly, add it now and skip steps 4 and 5.

2. Add 50 μL 1 mg/mL BSA. Let incubate 5 minutes. This passivates the surface and prevents nonspecific sticking of actin to the flow cell surface.

3. Repeat step 2.

4. During this incubation, prepare the myosin (with calmodulin if necessary, see ^{Note 16}).

5. Add 50 μL myosin. Let incubate 5 minutes.

6. During this incubation, prepare the activation buffer. Cut the tips off of the pipet tips before dispensing actin to minimize shearing of the filaments.

7. Wash the flow cell with 100 μL KMg25.

8. Add 100 μL activation buffer.

9. Briefly sonicate functionalized beads (<5 seconds) in a bath sonicator. Add ~4 μL to the flow cell to fill ~1/3 of the flow cell (see ^{Note 29}).

10. Seal the flow cell with vacuum grease to prevent evaporation and flow artifacts.

3.9 Performance of the Three-Bead Assay

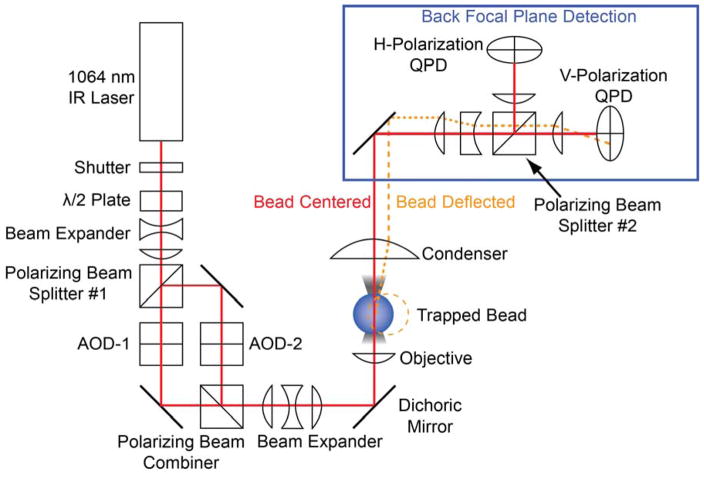
Dumbbells are formed by stringing an actin filament between two optically trapped beads. Therefore, a dual-beam optical trap must be employed (14). Our optical trapping instrument has been described previously (23). In our system, a 1064 nm solid-state laser beam is split into two polarization-separated beams using a half wave plate and a polarizing beam splitter (Fig. 3). These two beams can be independently steered by acoustic optical deflectors (AODs), enabling the manipulation of the beads necessary to form bead-actin-bead dumbbells. The beams are recombined in a prism, expanded, and then relayed through the objective to the sample plane. The detection of the optically-trapped beads occurs at the back-focal plane where movements of the optically-trapped beads relative to the center of the optical trap are detected using polarization separated quadrant photodiodes (QPDs). Back-focal plane detection measures forces (i.e., the relative displacement of the bead from the center of the optical trap) and not the absolute position of the beads in space. To identify single-molecule interactions, perform the following steps:

Figure 3.

Dual-beam optical trap layout. A 1064 nm wavelength laser passes through a half-wave plate and then the beam is separated into two beam paths (i.e., two traps) by a polarizing beam splitter. The two independent beams can then be independently steered by acoustic-optical deflectors (AODs) before being recombined by a polarizing beam combiner. Diffraction-limited optical traps are formed in the focal plane by a water immersion objective. After interacting with the beads, the laser light is collimated by a condenser lens, and the polarized beams are collected separately on two quadrant photodiodes (QPDs). The deflection of the laser beam on the QPDs reports the magnitude of the force on the beads, which can be converted to distance by dividing by the trap stiffness. Figure is adapted from (23).

1. Translate the flow chamber to the region where the beads are located. Optically trap two beads and position the traps approximately 10 μm apart.

2. Translate the flow chamber to move the trapped beads away from the free beads in solution. Visualize the fluorescent actin using epifluorescence. Bring one bead into contact with the end of an actin filament that is at least 10 μm long to attach one bead to the actin.

3. Move the stage so that the actin filament orients towards the second optically-trapped bead by hydrodynamic drag. Move the unattached bead so that it just touches the end of the actin filament and becomes attached.

4. Once the actin filament is stably attached to both beads, shutter the fluorescence excitation to prevent photobleaching of the actin.

5. Move the trapped beads close to the surface of the flow cell (i.e., the surface with the pedestal beads), near the height where data will be collected. Move the trapped beads toward each other so that there is no tension applied to the actin filament.

6. Zero the position of the beams on the quadrant photodiodes.

7. Record 5 s of data at 20 kHz, filtered at 10 kHz to measure the power spectral density (PSD) of the trapped beads (see (24), Fig. 4a). A Lorentzian function can be fit to the PSD to calculate the trap stiffness and the conversion between V and pN:

   $$\mathit{PSD}(f)=\frac{4\gamma k_{B}T}{C^2\left(1+\frac{f^2}{f_c^2}\right)}+y_0,$$

   where γ is the viscous drag coefficient, k_B is Boltzmann’s constant, T is the temperature, C is the calibration constant for pN/V, f is the frequency, f_c is the corner frequency, and y₀ is the noise floor. The viscous drag coefficient for a bead is given by γ = 6πηr where r is the radius of the bead and η is the viscosity of water. The trap stiffness, k, is related to the corner frequency by =2πηf_c .

8. Move one of the optically trapped beads to put tension on the actin filament. This “pretension” is critical to ensure that the bead-actin-bead linkages are stretched and are not more compliant than the myosin-pedestal attachment. A minimum of 2–4 pN of tension should be applied to each bead (see ^{Note 30}).

9. Carefully bring the bead-actin-bead dumbbell over a surface-bound pedestal bead. Use the piezoelectric stage to lower the dumbbell until the force on the beads increases due to the bending of the actin filament over the pedestal bead. Move away from the surface bead using the piezoelectric stage so that the beads are no longer deflected. The actin is now properly positioned to observe myosin-binding events.

10. Scan the surface of the pedestal for myosin binding events, waiting ~30 s at each position before moving. Binding events are identified by a change in the variance of the force on both beads (Fig. 4b). If binding events are not observed, move the actin filament to a new position on the pedestal in ~20 nm increments. Repeat this scanning until actomyosin binding is identified or until the surface of the pedestal has been scanned.

11. To ensure single-molecule conditions, only 1 in 10 beads should give binding interactions. At this density, the likelihood that a given bead has more than one myosin that can interact with the actin is less than 5% (25). Adjust the concentration of myosin to achieve these conditions.

12. Record actomyosin interactions at 2 – 20 kHz depending on the length of the binding interactions and required time resolution. Data should be filtered according to the Nyquist criterion (i.e., filtered at ½ of the sampling rate).

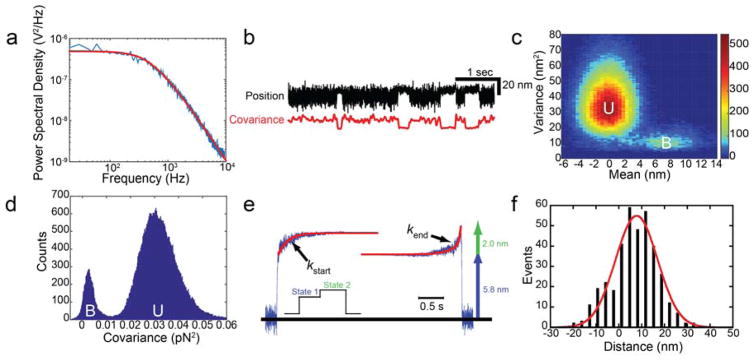
Figure 4.

Detection and measurement of the myosin working stroke. (a) Power spectral density (PSD) of an optically-trapped bead. The red line shows a fit of a Lorentzian function to the data. The corner frequency is 440 Hz and the calibration factor is 18 pN/V. (b, Upper trace) Sample data showing the position of one bead from a bead-actin-bead dumbbell as it interacts with Myo1c on an immobilized pedestal bead. (b, Lower trace) The covariance of the two optically-trapped beads. Binding interactions can clearly be resolved from both the reduction in variance of the black trace and covariance of the beads (red trace) with myosin binding. (c) Mean-variance histogram of Myo1c interactions with actin was generated by calculating the mean and variance of the bead position over a sliding window. The number of events at each point is shown via a color map. There are two resolvable distributions, one with a peak of ~0 nm displacement and high variance corresponding to an unbound (U) state and a second with a peak ~8 nm with a lower variance corresponding to the actin-bound (B) state. (d) Histogram of covariance values for interactions between actin and Myo1c calculated over the entire data trace. Two peaks are clearly resolved, one with high covariance corresponding to the unbound (U) state and one with low covariance corresponding to the bound (B) state. The minimum value between the two peaks is used as a covariance threshold in selection of events. (e) Ensemble averages of the Myo1c working stroke were generated as described in Subheading 3.12. The ensemble averages reveal that the Myo1c working stroke is composed of two substeps. The rates of the increase in position in the ensemble averages can be used to measure the lifetimes of state 1 and state 2. The total working stroke measured via ensemble averaging agrees well with the value measured via mean-variance analysis. Figure is adapted from (22). (f) Histogram of individual working stroke displacements for Myo1c selected by covariance thresholding. The data are well fit by a single Gaussian function centered at 7.8 nm, consistent with the measured values from the ensemble averages and mean-variance analysis. Figure is adapted from (22)

3.10 Identification of Binding Interactions

Several methods have been developed to detect actomyosin-binding interactions (Fig. 4). Most of these methods rely on changes in the Brownian motion of the optically-trapped beads when myosin binds to actin (e.g., (8, 23, 26–28)). The variance in the position of the beads is reduced when myosin binds to actin. The variance can be calculated over a sliding time window and a variance threshold can be chosen to discriminate bound and unbound states (29, 30). Alternatively, a sinusoidal waveform can be actively applied to one of the optically-trapped beads and the passive response of the second bead can be measured (31, 32). This methodology increases the temporal resolution by magnifying the difference in the variance between the bound and unbound states.

For our data analysis, we prefer using a covariance threshold since it utilizes information from both optically trapped beads (27, 33), which requires the simultaneous detection of forces on both beads (i.e., two QPDs are necessary; Fig. 3). In the absence of myosin binding, the two optically trapped beads are mechanically coupled through the actin filament. When myosin binds to actin, the coupling between the beads is reduced. The covariance, a measurement of bead motion coupling, is high in the absence of myosin binding and low when myosin binds. The covariance is calculated over a sliding time window (Fig. 4b) and a histogram of covariance values for the data trace can be calculated (Fig. 4d). The histogram should show two distributions with a peak of lower covariance corresponding to the actin-myosin bound state and a peak of higher covariance corresponding to the unbound state. The separation between the peaks will depend on the pretension of the actin filament and the stiffness of the myosin. These peaks can be used to select bound and unbound states.

To achieve good separation between the covariance distributions, there must be a measurable change in the covariance during a binding interaction over the averaging window. As such, increasing the pretension on the bead-actin-bead dumbbell will increase the separation between the peaks. Moreover, the size of the sliding window used to calculate the covariance can be increased. While increasing the size of the window will increase the separation between the covariance distributions, it will also make it impossible to detect binding events with durations smaller than the size of the window. Therefore, when analyzing a data set, there is a tradeoff between better covariance peak separation and temporal resolution.

The selection of binding events is based on the distribution of the covariances. One could define a binding event as one in which the covariance drops below a given threshold for at a user-specified amount of time (see ^{Note 31}). With good separation between the bound and unbound covariance peaks, it is useful to select the minimum value between the two peaks as the covariance threshold. These selection criteria will maximize the temporal resolution, but it will result in the identification of more “false positives”. Alternatively, one could require a binding event to start when the covariance value transitions from the value of the unbound peak to the value of the bound peak and then end once the covariance transitions from the value of the bound peak to the value of the unbound peak. This methodology limits the number of detected “false positive” events, but it also reduces the temporal resolution.

3.11 Analysis of the Actomyosin Lifetime

Once binding events are identified, it is possible to determine the lifetime of the bound states from the distribution of individual attachment durations. Several methods have been developed to determine actin-attachment lifetimes, but we prefer utilizing maximum likelihood estimation (MLE) of the data (34). MLE determines the optimum parameters of a model-dependent probability density function (PDF) from the data without the need for binning. This technique is appropriate for the analysis of single-molecule data for several reasons. Most importantly, single-molecule data are often not normally distributed, which is what is required in traditional least-squares fitting. Additionally, in experiments where the duration of short-lived binding interactions is similar to the dead time of the instrument, techniques such as averaging and fitting functions to histograms will lead to an over-estimate of the attachment lifetime. MLE does not have these limitations.

The interpretation of the data will depend on the number of processes observed. Statistical methods should be used when fitting models of increasing complexity to the data to justify model selection. When using MLE, the ratio of the log-likelihoods can be compared to a chi-squared distribution (35).

3.12 Measurement of the Myosin Working-Stroke Displacement

The displacement of the bead-actin-bead dumbbell during the myosin working stroke is often of the same magnitude as the variance in bead position due to thermally-driven motions of the dumbbell. Therefore, determining the magnitude of the myosin-driven displacement is not trivial. However, several methods have been utilized to measure this displacement, and some of these techniques have been successful in detecting and quantifying working-stroke sub-steps as has been seen in some myosin isoforms (10, 22, 32, 33, 36, 37). Here, we describe three of these techniques.

1. Mean-variance analysis (26). When myosin binds to actin and undergoes its working stroke, it causes a change in both the mean (due to the working stroke displacement) and variance (due to actin attachment) of the force/position of the optically trapped beads. To detect these changes, a sliding time window is used to calculate the mean and variance of the bead position/force over the entire data trace. Two distinct populations appear, one with no displacement and a higher variance corresponding to the unbound state and one with a finite displacement and a lower variance corresponding to the bound state (Fig. 4). By changing the width of the sliding time-window, the mean attachment duration can be calculated. This method is straightforward, since it does not require the investigator to resolve individual interactions. However, the method does not allow determination of the distribution of displacements from individual interactions.

2. Quantification of displacements of individual binding interactions. After selecting individual binding interactions, the average position of the trapped beads immediately before and during actomyosin interactions (as determined in Subheading 3.11) can be calculated to generate a histogram of displacements (Fig. 4f). The displacement distribution can be fit to an appropriate model, which in most published studies has been a Gaussian function. Because the average displacement is reported, substeps are not considered, which can result incorrect measurements of the final displacement. For example, if there is a substep with a large displacement within the last milliseconds of a 1s interaction, the overall displacement will be substantially underestimated due to averaging. Finally, bias in the position at which myosin binds trapped actin filaments may alter the observed working-stroke displacement (38).

3. Post-synchronization of individual interactions (i.e., ensemble averaging) (22, 32, 33, 36, 37, 39–41). Post-synchronized ensembles of single molecule events are created by temporally lining up many interactions at their start or end points and then averaging the data (Fig. 4e). The averaged traces reveal the dynamics of the molecules leading up to and following the synchronized transition, allowing information hidden in the noisy single trajectories to be analyzed (39). Post-synchronization is well suited for examining substep displacements and the kinetics of the working stroke, as shown in pioneering experiments (32, 37). A myosin with a two-substep working stroke will show a displacement increase after the initial attachment in the averages synchronized at myosin attachment, followed by an exponential increase in force that reports the lifetime of the first state, lower displacement state (State 1, Fig 4e). For a two-step displacement, ensemble averages created by synchronizing interactions at their endpoints will show an exponential increase in displacement to the level of the final displacement, with a lifetime equal to the state populated before detachment (State 2, Fig. 4e). This technique is very powerful since it allows one to examine both the kinetics and mechanics of the myosin working stroke. However, correctly identifying the starting and ending points of interactions is crucial for the averages to be useful. The reader is directed to kinetic tools that have been developed to analyze post-synchronized traces (39).

3.13 Measurement of Myosin’s Force-Dependent Properties

Myosins adjust their motile properties in response to mechanical forces on the lever arm, and several optical trapping techniques using the three-bead geometry have been used to measure the effects of these loads on actomyosin attachment durations. Some techniques use active force- or position- feedback loops to apply loads to myosin by steering the trapping beam using an acousto-optic deflector (AOD; Fig. 3). Other techniques apply forces without active feedback. Selected examples of these techniques are discussed below.

Active force feedback upon engagement of actomyosin relies on detecting a change in trap motion to identify binding events (e.g., variance) (8). Once a detection threshold is crossed for a given amount of time, the feedback is engaged. Active feedback loops can work by increasing the trap stiffness or moving the trap once a binding interaction is identified. Drawbacks of these techniques are that the feedback loops are necessarily slower since calculations must be done before engaging the feedback loop, and one must account for nonlinear series compliances in the bead-actin attachments. Techniques to speed up the feedback loops have been implemented where the bead-actin-bead dumbbell is oscillated, increasing the ability to distinguish binding interactions and activate the feedback loop (37, 42).

The isometric optical clamp is an active feedback loop developed by the Goldman and Shuman Laboratories (23, 43). This technique uses an active feedback loop in which one of the optically trapped beads (motor bead) is actively moved to maintain the other optically trapped bead (transducer bead) at a constant position. This is achieved using an AOD to steer the motor bead. This technique has the advantage that the feedback is always engaged and thus there is not a delay time beyond the time-constant of the feedback loop itself. Also, one need not correct for system compliances since the position of the transducer bead is held constant. The procedure for collecting data using the isometric optical clamp is similar to the procedure used to collect data in the absence of feedback. Before an experiment, the time constant of the feedback loop is adjusted to the desired value by forming a bead-actin-bead dumbbell, applying a square wave to the transducer bead, and then watching the time response of the motor bead. After the feedback loop time constant is set and a single active myosin on the surface is identified, the feedback loop is engaged and data are collected. Actin filaments have polarity and thus the feedback loop direction might need to be reversed to ensure that the applied forces oppose the myosin’s working stroke. Binding interactions are identified post acquisition using the covariance thresholding described earlier, and the attachment durations and the force on the myosin (exerted by the motor bead) can be measured.

The Spudich Laboratory implemented a novel method for measuring the force dependence of myosin interactions in which the stage is oscillated during an actomyosin attachment, resulting in the force of the stage oscillations being transferred to the myosin and the optically-trapped beads (44). This technique, dubbed harmonic force spectroscopy, has the advantage that the force is applied to the myosin rapidly, no feedback loops are required, and forces are not applied by expensive and difficult-to-align optical components. This method is well-suited for single force-dependent transitions that limit detachment over the range of all probed forces. However, this technique has the limitation that analysis of complex force-dependent processes will not be straightforward. For example this technique would not have allowed for the determination of the force-dependent mechanism of Myo1c or Myo6 (22, 45).

An ultra-fast feedback system was developed by the Capitanio Laboratory to enable the detection of binding events with sub-millisecond resolution (28). In this setup, force is applied to one of the optically-trapped beads, causing it to move at a constant velocity when no myosin is bound. When myosin binds, the force that was applied to the first bead is rapidly transferred to the myosin. By observing changes in the velocity of the beads, one can determine, with sub-millisecond resolution, when binding occurs. This technique gives excellent temporal resolution (28), but it is technically challenging to implement.

3.14 Analysis of Force-Dependent Data

To analyze the force-dependence of actomyosin detachment and attachment durations are measured over a range of forces. According to Arrhenius transition theory, force affects the rate of a transition by (46):

$$k(F)=k_0·e^{-\frac{\mathit{F}·\mathit{d}}{k_B·T}},$$ Eq. 1

where k₀ is the rate in the absence of force, F is the force, k_B is Boltzmann’s constant, T is the temperature, and d is the distance to the force-dependent transition state, also known as the distance parameter. Note that k(F) changes exponentially with the vector quantity d (i.e., it depends on the direction of the applied force). A larger d is indicative of a more force-sensitive transition. The probability density function is given by:

$$\mathit{PDF}=k(F)\ast e^{-k(F)\ast t}.$$ Eq. 2

As a consequence, if a single transition limits actomyosin dissociation at a given force, the distribution of attachment durations will be exponentially distributed at each force.

For data best fit by a simple exponential function, the reciprocal value of the mean attachment duration will equal the characteristic rate. Therefore, one method of analyzing the data is to plot the mean detachment rate at each force as a function of force and then fit Eq. 1 to the data using least-squares fitting to obtain the force dependence of the detachment rate. If the data are not exponentially distributed, this methodology will not work since the reciprocal value of the mean attachment duration will not equal the characteristic rate. There are two important situations where the data will not be exponentially distributed.

1. As described earlier, there will be a minimum observable attachment duration due to the instrumental dead time and as such, some short-lived binding events will be missed. Missing short-lived binding events will make the reciprocal value of the mean attachment duration appear slower than the true rate.

2. While Eq. 1 describes how force will affect the rate of a given transition, a single transition may not limit actomyosin dissociation, leading to a more complicated behavior. For example, in Myo1c and Myo1b, one transition limits detachment at low forces and a different transition limits detachment at higher forces (22, 33). There will exist a set of forces where the rates of these transitions are similar and the net detachment rate will not be exponentially distributed, skewing this analysis.

As described earlier (Subheading 3.11), these caveats mean that simple least-squares fitting of the mean values will not give the correct answer and MLE must be used (34, 47). To determine the errors in the MLE fitting and the sensitivity of the data to outliers, bootstrapping simulations can be used. In this method, a data set with N points is randomly resampled to generate a new data set with N points and then MLE is used to determine the values of the fitting parameters. By conducting a large number of simulations, it is possible to determine the uncertainty in each of the fit parameters.

3.15 Measurement of Myosin’s Stiffness

The abilities of myosin to generate and sense forces depend on the stiffness of the myosin. Several methodologies have been developed to measure myosin’s stiffness using the three-bead geometry. Here, we discuss selected methods. In one technique, a sinusoidal oscillation is applied to one bead and the passive response of the second optically-trapped bead is recorded (31). In the absence of myosin binding, the passive bead will follow the actively driven bead. When myosin binds to actin, the myosin acts as an additional elastic element in the system, damping the response of the passive bead to the active oscillations. By measuring the force on the actively driven bead and the position response of the passive bead, it is possible to measure the stiffness of the myosin. A method developed by the Sleep Laboratory uses a slow triangular wave applied to both optically-trapped beads (48). When the myosin binds to the actin, the myosin is stretched and a force-extension curve can be generated. A similar technique was applied to study muscle myosin-II filaments and the actin extension was corrected by measuring the position of a quantum dot covalently attached to the actin (49). In another method, passive response of the beads to Brownian motion in the presence and absence of myosin is measured (27, 48). As described earlier, when myosin binds to actin, the covariance between the two optically-trapped beads is reduced in proportion to the stiffness of the myosin. The correlation coefficient or the cross power spectral densities can be calculated to give the stiffness of the myosin.