Abstract
Discovering new energy materials is a key step toward satisfying the needs for next-generation energy conversion and storage devices. Among the various types of oxides, Ruddlesden–Popper (RP) oxides (A2BO4) are promising candidates for electrochemical energy devices, such as solid oxide fuel cells, owing to their attractive physicochemical properties, including the anisotropic nature of oxygen migration and controllable stoichiometry from oxygen excess to oxygen deficiency. Thus, understanding and controlling the kinetics of oxygen transport are essential for designing optimized materials to use in electrochemical energy devices. In this review, we first discuss the basic mechanisms of oxygen migration in RP oxides depending on oxygen nonstoichiometry. We then focus on the effect of changes in the defect concentration, crystallographic orientation, and strain on the oxygen migration in RP oxides. We also briefly review their thermal and chemical stability. Finally, we conclude with a perspective on potential research directions for future investigation to facilitate controlling oxygen ion migration in RP oxides.
Keywords: ruddlesden-popper oxides, perovskite oxides, layered perovskite oxides, mixed ionic and electronic conductors, oxygen ion migration, oxygen diffusion, anisotropy, solid oxide fuel cells, thermal expansion coefficients, chemical expansion
1. Introduction
To meet the increasing demand for electrochemical energy conversion and storage devices, including solid oxide fuel cells (SOFCs) and oxygen membranes, the development of new oxide materials is a critical element. So far, substantial efforts have been focused on developing ABO3 perovskite oxides, which exhibit fascinating physicochemical properties—i.e., high electronic and ionic conductivities and high catalytic activities [1,2,3]—for use in energy applications. Mixed ionic and electronic conductors (MIECs), such as La1−xSrxCoO3−δ (LSC113) [4,5,6,7,8,9,10,11,12] and La1−xSrxCo1−yFeyO3−δ (LSCF113) [13,14,15,16,17,18,19,20,21,22,23,24,25,26], that show high degrees of oxygen deficiency are commonly used to promote oxygen diffusivity and surface exchange kinetics at intermediate temperatures. However, these materials suffer from some serious inherent limitations, including poor thermal and chemical stability [27,28,29,30] and long-term instability [22,31,32,33,34].
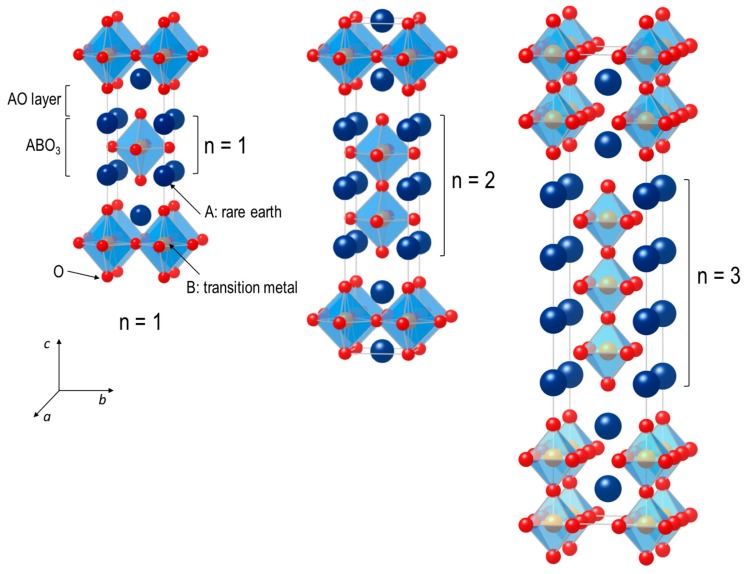
Ruddlesden–Popper (RP) oxides have shown very attractive and versatile physical properties such as superconductivity [35,36,37,38], magnetoresistance [39,40,41], and mixed ionic and electronic conductivity [42,43,44,45,46], which are beneficial for many energy and electronic devices. The general formula of RP phases can be written as An+1BnO3n+1 (n ≥ 1) [47]. The RP phases comprise n consecutive perovskite layers (ABO3) alternating with rock-salt layers (AO) along the crystallographic c-axis direction. Their formula can be represented by (AO)·(ABO3)n, where n represents the number of connected layers of vertex-sharing BO6 octahedra [48]. Figure 1 presents the ideal tetragonal unit-cells for n = 1, 2, and 3, which correspond to the stoichiometric compounds with the same space group, I4/mmm. For n > 1, the additional ABO3 blocks are introduced between two AO rock-salt layers. Commonly, these materials consist of rare or alkaline earth A-site cations with transition metals on the B site, forming an extensive series of compositions. The A-site cations have a coordination number of 9, locating at the boundary between the two types of layers, while the B-site cations are positioned at the center of an octahedron formed by six oxygen anions. Similar to ABO3 perovskite oxides, the RP phases show a rather high structural flexibility in the oxygen stoichiometry.
Figure 1.
Schematic crystal structures of n = 1, 2 and 3 members of Ruddlesden–Popper type An+1BnO3n+1 are shown. The denotation of n represents the number of stacked octahedral layers separated by a rock salt AO layer.
Of particular interest in the case of electrochemical energy applications such as SOFCs is the A2BO4 system (n = 1) because their oxygen surface exchange kinetics and oxygen diffusion are higher than those in ABO3 oxides [42,49,50,51,52,53]. Owing to the adjustment of two different structural units, i.e., ABO3 and AO, within the lattice, the A2BO4 structure exhibits strong anisotropic features. As described above, the B-site cations are coordinated by six oxygen anions, but the B-O bond lengths are different because of the Jahn–Teller effect caused by the valence state of the B-site cations [54]. This results in two types of oxygen species in the BO6 octahedra, which are referred to as “apical” and “equatorial” oxygen. In the A2BO4 system, interstitial sites are located in the AO layer, in which A2BO4 oxides can accommodate an excess oxygen as an interstitial oxygen defect. Oxygen vacancies can also be formed by appropriate doping in the system. Consequently, the oxygen transport properties of A2BO4 oxides can be strongly influenced by either oxygen interstitials or oxygen vacancies. In addition, different types of oxygen defects affect the oxidation states of transition metal cations of A2BO4 oxides as a result of changes in oxygen stoichiometry, and they thus lead to different lattice expansions.
A fundamental understanding of oxygen migration in A2BO4 oxides is therefore necessary to optimize superior oxygen ion transport for the development of applications in electrochemical energy devices, chemical sensors, and oxygen permeation membranes. This review aims to briefly review oxygen migration mechanisms depending on oxygen stoichiometry in the first member of the RP series (n = 1) and provide a rational idea of how to control oxygen ion migration in A2BO4 oxides. We first discuss the mechanisms of oxygen ion migration in oxygen-excess and oxygen-deficient A2BO4 oxides, providing an overview of reported experimental and theoretical results. We then cover in detail the effects of three factors—cation substitution, crystallographic orientation, and strain—on oxygen migration in A2BO4 oxides. The thermochemical stability of A2BO4 oxides is also briefly reviewed in a separate section. Finally, we provide a perspective on open questions on controlling oxygen ion migration in A2BO4 oxides and suggest some potential research directions to facilitate oxygen ion migration.
2. Oxygen Migration Mechanisms in Ruddlesden–Popper Oxides
In contrast to ABO3 oxides, which are generally known as oxygen-deficient perovskites because oxygen vacancies are their dominant anion defect, RP oxides can be both oxygen-deficient and oxygen-excess, depending upon their majority oxygen defects. In the case of oxygen-deficient RP oxides, oxygen nonstoichiometry (δ) arises from oxygen vacancies, whereas oxygen interstitials result in oxygen hyperstoichiometric RP oxides. Therefore, oxygen ion migration in RP oxides can occur via mechanisms associated with either oxygen vacancies or oxygen interstitials. The defect processes in RP oxides are dominated by anion Frenkel disorder [51,55,56] and can be expressed as
| OOx ⇔ VO¨ + Oi”. | (1) |
The oxygen diffusion coefficient DO can be expressed in terms of the defect concentrations and their diffusivities as [57]
| DO = DV[VO¨] + Di[Oi”] | (2) |
where DV and Di are the vacancy and interstitial diffusion coefficients, respectively. [VO¨] and [Oi”] represent the concentrations of oxygen vacancies and oxygen interstitials, respectively.
2.1. Oxygen-Excess RP Oxides
Many studies have shown oxygen ion transport properties in oxygen-excess RP oxides, mostly focusing on La2NiO4+δ (LNO214), which can accommodate excess oxygen by the incorporation of oxygen interstitials in the lattice [50,58,59,60,61]. Owing to the structural feature of RP oxides made of a stacking sequence of A2O2 and BO2 layers, LNO214 is a polar material and has an electric field gradient between the La2O22+ and NiO22− layers. Accordingly, the Coulomb potential leads to an expected large anisotropy in the oxygen transport by preventing the interstitial O2− ions from leaving the La2O22+ layer [50,62]. It is well known that oxygen diffusion along the a-b planes is much faster than in the c-direction [49,50,63,64,65]. Using atomistic simulation calculations, Minervini et al. [55] determined that the intrinsic disorder for LNO214 is anion Frenkel disorder with the oxygen vacancy residing on the equatorial site. According to the authors, oxygen ion migration in LNO214 occurs via an interstitialcy (or push–pull) mechanism, whereby at an apical site, the oxygen vacancy formed by the movement of apical oxygen into the interstitial sites in the rock salt layer is filled by a nearby interstitial oxygen. Consequently, the creation of Frenkel anionic defects, which are oxygen interstitials and oxygen vacancies, leads to additional oxygen content. Later calculations by Cleave et al. [66] showed that the most energetically favorable mechanism for oxygen migration in LNO214 is the vacancy mechanism in the a-b plane, where the equatorial oxygen vacancies are prone to migrate in the equatorial plane. Frayret et al. [67] also demonstrated an interstitial diffusion mechanism in LNO214 using density functional theory (DFT). The authors proposed that charge transfer phenomena play a minor role in the oxygen migration process, reporting that equatorial oxygen vacancies are energetically more favorable than apical oxygen vacancies to form Frenkel-type defects. More recently, molecular dynamics (MD) studies [63] showed that an interstitialcy mechanism—involving an interstitial oxygen, a neighboring apical oxygen, and an appropriate equatorial oxygen site—plays an important role in oxygen transport in LNO214.
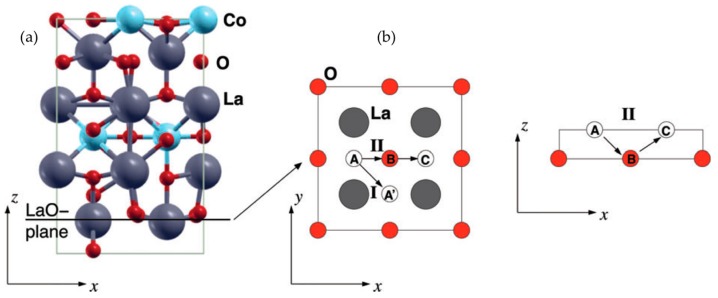
Similarly, MD simulations by Parfitt et al. [68] of Pr2NiO4+δ (PNO214) showed that oxygen ion migration is also highly anisotropic, occurring via an interstitialcy mechanism. The authors reported that the degree of excess oxygen strongly influences the activation energy for oxygen migration in PNO214. Similar to the case for LNO214, calculations for oxygen migration in La2CuO4+δ (LCuO214) by Allan et al. [69] showed that oxygen vacancies at the equatorial site are more favorable for migration in the equatorial plane, compared with interstitial oxygen. According to the calculated results from Kushima et al. [70], oxygen migrates dominantly via an interstitialcy mechanism in La2CoO4+δ (LCO214) (Figure 2). Kushima et al. performed both DFT and MD simulations, demonstrating that although the predicted activation energies for oxygen migration in DFT and MD are different from each other, oxygen migration via an interstitialcy migration mechanism has a significantly lower activation energy than migration via direct interstitial site exchange. The oxygen migration energies for oxygen-excess RP oxides are summarized in Table 1.
Figure 2.
(a) Relaxed configuration of the La2CoO4+δ model. Circled region represents an interstitial oxygen atom; and (b) migration paths in simulation. (I) indicates an interstitial migration mechanism where an oxygen interstitial atom at the A site directly hops to the adjacent interstitial site A’; (II) shows an interstitialcy migration mechanism. An oxygen interstitial atom at the A site kicks the oxygen atom at the B site out of the LaO plane, sending it to the next interstitial site C, and placing itself on the B site on the LaO plane. Reprinted from Ref. [70] with permission of The Royal Society of Chemistry
Table 1.
Oxygen ion migration energies in the a-b plane of various A2BO4+δ.
| Material | Ea/eV | Methodology | Mechanism | Ref. |
|---|---|---|---|---|
| La2NiO4+δ | 0.29 | MD | Interstitialcy mechanism | [55] |
| La2NiO4+δ | 0.55 | Static atomistic simulation | Vacancy mechanism | [66] |
| La2NiO4+δ | 1.2 | DFT | Interstitial mechanism | [67] |
| La2NiO4+δ | 0.51 | MD | Interstitialcy mechanism | [63] |
| Pr2NiO4+δ | 0.49–0.64 | MD | Interstitialcy mechanism | [68] |
| La2CoO4+δ | 0.31 | MD | Interstitialcy mechanism | [70] |
| La2CoO4+δ | 0.73–0.80 | DFT | Interstitialcy mechanism | [70] |
| La2CoO4+δ | 1.27–1.39 | DFT | Interstitial mechanism | [70] |
2.2. Oxygen-Deficient RP Oxides
The addition of acceptors to oxygen-excess RP oxides can drive the stoichiometry of RP oxides into oxygen deficiency [46,71,72]. For example, the substitution of an aliovalent cation such as Sr2+ (1.31 Å) for a cation such as La3+ (1.22 Å) on the A site leads to an increase of oxygen deficiency in RP oxides. Table 2 shows a summary of oxygen stoichiometry as a function of the strontium (Sr) content in RP oxides. Opila et al. [56] proposed the defect model for Sr-doped cuprates (La2−xSrxCuO4−δ), showing anisotropic oxygen transport properties. Owing to the formation of SrLa’ defects, charge compensation can occur by either electron holes or oxygen vacancies.
| 2SrLa’ + VO¨ = {(SrLa’)2VO¨}x. | (3) |
.
Table 2.
Oxygen stoichiometry in La2−xSrxMO4±δ (M = Cu, Ni, and Co) with various Sr contents. Oxygen nonstoichiometry of each of the samples was ascertained under reduction in air between 850 and 950 °C.
Then, the overall electroneutrality can be given by
| p + 2[VO¨] = n + 2[Oi”] + [SrLa’]. | (4) |
Opila et al. [56] suggested that a vacancy mechanism is responsible for oxygen migration in La2−xSrxCuO4−δ (LSCuO214) at low Sr contents (x < 0.07). MD simulations by Mazo et al. [73] of LSCuO214 (Sr = 0.37) demonstrated that a strong anisotropy of the crystal structure can lead to different oxygen transport properties in (La,Sr)O blocks and CuO2 layers, the latter being more favorable for oxygen transport via a conventional vacancy migration mechanism. More recently, Savvin et al. [74] also investigated the oxygen diffusion processes in LSCuO214 (Sr = 0.15 and 1.0) via MD simulations, demonstrating that oxygen migration occurs mainly in CuO2 layers as a result of a hopping mechanism. The authors proposed that, by jumping to the nearest position or along the CuO2 layers, oxygen can migrate in LSCuO214. In addition, they also pointed out that although the migration energy of oxygen vacancies at apical sites is much lower than that at the equatorial sites, oxygen migration along the c-direction can occur only with great difficulty, as vacancies at the apical sites must pass through the equatorial plane, resulting in an increase in the activation energy.
The oxide ion migration mechanisms of La2−xSrxCoO4±δ (LSCO214) for high Sr levels (x = 0.8 and 1.2) were reported by Tealdi et al. [79] via MD simulations (Figure 3). They proposed that oxygen diffusion in oxygen-deficient La0.8Sr1.2CoO3.9 is mainly attributable to the migration of oxygen vacancies within the perovskite layer, whereas an interstitialcy mechanism is dominant for interstitial oxygen transport in oxygen-excess La1.2Sr0.8CoO4.1. They further suggested that it is also possible for oxygen vacancies to migrate through long-range paths between adjacent layers. Schroeder et al. [45] investigated the oxygen transport property of polycrystalline La2−xSrxNiO4+δ (LSNO214, x = 0.5) samples by experimental results for the oxygen permeation flux. The authors claimed that oxygen migration in LSNO214 with Sr = 0.5 is mediated mainly by interstitial oxygens, occurring parallel to the layers of the structure, although the contribution of vacancy migration to the oxygen permeation process cannot be ruled out.
Figure 3.
(a) 3D representation of oxygen vacancy migration between equatorial and apical positions within a CoO6 octahedron (pink and red), between equatorial positions (green) and between apical positions belonging to separate layers (blue) in La10.8Sr1.2CoO3.9; (b) 3D representation of oxygen interstitial migration in La1.2Sr0.8CoO4.1. Each oxygen involved in the migration event is represented by a different color. Spheres of the same color indicate the positions occupied by a specific atom over the simulation time. Reprinted from Ref. [79] with permission of The Royal Society of Chemistry.
3. Control of Oxygen Migration in RP Oxides
As discussed earlier, oxygen migration in RP oxides is strongly dependent on the defect concentrations, which can change the degree of oxygen stoichiometry. In general, substitutions on the A or B sites of RP oxides are known to affect the oxygen stoichiometry, leading to a change in the oxygen transport properties [64]. In addition, the anisotropic nature of oxygen migration in RP oxides can cause two different behaviors in oxygen transport [50]. Furthermore, recent computational and experimental studies have shown that epitaxial strain in a thin film, induced by lattice mismatch, can alter oxygen migration in binary oxides [80,81,82,83,84] and ABO3 perovskite oxides [7,85,86]. In the following subsections, we focus on how these three factors, i.e., cation substitution, crystallographic orientation, and strain, can influence oxygen migration in RP oxides.
3.1. Influence of Cation Substitutions on Oxygen Migration
Cation substitutions have been widely used to facilitate the oxygen ion diffusion and oxygen surface exchange kinetics in ABO3 perovskites such as lanthanum (La)-based oxides, in which a hopping mechanism along the BO6 octahedron edge governs the oxygen vacancy migration [87,88]. It is well known that substituting Sr for La on the A-site of LSC113 results in an increase in oxygen vacancies and thus enhances the oxide ion diffusivity [10,89,90,91,92,93]. In addition, doping with different-size cations in ABO3 perovskites can also facilitate oxygen migration owing to a reduction in the ion migration energy [84]. The effect of Sr substitution on the activation energy for oxygen diffusion in LSC113, reviewed by Berenov et al. [5], is that the activation energy for oxygen diffusion decreases with increasing Sr content owing to the reduced vacancy formation energy. Cater et al. [15] compared the oxygen diffusivity between Sr-doped cobaltites and Sr-doped manganites, concluding that B-site cations with a lower valence state increase in oxygen diffusivity. In the case of RP oxides, however, the effect of cation substitutions on oxygen migration is poorly understood, compared with the case of ABO3 perovskites. In this section, we review oxygen diffusion depending upon either A-site or B-site substitution in the most widely studied RP nickelates, cuprates, and cobaltites.
3.1.1. Effect of Substitutions on the A-Site
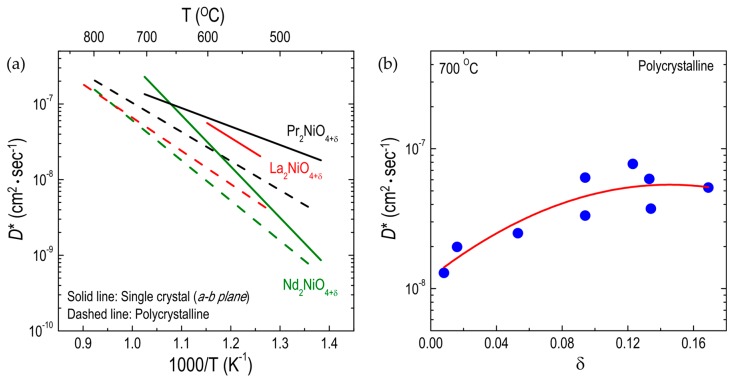
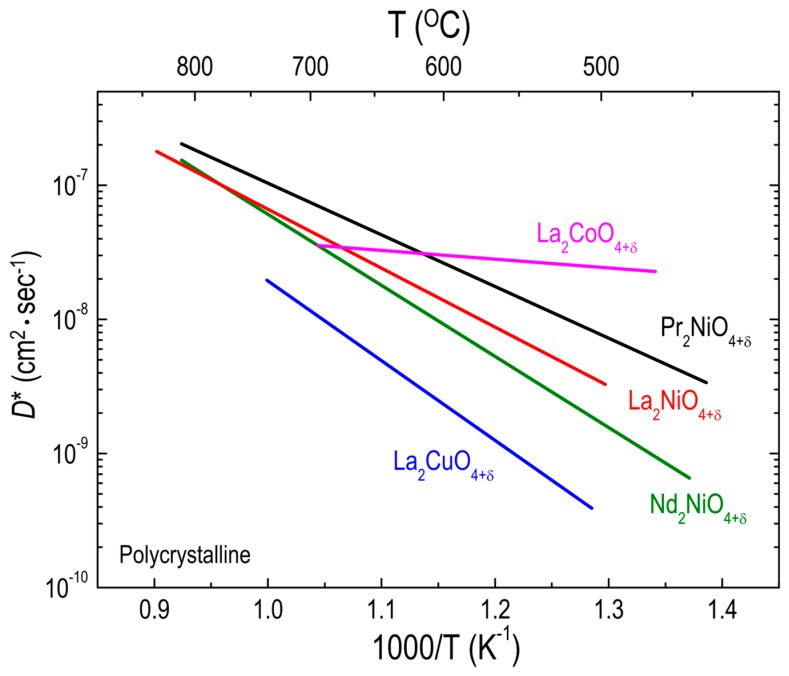
LNO214 is one of the most intensively studied RP oxides in terms of oxygen transport properties [51,61,72,94,95]. Using the isotope exchange depth profile method, the oxygen self-diffusion coefficient (D*) values of polycrystalline LNO214 samples were found to be higher than those of LSCF113 and similar to the diffusivity in LSC113 [53,96]. Later, Boehm et al. [51] reported a similar oxygen diffusivity for LNO214, showing the oxygen diffusivity of PNO214 and Nd2NiO4+δ (NNO214) polycrystalline samples as well (Figure 4a). In this study, the diffusivity of PNO214 was found to be the highest, with the lowest activation energy among the three RP nickelates in the temperature range of 550 to 850 °C. Recently, the D* values for the same RP nickelates were examined using single crystals [49,50,97] and showed a similar trend to that reported for polycrystalline samples (Figure 4a). The D* values along the a-b plane for PNO214 single crystals were found to be higher, with a significantly lower activation energy (0.67 eV), compared with NNO214 single crystals at low temperatures [49]. In the case of LNO214 single crystals, the D* values along the a-b plane and the activation energy (0.88 eV) for the diffusion were found to be comparable to the data observed in polycrystalline LNO214 [50]. The diffusivity measurements in the a-b plane for LNO214 single crystals were repeated by Burriel et al. [97]; their findings agreed well with the previous data [50]. They also demonstrated that the D* values along the a-b plane for LNO214 single crystals are comparable to those for PNO214 single crystals. Considering the oxygen nonstoichiometry (δ) determined in air at room temperature in PNO214 (δ = 0.21 [51]), LNO214 (δ = 0.13 [51]), and NNO214 (δ = 0.22 [51]), it was proposed that the larger δ value resulted in higher oxygen migration among the three RP nickelates, which have a sharp maximum D* value at a certain δ value (≈0.125) as a result of increased defect interactions [49,51] as shown in Figure 4b. However, this cannot explain the difference in oxygen transport in PNO214 compared with NNO214 despite the similar δ. Recently, Bassat et al. [49] suggested that an interplay between lattice dynamics and structural instabilities in RP structures may also lead to a difference in the oxygen migration between PNO214, LNO214, and NNO214, which may be responsible for the difference in oxygen transport between PNO214 and NNO214. Further investigation is needed to clarify the relationship between δ and D*. Activation energies for the oxygen diffusivities of various RP oxides are summarized in Table 3.
Figure 4.
Arrhenius plots of oxygen tracer diffusivity (D*) for different RP oxides: (a) Effect of A-site substitutions on D* for A2NiO4+δ (A = Pr, La, and Nd) single crystalline and polycrystalline oxides: single crystal (Ref. [49,97]) and polycrystalline (Ref. [51]); (b) Dependences of D* on the oxygen nonstoichiometry in A2NiO4+δ (A = Pr, La, and Nd) polycrystalline oxides (Ref. [51]).
Table 3.
Activation energies of oxygen self-diffusion in A2BO4+δ.
| Material | Ea/eV | Temperature Range/°C | Comment | Ref. |
|---|---|---|---|---|
| Pr2NiO4+δ | 0.67 | 450–700 | Single crystal, a-b plane | [49] |
| Pr2NiO4+δ | 1.10 | 450–700 | Single crystal, c-direction | [49] |
| Pr2NiO4+δ | 0.76 | 550–850 | Polycrystalline | [51] |
| La2NiO4+δ | 0.81 | 525–600 | Single crystal, a-b plane | [97] |
| La2NiO4+δ | 0.75 | 450–600 | Single crystal, c-direction | [97] |
| La2NiO4+δ | 0.87 | 500–850 | Polycrystalline | [51] |
| Nd2NiO4+δ | 1.38 | 450–700 | Single crystal, a-b plane | [49] |
| Nd2NiO4+δ | 1.27 | 450–700 | Single crystal, c-direction | [49] |
| Nd2NiO4+δ | 1.05 | 550–850 | Polycrystalline | [51] |
| La2CuO4+δ | 0.81 | 390–600 | Single crystal | [56] |
| La2CuO4+δ | 1.18 | 527–727 | Polycrystalline | [98] |
| La2CoO4+δ | 0.13 | 450–700 | Polycrystalline | [77] |
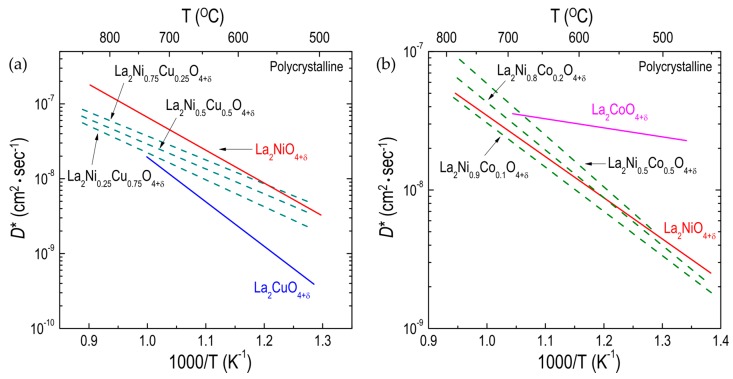
Investigations of the effect of A-site substitution on the oxygen transport properties of RP oxides have focused mainly on two material systems, LSNO214 and LSCuO214 [42,53,96,99,100]. Routbort et al. [100] measured the D* values for polycrystalline LSCuO214 oxides with a Sr content from 0.1 to 0.2, concluding that the decreased oxygen diffusion of LSCuO214 with increasing Sr content may be attributed to the immobilization of oxygen vacancies resulting from the addition of Sr. Using single crystals of LSCuO214 with Sr content from 0 to 0.12, Opila et al. [56] demonstrated the same trend of decreased oxygen diffusivity as Sr content increased. Similarly, LSNO214 polycrystalline oxides [51] were found to show a decrease in oxygen diffusivity with increasing Sr content. Likewise, Sr substitutions on the A-site of LSNO214 resulted in a reduction in the oxygen permeability [72]. The data are shown as part of the compilation of data in Figure 5. As discussed earlier, the ionic radii of Sr2+ and La3+ (1.31 Å and 1.22 Å, respectively [101]) are quite different. Therefore, substituting a larger cation for a cation ion on the A site in RP oxides leads to a structural stress relaxation, which in turn decreases the number of additional oxygen atoms required to stabilize the structure [102]. Consequently, the oxygen diffusion can decrease, owing to the decreased amount of additional oxygen. On the contrary, decreased δ may not always lead to a reduction in oxygen migration in RP oxides if the A-site cation is substituted by a cation with the same ionic radius and a smaller oxidation state, in accordance with a previous study on oxygen diffusion in calcium (Ca)-doped NNO214 (Ca = 0.2) [51]. One point to note from Figure 5 is that the oxygen diffusivity for LSCuO214 increases with increasing Sr content (Sr = 0.02) relative to LCuO214, whereas a further increase in the Sr content (Sr > 0.02) results in decreased oxygen diffusivity. Opila et al. [56] proposed that initially increased oxygen vacancies due to the Sr additions (Sr = 0.02) result in enhanced oxygen diffusivity, while further Sr additions (Sr > 0.02) cause oxygen vacancy ordering, decreasing the oxygen diffusivity. Although the trend toward reduction of the oxygen diffusivity with increasing Sr content in RP cuprates and nickelates has also been shown by other groups [61,95,99], most studies of the effects of Sr substitution on oxygen diffusivity in RP oxides have used a very narrow range of Sr content, from 0.0 to 0.2.
Figure 5.
Arrhenius plots of oxygen tracer diffusivity (D*) for different RP oxides. Effect of Sr substitution on the A site on D* for La2−xSrxCuO4+δ (Ref. [56]) single crystal and La2−xSrxNiO4+δ (Ref. [51]) polycrystalline oxides.
3.1.2. Effect of Substitutions on the B-Site
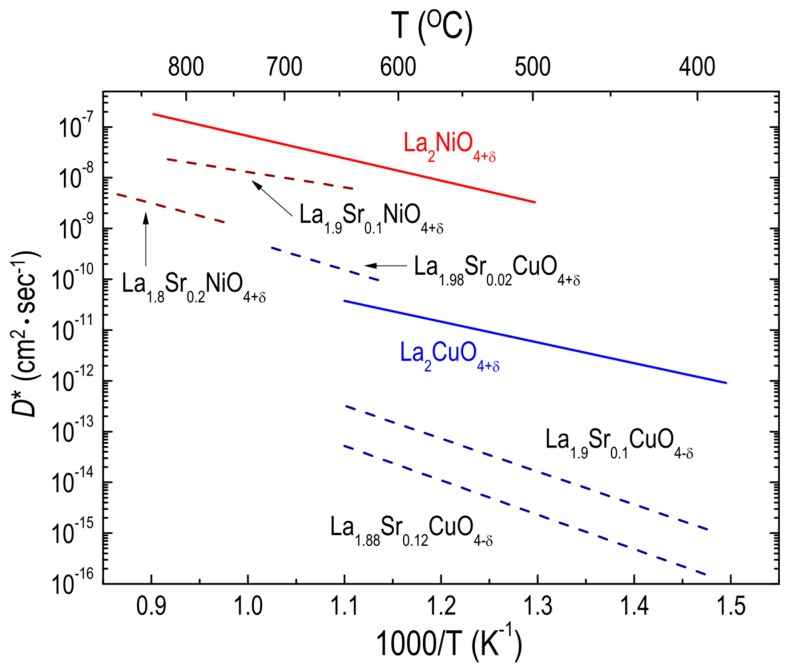
Munnings et al. [77] achieved a remarkably low activation energy (0.13 eV) for oxygen diffusion of polycrystalline LCO214 samples below 700 °C, above which LCO214 can be easily decomposed into LaCoO3 and La2O3. According to the comparison of the D* values for La2BO4+δ (B = Co [77], Ni [51], and Cu [98]) polycrystalline samples in Figure 6, LCO214 is the best material, with the highest oxygen diffusivity and the lowest activation energy in the temperature range of 450–700 °C where the oxygen diffusivity of LNO214 is higher than that of LCuO214. Moreover, the D* values for LCO214 appear much higher than those for both PNO214 and NNO214 below 630 °C. This fact implies that substitution on the B site has more influence on the oxygen ion transport in RP oxides than does A-site substitution. Considering that the concentration of oxygen interstitials in LCuO214 is much lower than in either LCO214 or LNO214, owing to the direct correlation between δ and B3+ content [103,104,105], a lower oxygen diffusivity for LCuO214 can be expected, as discussed in Section 3.1.1. However, the δ value of LCO214 (δ = 0.13 [77]) is highly comparable to that of LNO214 (δ = 0.13 [51]) and much smaller than that of PNO214 (δ = 0.21 [51]) and NNO214 (δ = 0.22 [51]) although the D* value for LCO214 is the highest among these materials at low temperatures. Although the defect concentration above a certain value may decrease the oxygen transport as a result of increased defect interactions, as discussed earlier, this possibility cannot address the LCO214 case. Thus, other factors, such as oxygen defect formation energy, may contribute to the oxygen diffusivity of RP oxides. Recently, Lee et al. [106] proposed that the oxygen 2p band center relative to the Fermi energy is an effective descriptor to predict the oxygen surface exchange as well as the activation energy for oxygen transport in RP oxides. According to this work, the calculated interstitial formation energies of La2BO4+δ (B = Co, Ni, and Cu) strongly depend on the B cation in the sequence LCuO214 > LNO214 > LCO214, which corresponds to the trend of B-cation–dependent oxygen diffusivity. More recently, Xie et al. [107] also calculated the formation energy of oxygen interstitials in the same RP oxide systems, demonstrating that, regardless of δ, the formation energy of oxygen interstitials decreases with decreasing the atomic number of the B cation, which is in good agreement with the data reported by Lee et al. [106].
Figure 6.
Arrhenius plots of oxygen tracer diffusivity (D*) for different RP oxides. Effect of B-site substitutions on D* for La2BO4+δ (B = Co, Ni, and Cu) polycrystalline oxides: La2CoO4+δ (Ref. [77]), La2NiO4+δ (Ref. [51]), and La2CuO4+δ (Ref. [98]). The D* values for Pr2NiO4+δ and Nd2NiO4+δ (Ref. [51]) are also plotted for comparison.
Boehm et al. [51,98] measured the oxygen diffusivity for polycrystalline La2Ni1−xCuxO4+δ (x = 0, 0.25, 0.5, 0.75, and 1.0), showing that the oxygen diffusion for La2Ni1−xCuxO4+δ decreases slightly as the copper (Cu) content increases (Figure 7a). The effect on oxygen diffusion of substituting cobalt (Co) for nickel (Ni) in La2Ni1−xCoxO4+δ has been evaluated by several different groups [51,77,94,108]. Kilner et al. [94] found that the activation enthalpy for oxygen migration in polycrystalline La2Ni1−xCoxO4+δ slightly increased with increasing Co content. Although the D* values for LCO214 have been measured by different groups, the overall trend is that the degree of change in oxygen diffusivity from partially substituting Co for Ni in La2Ni1−xCoxO4+δ is not significant, as shown in Figure 7b. The number of interstitial oxides of La2Ni1−xCuxO4+δ was found to slightly decrease with increasing Cu content [98], and partially substituting Co for Ni changed a small amount of δ in La2Ni1−xCoxO4+δ [94,108]. Therefore, this substitution may result in small changes in the D* values for La2Ni1−xB’xO4+δ when Ni is partially substituted by either Cu or Co. However, compared with the strong dependency of the D* of La2BO4+δ (B = Co, Ni, Cu) on the B-site cation, as discussed earlier, the degree of change in the oxygen diffusivity resulting from partial substitution on the B site is almost negligible. That finding suggests that the partial substitution of the B-site cation by other cations has a negligible effect on oxygen ion transport in La2B1−xB’O4+δ. It was assumed that partial substitution on the B site does not lead to significant changes in the oxygen-cation bonds in the BO6 octahedra and thus may have only a negligible effect on the oxygen diffusivity of La2Ni1−xBxO4+δ [51].
Figure 7.
Arrhenius plots of oxygen tracer diffusivity (D*) for different RP oxides: (a) effect of Ni substitution on the B site on D* for La2Ni1−xCuxO4+δ (Refs. [51,98]) polycrystalline; and (b) effect of Ni substitution on the B site on D* for polycrystalline La2Ni1−xCoxO4+δ (Refs. [77,94]) polycrystalline oxides.
3.2. Influence of Crystallographic Orientation on Oxygen Migration
As discussed earlier, the anisotropy of oxygen migration is one of the intrinsic properties of RP oxides owing to its structural feature. In the case of polycrystalline materials, the anisotropy is averaged; therefore, the D* value depends on the connectivity between grains. Introducing single crystals or epitaxial thin films has enabled investigation of the anisotropic nature of oxygen transport properties in RP oxides. For example, Burriel et al. [58] reported that the oxygen diffusion and oxygen surface exchange kinetics in the a-b plane are faster than those along the c-direction in epitaxial LNO214 thin films. Lee et al. [102] demonstrated that substituting Sr for La in LSNO214 thin films can result in the structural reorientation of the films because of the reduction in the surface energy of the (001) surface, reporting the anisotropic oxygen surface exchange kinetics. However, Chen et al. [109] did not obtain any orientation-dependent surface exchange kinetics in epitaxial La2−xSrxCoO4+δ (LSCO214, Sr = 0.25) thin films, in contrast to the observation that oxygen diffusion is orientation dependent.
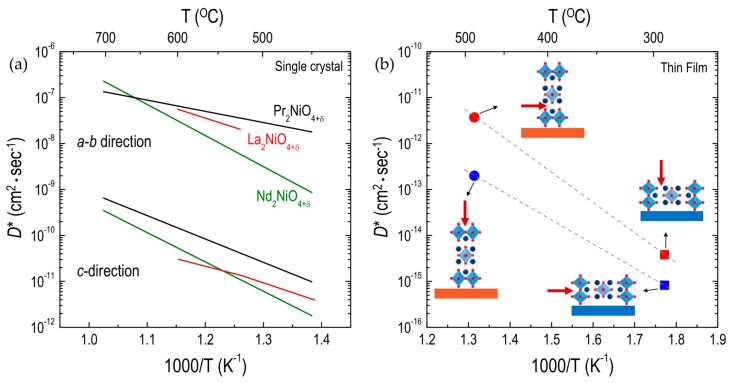
Anisotropic oxygen migration in RP oxides has been investigated, mainly focusing on RP nickelate single crystals, by Bassat and co-workers [49,50,97]. As shown in Figure 8a, three different RP nickelates (i.e., PNO214, LNO214, and NNO214) show a large anisotropy in the oxygen diffusion. In the temperature range of 450–700 °C, the oxygen diffusion along the a-b plane is about three orders of magnitude higher than that along the c-direction for all materials. Bassat et al. [49] suggested that the a-b plane diffusion process is dominant in polycrystalline samples, as the D* values along the a-b plane for single crystals are comparable to those for polycrystalline samples (Figure 4a). In addition, they found that the D* values along the a-b plane in RP nickelates are generally larger than those in ABO3 perovskites. Claus et al. also showed [99] anisotropic oxygen diffusion in single-crystal LCuO214, where the D* values along the a-b plane are two orders of magnitude higher than those along the c-direction.
Figure 8.
Arrhenius plots of oxygen tracer diffusivity (D*) for different RP oxides: (a) D* along the a-b plane and c-direction in A2NiO4+δ (A = Pr, La, and Nd, Refs. [49,97]) single crystalline oxides; and (b) D* along the a-b plane and c-direction in the (001)-oriented (circle) and the (100)-oriented (square) La1.75Sr0.25CoO4+δ thin films [109].
The effect of crystallographic orientation on the oxygen ion transport can be more clearly seen in thin films. Recently, Chen et al. [109] successfully fabricated LSC214 (Sr = 0.25) thin films grown in two different crystallographic orientations, i.e., (100) and (001), using (100) LaSrAlO4 (LSAO) and (001) SrTiO3 (STO) substrates. They demonstrated that the oxygen diffusivity along the a-b plane in the (100)-oriented LSC214 film was three orders of magnitude lower than that in the (001)-oriented LSC214 film (Figure 8b). Moreover, the D* value along the c-direction in the (001)-oriented LSC214 film was found to be one order of magnitude higher than that along the a-b plane in the (100)-oriented LSC214 film.
3.3. Influence of Strain on Oxygen Migration
The use of epitaxial strain induced in a thin film by lattice mismatch with a substrate has been intensively studied for control of oxygen migration and the formation of oxygen defects in binary oxides [80,81,82,83,110,111,112,113,114] and ABO3 perovskite oxides [7,85,86,115,116,117,118,119]. Theoretical studies [110,112] have shown that tensile (compressive) strain can decrease (increase) the formation energy of oxygen vacancies in CeO2. De Souza and co-workers [80] calculated the activation energies for oxygen migration in strained CeO2, demonstrating that the oxygen migration in tensile strain is remarkably faster than in compressive strain. Similar to research on binary oxides, Mayeshiba and Morgan [85] predicted the oxygen migration barriers in LaMO3 (M = Sc, Ti, V, Cr, Mn, Fe, Co, Ni, and Ga) perovskite oxides under tensile strain via DFT calculations. They demonstrated that tensile strain can significantly reduce the oxygen migration barriers, resulting in enhanced oxygen diffusion (one order of magnitude) at 500 °C compared with the diffusion under unstrained conditions. Kubicek et al. [7] synthesized LSC113 thin films on STO and LaAlO3 (LAO) substrates, which introduce tensile and compressive strain states, respectively, into the LSC113 films. They demonstrated that the D* values for tensile-strained LSC113 are two orders of magnitude higher than those for compressive-strained LSC113, postulating that an increase in the oxygen vacancies due to tensile strain may contribute to the enhanced oxygen diffusion. Similarly, SrCoO3−δ (SCO113) thin films revealed a sensitive response to strain, modifying the oxygen diffusion and activation [86,118].
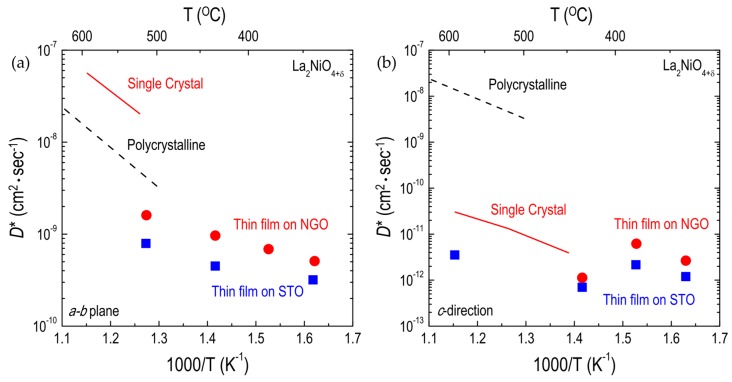
In contrast to binary oxides and ABO3 perovskite oxides, very few studies have reported the effects of strain on oxygen diffusion and surface exchange in RP oxides. Using pulsed laser deposition, Burriel et al. [58] fabricated (001)-oriented LNO214 films on STO and NdGaO3 (NGO) substrates, which led to bi-axial tensile and compressive strain states, respectively, along the a-b plane. They evaluated the oxygen diffusion and surface exchange kinetics for tensile- and compressive-strained LNO214 films, concluding that both compressive and tensile strain led to a reduction in the oxygen diffusivity in the first 175–200 nm of the film, whereas neither strain affected the oxygen surface exchange. Therefore, the D* values for the LNO214 films were found to be lower than those for either polycrystalline or single-crystal LNO samples regardless of the diffusion direction, as shown in Figure 9. However, Lee et al. [52] later showed that in (100)-oriented LNO214 thin films, tensile strain along the c-direction can lead to an increase in the driving force to form interstitial oxygen atoms in LNO214, resulting in enhanced oxygen surface exchange kinetics. Based on this work, the facilitated oxygen migration in tensile-strained LNO214 thin films can be inferred to show that more oxygen interstitials in RP nickelates can lead to enhancement of the oxygen diffusivity, as discussed in Section 3.1.1. More recently, Tsvetkov et al. [120] compared the δ values of tensile- and compressive-strained NNO214 thin films, demonstrating that the larger δ in tensile-strained NNO214 can enhance the oxygen surface exchange kinetics relative to those of compressive-strained NNO214 thin films. From this work, it can also be postulated that tensile-strained NNO214 would show increased oxygen migration. The discrepancy in the effects of strain on oxygen surface exchange kinetics in RP films, mentioned earlier, may be attributed to the fact that the critical thickness required to maintain an acceptable strain state is fairly smaller than what Burriel et al. [58] used. However, the effect of strain on oxygen migration in RP oxides needs further investigation.
Figure 9.
Arrhenius plots of oxygen tracer diffusivity (D*) for La2NiO4+δ films: (a) D* along the a-b plane; and (b) along the c-direction for La2NiO4+δ films on SrTiO3 (STO) and NdGaO3 (NGO). Thin film [58], single-crystal [97], and polycrystalline [51] data are comparatively shown.
4. Control of Oxygen Stability in RP Oxides
To implement oxide materials for practical applications, such as SOFCs and oxygen permeation membranes operated under a wide range of temperatures and oxygen partial pressures, oxide materials should possess high thermal and chemical stability. In the case of ABO3 perovskite oxides, a vast number of studies [1,20,21,26,28,29,30,32,33,121,122,123,124,125,126,127,128,129] related to the chemical stability and thermal expansivity of ferrites and cobaltites have been reported, as both material systems have high electronic and ionic conductivities useful in many applications [1,130,131,132]. However, ferrites and cobaltites exhibit high thermal expansion coefficients, as well as low chemical stability, because both materials can easily lose lattice oxygen, resulting in unfavorable expansion of the lattice in reducing atmospheres [28,133]. Here, we briefly review RP oxides based on nickelates, cuprates, and cobaltites with respect to their thermal and chemical stability.
LNO214 was found to have a structural transition from the Fmmm orthorhombic to the I4/mmm tetragonal structure between room temperature (RT) and 150 °C [134]. Huang et al. [135] also observed a structural transition (i.e., orthorhombic-tetragonal transition) of LNO214 between RT and 150 °C, above which no phase transition occurred. LSNO214 is expected to have a different thermal expansion behavior owing to a change in δ from adding Sr content [42,136,137,138]. Although the tetragonal structure of LSNO214 (Sr = 0.2 and 0.4) was retained over the temperature range between 600 and 900 °C, thermal expansion coefficients increased with increasing Sr content [138]. Makhnach et al. [136] reported significantly different high-temperature behavior of LSNO214 (Sr = 1.4) due to evolution of the Ni valence from Ni2+ to Ni3+ compared with LNO214. They found significantly larger variations of cell parameters a and c above 600 °C. Thermal expansion coefficients of ABO3 and A2BO4 oxides are shown in Table 4. The effect of partial substitution on the B-site in RP nickelates was investigated by Kharton and co-workers [139,140]. In these studies, the equilibrium chemical strains induced by the oxygen hyperstoichiometry variations in La2Ni1−xBxO4+δ (B = Fe, Co, and Cu) were found to be very low relative to ABO3 ferrites and cobaltites owing to a strongly anisotropic expansion of the RP structures [139]. However, at low oxygen partial pressure, the decomposition of Ni-containing phases was observed, which indicates that the partial substitution of other transition metal cations for Ni had no effect on the stability of LNO214 [140].
Table 4.
Thermal expansion coefficients (TEC) of ABO3−δ and A2BO4±δ.
| Material | TEC (×10−6 K−1) | Temperature/°C | Ref. |
|---|---|---|---|
| La0.8Sr0.2CoO3−δ | 19.1 | 30–1000 | [141] |
| La0.6Sr0.4CoO3−δ | 20.5 | 30–1000 | [142] |
| La0.8Sr0.2Co0.2Fe0.8O3−δ | 15.4 | 100– 800 | [143] |
| La0.6Sr0.4Co0.2Fe0.8O3−δ | 15.3 | 100–600 | [143] |
| La2NiO4+δ | 11.0 | 650–950 | [138] |
| La1.8Sr0.2NiO4+δ | 11.2 | 650–950 | [138] |
| La1.6Sr0.4NiO4+δ | 12.0 | 650–950 | [138] |
| La0.6Sr1.4MnO4±δ | 13.5 | 30–800 | [144] |
| La0.2Sr1.8MnO4±δ | 16.5 | 30–800 | [144] |
| La0.5Sr0.5Co0.5Fe0.5O4−δ | 13.5 | 30–700 | [145] |
| La2Ni0.9Co0.1O4+δ | 13.8 | 100–900 | [139] |
| La1.3Sr0.7CoO4−δ | 9.6 | 30–1000 | [27] |
| La1.4Sr0.6CoO4−δ | 10.1 | 30–700 | [145] |
| LaSrCoO4−δ | 14.3 | 30–1000 | [27] |
Kanai et al. [75] reported that the oxygen partial pressure for the decomposition of LSCuO214 is strongly dependent on the Sr contents. According to this work, although the decomposition of LSCuO214 is not dependent on oxygen partial pressure below Sr = 0.05, the dependence of decomposition on the oxygen partial pressure increases above Sr > 0.1. This suggests that an abrupt variation in the thermodynamic behavior of LSCuO214 occurs in the region between Sr = 0.05 and Sr = 0.1. In terms of thermal stability, LSCuO214 with Sr = 0.6 was found be more stable than LSCuO214 with Sr = 0.2 during heating in a vacuum because the higher Sr content prevented Cu+ formation and oxygen removal [78].
LSCO214 (0.5 ≤ Sr ≤ 1.5) showed stable reduction behaviors during heating and cooling between 300 and 1500 °C [46], whereas substituting a B cation for Co resulted in a slight increase in thermal expansion coefficients [145]. However, LCO214 without the Sr content was found to decompose into LaCoO3 and La2O3 above 700 °C [77], as discussed in Section 3.1.2. In addition, RP cobaltites and nickelates were found to have greater thermal stability than ABO3-based cobaltites and ferrites [27].
5. Conclusions
Developing high-performance energy and environmental devices, such as SOFCs, oxygen permeation membranes, and chemical sensors, requires discovering new oxide materials with high oxygen mobility and stability. In this regard, RP oxide materials (An+1BnO3n+1 with n = 1) have been considered as alternative materials to ABO3 perovskite oxides. In this review, we have briefly overviewed the fundamental mechanisms of oxygen ion migration, approaches to control oxygen transport, and stability in RP oxides, focusing on the A2BO4 system. A clear distinction between RP oxides and ABO3 oxides is that RP oxides can be both oxygen-deficient and oxygen-excess depending on the δ, which can determine whether the oxygen migration mechanism is driven by interstitialcy or vacancy. In addition, RP oxides have an anisotropic structure, which leads to highly anisotropic diffusion properties. Understanding how multiple factors associated with defect formation and structural features affect oxygen transport can provide insights into developing novel approaches to control oxygen migration in RP oxides.
The three factors discussed in this review—cation substitution, crystallography orientation, and strain—have an apparent influence on oxygen ion migration, remaining open questions with regard to the control of oxygen migration in RP oxides. To address these questions, two approaches are promising for further investigation. First, the development of descriptors, such as the metal d-band center and oxygen p-band center, by DFT calculations and MD simulations helps predict the trends associated with the changing nature of the A- and B-site cations. We discussed how the oxygen p-band center of lanthanum-based RP oxides correlates with the formation energy of oxygen defects. This concept can be extended to a series of various RP oxides, leading to an acceleration in the discovery of the best materials for applications requiring high oxygen mobility. High-throughput computational and combinatorial screening will also be helpful in identifying optimized materials. The second is the use of epitaxial thin films, which can be fabricated by pulsed laser epitaxy, sputtering, or molecular beam epitaxy. RP series oxides show strong anisotropic transport properties depending on the crystallographic direction, and epitaxial thin films enable the evaluation of anisotropic properties for different orientations and the implementation of strain for enhancing oxygen migration. Moreover, epitaxial thin films can be versatilely applied to real applications, in contrast to single crystals.
An additional comment is that higher-order RP series oxides (An+1BnO3n+1 with n ≥ 2) seem good candidates, as well, for the enhancement of oxygen transport properties. Although oxygen ion migration in higher-order RP oxides is not fully understood, these RP oxides exhibit higher electronic conductivity and thermal stability than the n = 1 RP oxides. Thus, exploring new RP systems will bring new opportunities for developing materials with fast oxygen migration.
Acknowledgments
This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division.
Author Contributions
Dongkyu Lee identified the most active and promising research topics in the field under review and analyzed the selected scientific literature. Ho Nyung Lee consulted the relevant studies and references. All authors contributed to the writing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Adler S.B. Factors governing oxygen reduction in solid oxide fuel cell cathodes. Chem. Rev. 2004;104:4791–4843. doi: 10.1021/cr020724o. [DOI] [PubMed] [Google Scholar]
- 2.Bhalla A.S., Guo R.Y., Roy R. The perovskite structure—A review of its role in ceramic science and technology. Mater. Res. Innov. 2000;4:3–26. doi: 10.1007/s100190000062. [DOI] [Google Scholar]
- 3.Voorhoeve R.J.H., Johnson D.W., Remeika J.P., Gallagher P.K. Perovskite oxides: Materials science in catalysis. Science. 1977;195:827–833. doi: 10.1126/science.195.4281.827. [DOI] [PubMed] [Google Scholar]
- 4.Adler S.B. Mechanism and kinetics of oxygen reduction on porous La1−xSrxCoO3−δ electrodes. Solid State Ion. 1998;111:125–134. doi: 10.1016/S0167-2738(98)00179-9. [DOI] [Google Scholar]
- 5.Berenov A.V., Atkinson A., Kilner J.A., Bucher E., Sitte W. Oxygen tracer diffusion and surface exchange kinetics in La0.6Sr0.4CoO3−δ. Solid State Ion. 2010;181:819–826. doi: 10.1016/j.ssi.2010.04.031. [DOI] [Google Scholar]
- 6.Crumlin E.J., Ahn S.J., Lee D., Mutoro E., Biegalski M.D., Christen H.M., Shao-Horn Y. Oxygen electrocatalysis on epitaxial La0.6Sr0.4CoO3−δ perovskite thin films for solid oxide fuel cells. J. Electrochem. Soc. 2012;159:F219–F225. doi: 10.1149/2.018207jes. [DOI] [Google Scholar]
- 7.Kubicek M., Cai Z.H., Ma W., Yildiz B., Hutter H., Fleig J. Tensile lattice strain accelerates oxygen surface exchange and diffusion in La1−xSrxCoO3−δ thin films. ACS Nano. 2013;7:3276–3286. doi: 10.1021/nn305987x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.La O’ G.J., Ahn S.J., Crumlin E., Orikasa Y., Biegalski M.D., Christen H.M., Shao-Horn Y. Catalytic activity enhancement for oxygen reduction on epitaxial perovskite thin films for solid oxide fuel cells. Angew. Chem. Int. Ed. 2010;49:5344–5347. doi: 10.1002/anie.201001922. [DOI] [PubMed] [Google Scholar]
- 9.Lee D., Lee Y.-L., Grimaud A., Hong W.T., Biegalski M.D., Morgan D., Shao-Horn Y. Enhanced oxygen surface exchange kinetics and stability on epitaxial La0.8Sr0.2CoO3−δ thin films by La0.8Sr0.2MnO3−δ decoration. J. Phys. Chem. C. 2014;118:14326–14334. doi: 10.1021/jp502192m. [DOI] [Google Scholar]
- 10.Mizusaki J. Nonstoichiometry, diffusion, and electrical properties of perovskite-type oxide electrode materials. Solid State Ion. 1992;52:79–91. doi: 10.1016/0167-2738(92)90093-5. [DOI] [Google Scholar]
- 11.Van der Haar L.M., den Otter M.W., Morskate M., Bouwmeester H.J.M., Verweij H. Chemical diffusion and oxygen surface transfer of La1−xSrxCoO3−δ studied with electrical conductivity relaxation. J. Electrochem. Soc. 2002;149:J41–J46. doi: 10.1149/1.1446874. [DOI] [Google Scholar]
- 12.Van Doorn R.H.E., Burggraaf A.J. Structural aspects of the ionic conductivity of La1−xSrxCoO3−δ. Solid State Ion. 2000;128:65–78. doi: 10.1016/S0167-2738(99)00282-9. [DOI] [Google Scholar]
- 13.Baumann F.S., Fleig J., Habermeier H.U., Maier J. Impedance spectroscopic study on well-defined (La,Sr)(Co,Fe)O3−δ model electrodes. Solid State Ion. 2006;177:1071–1081. doi: 10.1016/j.ssi.2006.02.045. [DOI] [Google Scholar]
- 14.Bouwmeester H.J.M., Kruidhof H., Burggraaf A.J. Importance of the surface exchange kinetics as rate-limiting step in oxygen permeation through mixed-conducting oxides. Solid State Ion. 1994;72:185–194. doi: 10.1016/0167-2738(94)90145-7. [DOI] [Google Scholar]
- 15.Carter S., Selcuk A., Chater R.J., Kajda J., Kilner J.A., Steele B.C.H. Oxygen transport in selected nonstoichiometric perovskite-structure oxides. Solid State Ion. 1992;53:597–605. doi: 10.1016/0167-2738(92)90435-R. [DOI] [Google Scholar]
- 16.Esquirol A., Brandon N.P., Kilner J.A., Mogensen M. Electrochemical characterization of La0.6Sr0.4Co0.2Fe0.8O3 cathodes for intermediate-temperature SOFCs. J. Electrochem. Soc. 2004;151:A1847–A1855. doi: 10.1149/1.1799391. [DOI] [Google Scholar]
- 17.Geary T.C., Lee D., Shao-Horn Y., Adler S.B. Nonlinear impedance analysis of La0.6Sr0.4Co0.2Fe0.8O3−δ thin film oxygen electrodes. J. Electrochem. Soc. 2016;163:F1107–F1114. doi: 10.1149/2.0851609jes. [DOI] [Google Scholar]
- 18.Ingram B.J., Eastman J.A., Chang K.C., Kim S.K., Fister T.T., Perret E., You H., Baldo P.M., Fuoss P.H. In situ X-ray studies of oxygen surface exchange behavior in thin film La0.6Sr0.4Co0.2Fe0.8O3−δ. Appl. Phys. Lett. 2012;101:051603. doi: 10.1063/1.4739518. [DOI] [Google Scholar]
- 19.Jiang S.P. A comparison of O2 reduction reactions on porous (La,Sr)MnO3 and (La,Sr)(Co,Fe)O3 electrodes. Solid State Ion. 2002;146:1–22. doi: 10.1016/S0167-2738(01)00997-3. [DOI] [Google Scholar]
- 20.Katsuki M., Wang S., Dokiya M., Hashimoto T. High temperature properties of La0.6Sr0.4Co0.8Fe0.2O3−δ oxygen nonstoichiometry and chemical diffusion constant. Solid State Ion. 2003;156:453–461. doi: 10.1016/S0167-2738(02)00733-6. [DOI] [Google Scholar]
- 21.Kuhn M., Fukuda Y., Hashimoto S., Sato K., Yashiro K., Mizusaki J. Oxygen nonstoichiometry and thermo-chemical stability of perovskite-type La0.6Sr0.4Co1−yFeyO3−δ (y = 0, 0.2, 0.4, 0.5, 0.6, 0.8, 1) materials. J. Electrochem. Soc. 2013;160:F34–F42. doi: 10.1149/2.050301jes. [DOI] [Google Scholar]
- 22.Lee D., Lee Y.-L., Hong W.T., Biegalski M.D., Morgan D., Shao-Horn Y. Oxygen surface exchange kinetics and stability of (La,Sr)2CoO4±δ/La1−xSrxMO3−δ (M = Co and Fe) hetero-interfaces at intermediate temperatures. J. Mater. Chem. A. 2015;3:2144–2157. doi: 10.1039/C4TA05795C. [DOI] [Google Scholar]
- 23.Lee D., Lee Y.-L., Wang X.R., Morgan D., Shao-Horn Y. Enhancement of oxygen surface exchange on epitaxial La0.6Sr0.4Co0.2Fe0.8O3−δ thin films using advanced heterostructured oxide interface engineering. MRS Commun. 2016;6:204–209. doi: 10.1557/mrc.2016.28. [DOI] [Google Scholar]
- 24.Lynch M.E., Yang L., Qin W.T., Choi J.J., Liu M.F., Blinn K., Liu M.L. Enhancement of La0.6Sr0.4Co0.2Fe0.8O3−δ durability and surface electrocatalytic activity by La0.85Sr0.15MnO3±δ investigated using a new test electrode platform. Energy Environ. Sci. 2011;4:2249–2258. doi: 10.1039/c1ee01188j. [DOI] [Google Scholar]
- 25.Steele B.C.H., Bae J.M. Properties of La0.6Sr0.4Co0.2Fe0.8O3−δ (LSCF) double layer cathodes on gadolinium-doped cerium oxide (CGO) electrolytes—II. Role of oxygen exchange and diffusion. Solid State Ion. 1998;106:255–261. doi: 10.1016/S0167-2738(97)00430-X. [DOI] [Google Scholar]
- 26.Tai L.W., Nasrallah M.M., Anderson H.U., Sparlin D.M., Sehlin S.R. Structure and electrical properties of La1−xSrxCo1−yFeyO3. Part 1. The system La0.8Sr0.8Co1−yFeyO3. Solid State Ion. 1995;76:259–271. doi: 10.1016/0167-2738(94)00244-M. [DOI] [Google Scholar]
- 27.Al Daroukh M., Vashook V.V., Ullmann H., Tietz F., Raj I.A. Oxides of the AMO3 and A2MO4-type: Structural stability, electrical conductivity and thermal expansion. Solid State Ion. 2003;158:141–150. doi: 10.1016/S0167-2738(02)00773-7. [DOI] [Google Scholar]
- 28.Chen X.Y., Yu J.S., Adler S.B. Thermal and chemical expansion of Sr-doped lanthanum cobalt oxide (La1−xSrxCoO3−δ) Chem. Mater. 2005;17:4537–4546. doi: 10.1021/cm050905h. [DOI] [Google Scholar]
- 29.Hashimoto S., Fukuda Y., Kuhn M., Sato K., Yashiro K., Mizusaki J. Thermal and chemical lattice expansibility of La0.6Sr0.4Co1−yFeyO3−δ (y = 0.2, 0.4, 0.6 and 0.8) Solid State Ion. 2011;186:37–43. doi: 10.1016/j.ssi.2011.01.014. [DOI] [Google Scholar]
- 30.Mastin J., Einarsrud M.A., Grande T. Structural and thermal properties of La1−xSrxCoO3−δ. Chem. Mater. 2006;18:6047–6053. doi: 10.1021/cm061539k. [DOI] [Google Scholar]
- 31.Benson S.J., Waller D., Kilner J.A. Degradation of La0.6Sr0.4Co0.8Fe0.2O3−δ in carbon dioxide and water atmospheres. J. Electrochem. Soc. 1999;146:1305–1309. doi: 10.1149/1.1391762. [DOI] [Google Scholar]
- 32.Ding H.P., Virkar A.V., Liu M.L., Liu F. Suppression of Sr surface segregation in La1−xSrxCo1−yFeyO3−δ: A first principles study. Phys. Chem. Chem. Phys. 2013;15:489–496. doi: 10.1039/C2CP43148C. [DOI] [PubMed] [Google Scholar]
- 33.Oh D., Gostovic D., Wachsman E.D. Mechanism of La0.6Sr0.4Co0.2Fe0.8O3 cathode degradation. J. Mater. Res. 2012;27:1992–1999. doi: 10.1557/jmr.2012.222. [DOI] [Google Scholar]
- 34.Simner S.P., Anderson M.D., Engelhard M.H., Stevenson J.W. Degradation mechanisms of La-Sr-Co-Fe-O3 SOFC cathodes. Electrochem. Solid State Lett. 2006;9:A478–A481. doi: 10.1149/1.2266160. [DOI] [Google Scholar]
- 35.Baledent V., Fauque B., Sidis Y., Christensen N.B., Pailhes S., Conder K., Pomjakushina E., Mesot J., Bourges P. Two-dimensional orbital-like magnetic order in the high-temperature La2−xSrxCuO4 superconductor. Phys. Rev. Lett. 2010;105:4. doi: 10.1103/PhysRevLett.105.027004. [DOI] [PubMed] [Google Scholar]
- 36.Cava R.J., Batlogg B., Palstra T.T., Krajewski J.J., Peck W.F., Ramirez A.P., Rupp L.W. Magnetic and electrical properties of La2−xSrxNiO4±δ. Phys. Rev. B. 1991;43:1229–1232. doi: 10.1103/PhysRevB.43.1229. [DOI] [PubMed] [Google Scholar]
- 37.Chaillout C., Cheong S.W., Fisk Z., Lehmann M.S., Marezio M., Morosin B., Schirber J.E. The crystal structure of superconducting La2CuO4.032 by neutron diffraction. Physica C. 1989;158:183–191. doi: 10.1016/0921-4534(89)90315-8. [DOI] [Google Scholar]
- 38.Meyer T.L., Jiang L., Park S., Egami T., Lee H.N. Strain-relaxation and critical thickness of epitaxial La1.85Sr0.15CuO4 films. APL Mater. 2015;3:126102. doi: 10.1063/1.4937170. [DOI] [Google Scholar]
- 39.Perry J.K., Tahir-Kheli J., Goddard W.A. Antiferromagnetic band structure of La2CuO4: Becke-3-Lee-Yang-Parr calculations. Phys. Rev. B. 2001;63:6. doi: 10.1103/PhysRevB.63.144510. [DOI] [Google Scholar]
- 40.Reehuis M., Ulrich C., Prokes K., Gozar A., Blumberg G., Komiya S., Ando Y., Pattison P., Keimer B. Crystal structure and high-field magnetism of La2CuO4. Phys. Rev. B. 2006;73:8. doi: 10.1103/PhysRevB.73.144513. [DOI] [Google Scholar]
- 41.Veith G.M., Chen R., Popov G., Croft M., Shokh Y., Nowik I., Greenblatt M. Electronic, magnetic, and magnetoresistance properties of the n = 2 Ruddlesden–Popper phases Sr3Fe2−xCoxO7−δ (0.25 ≤ x ≤ 1.75) J. Solid State Chem. 2002;166:292–304. doi: 10.1006/jssc.2002.9589. [DOI] [Google Scholar]
- 42.Aguadero A., Escudero M.J., Perez M., Alonso J.A., Daza L. Hyperstoichiometric La1.9Sr0.1NiO4+δ mixed conductor as novel cathode for intermediate temperature solid oxide fuel cells. J. Fuel Cell Sci. Technol. 2007;4:294–298. doi: 10.1115/1.2743075. [DOI] [Google Scholar]
- 43.Burriel M., Garcia G., Rossell M.D., Figueras A., Van Tendeloo G., Santiso J. Enhanced high-temperature electronic transport properties in nanostructured epitaxial thin films of the Lan+1NinO3n+1 Ruddlesden-Popper series (n = 1, 2, 3, ∞) Chem. Mater. 2007;19:4056–4062. doi: 10.1021/cm070804e. [DOI] [Google Scholar]
- 44.Ferkhi M., Khelili S., Zerroual L., Ringuede A., Cassir M. Synthesis, structural analysis and electrochemical performance of low-copper content La2Ni1−xCuxO4+δ materials as new cathodes for solid oxide fuel cells. Electrochim. Acta. 2009;54:6341–6346. doi: 10.1016/j.electacta.2009.05.082. [DOI] [Google Scholar]
- 45.Schroeder M., Dragan M.A. Oxygen transport in La2−xSrxNiO4+δ: Membrane permeation and defect chemical modelling. J. Mater. Sci. 2007;42:1972–1983. doi: 10.1007/s10853-006-0739-7. [DOI] [Google Scholar]
- 46.Vashook V.V., Ullmann H., Olshevskaya O.P., Kulik V.P., Lukashevich V.E., Kokhanovskij L.V. Composition and electrical conductivity of some cobaltates of the type La2−xSrxCoO4.5−x/2±δ. Solid State Ion. 2000;138:99–104. doi: 10.1016/S0167-2738(00)00774-8. [DOI] [Google Scholar]
- 47.Ruddlesden S.N., Popper P. The compound Sr3Ti2O7 and its structure. Acta Crystallogr. 1958;11:54–55. doi: 10.1107/S0365110X58000128. [DOI] [Google Scholar]
- 48.Brown I.D. Modeling the structures of La2NiO4. Z. Kristallogr. 1992;199:255–272. doi: 10.1524/zkri.1992.199.3-4.255. [DOI] [Google Scholar]
- 49.Bassat J.M., Burriel M., Wahyudi O., Castaing R., Ceretti M., Veber P., Weill I., Villesuzanne A., Grenier J.C., Paulus W., et al. Anisotropic oxygen diffusion properties in Pr2NiO4+δ and Nd2NiO4+δ single crystals. J. Phys. Chem. C. 2013;117:26466–26472. doi: 10.1021/jp409057k. [DOI] [Google Scholar]
- 50.Bassat J.M., Odier P., Villesuzanne A., Marin C., Pouchard M. Anisotropic ionic transport properties in La2NiO4+δ single crystals. Solid State Ion. 2004;167:341–347. doi: 10.1016/j.ssi.2003.12.012. [DOI] [Google Scholar]
- 51.Boehm E., Bassat J.M., Dordor P., Mauvy F., Grenier J.C., Stevens P. Oxygen diffusion and transport properties in non-stoichiometric Ln2−xNiO4+δ oxides. Solid State Ion. 2005;176:2717–2725. doi: 10.1016/j.ssi.2005.06.033. [DOI] [Google Scholar]
- 52.Lee D., Grimaud A., Crumlin E.J., Mezghani K., Habib M.A., Feng Z.X., Hong W.T., Biegalski M.D., Christen H.M., Shao-Horn Y. Strain influence on the oxygen electrocatalysis of the (100)-oriented epitaxial La2NiO4+δ thin films at elevated temperatures. J. Phys. Chem. C. 2013;117:18789–18795. doi: 10.1021/jp404121p. [DOI] [Google Scholar]
- 53.Skinner S.J., Kilner J.A. Oxygen diffusion and surface exchange in La2−xSrxNiO4+δ. Solid State Ion. 2000;135:709–712. doi: 10.1016/S0167-2738(00)00388-X. [DOI] [Google Scholar]
- 54.Gopalakrishnan J., Colsmann G., Reuter B. Studies on La2−xSrxNiO4 (0 ≤ x ≤ 1) system. J. Solid State Chem. 1977;22:145–149. doi: 10.1016/0022-4596(77)90031-7. [DOI] [Google Scholar]
- 55.Minervini L., Grimes R.W., Kilner J.A., Sickafus K.E. Oxygen migration in La2NiO4+δ. J. Mater. Chem. 2000;10:2349–2354. doi: 10.1039/b004212i. [DOI] [Google Scholar]
- 56.Opila E.J., Tuller H.L., Wuensch B.J., Maier J. Oxygen tracer diffusion in La2−xSrxCuO4-δ single-crystals. J. Am. Ceram. Soc. 1993;76:2363–2369. doi: 10.1111/j.1151-2916.1993.tb07778.x. [DOI] [Google Scholar]
- 57.Mott N.F., Gurney R.W. Electronic Processes in Ionic Crystals. Oxford University Press; London, UK: 1940. [Google Scholar]
- 58.Burriel M., Garcia G., Santiso J., Kilner J.A., Richard J.C.C., Skinner S.J. Anisotropic oxygen diffusion properties in epitaxial thin films of La2NiO4+δ. J. Mater. Chem. 2008;18:416–422. doi: 10.1039/B711341B. [DOI] [Google Scholar]
- 59.Burriel M., Santiso J., Rossell M.D., Van Tendeloo G., Figueras A., Garcia G. Enhancing total conductivity of La2NiO4+δ epitaxial thin films by reducing thickness. J. Phys. Chem. C. 2008;112:10982–10987. doi: 10.1021/jp7101622. [DOI] [Google Scholar]
- 60.Kim G., Wang S., Jacobson A.J., Chen C.L. Measurement of oxygen transport kinetics in epitaxial La2NiO4+δ thin films by electrical conductivity relaxation. Solid State Ion. 2006;177:1461–1467. doi: 10.1016/j.ssi.2006.07.013. [DOI] [Google Scholar]
- 61.Li Z.A., Haugsrud R., Norby T. Oxygen bulk diffusion and surface exchange in Sr-substituted La2NiO4+δ. Solid State Ion. 2011;184:42–46. doi: 10.1016/j.ssi.2010.10.009. [DOI] [Google Scholar]
- 62.Jorgensen J.D., Dabrowski B., Pei S., Richards D.R., Hinks D.G. Structure of the interstitial oxygen defect in La2NiO4+δ. Phys. Rev. B. 1989;40:2187–2199. doi: 10.1103/PhysRevB.40.2187. [DOI] [PubMed] [Google Scholar]
- 63.Chroneos A., Parfitt D., Kilner J.A., Grimes R.W. Anisotropic oxygen diffusion in tetragonal La2NiO4+δ: Molecular dynamics calculations. J. Mater. Chem. 2010;20:266–270. doi: 10.1039/B917118E. [DOI] [Google Scholar]
- 64.Kharton V.V., Viskup A.P., Kovalevsky A.V., Naumovich E.N., Marques F.M.B. Ionic transport in oxygen-hyperstoichiometric phases with K2NiF4-type structure. Solid State Ion. 2001;143:337–353. doi: 10.1016/S0167-2738(01)00876-1. [DOI] [Google Scholar]
- 65.Sayers R., Skinner S.J. Evidence for the catalytic oxidation of La2NiO4+δ. J. Mater. Chem. 2010;21:414–419. doi: 10.1039/C0JM02419H. [DOI] [Google Scholar]
- 66.Cleave A.R., Kilner J.A., Skinner S.J., Murphy S.T., Grimes R.W. Atomistic computer simulation of oxygen ion conduction mechanisms in La2NiO4. Solid State Ion. 2008;179:823–826. doi: 10.1016/j.ssi.2008.04.013. [DOI] [Google Scholar]
- 67.Frayret C., Villesuzanne A., Pouchard M. Application of density functional theory to the modeling of the mixed ionic and electronic conductor La2NiO4+δ: Lattice relaxation, oxygen mobility, and energetics of frenkel defects. Chem. Mater. 2005;17:6538–6544. doi: 10.1021/cm050195f. [DOI] [Google Scholar]
- 68.Parfitt D., Chroneos A., Kilner J.A., Grimes R.W. Molecular dynamics study of oxygen diffusion in Pr2NiO4+δ. Phys. Chem. Chem. Phys. 2010;12:6834–6836. doi: 10.1039/c001809k. [DOI] [PubMed] [Google Scholar]
- 69.Allan N.L., Mackrodt W.C. Oxygen ion migration in La2CuO4. Philos. Mag. A. 1991;64:1129–1132. doi: 10.1080/01418619108204884. [DOI] [Google Scholar]
- 70.Kushima A., Parfitt D., Chroneos A., Yildiz B., Kilner J.A., Grimes R.W. Interstitialcy diffusion of oxygen in tetragonal La2CoO4+δ. Phys. Chem. Chem. Phys. 2011;13:2242–2249. doi: 10.1039/C0CP01603A. [DOI] [PubMed] [Google Scholar]
- 71.Nakamura T., Yashiro K., Sato K., Mizusaki J. Oxygen nonstoichiometry and defect equilibrium in La2−xSrxNiO4+δ. Solid State Ion. 2009;180:368–376. doi: 10.1016/j.ssi.2009.01.013. [DOI] [Google Scholar]
- 72.Vashook V.V., Trofimenko N.E., Ullmann H., Makhnach L.V. Oxygen nonstoichiometry and some transport properties of LaSrNiO4−δ nickelate. Solid State Ion. 2000;131:329–336. doi: 10.1016/S0167-2738(00)00571-3. [DOI] [Google Scholar]
- 73.Mazo G.N., Savvin S.N. The molecular dynamics study of oxygen mobility in La2−xSrxCuO4−δ. Solid State Ion. 2004;175:371–374. doi: 10.1016/j.ssi.2003.12.028. [DOI] [Google Scholar]
- 74.Savvin S.N., Mazo G.N., Ivanov-Schitz A.K. Simulation of ion transport in layered cuprates La2−xSrxCuO4−δ. Crystallogr. Rep. 2008;53:291–301. doi: 10.1134/S1063774508020193. [DOI] [Google Scholar]
- 75.Kanai H., Mizusaki J., Tagawa H., Hoshiyama S., Hirano K., Fujita K., Tezuka M., Hashimoto T. Defect chemistry of La2−xSrxCuO4−δ: Oxygen nonstoichiometry and thermodynamic stability. J. Solid State Chem. 1997;131:150–159. doi: 10.1006/jssc.1997.7377. [DOI] [Google Scholar]
- 76.Teske K., Ullmann H., Trofimenko N. Thermal analysis of transition metal and rare earth oxide system-gas interactions by a solid electrolyte-based coulometric technique. J. Therm. Anal. 1997;49:1211–1220. doi: 10.1007/BF01983677. [DOI] [Google Scholar]
- 77.Munnings C.N., Skinner S.J., Amow G., Whitfield P.S., Davidson I.J. Oxygen transport in the La2Ni1−xCoxO4+δ system. Solid State Ion. 2005;176:1895–1901. doi: 10.1016/j.ssi.2005.06.002. [DOI] [Google Scholar]
- 78.Alyoshin V.A., Romanova I.P., Mikhailova D., Oswald S., Senyshyn A., Ehrenberg H. Oxygen nonstoichiometry of tetragonal La2−xSrxCuO4−δ (x = 0.15–1.2) and in situ XPS studies at elevated temperatures. J. Phys. Chem. A. 2010;114:13362–13369. doi: 10.1021/jp108648e. [DOI] [PubMed] [Google Scholar]
- 79.Tealdi C., Ferrara C., Mustarelli P., Islam M.S. Vacancy and interstitial oxide ion migration in heavily doped La2−xSrxCoO4±δ. J. Mater. Chem. 2012;22:8969–8975. doi: 10.1039/c2jm30769c. [DOI] [Google Scholar]
- 80.De Souza R.A., Ramadan A., Horner S. Modifying the barriers for oxygen-vacancy migration in fluorite-structured CeO2 electrolytes through strain: A computer simulation study. Energy Environ. Sci. 2012;5:5445–5453. doi: 10.1039/C2EE02508F. [DOI] [Google Scholar]
- 81.Jiang J., Hu X.C., Shen W.D., Ni C.Y., Hertz J.L. Improved ionic conductivity in strained yttria-stabilized zirconia thin films. Appl. Phys. Lett. 2013;102:143901. doi: 10.1063/1.4801649. [DOI] [Google Scholar]
- 82.Kushima A., Yildiz B. Oxygen ion diffusivity in strained yttria stabilized zirconia: Where is the fastest strain? J. Mater. Chem. 2010;20:4809–4819. doi: 10.1039/c000259c. [DOI] [Google Scholar]
- 83.Rushton M.J.D., Chroneos A. Impact of uniaxial strain and doping on oxygen diffusion in CeO2. Sci. Rep. 2014;4:6068. doi: 10.1038/srep06068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Yildiz B. “Stretching” the energy landscape of oxides-effects on electrocatalysis and diffusion. MRS Bull. 2014;39:147–156. doi: 10.1557/mrs.2014.8. [DOI] [Google Scholar]
- 85.Mayeshiba T., Morgan D. Strain effects on oxygen migration in perovskites. Phys. Chem. Chem. Phys. 2015;17:2715–2721. doi: 10.1039/C4CP05554C. [DOI] [PubMed] [Google Scholar]
- 86.Petrie J.R., Mitra C., Jeen H., Choi W.S., Meyer T.L., Reboredo F.A., Freeland J.W., Eres G., Lee H.N. Strain control of oxygen vacancies in epitaxial strontium cobaltite films. Adv. Funct. Mater. 2016;26:1564–1570. doi: 10.1002/adfm.201504868. [DOI] [Google Scholar]
- 87.Islam M.S., Cherry M., Catlow C.R.A. Oxygen diffusion in LaMnO3 and LaCoO3 perovskite-type oxides: A molecular dynamics study. J. Solid State Chem. 1996;124:230–237. doi: 10.1006/jssc.1996.0231. [DOI] [Google Scholar]
- 88.Cherry M., Islam M.S., Catlow C.R.A. Oxygen ion migration in perovskite-type oxides. J. Solid State Chem. 1995;118:125–132. doi: 10.1006/jssc.1995.1320. [DOI] [Google Scholar]
- 89.De Souza R.A., Kilner J.A. Oxygen transport in La1−xSrxMn1−yCoyO3±δ. Part I. Oxygen tracer diffusion. Solid State Ion. 1998;106:175–187. doi: 10.1016/S0167-2738(97)00499-2. [DOI] [Google Scholar]
- 90.Ishigaki T., Yamauchi S., Kishio K., Mizusaki J., Fueki K. Diffusion of oxide ion vacancies in perovskite-type oxides. J. Solid State Chem. 1988;73:179–187. doi: 10.1016/0022-4596(88)90067-9. [DOI] [Google Scholar]
- 91.Ishigaki T., Yamauchi S., Mizusaki J., Fueki K., Tamura H. Tracer diffusion-coefficient of oxide ions in LaCoO3 single-crystal. J. Solid State Chem. 1984;54:100–107. doi: 10.1016/0022-4596(84)90136-1. [DOI] [Google Scholar]
- 92.Routbort J.L., Doshi R., Krumpelt M. Oxygen tracer diffusion in La1−xSrxCoO3. Solid State Ion. 1996;90:21–27. doi: 10.1016/S0167-2738(96)00402-X. [DOI] [Google Scholar]
- 93.Van Doorn R.H.E., Fullarton I.C., De Souza R.A., Kilner J.A., Bouwmeester H.J.M., Burggraaf A.J. Surface oxygen exchange of La0.3Sr0.7CoO3−δ. Solid State Ion. 1997;96:1–7. doi: 10.1016/S0167-2738(97)00011-8. [DOI] [Google Scholar]
- 94.Kilner J.A., Shaw C.K.M. Mass transport in La2Ni1−xCoxO4+δ oxides with the K2NiF4 structure. Solid State Ion. 2002;154:523–527. doi: 10.1016/S0167-2738(02)00506-4. [DOI] [Google Scholar]
- 95.Li Z.A., Haugsrud R., Smith J.B., Norby T. Transport properties and defect analysis of La1.9Sr0.1NiO4+δ. Solid State Ion. 2009;180:1433–1441. doi: 10.1016/j.ssi.2009.08.011. [DOI] [Google Scholar]
- 96.Skinner S.J., Kilner J.A. A comparison of the transport properties of La2−xSrxNi1−yFeyO4+δ where 0 < x < 0.2 and 0 < y < 0.2. Ionics. 1999;5:171–174. [Google Scholar]
- 97.Burriel M., Téllez H., Chater R.J., Castaing R., Veber P., Zaghrioui M., Ishihara T., Kilner J.A., Bassat J.-M. Influence of crystal orientation and annealing on the oxygen diffusion and surface exchange of La2NiO4+δ. J. Phys. Chem. C. 2016;120:17927–17938. doi: 10.1021/acs.jpcc.6b05666. [DOI] [Google Scholar]
- 98.Boehm E., Bassat J.M., Steil M.C., Dordor P., Mauvy F., Grenier J.C. Oxygen transport properties of La2Ni1−xCuxO4+δ mixed conducting oxides. Solid State Sci. 2003;5:973–981. doi: 10.1016/S1293-2558(03)00091-8. [DOI] [Google Scholar]
- 99.Claus J., Borchardt G., Weber S., Hiver J.M., Scherrer S. Combination of EBSP measurements and sims to study crystallographic orientation dependence of diffusivities in a polycrystalline material: Oxygen tracer diffusion in La2−xSrxCuO4±δ. Mater. Sci. Eng. B. 1996;38:251–257. doi: 10.1016/0921-5107(95)01446-2. [DOI] [Google Scholar]
- 100.Routbort J.L., Rothman S.J., Flandermeyer B.K., Nowicki L.J., Baker J.E. Oxygen diffusion in La2−xSrxCuO4−δ. J. Mater. Res. 1988;3:116–121. doi: 10.1557/JMR.1988.0116. [DOI] [Google Scholar]
- 101.Shannon R.D., Prewitt C.T. Effective ionic radii in oxides and fluorides. Acta Cryst. 1969;B25:925–946. doi: 10.1107/S0567740869003220. [DOI] [Google Scholar]
- 102.Lee D., Lee Y.-L., Grimaud A., Hong W.T., Biegalski M.D., Morgan D., Shao-Horn Y. Strontium influence on the oxygen electrocatalysis of La2−xSrxNiO4±δ (0.0 ≤ xSr ≤ 1.0) thin films. J. Mater. Chem. A. 2014;2:6480–6487. doi: 10.1039/c3ta14918h. [DOI] [Google Scholar]
- 103.Allan N.L., Lawton J.M., Mackrodt W.C. A comparison of the calculated lattice and defect structures of La2CuO4, La2NiO4, Nd2CuO4, Pr2CuO4, Y2CuO4, Al2CuO4: Relationship to high-Tc superconductivity. Philos. Mag. B. 1989;59:191–206. doi: 10.1080/13642818908220171. [DOI] [Google Scholar]
- 104.Allan N.L., Mackrodt W.C. Defect chemistry of La2CuO4, Nd2CuO4 and Pr2CuO4 doped by tetravalent cations: Relevance to high-Tc behavior. Philos. Mag. Lett. 1989;60:183–186. doi: 10.1080/09500838908206455. [DOI] [Google Scholar]
- 105.Naumovich E.N., Patrakeev M.V., Kharton V.V., Yaremchenko A.A., Lopinovich D.I., Marques F.M.B. Oxygen nonstoichiornetry in La2Ni(M)O4+δ (M = Cu, Co) under oxidizing conditions. Solid State Sci. 2005;7:1353–1362. doi: 10.1016/j.solidstatesciences.2005.08.005. [DOI] [Google Scholar]
- 106.Lee Y.-L., Lee D., Wang X.R., Lee H.N., Morgan D., Shao-Horn Y. Kinetics of oxygen surface exchange on epitaxial Ruddlesden–Popper phases and correlations to first-principles descriptors. J. Phys. Chem. Lett. 2016;7:244–249. doi: 10.1021/acs.jpclett.5b02423. [DOI] [PubMed] [Google Scholar]
- 107.Xie W., Lee Y.-L., Shao-Horn Y., Morgan D. Oxygen point defect chemistry in Ruddlesden–Popper oxides (La1−xSrx)2MO4±δ (M = Co, Ni, Cu) J. Phys. Chem. Lett. 2016;7:1939–1944. doi: 10.1021/acs.jpclett.6b00739. [DOI] [PubMed] [Google Scholar]
- 108.Amow G., Skinner S.J. Recent developments in Ruddlesden–Popper nickelate systems for solid oxide fuel cell cathodes. J. Solid State Electrochem. 2006;10:538–546. doi: 10.1007/s10008-006-0127-x. [DOI] [Google Scholar]
- 109.Chen Y., Téllez H., Burriel M., Yang F., Tsvetkov N., Cai Z., McComb D.W., Kilner J.A., Yildiz B. Segregated chemistry and structure on (001) and (100) surfaces of (La1−xSrx)2CoO4 override the crystal anisotropy in oxygen exchange kinetics. Chem. Mater. 2015;27:5436–5450. doi: 10.1021/acs.chemmater.5b02292. [DOI] [Google Scholar]
- 110.Aidhy D.S., Liu B., Zhang Y.W., Weber W.J. Strain-induced phase and oxygen-vacancy stability in ionic interfaces from first-principles calculations. J. Phys. Chem. C. 2014;118:30139–30144. doi: 10.1021/jp507876m. [DOI] [Google Scholar]
- 111.Aidhy D.S., Zhang Y.W., Weber W.J. (001) SrTiO3 vertical bar (001) MGO interface and oxygen-vacancy stability from first-principles calculations. ACS Appl. Mater. Interfaces. 2014;6:15536–15541. doi: 10.1021/am504306t. [DOI] [PubMed] [Google Scholar]
- 112.Fronzi M., Cereda S., Tateyama Y., De Vita A., Traversa E. Ab initio investigation of defect formation at ZrO2-CeO2 interfaces. Phys. Rev. B. 2012;86:085407. doi: 10.1103/PhysRevB.86.085407. [DOI] [Google Scholar]
- 113.Shen W.D., Jiang J., Hertz J.L. Beneficial lattice strain in heterogeneously doped ceria. J. Phys. Chem. C. 2014;118:22904–22912. doi: 10.1021/jp506554z. [DOI] [Google Scholar]
- 114.Shen W.D., Jiang J., Ni C.Y., Voras Z., Beebe T.P., Hertz J.L. Two-dimensional vacancy trapping in yttria doped ceria. Solid State Ion. 2014;255:13–20. doi: 10.1016/j.ssi.2013.11.012. [DOI] [Google Scholar]
- 115.Cho S.Y., Chung Y.-C., Ahn K., Lee J.-H., Kim B.-K., Kim H. Oxygen transport in epitaxial La0.875Sr0.125CoO3−δ thin-film cathodes for solid oxide fuel cells: Roles of anisotropic strain. Scr. Mater. 2016;115:141–144. doi: 10.1016/j.scriptamat.2015.12.035. [DOI] [Google Scholar]
- 116.Gan L.-Y., Akande S.O., Schwingenschlogl U. Anisotropic O vacancy formation and diffusion in LaMnO3. J. Mater. Chem. A. 2014;2:19733–19737. doi: 10.1039/C4TA04119D. [DOI] [Google Scholar]
- 117.Kushima A., Yildiz B. Role of lattice strain and defect chemistry on the oxygen vacancy migration at the (8.3% Y2O3-ZrO2)/SrTiO3 hetero-interface: A first principles study. ECS Trans. 2009;25:1599–1609. [Google Scholar]
- 118.Petrie J.R., Jeen H., Barron S.C., Meyer T.L., Lee H.N. Enhancing perovskite electrocatalysis through strain tuning of the oxygen deficiency. J. Am. Chem. Soc. 2016;138:7252–7255. doi: 10.1021/jacs.6b03520. [DOI] [PubMed] [Google Scholar]
- 119.Xu T., Shimada T., Araki Y., Wang J., Kitamura T. Defect-strain engineering for multiferroic and magnetoelectric properties in epitaxial (110) ferroelectric lead titanate. Phys. Rev. B. 2015;92:104106. doi: 10.1103/PhysRevB.92.104106. [DOI] [Google Scholar]
- 120.Tsvetkov N., Lu Q., Chen Y., Yildiz B. Accelerated oxygen exchange kinetics on Nd2NiO4+δ thin films with tensile strain along c-axis. ACS Nano. 2015;9:1613–1621. doi: 10.1021/nn506279h. [DOI] [PubMed] [Google Scholar]
- 121.Bishop S.R., Duncan K.L., Wachsman E.D. Thermo-chemical expansion in strontium-doped lanthanum cobalt iron oxide. J. Am. Ceram. Soc. 2010;93:4115–4121. doi: 10.1111/j.1551-2916.2010.03991.x. [DOI] [Google Scholar]
- 122.Borovskikh L., Mazo G., Kemnitz E. Reactivity of oxygen of complex cobaltates La1−xSrxCoO3−δ and LaSrCoO4. Solid State Sci. 2003;5:409–417. doi: 10.1016/S1293-2558(03)00052-9. [DOI] [Google Scholar]
- 123.Cai Z.H., Kubicek M., Fleig J., Yildiz B. Chemical heterogeneities on La0.6Sr0.4CoO3-δ thin films-correlations to cathode surface activity and stability. Chem. Mater. 2012;24:1116–1127. doi: 10.1021/cm203501u. [DOI] [Google Scholar]
- 124.Hardy J.S., Templeton J.W., Edwards D.J., Lu Z.G., Stevenson J.W. Lattice expansion of LSCF-6428 cathodes measured by in situ XRD during SOFC operation. J. Power Sources. 2012;198:76–82. doi: 10.1016/j.jpowsour.2011.09.099. [DOI] [Google Scholar]
- 125.Hashimoto S., Fukuda Y., Kuhn M., Sato K., Yashiro K., Mizusaki J. Oxygen nonstoichiometry and thermo-chemical stability of La0.6Sr0.4Co1−yFeyO3−δ (y = 0.2, 0.4, 0.6, 0.8) Solid State Ion. 2010;181:1713–1719. doi: 10.1016/j.ssi.2010.09.024. [DOI] [Google Scholar]
- 126.Kahoul A., Hammouche A., Poillerat G., De Doncker R.W. Electrocatalytic activity and stability of La1−xCaxCoO3 perovskite-type oxides in alkaline medium. Catal. Today. 2004;89:287–291. doi: 10.1016/j.cattod.2003.12.003. [DOI] [Google Scholar]
- 127.Kharton V.V., Yaremchenko A.A., Patrakeev M.V., Naumovich E.N., Marques F.M.B. Thermal and chemical induced expansion of La0.3Sr0.7(Fe,Ga)O3−δ ceramics. J. Eur. Ceram. Soc. 2003;23:1417–1426. doi: 10.1016/S0955-2219(02)00308-4. [DOI] [Google Scholar]
- 128.Lugovy M., Aman A., Chen Y., Orlovskaya N., Kuebler J., Graule T., Reece M.J., Ma D., Stoica A.D., An K. In-situ neutron diffraction of LaCoO3 perovskite under uniaxial compression. II. Elastic properties. J. Appl. Phys. 2014;116:013504. doi: 10.1063/1.4884336. [DOI] [Google Scholar]
- 129.Samal D., Kumar P.S.A. A critical re-examination and a revised phase diagram of La1−xSrxCoO3. J. Phys. Condens. Matter. 2011;23:9. doi: 10.1088/0953-8984/23/1/016001. [DOI] [PubMed] [Google Scholar]
- 130.Baumann F.S., Fleig J., Cristiani G., Stuhlhofer B., Habermeier H.U., Maier J. Quantitative comparison of mixed conducting SOFC cathode materials by means of thin film model electrodes. J. Electrochem. Soc. 2007;154:B931–B941. doi: 10.1149/1.2752974. [DOI] [Google Scholar]
- 131.Steele B.C.H., Heinzel A. Materials for fuel-cell technologies. Nature. 2001;414:345–352. doi: 10.1038/35104620. [DOI] [PubMed] [Google Scholar]
- 132.Sun C.W., Hui R., Roller J. Cathode materials for solid oxide fuel cells: A review. J. Solid State Electrochem. 2010;14:1125–1144. doi: 10.1007/s10008-009-0932-0. [DOI] [Google Scholar]
- 133.Petric A., Huang P., Tietz F. Evaluation of La-Sr-Co-Fe-O perovskites for solid oxide fuel cells and gas separation membranes. Solid State Ion. 2000;135:719–725. doi: 10.1016/S0167-2738(00)00394-5. [DOI] [Google Scholar]
- 134.Skinner S.J. Characterisation of La2NiO4+δ using in-situ high temperature neutron powder diffraction. Solid State Sci. 2003;5:419–426. doi: 10.1016/S1293-2558(03)00050-5. [DOI] [Google Scholar]
- 135.Huang B.X., Malzbender J., Steinbrech R.W. Thermo-mechanical properties of La2NiO4+δ. J. Mater. Sci. 2011;46:4937–4941. doi: 10.1007/s10853-011-5406-y. [DOI] [Google Scholar]
- 136.Makhnach L.V., Pankov V.V., Strobel P. High-temperature oxygen non-stoichiometry, conductivity and structure in strontium-rich nickelates La2−xSrxNiO4−δ (x = 1 and 1.4) Mater. Chem. Phys. 2008;111:125–130. doi: 10.1016/j.matchemphys.2008.03.022. [DOI] [Google Scholar]
- 137.Millburn J.E., Green M.A., Neumann D.A., Rosseinsky M.J. Evolution of the structure of the K2NiF4 phases La2−xSrxNiO4+δ with oxidation state: Octahedral distortion and phase separation (0.2 ≤ x ≤ 1.0) J. Solid State Chem. 1999;145:401–420. doi: 10.1006/jssc.1999.8111. [DOI] [Google Scholar]
- 138.Nakamura T., Yashiro K., Sato K., Mizusaki J. Structural analysis of La2−xSrxNiO4+δ by high temperature X-ray diffraction. Solid State Ion. 2010;181:292–299. doi: 10.1016/j.ssi.2010.01.007. [DOI] [Google Scholar]
- 139.Kharton V.V., Kovalevsky A.V., Avdeev M., Tsipis E.V., Patrakeev M.V., Yaremchenko A.A., Naumovich E.N., Frade J.R. Chemically induced expansion of La2NiO4+δ-based materials. Chem. Mater. 2007;19:2027–2033. doi: 10.1021/cm070096x. [DOI] [Google Scholar]
- 140.Kharton V.V., Yaremchenko A.A., Shaula A.L., Patrakeev M.V., Naumovich E.N., Loginovich D.I., Frade J.R., Marques F.M.B. Transport properties and stability of Ni-containing mixed conductors with perovskite- and K2NiF4-type structure. J. Solid State Chem. 2004;177:26–37. doi: 10.1016/S0022-4596(03)00261-5. [DOI] [Google Scholar]
- 141.Tietz F., Raj I.A., Zahid M., Mai A., Stover D. Survey of the quasi-ternary system La0.8Sr0.2MnO3-La0.8Sr0.2CoO3-La0.8Sr0.2FeO3. Prog. Solid State Chem. 2007;35:539–543. doi: 10.1016/j.progsolidstchem.2007.01.028. [DOI] [Google Scholar]
- 142.Ullmann H., Trofimenko N., Tietz F., Stover D., Ahmad-Khanlou A. Correlation between thermal expansion and oxide ion transport in mixed conducting perovskite-type oxides for SOFC cathodes. Solid State Ion. 2000;138:79–90. doi: 10.1016/S0167-2738(00)00770-0. [DOI] [Google Scholar]
- 143.Tai L.W., Nasrallah M.M., Anderson H.U., Sparlin D.M., Sehlin S.R. Structure and electrical properties of La1−xSrxCo1−yFeyO3. Part 2. The system La1−xSrxCo0.2Fe0.8O3. Solid State Ion. 1995;76:273–283. doi: 10.1016/0167-2738(94)00245-N. [DOI] [Google Scholar]
- 144.Munnings C.N., Skinner S.J., Amow G., Whitfield P.S., Davidson L.J. Structure, stability and electrical properties of the La2−xSrxMnO4±δ solid solution series. Solid State Ion. 2006;177:1849–1853. doi: 10.1016/j.ssi.2006.01.009. [DOI] [Google Scholar]
- 145.Riza F., Ftikos C. Influence of A- and B-site doping on the properties of the system La2CoO4±δ. J. Eur. Ceram. Soc. 2007;27:571–573. doi: 10.1016/j.jeurceramsoc.2006.04.069. [DOI] [Google Scholar]