Structurally Linked Dynamics in Lactate Dehydrogenases of Evolutionarily Distinct Species

Abstract

We present new findings about how primary and secondary structure affects the role of fast protein motions in the reaction coordinates of enzymatic reactions. Using transition path sampling and committor distribution analysis, we examined the difference in the role of these fast protein motions in the reaction coordinate of lactate dehydrogenases (LDHs) of Apicomplexa organisms Plasmodium falciparum and Cryptosporidium parvum. Having evolved separately from a common malate dehydrogenase ancestor, the two enzymes exhibit several important structural differences, notably a five-amino acid insertion in the active site loop of P. falciparum LDH. We find that these active site differences between the two organisms’ LDHs likely cause a decrease in the contribution of the previously determined LDH rate-promoting vibration to the reaction coordinate of P. falciparum LDH compared to that of C. parvum LDH, specifically in the coupling of the rate-promoting vibration and the hydride transfer. This effect, while subtle, directly shows how changes in structure near the active site of LDH alter catalytically important motions. Insights provided by studying these alterations would prove to be useful in identifying LDH inhibitors that specifically target the isozymes of these parasitic organisms.

Graphical abstract

The effect of protein motion on both the mechanism and rate of enzymatic reactions has recently become a topic of significant research. A well-known example of this is that of dihydrofolate reductase (DHFR); millisecond scale motions, e.g., conformational changes, have been shown to play a critical role in the reaction coordinate of the enzyme.^1,2 Additionally, recent computational work has shown that much faster, subpicosecond protein motions coupled to the reaction coordinate, called rate-promoting vibrations (RPVs), are present in several types of enzymes, most notably in particle transfer enzymes such as alcohol dehydrogenase (ADH),^3,4 lactate dehydrogenase (LDH),^5–7 and human DHFR.⁸ Experimental studies augment this computational work, shedding further light on the role of fast protein motions on the chemical step, including LDH,⁹ purine nucleoside phosphorylase (PNP),¹⁰ and alanine racemase.¹¹ RPVs in particle transfer reactions usually consist of several residues relatively distant from the active site that push on the donor and acceptor before the transfer event, compressing the donor–acceptor distance and lowering the barrier to reaction. In particular, LDH is a target for the study of these motions, as it has been well studied experimentally^9,12–14 and computationally.^{5–7,15–17} LDH, typically a homotetramer, catalyzes the interconversion of pyruvate and lactate through the transfer of a proton from an active site histidine and a hydride from the nicotinamide adenine dinucleotide (NADH) cofactor. Previous work⁷ has determined that the human heart (hhLDH) and Geobacillus stearothermophilus (bsLDH) isozymes exhibit a four-residue promoting vibration consisting of a conserved active site arginine (R109) that pushes on the hydride acceptor, the pyruvate, and a three-residue feature (V32, G33, and M34 in hhLDH and V32, G33, and A34 in bsLDH), which pushes on the hydride donor, the NADH nicotinamide ring (note that all residue numbering in this paper follows that of dogfish LDH).¹⁸ We have previously shown, through calculation of the coherent dynamical structure factor in hhLDH,¹⁹ that equilibrium density fluctuations exhibit anisotropy along the RPV coordinate, indicating that motions along the RPV coordinate are long-lived, stable, and faster than motions along other axes in the enzyme. This provides confirmation of the nonstochastic nature of these motions.

While previous studies showed that these motions are found in some organisms with canonical LDHs,⁷ the sequences of these enzymes are highly conserved, and little significant research has probed how robust these motions are to changes in primary and secondary structure near the active site. Furthermore, there is a dearth of computational work examining noncanonical LDHs, or LDHs phylogenetically contained within the LDH-like malate dehydrogenase (MDH) family, a subgroup of the larger 2-ketoacid:NAD(P)-dependent enzyme superfamily (see refs ^20–22 for discussions of phylogeny and phylogenetic trees of these organisms and their dehydrogenases). A well-characterized sequence variation differentiates the majority of canonical LDHs from LDH-like MDHs; position 102, located adjacent to the substrate specificity loop that closes over the active site after binding to exclude water, is typically an uncharged residue such as glutamine in canonical LDHs and positively charged arginine in LDH-like MDH. This residue is known to be responsible for substrate specificity in LDHs and MDHs.²³

To examine differences in dynamics between canonical and noncanonical LDHs, we studied two related, but ultimately evolutionarily distinct, lactate dehydrogenases from Apicomplexa organisms, Plasmodium falciparum (pfLDH) and Cryptosporidium parvum (cpLDH).²² While both pfLDH and cpLDH are lactate dehydrogenases, they evolved through separate evolutionary events from a common LDH-like MDH ancestor; pfLDH evolved through a gene duplication before the evolutionary expansion of the Apicomplexa phylum,^21,22 whereas cpLDH likely evolved from its cytosolic LDH-like MDH through a separate gene duplication after it evolutionarily diverged from other Apicomplexa.^21,24 These LDHs are therefore evolutionarily distinct from other LDHs,^20–22 with pfLDH and cpLDH sharing 42% sequence homology with each other and 29 and 27% sequence homology with hhLDH, respectively.²⁵ Interestingly, while these enzymes catalyze the reaction characteristic of LDHs, they share sequence similarities with LDH-like MDHs, specifically a positively charged lysine at position 102 in pfLDH,²⁰ and a glycine at position 102 in cpLDH.²¹ Additionally, as a result of this parallel evolution, some members of Apicomplexa, such as Plasmodium²⁶ and Toxiplasmosa,²⁷ have a five-amino acid insertion (DKEWN sequence in most enzymes exhibiting it) in the previously mentioned substrate specificity loop of LDH. This loop insertion is unique to these LDHs and is not found in canonical LDHs or cpLDH. Furthermore, a conserved serine residue in all canonical LDHs (S163), which hydrogen bonds to the nicotinamide ring via a conserved water moiety, is instead a leucine in pfLDH and a methionine in cpLDH.¹⁴ The structural features described (the LDH active site, analogous RPV residues, M163 in cpLDH, and L163 in pfLDH) above can be seen in Figure 1. Multiple experimental studies have investigated the active site changes in pfLDH, showing that both the L163S mutation or completely removing the loop insertion from pfLDH destabilizes the enzyme such that it is unable to fold properly,¹³ and that larger active site loop causes the enzyme to be more intolerant of larger substrates.²⁸ Furthermore, experimental kinetic studies show that cpLDH²⁹ has a rate of turnover (k_cat) higher than that of pfLDH,³⁰ with respect to the conversion of pyruvate to lactate using NADH as a cofactor.

Figure 1.

Depiction of structural features in pfLDH (red) and cpLDH (blue). (a) Alignment of pfLDH and cpLDH crystal structures, showing the NADH (purple), substrate (dark blue), and loop insertion in pfLDH (yellow). Alignment performed with THESEUS.^31,32 (b) Active site of pfLDH (and representative of cpLDH). Important residues are labeled. (c) Active site of pfLDH, showing the QM region (dark blue), analogous RPV residues from hhLDH (red), and L163 (yellow). (d) Active site of pfLDH, showing the QM region (dark blue), analogous RPV residues from hhLDH (red), and M163 (yellow).

As discussed above, it has been established that fast protein motions are crucial to the chemical step in a number of enzymatic reactions. Investigating how coherent motions contribute to the chemical step provides insight into the role that protein structure plays in the function of enzymes. Knowledge of structure–function relationships in terms of how changes to primary and secondary structure alter motions and how those motions impact the chemistry of enzymatic reactions provides a set of tools that are useful in designing enzymes that incorporate and take advantage of those motions to catalyze complex reactions. In addition to these interesting biophysical questions, examining how potentially catalytically important motions are altered in pfLDH and cpLDH relative to human LDHs would benefit the search for small molecule drugs to target LDHs of these disease-causing organisms without the side effect of disrupting other LDHs necessary for normal human function. Previous work showed that RPV-mediated allostery of hhLDH through small molecule targeting of the RPV residues has the ability to alter the reaction coordinate of hhLDH,³⁵ and possibly inhibit catalysis. As P. falciparum³³ and C. parvum²¹ are both nearly dependent on glycolysis for ATP synthesis, LDH is a prime drug target for these organisms.

Herein, we present the findings of a computational investigation of the dynamics of these two LDHs, pfLDH and cpLDH. Using quantum mechanics/molecular mechanics (QM/MM) simulations and transition path sampling, we examined the relative role that subpicosecond protein motions play in the enzymes’ respective chemical step reaction coordinates. We found that both pfLDH and cpLDH exhibit a rate-promoting vibration analogous to that of the canonical LDHs from human heart and G. stearothermophilus. However, these motions contribute differently to the reaction coordinates of the two Apicomplexa enzymes. Through trajectory and committor analysis, we found that cpLDH mimics canonical LDHs while pfLDH makes a smaller contribution of the RPV to the overall reaction coordinate, possibly representing decoupling of the RPV from the hydride transfer event. This effect is subtle but shows how changes in active site structure can alter the reaction dynamics of isozymes. Additionally, it shows the power of computational simulations to interrogate slight alterations to dynamics that occur on time scales difficult to observe with experimental methods.

MATERIALS AND METHODS

System Setup

Simulations started with X-ray crystal structures of lactate dehydrogenase from P. falciparum³⁴ [Protein Data Bank (PDB) 1T2D] and C. parvum²⁹ (PDB entry 4ND4). The system setup followed that of previous studies,^3,35 and for the sake of completeness, a brief description of this procedure is provided here. All simulations were performed with the CHARMM^36,37 molecular dynamics package and the CHARMM27 force field for the classical region and the AM1 semiempirical method³⁸ for the quantum region. As pfLDH was crystallized with a substrate analogue, oxalate, this was changed to pyruvate for the purposes of this study. The active site of one monomer from each enzyme was partitioned into a quantum (QM) region consisting of 38 atoms: the pyruvate, the NADH nicotinamide ring, and the active site histidine side chain. Boundary atoms between the QM and MM regions, the C_α atom of the catalytic histidine and the NC1 atom of the nicotinamide ring, were treated with the generalized hybrid orbital (GHO) method.³⁹ The systems were solvated explicitly with TIP3 water in a nanosphere, to simulate bulk water and reduce edge effects, and neutralized with potassium ions. Each system proceeded with a two-step minimization: the first 100 steps of steepest descent minimization to remove bad contacts and clashes and then 1000 steps of adopted-basis Newton–Raphson (ABNR) minimization. Harmonic constraints were added to the protein (20 kcal mol⁻¹ Å⁻²), quantum region (50 kcal mol⁻¹ Å⁻²), and cofactor (20 kcal mol⁻¹ Å⁻²) during minimization and were progressively relaxed during the course of ABNR minimization. The solvated systems were then heated to 300 K and equilibrated for 300 ps, until the energy of the system plateaued. It should be noted that to successfully heat pfLDH while retaining an important hydrogen bond, harmonic constraints (20 kcal mol⁻¹ Å⁻²) were applied to the backbone and reduced while heating. Further discussion of this can be found below.

Transition Path Sampling

We used transition path sampling (TPS)^40–43 to harvest trajectories once the initial setup was complete. TPS is a Markov Chain Monte Carlo (MCMC) method with which rare events in complex systems can be studied without prior knowledge of the reaction coordinate, a substantial benefit in enzymatic systems that can have many thousands of degrees of freedom. Although knowledge of the reaction coordinate is not necessary to perform TPS, an order parameter describing the progress of the reaction, e.g., donor–acceptor distances, must be defined such that there are well-defined, metastable reactant and product wells. TPS is initiated by creating an initial reactive trajectory produced by constraining the product well order parameter such that the reaction is forced to occur. From this initial, constrained trajectory, a time slice is chosen at random, and its momentum is perturbed randomly per a Boltzmann distribution. A new trajectory is then initiated from this set of coordinates and perturbed momenta. To maintain a microcanonical ensemble, the velocities are rescaled after perturbation to keep the energy of the system constant. Using a microcanonical ensemble allows the typical Metropolis acceptance criterion to reduce to $P_{\mathrm{a}}^{0\to n}\text{cc}=h_{\mathrm{R}}({x_0}^n)H{\left({x_{\mathrm{T}}}^n\right)}_{\mathrm{P}}$, where h_R and H_P are Heaviside functions indicating commitment and visitation to the reactant and product wells, respectively. Plainly, if the new trajectory begins in the reactive well and ends in the product well, it is accepted and considered reactive.⁴⁰ Otherwise, the trajectory, considered nonreactive, is discarded, and a new trajectory with new randomly perturbed momenta is initiated from the same time slice. Through this iterative random sampling, using the previous accepted trajectory as a seed for the next trajectory, an ensemble of reactive trajectories that contains energetically allowable paths from reactants to products and produces thermodynamically correct statistics is created. This method has been used successfully to study protein dynamics and kinetics in a multitude of systems, such as YADH,^3,44 hhLDH,^6,35 DHFR,⁴⁵ PNP,⁴⁶ and base-catalyzed peptide hydrolysis.⁴⁷

For the purposes of this study, the order parameters chosen to describe the course of the reaction were the donor–acceptor distances for both the proton transfer and the hydride transfer. Trajectories were accepted if the particle–acceptor distance was <1.35 Å for both transfers. These criteria have been used successfully in a previous study of hhLDH.³⁵ For each system, we obtained an initial constrained reactive trajectory by applying harmonic constraints to the proton donor–acceptor, proton–donor, proton–acceptor, hydride donor–acceptor, hydride–donor, and hydride–acceptor distances. These distances are defined as follows: protonated nitrogen of the catalytic histidine, proton donor; carbonyl oxygen of the pyruvate substrate, proton acceptor; nicotinamide ring of the NADH, hydride donor; carbonyl carbon of the pyruvate substrate, hydride acceptor. These harmonic constraints were kept as weak as possible while ensuring a reactive trajectory, to introduce as little bias as possible into the system. Unconstrained trajectories for each system were initiated using these constrained trajectories as seeds, and the first 10 of each ensemble were discarded to allow decorrelation of the ensemble from initial biases. Subsequent trajectories were obtained by shooting from a random slice from the previous accepted trajectory. Each trajectory was 500 fs in length, with a time step of 1 fs.

Committor Analysis

We used committor analysis to determine commitment probabilities along a set of trajectories, to find transition states for those trajectories.⁴⁸ In committor analysis, we first initiate trajectories with random velocities from time slices along a reactive trajectory. Fifty trajectories of 250 fs were collected for each time slice along a reactive trajectory. These randomly initiated trajectories are used to calculate the commitment probability at each time slice, with the slice with a commitment probability of 0.5 denoting the separatrix, i.e., the point at which there is an equal chance that a trajectory initiated with random velocities will end in the reactant well and product well. This time slice is equated to the transition state. This technique has been used previously to determine transition states of enzymatic reactions in several recent studies.^35,46

To determine reaction coordinates for the two enzymes, we used committor distribution analysis. Starting from a transition state previously determined through committor analysis, a 250 fs trajectory is initiated, in which atoms and residues comprising an inferred reaction coordinate are constrained using harmonic constraints. From this constrained trajectory, 50 unconstrained trajectories are initiated with random velocities from every 10th time slice along the constrained trajectory, and commitment probabilities are calculated for each slice. If the inferred reaction coordinate accurately describes the reaction coordinate, the constrained trajectory will have performed a constrained walk along the separatrix, and the distribution of commitment probabilities will peak at 0.5. If not, a new constrained trajectory is initiated with a new inferred reaction coordinate and the process is repeated.

RESULTS AND DISCUSSION

Transition Path Ensembles

We created two transition path ensembles of 200 trajectories each, one each for pfLDH and cpLDH. The acceptance ratios were 18.1 and 14.5% for pfLDH and cpLDH, respectively. While a 40% acceptance ratio has been found to provide the best compromise between the number of accepted trajectories and decorrelation of the trajectories from one another,⁴¹ we find that a lower acceptance ratio provides quicker decorrelation from the initial constrained trajectory, especially in more complex systems such as enzymes. It should be noted that an initial pfLDH ensemble was created that provided spurious results due to L163 moving away from the nicotinamide ring of NAD during heating, breaking a hydrogen bond¹⁴ between the L163 backbone oxygen and the NAD amide group, as discussed above. As we do not want the equilibrated structure to differ significantly from the crystal structure, constraints were placed on the pfLDH backbone and relaxed during heating, preserving this hydrogen bond and producing the ensemble used for the rest of this study. This should provide a cautionary tale to the care needed to apply these methods to complex systems such as explicitly solvated enzymes.

Average representative distances from trajectories of the two ensembles are listed in Table 1. Representative trajectories of each system can be seen in Figure 2. Analysis of these trajectories shows several differences between the two enzymes. While the proton and hydride transfer from the same distances in the two enzymes, these transfers occur at different times relative to one another; cpLDH mimics canonical LDHs in transferring the proton prior to hydride transfer, but in the pfLDH ensemble, the proton was typically transferred after the hydride. This swap of transferring particle order has been previously seen between bsLDH and hhLDH;⁷ however, because of the very short time scales of these trajectories, both systems can reasonably be described as having concerted mechanisms, from an experimental point of view.

Table 1.

Time Lags (time between proton and hydride transfer) and Proton and Hydride Donor–Acceptor Distances (DAD) at the Time of Particle Transfer for the pfLDH and cpLDH Ensembles^a

system	time lag (fs)	proton DAD (Å)	hydride DAD (Å)
pfLDH	−52	2.50	2.75
cpLDH	63	2.52	2.71

^aNote that a positive time lag indicates the proton transfer occuring before the hydride transfer, with a negative time lag indicating the opposite.

Figure 2.

Representative trajectories of pfLDH and cpLDH. Note the proton donor–acceptor (red), hydride donor–acceptor (black), hydride–donor and –acceptor (solid blue and dashed blue), and proton–donor and –acceptor (solid green and dashed green) distances.

Transition States and Reaction Coordinates

We performed committor analysis of every 25th trajectory to calculate six transition states for pfLDH and seven transition states for cpLDH (Table 2). In cpLDH, the transition states lie between the hydride and proton transfers, with the proton already completely transferred. However, in pfLDH, the transition states lie closer to the hydride transfer, while the proton transfer has not yet been initiated. These distances agree with the visual interpretation of the trajectories.

Table 2.

Average Transition State Distances of Important Residues

system	H DAD (Å)	P DAD (Å)	H–donor (Å)	H–acceptor (Å)	P–donor (Å)	P–acceptor (Å)	I32–NC4
pfLDH	2.82	3.02	1.68	1.18	1.05	1.63	4.51
cpLDH	2.79	2.70	1.23	1.59	1.72	1.04	4.94

Three committor distributions, each obtained from three transition states, were obtained for both ensembles (Figure 3). Committor distributions constraining the reactive atoms, i.e., the hydride and proton to their donor and acceptor and the donor–acceptor to one another, as well as the hydride transfer dihedral, indicate that the chemically relevant atoms alone do not accurately describe the reaction coordinate (Figure 3a,b). This is evident in the diffusive nature of both distributions. Constraining the quantum region (Figure 3c,d) provides an initial glance into the role of protein dynamics in the reaction coordinate of these two enzymes. While the quantum region provides a fairly accurate description of the reaction coordinate in pfLDH, it does not in cpLDH. However, even in pfLDH, there is considerable distribution on the product side, away from the 0.5 peak expected of an accurate description of the reaction coordinate. This indicates that there are protein motions coupled to the reaction coordinate in both systems, though likely to varying degrees. As discussed above, an RPV involving several residues distal to the active site was previously discovered in both hhLDH and bsLDH, two canonical LDHs.⁷ Incorporating the analogous residues into the constraints indicates the extent to which protein motions contribute to the reaction coordinate (Figure 3e,f). Residues were constrained to each other in a daisy chain by their C_α atoms and, if applicable, C_β atoms, with the two residues closest to the active site, active site R109 and I32 behind the nicotinamide ring of NAD, constrained to the hydride acceptor and donor, respectively. This isoleucine takes the place of a Val typically found behind the hydride donor in canonical LDHs.⁴⁹ The addition of the canonical LDH RPV to the reaction coordinate of cpLDH indicates that the quantum region with the canonical LDH RPV provides a view of the reaction coordinate much more accurate than that of the quantum region alone. However, in pfLDH, the addition of the canonical LDH RPV, while improving the description of the reaction coordinate over that of the quantum region alone, does so to a degree significantly smaller than that in cpLDH. This difference is clear; including the RPV residues causes a significant sharpening of the committor distribution around 0.5 in cpLDH, while the effect is more subtle in pfLDH, showing a shift of some distribution from the product side to the middle. In other words, while both pfLDH and cpLDH have protein motion coupled to the reaction coordinate, those motions contribute less so to the reaction coordinate of pfLDH than to that of cpLDH. It is certainly to be expected that the contribution of protein dynamics to the reaction coordinate will vary for each enzyme, even for two enzymes as related as these two. As further evidence of an RPV in these two enzymes, we plotted I32 to hydride donor distance, which shows the motion of the RPV residues before the incident hydride donor–acceptor compression near the transfer event (Figure 4).

Figure 3.

Committor distributions of pfLDH (left) and cpLDH (right), with constraints on hydride and proton distances and the hydride dihedral (a and b), the quantum region (c and d), and the quantum region with residues analogous to the hhLDH RPV (I32, G33, G34, and R109) (e and f).

Figure 4.

Representative trajectories from pfLDH and cpLDH, showing the hydride transfer (donor in red, acceptor in black), hydride donor–acceptor (green), I32–NC4 distance (blue), and transition state, as determined by committor analysis (dashed black). These distances show RPV compression relaxation occurring at different times relative to hydride transfer in the two systems.

A possible explanation for this diminished contribution of protein dynamics to the reaction coordinate in pfLDH is weakened coupling of the RPV compression and hydride transfer events. We plotted the hydride transfer, hydride donor–acceptor, and I32–hydride donor (NC4) distances, i.e., the RPV, of a representative trajectory (Figure 4). It is immediately clear that the RPV compression is directly coupled with the hydride transfer in cpLDH, as the hydride donor–acceptor compression begins at the minimum of the I32–NC4 compression. On the other hand, this coupling is not seen to the same degree in pfLDH, with the hydride donor–acceptor compression beginning slightly after the I32–NC4 compression minimum. To show that this effect is present in all trajectories in each ensemble, we created three-dimensional histograms of the structures generated along all reactive trajectories projected onto the plane of I32–NC4 distance versus the difference of the hydride bond breaking and bond forming distances (Figure 5). The histograms show a distinct difference in the coupling of the two events between the two enzymes; in pfLDH, the I32–NC4 compression is at a minimum and relaxes entirely before the transfer of the hydride begins, as seen in the verticality of the donor well. On the other hand, the donor well in the cpLDH histogram is tilted, indicating that the hydride transfer begins as the compression of the RPV is at its minimum, before the compression relaxes. Furthermore, the pfLDH histogram exhibits more diffusivity in the product than that of cpLDH does. While the effect of this reduced coupling is subtle, it is evident that, though still present and relevant in the reaction coordinate, the RPV motion and resulting compression are less correlated to the transfer of the hydride in pfLDH than in cpLDH.

Figure 5.

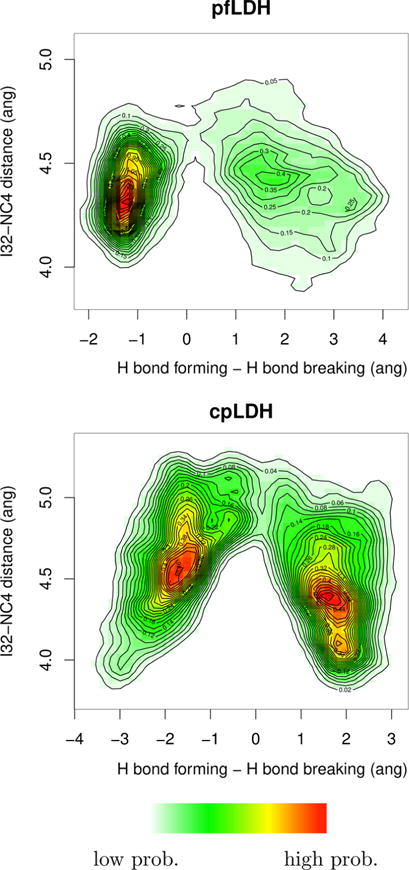
Three-dimensional histograms of all structures created along all reactive trajectories from pfLDH and cpLDH projected onto the plane of the I32–NC4, the closest RPV residue and the hydride donor, distance vs the hydride transfer (the difference of the hydride bond breaking and bond forming distances). In the heat map, red indicates relatively higher probability and white indicates relatively lower probability. Contour relief lines designate lines of equal probability. It is important to note that, as these are histograms, the probability of the two histograms cannot be compared to one another and that the relatively long I32–NC4 distance (4.0–5.0 Å) is due to the distance being measured from the I32 C_δ atom, not the C_δ hydrogens.

There are several structural differences between cpLDH and pfLDH that could explain this difference in the RPV contribution to the reaction coordinate. First, X-ray crystallography studies have indicated that differences in two residues in the cofactor binding pocket, I250P and T246P, offset the binding conformation of the cofactor such that the active site of pfLDH is more voluminous than that of canonical LDHs.¹² This larger active site relative to that of cpLDH could limit the ability of the RPV to contribute to the reaction coordinate, as motions are more difficult to sustain in a larger area. Second, as discussed above, LDHs traditionally have a serine at position 163 that hydrogen bonds with the carbonyl group of the NADH carboxamide. However, this position is occupied by M163 in cpLDH and L163 in pfLDH.¹⁴ We observe that the side chain of M163 mimics the placement of the canonical serine side chain and does not interact with the NADH nicotinamide ring. However, the bulky leucine side chain in pfLDH packs with the nicotinamide ring, behavior that accounts for its significantly better activity with the synthetic cofactor 3-acetylpyridine adenine dinucleotide (APADH) compared to human LDHs.^12,14 When NADH is bound, L163 interacts with the NADH ring and may disrupt its placement underneath the substrate. Mutagenic studies of bsLDH have indicated that the addition of the bulky leucine side chain to the active site (S163L) significantly disrupts the catalytic pathway, because of the lack of a stable volume in the active site.¹³

CONCLUSIONS

We have performed transition path sampling investigations of the effect of protein motions on the reaction mechanism in two noncanonical lactate dehydrogenases, those of P. falciparum and C. parvum, focusing on the specific active site changes in pfLDH compared to those in cpLDH. We found that these active site changes, S163L and a five-amino acid loop insertion in pfLDH, likely contribute to a decrease in the contribution of the canonical LDH RPV to the reaction coordinate in pfLDH, when compared to those of cpLDH and canonical LDHs. However, even with only moderate sequence homology, these two enzymes exhibit RPVs identical to those of the relatively evolutionarily distant LDHs from human heart and G. stearothermophilus. The fact that the same rate-promoting vibrations found in canonical LDHs are found in both pfLDH and cpLDH raises the question of what role evolution plays in the preservation of these motions through changes in reactive functionality and in active site sequence and structure. Symmetric coupling of vibrations absent in a pure antisymmetric, and hence Marcus,⁵⁰ model is found as a component of many enzymatic reaction coordinates. They are, however, not always equivalent in contribution, as shown here. Further studies, such as computational mutagenic studies involving L163 and insertion of the five-amino acid loop, could elucidate further the effects of these evolutionary changes on the role of motions in the chemical step of these Apicomplexa LDHs. We hope that this study will spur further experimental work on Apicomplexa LDHs, such as single-turnover kinetic studies that can interrogate these enzymes at time scales closer to those of our simulations.