Simulation-Based Design for Wearable Robotic Systems: An Optimization Framework for Enhancing a Standing Long Jump

Abstract

Goal

Technologies that augment human performance are the focus of intensive research and development, driven by advances in wearable robotic systems. Success has been limited by the challenge of understanding human–robot interaction. To address this challenge, we developed an optimization framework to synthesize a realistic human standing long jump and used the framework to explore how simulated wearable robotic devices might enhance jump performance.

Methods

A planar, five-segment, seven-degree-of-freedom model with physiological torque actuators, which have variable torque capacity depending on joint position and velocity, was used to represent human musculoskeletal dynamics. An active augmentation device was modeled as a torque actuator that could apply a single pulse of up to 100 Nm of extension torque. A passive design was modeled as rotational springs about each lower limb joint. Dynamic optimization searched for physiological and device actuation patterns to maximize jump distance.

Results

Optimization of the nominal case yielded a 2.27 m jump that captured salient kinematic and kinetic features of human jumps. When the active device was added to the ankle, knee, or hip, jump distance increased to between 2.49 and 2.52 m. Active augmentation of all three joints increased the jump distance to 3.10 m. The passive design increased jump distance to 3.32 m by adding torques of 135 Nm, 365 Nm, and 297 Nm to the ankle, knee, and hip, respectively.

Conclusion

Dynamic optimization can be used to simulate a standing long jump and investigate human-robot interaction.

Significance

Simulation can aid in the design of performance-enhancing technologies.

I. Introduction

Advances in robotic technology have recently enabled the development of wearable sensors and actuators aimed at assisting human movement. Robotic devices have been used successfully to assist patients with lower limb amputation in walking and climbing up and down stairs [1–6]. Augmentative devices for able-bodied individuals have also assisted with lifting and moving heavy loads [7], increased load carriage capacity during walking [8], and decreased the metabolic cost of hopping [9–12], but devices have had mixed results in decreasing the metabolic cost of walking and running [13–17].

Despite progress in wearable robotic systems, assisting able-bodied individuals has been limited by an insufficient understanding of the interaction between the neuromuscular system and assistive devices. Devices can change the operating length and velocity of muscles during a task, making them work suboptimally [9]. The neuromuscular system adapts when additional actuation is applied, and it can be difficult to predict how this adaptation will evolve [15]. Because of these challenges, much effort is currently spent in device testing and iteration, which slows the design process. Further, human subjects may be at risk of injury if devices apply large or poorly timed forces.

Two approaches will accelerate the development of wearable robotic systems. First, experimental robotic testbeds allow device developers to explore a wide range of forces and torques to examine the effects on human performance [18]. Second, modeling and simulation provide insight into variables that cannot be measured experimentally, which may improve designs of augmentative devices, as suggested by previous review papers [19, 20].

To investigate the potential of simulation to give insight into assistive device design, we developed a framework to improve standing long jump performance. Jumping is a prevalent motion used as a measure of human performance. The task requires coordinated timing of muscles to flex each of the lower limb joints and then rapidly extend for take-off. Although complex, the motion is tractable for simulation since the salient features of the jump occur in the sagittal plane [21] and thus can be captured with a planar model. Jumping also has an unambiguous, quantifiable goal: to maximize jump distance without injuring oneself.

A simulation for designing devices must represent the important features of movement dynamics (e.g., ground reaction forces, joint motions, and joint moments should approximate experimental measurements of these variables). Ashby and Delp [21] used dynamic optimization of the standing long jump to elucidate the role of the arms in enhancing jump performance. This simulation produced a similar velocity at take-off and jump distance compared to experimental data [22–24], but it is unclear if simulated ground reaction forces and joint moments were consistent with experimental measurements. Ridderikhoff et al. [25] used dynamic optimization to investigate differences in control strategy between standing long jumps and vertical jumps. The changes in simulated COM kinematics between vertical and horizontal jumping matched experimental trends, but ground reaction forces were not investigated. These studies provide a foundation for developing simulations using dynamic optimization, but more work is needed to rigorously validate simulations against experimental data before using this type of framework for simulation-based design.

The overall goals of this work were to investigate the utility of simulation for designing a wearable robotic system to augment a standing long jump and to explore the possibility of generating candidate designs and hypotheses about human performance. The first aim of this study was to develop a dynamic optimization framework that could synthesize a realistic standing long jump with a counter-movement, extension phase, take-off kinematics, ground reaction forces, and joint moments comparable to experiments. The second aim was to use this framework to design active and passive devices to increase simulated jump performance and elucidate the changes in jump strategy that account for the increase in jump distance.

II. Methods

We developed an optimization framework to generate a standing long jump and to predict performance changes due to added actuators (Fig. 1). We implemented a human model with physiological torque actuators based on muscle dynamics and geometry then used an optimizer to find the controls that maximized the model’s jump distance without incurring injury. We first synthesized an unassisted, or nominal, jump and compared the simulation to experimental data. To explore how augmentative devices could increase performance, we simulated both active and passive augmentation strategies, allowing the optimizer to choose human controls and device parameters simultaneously.

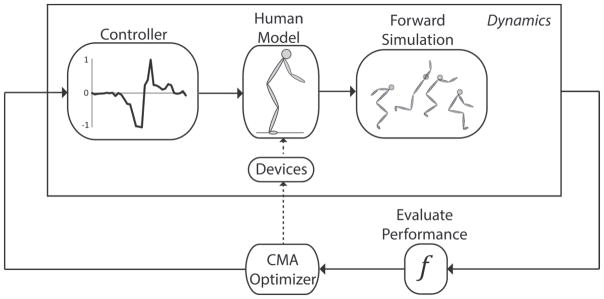
Fig. 1.

Flowchart of the framework used to optimize the standing long jump. In the dynamics block, a controller feeds activation patterns to the muscle torque actuators, which represent muscles in the human model. Integrating the equations of motion forward in time generates a forward simulation. An optimization loop is wrapped around the dynamics block. An objective function evaluates the performance of each forward simulation driven by the current set of activation patterns. The Covariance Matrix Adaptation (CMA) optimization algorithm uses the information from objective function evaluations to create the next set of activation patterns to be fed into the controller. To predict the performance of an augmentative device, a model of the device is added to the human model, and the optimizer adjusts the device parameters and activation patterns concurrently.

A. Human model, actuators, and controller

The human model was implemented in OpenSim [26] based on a model described by Ashby and Delp for generating simulations of standing long jumps with dynamic optimization [21]. The human model (Fig. 2) was composed of five rigid segments (foot, shank, thigh, pelvis-torso-head, and arm) and seven degrees of freedom (three for the location and orientation of the torso and four pin joints at the ankle, knee, hip, and shoulder). Since we assumed an identical control strategy for each side of the body, the right and left lower limbs and upper limbs and their corresponding joints were lumped together. Segmental parameters, including the mass, inertia, and length of each rigid segment, were based on a previous experimental study of untrained jumpers [22].

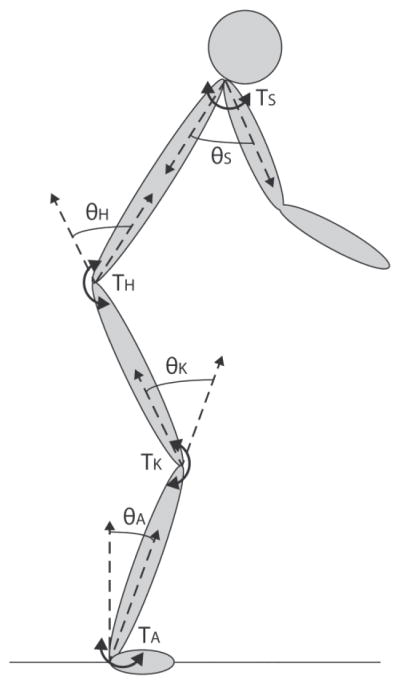
Fig. 2.

Planar human model used for dynamic optimization of standing long jumps. The model consists of six segments with seven degrees of freedom. The ankle, knee, hip, and shoulder joints are modeled as pin joints described by the angles θ_A, θ_K, θ_H, and θ_S, respectively, which are each actuated by a muscle torque actuator (T_A, T_K, T_H, and T_S). The elbow and neck joints are locked.

The model was driven by torque actuators at the ankle, knee, hip, and shoulder that represented the combined action of muscles crossing each joint. These physiological torque actuators were based on the combined muscle properties, including moment arms and length- and velocity-dependent force generation capacities, about each joint. The magnitude of the torque was dependent on activation (a), joint angle (q), and joint angular velocity (q̇):

$$T=a{T}_{\mathit{pos}}(q)T_{\mathit{vel}}(\stackrel{.}{q})$$ (1)

where T_pos is the maximum isometric torque as a function of joint angle and T_vel is a function that scales the maximum torque according to the joint angular velocity. There were eight different T_pos and T_vel curves describing torques about the ankle, knee, hip, and shoulder in flexion and extension. These curves were implemented as described by Ashby and Delp [27] and were based on experimental dynamometer data [28–35]. Activation ranged between −1 and 1, where negative values indicated extension torque and positive values indicated flexion torque. A controller governed the activation values for the four physiological torque actuators. Each actuator had its own control signal, which was constrained to be a piecewise linear function with nodes every 50 ms. Since muscles were represented by torque actuators with no delays, muscle activation dynamics, tendon dynamics, and muscle-tendon unit energy storage were not included in the model (see Discussion for implications of this assumption).

Ligaments were modeled by variable-stiffness springs at the ankle, knee, hip, and shoulder that engaged when a joint hyperextended or hyperflexed. The stiffnesses and angles at which the springs engaged were the same as those used by Ashby and Delp [27]. Ground contact was modeled as two point constraints: one at the heel and one at the toe. Each point constraint released when the vertical component of the ground reaction force reached 0, as determined by integration of the model’s equations of motion.

B. Optimization framework for generating a simulation of a standing long jump

We used dynamic optimization to solve for control signals to maximize standing long jump performance. In particular, the optimization (or design) variables were the values of the nodes for the controller signals, which were constrained by the optimizer to be between −1 and 1. There was a total of 132 design variables. At each optimization step, the equations of motion were integrated forward in time until the heel or toe’s vertical position returned to the ground after a successful take-off.

The optimizer sought to minimize the following objective:

$$f=-d+w_1(K_{\mathit{Cmx}}+K_{\mathit{CMy}})+w_2(K_{\mathit{injury}})+w_3(K_{\mathit{slip}})+w_4(K_{\mathit{time}})$$ (2)

The objective function rewards longer jump distances through the variable d, which defines the distance from the initial horizontal toe position to the horizontal heel position at landing, in meters. Jumps that were likely to fall at landing were penalized by K_CMx and K_CMy, which are the horizontal and vertical landing penalties if the position of the COM was too far behind the heel and too low to the ground, respectively. Jumps in which the person would become injured were penalized by K_injury, which penalizes the use of ligament torques. Compared to the previous study by Ashby and Delp, this formulation included two extra terms, K_slip and K_time, in the objective function. Slipping during take-off was penalized by K_slip, which discards jumps that would lead to slipping before take-off. Finally, jumps were penalized by K_time, which reduced the search space by discarding simulations where the model jumped immediately without a counter-movement; however, this formulation did not artificially enforce a counter-movement since a jump without a counter-movement could avoid this penalty by holding a static pose for sufficient time before jumping. The K_time penalty was inactive (i.e., yielded a value of zero) for the final optimized solutions. The weights, w_i, represent the relative importance of the high-level tasks related to each performance term. We report one set of values for the weights (see Appendix) which yielded results that were a good match with experiments. Details of all variables in the objective function are provided in the Appendix.

We used the Covariance Matrix Adaptation (CMA) optimizer [36], which has been used successfully for dynamic optimization of human movement [37]. CMA is an evolutionary algorithm that samples the design variable space by creating a set of candidate solutions (defined as a generation) given a specified population size (defined as the number of samples in each generation) and a mean, covariance matrix, and step size for the population. The algorithm updates the mean, covariance matrix and step size for each generation. Parameters for the optimizer were chosen empirically. The population size per generation was set as 98, and the initial step size was set as 0.01. Since the optimizer is stochastic and may yield different solutions each time, we re-ran an optimization with the same initial guess 20 times. The best result from these optimizations was used to seed another set of 20 optimizations until the final objective function value of each of the 20 optimizations did not improve compared to the seed’s objective function value.

The model was initialized with the lower limb joints in a standing posture, whereas Ashby and Delp’s simulation began in a crouched posture and did not include a countermovement. All initial coordinate velocities were set to 0 m/s or 0 rad/s. The initial controls were generated by hand tuning to find a jump with a forward velocity at take-off. We used the initial controls for the optimized nominal solution to seed the augmented jumps.

C. Validation of the Simulated Nominal Standing Long Jump

To assess how well the optimized solution captured realistic human movement, we compared the simulation to kinematic and kinetic data from experiments. Simulated kinematics at take-off, including body inclination angle and velocity of the COM, were compared to three previous studies with similar jump distances [22–24]. Lower body joint torques were compared to experimental data from Horita et al. [23] to validate the magnitude of peak torque and the timing of the extension phase. We compared horizontal and vertical ground reaction forces to experimental data from Ashby and Heegaard [22] to verify that there was a counter-movement followed by an extension phase. Specifically, we ensured that the vertical ground reaction force reached a minimum prior to the vertical ground reaction force increasing above body weight, and that both the vertical and horizontal ground reaction forces peaked just before take-off.

D. Augmenting the Standing Long Jump

Experimental studies show that maximal torque production occurs during the extension phase just before take-off [23]; thus, there is a clear need to increase this torque production. We first modeled an active device that could provide one burst of constant extension torque at one of the lower limb joints (the ankle, knee, or hip) with a 100 Nm limit. Previous work has shown that up to 175 Nm of torque can be generated from a lightweight device [18], thus we chose a torque well within the limit. We assumed each active device was massless. The control signal for each actuator had three parameters: the magnitude of the applied torque, the time when the torque was initially applied, and the duration of application. We optimized the device controls and the physiological torque controls by adding both controllers to the optimization framework. We tested four actuation conditions: 1) ankle, 2) knee, 3) hip, and 4) all three together (multi-joint active device).

We also modeled a multi-joint passive device by adding massless rotational springs to the ankle, knee, and hip. We again used our optimization framework, allowing the optimizer to choose each spring’s stiffness and equilibrium position (the joint position at which no torque is produced), along with the physiological torque controls.

After optimizing each device design and the corresponding physiological torque controls, we identified changes in the kinematics and kinetics of the augmented simulation compared to the nominal simulation. We analyzed changes in COM position and velocity at the instant of take-off. We also inspected the torque curves for the lower limb joints to study the optimal actuator design and changes to the human control strategy. All models and results from the simulations presented here are freely available at https://simtk.org/home/predictive_slj/.

III. Results and Discussion

A. Simulation of a nominal jump

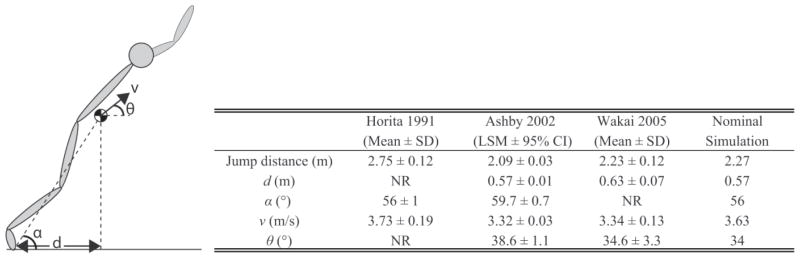
We first assessed if our dynamic optimization framework could reproduce a human standing long jump by comparing relevant kinematics and kinetics to experimental data. The framework was able to capture the salient features of a human standing long jump, including the counter-movement and extension phases, which led to realistic kinematics at take-off and total jump distance. In particular, the optimized, nominal jump entered the flight phase with kinematic parameters that were within 1 standard deviation (SD) of human subjects (Fig. 3), including body inclination angle (α) and the velocity vector of the COM, described by its magnitude (v) and angle with the horizontal (θ). The model jumped 2.27 m, which is also consistent with experimentally measured jump distances [22–24] (see Supplementary Material for a video of the simulated jumps).

Fig. 3.

Kinematic parameters of the center of mass (COM) at the instant of take-off from experimental data and from the nominal simulation. Parameters d and α describe the position of the COM with respect to the toe, and v and θ, respectively, describe the magnitude and direction of the COM velocity vector. Horita [23] and Wakai [24] reported results using the mean and standard deviation (Mean ± SD); Ashby [22] reported results using least squared mean and a 95% confidence interval (LSM ± 95% CI). Results that were not reported are denoted by NR.

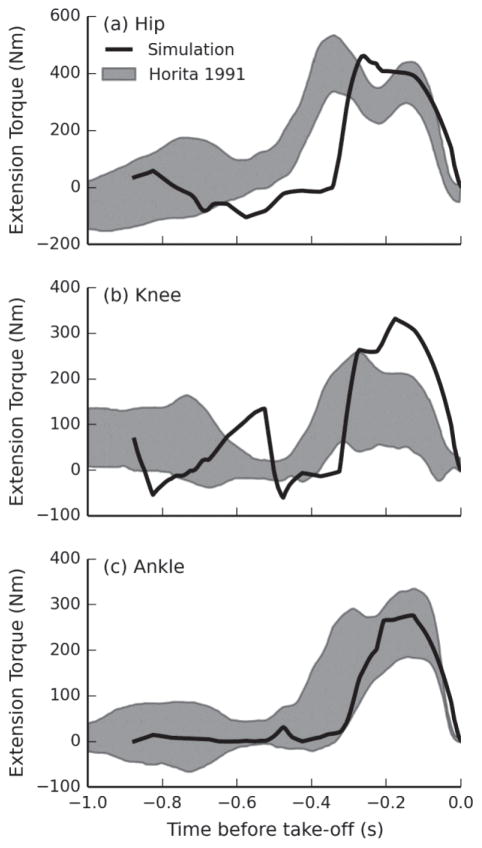
We also compared kinetics from the simulation to experimental data of human jumping (Fig. 4). For all three joints in the lower extremity, the peak torque values generated in the simulation were within 1 SD of the experimental values for the ankle and hip, and within 2 SD for the knee [23]. The simulation also produced a rapid extension torque phase just before take-off, as observed in experiments.

Fig. 4.

Joint torques about the (a) hip, (b) knee, and (c) ankle during the ground contact phase for the optimized nominal simulation. The shaded region shows the mean with one standard deviation from experiments. Joint torques from the nominal simulation are shown in the solid line.

We observed differences from experimental data, as the simulated hip and knee extension torques each had a delayed onset and faster rate of increase in preparation for take-off. Both of these differences are likely due to the lack of activation dynamics in the model, which allowed the model’s actuators to develop torque instantaneously. Consequently, the model had a later onset for hip and knee extension torque but still generated peak torques at the same time as peak torques measured in experiments.

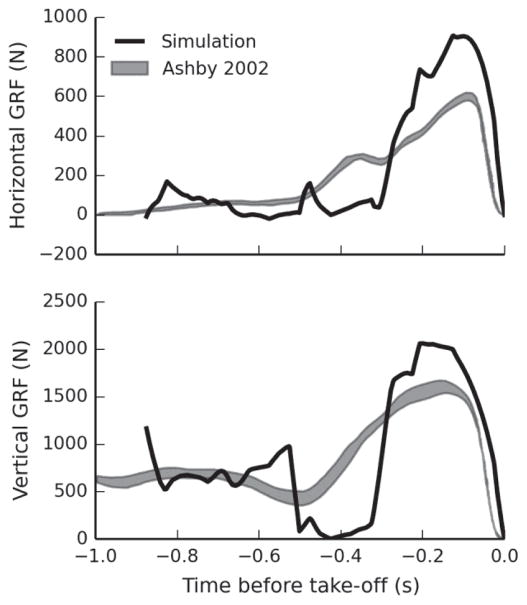
We also assessed whether key phases of a standing long jump were captured in the simulation by comparing simulated ground reaction forces to experimental ground reaction forces (Fig. 5). Both the horizontal and vertical ground reaction forces peaked just prior to take-off, as seen in experiments [22]. The simulated jump also captured the counter-movement phase, as seen by the dip in the vertical ground reaction force that starts approximately 500 ms before take-off.

Fig. 5.

Horizontal (top) and vertical (bottom) ground reaction force during the ground contact phase for the optimized nominal simulation. The shaded region shows the least squared mean and 95% confidence interval from experimental data. Ground reaction forces from the nominal simulation are shown by the solid line.

Discrepancies between the simulated and experimental vertical ground reaction force included a smaller minimum value during the simulated counter-movement, a steeper vertical ground reaction force curve both in initiation of the counter-movement and in the extension phase, and a peak vertical ground reaction force that was higher than in experiments. The lack of activation dynamics in the model allowed the ground reaction force to change instantaneously, contributing to these discrepancies. In addition, the population in Ashby and Heegaard’s study [22] consisted of untrained jumpers, who may perform suboptimal jumps with a shorter counter-movement phase. This would limit performance as a greater counter-movement time allows for a larger impulse from the ground reaction force to increase velocity at take-off. Finally, we used a simple two-constraint contact model, which could have also contributed to the difference between experimental and simulated ground reaction forces. Once the heel came off the ground, the only point of contact was a single point at the toe, which could not move until take-off. A contact model where the contact point could move horizontally along the foot would more realistically represent the application of the ground reaction force, which could lead to smoother ground reaction forces.

B. Simulation-based design of active augmentative devices

We used the framework to evaluate how augmentative devices might enhance a standing long jump. Active augmentative devices increased jump distance in all cases. In general, human control during the counter-movement phase was similar to the nominal case, but small changes during the extension phase prepared the human for the torque assistance. Increases in distance could be attributed to greater velocities and smaller body inclination angles at take-off.

In particular, single-joint active actuation yielded similar improvements in performance, increasing jump distance from 2.27 m for the nominal case to 2.49 m, 2.52 m, and 2.49 m, for the ankle, knee, and hip, respectively (Table I). Although the optimizer chose to use at least 99 Nm torque (of the 100 Nm possible) in all three cases, the kinematics at take-off varied for each type of joint assistance. For example, the model with a knee actuator jumped farther than the hip or ankle actuator cases, although the optimizer found a solution with a lower velocity at take-off. This lower take-off velocity was balanced by the jumper’s body configuration at take-off—the model with the knee actuator had the smallest body inclination angle (α in Fig. 3 = 55°) and its COM was the farthest ahead of the toes of all three cases (d in Fig. 3 = 0.62 m). An experimental study inspecting optimum take-off configuration of physically active individuals [24] noted that a lower take-off angle and higher take-off velocity are important for optimal jumps.

TABLE I.

Kinematic parameters of the center of mass at the instant of take-off for all simulation cases

	Nominal	Active: Multi-joint	Passive: Multi-joint	Active: Ankle	Active: Knee	Active: Hip
Jump distance (m)	2.27	3.10	3.32	2.49	2.52	2.49
d (m)	0.57	0.62	0.67	0.54	0.62	0.59
α (°)	56	54	50	58	55	55
v (m/s)	3.63	4.55	4.90	3.93	3.87	3.90
θ (°)	34	38	34	39	35	34

Parameters d, α, v, and θ are defined in Fig. 3.

When an external actuator was added to all three lower joints to test the multi-joint design, the jump distance increased to 3.10 m. This is greater than the projected jump distance of 2.96 m if the individual improvements from single-joint augmentation were summed. As expected, the magnitude of the take-off velocity was highest for this condition. The location of the COM led to a smaller body inclination angle than any of the single-joint cases (54°) and the COM was also far ahead of the toes at take-off (0.62 m).

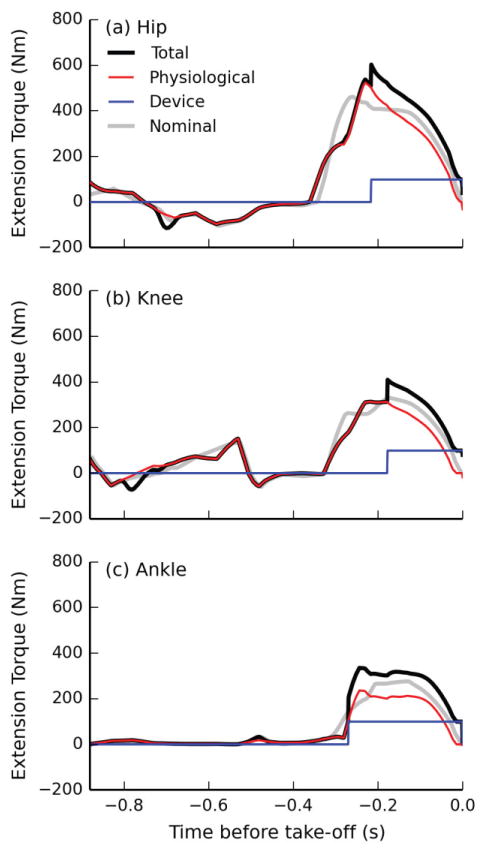
The human control strategy, as quantified by the torque-time profiles, remained similar in the counter-movement phase with the active actuation designs but changed during the extension phase in response to the added active assistance. Results for the multi-joint device are shown in Fig. 6, and similar trends were observed for single-joint assistance. During the counter-movement phase, the muscle strategy remained similar to the nominal case (compare Physiological and Nominal curves in Fig. 6), but at the start of the extension phase, we see changes in lower limb muscle coordination to maintain a good take-off pose while still generating as much torque as possible (i.e., each of the lower joint muscle torque actuators still reach a peak extension activation of at least 0.98). The higher total extension torques provided by the active assistive devices and physiological torques contribute to the increased take-off velocity. Furthermore, the device actuators were able to provide torque until take-off, in contrast to the physiological torques, which approach 0 Nm at take-off due to the high joint velocities and the torque-velocity relationship.

Fig. 6.

Joint torques during the ground contact phase for an optimized jump with the multi-joint active device. Shown are the total joint torque (black) and the individual physiological (red) and device (blue) torques. The total joint torque from the simulated nominal case (gray) is shown for reference. Extension torques about the (a) hip, (b) knee, and (c) ankle are shown. For comparison to human joint torque capacity, the peak isometric torque values for hip, knee, and ankle extension are 584 Nm, 529 Nm, and 400 Nm, respectively.

C. Simulation-based design of a passive augmentative device

We also evaluated how the framework might be used to optimize a passive device for a standing long jump. The optimized device parameters are provided in Table II. The passive device improved the jump distance to 3.32 m, more than 1 m longer than the nominal jump, which we attribute to the high joint torques delivered by the device (see Device curve in Fig. 7). Furthermore, a combination of the highest COM velocity, smallest body inclination angle, and farthest COM location past the toes at take-off also helped to increase jump distance.

TABLE II.

Optimized passive device spring parameters

	Ankle	Knee	Hip
Stiffness (Nm/rad)	113	265	144
Equilibrium position (°)	−45	39	4

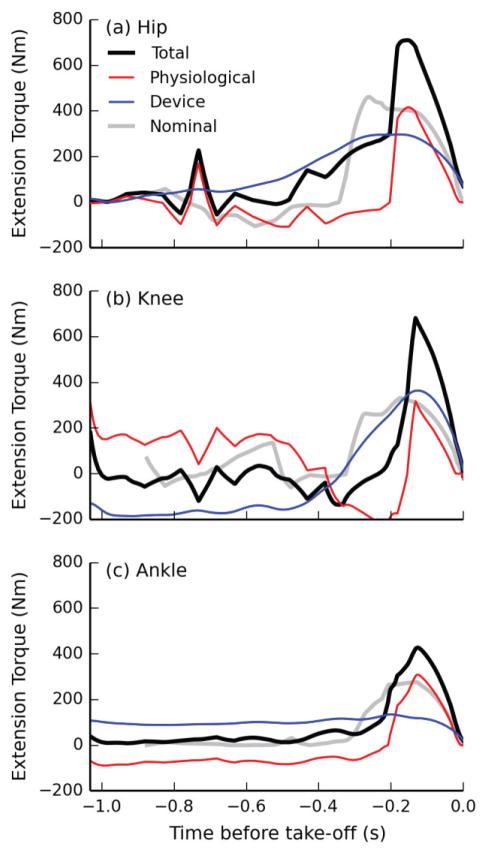
Fig. 7.

Joint torques during the ground contact phase for an optimized jump with the passive device. Shown are the total joint torque (black) and the individual physiological (red) and device (blue) torques. The total joint torque from the simulated nominal case (gray) is shown for reference. Extension torques about the (a) hip, (b) knee, and (c) ankle are shown. For comparison to human joint torque capacity, the peak isometric torque values for hip, knee, and ankle extension are 584 Nm, 529 Nm, and 400 Nm, respectively.

Torque–time plots (Fig. 7) show how the human model’s strategy adapted to the added springs and demonstrate that the springs have been optimized to maximize added extension torque. During the counter-movement phase, the muscle actuation strategy changed dramatically from the nominal case for the ankle and the knee (compare curves Physiological and Nominal in Fig. 7). The physiological torques changed to balance the added device torques so that the countermovement with the passive device is similar to the nominal case (compare curves Total and Nominal). Furthermore, the smaller device torques at take-off (see Device curve) demonstrate that the optimization framework set the equilibrium position of the rotational springs to maximize the extension torque provided by the springs before take-off. The data also show that significant energy was stored in the device at the beginning of the simulation for the knee and hip; however, given the physiological torque capacities of these joints, this initial pose is feasible to achieve.

Similar work has been done to investigate passive devices to assist in walking [38, 39] using exotendons. A key difference is that this previous work was based on cables passing over multiple joints, which coupled the assist torques about different joints. The model presented here used rotational springs about each lower-limb joint, which were uncoupled. The torques found here were also higher compared to the exotendon designs (e.g., 100s of Nm versus 10s of Nm), which is expected due to the higher torques needed for jumping compared to walking.

D. Injury analysis

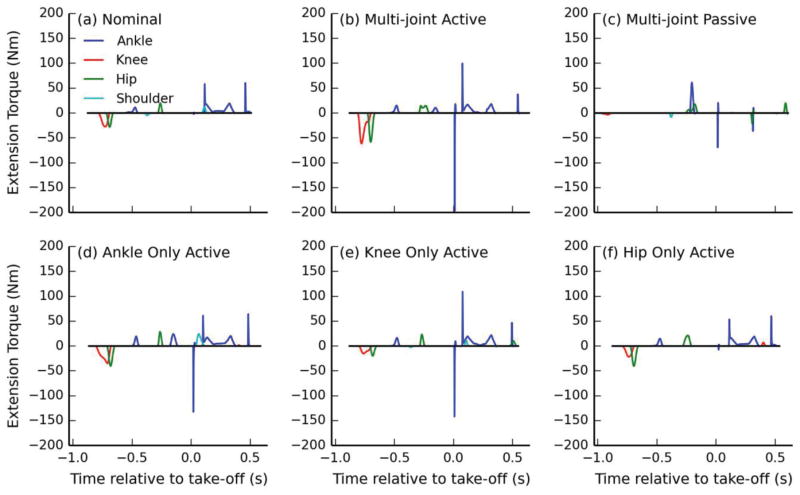
We investigated the potential for injury with all simulation cases by analyzing the use of the ligament torques (Fig. 8). For the nominal case (panel (a)), the ligament torque produced is small throughout the motion. The multi-joint, ankle only, and knee only active devices (panels (b), (d), and (e)) significantly engaged the ligament torque around the ankle just after take-off, while the multi-joint passive and hip only active devices (panels (c) and (f)) produced similar torque magnitude values as the nominal case. In all cases, these torques happened over a very small time range, but could lead to injuries with the higher torques. The engagement of the ligaments could be reduced by two methods. First, a joint stop could be added as part of the device design. Alternatively, an extra term in the optimization penalizing the maximum magnitude on the ligament torque could be used to avoid situations that would injure the joints.

Fig. 8.

Ligament torques plotted for the whole jump for all four joints in all six conditions simulated. Joint torques are only plotted when they are non-zero. The black line is plotted at 0 Nm torque for the duration of each simulation.

E. Limitations

The simplicity of the human model limits the questions that this study can address. For example, since the human model was driven by torque actuators that combined the action of multiple muscles, we cannot answer questions about the interaction of robotic systems with individual muscles. The physiological torque actuators could only extend or flex each joint and were independently controlled, so there could be no co-contraction or coupling of joint torques due to biarticular muscles. The lack of activation dynamics prohibits detailed analysis of the timing of muscle control, and the lack of tendon dynamics precludes the potential for energy storage and subsequent analysis. Finally, landing was controlled by a soft kinematic constraint, so questions about strategy after returning to the ground cannot be addressed. Addressing these limitations presents a challenge for future modeling and simulation work.

Assumptions in modeling the devices also limit the conclusions we can draw from this analysis. Both the active and passive devices were assumed to be massless; thus, the improvements in jump distance were likely overestimated, and we could not explore the trade-off between actuator size and jump performance. Furthermore, the torques produced by active devices were idealized, since they could produce torque instantaneously. Since timing is very important in jumping, the increase in performance of an actual device might be smaller than that predicted here. We also note that we cannot conclude that this passive device would outperform active devices since the active designs would likely lead to farther jump distances if they had an equivalent torque-generating capacity as the passive devices. Future work could include modeling designs with added mass, sensors, and more sophisticated controllers.

Further work is needed to validate the predicted changes in human control strategy presented here. We have presented one set of weighting coefficients in the objective function to represent the relative importance of motor subtasks. We did not perform a sensitivity analysis, but given the comparison to experimental data, we do not believe there would be a significant change in our results or conclusions from this study. Furthermore, while the performance simulated in this study is likely an upper bound on performance increases observed in practice, we believe the predicted adaptations to human jump strategy with actuation are reasonable since the torques in our model were constrained by experimentally measured relationships between joint position, velocity, and torque. Experiments are needed to test these conclusions.

Given the formulation of the optimization problem, we cannot guarantee that the solutions found here are the global optima, and the solutions are sensitive to initial conditions. We addressed this limitation by using a stochastic optimizer, rerunning the same optimization many times, and restarting optimizations as the solution evolved.

IV. Conclusion

We present a dynamic optimization framework that can synthesize human-like simulations of a standing long jump without requiring experimental data. Our simulations captured the salient features of a jump when compared to independent experimental kinematics, joint torques, and ground reaction forces. The framework enabled us to perform human-in-the-loop design, demonstrating that this method is flexible enough to optimize both active and passive devices acting at a single joint or multiple joints, along with the corresponding human control. Our framework generated several candidate designs all of which are achievable with currently-available lightweight actuators and springs. These candidate designs and hypotheses developed about jump performance must now be tested with experiments. In the future, this framework could be extended to include muscle models to elucidate how devices will interact on the individual muscle level and to optimize device design for more complex tasks such as walking and running.

Appendix

Parameters of the objective function are detailed here. The objective function was described by Eq. 2, and is provided here for convenience.

$$f=-d+w_1(K_{\mathit{Cmx}}+K_{\mathit{CMy}})+w_2(K_{\mathit{injury}})+w_3(K_{\mathit{slip}})+w_4(K_{\mathit{time}})$$ (A1)

• d: Distance from initial horizontal toe position to the horizontal heel position at landing in meters

• w₁ = 10.0, w₂ = 1.0 × 10⁻⁴, w₃ = 1.0, w₄ = 10.0: Penalty weights for 1) landing, 2) injury, 3) slip, and 4) time

• More details about each term K term are included below.

The landing penalty is composed of two parts, one for the horizontal direction and one for the vertical direction.

$$K_{\mathit{Cmx}}=max(q_x-q_{\mathit{Cmx}}-{\delta }_x,0)$$ (A2)

• q_x: Horizontal position of the heel at the time of landing

• q_CMx: Horizontal position of the center of mass at the time of landing

• δ_x = 0.17 m: If the horizontal distance to the heel from the center of mass is larger than this value, a penalty is applied. This value is based on experimental data of standing long jumps of active individuals [24].

$$K_{\mathit{CMy}}=max(q_y-q_{\mathit{CMy}}+{\delta }_y,0)$$ (A3)

• q_y: Vertical position of the heel at the time of landing

• q_CMy: Vertical position of the center of mass at the time of landing

• δ_y = 0.62 m: If the vertical distance to the heel from the center of mass is smaller than this value, a penalty is applied. This value is based on experimental data of standing long jumps of active individuals [24].

The injury penalty is based on using ligament torques due to hyperextension or hyperflexion.

$$K_{\mathit{injury}}={\int }_0^{t_f}\sum _{i=1}^n{T}_i^{2}dt$$ (A4)

• t_f: Final time of the simulation, when the feet first make contact at landing

• n = 4: The number of torques that represent ligaments in the model

• T_i: The ith ligament torque

The model cannot slip because contact is modeled by point constraints, so a penalty is applied when the ratio of the magnitude of the horizontal force to the vertical force is excessive.

$$K_{\mathit{slip}}={\int }_0^{t_{\mathit{take}-\mathit{off}}}\sum _{i=1}^{m}max\left(\left|F_x^{(i)}\right|-\mu F_y^{(i)},0\right)dt$$ (A5)

• t_take-off: Time of take-off, the instant both contact points are inactive

• F⁽ⁱ⁾: The force applied to the foot from the ground at the ith constraint

• m = 2: Number of points constraints modeling contact

• μ = 0.8: Coefficient of static friction

The time penalty decreases the search space of the optimizer, discarding trials and avoiding local minima where the model immediately jumps without a counter-movement.

$$K_{\mathit{time}}=\{\begin{array}{cc}\frac{1}{t_f^2}-\frac{1}{t_{\mathit{threshold}}^2},& t_f<t_{\mathit{threshold}}\\ 0& t_f\ge t_{\mathit{threshold}}\end{array}$$ (A6)

• t_f: Final time of the simulation, when the feet first make contact at landing

• t_threshold = 1.2 s: Threshold below which the time penalty is applied if the final time of the simulation is too short