Attention-related changes in correlated neuronal activity arise from normalization mechanisms

Abstract

Attention is believed to enhance perception by altering the correlations between pairs of neurons. How attention changes neuronal correlations is unknown. Using multi-electrodes in primate visual cortex, we measured spike-count correlations when single or multiple stimuli were presented, and stimuli were attended or unattended. When stimuli were unattended, adding a suppressive, non-preferred, stimulus beside a preferred stimulus increased spike-count correlations between pairs of similarly-tuned neurons, but decreased spike-count correlations between pairs of oppositely-tuned neurons. These changes are explained by a stochastic normalization model containing populations of oppositely-tuned, mutually-suppressive neurons. Importantly, this model also explains why attention decreased (attend preferred stimulus) or increased (attend non-preferred stimulus) correlations: as an indirect consequence of attention-related changes in the inputs to normalization mechanisms. Our findings link normalization mechanisms to correlated neuronal activity and attention, showing that normalization mechanisms shape response correlations and that these correlations change when attention biases normalization mechanisms.

Attention enhances perception by changing the responses of sensory neurons in the brain^1–4. For instance, attention can amplify the responses of neurons that represent an attended stimulus^5–11. Such attention-related changes in response strength can increase the effectiveness with which stimuli are represented because they elevate the signal above the noise^12,13.

Attention can also modify the correlation between the responses of pairs of neurons^7,8,14–20. These attention-related changes in response correlations have been suggested to be far more beneficial for improving the neuronal representations of stimuli than attention-related changes in the response strength^14,16. However, the mechanisms through which attention modifies response correlations remain unknown.

Attention-related changes in response correlations are commonly thought to result from an active process that directly modifies response correlations in order to flexibly adjust the quality of sensory representations depending on their behavioral relevance for the task at hand^14–18. For example, one recent study suggested that attention improves perceptual decisions that are based on the difference in the average activity of different pools of neurons by decreasing correlations within each neuronal pool, while increasing correlations between neurons in different pools¹⁵. However, it remains uncertain whether attention actively adjusts correlated responses to enhance perceptual behavior, or if instead these attention-related changes in response correlations are incidental to attention-related changes in the strength of neuronal responses.

Mounting evidence indicates that the magnitude of attention-related changes in the response strength of neurons are mediated by normalization mechanisms, which can greatly amplify attention-related changes in neuronal responses in some stimulus configurations^21–26. Normalization mechanisms operate in many sensory modalities and brain regions, underlying a range of neuronal phenomena such as surround suppression, contrast response functions and multisensory integration, to name a few²⁷. Yet, if and how normalization mechanisms influence correlated neuronal activity is unclear.

We examined how neuronal correlations relate to normalization mechanisms, and the mechanisms through which attention modifies neuronal correlations. We show that normalization mechanisms can either increase or decrease response correlations. We further show that attention can also increase or decrease response correlations. Importantly, our findings indicate that these attention-related increased or decreased neuronal correlations are an indirect consequence of attention-related changes in the inputs into normalization mechanisms. Finally, we show that similar mechanisms influence response correlations inside the classical receptive field and the surround; a finding that helps explain previously observed decreases in correlation by attention.

Results

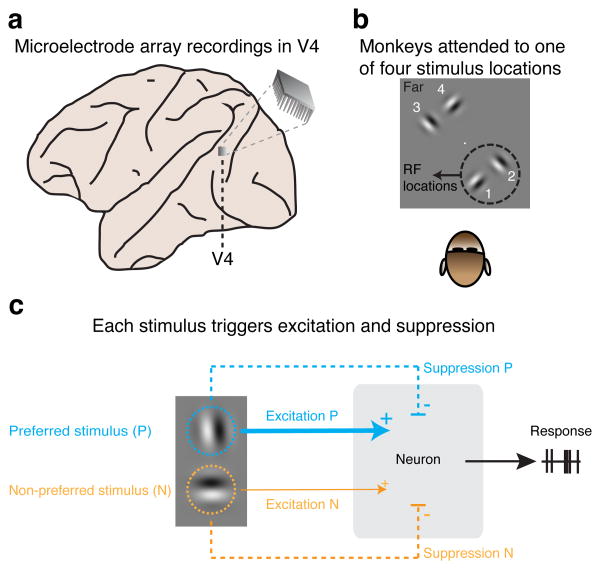
Using chronically implanted microelectrode arrays (Fig. 1a), we recorded from 12067 multi-units in visual area V4 in the left cerebral hemisphere of two rhesus monkeys (monkey M1: 4709; M2: 7358) while they performed a visual-detection task in which spatial attention was controlled (Online Methods). During task performance, we presented either single or paired stimuli near the receptive fields (RFs) of the recorded neurons, either inside the classical RF or in the RF-surround (Online Methods; Supplementary Fig. 1). During different blocks of trials, monkeys attended different stimulus locations, one attended location per block of trials. Attention was directed toward one of two stimulus locations near the neurons' RFs (Fig. 1b, locations 1, 2), or toward one of two stimulus locations far from the RFs, in the other visual hemifield (Fig. 1b, locations 3, 4).

Figure 1. Multi-electrode array recordings of neuronal activity in area V4 during a visual attention task.

a, Simultaneous recordings of the responses of multiple neurons in area V4 of rhesus monkeys. b, In separate blocks of trials, monkeys attended to one of four stimulus locations, either near the RFs of the recorded V4 neurons (location 1 and 2) or far from the RFs (location 3 and 4). The central white dot represents the fixation point on the display. c, Each of the two RF stimuli evokes excitation, which increases responses, and suppression, which decreases responses. Normalization mechanisms determine how neurons combine the suppressive and excitatory contribution of each stimulus into a response. By fitting a normalization model to the observed neuronal responses in all conditions, the excitatory and suppressive contribution of each stimulus were estimated.

Normalization mechanisms can increase or decrease spike-count correlations

We first examined how normalization mechanisms, in the absence of attention, affect spike-count correlations, i.e. the correlated fluctuations of neuronal responses across repeated presentations of the same stimuli.

In what follows, we will present a mechanistic model that explains the heterogeneous patterns in spike-count correlations observed in our data, with and without attention. In its steady state this mechanistic model closely resembles the classical normalization model (see Online Methods). The mechanistic model explains the patterns of spike-count correlations as a function of two factors, namely the excitatory and suppressive inputs received by neurons when stimuli are presented.

To show empirically that excitation and suppression play an important role in shaping correlations, one would ideally directly observe the excitatory and suppressive activity that drive a neuron's response. Unfortunately, this is not possible with extracellular recordings. However, using a normalization model, we could obtain good estimates of the suppression and excitation induced by stimuli in neurons. Specifically, when two stimuli are simultaneously presented, each stimulus contributes certain amounts of excitation and suppression to the neuronal response (Fig. 1c). Crucially for our purposes, the parameters of normalization models capture the amount of suppression and excitation induced by stimuli. Thus, by fitting a normalization model to neuronal responses across all stimulus conditions (Online Methods), we were able to estimate the excitation and suppression contributed by each of the two RF stimuli in a stimulus pair.

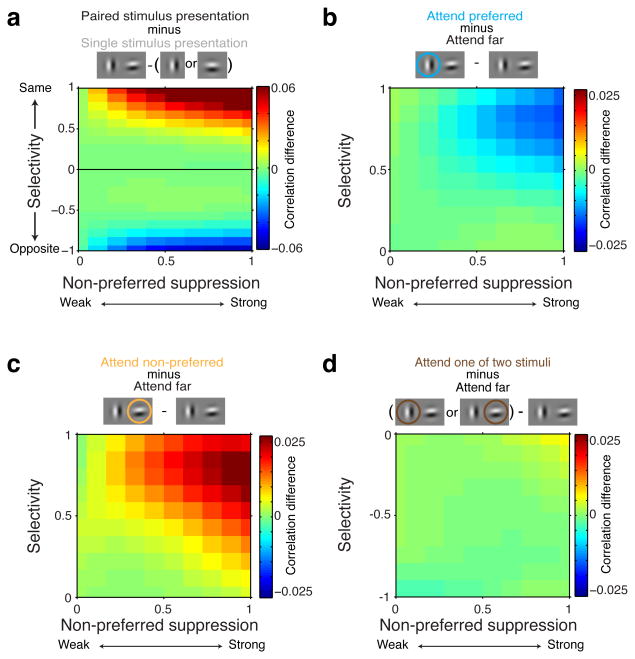
We found that two aspects of stimulus-related excitation and suppression are critical for understanding the effects of normalization on spike-count correlations. The first is whether the two neurons of a neuron pair prefer the same stimulus. For each neuron, we designated the preferred and non-preferred stimulus of a stimulus pair as the stimulus that contributed the most and least excitation, respectively. For each neuron pair, we defined a measure of selectivity (Online Methods) that was positive when both neurons of the pair preferred the same stimulus and negative when the two neurons preferred different stimuli, with larger magnitudes reflecting greater selectivity (Fig. 2a, blue arrows, y-axis). The second critical factor is how strongly the responses of each pair of neurons were suppressed by the non-preferred stimulus. We defined a measure of non-preferred suppression (Online Methods) that reveals whether the neurons of a pair both received weak (values near 0) or strong (values near 1) suppression from their non-preferred stimulus (Fig. 2a, orange arrows, x-axis).

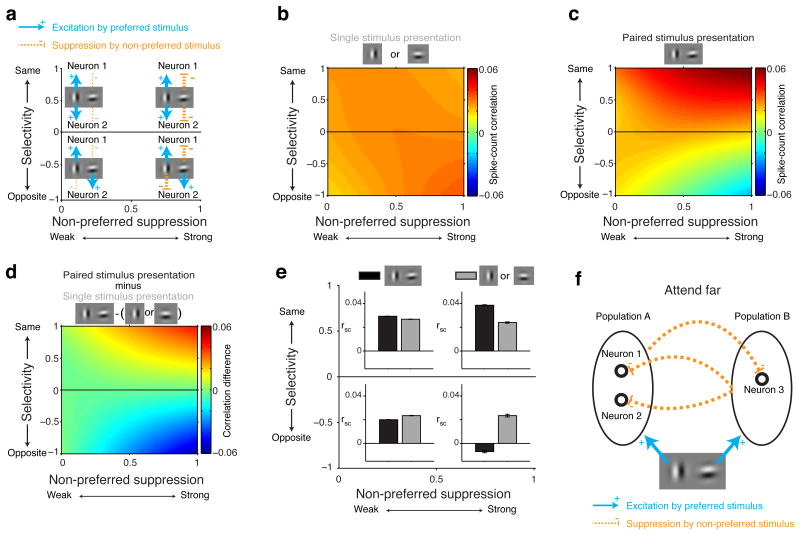
Figure 2. Normalization mechanisms determine spike-count correlations.

All data in these plots were obtained while monkeys' attention was directed far from the RF stimuli (locations 3, 4 Figure 1b). a, Each neuron's preferred stimulus in a stimulus pair was the stimulus that contributed most excitation (blue arrows). Positive selectivity indices refer to neuron pairs with the same stimulus preference (blue arrows upper half plot). Negative selectivity indices refer to neuron pairs with opposite stimulus preferences (blue arrows lower half plot). Values of non-preferred suppression near zero indicate that the two neurons of a neuron pair were weakly suppressed by their non-preferred stimulus (thin orange dashed line left side plot), values near one indicate strong suppression by their non-preferred stimulus (thick orange dashed line right side plot). For neurons with opposite selectivity (lower half plot), the preferred stimulus of one neuron is the non-preferred stimulus of the other neuron. b, Mean spike-count correlations, indicated by color, as a function of the selectivity and non-preferred suppression of neuron pairs, measured while a single stimulus was presented alone near the RF. c, Mean spike-count correlations during paired stimulus presentations. d, Difference in spike-count correlations between c and b. Plots based on regularized bilinear interpolation (Online Methods). e, Mean spike-count correlations (r_sc) computed on the data from four quadrants in the space spanned by selectivity and non-preferred suppression (quadrants defined as a combination of negative or positive selectivity, and non-preferred suppression < 0.5 or > 0.5). Black: paired stimulus presentations. Gray: Single stimulus presentations. Error-bars represent ± 1 SEM. f, Pattern of spike-count correlations can be explained by two oppositely-tuned neuronal populations, Population A and B, that mutually suppress each other's activity. Common suppression, evoked by neurons in Population B, correlates the activity of neuron 1 and 2 in Population A, but decorrelates the activity of neurons in different populations, e.g. neuron 1 and 3.

Using the very large set of V4 neuronal pairs, we could examine how selectivity and non-preferred suppression affect spike-count correlations in the absence of attention to stimuli inside the RF, i.e. during blocks of trials with attention directed far from the RF stimuli. Whenever a single stimulus (preferred or non-preferred) was presented alone, average spike-count correlations were small and positive for all neuron pairs, regardless of their selectivity and non-preferred suppression (Fig. 2b). However, adding a second stimulus changed the structure of spike-count correlations across the population of neuron pairs in a specific way: spike-count correlations increased between neuron pairs with the same selectivity, but only when both neurons of the pair were strongly suppressed by their non-preferred stimulus (upper right quadrant in Fig. 2c-e; main effect selectivity: P<0.0001, main effect suppression: P<0.0001, selectivity-suppression interaction: P<0.0001, linear regression, N=2533424 correlations, resulting from different combinations of neuron and stimulus pairs). Conversely, spike-count correlations decreased between neuron pairs with opposite selectivity, but again only when both neurons of the pair were strongly suppressed by each neuron's non-preferred stimulus. Notably, these neuron pairs became negatively correlated (lower right quadrant in Fig. 2c-e; main effect selectivity: P=0.02, main effect suppression: P=0.003, selectivity-suppression interaction: P<0.0001, N=1270826 correlations).

In the previous analyses we treated each pair of neurons as an independent sample for statistical purposes. We also performed an additional analysis on the average results from individual sessions and found similar results. Specifically, for each session, we computed the average difference in spike-count correlations between single and paired stimulus presentations within each quadrant of Figure 2e. Across sessions there was a significant effect of selectivity, non-preferred suppression and their interaction (p<0.0001 for all effects, 2-way repeated measures ANOVA). Similar effects were also observed when analyzing the data from the preferred and non-preferred stimulus separately (Supplementary Fig. 2).

A simple mechanism provides insights into the dynamics behind these changes in correlation. This mechanism incorporates two mutually-suppressive neuronal populations (Fig. 2f). Neurons with similar stimulus preferences belong to the same neuronal population, e.g. neurons 1 and 2 in Population A. Neurons in different neuronal populations have different preferred stimuli, e.g. neuron 1 in Population A and neuron 3 in Population B. Thus, the preferred stimulus of Population A is the non-preferred stimulus of Population B and vice versa. When a pair of stimuli is presented, neurons in both populations become active while also suppressing neurons in the other population (dashed orange lines). Suppression from Population B is shared among neurons in Population A, and this shared suppression produces a positive correlation between pairs of neurons in population A. Neuron pairs in population A that are more strongly suppressed by neurons in population B (non-preferred suppression near 1), receive more common suppression and become more positively correlated. The neuron pair consisting of neurons 1 and 2 in Population A might lie near the upper right corner of Figure 2a-e if the suppression they receive from Population B is strong, or near the upper left corner of Figure 2a-e if that suppression is weak.

While shared suppression results in positive correlations between neurons with similar preferences, neurons with opposite selectivity become negatively correlated. This follows from the same mutually-suppressive mechanisms: Larger responses in Population B more strongly suppress responses in Population A, causing neuronal responses in population A and B to become negatively correlated. Stronger suppression from the other population (non-preferred suppression near 1) will cause more decorrelation. The neuron pair consisting of neurons 1 and 3 in Figure 2f would lie near the lower right corner in Figure 2a-e if the suppression each receives from the other population were strong.

The striking pattern of stimulus-induced changes in spike-count correlations (Fig. 2c-e) suggests that normalization mechanisms strongly influence the structure of correlated neuronal activity.

Attention-related increased or decreased spike-count correlations arise from normalization mechanisms

Visual attention engages normalization circuitry^21–26 and influences neuronal correlations^7,8,14–20. We sought to determine whether attention-related changes in spike-count correlations arise from the same normalization mechanism described above. The effects of attention were measured with two stimuli simultaneously presented near the RFs, i.e. the same paired-stimulus configurations and neuron pairs for which selectivity and non-preferred suppression was measured in Figure 2.

Attention-related changes in spike-count correlations were robust only for neuron pairs with the same stimulus preferences (selectivity > 0). We first focus on these pairs in Figure 3 (see below for neuron pairs with opposite stimulus preferences). Attending to the preferred stimulus of similarly-tuned neurons decreased spike-count correlations relative to when attention was directed far from the RF (i.e. relative to Fig. 2c; see Fig. 3a, d; main effect non-preferred suppression: P=0.48, main effect selectivity: P<0.0001, selectivity-suppression interaction: P<0.0001, linear regression, N=1266712 correlations).

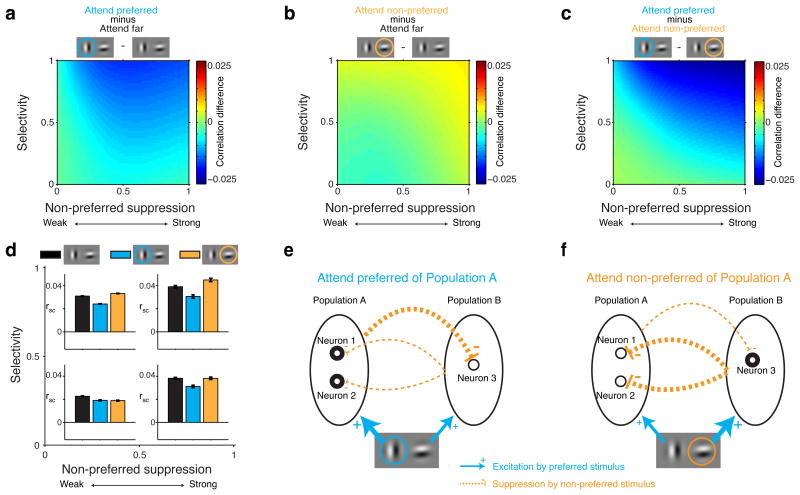
Figure 3. Visual attention engages normalization mechanisms to modulate spike-count correlations.

All data in these plots were obtained during paired stimulus presentations with attention directed to one of two RF stimuli (locations 1, 2 Figure 1b). Data are shown for neuron pairs with the same selectivity (selectivity > 0; see Figure 4 for opposite selectivity). a, Spike-count correlations decrease when the preferred stimulus is attended relative to when attention is directed far from the RF stimuli. b, Spike-count correlations increase when the non-preferred stimulus is attended relative to when attention is directed far from the RF stimuli. c, Attention modulation of spike-count correlations: comparing a and b. d, Mean spike-count correlations (r_sc) computed on the data from four quadrants in the space spanned by selectivity and non-preferred suppression in a, b and c (quadrants defined by a combination of selectivity < 0.5 or > 0.5 and non-preferred suppression < 0.5 or > 0.5). Black: attention directed far from the RF stimuli. Blue: attention directed to the preferred stimulus of neuron pairs. Orange: attention directed to the non-preferred stimulus of neuron pairs. Error-bars represent ± 1 SEM. e, Attending the preferred stimulus of neurons in Population A increases neuronal activity in Population A (thick circles), which increases suppression to neurons in Population B (thick orange line). The less active neurons in Populations B (thin circles) send less common suppression to neurons in Population B (thin orange line), thereby decorrelating activity in Population A. f, Attending the preferred stimulus of neurons in Population B increases neuronal activity within Population B, which increases common suppression to neurons in Population A, thereby correlating activity in Population A.

Attending to the non-preferred stimulus of these neurons increased spike-count correlations compared to when attention was directed far from the RF (Fig. 3b, d; main effect non-preferred suppression: P<0.0001, main effect selectivity: P<0.0001, selectivity-suppression interaction: P<0.0001, N=1266712 correlations). This was unexpected, because the effect of attention to a receptive field stimulus is typically described as reducing spike-count correlations^7,8,14–20.

We next compared the effects of attending to the preferred or non-preferred stimulus (Fig. 3a vs. 3b). When shifting attention between the preferred and the non-preferred stimulus, spike-count correlations modulate most for similarly-tuned neuron pairs that are most selective and are most suppressed by their non-preferred stimulus (Fig. 3c, d, upper right quadrant).

These results were confirmed in a session-by-session analysis: For each session we obtained the average attention modulation of spike-count correlations within each quadrant of Figure 3d. Across sessions there was a significant effect of selectivity (p=0.007), non-preferred suppression (p=0.006) and their interaction (p=0.04). Similar results were obtained when the average responses of pairs of neurons were matched across conditions (Online Methods).

These attention-related changes in spike-count correlations emanate from the same mutually-suppressing neuronal populations considered earlier (Fig. 3e, f). Attending to the preferred stimulus of neurons with the same selectivity, e.g. neurons 1 and 2 in Population A, increases their responses (thick circles in Fig. 3e; Supplementary Fig. 3). Following this increased activity in Population A, Population A more strongly suppresses neurons in Population B (thick dashed orange line in Fig. 3e), causing responses in Population B to decrease (thin circles in Fig. 3e). Because responses in Population B decrease, the correlating suppressive inputs from Population B into Population A become weaker (thin dashed orange lines in Fig. 3e), thereby decreasing the spike-count correlations within Population A, as in Figure 3a.

Conversely (Fig. 3f), attending to the non-preferred stimulus of neurons in Population A increases activity in Population B, because now Population B's preferred stimulus is attended. The increased activity in Population B amplifies the common suppression from Population B into Population A (thick dashed orange lines in Fig. 3f). This increased common suppression to Population A correlates activity in Population A, as in Figure 3b.

Thus attention-related changes in spike-count correlations stem from normalization mechanisms.

No attention-related changes in spike-count correlations for oppositely-tuned neurons

For pairs of neurons with opposite stimulus preferences (selectivity < 0), one neuron's preferred stimulus is the other neuron's non-preferred stimulus. Attend preferred and attend non-preferred are not defined for such pairs of neurons (attend preferred for one neuron of the pair is attend non-preferred for the other neuron of the pair). We therefore compared conditions in which attention was directed far from the RF to conditions in which attention was directed toward one of the two RF stimuli.

For oppositely-tuned pairs of neurons, attending to a RF stimulus had little effect on spike-count correlations relative to when attention was directed far from the RF (Fig. 4a, b). Such small effects of attention on the spike-count correlations of pairs of oppositely-tuned neurons are predicted by the normalization model with oppositely-tuned mutually-suppressive neuronal populations: Attending to the preferred stimulus of neurons in Population A increases the responses of these neurons (Fig. 4c). The stronger responses in Population A increase suppression toward Population B (thick dashed orange line in Fig. 4c), in which responses will decrease. Due to its decreased responses, Population B sends less suppression to Population A (thin dashed orange lines in Fig. 4c). Thus when attending the preferred stimulus of neurons in Population A, Population A sends more correlating suppression to Population B, which would normally result in more negative correlations between neurons in Population A and neurons in Population B (compared to attend Far). However, because Population B sends less correlating suppression to Population A, these same correlations become more positive (compared to attend Far). The increased correlating suppression in one direction and the decreased correlating suppression in the other direction act to cancel each other out. The result is that attention has little overall effect on the response correlations between neurons in Population A and neurons in Population B, i.e. neurons with opposite stimulus preferences.

Figure 4. Little attention modulation of spike-count correlations for neuron pairs with opposite selectivity.

For oppositely-tuned neuron pairs (selectivity < 0), attend preferred and non-preferred are not defined: one neuron's preferred stimulus is the other neuron's non-preferred stimulus. So we compared conditions in which attention was directed far from the RF stimuli to conditions in which attention was directed toward one of two RF stimuli. a, Attention modulation of spike-count correlations. b, Mean spike-count correlations computed on the data from four quadrants in the space spanned by selectivity and non-preferred suppression indices in a. Black: paired stimulus presentations with attention directed far from the RF stimuli. Brown: spike-count correlations with attention directed toward one of two RF stimuli. Error-bars represent ± 1 SEM. c, Correlations between neurons in Population A and neurons in Population B (e.g. neurons 1 and 3) change little compared to the condition with attention directed Far from the RF, because increased suppression in one direction is canceled by decreased suppression in the other direction.

Taken together, the findings from similarly- and oppositely-tuned neuron pairs illustrate the heterogeneous effects of attention on spike-count correlations under different neuron and attention conditions.

A stochastic normalization model accounts for the spike-count correlations

To validate the intuitions provided by the model in Figures 2-4, we developed a quantitative stochastic normalization model that formalizes the intuitive model presented thus far (Online Methods). As with the intuitive model, the quantitative model consists of two mutually-suppressive and oppositely-tuned neuronal populations. Critically, in the model attention operates solely by amplifying the excitatory contribution of the attended stimulus to the neuronal response: a gain change. Thus, attention-related changes in spike-count correlations can only appear as an indirect consequence of the response of the normalization mechanism to changes in its input: the attention-related increased excitatory inputs amplify the inhibitory outputs from a population, resulting in altered spike-count correlations.

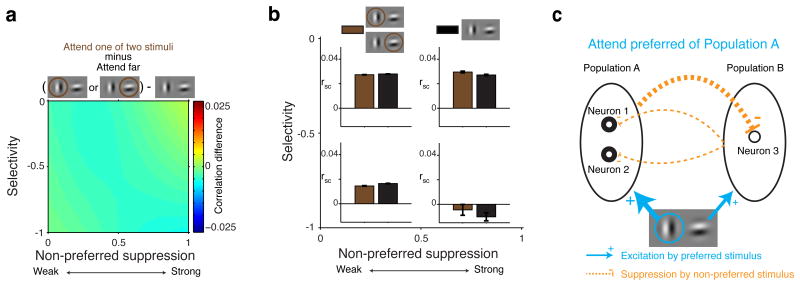
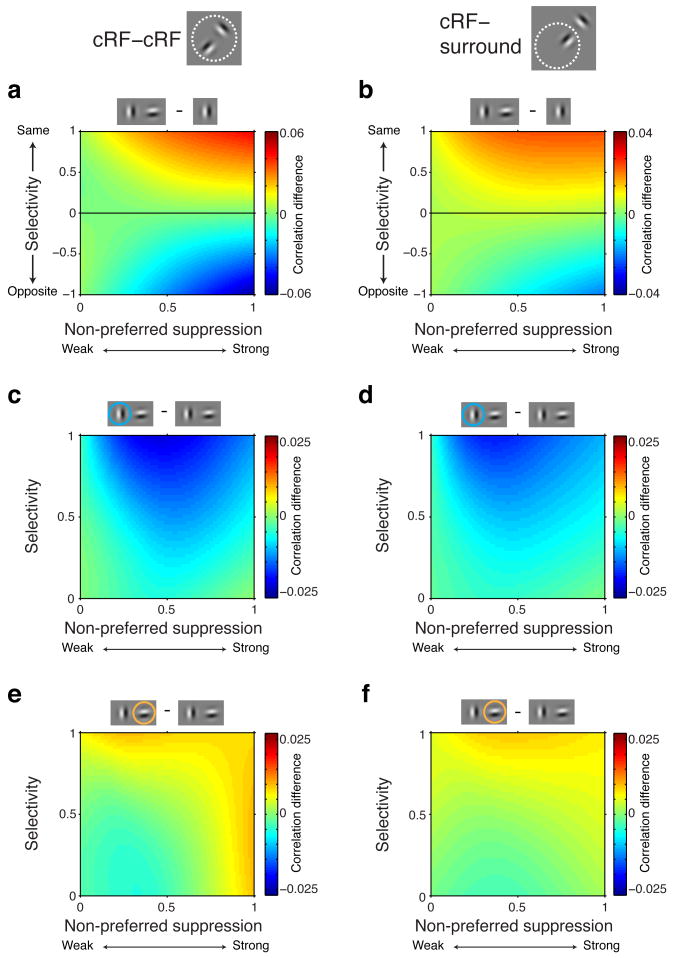
The stochastic normalization model captures all the main trends in the observed correlation structure: increased spike-count correlations for similarly-tuned neurons when attending far (Fig. 5a), decreased spike-count correlations for oppositely-tuned neurons when attending far (Fig. 5a), decreased correlations when attending to the preferred stimulus of similarly-tuned neurons (Fig. 5b), increased correlations when attending to the non-preferred stimulus of similarly-tuned neurons (Fig. 5c), and little attention modulation for oppositely-tuned neurons (Fig. 5d).

Figure 5. A stochastic normalization model accounts for the main trends in the observed correlations.

The model is based on two mutually-suppressive neuronal populations with opposite stimulus preferences. a, Model output for the conditions with attention directed far from the RF stimuli. Conventions as in Figure 2d. b, Model output for the conditions with attention directed to the preferred stimulus of similarly-tuned neuron pairs. Conventions as in Figure 3a. c, Model output for the conditions with attention directed to the non-preferred stimulus of neuron pairs with similar stimulus selectivity. Conventions as in Figure 3b. d, Model output for the conditions with attention directed to one of two receptive field stimuli for neuron pairs with opposite stimulus selectivity. Conventions as in Figure 4a.

Thus attention-related changes in spike-count correlations can be viewed as a consequence to attention-related changes in the strength of inputs to normalization mechanisms.

Normalization mechanisms in the classical receptive field and the surround shape response correlations similarly

The previous analyses averaged across stimulus configurations with both stimuli contained within the classical receptive field (cRF) and configurations with stimuli lying the neuron's surround. We next distinguished between these stimulus conditions and examined the effects of normalization mechanisms and attention on spike-count correlations inside the cRF and the surround.

We found that the effects of stimulus selectivity and suppression on spike-count correlations were similar for conditions with two stimuli both presented inside the classical receptive field (cRF-cRF) and stimulus conditions with one stimulus shown inside the cRF and another stimulus presented inside the surround (cRF-surround). In both stimulus configurations, we observed that selectivity and non-preferred suppression increased (similar selectivity) or decreased (opposite selectivity) spike-count correlations (Fig. 6a, b; cRF-cRF same selectivity: main effect selectivity: P<0.0001, main effect suppression: P=0.26, selectivity-suppression interaction: P<0.0001, linear regression. cRF-cRF different selectivity: main effect selectivity: P<0.0001, main effect suppression: P=0.76, selectivity-suppression interaction: P<0.0001. cRF-surround same selectivity: main effect selectivity: P<0.0001, main effect suppression: P=0.5, selectivity-suppression interaction: P<0.0001. cRF-surround different selectivity: main effect selectivity: P=0.001, main effect suppression: P=0.004, selectivity-suppression interaction: P=0.001) The effects were slightly smaller in the surround condition, as expected from the weaker suppression from stimuli inside the surround compared to stimuli inside the cRF²⁶.

Figure 6. Normalization mechanisms affect spike-count correlations similarly for stimuli inside the classical receptive field or in the surround.

Left column, stimulus configurations with two stimuli inside the cRF. Right column, stimulus configurations with one stimulus inside the cRF and one stimulus inside the surround. a and b, Same conventions as in Figure 2d. Note the different scale bars between a and b. c and d, Same conventions as in Figure 3a. e and f, Same conventions as in Figure 3b.

Attention also operated similarly in both stimulus configurations, decreasing spike-count correlations when directed to the preferred stimulus of a pair, and increasing response correlations when directed to the non-preferred stimulus (Fig. 6c-f; cRF-cRF attend preferred: main effect selectivity: P<0.0001, main effect suppression: P=0.69, selectivity-suppression interaction: P<0.0001, linear regression. cRF-cRF attend non-preferred: main effect selectivity: P<0.0001, main effect suppression: P=0.0003, selectivity-suppression interaction: P=0.003. cRF-surround attend preferred: main effect selectivity: P<0.0001, main effect suppression: P=0.04, selectivity-suppression interaction: P<0.0001. cRF-surround attend non-preferred: main effect selectivity: P<0.0001, main effect suppression: P=0.01, selectivity-suppression interaction: P=0.005). Note that for the cRF-surround condition, the surround stimulus is always the non-preferred stimulus because by definition neurons do not respond to stimuli inside the surround.

These results agree with a previous study that showed that normalization mechanisms and attention operate similarly on rate of firing for stimuli inside the classical receptive field (cRF) and the surround²⁶. Importantly, these analyses also help explain the well-established observation that attention reduces spike-count correlations when shifted to a single stimulus inside the RF^7,14,16,17. Specifically, in these experiments attention shifted between a stimulus in the opposite hemifield and a stimulus in the classical receptive field, a configuration that corresponds to the configuration with one stimulus inside the cRF and one stimulus inside the surround, for which we observe decreased correlations when the cRF stimulus is attended and which the model explains.

Discussion

We show that shared neuronal activity fluctuations within an area can be understood as arising from normalization mechanisms, providing a simple mechanistic explanation for a heterogeneous set of observations. A relationship between normalization mechanisms and spike-count correlations has been suggested previously^28–31, but the precise relationship remained unclear. Our findings show that normalization mechanisms can shape spike-count correlations through suppressive activity that affects the responses of populations of neurons. These suppressive influences can be shared among neurons with similar stimulus preferences, resulting in increased spike-count correlations, or antagonistic among neurons with opposite stimulus preferences, creating negative response correlations. Our results indicate that attention can bias suppressive activity as a result of elevating responses in one population of neurons, and that this bias can explain why we observed that attention decreased (attend preferred) or increased (attend non-preferred) spike-count correlations. A stochastic normalization model, consisting of two mutually-suppressive but opposite-tuned neuronal populations, explained all patterns of spike-count correlations.

Previous studies have suggested that spike-count correlations arise from shared inputs³² that might take the form of common gain modulations^33–35 or other shared modulatory signals^33,35,36. However details of the mechanisms that determine these common influences have remained obscure. Our findings show that shared activity fluctuations can be determined by normalization circuits in which suppressive activity can either increase or decrease response correlations. The influence of the suppressive activity on spike-count correlations can be strong: for pairs of neurons with strong preferences for the same stimulus, stimulus-induced suppression can double the spike-count correlations compared to those observed during single stimulus presentations. On the other hand, for pairs of oppositely-tuned neurons, stimulus-induced suppression can turn positive correlations into negative correlations. Thus, the suppression in normalization circuitries is an important factor in shaping correlated neuronal activity, potentially the dominant source.

Normalization mechanisms underlie a broad range of response properties of neurons in different brain areas, such as contrasts tuning³⁷, how responses to a stimulus are suppressed by nearby stimuli^38,39, multisensory integration⁴⁰, and how attention modulates neuronal responses^21–26. Given the importance of normalization mechanisms under various sensory and cognitive conditions, it is likely that the relationship between normalization mechanisms and correlated neuronal activity, as reported here, will explain spike-count correlations throughout the brain and for different experimental conditions. The current data provide one important example, showing that visual attention uses normalization mechanisms to correlate or decorrelate neuronal activity.

Visual attention engages normalization circuitry by amplifying the excitation and suppression associated with the attended stimulus^21–26. We reasoned that if attention-related changes in the rate of firing are influenced by normalization mechanisms, then the effects of attention on spike-count correlations should also follow from normalization mechanisms. We show that, depending on which stimulus is attended, attention can decrease (attend preferred stimulus) or increase (attend non-preferred stimulus) response correlations. These attention-related changes in spike-count correlations followed from the normalization model, as an indirect consequence of amplifying the excitation (gain) associated with the attended stimulus. The attention-related gain change biased the suppression between different neuronal populations in favor of the population preferring the attended stimulus, which in turn modified response correlations. Therefore, these findings provide strong support for normalization models of attention.

Conversely, because attention builds on normalization mechanisms to modify neuronal responses, we could test how perturbations in activity affect correlations in the normalization model of spike-count correlations that we propose. The findings show that increased or decreased activity in one population of neurons biases suppressive activity, which leads to predictable changes in spike-count correlations. Crucially, in the model attention is just one factor that can change the response strength of neurons, but other factors, like stimulus contrast, are expected to exert similar influences on response correlations.

Previous studies have shown that attending a single stimulus inside the receptive field decreases spike-count correlations relative to when a stimulus in the opposite hemifield is attended^7,14,16,17. Our model predicts such a decrease in correlation. Specifically, the conditions in these experiments correspond to the condition in which one stimulus is shown inside the cRF and another stimulus inside the surround (the stimulus in the opposite hemifield). Our data and model demonstrate that in such configurations spike-count correlations will be lower when the cRF stimulus is attended compared to when the surround stimulus is attended.

It has been suggested that attention actively modifies spike-count correlations, in a task and stimulus dependent way, to improve sensory encoding^14–18. How attention might achieve such a complex feat is unknown. Our findings provide a more parsimonious explanation, namely that spike-count correlations are indirectly modulated by the same normalization mechanisms that have been shown to modulate the average responses of individual neurons^21–26. Note, however, that our findings do not exclude the possibility that changes in the mean rate effected by normalization are incidental to changes in correlation, or that both mean rate and correlations matter for sensory processing. Our data suggest that mechanisms that are common across different tasks, like normalization mechanisms, contribute to shaping spike-count correlations.

Contrary to our findings, a previous study by Ruff and Cohen found increased spike-count correlations for pairs of neurons with opposite stimulus tuning¹⁵. However, there are at least two important differences between the two studies that make direct comparisons difficult: First, the other study defined selectivity based on neuronal responses to stimuli that were not used during the attention task. Specifically, they defined a neuron's selectivity (i.e., spatial selectivity) based on the responses to 100% contrast stimuli at one of two locations (same orientation), as measured during instruction trials in which only one stimulus was presented. During the task, however, stimuli of different contrasts were shown and these stimuli could be positioned at either of two receptive field positions. It is very likely that which stimulus the neurons preferred (for an individual stimulus presentation) depended on whether the high or low contrast stimulus was presented at the more or less responsive receptive field position. For example, a high contrast stimulus at the less responsive RF position may elicit a stronger response than the low contrast stimulus at the more responsive position. In that case, the neuron would actually prefer the “non-preferred” stimulus. In contrast to Ruff and Cohen, we always defined stimulus selectivity using the same stimuli (orientation and position) during the attention task (with attention directed away from the RF). Thus in Ruff and Cohen, stimulus selectivity is likely to have differed across the stimulus configurations they used to measure spike correlations, such that their average results for neurons with opposite stimulus preferences also included pairs of neurons with similar stimulus preferences.

Second, Ruff and Cohen used a different task that gave them less control over where monkeys attended. In their study the monkeys had to compare the contrast of two nearby stimuli. Consequently, their monkeys were encouraged to either pay attention to both stimuli or switch their attention between them (across or within trials). Their larger attentional field or their variable locus of attention would be expected to contribute to the differences between the studies.

Ruff and Cohen (2016) found a negative correlation between normalization and spike-count correlations³⁰. However, they did not separate the data according to stimulus selectivity. We also find a negative correlation between suppression and spike-count correlations, but only for pairs of neurons with opposite stimulus preferences.

Attention can also affect spike-count correlations if the state of attention varies from trial to trial, causing spike rates of neurons representing a stimulus to covary^33,41,42. Our findings did not rely on trial-by-trial changes in the state of attention to explain attention-related changes in spike-count correlations. In the stochastic normalization model the attention-related gain factor was constant and contributed no variability. Moreover, our data show that on a given trial and a given attentional state, attention modulation of correlated neuronal activity differs between pairs of neurons depending on their selectivity and the strength of their shared suppressive inputs. So variable attention states were not necessary to account for the observed correlations.

Mutually-suppressive neuronal populations with different stimulus tuning have also been proposed to underlie perceptual-decision making^27,43,44. Moreover, normalization mechanisms support diverse response properties across a broad range of brain areas^{27,37,38,45,46}. Thus it will be interesting to explore how the present results will bear on brain functions well beyond attention.

Online Methods

Surgical procedures

Two male rhesus monkeys (M1 and M2, Macaca mulatta, both 9 kg, 7 and 10 years old) were pair housed in standard 12:12 light-dark cycle and given food ad libitum. Before training, each animal was implanted with a head post. Following completion of the behavioral training (∼7 months), we implanted a 10 × 10 array of microelectrodes into area V4 of the left cerebral hemisphere, on the prelunate gyrus. Before surgery, animals were given buprenorphine (5.0 μg/kg, intramuscular) and flunixin (1.0 mg/kg, intramuscular) as analgesics, and a prophylactic dose of an antibiotic (Baytril, 5.0 mg/kg, intramuscular). They were then sedated with ketamine (15 mg/kg, intramuscular) and xylazine (2 mg/kg, intramuscular) and given atropine (50 μg/kg, intramuscular) to reduce salivation. Anesthesia was maintained with 1–2% isoflurane. Antibiotic was administered again 1.5 h into surgery; buprenorphine and flunixin were given for 48 h post-operatively. All procedures were approved by the Institutional Animal Care and Use Committee of Harvard Medical School.

Spatial attention task

As described in detail previously²⁶, we trained monkeys to perform a visual detection task in which spatial attention was manipulated. Each trial started when the monkey fixated a small spot in a virtual 1.5° square fixation window in the center of the video display for 240-700 ms. Eye movements were tracked using an infrared camera (EyeLink 1000) sampling binocularly at 500 Hz. The duration of the fixation period was randomly drawn from a uniform distribution. Following fixation a sequence of stimuli was presented, in which each stimulus presentation lasted 200 ms and was separated from other presentations by 200-1020 ms interstimulus intervals. The durations of the interstimulus intervals were randomly drawn from an exponential distribution (τ = 200 ms). During the interstimulus interval only a gray screen with the fixation dot was shown. The stimulus presentations were short to prevent animals from adjusting their attention within a stimulus presentation in response to the number or orientation of stimuli presented.

On each trial, stimuli appeared at two locations near the RFs of neurons, but the two locations differed between blocks of trials. One stimulus location (the middle location: location 1 in Supplementary Fig. 1a,b) never varied, but in different blocks of trials the second stimulus location was offset either clockwise (location 2 in Supplementary Fig. 1a) or counterclockwise (location 3 in Supplementary Fig. 1b). All stimulus locations were equidistant from the fixation point, and stimulus locations 2 and 3 were equidistant from stimulus location 1.

On each stimulus presentation within a trial, we presented one, two, or no stimuli at the two stimulus locations near the neurons' RFs. The stimuli could be of one of two orthogonal orientations. Each session, the stimulus orientation and location were optimized for a randomly selected unit, so that different orientations and locations were used across sessions. A representative set of nine possible stimulus combinations (for a particular orientation pair) is shown in Supplementary Figure 1c. Using these different stimulus combinations we could measure how the excitatory and suppressive contributions from different stimuli were combined into a neuronal response using a normalization model (see below).

Each stimulus location near the neurons' RFs (stimulus location 1, 2, 3 in Supplementary Fig. 1a,b) had a corresponding and equally eccentric stimulus location on the opposite side of the fixation point (e.g. stimuli near Far in Fig. 1b and Supplementary Fig. 1a,b). As outlined below, we instructed monkeys to direct their attention to one stimulus location, either near or far from the RFs. Using this approach we could measure not only how attention modulated correlated neuronal responses when directed to different stimuli near the neurons' RFs, but also measure stimulus selectivity and suppression with attention directed far from the neurons' RFs.

When Gabor pairs were presented near the neurons' RFs, their centers were separated by a median of 2.3° (range: 1.6°-4.8°), and always separated by at least six Gabor standard deviations (mean Gabor σ: 0.45°; range: 0.17°-0.50°). With such inter-stimulus spacing, two stimuli can fall within the RFs of a V4 neuron. We recorded simultaneously from several units, and therefore could not optimize the stimuli for most neurons. Depending on the precise size and locations of the neurons' RF, the two stimuli could both fall inside the cRF (cRF-cRF condition; Figure 6) or one stimulus could fall inside the cRF and the other inside the surround (cRF-surround; Figure 6; the condition with two stimuli inside the surround did not elicit responses and were not further analyzed).

Subjects were required to detect a faint white spot (Target; Supplementary Fig. 1e). The target appeared at one of the four stimulus locations (see above) during one stimulus presentation within a trial. The target never appeared on the first stimulus presentation of a trial, but could occur with equal probability on any other stimulus presentation (range: 2-8). Two to five percent of the trials contained no target and the monkey was rewarded for maintaining fixation until the trial ended. Targets were presented in the center of Gabor stimuli to encourage the monkeys to confine their attention to a restricted part of visual space near the cued stimulus location.

Task difficulty was manipulated by varying the target strength, defined as the opacity of the target (range of alpha-transparency values: 0.06-0.28). Each session we used six different target strengths (Supplementary Fig. 1e). The monkey was rewarded with a drop of juice for making a saccade to the target location within 350 ms of its appearance.

Attention was cued to a single location throughout each block of ∼150 trials. Before the start of each block the monkey performed three to five instruction trials in which stimuli were presented at a single (cued) location. The instruction trials cued the monkey to attend to that location during subsequent trials in which stimuli could occur at all four locations. No spatial cueing was provided after the instruction trials were completed.

Within a block of trials, the target appeared at the cued location in 91% of the trials (valid trials; position of the black circle in Supplementary Fig. 1d). In the remaining 9% of the trials (invalid trials) the target appeared at one of the three other (uncued) stimulus locations with equal probability (position of the yellow and green circles in Supplementary Fig. 1d). We used a single target strength for the invalid trials, as this allowed us to obtain reliable estimates of behavior at the unattended locations despite the small number of invalid trials. Using invalid trials, we could compare performance between attended and unattended locations. For both monkeys, the attention cue greatly affected behavioral performance in the task: targets were much more likely detected at a cued location than at an uncued location, even when the uncued location was adjacent to the cued location (Supplementary Fig. 1e).

Adaptation or repetition suppression/enhancement causes neuronal responses to a stimulus to decrease/enhance depending on the recent stimulus history. The magnitude of adaptation-related response changes may depend on the identity of the preceding stimulus⁴⁷. Such stimulus-dependent adaptation can potentially bias spike-count correlations, which are calculated across different repetitions of a stimulus with possibly different preceding stimuli. We mitigated adaptation-related correlation biases by keeping the recent stimulus history constant within a recording session, i.e. by assuring that each stimulus was always preceded by the same stimulus. For each daily recording session we used a new and randomly-ordered circular stimulus sequence (i.e. imagine placing the different stimuli of Supplementary Figure 1c in a random order on a rotating carousel). Each trial started at a random position within the sequence and subsequently the sequence progressed by the random number of stimulus presentations for that trial. This procedure was not employed during training sessions and stimuli containing the target were not counted as part of the sequence.

Visual stimulation and recordings

Stimuli were presented on a gamma-corrected cathode-ray tube (CRT) display with a 100 Hz frame rate (1024 × 768 pixels). Monkeys viewed the display from a distance of 57 cm. Stimuli consisted of full-contrast achromatic odd-symmetric static Gabor stimuli (0.6-2.2 cycles per degree; one spatial frequency per daily session) presented on a gray background (42 cd/m²), rendered online using custom software. The Gabor stimuli were truncated at three standard deviations from their center.

We recorded neuronal activity using a 10 × 10 array of microelectrodes (Blackrock Microsystems; impedances: 0.3-1.2 MΩ at 1 kHz; 1 mm electrodes; 0.4 mm between adjacent electrodes), chronically implanted into area V4 of the left cerebral hemisphere of each monkey. The data presented here are from 130 daily sessions of recording (Monkey M1: 52; Monkey M2: 78).

At the beginning of each recording session, we mapped the RFs and optimized stimulus parameters (position, orientation) for one randomly selected unit. The RFs of the units were located in the lower right quadrant at an average eccentricity of 3° for monkey M1 and 4° for monkey M2.

Statistics

We included only neuronal data from stimulus presentations from validly-cued correct trials. We excluded invalidly-cued trials, incorrect trials, instruction trials, trials with no target, the first stimulus presentation of a trial (on which no target could occur) and stimulus presentations with a target. Units were included in the analyses if they responded significantly above baseline to any single Gabor presented at any stimulus location in the attend far condition (ANOVA; α=0.05). Responses in the attend far condition were obtained by averaging the firing rates from the conditions in which attention was directed to either of the two stimulus locations furthest away from the receptive-field center of the neuron (Far in Fig. 1b). Similar results were obtained for each monkey, so the data from both monkeys were combined.

We examined the relationship between normalization mechanisms and spike-count correlations. Normalization mechanisms determine how neurons combine the suppressive and excitatory contributions triggered by each stimulus into one response^37,38. Because we only observe neuronal responses, we need a way to disentangle these different contributions to the neuronal response. We used a previously described divisive normalization model to estimate for each stimulus the strength of its excitatory and suppressive contribution to the neuronal response²⁶. This model successfully captures neuronal responses in all stimulus and attention conditions. Its basic form is given by:

$$R_{1,2}=\frac{L_1+L_2}{{\alpha }_1+{\alpha }_2+\sigma }$$ (1)

where R_1,2 is the neuronal response to a Gabor pair consisting of component Gabors 1 and 2. L₁ and L₂ are the excitatory contributions associated with each component Gabor. The α₁ and α₂ parameters determine the suppressive contribution of each component Gabor. Parameters α₁and alpha;₂ are each associated with one receptive-field location, and do not vary with the orientation of the stimuli shown at those locations. For simplicity, no contrast terms appear in Equation 1 because the Gabors were always presented at full contrast: when a single stimulus is presented in isolation, the L and α terms from the other stimuli are set to zero. Directing attention toward the first (R_1att,2; equation (2)) or second (R_1,2att; equation (3)) receptive-field location has a multiplicative effect on the parameters corresponding to the attended receptive-field location. This is described by the β parameter in equation (2) and (3):

$$R_{1\mathit{\text{att}},2}=\frac{\beta L_1+L_2}{\beta {\alpha }_1+{\alpha }_2+\sigma }$$ (2)

$$R_{1,2\mathit{\text{att}}}=\frac{L_1+\beta L_2}{{\alpha }_1+\beta {\alpha }_2+\sigma }$$ (3)

The model was fit to each unit's responses to all stimulus conditions: including conditions with single Gabors or Gabor pairs near the RF, and conditions with attention directed toward stimulus locations near the RF or far from it. All parameters were constrained to be nonnegative. The model was fit by minimizing the sum of squared error using a simplex optimization algorithm (MATLAB fminsearch; MathWorks). The model was fitted to 36 attention and stimulus combinations with ten parameters (see²⁶ for additional details). Across all units the median percentage explained variance of the model was 83%.

The model parameters provide information about each stimulus' suppressive and excitatory contribution to a unit's response. For each of the presented Gabor pairs, we quantified the relative excitatory and suppressive contribution of the component Gabors to each unit's response using two indices. First, we defined the selectivity of a unit for the two component Gabors of a Gabor pair as: $\mathit{\text{Selectivity}}=\frac{L_1-L_2}{L_1+L_2}$, where Gabor 1 is the preferred stimulus, i.e. L₁ > L₂.

Similarly, we defined for each Gabor pair the non-preferred suppression index as: $\text{non}-\text{preferred suppression}=\frac{{\alpha }_2}{{\alpha }_1+{\alpha }_2}$, where α₁ and α₂ correspond to the preferred and non-preferred stimulus respectively.

Selectivity and relative suppression indices were computed for each unit (N=12067 units) and all different Gabor pairs consisting of Gabors of different orientations and presented at different positions (Supplementary Fig. 1a-c).

To simplify the presentation of the results, in Figure 2 we excluded from the analysis 27% of unit pairs in which one unit received strong suppression from its preferred stimulus and the other unit received strong suppression from its non-preferred stimulus. However, similar results were obtained for this subset of unit pairs (see Supplemental Fig. 4).

Spike-count correlations were computed as the Pearson correlation coefficient between the spike counts of two units. For this purpose, spike counts were obtained from repeated presentations of the same stimulus in the same attention condition, and were measured in the interval from 50 ms to 300 ms after stimulus onset.

Spike-count correlations were computed for pairs of units, where each unit of a pair has its own selectivity and relative suppression index. For each index, the two indices of a correlation pair were combined using the geometric mean of both units' indices (e.g. ${\mathit{\text{Selectivity}}}_{\mathit{\text{pair}}1,2}=\sqrt{{\mathit{\text{Selectivity}}}_{\mathit{\text{unit}}1}\times {\mathit{\text{Selectivity}}}_{\mathit{\text{unit}}2}}$). Figure 2 and 3 are based on these combined indices. The combined selectivity index was subsequently signed: Positive selectivity indices correspond to pairs of units with the same stimulus preference, i.e. both units prefer the same component Gabor of a Gabor pair. Negative selectivity indices correspond to pairs of units with opposite stimulus preferences, e.g. unit 1 prefers Gabor1 while unit 2 prefers Gabor 2 of a Gabor pair. Selectivity was computed per Gabor pair and could depend on either spatial or orientation selectivity. The non-preferred suppression index ranges from zero to one. Values near zero indicate that each unit of a correlation pair is weakly suppressed by its non-preferred stimulus, relative to the suppression by its preferred stimulus. Values near one indicate that each unit of a correlation pair is strongly suppressed by its non-preferred stimulus, relative to the suppression by its preferred stimulus.

Similar results were obtained when equating the average response strength of pairs of neurons across conditions. For this purpose we matched the response-strength distributions (eight bins covering the range between the maximum and minimum response strength) between stimulus (Fig. 2e) or attention (Fig. 3d) conditions for each quadrant in the space spanned by selectivity and non-preferred suppression. The quadrants are those used in Fig. 2e, 3d and 4b. Here, response strength is defined by the geometric mean of the average neuronal responses of the two units of a correlation pair. Response-strength distributions were matched by randomly removing spike-count correlations.

Due to the chronic nature of our recordings, it is possible that some units were resampled across days. Because we adjusted the orientations and locations of the stimuli each day for a randomly selected unit, any such resampling would have rarely involved identical stimulus configurations.

A stimulus location was considered within the cRF if the unit responded significantly to any single stimulus (of either orientation) presented at that location, measured in the attend Far condition. A stimulus location was considered to be within the surround of a unit if the unit did not increase its firing rate significantly to any single stimulus (of either orientation; N>36 trials per stimulus) presented at that location, measured in the attend Far condition. Units for which a surround location was measured did respond significantly to at least one of the stimuli when it was presented inside the cRF instead of the surround.

The plots in Figure 2b-d, Figure 3a-c and Figure 4a were obtained using regularized (regularizing the gradient; smoothness=1) bilinear interpolation on the observed spike-count correlations from all Gabor pairs and all unit pairs (D'Errico, John (2005) Surface Fitting using gridfit (http://www.mathworks.com/matlabcentral/fileexchange/8998), MATLAB Central File Exchange). The data covered virtually the entire space spanned by the non-preferred suppression and selectivity indices (Supplementary Fig. 5).

No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to or lager than those reported in previous publications¹⁴.

Where linear regression and ANOVA analyses where used, the distribution of the residuals closely approximated a normal distribution (i.e. comparing the empirical residual distribution to the best-fitted Gaussian distribution), but did statistically deviate from normality (Kolmogorov-Smirnov test), as expected from the large sample size employed in the experiment. All statistical tests where two-tailed. Supplementary Fig. 6 shows the box-and-whisker plots for Figure 2e, 3d and 4b.

Data collection but not analysis was performed blind to the conditions of the experiments. No animals were excluded from the analysis.

Model

The intuitive model in Figure 2f and Figure 3e, f was formalized using a Poisson process with a rate governed by a system of coupled differential equations. Specifically, each neuron i generated spikes from a Poisson process with a random and time-varying mean spike rate λ_i(t). The mean spike rate of the neurons on a given trial evolved over time according to:

$$\tau \frac{d\lambda }{dt}=-\lambda +S(N\lambda +E)$$ (4)

Here, λ is a vector containing the spike rates λ_i(t) of each neuron i, τ is a time constant (i.e. 50 ms), S is a sigmoidal transfer function (i.e. logistic function) stabilizing the model, N is a normalization matrix capturing the coupling of the spike rates of the individual neurons thereby inducing spike-count correlations between the neurons, and E is a vector containing the excitatory inputs E_i to each neuron.

In the steady state, i.e. $\frac{d\lambda }{dt}=0$, this model is akin to a multivariate normalization model λ = E(I−N)⁻¹, where (I − N)⁻¹ functions as the normalizing denominator, I is the identity matrix, and we used the fact that most of the dynamics in λ occurs on the linear part of S so that S can be ignored.

Each trial, the excitatory input was assumed to be randomly distributed according to a Gaussian distribution, i.e. E ∼ N(Ē, σ_E). The Ē vector contained the mean excitatory inputs to each neuron and depends on each neuron's stimulus tuning (see below). The term σ_E is a covariance matrix, which contains all zeroes except on the diagonal where values were identical (i.e. 0.03). So the excitatory inputs E_i across neurons were independent of each other given the mean Ē.

Population A and B contained neurons with different stimulus preferences. For the simulations, neurons in different populations had different orientation preferences (preferred orientation population A: 45°; population B: 135°) with circular Gaussian (von Mises distribution) tuning curves. Neurons within a population had the same tuning curves. Similar to the experiment described in the results, we presented the model with pairs of stimuli such that the two stimuli in the stimulus pair had orthogonal orientations. Depending on where the stimulus orientations fell on the tuning curves of each neuron, stimuli elicited different amounts of excitation. Each stimulus of a stimulus pair contributed excitation, which was summed to obtain Ē_i, the average response of neuron i to that stimulus pair. A range of stimulus conditions was employed, consisting of stimulus pairs of different orthogonal orientations (covering 0°-180°) and resulting in different excitations. Selectivity was computed for pairs of neurons according to the definition given above, using the difference in excitatory drive from each stimulus.

Attending to a stimulus corresponded to multiplying the excitatory drive associated with the attended stimulus with a constant gain factor (i.e., 1.1). Aside from this gain change, attention exerted no other direct influence on the model parameters, only indirect influences that followed from the model dynamics.

For simplicity the simulations described in the text were performed using four neurons, two in population A, and two in population B, but the results do not depend on the number of neurons. Within a population, none of the neurons' spike rates were coupled to each other. Between populations, neurons' spike rates were negatively coupled to each other, thus creating mutual suppression between neuronal populations. So the matrix N consisted of zero (within populations) or negative (between populations) coupling values. A range of negative coupling values was employed (0 to -3.5) to simulate different amounts of non-preferred suppression. Non-preferred suppression indices were obtained by normalizing the coupling values to the range zero to one.

Once a stimulus is present, the evoked excitation E will elevate the responses of neurons, depending on their stimulus tuning. Thus the excitation E will increase the rate λ of the Poisson process (equation (4)). This rate gets multiplied by the normalization matrix N in equation (4), resulting in an increased inhibition towards the neurons in the other population. The elements of the normalization matrix N are the only parameters that describe the interaction between neurons in different populations. However, the strength of the interaction crucially depends on the strength of the stimulus-driven excitation: increased (decreased) excitation will result in more (less) inhibition towards the other population.

Using this model, we simulated 10000 trials per condition, i.e. for each combination of non-preferred suppression, selectivity and position of attention. Equation (4) was numerically solved using the Runge-Kutta method. For each condition we computed the spike-count correlation (Pearson correlation) based on the spikes simulated from the model in the interval from 50 ms to 300 ms after stimulus onset.