Motor Equivalence and Structure of Variance: Multi-Muscle Postural Synergies in Parkinson's Disease

Abstract

We explored posture-stabilizing multi-muscle synergies with two methods of analysis of multielement, abundant systems: (1) Analysis of inter-cycle variance; and (2) Analysis of motor equivalence, both quantified within the framework of the uncontrolled manifold (UCM) hypothesis. Data collected in two earlier studies of patients with Parkinson's disease (PD) were re-analyzed. One study compared synergies in the space of muscle modes (muscle groups with parallel scaling of activation) during tasks performed by early-stage PD patients and controls. The other study explored the effects of dopaminergic medication on multi-muscle-mode synergies. Inter-cycle variance and absolute magnitude of the center of pressure displacement across consecutive cycles were quantified during voluntary whole-body sway within the UCM and orthogonal to the UCM space. The patients showed smaller indices of variance within the UCM and motor equivalence compared to controls. The indices were also smaller in the off-drug compared to on-drug condition. There were strong across-subject correlations between the intercycle variance within/orthogonal to the UCM and motor equivalent/non-motor equivalent displacements. This study has shown that, at least for cyclical tasks, analysis of variance and analysis of motor equivalence lead to metrics of stability that correlate with each other and show similar effects of disease and medication. These results show, for the first time, intimate links between indices of variance and motor equivalence. They suggest that analysis of motor equivalence, which requires only a handful of trials, could be used broadly in the field of motor disorders to analyze problems with action stability.

Introduction

The term “synergy” has been used in the literature in different ways. In clinical literature, synergy usually means a pathological, stereotypical pattern of muscle activations interfering with purposeful actions (DeWald et al. 1995). Another meaning of synergy is a group of variables with proportional scaling of changes over time or with changes in task parameters (d'Avella et al. 2003; Ivanenko et al. 2004; Ting and Macpherson 2005). To avoid terminological confusion, we prefer to address such groups as modes (Krishnamoorthy et al. 2003) and use them as elemental variables in the analysis of synergies defined as neural organizations of elements (such as joints, limbs, digits, muscle groups, etc.) ensuring task-specific stability of salient performance variables (reviewed in Latash 2008, 2016).

A number of recent studies quantified multi-element motor synergies in different populations, including patients with Parkinson's disease (PD, reviewed in Latash and Huang 2015). These studies defined synergies as neural organizations of abundant sets of elements whose purpose is to provide stability of salient performance variables (reviewed in Latash 2012, 2016). In particular, synergies in the space of activations of muscle groups (M-modes) stabilizing coordinates of the center of pressure (COP) were studied (Falaki et al. 2016). This analysis was performed using the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; Latash et al. 2007) to quantify two components of inter-trial (or inter-cycle, for cyclical tasks) variance within the space of M-modes. The variance component within the UCM space (V_UCM) had no effect on the COP coordinate, whereas the variance component within the space orthogonal to the UCM (V_ORT) did. The normalized difference between V_UCM and V_ORT, quantified per dimension in each space, has been used as an index of stability (a synergy index). In this context, stability means an ability to return to a state or trajectory following a small transient perturbation or a change in initial state. Analysis of inter-cycle variance may be viewed as a method producing a proxy of stability (reviewed in Latash 2008, 2016). In particular, repeating a task from slightly different initial states is expected to lead to trajectories converging in more stable directions and diverging in unstable directions resulting in different variance indices within the UCM and ORT.

Two aspects of impaired control of stability in PD patients have been identified, namely, impaired stability and impaired agility (reviewed in Latash and Huang 2015). In particular, PD patients typically show weaker synergies stabilizing COP coordinates during steady-state tasks interpreted as signs of impaired stability. Weaker synergies in postural tasks have been documented in early-stage PD patients with no identifiable clinical signs of postural instability (Falaki et al. 2016). These changes in the synergy index show sensitivity to dopamine-replacement drugs (Park et al. 2014; Falaki et al. 2017).

One of the problems with using analysis of inter-trial variance in patient populations is the necessity to collect multiple trials to obtain clouds of data points (illustrated in Figure 1) to estimate V_UCM and V_ORT. Recently, another set of metrics has been developed within the framework of the UCM hypothesis, which can be measured in single trials. This analysis quantifies the magnitudes of motion of an abundant system within the UCM and ORT spaces (Scholz et al. 2007; Mattos et al. 2011, 2013, 2015). The within-UCM component, by definition, has no effect on the salient performance variable; it has been addressed as motor equivalent (ME). The ORT component, non-motor equivalent (nME), changes the performance variable.

Figure 1.

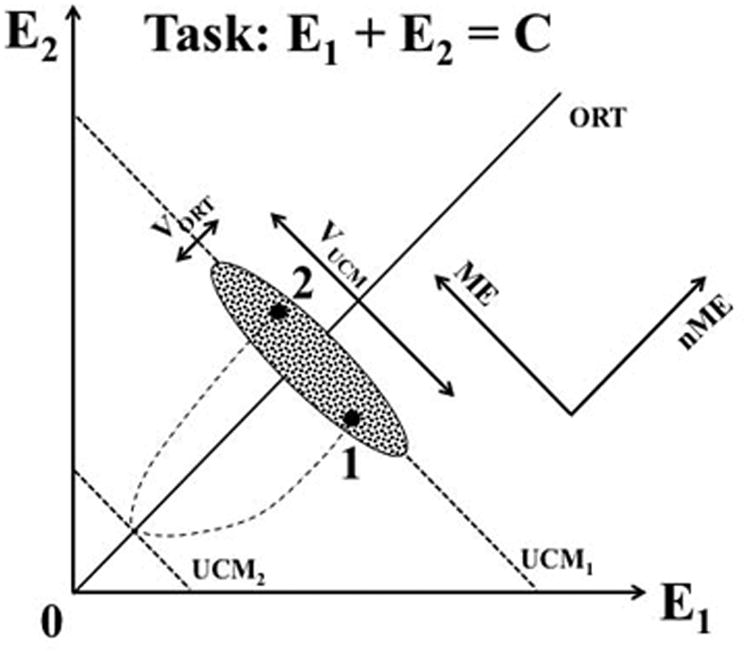
An illustration of the main notions for a simple task of producing a constant sum with two effectors: E₁ + E₂ = C. For a given C, the solution space is shown with the slanted dashed line (UCM₁). The cloud of data points measured in consecutive trials is elongated along the UCM (V_UCM > V_ORT). If the subject of this experiment is asked to produce a transient quick change in C and then come back to the initial value, motion to a new UCM (UCM₂) will be followed by a return motion ending up in a new point (2) that deviates from the original point (1) along the UCM more than along the orthogonal to the UCM direction (ME > nME).

Figure 1 illustrates the notions of V_UCM, V_ORT, ME and nME using a task of producing a particular magnitude of the sum of two variables: E₁ + E₂ = C. For a given C, the solution space is shown with the slanted dashed line (UCM₁). A synergy stabilizing (E₁ + E₂) is reflected in the cloud of data points measured in consecutive trials elongated along the UCM (V_UCM > V_ORT). If the subject of this experiment is asked to produce a transient quick change in C and then return to the initial value, motion to a new UCM (UCM₂) will be followed by a return motion ending up at a new point (2) that deviates from the original point (1) along the UCM more than along the orthogonal to the UCM direction (ME > nME).

Both the inter-trial variance analysis and the ME analysis provide proxies of stability of the performance variable (reviewed in Latash 2016, 2017). They are not identical, however, and a few recent studies have documented different statistical effects on the corresponding sets of metrics (Mattos et al. 2011, 2015). Note that ME analysis has never been performed in the space of muscle activations (or M-modes) during whole-body tasks. This analysis also has never been applied to data in neurological patients. In this study, we explore the links between the ME and variance analyses, and the potential usefulness of the ME analysis for clinical studies by reanalyzing data from two earlier experiments (Falaki et al. 2016, Falaki et al. 2017). Specifically, we addressed the following hypotheses. Hypothesis-1: PD patients will show smaller ME components during voluntary cyclical sway compared to control subjects (cf. smaller V_UCM in PD, Falaki et al. 2016). Hypothesis-2: PD patients will show smaller ME components off-drugs compared to the on-drug state (cf. smaller V_UCM off-drugs, Falaki et al. 2016). Hypothesis-3: the ME component will correlate with V_UCM, whereas the nME component will correlate with V_ORT. The last hypothesis is based on statistical considerations described in more detail in the Discussion.

We also explored the time profiles in the outcome indices within the sway cycle using a factor Phase. This exploration was based on earlier studies showing correlations of V_ORT with the rate of change of the salient performance variable and correlation of V_UCM with the magnitude of that variable (Latash et al. 2002; Scholz et al. 2002). These findings were interpreted later within a model of synergic control (Goodman et al. 2005), which assigned V_ORT to variance in setting timing parameters during a cyclical action and V_UCM to variance in setting spatial parameters. We expected similar relations between the rate of change of COP and nME, and between its magnitude and ME.

Methods

This paper reports results of additional analysis of the data collected in two studies and published earlier (Falaki et al. 2016, 2017). Here we briefly describe the materials and methods of the two studies.

Subjects

In the first experiment, 11 patients (6 females) diagnosed with PD at stage-II according to Hoehn and Yahr (HY; Hoehn and Yahr 1967), age 69 ± 6.3 years (mean ± standard deviation), and 11 healthy adults (age 65 ± 8.1 years, 5 females) volunteered to participate. In the second experiment, 10 PD patients (6 HY stage II and 4 HY stage III; age 69 ± 6.3; 5 females) participated. Three patients took part in both experiments. All of the participants were right-hand dominant according to their preferential hand use during writing and eating, except for one ambidextrous control subject (Sub #C07, experiment 1) and one ambidextrous patient (Sub #P17, experiment 2). Table 1 presents the general characteristics of the participants, as well as the Unified Parkinson's Disease Rating Scale (UPDRS-III) motor scores, disease duration since diagnosis, and the Levodopa equivalent dose (LED; Tomlinson et al. 2010). Control subjects were free from any diagnosed neurological or musculoskeletal disorder, and patients had no other known neurological or motor disorder except PD. None of the HY stage II patients showed signs of clinically identifiable postural instability (falls or positive responses to the shoulder pull test described in UPDRS) and no patient showed drug-induced dyskinesia on their prescribed medications. Participants were recruited from a large subject pool of an ongoing clinical study at the Penn State Milton S. Hershey Medical Center and were referred by their neurologist. All participants gave written informed consent according to the protocol approved by the Institutional Review Board of the Hershey Medical Center.

Table 1. Description of the participants.

Patients
Sub ID	Sex	Age	Symptom Onset	Duration (y)	UPDRS motor (Off)	UPDRS motor (On)	LED, mg/day	Experiment 1	Experiment 2
P01	F	72	R	3.5	—	11	300	✓	3 mo later
P02	F	73	L	4.5	—	18	480	✓
P03	F	72	L	4	—	38	300	✓
P04	F	70	Bilateral	0.8	—	13	500	✓	2.5 mo later
P05	M	72	R	4.6	—	15	167	✓
P06	M	69	Bilateral	1.6	—	8	195	✓
P07	M	79	R	2.2	—	8	500	✓	1 mo later
P08	M		L	7.6	—	5	738	✓
P09	M	71	R	3.1	—	21	400	✓
P10	F	55	R	2.2	—	2	250	✓
P11	F	63	R	4.7	—	18	700	✓
P12	M	63	L	11.7	21	13	667		✓
P13	M	64	R	8.6	46	30	635		✓
P14	M	71	Bilateral	1.5	19	8	250		✓
P15	F	64	R	12.2	16	9	550		✓
P04	F	70	Bilateral	1.1	37	33	500	✓	✓
P17	F	67	L	3.3	27	8	750		✓
P01	F	73	R	3.8	10	6	480	✓	✓
P19	F	67	R	4.8	38	25	700		✓
P20	M	75	L	8.6	31	18	650		✓
P07	M	79	R	2.3	29	25	600	✓	✓
Controls
Sub ID	Sex	Age
C01	M	56
C02	F	58
C03	F	67
C04	F	54
C05	M	77
C06	M	78
C07	M	69
C08	F	71
C09	M	64
C10	M	63
C11	F	61

Parkinson's disease participants who were common in both experiments are shown in bold. M/F: male/females, R/L: right/left, LED: levodopa equivalent dose

Apparatus

Subjects stood on a force platform (AMTI, OPTIMA) that recorded the horizontal and vertical components of the ground reaction force (F_X, F_Y, and F_Z, respectively), as well as the three moments of force about the XYZ axes (M_X, M_Y, and M_Z). In order to compute the coordinates of the center of pressure (COP), we used the platform coordinate system in which the X-axis was a horizontal axis pointing in the anterior direction, the Y-axis represented a horizontal axis pointing toward the right side of the subject's body, and the Z-axis was a vertical axis pointing downward (Fig. 2). Participants were provided with visual feedback on their COP coordinates in the anterior-posterior direction (COP_AP) and in the medial-lateral direction (COP_ML) computed using standard methods (Winter et al., 1996). This feedback was presented as a 5-mm white circle on a 23″ monitor mounted at eye level about 1.5 m away from the subject. To ensure safety and comfort, participants wore a safety harness affixed to the ceiling and an experimenter stood by them during the course of the experiment.

Figure 2.

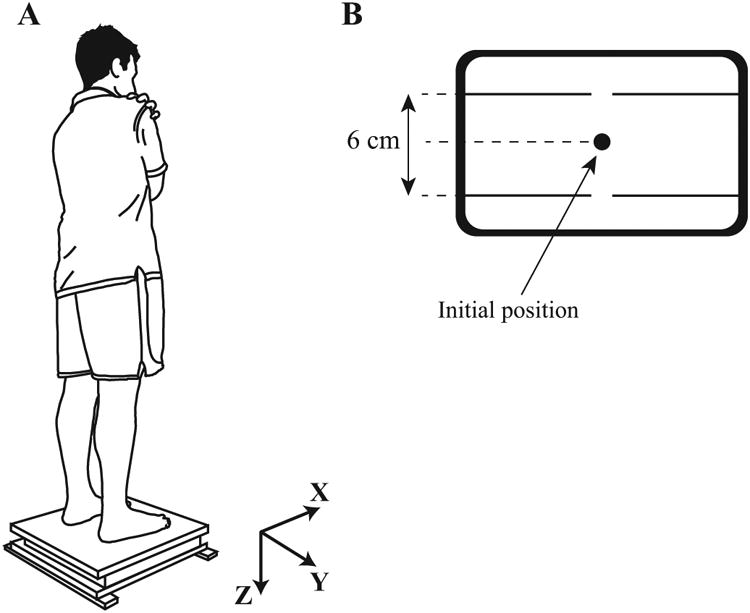
Experimental setup. A: Participants stood on the force platform with arms crossed over the chest and swayed mainly about ankle joints in the anterior-posterior direction. The platform coordinate system also is shown. A safety harness always was worn by participants (not drawn). B: Visual feedback of both COP_AP and COP_ML. Participants shifted their center of pressure between targets shown on the screen as two horizontal lines (6 cm peak-to-peak and symmetrical with respect to the initial standing position).

Surface electromyography (EMG) was recoded using rectangular-shaped active electrodes that housed built-in pre-amplifiers on the recording heads (Delsys, Trigno Wireless EMG). Electrodes were placed over the bellies of 13 leg and trunk muscles on the right side of the body: tibialis anterior (TA), soleus (SOL), gastrocnemius medialis (GM), gastrocnemius lateralis (GL), biceps femoris (BF), semitendinosus (ST), rectus femoris (RF), vastus lateralis (VL), vastus medialis (VM), tensor fasciae latae (TFL), lumbar erector spinae (ESL), thoracic erector spinae (EST), and rectus abdominis (RA). EMG sensors were placed according to published guidelines (Criswell and Cram, 2011) and subsequently confirmed by observing EMG patterns of related isometric contractions and free movements. We recorded EMGs on one side of the body based on earlier studies documenting bilateral changes in indices of synergies with no side differences in PD patients, even in those at Hoehn & Yahr stage-I that is defined clinically as the stage at which PD symptoms are limited to one side of the body (Park et al. 2012, 2014).

A data collection computer (Dell, Xenon 2 GHz) with a customized LabVIEW-based program (LabVIEW 2013, National Instruments) was used to digitize the EMG and force platform data at the sampling frequency of 1 KHz with a 16-bit resolution (PCI-6225, National Instruments).

Procedures

Initially, participants were asked to stand barefoot on the platform while keeping their feet parallel at shoulder width. We enforced the same initial posture throughout different trials by marking the position of each foot on the platform surface and asking subjects to reproduce this initial position at the beginning of each trial.

Quiet standing (QS) task

Each participant stood quietly on the force platform—with arms crossed over the chest and fingertips rested on the shoulders—for 30 s and tried to avoid body movements. This was the only task without visual feedback on the COP coordinates. The purpose of this task was to measure the baseline activity of recorded muscles for further correction and normalization of EMG signals (see ‘Data processing’) to facilitate between-subjects comparisons.

Voluntary sway (VS) task

Each participant stood on the platform and held the initial posture with arms crossed over the chest. The task was to perform continuous voluntary whole-body sway about the ankle joints in the anterior-posterior direction, shifting COP_AP between two targets shown as two horizontal lines on the screen, while trying to minimize COP_ML deviations (Klous et al. 2010; Falaki et al. 2016). During this task, visual feedback of both COP_AP and COP_ML was available on the screen (Fig. 2B). Positions of the targets were set at 3-cm posterior and 3-cm anterior to the neutral standing position (6 cm peak-to-peak amplitude). Each participant performed the VS task twice while being paced by a sound metronome at 0.5 Hz. The participants kept their feet in full contact with the platform during the course of the task, and each trial lasted 30 s. There was a 30-s rest period between trials. In case of excessive hip and/or knee joint involvement, the trial was repeated. Participants performed two practice trials, each lasting 15 s, prior to data collection. For the purposes of analysis, the time interval between two consecutive anterior-most COP_AP coordinates was defined as a VS cycle.

Experiment 1

In this experiment, patients were tested on their normal schedule of medication. The experiment started with measuring UPDRS-III motor scores by a trained clinician, after which all participants performed the QS task followed by the VS task.

Experiment 2

This experiment involved two sessions. The first session started early in the morning following an overnight withdrawal of the prescribed PD medication, prior to taking the first daily dose (off-drug condition). When participants finished the first session, they took their prescribed medication. The second session started one hour after taking the medication (on-drug condition). Each session started with measuring UPDRS-III motor scores followed by performing the QS and VS tasks.

Data processing

EMG and force platform signals were processed offline using a customized Matlab R2015a program. Prior to computing time-varying COP_AP coordinates (Winter et al, 1996), force platform signals were filtered with a 10 Hz low-pass, forth-order, zero-lag Butterworth filter. For VS trials, to avoid edge effects and incomplete cycles at the beginning and end of each trial, only the data within {3 s; 28 s} time interval were accepted. The time interval between two consecutive anterior-most COP_AP coordinates was defined as a sway cycle. On average, each participant performed 10 cycles within each VS trial. There was no statistically significant difference between the average number of cycles performed by PD and CO groups (Experiment 1), or between on-drug and off-drug conditions (Experiment 2). For the analysis of variance and motor equivalence, cycles that had an extra local COP_AP peak and those with the most anterior (posterior) COP_AP coordinates that differed from the corresponding means by more than ±2 SD were removed from further analysis. Such aberrant cycles likely reflected distracted attention by the subject; they had to be removed to satisfy one of the main assumption of the analysis, namely that the subjects were trying “to do the same” across cycles. The total number of rejected cycles varied between 0 and 3 per subject.

Raw EMG data were shifted 50 ms backward with respect to the force platform data to compensate for the electro-mechanical delay (Corcos et al. 1992; Cavanagh and Komi 1997), band-pass filtered (20-350 Hz) with a fourth-order, zero-lag Butterworth filter, and then rectified. A 100-ms window moving average filter then was used to create the envelope of the rectified EMG signals. For each participant, filtered EMG of each muscle was corrected for the background activity by removing the baseline muscle activity during the QS trial (EMG_QS) defined as the average value within the time period {13 s; 17 s}. Further EMGs were normalized by the peak value (EMG_PEAK) of the corresponding muscle across all sways.

$${\text{EMG}}_{\text{NORM}}=\frac{\text{EMG}-{\text{EMG}}_{\text{QS}}}{{\text{EMG}}_{\text{PEAK}}}$$ (1)

Defining muscle modes

We assumed that the central nervous system (CNS) organizes muscles into groups with close to parallel scaling of activation levels within each group (cf. d'Avella et al. 2003; Krishnamoorthy et al. 2003). We have defined these muscle groups as muscle modes or M-modes. To identify M-modes for each subject, the correlation matrix of EMG data normalized and averaged over each 50-ms time window (IEMG_NORM) from the VS trials was subjected to principal component analysis (PCA) with Varimax rotation and factor extraction (Krishnamoorthy et al. 2003; Danna-Dos-Santos et al. 2007). The first four PCs were selected, in the order of total variance for which they accounted, based on the Kaiser criterion, and confirmed by visual inspection of the inflection point of the scree plot. Additional criteria were that each muscle had to be significantly loaded (loading beyond ±0.5) on at least one of the four PCs and there could be no PCs without at least one significantly loaded muscle.

As in the aforementioned earlier studies, we decided to accept a fixed number of M-modes across groups and conditions rather than aim for a similar amount of total variance accounted for by the selected modes. Note that adding an M-mode to a set increases the UCM dimensionality without affecting ORT dimensionality (see later). Since variance magnitudes are normalized per dimension (whereas ME and nME indices are normalized per square root of dimensionality), this would result in unfair comparisons. Indeed, adding an M-mode that accounts for little variance would reduce variance within the UCM (and ME) after normalization without affecting variance within ORT (and nME). Moreover, adding a fifth M-mode would create more modes with only one muscle significantly loaded, which goes against the basic idea of identifying muscle groups with parallel scaling of activation.

We used PCA rather than the widely used non-negative matrix factorization method (NMF; Ivanenko et al. 2004; Ting and McKay 2007; d'Avella and Bizzi 2005) because PCA generates orthogonal eigenvectors while NMF generates a set of independent but not orthogonal vectors. Note that orthogonal bases are much more convenient for the analysis of variance and motor equivalence (see later). Also, note that an earlier study has shown comparable results from the PCA analysis with Varimax rotation and factor extraction and from NMF (Tresch et al. 2006).

Defining the Jacobian matrix

Linear relations between small changes in elemental variables (ΔM) and COP_AP shifts (ΔCOP_AP) were assumed (Krishnamoorthy et al. 2003; Danna-Dos-Santos et al. 2007). Averaged over each 50-ms time window, EMG and COP_AP data from all cycles during the VS task were used to run multiple linear regression analysis without intercept. For each participant, coefficients of the regression analysis defined the Jacobian (J) matrix:

$$\begin{array}{c}\mathrm{\Delta }{\text{COP}}_{\text{AP}}={\mathrm{k}}_1\mathrm{\Delta }{\mathrm{M}}_1+{\mathrm{k}}_2\mathrm{\Delta }{\mathrm{M}}_2+{\mathrm{k}}_3\mathrm{\Delta }{\mathrm{M}}_3+{\mathrm{k}}_4\mathrm{\Delta }{\mathrm{M}}_4\\ \mathbf{J}=[\begin{array}{cccc}{\mathrm{k}}_1& {\mathrm{k}}_2& {\mathrm{k}}_3& {\mathrm{k}}_4\end{array}]\end{array}$$ (2)

The J matrix determines how small deviations of M-mode magnitudes affect the selected performance variable (the COP_AP coordinate). Prior to the regression analysis, a fourth-order, zero-lag Butterworth filter was used to low-pass filter ΔCOP_AP and ΔM at 5 Hz to remove effects of high-frequency data components that were unrelated to voluntary body sway.

Analysis of variance

According to the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner, 1999), elemental variables (in this study M-modes) are organized to provide stability of a potentially important performance variable (in this study, COP_AP). Within this approach, two inter-trial (inter-cycle) variance components are quantified in the M-mode space. The first component is within the UCM (V_UCM, variance preserving the COP_AP coordinate), whereas the second component is in the orthogonal to the UCM sub-space (V_ORT, variance affecting the COP_AP coordinate). The M-mode space had the dimensionality of n = 4. Since the hypothesis of COP_AP stabilization accounted for one degree of freedom (d = 1), the UCM sub-space had the dimensionality of three.

For each participant, the duration of all of the accepted sway cycles during the VS task was normalized to 100%. For each time-normalized step (1% of the sway cycle), the mean vector of M-mode magnitudes across cycles (M̄) was subtracted from vectors of individual M-mode magnitudes from each cycle resulting in mean-free values of M-modes changes, ΔM_demeaned:

$$\mathrm{\Delta }{\mathbf{M}}_{\mathbf{\text{demeaned}}}=\mathbf{M}-\overline{\mathbf{M}}$$ (3)

To compute V_UCM and V_ORT, ΔM_demeaned was projected onto the UCM (f_UCM) and the ORT space (f_ORT). The null-space of the J matrix served as a linear approximation of the UCM. Variance within the UCM and ORT, normalized by dimension, was computed as:

$$\begin{array}{c}{V}_{\mathit{\text{UCM}}}={\sigma }_{\mathit{\text{UCM}}}^2=\frac{{\sum }_{i=1}^N|{\mathrm{f}}_{\mathit{\text{UCM}}}{|}^2}{(n-d)N_{\mathit{\text{trials}}}}\\ V_{\mathit{\text{ORT}}}={\sigma }_{\mathit{\text{ORT}}}^2=\frac{{\sum }_{i=1}^N|{\mathrm{f}}_{\mathit{\text{ORT}}}{|}^2}{d{N}_{\mathit{\text{trials}}}}\end{array}$$ (4)

Analysis of motor equivalence

The motor equivalence analysis (Mattos et al. 2011, 2013, 2015) quantifies the amount of deviations in the space of elemental variables (M-modes) that occurs in directions preserving (motor equivalent, ME), changing (non-motor equivalent, nME) the performance variable, COP_AP. For each subject and each time-normalized step, deviations of M-modes from one sway cycle to the next were projected onto the null-space of J (f_ME) and its orthogonal complement (f_nME):

$$\begin{array}{c}\mathrm{\Delta }\mathit{M}={\mathit{M}}_i-{\overline{\mathit{M}}}_{(i+1)}\\ {\mathrm{f}}_{\mathit{\text{ME}}}=\sum _{i=1}^{n-d}{({\varepsilon }_i^T•\mathrm{\Delta }M)}^T•{\varepsilon }_i^T\\ {\mathrm{f}}_{n\mathit{\text{ME}}}=\mathrm{\Delta }M-{({\mathrm{f}}_{\mathit{\text{ME}}})}^T\end{array}$$

In equation (5), ε_i stands for basis vectors that spanned the null-space of J. The length of this projection within the UCM sub-space was the ME component, whereas the length of the projection within the ORT reflected the nME component. For quantitative comparisons, ME and nME components were normalized by the square root of the dimension in the respective spaces (cf. Mattos et al. 2011):

$$\begin{array}{c}\mathit{\text{ME}}=\frac{\Vert {\mathrm{f}}_{\mathit{\text{ME}}}\Vert }{\sqrt{(n-d)}}\\ \mathit{\text{ME}}=\frac{\Vert {\mathrm{f}}_{\mathit{\text{nME}}}\Vert }{\sqrt{d}}\end{array}$$ (6)

For each subject, the average of the ME and nME components across time-normalized cycles was computed for statistical analyses. Note that we used average indices over all the cycles for this analysis. We viewed this as appropriate for the first step in using the ME analysis to identify postural stability problems in PD. In future, ME and nME indices can be computed as averages over 3-4 trials only, particular for non-cyclical tasks.

Statistics

Statistical analysis was performed with SPSS 21.0 (IBM Corp.). In the text and figures, data are shown as means ± standard errors (SE). To explore the dependence of outcome variables (kinematics of sway, V_UCM, V_ORT, ME and nME) on the phase of swaying, the factor Phase with four levels was used to represent four windows with a length equal to 11% of the sway cycle and centered about the maximum, minimum, and in-between phases of the cycle: ‘95-5%’ (representing 95-100% of cycle n-1 and 1-5% of cycle n), ‘20-30%’, ‘45-55%, and ‘70-80%’. In Experiment 1, two-way repeated measures ANOVAs were used to explore the effects of factor Phase (four levels) and Group (two levels: PD and CO) on the outcome variables. Repeated measures ANOVAs with factors Group, Variance (two levels: V_UCM and V_ORT), and/or Motor equivalence (two levels: ME and nME) were used to investigate effects of PD on the averaged across cycle variances and motor equivalence components. In Experiment 2, factor Medication (two levels: off-drug and on-drug) replaced factor Group in order to explore effects of the dopamine-replacement drug on the outcome variables. Data were checked for normality and sphericity. In case of violation of the assumption of sphericity, Greenhouse-Geisser correction was used for degrees-of-freedom adjustments. To explore significant effects at the level of p < 0.05, pairwise comparisons with Bonferroni corrections were performed. Correlations between variance components (V_UCM and V_ORT) and motor equivalence components (ME and nME) were explored using Pearson correlation coefficients. We present median values and inter-quartile ranges (IQR) for coefficients of determination (R²).

Results

Voluntary sway kinematics

All participants, including patients in the off-drug condition, were able to perform qualitatively similar ‘sine-like’ time-profile of COP_AP during the voluntary body sway task. Figure 3 shows the mean (top panels) and SD (bottom panels) of the COP_AP averaged over VS cycles and across participants separately for Experiment 1 and Experiment 2. Participants were at the anterior-most position at 0% and 100% of the time-normalized sway cycle, whereas they were at the posterior-most position approximately at 50% of the sway time. There was no statistically significant difference in the COP_AP coordinate at different sway phases between PD and control participants (Experiment 1), and between the off-drug and on-drug conditions (Experiment 2) in the two-way ANOVAs with factors Phase and Group (Medication). The ANOVA showed only the trivial main effect of Phase. The average peak rate of COP_AP shifts, averaged across forward and backward phases, (dCOP/dt)_MAX, however, was significantly smaller in PD subjects (19.4 ± 1.65 cm/s) than controls (25.9 ± 1.61 cm/s), confirmed by a oneway ANOVA with factor Group (F_(1,20) = 7.98; p < 0.05). Although the SD of the COP_AP was larger in controls, the group difference was non-significant (F_(1,20) = 3.83; p > 0.05). In Experiment 2, there was no statistically significant differences between (dCOP/dt)_MAX in the off-drug (19.1 ± 1.80 cm/s) and on-drug (20.9 ± 1.49 cm/s) conditions, and no difference between the SD of the COP_AP (off-drug: 0.82 ± 0.05; on-drug: 0.92 ± 0.07).

Figure 3.

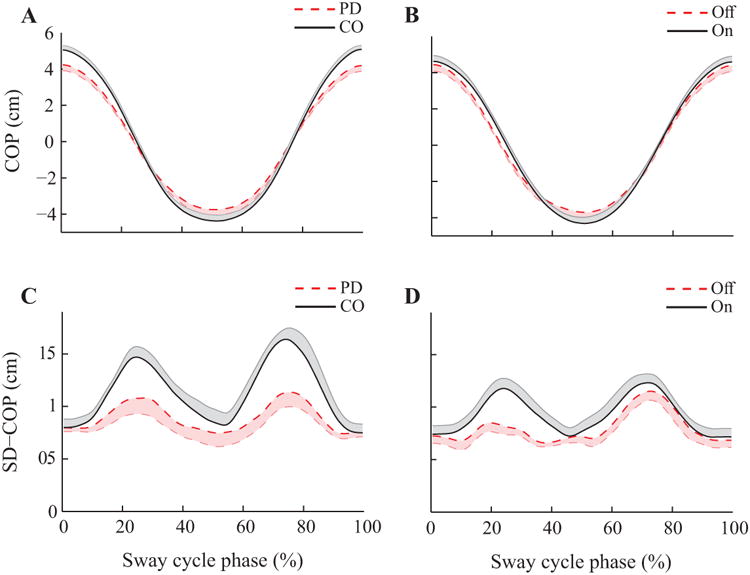
Time-normalized profiles of the center of pressure coordinate in the anterior-posterior direction (COP_AP; A and B) and the standard deviation of COP_AP (SD-COP; C and D) with standard error shades. Participants were at the anterior-most position at 0% and 100%, of the sway cycle. At about 50% of the sway cycle, participants were at the posterior-most position. A and C: Experiment 1. The dashed line represents the mean data for PD patients and the solid line represents the mean data for the controls. B and D: Experiment 2. The dashed line represents the mean data for the off-drug condition and the solid line represents the mean data for the on-drug condition.

Defining M-modes and Jacobians

Based on the criteria described in the Methods, four M-modes were identified in all subjects. Table 2 represents a typical set of muscle loadings for a PD participant in the on-drug and off-drug conditions. M₁-mode and M₂-mode typically involved significantly loaded dorsal or ventral muscles and are called either dorsal or ventral M-mode. The composition of those modes was similar in all subjects and did not differ in PD patients based on the side of symptom onset. The other two M-modes compositions were more variable across subjects. Loadings over 0.5 are shown in bold.

Table 2. Muscle loadings for the first four M-modes in a typical PD patient.

Muscle	Off-drug				On-drug
	M1	M2	M3	M4	M1	M2	M3	M4
TA	0.75	-0.38	-0.17	-0.18	0.73	0.40	-0.25	-0.03
SOL	-0.45	0.72	0.30	0.13	-0.37	-0.86	0.22	-0.03
GM	-0.46	0.77	0.26	0.10	-0.29	-0.91	0.14	-0.01
GL	-0.42	0.74	0.33	0.09	-0.23	-0.86	0.31	-0.01
BF	-0.01	0.90	0.03	-0.03	-0.37	-0.74	0.34	-0.04
ST	0.81	-0.09	-0.01	0.02	-0.17	-0.08	0.76	-0.07
RF	0.86	-0.31	-0.20	-0.06	0.81	0.43	-0.22	0.02
VL	0.78	-0.17	-0.29	0.15	0.82	0.40	-0.15	0.03
VM	0.88	-0.34	-0.09	-0.03	0.88	0.26	-0.14	0.04
TFL	0.87	-0.08	-0.18	0.03	0.85	0.08	-0.25	-0.01
ESL	-0.16	0.16	0.86	0.04	-0.21	-0.35	0.75	0.00
EST	-0.17	0.20	0.85	0.02	-0.23	-0.30	0.73	0.03
RA	0.02	0.08	0.04	0.98	0.02	0.03	-0.04	0.99

Loading factors after Varimax rotation for a typical Parkinson's disease patient in the off-drug and on-drug conditions. Significant loadings (greater than 0.5) are shown in bold. TA - tibialis anterior, SOL - soleus, GM - gastrocnemius medialis, GL - gastrocnemius lateralis, BF - biceps femoris, ST - semitendinosus, RF - rectus femoris, VL - vastus lateralis, VM - vastus medialis, TFL - tensor fasciae latae, ESL - lumbar erector spinae, EST - thoracic erector spinae, RA -rectus abdominis.

In Experiment 1, the four M-modes accounted for, on average, significantly less variance in the muscle activation space in the PD group compared to controls (71.5 ± 1.74% vs. 78.3 ± 1.74%; F_(1,20) = 7.969; p < 0.05). In Experiment 2, the M-modes accounted for significantly less variance in the muscle activation space in the off-drug condition compared to its respective value in the on-drug condition (68.6 ± 2.2% vs. 74.7 ± 2.4%; t₍₉₎ = -4.51, p < 0.01). In both Experiments, all M-modes were significant predictors of COP_AP shifts for each subject (p < 0.001).

Analysis of variance and motor equivalence

For each subject and/or medication condition, we used the framework of the UCM hypothesis to quantify two components of the inter-cycle variance in the M-mode space: the component affecting (V_ORT) and not affecting (V_UCM) the COP_AP coordinate during the VS task. The same data also were used to quantify the deviations in the M-mode space across consecutive cycles that preserved (ME) or changed (nME) the COP_AP coordinate. The time profiles of V_UCM and ME were similar to each other, whereas the time profiles of V_ORT and nME were aligned closely. Figures 4 and 5 present averaged time profiles over cycles of ME and nME (top panels) and V_UCM and V_ORT (bottom panels) for the two Experiments. Note the qualitative similarity of the top and bottom graphs. In particular, the nME and V_ORT plots show a two-peak profile resembling that expected for the absolute value of dCOP(t)/dt if COP(t) were a perfect sine wave (compare to the bottom panels in Fig. 3).

Figure 4.

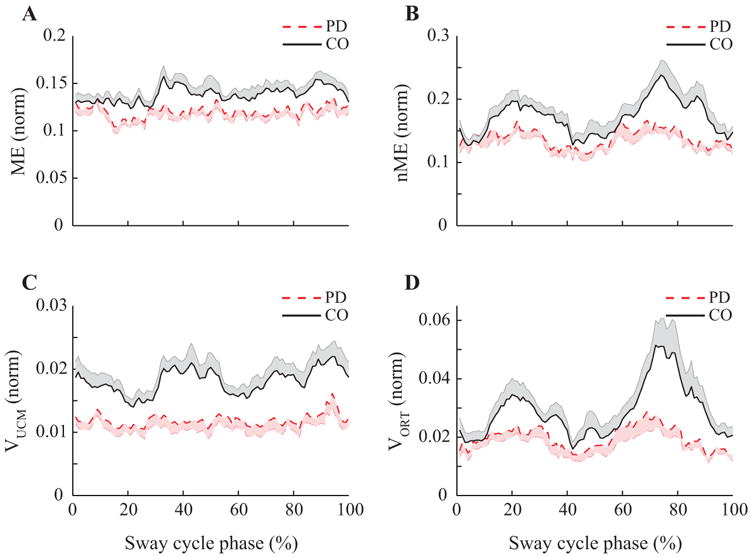
Results of the motor equivalence and variance analyses in Experiment 1. Time-normalized profiles of the motor equivalent (ME, panel A) and non-motor equivalent (nME, panel B) components, variance within the UCM (V_UCM, panel C), and within ORT (V_ORT, panel D) for PD patients (dashed line) and controls (CO, solid line). Note the higher magnitudes of all indices in the controls and the typical double-peaked patterns of nME and V_ORT.

Figure 5.

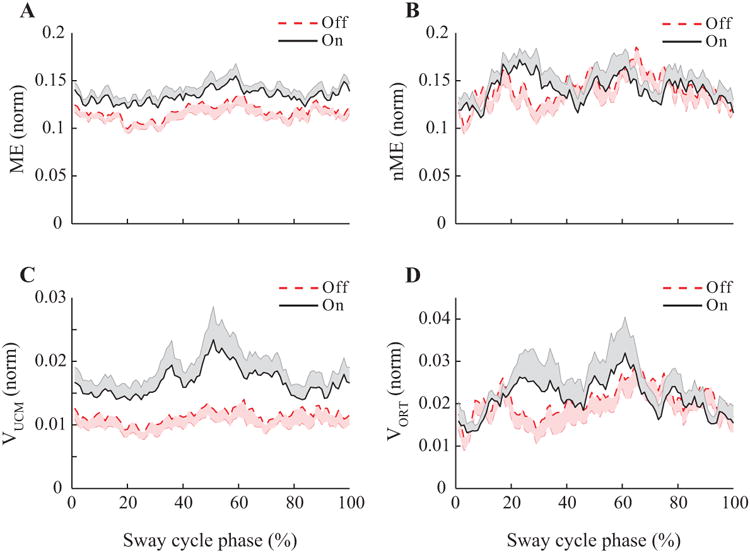
Results of the motor equivalence and variance analyses in Experiment 2. Time-normalized profiles of the motor equivalent (ME, panel A) and non-motor equivalent (nME, panel B) components, variance within the UCM (V_UCM, panel C), and within ORT (V_ORT, panel D) for PD patients off-drug (dashed line) and on-drug (solid line). Note the higher magnitudes of all indices on-drug and the typical double-peaked patterns of nME and V_ORT.

To explore possible links of the outcome variables to parameters of the task, such as COP(t) and dCOP(t)/dt, we used linear regression analysis. To explore the similarity between the pairs of outcome variables, V_UCM vs. ME and V_ORT vs. nME, we performed statistical analyses on the effects of the main factors (Phase, Group, and Medication) and correlation analyses within these pairs of variables.

Experiment 1

A two-way ANOVA, Group × Variance, showed that control subjects had significantly larger amounts of total inter-cycle variance in the M-mode space compared to PD patients (0.023 ± 0.002 vs. 0.016 ± 0.002; effect of Group F_(1,20) = 10.32; p < 0.01). Both V_UCM and V_ORT in the PD group (Vucm: 0.012 ± 0.001; V_ORT: 0.020 ± 0.003) were smaller compared to the control group (V_UCM: 0.018 ± 0.001; V_ORT: 0.029 ± 0.003). V_ORT was, on average, larger than Vucm (effect of Variance; F_(1,20) = 23.15; p < 0.001). A two-way ANOVA, Phase × Group, performed separately on V_UCM and V_ORT showed no significant modulation of V_UCM across the four phases of the sway cycle, whereas V_ORT showed a significant Phase effect (F_(3,60) = 12.80; p < 0.001), and a significant Group × Phase interaction (F_(3,60) = 3.39; p < 0.05). Pairwise comparisons revealed that V_ORT in phases 1 and 3 was smaller than its respective values in phases 2 and 4 (p < 0.05). The interaction reflected the fact that the effect of phase on V_ORT was significant in the control group only.

Hypothesis 1

Similar results were obtained in the analysis of motor equivalence. In particular, both ME and nME in PD (ME: 0.121 ± 0.005; nME: 0.139 ± 0.10) were significantly smaller than their respective values in controls (ME: 0.138 ± 0.005; nME: 0.171 ± 0.010). This was confirmed by a significant effect of Group (F_(1,20) = 8.24; p < 0.01) in a two-way ANOVA Group × Motor equivalence. The nME component was larger than the ME component in both groups (F_(1,20) = 14.64; p < 0.001) without an interaction. A two-way ANOVA, Group × Phase, on nME showed significant effects of Group (F_(1,20) = 5.50; p < 0.05), Phase (F_(3,60) = 14.54; p < 0.001), and a Group × Phase interaction (F_(3,60) = 2.97; p < 0.05). Similar to V_ORT, pairwise comparisons revealed smaller magnitudes of nME in phases 1 and 3 compared with phases 2 and 4 (p < 0.05). In PD patients, only the amount of nME in phase 2 was larger than in phase 3 (p < 0.05).

Further, we explored correlations between the nME (and V_ORT) indices and the derivative of the COP_AP (t) for each subject using a liner regression analysis: V_ORT (nME) = a + b |dCOP/dt|. The values of V_ORT (nME) and |COPap (t)/dt| were taken at each 1% from the time-normalized cycles. Table 3 summarizes the median, the first quartile, and the third quartile values. In 10 out of 11 controls, V_ORT was correlated linearly with |dCOP/dt|. A similar relationship existed between nME and |dCOP/dt|. For the PD group, these correlations were significant in seven out of 11 patients.

Table 3. Results of the correlation analysis.

Group	VORT vs. |dCOP/dt|		nME vs. |dCOP/dt|		VUCM vs. COP(t)		ME vs. COP(t)
	Median	Q1, Q3	Median	Q1, Q3	Median	Q1, Q3	Median	Q1, Q3
PD patients	0.11	0.04; 0.26	0.07	0.03; 0.20	0.17	0.13; 0.21	0.11	0.05; 0.19
Controls	0.37	0.24; 0.42	0.31	0.24; 0.47	0.26	0.05; 0.39	0.10	0.08; 0.18
PD off-drug	0.08	0.02; 0.16	0.07	0.04; 0.29	0.27	0.10; 0.38	0.09	0.02; 0.36
PD on-drug	0.06	0.02; 0.09	0.07	0.05; 0.11	0.18	0.04; 0.26	0.14	0.07; 0.24

The median and inter-quartile values of the correlation coefficients between the V_ORT (nME) indices and the derivative of the COP_AP (t), and between the V_UCM (ME) indices and COP_AP(t). Q₁: the first quartile, Q₃: the third quartile

The correlation between V_UCM and COP_AP (t) was also investigated using linear regression: V_UCM (ME) = a + b COP(t). The values of V_UCM and COP(t) were taken at each 1% of the sway cycle. V_UCM was correlated linearly with COP_AP (t) in nine controls and 10 PD patients. Comparing ME and COP_AP (t), a linear relation was observed in nine controls and nine PD patients.

Experiment 2

Dopaminergic medications led to an increase in the amount of V_UCM (0.017 ± 0.002 vs. 0.012 ± 0.002 on- and off-drug, respectively; F_(1,9) = 6.08; p < 0.05) without a change in V_ORT (0.021 ± 0.004 vs. 0.021 ± 0.003; on- and off-drug, respectively). There also was an effect of Phase (F_(3,54) = 3.96; p < 0.05) on V_UCM: On average, V_UCM in phase 2 (0.012 ± 0.001) was smaller than phase 3 (0.017 ± 0.002), as confirmed by pairwise comparisons. There were no significant effects of Phase on V_ORT.

Hypothesis 2

Similar results were obtained in the analysis of the ME and nME components. In particular, ME on-drug was larger compared to the off-drug condition (0.134 ± 0.005 vs. 0.118 ± 0.006; F_(1,9) = 17.60; p < 0.01). In contrast, there were no effects of Medication on the nME component (on-drug: 0.143 ± 0.008; off-drug 0.141 ± 0.010). There were no significant Phase effects on either ME or nME.

Overall, correlations between ME(t) and COP_AP(t) and between nME(t) and dCOP_AP(t)/dt were weak, although statistically significant in some of the patients. On-drug, the absolute value of dCOP(t)/dt was related linearly to V_ORT indices in seven patients and to the nME in eight patients. Off-drug, these relationships were significant for V_ORT in six patients and for nME in seven patients. In addition, there was a significant relationship between V_UCM and COP_AP (t) in seven patients and between ME and COP_AP (t) in nine patients in the on-drug condition. Off-drug, COP_AP (t) was correlated with V_UCM indices in nine patients and with ME in seven patients. A summary of the median and inter-quartile values is presented in Table 3.

Hypothesis 3

Correlations between ME and V_UCM, and between nME and V_ORT were explored using Pearson correlation coefficients. For each subjects, time-normalized data points of variance components (V_UCM and V_ORT) were averaged over the cycle and plotted against the respective motor equivalence components (ME and nME), also averaged over the cycle. Figure 6 represents scatter plots of V_UCM and ME, as well as V_ORT and nME for Experiment 1 (panels A and B) and Experiment 2 (panels C and D) with the lease squares line of best fit. In this Figure, data points refer to individual subjects. There was a significant correlation between V_UCM and ME (PD: R² = 0.49; CO: R² = 0.4; p < 0.05), and between V_ORT and nME component (PD: R² = 0.87; CO: R² = 0.84; p < 0.05) in Experiment 1. In Experiment 2, there also was a significant correlation between V_UCM and ME (off-drug: R² = 0.76; on-drug: R² = 0.42; p < 0.05), and between V_ORT and nME (off-drug: R² = 0.48; on-drug: R² = 0.91; p < 0.05).

Figure 6.

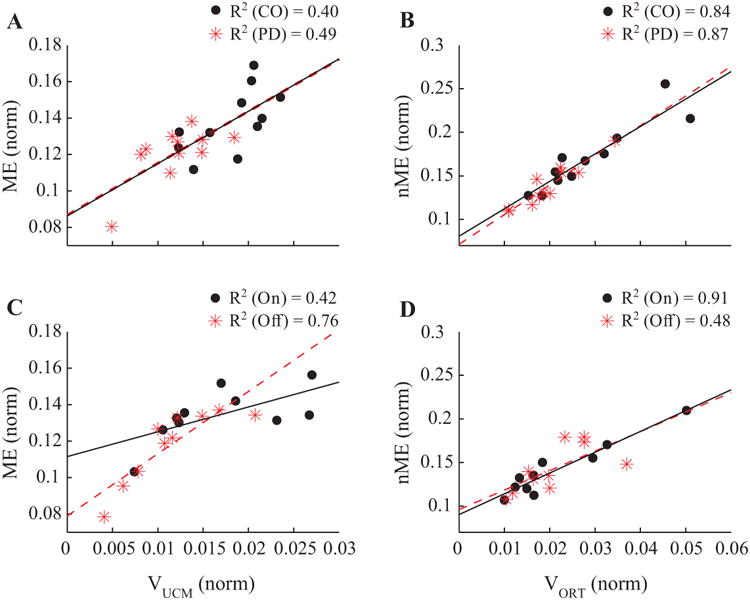
Scatter plots of the variance and motor equivalence indices across subjects. Correlations between V_UCM and the ME component for Experiment 1 (panel A) and Experiment 2 (panel C) and between V_ORT and the nME component for Experiment 1 (panel B) and Experiment 2 (panel D) are presented with regression lines and coefficients of determination.

We also quantified correlations between the same pairs of variables within each participant using cross-correlation analysis of time-normalized data points. Peak correlation coefficients were large for both Experiment 1 and Experiment 2. In Experiment 1, peak correlation coefficients between V_UCM and ME ranged from 0.35 to 0.87 for PD subjects (median: 0.77; IQR: 0.67, 0.84) and from 0.39 to 0.91 for controls (median: 0.73; IQR: 0.65, 0.79). For the analysis of V_ORT vs. nME, peak correlation coefficients ranged from 0.56 to 0.93 for PD subjects (median: 0.75; IQR: 0.70, 0.86) and from 0.55 to 0.96 for controls (median: 0.87; IQR: 0.76, 0.92). The time-lag of the peak correlation coefficient was close to zero in all comparisons (note that we used cycle percentage as a unit of time): The mean ± SE of the time-lag for the controls was –3.6 ± 3.35 in % cycle for the ME-V_UCM analysis and 0 ± 0 for the nME-V_ORT analysis. For PD patients, the time-lag of cross-correlation analysis was –1.9 ± 1.91 for the ME-V_UCM analysis and –1.3 ± 1.27 for the nME-V_ORT analysis. There was no statistically significant difference between the groups.

In Experiment 2, the time-lag was zero for all participants. For the off-drug condition, correlation coefficients between V_UCM and ME ranged from 0.68 to 0.90 (median: 0.84; IQR: 0.78, 0.88) and between V_ORT and nME ranged from 0.54 to 0.91 (median: 0.83; IQR: 0.77, 0.87). For the on-drug condition, correlation coefficients between V_UCM and ME ranged between 0.62 and 0.94 (median: 0.77; IQR: 0.70, 0.87) and between V_ORT and nME from 0.54 to 0.88 (median: 0.80; IQR: 0.76, 0.86). There was no statistically significant difference between correlation coefficients due to the medication that was confirmed by a one-way ANOVA.

Discussion

The three main hypotheses formulated in the Introduction have been supported by the data. Indeed, in Experiment-1, PD patients showed smaller motor equivalent (ME) components within the space of muscle modes during voluntary cyclical sway compared to control subjects in support of our Hypothesis-1. In Experiment-2, PD patients showed smaller ME components off-drugs compared to the on-drug state in support of Hypothesis-2. Both qualitative comparisons (Figures 4 and 5) and correlation analyses confirmed similar patterns between the ME component and the variance within the UCM (V_UCM) and between the nME component and the variance within the ORT space (V_ORT). Effects of the main factors on the metrics computed in the analysis of variance and in the analysis of motor equivalence were similar in both experiments. These observations support Hypothesis-3.

Our comparisons of the two types of indices, those reflecting inter-cycle variance structure (V_UCM and V_ORT) and those reflecting motor equivalence estimated across consecutive cycles (ME and nME), have shown that they both are sensitive to PD and dopamine-replacement medications. Note that our Experiment 1 involved PD patients at stage II according to Hoehn and Yahr (1967), which is defined as a stage without clinically identifiable postural instability. Nevertheless, both ME and variance indices showed significant differences between the PD and control groups. Both pairs of indices are proxies for the stability of a functionally important variable (COP_AP) estimated within the muscle mode space. The results suggest that indices of motor equivalence may be sensitive to emerging problems with postural stability even at stages when clinical examination fails to detect those problems. Experiment 2 confirmed that these indices also are sensitive to effects of dopamine-replacement medication. The fact that these two indices are correlated closely suggests that ME indices may become a practical measurement for clinical research to gauge synergic control of postural stability. Although we used averages over numerous cycles to produce ME indices in the current study, theoretically a few trials may be sufficient. This is something to explore in the future.

Synergies – mechanisms of task-specific stability

Our study is based on the concept of multi-element synergies stabilizing important, task-specific variables in a hierarchical system (reviewed in Latash 2010, 2016, 2017). This general theoretical framework is based on the idea of parametric control, i.e., the neural control of movements based on specifying time patterns of parameters of natural laws. It suggests that neural variables at a hierarchically high, task-specific level encode referent coordinates (RCs) for salient performance variables. Further, as a result of several few-to-many transformations, these task-specific RCs are transformed into RCs for individual effectors, joints, and muscles. At the muscle level, RC is equivalent to threshold of the tonic stretch reflex, as in the classical equilibrium-point hypothesis (Feldman 1966, 1986). The transformations are organized in such a way that spontaneous deviations of performance at the level of elements (due to changing intrinsic neural states and external forces) co-vary to keep variability of the salient variable relatively low. Such organizations have been addressed as synergies stabilizing those performance variables (Latash et al. 2007).

Note that proper stability, as ensured by synergies, is a crucial feature of all functional actions. For example, during steady-state performance, low stability may lead to failure and/or necessity to monitor performance and make corrections at all times. Another important aspect of synergies is their task-specificity: Different performance variables can be stabilized by the same set of elemental variables (e.g., M-modes) depending on the task. This allows several tasks to be performed with a single set of effectors and to avoid interference among salient performance variables when a few tasks are conducted simultaneously.

The story about synergies and their changes in neurological disorders would be incomplete without mentioning the phenomenon of anticipatory synergy adjustments (ASAs, Olafsdottir et al. 2005), which represents attenuation of a synergy in preparation for a quick action. This important functional mechanism allows a person to avoid fighting one's own synergies during quick actions. ASAs have been documented across systems and tasks (Shim et al. 2005; Klous et al. 2011; Krishnan et al. 2011, 2012). This mechanism is impaired in a variety of patients with both subcortical and cortical disorders (Park et al. 2012; Jo et al. 2016; reviewed in Latash and Huang 2015), which may lead to difficulty with movement initiation and even episodes of freezing.

Whereas mechanisms of synergies (those responsible for organizing muscles into M-modes and those responsible for M-mode synergies stabilizing salient performance variables) remain largely unknown, recent studies in neurological patients provide insights into possible neurophysiological mechanisms of synergic control of different sets of effectors, from multi-finger actions, to multi-joint reaching, and to multi-muscle whole-body actions (reviewed in Latash and Huang 2015). In particular, those studies have documented significantly impaired synergy indices during steady-state tasks in patients with subcortical disorders, but not following cortical stroke (Reisman and Scholz 2003; Jo et al. 2016). These findings are compatible with the idea of distributed processing modules (Houk 2005) involving loops through the basal ganglia and the cerebellum. In contrast, ASAs are reduced and decreased in magnitude in patients with both cortical and subcortical disorders (Park et al. 2012; Jo et al. 2016). Indices of synergic control are sensitive to very early stages of PD; they can be seen in the apparently non-involved hands of patients at HY stage-I (Park et al. 2012, 2014) and even in asymptomatic persons at elevated risk for parkinsonism, such as professional welders (Lewis et al. 2016).

So far, all the clinical studies of synergies have used analysis of the structure of inter-trial variance in two sub-spaces, the UCM where the salient performance variable does not change, and the ORT where it changes (see Fig. 1). These methods have provided a wealth of useful information. Their broad application, however, has been slowed by the necessity to analyze clouds of data points that requires collecting numerous trials in patients. This is not always feasible given that many patient populations are characterized by quick fatigue. One of the goals of our study has been to define whether a method that is capable of producing indices of stability based on a few trials, i.e. analysis of motor equivalence, is comparably sensitive to changes in synergies resulting from PD and/or dopaminergic medication. Whereas our experiment used indices of motor equivalence averaged over all of the cycles, such indices can be computed using individual cycles/trials and then averaged over only a few cycles or trials.

Indices of variance and motor equivalence

During cyclical tasks, analyses of inter-cycle variance and inter-cycle mean distances are linked if one assumes a perfectly normal distribution of the data. Indeed, if we assume that each measurement at a particular phase of the cycle represents a sample from a normal distribution, the difference between two random samples will be another normal distribution with the mean μ_D = 0 and standard deviation σ_D linearly related to standard deviation of the original distribution, σ_D =σ√2. In the analysis of motor equivalence, we computed absolute distances between data points in consecutive cycles (see Methods). This makes the distribution of those distances non-negative (folded) with a new mean (μ_X) and new standard deviation (σ_X). From classical statistics (Leone et al. 1961):

$$\begin{array}{c}{\mu }_X=\sigma \sqrt{2/\pi }\\ {\sigma }_X^2={\sigma }^2-{\mu }_X^2\end{array}$$ (7)

These equations can be applied separately to data in different sub-spaces of the original space. They suggest, in particular, that ME is expected to be proportional to the standard deviation within the UCM (σ_UCM), whereas nME is expected to be proportional to the standard deviation within the ORT space (σ_ORT). Correlations with squared magnitudes of standard deviations, V_UCM and V_ORT, also are expected, although they may be weaker.

Indeed, our analysis has shown that ME correlated with V_UCM, whereas nME correlated with V_ORT (see also the similar shapes of V_UCM and ME and of V_ORT and nME in Figs. 4 and 5). Although the current data set is limited and does not allow distinguishing between correlations with standard deviation and with variance (we explored both and found no significant differences), they allow drawing an important conclusion: At least in some tasks, indices of motor equivalence (ME and nME) can be used as synergy indices instead of metrics of intercycle variance. This conclusion is corroborated by the observations of similar significant differences in both variance indices and motor equivalence indices between the PD and control groups in Experiment 1 and between the PD patients on- and off-drug in Experiment 2. This result allows collecting only a handful of cycles/trials (< 5 trials) to obtain quantitative estimates of synergies stabilizing salient variables based on the ME and nME indices. As a result, analysis of motor equivalence may be applicable more easily to studies of populations with movement disorders who may be able to perform only a few cycles/trials of a given motor task.

The aforementioned statistical analysis potentially also can be applied to non-cyclical data. In discrete actions, however, it is more likely that individual trials differ from each other more than cycles within a continuous cyclical task due to the larger variance in setting central parameters that define the neural control process (cf. Friedman et al. 2009). As a result, a relatively small set of data points may deviate more from what is expected regarding a perfectly normal distribution. This may be the reason why, in some earlier studies, statistical effects on variance and motor equivalence indices were different (Mattos et al. 2011, 2015).

The time profiles of the ME and variance indices showed characteristic shapes, consistent across all subjects (Figures 4 and 5). In particular, ME and V_UCM showed a relatively flat time profile with a small peak in the middle, whereas nME and V_ORT showed double-peaked profiles with the peaks approximating the times of maximal COP_AP rate shifts. Such time profiles of V_ORT were reported earlier in studies of multi-finger force production (Latash et al. 2001, 2002; Scholz et al. 2002). Our correlation analyses confirmed associations between the COP_AP coordinate and both V_UCM and ME, and between the absolute magnitude of COP(t) rate and both V_ORT and nME in support of the model introduced earlier (Goodman et al. 2005; see Introduction).

The double-peaked profile of V_ORT and nME was more pronounced in the control subjects possibly reflecting two factors. First, the controls showed larger peak rates of COP_AP shift, which are expected to lead to higher V_ORT even if variance in setting the timing parameter is unchanged between the groups (see equations in Friedman et al. 2009). Second, variance in setting timing parameters across cycles also may be higher in PD as suggested by observations of higher temporal variability in motor performance in PD subjects (Wing et al. 1984; Pastor et al. 1992; Almeida et al. 2002).

Analysis of synergies as a sensitive clinical tool

Studies of action stability during whole-body movements have used a variety of methods applied to different patient populations and functional tasks including vertical posture (Hausdorff et al. 1985; Cavanaugh et al. 2005; Riva et al. 2013; van Emmerik et al. 2014). Studies of patients with postural disorders explored analysis of postural sway during quiet standing (Visser et al. 2008), postural preparation to self-initiated action (King et al. 2010; Rogers et al. 2011), and responses to unexpected postural perturbations (Boonstra et al. 2014). Some of these studies produced indices sensitive to early stages of postural problems and effects of treatment.

We would like to emphasize the following advantages of our approach based on quantifying multi-muscle synergies during postural tasks. First, this approach is theory-based and rooted deeply in both physics and physiology. It is linked intimately to the theory of control of movements with time-varying spatial referent coordinates organized in a hierarchical way, to the principle of abundance, to the uncontrolled manifold hypothesis, and to the idea of control with spatial RCs (reviewed in Latash 2010, 2016; Feldman 2015). Second, the approach has proven its specificity to subcortical neurological disorders (reviewed in Latash and Huang 2015) in support of the idea of distributed processing modules involving loops through the cerebellum and the basal ganglia (Houk 2005). Third, the approach is highly sensitive to very early stages of disorders (such as PD subjects in HY stage-I, Park et al. 2012, 2013, 2014) and even to subclinical changes in persons at elevated risk for parkinsonism (Lewis et al. 2016). Other mentioned approaches are typically computational, use behavioral indices with no clear links to physics and physiology, and/or are not as sensitive to disease-related changes.

Given the obvious importance of proper control of action stability for motor function, we believe that analysis of synergies should be incorporated broadly into clinical research. So far, applications of this analysis have been limited, partly due to the necessity to collect numerous trials for analysis of inter-trial variance. We hope that the current study will pave the way toward broader use of this method by showing that, at least for some tasks, analysis of only a few trials may be able to provide data sensitive to early-stage PD and the effects of medication. We would like to emphasize that our methods were able to detect significant changes in indices of postural stability in PD patients at HY stage II, i.e., those who show no detectable problems with postural stability during neurological examination.

Concluding comments

This study has lessons for both basic and clinical research. It shows that indices of inter-cycle (potentially also inter-trial) variance and those of motor equivalence are strongly correlated with each other and show similar statistical effects. Within the idea of movement control with changes in referent body configurations (RC, Latash 2010, Feldman 2015), muscle modes may be viewed as reflections of elemental changes in the body RC, which are used as the basis for a variety of whole-body actions (Latash 2016). The elemental RC changes are used as elemental variables to produce synergies stabilizing task-specific salient variables. Both inter-trial variance structure and ME deviations are natural consequences of this scheme: An input from hierarchically higher levels leads to deviations in less stable directions, i.e. within the UCM, rather than in directions leading to shifts of the salient variable (i.e., within ORT). This is true for spontaneous, natural variations in the task-specific input as well as for its purposeful changes. Within this scheme, loss of stability produced by synergies is expected to be reflected in both variance and ME indices, as demonstrated in our study. This makes both indices potentially sensitive to neurological disorders characterized by reduced action stability such as PD. The fact that ME indices can be measured in individual trials makes this index very attractive for clinical studies, particularly when examination time may be a limiting factor.

We would like to acknowledge limitations of our study. In particular, we recorded and analyzed EMG signals from one side of the body only. This approach was chosen based on earlier studies showing bilateral changes in synergy indices that demonstrated no side differences in PD patients, even in those with major bilateral differences in clinical symptoms (Park et al. 2012, 2014). As a result, we opted to analyze more muscles on one side of the body only given the limited number of EMG channels.