The use of permutation tests for the analysis of parallel and stepped-wedge cluster-randomized trials

Abstract

We investigate the use of permutation tests for the analysis of parallel and stepped-wedge cluster randomized trials. Permutation tests for parallel designs with exponential family endpoints have been extensively studied. The optimal permutation tests developed for exponential family alternatives require information on intraclass correlation, a quantity not yet defined for time-to-event endpoints. Therefore, it is unclear how efficient permutation tests can be constructed for cluster-randomized trials with such endpoints. We consider a class of test statistics formed by a weighted average of pair-specific treatment effect estimates and offer practical guidance on the choice of weights to improve efficiency. We apply the permutation tests to a cluster-randomized trial evaluating the effect of an intervention to reduce the incidence of hospital-acquired infection. In some settings, outcomes from different clusters may be correlated, and we evaluate the validity and efficiency of permutation test in such settings. Lastly, we propose a permutation test for stepped-wedge designs and compare its performance to mixed effect modeling, and illustrate its superiority when sample sizes are small, the underlying distribution is skewed, or there is correlation across clusters.

1. Introduction

Permutation tests have been used in parallel cluster-randomized trials to test the null hypothesis of no treatment effect [1, 2]. Gail et al. discussed randomization-based inference for matched and unmatched cluster intervention trials[3]. They considered both a strong null hypothesis that treatment has no effect on any cluster as well as a weak null hypothesis that treatment does not affect the average community response. Permutation tests have several advantages over parametric approaches: they are non-parametric and maintain size even if the test statistic is derived from a mis-specified model. For analysis of paired cluster intervention trials with person-time data, Brookmeyer and Chen compared the performance of permutation tests to that of the standard Mantel-Haenszel type of statistics ignoring intraclass correlation and the paired t-tests; they found that permutation tests performed well when the number of cluster pairs is small [4]. Murray et al. compared the performance of permutation test with the mixed-model regression methods for the analysis of simulated data in the context of a cluster-randomized trial for a wide range of settings including in the presence of measurable confounding and violations of normality assumptions underlying the mixed-effects models [5]. Their results indicated that permutation methods and model-based methods have similar performance in terms of size and power in most situations; when the normality assumptions are violated and the intraclass correlation is not small, say, greater than 0.01, the permutation test maintains the nominal type I error while the model-based test can be conservative.

The validity of permutation tests in cluster-randomized trials relies on the random allocation of treatment, and methods exist to assure validity in the presence of variable selection [6]. Many applications of permutation tests in other contexts do not begin with a randomized experiment, but rather with an assumption that the observations are statistically independent with certain symmetry properties. If a permutation test is justified by an assumption of independence, and if that assumption is false (e.g., unequal variance in two comparison treatment groups), then the nominal level of the test may be erroneous (see for examples, [7–9]). However, tests derived solely from randomization have the correct level whether or not potential responses under comparison treatment arms are independent [10–14].

The efficiency of permutation tests is affected by the choice of test statistic. Braun and Feng [15] develop optimal permutation tests for parallel cluster randomized trials with exponential family alternatives where the test statistic is a weighted sum of cluster errors with weights equal to the inverse of the total variance for each cluster. The total variance is a function of within cluster variation and intraclass correlation. They show that the weighted permutation test (i.e., the permutation test using a weighted test statistic) with properly chosen weights is more powerful than the unweighted permutation test, especially when cluster sizes vary substantially. However, optimal weights need to take into account the intraclass correlation. Weighting by cluster sizes alone does not guarantee improvement of the performance of the test.

In this paper, we investigate the use of permutation tests for the analysis of cluster-randomized trials in the following three areas. First, we consider matched and unmatched parallel cluster randomized trials with time-to-event endpoints and discuss choices of test statistic to achieve better efficiency. The optimal tests developed in Braun and Feng [15] do not apply to time-to-event endpoints because they require information on the intraclass correlation – a quantity has not been defined for time-to-event endpoints. In the setting of paired-matched trials, we consider the class of test statistics formed by taking a weighted average of estimated pair-specific treatment effect.We assess power associated with different choices of weights (with constant weights representing the unweighted test statistic) and offer practical recommendations on the choice of weights. This approach can be applied to unmatched trials by considering all possible treatment-control pairs.

In addition, we consider the setting where observations from different clusters may be correlated. While standard mixed-effects modeling methods take into account correlation among observations within the same cluster, they usually assume independence of observations from different clusters. This assumption may be violated in practice; for example, clusters that are physically near each other may share similar characteristics that induce correlation of outcomes from them. In cluster-randomized trials for HIV prevention, treatment contamination due to sexual relationships formed between communities randomized to opposite treatment arms can occur. We investigate the validity and efficiency of permutation tests in the presence of correlated outcomes across clusters.

Finally, we propose permutation tests for stepped-wedge designs and demonstrate their validity and, in some settings, superiority over parametric model-based modeling. In contrast to the parallel design for cluster-randomized trials discussed above where clusters are randomized to different treatment conditions at baseline, the stepped-wedge design allows clusters to cross over to the experimental intervention arm in a unidirectional manner at different times. The time of this crossover to the intervention arm is randomized. At each of the pre-selected time points, some clusters initiate the intervention; the response to the intervention in all clusters is measured. As discussed in Hussey and Hughes [16], this type of design can be especially useful when limited resources or geographical constraints make it logistically difficult to implement the intervention simultaneously in many communities. In addition, all clusters eventually receive the intervention - a feature that may reduce ethical concerns about evaluating the population-level impact of an intervention shown to be effective in an individually-randomized trial. Methods have been described to analyze the resulting data through the use of a mixed effects model where random effects model the correlation between individuals within the same cluster and the fixed effects model the time effects [16]. The use of permutation tests for cluster randomized trials with stepped-wedge designs have not been studied. The permutation tests for parallel designs rely on the random allocation of communities into treatment and control arms and cannot be applied to stepped-wedge designs because all communities will cross-over to the treatment arm over time. To overcome this challenge, we propose to construct permutation tests where the permutation distribution is generated by permuting the random order of the treatment assignment and compare the performance of such tests to their parametric counterparts.

The rest of the paper is organized as follows. In section 2, we investigate permutation tests for parallel cluster-randomized trials with time-to-event endpoints. In Section 2.1, we propose a class of test statistics based on pair-specific treatment effect estimates and investigate the impact of the choice of test statistic on efficiency. In Section 2.2, we evaluate the validity and efficiency of permutation tests when outcomes from different communities are correlated, and in Section 2.3, we describe the construction of such test statistics for unmatched parallel cluster-randomized trials and illustrate its use using data from a cluster-randomized trial evaluating effect of an intervention to reduce the incidence of hospital-acquired infection. In Section 3, we propose a permutation test for stepped-wedge designs and compare their performance with mixed-effects modeling. Section 4 provides a Discussion.

2. Parallel cluster randomized trials with time-to-event endpoints

Suppose that we have J pairs of communities in a matched-pair cluster-randomized trial to assess the effect of intervention versus control. We pair communities on the basis of demographic or other characteristics that are expected to be correlated with the outcome of interest and then randomly assign communities with each pair between two treatment arms. Let i = 1, 2 denote the intervention and control arms respectively. Let T_ijk, C_ijk, U_ijk = min(T_ijk, C_ijk) and δ_ijk = 1(T_ijk ≤ C_ijk) denote the time to event, the censoring time, the observed time to event or censoring, and the event indicator for individual k in community j on treatment i, j = 1, . . . , J, and k = 1, . . . , K_ij, where K_ij denote the sample size in jth community on treatment i. Here we use 1(·) to denote the indicator function. Let β denote the treatment effect and β̂_j denote the estimated treatment effect based on data from the jth pair. For example, β̂_j might be the estimated treatment effect obtained from a Cox model applied to data from individuals in the jth pair of clusters.

We consider the class of test statistics of the form

$$S^{\mathit{\text{obs}}}=\sum _{j=1}^J{w}_j{\widehat{\beta }}_j,$$

where w_j’s are weights allocated to β̂_j. Under the null hypothesis of no treatment effect, i.e., H₀: β = 0,

$$f({\widehat{\beta }}_1,{\widehat{\beta }}_2,\dots ,{\widehat{\beta }}_J)=f({\gamma }_1{\widehat{\beta }}_1,{\gamma }_2{\widehat{\beta }}_2,\dots ,{\gamma }_J{\widehat{\beta }}_J)$$

for any choices of γ_j = ±1. Here we use f(·) to denote the joint density function. The permutation distribution is formed by a collection of S^p = Σ w_jγ_jβ̂_j. Under the null hypothesis of no intervention effect in any community, H₀ : β = 0, the observed treatment effect can be viewed as a random sample of size 1 from the permutation distribution generated by randomly permuting the allocation of community between treatment arms [17]. The p-value is given by the proportion of test statistics resulting from permuted datasets that are more extreme than the observed test statistic among all possible permutations:

$$\frac{{\sum }_{j=1}^{M}I(|S_j^p|\ge |S^{\mathit{\text{obs}}}|)}{M},\text{ where }M\text{ is the number of all possible permutations}.$$

The number of all possible permutations M increases quickly with the number of units and is in general quite large so that enumerating all the possibilities becomes computational prohibitive. In practice, we take a random sample of permutations and approximate the p-value by

$$\frac{1+{\sum }_{j=1}^{m}I(|S_j^p|\ge |S^{\mathit{\text{obs}}}|)}{1+m},\text{ where }m\text{ is the number of sampled permutations}.$$

We add 1 to both the numerator and denominator to account for the observed test statistic. Gail et al. [3] considered a special case of this type of test statistics for continuous outcomes Y_ijk in analyzing parallel cluster randomized trials. More specifically, they considered pair-specific treatment effect estimate β̂_j as the difference in the sample average $K_{1j}^{-1}{\sum }_k{Y}_{1jk}-K_{2j}^{-1}{\sum }_k{Y}_{2jk}$ and all weights w_j = 1 for j = 1, . . . , J. Here, to handle time-to-event endpoints, β̂_j can be the estimated log-hazard ratio from Cox proportional hazard models as described below.

The choice of test statistic does not affect the validity of permutation test, which is ensured by randomization. However, the efficiency of permutation test is affected by the choice of test statistic. Analysis of data from cluster-randomized trials based on cluster-level summaries requires selection of weights used to create weighted averages of these summaries. Hayes and Moulton [17] discuss the trade-off between the weighted and the unweighted approaches, and recommend the latter in general for its robustness. The weighted approach may improve precision, but only when the weights are based on accurate unconditional variance estimates of the cluster-level summaries, which requires an accurate estimate of intraclass correlation[17]. Although optimal test statistics have been proposed for exponential family endpoints (e.g., continuous, binary, counts etc) [15], it is unclear how to construct the optimal test statistic for time-to-event endpoint. The optimal test statistic proposed in Braun and Feng [15] makes use of intraclass correlation – a quantity not yet been defined for time-to-event endpoint. Motivated by the uncertainty in choice of weights to improve efficiency and lack of optimal weights for time-to-event endpoints, we conduct a simulation study to compare two specific test statistics, unweighted and weighted according to the conditional within-cluster sampling variances of pair-specific treatment effect estimates.

2.1. Comparison between unweighted and weighted test statistics

We compare the performance of the permutation tests with various test statistics of the form Σ_j w_jβ̂_j, where j = 1, ⋯ , J and β̂_j denotes the estimated pair-wise treatment effect. In the first setting, we consider J = 10 pairs of communities, with sample sizes ranging from 100 to 1000, in increments of 100. The underlying clustered failure time data (e.g. times to infection) are generated by adding a frailty term in an accelerated failure time (AFT) model. Let T_ik denote the failure time of interest for the kth subject from the ith cluster, and X_i denote the treatment assigned to the cluster i.

$$\mathit{\text{log}}(T_{ik})=b_i+\alpha +\beta X_i-{\epsilon }_{ik},$$

where β measures treatment effect; $b_i\stackrel{i.i.d}{~}N(0,{\theta }^2)$ introduces correlation within communities. We first consider the setting where ε_ik follows an extreme value distribution $~G(\epsilon )=\mathit{\text{exp}}\{-\mathit{\text{exp}}(-\frac{\epsilon -\mu }{\sigma }\left)\right\}$, with μ = 0 and σ = 1. The censoring times are simulated from a uniform distributions with probability mass on interval [1, 2], thereby causing outcomes to be right-censored.

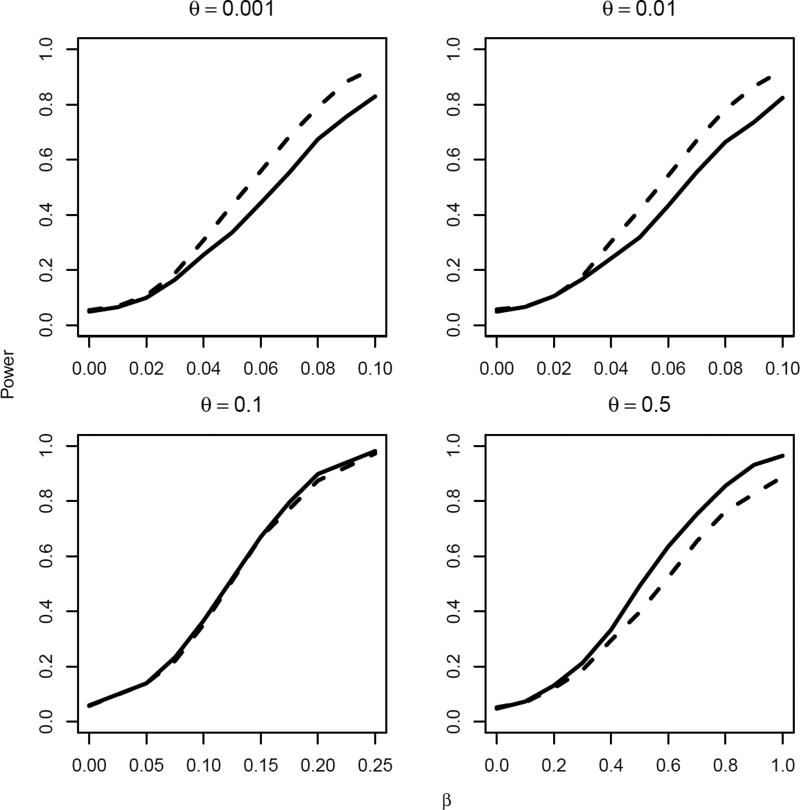
Communities with same sizes are pair-matched. We calculate a treatment effect estimate within each pair, β̂_j, using a Cox proportional hazard model. In this setting, T_ik follows an exponential distribution conditional on b_i and proportional hazards assumption is satisfied. For the unweighted permutation test, we use the sum of pair-wise treatment effect estimates (i.e., log hazard ratio) as the test statistic. For the weighted permutation test, we use the weighted sum, where the weights are based on the estimated sampling variance of β̂_j within each pair. For the null hypothesis of no treatment effect, β = 0, we can find the null distribution of this statistic by randomly re-assigning treatment to each of the paired communities and re-calculating the treatment effect. In pair-matched settings, re-assigning treatment to each of the paired communities only leads to a possible sign change in β̂_j. Figure 1 below compares size and power for permutation tests using the unweighted and weighted test statistics.

Figure 1.

Empirical size/power estimates for 0.05 level test of the null hypothesis H₀: β = 0 using the unweighted (solid lines) and weighted (dotted lines) test statistics, for right-censored endpoints and varying magnitude of treatment effect β and standard deviation of between-cluster variation θ, based on 1000 experiments. The underlying failure times T_ik’s were generated according to log(T_ik) = b_i + α + βX_i − ε_ik, where b_i ~ N(0, θ²) and ε_ik ~ exp{−exp(−ε)}. The censoring times were assumed to follow a uniform distribution with support on [1, 2].

As shown in Figure 1, the relative performance of the unweighted and weighted test statistics depends on the magnitude of intraclass correlation. The weighted test statistic achieves greater power than the unweighted when the between-cluster heterogeneity θ is small – in this simulation setting, < 0.1. The difference is substantial, especially for the effect sizes that are of practical relevance, i.e., those associated with power around 80%. For example, when θ = 0.01, for effect size β = 0.076, the weighted test statistic achieves 80% power for the given sample size whereas the unweighted test statistic is only associated with 70% power. As θ increases to values close to 0.1, their performances become almost identical – suggesting that unweighted test statistics may be preferable because of their simplicity. As θ becomes very large, e.g. 0.5, the unweighted test statistic is associated with greater power than the weighted test statistic.

We also evaluate a test statistic where the pairwise treatment effect estimate was obtained using a Cox proportional hazards model and its associated robust variance estimate that takes into account the correlation among time to event endpoints [18]. Our results revealed that this test statistic is associated with lower power than both the unweighted and weighted test statistics considered above, regardless of the magnitude of intraclass correlation. This may result from the fact that this robust variance approach was developed for settings with a large number of small clusters and does not work well for the settings with a small number of large clusters.

The relative performance of the unweighted and weighted test statistics depend crucially on the magnitude of intraclass correlation and the level of heterogeneity in cluster sample sizes. If the sample sizes for all clusters are equal, then the unweighted and weighted test statistics will lead to the same results irrespective of the magnitude of intraclass correlation. When sample sizes vary across clusters, the relative performance of these two test statistics may change depending on the magnitude of intraclass correlation. In these simulated settings, the intraclass correlation ρ for the underlying failure time (log-transformed) is given by $\frac{{\theta }^2}{{\theta }^2+{\sigma }^2}$. The results suggest that, for smaller ρ, e.g. ρ < 0.01 in the current setting, the weighted test statistic tends to be associated with greater power than the unweighted one; as ρ increases to greater than 0.01, the advantage of the weighted test statistic decreases. For larger ρ such as 0.2, the unweighted test statistic yields greater power than the weighted one. The results are not surprising as the optimal weight would likely be the inverse of accurate unconditional variance estimates for each pair of comparison as in other similar settings with exponential family endpoints [15, 17]. When the intraclass correlation is small, the effect of ignoring it tends to be small and the weights based on within cluster variances only are close to being optimal; when the intraclass correlation is large, weights based on within cluster variances alone would be further away from the optimal weights. For CRTs with a binary or continuous outcome, the optimal weights to be used in a weighted t-test are [17]

$$w_i=\frac{m_i}{1+\rho (m_i-1)},$$

where ρ denotes the intraclass correlation and m_i represents the sample size for cluster i. As can be seen from this formula, if the clustering effect is small so that ρ is close to 0, weights based on individual cluster sizes are close to the optimal weights; on the other hand, if ρ is large, the weights tend to be constant so that equal weights may be closer to the optimal weights.

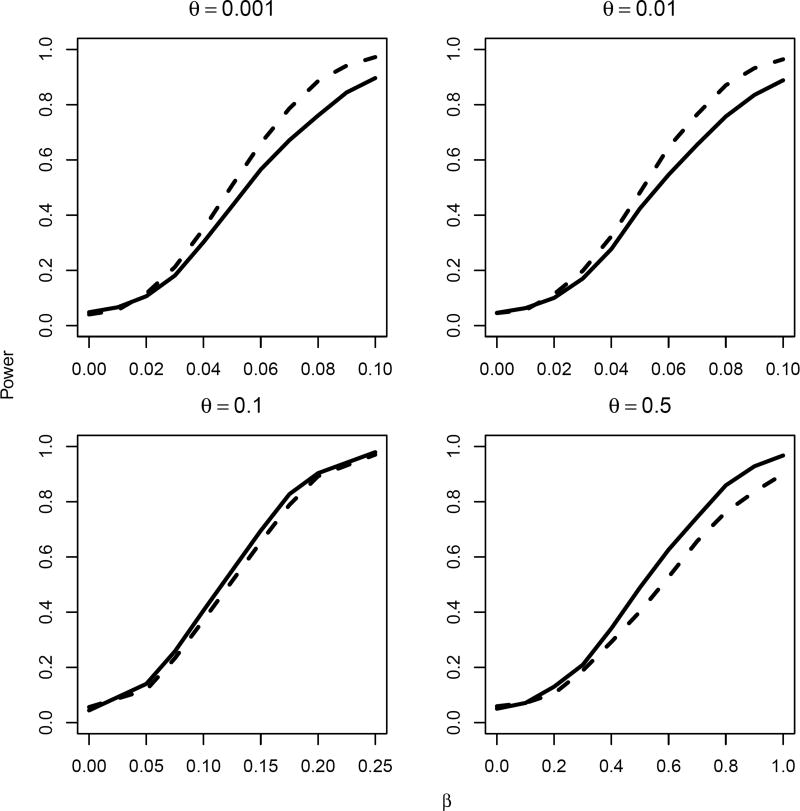
We also considered the setting where ε_ik follows a normal distribution N(0, 1), implying that T_ik follows a log-normal distribution conditional on b_i. The results are similar (Figure 2) irrespective of the underlying failure time distributions.

Figure 2.

Empirical size/power estimates for 0.05 level test of the null hypothesis H₀: β = 0 using the unweighted (solid lines) and weighted (dotted lines) test statistics, for right-censored endpoints and varying magnitude of treatment effect β and standard deviation of the between-cluster variation θ, based on 1000 experiments. The underlying survival times T_ik were generated according to log(T_ik) = b_i + α + βX_i + ε_ik, where b_i ~ N(0, θ²) and ε_ik ~ N(0, 1)}. The censoring times were assumed to follow a uniform distribution with support on [1, 2].

With right-censored time-to-event endpoints, we can not calculate the intraclass correlation ρ directly because the underlying failure times are not completely observed. We investigate the usefulness of estimating ρ based on the binary event indicator as an approximation of the ρ for the underlying log-transformed failure time. Note that when estimating ρ, only data from the control communities will be used to avoid the possible extra heterogeneity in outcomes caused by the treatment. Let p denote the overall proportion computed from all control clusters, m̄_H denote the harmonic mean of the individual cluster sizes, and s² denote the empirical variance of cluster proportions. The between-cluster variance ${\sigma }_B^2$ can be estimated as [17]:

$${\widehat{\sigma }}_B^2=s^2-\frac{p(1-p)}{{\overline{m}}_H}.$$

We can then estimate the intraclass correlation ρ as follows:

$$\widehat{\rho }=\frac{{\widehat{\sigma }}_B^2}{p(1-p)}.$$

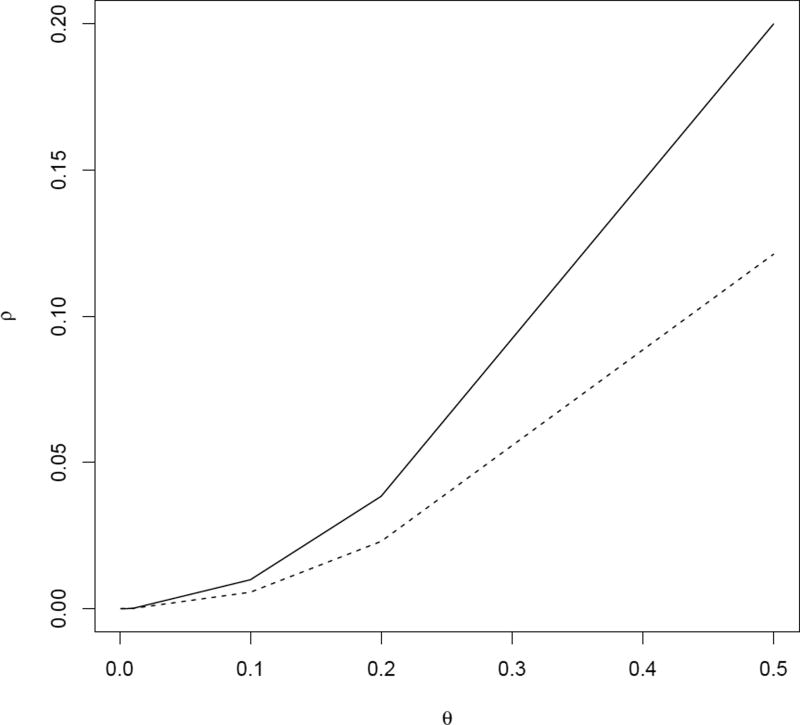
For the settings we consider, we find that the estimated ρ based on the binary event indicator is generally smaller than the true ρ, and the difference between them increases as ρ increases (Figure 3). Therefore, when prior knowledge of ρ is not available, we may in practice estimate ρ based on the binary event indicator data, but must recognize that this will underestimate the true ρ.

Figure 3.

True intraclass correlation for the underlying log-transformed failure time (solid lines) and estimated intraclass correlation based on binary event indicator (dotted lines) for varying magnitude of standard deviation of the between-cluster variability θ, based on 1000 experiments. The underlying failure times T_ik were generated according to log(T_ik) = b_i + α + βX_i + ε_ik, where b_i ~ N(0, θ²) and ε_ik ~ N(0, 1). The censoring times were assumed to follow a uniform distribution with support on [1, 2].

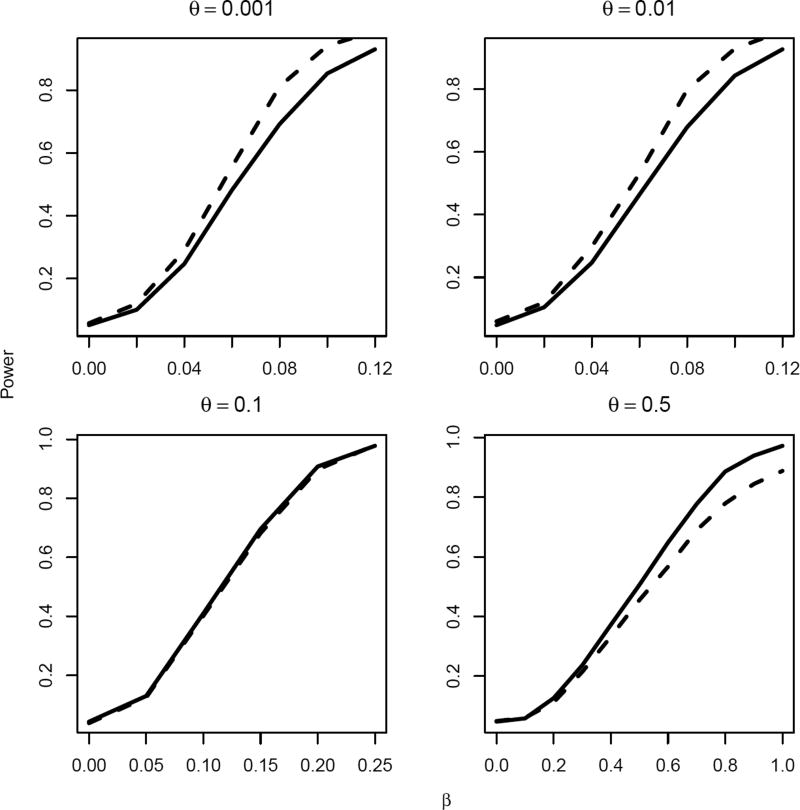
In addition to right-censored endpoint, we also consider interval-censored endpoints by setting two observational times, both distributed as uniform, on intervals [1, 2] and [2, 3], respectively. The pair-wise treatment effect estimates are obtained using Cox proportional hazards model for interval-censored observations using an R package “frailtypack”. Results are summarized in Figure 4. As before, when the between-cluster heterogeneity θ is small, the weighted test statistic achieves greater power than the unweighted test statistic, and their relative performance reverses when θ becomes large.

Figure 4.

Empirical size/power estimates for 0.05 level test of the null hypothesis H₀: β = 0 using the unweighted (solid lines) and weighted (dotted lines) test statistics, for interval-censored endpoints with varying magnitude of treatment effect β and standard deviation of the between-cluster variability θ, based on 1000 experiments. The underlying failure times T_ik were generated according to log(T_ik) = b_i + α + βX_i − ε_ik, where b_i ~ N(0, θ²) and ε_ik ~ exp{−exp(−ε)}. Interval-censored observations were generated by comparing the failure times to two observational times, both distributed as uniform, on intervals [1, 2] and [2, 3].

2.2. Correlated outcomes across communities

In some settings, outcomes from different communities may be correlated. For example, communities geographically near each other or clusters that share similar community characteristics may have outcomes that are more correlated with each other than they are with others. In the context of HIV prevention studies, outcome differences between the treatment arms may be diluted as a result of sexual contacts formed between intervention and control communities. The customary main aim of a CRT is to measure the overall treatment effect, defined as the difference in outcomes among interventions if they are implemented throughout populations under study. If there is a single intervention and a control condition, mixing between communities assigned to different treatment policies will tend to attenuate this overall effect. The term interference between units has been used to describe the phenomenon that outcomes of one unit may be affected by the treatment assignments of other units (see for example, [19]). Under the null hypothesis of no treatment effect, the permutation test has the correct type I error and remains valid as randomization is the sole basis for inference and no treatment effect implies no interference between units [14].

We investigate the validity and power of the permutation test in such settings by simulating outcome data from 10 pairs of communities and specifying correlated cluster-specific random effects b_is within and between pairs of communities. More specifically, we group 10 pairs into 5 blocks, where each block contains 2 pairs of communities and

$${(b_{2i-1,0},b_{2i-1,1},b_{2i,0},b_{2i,1})}^T~\mathit{\text{MV}}N({(0,0,0,0)}^T,R{\theta }^2),i=1,2,\cdots ,5,$$

where

$$R=\left(\begin{array}{cccc}1& {\rho }_w& {\rho }_b& {\rho }_b\\ {\rho }_w& 1& {\rho }_b& {\rho }_b\\ {\rho }_b& {\rho }_b& 1& {\rho }_w\\ {\rho }_b& {\rho }_b& {\rho }_w& 1\end{array}\right).$$

We generate the times to infection in community i from an exponential distribution with hazard rate λ₀ · exp(b_i)exp(βX_i), where X denotes the treatment indicator and exp(β) represents the treatment effect (hazard ratio comparing treatment with control). Throughout we fixed λ₀ = 0.2. Censoring times, C, were generated from a Uniform distribution with support [1,2]. Generated infection times were compared to the censoring times to create the time to event outcomes (U, δ), where U = min(T,C) and δ = 1(T ≤ C). Within each pair, we fitted a Cox proportional hazard model h(t) = h₀(t)exp(βX), where X denoted the treatment indicator, and obtained an estimate for β, β̂_i, and its standard error estimate s_i = ŝ(β̂_i). The unweighted and weighted test statistic considered were T_u = Σ_i β̂_i and $T_w={\sum }_i{s}_i^{-2}{\widehat{\beta }}_i$ as before. Table 1 summarizes the size and power of the permutation test using unweighted and weighted test statistics for varying treatment effect β and correlation structure. The permutation test has the correct Type I error and remains valid when the outcomes from different communities are corrected. When θ is small (e.g. intraclass correlation ρ < 0.01 in the current setting), the weighted test statistic is associated with greater power; as θ gets larger, the unweighted test statistic yields increasingly greater power.

Table 1.

Empirical estimates of P (reject H₀) for right-censored data for varying within- and between- cluster correlations (ρ_w and ρ_b), based on 10,000 experiments

		ρw = 0.5 ρb = 0.2		ρw = 0.2 ρb = 0.1		ρw = 0 ρb = 0
θ	β	Tu	Tw	Tu	Tw	Tu	Tw
0.001	0	0.049	0.050	0.050	0.050	0.050	0.050
	−0.1	0.499	0.598	0.498	0.598	0.499	0.598
	−0.2	0.930	0.988	0.931	0.988	0.930	0.989
0.1	0	0.049	0.050	0.046	0.046	0.048	0.050
	−0.1	0.366	0.388	0.306	0.319	0.280	0.285
	−0.3	0.985	0.998	0.975	0.989	0.965	0.981
0.5	0	0.047	0.047	0.046	0.048	0.046	0.048
	−0.2	0.186	0.161	0.135	0.120	0.116	0.108
	−0.5	0.754	0.672	0.573	0.492	0.482	0.412

2.3. Unmatched parallel cluster randomized trials

The class of test statistic we consider is based on pairwise treatment effect estimates. In matched-pair cluster-randomized trials, the pair-specific treatment effect estimates are obtained from data generated by each pair. We next consider extension of this approach to unmatched cluster randomized trials. Suppose that there are J₁ communities randomized to treatment and J₂ communities randomized to control. Let Z_j = 1 if cluster j is assigned to treatment and Z_j = 0 if this cluster is assigned to control so that $J_1={\sum }_{j=1}^{J_1+J_2}{Z}_j$. Let Z = (Z₁, . . . , Z_J1+J2) denote the vector of treatment status for the J₁ + J₂ clusters. Let D = (U, δ, X, Z) denote the data matrix consisting of the time-to-event outcomes (U, δ), covariates X, and treatment assignment Z. Let d^obs denote the observed data matrix for the realized assignment. Let D(ℓ) = D(Z^ℓ) = (U, δ, X, Z^ℓ) denote the permuted data matrix where Z^ℓ denote a re-randomization of Z. Under the null hypothesis H₀ of no treatment effect,

$$\mathit{\text{Pr}}(\mathbf{D}=\mathbf{d}({\mathbf{z}}^{\ell })|\mathbf{Z}\stackrel{p}{=}{\mathbf{z}}^{\mathit{\text{obs}}},\mathbf{D}=\mathbf{d}({\mathbf{z}}^{\mathit{\text{obs}}}))=M^{-1},$$

where we use $“\stackrel{p}{=}”$ to denote “is a permutation of” and M is the total number of permutations (J₁ + J₂)! (or $\left(\begin{array}{c}{J}_1+J_2\\ J_1\end{array}\right)$) if only distinct treatment assignments are considered). That is, the observed data matrix, d^obs, can be viewed as a randomly selected element from the set ∏, consisting of M matrices d(z^ℓ). It follows that if T = T(D) is any test statistic, the observed value of T can be viewed under H₀ as a random sample of size 1 from the resulting permutation distribution of values {T(d(z^ℓ)) | d(z^ℓ) ∈ ∏}. This provides the basis for valid inferences about H₀.

Here we consider a specific type of test statistic to be the weighted average of all pair-wise treatment effect estimates. More specifically, let θ̂_jj′ denote the treatment effect estimate based on data from jth community from the intervention arm and j′th community from the control arm. The test statistic we consider is Σ_j,j′ w_jj′θ̂_jj′. That is, we will estimate a treatment effect based on data from each of the all possible treatment-control pairs and use a weighted average of these pair-wise treatment effect estimates as the test statistic. Each permuted dataset is obtained by randomly allocating J₁ communities out of J₁ + J₂ communities to the intervention arm. The permutation distribution is then generated by evaluating the same test statistic on each permuted dataset. A p-value can be obtained as above. We note that alternative test statistics can also be used. For example, we can use treatment effect estimated from models for correlated failure time data. Commonly-used approaches include a pseudo-likelihood approach with a working independence assumption [20] and a frailty model approach where parametric random effects are used to capture the correlation among clustered data [21]

To illustrate, we use this permutation test to analyze data from a cluster-randomized trial evaluating the effect of surveillance for methicillin-resistant Staphylococcus aureus (MRSA) and vancomycin-resistant enterococcus (VRE) colonization and of the expanded use of barrier precautions compared with existing practice on the incidence of MRSA or VRE colonization or infection in adult ICUs [22]. This study enrolled 18 ICUs, 10 of which received intervention. Data on times to MRSA or VRE colonization or infection were collected. The total number of subjects included in the analysis was 3447; the sample sizes for individual ICUs varied from 105 to 315. For each pair of intervention-control ICUs, we calculate a treatment effect estimate using Cox proportional hazard model and its associated robust variance estimate [18]. We consider two test statistics, unweighted and weighted, with weights proportional to the inverse of the conditional within-cluster variance estimates. Usually the number of possible permutations is too large to enumerate all possibilities and p-values obtained from permutation tests are based on a sample of possible permutations. Therefore we present summary statistics of p-values from 100 permutation tests rather than one single p-value to reduce the reliance on the random seed. The p-values, each based on a sample of 2000 permutations, are fairly consistent across 100 permutation tests. The resulting p-values (median, [25th, 75th percentiles]) were 0.38 [0.37, 0.39] and 0.45 [0.44, 0.46] respectively, suggesting that the intervention under evaluation did not significantly reduce times to MRSA or VRE colonization or infection.

3. Cluster randomized trials with stepped-wedge design

In contrast to the parallel design for cluster-randomized trials mentioned above, the stepped-wedge design allows clusters to cross over to the experimental intervention in a unidirectional manner at different times. The time of this crossover to the intervention is randomized. At each time point, some clusters initiate the intervention; the responses in all clusters are measured. Permutation methods for parallel cluster-randomized trials involve random allocation of treatment assignment to clusters and do not apply to stepped-wedge design because clusters in a stepped-wedge cluster-randomized trials will all receive the intervention over time. Instead of randomly allocating treatment assignment, we propose to randomly assign the order of receiving the intervention.

Suppose there are J periods, each of which is denoted by j, j = 1, . . . , J. We let the first period (j = 1) serve as the the baseline period for all clusters. Suppose that at each subsequent period, j = 2, . . . , J, I_j clusters are randomized to initiate the intervention. Under the null hypothesis of no intervention effect, we can obtain the null distribution of the test statistic by permuting the order in which clusters start receiving intervention; we then compute the test statistic using the permuted order of assignment. We can then compare the observed test statistic to its permutation distribution under the null hypothesis. That is, we randomly assign each cluster to initiate treatment at one of possible periods while preserving the number of clusters assigned to the different treatment initiation periods as the observed data. Operationally, this is done by creating a vector of length I (the total number of clusters), denoted as ℐ. Each element of this vector indicates the period in which treatment is initiated; the elements of this vector ℐ are permuted to conduct the test. Permuting the elements of vector ℐ ensures I_j clusters assigned to each possible treatment starting points in the re-randomized datasets. The test statistic we consider is the estimated treatment effect from the mixed effect model for correlated outcomes with fixed period effects.

We simulate data from a stepped-wedge design with I clusters, J periods, I_j clusters are randomized to receiving the intervention at each period, and N individuals sampled per cluster per time interval. Let Y_ijk denote the response corresponding to individual k at time j from cluster i, and let Y_ij denote the mean for cluster i at time j. Y_ijk is generated under the model:

$$Y_{\mathit{\text{ijk}}}=\mu +{\alpha }_i+{\gamma }_j+X_{\mathit{\text{ij}}}\beta +e_{\mathit{\text{ijk}}},$$ (1)

where α_i is a random effect for cluster i, γ_j is a fixed effect for time interval j (j = 1, ⋯ , J, and γ₁ = 0), X_ij is an indicator of the treatment assignment for cluster i at time j and β is the treatment effect. We consider four distributions for e_ijk, including 1) Normal: e_ijk ~ N(0, 1); 2) Cauchy with location parameter 0 and scale parameter 1, i.e., $e_{\mathit{\text{ijk}}}~\frac{1}{\pi {(1+e_{\mathit{\text{ijk}}})}^2}$; 3)Lognormal where the mean and standard deviation of the logarithm were 0 and 1; and 4) Pareto with location parameter 1 and shape parameter 3, i.e., $e_{\mathit{\text{ijk}}}~\frac{3}{e_{\mathit{\text{ijk}}}^4}$, for e_ijk > 1.

Tables 2 − 3 summarize the empirical size (columns corresponding to β = 0) and power (columns corresponding to non-zero β) comparing two approaches: 1) fitting a mixed effect model for correlated outcomes with fixed time effects (MM); and 2) permutation test with the estimated treatment effect from the mixed effect model (T_MM). We first consider the settings where ${\alpha }_i\stackrel{i.i.d}{~}N(0,{\theta }^2)$ (see Table 2). When sample sizes are relatively large with I = 10 and N = 100, the usual mixed-effects model (MM) performs well, even when the error distributions deviate from the normal. T_MM has similar performance as MM. As sample size decreases to I = 5 clusters and N = 50 subjects per cluster at each time interval, the permutation tests generally control type I errors better than does MM. Comparing the settings where I = 5 and N = 50 to those where I = 10 and N = 25 (which preserves total sample size), the improvement in control of type I error associated with the permutation test is more evident when the number of clusters is small, rather than when the number of subjects within each cluster is small. This phenomenon is likely due to the fact that in the settings we considered, wherein θ = 0.1, the effective sample size accounting for intraclass correlation for I = 5 and N = 50 is smaller compared that for I = 10 and N = 25. In the settings we examined in Table 2, the power estimates associated with Cauchy distributed errors for both MM and T_MM remain very low even as the treatment effect β increases. This is due to the fact that Cauchy distribution has large spread leading to a very low signal to noise ratio for the range of β (from 0 to 0.3) considered here. Power will increase with substantial increases in β.

Table 2.

Empirical estimates of P(reject H₀) comparing the permutation approach(T_MM) and mixed-effects models (MM) for step-wedge design for number of periods J = 6, standard deviation of the cluster-specific random effect θ = 0.1, varying number of clusters I, number of individuals sampled per cluster at each time interval N, and the intervention effect β, based on 10,000 experiments

			β = 0		β = 0.1		β = 0.3
I	N	Error distribution	MM	TMM	MM	TMM	MM	TMM
10	100	Normal	0.056	0.049	0.629	0.581	1	1
		Cauchy	0.051	0.049	0.051	0.049	0.053	0.052
		Lognorm	0.059	0.047	0.221	0.186	0.928	0.898
		Pareto	0.059	0.053	0.756	0.723	1	0.999
10	25	Normal	0.061	0.050	0.257	0.213	0.953	0.929
		Cauchy	0.053	0.055	0.053	0.054	0.053	0.057
		Lognorm	0.059	0.053	0.108	0.097	0.475	0.432
		Pareto	0.060	0.050	0.334	0.292	0.978	0.968
5	50	Normal	0.070	0.044	0.244	0.167	0.945	0.858
		Cauchy	0.053	0.043	0.053	0.044	0.054	0.047
		Lognorm	0.060	0.044	0.106	0.076	0.466	0.343
		Pareto	0.068	0.045	0.322	0.232	0.974	0.935

Table 3.

Empirical size estimates comparing the permutation approach (T_MM) to mixed-effects models (MM) for step-wedge design for θ = 0.1, total number of periods J = 6, and varying ρ, ν, number of clusters I, and number of sampled subjects N per cluster at each time period, based on 10,000 experiments. The outcomes Y_ijk’s are generated according to Y_ijk = μ + α_i + γ_j + (αγ)_ij + X_ijβ + e_ijk, where (α₁, . . . , α_I)^T ~ M V N(0, Σ), Σ is an exchangeable variance-covariance matrix with variance θ² and covariance ρ * θ², and (αγ)_ij ~ N(0, ν²).

I	N	ρ	ν	MM	TMM
10	100	0	0.1	0.163	0.050
		0	0.2	0.374	0.051
		0.1	0	0.055	0.048
		0.2	0	0.057	0.048
10	25	0	0.1	0.085	0.051
		0	0.2	0.239	0.053
		0.1	0	0.060	0.053
		0.2	0	0.063	0.050
5	50	0	0.1	0.122	0.045
		0	0.2	0.166	0.048
		0.1	0	0.068	0.045
		0.2	0	0.065	0.042

Model (1) implies that observations in the same cluster at different periods have the same correlation as two in the same cluster in the same period. To reflect the setting where observations in the same cluster in the same period have stronger correlation than those in different periods, we can include a random interaction term in the model:

$$Y_{\mathit{\text{ijk}}}=\mu +{\alpha }_i+{\gamma }_j+{(\alpha \gamma )}_{\mathit{\text{ij}}}{X}_{\mathit{\text{ij}}}\beta +e_{\mathit{\text{ijk}}},$$ (2)

where (αγ)_ij ~ N(0, ν²). We also consider the settings in which data from different clusters may be correlated; here (α₁, . . . , α_I)^T ~ MV N(0, Σ) and Σ is an exchangeable variance-covariance matrix with variance θ² and covariance ρ * θ². In such settings, the permutation test approaches control type I error better than MM regardless of sample size (see Table 3). If the true data generating process includes an additional random interaction term that is ignored in data analysis, testing based on mixed effects model can lead to severely inflated type I error; in contrast, the permutation test remains valid.

4. Discussion

We consider a class of test statistics formed by a weighted average of pairwise treatment effect estimates and evaluate the effect of weights on efficiency. Accurate estimates of the unconditional variance of pairwise treatment effect estimates incorporating intraclass correlation would improve efficiency of the permutation test, but these are generally difficult to obtain. Therefore, using equal weights is an attractive approach, in terms both of efficiency (it may be closer to the optimal weights) and ease of implementation. If the individual cluster sample sizes vary substantially and the intraclass correlation is negligible, the weighted version of the test statistic may lead to greater power than the unweighted test statistic. This advantage decreases as the intraclass correlation increases. To guide the choice of test statistic, we may use prior knowledge on the intraclass correlation or estimate the intraclass correlation using a binary event indicator to provide a lower bound for the true intraclass correlation of the underlying failure time. Inference based on the same data set as that used for model selection may be subject to inflated type I error. In this case, we would expect the effect to be minimal because the selection is done based on second-order association parameters (ICCs) and does not target treatment effect. Furthermore, even if the estimated intraclass correlation is imprecise (e.g., in the case of time-to-event endpoints) and the weighted test statistic is in fact associated with lower power than the unweighted test statistic, it affects only the efficiency, not the validity, of the permutation test. For unmatched trials, we can construct the test statistic by considering all pairwise treatment-control comparisons. Taking into account correlation among β̂_ij and β̂_ij′ may further improve the efficiency of the test and is worthy of further investigation.

If we postulate a semiparametric or parametric model for the treatment effect, the permutation tests can be inverted to obtain point and interval estimates for the model parameters. For time-to-event outcomes, we may consider an accelerated failure time model. More specifically, let T₁ and T₂ denote survival times sampled from F₁(·) and F₂(·), the survival distributions of two treatment groups respectively and β > 0 is some positive constant. According to this model, T₁ has the same distribution as βT₂; or equivalently, F₂(t) = F₁(βt). Let β₀ be some specified value and consider testing H(β₀) : β = β₀. A point estimate for β is given by the value for which there is the least evidence against H(β₀) : β = β₀, say, by giving the largest p-value. A confidence interval of size 100(1 − α)% for β can be formed by the set of β₀ which are not rejected at the α level of significance. It is important to note that, for censored observations, the transformed data arise from two groups with equal underlying survival distributions but, in general, different underlying censoring distributions. The methods described in [23] can be used to construct the permuted datasets that are equally likely as the observed data to form the null distribution for the test statistics. Confidence intervals obtained by inverting the permutation tests will be similarly affected as the p-value in the sense that more efficient tests will be associated with narrower confidence intervals. Similar approach can be used for continuous outcomes generated under the model described in Section 3 to obtain confidence intervals. In this case, the test for H(β₀) : β = β₀ can be readily constructed by transforming the original outcomes Y_ij to $Y_{\mathit{\text{ij}}}^{\ast }=Y_{\mathit{\text{ij}}}-X_{\mathit{\text{ij}}}{\beta }_0$.

Test statistics of the class we consider are easy to implement, flexible, and useful in a variety of settings. Although motivated by analysis of cluster-randomized trials with time to event endpoints, the class we discuss applies to any type of endpoint. When estimating pairwise treatment effect, we can incorporate covariates, conduct variable selection on covariates, and accommodate missing data. For example, in the presence of missing data, the pairwise treatment effect estimate may be obtained from inverse probability weighted generalized estimating equations [24]. Variable selection can be done based on combined data from both arms. In addition, valid permutation tests are available by incorporating variable selection procedure in permutation tests [6, 25, 26]. One limitation of this approach arises in settings where the cluster-randomized trial includes a large number of small clusters. In this case, treatment effect estimates based on pairwise estimates may not be stable, and sometimes cannot be estimated due to sparseness of data.

In analyzing cluster-randomized trials, the permutation test provides an attractive alternative to its parametric counterparts for testing the null hypothesis of no treatment effect. It remains valid in small samples and in the presence of correlation across different clusters regardless of underlying data distribution, and is robust to mis-specification of the models used to construct the test statistic.