Selfing in Haploid Plants and Efficacy of Selection: Codon Usage Bias in the Model Moss Physcomitrella patens

Abstract

A long-term reduction in effective population size will lead to major shift in genome evolution. In particular, when effective population size is small, genetic drift becomes dominant over natural selection. The onset of self-fertilization is one evolutionary event considerably reducing effective size of populations. Theory predicts that this reduction should be more dramatic in organisms capable for haploid than for diploid selfing. Although theoretically well-grounded, this assertion received mixed experimental support. Here, we test this hypothesis by analyzing synonymous codon usage bias of genes in the model moss Physcomitrella patens frequently undergoing haploid selfing. In line with population genetic theory, we found that the effect of natural selection on synonymous codon usage bias is very weak. Our conclusion is supported by four independent lines of evidence: 1) Very weak or nonsignificant correlation between gene expression and codon usage bias, 2) no increased codon usage bias in more broadly expressed genes, 3) no evidence that codon usage bias would constrain synonymous and nonsynonymous divergence, and 4) predominant role of genetic drift on synonymous codon usage predicted by a model-based analysis. These findings show striking similarity to those observed in AT-rich genomes with weak selection for optimal codon usage and GC content overall. Our finding is in contrast to a previous study reporting adaptive codon usage bias in the moss P. patens.

Introduction

A long-term reduction in effective population size is expected to lead to a major shift in the evolution of genomes (Wright et al. 2008). In particular, because the efficacy of selection depends on the product of the effective population size and the selective coefficient of mutations, reduced effective population size will lead to decreased selection efficacy, given the same selective coefficient (Kimura 1968). Therefore, slightly deleterious mutations with small selection coefficient that would otherwise be removed from the population by purifying selection will become effectively neutral and start to accumulate with an accelerated rate (McVean and Charlesworth 1999). At the level of the genome, this is expected to lead to an increased rate of replacement mutations (Glémin 2007), decreased synonymous codon usage bias and ultimately to degeneration of the genome (Jarne 1995; Charlesworth and Wright 2001; Glémin et al. 2006; Glémin 2007; Qiu, Zeng, et al. 2011; Galtier 2012; Wright et al. 2008, 2013). Genomic features with the weakest selection coefficient, such as synonymous codon usage, should be the most sensitive to the reduction of the effective population size (N_e), because a large number of mutations will shift from the selectively driven to the effectively neutral class (McVean and Charlesworth 1999). Nevertheless, because it is genetic drift that is acting on these genomic features, phenomena associated with reduced N_e will occur rather slowly on the order of the mutation rate (Marais, et al. 2004a).

One evolutionary event that considerably reduces effective population size is the onset of self-fertilization (Pollak 1987; Nordborg 2000). This is because the rate of selfing affects the efficacy of natural selection in three ways: 1) In diploid-dominant organisms, complete selfing will half N_e through the nonrandom sampling of gametes compared with outcrossers (Pollak 1987; Nordborg 2000). Furthermore, 2) selfing will increase the level of genome-wide homozygosity and lead to decreased effective recombination rates. The drop in effective recombination rates will intensify the extent of Hill–Robertson interference of mutations and decrease local effective population size even further (Kaplan et al. 1989; McVean and Charlesworth 2000; Charlesworth 2012; Kamran-Disfani and Agrawal 2014). Finally, 3) population structure and population dynamics of selfers is expected to further lower species-wide and local effective population sizes due to the small size of local populations and intensive metapopulation dynamics (Pannell and Charlesworth 1999; Ingvarsson 2002). Although selfing can also increase the purging of recessive and strongly deleterious mutations by homozygote exposure, this does not appear to override the effect of N_e reduction (Galtier 2012; Arunkumar et al. 2015). Therefore, population genetic theory predicts severely reduced N_e in selfers, a prediction confirmed by experimental evidence (Wright et al. 2013).

The effect of selfing on codon usage bias has been extensively studied in animal and plant species that express sex in their diploid-dominant life cycle phase (Powell and Moriyama 1997; Ingvarsson 2007; Vicario et al. 2008; Qiu, Bergero, et al. 2011; Qiu, Zeng, et al. 2011; Ness et al. 2012; De La Torre et al. 2015; Szövényi et al. 2015). In contrast, species expressing sex in their dominant haploid life phase have been rarely investigated (Whittle et al. 2011, 2012; Gioti et al. 2013). Many species of bryophytes (liverworts, mosses, hornworts), fungi and algae have haploid-dominant life cycles and their individuals may be either unisexual or bisexual. Bisexual species frequently undergo a special type of selfing, referred to as haploid or intragametophytic selfing, in which genetically identical gametes produced by a single genetic individual fuse to form a completely homozygous diploid phase (Barner et al. 2011; Billiard et al. 2012). In such diploids, the effective recombination rate is essentially zero, leading to severely reduced effective size through Hill–Robertson interference (Hedrick 1987a, 1987b; Holsinger 1987). Therefore, N_e reduction in haploid selfers frequently undergoing intragametophytic selfing is expected to be even more severe than in their counterparts with a diploid-dominant life cycle. Consequently, in such organisms, codon-usage bias should be primarily driven by drift or mutational biases, rather than by natural selection.

In the moss family Funariaceae, monoecy (individuals are bisexual: Capable of producing both male and female reproductive structures) is assumed to be the ancestral state and phylogenetic evidence suggests that it has evolved once (Liu et al. 2012). This family consists of the model moss Physcomitrella patens and its relatives. In fact, all species of the family have bisexual gametophytes and are assumed to reproduce predominantly by intragametophytic selfing (Fife 1985; Perroud et al. 2011; McDaniel and Perroud 2012). Moreover, the family Funariaceae was estimated to have originated more than 100 Ma, suggesting persistence of the monoicous breeding system for a long period of time (Fife 1985; Liu et al. 2012). Therefore, it is thought that sufficient time has elapsed since the onset of the monoicous breeding system for the molecular consequences of self-fertilization to become apparent. In particular, species-wide effective population size of the model moss P. patens is assumed to be severely reduced owing to its high incidence of intragametophytic selfing (92–97% of the sexual reproduction events are of this type under controlled conditions [Perroud et al. 2011]), assumed ineffective long-distance dispersal (Beike et al. 2014), and extensive metapopulation dynamics (Liu et al. 2012; Szövényi et al. 2015). Long persistence of the monoicous breeding system and frequent intragametophytic selfing imply that synonymous codon usage of P. patens should be primarily driven by drift or mutational biases, rather than by natural selection (McDaniel and Perroud 2012; Hough et al. 2013). Yet very little is known on synonymous codon usage and its driving forces in P. patens, and previous studies came to contradictory conclusions. An early study concluded that synonymous codon usage in P. patens is driven by natural selection, contradicting expectations of evolutionary theory (Stenøien 2005). Nevertheless, this study only used a subset of the P. patens gene set and did not explicitly account for nucleotide compositional biases that may drive codon usage bias. In contrast, another study found that codon usage is less biased in the selfer P. patens than in the outcrosser Ceratodon purpureus, a dioecious moss from the family Ditrichaceae, implying reduced efficacy of selection in the former (Szövényi et al. 2015). Finally, it was also suggested that synonymous codon usage of P. patens can be partly explained by nucleotide biases across the genome (Camiolo et al. 2015). Therefore, it is not yet clear whether codon usage in the moss P. patens is primarily driven by natural selection or by neutral processes.

In this study, we test the hypothesis that in organisms frequently undergoing haploid (intragametophytic) selfing synonymous codon usage bias should be primarily driven by genetic drift or mutational biases rather than by natural selection owing to the severely reduced effective population size. To investigate this question, we provide a detailed analysis of synonymous codon usage in the highly selfing model moss P. patens. In particular, we use the entire P. patens proteome, large-scale gene expression data (microarray and RNA sequencing), and orthologous sequences from the moss C. purpureus to assess whether synonymous codon usage is mainly driven by drift or natural selection. We show that a weak correlation between gene expression level and synonymous codon usage bias seemingly supports the hypothesis of translational selection. Nevertheless, careful analysis shows that this correlation is primarily driven by variation in background nucleotide composition, which suggests that mutational biases are at work. We also found that, in contrast to what is expected under the translational/transcriptional selection scenario, increasing codon usage bias does not decrease the accumulation of synonymous substitutions between species. We further show that more broadly expressed genes that are under stronger purifying selection do not tend to have greater codon usage bias. Finally, by using a model-based approach we show that genetic drift and mutational biases are predominant in shaping codon usage bias in P. patens. Therefore, we argue that synonymous codon usage in P. patens is mainly driven by drift, potentially by background nucleotide content variation, and the effect of natural selection on synonymous codon usage bias is weak. We also found a significant relationship between tRNA gene copy numbers and preferentially used codons, which is best interpreted as secondary adaptation of the tRNA pool to the nucleotide content of the preferred set of codons.

Materials and Methods

Physcomitrella patens Genome, Proteome and Estimating Codon Usage Bias

We downloaded the P. patens genome version 1.6 (Zimmer et al. 2013) from Phytozome9 (Goodstein et al. 2012). We did not use the recent prerelease (version3) of the genome, because this assembly is still under embargo. Nuclear gene models were extracted from the genomic DNA using the gff3 file provided with the genome version. For each gene, we selected only one splice variant, in particular the one coding the longest protein sequence, which was used in all further analyses. As estimating the effective number of codons (ENC) statistic (Wright 1990) is problematic for short sequences, we discarded genes shorter than 50 amino acids, resulting in 31,708 genes out of 32,273 (Wright 1990).

Codon bias was estimated using three statistics that have different statistical and distributional properties. First, we used the ENC to measure codon bias of genes and also to identify optimal codons (Wright 1990). This statistic measures to what extent codon usage deviates from the equal usage of synonymous codons in a particular gene, with low values referring to highly biased (minimum 20) and high values to unbiased codon usage (maximum 61). One disadvantage of the statistic is that it is strongly influenced by the background nucleotide composition (especially GC content) of genes (Novembre 2000). Therefore, we also used a version of ENC, ENC′ (ENC “prime”) which estimates effective codon usage by taking into account background nucleotide frequencies (Novembre 2000). Maximum values of ENC and ENC′ can theoretically exceed 61 (the number of synonymous codons) for a standard genetic code. Therefore, values are usually rescaled to fall between 20 and 61. However, rescaling decreases the accuracy of estimates; hence, codon usage in genes with the very same ENC or ENC′ values might differ, leading to biased estimates. Furthermore, adjustment of the values will generate many ties that will weaken the power of further statistical tests, including correlation analysis. Therefore, we also used a third statistics, the proportion of optimal codons (F_op), which is strongly affected by background nucleotide composition but is devoid of the adjustment issues mentioned above. Nonetheless, estimating F_op requires a priory definition of the optimal set of codons, which we detail in the next paragraph. We calculated ENC and ENC′ using the software INCA (Supek and Vlahoviček 2004) which uses base composition of coding sequences (CDS) as the neutral reference. All other calculations were carried out in the statistical environment R (R Development Core Team 2008).

In previous studies, the optimal set of codons was identified using correspondence analysis on relative synonymous codon usage (RSCU) values (Rensing et al. 2005; Stenøien 2005; Szövényi et al. 2015). Nevertheless, this approach may lead to misleading conclusions, especially when mutational biases and selection on codon usage are acting in the same direction (Perrière and Thioulouse 2002) and (John Peden, http://www.molbiol.ox.ac.uk/cu (last accessed March 13, 2017), version 1.4.2). Therefore, we defined optimal codons as the synonymous codons of codon families that are more frequently used in genes with greater codon usage bias. Genes in which the codon family appeared less than ten times were discarded. We estimated codon usage bias of genes using the ENC statistic and its version that corrects for background nucleotide content (ENC′). To identify the optimal set of codons for each of the 18 amino acids that are coded by more than one codon, we correlated each alternative codon’s frequency in a given gene with the ENC and ENC′ statistics. We calculated nonparametric Spearman rank-correlation between ENC/ENC′ and the frequency of alternative codons per gene and optimal codons were those that showed the strongest significant correlation (P ≤ 0.05/n, where n is the number of codons encoding the amino acid in question) (Hershberg and Petrov 2009). Using the set of optimal codons, we also calculated the statistic F_op, the proportion of optimal codons per gene.

Gene Expression Data

We used both RNA-seq and microarray-based gene expression data sets to avoid the effect of technology-dependent biases that may influence our conclusions. To compile the RNA-seq data, we retrieved published data sets describing gene expression in the chloronemata (the early filamentous stage) and in the gametophore (the leafy shoot stage of the haploid phase) from the NCBI SRA database (SRR072918 and SRR060806). In addition, we generated RNA-seq data for three developmental stages of the P. patens sporophyte (diploid) (stages 20–23, 25–26, and 28 days after fertilization; all premeiotic, available in the European Nucleotide Archive under accession number PRJEB19978). The three RNA-seq libraries were prepared using the Truseq RNA-seq library preparation protocol including polyA selection and were sequenced on a Hiseq2000 machine (single end, 101 cycles) at the Functional Genomics Center Zurich. We trimmed and filtered the raw data sets using trimmomatic (Bolger et al. 2014; -phred33 ILLUMINACLIP: Hiseq_.fa:2:30:10:8:true LEADING:9 TRAILING:3 SLIDINGWINDOW:4:15 MINLEN:36) and mapped reads to the P. patens v1.6 (https://www.cosmoss.org/physcome_project/wiki/Downloads; last accessed May 1, 2017) genome using tophat2 (Kim et al. 2013). We used all these RNA-seq data to refine gene model annotations of the P. patens v1.6 gff files (link see above) using Cufflinks and Cuffmerge (Trapnell et al. 2012). We then ran CuffDiff (Trapnell et al. 2012) using the refined gtf files and obtained expression estimates for each gene in each expression data set as FPKM (fragment per kilobase of exon per million fragments mapped) values after quantile normalization. In the following analyses, estimated FPKM values were used as gene expression estimates.

RNA-seq technology is known to be more accurate in estimating gene expression than microarray technology, especially due to its greater dynamic range (Marioni et al. 2008; Zhu et al. 2015). Nevertheless, our RNA-seq data set is only restricted to five different developmental stages, which may introduce a bias in estimating gene expression. Therefore, we repeated the above-mentioned analyses using a recently published microarray-based gene expression atlas of P. patens including tissue samples from ten different parts/developmental stages of the plant (Ortiz-Ramírez et al. 2016). We used the average normalized gene expression estimates per each developmental stage and for each gene as given in the supplementary material 2 of the publication. For both type of data (RNA-seq and microarray), we used the maximum value of gene expression across all the developmental stages as a measure of gene expression level in all further analyses. We followed this strategy because global gene expression can be highly influenced by the number of tissues a gene is expressed in. This may generate spurious correlations between codon usage bias and gene expression that are primarily driven by expression breadth. Finally, the strength of translational selection acting on a gene is expected to be primarily determined by its maximum expression value. We, however, note that we repeated all analyses using the arithmetic average of gene expression values across developmental stages which did not change our conclusions qualitatively.

We also calculated the expression breadth of genes that was used later in the analysis. We chose the statistic τ (tau), which combines information on tissue specificity and expression level. This statistic was also shown to have the best properties among multiple indices used to describe tissue specificity of expression (Kryuchkova-Mostacci and Robinson-Rechavi 2017). We calculated τ as given in Kryuchkova-Mostacci and Robinson-Rechavi (2017). We estimated expression breadth using both the microarray and RNA-seq data set.

Correlation and Partial Correlation Analyses

Codon usage bias may be shaped by natural selection, genetic drift, or mutational processes. To test whether codon usage bias is primarily driven by natural selection or by neutral forces, we carried out the following analyses and tests. All our tests are based on nonparametric correlation analysis (partial Spearman rank-correlation), because statistical properties of the data did not satisfy those of parametric tests even after multiple rounds of data transformation.

(a) We first tested whether the predicted number of tRNA genes in the genome can explain the bias in synonymous codon usage. We retrieved the predicted number of tRNA genes in the P. patens genome from the recently updated GtRNAdb data base (http://gtrnadb.ucsc.edu/; last accessed November 10, 2016) (Chan and Lowe 2015). We then investigated the correlation (Spearman rank-correlation) between the genomic copy number of tRNA genes and the corresponding relative amino acid abundances in the proteome weighted by each gene’s expression level. If genomic copy number can be used as a proxy for the cellular concentration of isoacceptor tRNA species, we expect to find a significant correlation (Duret 2000).

We also investigated whether synonymous codon usage can be explained by the biased cellular concentration of tRNA genes. To test this, we calculated the relative gene frequency (RGF, is the observed tRNA-gene copy number in the genome divided by the frequency expected if all isoacceptor tRNA genes for that amino acid were equally frequent in the genome) of each tRNA gene in the P. patens genome and correlated it with the average RSCU (Sharp et al. 1986) of the corresponding codon in the 5% most highly expressed genes (calculated separately for the RNA-seq and for the microarray data sets). Because one tRNA gene can decode multiple codons, this correlation only partially reflects the coadaptation of tRNA abundance and codons. To correct for that, we did a second test in which we took into account classical and revised wobble rules to identify the correspondence among codons and their decoding tRNA genes: 1) GNN tRNAs can pair with both C and U ending codons; 2) ANN tRNA genes are modified to inosine and decode both U and G ending codons (Percudani 2001). We then calculated RGF for each isoaceptor tRNA. When grouping codons based on wobbling rules, we used average RSCU values. For this latter calculation, we skipped all amino acids for which all alternative codons were coded by the very same anticodon sequence.

(b) If codon usage bias is driven by translational selection, then genes expressed at a higher level should show greater codon bias (Akashi and Eyre-Walker 1998; Akashi 2001; Akashi et al. 2012). We calculated nonparametric Spearman rank-correlation between the maximum expression value and ENC, ENC′, and F_op. Nevertheless, a significant correlation between expression level and codon bias may also be a result of mutational biases that are correlated with the level of gene expression. Therefore, we also employed a third test.

(c) If translational selection is driving codon usage, then intensity of selection against unpreferred codons should be greater in more highly expressed genes, which should decrease the rate at which synonymous mutations accumulate between species. Therefore, we investigated the correlation between gene expression and synonymous divergence (K_s) of P. patens genes from the moss C. purpureus. We calculated the synonymous divergence of each P. patens gene from its C. purpureus ortholog using sequence data of the C. purpureus GG1 strain (Szövényi et al. 2015). We established one-to-one orthology between P. patens and C. purpureus GG1 protein sequences using the bidirectional best hit approach with an e-value threshold of 10⁻⁶ (Tatusov 1997). We then aligned protein sequences (P. patens vs. C. purpureus GG1) using the default parameters of muscle (Edgar 2004) and forced nucleotide alignments into the protein alignments using pal2nal (Suyama et al. 2006). Finally, we used K_a/K_s_calculator 2.0 (Wang et al. 2010) to calculate K_s values for each pair of orthologs with the YN model (Yang and Nielsen 2000). We additionally calculated the nonparametric correlation between K_s values and the maximum value of gene expression. To correct for alignment uncertainty and saturation biases, we only used orthologs with a K_s  ≤ 2 and carried out the correlation analyses at two stringency thresholds (K_s ≤ 1 and ≤2). The number of nonsynonymous substitutions per nonsynonymous sites divided by the number of synonymous substitutions per synonymous sites (the K_a/K_s statistic) can be used as an indicator of the strength of purifying selection acting on a gene (Nielsen and Yang 2003). Therefore, we also assessed the correlation between K_a/K_s values and codon usage bias while controlling for all other confounding genomic variables at two K_s thresholds as above (K_s≤1 and ≤2).

(d) It was reported that codon usage bias can also be influenced by expression breadth (Duret and Mouchiroud 2000; Urrutia and Hurst 2001; Ganko et al. 2007; Ingvarsson 2007, 2008). More broadly expressed genes are under greater purifying selection, which is expected to also act on synonymous codon usage. Therefore, we calculated Spearman rank-correlation between expression breadth (τ) and codon usage bias of genes and expected that if codon usage bias is driven by natural selection more broadly expressed genes will show greater codon usage bias.

Accounting for the Effect of Other Potentially Confounding Genomic Features

Synonymous codon usage and evolutionary rate of genes were also reported to be affected by other genomic variables that are themselves correlated with gene expression, including gene length, intron number, intron length, exon number, exon length, and GC content (Ingvarsson 2007; Stenøien 2007, 2005; Slotte et al. 2011; Yang and Gaut 2011; Camiolo et al. 2015; De La Torre et al. 2015; Kryuchkova-Mostacci and Robinson-Rechavi 2015). Therefore, a significant relationship between gene expression and synonymous codon usage can be potentially explained by the indirect effect of other genomic variables that correlate with gene expression. To take this into account in all previous statistical tests, we used nonparametric partial rank-correlation analysis to investigate pairwise correlation of variables while correcting for the effect of potential covariates (Kim 2015). We extracted the following genomic features from the P. patens genome’s gff file as potential covariates, because they were previously reported to affect either codon usage bias or evolutionary rates of genes: Gene and intron length on the chromosome in base pairs, percent GC content of genes, exons, third codon positions, and introns (Urrutia and Hurst 2001; Akashi 2001; Stenøien 2005, 2007; Akashi et al. 2012; De La Torre et al. 2015). Gene expression breadth was calculated using the RNA-seq and the microarray data sets separately, as explained above. Preliminary analyses suggested that the variable pairs intron number–intron length and CDS length–gene length are highly significantly correlated. Therefore, the variables intron number and CDS length were excluded and only intron length and gene length were included in the final analysis. Partial rank-correlation analysis was carried out using the package ppcor in the statistical language R (Kim 2015). We used the method of Benjamini and Hochberg (Benjamini and Hochberg 1995) to correct for multiple comparisons.

Assessing the Effect of Mutational Bias and Natural Selection on Codon Usage Bias Using a Stochastic Evolutionary Model of Protein Production Rate

The above-mentioned tests rely on correlation analyses or on divergence statistics which may lead to erroneous conclusions when selection is weak and mutation bias is strong (Lawrie et al. 2011, 2013). Therefore, we also used a Bayesian method (Ribosome Overhead Costs Stochastic Evolutionary Model of Protein Production Rate [ROC SEMPPR]) (Gilchrist et al. 2015) to model the effect of mutational bias and natural selection on synonymous codon usage in a proper population genetic framework. The model implemented in ROC SEMPPR is able to predict the probability of observing a given synonymous codon genotype for a gene based on its protein production rate. It is assumed that this probability is a combined function of the mutation bias and natural selection for translational inefficiency of which the latter is hypothesized to scale with the level of protein production and effective population size (Gilchrist 2007; Wallace et al. 2013; Gilchrist et al. 2015). Therefore, if N_e is sufficiently large, then the pattern of codon usage bias should provide sufficient information to accurately approximate protein production rates without gene expression information using the model. However, if N_e is low and codon usage bias is very weak and/or it does not scale with protein production rates, the fit between predicted production rates obtained with or without observed gene expression estimates included is expected to be poor. Furthermore, when selection on codon usage is very weak, the model will not be able to reliably estimate translational inefficiency parameter and thus identify the selectively preferred codon.

We fitted the model using the codon composition of the P. patens proteome and run two separate analyses with or without including our RNA-seq-based FPKM values as proxies of protein production rates. We run 10,000 iterations of the Markov chain Monte Carlo chain and then used the last 5,000 iterations to obtain posterior estimates of parameters (mutation bias: ΔM, translational inefficiency: Δη; and protein production: Φ). Initial values for mutation bias and translational inefficiency were obtained by multinomial logistic regression using observed RNA-seq expression values as explanatory variables. Initial protein production rates we directly obtained from the gene expression estimates of the RNA-seq data. We calculated point estimates of parameters as arithmetic means of their posterior distribution. We compared the fit between protein production rates of the two models (with and without observed gene expression estimates included) using regular linear regression. We also calculated the posterior mean of selection on codon usage per gene (SCU) (Wallace et al. 2013), which is the mean fitness advantage scaled by the effective population size, that the organism gains from the gene’s codon composition relative to an unselected synonymous alternative. When SCU is 1 or is smaller than 1, drift is dominant over natural selection. We carried out all analyses using the R package cubfits (Chen et al. 2014).

Results

Identification of Optimal/Major Codons

We first identified optimal codons per synonymous codon families that are significantly more frequently used in genes with greater overall codon usage bias as defined by the ENC or ENC′ statistics. Our analysis is based on 31,708 genes (genes with less than 50 codons were excluded). Both ENC and ENC′ values were relatively high, suggesting weak codon usage bias overall (ENC_mean=54.82, ENC_median=56.46, ENC_{IQR[Inter  Quartile  Range]}=52.78–58.94; ENC′_mean=57.00, ENC′_median=59.28, ENC′_IQR=55.95–61.00). A previous study identified optimal codons by performing a correspondence analysis on RSCU values (Szövényi et al. 2015); the results are shown along with results of the current analysis in table 1 and in the supplementary table 1, Supplementary Material online. The correspondence analysis and our correlation-based analysis using the statistic ENC′ identified the very same set of codons as optimal except in a single case. This slight discordance between the two approaches is likely due to a lower statistical power of the correlation analysis, because the optimal codon defined by the correspondence analysis turned out to be also more frequent in genes with greater codon usage bias, but the significance of the correlation did not pass the required threshold set by multiple testing. In contrast, using the ENC statistic that does not correct for background nucleotide content led to considerably less concordant results. Fourteen optimal codons that were recovered by both the correspondence and ENC′-based analyses were not identified as optimal codons in the ENC-based analysis (table 1). It is important to note that not all of the optimal codons identified by the ENC′ and correspondence analyses were found to be more abundant in the set of highly expressed genes, as would be expected under the translational selection hypothesis, and this finding was supported by both the microarray and the RNA-seq data (table 1, see italicized and underlined ΔRSCU values). In particular, 7 out of the 27 optimal codons supported by both the correlation and correspondence analyses were less frequent in the subset of most highly expressed genes, contradicting the simple translational selection hypothesis.

Table 1.

Optimal Codons per Synonymous Codon Families Identified by Correlation Analysis between Overall Codon Usage Bias of Genes (ENC and ENC′) and the Frequency of Codons per Each Gene

				Correlation analysis								Correspondence analysis
				Using ENC	Using ENC′	Microarray			RNA-seq
Number of Corresponding tRNA Genes in P. patens Genome	RGF	RGF Wobble	Amino Acids	Codons	Codons	RSCUhighly expressed	RSCUlowly expressed	ΔRSCU	RSCUhighly expressed	RSCUlowly expressed	ΔRSCU	Codons	High-Bias	Low-Bias	ΔRSCU
19	2.1111		Ala	GCT	GCT	1.3400	1.2070	0.1329	1.3623	1.1526	0.2097	GCT	0.7200	1.5200	−0.8000
0	0.0000	1.5833		GCC	GCC*	1.0127	0.8038	0.2088	1.0113	0.8775	0.1338	GCC*	1.1600	0.5500	0.6100
9	1.0000	0.7500		GCA	GCA	0.9004	1.1673	−0.2669	0.8923	1.1124	−0.2201	GCA	0.6000	1.5700	−0.9700
8	0.8889	0.6667		GCG	GCG*	0.7470	0.8218	−0.0749	0.7341	0.8575	−0.1234	GCG*	1.5200	0.3700	1.1500
8	1.2966		Arg	CGT	CGT	0.9886	0.7943	0.1943	1.0110	0.7264	0.2846	CGT	0.6000	0.7600	−0.1600
1	0.1621	1.2162		CGC	CGC*	1.1197	0.9054	0.2143	1.0981	0.9755	0.1227	CGC*	1.4300	0.3500	1.0800
7	1.1345	0.9459		CGA	CGA	0.8164	1.0329	−0.2164	0.8310	1.0296	−0.1985	CGA	0.6200	0.9400	−0.3200
5	0.8104	0.6757		CGG	CGG*	0.8206	0.9338	−0.1132	0.8232	0.9386	−0.1154	CGG*	1.4500	0.4600	0.9900
6	0.9724	0.8108		AGA	AGA	0.8939	1.1666	−0.2727	0.8915	1.1695	−0.2779	AGA	0.4800	2.3300	−1.8500
10	1.6207	1.3514		AGG*	AGG*	1.3607	1.1670	0.1937	1.3451	1.1605	0.1846	AGG*	1.4100	1.1600	0.2500
1	0.1333		Asn	AAT	AAT	0.8467	1.0670	−0.2203	0.8713	0.9727	−0.1014	AAT	0.5200	1.3400	−0.8200
14	1.8667	2.0000		AAC*	AAC*	1.1533	0.9330	0.2203	1.1287	1.0273	0.1014	AAC*	1.4800	0.6600	0.8200
0	0.0000		Asp	GAT	GAT	1.0151	1.0854	−0.0703	1.0033	1.0205	−0.0172	GAT	0.6700	1.4100	−0.7400
11	2.0000	2.0000		GAC*	GAC*	0.9849	0.9146	0.0703	0.9967	0.9795	0.0172	GAC*	1.3300	0.5900	0.7400
0	0.0000		Cys	TGT	TGT	0.7898	0.9278	−0.1380	0.6906	0.8315	−0.1409	TGT	0.4300	1.2100	−0.7800
7	2.0000	2.0000		TGC*	TGC*	1.2102	1.0722	0.1380	1.3094	1.1685	0.1409	TGC*	1.5700	0.7900	0.7800
9	0.9474	0.9474	Gln	CAA	CAA	0.7657	0.9658	−0.2001	0.7837	0.9190	−0.1352	CAA	0.4500	1.3300	−0.8800
10	1.0526	1.0526		CAG*	CAG*	1.2343	1.0342	0.2001	1.2163	1.0810	0.1352	CAG*	1.5500	0.6700	0.8800
7	0.6667	0.6667	Glu	GAA	GAA	0.7014	0.8470	−0.1456	0.7219	0.8236	−0.1017	GAA	0.4400	1.1800	−0.7400
14	1.3333	1.3333		GAG*	GAG*	1.2986	1.1530	0.1456	1.2781	1.1764	0.1017	GAG*	1.5600	0.8200	0.7400
0	0.0000		Gly	GGT	GGT	1.1190	0.9676	0.1514	1.1101	0.9205	0.1896	GGT	0.6400	1.2100	−0.5700
15	1.7143	1.2864		GGC	GGC*	0.9617	0.9708	−0.0091	0.9759	1.0439	−0.0680	GGC*	1.2400	0.7300	0.5100
9	1.0286	0.7719		GGA	GGA	1.2212	1.1394	0.0818	1.2122	1.1498	0.0623	GGA	0.9500	1.4600	−0.5100
11	1.2571	0.9434		GGG	GGG*	0.6980	0.9222	−0.2241	0.7018	0.8858	−0.1839	GGG*	1.1600	0.6000	0.5600
0	0.0000		His	CAT	CAT	0.8417	1.0529	−0.2112	0.8391	0.9619	−0.1228	CAT	0.6100	1.4100	−0.8000
9	2.0000	2.0000		CAC*	CAC*	1.1583	0.9471	0.2112	1.1609	1.0381	0.1228	CAC*	1.3900	0.5900	0.8000
12	2.2514		Ile	ATT	ATT	1.3376	1.2370	0.1007	1.3250	1.2036	0.1214	ATT	0.8000	1.3000	−0.5000
0	0.0000	1.5000		ATC*	ATC*	1.3535	1.1231	0.2304	1.3549	1.2422	0.1128	ATC*	1.9800	0.5500	1.4300
4	0.7505	0.5000		ATA	ATA	0.3088	0.6399	−0.3311	0.3201	0.5543	−0.2342	ATA	0.2200	1.1500	−0.9300
2	0.4796	0.4000	Leu	TTA	TTA	0.3412	0.5837	−0.2425	0.3684	0.5152	−0.1468	TTA	0.1300	1.2000	−1.0700
6	1.4388	1.2000		TTG	TTG	1.7998	1.4873	0.3125	1.8150	1.5153	0.2997	TTG	1.4400	2.1200	−0.6800
6	1.4388			CTT	CTT	1.1936	1.1819	0.0118	1.1359	1.0768	0.0591	CTT	0.5400	1.1900	−0.6500
1	0.2398	1.4000		CTC	CTC*	1.0424	0.9544	0.0880	1.0535	1.0195	0.0340	CTC*	1.0700	0.4900	0.5800
5	1.1990	1.0000		CTA	CTA	0.3789	0.5042	−0.1252	0.3761	0.4856	−0.1095	CTA	0.2000	0.5700	−0.3700
5	1.1990	1.0000		CTG*	CTG*	1.2440	1.2886	−0.0446	1.2511	1.3876	−0.1365	CTG*	2.6200	0.4300	2.1900
8	0.6667	0.6667	Lys	AAA	AAA	0.5422	0.7975	−0.2553	0.5538	0.7665	−0.2127	AAA	0.3300	1.0400	−0.7100
16	1.3333	1.3333		AAG*	AAG*	1.4578	1.2025	0.2553	1.4462	1.2335	0.2127	AAG*	1.6700	0.9600	0.7100
1	0.1333		Phe	TTT	TTT	0.8004	0.9593	−0.1589	0.8164	0.8849	−0.0686	TTT	0.4700	1.4000	−0.9300
14	1.8667	2.0000		TTC*	TTC*	1.1996	1.0407	0.1589	1.1836	1.1151	0.0686	TTC*	1.5300	0.6000	0.9300
13	2.0800		Pro	CCT	CCT	1.3234	1.2547	0.0687	1.3296	1.2101	0.1195	CCT	0.6800	1.4400	−0.7600
0	0.0000	1.5606		CCC	CCC*	1.1467	0.8594	0.2873	1.1198	0.8554	0.2644	CCC*	1.2300	0.4500	0.7800
8	1.2800	0.9604		CCA	CCA	0.9124	1.1249	−0.2125	0.9516	1.0821	−0.1305	CCA	0.5800	1.8100	−1.2300
4	0.6400	0.4802		CCG	CCG*	0.6174	0.7609	−0.1436	0.5990	0.8524	−0.2534	CCG*	1.5100	0.3000	1.2100
13	2.2928		Ser	TCT	TCT	1.2234	1.1860	0.0374	1.2445	1.1178	0.1267	TCT	0.5800	1.5000	−0.9200
0	0.0000	1.5294		TCC	TCC*	1.1210	0.9560	0.1650	1.1340	0.9735	0.1605	TCC*	1.2400	0.5200	0.7200
5	0.8818	0.5882		TCA	TCA	0.8221	0.9374	−0.1153	0.8223	0.9186	−0.0962	TCA	0.4000	1.6400	−1.2400
7	1.2346	0.8235		TCG	TCG*	0.9085	0.8898	0.0186	0.8819	0.9355	−0.0536	TCG*	1.7300	0.3500	1.3800
0	0.0000			AGT	AGT	0.8045	0.9291	−0.1246	0.7460	0.8680	−0.1220	AGT	0.4100	1.1800	−0.7700
9	1.5873	1.0588		AGC*	AGC*	1.1205	1.1017	0.0188	1.1712	1.1867	−0.0155	AGC*	1.6400	0.8100	0.8300
10	1.9048		Thr	ACT	ACT	1.2054	1.1451	0.0603	1.1815	1.0608	0.1208	ACT	0.5300	1.2900	−0.7600
0	0.0000	1.4286		ACC	ACC*	1.1632	0.8676	0.2957	1.1404	0.9640	0.1764	ACC*	1.2900	0.5600	0.7300
5	0.9524	0.7143		ACA	ACA	0.8646	1.1010	−0.2364	0.8708	1.0371	−0.1663	ACA	0.4500	1.8300	−1.3800
6	1.1429	0.8571		ACG	ACG*	0.7668	0.8864	−0.1196	0.8073	0.9381	−0.1309	ACG*	1.7200	0.3200	1.4000
0	0.0000		Tyr	TAT	TAT	0.6841	0.9464	−0.2622	0.7009	0.8084	−0.1075	TAT	0.4600	1.3300	−0.8700
8	2.0000	2.0000		TAC*	TAC*	1.3159	1.0536	0.2622	1.2991	1.1916	0.1075	TAC*	1.5400	0.6700	0.8700
13	0.5000		Val	GTT	GTT	1.0106	1.0558	−0.0452	1.0495	0.9711	0.0784	GTT	0.4600	1.4400	−0.9800
0	0.0000	1.5012		GTC	GTC*	0.8330	0.7387	0.0942	0.8373	0.8203	0.0170	GTC*	0.8100	0.5100	0.3000
2	0.0769	0.2309		GTA	GTA	0.4681	0.6084	−0.1403	0.4552	0.5732	−0.1180	GTA	0.2500	1.0000	−0.7500
11	0.4231	1.2702		GTG*	GTG*	1.6883	1.5970	0.0913	1.6580	1.6354	0.0226	GTG*	2.4800	1.0600	1.4200

Note.—RGF, relative gene frequency of tRNA genes in the genome (frequency of a codon per codon family/frequency assuming equal abundances of tRNA genes per codon family) not taking into account wobble rules; RGF wobble, relative gene frequency of tRNA genes taking into account revised wobble rules (codons were grouped according to wobble rules); RSCU_{lowly expressed}, average RSCU in the 5% least expressed genes; RSCU_{highly expressed}, average RSCU in the 5% most highly expressed genes; ΔRSCU, RSCU_{highly expressed} − RSCU_{lowly expressed}. Optimal codons identified in a previous study using correspondence analysis on RSCU are also shown along with the average RSCU values in the gene set with the highest and lowest codon usage bias (upper and lower 5%) (values are taken from the publication Szövényi et al. 2015). Optimal codons are labeled with an asterisk and optimal codons supported by more than one analysis are in bold. ΔRSCU values contradicting the translational/transcriptional hypothesis are underlined and in italics.

Coadaptation of tRNA Copy Number and Codon Bias

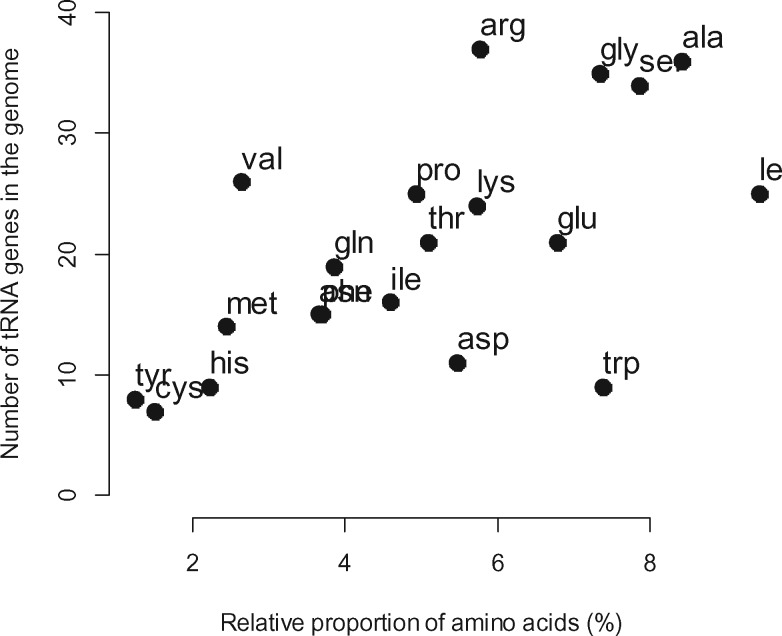
We found that estimated copy number of tRNA genes in the genome and the relative abundance of amino acids in proteins (weighted by their average expression level) were strongly and significantly correlated (Spearman’s rho [r_s] r_{s  microarray}=0.6468, P = 0.0021; r_{s  RNA-seq}=0.6543, P = 0.0017, fig. 1), as expected when genomic copy number of tRNA genes corresponds to their concentration in the cell. We also found that almost all optimal codons corresponded to the most abundant tRNA genes (table 1) and the proportion of preferred codons corresponding to the most abundant tRNA genes was greater than expected by random chance regardless whether wobble rules were taken into account (without wobble rules 61% and 100% with wobble rules; P_{getting greater values than observed by chance}<0.0001 for both). This was further supported by a strong and significant relationship between the RGF of cognate tRNA genes and the RSCU values of the corresponding codons in the 5% most highly expressed genes, regardless of accounting for the wobble rules (r_{s  microarray_no_wobble_rules}=0.4369, P = 0.0005; r_{s  RNA-seq_no_wobble_rules}=0.4607, P = 0.0002; r_{s  microarray_wobble_rules}= 0.7598, P ≪ 0; r_{s  RNA-seq_wobble_rules}= 0.7623, P ≪ 0). When we repeated this analysis with the 5% most weakly expressed genes, the strength of the correlation was significantly lower than that of the highly expressed gene set when taking into account wobble rules (r_{s microarray_wobble_rules}=0.5152, P = 0.0011; r_{s RNA-seq_wobble_rules}=0.5135, P = 0.0012), but not when wobble rules were not accounted for (r_{s microarray_no_wobble_rules}=0.4379, P = 0.0005; r_{s  RNA-seq_no_wobble_rules}=0.5452, P = 0.00001; r_{s microarray_wobble_rules}=0.5152, P = 0.0011; r_{s  RNA-seq_wobble_rules}=0.5135, P = 0.0012; z_{microarray_wobble_rule_lowly_vs._highly_expressed_genes} = −1.76, P = 0.0392; z_{RNA-seq_wobble_rule_lowly_vs._highly_expressed_genes}  = −1.79, P = 0.0367). These results imply that tRNA copy number and synonymous codon usage are coadapted and that codons with more abundant cognate tRNA genes in the genome are on average more preferentially used in highly expressed genes.

Fig. 1.

—Correlation between the number of tRNA genes in the P. patens genome and the relative proportion of the corresponding amino acids in the proteome. Amino acids are labelled with their three letter codes and their frequencies are weighted by the average expression of genes. For this figure, we used gene expression data from the microarray experiment.

Synonymous Codon Usage and Gene Expression Intensity

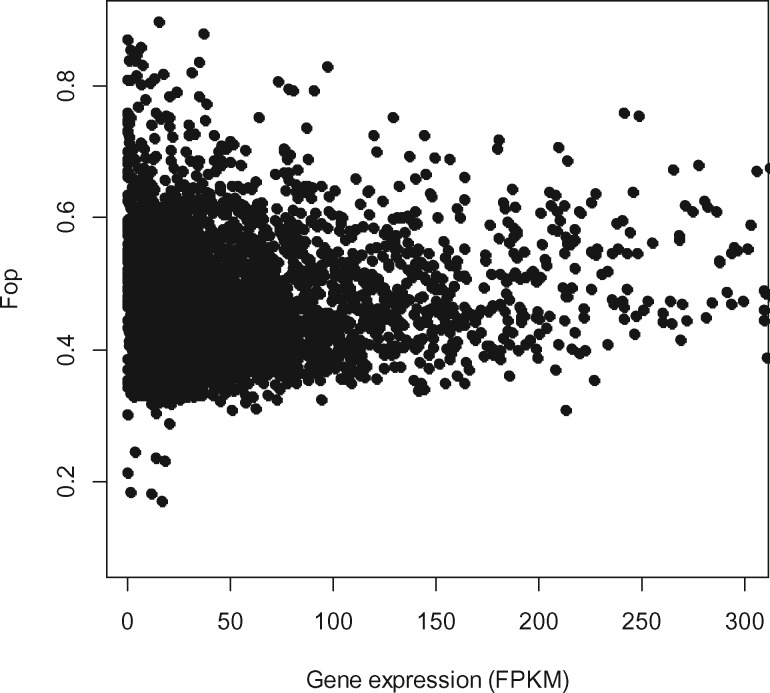
If codon usage of genes is driven by translational/transcriptional selection, then gene expression should be positively correlated with the measure of codon bias. That is, genes with greater codon bias should use optimal codons more frequently. We found a significant, but weak correlation between the statistics F_op/ENC and expression intensity of genes in a partial rank correlation analysis correcting for the effect of all other confounding variables (fig. 2, table 2). Furthermore, when we used the ENC′ statistic accounting for the unequal usage of synonymous codons due to background nucleotide content, partial correlation with expression level of genes was very weak and for the RNA-seq data nonsignificant (table 2).

Fig. 2.

—Correlation between the frequency of optimal codons (F_op) and gene expression (maximum value of RNA-seq expression estimate [FPKM]).

Table 2.

Partial Spearman Rank Correlation of Codon Bias Statistics and Genomic Variables

		Gene Expression				Expression Breadth (τ)				Ks				Ka/Ks				Ka				Gene Length		Intron Length		GC_CDS		GC_ third codon		GC_ intron
		Microarray		RNA-seq		Microarray		RNA-seq		Ks ≤2		Ks ≤1		Ks ≤2		Ks ≤1		Ks ≤2		Ks ≤1
		Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P	Rho	P
Codon usage bias statistic
ENC	vs.	−0.1208	2.5380E- 18	−0.0836	1.4840E- 09	0.0233	8.6452E- 02	0.0764	1.8114E- 08	−0.0991	1.0410E- 11	−0.0401	2.5855E- 02	0.1700	2.7720E- 32	0.1674	6.7550E- 21	0.1216	4.8000E- 17	0.0723	6.6000E- 05	−0.0569	4.9886E- 05	0.0421	2.6759E- 03	0.1029	3.0190E- 14	0.1698	1.0606E- 36	0.1400	2.9156E- 25
Fop	vs.	0.0647	3.9400E- 06	0.0387	5.3886E- 03	−0.0050	7.1610E- 01	0.0511	1.6971E- 04	0.1240	8.1000E- 18	0.0898	8.7120E- 07	−0.0790	8.8760E- 08	−0.0651	3.6670E- 04	−0.0656	7.6971E- 06	−0.0512	5.1389E- 03	−0.0456	1.2025E- 03	−0.0235	9.1829E- 02	0.4273	8.2376E- 264	0.9766	0.0000E+ 00	0.3879	1.1119E- 209
ENC_prime	vs.	−0.0536	1.9512E- 04	−0.0180	2.2357E- 01	−0.0456	1.3748E- 03	−0.0405	2.8932E- 03	−0.1253	1.4040E- 17	−0.0446	1.5730E- 02	0.1013	5.4600E- 12	0.0634	6.8209E- 04	0.0738	7.0500E- 07	0.0105	6.0351E- 01	−0.0396	5.4170E- 03	0.0925	3.6760E- 11	−0.1098	4.9028E- 16	−0.0342	1.1883E- 02	−0.0479	4.2922E- 04

Note.—Rank correlations presented are pairwise partial rank correlations in which all the other variables listed in the table were included as covariates. Rho, Spearman’s partial rank correlation statistic; K_s, number of synonymous substitutions per synonymous sites between P. patens and C. purpureus GG1; K_a, number of nonsynonymous substitutions per nonsynonymous sites between P. patens and C. purpureus GG1; Gene length, physical length of genes in nucleotides in the genome; Intron length, physical length of the introns in nucleotides in the genome; GC_CDS, GC content of coding regions; GC_thirdcodon, GC content of third codon positions; GC_intron, GC content of introns; p, Benjamini–Hochberg false discovery rate.

As we show below GC content of coding and noncoding regions is significantly positively correlated in the P. patens genome. Therefore, if local GC bias is a major driver of codon bias and GC bias is positively correlated with the level of gene expression, employing ENC′ in the analysis may have removed a true signal. Indeed, this is what we found in our analysis because ENC and F_op are more strongly correlated with gene expression than ENC′ (table 2). Nevertheless, if codon usage bias is primarily driven by local GC bias, both ENC and F_op statistics should show similar strength of correlation with GC content of noncoding and coding regions, which is what we observe (table 2). This implies that the effect of translational or transcriptional selection on synonymous codon usage is very weak and it is primarily driven by background nucleotide content.

GC Bias of Genes and Gene Expression

Average GC content of the P. patens genome is 38% which is on the lower end of values reported so far for land plants (Kejnovsky et al. 2012; Singh et al. 2016). Nevertheless, coding regions have a significantly higher GC content (∼48%) which is close to the average detected in land plants overall (Singh et al. 2016). Furthermore, GC content in coding regions varies considerably across the genome and is significantly higher than in intronic and intergenic regions (∼40%). GC content of coding and noncoding regions is highly interdependent. More specifically, GC content of CDS is significantly positively correlated with both GC content of introns and UTRs (r_{s GC_CDS_vs._GC_intron}=0.4676, P< 2.2 × 10⁻¹⁶; r_{s  GC3_CDS_vs._GC_intron}=0.5360, P< 2.2 × 10⁻¹⁶; r_{s GC_CDS_vs._GC_UTR}=0.2880, P< 2.2 × 10⁻¹⁶; r_{s GC3_CDS_vs._GC_UTR}=0.1960, P< 2.2 × 10⁻¹⁶) suggesting that mutational biases and/or transcription-coupled mutations have a significant effect on synonymous codon usage.

We showed that optimal codons in P. patens almost all end with G or C (table 1) (Szövényi et al. 2015) and it is known that GC content of genes and coding regions is frequently correlated with gene expression (Kudla et al. 2006). Therefore, we hypothesize that gene expression may drive GC content, which, in turn, drives the correlation between optimal codon frequency and gene expression independently of transcriptional/translational selection. Therefore, we calculated how GC content is correlated with codon usage of genes while controlling for the effect of the other confounding factors including gene and intron length on the chromosome in base pairs, and gene expression breadth. Therefore, rank correlations refer to pairwise partial rank correlations while controlling for the set of covariates mentioned. We found that overall GC content of CDS was weakly positively correlated with gene expression (r_{s  RNA-seq}=0.0610, P = 7.2081 × 10⁻⁰⁶; r_{s  microarray}=0.0578, P = 2.1928 × 10⁻⁰⁵). Moreover, GC content in third codon positions that are less selectively constrained and strongly influenced by mutational biases was strongly positively correlated with gene expression regardless of the data set used (r_{s RNA-seq}=0.2136, P = 5.0052 × 10⁻⁵⁸; r_{s  microarray}=0.1900, P = 8.0731 × 10⁻⁴⁶). Finally, GC content in intronic regions was also weakly positively correlated with gene expression (r_{s RNA-seq}=0.0759, P = 2.2509 × 10⁻⁸; r_{s  microarray}=0.0442, P = 0.0012). That is, GC bias of third codon positions is indeed increased by gene expression, which is also true for GC content of noncoding regions but with a lesser extent. We also note that our conclusions remain qualitatively the same when potential covariates are not accounted for in the correlations analysis. This suggests that GC content is primarily driven by the level of gene expression and this is true for both coding and surrounding noncoding regions.

Codon Usage and Synonymous and Nonsynonymous Divergence

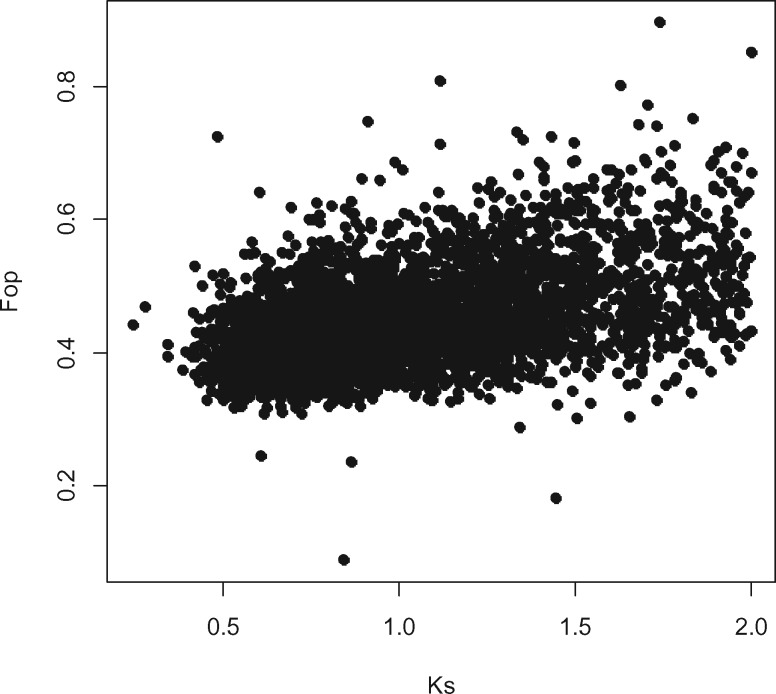
If codon usage bias is driven by natural selection, we expect that increased selection against unpreferred codons will decrease silent divergence (K_s) of genes from a closely related species (Akashi 2001). Nevertheless, as selection for synonymous codon usage is weak, this correlation is also expected to be weak (Powell and Moriyama 1997; Bierne and Eyre-Walker 2003; Marais et al. 2004b). We used divergence data from the moss C. purpureus and calculated the partial correlation between synonymous divergence (K_s) and codon usage bias statistics at two K_s divergence thresholds (K_s ≤2 and ≤1). We found 5,397 strictly one-to-one orthologous gene pairs between P. patens and C. purpureus, of which 4,485 and 3,190 gene pairs showed a K_s divergence value of ≤2 and ≤1, respectively. For all three codon usage bias statistics and for both K_s thresholds (K_s ≤2 and ≤1) we found that genes with greater codon usage bias showed greater silent divergence (fig. 3, table 2). These observations contradict the hypothesis that codon usage would be driven by selection in P. patens. We also tested whether this relationship is mainly explained by GC content of the CDS or that of GC content of third codon positions. Not controlling for GC content of third codon positions in the partial correlation analysis considerably increased the value of Spearman’s rho, especially at the K_s ≤2 threshold (GC content of third codon positions is not controlled for: K_s ≤2, F_op vs. K_sr_s=0.2851, P = 8.0714 × 10⁻⁹⁶; K_s ≤1, F_op vs. K_sr_s=0.1692, P = 3.5518 × 10⁻²²) while excluding GC content of exons had a slighter effect (dropping GC content exons: K_s ≤2 F_op vs. K_sr_s=0.1093, P = 1.6185 × 10⁻¹⁴; K_s ≤1: F_op vs. K_sr_s=0.0740, P = 2.8507 × 10⁻⁰⁵). Therefore, the positive correlation of K_s and codon usage bias can be at least partially explained by the GC content at third codon positions.

Fig. 3.

—Correlation between the frequency of optimal codons (F_op) and the number of synonymous substitutions per synonymous sites (K_s, calculated in comparison with the orthologous C. purpureus proteins).

The ratio of the number of nonsynonymous substitutions per nonsynonymous sites to the number of synonymous substitutions per synonymous sites (K_a/K_s) can be used as an indicator of the strength of purifying selection acting on a gene (Nielsen and Yang 2003). Therefore, we also assessed the correlation between K_a/K_s values and codon usage bias while controlling for all other confounding genomic variables at two K_s thresholds as above (K_s ≤1 and ≤2). We found that genes under more relaxed selective constraints (greater K_a/K_s) have slightly lower codon usage bias when using the F_op and ENC statistics (table 2). Nevertheless, correlation strengths were weak or very weak, especially when applying the more reliable K_s ≤1 threshold, at which the effect of alignment ambiguity and saturation issues are minimal. Moreover, when we used the ENC′ statistic, the correlation became even weaker especially at the K_s ≤1 threshold (table 2). We repeated the very same analysis for the number of nonsynonymous substitutions per nonsynonymous sites (K_a) which essentially led to the same conclusions.

Codon Usage Bias and Gene Expression Breadth

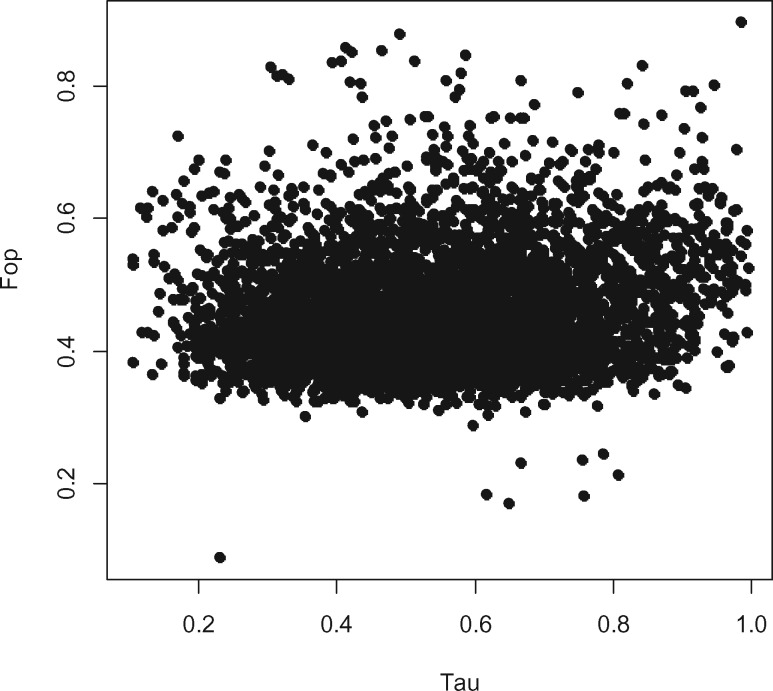
Gene expression breadth is known to be highly influential concerning the rate of purifying selection that acts also on synonymous codon usage (Duret and Mouchiroud 2000; Urrutia and Hurst 2001; Ingvarsson 2007, 2008; Szövényi et al. 2013; De La Torre et al. 2015). In line with that, multiple studies revealed greater synonymous codon usage bias in more broadly expressed genes in both plants and animals (Urrutia and Hurst 2001; Ganko et al. 2007; Ingvarsson 2007; De La Torre et al. 2015). We found that F_op and ENC were not significantly correlated with expression breadth (τ), whereas ENC′ showed a weak negative correlation with expression breadth in a partial correlation analysis (fig. 4, table 2). This result implies that tissue specificity either does not affect codon usage bias or increasing tissue specificity is associated with increasing codon usage bias. This is in contrast to the general observation that more broadly expressed genes show greater codon usage bias because they are under greater selective constraints.

Fig. 4.

—Correlation between gene expression breadth (Tau [τ]) and the frequency of optimal codons (F_op).

Model-Based Analysis Suggests Low Efficacy of Natural Selection on Codon Usage Bias

To assess the united effect of mutational bias and natural selection on synonymous codon usage, we fitted the Bayesian model ROC SEMPPR (Gilchrist et al. 2015) using codon composition of the P. patens proteome and our RNA-seq gene expression data set. This model assumes that codon usage of a gene is a combined function of mutation bias and natural selection for translational inefficiency of which the latter is expected to scale with protein production and effective population size. If N_e is sufficiently large, then this model is able to accurately predict protein production rates using only codon composition of genes. Moreover, adding experimental data on protein production rate estimates to the model should have negligible effect on protein production rate estimates. In line with our correlation-based analyses, we found that protein production rate estimates solely based on codon composition of the proteome poorly fitted the estimates obtained with a model including observed gene expression values (linear regression of estimated protein production rates obtained with a model including vs. excluding observed gene expression estimates: R²=0.7231, y= 0.0642 − 0.5031x). Furthermore, this regression line significantly deviated from the expected 1:1 relationship (z-test of difference from a slope of 1; P = 0.000002) with more than three-quarters of the observed data falling outside of the 95% confidence interval of the one-to-one line. That is, codon usage of genes itself does not contain sufficient information to predict protein production rates.

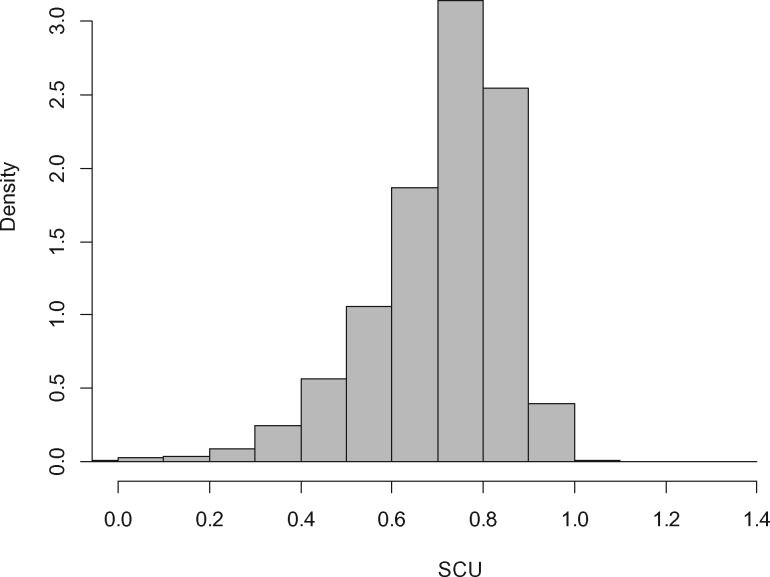
We also obtained model-based estimates of codon-specific translational inefficiencies (Δη), mutation bias (ΔM), and the per gene selection intensity on codon usage (SCU). When SCU ≤ 1, drift will dominate over natural selection. In line with the predicted low N_e, we found that the difference in translational inefficiency between the reference (optimal) and alternative synonymous codons was small ranging between 0.00047 and 0.016 with an average value of 0.00656. Nevertheless, the 95% confidence intervals did not overlap with zero suggesting the presence of weak selection (supplementary table 2, Supplementary Material online). We also found that all per gene SCU estimates (SCU_mean=0.7072, SD = 0.1507), but one, were below one that is codon usage bias is primarily driven by genetic drift (fig. 5). In contrast, codon-specific mutation bias estimates, the natural logarithm of the ratio of synonymous codon frequencies in the absence of selection, were considerable ranging between −0.4646 and 1.1165 with an absolute average of 0.2624 (supplementary table 3, Supplementary Material online).

Fig. 5.

—Histogram of SCU estimates (per gene selection intensity on codon usage).

Discussion

Here, we analyzed synonymous codon usage bias of genes in the model moss P. patens with a life cycle and breeding system implying low local and species-wide effective population sizes (Perroud et al. 2011). In line with predictions from population genetic theory, we found that the effect of natural selection on synonymous codon usage bias is weak. Our results well-fit the repeated pattern found in organisms with AT-rich genomes experiencing putatively weak selection on the genome, GC content and GC-ending codons overall (Hershberg and Petrov 2009, 2010; Lassalle et al. 2015; Rudolph et al. 2016). Therefore, we propose that synonymous codon usage is mainly driven by nucleotide compositional biases. Our finding is in contrast to a previous study reporting adaptive codon usage bias in the moss P. patens (Stenøien 2005). Our conclusion is supported by four lines of evidence that we further discuss below: 1) Very weak or nonsignificant correlation between gene expression and codon usage bias, 2) no or weak increase of codon usage bias in more broadly expressed genes, 3) no evidence that codon usage bias would constrain synonymous and nonsynonymous divergence, and 4) predominant role of genetic drift on synonymous codon usage predicted by a model-based analysis.

Weak and/or Nonsignificant Correlation between Codon Bias and Gene Expression

If codon usage bias is driven by translational or transcriptional selection, optimal codons are expected to be preferentially used in highly expressed genes (Akashi and Eyre-Walker 1998; Akashi 2001; Akashi et al. 2012). Nevertheless, a positive correlation can also arise when mutational biases are nonrandom and correlated with expression level of genes (Hershberg and Petrov 2009). Although we found a positive correlation between codon usage bias and gene expression level, this relationship was very weak (table 2). This implies that selection for optimal codon usage is at most weak and is primarily driven by nucleotide compositional biases.

Our result is in contrast to a previous study reporting a significant and substantial correlation between gene expression and codon usage bias for P. patens (Stenøien 2005). However, the former study used only a small set of the P. patens proteome, EST library-based gene expression estimates and codon bias indices (F_op and ENC) that do not account for background nucleotide biases. Furthermore, our analysis used a partial correlation approach that accounts for the effect of other genomic variables potentially affecting codon usage bias. Therefore, we argue that contrasting results obtained by our analyses and those of the mentioned study are primarily of methodological origin.

Our results are also in line with population genetic theory predicting that effective population size is key in determining whether codon usage bias is driven by natural selection or genetic drift (Ikemura 1985; Akashi 1996; Ingvarsson 2007; Stoletzki and Eyre-Walker 2007; Hershberg and Petrov 2008; Sharp et al. 2010; Burgarella et al. 2015). In particular, transition from an outcrossing to a selfing breeding system resulting in an overall effective population size reduction was shown to decrease the efficacy of selection acting on codon usage bias in plants and in animals (Sweigart and Willis 2003; Cutter et al. 2006; Foxe et al. 2008; Cao et al. 2011; Qiu, Zeng, et al. 2011; Ness et al. 2012; Slotte et al. 2013). This effect is expected to be especially strong if selfing is frequent and enough time has elapsed since the onset of selfing behavior to significantly affect codon usage (Morton and Wright 2007; Cutter et al. 2008).

Physcomitrella patens is frequently undergoing intragametophytic selfing which, in contrast to selfing in vascular plants, will lead to a fully homozygous diploid phase and should dramatically decrease effective population size (Perroud et al. 2011). Moreover, phylogenetic evidence strongly supports long-lasting persistence of the monoicous breeding system of P. patens. Breeding system of P. patens is shared by all species of the family Funariaceae estimated to have originated more than 100 Ma (Liu et al. 2012). Therefore, our data are in accordance with theory by showing that codon usage in P. patens is primarily driven by genetic drift and the effect of natural selection is weak at most.

K_s Is Not Negatively but Positively Correlated with Codon Bias

It is expected that, if synonymous codon usage is driven by natural selection, then genes with more biased codons should show reduced synonymous divergence from the corresponding gene sequences of a closely related species (Sharp and Li 1987; Akashi 2001; Drummond and Wilke 2008). This is because most synonymous mutations will change preferred codons to unpreferred codons, which, in turn, will decrease the number of synonymous mutations per synonymous sites that go to fixation. This effect, however, may be weak, especially if selection on codon usage bias is weak, as it is in species with reduced effective population sizes (Powell and Moriyama 1997; Bierne and Eyre-Walker 2003; Marais, Domazet-Lošo, et al. 2004).We found that increasing codon usage bias was positively and not negatively associated with the number of fixed synonymous changes. This is the opposite of what one would expect if selection would preserve preferred synonymous codons, which will in turn decrease the number of substitutions at synonymous sites. Nevertheless, we also showed that this effect can be well alleviated by correcting for biased nucleotide composition as well as for GC content. Therefore, GC content in third codon positions is at least partially responsible for the positive correlation and increased silent divergence.

One potential explanation for the positive correlation between K_s and codon usage bias is that preferred synonymous codons differ between the two species investigated (P. patens and C. purpureus). Nevertheless, this contradicts findings of a previous study describing the very same set of preferred codons in the two species (Szövényi et al. 2015). A potentially more likely explanation is that codon bias is primarily driven by mutational biases in P. patens whereas natural selection dominates in the outcrosser C. purpureus. This would be expected to drive synonymous codon usage of the two species apart and would lead to an increased number of synonymous substitutions, especially if mutational biases depend differently on genomic features/context in the two species. Finally, it is also possible that the positive correlation between synonymous divergence and codon usage is a result of a combination of strong mutational bias and weak purifying selection (Lawrie et al. 2011, 2013; Lawrie and Petrov 2014). Under such circumstances even increasing constraint can lead to accelerated evolutionary rates. This is a conceivable explanation because mutations are thought to be A/T-biased across all eukaryotes (Galtier et al. 2001; Smith and Eyre-Walker 2001; Hershberg and Petrov 2010) and our analysis suggests that purifying selection on codon usage bias is weak. Our data are insufficient to distinguish among these three alternative hypotheses but they all support the conclusion that natural selection on codon usage bias is rather weak in P. patens. We note that with more data on gene expression and genomic features in the moss C. purpureus the three alternative hypotheses will become testable.

Although the K_s–codon usage correlation analysis has been extensively used as a decisive test of the effect of natural selection on codon usage bias in many studies, it is not free of caveats (Ingvarsson 2007, 2008; Slotte et al. 2011; Hough et al. 2013; De La Torre et al. 2015). First of all, as all K_s-based tests it is designed to be used between relatively closely related species pairs. Unfortunately, high-quality sequence data are only available for C. purpureus which are estimated to have shared a common ancestor with P. patens about 200 Ma (Szövényi et al. 2015). We intended to correct for the deep divergence of the two species by limiting our analysis to less divergent orthologous gene pairs to avoid issues related to saturation of substitutions and alignment uncertainty. Nevertheless, we acknowledge that the deep divergence between the two species adds some uncertainty to our analysis which we could not easily resolve. For instance, our data are insufficient to decide whether efficacy of selection on codon usage bias was constantly low along the branch leading to P. patens or it was actually strong on the terminal branch leading to P. patens but this signal may have been diluted over the long evolutionary branch connecting the two species. Although we cannot unambiguously exclude this latter explanation we believe that it is unlikely because besides the K_s-based analysis our other tests are independent of any divergence statistics and support the conclusion that the effect of natural selection on codon usage bias is weak in P. patens.

Finally, assessing the correlation between K_a/K_s and codon usage bias led to similar conclusions, showing either a very weak correlation or no correlation at all (table 2). Altogether, these observations provide another line of evidence that in P. patens, characterized by a dramatically reduced effective population size, the efficacy of natural selection on codon usage bias is weak.

Gene Expression Breadth and Codon Usage Bias

Another important finding contradicting the hypothesis that codon usage bias is primarily driven by translational/transcriptional selection in P. patens is the sign of correlation between gene expression breadth and codon usage bias. Gene expression breadth was shown to be one of the main factors constraining molecular evolutionary rates of genes in a moss and in the model plant Arabidopsis thaliana (Slotte et al. 2011; Yang and Gaut 2011; Szövényi et al. 2013). That is, more broadly expressed genes have lower dN/dS values due to more efficient purifying selection. Therefore, expression breadth of genes can be used as a proxy for the strength of purifying selection (Urrutia and Hurst 2001). If codon usage bias is driven by translational or transcriptional selection, more broadly expressed genes should be under greater selective constraints and should exhibit greater codon usage bias. Our observation contradicts this hypothesis, as more broadly expressed genes have slightly less biased codon usage when nucleotide compositional biases are accounted for or the correlation is not significant at all. This suggests that the efficacy of natural selection on codon usage bias is weak.

Model-Based Estimates Also Suggest That Efficacy of Selection on Synonymous Codon Usage Is Weak

Correlation- and divergence-based tests assessing the effect of natural selection on synonymous codon usage may fail when mutation bias is strong and purifying selection is weak (Lawrie et al. 2011, 2013). Therefore, we also used a model-based analysis that is able to model the united effect of mutation bias, natural selection, and their often nonlinear dependence on gene expression level on synonymous codon usage (Gilchrist 2007; Gilchrist et al. 2015). Results of this analysis provide further support to the observation that the effect of natural selection on synonymous codon usage is rather weak in P. patens.

In particular, the model predicts that when N_e is sufficiently large, protein production rates can be accurately estimated using codon composition of genes. If this is true, adding experimental data on protein production rates to the model should have negligible effect on protein product rate estimates. We found that a model solely based on codon usage pattern of the proteome very poorly fit the estimates obtained with a model including experimental estimates of protein production. Previous studies showed that the model can accurately predict protein production rates in simulated and real data in which selection for optimal codons is considerable (Gilchrist 2007; Wallace et al. 2013; Gilchrist et al. 2015). Therefore, in accordance with the correlation-based analysis, this implies that synonymous codon usage of P. patens genes provides only limited information on protein production rates. This is in line with our hypothesis that P. patens has low overall N_e and selection for optimal codon usage is weak.

We also obtained model-based estimates for the two major parameters of the model, codon-specific translational inefficiencies (Δη) and mutation bias (ΔM) and the a composite parameter quantifying the per gene selection intensity on codon usage (SCU) (Gilchrist 2007; Wallace et al. 2013; Gilchrist et al. 2015). In brief, codon-specific translational inefficiency (η) is a parameter describing how codon usage of a given open reading frame alters the ratio of the expected cost of protein production over the expected benefit of protein synthesis (Gilchrist et al. 2015). It is assumed that natural selection favors codon usage that reduces this cost–benefit ratio and selection increases with protein production rates. More specifically, translational inefficiency (Δη) is the difference two codons make to η relative to the effect of genetic drift. Our analysis provided very small estimates for the translational inefficiency parameters implying that codon usage data predict only slight selective differences among alternative synonymous codons. Indeed, our estimates were more than ten times smaller than those obtained for yeast showing considerable selection for optimal codon usage (Gilchrist 2007; Wallace et al. 2013; Gilchrist et al. 2015).

To verify this observation, we also estimated a composite parameter describing the per gene selection intensity on codon usage (SCU). SCU is the mean fitness advantage scaled by the effective population size, that the organism gains from the gene’s codon composition relative to an unselected synonymous alternative (Wallace et al. 2013). When SCU ≤ 1, drift will dominate over natural selection. We found that all but one SCU estimates fell below 1. This is strikingly different from the observation made in yeast where most of the genes had SCU values over 1 (Gilchrist 2007; Wallace et al. 2013; Gilchrist et al. 2015). Because selection for optimal codon usage is considerable in yeast our finding on SCU implies that optimal codon usage is mainly driven by genetic drift rather than by natural selection.

Finally, we also obtained estimates for the mutational bias parameter (ΔM). The mutation bias parameter is the natural logarithm of the ratio of the frequencies of the reference codon to codon i in the absence of natural selection (Gilchrist et al. 2015). We found that our estimates were comparable to those found in previous studies in yeast (Gilchrist 2007; Wallace et al. 2013; Gilchrist et al. 2015). Therefore, the absolute strength of mutation bias does not seem to be strikingly different in the moss and in yeast but the overall efficacy of selection on codon usage is considerably weaker in the moss. Altogether, correlation-, divergence-, and model-based analyses all converge to the very same conclusion that natural selection is only a weak force shaping synonymous codon usage bias in P. patens.

Potential Driving Forces of Nucleotide Compositional Biases

Altogether, our observations suggest that codon usage bias of P. patens is primarily driven by nonselective forces that may be mutational bias and drift. This observation is in line with the life cycle characteristics of the species, implying highly reduced effective local and species-wide population sizes (Quatrano et al. 2007; Perroud et al. 2011; McDaniel and Perroud 2012). Moreover, our analysis also suggests that synonymous codon usage can be primarily explained by nucleotide biases, especially by variation in GC content across CDS. Nevertheless, the exact factors responsible for the compositional biases are unknown. In the next paragraphs, we provide some speculation about the potential molecular mechanisms that may be driving codon usage bias in P. patens.

The exact mechanism through which GC content of coding regions evolves is debated and used to be explained by three main processes: Mutational biases, synonymous codon usage bias, and GC-biased gene conversion (Glémin et al. 2014). Studies often prefer the latest as the most likely explanation (Glémin et al. 2014). Nevertheless, the effect of biased gene conversion in an intragametophytic selfer should be negligible (Burgarella et al. 2015). Furthermore, although nonallelic gene conversion may occur in P. patens, it is probably not GC-biased and unlikely to explain our findings (Assis and Kondrashov 2012). Therefore, we argue that weak selection for optimal codon usage bias and overall GC content may be more likely to explain GC variation of CDS in P. patens. This hypothesis is supported by the observation that GC content of coding and surrounding noncoding regions is positively correlated and they are all positively correlated with level of gene expression. This implies that GC content of genomic regions is considerably influenced by regional mutational biases which are positively correlated with expression of genes and codon usage bias. Nevertheless, the exact mechanisms through which gene expression or some other unknown genomic features that correlate with gene expression affect GC content of the genome or vice versa are currently unknown.

Finally, our findings are also strikingly similar to those observed in a wide-range of organisms with AT-rich genomes. There is indication that selection on optimal codon usage and GC content is overall weaker in AT-rich genomes (Hershberg and Petrov 2009, 2010; Lassalle et al. 2015; Rudolph et al. 2016). The observations from AT-rich genomes are in line with our findings: 1) A clear mismatch between optimal codons identified by the ENC and ENC′ statistics, 2) weak correlation between gene expression and codon usage bias, and 3) discordance between optimal codons and codons used in the set of highly expressed genes. Furthermore, we showed that noncoding parts of the P. patens genome are especially AT-rich among land plants (Kejnovsky et al. 2012; Singh et al. 2016). Therefore, our findings on the P. patens genome add additional support to the observation that overall selection for optimal codon usage and GC content is generally weak in AT-rich genomes.

Coadaptation of tRNA Gene Copy Numbers and Codon Usage Bias

The above-mentioned findings clearly support the idea that codon usage bias in the moss P. patens is driven by a combination of mutational biases and weak natural selection of which the former seem to be predominant. Nevertheless, we also report that tRNA gene numbers and their cognate codons seem to be significantly coadapted. That is, synonymous codons frequently used in highly expressed genes have also the most biased tRNA gene copy numbers. One possible interpretation of this pattern is that tRNA copy number is driving synonymous codon usage, which is an indication of translational selection. Nevertheless, it is also possible that codon usage bias is primarily driven by neutral forces, and this in turn drives the evolution of tRNA copy numbers. This latter hypothesis has been proposed earlier and was recently confirmed by experimental evidences (Hershberg and Petrov 2008, 2009; Trotta 2013). For instance, Yona et al. (2013) showed that adaptation to a perturbed tRNA pool can rapidly occur. Therefore, we argue that the tRNA abundance-codon usage correlation discovered here is the result of the adaptation of tRNA gene copy numbers to the optimal set of synonymous codons of which the latter is primarily driven by nucleotide compositional biases (Whittle et al. 2012). We note that this explanation does assume that the adaptation between tRNA copy numbers and synonymous codons is a result of natural selection. Nevertheless, it hypothesizes that the strength of natural selection exerted by each gene on tRNA copy numbers is very weak but it becomes sufficiently strong when it scales up to the level of the genome.

Conclusions

Altogether, our analyses suggest that codon usage bias in the moss P. patens is primarily driven by neutral processes, potentially by nucleotide biases, and the effect of natural selection is weak, albeit detectable. This is in line with evolutionary theory predicting strongly reduced effective population size and weak efficacy of natural selection in organisms frequently undergoing haploid (intragametophytic) selfing. Nevertheless, our data are insufficient to determine the key molecular processes driving biased nucleotide usage across the genome. Therefore, to gain detailed insights into the molecular mechanisms driving codon usage bias in P. patens, the relationship between nucleotide bias, codon usage bias, recombination rate, and genome-wide methylation should be determined. With data on these genomic features in P. patens, such analyses will be feasible in the future.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.