Short-range surface plasmonics: Localized electron emission dynamics from a 60-nm spot on an atomically flat single-crystalline gold surface

We demonstrate nanofocusing down to 60 nm with 800-nm light in atomically flat single-crystalline 22-nm-thick gold flakes.

Abstract

We experimentally and theoretically visualize the propagation of short-range surface plasmon polaritons using atomically flat single-crystalline gold platelets on silicon substrates. We study their excitation and subfemtosecond dynamics via normal-incidence two-photon photoemission electron microscopy. By milling a plasmonic disk and grating structure into a single-crystalline gold platelet, we observe nanofocusing of the short-range surface plasmon polariton. Localized two-photon ultrafast electron emission from a spot with a smallest dimension of 60 nm is observed. Our novel approach opens the door toward reproducible plasmonic nanofocusing devices, which do not degrade upon high light intensity or heating due to the atomically flat surface without any tips, protrusions, or holes. Our nanofoci could also be used as local emitters for ultrafast electron bunches in time-resolved electron microscopes.

INTRODUCTION

Short-range surface plasmon polaritons (SR-SPPs) have received less attention compared to long-range SPPs (LR-SPPs) (1–12) because they usually exhibit high damping losses, resulting in short propagation lengths. In metals, only a few attempts have been undertaken to explore the potential of short-range surface plasmons for imaging (13). Metal-insulator-metal waveguides have been used, where the plasmon wavelength was as short as 51 nm for a 650-nm light (14). One should mention that recent efforts in graphene or other layered materials, such as hexagonal boron nitride (h-BN), also yield extreme wavelength reduction using surface plasmons yet usually for infrared wavelengths (15–18).

Moreover, there are several approaches to focusing propagating surface plasmons (19–25). Short-range surface plasmon focusing on a silver–silicon nitride interface was introduced recently (26, 27), where near-field microscopy was used to resolve a minimum focal spot of 66 nm in a circular focusing device at λ = 633 nm. However, one has to distinguish such efforts in focusing propagating surface plasmons from other approaches, where light is squeezed into nanovolumes assisted by plasmonic structures (28), transmitted through a subwavelength hole (29), or focused beyond a super oscillatory plasmonic lens to perform high resolution imaging (30) because plasmon focusing allows for light localization on a perfectly flat and hence reproducible surface, without the dependence on holes, tops, or protrusions, which are susceptible to their exact shape or to potential damage.

SPP excitation and propagation take place at metal-dielectric interfaces (31–33). If a thin metal film is sandwiched between two different dielectric media at the top and at the bottom of the film, then there will be two plasmonic modes forming at the two interfaces. If the metal film becomes sufficiently thin, on the order of a few tens of nanometers, then the two plasmonic modes can hybridize and must be treated as coupled oscillators, where the long- and the short-range plasmon become the eigenmodes of the coupled system (34–37). Even for thicker films, the plasmonic modes at the upper and lower interface of the metal film will differ in phase and group velocity, and they will exhibit different decay lengths. Their properties will be determined by the complex refractive indices of the materials surrounding the metal film. An adjacent material with a high refractive index drastically reduces the wavelength of excited SPPs. Here, we aim at the excitation, dynamics, and nanofocusing of SPPs, implementing such a highly reduced wavelength system.

RESULTS AND DISCUSSION

We calculate the dispersion relation of LR-SPPs and SR-SPPs of a 20-nm-thick layer of gold, with optical properties discussed by Johnson and Christy (38), on a silicon substrate, which is covered with a 2.5-nm-thick layer of native SiO₂. We use analytical equations for complex propagation constants along the interfaces. The blue line in Fig. 1A represents the dispersion relation of LR-SPPs, whereas the red curve depicts the dispersion relation of SR-SPPs. We indicate the 800-nm excitation wavelength as a horizontal dashed black line. From its intersection points with the dispersion relation curves, we calculate LR-SPP and SR-SPP wavelengths as λ_LR-SPP = 787 nm and λ_SR-SPP = 176 nm, respectively. Furthermore, we calculate propagation length and phase velocity of SR-SPPs, which are 1.18 μm and 0.221c, respectively.

Fig. 1. Concept of SR-SPP imaging in 2PPE PEEM.

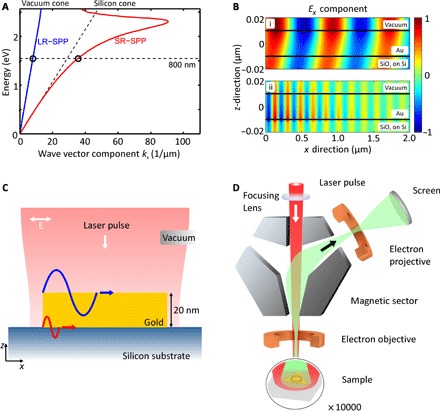
(A) Illustration of the SPP dispersion relations at gold-vacuum and gold-silicon interfaces. The dispersion relations are calculated from a 20-nm-thick gold film [with optical properties discussed by Johnson and Christy (38)] on a silicon substrate with a native SiO₂ layer. λ₀ = 800 nm (dashed black line) is the excitation wavelength for LR-SPPs (blue line) and SR-SPPs (red curve). Image (B) represents cross sections through the sample, together with the x component of the SPP electric field. In (i), LR-SPPs are illustrated, which are predominantly located at the gold-vacuum interface. In (ii), SR-SPPs are described, which mainly exist at the gold-silicon interface. They can extend to the gold-vacuum interface in the z direction if the gold thickness is small enough. (C) Illustration of the experimental concept: Single-crystalline gold platelets are deposited on silicon substrates. This allows SPP excitation at the material interfaces due to normal incident ultrashort laser pulses (<15 fs) of 800-nm wavelength with linear transversal magnetic (TM) polarization. LR-SPPs are indicated at the gold-vacuum interface (blue), and SR-SPPs are indicated at the gold-silicon interface (red). (D) SPP excitation and imaging are realized using two-photon photoemission microscopy at normal incidence. After SPP excitation, electrons are emitted from the sample and imaged with a nanometer resolution using electron optics. As recently demonstrated (41), the E_x component of the surface plasmon field along the incident polarization is responsible for the electron emission.

SPP waves are longitudinal waves and thus feature x components of an electric field, which can be imaged by electrons emitted from the surface that are detected in a two-photon photoemission electron microscopy (2PPE PEEM) experiment (39–41). In Fig. 1B, we show cross sections of our sample geometry overlaid with the E_x-field distribution colored in red for field maxima and in blue for field minima. The long-range plasmon in Fig. 1B (i) is mainly located at the gold-vacuum interface and propagates several tens of micrometers; however, the short-range plasmon in Fig. 1B (ii) predominantly exists at the gold-silicon interface and decays after roughly 1.2 μm of propagation in x direction when excited at x = 0.

The SR-SPP field decays exponentially in z direction away from the silicon surface toward the gold-vacuum interface. Hence, only very thin gold flakes on the order of 20 to 40 nm allow for large enough short-range plasmon fields at the gold-vacuum interface, to yield electron emission of these kinds of plasmons.

Figure 1C illustrates our experimental concept. Single-crystalline gold platelets, electrochemically grown with lateral sizes between 5 and 10 μm, are dispersed onto a silicon substrate, which is covered with a native oxide layer (SiO₂). The thickness of the oxide layer was determined to be 2.5 nm by ellipsometry. Because the gold-platelets have sharp and defined edges, they can provide the necessary momentum vector to excite femtosecond SPP pulses at the top and at the bottom of the gold platelet. After excitation, the SPP pulses propagate across the atomically flat surface, as indicated in Fig. 1C. LR-SPPs (indicated in blue) are predominantly localized at the gold-vacuum interface and, due to their only weakly bent dispersion, exhibit a slightly shorter wavelength than the exciting laser pulses. However, at the gold-SiO₂/Si interface, SR-SPPs (depicted in red) are excited. These are expected to exhibit a significantly shorter wavelength, due to the high refractive index of silicon and the resulting strongly bent dispersion.

Imaging of the SPPs was performed using a time-resolved 2PPE PEEM setup (42, 43). The recently established normal-incidence configuration (39) allows direct imaging of the excited SPPs in a direct conceptual visualization. Figure 1D illustrates the basics of the measurement principle. Linearly polarized <15-fs laser pulses of a central wavelength of 800 nm from a Ti:sapphire oscillator with a repetition rate of 80 MHz impinge onto one of the single-crystalline gold platelets. The work function of the Au has been sufficiently lowered by Cs deposition to enable emission of electrons via a two-photon process. Emitted electrons are collected by an electron objective, deflected in a magnetic prism, and focused to obtain an emission image with an electron-optical resolution of 11 nm. Details of the electron optics are discussed in the work of Schmidt et al. (44). This experimental setup can either be operated at a zero time delay (2PPE PEEM) or allow for time-resolved pump-probe measurements to study SPP dynamics (TR-PEEM). In the latter case, ultrashort laser pulses impinge on the sample along the surface normal and excite the SPPs. Time-delayed probe laser pulses interfere with the initially excited SPPs and provide sufficient energy to eject a conduction electron from the gold platelet into the vacuum via a two-photon emission pathway (40, 45).

Figure 2 depicts some of the PEEM results using single-crystalline gold platelets of different thickness. First, in Fig. 2A, a 120-nm-thick hexagonal platelet is used, where the wave pattern of LR-SPPs at the gold-vacuum interface is visible, following the polarization direction of the incident electric field vector (indicated as arrow). The PEEM image in Fig. 2B arises from a 37-nm-thick gold platelet where both LR-SPPs and SR-SPPs are visible. LR-SPPs propagate across the entire platelet surface. SR-SPPs with their much shorter plasmon wavelength are excited at the platelet edges and already decay after a few wavelengths of propagation.

Fig. 2. Normal-incidence 2PPE PEEM results.

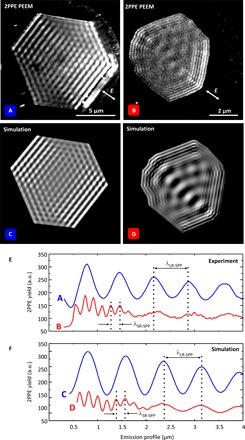
(A) Long-range plasmon wave pattern, excited with zero time delay pulses on a 120-nm-thick hexagonal platelet. (B) The platelet is 37 nm high and permits long- and short-range surface plasmon excitation simultaneously. (B) Snapshot at t₀ + 4.52 fs time delay, taken from a time-dependent series. (C and D) The PEEM results are modeled, taking all specifications from images (A) and (B) into account. (E) Emission profiles from platelets (A) and (B). From profile (A), the LR-SPP wavelength is determined as λ_LR-SPP = 785 nm. Profile (B) illustrates the superposition of LR-SPPs and SR-SPPs, where the SR-SPP wavelength is determined as λ_SR-SPP = 185 nm. (F) The emission profiles derived from the theoretical PEEM images.

In Fig. 2 (C and D), images of electron yield in the experiment were calculated from the combined electric field of the incident light pulses and the surface plasmons at the gold surface. The surface plasmons are initiated at the boundaries of the gold film and propagate inward. In the simulation, the boundary was approximated by a polygon of straight line segments, with each point on a segment being a source of circular Huygens plasmons. In effect, a beam of surface plasmon waves from each line segment was added to the total electric field over the surface of the film. The sum of the fields leads to interference effects. The plasmon electric field E_p was taken from the known plane-wave solutions for thin films on dielectrics, including the propagation losses (46)

$${\mathit{E}}_{\mathit{p}}(\mathit{r},\mathit{t})={\mathit{E}}_{\mathit{p}}\left(\frac{\mathit{i}\mathrm{\gamma }\widehat{\mathit{n}}-\mathrm{\alpha }\widehat{\mathit{z}}}{\mathit{k}}\right)\mathit{G}(\mathit{r},\mathit{t}-{\mathit{t}}_{\mathit{a}}){\mathit{e}}^{\mathit{i}(\mathrm{\alpha }\widehat{\mathit{n}}\cdot \mathrm{r}-\mathrm{\omega }(\mathit{t}-{\mathit{t}}_{\mathit{a}}))}$$

where $\widehat{\mathit{n}}$ is a vector in the plane of the gold film perpendicular to the boundary segment, and $\widehat{\mathit{z}}$ is normal to the film surface. The plasmon wave number is α, and γ² = α² − ϵ_mk² with ϵ_m for the relative complex permittivity of the metal near the surface. $\mathit{k}=\frac{\mathrm{\omega }}{\mathit{c}}$ is the free-space wave number, ω is the frequency of light, and c is the speed of light in vacuum. The plasmon amplitude is multiplied by a propagating Gaussian envelope G(r, t − t_a), centered at time t_a, to take account of the pulsed nature of the incident light.

Following the simplest possible yield model for field-enhanced 2PPE, the rate of emission of electrons from the surface via coherent two-photon absorption is proportional to ${\mathit{I}}^2(\mathit{r},\mathit{t})={|{\mathit{E}}_{\mathit{T}}^{*}(\mathit{r},\mathit{t})\cdot {\mathit{E}}_{\mathit{T}}(\mathit{r},\mathit{t})|}^2$, where E_T(r, t) is the sum of all the electric fields from the incident light and the surface plasmons. The simulated images represent the numerically evaluated time integration ${\displaystyle {\int }_{-\infty }^{\infty }}{\mathit{I}}^2(\mathrm{\tau },\mathit{r},\mathit{t})\mathit{d}\mathit{t}$ for a given delay time τ between the pump and the probe pulses.

To quantitatively analyze the two SPP signatures, we plot emission profile cross sections from Fig. 2A in blue and Fig. 2B in red directly on top of each other and display them in Fig. 2E. From the blue profile, we determine the wavelength of LR-SPPs (λ_LR-SPP) by measuring the distance between the maxima, which is 785 nm. As expected, this is slightly shorter than the excitation wavelength of 800 nm. The red emission profile shows a beating pattern, indicating the superposition of LR-SPPs and SR-SPPs. This interaction is possible because the top and bottom modes have the same energy but differ in wavelength. SR-SPPs are excited at the platelet’s edges and decay after approximately 1.5 μm of propagation. On the platelet in Fig. 2B, SR-SPPs exhibit a wavelength of 185 nm (λ_SR-SPP), which is in agreement with our theory. In Fig. 2F, we generate emission profiles from the simulations in Fig. 2 (C and D), which confirm all PEEM features with excellent agreement. The small deviations between theory and experiment may arise from the systematic magnification calibration error of the PEEM and lie within the standard deviations of the experimental values. These are 41 nm for the LR-SPP and 13 nm for the SR-SPP, respectively. Size calibration for the measured wavelengths in the PEEM image was inferred from the independently determined size of the gold platelet and the focused ion beam milled structure dimensions.

From time-resolved experiments, using a phase-stabilized Pancharatnam-type Mach-Zehnder interferometer that generates a pulse train of pairs of pulses impinging on the sample, we obtain information about the SR-SPP dynamics. In general, time-resolved PEEM images recorded in normal incidence geometry show distinct characteristic features as introduced in the study of Kahl et al. (40). Near the platelet edge, where laser pulses excite the SPP waves, both electric fields superpose and form a static pattern, which resembles the spatial cross-correlation pattern of the two pulses. A second feature arises, as SPP waves propagate away from their excitation region, which is referred to as dynamic area of the PEEM contrast.

In Fig. 3 , we use an atomically flat 22-nm-thick plasmonic gold surface to demonstrate the use of short-range surface plasmons for the creation of a highly reproducible, localized electron emission spot with the smallest dimension of 60 nm for a light wavelength of 800 nm. This is achieved in the center of a 2-μm-diameter flat disk, which was fabricated from a triangular single-crystalline gold platelet using a focused Ga ion beam. To create a particularly strong emission spot in the center of the disk, we structured four additional concentric rings with a distance of 150 nm around the disk to serve as a selective grating coupler for the SR-SPPs (see Fig. 3A). Figure 3B depicts the time-averaged 2PPE PEEM image from the sample. At the edges, the SR-SPPs are excited with an approximate wavelength of 180 nm and a decay length of 1 μm. Along the polarization direction in the central disk, an intense short-range surface plasmon pattern is observed. Because the momentum transfer at the grating coupler has been adjusted to only yield SR-SPP excitation, the LR-SPP mode is effectively suppressed. For excitation at the edges of the triangular platelet, this selectivity does not exist, and both LR-SPPs and SR-SPPs are excited at the edges of the platelet accordingly. At the corners of the triangle, the interference of the SR-SPPs that have been excited at different edges can also be identified. Because of the extremely high quality and the defect-free single crystallinity of the atomically flat gold film, hotspots at protrusions or extrusions are not at all present. Figure 3C displays a false-color PEEM image (inset) and the emitted electron intensity cross section in the polarization plane of the exciting laser pulses (dashed line in the inset). The central maximum exhibits a FWHM of 60 nm, corresponding to λ₀/13.3, whereas in the perpendicular direction (depicted in Fig. 3D), the FWHM is 120 nm. In terms of λ_SR-SPP, the central spot is ~λ/3, which is expected for a Bessel function J₀(r) of radial shape. [The exact value is 0.306λ, which is 2/1.22*λ/2, with 2*λ/W and 1.22*λ/D being the sizes of the central diffraction pattern for a linear slit of width W and circular opening with size D. The latter number arises from the first zero crossing of the circular Bessel function J₀(r).] The asymmetric shape of the focus originates from the polarization direction of the incident light. The 120-nm size is determined by the focusing properties of the grating coupler, whereas in the other direction, the focus spot is additionally reduced in size due to the transient formation of a standing SPP wave.

Fig. 3. Nanofocus formation.

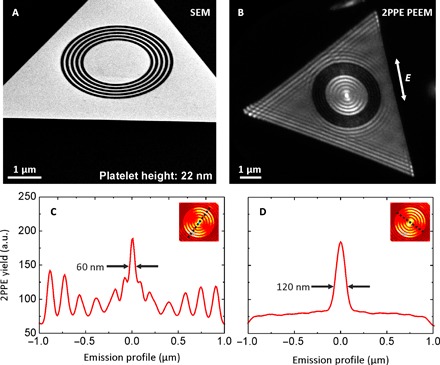
(A) SEM image of a 22-nm-high single-crystalline gold platelet, taken at an inclined angle of 54°, patterned with a circular grating of 150 nm period and a central disk with a diameter of 2 μm. (B) 2PPE PEEM at an 800-nm laser wavelength excites both long- and short-range surface plasmons on the structured platelet. Long-range surface plasmons of about 800-nm wavelength are hardly visible, whereas the short-range plasmons are predominant. Because of the surrounding grating, the short wavelength plasmon can couple into the central disk, which acts as a focusing device. At the focal spot, the highest electron emission is observed. From these time-integrated data, the emission profile is characterized perpendicular (C) and parallel (D) to occurring wavefronts. The focus size in profile (C) is determined by the full width at half maximum (FWHM) of the central peak and is 60 nm. (D) The focus width is 120 nm. The images and cuts present raw data without any postprocessing, which is characteristic of the extremely high sample quality and the noninvasive imaging process. They share the same y scale.

Because the intensity profiles in Fig. 3 depict the yield of nonlinearly photoemitted electrons, the central maximum resembles a defined electron emission spot in the focus of the disk. Considering the duration of the laser pulses (15 fs) and keeping in mind that the grating coupler used for SPP excitation consists of five grooves, we can conclude that this plasmonic electron emitter produces sub–30-fs bunches of electrons. Such an electron emitter could be used as a localized and ultrafast electron source for femtosecond electron microscopy (47, 48), permitting subwavelength imaging, as well as deep subwavelength imaging illumination and lithography.

In addition to the time-averaged picture in Fig. 3, we particularly investigated the temporal behavior of the short-range plasmon focus. More specifically, we use PEEM data at different pump-probe delays to characterize propagation and interference of counter-propagating SR-SPP waves inside the single-crystalline gold disk. Again, SR-SPPs are launched at the circular grating. Starting from opposite sides of the gold disk, SPP wave fronts propagate toward each other, superpose in the dynamic center, and focus to a small spot. Because of constructive and destructive interference of the two counter-propagating SPP waves with the oscillating light field, alternating maximum and minimum electron emission takes place in the focal spot. The minimum at the focus position arises from constructive interference of the fields at times when both of them are zero, which happens periodically in time at the focus position. Figure 4A shows the emission pattern at a delay time Δt = t₀ when the central spot constitutes an isolated emission maximum. At Δt = t₀ + 1.33 fs, after half an optical cycle, there is minimal electron emission in the focal spot, which is displayed in Fig. 4B. After one full optical cycle (2.66 fs), there is again maximum electron emission in the center of the disk. Figure 4 (C and D) reproduce the electron emission yield for a maximum and a minimum focus derived from our theoretical PEEM model. We characterize the electron emission cross sections parallel to the electric field vector and plot them in Fig. 4 (E to H), which illustrate the experimental and theoretical emission maximum and minimum, respectively. Here, the emission spot exhibits a FWHM of 60 nm as well. The full movie is available in the Supplementary Materials.

Fig. 4. Time-resolved PEEM measurements illustrate the dynamic SPP focus in the center of the 2-μm disk.

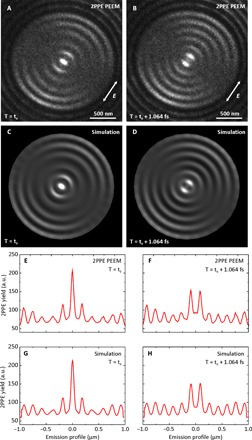
(A) The plasmon focus is at a relative maximum at delay time Δt = t₀ between pump and probe pulse. (B) At delay time Δt = t₀ + 1.33 fs, the PEEM image shows minimum electron emission at the central spot. Images (C) and (D) show the simulated PEEM images for the same delay times. Images (E) to (H) show the emission profiles from the PEEM measurements and simulations above. Profiles (E) and (G) illustrate the maximum case, where the FWHM of the central peak is 60 nm as well. The complete experimental and simulated movies are available in the Supplementary Materials.

In Fig. 5, emission profiles of different delay times between pump and probe pulses are taken through the center of the focus and plotted successively in one single diagram. From the dashed yellow line, the SR-SPP phase velocity can be calculated. It equals 0.22c₀, which is slightly less than a quarter of the velocity of light in vacuum c₀, in agreement with the theory above. Fitting a Gaussian profile to the wave pattern of propagating SR-SPPs allows experimental determination of the group velocity v_g as well, just as has been performed for LR-SPPs in the study of Kahl et al. (40). For a platelet with a thickness of comparable width to that in Fig. 5, we find v_g ≈ 0.1c₀; however, note that a different platelet thickness modifies the coupling strength between the SPP modes at the top and bottom interface. For thicker platelets, both the values of v_p and v_g have been found to be slightly higher. The experimental data can be found in fig. S1 for two platelets of different thickness.

Fig. 5. Sequence of emission profiles through the nanofocus (see inset) for increasing delay times up to 50 fs.

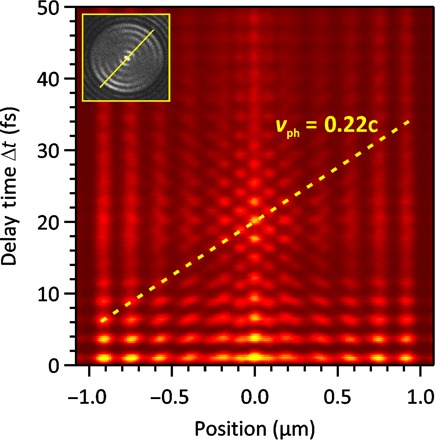
The plasmon waves counterpropagate from the edges into the central position 0 and superpose constructively and destructively with each other and the electric field of the pump laser pulse. At the focal spot, within an optical cycle, one emission maximum and one minimum occur. From the slope of the dashed yellow line, the phase velocity of SR-SPPs can be calculated, which is 0.22c.

CONCLUSION

Our concept of short-range plasmon focusing could open the door to a variety of applications. It could be implemented as a localized source for local heating in heat-assisted magnetic recording (49). Our concept does not suffer from the necessity to have a nanoantenna with sharp edges, or an intrusion or extrusion on a flat surface, which all suffer from degradation when exposed to strong laser fields, high average power, or thermal loads. The ring structure used for SPP excitation is located at areas of lower electric field and hence does not suffer that much from degradation.

Beyond this, our method could open up new paths in several plasmonic areas. One prominent example might be the use of refractory plasmonic materials (50, 51) such as TiN (if sputtered in an ultrasmooth fashion), which can withstand heating. Ideally, one would use a transparent substrate material of high refractive index, such as Si₃N₄, TiO_xN_y, or a semiconductor, which can also withstand heat and deposit a metallic film that can support the short-range surface plasmon. Even doped semiconductors could be used to support short-range surface plasmon excitation. One might even think of an intrinsic semiconductor substrate with a thin doped layer that supports the short-range surface plasmon. The high losses of the short-range plasmons are not problematic because we are dealing with short propagation distances. Also, very lossy materials with strong dispersion, such as copper, graphene, MoS₂, WS₂, WSe₂, or h-BN, could be used to study SR-SPP propagation and focusing.

There are more potential structure geometries to create plasmonic nanofoci by milling other appropriate grating structures [for example, ellipses (52)] into a surface that will create a sub–100-nm spot through interference. Carving Archimedean spirals into the films (53) leads to angular orbital momentum of the short-range surface plasmons (54). It is natural to use tapered structures for adiabatic focusing of SR-SPPs. This will avoid difficulties associated with long-range surface plasmons, which start at a much longer wavelength and then are compressed in a tapered or straight plasmonic waveguide (19, 55, 56), such as those used before for plasmon-induced electron emission (57, 58). Another possibility is the use of SR-SPP nanofoci on ultraflat surfaces for the generation of optical forces and trapping (59, 60).

In addition, enhanced light-matter interaction should occur when placing a quantum emitter directly into the nanofocus. This could also be useful for nanosensing with a very tightly focused spot that is well bound to the metal, particularly when combined with radially polarized excitation.

MATERIALS AND METHODS

2PPE PEEM

The experiments were performed using the time-resolved two-photon photoemission microscopy setup at the University of Duisburg-Essen. The setup combines a commercial low-energy electron microscope (ELMITEC LEEM) with a femtosecond laser (FEMTOLASERS). The ultrahigh-vacuum microscope provides for a 11-nm spatial resolution, and the specific design with an electron-optical beam splitter enables a normal-incidence beam-path for the femtosecond laser pulses (39). Ultrashort (12 to 15 fs) laser pulses of a central wavelength of 800 nm were created using a Ti:sapphire oscillator with a pulse rate of 80 MHz. The average laser power was approximately 600 mW, and the pulses were dispersion-corrected with chirped mirrors. For the time-resolved experiments, each individual laser pulse was split into two pulses, and these two pulses were mutually time-delayed with respect to each other in an actively phase-stabilized Mach-Zehnder interferometer (61). It was demonstrated earlier (62) that our setup provides a stability of better than 0.1 fs over a time of several hours. The contrast in the experiment is caused by a two-photon photoemission process. In brief, the first laser pulse excited a SPP at a suitable focused-ion beam-milled grating coupler. A delayed second laser pulse probed the SPP because the interference of the SPP’s electric field and the probing laser field resulted in a periodic modulation of the photoemission yield across the surface. Details of the origin of the 2PPE PEEM contrast for a time-resolved experiment are discussed in the study of Kahl et al. (40).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/7/e1700721/DC1

fig. S1. Determination of phase and group velocity of SR-SPPs.

movie S1. Nanofocusing movie experiment.

movie S2. Nanofocusing movie theory.