Abstract
Modern world has witnessed a dramatic increase in our ability to collect, transmit and distribute real-time monitoring and surveillance data from large-scale information systems and cyber-physical systems. Detecting system anomalies thus attracts significant amount of interest in many fields such as security, fault management, and industrial optimization. Recently, invariant network has shown to be a powerful way in characterizing complex system behaviours. In the invariant network, a node represents a system component and an edge indicates a stable, significant interaction between two components. Structures and evolutions of the invariance network, in particular the vanishing correlations, can shed important light on locating causal anomalies and performing diagnosis. However, existing approaches to detect causal anomalies with the invariant network often use the percentage of vanishing correlations to rank possible casual components, which have several limitations: 1) fault propagation in the network is ignored; 2) the root casual anomalies may not always be the nodes with a high-percentage of vanishing correlations; 3) temporal patterns of vanishing correlations are not exploited for robust detection. To address these limitations, in this paper we propose a network diffusion based framework to identify significant causal anomalies and rank them. Our approach can effectively model fault propagation over the entire invariant network, and can perform joint inference on both the structural, and the time-evolving broken invariance patterns. As a result, it can locate high-confidence anomalies that are truly responsible for the vanishing correlations, and can compensate for unstructured measurement noise in the system. Extensive experiments on synthetic datasets, bank information system datasets, and coal plant cyber-physical system datasets demonstrate the effectiveness of our approach.
Keywords: causal anomalies ranking, label propagation, nonnegative matrix factorization
1. INTRODUCTION
With the rapid advances in networking, computers, and hardware, we are facing an explosive growth of complexity in networked applications and information services. These large-scale, often distributed, information systems usually consist of a great variety of components that work together in a highly complex and coordinated manner. One example is the Cyber-Physical System (CPS) which is typically equipped with a large number of networked sensors that keep recording the running status of the local components; another example is the large scale Information Systems such as the cloud computing facilities in Google, Yahoo! and Amazon, whose composition includes thousands of components that vary from operating systems, application soft-wares, servers, to storage, networking devices, etc.
A central task in running these large scale distributed systems is to automatically monitor the system status, detect anomalies, and diagnose system fault, so as to guarantee stable and high-quality services or outputs. Significant research efforts have been devoted to this topic in the literatures. For instance, Gertler et al. [9] proposed to detect anomalies by examining monitoring data of individual component with a thresholding scheme. However, it can be quite difficult to learn a universal and reliable threshold in practice, due to the dynamic and complex nature of information systems. More effective and recent approaches typically start with building system profiles, and then detect anomalies via analyzing patterns in these profiles [5, 13]. The system profile is usually extracted from historical time series data collected by monitoring different system components, such as the flow intensity of software log files, the system audit events and the network traffic statistics, and sometimes sensory measurements in physical systems.
The invariant model is a successful example [13, 14] for large-scale system management. It focuses on discovering stable, significant dependencies between pairs of system components that are monitored through time series recordings, so as to profile the system status and perform subsequent reasoning. A strong dependency between a pair of components is called invariant (correlation) relationship. By combining the invariants learned from all monitoring components, a global system dependency profile can be obtained. The significant practical value of such an invariant profile is that it provides important clues on abnormal system behaviors and in particular the source of anomalies, by checking whether existing invariants are broken. Figure 1 illustrates one example of the invariant network and two snapshots of broken invariants at time t1 and t2, respectively. Each node represents the observation from a monitoring component. The green line signifies an invariant link between two components, and a red line denotes broken invariant (i.e., vanishing correlation). The network including all the broken invariants at given time point is referred to as the broken network.
Figure 1.
Invariant network and vanishing correlations(red edges).
Although the broken invariants provide valuable information of the system status, how to locate true, causal anomalies can still be a challenging task due to the following reasons. First, system faults are seldom isolated. Instead, starting from the root location/component, anomalous behavior will propagate to neighboring components [13], and different types of system faults can trigger diverse propagation patterns. Second, monitoring data often contains a lot of noises due to the fluctuation of complex operation environments.
Recently, several ranking algorithms were developed to diagnose the system failure based on the percentage of broken invariant edges associated with the nodes, such as the egonet based method proposed by Ge et al. [8], and the loopy belief propagation (LBP) based method proposed by Tao et al. [22]. Despite the success in practical applications, existing methods still have certain limitations. First, they do not take into account the global structure of the invariant network, neither how the root anomaly/fault propagates in such a network. Second, the ranking strategies rely heavily on the percentage of broken edges connected to a node. For example, the mRank algorithm [8] calculated the anomaly score of a given node using the ratio of broken edges within the egonet1 of the node. The LBP-based method [22] used the ratio of broken edges as the prior probability of abnormal state for each node. We argue that, the percentage of broken edges may not serve as a good evidence of the causal anomaly. This is because, although one broken edge can indicate that one (or both) of related nodes is abnormal, lack of a broken edge does not necessary indicate that related nodes are problem free. Instead, it is possible that the correlation is still there when two nodes become abnormal simultaneously [13]. Therefore the percentage of broken edges could give false evidences. For example, in Figure 1, the causal anomaly is node ⓘ. The percentage of broken edges for node ⓘ is 2/3, which is smaller than that of node ⓗ (which is equal to 1). Since there exists a clear evidence of fault propagation on node ⓘ, an ideal algorithm should rank ⓘ higher than ⓗ. Third, existing methods usually consider static broken network instead of multiple broken networks at successive time points together. While we believe that, jointly analyzing temporal broken networks can help resolve ambiguity and achieve a denoising effect. This is because, the root casual anomalies usually remain unchanged within a short time period, even though the fault may keep prorogating in the invariant network. As an example shown in Figure 1, it would be easier to detect the causal anomaly if we jointly consider the broken networks at two successive time points together.
To address the limitations of existing methods, we propose several network diffusion based algorithms for ranking causal anomalies. Our contributions are summarized as follows.
We employ the network diffusion process to model propagation of causal anomalies and use propagated anomaly scores to reconstruct the vanishing correlations. By minimizing the reconstruction error, the proposed methods simultaneously consider the whole invariant network structure and the potential fault propagation. We also provide rigid theoretical analysis on the properties of the proposed methods.
We further develop efficient algorithms which reduce the time complexity from 𝒪(n3) to 𝒪(n2), where n is the number of nodes in the invariant network. This makes it feasible to quickly localize root cause anomalies in large-scale systems.
We employ effective normalization strategy on the ranking scores, which can reduce the influence of extreme values or outliers without having to explicitly remove them from the data.
We develop a smoothing algorithm that enables users to jointly consider dynamic and time-evolving broken network, and thus obtain better ranking results.
We evaluate the proposed methods on both synthetic datasets and two real datasets, including the bank information system and the coal plant cyber-physical system datasets. Experimental results demonstrate the effectiveness of our methods.
2. BACKGROUND AND PROBLEM DEFINITION
In this section, we first introduce the technique of the invariant model [13] and then define our problem.
2.1 System Invariant and Vanishing Correlations
The invariant model is used to uncover significant pairwise relations among massive set of time series. It is based on the AutoRegressive eXogenous (ARX) model [10] with time delay. Let x(t) and y(t) be a pair of time series under consideration, where t is the time index, and let n and m be the degrees of the ARX model, with a delay factor k. Let ŷ(t; θ) be the prediction of y(t) using the ARX model parametarized by θ, which can then be written as
| (1) |
| (2) |
where θ = [a1,…,an, b0,…,bm, d]⊤ ∈ ℝn+m+2, φ(t) = [y(t−1),…,y(t−n), x(t−k),…,x(t−k−m), 1]⊤ ∈ ℝn+m+2. For a given setting of (n, m, k), the parameter θ can be estimated with observed time points t = 1,…,N in the training data, via least-square fitting. In real-world applications such as anomaly detection in physical systems, 0 ≤ n, m, k ≤ 2 is a popular choice [6, 13]. We can define the “goodness of fit” (or fitness score) of an ARX model as
| (3) |
where ȳ is the mean of the time series y(t). A higher value of F(θ) indicates a better fitting of the model. An invariant (correlation) is declared on a pair of time series x and y if the fitness score of the ARX model is larger than a pre-defined threshold. A network including all the invariant links is referred to as the invariant network. Construction of the invariant network is referred to as the model training. The model θ will then be applied on the time series x and y in the testing phase to track vanishing correlations.
To track vanishing correlations, we can use the techniques developed in [6, 15]. At each time point, we compute the (normalized) residual R(t) between the measurement y(t) and its estimate by ŷ(t; θ) by
| (4) |
where εmax is the maximum training error εmax = max1≤t≤N |y(t) − ŷ(t; θ)|. If the residual exceeds a prefixed threshold, then we declare the invariant as “broken”, i.e., the correlation between the two time series vanishes. The network including all the broken edges at given time point and all nodes in the invariant network is referred to as the broken network.
2.2 Problem Definition
Let 𝒢l be the invariant network with n nodes. Let 𝒢b be the broken network for 𝒢l. We use two symmetric matrices A ∈ ℝn × n, P ∈ ℝn × n to denote the adjacency matrix of network 𝒢l and 𝒢b, respectively. These two matrices can be obtained as discussed in Section 2.1. The two matrices can be binary or continuous. For binary case of A, 1 is used to denote that the correlation exists between two time series, and 0 denotes the lack of correlation; while for P, 1 is used to denote that the correlation is broken (vanishing), and 0 otherwise. For the continuous case, the fitness score F(θ) (3) and the residual R(t) (4) can be used to fill the two matrices, respectively.
Our main goal is to detect the abnormal nodes in 𝒢l that are most responsible for causing the broken edges in 𝒢b. In this sense, we call such nodes “causal anomalies”. Accurate detection of causal anomalous nodes will be extremely useful for examination, debugging and repair of system failures.
3. RANKING CAUSAL ANOMALIES
In this section, we present the algorithm of Ranking Causal Anomalies (RCA), which takes into account both the fault propagation and fitting of broken invariants simultaneously.
3.1 Fault Propagation
We consider a very practical scenario of fault propagation, namely anomalous system status can always be traced back to a set of root cause anomaly nodes, or causal anomalies, as initial seeds. As the time passes, these root cause anomalies will then propagate along the invariant network, most probably towards their neighbors via paths identified by the invariant links in 𝒢l. To explicitly model this spreading process on the network, we have employed the label propagation technique [16, 24, 26]. Suppose that the (unknown) root cause anomalies are denoted by the indicator vector e, whose entries ei’s (1 ≤ i ≤ n) indicate whether the ith node is the casual anomaly (ei = 1) or not (ei = 0). At the end of propagation, the system status is represented by the anomaly score vector r, whose entries tell us how severe each node of the network has been impaired. The propagation from e to r can be modeled by the following optimization problem
where D ∈ ℝn × n is the degree matrix of A, c ∈ (0, 1) is the regularization parameter, r is the anomaly score vector after the propagation of the initial faults in e. We can re-write the above problem as
| (5) |
where In is the identity matrix, Ã = D−1/2 AD−1/2 is the degree-normalized version of A. Similarly we will use P̃ as the degree-normalized P in the sequel. The first term in Eq. (5) is the smoothness constraint [26], meaning that a good ranking function should assign similar values to nearby nodes in the network. The second term is the fitting constraint, which means that the final status should be close to the initial configuration. The trade-off between these two competing constraints is controlled by a positive parameter c: a small c encourages a sufficient propagation, and a big c actually suppresses the propagation. The optimal solution of problem (5) is [26]
| (6) |
which establishes an explicit, closed-form solution between the initial configuration e and the final status r through propagation.
To encode the information of the broken network, we propose to use r to reconstruct the broken network 𝒢b. The intuition is illustrated in Figure 2. If there exists a broken link in 𝒢b, e.g., P̃ij is large, then ideally at least one of the nodes i and j should be abnormal, or equivalently, either ri or rj should be large. Thus, we can use the product of ri and rj to reconstruct the value of P̃ij. In Section 5, we’ll further discuss how to normalize them to avoid extreme values. Then, the loss of reconstructing the broken link P̃ij can be calculated by (ri · rj − P̃ij)2. The reconstruction error of the whole broken network is then . Here, ○ is element-wise operator, and M is the logical matrix of the invariant network 𝒢l (1 with edge, 0 without edge). Let B = (1 − c)(In − cÃ)−1, by substituting r we obtain the following objective function.
| (7) |
Figure 2.
Reconstruction of the broken invariant network using anomaly score vector r.
Considering that the integer programming in problem (7) is NP-hard, we relax it by using the ℓ1 penalty on e with parameter τ to control the number of non-zero entries in e [23]. Then we reach the following objective function.
| (8) |
3.2 Learning Algorithm
In this section, we present an iterative multiplicative updating algorithm to optimize the objective function in (8). The objective function is invariant under these updates if and only if e are at a stationary point [17]. The solution is presented in the following theorem, which is derived from the Karush-Kuhn-Tucker (KKT) complementarity condition [3]. Detailed theoretical analysis of the optimization procedure will be presented in the next section.
Theorem 1. Updating e according to Eq. (9) will monotonically decrease the objective function in Eq. (8) until convergence.
| (9) |
where ○, and are element-wise operators.
Based on Theorem 1, we develop the iterative multiplicative updating algorithm for optimization and summarize it in Algorithm 1. We refer to this ranking algorithm as RCA.
3.3 Theoretical Analysis
Algorithm 1.
Ranking Causal Anomalies (RCA)
3.3.1 Derivation
We derive the solution to problem (9) following the constrained optimization theory [3]. Since the objective function is not jointly convex, we adopt an effective multiplicative updating algorithm to find a local optimal solution. We prove Theorem 1 in the following.
We formulate the Lagrange function for optimization . Obviously, B, M and P̃ are symmetric matrix. Let F = (Bee⊤ B⊤) ○ M, then
| (10) |
It follows that
| (11) |
and thereby
| (12) |
Thus, the partial derivative of Lagrange function with respect to e is:
| (13) |
where 1n is the n × 1 vector of all ones. Using the Karush-Kuhn-Tucker (KKT) complementarity condition [3] for the non-negative constraint on e, we have
| (14) |
The above formula leads to the updating rule for e that is shown in Eq. (9).
3.3.2 Convergence
We use the auxiliary function approach [17] to prove the convergence of Eq. (9) in Theorem 1. We first introduce the definition of auxiliary function as follows.
Definition 3.1. Z(h, ĥ) is an auxiliary function for L(h) if the conditions
| (15) |
are satisfied for any given h, ĥ [17].
Lemma 3.1. If Z is an auxiliary function for L, then L is non-increasing under the update [17].
| (16) |
Theorem 2. Let L(e) denote the sum of all terms in L containing e. The following function
| (17) |
is an auxiliary function for L(e). Furthermore, it is a convex function in e and has a global minimum.
Theorem 2 can be proven in a similar way as [7] by validating Z(e, ê) ≥ L(e), Z(e, e) = L(e), and the Hessian matrix ∇∇eZ(e, ê) ⪰ 0. Due to space limitation, we omit the details.
Based on Theorem 2, we can minimize Z(e, ê) with respect to e with ê fixed. We set ∇eZ(e, ê) = 0, and get the following updating formula
| (18) |
which is consistent with the updating formula derived from the KKT condition aforementioned.
From Lemma 3.1 and Theorem 2, for each subsequent iteration of updating e, we have L(e0) = Z(e0, e0) ≥ Z(e1, e0) ≥ Z(e1, e1) = L(e1) ≥ … ≥ L(eIter). Thus L(e) monotonically decreases. Since the objective function Eq. (8) is lower bounded by 0, the correctness of Theorem 1 is proven.
3.3.3 Complexity Analysis
In Algorithm 1, we need to calculate the inverse of an n × n matrix, which takes 𝒪(n3) time. In each iteration, the multiplication between two n × n matrices is inevitable, thus the overall time complexity of Algorithm 1 is 𝒪(Iter · n3), where Iter is the number of iterations needed for convergence. In the following section, we will propose an efficient algorithm that reduces the time complexity to 𝒪(Iter · n2).
4. COMPUTATIONAL SPEED UP
In this section, we will propose an efficient algorithm that avoids the matrix inverse calculations as well as the multiplication between two n × n matrices. The time complexity can be reduced to 𝒪(Iter · n2).
We achieve the computational speed up by relaxing the objective function in (8) to jointly optimize r and e. The objective function is shown in the following.
| (19) |
To optimize this objective function, we can use an alternating scheme. That is, we optimize the objective with respect to r while fixing e, and vise versa. This procedure continues until convergence. The objective function is invariant under these updates if and only if r, e are at a stationary point [17]. Specifically, the solution to the optimization problem in Eq. (19) is based on the following theorem, which is derived from the Karush-Kuhn-Tucker (KKT) complementarity condition [3]. The derivation of it and the proof of Theorem 3 is similar to that of Theorem 1.
Theorem 3. Alternatively updating e and r according to Eq. (20) and Eq. (21) will monotonically decrease the objective function in Eq. (19) until convergence.
| (20) |
| (21) |
Based on Theorem 3, we can develop the iterative multiplicative updating algorithm for optimization similar to Algorithm 1. Due to page limit we skip the details. We refer to this ranking algorithm as R-RCA. From Eq. (20) and Eq. (21), we observe that the calculation of the inverse of the n × n matrix and the multiplication between two n × n matrices in Algorithm 1 are not necessary. As we will see in Section 7.4, the relaxed versions of our algorithm can greatly improve the computational efficiency.
5. SOFTMAX NORMALIZATION
In Section 3, we use the product ri · rj as the strength of evidence that the correlation between node i and j is vanishing (broken). However, it suffers from the extreme values in the ranking values r. To reduce the influence of the extreme values or outliers, we employ the softmax normalization on the ranking values r. The ranking values are nonlinearly transformed using the sigmoidal function before the multiplication is performed. Thus, the reconstruction error is expressed by , where σ(·) is the softmax function with:
| (22) |
The corresponding objective function in Algorithm 1 is modified to the following
| (23) |
Similarly, the objective function for Eq. (19) is modified to the following
| (24) |
The optimization of these two objective functions are based on the following two theorems.
Theorem 4. Updating e according to Eq. (25) will monotonically decrease the objective function in Eq. (23) until convergence.
| (25) |
where Ψ = {diag [σ(Be)] − σ(Be)σ⊤(Be)}.
Theorem 5. Updating r according to Eq. (26) will monotonically decrease the objective function in Eq. (24) until convergence.
| (26) |
where Λ = σ(r)σ⊤(r) and ρ = σ⊤(r)σ(r).
Theorem 4 and Theorem 5 can be proven with a similar strategy to that of Theorem 1. We refer to the ranking algorithms with softmax normalization (Eq. (23) and Eq. (24)) as RCA-SOFT and R-RCA-SOFT respectively.
6. TEMPORAL SMOOTHING ON MULTIPLE BROKEN NETWORKS
As discussed in Section 1, although the number of anomaly nodes could increase due to fault propagation in the network, the root cause anomalies will be stable within a short time period T [14]. Based on this intuition, we further develop a smoothing strategy by jointly considering the temporal broken networks. Specifically, we add a smoothing term to the objective functions. Here, e(t−1) and e(t) are causal anomaly ranking vectors for two successive time points. For example, the objective function of algorithm RCA with temporal broken networks smoothing is shown in Eq. (27).
| (27) |
Here, P̃(t) is the degree-normalized adjacency matrix of broken network at time point t. Similar to the discussion in Section 3.3, we can derive the updating formula of Eq. (27) in the following.
| (28) |
The updating formula for R-RCA, RCA-SOFT, and RRCA-SOFT with temporal broken networks smoothing is similar. Due to space limit, we skip the details. We refer to the ranking algorithms with temporal networks smoothing as T-RCA, T-R-RCA, T-RCA-SOFT and T-R-RCA-SOFT respectively.
7. EMPIRICAL STUDY
In this section, we perform extensive experiments to evaluate the performance of the proposed methods (summarized in Table 1). We use both simulated data and real-world monitoring datasets. For comparison, we select several state-of-the-art methods, including mRank and gRank in [8, 13], and LBP [22]. For all the methods, the tuning parameters were tuned using cross validation. We use several evaluation metrics including precision, recall, and nDCG [12] to measure the performance. The precision and recall are computed on the top-K ranking result, where K is typically chosen as twice the actual number of ground-truth causal anomalies [12, 22]. The nDCG of the top-p ranking result is defined as , where IDCGp is the DCGp value on the ground-truth, and p is smaller than or equal to the actual number of ground-truth anomalies. The reli represents the anomaly score of the ith item in the ranking list of the ground-truth.
Table 1.
Summary of notations
| Symbol | Definition |
|---|---|
|
| |
| n | the number of nodes in the invariant network |
| c, λ, τ | the parameters 0 < c < 1, τ > 0, λ > 0 |
| σ(·) | the softmax function |
|
| |
| 𝒢l | the invariant network |
| 𝒢b | the broken network for 𝒢l |
| A (Ã) ∈ ℝn × n | the (normalized) adjacency matrix of 𝒢l |
| P (P̃) ∈ ℝn × n | the (normalized) adjacency matrix of 𝒢b |
| M ∈ ℝn × n | the logical matrix of 𝒢l |
|
| |
| d(i) | the degree of the ith node in network 𝒢l |
| D ∈ ℝn × n | the degree matrix: D = diag(d(i), …, d(n)) |
|
| |
| r ∈ ℝn × 1 | the prorogated anomaly score vector |
| e ∈ ℝn × 1 | the ranking vector of causal anomalies |
|
| |
| RCA | the basic ranking causal anomalies algorithm |
| R-RCA | the relaxed RCA algorithm |
| RCA-SOFT | the RCA with softmax normalization |
| R-RCA-SOFT | the relaxed RCA with softmax normalization |
| T-RCA | the RCA with temporal smoothing |
| T-R-RCA | the R-RCA with temporal smoothing |
| T-RCA-SOFT | the RCA-SOFT with temporal smoothing |
| T-R-RCA-SOFT | the R-RCA-SOFT with temporal smoothing |
7.1 Simulation Study
We first evaluate the performance of the proposed methods using simulations. We have followed [8, 22] in generating the simulation data.
7.1.1 Data Generation
We first generate 5000 synthetic time series data to simulate the monitoring records2. Each time series contains 1,050 time points. Based on the invariant model introduced in Section 2.1, we build the invariant network by using the first 1,000 time points in the time series. This generates an invariant network containing 1,551 nodes and 157,371 edges. To generate invariant network of different sizes, we randomly sample 200, 500, and 1000 nodes from the whole invariant network and evaluate the algorithms on these sub-networks.
To generate the root cause anomaly, we randomly select 10 nodes from the network, and assign each of them an anomaly score between 1 and 10. The ranking of these scores is used as the ground-truth. To simulate the anomaly prorogation, we further use these scores as the vector e in Eq. (6) and calculate r (c = 0.9). The values of the top-30 time series with largest values in r are then modified by changing their amplitude value with the ratio 1+ri. That is, if the observed values of one time series is y1, after changing it from y1 to y2, the manually-injected degree of anomaly is equal to 1 + ri. We denote this anomaly generation scheme as amplitude-based anomaly generation.
7.1.2 Performance Evaluation
Using the simulated data, we compare the performance of different algorithms. In this example, we only consider the training time series as one snapshot; multiple snapshot cases involving temporal smoothing will be examined in the real datasets. Due to the page limit, we report the precision, recall and nDCG for only the top-10 items considering that the ground-truth contains 10 anomalies. Similar results can be observed with other settings of K and p. For each algorithm, reported result is averaged over 100 randomly selected subsets of the training data.
From Figure 3, we have several key observations. First, the proposed algorithms significantly outperform other competing methods, which demonstrates the advantage of taking into account fault prorogation in ranking casual anomalies. We also notice that performance of all ranking algorithms will decline on larger invariant networks with more nodes, indicating that anomaly ranking becomes more challenging on networks with more complex behaviour. However, the ranking result with softmax is less sensitive to the size of the invariant network, suggesting that the softmax normalization can effectively improve the robustness of the algorithm. This is quite beneficial in real-life applications, especially when data are noisy. Finally, we observe that RCA and RCASOFT outperform R-RCA and R-RCA-SOFT, respectively. This implies that the relaxed versions of the algorithms are less accurate. Nevertheless, their accuracies are still very comparable to those of the RCA and RCA-SOFT methods. In addition, the efficiency of the relaxed algorithms is greatly improved, as discussed in Section 4 and Section 7.4.
Figure 3.
Comparison on synthetic data(K, p = 10).
7.1.3 Robustness Evaluation
Practical invariant network and broken edges can be quite noisy. In this section, we further examine the performance of the proposed algorithms w.r.t. different noise levels. To do this, we randomly perturb a portion of non-broken edges in the invariant network. Results are shown in Figure 4. We observe that, even when the noise ratio approaches 50%, the precision, recall and nDCG of the proposed approaches still attain 0.5. This indicates the robustness of the proposed algorithms. We also observe that, when the noise ratio is very large, RCA-SOFT and R-RCA-SOFT work better than RCA and R-RCA, respectively. This is similar to those observations made in Section 7.1.2. As has been discussed in Section 5, the softmax normalization can greatly suppress the impact of extreme values and outliers in r, thus improves the robustness.
Figure 4.
Performance with different noise ratio(K, p = 10).
7.2 Ranking Causal Anomalies on Bank Information System Data
In this section, we apply the proposed methods to detect causal abnormal components on a Bank Information System (BIS) data set [8, 22]. The monitoring data are collected from a real-world bank information system logs, which contain 11 categories. Each category has a varying number of time series, and Table 2 gives five categories as examples. The data set contains the flow intensities collected every 6 seconds. In total, we have 1,273 flow intensity time series. The training data is collected at normal system states, where each time series has 168 time points. The invariant network is then generated on the training data as described in Section 2.1. The testing data of the 1,273 flow intensity time series are collected during abnormal system states, where each time series contain 169 time points. We track the changes of the invariant network with the testing data using the method described in Section 2.1. Once we obtain the broken networks at different time points, we will then perform causal anomaly ranking in these temporal slots jointly. Properties of the networks constructed are summarized in Table 3.
Table 2.
Examples of categories and monitors.
| Categories | Samples of Measurements |
|---|---|
| CPU | utilization, user usage time, IO wait time |
| DISK | # of write operations, write time, weighted IO time |
| MEM | run queue, collision rate, UsageRate |
| NET | error rate, packet rate |
| SYS | UTIL, MODE UTIL |
Table 3.
Data set description
| Data Set | #Monitors | #invariant links | #broken edges at given time point |
|---|---|---|---|
| BIS | 1273 | 39116 | 18052 |
| Coal Plant | 1625 | 9451 | 56 |
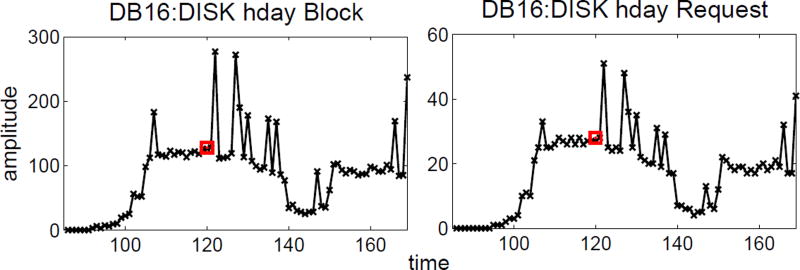
Based on the knowledge from system experts, the root cause anomaly at t = 120 in the testing data is related to “DB16”. An illustration of two “DB16” related monitoring data are shown in Figure 5. We highlight t = 120 with red square. Obviously, their behaviour looks anomalous from that time point on. Due to the complex dependency among different monitoring time series (measurements), it is impractical to obtain a full ranking of abnormal measurement. Fortunately, we have a unique semantic label associated with each measurement. For example, some semantic labels read “DB16:DISK hdx Request” and “WEB26 PAGE-OUT RATE”. Thus, we can extract all measurements whose titles have the prefix “DB16” as the ground-truth anomalies. The ranking score is determined by the number of broken edges associated with each measurement. Here our goal is to demonstrate how the top-ranked measurements selected by our method are related to the “DB16” root cause. Altogether, there are 80 measurements related to “DB16”, so we report the precision, recall with K ranging from 1 to 160 and the nDCG with p ranging from 1 to 80.
Figure 5.
Two example monitoring data of BIS.
The results are shown in Figure 6. The relative performance of different approaches is consistent with the observations in the simulation study. Again, the proposed algorithms outperform baseline methods by a large margin. To examine the top-ranked items more clearly, we list the top-12 results of different approaches in Table 4 and report the number of “DB16”-related monitors in Table 5. From Table 4, we observe that the three baseline methods only report one “DB16” related measurement in the top-12 results, and the actual rank of the “DB16”-related measurement appear lower (worse) than that of the proposed methods. We also notice that the ranking algorithms with softmax normalization outperform others. From Tables 4 and 5, we can see that top ranked items reported by RCA-SOFT and R-RCASOFT are more relevant than those reported by RCA and R-RCA, respectively. This clearly illustrates the effectiveness of the softmax normalization in reducing the influence of extreme values or outliers in the data.
Figure 6.
Comparison on BIS data.
Table 4.
Top 12 anomalies detected by different methods on BIS data(t:120).
| mRank | gRank | LBP | RCA | RCA-SOFT | R-RCA | R-RCA-SOFT |
|---|---|---|---|---|---|---|
|
| ||||||
| WEB16:NET eth1 BYNETIF | HUB18:MEM UsageRate | WEB22:SYS MODE UTIL | HUB17:DISK hda Request | DB17:DISK hdm Block | HUB17:DISK hda Request | DB17:DISK hdm Block |
| HUB17:DISK hda Request | HUB17:DISK hda Request | DB15:DISK hdaz Block | DB17:DISK hday Block | DB17:DISK hdba Block | DB15:PACKET Output | DB17:DISK hdba Block |
| AP12:DISK hd45 Block | AP12:DISK hd45 Block | WEB12:NET eth1 BYNETIF | HUB17:DISK hda Busy | DB16:DISK hdm Block | HUB17:DISK hda Busy | DB16:DISK hdm Block |
| AP12:DISK hd1 Block | AP12:DISK hd1 Block | WEB17:DISK BYDSK | DB18:DISK hdba Block | DB18:DISK hdm Block | DB17:DISK hdm Block | DB16:DISK hdj Request |
| WEB19:DISK BYDSK | AP11:DISK hd45 Block | DB18:DISK hdt Busy | DB18:DISK hdm Block | DB16:DISK hdj Request | DB17:DISK hdba Block | DB16:DISK hdax Request |
| AP11:DISK hd45 Block | AP11:DISK hd1 Block | DB15:DISK hdl Request | DB16:DISK hdm Block | DB18:DISK hdba Block | DB18:DISK hdm Block | DB18:DISK hdag Request |
| AP11:DISK hd1 Block | DB17:DISK hday Block | WEB21:DISK BYDSK | DB17:DISK hdba Block | DB16:DISK hdax Request | DB16:DISK hdm Block | DB18:DISK hdm Block |
| DB16:DISK hdm Block | DB15:PACKET Input | WEB27:FREE UTIL | DB17:DISK hdm Block | DB18:DISK hdag Request | DB18:DISK hdba Block | DB18:DISK hdbu Request |
| DB17:DISK hdm Block | DB17:DISK hdm Block | WEB19:NET eth0 | DB16:DISK hdba Block | DB18:DISK hdbu Request | DB17:DISK hday Block | DB18:DISK hdx Request |
| DB18:DISK hdm Block | DB16:DISK hdm Block | WEB25:PAGEOUT RATE | DB16:DISK hdj Request | DB16:DISK hdba Block | DB16:DISK hdba Block | DB18:DISK hdax Request |
| DB17:DISK hdba Block | DB17:DISK hdba Block | DB16:DISK hdy Block | DB18:DISK hdag Request | DB18:DISK hdx Request | DB16:DISK hdj Request | DB18:DISK hdba Block |
| DB18:DISK hdba Block | DB18:DISK hdm Block | AP13:DISK hd30 Block | DB16:DISK hdax Request | DB18:DISK hdax Request | DB18:DISK hdag Request | DB16:DISK hdx Request |
Table 5.
Number of “DB16” related monitors in top 32 results on BIS data(t:120).
| mRank | gRank | LBP | RCA | RCA-SOFT | R-RCA | R-RCA-SOFT |
|---|---|---|---|---|---|---|
| 10 | 7 | 4 | 14 | 16 | 13 | 17 |
As discussed in Section 1, the root anomalies could further propagate from one component to related ones over time, which may or may not necessarily relate to “DB16”. Such anomaly propagation makes anomaly detection even harder. To study how the performance varies at different time points, we compare the performance at t = 120 and t = 122, respectively in Figure 7 (p, K=80). Clearly, the performance declines for all methods. However, the proposed methods are less sensitive to anomaly propagation than others, suggesting that our approaches can better handle the fault propagation problem. We believe this is attributed to the network diffusion model that explicitly captures the fault propagation processes. We also list the top-12 abnormal at t = 122 in Table 6. Due to page limit, we only show the results of mRank, gRank, RCA-SOFT and R-RCA-SOFT. By comparing the results in Tables 4 and 6, we can observe that RCA-SOFT and R-RCA-SOFT significantly outperform mRank and gRank, the latter two methods based on the percentage of broken edges are more sensitive to the anomaly prorogation.
Figure 7.
Performance at t:120 v.s. t:122 on BIS data(p,K=80).
Table 6.
Top 12 anomalies on BIS data(t:122).
| mRank | gRank | RCA-SOFT | R-RCA-SOFT |
|---|---|---|---|
|
| |||
| WEB21:NET eth1 BYNETIF | WEB21:NET eth0 BYNETIF | DB17:DISK hdm Block | DB17:DISK hdm Block |
| WEB21:NET eth0 BYNETIF | WEB21:NET eth1 BYNETIF | DB17:DISK hdba Block | DB17:DISK hdba Block |
| WEB21:FREE UTIL | HUB18:MEM UsageRate | DB16:DISK hdm Block | DB16:DISK hdm Block |
| AP12:DISK hd45 Block | WEB21:FREE UTIL | DB18:DISK hdm Block | DB16:DISK hdj Request |
| AP12:DISK hd1 Block | WEB26:PAGEOUT RATE | DB16:DISK hdj Request | DB16:DISK hdax Request |
| DB18:DISK hday Block | AP12:DISK hd45 Block | DB18:DISK hdba Block | DB18:DISK hdm Block |
| DB18:DISK hdk Block | AP12:DISK hd1 Block | DB16:DISK hdax Request | DB18:DISK hdx Request |
| DB18:DISK hday Request | DB18:DISK hday Block | DB16:DISK hdba Block | DB18:DISK hdba Block |
| DB18:DISK hdk Request | DB18:DISK hdk Block | DB18:DISK hdx Request | DB16:DISK hdba Block |
| WEB26:PAGEOUT RATE | DB18:DISK hday Request | DB18:DISK hdbl Request | DB18:DISK hdax Request |
| DB17:DISK hdm Block | DB18:DISK hdk Request | DB16:DISK hdx Busy | DB16:PACKET Inputx |
| DB16:DISK hdm Block | AP11:DISK hd45 Block | DB16:DISK hdx Request | DB18:DISK hdbl Request |
We further validate the effectiveness of proposed methods with temporal smoothing. We report the top-12 results of different methods with smoothing at two successive time points t = 120 and t = 121 in Table 7. The number of “DB16”-related monitors in the top-12 results is summarized in Table 8. From Tables 7 and 8, we observe a significant performance improvement of our methods with temporal broken networks smoothing compared with those without smoothing. As discussed in Section 6, since causal anomalies of a system usually do not change within a short period of time, utilizing such smoothness can effectively suppress noise and thus give better ranking accuracy.
Table 7.
Top 12 anomalies reported by methods with temporal smoothing on BIS data(t:120–121).
| T-RCA | T-RCA-SOFT | T-R-RCA | T-R-RCA-SOFT |
|---|---|---|---|
|
| |||
| WEB14:NET eth0 BYNETIF | DB17:DISK hdm Block | WEB14:NET eth0 BYNETIF | DB17:DISK hdm Block |
| WEB16:DISK BYDSK | DB17:DISK hdba Block | WEB21:NET eth0 BYNETIF | DB17:DISK hdba Block |
| DB18:DISK hdba Block | DB16:DISK hdm Block | WEB16:DISK BYDSK PHYS | DB16:DISK hdm Block |
| DB18:DISK hdm Block | DB18:DISK hdm Block | WEB21:FREE UTIL | DB18:DISK hdm Block |
| DB17:DISK hdba Block | DB16:DISK hdj Request | DB15:PACKET Output | DB16:DISK hdj Request |
| DB16:DISK hdm Block | DB18:DISK hdba Block | DB16:DISK hdj Request | DB18:DISK hdba Block |
| DB17:DISK hdm Block | DB16:DISK hdax Request | DB17:DISK hdm Block | DB16:DISK hdax Request |
| DB16:DISK hdba Block | DB16:DISK hdba Block | DB16:DISK hdba Block | DB18:DISK hdx Request |
| DB16:DISK hdj Request | DB18:DISK hdx Request | DB17:DISK hday Block | DB16:DISK hdba Block |
| DB16:DISK hdax Request | DB18:DISK hdbl Request | DB16:DISK hdm Block | DB18:DISK hdbl Request |
| DB16:DISK hdx Busy | DB16:DISK hdx Busy | DB16:DISK hdax Request | DB16:DISK hdx Request |
| DB16:DISK hdbl Busy | DB16:DISK hdx Request | DB18:DISK hdba Block | DB16:DISK hdx Busy |
Table 8.
Comparison on the number of “DB16” related anomalies in top-12 results on BIS data.
| RCA | RCA-SOFT | R-RCA | R-RCA-SOFT | |
|---|---|---|---|---|
| Without temporal smoothing | 4 | 4 | 3 | 4 |
| With temporal smoothing | 6 | 6 | 4 | 6 |
7.3 Fault Diagnosis on Coal Plant Data
In this section, we test the proposed methods in the application of fault diagnosis on a coal plant cyber-physical system data. The data set contains time series collected through 1625 electric sensors installed on different components of the coal plant system. Using the invariant model described in Section 2.1, we generate the invariant network that contains 9451 invariant links. For privacy reasons, we remove sensitive descriptions of the data.
Based on knowledge from domain experts, in the abnormal stage the root cause is associated with component “X0146”. We report the top-12 results of different ranking algorithms in Table 9. We observe that the proposed algorithms all rank component “X0146” the highest, while the baseline methods could give higher ranks to other components. In Figure 8(a), we visualize the egonet of the node “X0146” in the invariant network, which is defined as the 1-step neighborhood around node “X0146”, including the node itself, direct neighbors, and all connections among these nodes in the invariant network. Here, green lines denote the invariant link, and red lines denote vanishing correlations (broken links). Since the node “Y0256” is top-ranked by the baseline methods, we also visualize its egonet in Figure 8(b) for a comparison. There are 80 links related to “X0146” in the invariant network, and 14 of them are broken. Namely the percentage of broken edges is only 17.5% for a truly anomalous component. In contrast, the percentage of broken edges for the node “Y0256” is 100%, namely a false-positive node can have a very high percentage of broken edges in practice. This explains why baseline approaches using the percentage of broken edges could fail, because the percentage of broken edges does not serve as a reliable evidence of the degree of causal anomalies. In comparison, our approach takes into account the global structures of the invariant network via network propagation, thus the resultant ranking is more meaningful.
Table 9.
Top anomalies on coal plant data.
| mRank | gRank | LBP | RCA | RCA-SOFT | R-RCA | R-RCA-SOFT |
|---|---|---|---|---|---|---|
|
| ||||||
| Y0039 | Y0256 | Y0256 | X0146 | X0146 | X0146 | X0146 |
| X0128 | Y0045 | X0146 | Y0045 | Y0256 | X0128 | X0166 |
| Y0256 | Y0028 | F0454 | X0128 | F0454 | F0454 | X0144 |
| H0021 | X0146 | X0128 | Y0030 | J0079 | Y0256 | X0165 |
| X0146 | X0057 | Y0039 | X0057 | Y0308 | Y0039 | X0142 |
| X0149 | X0061 | X0166 | X0158 | X0166 | Y0246 | J0079 |
| H0022 | X0068 | X0144 | X0068 | X0144 | Y0045 | X0164 |
| F0454 | X0143 | X0149 | X0061 | X0128 | Y0028 | X0145 |
| H0020 | X0158 | J0085 | X0139 | X0165 | X0056 | X0143 |
| X0184 | X0164 | X0061 | X0143 | X0142 | J0079 | X0163 |
| X0166 | J0164 | Y0030 | H0021 | H0022 | X0149 | J0164 |
| J0164 | H0021 | J0079 | F0454 | X0143 | X0145 | X0149 |
Figure 8.
Egonet of node “X0146” and “Y0256” in invariant network and vanishing correlations(red edges) on coal plant data.
7.4 Time Performance Evaluation
In this section, we study the efficiency of proposed methods using the following metrics: 1) the number of iterations for convergence; 2) the running time (in seconds) ; and 3) the scalability of the proposed algorithms. Figure 9(a) shows the value of the objective function with respect to the number of iterations on different data sets. We can observe that, the objective value decreases steadily with the number of iterations. Typically less than 100 iterations are needed for convergence. We also observe that our method with softmax normalization takes fewer iterations to converge. This is because the normalization is able to reduce the influence of extreme values [21]. We also report the running time of each algorithm on the two real data sets in Figure 10. We can see that the proposed methods can detect causal anomalies very efficiently, even with the temporal smoothing module.
Figure 9.
Number of iterations to converge and time cost comparison.
Figure 10.
Running time on real data sets.
To evaluate the computational scalability, we randomly generate invariant networks with different number of nodes (with network density=10) and examine the computational cost. Here 10% edges are randomly selected as broken links. Using simulated data, we compare the running time of RCA, R-RCA, RCA-SOFT, and R-RCA-SOFT. Figure 9(b) plots the running time of different algorithms w.r.t. the number of nodes in the invariant network. We can see that the relaxed versions of our algorithm are computationally more efficient than the original RCA and RCA-SOFT. These results are consistent with the complexity analysis in Section 4.
8. RELATED WORK
In this section, we review related work on anomaly detection and system diagnosis, in particular along the following two categories: 1) fault detection in distributed systems; and 2) graph-based methods.
For the first category, Yemini et al. [25] proposed to model event correlation and locate system faults using known dependency relationships between faults and symptoms. In real applications, however, it is usually hard to obtain such relationships precisely. To alleviate this limitation, Jiang et al. [13] developed several model-based approaches to detect the faults in complex distributed systems. They further proposed several Jaccard Coefficient based approaches to locate the faulty components [14, 15]. These approaches generally focus on locating the faulty components, they are not capable of spotting or ranking the causal anomalies.
Recently, graph-based methods have drawn a lot of interest in system anomaly detections [2, 5], either in static graphs or dynamic graphs [2]. In static graphs, the main task is to spot anomalous network entities (e.g., nodes, edges, subgraphs) given the graph structure [4, 11]. For example, Akoglu et al. [1] proposed the OddBall algorithm to detect anomalous nodes in weighted graphs. Liu et al. [18] proposed to use frequent subgraph mining to detect non-crashing bugs in software flow graphs. However, these approaches only focus on a single graph; in comparison, we take into account both the invariant graph and the broken correlations, which provides a more dynamic and complete picture for anomaly ranking. On dynamic graphs, anomaly detection aims at detecting abnormal events [19]. Most approaches along this direction are designed to detect anomaly time-stamps in which suspicious events take place, but not to perform ranking on a large number of system components. Sun et al. proposed to use temporal graphs for anomaly detection [20]. In their approach, a set of initial suspects need to be provided; then internal relationship among these initial suspects is characterized for better understanding of the root cause of these anomalies.
In using the invariant graph and the broken invariance graph for anomaly detection, Jiang et al. [14] used the ratio of broken edges in the invariant network as the anomaly score for ranking; Ge et al. [8] proposed mRank and gRank to rank causal anomalies; Tao et al. [22] used the loopy belief propagation method to rank anomalies. As has been discussed, these algorithms rely heavily on the percentage of broken edges in egonet of a node. Such local approaches do not take into account the global network structures, neither the global fault propagation spreading on the network. Therefore the resultant rankings can be sub-optimal.
9. CONCLUSIONS
Detecting causal anomalies on monitoring data of distributed systems is an important problem in data mining research. Robust and scalable approaches that can model the potential fault propagation are highly desirable. We develop a network diffusion based framework, which simultaneously takes into account fault propagation on the network as well as reconstructing anomaly signatures using propagated anomalies. Our approach can locate causal anomalies more accurately than existing approaches; in the meantime, it is robust to noise and computationally efficient. Using both synthetic and real-life data sets, we show that the proposed methods outperform other competitors by a large margin.
Acknowledgments
Wei Wang is partially supported by the National Science Foundation grants IIS-1313606, DBI-1565137, by National Institutes of Health under the grant number R01GM115833-01.
Footnotes
CCS Concepts
•Security and privacy → Pseudonymity, anonymity and untraceability;
An egonet is the induced 1-step subgraph for each node.
References
- 1.Akoglu L, McGlohon M, Faloutsos C. Oddball: Spotting anomalies in weighted graphs. PAKDD. :410–421. [Google Scholar]
- 2.Akoglu L, Tong H, Koutra D. Graph-based anomaly detection and description: A survey. CoRR. 2014 [Google Scholar]
- 3.Boyd S, Vandenberghe L. Convex Optimization. Cambridge University Press; 2004. [Google Scholar]
- 4.Breunig MM, Kriegel H-P, Ng RT, Sander J. Lof: Identifying density-based local outliers. SIGMOD. 2000:93–104. [Google Scholar]
- 5.Chandola V, Banerjee A, Kumar V. Anomaly detection: A survey. ACM Computing Surveys. 2009;41(3):1–58. [Google Scholar]
- 6.Chen H, Cheng H, Jiang G, Yoshihira K. ICDM. 2008. Global invariants for the management of large scale information systems. [Google Scholar]
- 7.Ding C, Li T, Peng W, Park H. KDD. 2006. Orthogonal nonnegative matrix t-factorizations for clustering; pp. 126–135. [Google Scholar]
- 8.Ge Y, Jiang G, Ding M, Xiong H. Ranking metric anomaly in invariant networks. TKDD. 2014 Jun;8(2) [Google Scholar]
- 9.Gertler J. Fault Detection and Diagnosis in Engineering Systems. Marcel Dekker; 1998. [Google Scholar]
- 10.System Identification (2nd Ed.): Theory for the User. 1999. Gertler: 1998. [Google Scholar]
- 11.Henderson K, Eliassi-Rad T, Faloutsos C, Akoglu L, Li L, Maruhashi K, Prakash BA, Tong H. KDD. 2010. Metric forensics: a multi-level approach for mining volatile graphs; pp. 163–172. [Google Scholar]
- 12.Jarvelin Kalervo, Kekalainen Jaana. Cumulated gain-based evaluation of IR techniques. TIS. 2002;20(4):422–446. [Google Scholar]
- 13.Jiang G, Chen H, Yoshihira K. Discovering likely invariants of distributed transaction systems for autonomic system management. Cluster Computing. 2006;9(4):385–399. [Google Scholar]
- 14.Jiang G, Chen H, Yoshihira K. Modeling and tracking of transaction flow dynamics for fault detection in complex systems. TDSC. 2006;3(4):312–326. [Google Scholar]
- 15.Jiang G, Chen H, Yoshihira K. Efficient and scalable algorithms for inferring invariants in distributed systems. TKDE. 2007;19(11):1508–1523. [Google Scholar]
- 16.Kim TH, Lee KM, Lee SU. ECCV. 2008. Generative image segmentation using random walks with restart; pp. 264–275. [Google Scholar]
- 17.Lee DD, Seung HS. NIPS. 2000. Algorithms for non-negative matrix factorization; pp. 556–562. [Google Scholar]
- 18.Liu C, Yan X, Yu H, Han J, Yu PS. SDM. 2005. Mining behavior graphs for ”backtrace” of noncrashing bugs; pp. 286–297. [Google Scholar]
- 19.Rossi RA, Gallagher B, Neville J, Henderson K. Modeling dynamic behavior in large evolving graphs. WSDM. 2013:667–676. [Google Scholar]
- 20.Sun J, Tao D, Faloutsos C. Beyond streams and graphs: Dynamic tensor analysis. KDD ’06. 2006:374–383. [Google Scholar]
- 21.Sutton RS, Barto AG. Reinforcement Learning: An Introduction. The MIT Press; Cambridge, MA: 1998. [Google Scholar]
- 22.Tao C, Ge Y, Song Q, Ge Y, Omitaomu F. ICDM. 2014. Metric ranking of invariant networks with belief propagation. [Google Scholar]
- 23.Tibshirani RJ. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B. 1996;58(1):267–288. [Google Scholar]
- 24.Tong H, Faloutsos C, Pan J-Y. ICDM. 2006. Fast random walk with restart and its applications; pp. 613–622. [Google Scholar]
- 25.Yemini SA, Kliger S, Mozes E, Yemini Y, Ohsie D. High speed and robust event correlation. IEEE Communications Magazine. 1996;34:82–90. [Google Scholar]
- 26.Zhou D, Bousquet O, Lal TN, Weston J, Schölkopf B. NIPS. 2003. Learning with local and global consistency; pp. 321–328. [Google Scholar]