Estimating 4D‐CBCT from prior information and extremely limited angle projections using structural PCA and weighted free‐form deformation for lung radiotherapy

Abstract

Purpose

To investigate the feasibility of using structural‐based principal component analysis (PCA) motion‐modeling and weighted free‐form deformation to estimate on‐board 4D‐CBCT using prior information and extremely limited angle projections for potential 4D target verification of lung radiotherapy.

Methods

A technique for lung 4D‐CBCT reconstruction has been previously developed using a deformation field map (DFM)‐based strategy. In the previous method, each phase of the 4D‐CBCT was generated by deforming a prior CT volume. The DFM was solved by a motion model extracted by a global PCA and free‐form deformation (GMM‐FD) technique, using a data fidelity constraint and deformation energy minimization. In this study, a new structural PCA method was developed to build a structural motion model (SMM) by accounting for potential relative motion pattern changes between different anatomical structures from simulation to treatment. The motion model extracted from planning 4DCT was divided into two structures: tumor and body excluding tumor, and the parameters of both structures were optimized together. Weighted free‐form deformation (WFD) was employed afterwards to introduce flexibility in adjusting the weightings of different structures in the data fidelity constraint based on clinical interests. XCAT (computerized patient model) simulation with a 30 mm diameter lesion was simulated with various anatomical and respiratory changes from planning 4D‐CT to on‐board volume to evaluate the method. The estimation accuracy was evaluated by the volume percent difference (VPD)/center‐of‐mass‐shift (COMS) between lesions in the estimated and “ground‐truth” on‐board 4D‐CBCT. Different on‐board projection acquisition scenarios and projection noise levels were simulated to investigate their effects on the estimation accuracy. The method was also evaluated against three lung patients.

Results

The SMM‐WFD method achieved substantially better accuracy than the GMM‐FD method for CBCT estimation using extremely small scan angles or projections. Using orthogonal 15° scanning angles, the VPD/COMS were 3.47 ± 2.94% and 0.23 ± 0.22 mm for SMM‐WFD and 25.23 ± 19.01% and 2.58 ± 2.54 mm for GMM‐FD among all eight XCAT scenarios. Compared to GMM‐FD, SMM‐WFD was more robust against reduction of the scanning angles down to orthogonal 10° with VPD/COMS of 6.21 ± 5.61% and 0.39 ± 0.49 mm, and more robust against reduction of projection numbers down to only 8 projections in total for both orthogonal‐view 30° and orthogonal‐view 15° scan angles. SMM‐WFD method was also more robust than the GMM‐FD method against increasing levels of noise in the projection images. Additionally, the SMM‐WFD technique provided better tumor estimation for all three lung patients compared to the GMM‐FD technique.

Conclusion

Compared to the GMM‐FD technique, the SMM‐WFD technique can substantially improve the 4D‐CBCT estimation accuracy using extremely small scan angles and low number of projections to provide fast low dose 4D target verification.

1. Introduction

Reducing target localization errors is important for radiation therapy treatments. Previous studies showed that reducing target localization errors was correlated with improved tumor control and reduced normal tissue toxicity.^{1, 2} This is especially important for lung cancer treatments due to the uncertainties caused by tumor motions.^{3, 4} Stereotactic body radiation therapy (SBRT) is becoming an emerging and effective treatment paradigm in radiation therapy to treat early stage non‐small cell lung cancer with promising early clinical outcome.^{5, 6} Compared to traditional fractionated radiotherapy, SBRT delivers much higher radiation dose per fraction in no more than five fractions. On‐board 4D volumetric verification of the target location before or during the treatment is critical for lung SBRT treatments due to its tight PTV margin, high fractional dose, and long treatment time.

4D Cone‐beam CT (CBCT) and 4D digital tomosynthesis (DTS) have been developed recently to provide on‐board 4D localization of moving targets.^{7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17} Conventional 4D‐CBCT reconstructed by the Feldkamp–Davis–Kress (FDK) algorithm requires the acquisition of 4D projections over a full rotation angle. This leads to long acquisition time (~a few minutes) and high imaging dose to patients (~2 cGy at isocenter and skin dose ~1 −3.5 cGy).¹² Additionally, the gantry may not be cleared to perform the full rotation scan especially when imaging tumors in the peripheral region. 4D‐DTS acquires only limited angle projection data for reconstruction; therefore, it requires much less scan time and lower imaging dose. However, 4D‐DTS is limited by its degraded resolution along the plane‐to‐plane direction without full volumetric information.^{15, 18}

Previously, a CBCT estimation method using global motion‐modeling and free‐form deformation (GMM‐FD) was developed to estimate 4D‐CBCT from limited angle projections using prior knowledge and deformation models.^{19, 20} One limitation of this method is that the global PCA model assumes a fixed correlation between motion patterns of different anatomical structures in the body from planning‐CT to on‐board CBCT, which may not be true. The invalidation of this assumption led to estimation errors in the final results when the scan angle was less than 30° orthogonal. This prevents us from further reducing the scan angles to reduce the imaging dose and improve the efficiency of the technique for inter‐ or intrafraction verification of the target location.

In this study, a new structural PCA‐based motion modeling method was developed to improve the accuracy of the motion modeling by accounting for potential relative motion pattern changes between the target and the body from simulation to treatment. Weighted free‐form deformation was employed to introduce flexibility in adjusting the weighting of different regions in the data fidelity constraint based on the clinical interests. The accuracy of the developed method was evaluated for different patient scenarios and scanning parameters using the XCAT phantom, and was compared with the GMM‐FD method developed previously.

2. Methods and materials

In the GMM‐FD method developed previously, each phase of the new on‐board CBCT (CBCT_new) is considered as a deformation of the CT volume (CT_prior) acquired previously for treatment planning. The CBCT_new at each phase is generated by deforming CT_prior using a deformation field map (DFM).

$$CBC{T}_{new}(i,j,k)=C{T}_{prior}\left(i+D_x(i,j,k),j+D_y(i,j,k),k+D_z(i,j,k)\right)$$ (1)

D_x, D_y, and D_z represent the deformation fields along the three canonical directions of the Cartesian coordinate system.

To solve for the optimal deformation field, we use a data fidelity constraint which requires the DRRs of the CBCT_new to match with the acquired on‐board projections. The GMM‐FD method developed previously uses two deformation models to solve the DFM: motion‐modeling and free‐form deformation. This study has two aims: (1) to develop a motion modeling method that better models the relative motion between the tumor and the body, and (2) to add weightings to a region of interest (ROI) around the tumor within the data fidelity constraint of the free‐form optimization to better estimate tumor volume.

2.A. Structural‐based PCA motion modeling

First, the end‐expiration phase of an n‐phase 4D‐CT previously acquired for planning is selected as CT_prior in this study due to its relative stability. All the other (n−1) phases of the 4D‐CT are deformed to CT_prior using deformable image registration software to obtain (n−1) DFMs. The DFMs are divided into two structures: tumor and body excluding tumor (called ‘body’ from here on out). To determine the region of the tumor structure, the internal target volume (ITV) was estimated from the 4D‐CT, and then the tumor region used for the structural motion modeling was calculated by taking a rectangular region around the ITV by expanding about 10 mm in the lateral direction, and 15 mm in the AP and SI directions. Then, principal motion modes $\{{\tilde{D}}_{0,tumor}^j\}$ and $\{{\tilde{D}}_{0,body}^j\}$ are extracted from the DFMs for the two structures based on principal component analysis (PCA). The deformation field map, D is represented by a weighted linear combination of the first three principal motion modes for each structure shown in Eq. (2).

$$D=D_{0,ave}+\sum _{j=1}^3{w}_{j,tumor}{\tilde{D}}_{0,tumor}^j+\sum _{j=1}^3{w}_{j,body}{\tilde{D}}_{0,body}^j$$ (2)

D _0,ave is the average of DFMs obtained from 4D‐CT, as explained above. The weightings $w_{j,tumor}$ and $w_{j,body}$ of the PCA eigenvectors are structure specific, and they are the variables to be solved in the algorithm. The data fidelity constraint is used to solve for $w_{j,tumor}$ and $w_{j,body}$, as shown in Eq. (3).

$$M\ast CBC{T}_{new}(D,C{T}_{prior})=P$$ (3)

M represents the projection matrices that project the 3D volume CBCT_new to digitally reconstructed radiographs (DRRs) according to the cone‐beam geometry. P is the on‐board projection data acquired. In the clinic, the data fidelity constraint, as shown in Eq. (3), may not be satisfied due to errors caused by the gray level difference between the DRRs and the on‐board projections and image artifacts. To solve this problem, we use the normalized cross correlation (NCC) metric for the data fidelity constraint, as was used in our previous study.²⁰ The data fidelity constraint is then enforced by minimizing the negative value of the NCC as shown in the following objective function:

$$f(D)=-NCC\left(M\ast CBC{T}_{new}(D,C{T}_{prior}),P\right)$$ (4)

A gradient descent optimizer is adopted to minimize the objective function shown in Eq. (4). To maintain the smoothness of the deformation field around the boundary between the tumor and body structures, a smoothing constraint is applied after each iteration of the data fidelity optimization. The smoothing constraint is to minimize the deformation energy around the boundary between the two structures defined in the motion model. The deformation energy of the entire DFM can be defined by Eq. (5).²¹

$$E(D)={\sum }_{i=1}^{n_i}{\sum }_{j=1}^{n_j}{\sum }_{k=1}^{n_k}{\sum }_{m=1}^3\left({\left(\frac{\mathit{\partial }{D}_m(i,j,k)}{\mathit{\partial }x}\right)}^2+{\left(\frac{\mathit{\partial }{D}_m(i,j,k)}{\mathit{\partial }y}\right)}^2+{\left(\frac{\mathit{\partial }{D}_m(i,j,k)}{\mathit{\partial }z}\right)}^2\right)$$ (5)

2.B. Weighted free‐form deformation

After the motion modeling optimization, a free‐form deformation model is applied to better fine tune the deformation field voxel by voxel. A more comprehensive analysis of the methods and the implementation of the original free‐form deformation algorithm can be found in.¹⁹ In brief, the free‐form deformation model allows each voxel to move independently to meet the data fidelity constraint. Deformation energy [Eq. (5)] of the entire deformation field is also minimized in the process to regulate the DFMs and preserve their smoothness.

In this study, the FD part of the GMM‐FD method was improved by introducing additional weightings in the target region in the data fidelity constraint of the free‐form optimization. The weightings were added within a region of interest (ROI) around the tumor in the on‐board projections. These weightings give more flexibility in adjusting the importance of matching to different regions in the projection data in the data fidelity constraint based on the clinical interests. The objective function of the data fidelity constraint now becomes the following:

$$f(D)=-[(1-w)NC{C}_{global}+wNC{C}_{ROI}]$$ (6)

In Eq. (6), w is the weighting coefficient, which ranges from 0 to 1. The ROI is chosen by selecting a region around the planned tumor positions in the projections with a ~10–15 mm margin added around the tumor. One fixed ROI was selected for a given scan angle since the angular dependence of the ROI location is minimal for the very small scan angles used. For examples, with scan angles of orthogonal‐view 15°, one ROI was selected for the projections from 0–15°, and a second ROI was selected for projections from 90–105°. If the scan angle is single‐view 15°, there would be one ROI for the entire 0–15° projections.

The goal of the weighted free‐form deformation optimization is now to find the deformation field map D satisfying Eq. (7), subject to the new data fidelity constraint shown in Eq. (8)

$$D=\text{argmin}E(D)$$ (7)

where E(D) is the deformation energy.

$$f(D)=1-[(1-w)NC{C}_{global}+wNC{C}_{ROI}]\le \mathit{\epsilon }$$ (8)

ε here accounts for the fact that DRRs cannot be exactly matched to on‐board projections even when the DFMs are perfect. Equation (7) is applied to find the smoothed DFMs by decreasing the deformation energy while reducing the data fidelity error. To solve the constrained optimization problem, an adaptive steepest descent free‐form deformation (ASD‐FD) algorithm is used similar to the one used in the previous work.¹⁹ The deformation energy minimization and the data fidelity constraint are enforced consecutively through gradient descent optimization to adaptively control the step size of the deformation energy minimization to reach final convergence.

The final deformation field is then applied to the CT_prior image using Eq. (1) to obtain that CBCT_new image. Note that the projection data P in the equations are sorted into different phase bins, and the proposed method is applied to projection data from individual phase bins to obtain the CBCT images at each phase.

2.C. Evaluation study

Studies using a digital anthropomorphic phantom, XCAT, and three patients' data²² were conducted to evaluate the accuracy of the new structural‐based motion modeling and weighted free‐form deformation method.

2.C.1. Simulation study using 4D digital extended‐cardiac torso phantom (XCAT)

A digital anthropomorphic phantom, XCAT, was used to simulate the prior 4D‐CT set, on‐board CBCT images, and on‐board CBCT projections. XCAT uses nonuniform rational B‐spline surfaces to model detailed human anatomy based on databases from the National Library of Medicine and patient datasets.²³ The respiratory motion of both the body volume and user defined lesion volume of the 4D XCAT images can be controlled separately by two respiratory curves: the diaphragm curve and the chest wall curve. The diaphragm curve mainly determines the motion in the superior‐inferior (SI) direction and the chest wall curve mainly controls the motion in the anterior‐posterior (AP) direction.

Prior 4D‐CT simulation

A spherical lesion of 30 mm diameter was simulated in the middle of the lung in XCAT. Both the body volume and lesion volume were simulated to move according to the same diaphragm and chest wall curves with a respiratory cycle of 5 s. The peak‐to‐peak amplitudes of the diaphragm curve and the chest wall curve were set to 3 and 2 cm, respectively. This corresponds to lesion peak‐to‐peak amplitude of 0.8 cm in SI direction and 1.5 cm in AP direction. There was no lateral motion. A ten‐phase 4D‐CT was then simulated as the prior 4D‐CT. The 4D‐CT volumes were simulated using a monochromatic CT source spectrum with the energy set to 40 keV, in order to approach the effective energy of a ~120 kVp polychromatic spectrum used in clinical CT scans. The CT volume of each phase was composed of 256 × 256 × 150 voxels, with each voxel measuring 1.67 × 1.67 × 1.67 mm in dimension. The end‐expiration phase of the prior 4D‐CT was selected as CT_prior.

On‐board volume and cone‐beam projection simulation

On‐board patient 4D‐CBCT sets were generated with the same patient parameters as 4D‐CT. To simulate on‐board volume sets to reflect different on‐board respiratory or anatomical variations, eight patient scenarios were generated.

1. Body volume and lesion move according to the same diaphragm curve and chest wall curve, but peak‐to‐peak amplitude of diaphragm curve changes to 2 cm and that of the chest wall curve changes to 1.2 cm. This corresponds to lesion peak‐to‐peak amplitude of 0.8 cm in SI direction and 1 cm in AP direction.

2. Based on scenario 1, also with lesion's diameter shrinking to 25 mm.

3. Based on scenario 1, also with lesion's diameter expanding to 40 mm.

4. Based on scenario 1, also with lesion's average position shifted in SI direction by 8 mm.

5. Based on scenario 1, also with lesion's average position shifted in AP direction by 8 mm.

6. Based on scenario 1, also with lesion's average position shifted in SI, AP and lateral directions by 5 mm each

7. Based on scenario 1, but with lesion having 20% phases shift relative to the body volume respiratory cycle.

8. Body volume and lesion move according to different diaphragm and chest wall curves: the peak‐to‐ peak amplitudes of the diaphragm curve for body and lesion are 2 and 4 cm, respectively; and those of chest wall curve for body and lesion are 1.2 and 3 cm respectively. The lesion peak‐to‐peak amplitude is 1.2 cm in SI direction and 2.2 cm in AP direction.

Based on the simulated ground‐truth 4D‐CBCT, on‐board cone‐beam projections of different phases were also simulated based on Siddon's ray racing techniques.^{24, 25} The source to isocenter distance was set to 100 cm, and the isocenter to detector distance was set to 50 cm. Each projection contains 512 × 384 pixels, with each pixel being 0.78 × 0.78 mm in dimension. Note that the projections were all simulated as full‐fan acquisition which led to a limited field of view (FOV) of ~27 diameter (axial) and ~20 cm length (longitudinal). Part of the phantom was truncated and outside of the FOV.

Weighting coefficient study

To investigate the effects of weighting coefficients used in the free‐form deformation on the estimation accuracy, w values in Eq. (8) were set to 0, 0.1, 0.2, 0.5, and 1 for different XCAT scenarios for comparison.

Scan angle study

To determine the effects of different scan angles on the estimated results of the structural motion modeling and weighted free‐form deformation (SMM‐WFD) technique in comparison to the previous global motion modeling and free‐form deformation (GMM‐FD) technique, projections of different acquisition scenarios were generated:

1. Single‐view 30°

2. Orthogonal‐view 15°

3. Orthogonal‐view 10°

4. Orthogonal‐view 5°

For the single‐view 30° acquisition, projections were acquired within one limited scan angle along the AP direction. For the orthogonal‐view acquisitions, projections were acquired within two orthogonal scan angles: AP and left‐lateral directions. Two angular spacing techniques were evaluated. The first approach was to set the angular spacing between projections to around 0.5° for all the different acquisition angles. This resulted in acquiring 51, 52, 42, and 22 projections for single‐view 30°, orthogonal‐view 15°, orthogonal‐view 10°, and orthogonal‐view 5°, respectively. The second approach was to fix the total number of projections for each acquisition scenario to be 52 projections to investigate the effects of scan angle while fixing the imaging dose. This resulted in setting the angular spacing between projections to 0.6°, 0.4° and 0.2° for orthogonal‐view 15°, orthogonal‐view 10°, and orthogonal‐view 5°, respectively.

Projection number study

To investigate how sparseness of the projection sampling affects the SMM‐WFD technique, different numbers of projections were also simulated for orthogonal‐view 15° acquisition and orthogonal‐view 30° acquisition. For the orthogonal‐view 15° acquisition, 52, 22, 12, and 4 projections were simulated and used in evaluation. For the orthogonal‐view 30° acquisition, 102, 52, 26, 14, 8, and 4 projections were simulated and used in evaluation.

Lesion contrast study

To investigate the effects of lesion contrast on the estimation accuracy, various lesions to lung contrast values were investigated. The lung HU value was set to −700, and lesion HU value was set to −100, −50, 0, 50, and 100 as typical tumor HU values vary between −100 and 100. This corresponds to a lesion to lung contrast of 600, 650, 700, 750, and 800, respectively.

Noise study

To investigate the effects of noise on the estimation accuracy, we incorporated noise in the projections for the study using patient scenario 2 as an example, similar to the noise study performed in.¹⁹ Specifically, noise was simulated according to Eq. (9) and added to the projection images directly.

$$P_i^{\prime }=-{log}_e\left(\frac{\text{Poisson}(I_0{e}^{-P_i})+\text{Normal}(0,{\mathit{\sigma }}^2)}{I_0}\right)$$ (9)

P _i is the ray sums of the attenuation coefficients at point i of each projection. I ₀ is set to 10⁵ to signify intensity of incident photons. Noise was added with the variation level in the normal distribution (σ ²) equal to 0, 10, 50, and 100.

2.C.2. Patient study

Three patients' data were also used in this study. The images for all three patients were acquired under an IRB‐approved protocol at MD Anderson Cancer Center. The 4D‐CTs were acquired on a CT scanner (LightSpeed, GE Healthcare, Milwaukee, WI) in cine mode.²² Scan parameters were set at 120 kVp, 100 mA, 0.5 s cine time, and cine duration of average breathing cycle plus 1 s. For 4D‐CBCT acquisition, 200° on‐board full‐fan projections of each patient were acquired within 2 weeks from the 4D‐CT acquisition, using an adaptive‐speed slow gantry rotation setting²² using 120 kVp, 80 mA, and 25 ms. The projections were phase‐sorted using an in‐house developed Fourier‐transform‐based method.^{26, 27} The average sampling intervals of phase‐binned projections for patient 1, 2, and 3 are 0.9 ± 1.0°/proj, 0.9 ± 0.9°/proj, and 1.1 ± 1.2°/proj, respectively. Full 200° projections were used to reconstruct the reference clinical 4D‐CBCT and orthogonal‐view 10° projections around the posterior‐anterior (PA) (170°~180°) and the right‐lateral (RL) (260°~270°) directions were used for the estimation technique.

2.C.3. Evaluation methods

The estimation accuracy for lesion location and volume in the on‐board CBCT was evaluated at the end‐inspiration phase since this phase has the largest deformation from end‐expiration CT_prior images, and therefore, the largest estimation errors. This was proven in the previous work.¹⁹

For the XCAT study, the lesions were automatically contoured based on a threshold voxel value in both the estimated images and the ground‐truth CBCT images for comparison. Two metrics were defined to quantify the accuracy of the estimated lesion volume: volume percent difference (VPD) and center‐of‐mass‐shift (COMS).

$$\text{VPD}=\frac{|V\cup V_0-V\cap V_0|}{V_0}\ast 100\%$$ (10)

V is the lesion volume contoured in the estimated image and V ₀ is that contoured in the “ground‐truth” image.

$$\text{COMS}=\sqrt{\mathrm{\Delta }{x}^2+\mathrm{\Delta }{y}^2+\mathrm{\Delta }{z}^2}$$ (11)

∆x, ∆y, and ∆z are center‐of mass distances from V to V ₀.

These accuracy metrics were used to compare between the following methods: (a) global PCA motion modeling (GMM) versus structural PCA motion modeling (SMM) to study the effects of structure‐based motion modeling; (b) structural PCA motion modeling with free‐form deformation with no weights (SMM‐FD) versus structural PCA motion modeling with weighted free‐form deformation (SMM‐WFD) to study the effects of weighting in FD; (c) global PCA motion modeling and free‐form deformation (GMM‐FD) versus structural PCA motion modeling with weighted free‐form deformation (SMM‐WFD) to study the combined effects of structure‐based motion modeling and weighted FD; (d) Varying the weightings within the free‐form deformation of the SMM‐WFD technique; (e) Varying the scanning angles; (f) Varying the projection numbers; and (g) Varying amounts of noise in the projection data.

3. Results

3.A. Structural PCA

Figure 1 shows the images for prior image, ground‐truth (GT) CBCT, estimated CBCT using the global PCA motion model (GMM), and estimated CBCT using the structural based PCA motion model (SMM) based on orthogonal‐view 15° scan angle for (a) XCAT scenario 5, (b) XCAT scenario 6, and (c) XCAT scenario 8. Figure 2 shows the subtraction images for GT minus prior, GT minus estimated with GMM and GT minus estimated with SMM for (a) XCAT scenario 5, (b) XCAT scenario 6, and (c) XCAT scenario 8. The images used for ground‐truth CBCT and estimated CBCTs were images of the end‐inspiration phase as to show the most deformation from the prior volume.

Figure 1.

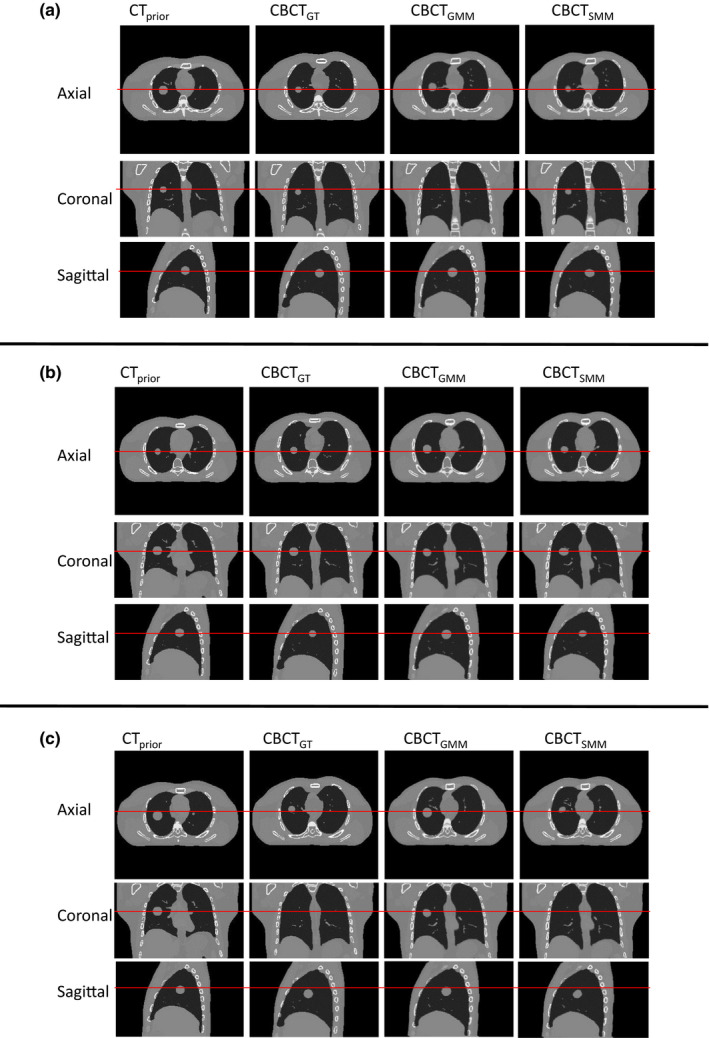
Comparison of CBCT _prior at end‐expiration phase, ground‐truth CBCT (CBCT_GT ) at end‐inspiration phase, estimated CBCT using global MM (CBCT_GMM ) and estimated CBCT using structural MM (CBCT_SMM ) using orthogonal‐view 15° scan angle with 52 projections for (a) XCAT scenario 5, (b) XCAT scenario 6, and (c) XCAT scenario 8. [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 2.

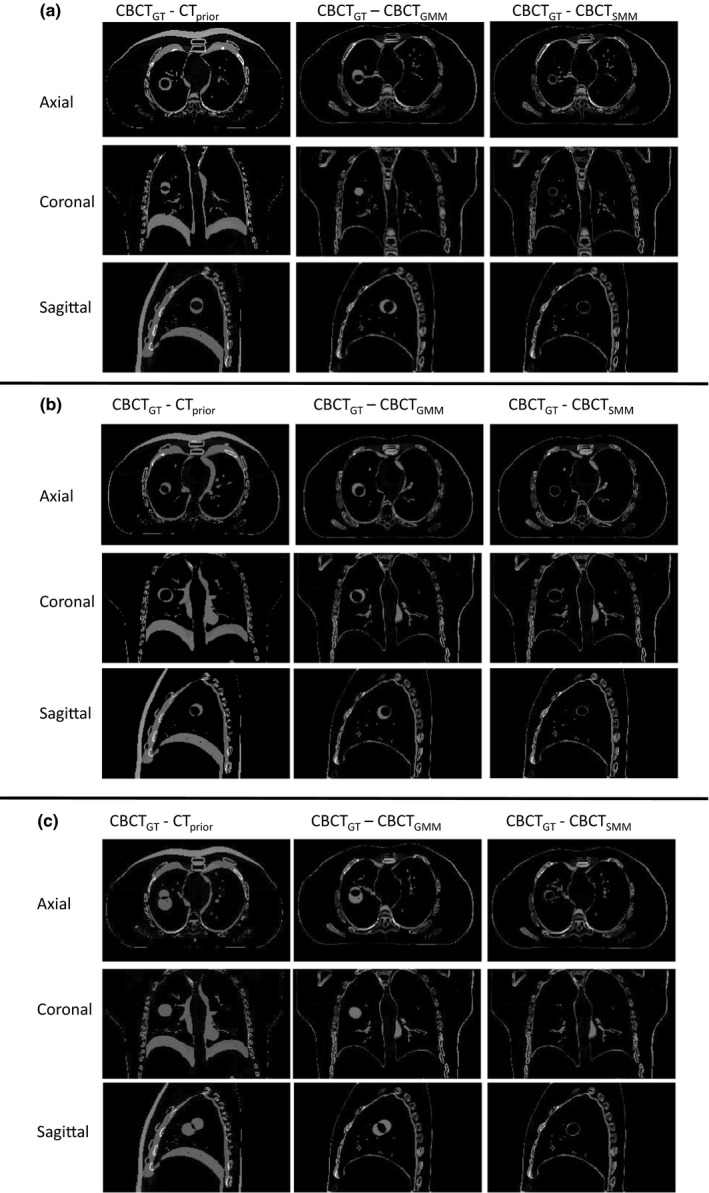
Subtraction images for axial, coronal, and sagittal images shown in Fig. 1(a), (b), and (c), respectively.

Table 1 shows the VPD and the COMS results from CBCTs estimated using GMM and SMM for all eight XCAT scenarios. The results shown in Table 1 are generated from the estimated CBCTs in the end‐inspiration phase. Using global PCA motion models resulted in a mean VPD and mean COMS of 64.71 ± 30.80% and 5.70 ± 3.92 mm across all eight XCAT scenarios using orthogonal‐view 15° scan angle, and 63.72 ± 31.30% and 5.96 ± 383 mm using single‐view 30°. Using the structural‐based PCA motion models resulted in a mean VPD and mean COMS of 21.02 ± 9.52% and 0.84 ± 0.55 mm using orthogonal‐view 15° scan angle, and 31.79 ± 17.62% and 2.69 ± 2.31 mm using single‐view 30°.

Table 1.

VPD and COMS for XCAT scenarios with CBCT estimation from global PCA motion modeling (GMM) and structural‐based PCA motion modeling (SMM) for single‐view 30° projections and orthogonal‐view 15° projections. The number of projections was 51 and 52 for single‐30° and ortho‐15° acquisitions, respectively

Scenarios			1	2	3	4	5	6	7	8
VPD (%)	Single 30°	GMM	38.29	76.25	53.76	64.04	72.25	65.91	15.73	123.50
		SMM	17.42	31.27	37.23	20.08	37.50	24.40	16.26	70.16
	Ortho 15°	GMM	28.32	78.29	53.28	69.74	79.22	75.21	18.62	115.01
		SMM	14.61	32.73	38.31	12.49	15.70	16.73	15.10	22.48
COMS (mm)	Single 30°	GMM	3.82	3.83	4.00	6.42	7.52	7.02	1.17	13.91
		SMM	1.22	1.12	3.40	1.53	3.78	1.75	0.95	7.77
	Ortho 15°	GMM	2.67	2.69	2.87	7.12	8.31	7.87	1.39	12.70
		SMM	0.44	1.30	1.99	0.43	0.70	0.80	0.68	0.40

3.B. Weighted free‐form deformation

A value of w   = 0.1 was chosen for all the results below labeled ‘SMM‐WFD’. Section 3.C. shows results with various w values. Figure 3 shows an example of the ROI chosen within a projection. Figure 4 shows the images for prior image, ground‐truth CBCT, estimated CBCT using the global PCA motion model and free‐form deformation (GMM‐FD), and estimated CBCT using the structural based PCA motion model and weighted free‐form deformation (SMM‐WFD) using orthogonal‐view 15° scan angle for (a) XCAT scenario 5, (b) XCAT scenario 6, and (c) XCAT scenario 8. Figure 5 shows the subtraction images for GT minus prior, GT minus estimated with GMM‐FD and GT minus estimated with SMM‐WFD for (a) XCAT scenario 5, (b) XCAT scenario 6, and (c) XCAT scenario 8. The images used for ground‐truth CBCT and estimated CBCTs were images from the end‐inspiration phase as to show the most deformation from the prior volume.

Figure 3.

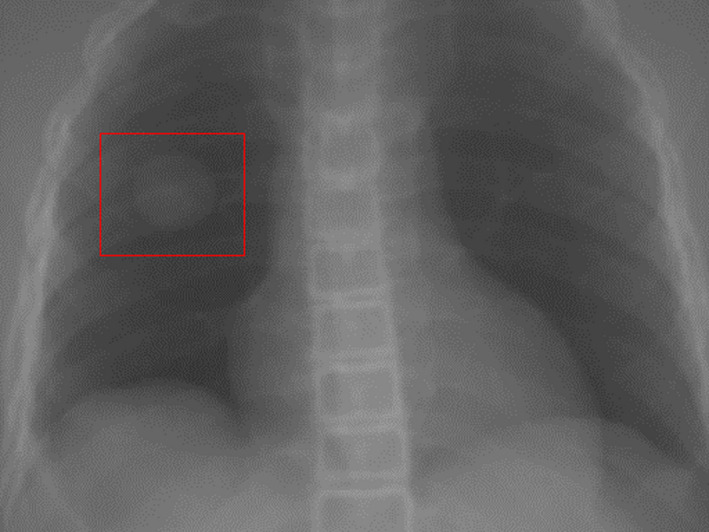
This is an example of the ROI selected within a projection image. The weightings would be applied everywhere inside the ROI within the data fidelity constraint of the free‐form deformation model. [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 4.

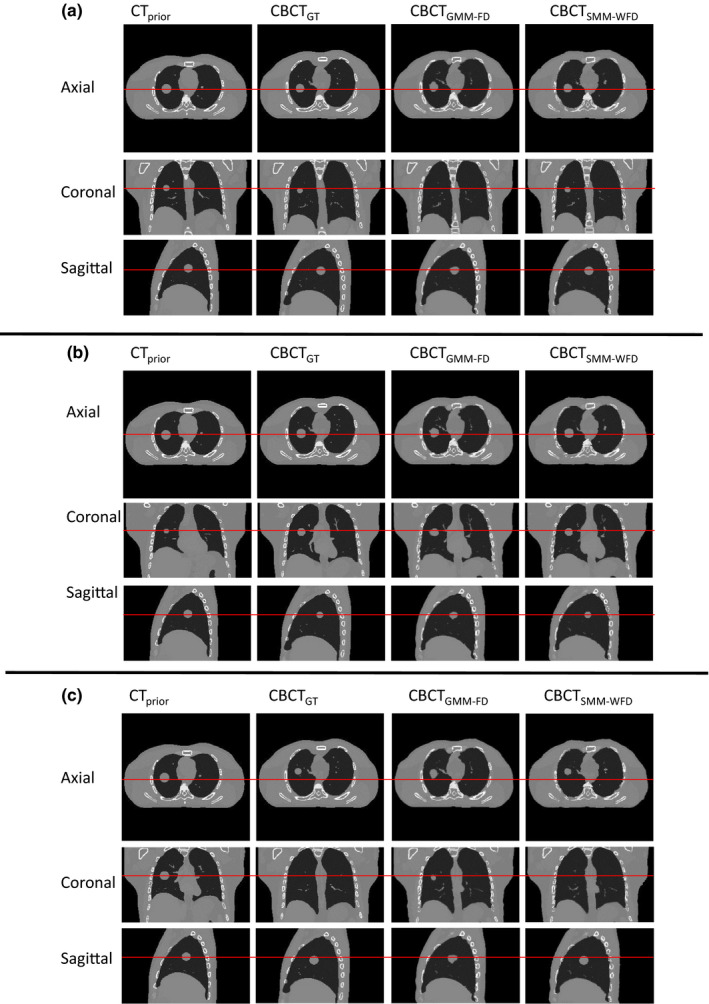
Comparison of CBCT _prior at end‐expiration phase, ground‐truth CBCT (CBCT_GT ) at end‐inspiration phase, estimated CBCT using global MMFD (CBCT_GMMFD ) and estimated CBCT using structure MM‐WFD (CBCT_{SMM ‐ WFD} ) using orthogonal‐view 15° projection acquisition with 52 projections for (a) XCAT scenario 5, (b) XCAT scenario 6, and (c) XCAT scenario 8. [Colour figure can be viewed at wileyonlinelibrary.com]

Figure 5.

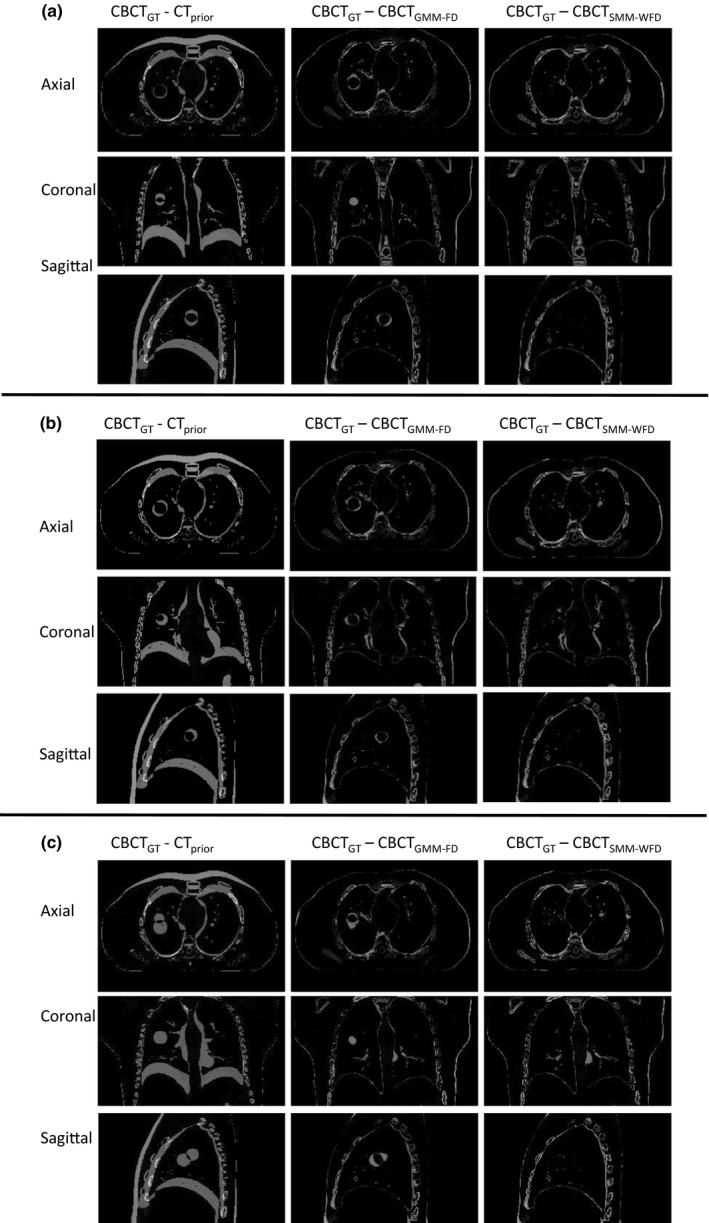
Subtraction images for axial, coronal and sagittal images shown in Fig. 4(a), (b), and (c), respectively.

Table 2 shows the VPD and the COMS results from CBCTs estimated using GMM‐FD and SMM‐WFD for all eight XCAT scenarios with single‐view 30° scan angles, and CBCTs estimated using GMM‐FD, SMM‐FD, and SMM‐WFD for all XCAT scenarios with orthogonal‐view 15° scan angels. The results shown in Table 2 are generated from the estimated CBCTs in the end‐inspiration phase. Using GMM‐FD resulted in a mean VPD and mean COMS of 25.23 ± 19.01% and 2.58 ± 2.54 mm across all eight XCAT scenarios using orthogonal‐view 15° scan angle and 32.00 ± 23.81% and 3.39 ± 3.06 mm using single‐view 30°. Using the SMM‐WFD resulted in a mean VPD and mean COMS of 3.47 ± 2.94% and 0.23 ± 0.22 mm using orthogonal‐view 15° scan angle and 13.82 ± 11.82% and 1.50 ± 1.49 mm using single‐view 30°. Using SMM‐FD resulted in a mean VPD and mean COMS of 9.96 ± 4.39% and 0.37 ± 0.20 mm using orthogonal‐view 15° scan angles.

Table 2.

VPD and COMS for XCAT scenarios with CBCT estimation from global PCA motion modeling with free‐form deformation (GMM‐FD), structural‐based PCA motion modeling with free‐form deformation (SMM‐FD), and structural‐based PCA motion modeling with weighted free‐form deformation (SMM‐WFD) for different scan angle acquisitions

Scenarios			1	2	3	4	5	6	7	8
VPD (%)	Single 30°	GMM‐FD	16.11	27.29	30.64	25.97	46.89	19.97	5.99	83.10
		SMM‐WFD	8.33	8.42	14.36	8.35	12.17	11.16	5.51	42.26
	Ortho 15°	GMM‐FD	7.67	13.86	28.93	20.47	34.09	25.17	6.24	65.44
		SMM‐FD	6.49	12.49	19.23	6.71	7.08	9.83	6.73	11.14
		SMM‐WFD	1.30	2.89	10.30	2.12	1.96	4.57	1.65	2.96
COMS (mm)	Single 30°	GMM‐FD	1.83	2.34	2.60	2.73	5.42	2.05	0.13	10.04
		SMM‐WFD	0.91	0.78	2.13	0.69	1.47	0.66	0.44	4.92
	Ortho 15°	GMM‐FD	0.44	1.03	2.28	2.06	3.95	2.76	0.08	8.03
		SMM‐FD	0.16	0.43	0.46	0.27	0.42	0.73	0.08	0.43
		SMM‐WFD	0.06	0.15	0.63	0.05	0.18	0.53	0.11	0.16

3.C. Effects of weighting coefficient

Table 3 shows VPD/COMS with weighting coefficients w = 0, 0.1, 0.2, 0.5, and 1 for XCAT scenario 2, 5, and 8. A value of w = 0.1 was chosen to use in all SMM‐WFD results since it provided the best accuracy compared to other weighting coefficient values.

Table 3.

The effects of weighting coefficient based on orthogonal‐view 15° scan angle with 52 projections using SMM‐WFD for XCAT scenarios 2, 5, and 8

w		0	0.1	0.2	0.5	1
VPD (%)	Scenario 2	12.49	2.89	3.41	6.39	6.24
	Scenario 5	7.08	1.96	2.05	4.18	4.75
	Scenario 8	11.14	2.96	3.50	5.67	6.26
COMS (mm)	Scenario 2	0.43	0.15	0.32	0.28	0.25
	Scenario 5	0.42	0.18	0.10	0.13	0.14
	Scenario 8	0.43	0.16	0.19	0.14	0.25

3.D. Effects of scanning angles

Table 4 shows the image estimation results for the SMM‐WFD technique using single‐view 30°, orthogonal‐view 15°, orthogonal‐view 10°, and orthogonal‐view 5° scan angle acquisition for all XCAT scenarios with equal spacing between projections (~0.5°). It can be observed that (a) orthogonal‐view 15° achieved substantially better results than single‐view 30° with the same total scanning angle; (b) although the estimation accuracy degrades slightly as the orthogonal‐view scan angle decreases, orthogonal‐view 10° provided high accuracies in both VPD and COMS. The mean VPD and COMS among all XCAT scenarios for single‐view 30° was 13.82 ± 11.82% and 1.50 ± 1.49 mm. The mean VPD and mean COMS among all XCAT scenarios for orthogonal‐view 15° was 3.47 ± 2.94% and 0.23 ± 0.22 mm. Using orthogonal‐view 10°, the mean VPD and mean COMS among all XCAT scenarios was 6.21 ± 5.61% and 0.39 ± 0.49 mm. Using orthogonal‐view 5°, the mean VPD and mean COMS among all XCAT scenarios was 12.64 ± 9.40% and 0.94 ± 1.03 mm.

Table 4.

VPD and COMS for XCAT scenarios with CBCT estimation from structural PCA motion modeling with weighted free‐form deformation (SMM‐WFD) technique using single‐view 30° (51 projections), orthogonal‐view 15° (52 projections), orthogonal‐view 10° (42 projections), and orthogonal‐view 5° (22 projections)

Scenarios			1	2	3	4	5	6	7	8
VPD (%)	Single 30°	51 Proj	8.33	8.42	14.36	8.35	12.17	11.16	5.51	42.26
	Ortho 15°	52 Proj	1.30	2.89	10.30	2.12	1.96	4.57	1.65	2.96
	Ortho 10°	42 Proj	2.10	5.01	18.10	2.88	3.10	11.11	2.41	5.02
	Ortho 5°	22 Proj	7.08	17.98	32.91	7.39	5.06	9.89	5.59	15.20
COMS (mm)	Single 30°	51 Proj	0.91	0.78	2.13	0.69	1.47	0.66	0.44	4.92
	Ortho 15°	52 Proj	0.06	0.15	0.63	0.05	0.18	0.53	0.11	0.16
	Ortho 10°	42 Proj	0.09	0.41	1.46	0.12	0.11	0.72	0.10	0.11
	Ortho 5°	22 Proj	0.32	0.80	3.26	0.31	0.19	0.95	0.31	1.40

Table 5 shows the image estimation results for the SMM‐WFD technique using, orthogonal‐view 15°, orthogonal‐view 10°, and orthogonal‐view 5° scan angle acquisition for all XCAT scenarios with all using 52 projections. This study is to investigate the effects of scan angle reduction when the imaging dose is fixed.

Table 5.

VPD and COMS for XCAT scenarios with CBCT estimation from structural PCA motion modeling with weighted free‐form deformation (SMM‐WFD) technique using orthogonal‐view 15°, orthogonal‐view 10°, and orthogonal‐view 5°. Each set of scan angle had 52 projections

Scenarios		1	2	3	4	5	6	7	8
VPD (%)	Ortho 15°	1.30	2.89	10.30	2.12	1.96	4.57	1.65	2.96
	Ortho 10°	2.69	2.93	16.43	2.76	7.10	6.59	2.27	4.06
	Ortho 5°	4.64	12.20	30.29	6.15	3.87	11.88	4.43	7.67
COMS (mm)	Ortho 15°	0.06	0.15	0.63	0.05	0.18	0.53	0.11	0.16
	Ortho 10°	0.07	0.12	1.47	0.08	1.16	0.58	0.11	0.19
	Ortho 5°	0.15	0.37	3.25	0.10	0.08	1.18	0.14	0.26

3.E. Effects of the projection number

Tables 6 and 7 list the image estimation results using different number of projections for orthogonal‐view 30° scan angle acquisition and orthogonal‐view 15° scan angle acquisition, respectively. XCAT scenario 2 was used in this study as it has both motion pattern change and tumor size change.

Table 6.

VPD and COMS for XCAT scenario 2 using orthogonal‐view 30° angle with varying number of projections

Projection number		102	52	26	14	8	4
VPD (%)	GMM‐FD	8.14	7.81	12.68	23.08	27.53	31.65
	SMM‐WFD	1.56	1.14	3.26	6.86	15.89	29.09
COMS (mm)	GMM‐FD	0.53	0.60	0.92	1.37	1.33	1.31
	SMM‐WFD	0.24	0.19	0.25	0.47	1.08	2.00

Table 7.

VPD and COMS for XCAT scenario 2 using orthogonal‐view 15° angle with varying number of projections

Projection number		52	22	8	4
VPD (%)	GMM‐FD	13.86	19.73	34.34	35.95
	SMM‐WFD	2.89	4.64	12.77	25.21
COMS (mm)	GMM‐FD	1.03	1.47	1.91	2.02
	SMM‐WFD	0.15	0.23	0.55	1.31

3.F. Lesion contrast study

Table 8 shows results for tumor estimation accuracy for lesion to lung contrast values of 600, 650, 700, 750, and 800. The lung HU value was set to −700, and lesion HU value was set to −100, −50, 0, 50, and 100. The SMM‐WFD method achieved high accuracy for all tumor HU values typically seen in the clinics. The estimation accuracy was improved as the HU values of the tumor increased with better contrast to the lung.

Table 8.

VPD and COMS values for XCAT scenario 2 with various amounts of lesion contrast. Each column corresponds to HU_lesion set to −100, −50, 0, 50 and 100, respectively. Calculations were done using the SMM‐WFD technique with 15° orthogonal scan angles (52 projections)

HUlesion	−100	−50	0	50	100
VPD (%)	6.53	4.35	3.36	2.89	1.75
COMS (mm)	0.23	0.17	0.23	0.15	0.14

3.G. Noise study

Figure 6 and Table 9 show the results of the noise study. No noise correction like smoothing or filtration has been applied in the image estimation process. The noise level of that within the Poisson distributed noise (shown in Fig. 6(b)) was closer to that seen in a real clinically acquired projection.

Figure 6.

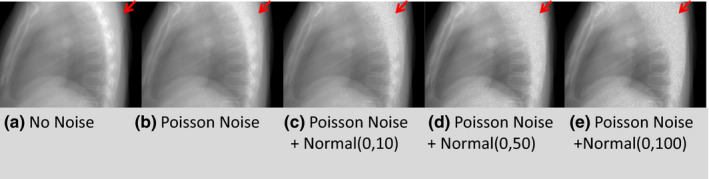
Visual comparison of the same projection images for XCAT scenario 2. The arrows indicate the level of noise in the bony region of the projection images. The noise level gradually increased from left to right: (a) No noise, (b) Poisson noise, (c) Poisson noise + normal(0, 10), (d) Poisson noise + normal(0, 50), and (e) Poisson noise + normal(0, 100). [Colour figure can be viewed at wileyonlinelibrary.com]

Table 9.

VPD and COMS for XCAT scenario 2 using orthogonal‐view 15° angle (52 projections) and orthogonal‐view 30° angle (102 projections) for various levels of noise within the projection data using both the GMM‐FD and SMM‐WFD methods

			No noise	Poiss noise	Poiss noise + norm(0, 10)	Poiss noise + norm(0, 50)	Poiss noise + norm (0, 100)
VPD (%)	Ortho 30°	GMM‐FD	8.14	12.25	14.71	15.52	19.02
		SMM‐WFD	1.56	6.29	6.39	8.37	11.78
	Ortho 15°	GMM‐FD	13.86	28.48	27.06	31.55	33.25
		SMM‐WFD	2.89	15.94	15.85	15.33	17.36
COMS (mm)	Ortho 30°	GMM‐FD	0.53	1.05	1.27	1.31	1.53
		SMM‐WFD	0.24	0.40	0.48	0.55	0.54
	Ortho 15°	GMM‐FD	1.03	2.08	2.00	2.22	2.05
		SMM‐WFD	0.15	0.43	0.36	0.31	0.41

3.H. Patient study

Figure 7 shows the results from the patient study. ‘CT_Prior’ image refers to the end‐expiration phase image of the 4D‐CT, ‘Clinical CBCT’ image refers to the CBCT image at end‐expiration phase reconstructed with 200° projections using FDK, ‘GMM‐FD’ image refers to the CBCT image at end‐expiration phase reconstructed with 10° orthogonal scan angles using the GMM‐FD technique, and ‘SMM‐WFD’ image refers to CBCT image at end‐expiration phase reconstructed with 10° orthogonal scan angles using the SMM‐WFD technique. It can be observed that in each case illustrated in Fig. 7, the SMM‐WFD technique achieved a better match with the clinical CBCT image than the GMM‐FD technique when using only 10° orthogonal scan angles.

Figure 7.

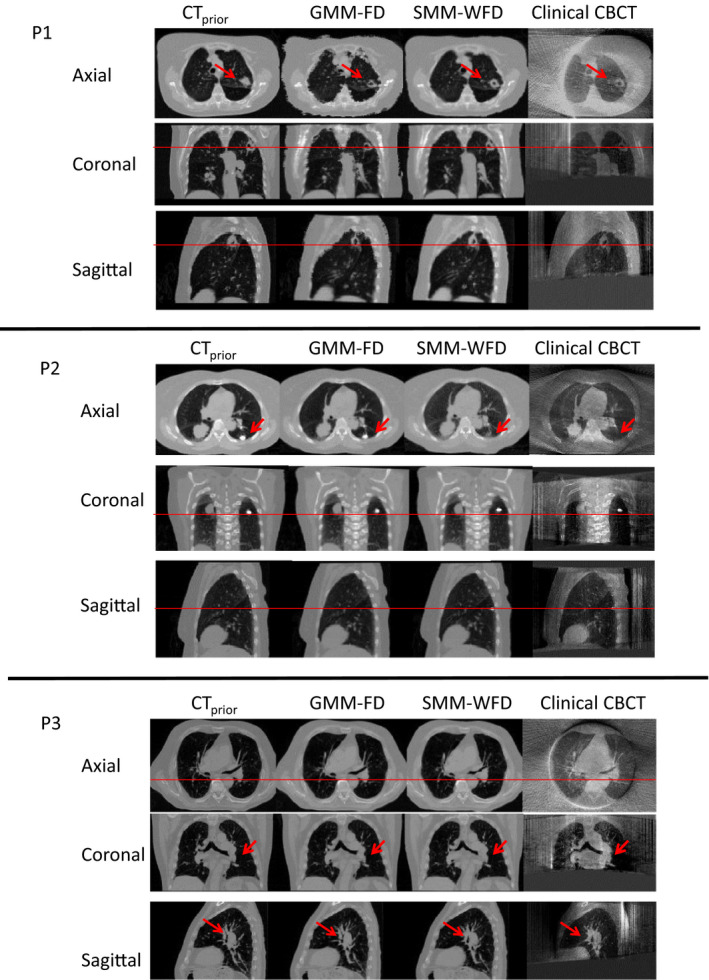
Patient image results for patient 1 (P1), patient 2 (P2), and patient 3 (P3). ‘CT_{P rior}’ image refers to the end‐expiration phase image of the 4D‐CT, ‘Clinical CBCT’ image refers to the CBCT image reconstructed with 200° projections using FDK in the end‐expiration phase, ‘GMM‐FD’ image refers to the end‐expiration phase CBCT image reconstructed with 10° orthogonal scan angles using the GMM‐FD technique, and ‘SMM‐WFD’ image refers to the end‐expiration phase CBCT image reconstructed with 10° orthogonal scan angles using the SMM‐WFD technique. The arrows and horizontal line provide references for evaluating the tumor volume differences in the images. [Colour figure can be viewed at wileyonlinelibrary.com]

4. Discussions

4.A. SMM‐WFD vs GMM‐FD

The structural‐based PCA motion modeling is innovative in that it decouples the correlation between motion patterns of different anatomical structure and allows relative motion between anatomical structures to change from CT to CBCT, which is more clinically realistic. The weighted free‐form deformation gives extra freedom for adjusting weightings of different regions in the data fidelity constraint to optimize the image estimation accuracy of the region of the most clinical interests. The structural‐based PCA motion modeling along with the weighted free‐form deformation methods can improve the accuracy of the 4D‐CBCT estimation substantially, especially when using extremely small scan angles or low number of projections. This allows us to significantly reduce the imaging dose and time to achieve fast 4D‐CBCT imaging for either inter‐ or intrafraction verification to improve the treatment accuracy, which is especially critical for SBRT treatments.

Results in Table 1 showed that the CBCT estimation based on structural‐based PCA motion modeling achieved better accuracy for tumor localization than that of the global PCA motion modeling. Results in Table 2 showed that the CBCT estimation based on using weightings in the free‐form deformation optimization achieved better accuracy than when all structures were weighted equally. This is because more importance was given to the areas within the projection data that included the tumor volume during the optimization.

Regarding the weighting factor used in the weighted free‐form deformation method, Table 3 showed the estimation improved significantly from w = 0 to w = 0.1, and then slightly decreased from w = 0.1 to w  = 1 for different XCAT scenarios. Therefore, w = 0.1 was used for the SMM‐WFD method in all other studies since it provided the most accurate tumor estimation.

In our studies, we consider 20% VPD and 2 mm COMS as the criteria to judge if the estimation accuracy of the method is clinically acceptable. To justify that, we simulated different amount of shift of the 3 cm diameter tumor used in the XCAT study to simulate different localization errors of the tumor. Calculation showed that a 1 mm, 2 mm, and 3 mm COMS of the tumor correspond to VPD = 10.32%, 19.37%, and 29.27%, respectively. Considering the voxel size of 1.67 mm³ in the simulation study, and the fact that a 5 mm ITV‐PTV margin is typically used in lung SBRT, we believe a clinically acceptable target localization error is < 2 mm, which corresponds to VPD ~ = 20% and COMS = 2 mm.

4.B. Effects of scanning angles

Table 2 showed that orthogonal‐view 15° scan angle yielded more accurate estimation than single‐view 30° scan angle for both GMM‐FD and SMM‐WFD. Single‐view 30° still gave accurate estimation for seven out of the eight XCAT scenarios when using the SMM‐WFD technique, whereas single‐view 30° only gave accurate estimation for two out of the eight XCAT scenarios when using the GMM‐FD technique. Tables 4 and 5 showed that reducing the scan angles to orthogonal‐view 10° and orthogonal‐view 5° degraded the estimation accuracy for SMM‐WFD as compared to using orthogonal‐view 15° scan angles. However, the SMM‐WFD method was still able to achieve less than 20% for VPD and 2 mm for COMS for all XCAT scenarios using orthogonal‐view 10° scan angles. In contrast, the GMM‐FD method failed for most XCAT scenarios even using orthogonal‐view 15° scan angles, as shown in Table 2.

4.C. Effects of projection number

Results in Tables 6 and 7 showed that the SMM‐WFD method is much more robust than the GMM‐FD method against reduction in the projection number. The GMM‐FD technique had a significant decrease in accuracy when there were less than 52 projections using orthogonal‐view 15° scan angles or less than 26 projections using orthogonal‐view 30° scan angles. In contrast, the SMM‐WFD technique was robust against reduction of projection numbers down to only 8 projections in total for both orthogonal‐view 30° scan angles and orthogonal‐view 15° scan angles. Note that this brings projection number down significantly in comparison to Ref. 19 which found that 26 projections using orthogonal‐view 30 ° scan angle were needed to maintain the estimation accuracy. It is important to mention that the number of projections here only estimates one phase image of the on‐board 4D‐CBCT, so for 10 phases, the number of projections would need to be multiplied by 10 to estimate the whole 4D‐CBCT set. Using 8 projections for one phase image (or 80 projections for entire 4D set) is much smaller than that of a traditional static CBCT scan. This indicates a substantial reduction in the imaging dose to patients.

4.D. Effects of noise

Results in Table 9 showed that the SMM‐WFD method was more robust than the GMM‐FD method against increasing levels of noise. In both estimation methods, the estimation accuracy declines as the noise level increases. Both the SMM‐WFD and GMM‐FD methods achieved better accuracy with increased noise when using orthogonal‐view 30° scan angles than using orthogonal‐view 15° scan angles. Note that the SMM‐WFD technique achieved VPD < 20% and COMS< 2 mm even in the highest amounts of noise for the orthogonal‐view 15° scan angle.

4.E. Convergence speed study

Figure 8 shows the convergence plots for estimation of XCAT scenario 8 based on SMM‐WFD and GMM‐FD using orthogonal‐view 15° scan angle with 52 projections. The convergence speed was similar for the two methods. As shown in Fig. 8, the data fidelity error of the ROI of the projection images was significantly less for the SMM‐WFD technique as compared to the GMM‐FD technique.

Figure 8.

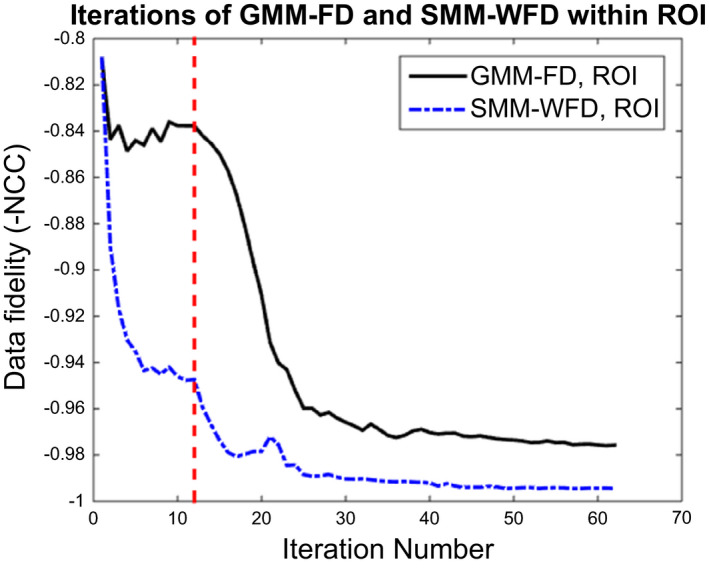
Data fidelity errors of the GMM‐FD and SMM‐WFD techniques for image estimation of XCAT scenario 8 using orthogonal‐view 15° scan angle with 52 projections. The dashed line shows where the motion modeling optimization converges, and where the free‐form deformation starts. The data fidelity error was calculated within the ROI around the tumor in the projection data. [Colour figure can be viewed at wileyonlinelibrary.com]

4.F. Clinical impact of reducing scanning dose and scanning time

Reducing the scanning angle and number of projections needed to accurately reconstruct 4D‐CBCT can substantially reduce the scanning dose and scanning time for the patient. Santoso et al. found that for a full 4D‐CBCT acquisition using about 3000 projections resulted in an absorbed dose of ~8.5 cGy.²⁸ In comparison, our patient study showed that the SMM‐WFD method was able to reconstruct 4D‐CBCT using 250 projections in total (25 projections per phase) acquired within orthogonal‐view 10° scanning angles. If we assume a linear relationship between projection number and dose, the SMM‐WFD method would result in a scanning dose of ~0.7 cGy, which is approximately a 12‐fold reduction of the conventional 4D‐CBCT dose.

The total scanning time of the SMM‐WFD method includes the scanning time for each limited scan angle and the gantry rotation time between the orthogonal scan angles. The scanning for each limited angle will be performed with slow gantry rotation speed, while the gantry rotation between the orthogonal scan angles will be performed with the fastest gantry rotation speed, i.e., 6°/s. With this in consideration, we can calculate the total scanning time as the following:

1. Limited angle slow gantry rotation scan: Slow gantry rotation mode was used for the limited angle scan in both XCAT and patient studies. We can estimate total scanning time, t, to be the number of projections for each phase, n, multiplied by the breathing cycle, T. The gantry rotation speed, ω, can be calculated as:

   $$\mathrm{\omega }=\frac{\mathit{\alpha }}{\mathrm{t}}=\frac{\mathit{\alpha }}{\mathrm{nT}},$$

   where α is the scanning angle. For the XCAT scenario with α = 15°, n = 4, and T = 5 s, we can calculate the gantry rotation speed to be 0.75°/s with a scanning time of t = 20 s. In the patient study, the 4D‐CBCT scan time for the 200° slow gantry rotation ranged from 3.3 to 6.6 min for the average breath cycle of 3–6 s.²² Based on this, we can proportionally calculate that it would take ˜10–20 s for each 10° scanning angle in the orthogonal‐view 10° acquisition.

2. Gantry rotation between orthogonal scan angles: Since the gantry rotates at 6°/s between the orthogonal scan angles, the rotation time would be ˜ 90°/(6°/s) = 15 s.

Overall, the total scanning time for our method in the patient study would be 35–55 s, including 10–20 s for the first 10° scan, 15 s for rotation between scans, and 10–20 s for second 10° scan. This represents a substantial reduction of the 3.3–6.6 min scanning time for the full rotation 4D‐CBCT scan.

4.G. Limitations

It is important to note that this study first aimed at investigating the feasibility of reducing scan angles and number of projections for accurate on‐board 4D‐CBCT estimation and localization using a structural‐based PCA motion model and weighted free‐form deformation. Two structures were used in the motion model in this study – tumor and body excluding tumor. Results using these two structures yielded accurate estimation for on‐board CBCT imaging using as few as orthogonal‐view 10° scan angles, or as few as 8 projections using orthogonal‐view 15° scan angle, in comparison with orthogonal 30° and 26 projections needed for the previous GMM‐FD method. Further investigation will be carried out to build a more comprehensive multiple organ‐specific structures to model the motion pattern of each organ to further improve the estimation accuracy of the method using extremely small scan angles or low number of projections.

Our current studies have been focusing on the application of the developed technique for imaging lung cancer, which typically has high contrast between the tumor and the surround lung tissues. It may be more challenging to apply this technique to reconstruct soft tissue structures in a low contrast region, such as the abdominal region. This is a limitation of any deformable registration algorithm for low contrast regions. Contour‐ or control point‐based deformation models can potentially be used to improve the reconstruction accuracy based on anatomical features in the low contrast region.

Another aspect that was not investigated in this study due to limited patient data is the effects of patient weight loss on the reconstruction accuracy. Patient weight loss would alter the peripheral body volumes, which could affect the reconstruction accuracy of the tumor volume inside the body. In such a scenario, a new planning 4D‐CT can be acquired during the treatment course to update the patient anatomy. Also, it is worthy to mention that as this technique was developed primarily for SBRT treatment verification, it is less likely that substantial weight loss will happen due to the short treatment course in SBRT.

Additionally, there may be concerns about the algorithm's performance when the lesion is located in the upper lobe of lung and the diaphragm is not included in all CBCT projections. We did a XCAT study simulating XCAT scenario 2, but with the lesion located high in the upper lobes of the lungs. Figure 9 shows the CT_prior and a sample on‐board CBCT projection image for the simulation. We found that when using 15° orthogonal scan angles with 52 projections, the GMM‐FD method achieved VPD/COMS of 31.10%/1.11 mm and the SMM‐WFD method achieved VPD/COMS of 13.88%/0.44 mm demonstrating the substantial improvements by the SMM‐WFD method.

Figure 9.

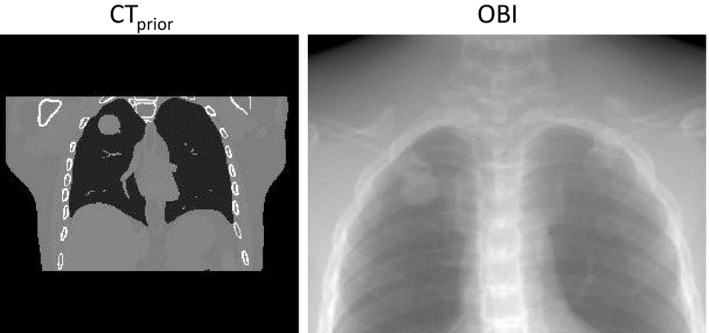
CT _prior and sample on‐board CBCT projection image for the XCAT simulation with a tumor in the upper lobe of the left lung.

Also, the gray value mismatch between CT and CBCT and image artifacts can potentially affect the accuracy of the reconstruction. Different approaches have been developed in the past to address this issue. Wang et al.¹⁶ and Li et al.¹⁷ proposed to address this issue by linearly scaling the on‐board projections, and demonstrated the efficacy of their methods through patient studies. We proposed to address this issue using normalized cross correlation (NCC) as the data fidelity metric,²⁰ which was proven to be more robust than image differences against intensity mismatches and artifacts in patient studies. Potential further improvements can be made by incorporating accurate scatter correction algorithms or modeling beam hardening in the projection images^{29, 30, 31, 32, 33} to improve the performance of current algorithm.

Lastly, for the examples using orthogonal‐view 15° scanning angles, we can estimate that we have captured 8 breathing cycles based on the calculations performed in Section 2.F. Because we have only captured a small number of breathing cycles, the 4D‐CBCT estimation may be affected more by breathing irregularity, such as patient coughing. The magnitude of the effects will depend on the amount of the irregularity. To mitigate this problem, we can monitor the patient breathing curves, such as RPM signal, during the acquisition to avoid or minimize breathing irregularity in the short scan for our method.

5. Conclusions

The structural‐based PCA MM with weighted free‐form deformation technique can estimate 4D‐CBCT images using extremely small scan angles and small number of projections. The technique provides a promising tool for fast low dose 4D imaging for both inter‐ and intrafraction verification in lung radiation therapy.

Conflict of Interests

None.