Bistability and oscillations in co-repressive synthetic microbial consortia

Abstract

Synthetic microbial consortia are conglomerations of multiple strains of genetically engineered microbes programmed to cooperatively bring about population-level phenotypes. By coordinating their activity, the constituent strains can display emergent behaviors that are difficult to engineer into isogenic populations. To do so, strains are engineered to communicate with one another through intercellular signaling pathways. As a result, the regulatory networks that control gene transcription throughout the population are sensitive to the extracellular concentration of the signaling molecules, and hence the relative densities of constituent strains. Here, we use computational modeling to examine how the behavior of a synthetic microbial consortium results from the interplay between the population dynamics governed by cell growth and the internal transcriptional dynamics governed by cell-to-cell signaling. Specifically, we examine a synthetic microbial consortium in which two strains each produce signals that down-regulate transcription in the other. Within a single strain this regulatory topology is called a “co-repressive toggle switch” and can lead to bistability. We find that in a two-strain synthetic microbial consortium the existence and stability of different states depends on the population-level dynamics of the interacting strains. As the two strains passively compete for space within the colony, their relative fractions can fluctuate and thus alter the strengths of intercellular signals. These fluctuations can drive the consortium to alternative equilibria. Additionally, if the growth rates of the strains depend on their transcriptional states, an additional feedback loop is created that can generate relaxation oscillations. These findings demonstrate that the dynamics of microbial consortia cannot be predicted from their regulatory topologies alone, but also is determined by interactions between the strains.

1 Introduction

A major goal of synthetic biology is the construction of genetic circuits that endow cells and organisms with novel functions. Synthetic gene circuits provide the basis for technologies such as gene therapy [1], biofuel and biopharmaceutical production [2], and have a range of environmental applications [3]. In addition, they allow for unprecedented control of biological systems thus opening new avenues in biological research [4]. The majority of currently available synthetic gene circuits have been built within a single strain and operate at the single-cell level. However, to realize the full potential of synthetic biology we need to be able to design consortia of interacting cells and organisms. Cooperating cells can specialize and assume different responsibilities within a consortium [5]. This allows bacterial consortia to be more efficient, and have a wider range of functions than monocultures. In such consortia, the signals within and between bacterial populations shape the response of genetic networks within cells. The activity of the population, in turn, arises from the coordinated activity of individuals [6, 7]. Consortia can thus perform computations and make decisions that are far more sophisticated than those of a single bacterium [8, 9].

To understand the behaviors of naturally occurring microbial consortia and to engineer synthetic consortia for practical applications, it is necessary to develop mathematical and computational models that describe their behavior. Such multi-scale models must simultaneously describe transcriptional dynamics within cells, interactions between cells due to cell-to-cell communication, and population-level dynamics that arise as different cell types compete for limited resources [10, 11]. To further complicate matters, each of these levels of organization is linked to the others. Transcriptional dynamics within single cells are affected by intercellular signaling molecules. The concentrations of signaling molecules, in turn, are determined by gene network activity and total strain density. Strain density is also affected by transcriptional dynamics, as protein production can affect the growth rate of cells [12, 13, 14]. Therefore, to understand and predict the dynamics of microbial consortia, one must consider the dynamic interplay of multiple levels of organization.

Here we introduce a class of models describing the dynamics of synthetic microbial consortia in which two strains transcriptionally repress each other. We first introduce a deterministic model to describe the average behavior of cells within each population, their global interactions, and the resulting emergent dynamics. Furthermore, we show how to extend this model to include stochastic effects due to small population size and small molecular counts within each cell. This stochastic model has the deterministic model as its mean field approximation while it is able to capture fluctuations within cells and across strains as well as strain extinctions.

The co-repressive microbial consortium is a generalization of the well-known synthetic toggle switch that operates in a single bacterium [15] (See Fig. 1a). In single cells, the co-repressive toggle switch can exhibit transcriptional bistability with two mutually exclusive gene expression states: 1) expression of tetR and repression of lacI; or 2) expression of lacI and repression of tetR. The analogous synthetic co-repressive microbial consortium, shown in Fig. 1b, might be constructed with two strains using two orthogonal quorum sensing systems (here cinI/R and rhlI/R) [16, 17], and two transcriptional inverters [18]. When one strain is active, it produces an intercellular signal that transcriptionally represses the opposing strain. Unlike its bistable single strain counterpart, the co-repressive consortium may exhibit more complicated behaviors. In particular, we show that the co-repressive consortium can oscillate if the growth rates of the strains depend on their transcriptional state, which can occur when heterologous protein is produced [12, 13].

Figure 1.

Single- and two-strain toggle switch. (a) Gene circuit diagram of a single cell co-repressive toggle switch [15]. (b) Proposed synthetic microbial consortium with a co-repressive network. Each strain contains a transcriptional inverter (mediated by LacI) and an enzyme that creates a quorum sensing molecule. Repression occurs when the quorum sensing molecule from one strain diffuses into the other strain, up-regulating the target transcriptional inverter (green dashed arrows). That inverter down-regulates production of the second, orthogonal quorum sensing molecule.

While we only consider the dynamics of co-repressive microbial consortia, our modeling approach can be extended to any consortia of fixed size when spatial effects are negligible. Both our deterministic and stochastic models can be easily modified to describe different gene circuits and cell-to-cell interactions. We thus provide a general framework for modeling and analyzing the interplay between population and gene circuit dynamics that drives the behavior of microbial consortia.

2 The dynamics of the two-strain co-repressive consortium

We first consider the deterministic dynamics of a two-strain consortium growing in a small, well-mixed turbidostat, such as a microfluidic trap [19]. Since such traps have fixed volume, we assume that the total population size and cellular volume of the consortium remain constant. To maintain a fixed population size whenever a cell divides, we assume that a randomly chosen cell from the consortium exits the chamber. For simplicity, we assume that all cells in the consortium have equal size. The fraction of strain 1 within the chamber is then defined by the ratio r = V₁/V = n₁/N where V₁ is the volume occupied by strain 1, V is the total volume, n₁ is the number of cells in strain 1, and N is the total number of cells. Note that the ratio r is treated as a real number that can vary between 0 and 1. Moreover, denoting the volume occupied by strain 2 by V₂ and the number of cells in strain 2 by n₂, we have V₁ + V₂ = V and n₁ + n₂ = N. Therefore, the fraction of strain 2 in the chamber is given by 1 − r = V₂/V = n₂/N.

We model the dynamics of a single gene within each strain. We assume that the production of an enzyme that creates a signaling molecule is repressed by the presence of the signaling molecule produced by the other strain. Further, the concentration of a signaling molecule is assumed to be spatially homogeneous and directly proportional to the total concentration of its enzyme within the culture (i.e., the product of the average intracellular concentration of the enzyme and the number of cells containing it). Therefore the time evolution of the average concentrations x₁ and x₂ of the corresponding enzymes can be described by:

$$\begin{array}{c}{\dot{x}}_1=\alpha f_1(x_2,r)-{\beta }_1{x}_1,\\ {\dot{x}}_2=\alpha f_2(x_1,r)-{\beta }_2{x}_2,\end{array}$$ (1)

where

$$f_1(x_2,r)=\frac{1}{1+{((1-r)N{x}_2/\theta )}^n},f_2(x_1,r)=\frac{1}{1+{(rN{x}_1/\theta )}^n}.$$ (2)

Here α is the maximal production rate of the proteins, θ is a scaling parameter that determines half-maximal repression, and β₁ and β₂ are the growth rates of strains 1 and 2, respectively. The proteins are assumed to be stable and decrease in concentration only through cellular growth and division at a rate proportional to the growth rates. It is assumed that the volume is measured in units of single cells so that the total cellular volume is V = N. Moreover, we assume that there is a linear relation between the expression of the signaling molecule and protein within a single cell. Therefore protein production in strain 2 is repressed in proportion to the total protein signal V₁x₁ = rVx₁ = rNx₁ from strain 1. Similarly, the protein production in strain 1 is repressed by the total protein signal (1 − r)Nx₂ from strain 2. Note that this approximation for the amount of signaling molecule assumes that: 1) the transient dynamics of the signaling molecule are fast with respect to changes in the corresponding protein concentration x_i, and 2) the quasi-equilibrium concentration of the signaling molecule is linearly proportional to the amount of enzyme making it. The first approximation is generally valid provided that the growth chamber is small enough and that diffusion across cell walls is fast. The second approximation is valid provided that the presence of the signaling molecule does affect the enzyme's ability to make it.

Next, we describe a deterministic model of the dynamics of the population ratio r assuming that the number of cells within each strain can be described by a birth–death process. A new cell is born at cell division, while a “death” occurs when a cell is removed from the chamber. Recall that n₁ and n₂ are the number of cells in strains 1 and 2, respectively, so that n₁ + n₂ = N is constant. Left on their own, the two strains would grow exponentially with rates β₁n₁ and β₂n₂, respectively. To keep the total population size constant, we set the total rate at which cells are removed from the population to β₁n₁ + β₂n₂. If all cells are equally likely to be removed, the probability that a cell is removed from strain i is n_i/N , giving a death rate of $({\beta }_1{n}_1+{\beta }_2{n}_2)\frac{n_i}{N}$. The deterministic birth-death process of the strain 1 can then be described by the differential equation

$${\dot{n}}_1={\beta }_1{n}_1-({\beta }_1{n}_1+{\beta }_2{n}_2)\frac{n_1}{N}.$$ (3)

Substituting n₁ = rN and n₂ = (1 − r)N into (3), we obtain the logistic equation

$$\dot{r}=({\beta }_1-{\beta }_2)r(1-r),$$ (4)

for the ratio r of the strain 1 in the chamber.

2.1 Bistability in the absence of metabolic loading

There are many reasons why protein production might influence the growth rate of a cell. For instance, heterologous protein expression may slow growth due to metabolic loading [12, 13], or transcription of a suicide gene may be linked to one of the two states [20, 21]. For simplicity, we will refer to these phenomena collectively as “metabolic loading” – a burden imposed by the production of heterologous protein.

In the absence of metabolic loading, the growth rates of the two strains are not affected by the production of the enzymes and hence will remain constant. If the two strains grow at the same rate β₁ = β₂, Eq. (4) implies that the ratio r will remain fixed at its initial value. Then we can treat r as a parameter in Eq. (1) and the equilibria $x_1^{\ast }$ and $x_2^{\ast }$ are given by

$$\begin{array}{c}{\beta }_1{x}_1^{\ast }=\alpha f_1(x_2^{\ast },r),\\ {\beta }_2{x}_2^{\ast }=\alpha f_2(x_1^{\ast },r).\end{array}$$ (5)

Indeed, the equilibria are the solutions of $x_1^{\ast }=h_1(h_2(x_1^{\ast }))$, where h_i = αf_i/β_i. Since h₁ and h₂ are monotonically decreasing sigmoidal functions, h₁ ∘ h₂ is a monotonically increasing sigmoidal function and it intersects the diagonal in 1, 2, or 3 points which correspond to the equilibria.

Fig. 2a shows a typical example of how $x_1^{\ast }$ changes with the ratio r. If the ratio r is high or low, there exists a unique equilibrium (solid line) and one of the strains dominates the trap; the dominant strain will be expressed and the opposite strain repressed. For mid values of r, the system is bistable with two stable equilibria (solid lines) and an unstable equilibrium in the middle (dashed line). This region of bistability is bounded by bifurcations at which two of the equilibria disappear in a saddle–node collision. That is, the consortium behaves like a toggle switch for a range of strain ratios. Unlike switches that operate on the level of single cells, bistability in the present case depends on the ratio of the strains in the trap.

Figure 2.

Two-strain population toggle with equal growth rates. (a) The equilibrium $x_1^{\ast }$ as a function of population ratio r. The dashed and solid lines correspond to unstable and stable equilibria, respectively. (b) Two trajectories of Eq. (1) approaching one of the two stable equilibria marked by ( ) and ( ) based on the initial conditions. The third, unstable equilibrium is denoted by ( ). The gray dashed line shows the separatrix between the two basins of attraction of the stable equilibria. The parameters are chosen as β₁ = β₂ = 0.023 min⁻¹ corresponding to E. coli's cell cycle of approximately 30 minutes, α = 10 min⁻¹, θ = 500, N = 200, and n = 2. The simulations are carried out for constant population ratio r = 0.4 and initial conditions (x₁(0), x₂(0)) = (100, 200) proteins per cell and (x₁(0), x₂(0)) = (300, 100) proteins per cell.

Fig. 2b shows simulations of Eq. (1) with equal growth rates β₁ = β₂ for two different sets of initial conditions where the ratio r is chosen from the bistable domain. If the initial conditions fall below the gray dashed separatrix (given by the stable manifold of the unstable equilibrium denoted by ), the system approaches the equilibrium denoted by . The simulations starting above the separatrix approach the other stable equilibrium denoted by . Note that the slope of the separatrix is equal to 1 for ratio r = 0.5, and decreases with decreasing r.

When the difference β₁ − β₂ between the growth rates of the two strains is small, r changes slowly according to Eq. (4). Let us assume that

$$\begin{array}{c}{\beta }_1={\beta }_0(1+\epsilon ),\\ {\beta }_2={\beta }_0,\end{array}$$ (6)

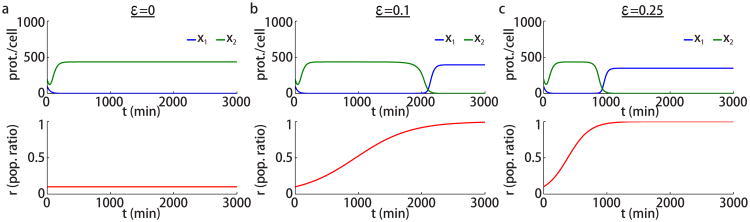
where ε reflects the relative difference between the growth rates of the two strains. We only consider ε ≥ 0, since if ε < 0 the roles of strains 1 and 2 can be reversed. When ε is small, Eqs. (1), (2), and (4) form a slow-fast system. Thus the concentrations x₁ and x₂ track a stable equilibrium until it disappears in a sadddle-node bifurcation [22] (see Fig. 2a). Once an equilibrium disappears, the system jumps to the other stable equilibrium, and a switch in expression levels occurs. For example, as shown in Fig. 3b,c, when ε > 0 and r is initially close to 0, the concentration x₁ initially approaches the lower equilibrium value (repressed state) and stays close to it as r increases slowly due to the larger growth rate of the first population. After the ratio r passes through the critical value at which the lower equilibrium disappears, x₁ switches to the higher equilibrium (expressed state). Fig. 3b,c show such transitions for small and intermediate differences in growth rates. Notice that the transition occurs earlier in time as ε increases. On the other hand when the growth rates are equal, no transition occurs as the ratio r remains constant; see Fig. 3a. While the dynamics for different values of ε > 0 are similar, the slow-fast approach is valid only when ε is small.

Figure 3.

Two-strain population toggle with different growth rates. Simulations of Eqs. (1), (4), and (6) with β₀ = 0.023 min⁻¹ and different ε values as indicated. Other parameters are the same as in Fig. 2. Initial protein concentrations are (x₁(0), x₂(0)) = (100, 200) proteins per cell and initial population ratio is r(0) = 0.1.

When the two strains have identical growth rates, the two-strain microbial consortium behaves like a single-strain toggle switch: gene expression in the two strains is bistable for a range of population ratios r. However, if one strain has a larger growth rate, the opposite strain eventually disappears from the trap. Even before it is driven to extinction, the less numerous strain becomes fully repressed.

2.2 Impact of metabolic loading on population toggle dynamics

We next investigate the dynamics of the co-repressive consortium in the presence of metabolic loading, i.e., when the growth rates of the two strains depend on their transcriptional states. If a balance of population sizes is necessary to maintain a particular behavior then any change in the growth rates can affect the dynamics of the consortium. To gain insight as to how metabolic loading in the two-strain toggle consortium can lead to relaxation oscillations, assume that the cells with higher expression rate experience an increased metabolic burden, and thus grow slower. This, in turn, allows cells in the repressed state to increase their relative population size. Once these cells dominate the trap, they are no longer repressed. As they reach high expression levels, they experience higher metabolic load and the process repeats.

To demonstrate such relaxation oscillations in the co-repressive consortium, we assume that the growth rates of both strains depend on the rate of expression of each gene, f₁ and f₂ defined in Eq. (2). In particular Eq. (6) is replaced by

$$\begin{array}{c}{\beta }_1={\beta }_0(1+\epsilon )(1-\rho f_1(x_2,r)),\\ {\beta }_2={\beta }_0(1-\rho f_2(x_1,r)),\end{array}$$ (7)

where the parameter 0 < ρ < 1 determines the impact of the metabolic load on the growth rates, such that ρ ≈ 0 corresponds to a low and ρ ≈ 1 corresponds to a high impact. The growth rate of a strain is therefore largest when gene expression is at its minimum. Here the parameter e determines the difference between the maximal growth rates of the two strains.

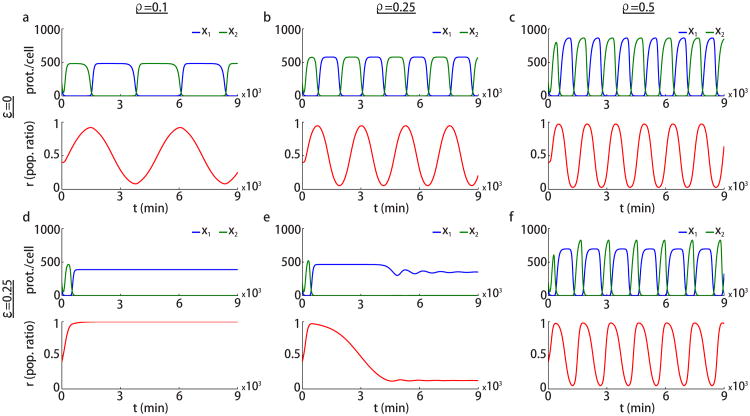
Fig. 4 shows solutions of Eqs. (1), (4), and (7) for different values of the parameters ε and ρ. When ε = 0, the system exhibits oscillations for all values of ρ > 0, see Fig. 4a-c (recall that for ρ = 0 case, we have the bistable system shown in Fig. 2a). The frequency and amplitude of these oscillations increase with the impact of the metabolic loading ρ. Fig. 5a–c show the bifurcation diagrams while using ρ as the bifurcation parameter for the case ε = 0. In Fig. 5a, three unstable equilibria are shown as a function of ρ. Fig. 5b shows the value of the population ratio r for these unstable equilibria. Fig. 5c shows the amplitude of the oscillations as a function of ρ.

Figure 4.

Metabolic loading leading to relaxation oscillations. Simulations of Eqs. (1),(4), and (7) for different values of ε and ρ as indicated. Parameters are β₀ = 0.023 min⁻¹, α = 10 min⁻¹, θ = 500, N = 200, and n = 2. Initial conditions are (x₁(0), x₂(0)) = (100, 200) proteins per cell and r(0) = 0.4.

Figure 5.

Bifurcation diagrams for the two-strain toggle under metabolic load. In panels (a,b,d,e), solid and dashed lines denote stable and unstable equilibria, respectively. In panels (d,e,f), the markers × and * indicate transcritical and Hopf bifurcations, respectively. The solid magenta line in panels (c,f) shows the amplitude of the periodic solution. In panel (f) the periodic solution emerges from a Hopf bifurcation. Parameters are the same as in Fig. 4.

Fig. 4d–f shows numerical simulations of (1), (4), and (7) for different ρ values where ε = 0.25 is kept fixed. We observe that when ε > 0, oscillations occur only when metabolic loading is sufficiently large. The bifurcation diagrams for the case ε = 0.25 are shown in Fig. 5d–f. When ρ is close to zero the equilibrium r* = 1 is stable. An increased metabolic load, ρ, leads to the appearance of a stable equilibrium for which 0 < r* < 1 (red line in Fig. 5d,e) that emerges via a transcritical bifurcation indicated by × in Fig. 5d,e. This equilibrium is stable over a small range of the parameter ρ, then undergoes a supercritical Hopf bifurcation (marked by *) leading to stable oscillations. Note that if we continue the equilibrium shown by the red branch to lower ρ values, the corresponding population ratio r* is larger than 1 and physically not meaningful. Therefore, this branch section is not shown here. The amplitude of the periodic orbit is shown in Fig. 5f. The middle equilibrium (red branch) is also included in Fig. 5f as a steady state with zero amplitude. The amplitude of the oscillations arising from the Hopf bifurcation grows explosively over a small parameter range after the bifurcation. We conjecture that this is due to a canard explosion [23].

3 Small population effects

In smaller traps, or confined geometries, the number of cells may be sufficiently small for stochastic fluctuations in population size and gene expression to become appreciable. We therefore describe a full stochastic model of the dynamics of intracellular proteins, as well as the birth and removal of cells in the two strains. We work under the same assumptions as in the previous section: the number of cells, n₁ + n₂ = N, in the trap is fixed, and is maintained by following each birth by a removal of a randomly chosen cell. We again neglect spatial effects.

We model protein dynamics separately in each cell. Let x_i,j be the number of proteins in cell j of strain i, so that i ∈ {1,2}, and j ∈ {1, 2, ⋯, n_i}. We therefore have a set of N birth processes modeling protein production

$$\begin{array}{cc}\varnothing \stackrel{\alpha f_1}{\to }{x}_{1,1}& \varnothing \stackrel{\alpha f_2}{\to }{x}_{2,1}\\ \varnothing \stackrel{\alpha f_1}{\to }{x}_{1,2}& \varnothing \stackrel{\alpha f2}{\to }{x}_{2,2}\\ ⋮& ⋮\\ \varnothing \stackrel{\alpha f_1}{\to }{x}_{1,n_1}& \varnothing \stackrel{\alpha f_2}{\to }{x}_{2,n_2}.\end{array}$$ (8)

The rate of protein production in each cell in strain i is αf_i, where

$$f_1=\frac{1}{1+{\left(\frac{x_{2,1}+x_{2,2}+\cdots +x_{2,n_2}}{\theta }\right)}^n},\text{and}{f}_2=\frac{1}{1+{\left(\frac{x_{1,1}+x_{1,2}+\cdots +x_{1,n_1}}{\theta }\right)}^n},$$ (9)

cf. (2). Note that we do not model protein degradation explicitly, as we assume that proteins are relatively stable. Approximately fixed concentrations are maintained by dilution through division, as explained further below.

We separately model the division (birth) and removal (death) of cells from the trap. The rates of these processes are as described in the derivation of Eq. (3). The number of cells n₁ and n₂ in each strain is governed by the coupled birth and death processes

$$\begin{array}{c}\varnothing \stackrel{{\beta }_1{n}_1}{\to }\text{One cell in strain}1\text{divides and}\{\begin{array}{c}\text{a cell from strain}1\text{is removed with probability}{n}_1/N,\\ \text{a cell from strain}2\text{is removed with probability}{n}_2/N,\end{array}\\ \varnothing \stackrel{{\beta }_2{n}_2}{\to }\text{One cell in strain}2\text{divides and}\{\begin{array}{c}\text{a cell from strain}1\text{is removed with probability}{n}_1/N,\\ \text{a cell from strain}2\text{is removed with probability}{n}_2/N.\end{array}\end{array}$$ (10)

The two population sizes therefore follow Moran dynamics [24, 25]: whenever a cell divides, another randomly chosen cell is removed.

We use Gillespie algorithm to sample trajectories from the processes described by Eqs. (8) and (10). At each step of the Gillespie algorithm, the possible events and their probabilities are given by these two equations. There are N + 2 possible events that can occur in each step of the algorithm: a birth (division) in either strain, accompanied by the removal of a random cell, and a birth (formation) of a protein in one of the N cells. The rate at which a division occurs in strain i is given by β_in_i where β_i are given by Eq. (7), i.e.,

$$\begin{array}{c}{\beta }_1={\beta }_0(1+\epsilon )(1-\rho f_1),\\ {\beta }_2={\beta }_0(1-\rho f_2),\end{array}$$ (11)

where the protein production rates, f₁ and f₂, are defined in Eq. (9).

When a cell divides, its cellular material, including all proteins, is divided between the two daughter cells. Let the index pair (i, j) correspond to cell j in strain i, so that i ∈ {1, 2} and j ∈ {1, 2, …, n_i}. If an event corresponds to division in strain 1, we pick a random cell in that strain with index (1, b), to be divided into two. If the cell to be removed comes from the same strain, say it has index (1, d), we replace cell (1, d) with a new cell, and divide the proteins from cell (1, b) into two groups by sampling from a binomial distribution. One of the two groups is assigned to cell (1, b), while the other is transferred to the new cell with index (1, d). In this case, the cell counts n₁ and n₂ remain constant. If one of the cells in the strain 2 is chosen to be removed, say cell (2, d), we add an additional cell with index (1, n₁ + 1) to strain 1. We again partition the proteins from the dividing cell (1, b) between the mother and daughter cell. We then remove the cell (2, d) from strain 2 and renumber the remaining cells in strain 2 to close the resulting gap, that is x_2,j ← x_2,j+1, for j = d, d + 1, …, n₂. In this second case, n₁ increases by 1 and n₂ decreases by 1. The algorithm is equivalent if a cell divides in strain 2. Also a modeling assumption in this algorithm is that the birth and removal of cells happen concurrently, not allowing for the cell that is just born to be removed.

Next we explore the effects of stochasticity on the dynamics of the two-strain toggle consortia.

3.1 Stochastic dynamics in the absence of metabolic loading

With no metabolic loading, i.e., when ρ = 0, the growth rates of the two strains are constant. The slower growing strain is more likely to disappear from the trap. However, even if the two growth rates are equal, random fluctuations eventually lead to the extinction of one strain.

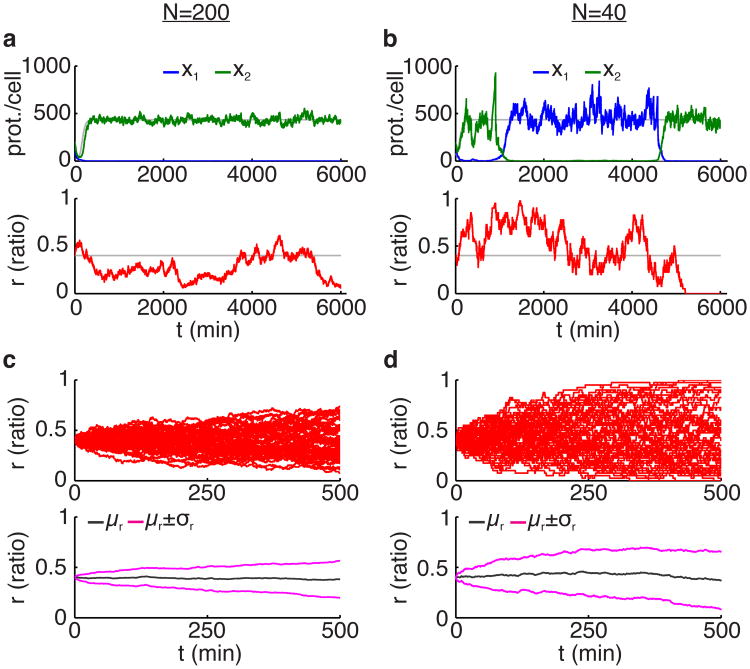
When the two strains of bacteria have equal growth rates, the probability of a strain dominating the whole population is equal to the initial proportion of that strain in the trap [25]. For example, the probability that the strain 1 will take over is n₁(0)/N. Fig. 6 shows simulations of the stochastic model described by Eqs. (8)-(11) with ρ = 0 and when the two strains have equal growth rates, i.e., ε = 0, for different population sizes N. In Fig. 6a,b, the blue and green curves show the mean number of proteins in strains 1 and 2, respectively. The gray curves represent the solutions of corresponding deterministic system described by Eqs. (1) and (4) with the same parameters. When the population size is smaller the effects of random fluctuations are more pronounced. This can be observed when comparing Fig. 6a and Fig. 6b. In Fig. 6a, where the total cell number N is larger, the protein concentrations x₁ and x₂ follow the deterministic model (shown by the gray curves) fairly close so that x₁ approaches the repressed state and x₂ approaches the expressed state. The ratio r oscillates around the initial value of r = 0.4. In Fig. 6b, initially the genes in strain 2 are expressed while the genes in strain 1 are repressed. However, as the total cell population is smaller, the fluctuations in the population ratio r are larger and the likelihood of a switch taking place in the gene expression states is bigger. Therefore, we observe more switches between the gene expression states in Fig. 6b. This behavior cannot be predicted by the deterministic model. In larger cell populations, the fluctuations in the population ratio are not strong enough and a swicth in the gene expression states is less likely to occur. Furthermore, in a stochastic model random fluctuations always drive one population to extinction. However, in the deterministic model when growth rates are equal, no extinctions occur as the ratio remains constant.

Figure 6.

Stochasticity in the dynamics of the two-strain toggle consortium. (a,b) Simulations of Eqs. (8)-(11) with no metabolic loading (ρ = 0) and equal growth rates (ε = 0) for different population sizes as indicated. The blue and green curves show the mean number of proteins in strains 1 and 2, respectively. The red curve shows the population ratio. Simulations of the deterministic system from Eqs. (1) and (4) are also shown using gray curves. Parameters are the same as in Fig. 4. Initial protein counts are x_1,i(0) = 100, i = 1, …, n₁, x_2,j(0) = 200, j = 1, …, n₂, and initial ratio of strain 1 is r(0) = 0.4. (c,d) Different stochastic simulations of the population ratio corresponding to panels (a,b), respectively, as well as the mean (μ_r) and the standard deviation (σ_r).

Fig. 6c,d show the time evolution of the population ratio r obtained by running 50 simulations of the stochastic model from Eqs. (8)-(11). For N = 200, the variability in the population ratio is observed to be smaller than that observed in for N = 40. In the bottom plots in Fig. 6c,d, the standard deviation of the population ratio (σ_r) and the mean (μ_r) are shown versus time. In the case that the total population size is smaller (panel d), the variance of population ratio r grows faster with time.

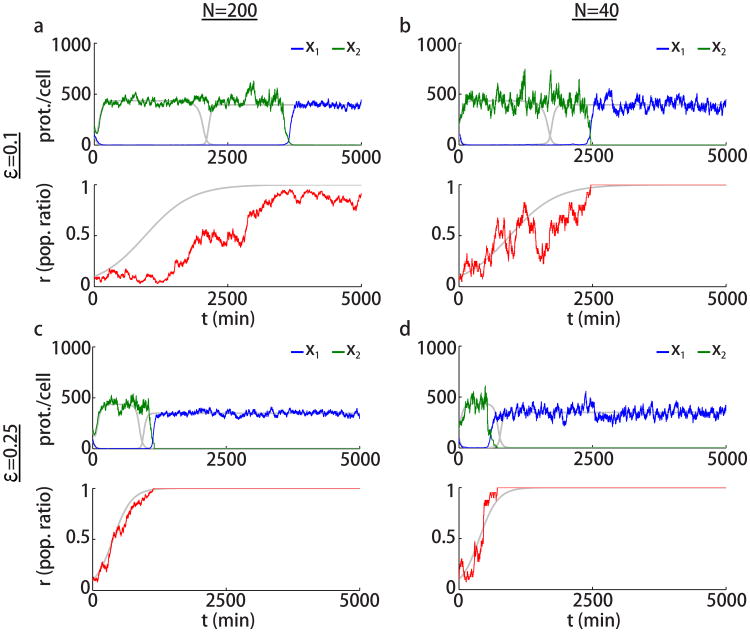
When the two strains have different growth rates, the likelihood that the strain with a lower growth rate goes extinct increases. Fig. 7 shows the simulations of the stochastic model from Eqs. (8)-(11) for cases ε = 0.1 and ε = 0.25 each with population sizes N = 200 and N = 40. Simulations of the deterministic model using the same parameters are also shown as gray curves. As predicted by the deterministic model, starting from 0.1, the population ratio r increases and crossing a critical value a switch happens in the gene expression states. However, the time at which this switch occurs depends on the random fluctuations in the population ratio and could be either before or after the time predicted by the deterministic model. It can also be the case that strain 1 goes extinct (r becomes 0) and no switches occur. When ε is larger (Fig. 7c,d), the switch occurs faster and the stochastic dynamics are closer to those of the deterministic model.

Figure 7.

Simulations of Eqs. (8)-(11) with unequal growth rates of the strains and no metabolic loading (ρ = 0) with different ε and N values as indicated. The gray curves show the corresponding simulations of the deterministic model. Parameters are the same as in Fig. 4. Initial conditions are x_1,i(0) = 100 proteins, i = 1 …, n₁, x_2,j(0) = 200 proteins, j = 1, …, n₂, and initial ratio of strain 1 is r(0) = 0.1.

3.2 The impact of metabolic loading on stochastic growth dynamics

We next simulate the stochastic model given by Eqs. (8)-(11) taking into account the effect of metabolic loading on the growth rates of the bacterial strains by setting 0 < ρ < 1 in Eq. (11). As Fig. 8 shows, the oscillations occur when the metabolic load is taken into account. However, when the total population size is small, the likelihood that one of the strains goes extinct increases. Therefore, as shown in Fig. 8(b), the oscillations can stop early due to extinction.

Figure 8.

Effects of the metabolic load on the stochastic dynamics of the two-strain toggle. Simulations of Eqs. (8)-(11) with metabolic loading ρ = 0.5 and ε = 0 for different populations sizes as indicated. The gray curves show the simulations of the deterministic model. Parameters are the same as in Fig. 4. Initial conditions are x_1,i(0) = 100 proteins, i = 1, …, n₁, x_2,j(0) = 200 proteins, j = 1, …, n₂, and initial ratio of strain 1 is r(0) = 0.4.

Next we ask whether metabolic loading affects the extinction time. Our deterministic analysis showed that metabolic loading increases the frequency of the oscillations in the population ratio r. Therefore, for smaller populations, one expects that the chance of extinction increases as the population ratio gets close to 0 or 1 more frequently. To test this hypothesis numerically, for each of the cases ρ = 0 (no metabolic loading), ρ = 0.5, and ρ = 0.9, we run 500 simulations of the stochastic model from Eqs. (8)-(11). The histograms of the extinction times are shown in Fig. 9. Note that the extinction time is determined when either one of the populations goes extinct, i.e., the time at which r = 0 or r = 1. We see that the distribution of the extinction times gets narrower as the metabolic load increases. For higher metabolic loads, the change in the mean and variance of the distribution is more pronounced.

Figure 9.

Effects of the metabolic load on the extinction times of the two-strain consortium. Normalized histograms of the extinction times for different values of ρ obtained from 500 simulations of the stochastic model from Eqs. (8)-(11) with N = 40 and ε = 0. Parameters are the same as in Fig. 4. Initial conditions are x_1,i(0) = 100 proteins, i = 1, …, n₁, x_2,j(0) = 200 proteins, j = 1, …, n₂, and initial population ratio is r(0) = 0.5.

4 Discussion

We have shown that population growth can significantly alter the dynamics of synthetic microbial consortia. Differential growth between the strains which constitute the consortium, whether due to random fluctuations or changes in growth rate due to protein production, can lead to an imbalance in population sizes and alter the strength of signals between cells. Further, when the growth rates of cells are directly affected by protein production, “hidden” feedback loops arise that can change the dynamical landscape of the consortium. For instance, the regulatory structure of the two-strain co-repressive consortium forms a positive feedback loop. Positive feedback loops generally do not permit oscillatory solutions. However, we showed that growth rate changes due to metabolic load can create a hidden negative feedback loop that acts on a slow time scale. Therefore, the entire system has a fast positive feedback loop (due to signaling) and a slow negative feedback loop (due to metabolic loading) – the hallmark of relaxation oscillators [26]. A two-strain toggle consortium where the growth rates of the strains are affected by the metabolic load on the cells can therefore exhibit relation oscillations, a behavior that cannot be observed in the single-strain toggle switch. It is also shown that under the circumstances where the strains have an identical growth rate not affected by metabolic loading, the consortium shows bistability similar to the single-strain counterpart.

The perturbations due to the random partitioning of proteins at the time of cell division can have a strong effect on internal cell dynamics [27]. With metabolic loading internal and external fluctuations are even more strongly coupled. Variations in the ratio between the strains can change the expression within each cell. On the other hand, internal fluctuations within cells can affect growth, and thus the ratio between strains. Our model captures this interaction of fluctuations across scales, and can be extended to describe more details of local and global processes, or different dynamical behaviors.

In particular, our analysis could be extended to include spatial effects. Such effects will be most important for consortia that are not well-mixed or are large enough to limit intercellular signaling. As strains grow and compete for space within the colony, their spatial arrangement within the colony will change in time. Therefore, the regulatory “topology” of such a system will depend on both time and space, significantly complicating resulting dynamics. Any model that accurately recapitulates such a situation must include the internal dynamics of proteins within cells, the spatiotemporal dynamics of intercellular signals, the growth rate dynamics of the strains, and the time-dependent rearrangement of boundaries between cell types.