Pushing NMR sensitivity limits using dynamic nuclear polarization with closed-loop cryogenic helium sample spinning

The cooler the better. We report a strategy to push the limits of solid-state NMR sensitivity far beyond its current state-of-the-art.

Abstract

We report a strategy to push the limits of solid-state NMR sensitivity far beyond its current state-of-the-art. The approach relies on the use of dynamic nuclear polarization and demonstrates unprecedented DNP enhancement factors for experiments performed at sample temperatures much lower than 100 K, and can translate into 6 orders of magnitude of experimental time-savings. This leap-forward was made possible thanks to the employment of cryogenic helium as the gas to power magic angle sample spinning (MAS) for dynamic nuclear polarization (DNP) enhanced NMR experiments. These experimental conditions far exceed what is currently possible and allows currently reaching sample temperatures down to 30 K while conducting experiments with improved resolution (thanks to faster spinning frequencies, up to 25 kHz) and highly polarized nuclear spins. The impressive associated gains were used to hyperpolarize the surface of an industrial catalyst as well as to hyperpolarize organic nano-assemblies (self-assembling peptides in our case), for whom structures cannot be solved using diffraction techniques. Sustainable cryogenic helium sample spinning significantly enlarges the realm and possibilities of the MAS-DNP technique and is the route to transform NMR into a versatile but also sensitive atomic-level characterization tool.

Introduction

Solid-state nuclear magnetic resonance (ssNMR) is an indispensable tool for biological, chemical, and physical analysis. However, one important weakness of the technique is its lack of sensitivity, with some experiments lasting weeks and others being completely infeasible. Nevertheless, recent technological advancements pioneered by Griffin and co-workers,¹ which have now been commercialized,² have permitted huge sensitivity gains by combining high magnetic fields, sample rotation at the so-called magic angle, and dynamic nuclear polarization (DNP).^3–6 DNP involves the microwave-driven transfer of the substantial spin polarization of unpaired electrons to nuclear spins, increasing nuclear polarization (and thus NMR sensitivity), and reducing experimental times by many orders of magnitude. The current state-of-the-art technology for DNP-enhanced ssNMR allows experiments to be performed at a temperature of ∼100 K, with magic angle spinning (MAS) frequencies up to 15 kHz for a 3.2 mm diameter rotor, using cold nitrogen gas to both cool the sample and pneumatically spin it to the desired rotation frequency.²

Despite the very large success of MAS-DNP, there are still significant improvements that can be made to push further the limits of sensitivity. One of the current limitations of the approach is the use of cold nitrogen gas to power the pneumatic rotation of the turbine. This prevents working temperatures below 100 K, which would be required to avoid the use of expensive high-power, high-frequency microwave (μw) sources (e.g. gyrotrons). In addition, the fluidic properties of cold nitrogen strongly limit the maximum sample spinning frequency as compared to room temperature nitrogen gas. To overcome these limitations, helium (He) presents itself as a highly pertinent gas for MAS at or below 100 K due to its fluidic properties,⁷ with the speed of sound in He being much higher than in nitrogen (N₂) gas. However, it was up to now not clear that fast and stable spinning could be achieved at such temperatures without significant modifications of the rotor/stator design.^8–10 So far, only moderate sample spinning was demonstrated using pressurized helium tanks.^8,11–13 In addition, in He gas close to ambient pressure, the critical electric rf-field strength for voltage breakthrough is relatively low and may lead to arcing, a well-known issue in NMR probe operation at cold helium temperatures. Moreover, cooling to cryogenic temperatures the high flows of He gas needed for both cooling and pneumatic spinning the sample rotor is a technological challenge, especially considering the cost and sustainability of He.¹⁴ For these reasons, some designs for “ultra-low” temperature MAS (ULT-MAS) employ N₂ gas for spinning the sample and He gas for cooling.^15,16 Nevertheless, this requires a separation of the two gases so that N₂ is not liquefied or even solidified during sample rotation. This elegant approach has been demonstrated to work for large and elongated 4 mm rotors.^15,16

In this work we demonstrate an alternative route whereby the use of cryogenic helium gas enables reaching much faster MAS rates and much lower temperatures, the latter increasing significantly the hyperpolarization efficiency of the cross-effect (CE) MAS-DNP mechanism^17,18 as compared to 100 K measurements. These results, obtained using a magnetic field strength of 10 T, are of primary importance for the development of MAS-DNP at higher magnetic fields and should allow extending significantly the range of polarizing agents that can be employed efficiently (biradicals,^19–21 organic radicals with narrow EPR resonances,²² metal ions,²³ intrinsic paramagnetic defects²⁴ etc.). This is of course of direct relevance for the study of systems with extremely low sensitivity and/or those that require multidimensional homonuclear correlation experiments involving nuclides with low natural abundance,^25–29 as well as for the study of low gyromagnetic ratio³⁰/quadrupolar nuclei.^31–34 This original approach is the first step towards sustainable helium spinning and is fully compatible with the use of smaller diameter rotors for ultra-fast sample spinning.

Experimental

DNP samples

The cellulose sample was obtained by suspending cellulose in a solution of 20 mM TOTAPOL, [D₈]-glycerol, D₂O, and H₂O (60/30/10, v/v/v), which was then packed into a 3.2 mm outer-diameter zirconia rotor. To test DNP sensitivity, solutions of 2 M ¹³C-urea in [D₈]-glycerol, D₂O, and H₂O (60/30/10, v/v/v) with different concentrations (given in the text) of the polarizing agents TOTAPOL³⁵ and AMUPol¹⁹ were used, and packed into 3.2 mm outer-diameter sapphire rotors. The γ-alumina sample was impregnated with a solution of [D₆]-DMSO, D₂O, and H₂O (78/14/8, w/w/w) containing 10 mM AMUPol and packed into a 3.2 mm outer-diameter zirconia rotor. Nanotubes of the cyclic dipeptide cyclo-diphenylalanine were prepared using a Matrix-Free approach²⁵ so that TOTAPOL could be dispersed within the powdered sample, giving good sensitivity for MAS-DNP experiments.

DNP experiments

All DNP experiments were performed with a 9.4 T Bruker BioSpin solid-state DNP-NMR spectrometer,² equipped with a 263 GHz gyrotron and a modified low-temperature triple-resonance MAS probe suitable for 3.2 mm outer-diameter rotors. To reach cryogenic temperatures, the probe was connected to the here presented closed-loop NUMOC system. The sample temperature was measured using a thermocouple placed near the rotor, with corrections according to measurements of the saturation-recovery buildup times of ⁷⁹Br in an external reference of KBr.³⁶

Results and discussion

The cryostat

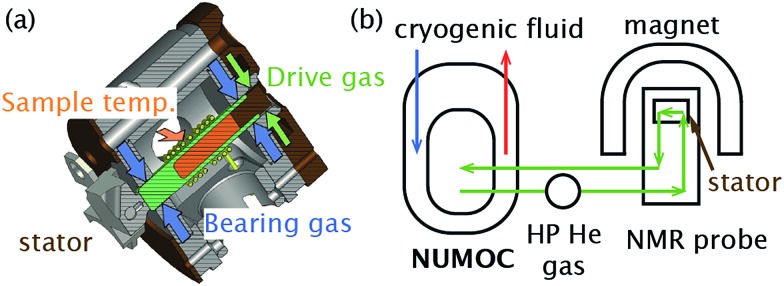
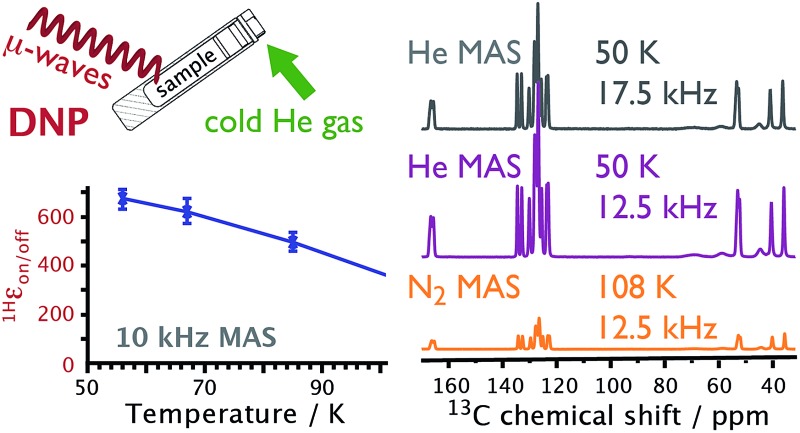
Fig. 1 shows schematics for both the MAS stator and the device we have named NUMOC (NUclear magnetic resonance spinning MOdule Cryostat) that is used to cool He gas, which is subsequently sent to the stator in three separate lines to provide bearing gas (to cushion the rotor), drive gas (to spin the rotor), and cooling gas (to vary the sample temperature). Cold He gas then leaves the stator, is recovered and recycled through NUMOC in a closed-loop circuit to continue cooling and rotating the sample. The simultaneous cooling of all three lines of He gas to similar temperatures prevents temperature gradients across the sample, ensures easy recuperation of the gas, and permits fast sample spinning. Thus, combining NUMOC and a 3.2 mm MAS test stator only (i.e., without a full NMR probe) MAS rates of 5 kHz at 10 K and 25 kHz at 90 K were achieved.

Fig. 1. Schematics of (a) an NMR stator and (b) the ultra-low-temperature MAS-DNP setup called NUMOC.

The He_(liquid) consumption of NUMOC is 5 to 25 L h^–1 depending on the desired sample temperature (30–90 K) and spinning frequency (up to 25 kHz for a 3.2 mm rotor). Note that NUMOC can be used instead with N_2(liquid) as the cryogen, with a consumption of approximately 10 L h^–1, to achieve sample temperatures > 90 K. As a comparison, the commercial system requires 10–20 L h^–1 of N_2(liquid) to reach a minimum sample temperature of approximately 100 K at maximum spinning frequencies of 15 kHz. The He_(gas) consumption of NUMOC is ≪1 L h^–1 to compensate for leaks in the closed-loop He_(gas) circuit and for pneumatic insertion/ejection of the sample (c.f. ≫1000 L h^–1 of N_2(gas) for the commercial system, since there is no closed-loop). The low temperature operation with stable sample spinning (±few Hz) can be maintained as a function of the size of the He_(liquid) vessel connected to NUMOC. A 200 L tank of He_(liquid) will thus enable ∼10 h of stable operation. A fully autonomous system where the He_(liquid) consumption is zero thanks to the use of suitable cryo-coolers is currently under testing.

The Bruker Biospin ULT-MAS-DNP functional prototype probe is based on a similar design to the LT-MAS-DNP probe used for 100 K measurements. The probe was modified to prevent any cold gas leakage and to allow spinning and cooling the rotors using a closed-loop circuit powered by a unique compressor. The nominal pressure of the cryostat was chosen to be higher than atmospheric pressure to prevent any air contamination that could result in ice formation and partial blockages in the system. The helium circuit was also connected to a high-pressure helium tank to ensure constant gas volume operation and compensate for any helium leaks if present. The rotor insert/eject system was also optimized to allow safe operation at cryogenic temperatures between 30 K and 100 K.

DNP results at fast MAS frequencies

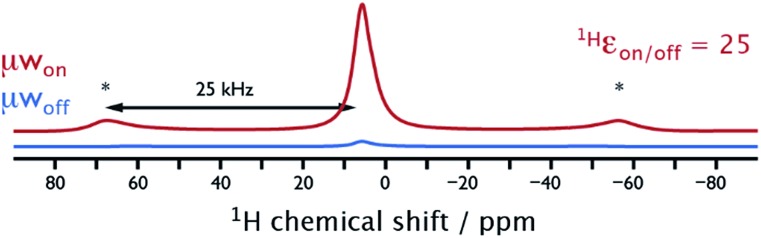
When combining NUMOC with the ULT-MAS-DNP probe and using liquid N₂ as the cryogenic fluid to cool the He gas lines, sample temperatures similar to the commercial setup (∼90 K) are obtained. However, as shown in Fig. 2, MAS is then not limited any more by the fluidic properties of N₂ at ∼100 K (maximum MAS frequency of 15 kHz for 3.2 mm rotors), and stable spinning frequencies up to 25 kHz ± 10 Hz can be easily achieved with He gas. This corresponds otherwise to the maximum spinning frequency specification of 3.2 mm probes at room temperature. For high-magnetic field ssNMR fast sample spinning is required to average chemical shift anisotropy (CSA) interactions, which are proportional to the external magnetic field strength. Moreover, faster sample spinning contributes to spectral linewidth narrowing, increasing thus signal-to-noise and resolution. This is especially true for ¹H resonances, which are usually broadened by strong homonuclear dipolar couplings, and for quadrupolar nuclei such as ¹⁷O, ²⁷Al, and ⁴³Ca that experience a broadening due to the second order quadrupolar interaction. Interestingly, the DNP enhancement, defined as the ratio of the returned signal intensities measured in the presence and absence of μw irradiation (ε _on/off), is similar in this fast spinning regime (^1H ε _on/off@25 kHz = 25) to that measured at a MAS frequency of 8 kHz (^1H ε _on/off@8 kHz = 20).

Fig. 2. ¹H Hahn-echo NMR spectra recorded with (red) and without (blue) μw irradiation suitable for CE-DNP on the cellulose sample. The experiments were performed with the setup shown in Fig. 1b with He gas to achieve a MAS frequency of 25 kHz at a sample temperature of ∼90 K. Asterisks denote spinning sidebands.

DNP results at temperatures ≪100 K

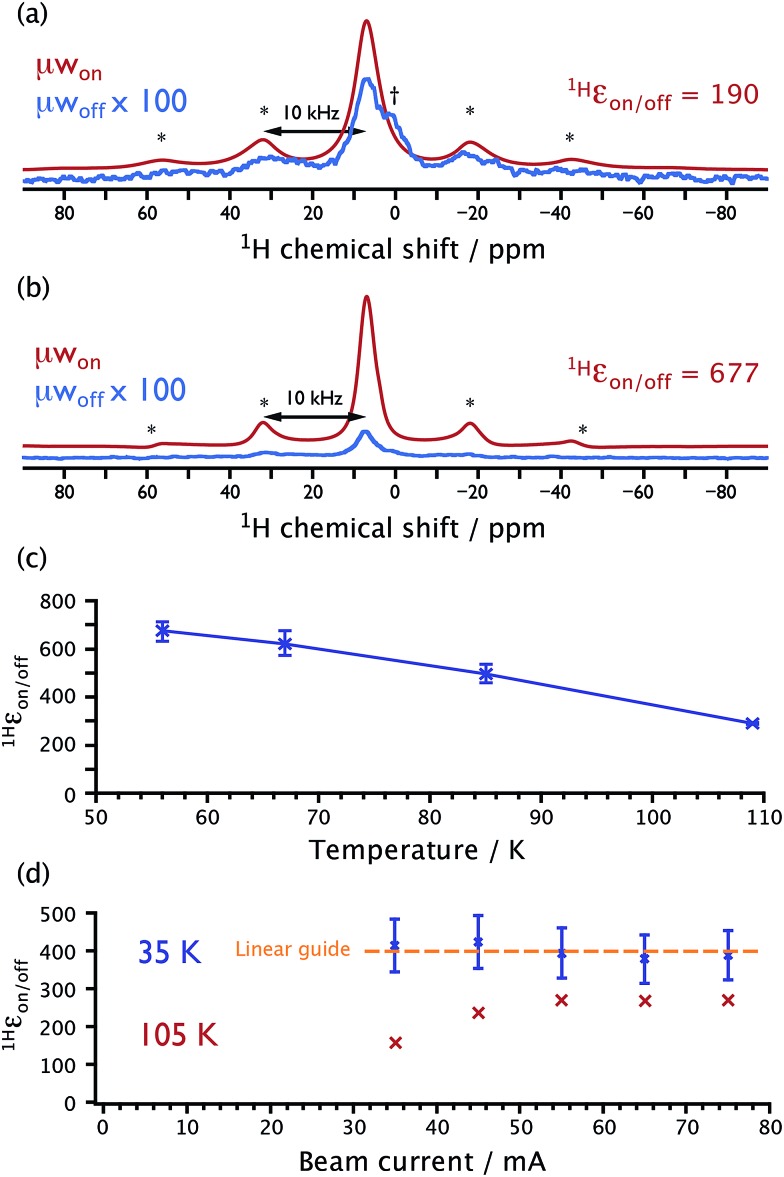
By changing the cryogenic N₂ fluid used to cool the He gas lines to He, much lower sample temperatures can be achieved with the described setup. Fig. 3a shows ¹H spectra recorded at 55 K on the model system of ¹³C-urea in a glass-forming matrix along with the binitroxide polarizing agent TOTAPOL³⁵ (20 mM) that has been introduced for CE-DNP. At a MAS frequency of 10 kHz, reducing the sample temperature to ∼55 K leads to a DNP enhancement ^1H ε _on/off@55 K = 190, which is three-fold higher than the enhancement obtained with standard conditions; at 110 K, ^1H ε _on/off@110 K = 60. Using AMUPol¹⁹ (5 mM), a biradical specifically designed to optimize CE-DNP efficiency, enhancement of ^1H ε _on/off@110 K = 290 is obtained for a similar sample of ¹³C-urea at 110 K (Fig. 3b). Fig. 3c shows that reducing the sample temperature leads to a strong increase of the DNP enhancement ^1H ε _on/off. At 55 K, ^1H ε _on/off@55 K = 677 ± 34, as shown in Fig. 3b. This value can be surprising at first sight as it is close to the theoretical enhancement maximum, given by γ _e/γ _1H = 658. It is here important to note that the reported values of ^1H ε _on/off do not account for nuclear depolarization, which results in a loss of nuclear magnetization at steady-state in absence of μw irradiation and under MAS when compared to Boltzmann equilibrium.^37,38 This explains why ^1H ε _on/off may exceed the theoretical enhancement maximum. To correct ^1H ε _on/off towards the real enhancement gain taking into account depolarization would have required measurement of the static ¹H resonance.³⁸ However, for static samples, it is difficult with our experimental setup to achieve long-term temperature stability, which would be required for a reliable estimation of the depolarization. Nevertheless, even without accounting for depolarization, it is evident that substantial gains in sensitivity can be obtained by DNP at reduced temperatures (vide infra).

Fig. 3. ¹H Hahn-echo NMR spectra recorded with (red) and without (blue) μw irradiation suitable for CE-DNP on the ¹³C-urea model solution containing 20 mM TOTAPOL (a) or 5 mM AMUPol (b), at a sample temperature of 55 K and a MAS frequency of 10 kHz. The signals recorded in the absence of μw irradiation have been magnified by a factor of 100 for illustrative purposes. Asterisks and daggers denote spinning sideband and ‘plug’ signals, respectively. (c) The measured DNP-enhancement ratio as a function of sample temperature for the sample from (b). (d) The measured DNP-enhancement ratio as a function of the gyrotron beam current, which has been checked to be proportional to μw power, for a ¹³C-urea model solution containing 12 mM AMUPol, recorded at a MAS frequency of 5 kHz and sample temperatures of 105 K (red) and 35 K (blue).

Since sensitivity is defined as the signal-to-noise ratio per unit square root of time, (S/N)_√t, the rate at which the experiment can be repeated is crucial. Usually, this rate is limited by the nuclear spin-lattice relaxation time constants (T _1n). One assumed drawback of lowering the sample temperature was the lengthening of these characteristic times that would be deleterious for the sensitivity. However, we observe experimentally in this study that the magnetization build-up times (after saturation), both in the presence and absence of μw irradiation, do not change significantly as the temperature is decreased below 100 K for samples that experience the CE. Using the model sample of ¹³C-urea, build-up time constants of 10.7 s (with 5 mM AMUPol) and 3.0 s (with 12 mM AMUPol) were recorded at 110 K. When the sample temperature was lowered to 35 K, build-up constants of 12.3 s (5 mM AMUPol) and 3.8 s (12 mM AMUPol) were obtained, respectively. Interestingly, T _1n is therefore not the limiting factor for the build-up rate, since in the absence of biradicals, ^1H T _1n > 60 s at 100 K for this sample. Furthermore, induced relaxation by the presence of the paramagnets is also not responsible for the build-up rates since this would induce large changes with temperature.³⁹ The magnetization saturation-recovery build-up times must then be determined by both the CE and spin-diffusion, which respectively exchanges electron polarization difference with the nuclear spins and spreads hyperpolarization throughout the sample. Its theoretical dependence as a function of temperature is certainly complicated. In the experimental frame of this study, lowering the temperature here does not impact significantly on the optimum experimental repetition rate, and is therefore not prohibitive in terms of (S/N)_√t.

Fig. 3d depicts a further advantage of lowering the sample temperature. To obtain an efficient CE-DNP mechanism, sufficient μw power must be used to create a large polarization difference between electron spins of the polarizing agent. The required power depends on the relaxation properties of the electronic spins (T _1e and T _2e). At lower temperature, nitroxide electron relaxation time constants are increased,⁴⁰ and less μw power is needed to saturate the spin transitions. At 105 K, high μw power from the gyrotron (a few watts at the sample) is needed for maximum DNP enhancement, as shown in Fig. 3d. However, at 35 K the μw power can be reduced by more than half without a noticeable change in the DNP enhancement. Therefore, less expensive, more adaptable (broadband, pulsed etc.), lower-power alternative μw sources may be suitable for efficient CE-DNP at temperatures ≪100 K, replacing the expensive, high-power, narrowband, and continuous-wave gyrotrons.

DNP results on γ-alumina

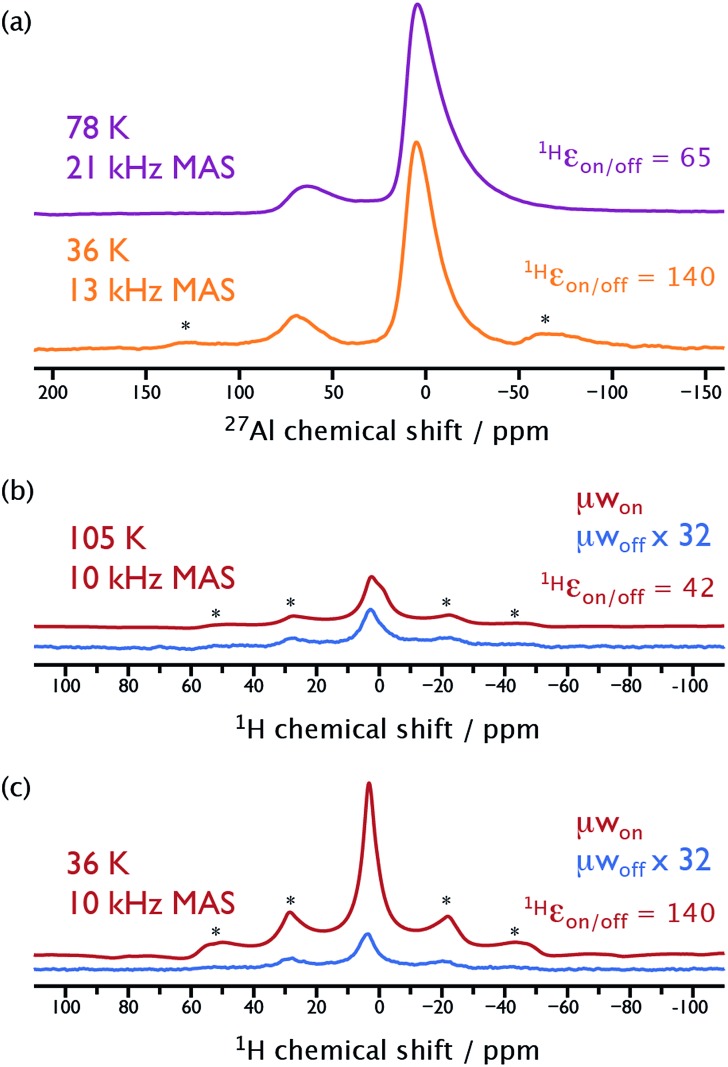
The sample of γ-alumina (Al₂O₃), which we recently studied at 104 K with MAS-DNP using N₂ for sample spinning at ∼14 kHz,⁴¹ was selected to highlight the importance of faster sample spinning using cold He gas. The catalytic surface of this material of high industrial relevance can be studied by central-transition (CT)-selective cross-polarization (CP) to ²⁷Al nuclei from surface protons.⁴¹ In Fig. 4a the ²⁷Al spectrum recorded using a MAS frequency of 21 kHz is completely free from spinning sidebands and spectral distortions. This is essential for higher-field studies where these distortions worsen at limited spinning rates and prevent crucial spectral data fitting. Interestingly, the peaks in the ²⁷Al spectrum at 21 kHz MAS are significantly broader than those of the corresponding spectrum acquired at 13 kHz MAS. This is the result of a better excitation at high MAS frequencies of ²⁷Al nuclei with large quadrupolar coupling constants. This leads to the observation of ²⁷Al species that were previously “invisible” at lower spinning speeds, again highlighting the importance of rapid sample rotation.

Fig. 4. NMR spectra recorded on the γ-alumina sample. (a) {¹H-}²⁷Al CT-CP spectra recorded at sample temperatures of ∼78 K (top, purple) and ∼36 K (bottom, orange) using MAS frequencies of 21 kHz and 13 kHz, respectively. (b) ¹H Hahn-echo spectra recorded at a sample temperature of ∼105 K and a MAS frequency of 10 kHz with (red) and without (blue) μw irradiation suitable for CE-DNP. (c) The same as for (b) at the same intensity scaling, but at a sample temperature of ∼36 K. The signals in (b) and (c) recorded in the absence of μw irradiation have been magnified by a factor of 32 for illustrative purposes. Asterisks denote spinning sideband signals.

Fig. 4b and c highlight the gain in sensitivity obtained by performing MAS-DNP experiments at lower temperatures. While ^1H ε _on/off has increased by a factor of 3.3 from 42 at 105 K to 140 at 36 K, more importantly (S/N)_√t, which is the real measure of the sensitivity gain, has increased by a factor of 2.3, resulting in five-times faster experiments. This sensitivity gain is however less than the expected factor of ∼10 resulting from the multiplicative increased contributions from the ^1H ε _on/off ratio (factor of 3.3) and Boltzmann equilibrium polarization (factor of 2.9, ignoring changes in rf-circuit sensitivity). The difference most likely comes from the aforementioned nuclear depolarization,³⁷ which increases at lower temperatures, leading to a stronger overestimation of ^1H ε _on/off with respect to the real DNP gain over the nuclear Boltzmann polarization. Depolarization amounts can be crudely estimated from Fig. 4b and c. In the absence of μw irradiation (blue spectra), the S/N is approximately the same at both temperatures, even though the expected S/N should be ∼3 times greater for the about thrice colder sample, owing merely to the increased Boltzmann polarization. This indicates that the nuclear depolarization is approximately 3 times as large in the sample at 36 K compared to that at 105 K. The biradical AMUPol may therefore not be optimal for this ULT-MAS-DNP regime and may be best suited for experiments at higher temperatures. Alternative polarizing agents, specifically designed for this temperature regime, are currently under investigation in our laboratory.

Experiments on γ-alumina give further evidence for the polarization build-ups being dominated by CE-DNP and not T _1n. For this sample preparation, ²⁷Al spins do not experience any (observed) direct hyperpolarization. The polarization build-up time constant for ²⁷Al nuclei after saturation changes from 5 s at 100 K to 18 s at 40 K. However, ¹H nuclei, which do experience CE-DNP, display almost no change in their build-up time constants, with values of 3.5 s at 100 K and 4 s at 40 K. Lowering the temperature in the presence of the CE mechanism has only negligible effect on the polarization build-up times, and does not therefore induce any loss of sensitivity.

DNP results on cyclo-FF

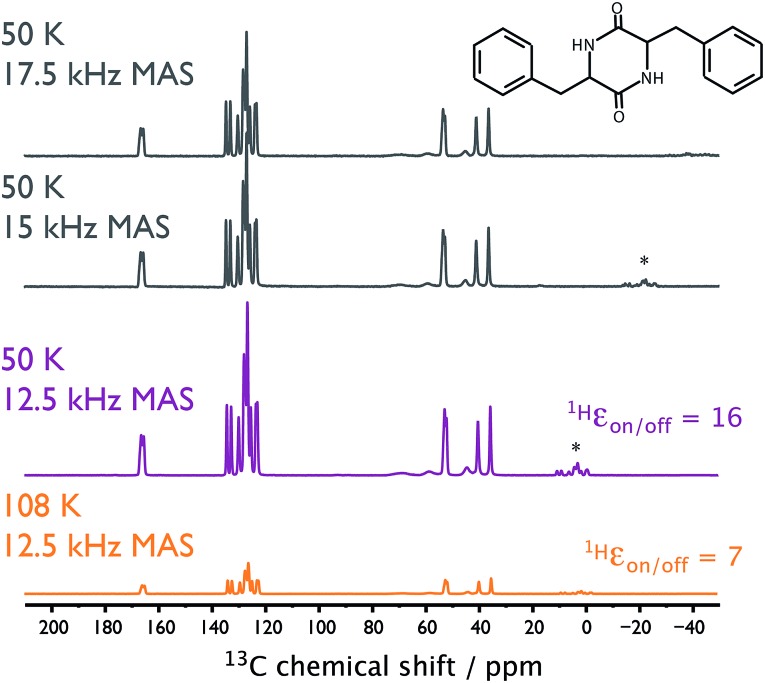
Cyclo-diphenylalanine (cyclo-FF; shown in Fig. 5) can be prepared so as to self-assemble into semiconducting nanotubes. A special sample preparation procedure, which uses the TOTAPOL biradical, makes these nanotubes suitable for analysis by MAS-DNP.²⁵ Fig. 5 shows the gain in (S/N)_√t when performing DNP-enhanced experiments on this sample at ∼50 K compared to ∼110 K. Already at ∼110 K, MAS-DNP experiments gave (S/N)_√t values that were 2 orders of magnitude larger than conventional ssNMR under ambient conditions.²⁵ Here, lowering the sample temperature to ∼50 K results in 5.6 times further (S/N)_√t increase, corresponding to an experimental time-saving of 6 orders of magnitude compared to conventional ssNMR. Again, using He gas for the sample spinning permitted spectra to be recorded at higher MAS frequencies than were previously possible at 100 K using N₂ gas (see Fig. 5).

Fig. 5. NMR spectra recorded on the cyclo-FF (top right) sample. DNP-enhanced {¹H-}¹³C CP spectra recorded at sample temperatures of ∼108 K (orange) and ∼50 K (purple) using MAS frequencies of 12.5 kHz. Also shown (gray) are similar spectra recorded at ∼50 K using various MAS frequencies. 100 kHz of SPINAL-64 decoupling⁴² was used for the 30 ms of acquisition without any evidence of arcing. The spectra have been scaled relative to their (S/N)_√t. Asterisks denote spinning sideband signals.

Unlike the sample of γ-alumina, which was studied by MAS-DNP using the AMUPol biradical (vide supra), the TOTAPOL biradical employed for the cyclo-FF sample shows no evidence of causing further depolarization at 50 K compared to 110 K. It should also be noted that the polarization build-ups under these CE-DNP conditions were 3 and 4 s at 108 and 50 K, respectively.

For this last tested sample it was necessary to utilize high-power heteronuclear decoupling to produce the thin peaks seen in Fig. 5, owing to the strongly coupled protons in the analyte. As stated above, there is a risk of electric arcing when using rf irradiation in a He gas environment. However, when applying the required long duration of high-power decoupling, no evidence of arcing was observed. This shows that sample spinning using a closed-loop cold He gas supply produced through NUMOC is fully compatible with state-of-the-art DNP-enhanced ssNMR. Moreover, it allows for faster sample spinning and experiments with much increased sensitivity.

Conclusions

To summarize, we have demonstrated here that orders of magnitude of additional time-savings can be achieved by performing MAS-DNP experiments at temperatures much lower than 100 K. To achieve these results, we developed a cryostat that allows sustainable fast MAS using recycled cold helium gas. Firstly, sample spinning with helium gas permits much higher MAS frequencies than with conventional nitrogen gas, facilitating complex solid-state NMR measurements. Secondly, the potential drawback of decreasing the temperature, namely the increase in experimental repetition delays due to longer nuclear relaxation times, is bypassed by the use of CE-DNP. With this mechanism, the nuclear (hyper)polarization is built-up via CE and diffusion-type processes, which are shown to be quite insensitive to the temperature in the considered range. Finally, this approach leads to larger hyperpolarization and, more importantly, higher absolute sensitivity. It was demonstrated here at 10 T with 3.2 mm rotors, but it is fully compatible with even faster spinning and higher magnetic fields. Therefore, this approach will pave the way to the successful extension of MAS-DNP experiments to these higher fields as well as to envision the use of lower power and less expensive microwave sources, making the technique accessible to a wider community. This will open up possibilities for more comprehensive future biological, chemical, and physical studies.