Single pulse two photon fluorescence lifetime imaging (SP-FLIM) with MHz pixel rate

Abstract

Two-photon-excited fluorescence lifetime imaging microscopy (FLIM) is a chemically specific 3-D sensing modality providing valuable information about the microstructure, composition and function of a sample. However, a more widespread application of this technique is hindered by the need for a sophisticated ultra-short pulse laser source and by speed limitations of current FLIM detection systems. To overcome these limitations, we combined a robust sub-nanosecond fiber laser as the excitation source with high analog bandwidth detection. Due to the long pulse length in our configuration, more fluorescence photons are generated per pulse, which allows us to derive the lifetime with a single excitation pulse only. In this paper, we show high quality FLIM images acquired at a pixel rate of 1 MHz. This approach is a promising candidate for an easy-to-use and benchtop FLIM system to make this technique available to a wider research community.

1. Introduction

Nonlinear optical microscopy is a powerful technique in bio-molecular science that allows to gain a better understanding of biochemical processes on a cellular level. The main goal is to identify not only morphology but also the chemical composition of a sample. Amongst many other modalities with molecular and functional contrast, two-photon excited fluorescence (TPEF) microscopy is a very promising and already widely applied imaging modality [1]. Different molecules can be discriminated by their different fluorescence spectra and, furthermore, the nonlinear nature of TPEF allows for inherent 3D sectioning of thick tissue [2, 3]. But there is even more information one can gain from TPEF microscopy. In fluorescence lifetime imaging (FLIM), fluorophores with similar emission spectra are distinguished by the decay time of their fluorescence emission. Different fluorophores may not only have different lifetimes, but more importantly, also the lifetime of one and the same molecule can critically depend on its molecular environment. This can yield valuable information about electronic interactions, steric configuration and vibrational coupling [4]. With this wealth of information, TPEF microscopy combined with FLIM is a valuable tool for researchers throughout many fields of bio-molecular science [5–7].

The current gold standard for FLIM is time correlated single photon counting (TCSPC) [8]. There, the time of arrival of the first fluorescence photon after an excitation pulse is measured. By recording a large number of such arrival times, the fluorescence decay can be represented by a photon histogram. An important constraint of this approach is that only one fluorescence photon can be detected between two excitation pulses. If more photons are emitted by a fluorophore, the lifetime is biased towards a shorter lifetime as the detection electronics has a dead-time and later arriving photons are less likely detected. Therefore, the rate at which fluorescence photons are created has to be lowered to about a 10th to a 100th of the excitation pulse rate in order to lower the probability of missing the detection of fluorescence photons. Ti:Sa lasers, which are typically applied today, have pulse repetition rates of ~100 MHz. Taking into account the constraint mentioned above, a maximum photon count rate of about 1 MHz can be achieved. If an accurate lifetime measurement requires 100 or more photons, the maximum pixel rate for a FLIM image is already reduced to ~10 kHz resulting in an acquisition time of more than 1.5 minutes for a 1024 × 1024 pixel image. Highly sophisticated counting modules from companies like PicoQuant or Becker & Hickl can extend the count rates of TCSPC systems up-to 40 Mcounts/s using fastest counting electronics [9]. However, this increase in speed comes with a loss in accuracy of the lifetime measurement because of pile-up effects [10].

To overcome this speed limitation without sacrificing temporal resolution, direct sampling approaches have been proposed where the fluorescence signal is measured directly in time domain [11–14]. Using such an approach, Giacomelli et al. have demonstrated that large area biopsies can be assessed rapidly to give physicians a direct feedback during a surgical resection of malignant tissue [11].

However, an even wider range of applications of these techniques is currently hindered by the need for a complex and expensive excitation source. Like all nonlinear imaging techniques, TPEF- and two-photon FLIM-imaging require very high peak power with low duty cycle. The high power is necessary for a strong signal and the low duty cycle ensures that the average power is kept on a moderate level in order to avoid sample damage. Currently, the work horses for this kind of excitation are ultra-short pulse Ti:Sa lasers with pulse durations of ~100 fs and a repetition rate of ~100 MHz [15]. As these lasers tend to be bulky, expensive, and not fiber compatible, there is a demand for new, easier to use excitation sources to make the wealth of information provided by non-linear fluorescence microscopy available to more researchers and to expedite the translation of this technique into the clinic.

Especially fiber based sources have proven to be favorable as they are very robust, alignment and maintenance free, and less expensive compared to bulk optic excitation sources. Although they usually do not achieve as short pulses as bulk optic lasers do, picosecond fiber lasers have been successfully applied for TPEF imaging [16–22] and it has been shown that the image quality compared to a Ti:Sa is the same if the same duty cycle is applied [14,23].

In this paper, we present a new system which exhibits the advantages of both approaches. We use a sub-nanosecond pulsed fiber laser as excitation source and direct high analog bandwidth signal sampling. Compared to ultra-short pulsed lasers, we use pulses in the 100 ps regime which produce many more fluorescence photons per shot generating higher signal levels. This makes the electronic signal of our single pulse FLIM (SP-FLIM) system very robust against electronic noise. The applicability of direct sampling for FLIM was shown already in [11]. However, instead of using only the ratio of two values of the digitized signal for differential lifetime analysis, our high signal levels allow for a real exponential curve fitting at every pixel in the image. This yields highly differentiated FLIM images, even at speeds of 1 MHz pixel rate.

2. Methods

2.1 Basic concept

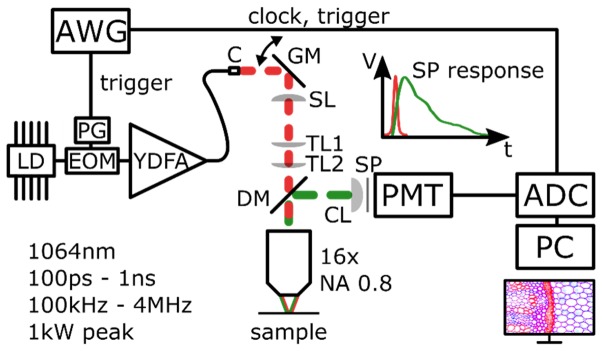
The basic concept of our approach is illustrated in Fig. 1. We use an actively modulated fiber laser with typically 100 ps long pulses at an adjustable repetition rate – typically set to 1 MHz – and peak powers of about 1 kW as an excitation source. The light is coupled into a self-built microscope where two galvanometric mirrors scan the beam on the sample. The generated fluorescence light from the sample is separated from the excitation light by a dichroic mirror (DM) and is detected with a fast photomultiplier tube (PMT) in a non-descanned detection configuration. The output signal of the PMT is digitized with a fast analog-to-digital converter (ADC) at 12 Bit and 4 GSample/s with a high analog bandwidth (2 GHz) in real time. The excitation laser and the ADC are synchronized by a phase locked arbitrary waveform generator (AWG). More details on the experimental realization are given in the following sections.

Fig. 1.

Basic concept of the single pulse FLIM setup. An arbitrary waveform generator (AWG) provides trigger and timing signals for the laser pulse generation and the digitization. Excitation pulses are provided by an all fiber master oscillator power amplifier (MOPA). Briefly, the output of a laser diode (LD) is modulated to short pulses by an electro optic modulator (EOM), driven by a high speed pulse generator (PG). These typically 100 ps seed pulses with 1 MHz repetition rate are amplified by ytterbium doped fiber amplifiers (YDFA) to ~1 kW of peak power. The fiber output gets collimated (C) and galvanometric mirrors (GM) are used for beam steering to raster-scan the sample. There, one single pulse has enough energy to excite many fluorophores so that many fluorescence photons can be detected by a photomultiplier tube (PMT). A fast time response of the PMT and high bandwidth of the analog to digital converter (ADC) ensure a high time resolution for accurate lifetime measurements. SL: scan lens; TL1, TL2: tube lens; CL: condenser lens; SP: short pass filter; DM: dichroic mirror.

2.2 Excitation laser source

The all fiber excitation laser is a self-built master oscillator power amplifier (MOPA), based on ytterbium doped fiber amplifiers (YDFA). The continuous wave and spectrally narrowband 1064 nm output of a laser diode (Innolume, LD-1064-FBG-400) is amplitude modulated with a 12 GHz electro-optic modulator (EOM, Photline, NIR-MX-LN 10). The electronic driving signal for the EOM is generated by a short pulse generator (PG, Alnair, EPG-210) where the pulse length can be adjusted continuously from 50 ps to 250 ps. This concept of actively modulating the pulses allows for freely selectable repetition rate and an easy synchronization with the detection. These seed pulses with a peak power of ~100mW out of the EOM are amplified in two core-pumped and one cladding-pumped YDFAs to peak powers of up to 1kW. The main limitation for higher power levels is stimulated Raman scattering (SRS) in the delivery fiber. Either by shortening the currently ~4m of standard single mode fiber (Corning SMF28e) or by replacing it with a large mode area (LMA) fiber, this limitation can be overcome if necessary. However, SRS can even be used to provide additional excitation wavelengths [24–26]. With such an extension, most of the prominent red fluorescence proteins can be addressed [27, 28]. For the measurements presented below, the pulse width was set to 100 ps and the pulse repetition to 1 MHz.

2.3 TPEF microscope setup

Our self-built multi-photon microscope follows partly the design concept presented in [29]. Briefly, the light output of the fiber laser is collimated with an aspheric lens with a focal length of 18.57 mm (C, Thorlabs, C280TME-1064). The output beam with a diameter of 4.1 mm is deflected by two galvanometric mirrors (GM, Thorlabs, GVS002). The pivot point of the galvanometric mirrors is relay imaged to the back focal plane of the microscope objective with a 75 mm achromatic lens (SL, Thorlabs, AC508-075-C-ML) as scan lens and a combination of a 300 mm (TL1) and a 400 mm lens (TL2) (Thorlabs, AC508-300-C-ML, AC508-400-C-ML) as tube lens. Thus, the output beam is magnified 2.8-fold with a resulting beam diameter of 12.3 mm before the objective. With an NA 0.8 16x objective (Nikon, CFI75 LWD 16xW) this results in a spot size of 1.6 µm for 1064 nm. The overall transmission from the fiber output to the focal plane was measured to be 46%. On the way back, a dichroic mirror (DM, Thorlabs, DMLP950R) separates the fluorescence light from the excitation light and deflects it onto a fast multi-alkali photomultiplier tube (PMT, Hamamatsu, H12056-20). The PMT has a quantum efficiency of ~16% at 600nm. To further suppress remaining excitation light, an additional short pass filter (SP, Edmund Optics, SP1000 OD2) is placed before the PMT.

2.4 Electronics and digitization

A crucial part of our concept is an accurate synchronization of the excitation pulses with the detection electronics to minimize timing jitter. To achieve this, we employed a 100 MS/s four channel inter-channel locked arbitrary waveform generator (AWG, TTi, TGA12104). This function generator provides trigger signals for the excitation laser and the data acquisition card. The digitizer is a 2 GHz bandwidth high speed 12 Bit analog-to-digital converter card (ADC, Alazartech, ATS9373) (cf. Figure 1). With a data throughput, of 6.8 GByte/s and data packing, it is possible to continuously stream the acquired data into the PC memory. An internal phase locked loop (PLL) on the ADC card is used to multiply the 10 MHz reference signal from the AWG to 4 GHz which is used as the sampling clock. Together with the trigger signals, this allows us to calculate the exact sample location where the signal occurs for every excitation pulse.

The fluorescence light is detected with the fast PMT with a rise time of ~600 ps. The current output of the PMT is converted to a voltage by a 50 Ohm resistor directly at the output, which also matches the impedance of the BNC signal cable. Together with the 50 Ohm terminated input of the ADC card, a total current to voltage conversion of 25 V/A is achieved. At a typical PMT control voltage of 800 mV, the internal gain is $g~3·{10}^5$. Thus, at a gating time of $\tau ~1 ns$, a single photon event produces a current of $I=e·g/\tau ~48 \mathit{\mu }A$ resulting in a voltage amplitude of $U=R·I~1.2 mV$. Assuming a linear response of the PMT our full range of the ADC corresponds to a total of ~400 detectable photons per time gate.

2.5 Data processing and fluorescence lifetime fits

The acquired data is continuously streamed to the PC memory. With the synchronized detection, only the samples with TPEF information are stored in a data array for further processing in order to reduce the total amount of data. 40 to 100 samples -an equivalent of 10 to 25 ns- around the time of the excitation are stored for the determination of the TPEF intensity and for fluorescence lifetime fitting. Because the data is streamed continuously, it will be possible to implement real time analysis on a graphics processing unit (GPU) for live video rate FLIM imaging. We have demonstrated such a processing at comparable data rates for live 4D-OCT imaging [30].

For TPEF intensity images, the maximum value of the acquired data points of the transient measured with the ADC is used. To determine the fluorescence lifetime, an exponential lifetime model is fitted to the data points. For most of the presented images, we applied a 3x3 pixel binning to improve the lifetime measurement quality.

We use two different approaches to obtain the fluorescence lifetime of a given sample. In the first method, we assume that the recorded data is dominated by the time characteristics of the fluorescence decay. Then, fitting the exponential tail starting a few samples after the excitation pulse is performed. As this does not take into account the systems time response, it does not deliver an exact time constant of the fluorescence decay. However, this relatively fast fitting method can be used to distinguish areas with different decay constants and is therefore useful to implement a lifetime color contrast in FLIM images.

To obtain a more accurate decay time value, the instrument response function (IRF) has to be taken into account as the actual measured data is a convolution of the fluorescence decay and the time response of the measurement system, the IRF. The IRF can be measured by recording a kinetic with quasi instantaneous time response like second harmonic generation (SHG). The straight-forward way to use a deconvolution on the measured data with the measured IRF is usually not working very well as this approach is quite sensitive to noise. A more robust way to get an accurate decay constant is to create a model exponential decay with a set of start parameters and convolute it with the measured IRF. This function is then fitted to the measured lifetime data.

To form a colored FLIM image, the fitted parameters are mapped to a color using the HSV (hue, saturation, value) color space for each pixel. The HSV value of a pixel is set according to the fluorescence amplitude and the HSV hue according to its lifetime. The saturation can be used to display a quality of fit parameter or is set to 1. Usually, the values of the single components are mapped by a linear transformation. For some images, a nonlinear transformation was chosen to achieve a better visualization, for example a logarithmic transformation for the intensity to brighten up dim features. This is indicated for each image individually.

3. Results and discussion

3.1 Instrument response function (IRF)

In contrast to TCSPC, the IRF or apparatus function is given by the electronic bandwidth of the overall system in the SP-FLIM approach. To measure the IRF, we imaged a slide of Urea crystals. The second harmonic signal of these crystals represents an instantaneous response of the sample under investigation. Therefore, only the time characteristics of the laser system and the detection system influence the acquired data.

Figure 2(b) shows the image of Urea crystals. It has a size of 512 × 512 pixels and was acquired with 1 MHz pulse repetition rate and a single pulse per pixel. This led to a total acquisition time of 670 ms. The discrepancy between a theoretical acquisition time of 260 ms and the mentioned 670 ms is due to the fact that we currently have not implemented bidirectional scanning. We use only about 80% of one direction of our scan range for imaging, to avoid nonlinear image distortion due to the slow mechanical response of our scan mirrors. The intensity in the image is displayed on a logarithmic scale to better visualize dim features.

Fig. 2.

Instrument response function (IRF) determination with second harmonic signal (SHG) of Urea crystals. Blue curves indicate measurements, red curves Gaussian fits. a) unaveraged SHG signal of a single excitation pulse at pixel P1 as a representative of an IRF. The FWHM of a Gaussian fit is 1.34 ns b) 512 × 512 pixel image of Urea crystal acquired with a single pulse per pixel at a pixel rate of 1 MHz acquired within 670 ms (raw data acquisition time 260ms, see text). The intensity is displayed on a logarithmic scale to better visualize dim features. The coloring represents the FWHM of a Gaussian fit of a single pixel. The homogeneous color distribution indicates that the variation of the FWHM of the systems time response is small. c) Histograms of the center position and the FWHM of the Gaussian fits of all pixels of image b). Scale bar 100 µm.

For each pixel, 60 samples (15 ns) are acquired and fitted to a Gaussian model function. The signal of a representative pixel (indicated as P1 in Fig. 2(b)) is depicted in Fig. 2(a). The FWHM of a Gaussian fit of the recorded SHG signal at P1 is 1.34 ns. The mean value of the FWHM of all pixels in the image is 1.30 ns. This represents the apparatus function of our system. However, even shorter lifetimes can be extracted with a suitable fit method. Then, the time resolution is given by the variation of the width of the apparatus function. We determined a standard variation of 63 ps (cf. Figure 2(c)) of the FWHMs of the Gaussian fits of all pixels in image Fig. 2(b). This means that for low noise signals we can expect to get reliable access to lifetimes <<1ns by deconvolution. We also measured a jitter of the center of the apparatus function of 136 ps (cf. Figure 2(c)) by analyzing the center of the Gaussian fit for all pixels in the image. This jitter is caused by the triggering electronics of the 100 MS/s AWG. However, because of our high signal fidelity, we can apply an appropriate fit model accounting for the jitter of the time zero. Thus, in our case the time resolution of the lifetime measurement is not directly affected by the jitter of the time zero. Also, a higher bandwidth trigger signal would reduce this effect.

3.2 Lifetime of a sample exhibiting a single exponential decay

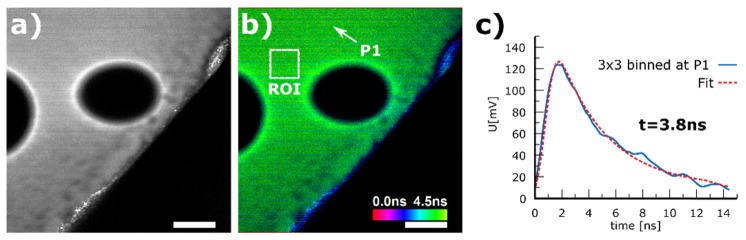
The quality of the applied lifetime fitting method is validated by measurement of a sample with known lifetime and single exponential decay characteristics. We dissolved Rhodamine 6G in methanol and further diluted the solution to a concentration of approximately 10 mM. A drop of the solution was placed on a microscope slide, covered with a No. 1 cover slip and sealed with nail-polish (On the microscope slide, a thin (~150 µm) compartment was made by pieces of a No. 1 coverslip). An image of a region of 0.5 × 0.5 mm was acquired with 1024 × 1024 pixels at a total acquisition time of 1.9 s. The raw data acquisition time was only 1.0 s. Figure 3(a) shows the acquired region of the Rhodamine sample with intensity contrast. The holes are air bubbles within the sample and the edge stems from the glass spacer used to make the compartment. The lifetime distribution is depicted in Fig. 3(b). The lifetime is mapped to color as specified in the scale bar and the TPEF intensity values are used for brightness. For this image, 3 × 3 pixels are binned and the lifetime is fitted for the binned pixels with a model taking the IRF into account. An example pixel is presented in Fig. 3(c). The fit reveals a fluorescence lifetime of 3.8 ns. A region of interest (ROI, Fig. 3(b)) was selected to analyze the variation of the lifetime within the image. There, the standard deviation was 270 ps at a mean lifetime of 3.6 ns which is in good agreement with a literature value of 3.7 ns for the molecular lifetime of Rhodamine 6G [31]. As the color distribution in the areas around the air bubbles in Fig. 3(b) shows, the lifetime distribution is very homogenous. However, the lifetime strongly changes towards the interface between the dye solution and the piece of glass. While the intensity image (Fig. 3(a)) reveals only a slight change in structure, the lifetime image clearly shows that the lifetime is much shorter in this region which is an indicator for a higher Rhodamine concentration [31].We suggest that the lifetime change is due to the drying of the solution at the interface and Rhodamine molecules are strongly aggregated. Overall, these results demonstrate the applicability of the SP-FLIM method to accurately measure lifetimes.

Fig. 3.

Single exponential decay of Rhodamine 6G dissolved in methanol. a) Intensity image, size 0.5 × 0.5 mm at 1024 × 1024 pixel acquired within 1.9 s (raw data acquisition time: 1.0 s, see text) b) SP-FLIM image with 3x3 pixel binning for the lifetime map. A region of interest (ROI) was selected to determine the lifetime variation (see text) c) Single exponential decay lifetime fit of a 3x3 binned pixel taking IRF into account. Scale bar 100 µm.

3.3 Lifetime imaging with 1 MHz pixel rate

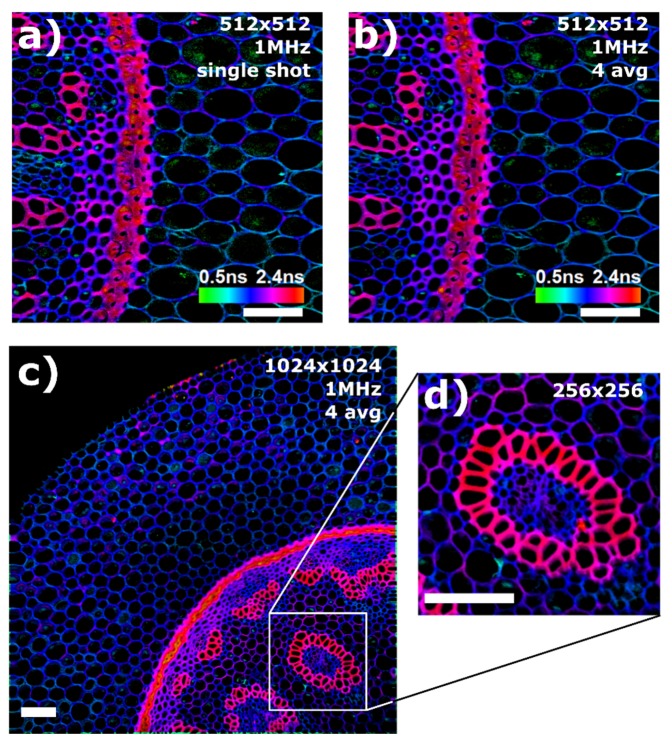
To show the performance of our SP-FLIM system, we present SP-FLIM images of a convalaria majalis stem stained with acridine orange (Lieder GmbH) in Fig. 4. All images were acquired with an excitation power of ~30 mW on the sample. The upper images (Fig. 4(a) and 4(b)) show a region of 0.5 × 0.5 mm² with a resolution of 512 × 512 pixel. The hue in the images is set by a linear transformation of the fluorescence lifetime. For lifetime determination, 3x3 pixels were binned. Since the dynamic range of the TPEF signal is too large to be displayed directly, we apply a non-linear high dynamic range (HDR) mapping of the brightness data. The brightness is given by the intensity of the logarithmically scaled TPEF signal to better visualize areas with a weak signal in these high dynamic range images. It should be mentioned, that the logarithmic scaling of the brightness gives the visual impression of a somewhat reduced transverse resolution in the appearance of the image. The left image Fig. 4(a) was acquired with a single excitation pulse per pixel at a pixel rate of 1 MHz. The total acquisition time was 670 ms. As mentioned above, the actual data recording time for the 512 × 512 pixel SP-FLIM image was only 260 ms (512 × 512/1 MHz). Since we did not employ bidirectional scanning and the scanner showed a strong non-linearity at the turning points, we omitted most of the scan time for a distortion and wobble free image. In the future, this problem will be solved by applying bidirectional scanning protocols and numerical removal of “zipper” artifacts in post processing as shown earlier [32]. At typical 80% scanning duty cycle, an acquisition time for one frame of 330 ms is realistic for non-resonant scanners.

Fig. 4.

SP-FLIM images of a convalaria majalis stem. The upper images show a region of 0.5 × 0.5 mm² with a resolution of 512 × 512 pixel. 3x3 pixels were binned for lifetime measurements. a) Single pulse excitation per pixel at a pixel rate of 1 MHz, the total acquisition time was 670 ms (see text). b) The same region 4 × averaged, acquired within 2.7 s. c) 1.2 × 1.2 mm² at 1024 × 1024 pixel resolution, acquired within 7.6 s. d) Zoom-in into a region of interest. Scale bar 100 µm.

The right image (Fig. 4(b)) shows the same region four times averaged and was acquired within 2.7 s. The lower image (Fig. 4(c)) shows a larger region of 1.2 × 1.2 mm² of the same sample with a resolution of 1024 × 1024 pixel. With an excitation rate of 1 MHz and four times averaging, the total acquisition time was 7.6 s.

Despite the high acquisition speed, Fig. 4(a) shows that the quality of a single shot lifetime acquisition is very high. Clearly, the plant cell walls (blue color) can be distinguished from the vascular bundle (red color) and chloroplasts within the cells (green color).

In cases where a sample exhibits lower fluorescence signals, frame averaging might be necessary. Since all components are synchronized, averaging is straightforward, as shown in Figs. 4(b)-4(d). Almost no loss of resolution is observed, indicating very good repeatability of the scans. While the single pulse FLIM image in Fig. 4(a) exhibits some noise, the four times averaged image reveals the same structural elements of the sample at an even higher image quality, with still a very fast total acquisition time of only 2.7 s. Furthermore, this high acquisition speed makes it possible to acquire a large area of view at a high resolution. For example, Fig. 4(c) has a size of 1024 × 1024 pixels and was acquired within 7.6 s. This allows to zoom into areas of interest to analyze it further as shown in Fig. 4(d).

3.4 Multi-species contrast

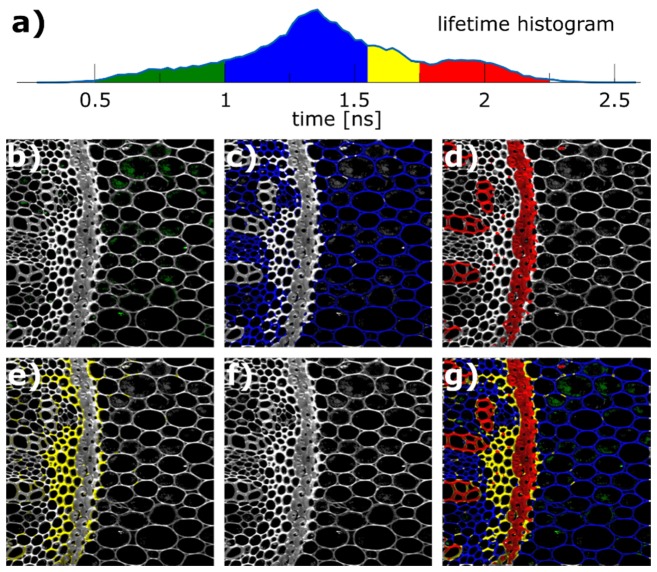
The purpose of Fig. 5 is to investigate how much more information is contained in the lifetime measurements compared to a TPEF intensity image and how well different time decay constants correspond to specific sites in the sample. In Fig. 5(a) the lifetime histogram of all pixels (not weighted by intensity) of the convalaria majalis image presented in Fig. 4(b) is shown (512 × 512 pixels, 2.7 s acquisition time). We analyzed the multi-peak structured histogram distribution and can identify four different regions. The most dominant peak is at 1.3 ns and two other peaks can be identified at 0.7 ns and at 1.9 ns. Additionally, the peak at 1.3 ns exhibits a slight shoulder around 1.6 ns. We assume that every individual peak or shoulder is indicative for an individual component or molecular species. To represent this multi-component structure, the histogram is divided into four sections and used to color code pixels for the regions individually as follows: pixels with a lifetime between 0.5 ns and 1.0 ns are colored green, from 1.0 ns to 1.55 ns blue, 1.55 ns to 1.75 ns yellow, and from 1.75 ns to 2.5 ns red. In Figs. 5(b)-5(e) the images are colored accordingly. It is obvious that the individually colored areas – distinguished by different lifetime bins – are representing various functional sites of the plant stem. These topologically ordered structures are hard to identify within the image showing TPEF intensity contrast only (Fig. 5(f)). In total, the image shows that the variation within the lifetime distribution does not stem from system imperfections but that it is based on the different lifetimes of the various components of the sample. Although, we would expect that photon counting systems produce higher quality lifetime measurements, our signal and dynamic range is sufficient to clearly identify 4 different species in this case.

Fig. 5.

Individual colorings of different lifetime regions of Fig. 4 b). 512 × 512 pixel, 1 MHz pixel rate, 4 × averaged, total acquisition time 2.7 s. a) Lifetime histogram over all pixels. b) - e) Individually colored areas distinguished by different lifetime bins representing various functional sites of the plant stem. f) TPEF intensity. g) Overlay of colored images.

4. Conclusion

With the presented results, we show that longer pulses in the many-10ps to nanosecond regime are not only suitable for TPEF imaging but also allow for fast FLIM imaging. The high energy pulses in the sub-ns regime produce enough fluorescence photons to determine the lifetime directly from a single shot. This makes very fast FLIM imaging with 1 MHz pixel rate possible and even higher pixel rates could be feasible. Moreover, in cases, where it is important to not only contrast an image by lifetime differences but also extract substantial information from the lifetime itself, it is essential to derive the actual decay constant. With the data presented above, we have demonstrated that this is possible due to the strong signal produced by longer pulses, the high bandwidth detection, and an appropriate fit algorithm. The time resolution has proven to be sufficient to distinguish in our case 4 different species with lifetimes close to each other. Furthermore, the technological advance in high speed data acquisition will make even higher time resolution possible and close the gap to TCSPC systems. Additionally, the implementation of the system is very compatible to other microscopic imaging modalities, like fast 4D OCT [30] and TICO (time-encoded) stimulated Raman sensing [26]. It can even be envisioned that the Fourier Domain Mode locked (FDML) laser [33–36], which is used for MHz-OCT [32, 37, 38] and for TICO-Raman, is compressed by a long highly dispersive fiber and then used as pump source [39]. In conclusion, we think SP-FLIM with the all fiber based excitation source and accurate decay time determination by high speed analog detection and real exponential curve fitting is a promising technology to bring 2-photon FLIM imaging out of optics labs to the work-benches of researchers or into clinics for medical diagnosis. Also, this system can be a big step towards fast and reliable, cost effective multi-modal non-linear endoscopes.

Funding

European Union project ENCOMOLE-2i (Horizon 2020, ERC CoG no. 646669); German Research Foundation (DFG project HU1006/6 and EXC 306/2).