Abstract
Optical coherence tomography (OCT) has become one of the most successful optical technologies implemented in medicine and clinical practice mostly due to the possibility of non-invasive and non-contact imaging by detecting back-scattered light. OCT has gone through a tremendous development over the past 25 years. From its initial inception in 1991 [Science 254, 1178 (1991)] it has become an indispensable medical imaging technology in ophthalmology. Also in fields like cardiology and gastro-enterology the technology is envisioned to become a standard of care. A key contributor to the success of OCT has been the sensitivity and speed advantage offered by Fourier domain OCT. In this review paper the development of FD-OCT will be revisited, providing a single comprehensive framework to derive the sensitivity advantage of both SD- and SS-OCT. We point out the key aspects of the physics and the technology that has enabled a more than 2 orders of magnitude increase in sensitivity, and as a consequence an increase in the imaging speed without loss of image quality. This speed increase provided a paradigm shift from point sampling to comprehensive 3D in vivo imaging, whose clinical impact is still actively explored by a large number of researchers worldwide.
OCIS codes: (170.0170) Medical optics and biotechnology, (170.4500) Optical coherence tomography, (030.4280) Noise in imaging systems
1. Introduction
Optical Coherence Tomography (OCT) is analogous to ultrasound imaging, where a sound pulse is launched and the reflections (echoes) are measured to create an image of tissue. In OCT light reflections are measured by a Michelson interferometer, using the low coherence properties of a broadband light source: only light that has traveled approximately the same distance in the two arms of the interferometer to within the coherence length of the source is able to create interference fringes. By measuring this interference, the location and strength of the reflections can be determined. In its original inception, depth profiles (A-lines) of the tissue were acquired by scanning the length of the reference arm to map out the tissue reflectivity. This approach has been retrospectively named Time Domain OCT (TD-OCT). Although historically names for the different techniques have been used interchangeably, we used the following nomenclature for this review. The alternative approach to TD-OCT, and the topic of this review paper, is named Fourier Domain OCT (FD-OCT). Fourier domain OCT detection can in principle be performed in two ways: either by using a spectrometer (called Spectral Domain OCT or spectral OCT) or by using a rapidly tunable laser (called Swept Source OCT or Optical Frequency Domain Imaging). Both approaches have in comon that the reflectivity along a depth profile is measured for a multitude of wavelengths separately. For a single wavelength, the reflectivity of a sample is determined by the periodicity of the refractive index modulation along the beam, in analogy with e.g., a fiber Bragg grating [2]. A single wavelength provides information on the strength of the periodic refractive index modulation (Fourier component) along the beam with a periodicity determined by the wavevector , with the wavelength. By combining the information of a multitude of wavelengths, a depth profile can be created by a Fourier transformation of the reflectivity as a function of wavevector, thus the name Fourier Domain OCT. Two dominant implementations of FD-OCT have emerged over the past 15-20 years: Spectral Domain OCT (SD-OCT), where the wavelength dependent reflectivity is measured using a broad band light source and a spectrometer, and Swept Source OCT (SS-OCT), also called Optical Frequency Domain Imaging (OFDI), where the wavelength dependent reflectivity is measured with a single (balanced) detector, and where a narrow band light source is rapidly tuned over a large optical bandwidth. Both implementations have in common that the wavelength dependent reflectivity is determined, and a depth profile is obtained by a Fourier transformation.
The key feature of FD-OCT over TD-OCT is the improved sensitivity, which will be discussed in more detail and with mathematical rigor in the next section. An in depth analysis reveals that the improved sensitivity is not a consequence of an increase of the signal, but follows from a fundamental reduction of the noise, which leads to the significant Signal to Noise Ratio (SNR) improvement. Although it has been argued that the SNR improvement follows from the feature that FD-OCT measures a full depth profile in a single shot, this holds only for SD-OCT, but not for SS-OCT, where the wavelength dependent reflectivity is measured sequentially. Moreover, an implementation that also provided a single shot depth profile did not result in an improved SNR [3,4]. Key to the SNR improvement is the detection of sample reflectivity as a function of wavelength. The best achievable performance of an OCT system is reached in the shot noise limit, meaning that shot noise is the dominant noise contribution. In an OCT system one assumes that the sample arm light is orders of magnitude weaker than the reference arm, and the shot noise is generated by the reference arm intensity only. OCT is an interferometric technique, relying on the detection of interference of sample and reference arm light, and this provides a key insight into the signal formation. Interference will only be observed between electromagnetic fields that differ in frequency by less than the detection bandwidth. In the near IR region for a detection bandwidth of 1 GHz this corresponds to optical frequency differences of a few parts per million. Thus, interference is only observed for (virtualy) identical wavelengths. In an optimal OCT system, a detector should measure only virtually identical wavelengths, since if more wavelengths are present (and thus more intensity will fall on the detector), the shot noise will increase.
The principle of FD-OCT was demonstrated earlier, SD-OCT in 1995 by Fercher et al. [5] and SS-OCT between 1997 and 1999 [6–11] however, the sensitivity advantage was not recognized nor demonstrated. The first theoretical hints at the sensitivity advantage were provided by Andretzky et al. and Mitsui in 1998 [12,13]. Although Andretzky's paper was intensely debated at that time and Mitsui's paper was overlooked by the community, the results were not generally accepted, partly due to incomplete derivations, a confusion of sensitivity with dynamic range, and a lack of solid experimental confirmation. The firm establishment and acceptance of FD-OCT as a superior technology over TD-OCT took another 5 years and came in 2003, with three papers (Leitgeb et al., de Boer et al., Choma et al.) providing both a theoretical derivation and an experimental confirmation of the sensitivity advantage of both SD-OCT [14,15] and SS-OCT [16]. It is hard to overstate the impact of FD-OCT on the success of OCT as an in vivo medical imaging technology. Image speeds increased from the first TD-OCT systems at 2 A-scans/second to speeds up to few millions A-scan/second using SS-OCT with high speed swept source technology [17]. Such a dramatic development (an increase of 6 orders of magnitude in acquisition speed within 25 years) has opened new fields of applications and contributed to the success of OCT.
In this paper we present a general overview of the basics of Fourier Domain OCT method and its main advantage of sensitivity improvement, enabling the rapid acquisition rates that are necessary to reduce motion artifacts in vivo. In order to illustrate the fundamental principles of the method we used examples of ophthalmic imaging, which is currently the most evolved application of Fourier Domain OCT.
2. Historical overview
The first ideas of Fourier interferometric detection reach back to nineteenth century - the golden age of interferometry. The concept of dispersing the spectrum in the interferometric set-up was initially introduced for speeding-up an adjustment procedure in white light interferometric experiments since the spectrally resolved interference signal was detectable over much larger path length differences than that observed directly, without spectrally dispersing [18].
The first application of one dimensional distance ranging of biological tissue by FD-OCT was presented in 1995 by Fercher et al. for corneal thickness measurement [5]. Three years later Hausler and Lindner demonstrated the first tomograms of skin measured by so called spectral radar which was similar to Fercher’s spectral interferometric instrument [19]. In both papers, however authors used relatively narrow spectral bandwidths and the quality of the resulting cross-sectional images were not close to what could ultimately be achieved. The next step in the technology development was initiated between 1999 and 2003 by Wojtkowski and Leitgeb, who demonstrated the first decent quality SD-OCT images of the in vivo retina and anterior segment SD-OCT by solving basic physical limitations including removal of DC and autocorrelation components, mapping lambda to k-space before the Fourier transformation and reducing the exposure time to avoid strong fringe wash-out [20,21]. At that time it was also demonstrated that SD-OCT could be a promising candidate for the assessment of functional parameters by recording spectroscopic, polarization and Doppler dependent data [22–25].
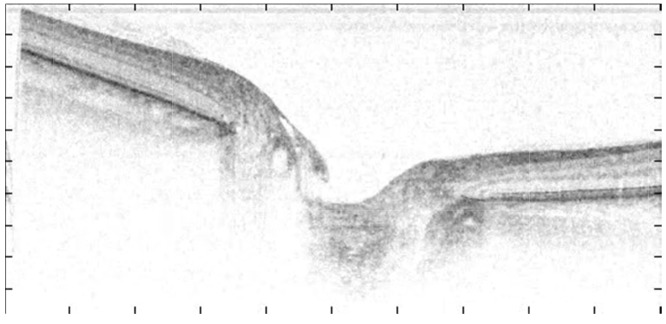
Another major step in development of SD-OCT was the first demonstration of the improved speed of OCT in vivo retinal imaging at 15,000 A-scans/s, albeit at bursts of 128 A-lines (8 ms) for a single B-scan, followed by a 150 ms dead time for A/D conversion and data transfer using a camera with a matrix CCD acting simultaneously as a linear detector and a storage media [26,27]. Fig. 1 and the embedded movie demonstrate one of the first high speed retinal SD-OCT imaging showing pulsation of blood vessel obtained with the experimental OCT system mentioned above.
Fig. 1.
Fourier domain OCT is able to visualize dynamics of the retina: comparison of OCT movie (Visualization 1 (449.8KB, MOV) ) showing a sequence of real-time SD-OCT cross-sectional images of peripheral part of human optic disc in vivo: measured by the experimental system using a matrix CCD [26] as discussed in the text.
The full potential of SD-OCT and a breakthrough in retinal imaging speed and quality was demonstrated in 2004 by Nassif et al. at 830 nm, showing continuous acquisition at 29.000 A-lines per second and 1000 A-lines per B-scan for video rate high quality imaging of the human retina in vivo [28,29]. Figure 2 and the embedded movie shows results from this system acquired in 2003. The system used a spectrometer with linear CCD array (Atmel TH7814A Linear CCD), real time data transfer to the host PC at a 10 bit/pixel resolution with a 98% duty cycle, demonstrating shot noise limited detection and a sensitivity of 98.4 dB at 600 μW of sample arm power. A key feature that enabled high speed acquisition was the realization that 10 bit/pixel resolution was sufficient to reach a dynamic range of 40-60 dB in an A-line, and that even with the relatively small well depth of each pixel (180.000 electrons) shot noise limited detection was already reached at only 6% of the saturation value for each pixel.
Fig. 2.
Single frame of a movie (Visualization 2 (7.1MB, MP4) ) (9.4 MB) of a region around the optic nerve head, acquired in 13.1 seconds at a rate of 29 fps with 1000 A-lines/frame. Each image is 6.4 mm wide x 1.7 mm deep. The sequence sweeps over a region 5.12 mm long, with one frame out of 380 shown above. The retinal vasculature is seen both in the layers of the retina and converging in the optic nerve head itself. Reproduced from Ref [29] with permission of the Optical Society of America.
The availability of InGaAs linear arrays, albeit with a poorer performance in terms of pixel number, noise performance and speed allowed the first demonstration at 1300 nm and 18,000 A-scans/s in 2003 of a human finger [30]. The first video rate SD-OCT demonstration was quickly followed by Ultra High Resolution retinal imaging [31], and video rate Ultra High Resolution retinal imaging including numerical compensation of dispersion for these very large bandwidth sources [32,33]. The first clinical results in ophthalmology obtained with SD-OCT demonstrated the diagnostic advantage of volumetric OCT images. Linear CCD and CMOS arrays have since become the standard for SD-OCT, achieving 50,000 A-scans/s in 2007 [34] and 310,000 A-scans/s in 2008 [35].
The first demonstration by Choma et al. in 2003 [16] that SS-OCT provided the same SNR advantage as SD-OCT was quickly followed by the first high speed SS-OCT system at an A-line rate of 15.7 kHz and a sensitivity of 110 dB at 6 mW source power [36] starting a rapid development in sources and systems that has culminated in state of the art systems exceeding MHz A-line rates [17,37].
3. Theoretical advances
The most striking feature of FD-OCT is the sensitivity advantage that has enabled a gain in acquisition speed by several orders of magnitude as compared to time domain OCT without compromising image quality. In the following we give both a short explanation for this advantage as well as rigorous mathematical treatment, after describing the key parameters to quantify OCT system performance.
To start, we need to define sensitivity and signal-to-noise ratio (SNR). In OCT we define SNR as the quotient of the average squared signal divided by the noise variance, i.e., . The angle brackets define ensemble averaging, which in case of ergodic signals is equal to the time averaging. Usually SNR is given in decibels as . The sensitivity is defined as the inverse of the smallest sample reflectivity Rs, min, for which the SNR equals 1, i.e., .
In TD-OCT we observe the interference signal at a single axial location or delay at a time. Hence, the detection system records at each axial location over the full spectral bandwidth the summed power reflected from all depth locations, whereas the actual OCT signal is present only within the temporal coherence gate, i.e., the light reflected from a thin tissue slice with a thickness corresponding to the coherence length of the source. Thus only a small part of the received sample arm light actually contributes to the OCT signal, which fraction is given by the ratio of round trip coherence length to the full depth scanning range.
In FD-OCT only a narrow optical bandwidth corresponding to a long coherence length on the order of millimeters is measured by each detector element (SD-OCT) or sequentially in time by a single detector element (SS-OCT). Thus, light backscattered from all depth regions corresponding to the coherence length interfere with the reference beam at the detector and contribute to the spectrally resolved interference pattern. Fourier analysis of the spectrally resolved interference pattern obtains the full axial structure in parallel, the recorded signal contributes in its entirety to the axial structure. In contrast, for a single detector TD-OCT system, the full optical bandwidth reaches a single detector element. Interference will only occur between electromagnetic fields of (virtually) the same optical frequency or wavelength. The carrier frequency of the interference at this wavelength is given by , with the reference arm mirror (group) velocity [38]. At the same time due to the white noise characteristic, the shot-noise generated by the power density at one particular wavelength is present at all electronically detected frequencies, and therefore adversely affects the SNR at all other carrier frequencies and consequently wavelengths . By spectrally dispersing each wavelength to a separate detector in space (SD-OCT) or time (SS-OCT), the cross shot-noise term is eliminated in both hybrid and fully parallel SD/SS-OCT systems while the full interference signal is preserved [15]. Both SD-OCT and SS-OCT have this key feature in common. Altogether, this immediately translates into higher detection sensitivity as compared to the case of TD-OCT.
The above explanation for the sensitivity advantage holds in case photon or shot noise is the dominating noise source. For a rigorous mathematical treatment, we also consider excess, and receiver noise. To facilitate the noise analysis in the case of SD- and SS-OCT, the signal and noise terms will be expressed in number of photo-electrons. The number of photo-electrons is related to the number of incident photons via the conversion factor as , where P is the total incident power on the detector, is the photon energy at optical frequency with Planck's constant. For SD-OCT the integration time per detector element is , where each detector element detects an optical bandwidth . For SS-OCT the integration time needs to be replaced by , the single detector sampling time, where during time interval the detector detects an optical bandwidth . This results in a spectral interference signal term for SD-OCT,, per spectral detector element for a reflecting surface at location expressed in electron charge given by [14,15],
| (1) |
with Pref and Psample the total reference arm and sample arm power integrated over the optical bandwidth of the source in the detection arm, respectively, N the number of spectral detection channels of width , and where is the electron charge. Equation (1) assumes a flat constant source spectrum covering a spectral width of .
For SS-OCT the spectral interference signal term,, per detector sampling time and a reflecting surface at location expressed in electron charge is given by [16,36],
| (2) |
with Pref and Psample now determined by the full power of the swept source emitted within the optical bandwidth over time interval . Noting that for equal A-line rates the detector sampling time in SS-OCT is equal to the integration time divided by the number of detector elements in SD-OCT, it is immediately observed that Eqs. (1) and (2) for and , respectively, are identical.
Figure 3 illustrates further the relation between the energy detected by each element in SD-OCT during integration time and by the single element in SS-OCT during sampling time .
Fig. 3.
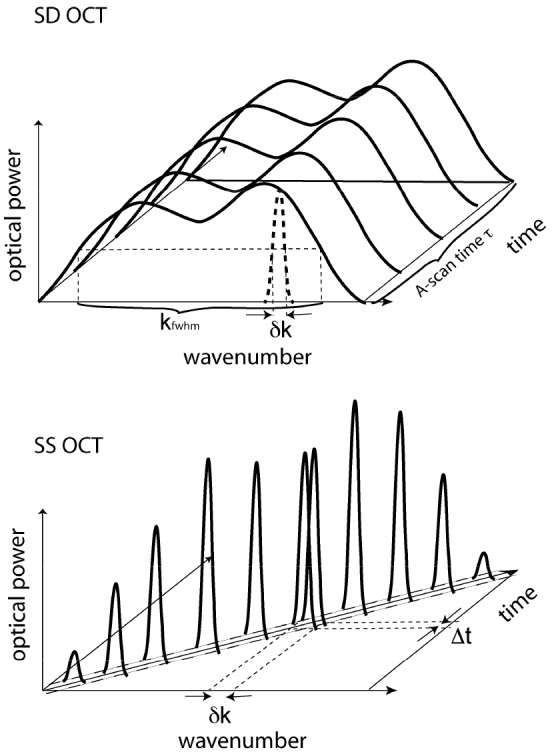
Deposited energy at the detector for SD-OCT compared to SS-OCT. A) In SD-OCT the total source power is emitted over optical bandwidth and distributed over N detector elements. The energy deposited at a single detector element is given by the fraction of the source power times the integration time , giving an energy per detector element of . B) In SS-OCT the total source power is emitted over optical bandwidth . The energy deposited at a single detector element is given by the total source power times the sampling time , giving an energy per detector sampling time of . With the relations and the deposited energies within optical bandwidth are equal, . (reproduced from [39])
The non-interfering term per detection element, also called DC term, is given for SD-OCT and SS-OCT, respectivley, by
| (3) |
In case of TD-OCT we follow a derivation in units photocurrent, and the single detector (N = 1) reads a signal current, that can be related to the optical power P as . The interference term for TD-OCT is given by
| (4) |
with the coherence envelope of the low coherence source. With those definitions the SD-OCT, SS-OCT and TD-OCT signal powers can be written in analogy with the definition of Sorin and Baney as [40],
| (5) |
| (6) |
| (7) |
The noise contributions are shot noise and Relative Intensity Noise (RIN), also known as Bose Einstein (BE) noise, for SD- SS- and TD-OCT, and CCD detector read-out and dark noise for SD-OCT, and thermal noise for SS-OCT and TD-OCT. These noise terms are additive on the level of variances.
The read-out and dark noise for SD-OCT, and thermal noise for SS-OCT and TD-OCT, do not depend on the incident optical power. In case of integrating sensors such as CCDs it is described by read noise and dark noise in terms of number of electrons. For photocurrent detectors, such as PIN diodes, the thermal noise is described per unit bandwidth using noise equivalent current. The relation between variances of photo-electrons fluctuations and photo-current fluctuations is .
Shot noise itself describes the signal fluctuation due to the random arrival of photons at the detector and follows a Poisson distribution. The shot noise variance is therefore given directly by the number of detected photo-electrons . For OCT, the noise is dominated by the DC contribution of the signal. Assuming further that the power of the reference arm is much larger than the power of the sample arm, the shot noise per detector element in SD- and SS-OCT becomes, respectively,
| (8) |
In TD-OCT the photocurrent associated with the OCT signal is recorded with an electronic detection bandwidth B. The shot noise in case of photo current reads , assuming again dominant reference arm power. The shot noise per unit bandwidth is then given by,
| (9) |
The RIN or BE noise term expresses random fluctuations in intensity, which scales inversely with the optical bandwidth per detector element, and quadratic with the optical power. The total noise variance in detected photo-electrons squared per read out cycle and per spectral detector element for SD-OCT is given by [14,15].
| (10) |
For SS-OCT the total noise variance in detected photo-electrons squared per sampling time is given by,
| (11) |
and for TD-OCT the total noise variance in photocurrent squared is given by [40,41].
| (12) |
The RIN noise term is proportional to and for SD- and SS-OCT, respectively, and is given assuming a thermal light source, for which the inverse optical bandwidth per detection element can been expressed by the coherence time as [42],
| (13) |
with c the speed of light, the center wavelength of the source, and the spectral width detected by a single detector element for SD-OCT or the instantaneous laser line width for SS-OCT, respectively. In SS-OCT the laser source RIN is in general much smaller than for a thermal light source.
The expressions for the signal and noise in the Fourier domain have been expressed as a function of wavevector in relation to a single detection element (SD-OCT) or a single sample interval (SS-OCT). The actual FD-OCT signal is obtained by Fourier transform (FT) of the recorded spectral interference pattern or . We therefore need to translate the expressions for the recorded signal and noise to the space domain. Parseval's theorem states that the integrated power before and after the FT is conserved. Since the noise is white, the noise power of each detector element in the spectral domain as expressed by the variance in Eqs. (10) and (11), will therefore be equal to the noise power per detector element after Fourier transformation. Hence, the noise variances after FT, and , are related to the noise variance in the Fourier domain as and . For the signal power also Parseval's theorem holds, but where the signal power in the Fourier domain is distributed equally over the spectrum (see Eqs. (5) and (6)), after the FT all the power will be concentrated in 2 pixels, one at positive and one at negative depth location. The signal amplitude after FT for SD-OCT and SS-OCT will then be, respectively,
| (14) |
| (15) |
The final SNR of SD-OCT becomes then,
| (16) |
and for SS-OCT,
| (17) |
where we assumed that . In case of shot noise limited detection, i.e., or , the expression for the SNR in the shot noise limit becomes [14–16,36],
| (18) |
This expression can be compared to the respective expression for TD OCT which reads
| (19) |
We immediately observe that both expressions for the SNR for the time domain and the Fourier domain are formally identical through the relation between electronic detection bandwidth B and integration or sampling time, for SD-OCT, for SS-OCT, respectively. The important difference between the actual measured SNRs becomes clear by expressing the electronic bandwidth of TD-OCT into the integration time for SD-OCT or the sampling interval for SS-OCT. The carrier frequency generated by wavelength for a reference arm mirror moving at velocity is given by . The electronic bandwidth of the signal for TD-OCT is given by [38],
| (20) |
where is defined by the spectral width of the source and vg is the group velocity, which can be assumed as the axial scanning velocity in TD-OCT. The group velocity of the TD-OCT measurement is given by the depth range divided by the time to acquire a single A-line,
| (21) |
The corresponding −6 dB fall off depth range in SD- or SS-OCT is given by (see Izatt et al. [43] for an in depth analysis of ranging depth expressed in sampling interval or spectral resolution),
| (22) |
with the spectrometer resolution or the instantaneous laser line width, respectively. Combining Eqs. (20)-(22) and assuming an optimal configuration where the sampling interval in k-space is equal to the spectrometer resolution or the instantaneous laser line width and sampling the spectral width with N measurement such that results in,
| (23) |
Inserting this bandwidth into Eq. (19), the SNR for TD-OCT can be directly compared to that of SD- and SS-OCT, showing that the SNR for SD- and SS-OCT is better by approximately a factor N/2,
| (24) |
Examining the SNR expressions for SD- and SS-OCT in Eq. (18) in more detail, it is observed that for a single sample arm photon being detected per measurement time , the SNR is already 1, meaning that FD-OCT is sensitive to a single photon, and it is hard to imagine that this can be improved upon within the realm of classical optics. The second observation is that the SNR in FD-OCT does not depend on the bandwidth of the source. In TD-OCT the SNR (Eq. (19)) depends on the optical bandwidth of the source through the electronic bandwidth B. When the optical bandwidth increases, also the electronic bandwidth needs to increase (Eq. (20)), leading to a lower SNR. As a consequence, FD-OCT is ideally suited for Ultra High Resolution (UHR) OCT compared to TD-OCT. However, since in FD-OCT the number of photons detected from within a tissue slice is proportional to the system resolution, the total number of detected photons per depth resolution will be lower in an UHR FD-OCT system compared to a standard FD-OCT system.
A difference between SD- and SS-OCT is the magnitude of the RIN noise term. From Eqs. (10) - (11),
| (25) |
It is clear the RIN noise for SS-OCT is orders of magnitude larger. Therefore, balanced detection is in general used in SS-OCT systems to cancel or significantly suppress the RIN noise, although the laser source RIN is in general much smaller than for a thermal light source, which was assumed here.
The sensitivity is obtained by setting Eq. (16) or Eq. (17) equal to one, and expressing for the inverse sample reflectivity 1/Rsample, assuming . Sensitivity in FD-OCT is best understood by plotting the sensitivity contributions as function of reference arm power Pref. The graphics in Fig. 4 assumes again Pref>>Psample. For small Pref the receiver noise contribution dominates and the sensitivity increases linearly with Pref until it comes close to the shot noise limit. Shot noise limited SNR and sensitivity is independent of Pref, and depends only on the amount of photons being backscattered from the sample Psample . If the reference arm power is further increased, RIN becomes dominant, and the sensitivity decreases inversely proportional with Pref. In case of ideal balanced detection, RIN will be suppressed, and the sensitivity approaches asymptotically the shot noise limited value with increased Pref. Sensors with a low receiver noise, such as charge coupled devices (CCDs), allow achieving shot noise limited detection already with low power levels. Even at high frame rates of CMOS sensors, which usually exhibit higher noise than scientific grade CCDs, the reference arm power may be adjusted to come close to shot noise limit. At high frame rates of several 100kHz, RIN noise might however become dominant before the shot noise limit can be reached.
Fig. 4.
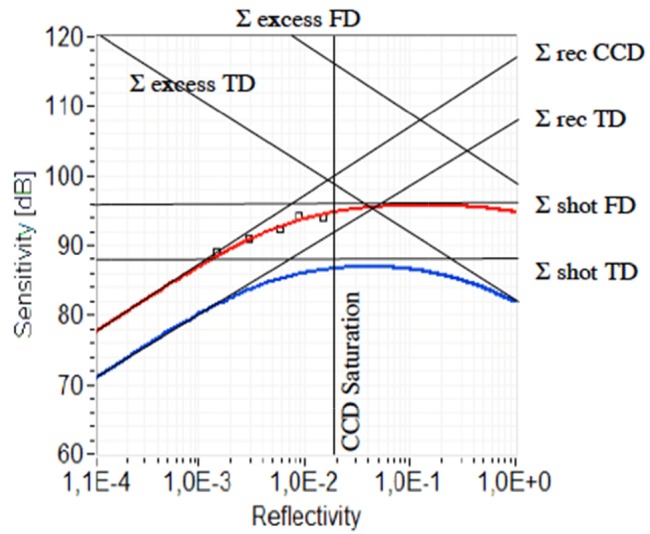
The red line shows the theoretical sensitivity Σ for FD-OCT, employing a CCD sensor, according to Eq. (16) with Pref = 0.15P0, Psample = 0.07 P0, ρ = 0.19, η = 0.4, P0 = 175μW, τi = 1 ms, σr + d = 250 e-(at room temperature), FWC = 400 ke- The blue line is the TD-OCT sensitivity for an unbalanced configuration, with Pref = 0.25 P0, B = 113 kHz, NEC = 0,5pA/√Hz. The squared dots are the actual measured system sensitivities. (reproduced from Leitgeb et al. [14]). The saturation of the CCD sets the ultimate limit to the achievable sensitivity in SD-OCT.
4. Experimental implementation
The core of an Fourier domain-OCT systems is a Michelson or Mach-Zehnder interferometer with either a spectrometer in the detection arm (SD-OCT) or tunable light source and a single pixel photoreceiver (SS-OCT). A careful analysis of the noise terms in experimental Fourier domain OCT systems is essential for optimal performance of the system, and we will use the earlier derived equations.
Noise analysis of FD-OCT and optimal performance parameters using charge coupled devices (CCD’s)
To reach the optimal performance of an FD-OCT system the shot noise should dominate other noise terms. For SS-OCT systems this depends mainly on the magnitude of the laser source RIN and the ability to suppress RIN by balanced detection, which requires careful experimental evaluation. For SD-OCT balanced detection is in general not an option, however since RIN is orders of magnitude smaller than for SS-OCT (see Eq. (25)) balanced detection is not necessary to reach shot noise limited detection. The signal and noise for SD-OCT were earlier derived in Eq. (14) and Eq. (10), respectively [14,15]. The three noise terms in Eq. (10) (using the earlier derived equivalence ) are the sum of read out and dark noise of the CCD array, , shot noise which is proportional to the reference arm power and the integration time, and the relative intensity noise for a thermal light source,which is proportional to the reference arm power squared, the integration time and the coherence time (Eq. (13)). The optimal signal to noise performance is achieved when shot noise dominates both read-out noise and relative intensity noise (RIN) [40]. Shot noise dominates read-out and dark noise when their ratio is larger than 1, i.e., . Shot noise dominates RIN when their ratio is larger than one, i.e., . The optimal reference arm power is found when read-out noise and dark noise are equal to the RIN [30].
| (26) |
Thus, for a system to operate close to shot noise limited performance, shot noise should dominate read-out noise and dark noise and RIN noise at the optimal reference arm power,
| (27) |
At this optimal reference arm power, the inequalities describing shot noise dominance over read-out noise and RIN, respectively, reduce to the same equation,
| (28) |
Since the A-line rate is inversely proportional to the integration time one would like to choose the integration time as short as possible, and since the coherence time is inversely related to the spectral resolution of the spectrometer which in turn relates linearly to the maximum depth range of the system, one would like to choose the coherence time as long as possible. Equation (28) describes the tradeoff between these performance parameters for an SD-OCT system with respect to remaining in the shot noise limited sensitivity region.
Autocorrelation noise
Fourier Domain OCT is based on spectral interferometry, where recombined light from reference and sample arms is spectrally separated, detected and converted into a depth profile. The detected interference signal at the spectrometer may be expressed as [44].
| (29) |
where and are the wavelength-dependent intensities reflected from reference and sample arms, respectively, and k is the wave number. The second term on the right hand side of Eq. (29) represents the interference between light returning from reference and sample arms. is the square root of the sample reflectivity at depth . Depth information is retrieved by performing an inverse Fourier transform of Eq. (29), yielding the following convolution [44].
| (30) |
with Γ(z) representing the envelope of the coherence function. The first term in the braces on the right hand side describes the autocorrelation signal from the reference arm and has magnitude unity. The second and third terms are due to interference between light returning from reference and sample arms and form two images, where each has magnitude on the order of . These two terms provide mirror images, where one is retained. The final term, with magnitude on the order of , describes autocorrelation noise due to interference within the sample arm [20,44]. Is and Ir represent the total intensity reflected from sample and reference arms, respectively. For SS-OCT the first and third term are significantly suppressed by balanced detection, for SD-OCT Eq. (30) indicates that the relative contribution of sample autocorrelation noise can be reduced by increasing the reference arm power with respect to the signal, decreasing the ratio and consequently reducing the contribution of autocorrelation noise in ultra-high-speed FD-OCT.
Dynamic range and digitization depth
Earlier SD-OCT system designs emphasized the necessity of large well depth (number of electrons that could be stored in a single element of the CCD) and large bit depth as an important consideration to realize the high sensitivity and dynamic range that can be achieved by OCT. Sensitivity is the ratio of maximum signal over noise floor, where the maximum signal is defined by placing a perfect reflector in the sample arm. The dynamic range of a system is the maximum signal over the noise floor that a particular system can measure without e.g., saturating a detector, overloading an amplifier or exceeding a digitization range. In practice, no TD or SD-OCT system realizes a dynamic range equal to the sensitivity, which can easily be over 100 dB. In general, this is not necessary, since tissue reflectivity is at least 4 orders of magnitude smaller than a perfect reflector. A system dynamic range of 40-60 dB suffices in most cases.
A 60 dB dynamic range in a TD-OCT system would require at least a 10 bit A/D range (6 dB per bit) digitizing the interference modulation on the DC background. An advantage of TD-OCT and SS-OCT systems is that balanced detection can be implemented easily and that the signal can be high pass filtered to remove the DC component and only pass the interference modulation to the digitization circuitry. In SD-OCT, the CCD detectors do not easily permit balanced detection and removal of a DC component, and considerations similar to that for a TD-OCT system suggest that for an SD-OCT system the A/D range needed to capture the interference modulation on top of the DC background with sufficient resolution to provide 40-60 dB dynamic range would require an A/D resolution significantly exceeding that of a TD-OCT system. Fortunately, the required bit resolution capturing the interference modulation to achieve 40-60 dB dynamic range turns out to be much smaller.
In SD-OCT the reflectivity in z-space is given by the summed square of a single cosine modulation in k-space. The resolution of reflectivity in z-space is proportional to the resolution of the modulation depth of the spectrum, multiplied by the number of illuminated pixels of the camera (on the order of ~1000). Thus, a relative small resolution of the modulation depth of the spectrum (on the order of a few bits) gets amplified by the number of illuminated pixels, easily providing a dynamic range in z-space exceeding 40-60 dB. The same argument is valid for SS-OCT systems. The presence of multiple reflecting structures complicates matters. For example, two strong reflectors in the sample arm each create a periodic modulation of the spectrum. These modulations are summed and create a larger modulation depth of the spectrum on the DC background that should be captured without saturation of the CCD or clipping of the digitization circuitry. Therefore, the calculation of the dynamic range of a FD-OCT system is not a straightforward calculation of the strongest single reflector that can be measured, but depends on the total power reflected by the sample. As the total reflected power increases, the dynamic range with which the reflectivity of a particular location can be measured decreases for a given A/D resolution.
Experimental demonstration of SNR advantage
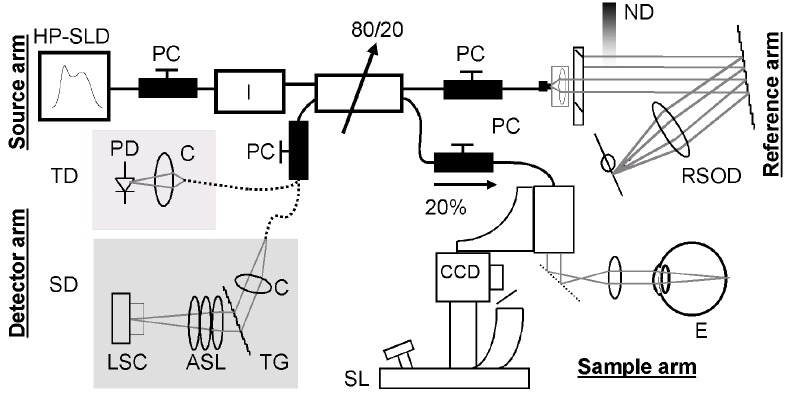
A direct comparison between the SNR of a TD-OCT versus a SD-OCT was presented by de Boer et al. [28]. To compare directly the SNR performance they used a combined TD-OCT and SD-OCT set-up presented in Fig. 5.
Fig. 5.
Time and Spectral domain system integrated into a single instrument for a direct comparison of the SNR. Reproduced from Ref [28]. with permission from the Optical Society of America.
The power reflected by the weak reflector in the sample arm measured at the fiber tip in the detection arm was 1.3 nW. The polarization states of sample and reference arm light were carefully aligned to maximize interference. First, 256 depth profiles at a speed of 4 ms per depth profile were acquired with the TD-OCT system, scanning over a depth of 1.4 mm in air. The signal pass bandwidth (BW) was 100 kHz. Then the detection arm was connected to the spectrometer, and 256 spectra were acquired at a speed of 100 μs per spectrum. To reduce fixed pattern noise in the SD-OCT measurement [14], each individual spectrum was divided by the average spectrum of 1000 reference arm spectra. The resulting spectrum was multiplied by a Gaussian to reshape the spectrum [45]. A Fourier transform links z and k space. Because of the non-linear relation between k and λ, the spectra were interpolated to create evenly-spaced samples in the k domain [20] before Fourier transformation of the spectra to generate depth profiles.
Figure 6 shows the averaged depth profiles acquired with the respective configurations, demonstrating a SNR of 44.3 and 50 dB for TD- and SD-OCT respectively. Both depth profiles were normalized on the reflectivity peak. The TD measurement was shifted such that the peaks coincide. Some fixed pattern noise was still present in the SD-OCT measurement, resulting in peaks at 84 and 126 μm. Since the SD-OCT system was 5.7 dB more sensitive, operated at a speed 40 times faster (corresponding to 16 dB) than the TD-OCT system, the combined sensitivity improvement was 21.7 dB or a factor of 148. The theoretical shot noise limited SNR in TD and SD are given by, respectively(see Eq. (19) and Eq. (18)) [14,15],
| (31) |
resulting in 46.7 dB (TD) and 51.9 dB (SD), where = 0.85 was used for a PIN diode in TD. The measured TD and SD SNR’s were respectively 2.4 and 1.9 dB less than the theoretical optimal performance, where 1 dB in TD was determined to be due to thermal noise contributing to the total noise. The measured coherence function FWHM in air was 6.3 μm in both TD- and SD-OCT.
Fig. 6.
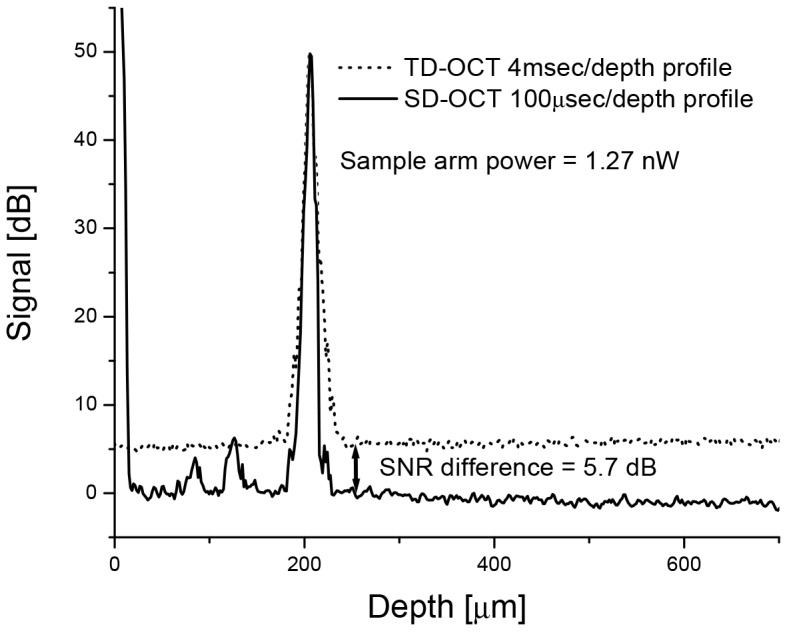
Direct comparison of the SNR between SD and TD-OCT. Reproduced from Ref [28]. with permission from the Optical Society of America.
Shot noise limited detection
The different noise components present in the system were measured and analyzed to demonstrate that performance was shot-noise-limited. The read-out and shot noise at a 29.3 kHz read-out rate are shown in Fig. 7.
Fig. 7.
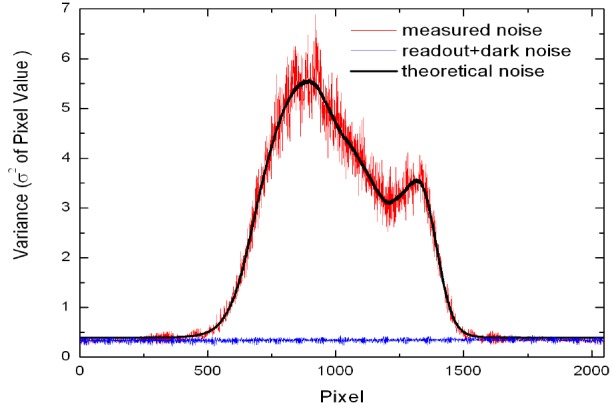
Noise components in the detector. The shot noise level was determined with illumination of the reference arm only, and was used to determine the A/D resolution of the detector. The theoretical shot noise curve was fit using Eq. (32) to the measured noise, giving a Δe of 173 electrons and a corresponding well depth of 177,000 electrons. Reproduced from Ref [29]. with permission from the Optical Society of America.
The noise was determined by calculating the variance at each camera pixel for 1000 consecutive spectra. Dark noise measurements were taken with the source light off. Only light returning from the reference arm was used to measure the shot noise in the system. The shot noise expressed in number of electrons is , where is the pixel value corresponding to the intensity at each CCD element, with values ranging from 0 to 1024 (10-bits) and Δe is the analogue-to-digital conversion resolution, which corresponds to the number of electrons required for an incremental increase of 1 pixel value. Thus, the variance as measured in pixel values is defined as:
| (32) |
The first term on the right hand side of Eq. (32) is the shot noise contribution and the second term is the read-out contribution to the total noise. The CCD well depth was determined by fitting the theoretical expression for shot noise to the measured shot noise, using Δe as the fitting parameter and limiting the fit to the central 700 pixels. From this measurement, Δe was calculated to be 173 electrons. Assuming that the maximum pixel value corresponds to the full well depth, a well depth of 177,000 electrons was calculated, in agreement with our previously published result [28]. Shot noise dominated read-out and dark noise when the intensity reached 6% of the saturation value. Relative intensity noise (RIN) was never dominant in this setup, since the maximum power per pixel (4.6 nW) at a 34.1 μs integration time does not meet the criteria for RIN dominated noise [28].
Remapping to k-space; sensitivity drop off as a function of depth; spectrometer resolution, fixed pattern noise removal
In FD-OCT, the structural information, i.e. the depth profile (A-line), is obtained by Fourier transforming the optical spectrum of the interference as measured by a detector at the output of a Michelson interferometer [5,20]. Fourier transformation relates the physical distance (z) with the wave number (k = 2π/λ). The spectra obtained with FD-OCT are not necessarily evenly spaced in k-space. The importance of proper wavelength assignment for FD-OCT was first described by Wojtkowski and Leitgeb [20]. Incorrect wavelength mapping generates a depth-dependent broadening of the coherence peak similar in appearance to dispersion in structural OCT images. A proper depth profile can be obtained only after preprocessing to obtain data that is evenly spaced in k-space, and this requires accurate assessment of the wavelength corresponding to each spectral element.
Depth dependent sensitivity
In all FD-OCT methods, the sensitivity is dependent on the depth within an image. This roll-off in sensitivity is related to the spectral resolution with which the signal can be detected. For SD-OCT systems the roll-off is caused by the inability to accurately measure the high frequency modulation of the detected spectrum, which is a combination of the effect of the finite pixel size of the array [14] and the finite spectral resolution of the spectrometer [30]. For SS-OCT the roll-off depends on the instantaneous line width of the light source and the detection bandwidth of the photodiode and digitizer. Figure 8 shows an example of this effect, where a weak reflector was placed in the sample arm at different depths. For an ideal system, one would expect that each peak would have the same height.
Fig. 8.
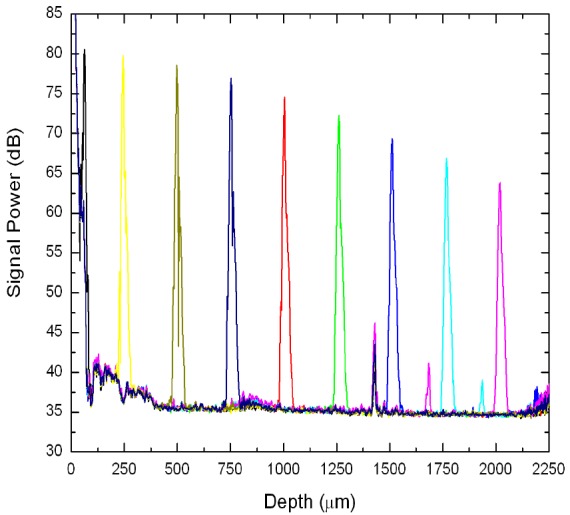
The depth dependent loss in signal sensitivity from a weak reflector. The signal decayed 16.7 dB between 0 and 2 mm. The peaks at 1.4 mm, 1.6 mm, and 1.85 mm are fixed pattern noise. Reproduced from Ref [29]. with permission from the Optical Society of America.
Combining both effects by convolution of the finite pixel size with the Gaussian spectral resolution for SD-OCT or the instantaneous linewidth for SS-OCT yields the following expression for the sensitivity reduction, R, as a function of imaging depth, z [30],
| (33) |
where d is the maximum scan depth, and ω is the ratio of the spectral resolution to the sampling interval. Equation (33) was fit to the signal decay data presented in Fig. 8 with ω as a free parameter. Due to its proximity to the autocorrelation peak, the first data point was not included in the fit. The value for ω obtained from the fit was 1.85, demonstrating that the working spectral resolution was 0.139 nm. For an SS-OCT system this would have corresponded to an instantaneous line width of 0.139 nm.
There are significant differences in depth dependent sensitivity performance between SD-OCT and SS-OCT. Technologically it is much easier to achieve a narrow instantaneous line width in tunable light source than to manufacture a spectrometer covering more than 100 nm optical bandwidth with very high spectral resolution. This is especially true for short cavity lasers like VECSELs, with coherence lengths corresponding to centimeters of OCT ranging depth [46–48].
Motion artifacts and fringe washout
As OCT utilizes lateral point-scanning, motion of the sample or scanning beam during the measurement causes SNR reduction and image degradation in both: SD-OCT and SS-OCT [49]. Yun et al. theoretically investigated axial and lateral motion artifacts in continuous wave (CW) SD-OCT and SS-OCT, and experimentally demonstrated reduced axial and lateral motion artifacts using a pulsed source and a swept source in endoscopic imaging of biological tissue [49,50]. Stroboscopic illumination in full field OCT was demonstrated, resulting in reduced motion artifacts for in-vivo measurement [51]. In ophthalmic applications of SD-OCT, SNR reduction caused by high speed lateral scanning of the beam over the retina may be dominant over axial patient motion. Pulsed illumination can reduce lateral motion artifacts, however care should be taken as pulsed illumination increases the RIN noise [50].
5. Complex representation of the fourier domain OCT signal
Fourier transformation of the real valued spectral fringe OCT signal results in a linear summation of the structural information and two extra terms, the total intensity of the signal that appears as DC term at z = 0 and self- cross correlations between fields back reflected at individual sample structure layers (Eq. (30)). These latter terms are commonly referred to as auto-correlation or coherence noise terms [29,52]. There is also another side effect, which is an ambiguity with respect to the zero delay associated with the Hermitian nature of the inverse Fourier transform as it is applied to the real valued signal I(k). As a result, each structure term has its mirror image in the inverse Fourier space corresponding to negative positions with respect to zero optical path delay. Therefore, all structure terms should be confined to one half of the Fourier space to avoid an overlap between various signal component. In practice the imaging system should be designed in such way that an imaging depth should be significantly larger than the thickness of an imaged object. In such situation it is enough to adjust the reference arm delay to position the object within the range corresponding to half of the Fourier space. Such a simple procedure enables distinguishing between the cross-sectional image and coherence noise artifacts. In case the object thickness is longer than the distance corresponding to the half of Fourier space the coherence noise terms and symmetrical images mix together with the signal representing the actual axial sample structure and direct reconstruction of the true architecture of the measured sample becomes impossible.
The reconstruction of the complex representation of the spectral fringe signal resolves this ambiguity and the image space can be doubled. As the complex space is dual (consisting sin and cos) it requires at least two phase-shifted copies (so-called frames) of the spectral fringes to calculate the complex signal. One of the most straightforward ways of the complex reconstruction is based only on two frames with a relative phase shift of [53,54]. A simple combination of two shifted spectra will still have a strong DC component as well as coherence noise terms. To use this technique, the reference intensity needs to be much larger than the sample intensity – a condition often fullfilled in biomedical applications. Then it is sufficient to subtract the reference spectrum from each spectral interference pattern to suppress the DC term along with the cross correlation terms.
Mathematically the determination of the complex representation from real interferometric signals requires a minimum of three linearly independent equations [55]. This can be done by measuring at least three times the intensity signal with an additional phase shift introduced to each interference fringe pattern. The phase shift between measured fringe signals can be anything between 0 and . In order to reduce the influence of phase shift errors it is also possible to create an over-determined system of equations measuring N fringe patterns with additional n phase shifts.
There are many possible algorithms retrieving the phase information based on extended set of measurements with linear phase shifts including, three-, four-, five- and six frames techniques [55]. Initially the five frame method has been chosen for OCT applications because of its optimal performance in phase reconstruction [56,57]. In this technique five consecutive measurements of the spectral fringes Ι(ω) are needed with a phase increment of π/2.
Figure 9 shows a results of complex SD-OCT imaging of a rabbit eye in vitro The autocorrelation terms located close to the zero path difference (central white stripe) and the superimposed mirror image are clearly visible. The five-frame technique efficiently reduces these artifacts and uncovers the details of the sample (Fig. 9, right panel).
Fig. 9.
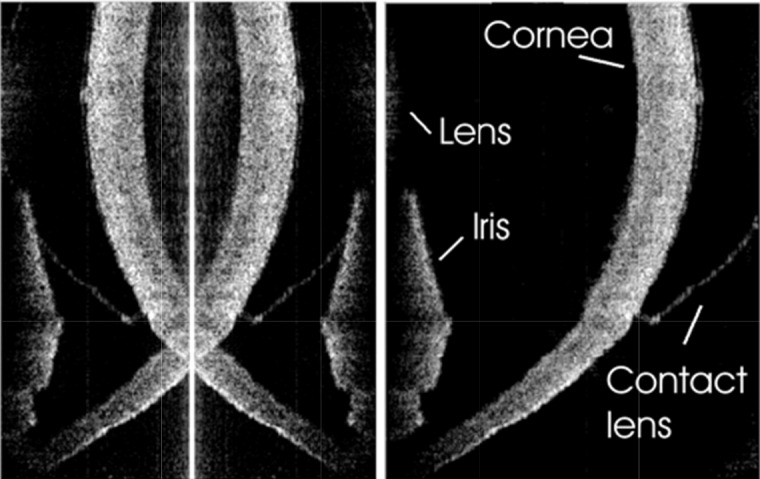
SD-OCT Cross-sectional image of a hard contact lens on the rabbit eye in vitro: left, standard SD-OCT, right, complex(five–frame) SD-OCT. Image reprinted from [58]
The easiest way to introduce the phase shift is by changing the path length of the reference arm using for example a mirror mounted on a moving mechanical element. A more efficient way of shifting the optical delay in the reference arm is by using acousto-optic or electro-optic modulators. For SS-OCT, Yun et al. demonstrated already in 2004 removal of the depth-degeneracy with frequency shifting using an acousto-optic modulator [59]. Gotzinger et al. used an electro-optic modulator for an SD-OCT system [60]. For SD-OCT systems the array detectors cannot follow the fast signal modulations in the MHz range. Bachmann et al. demonstrated a solution using two slightly detuned AOFS in the sample and reference arm respectively [61]. A quadrature detection scheme is realized by locking the array detector to the resulting lower beating frequency and recording the shifted spectral interference patterns via an integrated bucket method. This method has the potential together with array detectors based on CMOS technology to perform true heterodyne detection with Spectral Domain OCT. CMOS technology allows on-chip demodulation of the heterodyne signal such that only the AC part will subsequently be amplified and digitized. In an alternative approaches phase shifted spectra were recorded simultaneously on different lines of 2D detector [62]. Choma et al. followed a completely different approach by using the phase relation between the arms of a 3x3 fiber coupler and recording two phase shifted copies of the interference pattern on separate detectors [63,64].
Another interesting concept for a complex OCT system combining heterodyne time domain beating with Fourier Domain detection was proposed by Yasuno et al. [65] and Makita et al [66]. This technique is analogous to the heterodyne complex method presented by Yun et al [59]. Instead of a carrier frequency in a single A-scan introduced by the phase modulator the entire set of cross-sectional OCT data is analyzed. The phase modulation is introduced by periodical and continuous phase modulation of the reference beam. The time dependent lateral scanning and time dependent phase modulation mix together. Assuming low speed of the transverse scanning and analyzing each optical frequency separately, the low frequency light intensity modulation caused by the lateral structure of an object and speckle pattern is now shifted by the frequency introduced by the beating of the time domain signal. In turn the low frequency cross-correlation and DC terms are separated from the signals corresponding to the lateral structure of measured object by numerical Hilbert transformation, which together with high-pass filtering enables reconstruction of the complex and coherence noise free Fourier domain OCT signal. The same method is applied by introducing a lateral scanning induced carrier frequency through a simple shift of the sample beam from the pivot position on the scanning mirror. This method does not need any additional phase shifting device, but comes at the price of rigid setting of scanning field of view and speed [67].
An attractive alternative to complex signal retrieval for full range imaging in FD-OCT is dispersion encoded full range OCT. There, one uses the fact that the complex conjugate signal term is affected asymmetrically by higher order dispersion. Hence, iterative post-processing algorithms allow dispersing the complex conjugate terms below noise in favor of the actual sample terms [68]. Passive suppression of mirror terms as well as off-setting the sensitivity roll-off envelope to larger depth positions is achieved by Talbot band imaging [69].
For SS-OCT it is possible to perform true heterodyne detection by locking the detector to a sinusoidal reference arm delay modulation. It is relatively easy to implement frequency shifting devices such as acousto-optic frequency shifters (AOFS) allowing for high speed quadrature detection with fast PIN diodes [59,70,71]. As a result it is possible to introduce the carrier frequency to the spectral fringe signal and remove the complex conjugate artifacts by quadrature detection without doubling the measurement range. In the case of frequency shifting of the spectral fringe signal the carrier frequency introduced by the phase modulator placed in the reference arm of the OCT interferometer establishes the reference point for the zero optical path delay.
In general full range imaging has its importance for spectrometer based SD-OCT, where on the one hand spectral sampling and the related maximal depth range is limited by the finite number of linear sensor elements, and on the other hand the strong SNR roll-off in depth can be relaxed by imaging across the zero delay position. SS-OCT, however, is more flexible concerning the spectral sampling, usually exhibiting exceptional depth ranging capabilities with low SNR roll-off. Full range imaging has therefore become less important for classical point scanning SS-OCT. The situation is different in full field SS-OCT, where an array sensor samples the spectrum over time. Since available array sensors are still relatively slow, the number of recorded points needs to be kept small to avoid large measurement times and resulting motion distortions of the spectral interference fringe signal. Applying a simple method of reference arm tilting with respect to the sample arm at the sensor plane introduces a lateral spatial modulation just as in holography [62]. Spatial frequency filtering extracts the interference signal, and allows again for complex OCT signal reconstruction. Thereby the needed number of spectral samples can be reduced by a factor of two to facilitate sufficient axial range for in-vivo OCT imaging [72,73].
6. Phase stability and its impact on functional OCT
In SD-OCT, a phase-sensitive image is generated by simply determining the phase difference between points at the same depth in adjacent A-lines. This parallels the time domain method pioneered by Zhao et al. [74,75] The superior phase stability of SD-OCT, due to the absence of moving parts, was demonstrated by White et al. [25] The data was acquired with a stationary mirror in the sample arm, without scanning the incident beam. Ideally, interference between sample and reference arm light should have identical phase at the mirror position for all A-lines. This condition underlies the assumption that any phase difference between adjacent A-lines is solely due to axial motion within the sample. The actual phase varies in a Gaussian manner about this ideal, where we present the measured probability distribution of phase differences with a standard deviation of 0.296 ± 0.003°. This value is over 25 times lower than previously quantified figures for TD-OCT systems [76,77]. Phase sensitive detection is of particular interest for quantifying axial motion, which is the subject of Doppler OCT or OCT elastography. It has also been used in polarization sensitive OCT to calculate phase retardation, as well as for phase contrast microscopy.
6.1. Doppler OCT and OCT angiography
The main short-coming of OCT based on backscattering alone is its missing specificity to biological structures of interest. Functional extensions allow partially mitigating this deficiency by providing label-free intrinsic contrast of tissue. Doppler OCT as one of the most promising functional OCT candidate, provides depth resolved quantitative information on blood flow and velocity thereby generating angiographic maps without the need of contrast agents. The first Doppler OCT images based on TD-OCT were already presented in 1997 by Chen et al. and Izatt et al. [78,79]. In the past, phase-resolved Doppler OCT (D-OCT) based on time domain OCT (TD-OCT) was proven able to make high-resolution, high-velocity-sensitivity cross-sectional images of in vivo blood flow [74,75,77,80–82]. D-OCT measurements of blood flow in the human retina have been demonstrated [83,84], yet the accuracy and sensitivity was compromised by A-line rate and patient motion artifacts, which can introduce phase inaccuracy and obscure true retinal topography. As a result, they were too slow to assess retinal vasculature over a large range of vessel sizes and were limited in field of view [85]. In addition, for precise flow quantification information about the illumination angle with respect to the flow direction is needed [86]. Combining Optical Doppler Tomography with the superior sensitivity and speed of SD-OCT has allowed a significant improvement in detecting Doppler signals in vivo. In the first combination of these technologies, velocity of a moving mirror and capillary tube flow was demonstrated [87], followed by in vivo demonstration of retinal blood flow [24,25].
In case of Doppler SD-OCT, operating at an acquisition speed of 29kHz, a phase standard deviation of 0.296°, as demonstrated in Fig. 10, corresponds to a minimum detectable Doppler shift fD of ± 25 Hz. With the relation between Doppler frequency shift and axial velocity being , the minimum Doppler shift corresponds to a minimum axial velocity of only about 10µm/s assuming a central wavelength 840nm. The sensitivity to low flow velocities could be considerably improved by increasing the time delay between A-line measurements, as has been demonstrated by Refs [88–91]. For rapid flow, the fact that axial velocity is determined from circular phase shifts might result in phase wrapping. The unambiguous axial velocity range is determined as With a time difference of 34.1 μs between acquired A-lines, phase wrapping occurs at Doppler shifts greater than 15 kHz. High speed D-OCT at up to 300 k A-lines/sec enhances the velocity range, allowing to resolve unambiguously flow in vessels with larger diameter present for example in the region of the optic nerve head [92]. The improved phase stability for SD-OCT is not necessarily shared by SS-OCT due to the in most cases mechanical tuning of the sources together with electronic trigger jitter. In particular the latter leads to depth dependent phase error that is difficult to be corrected in post processing. Several solutions have been proposed to recover also for SS-OCT the intrinsic phase stability provided by the static reference mirror of FD-OCT systems [93–96]. Systems employing akinetic tuning sources show in fact similar phase stability as SD-OCT [97]. Ultimately, higher recording speed especially for SS-OCT results in reduced motion induced phase fluctuations during in-vivo assessment.
Fig. 10.
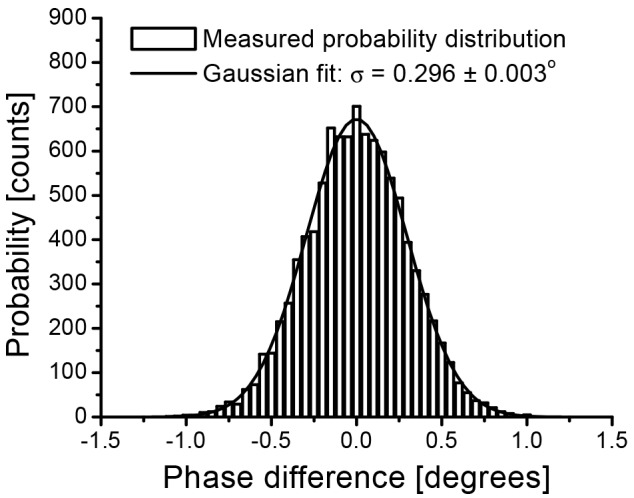
Probability distribution of the measured phase difference between adjacent A-lines in SD-OCT, with a stationary reflector in the sample arm. Bars: Counted phase difference for 9990 A-lines. Bin size = 0.05°. Solid line: Gaussian fit to the distribution, with a measured standard deviation of 0.296 ± 0.003°. Reproduced from Ref [25]. with permission from the Optical Society of America.
Recording full structural volumes together with phase information enabled the first attempts to overcome the Doppler angle ambiguity [98,99]. Their accuracy in determining flow suffered however from still present motion artifacts. Yet, the high speed of FD-OCT enabled dynamic imaging of relative pulsatile flow within individual vessels [25,100,101]. Ultimately, dynamic FD ODT could resolve pulsatile flow in a reliable quantitative manner, independent on the vessel direction, based on multi-beam [102–107] or volume acquisition schemes [108,109]. The high acquisition speed allowed furthermore for novel flexible scanning schemes to obtain 3D angiographic maps without compromising overall imaging time [88,91,110].
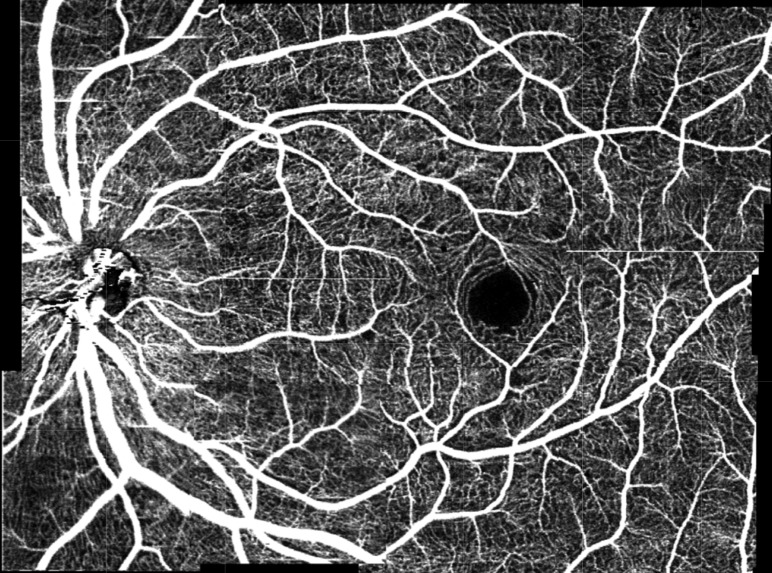
Algorithms to produce vascular contrast alone have been introduced already in TD-OCT using phase variance or displaying power Doppler maps [74,77]. In FD-OCT, alternative methods exploiting the intrinsically higher speed are resonant Doppler imaging [111], optical microangiography [112], joint frequency and time domain Doppler OCT [113], dual beam angiography [89,90], and other different flow filtering methods [114,115]. Modern OCT angiography (OCTA) displays signal differences between successive tomograms, being thereby sensitive to motion of red blood cells, and achieves high micro-vascular contrast down to the level of smallest capillaries [88,91,112,116–122]. Furthermore, OCTA is intrinsically co-registered with OCT structural information. Such label-free OCT angiography is becoming a clinical standard in retinal OCT nowadays establishing vascular structural pathologies as novel biomarker of retinal disease. Apart from ophthalmic applications, OCTA also pushes other fields of application such as dermatology [123], or endoscopy [124]. An example of a retinal OCTA image is shown in Fig. 11.
Fig. 11.
Example of OCTA mage showing the retinal vasculature down to the capilaries. Figure reproduced from Ref [91].
7. Advantages in clinical Fourier domain OCT imaging
One of the most important implication of introducing Fourier Domain detection to OCT imaging is the substantial improvement in the quality of cross-sectional images acquired at high speeds. Figure 12 shows an example of the evolution of Fourier domain OCT imaging quality within a decade starting from the first in vivo eye imaging measurements performed in 2002 up to 2012 when well optimized and developed instrumentation had evolved. For example, a substantial increase of axial resolution could be obtained because of a lack of a fundamental relationship between imaging sensitivity and axial resolution in the case of Fourier Domain detection [52,125]. In addition, in FD-OCT the interference fringe signal is not processed by analog electronics, and all operations enabling object reconstruction are performed on digital data. This allows for a better compensation of unfavorable effects influencing the loss of signal and the resolution than in the case of TD-OCT.
Fig. 12.
: One decade of progress in ophthalmic FD-OCT imaging: Left data published in 2002 [21,53,126] and FD-OCT cross-sectional ophthalmic images published in 2012 [127].
The improvement of imaging sensitivity of FD-OCT systems implies the possibility of measuring OCT data in all three dimensions in a time shorter than 1 second. This in turn enables to create virtual volumetric (3D) reconstruction of the tissue in clinical conditions. The full volumetric information gives access to a reconstruction of any cross-sectional image along any arbitrarily chosen plane. The combination of imaging in three dimensions with high resolution enables to localize precisely the position of cross-sections. The practical use of volumetric data is far greater than the selection of a cross-sectional images. One of the main practical advantages of having access to volumetric data is the possibility of an accurate registration of cross-sectional images to other optical imaging techniques, which are currently treated as gold standards in medical imaging either for diagnosis or treatment monitoring. Three-dimensional FD-OCT imaging also helped to introduce quantitative and clinically relevant morphometric analysis. An accurate quantitative data processing of various physical parameters including: thickness of layers, distances between characteristic points, the volume of chosen structures or the volume of structures of interest help to provide more objective diagnosis and accurate monitoring of disease progression and treatment success. Another very practical advantage is the possibility of obtaining clinically relevant information with a single OCT instrument, where previously several diagnostics devices were needed.
In ophthalmology for example it is possible to reconstruct images of the eye’s fundus analogous to images obtained by scanning laser ophthalmoscopy [125,128,129], by averaging the backreflected intensity along the axis determined by the direction of light propagation. Such a FD-OCT fundus image clearly reconstructs the retinal vasculature and, in the case of diseases it provides information about the location and extension of pathologic changes. The retinal vasculature creates a unique pattern and may be used for very precise localization of OCT data with respect to the classical fundus photo or angiography. Once the volumetric OCT data are acquired, it is also possible to generate projections using only a fragment of the volume. In the case of the retina we may choose data corresponding to a specific tissue layer and create its projection [128,130–132]. One of the most important steps in ophthalmic OCT applications is incorporation of standard surgical microscopes with FD-OCT [133–135]. This enables to take full advantage of the excellent optics of current microscope systems and add another dimension delivered by OCT. The challenge here is to have high quality cross-sectional images in the shortest possible time to improve the precision of manual surgery procedures. It is also important to ensure that cross-sectional images are visible in real time through the microscopic ocular.
High speed OCT imaging using Fourier domain detection can also be beneficial in applications other than ophthalmology. For example, in cardiology one of the main challenges is large scale imaging while searching for small focal (localized) regions to understand coronary atherosclerosis and to monitor the response to intravascular interventions such as implementation of stents or angioplasty. Fourier Domain OCT imaging has also the potential of providing the ability to survey large tissue volumes in real time in endoscopic and laparoscopic applications. In contrast to excisional biopsy, OCT examination enables for screening of early neoplastic localized changes in large luminal surface areas. Another interesting example of applications demonstrating the capabilities of high-speed Fourier domain OCT imaging is developmental biology. The ability to directly image dynamic changes in the cellular architecture enhances understanding of normal development as well as congenital abnormalities in live model systems [136–140].
8. Parallel FD-OCT
A main success of FD-OCT was to achieve high A-scan rates that enabled comprehensive 3D images of tissue structures. SS-OCT has shown up-to-date the highest data recording rates at several million A-scan per second [141]. The gain in speed comes however at the cost of expensive light source technology, as well as complex data acquisition and system synchronization. Thus, MHz swept source technology is still a challenge for clinical use, although it is desirable to cover large field of views both in standard OCT as well as for OCTA without compromising lateral sampling density. Even if the technological challenges are solved, point-scanning FD-OCT systems ultimately hit the physical boundary given by the detection process itself. According to Eq. (18), the sensitivity of FD-OCT systems in the shot noise limit is proportional to the power illuminating the sample and inversely proportional to imaging speed, expressed by the A-scan rate or . Increasing the speed, therefore, requires an equal increase in sample beam intensity to keep the sensitivity constant. This is particularly critical for in-vivo imaging, since the applied optical power is limited by laser safety regulations. The situation is relaxed for parallel image acquisition schemes using extended illumination, such as in line- or full-field OCT, where higher power can be applied for the same exposure time settings. Although, first parallel OCT schemes have been introduced already for TD-OCT, the combination with FD-OCT is promising for actual in-vivo applications regarding sensitivity and imaging speed.
The principle of line field (LF) FD-OCTwas first demonstrated by Zuluaga and Richards-Kortum [142]: a cylindrical lens produces a line illumination at the sample, that is then imaged onto a 2D sensor after having been dispersed into its spectral components by passing a diffraction grating. The 2D sensor acquires then the information of a full B-scan, where typically the vertical sensor coordinate samples the lateral object structure whereas the horizontal coordinate records the spectral interference pattern at each lateral position. First in-vivo tomograms of the human eye using LF FD-OCT have been presented by Grajciar et al. [143]. 3-D human retinal images have been shown by Nakamura et al. [144]. As has been outlined earlier, SD-OCT suffers from pixel cross talk resulting in strong sensitivity roll-off. SS-OCT is superior with respect to roll-off, as it samples the spectral data separated in time, and the instantaneous coherence length of the source itself ultimately determines the axial SNR roll-off performance. Parallel SS-OCT is in fact the most simple OCT configuration, as it does not require any lateral beam steering in case of full-field illumination: a full volume is recorded with a single wavelength sweep [145,146]. The only limitation in case of full-field SS-OCT is the frame rate of the sensor, as well as loss in structural contrast due to the missing confocal gating mechanism. Equipped with expensive high-speed sensor technology, Bonin et al. demonstrated retinal volumetric imaging with several MHz equivalent A-scans/sec [147]. Line-field illumination on the other hand maintains half of the confocal gating of out-of-focus stray light. Fechtig et al. showed retinal line-field SS-OCT with off-shelve CMOS sensor technology at up to 1MHz A-scan rate with a single frame sensitivity of more than 93dB [72] (Fig. 13). In order to keep sufficient axial samples, given the speed restrictions of the sensor, a hybrid holographic and FD-OCT configuration has been employed using off-axis reference arm illumination, which enables full range FD-OCT imaging without active phase shifting [73,148]. Parallel signal acquisition promises comprehensive in-vivo images both for OCT and OCTA, and exhibits in addition higher phase stability along the parallel direction, enabling wavefront sensing and correction via digital adaptive optics [149,150].
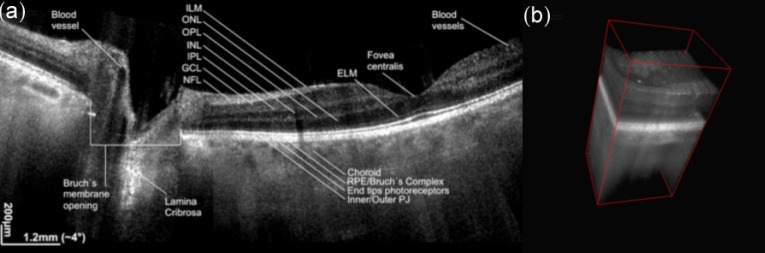
Fig. 13.
: (a) Stitched widefield retinal tomogram across central retina. The total field of view is approx. 30° (b) Volume rendered image of 6x6deg across optic nerve head. (ILM - internal limiting membrane, ONL - outer nuclear layer, OPL - outer plexiform layer, INL - inner nuclear layer, IPL - inner plexiform layer, GCL - ganglion cell layer, NFL - nerve fiber layer, ELM - external limiting membrane, RPE - retinal pigment epithelium, PJ – inner-outer photoreceptor segment junction) (reproduced from [72])
9. Summary
Although the principle of spectral channeling of interference signals has been known earlier and first demonstration of the principle in the context of biometry had been demonstrated, the real impact came with the recognition and demonstration of the intrinsic advantage in sensitivity of Fourier Domain OCT. This set the basis for modern structural as well as functional OCT systems as well as for future developments to further improve OCT imaging performance. The advantage in sensitivity immediately translates into higher imaging speed, resulting in improved image contrast, full volumetric tissue information, supporting high resolution in all three dimensions. This dramatic improvement in performance had an immediate impact on clinical applications, and paved the way for a new understanding of tissue physiology, pathogenesis. Ophthalmology has profited most of those developments; as of today every second worldwide a retinal scan is taken with modern OCT devices in a fully non-invasive and contact-free manner. Novel developments, that are currently in translation into clinical practice, such as contrast agent free OCT angiography, are changing the paradigms of clinical treatment monitoring. New biomarkers of disease based on vascular pattern, and tissue structure resolved with close to cellular resolution are becoming important tools for the development of novel treatment methods and are setting the basis for early diagnosis of major diseases, including cancer, diabetes, and age related and neurodegenerative diseases, such as AMD, Alzheimer’s, or Parkinson’s disease.
Although it is doubted that OCT will experience a similar disruptive technological change as with the recognition of the FD-OCT advantage, further improvements in imaging performance can be still expected. In particular the improvement in imaging speed over the last decade has been impressive, reaching nowadays several hundreds of thousands of A-scans/second for clinical systems and even several millions of A-scans/sec for research systems. Improved speed is of critical importance for several reasons: it allows enhancing the field of view for comprehensive wide-field imaging, helps to keep imaging times low to avoid motion distortions, results in enhanced image contrast through speckle averaging, and supports real time view not only of tomograms, but already of full 3D rendered volumes. The last feature is currently in translation into intrasurgical OCT, for accurate surgical guidance in 3D.
Advanced swept source technology such as akinetic sources or electronically pumped VCSELs promises high speed imaging at ultimately lower cost, with the further potential to be fully integrated into single photonic chips. Again, the intrinsic advantage in sensitivity of FD-OCT helps to overcome limitations related to coupling losses and waveguide losses, and will allow for competitive image quality of pocket size OCT devices in the near future.
Still point scanning OCT ultimately hits the physical boundary of detection sensitivity when further increasing imaging speed. Multibeam OCT scanning different tissue regions in parallel, or parallel OCT relax this boundary and promise further improvement in imaging speed keeping clinically relevant imaging performance. Parallel imaging in addition with its intrinsic phase stability over the full field of view opens new methods for wavefront manipulation and control, to realize cellular tissue imaging along an extended depth of focus, and aberration correction without the need of hardware adaptive optics components.
After almost two decades, FD-OCT is still an exciting and a dynamic field of engineering and development, extending continuously its application to new fields in medicine and biology. This excitement is driven by the great impact of OCT technology made on lives of a large number of humans worldwide, whose health condition can be screened and monitored by OCT instruments. This would not be possible without one of the most important turning points in the history of OCT technology development, which was the application of Fourier domain detection enabling for comprehensive 3D in vivo imaging.
Acknowledgment
JFdB would like to acknowledge his former colleagues at the Wellman Lab for Photomedicine, B.E. Bouma, G. J. Tearney and S.H. Yun, and the many PhD students and Postdocs that contributed to the work.
RL would like to acknowledge his colleagues at the Medical University of Vienna, Austria, A. F. Fercher, C.K. Hitzenberger, W. Drexler, L. Schmetterer, U. Schmidt-Erfurth, as well as T. Lasser at the Ecole Polytechnique de Lausanne, Switzerland, and the many PhD students and PostDocs that contributed to the work.
MW would like to acknowledge contribution of Prof Andrzej Kowalczyk, Prof. James G. Fujimoto from Massachusetts Institute of Technology, Cambridge, USA; Prof. Adolf F. Fercher from Medical University of Vienna, Austria; Maciej Szkulmowski and Tomasz Bajraszewski and other past and current members of Optical Biomedical Imaging Group from Nicolaus Copernicus University.
Funding
Netherlands Organisation for Scientific Research (NWO) with a Vici (JFdB); the Dutch Technology Foundation STW (grant number 12822 and grant number 13936); the Netherlands Organisation for Health Research and Development ZonMW (grant number 91212061); the Ministry of Economic Affairs, European Union's Horizon 2020 research and innovation program (654148, 666295, 732969, MOON; grant agreement No 667933-2, MIB); LaserLaB Europe; the Austrian Federal Ministry of Science, Research and Economy; Austrian Science Foundation (FWF, grant 29093-N36).
References and links
- 1.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical Coherence Tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fercher A. F., Drexler W., Hitzenberger C. K., Lasser T., “Optical coherence tomography - principles and applications,” Rep. Prog. Phys. 66(2), 239–303 (2003). 10.1088/0034-4885/66/2/204 [DOI] [Google Scholar]
- 3.Koch P., Hellemanns V., Huttmann G., “Linear optical coherence tomography system with extended measurement range,” Opt. Lett. 31(19), 2882–2884 (2006). 10.1364/OL.31.002882 [DOI] [PubMed] [Google Scholar]
- 4.Froehly L., Leitgeb R., “Scan-free optical correlation techniques: history and applications to optical coherence tomography,” J. Opt. 12(8), 084001 (2010). 10.1088/2040-8978/12/8/084001 [DOI] [Google Scholar]
- 5.Fercher A. F., Hitzenberger C. K., Kamp G., Elzaiat S. Y., “Measurement of Intraocular Distances by Backscattering Spectral Interferometry,” Opt. Commun. 117(1-2), 43–48 (1995). 10.1016/0030-4018(95)00119-S [DOI] [Google Scholar]
- 6.Chinn S. R., Swanson E. A., Fujimoto J. G., “Optical coherence tomography using a frequency-tunable optical source,” Opt. Lett. 22(5), 340–342 (1997). 10.1364/OL.22.000340 [DOI] [PubMed] [Google Scholar]
- 7.Golubovic B., Bouma B. E., Tearney G. J., Fujimoto J. G., “Optical frequency-domain reflectometry using rapid wavelength tuning of a Cr/sup 4+/:forsterite laser,” Opt. Lett. 22(22), 1704–1706 (1997). 10.1364/OL.22.001704 [DOI] [PubMed] [Google Scholar]
- 8.Lexer F., Hitzenberger C. K., Fercher A. F., Kulhavy M., “Wavelength-tuning interferometry of intraocular distances,” Appl. Opt. 36(25), 6548–6553 (1997). 10.1364/AO.36.006548 [DOI] [PubMed] [Google Scholar]
- 9.Hiratsuka H., Kido E., Yoshimura T., “Simultaneous measurements of three-dimensional reflectivity distributions in scattering media based on optical frequency-domain reflectometry,” Opt. Lett. 23(18), 1420–1422 (1998). 10.1364/OL.23.001420 [DOI] [PubMed] [Google Scholar]
- 10.Haberland U. H. P., Blazek V., Schmitt H. J., “Chirp Optical Coherence Tomography of Layered Scattering Media,” J. Biomed. Opt. 3(3), 259–266 (1998). 10.1117/1.429889 [DOI] [PubMed] [Google Scholar]
- 11.He Z. Y., Hotate K., “Synthesized optical coherence tomography for imaging of scattering objects by use of a stepwise frequency-modulated tunable laser diode,” Opt. Lett. 24(21), 1502–1504 (1999). 10.1364/OL.24.001502 [DOI] [PubMed] [Google Scholar]
- 12.P. Andretzky, M. W. Lindner, J. M. Herrmann, A. Schultz, M. Konzog, F. Kiesewetter, and G. Hausler, “Optical Coherence Tomography by “spectral radar”: dymanic range estimation and in vivo measurements of skin,” in Proc. SPIE 3567 Optical and Imaging Techniques for Biomonitoring IV, 1999), 78. [Google Scholar]
- 13.Mitsui T., “Dynamic range of optical reflectometry with spectral interferometry,” Jpn. J. Appl. Phys. 10(38), 6133–6137 (1999). 10.1143/JJAP.38.6133 [DOI] [Google Scholar]
- 14.Leitgeb R., Hitzenberger C. K., Fercher A. F., “Performance of fourier domain vs. time domain optical coherence tomography,” Opt. Express 11(8), 889–894 (2003). 10.1364/OE.11.000889 [DOI] [PubMed] [Google Scholar]
- 15.de Boer J. F., Cense B., Park B. H., Pierce M. C., Tearney G. J., Bouma B. E., “Improved signal-to-noise ratio in spectral-domain compared with time-domain optical coherence tomography,” Opt. Lett. 28(21), 2067–2069 (2003). 10.1364/OL.28.002067 [DOI] [PubMed] [Google Scholar]
- 16.Choma M. A., Sarunic M. V., Yang C. H., Izatt J. A., “Sensitivity advantage of swept source and Fourier domain optical coherence tomography,” Opt. Express 11(18), 2183–2189 (2003). 10.1364/OE.11.002183 [DOI] [PubMed] [Google Scholar]
- 17.Wieser W., Biedermann B. R., Klein T., Eigenwillig C. M., Huber R., “Multi-Megahertz OCT: High quality 3D imaging at 20 million A-scans and 4.5 GVoxels per second,” Opt. Express 18(14), 14685–14704 (2010). 10.1364/OE.18.014685 [DOI] [PubMed] [Google Scholar]
- 18.P. Hariharan, Basics of interferometry (Academic Press, Boston, 1992), pp. xvii, 213 p. [Google Scholar]
- 19.Häusler G., Lindner M. W., “Coherence Radar and Spectral Radar - new tools for dermatological diagnosis,” J. Biomed. Opt. 3(1), 21–31 (1998). 10.1117/1.429899 [DOI] [PubMed] [Google Scholar]
- 20.Wojtkowski M., Leitgeb R., Kowalczyk A., Bajraszewski T., Fercher A. F., “In vivo human retinal imaging by Fourier domain optical coherence tomography,” J. Biomed. Opt. 7(3), 457–463 (2002). 10.1117/1.1482379 [DOI] [PubMed] [Google Scholar]
- 21.Kaluzny J. J., Wojtkowski M., Kowalczyk A., “Imaging of the anterior segment of the eye by spectral optical coherence tomography,” Opt. Appl. 32, 581–589 (2002). [Google Scholar]
- 22.Leitgeb R., Wojtkowski M., Kowalczyk A., Hitzenberger C. K., Sticker M., Fercher A. F., “Spectral measurement of absorption by spectroscopic frequency- domain optical coherence tomography,” Opt. Lett. 25(11), 820–822 (2000). 10.1364/OL.25.000820 [DOI] [PubMed] [Google Scholar]
- 23.Yasuno Y., Makita S., Sutoh Y., Itoh M., Yatagai T., “Birefringence imaging of human skin by polarization-sensitive spectral interferometric optical coherence tomography,” Opt. Lett. 27(20), 1803–1805 (2002). 10.1364/OL.27.001803 [DOI] [PubMed] [Google Scholar]
- 24.Leitgeb R. A., Schmetterer L., Drexler W., Fercher A. F., Zawadzki R. J., Bajraszewski T., “Real-time assessment of retinal blood flow with ultrafast acquisition by color Doppler Fourier domain optical coherence tomography,” Opt. Express 11(23), 3116–3121 (2003). 10.1364/OE.11.003116 [DOI] [PubMed] [Google Scholar]
- 25.White B. R., Pierce M. C., Nassif N., Cense B., Park B. H., Tearney G. J., Bouma B. E., Chen T. C., de Boer J. F., “In vivo dynamic human retinal blood flow imaging using ultra-high-speed spectral domain optical Doppler tomography,” Opt. Express 11(25), 3490–3497 (2003). 10.1364/OE.11.003490 [DOI] [PubMed] [Google Scholar]
- 26.Wojtkowski M., Bajraszewski T., Targowski P., Kowalczyk A., “Real-time in vivo imaging by high-speed spectral optical coherence tomography,” Opt. Lett. 28(19), 1745–1747 (2003). 10.1364/OL.28.001745 [DOI] [PubMed] [Google Scholar]
- 27.Wojtkowski M., Bajraszewski T., Targowski P., Kowalczyk A., “Real-time in vivo ophthalmic imaging by ultra fast spectral Optical Coherence Tomography,” Coherence Domain Optical Methods and Optical Coherence Tomography in Biomedicine VII 4956, 50–54 (2003). 10.1117/12.477634 [DOI] [Google Scholar]
- 28.Nassif N., Cense B., Hyle Park B., Yun S. H., Chen T. C., Bouma B. E., Tearney G. J., de Boer J. F., “In vivo human retinal imaging by ultrahigh-speed spectral domain optical coherence tomography,” Opt. Lett. 29(5), 480–482 (2004). 10.1364/OL.29.000480 [DOI] [PubMed] [Google Scholar]
- 29.Nassif N. A., Cense B., Park B. H., Pierce M. C., Yun S. H., Bouma B. E., Tearney G. J., Chen T. C., de Boer J. F., “In vivo high-resolution video-rate spectral-domain optical coherence tomography of the human retina and optic nerve,” Opt. Express 12, 367–376 (2004). [DOI] [PubMed] [Google Scholar]
- 30.Yun S. H., Tearney G. J., Bouma B. E., Park B. H., de Boer J. F., “High-speed spectral-domain optical coherence tomography at 1.3 mu m wavelength,” Opt. Express 11(26), 3598–3604 (2003). 10.1364/OE.11.003598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Leitgeb R. A., Drexler W., Unterhuber A., Hermann B., Bajraszewski T., Le T., Stingl A., Fercher A. F., “Ultrahigh resolution Fourier domain optical coherence tomography,” Opt. Express 12(10), 2156–2165 (2004). 10.1364/OPEX.12.002156 [DOI] [PubMed] [Google Scholar]
- 32.Cense B., Nassif N. A., Chen T. C., Pierce M. C., Yun S. H., Park B. H., Bouma B. E., Tearney G. J., de Boer J. F., “Ultrahigh-resolution high-speed retinal imaging using spectral-domain optical coherence tomography,” Opt. Express 12(11), 2435–2447 (2004). 10.1364/OPEX.12.002435 [DOI] [PubMed] [Google Scholar]
- 33.Wojtkowski M., Srinivasan V. J., Ko T. H., Fujimoto J. G., Kowalczyk A., Duker J. S., “Ultrahigh-resolution, high-speed, Fourier domain optical coherence tomography and methods for dispersion compensation,” Opt. Express 12(11), 2404–2422 (2004). 10.1364/OPEX.12.002404 [DOI] [PubMed] [Google Scholar]
- 34.Bajraszewski T., Wojtkowski M., Szkulmowski M., Szkulmowska A., Huber R., Kowalczyk A., “Improved Spectral Optical Coherence Tomography using Optical Frequency Comb,” Opt. Express 16(6), 4163–4176 (2008). 10.1364/OE.16.004163 [DOI] [PubMed] [Google Scholar]
- 35.Potsaid B., Gorczynska I., Srinivasan V. J., Chen Y., Jiang J., Cable A., Fujimoto J. G., “Ultrahigh speed spectral / Fourier domain OCT ophthalmic imaging at 70,000 to 312,500 axial scans per second,” Opt. Express 16(19), 15149–15169 (2008). 10.1364/OE.16.015149 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yun S. H., Tearney G. J., de Boer J. F., Iftimia N., Bouma B. E., “High-speed optical frequency-domain imaging,” Opt. Express 11(22), 2953–2963 (2003). 10.1364/OE.11.002953 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Klein T., Huber R., “High-speed OCT light sources and systems [Invited],” Biomed. Opt. Express 8(2), 828–859 (2017). 10.1364/BOE.8.000828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Swanson E. A., Huang D., Lin C. P., Puliafito C. A., Hee M. R., Fujimoto J. G., “High-Speed Optical Coherence Domain Reflectometry,” Opt. Lett. 17(2), 151–153 (1992). 10.1364/OL.17.000151 [DOI] [PubMed] [Google Scholar]
- 39.R. A. Leitgeb, “Current Technologies for High-Speed and Functional Imaging with Optical Coherence Tomography,” in Advances in Imaging and Electron Physics, Vol 168, P. W. Hawkes, ed. (Elsevier Academic Press Inc, San Diego, 2011), pp. 109–192. [Google Scholar]
- 40.Sorin W. V., Baney D. M., “A Simple Intensity Noise-Reduction Technique for Optical Low- Coherence Reflectometry,” IEEE Photonics Technol. Lett. 4(12), 1404–1406 (1992). 10.1109/68.180591 [DOI] [Google Scholar]
- 41.Hoeling B. M., Fernandez A. D., Haskell R. C., Huang E., Myers W. R., Petersen D. C., Ungersma S. E., Wang R. Y., Williams M. E., Fraser S. E., “An optical coherence microscope for 3-dimensional imaging in developmental biology,” Opt. Express 6(7), 136–146 (2000). 10.1364/OE.6.000136 [DOI] [PubMed] [Google Scholar]
- 42.Mandel L., Wolf E., “Measures of Bandwidth and Coherence Time in Optics,” Proc. Phys. Soc. Lond. 80(4), 894–897 (1962). 10.1088/0370-1328/80/4/311 [DOI] [Google Scholar]
- 43.J. A. Izatt, M. A. Choma, and A.-H. Dhalla, “Theory of Optical Coherence Tomography,” in Optical Coherence Tomography: Technology and Applications, Second ed., W. Drexler and J. G. Fujimoto, eds. (Springer, Heidelberg, 2015), pp. 65–94. [Google Scholar]
- 44.Häusler G., Lindner M. W., “Coherence Radar and Spectral Radar - new tools for dermatological diagnosis,” J. Biomed. Opt. 3(1), 21–31 (1998). 10.1117/1.429899 [DOI] [PubMed] [Google Scholar]
- 45.Tripathi R., Nassif N., Nelson J. S., Park B. H., de Boer J. F., “Spectral shaping for non-Gaussian source spectra in optical coherence tomography,” Opt. Lett. 27(6), 406–408 (2002). 10.1364/OL.27.000406 [DOI] [PubMed] [Google Scholar]
- 46.Wieser W., Draxinger W., Klein T., Karpf S., Pfeiffer T., Huber R., “High definition live 3D-OCT in vivo: design and evaluation of a 4D OCT engine with 1 GVoxel/s,” Biomed. Opt. Express 5, 2963–2977 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bonesi M., Minneman M. P., Ensher J., Zabihian B., Sattmann H., Boschert P., Hoover E., Leitgeb R. A., Crawford M., Drexler W., “Akinetic all-semiconductor programmable swept-source at 1550 nm and 1310 nm with centimeters coherence length,” Opt. Express 22(3), 2632–2655 (2014). 10.1364/OE.22.002632 [DOI] [PubMed] [Google Scholar]
- 48.Wang Z., Potsaid B., Chen L., Doerr C., Lee H. C., Nielson T., Jayaraman V., Cable A. E., Swanson E., Fujimoto J. G., “Cubic meter volume optical coherence tomography,” Optica 3(12), 1496–1503 (2016). 10.1364/OPTICA.3.001496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yun S. H., Tearney G. J., de Boer J. F., Bouma B. E., “Motion artifacts in optical coherence tomography with frequency-domain ranging,” Opt. Express 12(13), 2977–2998 (2004). 10.1364/OPEX.12.002977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yun S. H., Tearney G. J., de Boer J. F., Bouma B. E., “Pulsed-source and swept-source spectral-domain optical coherence tomography with reduced motion artifacts,” Opt. Express 12(23), 5614–5624 (2004). 10.1364/OPEX.12.005614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Moneron G., Boccara A. C., Dubois A., “Stroboscopic ultrahigh-resolution full-field optical coherence tomography,” Opt. Lett. 30(11), 1351–1353 (2005). 10.1364/OL.30.001351 [DOI] [PubMed] [Google Scholar]
- 52.Wojtkowski M., “High-speed optical coherence tomography: basics and applications,” Appl. Opt. 49(16), D30–D61 (2010). 10.1364/AO.49.000D30 [DOI] [PubMed] [Google Scholar]
- 53.Wojtkowski M., Leitgeb R., Kowalczyk A., Bajraszewski T., Fercher A. F., “In vivo human retinal imaging by Fourier domain optical coherence tomography,” J. Biomed. Opt. 7(3), 457–463 (2002). 10.1117/1.1482379 [DOI] [PubMed] [Google Scholar]
- 54.Leitgeb R. A., Hitzenberger C. K., Fercher A. F., Bajraszewski T., “Phase-shifting algorithm to achieve high-speed long-depth-range probing by frequency-domain optical coherence tomography,” Opt. Lett. 28(22), 2201–2203 (2003). 10.1364/OL.28.002201 [DOI] [PubMed] [Google Scholar]
- 55.Creath K., “Phase-measurement interferometry techniques,” Prog. Opt. 26, 349–393 (1988). 10.1016/S0079-6638(08)70178-1 [DOI] [Google Scholar]
- 56.Schmit J., Creath K., “Extended Averaging Technique for Derivation of Error-Compensating Algorithms in Phase-Shifting Interferometry,” Appl. Opt. 34(19), 3610–3619 (1995). 10.1364/AO.34.003610 [DOI] [PubMed] [Google Scholar]
- 57.Wojtkowski M., Kowalczyk A., Leitgeb R., Fercher A. F., “Full range complex spectral optical coherence tomography technique in eye imaging,” Opt. Lett. 27(16), 1415–1417 (2002). 10.1364/OL.27.001415 [DOI] [PubMed] [Google Scholar]
- 58.Wojtkowski M., Kowalczyk A., Targowski P., Gorczynska I., “Fourier-domain optical coherence tomography: next step in optical imaging,” Opt. Appl. 32, 569–580 (2002). [Google Scholar]
- 59.Yun S. H., Tearney G. J., de Boer J. F., Bouma B. E., “Removing the depth-degeneracy in optical frequency domain imaging with frequency shifting,” Opt. Express 12(20), 4822–4828 (2004). 10.1364/OPEX.12.004822 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gotzinger E., Pircher M., Leitgeb R. A., Hitzenberger C. K., “High speed full range complex spectral domain optical coherence tomography,” Opt. Express 13, 583–594 (2005). 10.1364/OPEX.13.000583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Bachmann A. H., Leitgeb R. A., Lasser T., “Heterodyne Fourier domain optical coherence tomography for full range probing with high axial resolution,” Opt. Express 14(4), 1487–1496 (2006). 10.1364/OE.14.001487 [DOI] [PubMed] [Google Scholar]
- 62.Yasuno Y., Makita S., Endo T., Aoki G., Sumimura H., Itoh M., Yatagai T., “One-shot-phase-shifting Fourier domain optical coherence tomography by reference wavefront tilting,” Opt. Express 12(25), 6184–6191 (2004). 10.1364/OPEX.12.006184 [DOI] [PubMed] [Google Scholar]
- 63.Sarunic M. V., Choma M. A., Yang C. H., Izatt J. A., “Instantaneous complex conjugate resolved spectral domain and swept-source OCT using 3x3 fiber couplers,” Opt. Express 13(3), 957–967 (2005). 10.1364/OPEX.13.000957 [DOI] [PubMed] [Google Scholar]
- 64.Choma M. A., Yang C., Izatt J. A., “Instantaneous quadrature low-coherence interferometry with 3 x 3 fiber-optic couplers,” Opt. Lett. 28(22), 2162–2164 (2003). 10.1364/OL.28.002162 [DOI] [PubMed] [Google Scholar]
- 65.Y. Yasuno, S. Makita, T. Endo, G. Aoki, M. Itoh, and T. Yatagai, “High-speed full-range Fourier domain optical coherence tomography by simultaneous B-M-mode scanning,” in Coherence Domain Optical Methods and Optical Coherence Tomography in Biomedicine IX, (SPIE, 2005), 137–142. [Google Scholar]
- 66.Makita S., Fabritius T., Yasuno Y., “Full-range, high-speed, high-resolution 1 microm spectral-domain optical coherence tomography using BM-scan for volumetric imaging of the human posterior eye,” Opt. Express 16(12), 8406–8420 (2008). 10.1364/OE.16.008406 [DOI] [PubMed] [Google Scholar]
- 67.Leitgeb R. A., Michaely R., Lasser T., Sekhar S. C., “Complex ambiguity-free Fourier domain optical coherence tomography through transverse scanning,” Opt. Lett. 32(23), 3453–3455 (2007). 10.1364/OL.32.003453 [DOI] [PubMed] [Google Scholar]
- 68.Hofer B., Povazay B., Hermann B., Unterhuber A., Matz G., Drexler W., “Dispersion encoded full range frequency domain optical coherence tomography,” Opt. Express 17(1), 7–24 (2009). 10.1364/OE.17.000007 [DOI] [PubMed] [Google Scholar]
- 69.Podoleanu A. G., “Unique interpretation of Talbot Bands and Fourier domain white light interferometry,” Opt. Express 15(15), 9867–9876 (2007). 10.1364/OE.15.009867 [DOI] [PubMed] [Google Scholar]
- 70.Davis A. M., Choma M. A., Izatt J. A., “Heterodyne swept-source optical coherence tomography for complete complex conjugate ambiguity removal,” J. Biomed. Opt. 10(6), 064005 (2005). 10.1117/1.2136147 [DOI] [PubMed] [Google Scholar]
- 71.Zhang J., Nelson J. S., Chen Z. P., “Removal of a mirror image and enhancement of the signal-to-noise ratio in Fourier-domain optical coherence tomography using an electro-optic phase modulator,” Opt. Lett. 30(2), 147–149 (2005). 10.1364/OL.30.000147 [DOI] [PubMed] [Google Scholar]
- 72.Fechtig D. J., Grajciar B., Schmoll T., Blatter C., Werkmeister R. M., Drexler W., Leitgeb R. A., “Line-field parallel swept source MHz OCT for structural and functional retinal imaging,” Biomed. Opt. Express 6(3), 716–735 (2015). 10.1364/BOE.6.000716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Hillmann D., Lührs C., Bonin T., Koch P., Hüttmann G., “Holoscopy - holographic optical coherence tomography,” Opt. Lett. 36(13), 2390–2392 (2011). 10.1364/OL.36.002390 [DOI] [PubMed] [Google Scholar]
- 74.Zhao Y. H., Chen Z. P., Saxer C., Shen Q. M., Xiang S. H., de Boer J. F., Nelson J. S., “Doppler standard deviation imaging for clinical monitoring of in vivo human skin blood flow,” Opt. Lett. 25(18), 1358–1360 (2000). 10.1364/OL.25.001358 [DOI] [PubMed] [Google Scholar]
- 75.Zhao Y. H., Chen Z. P., Saxer C., Xiang S. H., de Boer J. F., Nelson J. S., “Phase-resolved optical coherence tomography and optical Doppler tomography for imaging blood flow in human skin with fast scanning speed and high velocity sensitivity,” Opt. Lett. 25(2), 114–116 (2000). 10.1364/OL.25.000114 [DOI] [PubMed] [Google Scholar]
- 76.de Boer J. F., Saxer C. E., Nelson J. S., “Stable carrier generation and phase-resolved digital data processing in optical coherence tomography,” Appl. Opt. 40(31), 5787–5790 (2001). 10.1364/AO.40.005787 [DOI] [PubMed] [Google Scholar]
- 77.Yang V. X. D., Gordon M. L., Qi B., Pekar J., Lo S., Seng-Yue E., Mok A., Wilson B. C., Vitkin I. A., “High speed, wide velocity dynamic range Doppler optical coherence tomography (Part I): System design, signal processing, and performance,” Opt. Express 11(7), 794–809 (2003). 10.1364/OE.11.000794 [DOI] [PubMed] [Google Scholar]
- 78.Chen Z. P., Milner T. E., Srinivas S., Wang X. J., Malekafzali A., vanGemert M. J. C., Nelson J. S., “Noninvasive imaging of in vivo blood flow velocity using optical Doppler tomography,” Opt. Lett. 22(14), 1119–1121 (1997). 10.1364/OL.22.001119 [DOI] [PubMed] [Google Scholar]
- 79.Izatt J. A., Kulkarni M. D., Yazdanfar S., Barton J. K., Welch A. J., “In vivo bidirectional color Doppler flow imaging of picoliter blood volumes using optical coherence tomography,” Opt. Lett. 22(18), 1439–1441 (1997). 10.1364/OL.22.001439 [DOI] [PubMed] [Google Scholar]
- 80.Rollins A. M., Yazdanfar S., Barton J. K., Izatt J. A., “Real-time in vivo color Doppler optical coherence tomography,” J. Biomed. Opt. 7(1), 123–129 (2002). 10.1117/1.1428291 [DOI] [PubMed] [Google Scholar]
- 81.Westphal V., Yazdanfar S., Rollins A. M., Izatt J. A., “Real-time, high velocity-resolution color Doppler optical coherence tomography,” Opt. Lett. 27(1), 34–36 (2002). 10.1364/OL.27.000034 [DOI] [PubMed] [Google Scholar]
- 82.Ding Z. H., Zhao Y. H., Ren H. W., Nelson J. S., Chen Z. P., “Real-time phase-resolved optical coherence tomography and optical Doppler tomography,” Opt. Express 10(5), 236–245 (2002). 10.1364/OE.10.000236 [DOI] [PubMed] [Google Scholar]
- 83.Yazdanfar S., Rollins A. M., Izatt J. A., “Imaging and velocimetry of the human retinal circulation with color Doppler optical coherence tomography,” Opt. Lett. 25(19), 1448–1450 (2000). 10.1364/OL.25.001448 [DOI] [PubMed] [Google Scholar]
- 84.Yazdanfar S., Rollins A. M., Izatt J. A., “In vivo imaging of human retinal flow dynamics by color Doppler optical coherence tomography,” Arch Ophthalmol-Chic 121(2), 235–239 (2003). 10.1001/archopht.121.2.235 [DOI] [PubMed] [Google Scholar]
- 85.Kulkarni M. D., van Leeuwen T. G., Yazdanfar S., Izatt J. A., “Velocity-estimation accuracy and frame-rate limitations in color Doppler optical coherence tomography,” Opt. Lett. 23(13), 1057–1059 (1998). 10.1364/OL.23.001057 [DOI] [PubMed] [Google Scholar]
- 86.Leitgeb R. A., Werkmeister R. M., Blatter C., Schmetterer L., “Doppler Optical Coherence Tomography,” Prog. Retin. Eye Res. 41, 26–43 (2014). 10.1016/j.preteyeres.2014.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.R. Leitgeb, L. F. Schmetterer, M. Wojtkowski, C. K. Hitzenberger, M. Sticker, and A. F. Fercher, “Flow Velocity Measurements by Frequency Domain Short Coherence Interferometry,” SPIE Proceedings 4619, 16–21 (2002). 10.1117/12.470477 [DOI] [Google Scholar]
- 88.Grulkowski I., Gorczynska I., Szkulmowski M., Szlag D., Szkulmowska A., Leitgeb R. A., Kowalczyk A., Wojtkowski M., “Scanning protocols dedicated to smart velocity ranging in Spectral OCT,” Opt. Express 17(26), 23736–23754 (2009). 10.1364/OE.17.023736 [DOI] [PubMed] [Google Scholar]
- 89.Makita S., Franck J., Yamanari M., Miura M., Yasuno Y., “Comprehensive in vivo micro-vascular imaging of the human eye by dual-beam-scan Doppler optical coherence angiography,” Opt. Express 19(2), 1271–1283 (2011). 10.1364/OE.19.001271 [DOI] [PubMed] [Google Scholar]
- 90.Zotter S., Pircher M., Torzicky T., Bonesi M., Gotzinger E., Leitgeb R. A., Hitzenberger C. K., “Visualization of microvasculature by dual-beam phase-resolved Doppler optical coherence tomography,” Opt. Express 19(2), 1217–1227 (2011). 10.1364/OE.19.001217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Braaf B., Vermeer K. A., Vienola K. V., de Boer J. F., “Angiography of the retina and the choroid with phase-resolved OCT using interval-optimized backstitched B-scans,” Opt. Express 20(18), 20516–20534 (2012). 10.1364/OE.20.020516 [DOI] [PubMed] [Google Scholar]
- 92.Schmoll T., Kolbitsch C., Leitgeb R. A., “Ultra-high-speed volumetric tomography of human retinal blood flow,” Opt. Express 17(5), 4166–4176 (2009). 10.1364/OE.17.004166 [DOI] [PubMed] [Google Scholar]
- 93.Vakoc B. J., Yun S. H., de Boer J. F., Tearney G. J., Bouma B. E., “Phase-resolved optical frequency domain imaging,” Opt. Express 13(14), 5483–5493 (2005). 10.1364/OPEX.13.005483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Braaf B., Vermeer K. A., Sicam V. A. D. P., van Zeeburg E., van Meurs J. C., de Boer J. F., “Phase-stabilized optical frequency domain imaging at 1-mu m for the measurement of blood flow in the human choroid,” Opt. Express 19(21), 20886–20903 (2011). 10.1364/OE.19.020886 [DOI] [PubMed] [Google Scholar]
- 95.Choi W., Potsaid B., Jayaraman V., Baumann B., Grulkowski I., Liu J. J., Lu C. D., Cable A. E., Huang D., Duker J. S., Fujimoto J. G., “Phase-sensitive swept-source optical coherence tomography imaging of the human retina with a vertical cavity surface-emitting laser light source,” Opt. Lett. 38(3), 338–340 (2013). 10.1364/OL.38.000338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Hendargo H. C., McNabb R. P., Dhalla A. H., Shepherd N., Izatt J. A., “Doppler velocity detection limitations in spectrometer-based versus swept-source optical coherence tomography,” Biomed. Opt. Express 2(8), 2175–2188 (2011). 10.1364/BOE.2.002175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Chen Z., Liu M. Y., Minneman M., Ginner L., Hoover E., Sattmann H., Bonesi M., Drexler W., Leitgeb R. A., “Phase-stable swept source OCT angiography in human skin using an akinetic source,” Biomed. Opt. Express 7(8), 3032–3048 (2016). 10.1364/BOE.7.003032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Michaely R., Bachmann A. H., Villiger M. L., Blatter C., Lasser T., Leitgeb R. A., “Vectorial reconstruction of retinal blood flow in three dimensions measured with high resolution resonant Doppler Fourier domain optical coherence tomography,” J. Biomed. Opt. 12(4), 01213 (2007). 10.1117/1.2771553 [DOI] [PubMed] [Google Scholar]
- 99.Makita S., Fabritius T., Yasuno Y., “Quantitative retinal-blood flow measurement with three-dimensional vessel geometry determination using ultrahigh-resolution Doppler optical coherence angiography,” Opt. Lett. 33(8), 836–838 (2008). 10.1364/OL.33.000836 [DOI] [PubMed] [Google Scholar]
- 100.Schmoll T., Kolbitsch C., Leitgeb R. A., “Ultra-high-speed volumetric tomography of human retinal blood flow,” Opt. Express 17(5), 4166–4176 (2009). 10.1364/OE.17.004166 [DOI] [PubMed] [Google Scholar]
- 101.Rao B., Yu L. F., Chiang H. K., Zacharias L. C., Kurtz R. M., Kuppermann B. D., Chen Z. P., “Imaging pulsatile retinal blood flow in human eye,” J. Biomed. Opt. 13(4), 040505 (2008). 10.1117/1.2967986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Werkmeister R. M., Dragostinoff N., Pircher M., Götzinger E., Hitzenberger C. K., Leitgeb R. A., Schmetterer L., “Bidirectional Doppler Fourier-domain optical coherence tomography for measurement of absolute flow velocities in human retinal vessels,” Opt. Lett. 33(24), 2967–2969 (2008). 10.1364/OL.33.002967 [DOI] [PubMed] [Google Scholar]
- 103.Werkmeister R. M., Dragostinoff N., Palkovits S., Told R., Boltz A., Leitgeb R. A., Gröschl M., Garhöfer G., Schmetterer L., “Measurement of Absolute Blood Flow Velocity and Blood Flow in the Human Retina by Dual-Beam Bidirectional Doppler Fourier-Domain Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 53(10), 6062–6071 (2012). 10.1167/iovs.12-9514 [DOI] [PubMed] [Google Scholar]
- 104.Blatter C., Grajciar B., Schmetterer L., Leitgeb R. A., “Angle independent flow assessment with bidirectional Doppler optical coherence tomography,” Opt. Lett. 38(21), 4433–4436 (2013). 10.1364/OL.38.004433 [DOI] [PubMed] [Google Scholar]
- 105.Pedersen C. J., Huang D., Shure M. A., Rollins A. M., “Measurement of absolute flow velocity vector using dual-angle, delay-encoded Doppler optical coherence tomography,” Opt. Lett. 32(5), 506–508 (2007). 10.1364/OL.32.000506 [DOI] [PubMed] [Google Scholar]
- 106.Haindl R., Trasischker W., Baumann B., Pircher M., Hitzenberger C. K., “Three-beam Doppler optical coherence tomography using a facet prism telescope and MEMS mirror for improved transversal resolution,” J. Mod. Opt. 62(21), 1781–1788 (2015). 10.1080/09500340.2014.983569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Peterson L. M., Gu S., Jenkins M. W., Rollins A. M., “Orientation-independent rapid pulsatile flow measurement using dual-angle Doppler OCT,” Biomed. Opt. Express 5(2), 499–514 (2014). 10.1364/BOE.5.000499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Baumann B., Potsaid B., Kraus M. F., Liu J. J., Huang D., Hornegger J., Cable A. E., Duker J. S., Fujimoto J. G., “Total retinal blood flow measurement with ultrahigh speed swept source/Fourier domain OCT,” Biomed. Opt. Express 2(6), 1539–1552 (2011). 10.1364/BOE.2.001539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Schmoll T., Leitgeb R. A., “Heart-beat-phase-coherent Doppler optical coherence tomography for measuring pulsatile ocular blood flow,” J. Biophotonics 6(3), 275–282 (2013). 10.1002/jbio.201200029 [DOI] [PubMed] [Google Scholar]
- 110.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). 10.1364/OE.14.007821 [DOI] [PubMed] [Google Scholar]
- 111.Bachmann A. H., Villiger M. L., Blatter C., Lasser T., Leitgeb R. A., “Resonant Doppler flow imaging and optical vivisection of retinal blood vessels,” Opt. Express 15, 408–422 (2007). [DOI] [PubMed] [Google Scholar]
- 112.An L., Wang R. K., “In vivo volumetric imaging of vascular perfusion within human retina and choroids with optical micro-angiography,” Opt. Express 16(15), 11438–11452 (2008). 10.1364/OE.16.011438 [DOI] [PubMed] [Google Scholar]
- 113.Szkulmowski M., Szkulmowska A., Bajraszewski T., Kowalczyk A., Wojtkowski M., “Flow velocity estimation using joint Spectral and Time Domain Optical Coherence Tomography,” Opt. Express 16(9), 6008–6025 (2008). 10.1364/OE.16.006008 [DOI] [PubMed] [Google Scholar]
- 114.Tao Y. K., Davis A. M., Izatt J. A., “Single-pass volumetric bidirectional blood flow imaging spectral domain optical coherence tomography using a modified Hilbert transform,” Opt. Express 16(16), 12350–12361 (2008). 10.1364/OE.16.012350 [DOI] [PubMed] [Google Scholar]
- 115.Kolbitsch C., Schmoll T., Leitgeb R. A., “Histogram-based filtering for quantitative 3D retinal angiography,” J. Biophotonics 2(6-7), 416–425 (2009). 10.1002/jbio.200910026 [DOI] [PubMed] [Google Scholar]
- 116.Mariampillai A., Standish B. A., Moriyama E. H., Khurana M., Munce N. R., Leung M. K. K., Jiang J., Cable A., Wilson B. C., Vitkin I. A., Yang V. X. D., “Speckle variance detection of microvasculature using swept-source optical coherence tomography,” Opt. Lett. 33(13), 1530–1532 (2008). 10.1364/OL.33.001530 [DOI] [PubMed] [Google Scholar]
- 117.Blatter C., Klein T., Grajciar B., Schmoll T., Wieser W., Andre R., Huber R., Leitgeb R. A., “Ultrahigh-speed non-invasive widefield angiography,” J. Biomed. Opt. 17(7), 070501 (2012). 10.1117/1.JBO.17.7.070505 [DOI] [PubMed] [Google Scholar]
- 118.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). 10.1364/OE.14.007821 [DOI] [PubMed] [Google Scholar]
- 119.Kim D. Y., Fingler J., Werner J. S., Schwartz D. M., Fraser S. E., Zawadzki R. J., “In vivo volumetric imaging of human retinal circulation with phase-variance optical coherence tomography,” Biomed. Opt. Express 2(6), 1504–1513 (2011). 10.1364/BOE.2.001504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Schmoll T., Singh A. S. G., Blatter C., Schriefl S., Ahlers C., Schmidt-Erfurth U., Leitgeb R. A., “Imaging of the parafoveal capillary network and its integrity analysis using fractal dimension,” Biomed. Opt. Express 2(5), 1159–1168 (2011). 10.1364/BOE.2.001159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Jia Y. L., Tan O., Tokayer J., Potsaid B., Wang Y. M., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Ginner L., Blatter C., Fechtig D., Schmoll T., Gröschl M., Leitgeb R., “Wide-Field OCT Angiography at 400 KHz Utilizing Spectral Splitting,” Photonics 1(4), 369–379 (2014). 10.3390/photonics1040369 [DOI] [Google Scholar]
- 123.Blatter C., Weingast J., Alex A., Grajciar B., Wieser W., Drexler W., Huber R., Leitgeb R. A., “In situ structural and microangiographic assessment of human skin lesions with high-speed OCT,” Biomed. Opt. Express 3(10), 2636–2646 (2012). 10.1364/BOE.3.002636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Tsai T.-H., Ahsen O. O., Lee H.-C., Liang K., Figueiredo M., Tao Y. K., Giacomelli M. G., Potsaid B. M., Jayaraman V., Huang Q., Cable A. E., Fujimoto J. G., Mashimo H., “Endoscopic Optical Coherence Angiography Enables 3-Dimensional Visualization of Subsurface Microvasculature,” Gastroenterology 147(6), 1219–1221 (2014). 10.1053/j.gastro.2014.08.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Wojtkowski M., Bajraszewski T., Gorczynska I., Targowski P., Kowalczyk A., Wasilewski W., Radzewicz C., “Ophthalmic imaging by spectral optical coherence tomography,” Am. J. Ophthalmol. 138(3), 412–419 (2004). 10.1016/j.ajo.2004.04.049 [DOI] [PubMed] [Google Scholar]
- 126.Wojtkowski M., Leitgeb R., Kowalczyk A., Fercher A., “Fourier domain OCT imaging of human eye in vivo,” Coherence Domain Optical Methods in Biomedical Science and Clinical Applications VI 4619, 230–236 (2002). 10.1117/12.491311 [DOI] [Google Scholar]
- 127.Szkulmowski M., Gorczynska I., Szlag D., Sylwestrzak M., Kowalczyk A., Wojtkowski M., “Efficient reduction of speckle noise in Optical Coherence Tomography,” Opt. Express 20(2), 1337–1359 (2012). 10.1364/OE.20.001337 [DOI] [PubMed] [Google Scholar]
- 128.Wojtkowski M., Srinivasan V., Fujimoto J. G., Ko T., Schuman J. S., Kowalczyk A., Duker J. S., “Three-dimensional retinal imaging with high-speed ultrahigh-resolution optical coherence tomography,” Ophthalmology 112(10), 1734–1746 (2005). 10.1016/j.ophtha.2005.05.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Schmidt-Erfurth U., Leitgeb R. A., Michels S., Povazay B., Sacu S., Hermann B., Ahlers C., Sattmann H., Scholda C., Fercher A. F., Drexler W., “Three-dimensional ultrahigh-resolution optical coherence tomography of macular diseases,” Invest. Ophthalmol. Vis. Sci. 46(9), 3393–3402 (2005). 10.1167/iovs.05-0370 [DOI] [PubMed] [Google Scholar]
- 130.Sikorski B. L., Wojtkowski M., Kaluzny J. J., Szkulmowski M., Kowalczyk A., “Correlation of spectral optical coherence tomography with fluorescein and indocyanine green angiography in multiple evanescent white dot syndrome,” Br. J. Ophthalmol. 92(11), 1552–1557 (2008). 10.1136/bjo.2007.135863 [DOI] [PubMed] [Google Scholar]
- 131.Wojtkowski M., Sikorski B., Gorczynska I., Gora M., Szkulmowski M., Bukowska D., Kaluzny J. J., Fujimoto J. G., Kowalczyk A., “Comparison of reflectivity maps and outer retinal topography in retinal disease by 3-D Fourier domain optical coherence tomography,” Opt. Express 15, 4189–4207 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Gorczynska I., Srinivasan V. J., Vuong L. N., Chen R. W., Liu J. J., Reichel E., Wojtkowski M., Schuman J. S., Duker J. S., Fujimoto J. G., “Projection OCT fundus imaging for visualising outer retinal pathology in non-exudative age-related macular degeneration,” Br. J. Ophthalmol. 93(5), 603–609 (2009). 10.1136/bjo.2007.136101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Hahn P., Migacz J., O’Connell R., Day S., Lee A., Lin P., Vann R., Kuo A., Fekrat S., Mruthyunjaya P., Postel E. A., Izatt J. A., Toth C. A., “Preclinical evaluation and intraoperative human retinal imaging with a high-resolution microscope-integrated spectral domain optical coherence tomography device,” Retina 33(7), 1328–1337 (2013). 10.1097/IAE.0b013e3182831293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Tao Y. K., Srivastava S. K., Ehlers J. P., “Microscope-integrated intraoperative OCT with electrically tunable focus and heads-up display for imaging of ophthalmic surgical maneuvers,” Biomed. Opt. Express 5(6), 1877–1885 (2014). 10.1364/BOE.5.001877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Heindl L. M., Siebelmann S., Dietlein T., Huttmann G., Lankenau E., Cursiefen C., Steven P., “Future prospects: assessment of intraoperative optical coherence tomography in ab interno glaucoma surgery,” Curr. Eye Res. 40(12), 1288–1291 (2015). 10.3109/02713683.2014.995311 [DOI] [PubMed] [Google Scholar]
- 136.Vakoc B. J., Shishko M., Yun S. H., Oh W. Y., Suter M. J., Desjardins A. E., Evans J. A., Nishioka N. S., Tearney G. J., Bouma B. E., “Comprehensive esophageal microscopy by using optical frequency-domain imaging (with video),” Gastrointest. Endosc. 65(6), 898–905 (2007). 10.1016/j.gie.2006.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Mariampillai A., Standish B. A., Munce N. R., Randall C., Liu G., Jiang J. Y., Cable A. E., Vitkin I. A., Yang V. X., “Doppler optical cardiogram gated 2D color flow imaging at 1000 fps and 4D in vivo visualization of embryonic heart at 45 fps on a swept source OCT system,” Opt. Express 15(4), 1627–1638 (2007). 10.1364/OE.15.001627 [DOI] [PubMed] [Google Scholar]
- 138.Jenkins M. W., Adler D. C., Gargesha M., Huber R., Rothenberg F., Belding J., Watanabe M., Wilson D. L., Fujimoto J. G., Rollins A. M., “Ultrahigh-speed optical coherence tomography imaging and visualization of the embryonic avian heart using a buffered Fourier Domain Mode Locked laser,” Opt. Express 15(10), 6251–6267 (2007). 10.1364/OE.15.006251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Tearney G. J., Waxman S., Shishkov M., Vakoc B. J., Suter M. J., Freilich M. I., Desjardins A. E., Oh W. Y., Bartlett L. A., Rosenberg M., Bouma B. E., “Three-dimensional coronary artery microscopy by intracoronary optical frequency domain imaging,” JACC Cardiovasc. Imaging 1(6), 752–761 (2008). 10.1016/j.jcmg.2008.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Larina I. V., Furushima K., Dickinson M. E., Behringer R. R., Larin K. V., “Live imaging of rat embryos with Doppler swept-source optical coherence tomography,” J. Biomed. Opt. 14(5), 050506 (2009). 10.1117/1.3241044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Kolb J. P., Klein T., Kufner C. L., Wieser W., Neubauer A. S., Huber R., “Ultra-widefield retinal MHz-OCT imaging with up to 100 degrees viewing angle,” Biomed. Opt. Express 6(5), 1534–1552 (2015). 10.1364/BOE.6.001534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Zuluaga A. F., Richards-Kortum R., “Spatially resolved spectral interferometry for determination of subsurface structure,” Opt. Lett. 24(8), 519–521 (1999). 10.1364/OL.24.000519 [DOI] [PubMed] [Google Scholar]
- 143.Grajciar B., Pircher M., Fercher A., Leitgeb R., “Parallel Fourier domain optical coherence tomography for in vivo measurement of the human eye,” Opt. Express 13(4), 1131–1137 (2005). 10.1364/OPEX.13.001131 [DOI] [PubMed] [Google Scholar]
- 144.Nakamura Y., Makita S., Yamanari M., Itoh M., Yatagai T., Yasuno Y., “High-speed three-dimensional human retinal imaging by line-field spectraldomain optical coherence tomography,” Opt. Express 15(12), 7103–7116 (2007). 10.1364/OE.15.007103 [DOI] [PubMed] [Google Scholar]
- 145.Choma M. A., Ellerbee A. K., Yang C., Creazzo T. L., Izatt J. A., “Spectral-domain phase microscopy,” Opt. Lett. 30(10), 1162–1164 (2005). 10.1364/OL.30.001162 [DOI] [PubMed] [Google Scholar]
- 146.Považay B., Unterhuber A., Hermann B., Sattmann H., Arthaber H., Drexler W., “Full-field time-encoded frequency-domain optical coherence tomography,” Opt. Express 14(17), 7661–7669 (2006). 10.1364/OE.14.007661 [DOI] [PubMed] [Google Scholar]
- 147.Bonin T., Franke G., Hagen-Eggert M., Koch P., Hüttmann G., “In vivo Fourier-domain full-field OCT of the human retina with 1.5 million A-lines/s,” Opt. Lett. 35(20), 3432–3434 (2010). 10.1364/OL.35.003432 [DOI] [PubMed] [Google Scholar]
- 148.Fechtig D. J., Schmoll T., Grajciar B., Drexler W., Leitgeb R. A., “Line-field parallel swept source interferometric imaging at up to 1 MHz,” Opt. Lett. 39(18), 5333–5336 (2014). 10.1364/OL.39.005333 [DOI] [PubMed] [Google Scholar]
- 149.Kumar A., Drexler W., Leitgeb R. A., “Numerical focusing methods for full field OCT: a comparison based on a common signal model,” Opt. Express 22(13), 16061–16078 (2014). 10.1364/OE.22.016061 [DOI] [PubMed] [Google Scholar]
- 150.Kumar A., Drexler W., Leitgeb R. A., “Subaperture correlation based digital adaptive optics for full field optical coherence tomography,” Opt. Express 21(9), 10850–10866 (2013). 10.1364/OE.21.010850 [DOI] [PubMed] [Google Scholar]