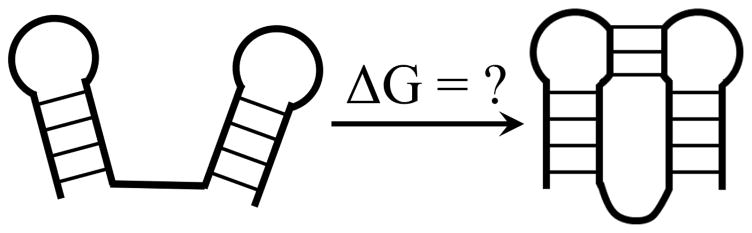Theory and Modeling of RNA Structure and Interactions with Metal Ions and Small Molecules

Abstract

In addition to continuous rapid progress in RNA structure determination, probing, and biophysical studies, the past decade has seen remarkable advances in the development of a new generation of RNA folding theories and models. Here, we review RNA structure prediction models and models for ion-RNA and ligand-RNA interactions. These new models are becoming increasingly important for mechanistic understanding of RNA function and quantitative design of RNA nanotechnology. We focus on new methods for physics-based, knowledge-based, and experimental data-directed modeling for RNA structures, and explore the new theories for the predictions of metal ion and ligand binding sites and metal ion-dependent RNA stabilities. The integration of these new methods with theories for the cellular environment effects, such as molecular crowding and cotranscriptional folding, may ultimately lead to an all-encompassing RNA folding model.

INTRODUCTION

RNA functions, such as the replication of RNA viruses and RNA-mediated regulation of gene expression, depend on RNA structures and the ability to adopt a variety of conformational states. It is therefore essential to be able to quantitatively model RNA structures from the sequence and to predict folding stability in proper solution conditions. Moreover, because RNA is highly charged, metal ions are critical for RNA folding and ions in the solution are probably the most important solution condition for RNA folding. Therefore, a reliable RNA model must consider the metal ion effects. In this review we mainly focus on RNA structure prediction and the modeling of ion effects in RNA folding.

The past decade has seen remarkable progress in RNA structure prediction, especially for small size RNAs (33, 34, 41, 79, 130). However, the prediction accuracy for medium to large (longer than 100 nucleotides) structures has been inconsistent for different RNA structures and sequences, even with the input from experimental data (101). The major problem comes primarily from structures with multibranched loops, base-base and base-backbone noncanonical interactions, and other long-range tertiary contacts. Furthermore, the problem of accurate prediction for ion and ligand binding sites and their binding affinities still remains unsolved, and the accuracy of theoretical predictions is usually acceptable only at low resolution level. The challenges mentioned above stem partly from the limited amount of experimental structural and biophysical data and partly from lack of physics-based free energy models for RNA tertiary folds. This review places emphasis on both the knowledge-based and physics-based approaches for the prediction of structures and modeling of ion and ligand binding.

TWO-DIMENSIONAL (2D) STRUCTURE PREDICTION

The fact that base pairing and stacking are dominant stabilizing forces in RNA structure supports the validity of a two-step structure prediction algorithm: first predict the two-dimensional (2D) structure of an RNA, then predict the three-dimensional (3D) structure based on the 2D structure. A 2D structure, like a contact map, describes the structure in terms of base pairs. A 2D structure can describe secondary as well as tertiary structural motifs, such as kissing loops and pseudoknots, at the base pairing level. Such a thermodynamics-based 2D to 3D approach, to some extend, bears resemblance the kinetic hierarchical pathway in RNA folding (15, 59).

Multiple sequence alignment (60, 108) can provide reliable predictions for the base pairs. However, the method is restricted by the availability of the homologous sequences, and the method can only provide conserved base pairs. For a given sequence, we often need a separate model to predict the remaining (non-conserved) base pairs. Helix assembly-based methods (9, 119) allow us to sample large, complex pseudoknotted 2D structures. However, without considering loop free energies, the prediction accuracies are not consistent, especially for large RNAs. Experimental data-directed free energy minimization approaches, such as chemical mapping, are highly promising (32, 42, 62, 73, 120). However, to interpret and understand the ambiguity of the experimental data for structured loops and populated distribution of multiple conformers requires a rigorous physical model.

A central issue in the physics-based 2D structure prediction is the free energy model, including the entropy model, for tertiary folds. Although folding entropy often receives less appreciation than energy in the field, it plays a significant role in the overall folding stability. For example, a rough estimate indicates that at room temperature, the loop entropy term TΔS_loop for the T4-35 pseudoknot contributes a significant portion (~ 7.5 kcal/mol) to the total folding free energy ΔG (~ 9.0 kcal/mol) (19).

One of the most significant distinctions between the free energy calculations for secondary and tertiary structures is the additivity issue. For secondary structures, one typically adds the free energies of the helices and loops, which can be calculated from the experimentally determined parameters (Turner Rules) (99), to estimate the total free energy. However, because the long-range cross-linkage causes coupling between the different loops and helices, the free energy, especially the entropy, is nonadditive for tertiary folds. The nonadditivity underscores the importance to treat a tertiary fold as a whole in the entropy calculation. Due to the holistic nature of the tertiary structure entropy and the large number of tertiary motif types, it is unrealistic to rely on experiments to measure all the parameters. Instead, we need a theory to compute the parameters. By considering the nonadditivity effect, researchers have developed and applied a variety of free energy models for tertiary motifs, such as the following.

• Dirks and Pierce developed an empirical energy model (48) for multiloops/pseudoknots, where the parameters are optimized through training with both negative (non-pseudoknotted structures) and positive (pseudoknotted structures) controls.

• From the knowledge of end-to-end distance distribution for the two-length-scale (one for unpaired segments, one for paired segments) freely jointed chains, Aalbert et al. developed polymer theory-based entropy models for pseudoknot loops (1) and kissing hairpin loops (100), respectively.

• Chen et al. developed a statistical mechanics-based virtual bond lattice model (“Vfold”) to compute the entropy parameters through conformation enumeration for pseudoknotted structures, kissing loops, and RNA-RNA kissing complexes (19, 20, 23, 90).

• Based on a topological genus-based structure classification, Bon & Orland developed a free energy model for pseudoknots according to their genus (11).

• To predict pseudoknotted 2D structures using selective 2′-hydroxyl acylation analyzed by primer extension (SHAPE) data, Mathews and Weeks et al. (62) proposed a heuristic free energy scoring function, where a jackknife approach is used to fit parameters from a training set with non-pseudoknotted and pseudoknot-containing RNAs.

• For unimolecular kissing hairpins (Fig. 1), Sperschneider et al. (131) developed a heuristic approximation: ΔG (the total free energy) = sum of the helix free energies and a weighted sum of the number of the unpaired nucleotides in the different loop segments, where the weight coefficients are trained to fit the known structures.

Figure 1.

Loop entropy and free energy parameters for the formation of a unimolecular long-range kissing structure.

These and other entropy/free energy parameters for tertiary folds have led to notable improvements in 2D structure prediction. However, the applicability of the parameters is still quite limited due to the following two reasons.

• Lack of sequence-dependence. For loops involving strong sequence-specific interactions, such as loop-helix triple base interactions, the loop free energy parameters require sequence-specific modifi-cations (21).

• Structure-specificity. The above parameters may not be useful for other tertiary motifs. The non-physics-based parameters may not be transferable between the different structures and can thus cause inaccuracy in structure predictions (131).

We need an entropy/free energy model that is based on rigorous statistical mechanics. Developing such a model and parameter set demands a large-scale systematic computations for the various types of tertiary motifs/folds. The Vfold model above has the advantage of accounting for the chain connectivity and excluded volume effects while keeping the conformational realism. Computations with the Vfold model have demonstrated the ability to successfully predict the entropy parameters for a variety of tertiary motifs. Integrated with a proper sampling method, Vfold may serve as a promising framework for systematic calculations for various types of tertiary motifs. Furthermore, entropy is intrinsically tied to the conformational statistics and is thus a problem at the 3D conformational level (19, 20, 144). With advances in 3D structure modeling, we expect continuous improvements in the entropy model and hence the 2D structure prediction accuracy (93, 95, 99, 128).

THREE-DIMENSIONAL (3D) STRUCTURE PREDICTION

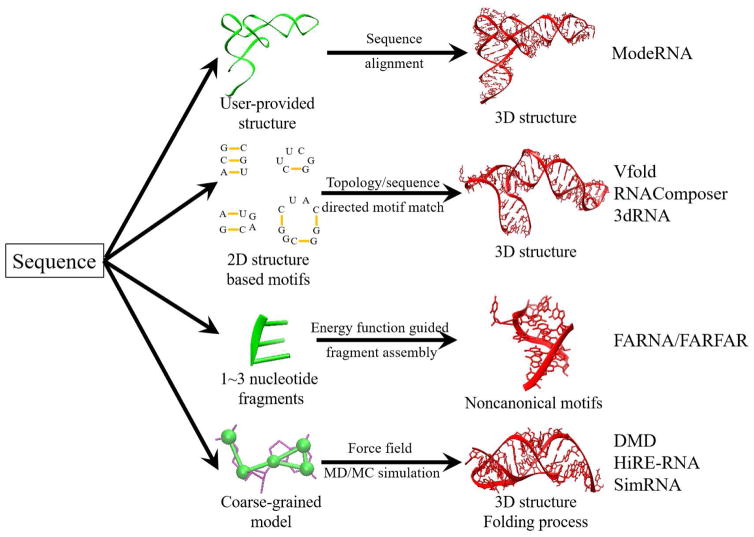
Two main ingredients for a 3D structure prediction method are conformational sampling and scoring. For sampling, one may generate conformations through molecular dynamics (MD) or Monte Carlo simulations, or through assembly of the fragments/templates extracted from the known structures. For scoring, one may use sequence similarity, knowledge-based statistical potential, or molecular mechanics-based force field to rank candidate structures. The combinations of the different sampling and scoring methods lead to different 3D structure prediction methods. In fact, sampling and scoring can be interwoven with each other and the boundary between the different methods is blurry. For example, template-based sampling can dramatically reduce the search space for physics-based methods and physics-based energy functions can provide effective guidance for structure assembly in template-based approaches. In Table 1, Fig. 2, and Table S1, we summarize a set of selected methods.

Table 1.

An overview of a selected set of 3D structure prediction models

Name/Reference	Operation material	Sampling technique	Scoring function
FARNA/FARFAR(38,40)	Trinucleotide fragment	Monte Carlo fragment assembly	Knowledge-based/full atomic force field
MC-Fold/MC-Sym(111)	Nucleotide cyclic motif	Las Vegas algorithm	Knowledge-based scoring function
RNA2D3D(98), Assemble(69)	User-defined	Interactive graphical editing	User-defined
RNABuilder(54)	Whole structure	User-defined constraints satisfaction	User-defined
ModeRNA(121)	Whole structure	Sequence alignment	Sequence similarity
Vfold(22)	2D structure based templates	Template match	Loop size and sequence similarity
RNAComposer(117)	Stems, loops and single strands	Fragment match	2D structure topology and sequence similarity
3dRNA(147)	Smallest secondary elements (SSEs)	SSE topology match	Sequence identity
RNA123(53)	Fragment and template	Template match	Knowledge-based force field
Graph theory approach(70, 72)	Graph representation	Monte Carlo graph sampling	Knowledge-based energy function
DMD(46), HiRE-RNA(34), SimRNA(12)	Coarse-grained beads	MD/MC simulation	Knowledge/physics-based force field

Figure 2.

The main elements for several computational approaches for RNA 3D structure modeling. Other models, such as MC-Fold/MC-Sym (111), may use a hybrid form of the elements listed in the figure.

Template-based methods

Template database: fragments vs. motif-based templates

A knowledge-based structure prediction method relies on a reference template database (22, 53, 54, 69, 98, 117, 121, 147). The database ranges from the whole structure (54, 121) to various structure motifs (22, 53, 117), including helices, hairpins, internal/bulge loops, pseudoknot loops, and junctions, down to small fragments with different chain lengths such as nucleotide cyclic motifs, trinucleotide fragments, and single base pairs (38, 40, 111). Recent studies on RNA-RNA interaction networks uncovered specific sequence patterns in many tertiary structural modules, including A-minors, ribose zippers, tetraloop receptors, and K-turns (18, 86). These structural modules can serve as excellent building blocks (templates) for 3D structure prediction. We refer to Westhof’s article in this volume for more details about structural modules and related computational tools.

The performance of the different fragment/template methods varies from structure to structure (36, 79) and a single universal ranking of the different methods may not be available. In general, when there are reliable templates in the database, many different methods can provide reasonably good predictions. For instance, for the tRNA structures, the Root Mean Square Deviation (RMSD) given by various approaches ranges from 3.6 Å to 6.1 Å(22, 117, 121, 147). On the other hand, as indicated by Problem 3 in the blind test RNA-Puzzles (36) (see Westhof’s article in this volume), the models that use relatively large size templates, such as Vfold (22), which searches the templates based on the whole loop/junction, have the advantage of accurately capturing the nonlocal intraloop interactions. In contrast, methods that use small size templates (fragments), such as SWA developed by Das et al. (36), have the advantage to accurately capture the local features, especially the local non-canonical interactions. Therefore, at the cost of a higher failure rate to find a template with an ideal match, the motif template-based methods, such as Vfold (22) and RNAComposer (117), may predict a reliable structure for complex structures such as multibranched loops and pseudoknot-ted loops (if the appropriate template is available). However, such motif-based templates are not always available. In that case, fragment-based methods, such as FARNA/FARFAR (38, 40) are particularly useful for generating 3D structures.

Sampling techniques: beyond the boundary of the template database

For template-based methods, the bottleneck is the lack of proper templates. Several novel methods have been developed to partially circumvent this problem. In RNAComposer, Adamiak et al. (117) utilized the machine translation system, where the translation search engine operates on the dictionary that maps the RNA 2D structure to 3D structure elements. In FARNA/FARFAR, Das et al. (132) developed an enumerative and recursive stepwise ansatz which enables the systematic sampling of RNA loop conformations at the atomic level. The fragment-based methods can be limited by the discrete nature of the fragments and their non-probabilistic nature. To remove the sampling limitations in the fragment assembly methods, Hamelryck and co-workers (55) developed a probabilistic model (BARNACLE) that allows efficient sampling of RNA conformations in continuous space with the associated probabilities. The Vfold (22) method exploits the fact that a 2D structure can be dynamic, especially at the loop-helix interface. The model allows a variable loop/junction size by closing/opening loop-closing base pairs. The approach can significantly augment the template database and enhance the possibility of finding the appropriate template.

In addition to the above sampling techniques for the candidate structures, global structural constraints encoded in the 2D structure can also be used to enhance the sampling efficiency, because the global constraints can influence the local structural preferences (7, 105). For example, the helix orientations (coaxial stacking, parallel, antiparallel, or perpendicular arrangement) in two-way (6), three-way (87), or higher-order junctions may subject to the restriction imposed by the long-range kissing contacts. A recent hierarchical graph theoretic algorithm guided by a knowledge-based scoring function (70, 72) shows great promise for efficiently sampling of large structures by incorporating the constraints from the 2D structure.

Scoring functions: guiding sampling/assembly process and evaluating structure candi-dates

A reliable scoring function is crucial for guiding the conformational sampling and ranking candidate structures. Ideally, such a function should be based on rigorous physics. The essential elements for a physically reliable force field and scoring function will be discussed in “Physics-based methods” section below.

Physics-based methods

Energy functions

In Table S1, we summarize the energy/scoring functions, including CG energy functions, for RNA structure prediction. Atomistic models, such as FARFAR (40) and RASP (24), use an AMBER/CHARMM-like force field for local interactions and various forms of potential energies for nonlocal interactions. For CG models, based on fewer degrees of freedoms, the force field can be both distance- and orientation-dependent and is often model-dependent. CG energy functions describe base stacking and base pairing interactions by incorporating simple geometric constraint (68), pairwise (140) and many-body distance-dependent (46, 125) potentials, and specific distance- and orientation-dependent functions (34, 44, 65), or more sophisticated multi-atom potentials in the form of multidimensional grids (12). CG models based on highly simplified low-resolution representation (e.g., less than three interaction sites per nucleotide) cannot provide sufficient details for noncanonical base pairing (85) and base-phosphate interactions (148). Furthermore, most CG models tend to use the Debye-Hückel potential with the (partially) neutralized backbone charges (44, 125) to model the salt effect. The Debye-Hückel model has the advantage of being computationally efficient. However, the validity of this model for multivalent ions, such as Mg²⁺ ions, requires further rigorous tests with experimental data or detailed all-atom simulations.

Parameterization of the energy/scoring functions

There are two types of methods to derive the energy functions (109): physics-based and knowledge-based approaches. Physics-based methods are based on statistical mechanics models and compute energy parameters from thermodynamic data or atomistic force fields (17, 65). Knowledge-based methods use the probability distribution p_sta (x) for the different structure elements x (e.g. torsional angles, base stacks, loops) from the known structures, and extract the statistical potential energies from the inverse of Boltz-mann: U(x) = −k_BT ln[p_sta(x)/p_ref (x)]. Here p_ref (x) is the probability distribution in the reference state. Compared to the physics-based method, the knowledge-based approach has the advantage of being mathematically simple. However, unlike the physics-based energy functions, the knowledge-based energies suffer from two disadvantages: (a) bias toward the native structure and (b) the challenge to select a physically valid reference state.

A physical reference state should correctly reflect the inherent chain connectivity and excluded volume effects, and depending on the potential to be extracted, may also need to account for the correlation between the different intrachain contacts such as canonical and noncanonical base pairs. These features, however, are not fully captured in the current RNA models that use simplified reference states, such as the non-interacting ideal gas state (140), state treated with quasi-chemical approximation (8, 12) or uniform distribution in the reaction coordinate space (24, 34, 40, 125, 140). In a CG RNA loop structure prediction model, Liu and Chen (90) employed an iterative method, which was originally developed for protein folding (137), to circumvent the reference state problem. The model leads to much improved loop structure predictions at the CG level (90). Essentially, the iterative method exploits statistical potentials such that the structure database-derived parameters can best reproduce the thermal equilibrium distribution for the complete conformational ensemble, including nonnative conformations, for the sequences in the training database. The method has the advantage of accounting for the full energy landscape, including the effects from nonnative structures.

Success and challenges

Simulations based on force fields such as AMBER or CHARMM have enabled us to extract detailed structural information about the native and alternative structures and folding and unfolding dynamics for small RNA structures (14,27,30,145) such as duplexes, hairpins, and pseudoknots. Moreover, other atomic force fields have been used to predict noncanonical motifs (40), to assess 3D structures (24), and to identify native-like conformations (8). Similarly, CG energy (scoring) functions have also led to success in structure prediction for small RNA (12, 34, 46, 125, 140), folding thermodynamics predictions for secondary structures and pseudoknots (34, 44, 46), and 3D structure refinement with structural constraints from experimental data (12, 68, 140). Furthermore, by taking noncanonical base pairs into account, CG models, such as HiRE-RNA (34) and SimRNA(12), can fold pseudoknots directly from the sequence (12, 34) and provide insights into the folding pathways of pseudoknots (12, 46), including triple helix pseudoknots (34).

However, all-atom and CG structure prediction remains a challenge even for medium size (e.g., 50–80 nts) RNAs. It suffers from three main problems. First, the force field needs further improvement. Even for the long-time tested AMBER and CHARMM force fields, folding studies for small systems such as an 8-nt tetraloop-forming hairpin (30) suggest the need for reparametrization of the force field. We expect the release of Amber16 force field, especially with the more accurate force field for metal ions (26), will lead to further improvements in prediction accuracy. For CG models, the energy function often lacks sufficiently detailed description for noncanonical base pairs and base-phosphate interactions. A correlated, many-body CG potential function may provide a viable way to alleviate the limitation. Second, efficient sampling of RNA conformations, especially for large RNAs, demands new approaches. Low-resolution representation, such as NAST (68), or modified force fields, such as DMD (46), can enhance the sampling efficiency, albeit at the cost of losing details about essential features for noncanonical interactions. Third, accurate modeling of RNA structures should consider the effect of the cellular environment. The problem requires incorporation of more sophisticated solvent models that can account for the effects from metal ions and other cofactors, including the molecular crowding effects, into the energy function.

DATA-DIRECTED STRUCTURE PREDICTION

Structural probing experiments, such as SHAPE (42, 62, 120), DMS (32) (dimethyl sulfate) structure detection, MOHCA (39) (multiplexed hydroxyl radical cleavage analysis), RING-MaP (66) (RNA interaction groups by mutational profiling), can provide a variety of low-resolution structure information. Other experiments, such as SAXS (small angle X-ray scattering) and Cryo-EM (cryogenic electron microscopy), can provide global shape of the structure. Integrating the experiment-generated low-resolution structure data into computational models can significantly reduce the conformational search space and remarkable improvements in the scope and accuracy of structure prediction. Indeed, some of the most actively pursued structure prediction methods in recent years are based on data-directed algorithms, as shown in the following for several examples.

• Chemical mapping data (such as SHAPE)-directed 2D structure prediction based on data-derived pseudo-energy terms (32, 42, 62, 120);

• HRP (hydroxyl radical probing)-aided 3D structure refinement (47), and ¹H NMR chemical shifts-guided structure determination for noncanonical interactions (133);

• Multidimensional chemical mapping-guided structure prediction with Rosetta (39, 73);

• Chemical probing data-assisted discrete molecular dynamics simulation for 3D structure refinement (66);

• SAXS data-directed selection of the most native-like structure from decoys generated by MC-Fold/MC-Sym (142), NAST (68) or other CG models (140).

Although the data-assisted algorithms have led to remarkable success in RNA structure prediction. such algorithms cannot always lead to accurate structure predictions (74, 94), unless the data is properly interpreted and implemented. As indicated by Weeks et al. (66), the long-range tertiary interactions can be cooperatively coupled, thus, the structure determination should contain all the essential data for the tertiary interaction network. However, over-constraint by experimental data may cause trapping in local minimal for conformational sampling. How to use the data in an optimal way for computational modeling remains a nontrivial problem. Furthermore, as shown by Das and co-workers (39), the correlation between experimental data (e.g., strength of hits) and certain reaction coordinate (e.g. the pairwise distance between residues), can sometimes be poor. The situation highlights the demand for a physical model to correctly interpret the data and to eliminate the background noise, data fluctuation, and redundant/incorrect experimental information (139).

In the aforementioned RNA structure prediction models, ion-mediated electrostatic interactions are often treated by simplified models such as the counterion Condensation (CC) model or the Debye-Hückel model. However, the role of ions, especially the Mg²⁺ ions, goes beyond the description of these mean-field ion electrostatic models. A more accurate description for the ion effects is needed. Ion-RNA interactions can be roughly classified into two types: site-specific and nonspecific binding. Because the two types of interactions show quite different features and thus require different methods to model, we discuss them separately in the following sections.

ION EFFECTS: SPECIFIC BINDING

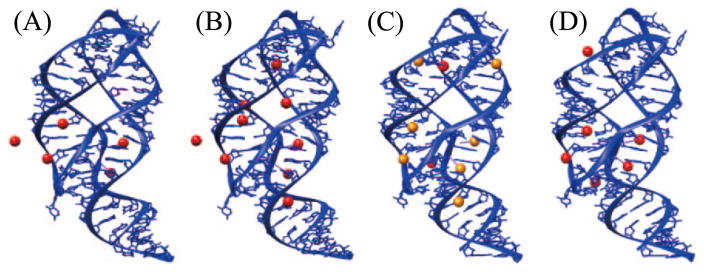
A fully hydrated Mg²⁺ ion has six water molecules in the first hydration shell and twelve in the second shell (97, 112). Specific binding of an ion is often associated with ion dehydration at various levels. For example, in the crystal structures of adenine riboswitch (PDB ID: 1Y26 (124) and 4TZX (146), shown in Figs. 3A and B), Mg²⁺ ions keep only one water molecule at certain binding sites and retain several water molecules in other binding sites. Theoretical calculations show that the dehydration of the first and second shells cost 303.9 Kcal/mol and 156.9 Kcal/mol, respectively (112). Using MD simulations, Chen and coworkers investigated the dehydration of monovalent ions (Na⁺, K⁺, and Cs⁺) bound to specific sites in an RNA kissing loop (28). The simulation led to the conclusion that (a) water molecules around smaller ions are bound more tightly thus smaller ions are less likely to dehydrate, and (b) ions at sites with strong ion-RNA attraction are more likely to dehydrate.

Figure 3.

Specific binding of ions in the adenine riboswitch. (A) PDB ID: 1Y26 (124), [Mg²⁺]=200mM; (B) PDB ID: 4TZX (146), [Mg²⁺]=200mM; (C) PDB ID: 4TZY (146), [Mg²⁺]=150mM and [Sr²⁺]=50mM; (D) PDB ID: 4NXR (91), [Mg²⁺]=100mM. The red and orange balls present Mg²⁺ ions and Sr²⁺ ions.

The specific ion binding sites are sensitive to ion species. Moreover, a recent study for ion binding to adenine riboswitch (146) (see Fig. 3C) showed that common binding sites for the different ion species can induce a competition between the different ions in RNA binding. Although Mg²⁺ has smaller radius (0.72 Å), Sr²⁺ (1.18 Å) appears to be a stronger competitor in this case as it replaces Mg²⁺ in several binding sites. The result depends on the interplay between Coulomb interaction, volume exclusion, and dehydration state of the ions. Because dehydration can reduce the effective size of an ion (97), smaller ions, which are less likely to dehydrate, may have a larger hydrated radius than an dehydrated ion (75). The large hydrated radius can cause stronger volume exclusion and weaker ion-RNA attraction. Similar competition has also been observed for Cu²⁺ and Ca²⁺ ions in the A-form RNA helix (123), Ca²⁺ and Mg²⁺ in the Thi-Box Riboswitch (50), and Mn²⁺ and Mg²⁺ in tetraloop-receptor complex (67).

Some binding sites can recognize only specific types of ions. An example is the Mg²⁺ ion trapped in the kissing loop of the adenine riboswitch. The specific binding may result from the direct binding between the ion and specific atoms of RNA such as the phosphate oxygen (123) instead of water-mediated indirect interactions. To quantitatively estimate the competition between the different types of ions, an atomistic model is needed. Recently, Panteva and coworkers (110) improved the force fields for Mg²⁺, Mn²⁺, Zn²⁺, and Cd²⁺ ions using a “12–6–4” potential (88) to account for the electrostatic interaction and volume exclusion. The theory gives promising theory-experiment agreement (deviation within 0.1 Kcal/mol) for the binding free energies for four types of ions tested with different nucleic acid systems.

The specific binding is also dependent on the background salt conditions. In Fig. 3B (PDB ID: 4TZX (146)) and Fig. 3D (PDB ID: 4NXR (91)), we show a comparison of the site-specific binding of Mg²⁺ ions at high ([Mg²⁺]=200mM) and low ([Mg²⁺]=100mM) salt concentrations. The figures show that the low and high [Mg²⁺] lead to four binding sites in common. Five binding sites at high [Mg²⁺] disappear at dilute [Mg²⁺] and, surprisingly, two other binding sites observed at dilute [Mg²⁺] are missing at high [Mg²⁺]. This phenomenon may result from two competitive effects induced by the change of the bulk ion concentration (84). An increase in the bulk concentration would cause more ions accumulated around the RNA. As a result, each binding site has a higher probability to capture an ion. However, accumulated ions tend to displace other like charge ions from the binding sites through Coulomb repulsion and volume exclusion, resulting in a negative impact on the specific binding.

Currently, both MD simulation-based and knowledge-based algorithms have been developed for the prediction of ion binding sites. For example, Philips and coworkers recently developed a knowledge-based algorithm to predict ion binding sites (114). The model uses more than one hundred ion-bound RNA crystal structures to deduce a statistical potential for metal ions such as Mg²⁺, Na⁺, and K⁺. In a different approach, using MD simulation, Denesyuk and Thirumalai (45) investigated the effects of specific binding of ions for ribozyme folding. The theory predicted the binding sites for Mg²⁺ ions, including the two locations of co-binding Mg²⁺ ions at the active site. Based on a similar simulational approach, Lee and coworkers (82) found that the two co-binding Mg²⁺ ions can assist catalysis in different steps of the reaction. MD simulations have also been applied to the prediction of specific ion binding in other RNAs, including the 5S rRNA Loop E Motif (3), Hepatitis Delta Virus (HDV) Ribozyme (76), and HIV-1 TAR RNA (49).

ION EFFECTS: NONSPECIFIC BINDING

Nonspecific Coulombic attraction between RNA and ions results in significant accumulation of ions around the RNA. The pronounced ion accumulation could extend more than 20 Åaway from the surface of RNA (63). Because of the large number of bound ions, the nonspecific ion binding contributes significantly to the overall RNA folding stability (102). In recent years, several novel experimental methods, such as “ion counting” (IC) (4, 56), SAXS (5), X-ray scattering interferometry (XSI) (126), and single-molecule optical trapping (SMOT) (2, 10) methods have been developed to probe ion binding properties. These experiments provided highly needed information about ion distribution and the number of bound ions around an RNA. In parallel with the experimental development, several new theories have been proposed to predict ion distribution and electrostatic free energies of the system.

Traditional theories such as counterion condensation theory (CC) and nonlinear Poisson-Boltzmann equation (NLPB) can give accurate treatment for monovalent ion solutions. However, for multivalent ions, such as Mg²⁺, the traditional theories become less reliable. For example, for a tethered 12-basepair DNA duplex in a Mg²⁺ solution (5), NLPB significantly underestimates the fraction of the relaxed conformations and the number of excess Mg²⁺ ions around the DNA (4). More recently, Gebala et al. found that NLPB also underestimates the excess number of monovalent cations in a high concentration salt solution due to neglecting the cation-anion correlation effect (56).

One of the problems in the traditional theories is neglecting ion correlation and fluctuation effects. When ions accumulate around the RNA surface, ions are close to each other. The high local concentration of the bound ions leads to two effects. First, the long-range strong Coulomb force can cause a strong coupling between the ions, such that ion binding at one location is correlated to the binding of ions at other locations. Second, the electrostatic interactions become highly sensitive to the discrete distributions as well as the discrete properties (such as the size) of the ions.

MD simulations with proper force field with explicit ions and solvents can intrinsically account for ion-ion correlations. Indeed, simulations have provided significant insights into the detailed information about ion-RNA interactions (28, 29, 45). A meaningful simulation requires a large number of ions in the systems, rendering a large simulation system and long simulation time. The problem is more pronounced for low ion concentration solutions. The difficulty in MD simulation has inspired the development of alternative approaches, such as the modified CC-like and NLPB-like theories (64,96), the three dimensional interaction site model (3D-RISM) (57), and the Tightly Bound Ions model (134, 136).

In the generalized Manning condensation (GMC) model (64), an explicit Mg²⁺–Mg²⁺ ion correlation term is introduced to the classical Manning’s ion condensation layer, and interaction potentials for the three different types of ions (explicit, condensed, and screening ions) are used in the Langevin dynamics. Moreover, to account for the volume exclusion effect of ions, the size-modified Poisson–Boltzmann equation (SMPBE) was developed by incorporating the finite ion sizes into NLPB through a lattice gas formulation (13). Applications of the SMPBE to ion-RNA interactions have led to improved predictions for the ion distributions (31).

Furthermore, in a recent study, Sushko et al. treated ion correlation and solvation effects in a density functional framework (135). Comparisons with SAXS data for the ion distribution support the importance of ion-ion correlation and hydration effects. 3D-RISM is another promising model for solvation and correlation effects based on the density distribution of ions (57). The model solves the Ornstein and Zernike (OZ) integral equation by averaging the solvent degrees of freedom. Applications of the 3D-RISM model to ion distribution around nucleic acids have led to reliable results. For example. the model gives two peaks in the ion density distribution around a nucleic acid helix, a result observed in explicit MD simulation. Because the 3D-RISM model takes into account both the ion-ion and the ion-solvent correlations, it can also be used to investigate specific binding of ions (118).

To treat ion correlation and fluctuation effects, Chen et al. developed the Tightly Bound Ion (TBI) model (136) in the statistical mechanical framework. The basic idea in the TBI model is to enumerate discrete ion distributions for strongly correlated ions (“tightly bound ions”), which are distributed in a thin layer around the RNA, and to use NLPB to treat the rest (weakly correlated) ions. For the original TBI model (136), the computational efficiency is severely limited by the time-consuming enumeration of the discrete ion distributions. As a result, the applicability of the model is restricted to RNAs less than 80 nucleotides long. Recently, using Monte Carlo simulation to sample the ion distributions (134), Chen et al. developed a new generation of the TBI model (“MCTBI”). The MCTBI model allows users to treat large RNAs of several hundreds of nucleotides long. The key idea in the new TBI model is a re-sampling algorithm for ion distribution: using Metropolis algorithm, to first randomly insert the tightly bound ions with bias toward low electric potential sites, followed by random removal of the ions with bias toward high electric potential sites.

LIGAND BINDING

Inspired by the tremendous potential of RNA-targeted therapeutics (127), researchers have developed a numbers of docking/scoring models for RNA-ligand binding (116). Different from ion binding, where an ion can be approximately modeled as a sphere, ligand binding models involve sampling of different orientations of the (anisotropic) ligand. In Table 2 we show several computational tools developed in recent years. As shown in the table, these docking/scoring tools involve a variety of sampling and physics-based or knowledge-based scoring methods, and have been successful at different levels. In contrast to ligand-protein docking models, which are supported by extensive database of the available compounds and the affinity data, such a database for ligand-RNA docking is highly limited. Therefore, physics-based modeling may be an important approach of choice. In the future model development, a successful physics-based for ligand-RNA binding should account for several unique, important factors for ligand-RNA binding, including the ones listed below.

Table 2.

Summary of a selected set of ligand-RNA docking tools

Name/Reference	Binding target(s)	Descriptions
DrugScoreRNA (77, 113)	RNA	The knowledge-based scoring function contains a set of distance-dependent potentials between two atoms in ligand and flexible target, respectively.
MORDOR (61)	RNA and Protein	The CHARMM-27 and general AMBER force fields are applied to RNA and ligand, respectively. The model considers flexible conformations of the ligand and the RNA target.
DOCK6 (80)	RNA and Protein	An extended version is developed for targeting RNA. The physics-based scoring function contains the effects of solvation and sodium ion effects on docking.
ligandRNA (115)	RNA	The model scores and ranks ligand poses in ligand-RNA complexes. The knowledge-based function contains a set of distance- and angle-dependent statistical potentials for atom pairs between ligand and RNA.
rDOCK(104, 122)	Nucleic acids and protein	The package is open source. The scoring function is specifically developed for RNA-ligand docking by taking into account the stacking interactions and the charge-distributions in both RNA and ligand.

First, ligand-RNA interaction is highly sensitive to the charge distribution on the ligand. A ligand may contain positively charged (protonated) subunits such as amidinium, guanidinium and imidazole, and negatively charged (deprotonated) subunits such as ethanesulfonic acid and acetic acid. The positively charged subunits are more likely to be attracted to the (negatively charged) RNA backbone. For example, amino-glycosides that contain several positive charges are potent inhibitors for RNA binding (52). By comparing the binding affinities between the different aminoglycosides, including paromomycin, kanamycin-B, gen-tamycin, and tobramycin, Smith et al. demonstrated that the charge distribution is critical for specific binding (129). To model the effect, Moitessier and coworkers developed a specific scoring function for aminoglycosides-RNA binding (103).

Second, the nucleobase elements in some ligands can induce specific hydrogen bonding and stacking interaction. Experimental evidence shows that 2,6-diaminopurine could bind to the C74U mutation of the guanine riboswitch because of the formation of eight hydrogen bonds, while benzimidazole couldn’t bind to the same riboswitch because it could only form two hydrogen bonds (58). In general, stacking interaction is much stronger than hydrogen bonding and hence stacking interaction is quite common in the stabilization of a ligand-riboswitch complex. For example, SAM riboswitch involves a full stacking between two nucleotides (92) at the ligand binding site.

Third, the interactions between RNA and the different cofactors, such as ions, proteins, and ligands, are often cooperatively or competitively coupled. For example, aminoglycoside binding to the bacterial ribosomal A-site RNA is in competition with metal ion binding, and binding of a synthetic ligand for an HCV RNA target is also found to be in competition with Mg²⁺ binding (25). For many riboswitches, ions facilitate ligand-induced conformational switch. For example, without Mg²⁺, the ligand binding may not be sufficient to cause the structure change in the expression platform (83). Similarly, for a large class of riboswitches, such as metal ion sensing riboswitches (35,37), the thiamine pyrophosphate (TPP) riboswitches (141), and glycine riboswiches (89), specific ion-binding is often required for ligand binding.

Furthermore, ligand structure is often sensitive to RNA structural changes in the ligand-RNA binding process, such as the binding of RBT550 to HIV-1 TAR RNA (PDB ID: 1UTS) (106) and Argininamide to HIV-2 TAR RNA (PDB ID: 1AJU) (16). Therefore, conformational flexibility is another critical challenge that must be taken in account in ligand-RNA interaction models.

CONCLUSIONS

In the past decade we witnessed substantial achievements in physics-based and knowledge-based predictions for RNA folding. With the remarkable progress in structural and biophysical experiments, such as chemical mapping of RNA structures, SAXS and ion counting experiment for the probing of ion distributions and the number of bound ions, we begin to see successful integration of physics-based theoretical models for RNA folding and experimental data for the predictions of large RNA structures and the detailed mechanism of ion-RNA interactions. Furthermore, with the expansion of our knowledge about the known structures, we can realistically expect continuous improvements in the accuracy of knowledge-based structure predictions. Nevertheless, accurate predictions for large structures and for folding under cellular conditions are not solved problems. Many of the limitations in the current models stem from the inaccuracy in physics-based free energy models for RNA tertiary folds and ion binding and dehydration models of multivalent metal ions.

Furthermore, to understand RNA function, we need models for RNA folding in vivo. In the cellular environment, an RNA is surrounded by other macromolecules and small molecules, causing a crowded environment with up to 30% volume fraction(51). Crowders can cause significant differences between in vivo and in vitro RNA structures (78, 138). Recent experimental and theoretical analyses suggested that the excluded volume of the crowders can reduce the accessible space of RNA conformations, especially for the unfolded state, resulting in stabilization of the folded state (43, 71, 78, 107). Furthermore, recent theoretical studies demonstrated that organic crowders can weaken or strengthen ion-RNA binding as a result of the interplay between three crowding effects: steric competition between ions and crowders in RNA binding, crowder-induced change in the dielectric environment, which can change ion-RNA Coulomb interaction strength, and changes in the hydration state due to crowder-RNA binding(143).

In addition, RNA folding in vivo is cotranscriptional and kinetically controlled. Co-transcriptional folding of RNA often leads to very different structures (81) from in vitro refolding. The above complications combined highlight the demand for an all-encompassing physical model to incorporate the in vivo solution effect and cotranscriptional kinetics into structure prediction.