Building an experimental model of the human body with non-physiological parameters

Abstract

New advances in engineering and biomedical technology have enabled recent efforts to capture essential aspects of human physiology in microscale, in-vitro systems. The application of these advances to experimentally model complex processes in an integrated platform — commonly called a ‘human-on-a-chip (HOC)’ — requires that relevant compartments and parameters be sized correctly relative to each other and to the system as a whole. Empirical observation, theoretical treatments of resource distribution systems and natural experiments can all be used to inform rational design of such a system, but technical and fundamental challenges (e.g. small system blood volumes and context-dependent cell metabolism, respectively) pose substantial, unaddressed obstacles. Here, we put forth two fundamental principles for HOC design: inducing in-vivo-like cellular metabolic rates is necessary and may be accomplished in-vitro by limiting O₂ availability and that the effects of increased blood volumes on drug concentration can be mitigated through pharmacokinetics-based treatments of solute distribution. Combining these principles with natural observation and engineering workarounds, we derive a complete set of design criteria for a practically realizable, physiologically faithful, five-organ millionth-scale (× 10⁻⁶) microfluidic model of the human body.

0. INNOVATION

An integrated experimental model of the human body (a “human-on-a-chip” or HOC) holds great promise for drug discovery, personalized medicine and basic research. Despite recent achievements in this field, substantial challenges remain in faithfully recapitulating macro human function at a micro scale. Breaking with convention, we propose that non-physiologic design parameters (e.g. low “blood” oxygen carrying capacity) can be employed to induce in-vivo-like HOC behavior. We apply this strategy — supported by experimental and theoretical evidence — to provide detailed design criteria for a five-organ HOC capable of matching macro human function across key criteria.

1. INTRODUCTION

Advances in micro-scale engineering, cell sourcing and culture techniques are presenting new opportunities to recapitulate key structural and functional characteristics of the human body in controlled, in-vitro, experimental systems. Already, organ-level devices (commonly called ‘organs-on-a-chip’) are quite prolific^1–3. Efforts at devising systems-level platforms (i.e. HOCs) hold even greater promise^4–7. Ideally, these small HOCs would predict the effects of potential drugs or toxins on the human body^8–10, significantly reducing costs associated with animal and human clinical trials in the drug discovery pipeline, clarifying mechanisms of human health and disease and introducing new opportunities in personalized medicine. However, unresolved issues in both the design and fabrication of such systems present scientists and engineers with a complex, interdependent set of problems.

Animal basal metabolic rate (BMR) has been shown to scale with animal mass raised to some power¹¹. Although there remains some debate as to the exact value of the exponent¹², recent research has focused on how nutrient distribution networks generally control the relationship between organism size and metabolism^13,14. Thus, many important physical parameters scale with organism mass (M) raised to the power of a multiple of ¼ (e.g. metabolic rate, M^¾; heart rate, M^−¼; and blood volume, M¹), called quarter-power scaling relationships (QPSRs). These QPSRs^6,15,16, along with order of magnitude estimates^17,18, residence time and physiologically based pharmacokinetic/pharmacodynamic (PB-PKPD) models^{4,5,8,19–21}, empirical allometry^22,23 and functional approaches^22–24 have all been used in the design of HOCs. Although these approaches do inform values for organ compartment size and other physiological parameters, they also present two classes of intractable problems in the design and construction of such systems. The first type of problem is purely technical in nature (e.g. the need for microfluidic systems of low circulating fluid volume, but sufficient tissue volume) and may eventually be solved by steady improvement in techniques and capabilities^2,7,18,21,22. Fundamental problems (e.g. the context-dependent change in cellular BMR), however, can only be addressed by a thoughtful and deliberate design strategy^25–28.

We propose that these challenges themselves only merit concern so far as they affect the end output of the HOC. That is, the structure of a ×10⁻⁶ HOC may assume strange and unexpected forms so long as the function — the cellular- and system-level behavior of the HOC — is accurate and relatable to human physiology. Therefore, discrete parts of an HOC need not necessarily be confined by conventional notions of what constitutes “normal” or “physiologic”. To that end, we focus on designing a ×10⁻⁶ HOC capable of mimicking key functions of a macro human, specifically (1) cellular- and macro-scale BMRs and (2) basic pharmacokinetics. We further demonstrate how naturally-occurring biological systems may stray from structures of typical physiology (e.g. a hemoglobin-free vertebrate), yet produce species capable of adapting and surviving nonetheless. As modification of any particular system parameter necessarily affects all others, both natural and artificial design alterations demand a holistic approach. Applying these general principles, we propose specific design parameters for an HOC that is practical in terms of fluid-to-cell ratios and is a ×10⁻⁶ miniaturization of the human body with regard to total cell mass, yet remains a faithful model of macroscopic human physiology with regards to cellular BMR, basic pharmacokinetics and inter-organ scaling.

2. CONTROL OF CELLULAR BMR

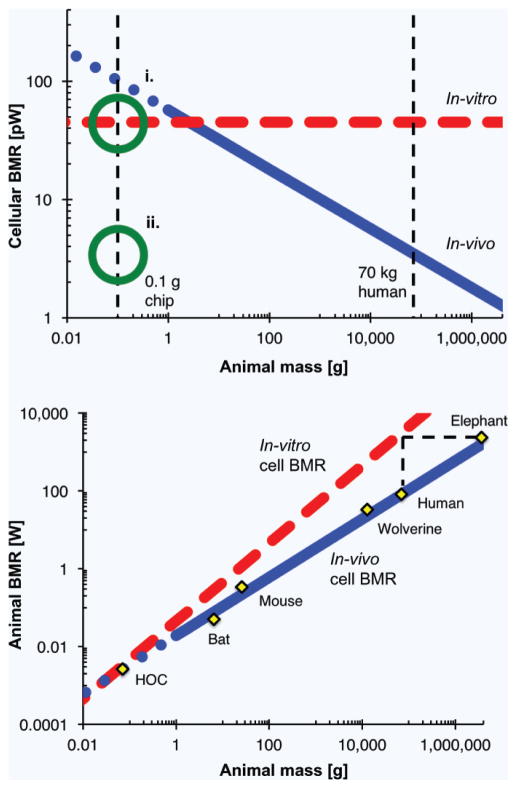
As predicted by QPSRs, cellular metabolic rate scales with animal mass^25,26,28. However, cells cultured in-vitro tend to operate at an elevated metabolic rate regardless of their organism of origin (Fig. 1a)^25,27. Without accounting for this phenomenon, cells in an in-vitro HOC would have a high cellular BMR, more akin to cells in a mouse than in a human. Thus, the system BMR of the animal-on-a-chip diverges from that of the corresponding real animal; the magnitude of the error increases with animal size as ∝^M¼ (Fig. 1b). For example, failure to consider the context-dependent behavior of cells in attempting to design a ×10⁻⁶ model of a human would result in an HOC wherein the cellular BMR is high and thus approximates that of a mouse and the system BMR is also high and approximates that of a ×10⁻⁶ elephant! Because of this non-linearity in scaling (i.e. M raised to a power ≠ 1), rational design — and control — of the metabolic infrastructure of an HOC is crucial. We have previously proposed that designers must force cells in an HOC to function as they would in the macroscopic human body — that is, designers must suppress cellular BMR to match in-vivo levels outlined in Fig. 1a, in a strategy termed metabolically supported scaling²⁴.

Figure 1.

Consequences of context-dependent cellular basal metabolic rate (BMR). (a) Cellular BMR scales as ∝M^−¼ in-vivo but mammalian cells cultured in-vitro have the same cellular BMR regardless of the mass of the source organism (∝M⁰). (a–i) In-vitro cell culture of human cells leads to a cellular BMR ~one order of magnitude larger than that of a normal human^25,27. (a–ii) A high-fidelity, physiologically relevant human-on-a-chip (HOC) should be designed with mechanisms to ensure cellular BMR matches typical in-vivo values for the organism to be modeled. (b) Failure to account for the context-dependent behavior of cells can substantially alter the modeled system BMR, especially for larger animals^25,28. Graphs reproduced using previously published data and relationships^25,28,72.

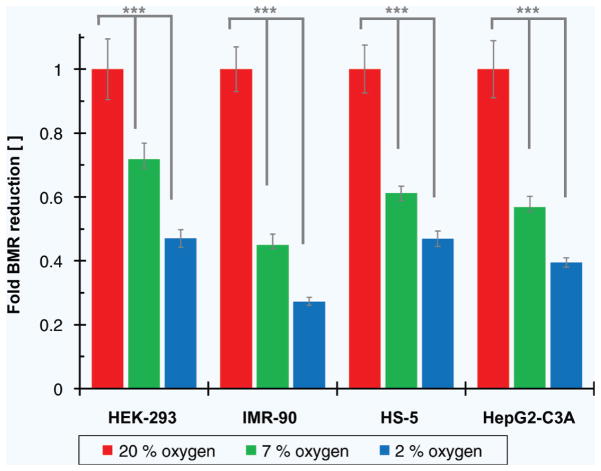
Although others have demonstrated metabolic control by regulating glucose²⁹, ions³⁰, extracellular matrix (ECM) cues³¹ and oxygen²⁴, we propose to limit O₂ availability for the expressed purpose of suppressing cellular BMR and inducing a more in-vivo like response from an HOC. Not only does this approach more closely approximate conditions in the body than the hyperoxic conditions of incubator cell culture, but in-situ microfluidic O₂ sensing and control is an established and active area of research^32–34. To demonstrate that O₂ deprivation is a viable method for controlling cellular metabolic rate, we examine the behavior of human cell lines in atmospheric (20%) and physiotypic (7% and 2%) oxygen environments. Using AlamarBlue as an indicator of cellular respiration, we show that HepG2-C3A, HS-5, IMR-90 and HEK-293 cells all demonstrate significant (p < 0.001) oxygen conformance. A similar effect has been noted by measuring oxygen consumption rather than AlamarBlue reduction as well as predicted numerically^35,36. As oxygen decreases, cellular metabolism follows — at physiotypic oxygen tension, cellular respiration is reduced by nearly fivefold (Fig. 2). Importantly, in no cases did AlamarBlue metabolism drop to zero indicating that, even after four hours culture in each O₂ atmosphere, the cells remained viable. Total cellular BMR is likely to be slightly higher than these measured values since our AlamarBlue indicator fails to respond to the anaerobic ATP production which yields ~10× less energy than aerobic processes.

Figure 2.

AlamarBlue metabolic indicator was used to measure cellular BMR in different oxygen tension environments. Correcting for the effect of oxygen on AlamarBlue fluorescence, we observed a marked decrease in respiration with falling oxygen levels across four different cell lines. A 10-fold reduction in oxygen reduced cellular respiration by a factor of nearly five. Data plotted as average ± standard deviation for n = 7. *** indicates p < 0.001 by one-way ANOVA with Tukey post-test.

Although cellular BMR saw at most a fivefold reduction, compared to the 10× theoretical difference between cells in-vivo and in-vitro (Fig. 1a), these results demonstrate that oxygen deprivation is a viable strategy for reducing cellular BMR to be more in line with “natural” levels. Moreover, the results demonstrate that cells remained viable in pO₂ up to 10× lower than a conventional cell culture incubator (perhaps unsurprising given that such low O₂ levels are part of the in-vivo environment for most cells). While we do not claim that data implies a specific O₂ range for “optimal” cell function, it does, combined with existing theory, suggest a more “in-vivo-like” set of parameters than those used in conventional cell culture. While it is likely that other processes may be affected by this change in cell BMR (e.g. drug metabolism) that is precisely the point, as these changes are likely to more accurately reflect cell behavior in the body. Therefore, in contrast with suggested strategies to create a suitable oxygen-rich blood substitute for use in an HOC^22,23,37, we propose limiting oxygen availability to manipulate cellular BMR²⁴. Combined with other O₂ sensing and control systems^32–34, we may achieve normoxic or (where necessary) hypoxic conditions in-situ to ensure that both cell- and system-level metabolic rates are appropriately scaled to those of a full-size human.

3. AN EXAMPLE OF EXTRA-PHYSIOLOGIC SURVIVAL: THE ICEFISH

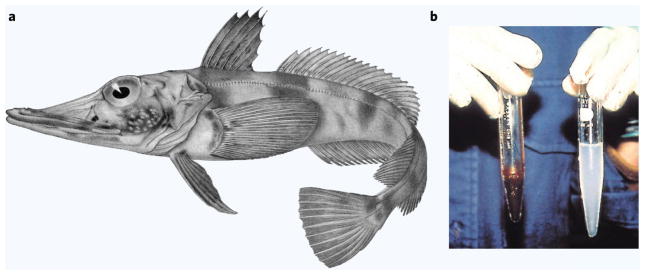
The design modifications proposed in the previous section beg the question of whether such extreme departures from expected physiologic parameter values are acceptable. Would an organism with drastically altered blood O₂ carrying capacity or completely lacking hemoglobin be viable at all? Fortunately, Nature herself has provided a unique example of such extra-physiologic adaptation and survival. The family Channichthyidae (sometimes called ‘icefish’) comprises hemoglobin-negative (Hb−) fish living in the Antarctic waters of the Southern Ocean. First documented in the 1840s, initial attempts to examine the fish were thwarted by an uncooperative cat who absconded with the specimen before it could be further studied³⁸. Subsequent investigations highlighted family members’, including Chaenocephalus aceratus’ (Fig. 3a), startling lack of blood pigment and hemoglobin (Fig. 3b)^39–42. Just as technical and fundamental limitations force HOC designers to contort system parameters in strange or unexpected ways, so too has nature forced C. aceratus to counter its own maladaptation in order to survive.

Figure 3.

(a) Artist’s rendering of C. aceratus, a hemoglobin-free fish living in the Southern Ocean near Antarctica. Used with permission of Regan³⁹. (b) Freshly drawn blood from C. aceratus (right) is milky white while blood from Hb+ N. coriiceps is a familiar shade of red (left). Adapted with permission from Sidell & O’Brien⁴².

To demonstrate, and perhaps learn from, this extra-physiologic survival, we examine the fish in more detail. As a control, we use a cousin of C. aceratus, Notothenia coriiceps (also called neglecta), from the common suborder Notothenioidei⁴³. N. coriiceps shares a similar environment and metabolic rate (measured by oxygen consumption) as C. aceratus^44–46, but unlike the icefish, produces Hb at normal levels. Starting from a healthy N. coriiceps, we remove Hb and then apply the adaptations that allow C. aceratus to thrive: increasing cardiac output by a factor of nearly two and allowing for increased cutaneous respiration^{40,41,44–48}. The result is a test-fish with several surprising extra-physiologic features, but nevertheless capable of survival (Table 1 and Supplementary Information SI1.1). In particular, the ability of C. aceratus to absorb oxygen through its skin evokes polydimethylsiloxane (PDMS) — a common polymer in microfluidic and biomedical research applications that has similar properties of gas permeability (Supplementary Information S1.2).

Table 1.

Physiological values for a hypothetical 1 kg test-fish as hemoglobin (Hb) is removed and icefish characteristics introduced.

Condition imposed on the test-fish	O2 solubility in blood [mg/mL]*	Cardiac output (Q) [mL/h]	Cutaneous respiration [mg O2/h]	Maximum O2 delivery [mg/h]
Normal	0.08540	3,90064	—	330
−Hb	0.009540	3,90064	—	37
−Hb, ↑Q	0.009540	7,14048	—	68
−Hb, ↑Q, +C. Resp.	0.009540	7,14048	1041	78
		N. coriiceps resting VO2 = 42 mg O2/h45,46
		C. aceratus resting VO2 = 32 mg O2/h44–46

^*Measured at 0°C and 101.3 kPa.

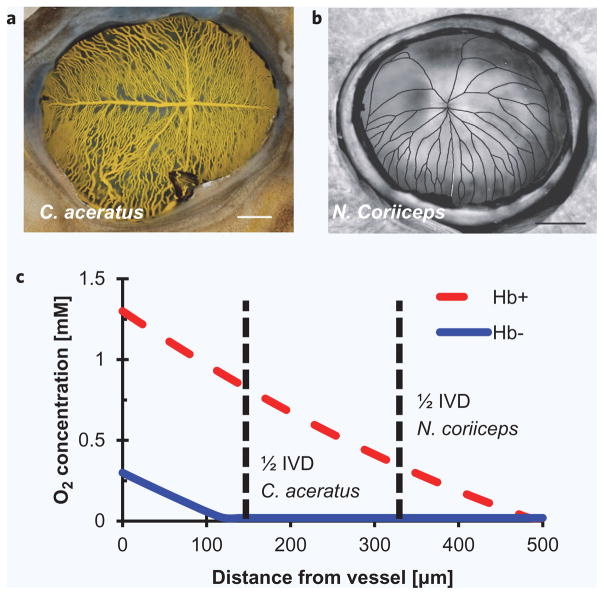
In addition to larger-than-expected cardiac output, C. aceratus also has a blood volume of ~90 mL/kg, nearly twofold greater than the ~50 mL/kg expected for a fish its size^{42,46,49–51}. Another member of Channichthyidae, C. hamatus, has a blood volume over twofold its predicted value⁴⁹. These Hb− fish substantially exceed expected blood volumes yet thrive (Supplementary Information S1.3), reinforcing the idea that extra-normal physiology can be an acceptable mechanism to survive in the face of limitations. Related to that increased blood volume, C. aceratus also exhibits increased capillary density. Recent results demonstrated that three different metrics of vascularization were all ~twofold greater in C. aceratus than in N. coriiceps (Figs. 4a and 4b)⁵². Therefore, even though blood flow rates are double in C. aceratus, so too is organ blood volume, indicating that tissue residence times — a key parameter in PB-PKPD models — should also remain unchanged between it and N. coriiceps.

Figure 4.

O₂ delivery in Notothenioidei. Retinal micrographs of (a) C. aceratus (b) N. co riiceps demonstrate the difference in capillary density and intervessel distance (IVD) between the two fish. Reprinted with permission from Wujcik et al.⁵². (c) These decreased intervessel distances help compensate for blood O₂ levels in C. aceratus. A similar effect should act on other solute (e. growth factors or drugs) diluted by larger blood volumes as well. Equation (1) solved numerically using MatLab and data from Refs. 17, 40, 52 and 53; full list of parameter values can be found in Supplementary Information S1.4.

This increased vascularity also helps compensate for dilution of soluble factors (e.g. O₂, drugs or hormones) due to increased blood volume. At steady state the perfusion-limited diffusion of molecules from blood into tissue is described by Equation (1):

$$D·{\nabla }^{2}C=R,$$ (1)

where C is the concentration, D is the diffusion coefficient and R is the uptake of solute by cells, governed in this case by Michaelis–Menten kinetics^17,53. Although a decrease in blood concentration leads to a decrease in potential gradient to drive diffusion, a corresponding decrease in intervessel distance (IVD) suggests that solute penetration may be similar, shown here specifically for O₂ (Fig. 4c; parameter values in Supplementary Information S1.4). This icefish adaptation is another example of nature finding a holistic, multi-faceted solution to physiologically challenging conditions. Of course, applying designs such as these to an HOC may still introduce problems with drugs or molecules that act in a concentration-dependent manner on the blood vessels themselves as well as other unforeseen consequences. Conversely, these data also suggest that depletion of soluble factors (e.g. oxygen) could be achieved over shorter distances, an important design consideration for engineering organ compartments such as the liver^17,54. Nevertheless, this preliminary analysis demonstrates that blood O₂ carrying capacity and the presence of Hb may be tuned to counter maladaptations — or possibly induce more appropriate cellular metabolic behavior. The icefish further suggests that increased blood volumes may be accommodated without drastically altering organism pharmacokinetics or certain stromal solute concentration gradients.

4. A DISTRIBUTION-INFORMED APPROACH TO HOC BLOOD VOLUME

Designing an HOC according to QPSRs alone would result in a system blood volume of ~6 μL, too small for even cutting-edge microfluidics and an acknowledged problem in the field^{7,18,21,22,24}. Although a 10× (or greater) increase would yield an HOC with a more manageable circulating volume, it would also dilute soluble factors and strain physiology to a much greater extent than the ~twofold increase in volume observed in C. aceratus. Therefore, we adopt a pharmacokinetic approach to investigate whether and to what extent the blood volume of an HOC can be increased while maintaining physiological relevance.

When a drug is administered, only a portion circulates dissolved in the blood. Accordingly, pharmacologists define volume of distribution, V_D, to describe how much drug is available in the plasma compared to the initial dose^55,56. Conceptually, V_D closely resembles a partition coefficient describing the equilibrium distribution of a drug between the body and the blood. Using a slightly different approach, we consider the distribution of a drug between body water — including blood — and tissue. Therefore, this treatment is most applicable to small, perfusion-limited drugs without substantial serum protein binding. This ratio, K, is defined by Equation (2):

$$K=\frac{C_T}{C_W},$$ (2)

where K is the partition or distribution coefficient, C_T is the concentration of drug in body tissue and C_W is the concentration of drug in body water. Ignoring excretion and metabolism and devolving the concentration terms to amount over volume,

$$K=\frac{\raisebox{1ex}{$\left(\mathit{Dose}-X_W\right)$}\!\left/ \!\raisebox{-1ex}{$V_T$}\right.}{\raisebox{1ex}{$X_W$}\!\left/ \!\raisebox{-1ex}{$V_W$}\right.},$$ (3)

where Dose is the total amount of drug in the system, X_W is the amount of drug in the body water, V_T is the tissue volume and V_W is the volume of body water. Assuming no difference in concentration of drug in body water and concentration of drug in blood (C_B) and introducing V_O for non-blood body water volume (i.e. V_W = V_B + V_O), we rearrange to obtain Equation (5):

$$K+\frac{X_W·V_W}{V_T·X_W}=\frac{\mathit{Dose}}{V_T·C_B},\text{and}$$ (4)

$$C_B=\frac{\mathit{Dose}}{\left(V_O+V_B\right)+K·V_T}.$$ (5)

If we apply an arbitrary Z-fold increase to the blood volume compartment and normalize the result to the Z = 1 condition, C_B0, Equation (6) follows:

$$\raisebox{1ex}{$C_B$}\!\left/ \!\raisebox{-1ex}{$C_{B0}$}\right.=\frac{\left(V_o+V_B\right)+K·V_T}{\left(V_o+Z·V_B\right)+K·V_T}.$$ (6)

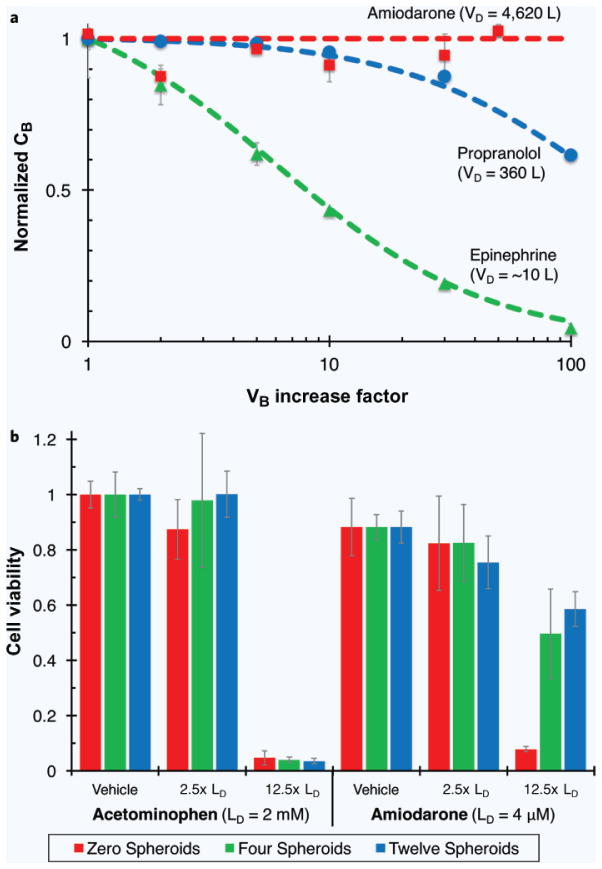
In general, C_B falls as 1/Z. However, the partitioning properties of the drug and the fact that V_B is a small fraction of the total system water volume serve to substantially temper the effect of increasing Z on blood concentration (Supplementary Information S2). For example, this treatment suggests that a highly hydrophilic drug, epinephrine, can tolerate ~10× increase in blood volume with only a ~twofold change in blood concentration. More hydrophobic drugs, such as amiodarone, are predicted to show almost no change in blood level at higher values of Z, and would require ~10⁶ increase in blood volume to approach that same two-fold dilution.

To test these predictions, we construct a simple model of the body mimicking the two-compartment structure of our theoretical treatment. The water compartment, including variable blood volume, is represented by phosphate buffered saline and tissue is represented by an organic liquid (here, 1-octanol). The concentration of three small-molecule drugs — epinephrine, propranolol and amiodarone — was measured and normalized to the Z = 1 condition. The data (mean ± S.D.), along with curves representing the values predicted by Equation (6) are plotted in Fig. 5a. All three cases show reasonable agreement between predicted and experimental values. For scenarios where even these small dilutions are unacceptable, or in instances where the preceding treatment does not apply, other pharmacokinetic-based approaches may be useful, especially if PDMS or another gas-permeable material is used to decouple O₂ delivery from blood flow rate (Supplementary Information S3).

Figure 5.

Altering aqueous to organic volume proportions affects concentration and toxicity of various drugs. (a) Increased blood volumes minimally effect blood concentration depending on drug properties for perfusion-limited drugs according to Equation (6). Hydrophobic drugs (e.g. amiodarone) partition mostly to tissue and blood concentration is largely unaffected by changes in blood volume. More hydrophilic drugs (e.g. epinephrine) partition largely to the blood and are more affected by large changes in blood volume. (b) In a live-cell experiment, increasing mass of the organic phase (i.e. addition of more adipospheroids) rescues HepG2-C3A liver cells from toxicity of a hydrophobic drug (Amiodarone, lethal dose 4 μM), but not a hydrophilic drug (acetaminophen, lethal dose 2 mM). Data plotted as average ± S.D. for n = 7.

*** indicates p < 0.001 by two-way ANOVA with Tukey post-test.

To illustrate this concept another way, we hold the aqueous phase constant, vary the mass presence of an organic depot (here represented by adipose spheroids instead of octanol) and assay for health of a HepG2 liver cell monolayer in the presence of differing concentrations of hydrophobic (amiodarone; V_D = 4,260 L for a 70-kg man) and hydrophilic (acetaminophen; V_D = 66.5 L) drugs. According to Equation (6), the high value of K for a hydrophobic compound amplifies the effects of increasing organic phase mass, leading to substantial protection of the HepG2 monolayer even at >10× the lethal concentration of amiodarone; the same changes in the face of increasing acetaminophen dosing shows no such effect (Fig. 5b). Combined with the theoretical treatment developed here for solutes of varying hydrophobicity in aqueous and organic phases of varying volume, these results demonstrate that HOC designers may be able to systematically predict the effects of changing system fluid volumes and therefore compensate for such changes in their experimental design.

5. HOC DESIGN

5.1 Organ compartment design strategy

To design each organ compartment, we build on metabolically supported functional scaling (MSFS) strategies proposed previously, as well as other, similar, schemes^22,24,57. The specific approach of Moraes et al. classifies organs according to principle function: two-dimensional (F-2D) or membranous tissue (e.g. lung) is scaled by surface area while functionally three-dimensional (F-3D) or lobular tissue (e.g. adipose) is scaled by volume²⁴. Since this approach relies on principles of Euclidian geometry, it avoids inconsistencies that appear when empirical laws are extrapolated outside the range of the original dataset — a key problem for applying empirical, allometric organ–organism size relationships to HOC design^22,23. Design parameters for F-2D organs are achieved by scaling according to surface area and compartment size is selected to match fluidic shear values found in-vivo for each tissue. F-3D organs are simply scaled by mass. For more complicated organs that may be classified as both F-2D and F-3D (e.g. liver), we used a two-compartment approach: one section with high surface area and another with high mass that together approach the appropriate values (Table 2). Spheroids and other tissue aggregation strategies may be particularly useful in these cases (Supplementary Information S4).

Table 2.

Design strategy for different HOC organ compartment classes defined by metabolically supported functional scaling (MSFS) theory.

HOC organ compartment class	Tissue size	Blood volume
F-2D	Surface area constrained, ∝M1 scaling from macro human	Dimensions selected to maintain physiologic shear given fractional cardiac output
F-3D	Volume constrained, ∝M1 scaling from macro human	Calculated so that organ blood volume matches target fractional organ mass of whole body
F-2.5D	Divided into F-2D and F-3D domains with each domain scaled per F-2D or F-3D design rules

The endothelium presents another special case. Since several sources estimate the endothelial surface area of the body at 1,000 m² or greater^58–60, including the whole of the endothelium in this HOC would be an impossible undertaking. Since the endothelium mainly acts in concert with its associated organ rather than as a distinct entity, we include only endothelial tissue from organs already represented in this model (lung and liver). These tissues serve to recapitulate endothelial cell function within the organs included in this design and also provide a readout for general endothelial “health” across the HOC.

In addition to the organs explicitly included in this HOC design, we must also account for the body volume not represented by any of the designated organ compartments. Including a blank “other organs” zone to represent implied (but absent) organs ensures that our total system mass will be commensurate with that of a macro version and other groups have included “missing organ formulators” and “other tissues” compartments to similar ends^19,20,22,24. Importantly, since we justify a substantially increased blood volume based in part on a volume distribution-based treatment that considers the entire body volume, it is critical that volume be faithfully replicated in our model system.

5.2 Overall design parameters

The insights provided by our examinations of metabolic scaling, C. aceratus’ unique physiology, and volume of distribution considerations indicate that we need not be confined by preconceived notions of what is or is not “physiologic” in designing an HOC. Instead, it is the ultimate response — the function — of the HOC and not the underlying structure that is paramount. Specifically:

1. Without additional controls, on-chip cellular BMR will exceed in-vivo levels and cause a fundamental mismatch between the model system and reality. We propose limiting oxygen delivery as one effective mechanism for controlling cellular BMR.

2. Lack of Hb or an Hb substitute does not doom a vertebrate organism (or an HOC) ex ante. In fact, by introducing systemic redundancies and extra-normal physiologic values nature has, and engineers may, successfully addressed such anomalies.

3. Blood volume increases are necessary to address technical limitations of current tissue engineering and microfabrication techniques. A distribution-based treatment of supra-physiologic blood volumes and the example of the icefish indicate that designers have some latitude in determining HOC blood volume, especially for perfusion-limited drugs.

It is necessary to note here that increasing blood volume is not at odds with our proposal to limit oxygen supply. Since Henry’s law dictates that the concentration of gas dissolved in a liquid is proportional to the partial pressure of that gas in the atmosphere and (as Fig. 2 demonstrates) cell consume oxygen in a concentration dependent manner, the overall blood volume should have little bearing on the matter in an oxygen controlled environment. If, rather than controlling the pO₂ of the culture atmosphere, a researcher sought to generate low O₂ by balancing gas exchange, consumption and flow⁶¹, then changing blood volume may indeed necessitate a careful balance of various parameters (e.g. flow, volume, cellular O₂ consumption and media oxygen concentration).

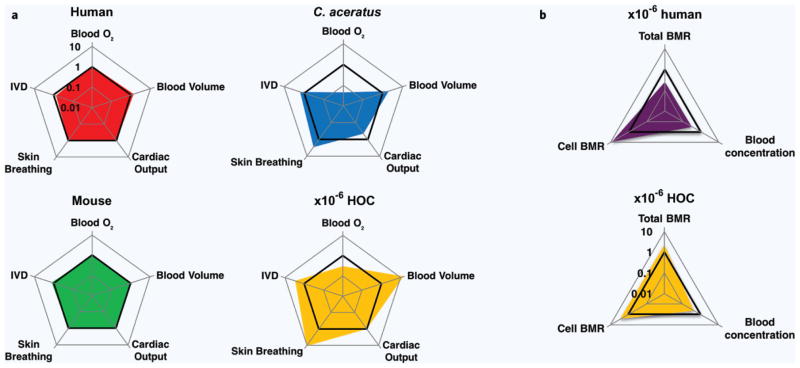
Finally, we formalize a complete set of design parameters for a lung, liver, endothelium, fat, and heart ×10⁻⁶ HOC (Table 3, other tables and comparisons in Supplementary Information S5, Supplementary Tables 3–6) that follows the design principles laid out here. We further compare relevant design criteria of this more practical ×10⁻⁶ HOC to C. aceratus, a standard human, and a mouse (Fig. 6a). Values for this five-parameter comparison across blood oxygen content (blood O₂), intervessel distance (IVD), skin gas exchange, cardiac output and blood volume were drawn from many sources and normalized against values predicted by QPSRs^{17,23,40,46,48,49,51,52,62–72}. For details, see Supplementary Information S6 and Supplementary Tables 7 and 8. Another set of charts predicting behavior based on these parameters is calculated and shown in (Fig. 6b), demonstrating the superiority of our holistic design strategy over an unmodified approach.

Table 3.

A comprehensive table of design parameters for a five-organ ×10⁻⁶ HOC. We propose increasing blood volume levels beyond those called for by conventional quarter-power scaling relationships (QPSRs) to account for engineering limitations in organ design. Chamber dimensions are selected to match in-vivo shear levels (F-2D) or match in-vivo mass (F-3D).

Organ		Class	×10−6 HOC
			Surface area [mm2]	Tissue mass [mg]	Blood volume (BV) [μL]	% BV	% CO	Compartment dimension
								Length [mm]	Width [mm]	Height [mm]
Lung	Endothelium	F-2D	30	0.12	1.1	—	—	—	—	—
	Non-EC	F-2D	40	0.16	1.4	—	—	—	—	—
	Total	F-2D	70	0.28	2.5	4	100	9.02	7.76	0.035
Liver	Endothelium	F-2D	80	0.32	2	—	—	14.87	5.38	0.025
	Non-EC	F-3D	34	1.75	1.03	—	—	1.57	1.57	1
	Total	F-2/3D	114	2.07	3.03	5	25	—	—	—
Heart		F-3D	—	0.33	0.28	0.5	4	1.06	1.06	0.5
Fat		F-3D	—	12.5	10.7	18	5	4.96	4.96	1
Blood		—	—	—	60	—	—	—	—	—
“Other Tissues”		F-3D	—	48.8	43.5	73	66	6.6	6.6	1
Blood Oxygen Content [BLO2; mM]						~2
Cutaneous Respiration [mol/m/s/mmHg]						≤3.8 × 10−11
Cardiac Output [mL/s]						3.4 × 10−3
Intervessel Distance [IVD; μm]						250

Figure 6.

Design and performance of natural and artificial physiological systems. (a) Radar charts comparing design parameter values for a human, a mouse, the Hb− icefish C. Aceratus, and a ×10⁻⁶ miniaturized HOC. Values plotted on a log scale and normalized to QPSR estimates for all graphs. Note that observed values for the mouse and human match QPSR estimates (bold lines) closely while the general shape of the charts for C. Aceratus and the HOC have similar shapes. A ×10⁻⁶ human designed only according to QPSRs would lie exactly along the bolded line representing a normalized value of 1. Without additional controls, this ×10⁻⁶ model would have abnormally high per cell and system metabolism. (b) Applying the modifications proposed here to build a ×10⁻⁶ HOC is predicted to lead to a more accurate model of the human body measured across three key functional parameters. Compared to an QPSR-scaled ×10⁻⁶ human with a minimum blood volume limited by technical challenges (top) and despite straying from conventional parameters, our design strategy yields a ×10⁻⁶ HOC (bottom) that more closely matches human levels of cellular BMR, system BMR and blood concentration of a low volume distribution drug (e.g. epinephrine). Computed using data from Refs. 17, 23, 40, 46, 48, 49, 51, 52, 62–72.

Inspired by the example of C. aceratus and motivated to suppress cellular BMR to physiologic levels (and to avoid the challenges inherent in developing a synthetic substitute), we have deliberately excluded Hb from this HOC design in order to restrict oxygen availability and limit cellular BMR. However, Hb also plays a key role in transporting carbon dioxide away from metabolically active tissues — carrying up to 30% of the CO₂ transported in blood⁷⁰. In this HOC design, we justify ignoring these effects because CO₂ transport can occur by other means. At 35°C, PDMS is nearly five times more permeable to carbon dioxide than oxygen⁷³. Similarly, the solubility of CO₂ and NO (nitrous oxide, an important signaling molecule) in water are both orders of magnitude greater than O₂74–76. Beyond oxygen transport, Hb plays important roles in other aspects of physiology including NO catalysis⁷⁰. Depending on the specific application, each function may need to be explicitly accounted for in HOC design.

For this (or any) HOC system to be accepted as a microphysiological model of the body, some method of validating the underlying design strategy is necessary. Although directly testing such a system against humans may be challenging, we can apply the same design criteria outlined here to build rats-, mice-, etc.-on-a-chip. Parallel studies comparing the response of the microphysiological model system to the genuine animal will provide information on areas where HOCs may be particularly well- (or ill-)suited to serve as a complimentary research tool. A second approach may be to test whether an HOC is able to maintain key homeostatic parameters (e.g. blood glucose level) in the face of a reasonable challenge (e.g. bolus injection of glucose). In and of themselves, these experiments may also yield new mechanistic insights into previously unexplored aspects of common biomedical research models.

6. CONCLUSION

This work makes several key assumptions that should be verified, or at least noted, in further research. Although the section on ‘Control of Cellular BMR’ makes clear that we may indeed induce a more in-vivo-like BMR in cells by controlling the concentration of oxygen available in culture, this is not the only criterion necessary for success. Many other factors including ECM support and cell–cell interaction, and likely some yet to be discovered factors, also drive in-vivo-like phenotypes and must be carefully considered as part of any HOC effort. Furthermore, for the treatment of the proposed distribution-informed approach to HOC blood volume to be valid, experimentalists must know, or at least be able to suspect, the chemical properties of all drugs, metabolites and other molecules of interest within a system. To be exhaustive within a generalized experimental model, it may be necessary for researchers to use iterative processes, where a system is screened for compounds of interest then tuned accordingly and rescreened. Finally, the F-2D and F-3D classification proposed for HOC designs is likely too simplistic. While some organs fall readily into one category or the other, the truth is that most all organs behave somewhat like the liver — each has critical dependencies on both surface area and volume. To most accurately represent this reality, engineered, organ-specific on-chip systems would ideally represent organ compartment. However, in many cases constraints on resources and/or complexity will mean that F-2D and F-3D idealizations are sufficient in most instances.

Quarter power scaling relationships are both empirically and theoretically supported and provide guidance for sizing physiologic parameters in the face of changing system size. Their application to the development of microphysiological models of the body or “HOCs” however introduces both fundamental and technical challenges which currently frustrate efforts at design and construction of a relevant, feasible system. We posit that HOC designers may avoid these issues by selecting parameters outside the realm of what is considered physiologic so long as the ultimate function of the system is preserved. Since cell behavior is context dependent, suppressing cellular BMR on-chip to mimic in-vivo levels is crucial to designing a physiologically relevant HOC. We observe O₂-dependent decreases in cell metabolism across four different cell types to demonstrate the feasibility of this approach. We use a natural experiment, the icefish, to conceptually justify this approach and demonstrate how extra-physiologic parameters may interact to give a normal physiologic response. Further study of an HOC system through a distribution-informed treatment of blood concentration of small-molecule drugs indicates that we may indeed increase HOC blood volumes with only minor consequences. In cases where even that is unacceptable, we provide frameworks to estimate the magnitude of and/or mitigate the error. Integrating these lessons in the design of a liver–lung–heart–fat–blood system, we propose a complete set of design parameters for a ×10⁻⁶ miniaturized HOC system. This work forms a basis of a nature-inspired approach to govern the design of in-vitro model systems.

7. METHODS

7.1 Oxygen conformance and cellular BMR suppression

All cell lines were obtained from ATCC and cultured in Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% Fetal Bovine Serum (FBS) and 1% antibiotic/antimycotic (anti/anti). The day before the experiment, cells were seeded in 96-well plates at 25,000 cells/well and allowed to adhere overnight. OxyCycler atmosphere control chambers (BioSphyrix, New York) were set to 2% and 7% oxygen, both with 5% CO₂. The day of the experiment, media was changed to DMEM and anti/anti without FBS and one plate was placed in each oxycycler chamber, as well as a third plate in a standard cell culture incubator (20% O₂ and 5% CO₂) and allowed to equilibrate for four hours. At that point, the media was changed again and replaced with DMEM, anti/anti and AlamarBlue metabolic indicator (Invitrogen). After a two-hour incubation, the level of reduced AlamarBlue was measured using a fluorescent plate reader (BioTek Synergy Neo) at 560/590 nm (excitation/emission).

AlamarBlue indicates cell metabolic activity by serving as an oxidizing agent during aerobic respiration, competing with oxygen for electrons at the end of the electron transport chain^70,77. Changing oxygen levels, therefore, affect the frequency at which AlamarBlue is reduced and therefore the levels of fluorescence observed across each cell culture plate at the end of the experiment. To correct for this effect, we use Equation (7) to estimate cellular metabolic activity in the face of changing oxygen level:

$$\mathit{Cellular}\mathit{BMR}=A{B}_{\mathit{Red}}·\frac{\mathrm{\Delta }{P}_{AB}+X·\mathrm{\Delta }{P}_{O2}}{\mathrm{\Delta }{P}_{AB}},$$ (7)

where Cellular BMR is the corrected, unitless cellular metabolic rate measured by AlamarBlue, AB_Red is the fluorescent measurement from the assay, ΔP_AB is the difference in reduction potential between AlamarBlue and cytochrome C, the ultimate reducing agent of oxygen in aerobic respiration, X is the fractional reduction of oxygen tension compared to a 20% O₂ atmosphere (typical for a laboratory cell culture incubator) and ΔP_O2 is the difference in reduction potential between O₂ and cytochrome C. Using standard values to calculate ΔP⁷⁷, we can generate a corrected cellular BMR. We may use this unitless metric to compare relative cellular BMRs and to demonstrate the effect of oxygen tension on cellular metabolic activity. Two caveats must apply to this analysis, however. First, the cellular BMR values compared here are aerobic only; we make no effort to measure energy derived from fermentation. As respiration is an order of magnitude more efficient, any error introduced by this approach is likely to be sufficiently small. Second, while these cellular BMRs are purely relative measurements, one may theoretically use a series of calibration experiments to arrive at a set of absolute measurements for cellular metabolic rates.

7.2 Distribution-informed approach to HOC blood volumes

To test the theoretical predictions of Equation (6) regarding the behavior of small-molecule drugs in the face of changing blood volumes, we constructed a crude, ×10⁻⁵ “pharmacokinetics-in-a-tube” system. A glass vial containing 280 μL of 1-octanol (Sigma) was used to model the tissue volume of a ×10⁻⁵ human and 360 μL of pH 7.4 phosphate-buffered saline (PBS, Life Technologies) represented the non-blood body water volume^55,56. A variable amount of PBS was used to represent Z = 1, 2, 5, 10, 30, 50 and 100 conditions, where Z = 1 corresponded to a blood volume of 60 μL. The relevant drug was added to the vial, agitated, and allowed to equilibrate for ~two hours in a 5% CO₂ incubator at 37°C. After ~two hours, the organic and aqueous phases were well separated and the appropriate phase was sampled and analyzed. Each condition was performed in triplicate. For epinephrine (Sigma), a total dose of 100 μg/vial was used and the lower (aqueous) phase was sampled. Epinephrine levels were detected by an Acquity UPLC system (Waters) with a reverse-phase C18 column (Waters) and a UV-vis detector measuring absorbance at 210 nm. The mobile phase was 99% 20 mM NaH₂PO₄ at pH 2.5 and 1% MeOH. For propranolol, a total dose of 1 mg/vial was used and the aqueous phase was sampled. Propranolol (Sigma) levels were detected on a Synergy plate reader (BioTek) by reading fluorescence at 289/353 nm. For amiodarone (Sigma), the total dose/vial was 0.56 mg and the upper (organic) phase was sampled. Amiodarone levels were detected by fluorescence at 388/475 nm.

To investigate the implications of changing organic phase mass on a living system, we used a liver-adipospheroid co-culture platform. 3T3-L1 preadipocytes were expanded and differentiated into adipose tissues in 3D spheroid culture as described previously with 8,000 cells per spheroid²⁴. HepG2-C3A liver cells were seeded in a clear bottom, black-wall 96-well plate (Corning Costar) at a density of 10,000 cells/well and given six hours to attach. After adipose spheroid differentiation, the spheroids were collected from the hanging drop plate and added to the 2D liver cell culture (0, 4 or 12 per well) in 30 μL of media volume. Amiodarone (dissolved in DMSO) and acetaminophen were then added to the culture wells and incubated for 24 hours. After the incubation period, media and spheroids were aspirated and the HepG2-C3A monolayer was washed once gently and AlamarBlue indicator was added. HepG2 viability was measured by taking a fluorescence reading at 560/590 (ex/em) after two hours. Data was analyzed using two-way ANOVA with Tukey’s post-test.