Work-Education Mismatch: An Endogenous Theory of Professionalization

Abstract

We model the education-workforce pipeline and offer an endogenous theory of professionalization and ever-higher degree attainment. We introduce two mechanisms that act on the education enterprise, causing the number of educated people to increase dramatically with relatively short-term changes in the job market. Using our illustrative dynamic model, we argue that the system is susceptible to small changes and the introduced self-driving growth engines are adequate to over-incentivize degree attainment. We also show that the mechanisms magnify effects of short-term recessions or technological changes, and create long-term waves of mismatch between workforce and jobs. The implication of the theory is degree inflation, magnified pressures on those with lower degrees, underemployment, and job market mismatch and inefficiency.

1. Introduction

Can we claim that the education industry is now providing a more effective and efficient service to the entire population of K-Graduate School students? At least across the developed world, educational attainment levels have been increasing continually. By comparing the education levels of different age groups, we see a clear indication of the growing trends. In 2011, 82% of the 25–34 age group of OECD countries had completed upper secondary education or higher, compared to 64% of the 55–64 age group (OECD, 2013). This trend continues into tertiary education, where in 2011 some 39% of the 25–34 age group had completed tertiary education, compared to 24% of the 55–64 age group (OECD, 2013). The increasing trend has even gone above the PhD level, and now years of postdoctoral work are becoming commonplace for many newly minted PhDs. The number of postdocs in U.S. institutions has more than tripled in the past 30 years (National Science Foundation, 2011). The demand for higher education has also increased, as shown in the number of applications for graduate programs in U.S. universities: a rise from 955,000 applicants for graduate programs in 1991 to 1.768 million in 2010 (FASEB, 2012). The overall trend is the growth of degree attainment.

The growth in higher education is in line with educational policies in developed countries. Governments have increasingly encouraged the pursuit of education to spur economic growth, raise productivity, and increase innovation and the general wellbeing of society (Te Riele & Crump, 2003). However, these policies include several inherent assumptions about the demand for more educated workers and the education industry. In fact, there is evidence for the opposite: inefficiency in labor markets and education systems.

Take the STEM (Science, Technology, Engineering, and Math) workforce as an example. On the one hand, there have been arguments claiming a shortage of STEM workers in the United States; evidence of this shortage includes the higher salaries and benefits for STEM professionals. The arguments have prompted various government initiatives to incentivize foreign workforce immigration (U.S. House of Representatives, 2012). On the other hand, many STEM graduates have difficulty finding jobs that match their training, and there is an abundant supply of STEM PhD graduates who cannot land academic positions (Larson et al., 2014; Ghaffarzadegan et al., 2015). Xue and Larson (2015) point to variation of the problem across STEM fields. While many PhD graduates decide to take postdoc positions and wait in the “postdoc queue” until finding permanent tenure-track academic positions, eventually, only about 15% of them succeed (Andalib et al., 2016).

Educational attainment and general job market needs do not appear to be closely matched. Many people are employed for jobs that do not require the level of education they attained: college graduates performing jobs that do not require a Bachelor’s degree, or PhD graduates taking master’s-level jobs, and postdoctoral work becoming a common practice for getting an academic position (Battu and Sloane, 2000). With the U.S. national student debt growing to $1.2 trillion and two thirds of U.S. college graduates leaving school with some level of debt (an average borrower will graduate with $26,600 in debt), there remains a puzzle regarding the incentives and mechanisms behind increasing degree attainment (Chopra, 2013; Institute for College Access and Success, 2012). These patterns make us doubt whether the efficiency and effectiveness of the education sector are truly increasing, and raise a question: What are the drivers of increased degree acquisition?

This paper offers a dynamic theory of educational attainment and inefficiency in education systems. We develop an operational model of the workforce pipeline to represent flow of people through different levels of education and degree credentials, and conduct simulation-based analyses to explain how degree attainment can get triggered endogenously and how the supply of a highly degreed workforce may not necessarily follow market demand.

2. Background

2.1. Complexities and Mismatch in STEM workforce

The growth in education might be explained by technological advancements, changes in net-economic return of education, or signaling theories of education, among other socio-economic theories of education policy and labor economics. Let’s start with technology; ideally, the trend toward increased educational attainment in the workforce should be linked to demand for a more educated workforce due to an increasingly complex technological world. Let us take Moore’s law (Moore, 1965) as a description of technological growth: Moore’s Law says, roughly, that the power of computers doubles approximately every two years. This law has been operating at least since 1958, indicating 29 doublings of computers’ abilities. If there is such a rapid growth in technological capabilities, one might conclude that complexities of production lines and factories that produce such devices should increase at the same pace and so too should the need for a more highly educated workforce. Put simply, new technological advancements require a more educated workforce. This argument implies that higher degree attainment is a rational response to such a need.

Such a technology driven hypothesis succeeds in explaining why there should be a growth in degree attainment; the growth is a rational response to market needs and should help a better match between market needs and supply of the workforce. However, the existing mismatches in the job market indicate an inefficient education and degree attainment system or marketplace. There is evidence that workers are hired into jobs that do not require their current educational credentials. Vedder et al. (2013) estimate that about half of employed college graduates are in jobs that require less than a four-year college education; of these, about 5 million are in jobs that do not require even a high school education. They report that more than 14 percent of waiters, bartenders, and counter and sales clerks hold college degrees. The exogenous theory does not explain these patterns. In 2010, the Bureau of Labor Statistics (BLS) reported that there are 28.6 million jobs requiring a college degree, but at the same time the number of people with a bachelor’s degree and higher in the workforce was around 43.8 million (Bureau of Labor Statistics, 2013b). Figure 1 shows the increasing gap over the past two decades between the number of employed people with bachelor’s degree and the number of jobs that require such degrees. Were the rise in degree attainment a response to the need in labor force and growth in technological capability, one would expect more educational training to lead to a better match between supply and demand of degrees.

Figure 1.

Increasing gap in the employment levels of bachelor’s degree holders or higher in the civilian labor force compared with the employment opportunities requiring bachelor’s degree or higher between 1994 and 2010 (Source: Bureau of Labor Statistics 2010, 2013a).

Net economic return of education is also a potential reason for the growth in education. A common and robust finding in economic studies of education is that there is simply a positive relation between education and earning (Card 1999). Thus, one can expect to see more incentives for pursuing higher education if the net return of attaining a degree increases. Also, at a policy-level, education is known to be one of the best investments in developing countries (Psacharopoulos, 1994). Given the economic growth and increasing capacities of developing countries, and the decreasing costs of education in home-countries, the positive trends in education investment are not a surprise. The increasing economic return of education can explain the growth in degree attainment but cannot necessarily explain the mismatch between education and job requirements. Given the increasing trend of education costs (e.g., inflation-adjusted university tuition in US has almost doubled in the past 20 years (United State Department of Education, 2015)), the benefits of education would have to increase commensurately to justify the inflated costs of education.

Another explanation for incentives for education comes from the signaling theory of education (Spence 1973). The main logic in the theory is that hiring is a kind of investment under uncertainties, and with more uncertainties about individuals’ skills, education can play a role by showing a person’s capabilities. People with higher education (an observable signal) also have higher skills (initially, difficult to observe for employers). In simple words, more degrees equal more skills. The theory is rooted in the asymmetric nature of information about employees’ skills and the fact that employers face lots of uncertainties in assessing job applicant, thus they rely on their educational degrees. In return, higher skilled individuals get more education to be more competitive in the market. The inherent assumption in this argument is that education is less costly for skilled individuals.¹ Empirical evidence suggests that even in a constant level of skill, education can provide a positive signal (Tyler et al. 2000). The signal theories of education, however, don’t explain why the mismatch between education and works has been growing overtime. While in 1970, less than 1% of taxi drivers and 2% of firefighters had college degrees, now more than 15% have college credentials in both jobs (Vedder et al., 2013). This can contradict the Bayesian updating process which is assumed in most signaling literature, that is, an employer eventually learns the actual value of a degree.

In all these explanations, a factor from outside of the education system influences growth in degree attainment.

2.2. Methodological Foundation of Our Theory

In this paper, we provide a different theory, an endogenous theory, to characterize the situation. Our approach is in line with a group of operational research studies that develop simple stylized models for the purpose of theory building with stress on feedback loops as sources of complexities. Specifically, consistent with many operational research models, the foundation of our model is a representation of the physics of the system (flow of population through the pipeline of education and workforce) which we combine with behavioral feedback loops that influence individuals’ decision making stressed in the system dynamics school of thought (Forrester 1961, Lane 1999, Sterman 2000).

Richardson (2011) reviews the history of system dynamics reflecting on his past thirty years of experience and seminal articles of Forrester, and concludes that the foundation of the approach is the “endogenous perspective”, the perspective that became more apparent as the field grew and more models were applied to policy studies. This is the central theme in our theory which differentiates it with many other studies, especially econometric models, in the domain of higher education policy. We also utilize simulation and experimentation to develop coherency within the theory, and offer a platform for future empirical studies.

2.3. Other Endogenous Theories of Education

There are several feedback-rich models in the domain of education. Kennedy (2011) provides a comprehensive review of system dynamics models of educational policy issues and classifies them based on their areas of concern and levels of analysis (national, regional, university, and K-12). Based on his taxonomy, the majority of the models are models of organizational level dynamics developed to improve management level decisions at universities such as planning and budgeting decisions. An exception is Mashayekhi’s (1977) policy model of education growth which focuses on developing countries. His model shows that education systems in developing countries can depict cyclic behaviors if the planners focus on the production sector without paying careful attention to syncing education and production.

Several recent systems models of education have focused on the growing trends in the population of scientists in developed countries (Larson et al. 2014; Ghaffarzadegan et al., 2015; 2017). These models have been pointing to what is referred to as the “systemic flaws” and “structural disequilibria”, particularly, in US biomedical sciences (Teitelbaum, 2008; Alberts et al., 2014). The main mechanism behind these models is the “birth rate” in academia: professors creating PhD students, a portion of which will become future professors (Ghaffarzadegan et al., 2015). Larson et al. (2014) point out that, if we assume the number of faculty positions is constant, in aggregate, each PhD graduate can replace his/her advisor, sooner or later. Since, on average, each faculty member is graduating much more than one PhD student (in engineering, about 7.8 PhD graduates per faculty member) a considerable portion of the graduates end up not finding a tenure-track position in academia.

Other models have looked at research funding fluctuations (Larson et al., 2012), effects of change in retirement age (Larson and Gomez, 2012), and effects of change in postdoc period (Ghaffarzadegan et al., 2014) on the science community. Overall, these models share the insights that the higher education and research enterprises are complex systems which often react unpredictably to change in policies (e.g., Hur et al., 2015; Vakili et al., 2015).

The main difference between our model and past feedback-rich education models is related to the purpose of the model; ours is specifically developed to offer an explanation for the work-education mismatch problem, beyond what is usually offered in the exogenous explanations.

3. The Endogenous Theory

We discuss briefly the theory of endogenous growth in degree attainment, and describe two major mechanisms that are rooted in the education system and lead to the growth in degree attainment.

Mechanism 1: Pipeline Cascading Effect

It is no surprise that many popular charts and analyses show that obtaining a university degree boosts the chances of getting a job. In the United States, there is significant evidence that unemployment is more prevalent for those with lower skills, education, and experience. Looking at data from the 2008 recession, college graduates were the only employment group that had more people employed in April 2013 than when the recession began. However, over the same time period, the majority of the jobs created were low-skilled and low-wage jobs in food and retail services (Rampell 2013). This suggests that bachelor’s degree holders had a competitive edge over their less-educated peers and that employers were hiring college graduates for jobs that did not require college-level skills.

If we assume, holding everything else constant (such as salary), there is a preference for hiring more educated people, an important mechanism emerges which magnifies unemployment rates for lower educated people. Suppose there are n steps of educational attainment. Let’s divide the workforce population to n subpopulations based on their latest degree attainment. Suppose each of the n layers has X=10% more qualified people than available jobs, and for simplicity suppose that the same number of jobs are available at each level. Then, at top level n, all jobs are filled by the top qualified, and the remaining top qualified people take 10% of the jobs at level n–1. That leaves only 90% of n–1 level jobs for the people qualified directly for these jobs. So, all of these 90% are taken by level n–1 people, who also take 20% of the n–2 level jobs. The level n–2 people take all 80% of their available jobs but an additional 30% take level n–3 jobs, and so on and so on. In this simple example, the entire mechanism results in a snowballing, reinforcing cascade, pushing otherwise qualified individuals into lower and lower job categories, as evidenced by Battu and Sloane (2000). In response, we obtain a feedback loop with considerable incentive to move up the education ladder and attain higher degrees.

The entire push-down and then feedback-up processes, which we label as “the cascading effect,” may result from certification and not from job qualifications per se.

Mechanism 2: Pipeline Reinforcing Effect

Education costs have been continually growing and academic institutions have tried various strategies to protect their institutions financially. Greater revenues can be achieved by increasing tuition and admitting more students. Between 1967 and 2010, the total undergraduate enrollment in degree-granting institutions tripled from 6 million to 18 million (Snyder and Dillow, 2012). More students require a larger teaching workforce, and the abundant supply of PhD students and graduates give universities the opportunity to hire them into temporary teaching positions at lower costs. Thus, while the full-time-equivalent (FTE) student-to-faculty ratio hovered around 16:1 between 1976 and 2009 (Snyder and Dillow, 2012) the share of part-time faculty (adjuncts) increased from around 24% to 42% over approximately the same period (Curtis and Thornton, 2013). Meanwhile, tenured and tenure-track faculty dropped from around 45% of instructional staff to less than one-fourth. This points to an increasing trend of hiring PhDs into non-tenure track academic positions to maintain the FTE student-to-faculty ratio (Curtis 2013).

With an increase in the number of doctorates, many of those desiring tenure-track academic positions end up being employed instead in lower paying, non-tenure track positions. For example, the number of engineering PhDs in non-tenure positions in academia has increased by about 60% in the past 10 years (National Science Foundation, 2011). With this additional workforce, education enterprises have been able to expand their capacity and admit more students, reinforcing the sheer number of educated people. With the increase in low-paid positions displacing work traditionally occupied by tenure-track professors, the university’s production capacity for all degree levels also increases.

Furthermore, professors who would like to focus more on research activities can buy out their teaching load, and universities can then hire lower-waged lecturers and postdocs to teach a variety of courses, especially undergraduate courses. This displaces the time professors had to spend on lecturing, and allows them to focus instead on research. A byproduct of research activities is the training and production of PhD students, leading to more PhD admissions and PhD graduates.

We argue that the described mechanisms form a reinforcing feedback loop and can magnify small exogenous shocks in the job market. Such a mechanism can result in long-term lasting waves of an abundant educated workforce, demand for higher education, and mismatch between job market requirements and workforce degree attainment.

In the following sections, we implement the model and further develop the theory to capture effects of small shocks to the system, representing short-term economic downturns, and changes in distribution of jobs, representing technological shifts in workplaces.

4. Modeling

We develop a system dynamics model of the workforce and credential-based job market. We explore the effects of the described mechanisms under two simulation scenarios: 1) a short-term economic downturn, and 2) a technological shift that permanently changes the distribution of education requirements.

We represent the workforce population in an aggregated pipeline where people move within the pipeline as they receive more education. Each step in this pipeline will represent a subpopulation of the workforce. The population of the pipeline increases as new people enter the pipeline and decreases as people leave the pipeline due to retirement or for other personal reasons. The model is based mainly on three major rules:

• Matching: In each time period, the active workforce population is matched to the available jobs. The workforce population is evaluated based on their highest level of education. If the number of jobs is less than the number in the workforce, some people will not find jobs and some will take jobs for which they are overqualified. In this model, we assume that people in the workforce prefer to take jobs that match their credentials (i.e., their education degree), the ones with higher degrees have competitive advantage over the ones with lower degrees, and people cannot take jobs that require higher degrees than what they have attained.

• Education for current workforce: In each time period, there is a normal ratio of people who join an education program to receive more education. In addition, we include a decision making rule to represent job market-related incentives for education: when one does not find a job, he/she has more incentive to obtain education to improve his/her competitiveness in the job market. We see this trend most prominently during economic recessions. For example, data (Cowan and Kessler, 2013) have shown that the MBA application volume follows the inverse of the business cycle.²

• University expansion: We assume a portion of people at the end of the pipeline who do not find a fitting job take temporary academic positions such as teaching positions. This, in the real world, is analogous to PhD or Master graduates taking temporary lecturer positions. These positions are economical for universities.

In the following section, we discuss these rules and represent them within the model structure. All formulation details and parameter values are presented in the Appendix. The goal of our simulation experiments is to offer a coherent and empirically testable theory regarding the dynamics of unemployment and underemployment as affected by education. The model represents a hypothetical context; we make no claim that it depicts U.S. or other labor markets precisely. Rather, we seek to understand first-order dynamics, given our postulated assumptions.

4.1. Workforce pipeline

For n steps of degree attainment, the workforce population can be divided into n subpopulations based on each individual’s highest attained degree. Subpopulation i will represent people whose highest degree is the degree level i. Let W_i represent the active workforce in the ith subpopulation. The pipeline also includes people who are in schools receiving more education, and therefore are not active in the market. We represent number of students who are attaining the ith level degree as S_i. Similarly, let J_i represent number of jobs that require at least degree i of education. We can write:

$$\begin{array}{l}\mathit{Total}“\mathit{active}”\mathit{workforce}=W_{\mathit{1}}+W_{\mathit{2}}+\dots +W_i+\dots +W_n\\ \mathit{Total}\mathit{students}=S_{\mathit{2}}+S_{\mathit{3}}+\dots +S_i+\dots +S_n\\ \mathit{Total}\mathit{jobs}=J_{\mathit{1}}+J_{\mathit{2}}+\dots +J_i+\dots +J_n\end{array}$$

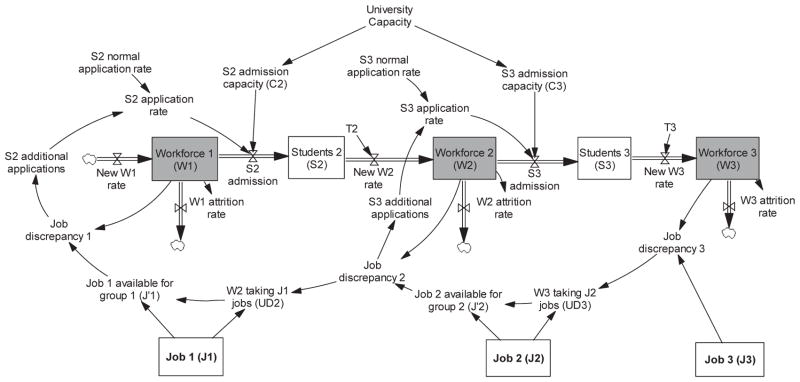
In the interest of parsimony, let us analyze the system for n=3, as Figure 2 depicts. In this model, we have three different subpopulations of active workforce (boxes in grey: W₁, W₂, and W₃), and two stages of education (boxes in white: S₂, and S₃) working as transition stages between W₁ to W₂, and W₂ to W₃, respectively. To offer a concrete example for this categorization, W₁ can represent people with a high school degree, and W₂ and W₃ can represent two stages of education such as undergraduate and graduate degrees. In this example, S₂ will be undergraduate students and S₃ will be graduate students.

Figure 2.

Stock-Flow representation of workforce group i

We assume, in each time period, a constant flow of people enter W₁. In each period, some members of the W₁ workforce exit the pipeline due to retirement or other personal reasons (W₁ attrition rate), some stay in the active workforce population, and some decide to obtain more education (S₂ admission). People in the S₂ stage receive more education and enter the W₂ subpopulation with a delay representing the time it takes to earn the degree. People who newly join W₂ may move to S₃ (immediately or with a delay) to obtain more education, or may stay in W₂ until retirement. In this simple model, W₃ is the end point, while in reality the pipeline may have additional stages (such as postdoctoral trainings).

4.2. Matching mechanism

We intuitively expect that the distribution of workforce and jobs do not necessarily match. Consequently, in each subpopulation, we have unemployed (people who do not find a job) and underemployed people (people who take jobs for which they are overqualified). Figure 3 depicts how jobs are taken by different subpopulations in our model. In the figure, while the workforce moves from left to right (from W₁ to W₃), jobs are distributed from right to left (from J₃ to J₁).

Figure 3.

Flows and distribution of workforce and jobs

In this model, we first estimate the shortage in the number of jobs for the most-educated workforce (W₃). The shortage is represented by the variable Job discrepancy 3. It is basically the difference between the number of people in the subpopulation and the number of jobs. For positive values, this variable indicates that there are people in the subpopulation W₃ who do not find a job fitting their level of educational attainment.

A portion of the people who do not find a fitting job remain unemployed and a portion become underemployed taking J₂ level jobs (in Fig 3: UD₃). The remaining jobs (in Fig 3: J’₂) will be taken by W₂. Similarly, underemployment is calculated for the rest of the pipeline.

4.3. Education for current workforce

In each time period, a portion of the population decides to pursue higher education and move up the pipeline. In addition to societal and personal reasons that incentivize higher education, one reason for receiving more education is to get a better job. The latter motivation makes more sense in particular when one’s chance of employment significantly increases by obtaining more education. Figure 3 includes job market incentives to pursue education.

We formulate the tendency to seek an education level (represented by S₂ application rate and S₃ application rate in Figure 3), as a function of normal rate of education and job discrepancy, the latter representing job market incentives to study more. The normal rate represents all other personal and social incentives and is set to create a netflow of people who replace the ones permanently exiting the workforce. In our model, university admissions (S₂ admission and S₃ admission) are constrained by university capacities (C₂ and C₃). We agree that this is a simplifying assumption; in the real world admission rate may be a function of enrollment. We later conduct sensitivity analysis for change in admission decision rules.

The links from job discrepancies (Job discrepancy 1 and Job discrepancy 2) to university admissions (S₂ and S₃) close several feedback loops as presented in Figure 3. For example, as we face more job shortages for group 1, Job discrepancy 1 increases, and there is more incentive to pursue education among W₁. Therefore, S₂ admission rises. As more W₁ leaves to attain S₂ education, W₁ declines, in turn compensating for job shortages (a short-term balancing loop). However, in a longer time period, as the number of people in W₂ increases, more of them take J₁ jobs, fewer jobs become available for W₁, and more individuals of W₁ obtain education, adding to the W₂ subpopulation (a reinforcing loop). A simulation analysis of the interactions between these reinforcing and balancing loops can reveal which ones are dominant.

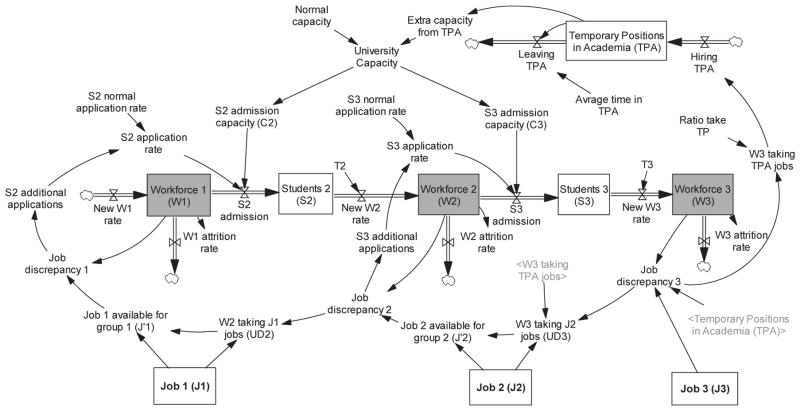
4.4. University Capacity Dynamics

Universities tend to expand their capacities by hiring the most-educated subpopulation for temporary teaching positions. We formulate University Capacity as a function of permanent positions and temporary positions (in Figure 4, normal capacity and temporary positions in academia (TPA), respectively). We assume a constant value for permanent positions. In our model, temporary positions are taken by people in the workforce group W₃ who do not find a fitting job. For simplicity, we assume that universities are always willing to hire a portion of individuals in W₃ who do not find a fitting job. We think this is reasonable since the pay for these positions is very low in comparison to permanent positions, and with more TPA positions, universities admit more students and increase their revenue. Later we analyze sensitivity of the results to setting a ceiling on hiring TPA. Figure 4 shows the resulting feedback structures.

Figure 4.

Temporary positions in universities and resulting feedback loops

In this figure, as more people obtain the highest degree, some are offered temporary positions in academia contributing to training more S₂ and S₃ students (reinforcing loops). However, these positions decrease the number of people in W₃ who need to take J₂ level jobs, which in turn raises jobs that are available for W₂ people (a balancing loop). The ratio of people who take temporary positions is also a parameter in our sensitivity analysis.

The described model can be simulated after parameterization. Consistent with the goal of our simulation as a proof of concept model (rather than an empirical replication of a specific market), we set the model parameters. Details of the formulations and parameter values are documented in Appendix I.

5. Simulation

As stated, we conduct two experiments, each representing one of the scenarios. In each experiment, an exogenous shock is introduced to the system and we then examine how the system reacts to those shocks. The exogenous shock for the first experiment is a short-term decline (negative pulse) in the number of jobs, and in the second experiment it is a shift in the distribution of jobs while keeping the total number of jobs constant.

We assume that in the steady state in each of the three subpopulations there is an active workforce of 1,000 people. We also assume that for each subpopulation there are 1,000 jobs (an active workforce totaling 3,000 people, and 3,000 jobs). Thus, initially, no unemployment or underemployment exist. We first conduct the experiments with the model for a specific set of parameters and then conduct a broader sensitivity analysis.

5.1. Experiment 1: a short-term economic downturn and loss in number of jobs

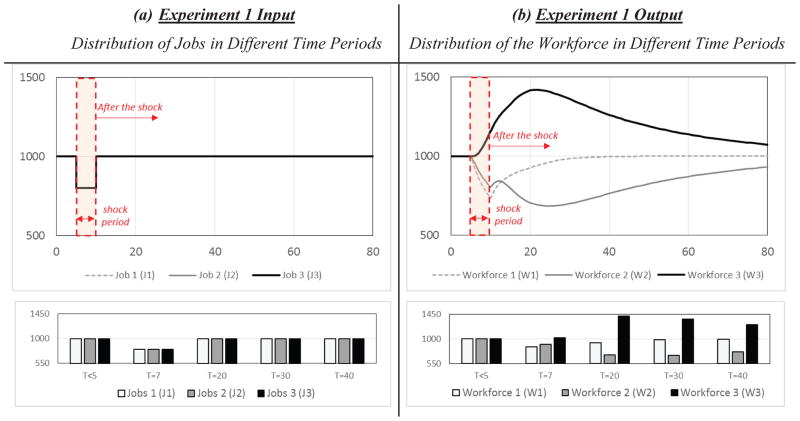
Let us assume at t=5 that there is a 20% shortage in the number of jobs at all levels due to a short-term economic recession for 5 years, and then at t=10 we go back to the initial number of 3,000 jobs and remain there. We expect the workforce to react to the shock, and in the recession period some people lose jobs, some take jobs for which they are overqualified to avoid unemployment, some remain unemployed, and some pursue more education to improve their chances of getting a job. One might think that after job market recovery at t=10, the system should return very quickly to its stage prior to the recession, with everyone having an appropriate job. Our simulation result does not support this intuition. Figure 5a shows how the shock is entered to the model as input; Figure 5b shows simulation outputs.

Figure 5.

Effects of a pulse decline in number of jobs available at 5 ≤ time ≤ 10 (a) on the distribution of workforce overtime (b)

As the figure shows, the 20% shock during 5 ≤ time ≤ 10 creates overshoot and undershoot in the workforce numbers in different groups. The number of the most-educated population increases beyond the equilibrium value and shows an overshoot pattern. The distribution of the workforce also changes, and for a long time we see a non-uniform distribution with a shortage of people in the middle-skilled workforce. As the figure shows, changes in the distributions of the workforce last for a long time before the distributions eventually return to the steady state.

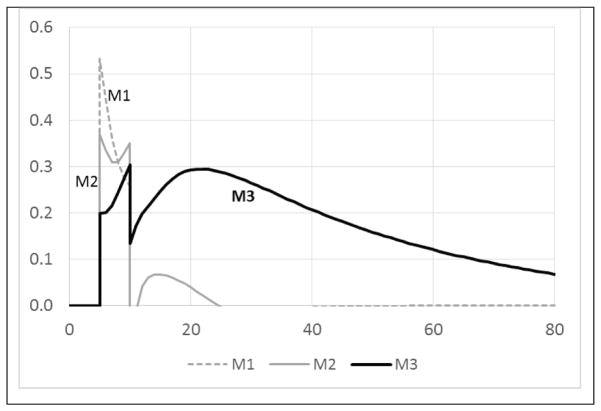
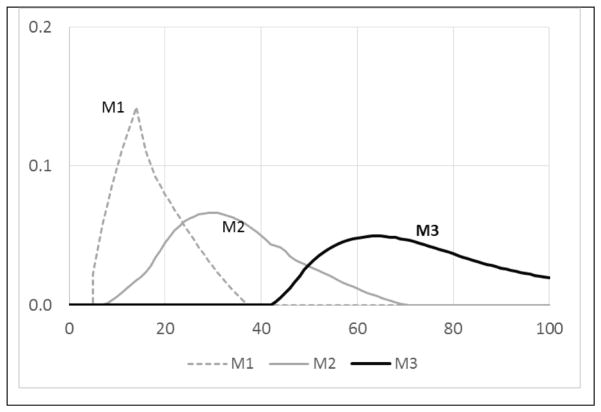
As a measure of efficiency, we are interested in measuring the mismatch between education and job types in each group and capturing the ratio of people who take jobs for which they are overqualified. The measure of mismatch, M_i, is defined as the ratio of people in group W_i who do not find a J_i type of work:

$$M_i=\frac{\mathit{Max}(\mathit{Job}\mathit{descripancy}i,0)}{W_i}$$

Figure 6 shows the trend of the mismatch for each workforce group during the recession and for a long time after. There are two different trends of mismatch: one short term as a quick response to the recession, and one long term. In the short run, the lower-skilled workforce experiences most of the economic recession burden and people with higher skills take their jobs (see M₁). In the long run, however, as people respond to the recession and try to move up the workforce pipeline, the ones with higher education experience more mismatch and underemployment (see M₃).

Figure 6.

Mismatch index in each workforce subgroup as results of a short-term recession between t=5 and t=10.

As the figure shows due to the flow of the workforce to attain more education, the mismatch remains in the system long after the recession, until the overeducated workforce retires from the pipeline. Let us recall that the entire recession is operationalized as a short-term pulse function and that the number of jobs returns to its previous stage at t=10, so the second wave of pressure on the workforce comes as an endogenous response to the flow of the workforce. In other words, after t=10, the job market for the highly educated population has become tight due to internal feedbacks within the workforce and education system.

Overall, the change in the distribution of the workforce causes many people to take jobs for which they are overqualified, an indicator for lack of efficiency in the system. One can imagine how the most-educated population will feel around time=20: “The economic recession finished 10 years ago, jobs are back, but somehow we still feel recessionary pressures!” Seeing a small picture of the entire system, the most-educated group may not even agree that the economic recession is gone and their past response to acquire education is the source of the new job market pressures.

5.2. Experiment 2: an upward shift in the distribution of jobs

Let us represent technological shifts in the society by changing the distribution of the jobs at t=5 to create greater demand for higher levels of education. In this simulation experiment, the numbers of jobs in each category changes from J₁=J₂=J₃=1,000 jobs to J₁= 750, J₂=1000, and J₃=1250 in a period of 10 years, and stays the same thereafter. The total number of jobs before and after the exogenous shock is the same (total of 3,000 jobs), and the only change is the distribution in favor of the most-educated group of the population. We expect the shock to provide more incentives for the workforce to attain higher degrees, and would like to examine the transition to the new steady-state condition. Figure 7a shows how input to our model is formulated, and Figure 7b shows the effects on the workforce population.

Figure 7.

Magnified effects of a change in the distribution of jobs available representing a technological change (a) on the distribution of workforce overtime (b)

As the figure indicates, the workforce overreacts for a long time, and each group experiences overshoot or undershoot in different time periods until, after a long delay, it reaches equilibrium.

Figure 8 shows the trend of mismatch in different workforce subpopulations. The shift in technology first affects the lower-skilled workers (see M₁), but with delays two separate waves emerge affecting other subpopulations (M₂ and M₃). It is interesting to note that the wave reaches the most-educated population (see M₃) when we do not see any mismatch among the least-educated population. We can imagine how the most-educated population will feel: Technology has changed in favor of us, we responded intelligently and studied more, there are more jobs for us, but somehow it seems we have wasted our time and are taking jobs that do not require our education! Seeing a small picture of the whole system, the most-educated group may not even agree that the number of jobs for the most-educated workforce has increased, and the mismatch comes as result of their “intelligent” reactions.

Figure 8.

Mismatch index in workforce subgroup as results of a shift in the distribution of jobs at t=5.

These two experiments simply represent a short-term decline in the number of jobs and a change in the distribution of jobs. In the real world, these changes can happen as results of short-term economic declines, technological shifts, or both. Our theory predicts long-term lasting effects that cascade to the most-educated population. The magnified effects go beyond short-term pressures and can create long-term waves in the job market that are reinforced endogenously by delays and feedback loops. They eventually affect the most-educated population by causing them to take jobs for which they are overqualified.

The model is simple and is run with hypothetical parameter values to develop a coherent theory. However, sensitivity analysis on major parameters helps us generalize the arguments and find the conditions under which we might observe more endogenously generated mismatch.

5.3. Simulation for a larger range of parameters

We extend our analysis to a larger parameter space: experiment 1 with different sizes of economic shocks, and experiment 2 with different magnitudes of technological shifts, both in interaction with different values for temporary positions in academia. The reason we test the effect of temporary positions in academia is that there has been a huge debate on potential effects of postdoc positions and other temporary positions in academia. Many argue these positions are mainly “holding positions” and help people wait for a longer time period before finding permanent positions (e.g., Zumeta 1985). Many times resources for these temporary positions are government grants (e.g., National Institutes of Health grants in U.S.), thus understanding the effects has policy implications too.

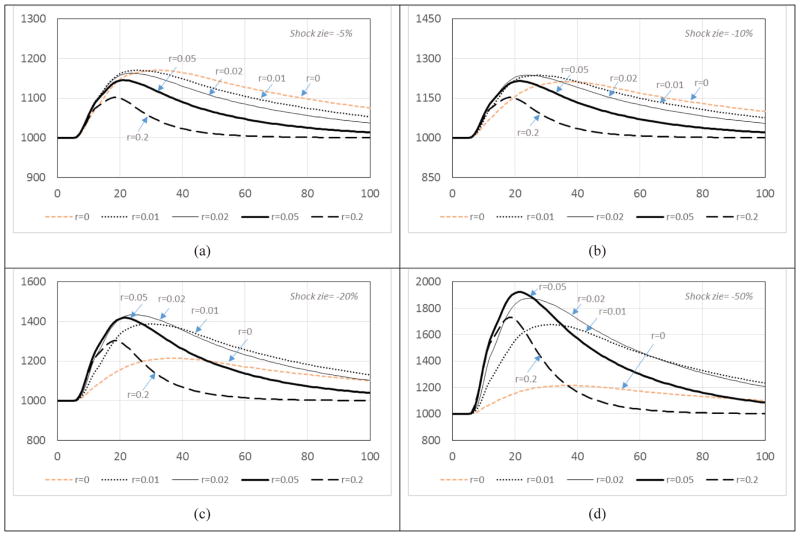
First, we simulate the model for different values of short-term economic shocks ranging from 0% to 30% decline in the number of jobs for 5 years times different values of r. Figure 9 depicts a few selected simulations for 4 sizes of economic shocks (−5%, −10%, −20%, and −50% shocks in figures 9a, 9b, 9c, and 9d, respectively). Each graph shows the result of a different value for the ratio that take temporary positions (r = 0, 0.01, 0.02, 0.05 and 0.2). The r = 0 conditions represent the dynamics of economic shock in the absence of any temporary positions in academia. Higher values of r demonstrate the effects of adding these temporary positions.

Figure 9.

Number of the most-educated group (W₃) in different scenarios. Note: r represents the ratio of highly educated people who do not find fitting jobs and take temporary positions in academia.

In all simulation runs, we see the overshoot pattern in which the magnitude of the overshoot is higher for stronger economic shocks. However, r has an interactive effect: for smaller economic shocks (see Fig. 9a), we see that the magnitude of overshoot declines for higher values of r, implying that more temporary positions decrease the overshoot; for larger values of economic shocks (see Fig. 9d), the magnitude of overshoot increases with larger values of r. In addition, very large values of r help dampen the overshoot more quickly.

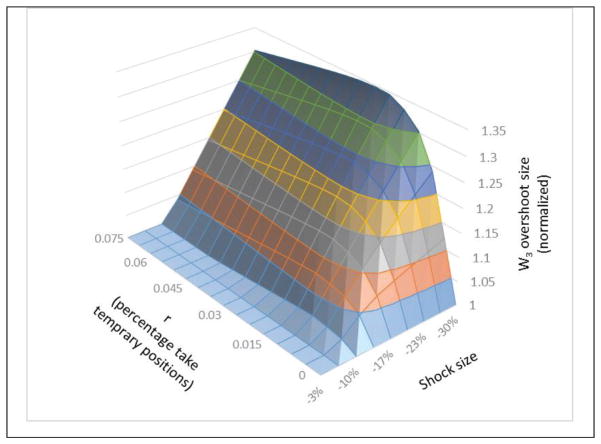
For a systematic examination of the magnitude of overshoot in W₃ (the most-educated workforce) in different conditions, we can examine the ratio of the maximum magnitude of the long-term wave in W₃ to the same variable in the corresponding r = 0 condition. We name this variable Normalized W₃ overshoot size. Put simply, the Normalized W₃ overshoot size for shock size = −20% and r = 0.05 will show the ratio of the overshoot size in this condition to the condition with shock size = −20% and r = 0. Higher values of the Normalized W₃ overshoot size would mean we have had larger amplitudes in long-term waves. Figure 10 shows the results.

Figure 10.

The size of overshoot in the number of the most-educated group (W₃) for different values of short-term economic shock size vs. r (percentage of people taking temporary positions)

The results imply two major points. First, as we expect, larger short-term economic shocks result in larger mismatches in the highest-educated group. In the figure, as shock size increases we see a larger value for W₃ overshoot size. Second, temporary positions in academia have interactive effects with the magnitude of long-term shocks, with a tipping point (Repenning et al., 2001; Morrison 2012) after which the direction of effect of temporary positions on overshoot changes. In major recessions, as more people are hired into temporary academic positions (e.g., in Fig. 10, see Shock Size = −30% and r between 0 and 0.03) we see that the long-term mismatch sharply increases. This is due to the dominance of the pipeline reinforcing effect that results in training more and more people in academia, with society ending up with an abundant number of highly educated people, more than what the job market desires. Notably, there is a tipping point after which the effect of r reverses. This is more apparent for smaller shocks: temporary positions help dampen economic shocks (e.g., in Fig. 10, see Economic Shock Size = −10% and r between 0 and 0.075). The reason is that these positions absorb people who do not find permanent jobs during short-term recessions, dampening the cascading effect and therefore mitigating what could have been extra pressure on the lower-educated population.

The bottom line is that for the range of parameters we tested, the endogenous growth in mismatch showed up, but the effect is worse for major recessions and during these the effects are likely to be magnified with temporary positions in academia. In smaller economic shocks, however, temporary positions can dampen the shocks, working as a buffer and absorbing highly educated people who otherwise would have taken the jobs of relatively lower-educated groups.

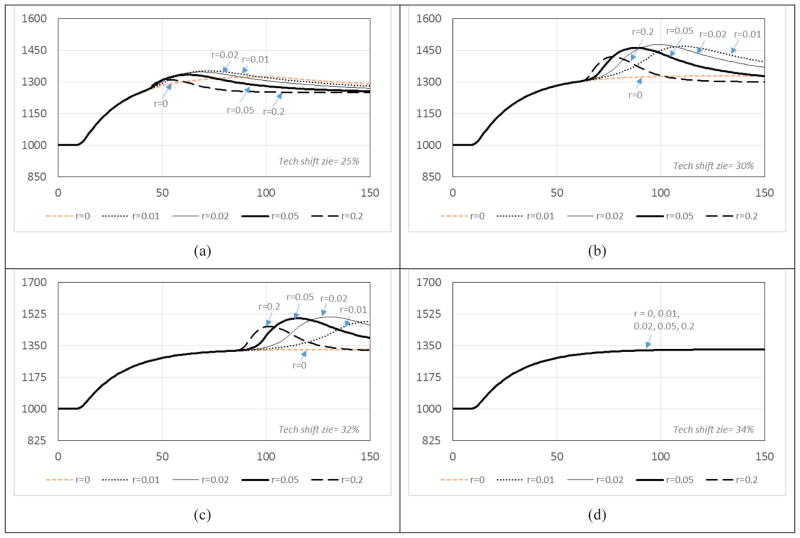
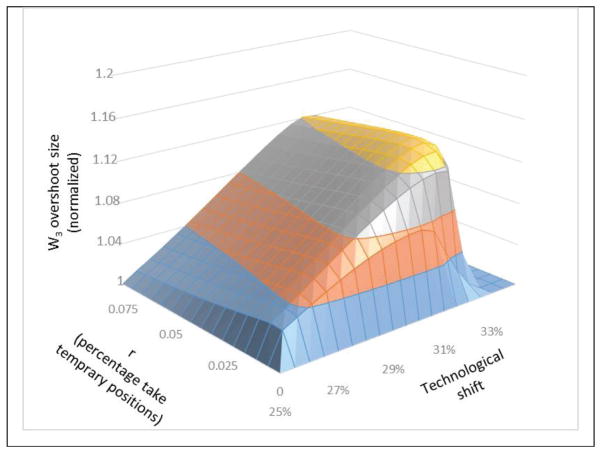
Next, we simulate the model for different values of the technological shift (the number of jobs taken from J₁ and added to J₃) times different values of r. Figure 11 depicts a few selected simulation runs over time for 4 sizes of technological shifts (25%, 30%, 32%, and 34% shocks in figures 11a, 11b, 11c, and 11d, respectively). Each graph shows the result of a different value for the ratio of people who take temporary positions (r = 0, 0.01, 0.02, 0.05, and 0.2).

Figure 11.

Number of the most-educated group (W₃) in different scenarios. Note: r represents the ratio of highly educated people who do not find a fitting a job and take temporary positions in academia.

In simulation runs for r = 0, we see a goal-seeking pattern. As the value of r increases in Figs. 11a, b, and c, an overshooting pattern emerges in Figs 11b and 11c. This shows there is a window of parameters for technological shift within which we see a large overshoot. In Figures 11a, b, and c, we can see the magnifying effect on overshoot of r. Higher values of r lead to a faster appearance of overshoot, and faster dampening.

Figure 12 shows a more systematic comparison of the magnitude of overshoot in the number of the most-educated workforce. The figure shows that there is a window of parameter values for a technological shift to result in long-term waves of underemployment. Smaller technological changes does not result in overshoot, and the workforce slowly adapts itself to the new equilibrium. However, as the shift passes a tipping point (in our model, 25%) and creates enough incentive to attain more education, more people go to schools and once the new wave of the students graduates, the job market ends up with an abundance of highly educated individuals. Notably, very large technological changes also will not result in mismatches for the highest-educated workforce. This is mainly due to absorbing all people who obtain education into new high-tech positions.

Figure 12.

The size of overshoot in number of the most-educated group (W₃) for different values of technological shift vs. r (percentage of people taking temporary positions)

The U-shaped effect of r is also worth mentioning. As people are hired into temporary positions (r > 0), the magnitude of overshoot increases until a tipping point, after which it declines. This is related to the range of parameters in which the pipeline reinforcing effect becomes dominant over the buffering effect of temporary positions. While the actual values of this parameter are empirical questions, our model predicts that overshoot emerges in a specific range of technological shifts in the market.

5.4. Sensitivity analysis

We used Vensim DSS for sensitivity analysis, and ran eight major sensitivity tests. Each test is about analyzing effects of change in one specific parameter. In each test, we conducted 1000 simulation runs changing the value of the test parameter in a predefined range (such as ±100% of its original value). Then we looked at the distribution of the results and examined the range of change in simulation outcomes, depicted by 50%, 75%, 95% and higher confidence interval ranges. Detailed results are reported in Appendix 2. Summary of the results are in Table A2 of the Appendix, and more information is provided in Figures A1–A17. In summary, the model’s predictions remained qualitatively similar in our tests for reasonable changes in different parameters. Here, we provide a brief summary.

In test 1, we examined effects of our assumption about speed of change in technological shift (from a step function to a ramp function over 20 years). Similar patterns of change in workforce happen for slower slopes of technological shifts while the size of overshoot declines. In tests 2 and 3 we analyzed effects of change in education duration for graduate and undergraduate degrees. For reasonable ranges (education duration between 1–10 years) the results are similar. In tests 4 and 5, we changed average time in TPA, and capped number of TPA positions. Within reasonable ranges of change in TPA duration (between one year and six years) and TPA cap (between 20%–50%, consistent with the past data (Curtis and Thornton 2013)), results are unchanged.

The last three tests results are also informative and in line with our theory’s prediction. In test 6, we changed the value for ratio willing to remain unemployed. This parameter represents the proportion of people who are not willing to get education to move up the ladder and not willing to take lower level jobs. In simple words, by people not reacting to job shortage, our mechanism one weakens and the size of overshoot in W₃ declines. In test 7, we specifically focused on the fraction who decide to study. With lower ratios, the flow in the education-workforce pipeline declines, weakens the first mechanism, which decreases the size of the overshoot. In test 8, we decreased the ratio willing to take TPA positions (r) which was analyzed in the previous section in details. The model’s outcomes remained unchanged for reasonable changes in these parameters (see Appendix 2), however, consistent with the predictions of our theory, overshoot patterns weakened in extreme condition tests. In simple words, if everyone is willing to stay unemployed rather than study, we will not have an overshoot.

The main insights from the sensitivity analysis are that 1) the model can reproduce overshoot patterns for a wide range of changes in parameters, and 2) results are sensitive to extreme changes in the parameters that affect our two mechanisms: if more people are willing to get education or take lower level jobs or take temporary positions in academia which all seem to be rational decisions at the individual level, in aggregate we see larger mismatch between workforce and jobs. In simple words, the consistent finding is that as individuals are more willing to react rationally, we see a more inefficient system in terms of mismatch.

6. Discussion and Conclusion

We presented a simple model to capture how feedback structures within labor and education sectors can lead to excess degree accumulation, magnified pressures on those with lower degrees, underemployment, and long-term pressures on people with higher degrees. We introduced two major feedback mechanisms that act on the education enterprise and cause the number of educated people to increase dramatically, with relatively short-term changes in the job market. First, we introduced a cascading effect that represents how job shortages throughout the pipeline cascade toward lower-skilled individuals as people with more education take jobs for which they are overqualified. The mechanism also creates incentives to move up the workforce pipeline. Second, we introduced a capacity reinforcing mechanism that results in increasing the population of PhDs by employing a portion of them in temporary academic positions. These two mechanisms create self-driving growth engines that are adequate to over-incentivize degree attainment, and can affect the long-term match between supply and demand for college-educated labor.

We provide simulation-based evidence that for a wide range of parameter values the education system can create magnified pressures endogenously on those with lower degrees, and long-term waves of pressures on those with higher degrees. The main driver of these dynamic patterns is the structure of the system: the reinforcing loops to push down short-term job shortages to the lower-educated population and incentivize more education, and to take temporary positions in academia, adding to the capacity of universities and future outputs. Delays in attaining a degree also contribute to overshoot in workforce numbers for a limited number of jobs. These mechanisms make the system vulnerable to small and short-term external shocks. As a result, we end up with individuals who attain higher degrees of education to take jobs that do not require these degrees, but give them a competitive advantage over people without those degrees. The implication at the societal level is inefficiency in the education system.

The behavior is similar to the bullwhip effect in supply chains and demand amplifications throughout supply chains (Lee et al., 1997; Sterman, 1989 and 2000). It is shown that a small external shock (or just expecting a shock (Croson et al., 2014)) creates long-term waves of backlog and inventory, and overall inefficiency throughout the chain. In supply chains, however, providing clear information may help correct the bullwhip effect. Here, we cannot easily argue that the problem of self-driving growth engines in education stems solely from a lack of information. Individuals seeking fitting jobs face competitors with higher degrees, as if the rules of the game are changed. Furthermore, the abundance of PhDs (Larson et al., 2014) who decide to look for non-academic positions end up applying for different positions in research centers, many of which do not need their specific and narrow PhD training. However, these PhDs are likely to win the competition over applicants with master’s degrees, persuading the latter that one needs a PhD to get any research position. And the story continues making a college degree a must for jobs that do not necessarily benefit from the type of training offered in colleges.

We tried to simplify the analysis by designing two clear experiments with the model. We investigated the effects of a pulse shock and a change in the distribution of jobs separately to capture effects of change in the average number of jobs and change in the distribution of jobs one at a time, while controlling for the other. In the real world, they are likely to happen concurrently. For example, there is no guarantee that for each W₁ job that disappears exactly one W₃ job emerges; in fact, one might expect that the number of high-tech jobs that are replacing former low-tech jobs is smaller. This adds to the magnitude of long-term waves throughout the education pipeline and makes the system more vulnerable. Overall, the education system seems to be in structural disequilibria (Teitelbaum, 2008).

Our study has several limitations. The model was offered to develop a theory, and as stated, we made no claim that our simulation model precisely depicts detailed labor markets in the United States or elsewhere. Rather, we tried to understand first-order dynamics, given our postulated assumptions. Future models can address more layers of complexities and include more details. They can also be calibrated to reproduce real-world patterns using different parameter estimation methods (e.g., Homer, 2012; Hosseinichimeh et al., 2016) and be validated against different cases (Forrester and Senge, 1980; Groesser and Schwaninger, 2012). The model can also be further developed to include potential changes in people’s willingness to stay unemployed or educated individuals to take temporary positions as endogenous variables in the system. From a modeling perspective, we have made simplifying assumptions about university capacities and admission rates. More complex models can consider effects of funding, facilities, ratio of professors to enrolled students, and many other similar variables. We leave these opportunities for future modelers.

Furthermore, our study focused on a specific type of mismatch. However, the problem of mismatch between education and job market goes much beyond the analysis in this study. Our model depicts a simple one-dimensional mismatch between the level of degree and job requirement; in the real world, there are multiple dimensions of mismatch between training and job requirements. For example, people may undergo training that lags behind technologies used in a given industry. The delay between education colloquia and industry needs may result in teaching techniques that are outdated. More elaboration on the dynamics of mismatch between education and industry is a future avenue of research.

In summary, we offered a new explanation for inefficiency in the education sector. We hypothesized that in this context, people end up obtaining education only to have a competitive advantage during the hiring period, without any further use. The overall result is extra spending on education, a corresponding loss of working years, and an increase in student debt.

Highlights.

• Education-job mismatch emerges endogenously.

• Pipeline cascading effect magnifies pressures on lower-educated workforce.

• Pipeline reinforcing effect can result in abundant educated workforce.

• In interaction, they can magnify effects of recessions and technological changes.

• The system creates long-term waves of mismatch between workforce and jobs.