Abstract
The design of effective electroporation protocols for molecular delivery applications requires the determination of transport parameters including diffusion coefficient, membrane resealing, and critical electric field strength for electroporation. The use of existing technologies to determine these parameters is time-consuming and labor-intensive, and often results in large inconsistencies in parameter estimation due to variations in the protocols and setups. In this work, we suggest using a set of concentric electrodes to screen a full range of electric field strengths in a single test to determine the electroporation-induced transmembrane transport parameters. Using Calcein as a fluorescent probe, we developed analytical methodology to determine the transport parameters based on the electroporation-induced pattern of fluorescence loss from cells. A monolayer of normal human dermal fibroblast (NHDF) cells were pre-loaded with Calcein and electroporated with an applied voltage of 750 V with 10 and 50 square pulses with 50 μs duration. Using our analytical model, the critical electric field strength for electroporation was found for the 10 and 50 pulses experiments. An inverse correlation between the field strength and the molecular transport time decay constant, and a direct correlation between field strength and the membrane permeability were observed. The results of this work can simplify the development of electroporation-assisted technologies for research and therapies.
Keywords: Electroporation, High-throughput experiments, Concentric electrode system, Cell membrane permeability, Transport parameters
1. Introduction
Electroporation (EP) is a commonly-used technique in biotechnology and medicine in which an externally-applied, pulsed electric field is used to increase cell membrane permeability [1]. If the resultant membrane permeability is reversible, the procedure is called reversible electroporation (RE). If the resultant membrane permeability is irreversible, the procedure is called irreversible electroporation (IRE). During IRE the cell dies; in RE, however, cells could survive the exposure to the electric fields. In the past decades, reversible and irreversible electroporation have found diverse applications in food processing [2], the pharmaceutical industry [3] and in medicine [4], [5].
The most widely considered theory to describe the electroporation phenomena is the “aqueous pore” theory [6]. The aqueous pore theory suggests that the application of a pulsed electric field causes the formation of nano-scale pores in the cell membrane [6]. Today, there is no single definition for the aqueous pore. One definition includes a regular static toroidal pore with smooth sides [7], an another one, in contrast, includes an irregular pathway where there is a flow of phospholipids [8]. Large pores that are probably derived from the primary pores have been observed in cell electroporated in hypoosmotic conditions [9]. In addition, researchers attempted to directly observe pores by scanning electron microscopy using hepatocytes cells in irreversible electroporation [10]. The recent molecular dynamics simulations support this hypothesis of the dynamic aqueous pore formation [11,12], however, final experimental proof of the existence of primary electroporation pores has yet to be established [13].
This pulsed electric field induced membrane permeability change allows for the transport of otherwise-impermeable molecules such as mRNA, nanoparticles, proteins and sugars [14]. The minimum required electrical field strength that results in increased membrane permeability, pulse duration and frequency, the kinetics of pore closure, and the maximum field strength, above which pore formation is irreversible, are all important parameters that determine the yield of transport for the desired molecules into and out of the cell. The electric field and transport parameters are cell- and molecule-type specific and must be optimized for a given experimental setup.
One of the most important tasks in optimizing electroporation experiments is to determine the electric fields on the interface between IRE/RE (irreversible electroporation threshold, Eirrev) and RE/no-EP (reversible electroporation threshold, Erev) regions [15,16]. To determine Erev and Eirrev, the current practice consists of a series of experiments with increasing electric field strength to find EP boundaries for a specific cell/molecule system [17]. This is a time and labor-intensive task. It is, moreover, cumbersome to estimate the local electric field distribution for different systems because of changes in impedance/conductance during electroporation protocols due to membrane resealing. To facilitate the optimization processes, a concentric electrodes electroporation system that allows for determining IRE/RE electric field threshold for bacteria inactivation in a single experiment has been previously introduced [18]. There is still a need for an experimental system that can offer a determination of the RE/no-EP and electroporation mediated molecular transport parameters in a single experiment. Such a system will enable rapid screening of electric field strength for optimization of electroporation parameters for its application biotechnology and medical applications [4].
In this work, we developed a rapid and convenient method to determine the critical electroporation and transport parameters for adherent cells in a single experiment. To this end, we used an electroporation system with concentric electrodes, which generated a radial gradient of electric field strength. We also developed a biophysical model of cell membrane electroporation that allows for the determination of critical electroporation parameters. Our method eliminates the need for multiple experiments for the determination of critical electroporation and mass transport parameters.
2. Theory
2.1. Electroporation-induced mass transport modeling
The application of electric field pulses could generate pores in the cell membrane, which can reversibly seal or irreversibly expand. These pores enable nonspecific, bidirectional transport across the cell membrane. In our theoretical description of the transport, the membrane pores are initially generated during the application of electric field and the pores start resealing immediately following the removal of electric field.
For the specific purpose of this paper, the experimental design was as follows: the cells were loaded with a fluorescent stain before the electroporation procedure. After electroporation, the fluorescent material left the cell through the pores created in the membrane until the size of pore was larger than the size of the molecule. In the simplest form, the transient flux of fluorescent molecules leaving the cells through the available pore area is directly proportional to the concentration gradient across the membrane [19]:
| (1) |
where N (moles) is the number of moles of the molecule of interest within the cell, t (s) represents the elapsed time post-electroporation, P (m s−1) is the proportionality constant also known as the permeability coefficient through the membrane. In general, P may be described as P = KD/Δx, where D (m2 s−1) is the diffusion coefficient, Δx (m), is the membrane thickness, and K is a correlation coefficient, which may also be physically interpreted as solubility of the molecule in the membrane [20]. In the above equation, D and Δx are physical constants. Hence, the only parameter that maybe affected by electroporation is K. The solubility of the molecule in the membrane reflects on the physical interactions between the membrane and the molecule such as polarity and charge and size. Hence, electroporation assisted increase in P arguably incorporates the effect of all these parameters as P is a direct function of K. A (m2) is the permeabilized area of the cell membrane, and Ci and Ce (mol L−1) are intra- and extracellular concentrations of molecules of interest, respectively.
In this formulation, we assumed intra- and extracellular distributions of the molecule of interest are uniform. In Eq. (1), A is a transient property due to pore resealing, and may be described as a fraction of the total cell surface area:
| (2) |
where φ(t) is permeabilized area fraction, which be defined as the ratio between the permeabilized membrane surface area (area of the membrane which contains pores large enough to facilitate specific molecular transport, and is a function of elapsed post-electroporation time (t)) to the total membrane surface area (Acell). It should be noted that our model does not include possible interactions of the pore forming lipids with electric field induced byproducts such reactive oxygen species. These reactions could play an important role in transport dynamics, yet very few information on them is currently available [7].
Assuming that the total cell volume does not change during pore resealing, Eq. (1) can be written as a function of the concentration of molecules, across the cell membrane:
| (3) |
where Vcell (m3) is the volume of the cell, Ci is the internal concentration of molecules and changes with time, Ci = Ci(t), and Ce is the external concentration of molecules, which is assumed to be constant. The assumption that the cell volume does not change during long term transport process is valid, as previous experimental studies showed rapid cell swelling in the first seconds after electroporation, and little further change in the cell volume in the following minutes [21].
The equivalent permeable area fraction is a complex non-linear function of elapsed post-electroporation time [22]. The rate of change of φ(t) per given electrical strength can be approximated using kinetic model with two time constants mimicking short term in scale of a fraction of a second, and longer time changes in scale of few seconds up to a minutes similar to [22]. The rate of change is given by:
| (4) |
where τ1,and τ2, are time decay constants that represent short term and long term scales, respectively.
These time constants model the different rates of decrease of the concentration observed after the electric field has been removed [22]. The solution of Eq. (4) for φ with two exponents is:
| (5) |
The work in [22], and [23], have shown that, immediately after removal of the electrical field, multiple exponential functions were required to closely describe the membrane resealing phenomenon at very small time scales (1 ms and smaller). However, the approximation using one exponent, was shown in [22] and [24] to agree very well with experimental data for times over 1 s and pulse voltage of 800 (V). Since the main focus of this work, is to quantify the effect of the electroporation in scale of few minutes, we can neglect the shorter term decay constants, and use only one decay exponent, related to longer scale changes of the equivalent permeable area fraction:
| (6) |
where τ the equivalent (molecular transport) decay constant, that represent the changes in scale of minutes after electroporation. The approximation using one exponent, were shown to give good results for time.
The initial fraction of electroporated membrane surface area, changes with the electric field strength. Thus, in a system with concentric electrodes, φ(t) depends on the radii:
| (7) |
Eqs. (6) and (7) imply that the change of permeabilized fraction of the cell membrane can be assumed to behave with the first order kinetics.
After substituting Eq. (7) in Eq. (3), and rearranging the terms and integrating both sides, and assuming that the extracellular concentration is very dilute, i.e. Ce ≅ 0 the equation to describe intracellular concentration is obtained:
| (8) |
where Ci and Ci0 are the intracellular concentration of the molecule of interest at time t and at time 0 respectively (time starts immediately after the last electric pulse).
In Eq. (8),Acell, and Vcell can be approximated for the chosen cell type. The parameters φ0, P, and τ are not known, and can be obtained by fitting Eq. (8) to experimental data. Assuming a spherical cell, the total electroporated area of the membrane at time zero, φ0, can be expressed as:
| (9) |
where R is the radius of the spherical cell, and θ0 is the opening angle which limits the electroporated area of the membrane at time zero (Schematic 1).
Schematic 1.
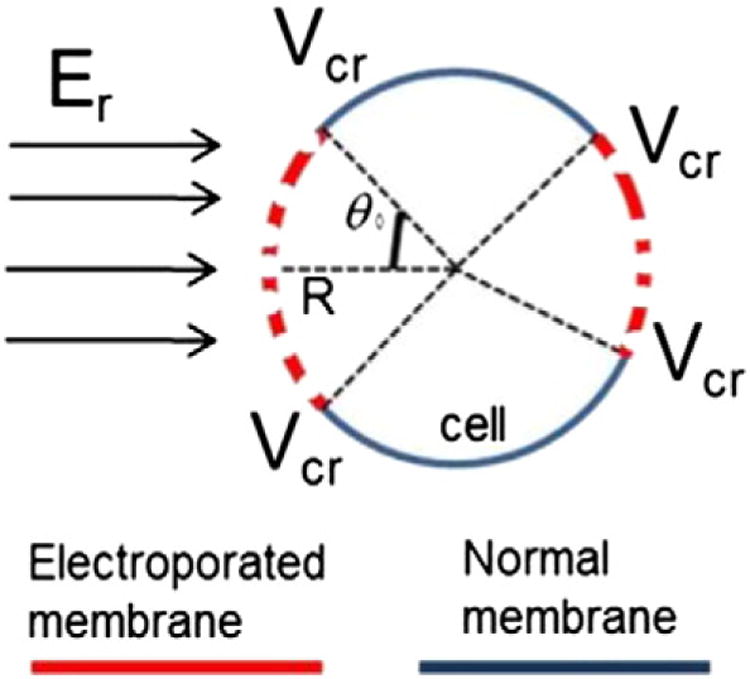
Biophysical model of cell membrane electroporation.
Induced transmembrane potential (V) for a single spherical cell with a nonconductive plasma membrane can be determined analytically by solving Laplace equation in the spherical coordinate system, yielding the expression often referred to as the steady-state Schwan equation [25]:
| (10) |
The Schwan equation inherently follows that the system is quasi-electrostatic, meaning that the driving electric fields are applied at speeds that are slow compared to the phenomenon observed (i.e. pulses are delivered at sufficiently low frequencies). When the duration of electric pulses is on μs scale, this gives significant time for the system to come to the steady-state, justifying the use of Schwan equation [26]. The induced transmembrane potential depends on the amplitude of the local electric field (Er) and the size of the cell (R) (i.e. the same electric field induces larger potential in larger cells) and 3) location on the membrane relative to the direction vector of the electric field (θ, is the angle between the specific location of the membrane and the direction vector of the electric field). Even though this induced transmembrane potential can analytically be calculated for spheroids, it has to be determined either numerically or measured experimentally for realistic cell shapes [27,28].
The minimum transmembrane potential that leads to cell membrane permeabilzation (critical potential, Vc) defines θ0 as the opening angle which limits the electroporated area of the membrane at time zero for each cell. However, in the concentric electrode system, at the border between RE/no-EP areas, θ0 = 0 and therefore: [MATH]. The membrane opening angle at time zero, θ0, can be calculated by:
| (11) |
where Er, is the local field strength and is a function of the radial distance r, from the central electrode, and Ecr is the minimum field strength (or critical field strength) required for formation of pores.
In a concentric electrodes electroporation system used in this study, the electrical field strength is a function of radius and applied voltage (v) [18]:
| (12) |
where r is the radial distance from the center electrode, Δv is the potential difference between the electrodes, and R1 and R2 are the radii of the center and circular electrodes, respectively.
The initial fraction of electroporated membrane surface area φ0 for concentric electrodes is a function of r and V, and can be obtained as follows.
| (13) |
Where is the radius of critical pore formation below which (r < rcr) pores would be formed. The value of rc can be approximated from the experimental data by measuring the radius after which there is no drop in florescence of cells before and after application of electric fields.
To further simplify the model, Eq. (8) can be solved for the final condition when t→°°:
| (14) |
In the above equation, the values of Ci0(r) and Ci∞(r) can be experimentally determined. The value of φ0 can be independently obtained after experimental determination of rcr. Hence, Eq. (14) defines a relationship between P and τ.
By substituting Eq. (14) back into Eq. (8) and rearranging, we obtain the following solution for the concentration:
| (15) |
The equivalent time decay τ, depends on the electrical strength (or the radii), τ = τ(r) and can be found by fitting to experimental data available for Ci to Eq. (15). This is equivalent to finding the time instance for each radii where concentration losses 63.2% of its initial value. After deriving the resealing constant, the cell permeability P can be found by substituting τ into Eq. (14).
3. Materials and methods
3.1. Cells and cell culture
Normal human dermal fibroblasts (NHDF) were obtained from ATCC (Manassas, VA). The cells were cultured in 75 cm2 flasks in Dulbecco’s minimum essential medium (DMEM, Life Technologies, Grand Island, NY) in 10% CO2 at 37°C. For the experiments, the cells were detached from the flasks by incubating with trypsin-EDTA (Life Technologies, Grand Island, NY) for 10 min before addition of equal volume medium. The cell suspension wascentrifugesat175gfor5min and the pellet was re-suspended in warm DMEM and the density was adjusted to 1 × 105 cell/ml. A volume of 1 ml of cell suspension was added per 35 mm cell culture dish and the dishes were left in the incubator at 37 °C and 10% CO2.
3.2. Electroporation procedure
About 24–48 h after seeding when the cells became nearly 100% confluent, the cells were incubated with 2 μM Calcein-AM in DMEM for 30 min at 37°C. Before electroporation, the staining medium was aspirated and the plates were washed twice with room-temperature Ca- and Mg-free PBS.1mmoffresh PBS was added to the dish for electroporation. The dishes were placed on the microscope stage and the concentric electrodes (diameter of internal electrode was1 mm the diameter of the external electrode was 24 mm) were placed and fixed on the dish bottom (Schematic 2A). The electrode material was stainless steel. Pulses were delivered using a BTX 830 pulse generator (Harvard Apparatus Inc., Holliston, MA, USA). The following electroporation settings were used: applied voltage of 750 V; 50 μs pulse duration; 2 Hz pulse frequency, 10 (n = 4) or 50 rectangular pulses (n = 3). These experiments enable to evaluate model parameters for the given frequency and pulse number values. Further validation, can be done with more experimental conditions and other sets of pulse frequencies.
Schematic 2.
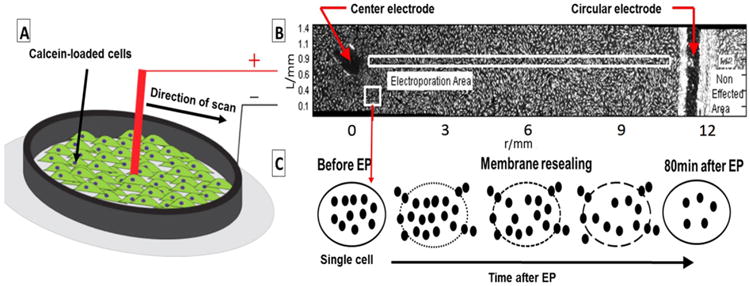
(A) A schematic of the electrode-cell monolayer setup in this study. The central electrode (+) and circular electrode (−) position on the cell monolayer loaded with Calcein in a 35 mm dish (B) A radial slice of the disk and the attached cells before start of experiment (C) Illustration of the effect of electroporation on the cell from electroporated area marked by white rectangular in (B). The black dots represent the fluorescent molecules.
3.3. Microscopic imaging
The initial set of overlapping images were acquired using a 5× objective in ∼6–7 spots from the center electrode toward the edge of the circular electrode, to cover a full radial distance with ∼10–15% overlapping (Schematic 2B). The spots were randomly chosen on the initial image after electroporation. The observation time was 90 min, which was larger than the reported full stabilization of the molecular transport of around 20 min after electroporation [29,30]. To closely capture the rate of fluorescence loss from the cells, the images were taken every minute for the first 10 min, and every 5 min till the end of observation (90 min post-electroporation). Using the pre-electroporation initial images, the exposure time was measured and set for the software to avoid over-exposed imaging (600 μs).
Fig. 2.
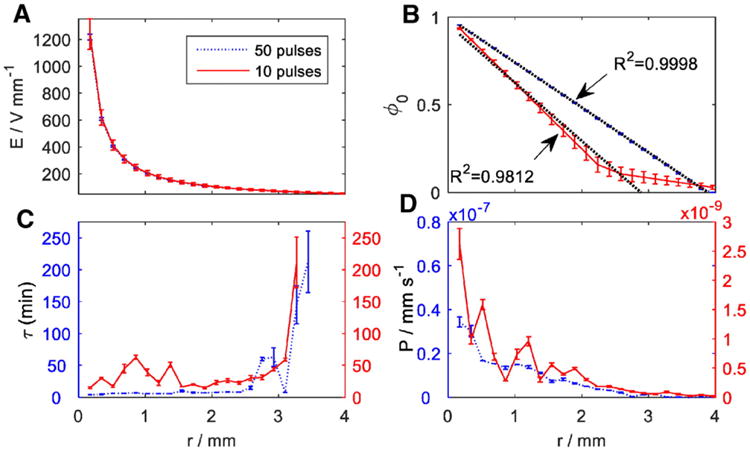
(A) The distribution of electric field strength from the center toward the circular electrode, (B) Distribution of initial pore fraction, ϕ0, at m = 10 and 50 pulses with linear regression fitting till the critical radii, (C) Best-fit values for pores time decay vs. distance for the center electrode (D) Best-fit values for permeability coefficient of Calcein obtained for m = 10 and 50 pulses vs. radial distance from the center electrode.
3.4. Image processing and data analysis
The set of time-lapsed images were stitched together using Image J software [31]. Schematic 2B shows a rectangular slice of one of the disks and Calcein-loaded fibroblasts before electroporation. The cells appear as bright dots, the black empty area on the left and the vertical black curve on the right are the places where the central and circular electrodes were placed on the bottom pf the dish and scraped the cells off the surface. The area between the electrodes was affected by electroporation. The region on the right side of the external electrode was unaffected and was used as reference to correct for fluorescence loss over time due to quenching and intrinsic membrane permeability.
The rectangular regions covering the radial distance between the center and the circular electrodes in Schematic 2B were analyzed. The fluorescence intensity, denoted by I, was directly translated to concentration of intracellular fluorescent material, Ci. A schematic representation of diffusion of intracellularly-loaded dye molecules through the pores after electroporation is presented in Schematic 2C. The stitched images over each time stamp were analyzed using MATLAB(R) (2015a, the MathWorks) software. Possible time-dependent fluorescent intensity change over time due to changes in the experiment conditions was corrected with the intensity in the non-affected areas (in the right side of Schematic 2B), similar to [24]. To account for the differences in intensity due to cell size, movement, deformation and discontinuities in cell distribution between the electrodes, cell boundaries were tracked over time in square areasof∼165 μm × 165 μm containing an average of 30 cells. The cell auto-fluorescence intensity level was subtracted from the total intensity, and then the cell intensities were normalized to their initial local intensities which were acquired immediately before the start of the procedure. The average intensity of each box, after background subtraction, represented one data point. The normalized intensity, which represent the relative concentration, was then expressed in the scale of 0 (cell auto-fluorescence intensity) to 1 (cell initial intensity) and is denoted as I/I0.
The solution in Eq. (15) is very sensitive to local changes in the value of Ci∞. To filter out estimation noise, a sigmoid fitting was used. This fitting includes a low pass filtering aggregated with empirical a-priori statistical knowledge about the electroporation properties [32]. The symmetrical sigmoid function to estimate the final condition concentration C∞ as a function of radial distance, r is:
| (16) |
Where Ĉi∞(r) is the fitted sigmoid, r is the radial distance, and rC50 is the radius at which the concentration (intensity of the fluorescent material) dropped to 50% of its maximum value, and α is spatial decay factor that is obtained by fitting Eq. (16) to Ci∞ using least-square error criterion.
By substituting Eq. (16) back to Eq. (15) we obtain the concentration as a function of only unknown parameter τ. Then the problem becomes a fitting of the experimental data to the model for τ using the least square error criterion [24]. The estimated value of τ was used to estimate the initial pore area, φ0, and the permeability, P, using Eq. (14).
4. Results
4.1. Single-experiment determination of critical electroporation parameters
Immediately upon electroporation, intracellularly-trapped Calcein diffused toward the extracellular solution through the permeabilized membrane and caused the fluorescence intensity of cells to be reduced over time. Due to excess volume of the medium, the extracellular concentration of Calcein could be practically considered negligible. The rate and the magnitude of fluorescence loss were affected mainly by the available area for transport, which was a function of initial area with a changed permeability (φ0), and by the kinetics of pore closure (τ). In Fig. 1A, time-lapse images of one of the disks after the electroporation with 10 pulses is presented. The intensity was normalized, artifacts were removed and corrected with the intensity in the non-affected areas similar to [24]. Fig. 1B shows the normalized fluorescence intensity loss in the same disk. The sigmoid presented in Eq. (16) was used to fit the data. The fitting result is presented by solid lines corresponding to each time point, and R2 values are the coefficient of determination. Fig. 1C and D display similar data and results with another disk electroporated with 50 pulses under similar conditions.
Fig. 1.
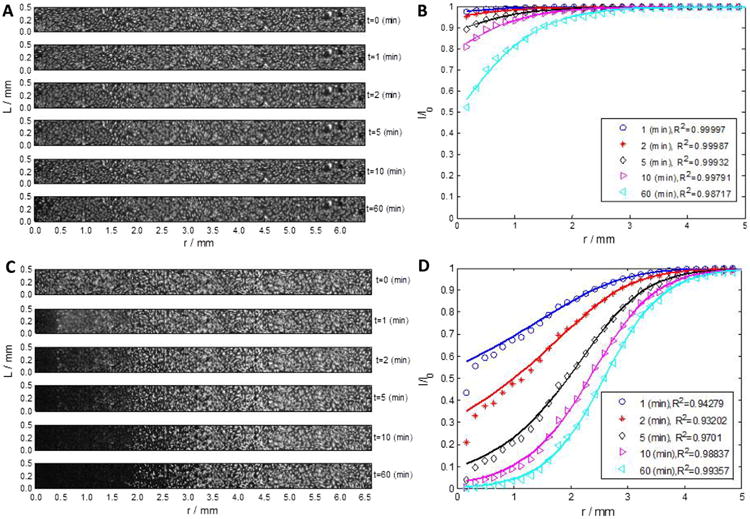
(A, C) Reconstructed images of the entire plate at time t = 0, 1, 5, 10 and 60 min demonstrated the transient loss of fluorescence in electroporated cells for m = 10 (TOP image) and m= 50 pulses (BOTTOM image), respectively (B, D) The measured fluorescence intensity loss and the model fit to the data with two fitting parameter tau and P for m = 10 and m = 50 pulses, respectively.
For both experimental conditions (m = 10, and m = 50 pulses), the loss of fluorescence intensity was more evident in cells closer to the center electrode, where the electrical field is stronger. This fluorescence loss was more pronounced and prolonged in m = 50 pulses than in m = 10 pulses. Nonetheless, at distances of r>2.9, and r>3.9 mm from the center, for 10, and 50 pulses respectively, the change in the fluorescence intensity of the cells is less significant (<10%). These values were used as an approximation to the critical field strengths, Ecr and the critical radii for electroporation, rcr, in Eq. (13) and are reported in Table 1. The change in concentration, as measured by the normalized fluorescence intensity, I/I0, occurred slower for m = 10, compared to m = 50 pulses. For both conditions, after 10 min, the concentration loss reached almost its maximal value, which can be roughly estimated by the values at 60 min [29], [30]. The loss rate for the higher pulse rate was significantly higher than the one of the low rate, as expected. The concentration loss rate decrease with distance, and reached a plateau at the critical radii for both conditions.
Table 1.
Parameter estimated parameters and their estimation quality.
| Number of pulses | rcr (mm) | Ecr (V mm−1) | τ center (min) | τr=rcr (min) | Pcenter (m s−1) | Pr=rcr (m s−1) |
|---|---|---|---|---|---|---|
| 10 | 2.9 ± 0.3 | 72.8 ± 6.6 | 28.7 ± 7.6 | 76.7 ± 23.0 | 0.52 ± 0.2 × 10−9 | 1.56 ± 0.4 × 10−10 |
| 50 | 3.9 ± 0.1 | 52.9 ± 0.9 | 7.6 ± 0.6 | 335 ± 91.0 | 0.57 ± 0.1 × 10−8 | 0.35 ± 0.4 × 10−10 |
*rcr and Ecr are the critical radius and field strength for pore formation, τcenter and τr=rcr are the time decay and Pcenter and Pr=rcr are the permeability coefficients at the center of the disk and at the critical radius.
As observed in Fig. 1, the proposed transport model (based on the sigmoid approximation) fits the experimental data very closely (R2 > 0.95 in average). With m = 50 pulses, the change in the fluorescence intensity was more rapid compared to 10 pulses, in particular closer to the center electrode. Though the overall fitting accuracy was very high, though at earlier time points, close to the center after electroporation, there is small discrepancy between the model and the data. This can explained by sensitivity of the model to small estimation errors in the estimation of rC50, or by non-linear effects. Furthermore, since the main purpose of the use of the fitting is to exclude experimental errors in the value of Ci∞, and the model is fitted to all the experimental data, the effect of this discrepancy on parameter fitting can be considered negligible.
The change of model parameters, φ0,τ, and P, over the radial distance from the center electrode for the different number of pulses are shown in Fig. 2. The data and the error bars in Fig. 2 represent the average values and standard error of the model parameters per cell. The statistics was obtained by fitting the model to the experimental data using 4 different disks (n = 4) for 10 pulses, and 2 (n = 3) for 50 pulses. Fig. 2A displays the calculated change in electrical field from the center to the edge electrode. Since the same voltage was applied in both experiments (10 and 50 pulses), the field gradients were identical in both experiments. The small error bars are due to the error in the placement of the center electrode. As calculated, the electrical field rapidly decreased from center toward the circular electrode. In a radial distance 0.5 <r<4 mm, the field decreased approximately two orders of magnitude. The critical field strength, Ecr, for the two experiment conditions was found by matching the field strength with the final distribution of intensity (for NHDF cells in this study). The values were 72.8 ± 6.6, and 52.9 ± 0.9 V mm−1, for critical radii of rcr=2.9 and 3.9 mm, for m = 10, and m = 50 pulses, respectively. This field strength reflects on the effective permeabilization of the cell membrane, and the results shows an inverse correlation between the number of pulses and the Ec (Table 1), which is corroborating to [33].
The value of φ0, is obtained by substituting the values of the critical radii into Eq. (13). Fig. 2B shows the distribution of the values calculated for φ0. The value of this parameter represents the initial pore fraction of the cell surface area available for free transport immediately after termination of the electroporation and before the start of imaging. The initial permeabilized area of the membrane decreases to zero at the critical radius (2.9 mm and 3.9 mm for m = 10 and m = 50 pulses, respectively), linearly (R2 > 0.98). This supports the model assumptions as result in Eq. (13). Interesting to observe, that in the area beyond the critical radius, in particular for the case of the lower number of pulses, the decrease in the pore area is not linear. This can be explained by the larger influence of reversible electroporation in these areas, which makes the pores coincide fast after the electroporation pulses.
An important parameter affecting the outcome of electroporation in terms of reversibility of the process is the time decay (τ). The value of τ describes a characteristic time pertaining to 63.2% loss in fluorescence intensity. Hence, a smaller value for τ corresponds to a more effective electroporation. In Fig. 2C, the value of τ are plotted versus the radial distance from the center electrode and the respective electric field. The time decay constant for m = 10 and 50 pulses fluctuate along their average value for small radii and when approaching the critical area, where the electrical field is very low, the time decay constants increase rapidly, which reflect the area of no effect on the cells. These results are consistent with previous observations in [29], [30], [34]. The difference between the results for m = 10 and 50 pulses were statistically significant (P value < 10−5), suggesting that the value of τ directly correlated with increasing number of pulses, as was also shown in [35] and [36]. The larger value of τm =10 indicates a longer time for the cells to lose signal intensity compared to 50 pulses (30–60 min vs. 3–8 min within the effective electroporation region, respectively). In both conditions, the values of τm =10, and τm=50 exhibited a clear dependence on radius, increasing with decreasing field strength. The values of τ for both m = 10 and 50 pulses significantly increased at the respective rc (Fig. 2D) implying a very long time for fluorescence loss. This can be explained by the very small permeability of Calcein through the intact membrane.
Another parameter in our model was the permeability P of Calcein molecules through the collective pore area toward the solution. In this study, we assumed that Calcein permeability through the intact cell membrane is negligible, and is only enhanced when the pores form on the cell membrane due to electroporation. Based on Eq. (7), it is expected that the permeability would be affected when the permeabilized area changed over time. In Fig. 2D, the value of P exhibited a clear dependence on the field strength, ranging from 10−7 mm s−1 close to the center electrode (Pcenter) to 10−9 mm s−1 at the boundary of electroporated region (Pr=rcr) for m = 50 pulses. In a similar distance, the permeability for m = 10 pulses decreased from 10−9 to 10−11 mm s−1. The permeability with m = 50 pulses was much higher than with m = 10 pulses within the effective electroporation distance. At farther distances toward the circular electrode, both permeabilities converged to very small values (<10−11 mm s−1).
To evaluate the estimation quality and to validate the model, the parameters were estimated using a test dataset that was not used to fit the data. For this a subset of the data which was non-inclusive to the other (“leave one out”) was used to derive Minimal Mean Square Root estimations for each data set separately. The parameter estimation mean, and their related average estimation error are given for τcenter,τr=rcr,Pcenter, and Pr=rcr in Table 1.
5. Discussion
Electroporation-based technologies are very attractive media for the application of novel therapies. Reversible electroporation has found applications in electro-chemotherapy and gene-electrotherapy for the delivery of small molecules and genes in tissues to improve health [4, 37, 38]. Irreversible electroporation (IRE) is utilized for direct, non-thermal ablation of solid tumors [39]. Electroporation is a common tool in genetic engineering and manipulation of multiple cell types in medical and biotechnology research studies. Specific protocols have been developed for electroporation of hMSC [40], adipocytes [41], hESC [40], riPSC [10], neural precursor [42], Schwann cells [43] human umbilical blood [44], to name a few. Recently, electroporation was used to generate human iPSC from fibroblasts [45]. For cancer immunotherapy, electroporation was used for RNA programming of T cells [46], D-cell activation [47], and whole-tumor lysate expression [48]. There are different models for electroporation-based mass transport, reviewed in [49]. Yet, some of the electroporation-mediated transport mechanism of molecules into cells is not fully known [33] and the major challenge in experimental electroporation still is to rapidly optimize the protocols and derive critical electroporation mediated molecular transport parameters.
In this study, we introduced a simple single-step method to screen the electrical field strengths for optimal electroporation. Our method includes a transport model combined with an experimental setup for estimation of the major electroporation parameters, i.e. cell type-dependent membrane time decay τ, and molecule type-dependent permeability, P. We used a transport model that incorporated the biophysical description of the cell membrane-molecule system. Given the description of our transport model, some limitations may be imposed due to differences in the cell shape and how the membrane of adherent cells may behave differently than a cell in suspension (derivation of Eq. (9)) or cells in the native environment. More accurate description than the used here spherical cell model could provide a more precise description of local electric field distribution [50–52]. The membrane resealing is a multi-step process, that not always can be approximated with first order kinetics [53]. Yet, the fitting results for the model parameters match those available in the literature (permeability coefficient, P) or those that could be directly extracted from the data (τ for m = 50 pulses [22]). These estimated model parameters could then be used to predict the behavior of cells in different settings (cell culture and tissues) and determination of effective electroporation boundaries.
Applying pulsed electric fields to cells may result in one of the following outcomes: irreversible electroporation, reversible electroporation, and ineffective electroporation. The method to differentiate between IRE/RE areas in a single experiment was previously shown in [18]. In this work, we show how to identify the effective and ineffective electroporation for a specific molecule and how to derive some of the critical electroporation parameters of molecular transport. We demonstrated this approach using the fluorescent molecule Calcein. In this study we did not take into account the possible effects of Ca+2 ion on Calcein florescence and future studies should incorporate these synergistic impacts. The boundary between the electroporated and nonelectroporated regions in this setup can be precisely and easily distinguished using the introduced imaging processing tools. In a mechanistic description, the critical electric field strength creates pores that are larger than the size of the molecule of interest thereby allowing the transmembrane movement of the molecule (permeabilization of the membrane to the specific molecule). A limitation of this description is that it does not take into account the steric hindrance, charge, polarity, and other physical quantities that may affect the transport system. Therefore, this model may not be appropriate for physical description of the transport of DNA and polynucleotides where such interactions would dominate the transport, and extra parameters need be added to the model. Moreover, previous work on the membrane resealing kinetics showed that under certain conditions, two or three exponential functions best describe the resealing after electroporation instead of a single exponential function used in this work [54]. Using a single function instead of three function can decrease the errors in the parameters estimation.
For the system of NHDF cells and Calcein, the estimated Ecr required for effective permeabilization and their standard deviation were 72.8 ± 6.6 and 52.9 ± 0.9 V/mm−1 for m=10 and m = 50 pulses, respectively. These values for Ecr corresponded to voltages of 0.78, and 0.97 V for 50 (n = 3 repeats) and 10 (n = 4 repeats) pulses respectively (assuming a diameter of 10 μm for cells). These values are within the range of previously reported critical transmembrane voltages required for electroporation (0.2–1 V) [55].
Using these methods enable estimation of the membrane permeability to Calcein. In this study, the value for the Calcein membrane permeability ranged from the minimum of 10–12 mm s−1 in the nonelectroporated region (passive permeability) to a maximum of 0.5 × 10−7 mm s−1 close to the center electrode and corresponding to the highest field strength. Permeabilization of the membrane by pulsed electric field significantly increased the permeability, as high as 4 orders of magnitude. In the non-EP region, the value of permeability corresponded to the value of permeation through an intact membrane, which was in close agreement with previously reported values for Calcein-liposome system (∼10−10 mm s−1) [56]. Therefore, within the limitations of our physical description of the system, the approximated values of fitted parameters closely matched previous results.
The value of time decay constant, τ, is a property of the cell membrane and other environmental conditions such as temperature and pH [29]. In our experiments, pH of the medium was regulated using phosphate buffered saline buffer and we assumed the change in the osmolality of the solution due to evaporation during the course of the experiments (90 min) to be negligible. However, the value of τ could be different if the experiments were performed at 37 instead of room temperature. Nonetheless, in our results, the value of τ did not exhibit a strong dependence on initial pore fraction and electric field strength. However, it was found to be decreasing with increase in the number of pulses. This is consistent with previous reports that showed the membrane resealing kinetics depend on the number of pulses. This observation can be explained by the electro-transport domain theory, reviewed elsewhere [57]. According to this theory, the strength of externally-applied electric field controls the area of cell membrane which is electroporated [36]. However, within the permeabilized area, the extent of permeabilization is not a function of the field strength, but it is controlled by the number and duration of pulses [19,57,36]. Accordingly, under the same electric field strength, 10 pulses led to the lesser extent of the membrane permeabilization than 50 pulses.
6. Summary
Experimental determination of the parameters governing the electroporation-facilitated transport is a resource intensive procedure. In this work, we introduced a simple experimental setup combined with a biophysical model of transport that allowed estimation of the critical electroporation parameters in a single experiment. The parameters that are evaluated using this methodology are: 1) the minimum field strength required for effective electroporation of the given cell type; 2) effective membrane permeability for a given cell-molecule system as a function of the field strength; 3) time that the membrane remains permeable for the concentration of the tested molecule to change 63.2% after the electric field is removed. Despite the idealistic assumptions incorporated in the transport model proposed in this study, this method can facilitate the experimental investigation of the parameters that influence the electroporation efficiency, including the effective range of electric field strength for the delivery/release of different types of target molecules (sugars, mRNA, cDNA, etc.). However, the fluorescent probe used for imaging should be selected so to closely resemble the target molecule in size and charge for a more accurate calculation of permeability coefficient. Further experiments will determine the dependence of pore closure constant τ on the number of pulses, and will allow for the analysis of the electroporation phenomena at a single cell level. We envision that automation of the introduced system will facilitate the application of electroporation-assisted technologies in a variety of technologies in the medicine, biotechnology and food industry where electroporation procedures are commonly utilized.
Acknowledgments
Alireza Abazari held a postdoctoral fellowship from the Natural Sciences and Research Council (NSERC) of Canada. The authors like to thank Dr. Kyle Smith from the Center for Engineering in Medicine and The BioMEMS Resource Center at Massachusetts General Hospital and Harvard Medical School for constructive comments. This research was partially supported by Eshkol Fund, 3-11034/3804851, of Israeli Ministry of Science and Technology.
Footnotes
Transparency document: The Transparency Document associated with this article can be found, in online version.
References
- 1.Neumann E, Schaefer-Ridder M, Wang Y, Hofschneider PH. Gene transfer into mouse lyoma cells by electroporation in high electric fields. EMBO J. 1982 Jan;1(7):841–845. doi: 10.1002/j.1460-2075.1982.tb01257.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Rubinsky B, editor. Irreversible Electroporation. Springer Berlin Heidelberg; Berlin, Heidelberg: 2010. [Google Scholar]
- 3.Golberg A, Belkin M, Rubinsky B. Irreversible electroporation for microbial control of drugs in solution. AAPS PharmSciTech. 2009 Jan;10(3):881–886. doi: 10.1208/s12249-009-9277-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yarmush ML, Golberg A, Serša G, Kotnik T, Miklavčič D. Electroporation-based technologies for medicine: principles, applications, and challenges. Annu Rev Biomed Eng. 2014 Jul;16:295–320. doi: 10.1146/annurev-bioeng-071813-104622. [DOI] [PubMed] [Google Scholar]
- 5.Rubinsky B, Onik G, Mikus P. Irreversible electroporation: a new ablation modality–clinical implications. Technol Cancer Res Treat. 2007;6:37–48. doi: 10.1177/153303460700600106. [DOI] [PubMed] [Google Scholar]
- 6.Weaver JC, Chizmadzhev YA. Theory of electroporation: a review. Bioelectrochem Bioenerg. 1996 Dec;41(2):135–160. [Google Scholar]
- 7.Son RS, Smith KC, Gowrishankar TR, Vernier PT, Weaver JC. Basic features of a cell electroporation model: illustrative behavior for two very different pulses. J Membr Biol. 2014 Dec;247(12):1209–1228. doi: 10.1007/s00232-014-9699-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Delemotte L, Tarek M. Molecular dynamics simulations of lipid membrane electroporation. J Membr Biol. 2012;245(9):531–543. doi: 10.1007/s00232-012-9434-6. [DOI] [PubMed] [Google Scholar]
- 9.Chang DC, Reese TS. Changes in membrane structure induced by electroporation as revealed by rapid-freezing electron microscopy. Biophys J. 1990;58(1):1–12. doi: 10.1016/S0006-3495(90)82348-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee EW, Wong D, Prikhodko SV, Perez A, Tran C, Loh CT, Kee ST. Electron microscopic demonstration and evaluation of irreversible electroporation-induced nanopores on hepatocyte membranes. J Vasc Interv Radiol. 2012;23(1):107–113. doi: 10.1016/j.jvir.2011.09.020. [DOI] [PubMed] [Google Scholar]
- 11.Böckmann RA, de Groot BL, Kakorin S, Neumann E, Grubmüller H. Kinetics, statistics, and energetics of lipid membrane electroporation studied by molecular dynamics simulations. Biophys J. 2008 Aug;95(4):1837–1850. doi: 10.1529/biophysj.108.129437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tarek M. Membrane electroporation: a molecular dynamics simulation. Biophys J. 2005;88:4045–4053. doi: 10.1529/biophysj.104.050617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rols MP. Electropermeabilization, a physical method for the delivery of therapeutic molecules into cells. Biochim Biophys Acta. 2006;1758(3):423–428. doi: 10.1016/j.bbamem.2006.01.005. [DOI] [PubMed] [Google Scholar]
- 14.Potter H, Heller R. Transfection by electroporation. Curr Protoc Neurosci. 2011 doi: 10.1002/0471142301.nsa01es57. [DOI] [PubMed] [Google Scholar]
- 15.Garcia PA, Davalos RV, Miklavcic D. A numerical investigation of the electric and thermal cell kill distributions in electroporation-based therapies in tissue. PLoS One. 2014 Aug;9(8):e103083. doi: 10.1371/journal.pone.0103083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Weaver JC, Smith KC, Esser AT, Son RS, Gowrishankar TR. A brief overview of electroporation pulse strength-duration space: a region where additional intracellular effects are expected. Bioelectrochemistry. 2012 Oct;87:236–243. doi: 10.1016/j.bioelechem.2012.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Neumann E, Toensing K, Kakorin S, Budde P, Frey J. Mechanism of electroporative dye uptake by mouse B cells. Biophys J. 1998 Jan;74(1):98–108. doi: 10.1016/S0006-3495(98)77771-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fernand F, Rubinsky L, Golberg A, Rubinsky B. Variable electric fields for high throughput electroporation protocol design in curvilinear coordinates. Biotechnol Bioeng. 2012 Aug;109(8):2168–2171. doi: 10.1002/bit.24479. [DOI] [PubMed] [Google Scholar]
- 19.Rols MP, Teissié J. Electropermeabilization of mammalian cells. Quantitative analysis of the phenomenon. Biophys J. 1990 Nov;58(5):1089–1098. doi: 10.1016/S0006-3495(90)82451-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Walter A, Gutknecht J. Permeability of small nonelectrolytes through lipid bilayer membranes. J Membr Biol. 1986;90(3):207–217. doi: 10.1007/BF01870127. [DOI] [PubMed] [Google Scholar]
- 21.Pavlin M, Kanduser M, Rebersek M, Pucihar G, Hart FX, Magjarevic R, Miklavcic D. Effect of cell electroporation on the conductivity of a cell suspension. Biophys J. 2005;88(6):4378–4390. doi: 10.1529/biophysj.104.048975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pucihar G, Kotnik T, Miklavcic D, Teissie J. Kinetics of transmembrane transport of small molecules into electropermeabilized cells. Biophys J. 2008;95(6):2837–2848. doi: 10.1529/biophysj.108.135541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.He H, Chang DC, Lee YK. Nonlinear current response of micro electroporation and resealing dynamics for human cancer cells. Bioelectrochemistry. 2008;72(2):161–168. doi: 10.1016/j.bioelechem.2008.01.007. [DOI] [PubMed] [Google Scholar]
- 24.Blumrosen G, Abazari A, Golberg A, Tonner M, Yarmush ML. Efficient Procedure and Methods to Determine Critical Electroporation Parameters. 2014 May;:314–318. [Google Scholar]
- 25.Pauly H, Schwan HP. {Ü }ber die Impedanz einer Suspension von kugelformigen Teilchen mit einer Schale - Ein Modell f{ü }r das dielektrische Verhalten von Zellsuspensionen und von Proteinl{ö }sungen. Z Naturforsch. 1959;14b:125–131. [PubMed] [Google Scholar]
- 26.Kotnik T, Miklavčič D, Slivnik T. Time course of transmembrane voltage induced by time-varying electric fields – a method for theoretical analysis and its application. Bioelectrochem Bioenerg. 1998;45(1):3–16. [Google Scholar]
- 27.Kotnik T, Miklavcic D. Analytical description of transmembrane voltage induced by electric fields on spheroidal cells. Biophys J. 2000;79(2):670–679. doi: 10.1016/S0006-3495(00)76325-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Valic B, Golzio M, Pavlin M, Schatz A, Faurie C, Gabriel B, Teissié J, Rols MP, Miklavcic D. Effect of electric field induced transmembrane potential on spheroidal cells: theory and experiment. Eur Biophys J. 2003;32(6):519–528. doi: 10.1007/s00249-003-0296-9. [DOI] [PubMed] [Google Scholar]
- 29.Saulis G. Pore disappearance in a cell after electroporation: theoretical simulation and comparison with experiments. Biophys J. 1997 Sep;73(3):1299–1309. doi: 10.1016/S0006-3495(97)78163-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bier M, Hammer SM, Canaday DJ, Lee RC. Kinetics of sealing for transient electropores in isolated mammalian skeletal muscle cells. Bioelectromagnetics. 1999;20(3):194–201. doi: 10.1002/(sici)1521-186x(1999)20:3<194::aid-bem6>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 31.Schneider CA, Rasband WS, Eliceiri KW. NIH image to ImageJ: 25 years of image analysis. Nat Methods. 2012 Jun;9(7):671–675. doi: 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dermol J, Miklavčič D. Predicting electroporation of cells in an inhomogeneous electric field based on mathematical modeling and experimental CHO-cell permeabilization to propidium iodide determination. Bioelectrochemistry. 2014 Mar; doi: 10.1016/j.bioelechem.2014.03.011. [DOI] [PubMed] [Google Scholar]
- 33.Pucihar G, Krmelj J, Reberšek M, Napotnik TB, Miklavčič D. Equivalent pulse parameters for electroporation. IEEE Trans Biomed Eng. 2011;58(11):3279–3288. doi: 10.1109/TBME.2011.2167232. [DOI] [PubMed] [Google Scholar]
- 34.Bier M, Chen W, Gowrishankar TR, Astumian R Dean, Lee RC. Resealing dynamics of a cell membrane after electroporation. Phys Rev E Stat Nonlinear Soft Matter Phys. 2002;66(6):3–6. doi: 10.1103/PhysRevE.66.062905. [DOI] [PubMed] [Google Scholar]
- 35.Gowrishankar TR, Pliquett U, Lee RC. Dynamics of membrane sealing in transient electropermeabilization of skeletal muscle membranes. Ann N Y Acad Sci. 1999;888:195–210. doi: 10.1111/j.1749-6632.1999.tb07957.x. [DOI] [PubMed] [Google Scholar]
- 36.Rols MP, Teissié J. Electropermeabilization of mammalian cells to macromolecules: control by pulse duration. Biophys J. 1998;75(3):1415–1423. doi: 10.1016/S0006-3495(98)74060-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mir LM, Gehl J, Sersa G, Collins CG, Garbay JR, Billard V, Geertsen PF, Rudolf Z, O’Sullivan GC, Marty M. Standard operating procedures of the electrochemotherapy: instructions for the use of bleomycin or cisplatin administered either systemically or locally and electric pulses delivered by the CliniporatorTM by means of invasive or non-invasive electrodes. Eur J Cancer Suppl. 2006 Nov;4(11):14–25. [Google Scholar]
- 38.Sersa G, Jarm T, Kotnik T, Coer A, Podkrajsek M, Sentjurc M, Miklavcic D, Kadivec M, Kranjc S, Secerov A, Cemazar M. Vascular disrupting action of electroporation and electrochemotherapy with bleomycin in murine sarcoma. Br J Cancer. 2008 Jan;98(2):388–398. doi: 10.1038/sj.bjc.6604168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Golberg A, Yarmush ML. Nonthermal irreversible electroporation: fundamentals, applications, and challenges. IEEE Trans Biomed Eng. 2013;60(3):707–714. doi: 10.1109/TBME.2013.2238672. [DOI] [PubMed] [Google Scholar]
- 40.Helledie T, Nurcombe V, Cool SM. A simple and reliable electroporation method for human bone marrow mesenchymal stem cells. Stem Cells Dev. 2008 Aug;17(4):837–848. doi: 10.1089/scd.2007.0209. [DOI] [PubMed] [Google Scholar]
- 41.Flanagan M, Gimble JM, Yu G, Xia X, Bunnell BA, Li S. Competitive DNA transfection formulation via electroporation for human adipose stem cells and mesenchymal stem cells. Biol Proced Online. 2012 Jan;14(1):7. doi: 10.1186/1480-9222-14-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Richard I, Ader M, Sytnyk V, Dityatev A, Richard G, Schachner M, Bartsch U. Efficient transfection of neural stem cells by electroporation. ARVO Meet Abstr. 2003 May;44(5):2338. [Google Scholar]
- 43.Haastert K, Mauritz C, Matthies C, Grothe C. Autologous adult human Schwann cells genetically modified to provide alternative cellular transplants in peripheral nerve regeneration. J Neurosurg. 2006 May;104(5):778–786. doi: 10.3171/jns.2006.104.5.778. [DOI] [PubMed] [Google Scholar]
- 44.Lim JY, Park SH, Jeong CH, Oh JH, Kim SM, Ryu CH, Park SA, Ahn JG, Oh W, Jeun SS, Chang JW. Microporation is a valuable transfection method for efficient gene delivery into human umbilical cord blood-derived mesenchymal stem cells. BMC Biotechnol. 2010 Jan;10(1):38. doi: 10.1186/1472-6750-10-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Okita K, Matsumura Y, Sato Y, Okada A, Morizane A, Okamoto S, Hong H, Nakagawa M, Tanabe K, Tezuka K, Shibata T, Kunisada T, Takahashi M, Takahashi J, Saji H, Yamanaka S. A more efficient method to generate integration-free human iPS cells. Nat Methods. 2011 May;8(5):409–412. doi: 10.1038/nmeth.1591. [DOI] [PubMed] [Google Scholar]
- 46.Mitchell DA, Karikari I, Cui X, Xie W, Schmittling R, Sampson JH. Selective modification of antigen-specific T cells by RNA electroporation. Hum Gene Ther. 2008 May;19(5):511–521. doi: 10.1089/hum.2007.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Michiels A, Tuyaerts S, Bonehill A, Heirman C, Corthals J, Thielemans K. Delivery of tumor-antigen-encoding mRNA into dendritic cells for vaccination. Methods Mol Biol. 2008 Jan;423:155–163. doi: 10.1007/978-1-59745-194-9_10. [DOI] [PubMed] [Google Scholar]
- 48.Weiss JM, Allen C, Shivakumar R, Feller S, Li LH, Liu LN. Efficient responses in a murine renal tumor model by electroloading dendritic cells with whole-tumor lysate. J Immunother. 2005 Jan;28(6):542–550. doi: 10.1097/01.cji.0000179437.95335.23. [DOI] [PubMed] [Google Scholar]
- 49.Golberg A, Rubinsky B. Transport in Biological Media. Elsevier; 2013. Mass transfer phenomena in Electroporation; pp. 456–492. [Google Scholar]
- 50.Pucihar G, Miklavčič D, Kotnik T. A time-dependent numerical model of transmembrane voltage inducement and electroporation of irregularly shaped cells. IEEE Trans Biomed Eng. 2009;56(5):1491–1501. doi: 10.1109/TBME.2009.2014244. [DOI] [PubMed] [Google Scholar]
- 51.Pucihar G, Kotnik T, Valič B, Miklavčič D. Numerical determination of transmembrane voltage induced on irregularly shaped cells. Ann Biomed Eng. 2006;34(4):642–652. doi: 10.1007/s10439-005-9076-2. [DOI] [PubMed] [Google Scholar]
- 52.Pavlin M, Leben V, Miklavcic D. Electroporation in dense cell suspension-theoretical and experimental analysis of ion diffusion and cell permeabilization. Biochim Biophys Acta. 2007;1770(1):12–23. doi: 10.1016/j.bbagen.2006.06.014. [DOI] [PubMed] [Google Scholar]
- 53.Schmeer M, Seipp T, Pliquett U, Kakorin S, Neumann E. Mechanism for the conductivity changes caused by membrane electroporation of CHO cell-pellets. Phys Chem Chem Phys. 2004 Dec;6(24):5564. [Google Scholar]
- 54.Pucihar G, Kotnik T, Miklavcic D, Teissié J. Kinetics of transmembrane transport of small molecules into electropermeabilized cells. Biophys J. 2008;95:2837–2848. doi: 10.1529/biophysj.108.135541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Weaver JC. Electroporation: a general phenomenon for manipulating cells and tissues. J Cell Biochem. 1993 Apr;51(4):426–435. doi: 10.1002/jcb.2400510407. [DOI] [PubMed] [Google Scholar]
- 56.Maherani B, Arab-Tehrany E, Kheirolomoom A, Geny D, Linder M. Calcein release behavior from liposomal bilayer; influence of physicochemical/mechanical/structural properties of lipids. Biochimie. 2013 Nov;95(11):2018–2033. doi: 10.1016/j.biochi.2013.07.006. [DOI] [PubMed] [Google Scholar]
- 57.Escoffre JM, Portet T, Wasungu L, Teissié J, Dean D, Rols MP. What is (still not) known of the mechanism by which electroporation mediates gene transfer and expression in cells and tissues. Mol Biotechnol. 2009 Mar;41(3):286–295. doi: 10.1007/s12033-008-9121-0. [DOI] [PubMed] [Google Scholar]


