Proton Transport Mechanism of M2 Proton Channel Studied by Laser-Induced pH Jump

Abstract

The M2 proton transport channel of the influenza virus A is an important model system because it conducts protons with high selectivity and unidirectionally when activated at low pH, despite the relative simplicity of its structure. Although it has been studied extensively, the molecular details of the pH-dependent gating and proton conductance mechanisms are incompletely understood. We report direct observation of the M2 proton channel activation process using a laser-induced pH jump coupled with tryptophan fluorescence as a probe. Biphasic kinetics is observed, with the fast phase corresponding to the His37 protonation, and the slow phase associated with the subsequent conformation change. Unusually fast His37 protonation was observed (2.0 × 10¹⁰ M⁻¹ s⁻¹), implying the existence of proton collecting antennae for expedited proton transport. The conformation change (4 × 10³ s⁻¹) was about 2 orders of magnitude slower than protonation at endosomal pH, suggesting that a transporter model is likely not feasible.

Graphical Abstract

■ INTRODUCTION

Protein-mediated proton transport through active pumps or passive channels plays a crucial role in many biological processes, including oxidative phosphorylation, photophosphorylation, viral replication, and enzyme catalysis. The structure and function of proton pumps and channels have been the subjects of intensive studies aimed at a better understanding of proton transfer mechanisms.^1,2 The M2 proton channel of the influenza virus has been one of the most widely studied proton channels because of its relative simplicity and promise as a target for anti-influenza drug development. M2 is an ideal model system because it forms a minimalistic ion channel with interesting characteristics such as pH-dependent gating, high selectivity,³ and unidirectional conductance.⁴

After endocytosis of a viral particle, the homotetrameric M2 proton channel is activated under lysosomal acidic pH, switching on proton conductance and acidifying the viral lumen to release viral ribonucleoproteins into the host cell cytosol.⁵ The gating and proton conductance mechanisms that control these processes have been investigated extensively.^6–8 It is generally accepted that the His37 tetrad in the trans-membrane domain is repeatedly protonated and deprotonated, likely alternating between the 2⁺ and 3⁺ states during the proton translocation cycle. This so-called proton shuttle mechanism of M2 proton channel is supported by the slow proton conduction rate (10–1000 H⁺/s), rectification, and the large deuterium isotope effect.^6,8,9 The shuttle mechanism also explains the leveling off of the conductance rate below pH 6.^10,11

The conformational switch model postulates that proto-nation of His37 plays a central role in the gating of M2 proton channel.⁶ In this model, the M2 proton channel forms a tightly packed tetramer structure under basic to neutral pH conditions with the His37 tetrad postulated to be in protonation states between 0 and +2. Positively charged residues may be stabilized in the relatively low dielectric environment of the channel interior by hydrogen bonding with water molecules and cation–π interactions (Figure 1a). As the pH is lowered to its endosomal value, the remaining histidines of the His37 tetrad are protonated, increasing the repulsion among the positively charged imidazolium cations, which subsequently induces dilation of the C-terminal ends of the M2 structure (Figure 1b).^6,8,12–18 In this activated form at acidic pH, the indole side chains of the Trp41 tetramer located near the C-termini, which were initially packed tightly at high pH, are loosened and more dynamic, and the channel becomes more accessible to water molecules.^7,19–21 A pH-dependent channel conformation change is supported by high-resolution structures at various pH values that exhibit a more dilated C-terminus at lower pH,⁶ which is in agreement with molecular dynamics (MD) simulations.²² Moreover, NMR studies have observed peak broadening at low pH, indicating increased conformational fluctuations of the activated form.^15,18,23 A detailed model of the channel opening and acid activation mechanism has been proposed based on multiscale reactive molecular dynamics and QM/MM calculations of the explicit proton transport behavior, including proton shuttling and charge delocalization on the His37 tetrad and pore water molecules.^24,25 This model accurately fits the available experimental data for the conductance and deprotonation rates.

Figure 1.

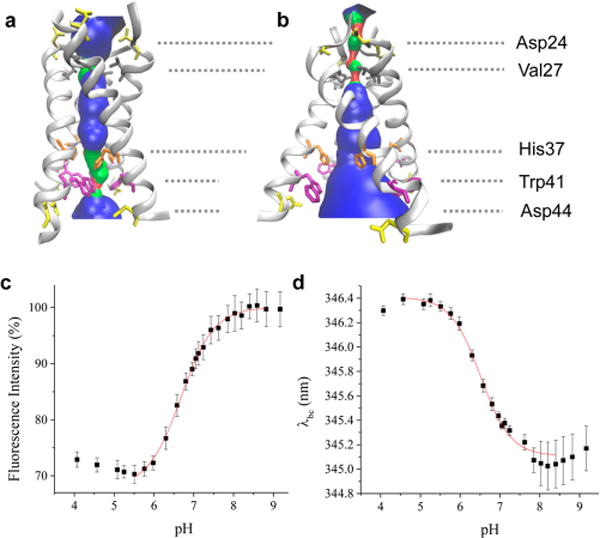
pH dependence of the equilibrium structure of the M2TM tetramer. (a) M2TM structure from ssNMR spectroscopy at pH 6.5 (PDB ID 2L0J). (b) 3.5 Å X-ray structure of M2TM at pH 5.3 (PDB ID 3C9J). Pore-lining residues and aspartic acid side chains are shown as sticks. The pore radius profile indicated with blue shading was calculated using the HOLE program.³⁷ (c) pH dependence of Trp fluorescence intensity and (d) of Trp fluorescence barycenter for the M2TM tetramer reconstituted in a DPPC bicelle. Solid red lines are fits to the Hill equation.

While this model is supported by equilibrium data from various techniques, the interconversion between opened (activated, Figure 1b) and closed (inactivated, Figure 1a) conformations of the C-terminus has not been observed directly. Furthermore, there are still many gaps to be filled to complete the proton conductance mechanism of M2 proton channel. In particular, it is still unclear whether proton conductance is transporter-like, in which the M2 proton channel alternates between closed and opened conformers during each proton transport cycle.²⁶ The rate of His37 protonation and conformational interconversion between the activated and inactivated forms need to be measured to resolve this question. However, most studies of M2 function have been conducted under equilibrium conditions at constant pH, and presteady-state kinetics experiments have not been possible, primarily because the kinetics of the pH-dependent processes are too fast. Specifically, protonation of the His37 tetrad along with the M2 proton channel activation occurs in the submillisecond time regime, which is inaccessible by conventional rapid mixers.

We have developed a new approach to study pH induced protein conformational dynamics that employs a rapid laser-induced pH jump to trigger M2 activation, coupled with time-resolved tryptophan (Trp) fluorescence spectroscopy to probe the protein response. The pH jump is accomplished by photolysis of a photoacid, which releases free H⁺ in a few tens of nanoseconds.^27–29 Similar approaches have been used to measure submillisecond time scale kinetics of protonation and subsequent processes, such as proton transfer processes in GFP variants,^30,31 α-helix formation in poly-L-glutamate,^32,33 histidine ligand dissociation from the heme of partially denatured cytochrome c,³⁴ acid-induced unfolding of myoglobin,³⁵ and leuicine zipper folding.³⁶ In the present study, native Trp fluorescence was utilized as a probe to reveal the proton transfer and channel activation mechanism without perturbing the structure or dynamics of the system. This approach is technically challenging and represents the first instance of using Trp fluorescence as a nonperturbing probe for laser pH-jump experiments.

Using this approach, we detect the His37 protonation and the subsequent response of M2 proton channel on the submillisecond time scale. The Trp fluorescence decays in response to the rapid pH jump, in two well-separated kinetics phases. The fast phase is attributed to the protonation of His37 based on its pH dependence, and the slow phase is assigned to the subsequent conformation change, specifically C-terminus dilation, confirming previous postulations from equilibrium studies. The His37 protonation kinetics is comparable to that of a surface-exposed ionizable residue, implying the presence of proton-collecting antenna residues near the channel orifice. The rate of conformational change of M2 proton channel after protonation of the His37 tetrad is about 2 orders of magnitude slower than the protonation rate at lysosomal pH, which is difficult to reconcile with a transporter-like mechanism. Instead, we propose that each proton transport cycle does not necessarily require a conformational change once M2 is activated.

■ EXPERIMENTAL SECTION

Peptide Synthesis

Influenza A Udorn strain M2 proton channel transmembrane domain (M2TM) (Ser22 to Leu46: SSDPLVVAASII-GILHLILWILDRL) was synthesized via standard 9-fluorenylmethoxycarbonyl (Fmoc)-based solid-phase chemistry in a microwave peptide synthesizer (CEM). Fmoc-PAL-PS resin (Applied Biosystems, Foster City, CA) was used to form a peptide amide. Peptide cleavage was performed using a cocktail of 90% trifluoroacetic acid (TFA), 5% thioanisole, 3% ethanedithiol, and 2% anisole for 180 min. The resulting mixture was filtered and precipitated in ice-cold ether. The peptide was purified by reverse phase-HPLC on a C-3 preparative column with a linear gradient of buffer A (0.1% TFA in H₂O) and buffer B (60% isopropyl alcohol, 30% acetonitrile, 10% H₂O, 0.1% TFA).³⁸ The peptide eluted at 65% of buffer B. The purified peptide was verified by MALDI mass spectroscopy and then lyophilized.

Sample Preparation

All detergents and lipids were purchased from Avanti Polar Lipids. The concentration of M2TM in ethanol was calculated from its UV–vis absorption spectrum using ε₂₈₀ = 5850 M⁻¹·cm⁻¹.³⁹ M2TM tetramers were reconstituted in bicelles by codissolving 273 μg of M2TM peptide (0.1 μmol) in ethanol with 24.1 mg of 1,2-diheptanoyl-sn-glycero-3-phosphocholine (DHPC) (50 μmol) and 7.3 mg of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) (10 μmol) in chloroform. The peptide to lipid ratio (M2TM:DPPC) was 1:100 (mol:mol) to ensure that M2TM tetramer was sufficiently formed in the lipid bilayer.^40,41 After thorough mixing, the lipid cake was prepared by drying under a N₂ stream and then under high vacuum for 2 h. The lipid cake was hydrated by adding 1 mL of buffer solution and then repeating multiple freeze/thaw cycles. In every freeze and thaw cycle, the solution was thoroughly sonicated, and the cycle was repeated at least 10 times until the solution became clear. Drug binding is a well-established indicator of the formation of the functional tetramer; for our conditions, amantadine binding to the M2 tetramer was verified by circular dichroism (CD) and fluorescence titrations (Figures S5–S7).

1-(2-Nitrophenyl)ethyl sulfate (NPE-sulfate) was synthesized as previously described.⁴² The concentration of NPE-sulfate was calculated from its UV–vis absorption spectrum using ε₃₅₅ = 500 M⁻¹·cm⁻¹. To prepare CO₂-free water, deionized water was boiled for 10 min and cooled under an Ar atmosphere. For the pH jump experiment, a bicelle sample containing 0.8 mM NPE-sulfate, 10 μM M2TM, 1 mM DPPC, 5 mM DHPC, and 100 mM NaCl was prepared and its pH was adjusted by NaOH under a N₂ stream. For steady-state measurements, samples in the pH range 3.0–7.5 were prepared in 100 mM citrate–phosphate buffer, and samples in the pH range 7.5–9.0 were prepared in 100 mM Tris buffer.

Laser-Induced pH Jump Probed with Time-Resolved Trp Fluorescence

A schematic of the pH jump experiment is shown in Figure S1. A third harmonic pulse (355 nm, 10 ns, maximum power: ~50 mJ) from a Q-switched Nd:YAG laser (Quanta-ray GCR IV, Spectra Physics) was passed through a quartz cuvette (2 mm × 10 mm) along the 2 mm path to photolyze the photoacid. The probe beam (283 nm) was obtained by frequency tripling the 849 nm output of a mode-locked femtosecond Ti:sapphire laser (Mira 900, Coherent). Pump and probe beams were made colinear using a dielectric mirror (CVI Melles Griot) to reflect the 355 nm pump and transmit the 283 nm probe to ensure they are completely overlapped in the sample. The pump beam diameter was about 3 mm, and the probe beam illuminated the center of the activated volume. The fluorescence signal was measured orthogonally to the pump beam. The fluorescence emission was filtered by long-pass filters to reject light at wavelengths below 300 nm and then detected by a gated PMT (Hamamatsu, H11526). To minimize stray light, two polarizers were installed in a cross-oriented configuration. A delay generator (DG535, Stanford Research System) controlled the timing of the gating signal. A photodiode detected the pump laser pulse as a timing signal for triggering data acquisition by a digitizing oscilloscope (Lecroy Wavesurfer 62MXS-B, 600 MHz, 10 Gs/s). Under ideal conditions with minimal scattering, the time resolution is limited by the laser pulse width (10 ns) and the detector response (similar time scale), but with a large scattering peak and the necessity to gate the detector off/on, the actual time resolution is limited to ~2.5 μs. During the pH jump experiment, the sample is illuminated by the probe beam only during data acquisition by using a shutter (Uniblitz), and the sample cuvette was flushed with nitrogen to prevent CO₂ uptake. A temperature-controlled cuvette holder regulated the sample temperature. The concentration of NPE-sulfate was limited to 0.8 mM because it absorbs the 280 nm probe beam intensively. Because Trp fluorescence is weak and single-shot experiments produce a low signal-to-noise ratio (SNR), a probe beam power of ~3 mW was used to increase the SNR. Baseline correction was accomplished by subtracting spectra measured without the pump beam. The initial pH was kept below pH 8.0 to avoid a high concentration of OH⁻, which rapidly scavenges H⁺ released from the photoacid. The time constant of protonation of WK dipeptide measured with this setup agrees with that of diffusion-limited protonation of pH indicator molecules.

Steady-State Fluorescence Measurements

All fluorescence spectra were measured by exciting Trp at 280 nm using a Fluoromax (Jovin Yvon Horiba) dual fluorometer. The spectral barycenter (λ_bc) was calculated according to the following equation:

$${\lambda }_{\mathrm{\text{bc}}}=\frac{{\sum }_n(I_n{\lambda }_n)}{{\sum }_n{I}_n}$$

■ RESULTS AND DISCUSSION

Tryptophan Fluorescence Detects Protonation of His37 Tetrad of M2TM in DPPC Bicelles

The transmembrane domain of M2 proton channel (residues 25–46, M2TM) was used in this study because it represents a minimal but sufficient model that exhibits most of the functions of full length M2, including homotetrameric channel formation, selective proton transport, gating, vectorial conductance, and drug binding.^38,39,43 M2TM proton channel exhibits a high proton selectivity of at least 10⁶ over other biological monovalent cations such as potassium or sodium ions.³ His37 is essential for this high selectivity as well as acid activation of M2TM proton channel. M2TM proton conductance is also unidirectional, from N-terminus to C-terminus. This rectification likely originates from Trp41 enclosing the N-terminal exit of the TM domain, which acts as a gate that prevents backward flow of protons.^4,25 M2TM was reconstituted as the homotetramer in DPPC:DHPC bicelles with q (DPPC:DHPC) = 0.2 and a diameter of about 4 nm,^44,45 to minimize light scattering from the membrane. Previous work has demonstrated that M2 proton channel can be reconstituted in bicelles with its native conformation and activity.⁴⁶

The Trp fluorescence of M2TM in DPPC bicelles exhibits a pH dependence as shown in Figure 1, in agreement with previous studies.^47,48 As the pH is made acidic, the fluorescence intensity decreases (Figure 1c) and its barycenter (λ_bc) is red-shifted (Figure 1d) due to protonation of the His37 tetrad and the associated conformational rearrangement. The fluorescence intensity is a sensitive probe of the protonation state of His37 because protonated imidazole is an efficient quencher of Trp fluorescence; therefore, its interaction with Trp41 causes a decrease in the fluorescence quantum yield.⁴⁹ Trp41 and His37 are located one helical turn away from one another and form a stabilizing cation–π intramonomer interaction when His37 is protonated.⁵⁰ This effect is additive as the His37 is progressively protonated to form multiple cation–π interactions. The fluorescence barycenter is sensitive to the degree of hydration of Trp, with increasing hydration causing it to red shift. At pH 8, the λ_bc of M2TM was 345.1 nm whereas at pH 5 it was 346.4 nm, indicating the Trps of M2TM in the lipid bilayer are more hydrated at acidic pH. This observation is consistent with the postulated C-terminal dilation of M2TM (Figure 1b), which alters the accessibility of Trp to water molecules as indicated by Stern–Volmer fluorescence titration^48,51 and ssNMR experiments.¹⁹

Because the Trp fluorescence reports on both the progressive protonation of the His37 tetrad and on the channel opening once the more fully protonated states are populated, we expected to observe multiple steps in the titration from pH 8 to 5. However, both the intensity and barycenter profiles were adequately fit to a single transition as shown in Figure 1. Each titration curve was fit with the Hill equation in an attempt to account for multiple proton binding steps and to assess possible cooperativity, yielding a pK_a value of 6.68 ± 0.03 and a Hill coefficient of 1.1 ± 0.1 for fluorescence intensity (Figure 1c), and a pK_a value of 6.51 ± 0.03 and Hill coefficient of 1.2 ± 0.1 for the barycenter (Figure 1d). The inability to resolve multiple steps may be due to significant overlap of the transitions, combined with the lack of specificity of the fluorescence changes. Above pH 8 and below pH 5.5, the pH profile does not reach a stable baseline, most likely due to the decreased stability of the tetramer above and below the physiological pH range,^39,43 making it difficult to fit the data to a multistate model. Nevertheless, the different apparent pK_a values observed for the fluorescence intensity and barycenter suggests that the transition is not a simple two-state process. Furthermore, the protonation and channel opening processes are cleanly separated in time as shown below, making it possible to distinguish the protonation steps and their pK_a values in the pH jump kinetics experiments.

M2TM Proton Channel Dynamics Triggered by a Laser pH Jump

Pulsed laser excitation of NPE-sulfate results in photochemical release of a proton and thus a jump to lower pH in ~100 ns; the transient fluorescence response is measured by continuous excitation of Trp at 280 nm and integrating the fluorescence signal as a function of time using a fast PMT detector. No change in Trp fluorescence was observed for control experiments with M2TM sample containing no NPE-sulfate, confirming that the transient fluorescence decrease is due to the pH jump and not a bleach of the Trp absorption by the intense pump pulse. Figure 2a shows the transient Trp fluorescence signal in response to the laser pH jump from pH 8.0 to 6.0 for M2TM reconstituted in DPPC bicelles. The fluorescence transient was fit to a double exponential function in this case, although jumps to higher final pH values were well fit by a single exponential.

Figure 2.

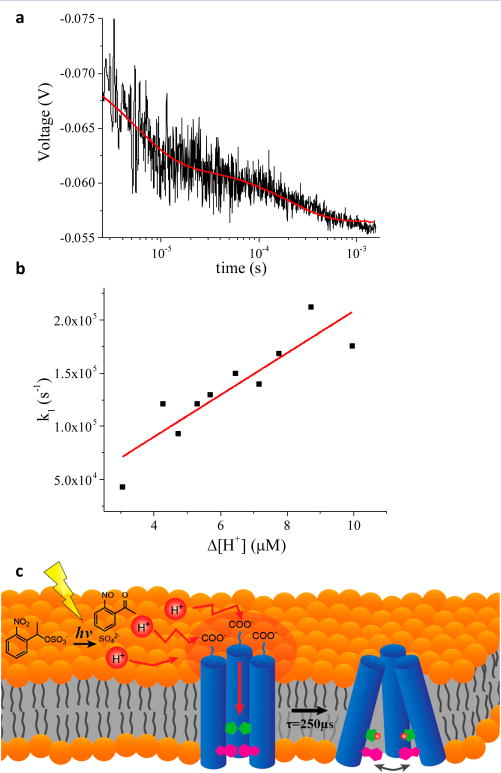
M2TM dynamics triggered by a laser-induced pH jump. (a) Time-dependent Trp fluorescence emission signal of a solution containing NPE-sulfate (0.8 mM) and M2TM reconstituted in a DPPC bicelle following a pH jump from pH 8.0 to 6.0, initiated with a 355 nm laser pulse. The data represent an average of 10 laser shots and were fit to a double exponential decay (red curve). (b) Dependence of the rate constant k₁ of M2TM as a function of Δ[H⁺] at 25 °C. The red line is a linear fit to the data. (c) Schematic representation of the proton transfer pathway and proton channel activation process.

The fast phase (k₁) showed a Δ[H⁺] dependence (Figure 2b), indicating that this process is the bimolecular protonation of His37. In contrast, the slow phase (k₂) did not exhibit any Δ[H⁺] dependence within the noise of the measurement (Figure S8) and the rate was about 2 orders of magnitude slower than the fast phase. Hence, k₂ is ascribed to a conformational change subsequent to His37 protonation that increases the accessibility of the tryptophans to water, further quenching the fluorescence. A schematic representation of these processes is shown in Figure 2c. The protonation rate constant, k_p = (2.0 ± 0.4) × 10¹⁰ M⁻¹ s⁻¹ and deprotonation rate constant k_d = (1 ± 2) × 10⁴ s⁻¹ were obtained by fitting the [H⁺]-dependent transients to a pseudo-first-order kinetics model (Figure 2b). Considering that the previously measured rate of protonation of a solvent-exposed His is 5 × 10⁹ M⁻¹ s⁻¹, in agreement with the prediction of the Debye–Smouluchow-ski equation for the protonation of an uncharged residue on a protein surface,¹ a protonation kinetic constant of His37 that is comparable to that of a surface-exposed carboxylate residue might seem unreasonable. The problem is exacerbated by the location of His37, buried in a pore with a constricted diameter, because histidine in this less accessible environment might be expected to exhibit slower protonation kinetics compared to an exposed histidine residue.

Unusually rapid proton transfer from bulk solution to a protonatable residue inside a protein has been observed previously for other proton channels and enzymes.⁵² For example, the rate of proton transfer from bulk solution to the catalytic center of cytochrome c oxidase from Rhodobacter sphaeroides (CcO) was estimated to be 10¹⁰ M⁻¹·s⁻¹ at pH 6.5 based on the steady-state O₂ reduction rate, and increased to ~7 × 10¹¹ M⁻¹·s⁻¹ at pH 9, assuming that protonation is the rate-limiting step.^53,54 Protonation kinetics of E286 near the catalytic center was measured by a flow-flash experiment at pH 9.8, from which a rate of greater than 2 × 10¹³ M⁻¹·s⁻¹ was determined for proton transfer through the D-pathway.⁵⁵ Kinetics of proton-coupled electron transfer in CcO triggered by CO photolysis at pH 9.5 showed a proton transport rate of ~2 × 10¹³ M⁻¹·s⁻¹ through the K-pathway.⁵⁶ For bacterial reaction centers at pH 8, a proton transport rate of ~1.5 × 10¹¹ M⁻¹·s⁻¹ was calculated from the steady-state turnover rate.⁵³ A fast protonation rate of 4 × 10¹¹ M⁻¹·s⁻¹ was measured for a protonatable residue in a Ca²⁺ channel.⁵⁷ The proton conductance rate of the CF₀, proton channel of H⁺-ATPase, was 2 × 10⁵ s⁻¹ in the range of pH 5.6 to 8.0, which corresponds to a proton transfer rate in the range of 8 × 10¹⁰ to 2 × 10¹³ M⁻¹·s⁻¹.⁵⁸ Finally, the high catalytic activity (7000 s⁻¹) of [FeFe]-hydrogenase from Desulfovibrio desulfurican at pH 8 requires a rapid proton uptake rate of ~1.5 × 10¹² M⁻¹·s⁻¹.⁵⁹

All of these examples exhibit protonation rates exceeding the diffusion-limited rate constant of proton transfer in aqueous solution (2–6 × 10¹⁰ M⁻¹·s⁻¹). Protonated groups acting as a proton reservoir might facilitate the enhanced proton transport rates in some of these systems. For example, in CcO protonated E286 acts as a primary proton donor for both the pumping and chemical steps in O₂ reduction. Proton antennas on the protein surface have been suggested as another explanation for enhanced proton transport rates. Ionizable residues near the entrance of the proton transfer pathway can effectively capture protons from bulk solution and then rapidly funnel them toward the channel orifice.⁶⁰ This idea has been tested for CcO by replacing ionizable residues near the entrance of proton transfer pathway with nonionizable residues, which slows the proton relay.^56,61–63

We speculate that the higher than diffusion-limited protonation rate of the His37 tetrad in M2TM is due in part to such a proton-collecting antenna. Both influenza A and B M2 proton channels have negatively charged residues near the channel entrance which are highly conserved among different strains, specifically Asp21 and Asp24 for influenza A, and Glu3 for influenza B M2 proton channel. Because M2TM tetramer has only Asp24, a total of four aspartic acid carboxylate side chains in the ectodomain form a possible proton-collecting antenna as shown in Figure 3a. Each negatively charged carboxylate has a coulomb cage, in which electrostatic interaction between positively charged proton and negatively charged residue is stronger than the thermal energy (k_BT). Due to their close proximity, their coulomb cages can merge and widen the proton-capturing surface network, enhancing proton harvesting from bulk aqueous phase (Figure 3b). Because the four aspartic acids work collectively, the apparent kinetic constant of protonation can exceed that of the diffusion-limited protonation rate of a single aspartic acid. We emphasize that this model is testable by mutation of Asp24 to a nonionizable residue.

Figure 3.

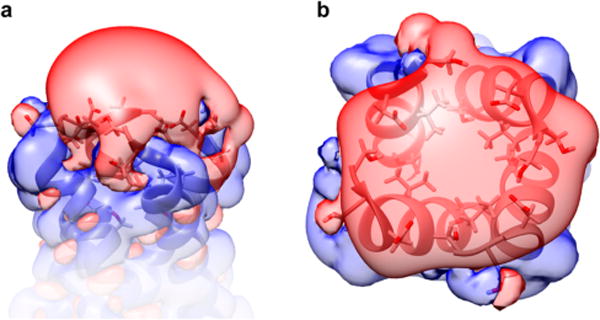
Electrostatic properties of the N-terminal region of M2TM tetramer (PDB ID 2L0J). (a) Side view and (b) top view of potential isocontour surfaces, shown at +1 kT/e (blue) and −1 kT/e (red). Electrostatic potential was computed using the Adaptive Poisson–Boltzmann Solver (APBS) software package⁶⁹ for an ionic strength of 100 mM and fixing the charge of the N-terminus at zero.

There is growing evidence that protons can diffuse through the membrane–water interface with a faster diffusion rate than in bulk aqueous solution. A more rapid protonation rate of the pH indicator fluorescein on membrane surfaces has been observed experimentally compared to that in bulk solution, although the mechanism is not clearly understood.^64–68 Also, the NPE-sulfate photoacid used in the present work can interact with lipid headgroups, and it is adsorbed on a phosphatidylcholine (PC) membrane surface with an adsorption constant of ~100 M⁻¹ (Figure S2). Interaction with the membrane increases the concentration of photoacid as well as released protons near the membrane surface compared to the bulk. Coupled to enhanced interfacial proton diffusion, this may expedite proton transport to M2TM.

After rapid initial protonation of the aspartic acid groups at the channel entry, the protons must dissociate to enter the channel. Considering the Asp pK_a of ~4, the deprotonation rate would be about 10⁶ s⁻¹, meaning proton dissociation occurs within 1 μs. Following dissociation, protons are likely transported to the His37 tetrad within the pore through water wires that are formed by fluidic water molecules hydrating the pore.⁷⁰ Before protons enter the channel they pass through the Val27 neck, which is narrow enough to break the water wire and therefore might slow proton entry into the pore to some extent. However, MD simulations suggest that the impact of the Val27 neck may not be significant because it dynamically interconverts between open and closed states with lifetimes in the nanosecond regime. The fast interconversion may allow water molecules to form a transient hydrogen bonding network to facilitate proton transport through the Val27 neck.^26,71,72 The proton free energy profile (PMF) calculated by multiscale reactive molecular dynamics combined with QM/MM shows a relatively low 4.7 kcal/mol barrier from the viral exterior to the Val27 in the unprotonated state, which could be partially compensated by the proton gradient.²⁵ The PMF also shows a barrier from Val27 to His37 that might be due to electrostatic repulsion between the positively charged His37 and the incoming proton, hindering proton transfer. Hence, the overall protonation rate of His37 is faster than those of ionizable residues inside a pore without proton-collecting antenna residues but in the range of the diffusion-limited rate due to the Val27 neck. This protonation rate is also in agreement with the rapid NH⋯N exchange rate of His37 (10⁵ s⁻¹) measured by ssNMR at pH 5.2.⁷³

We assign the slow kinetics phase to a conformation change of the channel, specifically C-terminus dilation subsequent to His37 protonation. Opening of the channel produces a more hydrated environment that further quenches the Trp fluorescence. The rate of channel opening was calculated as k₂ = (4 ± 2) × 10³ s⁻¹ from k₂^app. Compared to k₁, it is about 2 orders of magnitude slower, suggesting that the interconversion between activated and inactivated conformers might not occur during proton conductance. The proton conductance rate of M2 proton channel has been reported in the range of 10–1000 s⁻¹. Because the conformation change can be completed within a single conductance cycle at the upper limit of this range, the transporter model cannot be completely ruled out. The reverse transition from the open to closed conformation is likely faster compared to the forward one, because the membrane exerts lateral pressure in the direction of the closed state. Because the protonation rate is much faster than any conformational rearrangement of channel backbones, however, it is more likely that deprotonated His37 would be reprotonated before the conformation change proceeds. This may explain why a large-amplitude motion between activated and inactivated conformations has not been observed by NMR under equilibrium conditions. However, the transporter model might still be feasible under certain conditions for which the proton entry rate is significantly slowed. It was proposed that the Val27 valve is blocked in the activated form, which might provide enough time for the channel to return to its closed form.²⁶ In counterpoint, MD simulations⁷² and more rigorous multiscale reactive molecular dynamics combined with QM/MM calculations²⁴ suggested that Val27 is not completely closed even when three or four His37 are protonated. The simulations are consistent with NMR experiments that reveal a highly dynamic structure of the activated channel that allows the Val27 valve to fluctuate between open and closed configurations.

The rate-limiting step for proton conductance is thought to be proton dissociation from His37. Considering the proto-nation rate of (4 ± 2) × 10¹⁰ M⁻¹·s⁻¹ and the pK_a ~ 6.5 of His37, it follows that the deprotonation rate is ~10⁴ s⁻¹, which is one to 3 orders of magnitude faster than the reported conductance rate. This disparity can be rationalized by futile cycles, in which protons are dissociated back in the direction of the channel entrance instead of out the channel exit. It could also be explained by the role of the Trp41 gate, because the calculated free energy barrier is highly asymmetric with a significantly higher barrier for His37 deprotonation.^24,25 The conductance is increased when Trp41 is mutated to Cys, Gly, Ala, or Phe, indicating that Trp41 slows proton transport from His37 to the viral lumen.⁴

Resolution of Multiple His37 Tetrad Protonation Steps

In contrast with steady-state experiments, the pH jump measurements resolve the individual contributions of the protonation and conformation change steps to the fluorescence intensity change, because they are well separated in time. The fast phase originates from protonation of the His37 tetrad, and only a single lifetime was observed for this process, although multiple protonation steps occur. Because the protonation rates are all similar to one another, different deprotonation rates would be necessary to produce different pK_a values for the various His37 of the tetrad. The slow phase corresponds to the conformation change, and thus it occurs only after protonation of the third His37, but not before.

We built a polyprotic model (Figure 4a) to describe the equilibrium pH dependence of the Trp fluorescence, based on the kinetic resolution of the protonation and conformational change steps and a few reasonable assumptions. The amplitude change of both fast and slow phases as a function of final pH represents the population change of each protonation state. The M2TM tetramer can adopt multiple protonation states of the His37 tetrad, from 0 to 4⁺ (Figure 4a). After a pH jump, the population distribution of these protonation states is shifted to more highly protonated states. The amplitudes of the fast and slow kinetic phases as a function of final pH are plotted in Figure 4b. A rough estimate of the maximum signal change as a percent of the total fluorescence intensity for each kinetics phase was obtained from the fits, giving 20 ± 3% for the fast phase and 10 ± 3% for the slow phase. Because the fast phase corresponds to a convolution of all four protonation steps of the His37 tetrad, if we assume that the protonation of each His37 contributes equally to the Trp fluorescence quenching, then each step reduces the total fluorescence intensity by 5%. If we also assume that the conformation change occurs only for the transition from the 2⁺ to 3⁺ state (consistent with simulations), the additional 10% decrement of the fluorescence intensity in the slow phase can be attributed to this transition. As a result, the relative fluorescence intensity was modeled as 100% for the 0 state, 95% for the 1⁺ state, 90% for the 2⁺ state, 75% for the 3⁺ state, and 70% for the 4⁺ state. Finally, we assumed that protonation steps 1 and 2 (pK_a1) and steps 3 and 4 (pK_a2) are cooperative, because the change in fluorescence intensity occurred in such a narrow range (pH 7.5–6), and cooperativity was observed in other studies of M2.^25,74

Figure 4.

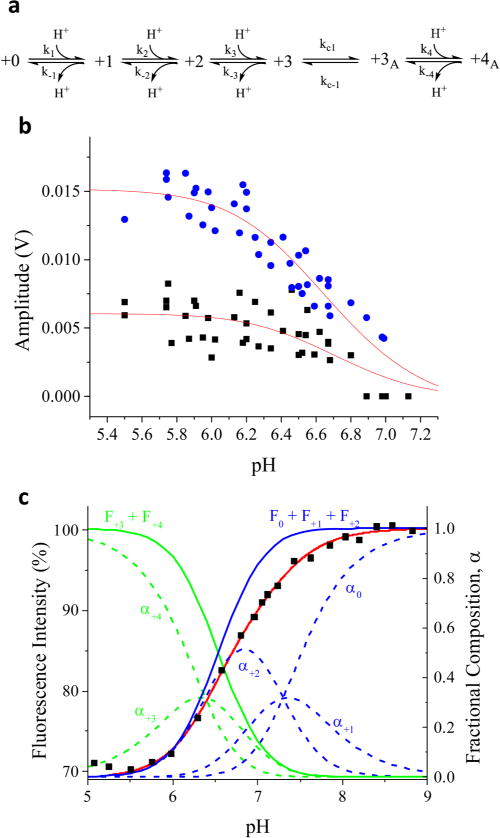
Kinetic resolution of multistep protonation of M2TM. (a) Reaction scheme for progressive protonation and conformational change of M2TM. (b) Fluorescence amplitude change of k₁^app (circles) and k₂^app (squares) for M2TM in DPPC bicelles measured by pH jumps from an initial pH 7.5, as a function of final pH at 25 °C. (c) Steady-state pH dependent M2TM fluorescence intensity change (squares) along with the fit (red line) based on the polyprotic model shown in part a, with fluorescence intensities of 100% for 0 state, 95% for +1 state, 90% for +2 state, 75% for +3 state, and 70% for +4 state. The fraction of each protonation state of M2TM (dashed lines) was also calculated from the pK_a values obtained from this model.

We tested whether this polyprotic model fits the equilibrium pH-dependent fluorescence data (Figure 4c). The model has two adjustable parameters, pK_a1 and pK_a2. The fitting procedure calculates the population of each state, from which its weighted contribution to the total fluorescence intensity is determined based on the model described above (see Supporting Information for fit equations). The procedure is iterated to produce the best fit to the observed fluorescence intensities (red curve in Figure 4c), yielding pK_a1 = 6.38 ± 0.03 and pK_a2 = 7.30 ± 0.03. This model fits that data well and is more physically realistic than the overly simplified monoprotic model that we used at first (Figure 1c). The pK_a values are relatively high compared to previously reported values, but this is likely due to different membrane environments. A wide range of pK_a values has been reported for the His37 tetrad of M2TM, which has been rationalized in terms of the various conditions employed in these studies.²³ It is possible that our experiments in DPPC bicelles shift the pK_a values up due to the lack of cholesterol in the membrane preparations.

The pK_a1 values obtained by fitting the amplitudes of the slow and fast kinetics phases (Figure 4b) were 6.56 ± 0.09 and 6.48 ± 0.04, respectively; pK_a2 was fixed at 7.3 for this calculation, based on its value derived from the steady state pH-dependent fluorescence data. The pK_a1 values determined from equilibrium (6.38) and kinetics (6.48) experiments are close and likely the same within error, considering the noise level of the single-shot kinetics experiments. However, we note that the pK_a values determined from the kinetics experiment are not necessarily the same as those measured at equilibrium. During the pH jump experiment, protonation occurs before the conformation change, whereas, during a steady-state experiment, one can only measure properties of M2 channels that have already completed the conformation change. Therefore, it is possible that the kinetics experiment observes the pK_a of M2TM before activation, which could be different from that of the activated form populated in steady-state measurements.

■ CONCLUSIONS

A laser-induced pH jump coupled with time-resolved Trp fluorescence spectroscopy was used to measure the rapid protonation of His37 of M2TM and a subsequent conformational change that perturbs the microenvironment around Trp41. An unusually fast protonation rate for His37 (k_p = 1.6 ± 0.4 × 10¹⁰ M⁻¹ s⁻¹) in the pore of M2 proton channel was observed, implying a role of the Asp24 residues in the N-terminal domain of M2TM (and Asp 21 for full-length M2 proton channel) as proton-collecting antenna residues. Protonation of the His37 tetrad induces opening of the C-terminal end of the channel and exposure of Trp41 to water, with a rate of (4 ± 2) × 10³ s⁻¹. This temporal decoupling of the protonation step from the conformational change suggests that the transporter-like mechanism is probably not feasible. Instead, we propose that each proton transport cycle does not require a further conformational change after the activation of M2 by the channel opening, in agreement with QM/MM simulations.²⁵ Because M2 proton channel is sensitive to the environment, future experiments with different membrane compositions would be required to elucidate the specific impacts of the membrane structure and dynamics. Also, the addition of the C-terminal amphipathic helices to M2TM could affect its conformational dynamics. Finally, many other protein systems are amenable to this approach, such as ATP synthase, uncoupling protein, and hemagglutinin, all of which undergo functional conformational transitions induced by a change in pH. The laser pH-jump technique coupled with time-resolved Trp fluorescence spectroscopy provides a powerful new methodology to study proton transport processes in general without perturbing their structure and function.