Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Jun 1;29(13):5654–5662. doi: 10.1021/acs.chemmater.7b01393

Isothermal Crystallization Kinetics and Time–Temperature–Transformation of the Conjugated Polymer: Poly(3-(2′-ethyl)hexylthiophene)

Liyang Yu †,*, Emily Davidson ‡, Anirudh Sharma §, Mats R Andersson §, Rachel Segalman ‡,∥, Christian Müller †,*
PMCID: PMC5509438  PMID: 28713199

Abstract

graphic file with name cm-2017-01393r_0004.jpg

Thermal annealing strongly impacts the nano- and microstructure of conjugated polymers. Despite the fundamental importance for the resulting optoelectronic behavior of this class of materials, the underlying crystallization processes have not received the same attention that is encountered in other disciplines of materials science. The question arises whether classical treatment of nucleation and growth phenomena is truly applicable to conjugated polymers? Here, the isothermal crystallization behavior of the conjugated polymer poly(3-(2′-ethyl)hexylthiophene) (P3EHT) is monitored with differential scanning calorimetry (DSC). Avrami analysis reveals growth- and nucleation-limited temperature regimes that are separated by the maximum rate of crystallization. The molecular weight of the polymer is found to strongly influence the absolute rate of crystallization at the same degree of undercooling relative to the melting temperature. A combination of optical microscopy and grazing-incidence wide-angle X-ray scattering (GIWAXS) confirms that the resulting nano- and microstructure strongly correlate with the selected isothermal annealing temperature. Hence, this work establishes that classical nucleation and growth theory can be applied to describe the solidification behavior of the semicrystalline conjugated polymer P3EHT.

Introduction

Conjugated polymers attract considerable attention because they combine a promising optoelectronic performance in field-effect transistors, light-emitting diodes, solar cells, and thermoelectric devices with cost-effective solution processability. For many materials systems, a strong correlation is observed between the device performance and the solid-state nanostructure in terms of the degree of crystalline order, the size and texture of ordered domains and the presence of grain boundaries.1−6 Hence, significant efforts are being dedicated to the development of processing protocols that permit to control and manipulate crystallization. A number of key factors have been identified including the regioregularity7,8 and molecular weight of the polymer,9 preaggregation,10 the rate of solvent removal,11 substrate interactions5 and nucleation conditions,12,13 chain entanglement,14 and chain conformations.7,9,15

However, the focus on solution processing has diverted attention from classical treatment of crystallization phenomena that is commonly used in other branches of materials science to describe the behavior of, e.g., metals, inorganic semiconductors, and bulk polymers. To understand crystallization a number of tools are available that lend predictive power. Isothermal crystallization experiments can be used to study the crystallization rate, which allow the construction of time–temperature–transformation (TTT) diagrams.16 With those, it is possible to identify conditions where nanostructure formation is governed by nucleation or crystal growth. In addition, solidification protocols can be selected that result in a well-controlled crystallinity and crystal size. A textbook example is isothermal crystallization of poly(ethylene terephthalate) (PET), which displays a glass transition and melting temperature of Tg ≈ 70 °C and Tm ≈ 265 °C, respectively. The highest crystallization rate is observed at an intermediate isothermal crystallization temperature of about Tc ≈ 170 °C, which depends on the molecular weight of the polymer.17,18 Detailed knowledge about the crystallization kinetics of PET has enabled the manufacture of foils and bottles with a high degree of optical transparency and mechanical strength. Processing protocols are chosen that involve rapid cooling of molten material to temperatures below Tg, which results in an amorphous film or preform. Then, biaxial film drawing or stretch blow molding just above Tg leads to strain induced crystallization.19

Several recent reviews have pointed out that the increased use of similar rationales may be key to further advance the field of organic electronics,20−22 as exemplified by a recent study that employed film thickness variations to tailor the crystal morphology of a large collection of materials.23 However, only a few studies exist where the crystallization kinetics of an organic semiconductor have been systematically mapped. For instance, Lindqvist et al. used optical microscopy to monitor the nucleation and growth of fullerene crystals in an initially glassy polymer:fullerene bulk-heterojunction blend during annealing above its Tg ≈ 110 °C.24 For single organic semiconductors, such studies can be challenging to carry out because their strong tendency to π-stack makes it difficult to reach a truly amorphous state from which controlled annealing can be carried out.25 Crossland et al. circumvented this complication by designing a suitable solvent vapor annealing protocol that for the first time permitted micrometer-sized spherulites in thin films of poly(3-hexylthiophene) (P3HT) to be grown.13 Instead, Brande et al. used chip calorimetry to study the nonisothermal crystallization of P3HT and found that the crystallization rate of the polymer peaks halfway between its Tg ≈ 10 °C and Tm ≈ 230 °C.26 Chip calorimetry allowed two processing protocols to be compared that (1) involved either rapid quenching from the melt to below Tg with a rate of 30 000 K/s, followed by controlled annealing above Tg, or (2) immediate rapid quenching to a desired isothermal crystallization temperature.26

Studies on isothermal crystallization were suggested to be a powerful method for analyzing the crystallization behavior of conjugated polymers.27,28 One conjugated polymer that is particularly suitable for isothermal annealing experiments is poly(3-(2′-ethyl)hexylthiophene) (P3EHT).29 P3EHT features a particularly low crystallization rate and hence only crystallizes slowly over the course of several hours, which facilitates quenching to a truly amorphous state.30,31 Moreover, the relatively low Tm ≈ 80 °C of P3EHT means that the polymer can be isothermally annealed for long periods of time without the risk of thermal degradation and oxidation. Thus, P3EHT lends itself as an ideal model compound for isothermal crystallization studies. Previously, Boudouris et al. have exploited the low crystallization rate to follow the crystallization process in situ with grazing incidence wide-angle X-ray scattering (GIWAXS) and correlated the nanostructure development at room temperature with electronic charge transport in field-effect transistors.32 Here, we employ thermal analysis to map the nucleation- or growth-dominated crystallization of P3EHT and explore its effect on the resulting nano- and microstructures.

Experimental Section

Materials

P3EHTs with number-average molecular weights of Mn ≈ (PDI 1.4) and 24 (PDI 1.8) kg/mol were synthesized using the GRIM procedure as established in the literature.33

Size Exclusion Chromatography (SEC)

SEC was carried out on an Agilent PL-GPC 220 Integrated High Temperature GPC/SEC system in 1,2,4-trichlorobenzene at 150 °C using polystyrene standards as a reference to obtain “polystyrene equivalent” molecular weights.

Dynamic Mechanical Analysis (DMA)

DMA measurements were performed on a TA Q800 DMA. The DMTA measurements were performed in strain-controlled mode (maximum strain <0.1%) at a frequency of 1 Hz. P3EHT was embedded in a glass fiber mesh (E-glass supplied by Hexcel) by casting from a 20 mg/mL chloroform solution followed with drying under vacuum at 40 °C for 30 min. The glass mesh was cut into strips at a 45° angle with respect to the fiber elongation to avoid any continuous fibers crossing the length of the sample and contributing to the DMA response (see ref (32) for details).34 All samples were measured under a continuous flow of N2 at 60 mm/min, and the rate of heating was set to 3 °C/min.

Differential Scanning Calorimetry (DSC)

Isotherms were recorded under nitrogen using a heat-flux differential scanning calorimeter (DSC) from Mettler Toledo (DSC2) equipped with a high-sensitivity sensor (HSS9+) and a TC-125MT intracooler. Mettler 20 μL Al crucible light sample pans were used; the sample weight was around 6 mg. Samples were first molten at 130 °C, which is significantly above Tm in order to remove seed crystals, for 30 min followed by rapid cooling at rate of −100 °C/min to the desired isothermal crystallization temperature between 20 to 75 °C, where isotherms were recorded over the course of up to 30 000 s. A data point was taken every 3 s. The original data was smoothed with a Savitzky–Golay method where the window size was set to be 200 data points. After that, a baseline was subtracted (the data processing is demonstrated in Figure S2). Origin 8 was used to fit processed data with a 3-parameter Avrami eq (eq 2).

Thin Film Preparation

A thin film of P3EHT was prepared by wire bar coating a solution of P3EHT dissolved in o-xylene (10 mg/mL) on a glass slide with a RK-print K Control Coater. The sample was heated to 130 °C for 10 s and then moved to a Wagner & Munz Kofler hot bench and kept in air in the dark. The Kofler hot bench was calibrated with an azobenzene standard (Tm = 68 °C). The sample was removed from the hot bench after 48 h. The thin film thickness was measured with a KLA-Tencor Alpha-Step D-100 Stylus Profiler.

Optical Microscopy

Transmission optical micrographs were recorded with a Zeiss Axio Scope A1 equipped with a pair of crossed polarizers.

Ultraviolet–Visible Absorption (UV–vis)

UV–vis spectra were obtained with a PerkinElmer Lambda 900 UV/vis/NIR spectrometer.

Grazing-Incidence Wide-Angle X-ray Scattering (GIWAXS)

GIWAXS measurements were performed at the D-line, Cornell High Energy Synchrotron Source (CHESS) at Cornell University. The X-ray beam with a wavelength of 1.162 Å and size of about 0.5 mm was directed to the thin film at an incident angle of 0.15°. An optical microscope was located vertically above of the sample and was used to monitor the beam and sample location. A Pilatus 200k detector located 169.5 mm from the sample was used with an exposure time of 10 s and a lateral sample scanning step of 0.2 mm.

Results and Discussion

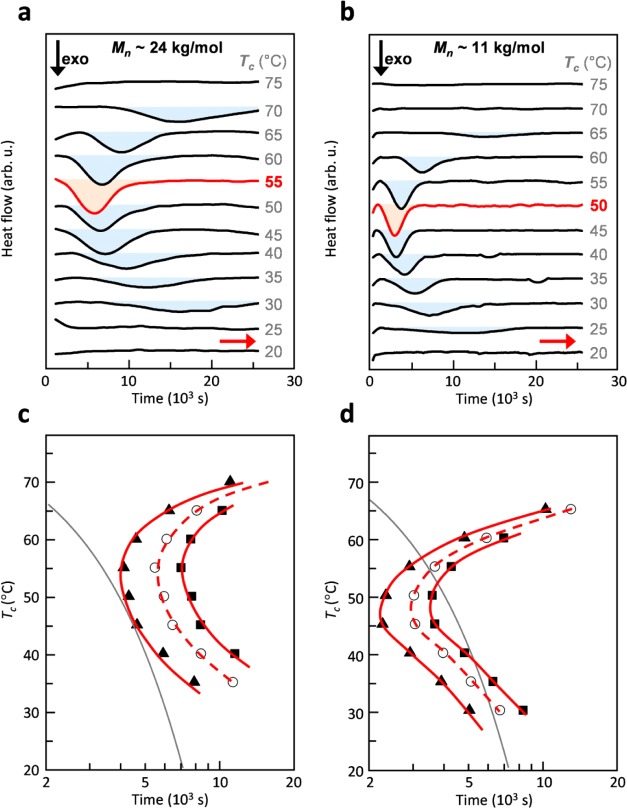
We started our investigation by analyzing the crystallization kinetics of two batches of P3EHT, which differed in molecular weight, for a wide range of undercooling. We employed differential scanning calorimetry (DSC) to record a series of isotherms at temperatures ranging from 20 to 75 °C (Figure 1a,b). As reported previously, crystallization of this polymer takes place over the course of several hours.32 For the higher molecular-weight batch with a number-average molecular weight Mn ≈ 24 kg/mol, we find that crystallization occurs most rapidly at 55 °C. For both higher and lower temperatures, the onset and endset of the crystallization exotherm shift to later times and are absent below 30 and above 70 °C, the latter because of the low degree of undercooling relative to the Tm ≈ 76 °C. The lower molecular-weight batch with Mn ≈ 11 kg/mol displayed qualitatively similar behavior but crystallized more quickly with the fastest crystallization occurring at a slightly lower temperature of 45 to 50 °C. Due to the slightly lower Tm ≈ 69 °C, no crystallization was observed above 65 °C. The temperature range where we observed isothermal crystallization was also in agreement with a glass transition temperature Tg ≈ 24 °C (30 °C) of higher (lower) molecular P3EHT, as measured with dynamic mechanical analysis (DMA) using the peak of the loss tangent tan δ (Figure S3). The melting behavior of these crystallized solids was also monitored (Figure S4). For further discussion on the sequential melting after isothermal crystallization, see refs (28 and 29).

Figure 1.

Figure 1

Open in a new tab

(a,b) Differential scanning calorimetry (DSC) isotherms of P3EHT with Mn ≈24 kg/mol (a) and Mn ≈ 11 kg/mol (b). (c,d) TTT diagram of P3EHT with Mn ≈ 24 kg/mol (c) and Mn ≈ 11 kg/mol (d). Isenthalpic lines correspond to the times required for the enthalpy of crystallization to reach values of 1 (▲), 5 (○), and 10 J/g (■). The gray lines represent a constant cooling rate of 0.4 °C/min from 80 °C and form a tangent with the isenthalpic line that corresponds to ΔH ≈ 1 J/g for the higher molecular-weight material.

To construct TTT diagrams, we extracted the time required for the crystallization to release 1, 5, and 10 J/g of heat (i.e., partial enthalpy ΔH). Note that, at some annealing temperatures, more than 10 J/g of heat was released in total (Table 1). We then plotted isenthalpic lines that correspond to the extracted partial enthalpies. The resulting TTT diagrams display the familiar U-shape with peaks at 55 and 45 °C in the case of high and low molecular-weight material, respectively (Figure 1c,d). From these diagrams it is now possible to estimate cooling rates that result in a certain degree of crystallization. For instance, a cooling rate of 0.4 °C/min from 80 °C to room temperature will result in a heat release of about 1 J/g in the case of higher molecular-weight P3EHT (cf. Figure 1c). In a typical TTT diagram such “fast” crystallization implies the formation of a large number of nuclei. Slower cooling would instead result in a more balanced nucleation and crystal growth process (cf. discussion below on impact on microstructure). The same effect is achieved when reducing the molecular weight. A cooling rate of 0.4 °C/min from 80 °C will result in a heat release of more than 10 J/g for the lower molecular-weight material (Figure 1d).

Table 1. Isothermal Crystallization Temperature Tc, Crystallization Enthalpy ΔH0, Avrami Coefficient m, Lag Time t0, Time Constant τ, Relative Rate of Nucleation dN/dt ∝ 1/t0, and Crystal Growth Rate dXc/dt|t=τ+t0 = m/eτa.

molecular weight temperature crystallization enthalpy Avrami factors
 nucleation rate crystal growth rate
Mn (kg/mol) Tc (°C) ΔH0 (J/g) m t0 (1000 s) τ (1000 s) l/t0 (1/1000 1/s) m/eτ (1/1000 1/s)
24 35 7.7 3.4 3.67 11.56 0.27 0.11
40 10.7 3.1 2.88 9.36 0.35 0.12
45 11.1 3.0 2.34 6.95 0.43 0.16
50 11.9 2.9 2.33 6.12 0.43 0.18
55 11.7 2.9 2.52 5.04 0.40 0.21
60 12.2 3.1 2.76 5.88 0.36 0.19
65 11.4 3.0 4.53 7.15 0.22 0.15
70 5.7 3.6 8.28 10.69 0.12 0.12
11 30 13.7 2.3 4.13 5.75 0.24 0.14
35 14.1 2.7 2.60 4.63 0.38 0.21
40 14.7 3.3 1.27 4.14 0.79 0.29
45 17.4 3.1 1.01 3.21 0.99 0.36
50 16.3 3.1 1.30 2.69 0.77 0.42
55 16.8 2.8 2.01 2.95 0.50 0.35
60 12.6 2.1 4.91 3.46 0.20 0.22
65 8.7 2.5 9.80 8.40 0.10 0.11
Open in a new tab
a

The dominant error arises from baseline selection during data processing (see Figure S2). We estimate the following errors: Δ(ΔH0) < 1 J/g, Δ(m) < 0.5, and Δ(t0) < 500 s (200 s) for higher (lower) molecular-weight P3EHT.

We noticed that the total enthalpy of crystallization varies among the isotherms (see Table 1). As expected for a polymer, crystallization is arrested long before the absolute crystallinity reaches 100%. To quantitatively analyze the crystallization kinetics, a common practice is to extract the relative crystallinity Xc(t):35

graphic file with name cm-2017-01393r_m001.jpg 1

where ΔH(t) is the partial enthalpy obtained by integrating isotherms up to time t and ΔH° is the total enthalpy of crystallization that corresponds to the total area of an isotherm (see Figure S2 for details on baseline correction and selection of integration limits). Note that we did not consider the influence of the crystal size when estimating the relative crystallinity from the enthalpy of crystallization.36

We then used the three-parameter Avrami equation to describe the evolution of Xc(t) with time:

graphic file with name cm-2017-01393r_m002.jpg 2

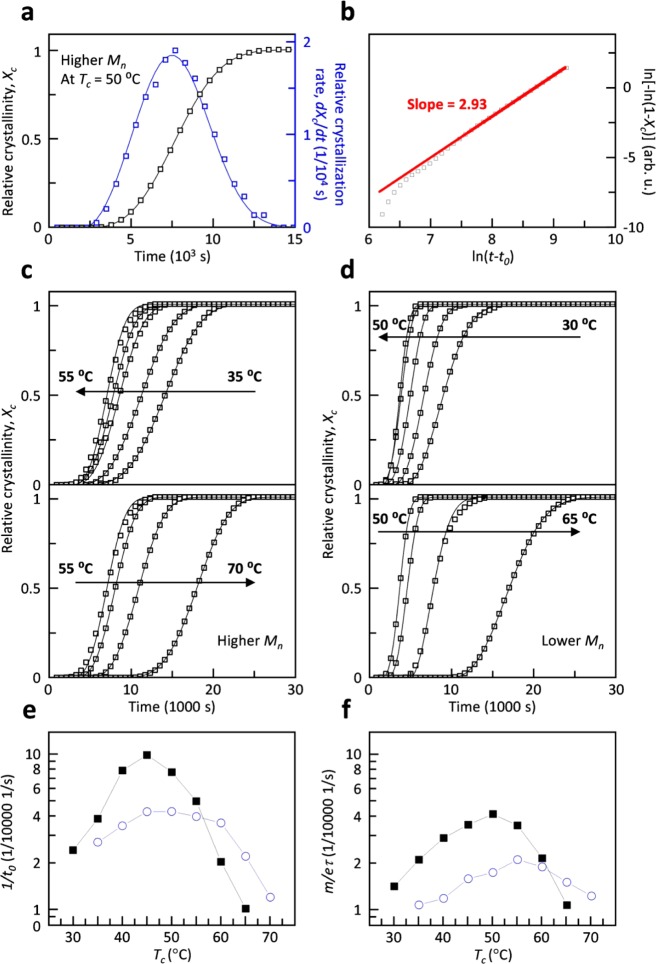
where the parameters t0, τ, and m are the lag time, time constant, and Avrami coefficient, respectively. Here, it should be noted that, as concluded by Wunderlich, “without the parallel knowledge of the microscopic, independently proven mechanism, the macroscopic, experimentally derived Avrami equation and Avrami parameters are only a convenient means to represent empirical data of crystallization”.37 While the Avrami equation was originally developed for crystalline materials,38 it is also commonly used to describe the crystallization kinetics of semicrystalline polymers. We fitted Xc(t) with eq 2 using a reiterative process, keeping t0, τ, and m as free fit parameters (cf. Table 1 for values obtained from best fits). A typical best fit for the relative crystallinity Xc(t) as well as the relative crystallization rate dXc(t)/dt is shown in Figure 2a.

Figure 2.

Figure 2

Open in a new tab

(a) Representative linear plot of Xc(t) (□) as well as the relative crystallization rate dXc/dt (blue square) of higher molecular-weight P3EHT at 50 °C, and (b) corresponding double-logarithmic, linearized Avrami plot of measured relative crystallinity Xc(t) and a straight line fit (red line) with a slope of m = 2.93. Xc(t) of (c) higher and (d) lower molecular-weight P3EHT for a range of isothermal crystallization temperatures. (e) Relative rate of nucleation dN/dt ∝ 1/t0, and (f) maximum rate of crystallization dXc/dt|t=τ+t0 = m/eτ for higher (blue circle) and lower (■) molecular-weight P3EHT.

In order to determine for which time interval the obtained fits accurately describe Xc(t), we examined the linearized form of the Avrami equation:

graphic file with name cm-2017-01393r_m003.jpg 3

which allows m and τ to be extracted from the slope and intersect of plots of ln(−Xc(t))) vs ln(t – t0). Generally, we find that the obtained fits describe the raw data well. A typical linearized Avrami plot of the raw data together with the predicted evolution of Xc(t) is shown in Figure 2b. The best fit describes the raw data well at times larger than ln(t – t0) > 7.5, i.e., t – t0 > 1808 s, which corresponds to Xc(t) > 0.02%. We ascribe the poor fit at the early stages of crystallization to the error in selecting the integration limits when extracting ΔH(t) from DSC isotherms (see Figure S2).

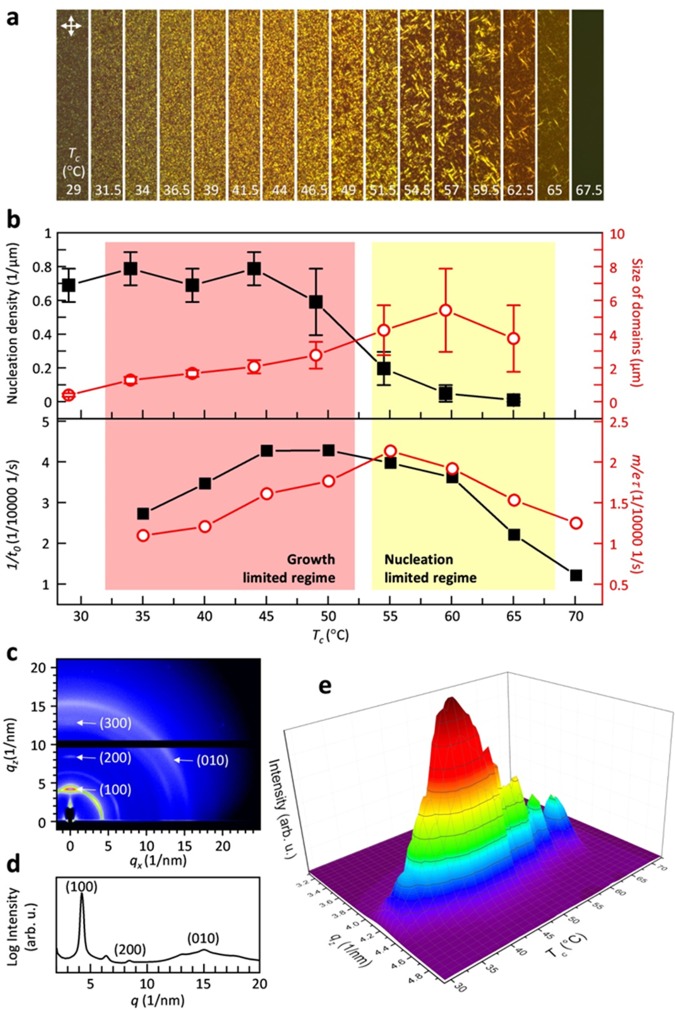
We carried out the same fitting procedure for all recorded DSC isotherms (Figure 2c,d). The Avrami coefficient m adopts a value of about 3 for most isothermal crystallization temperatures (Table 1). Since we estimate an error of Δm < 0.5, we can only conclude that m does not strongly vary with temperature. The Avrami coefficient is often interpreted as representing the dimension of crystal growth. A value of m ≈ 3 is consistent with either three-dimensional crystal growth and heterogeneous nucleation or two-dimensional growth and homogeneous nucleation where the latter is less likely in the bulk.39 In contrast, a number of previous studies have found a value close to m ≈ 1 for polythiophenes including P3HT and P3EHT,40−43 which indicates one-dimensional growth. We rationalize this difference in behavior with the large nucleation density that is commonly encountered in polythiophenes, which leads to one-dimensional growth of nanofibrils. For P3HT as well as other conjugated polymers, a reduction in nucleation density can result in the development of a spherulitic microstructure,13,44 which implies three-dimensional growth. Polarized optical microscopy of isothermally crystallized P3EHT reveals the presence of spherulites (Figure 3a), and therefore, we argue that the deduced Avrami coefficient of m ≈ 3 arises because of three-dimensional crystal growth and heterogeneous nucleation.

Figure 3.

Figure 3

Open in a new tab

(a) Polarized optical micrographs of higher molecular-weight P3EHT thin films after isothermal crystallization at the indicated temperatures for 48 h; the width of each micrograph is 10 μm. (b) Nucleation density (■) and size of domains (red circle) estimated from polarized optical micrographs of higher molecular-weight P3EHT thin films (top), and corresponding relative rate of nucleation (■), and maximum rate of crystallization (red circle) for bulk samples from Avrami analysis (cf. Figure 2e,f). (c) GIWAXS image of the thin film in (a) for Tc = 50 °C. (d) Diffraction intensity I100 against qz value plot obtained from (c). (e) A plot illustrating the evolution of the diffraction intensity at qz with Tc, obtained from the GIWAXS mapping of the thin film in (a).

In contrast to m, the lag time t0 and time constant τ strongly vary with temperature (Table 1). For both the low and higher molecular-weight P3EHT material, we find that the onset of crystallization shifts to earlier times with increasing degree of undercooling, reaching the lowest value of t0 ≈ 1000 and 2300 s at 45 and 50 °C, respectively. Conversely, at lower temperatures the onset of crystallization again shifts to later times. The lag time t0 corresponds to the time that is required for crystallization to commence, and thus, we chose to use the term 1/t0 to describe the relative rate of nucleation at different isothermal crystallization temperatures (Figure 2e). We find that for both molecular weights of P3EHT the temperature dependence of the nucleation rate resembles the U-shape encountered in the TTT diagrams (cf. Figure 1c,d). Low and higher molecular-weight P3EHTs show a distinct peak at 45 °C and a broad peak around 45 to 50 °C, respectively. At most temperatures, i.e., between 35 and 55 °C, the lower molecular-weight material features a higher nucleation rate, which we explain with more rapid diffusion of shorter polymer chains. Instead, at 60 °C and above the higher molecular-weight P3EHT features a higher nucleation rate because of the slightly lower Tm of the lower molecular-weight material.

The rate of crystallization varies with time, and can be described by the first derivative of Xc(t), which reaches zero at t = t0 as well as t ≫ τ (cf. Figure 2a):

graphic file with name cm-2017-01393r_m004.jpg 4

The maximum rate of crystallization can be found by setting the second derivative of Xc(t) to zero:

graphic file with name cm-2017-01393r_m005.jpg 5

The maximum rate of crystallization is found at m(tmax – t0)m + τm(1 – m) = 0:

graphic file with name cm-2017-01393r_m006.jpg 6

which yields for m = 3 a value of tmax ≈ 0.87τ + t0. We, therefore, chose to compare the rate of crystallization at t = τ + t0, which is close to tmax and yields

graphic file with name cm-2017-01393r_m007.jpg 7

We used eq 7 to plot the maximum crystallization rate for both investigated P3EHT batches as a function of isothermal crystallization temperature (Figure 2f and Table 1). Again, we observe a U-shaped trend with a peak that shifts to a higher temperature with increasing molecular weight. We find the highest crystallization rate at 50 and 55 °C for the lower and higher molecular-weight polymers, respectively. Similar to the relative nucleation rate, the crystallization rate of the lower Mw P3EHT is higher for most isothermal crystallization temperatures but 65 and 70 °C, which are close to the melting temperature.

In a further set of experiments, we employed polarized optical microscopy to visualize the influence of the crystallization kinetics on the resulting microstructure. To this end thin films of the higher molecular-weight P3EHT with a thickness of 52 ± 3 nm were isothermally crystallized for 48 h. To ensure identical crystallization conditions, we used a Kofler hot bench to generate samples with a continuous temperature gradient from about 30 to 130 °C (see Figure S5). We then recorded micrographs that correspond to isothermal crystallization temperatures ranging from 29 to 67.5 °C (Figure 3a). Qualitative inspection reveals that the number and size of individual crystallites strongly vary with crystallization temperature. A low degree of undercooling at a Tc ≈ 60 to 65 °C resulted in the formation of few large birefringent domains with a length of up to 10 μm. In contrast, at lower temperatures, we observe numerous smaller domains. We counted the number and measured the length of individual birefringent domains, in order to quantify the relative influence of the nucleation and growth rate on the crystallization kinetics. For the number of domains, we find a constant value of about 0.7 to 0.8 domains per μm2, which decreases above 50 °C to only 0.01 domains per μm2 at 65 °C (Figure 3b). Conversely, the size of birefringent domains increases with temperature from less than 0.5 μm at 35 °C to about 4–6 μm at Tc ≈ 55 to 65 °C. Comparison of the density and size of domains suggests a regime at Tc < 50 °C where nucleation dominates the crystallization process (i.e., the process is growth limited), which leads to a fine distribution of domains. The prominence of nucleation at these temperatures is corroborated by the relative nucleation rate 1/t0 obtained from DSC, which peaks around 45 to 50 °C (Figure 3b, bottom panel). Instead, for Tc > 50 °C, we observe a different regime where crystal growth is more prominent (i.e., the process is nucleation limited), which leads to the formation of fewer but larger birefringent domains. Interestingly, the highest rate of crystallization at Tc ≈ 55 °C that we obtained from DSC (cf. Figure 3b, bottom panel) corresponds to the crossover from the nucleation to the growth dominated regime. This can be rationalized by the cooperative effect of nucleation and growth to the overall crystallization rate.

The observed influence of Tc on the crystallization behavior is corroborated by grazing-incident wide-angle X-ray scattering (GIWAXS) mapping and UV–vis spectroscopy of the graded sample discussed above (Figure 3c–e and Figure S6). Edge-on orientation of the molecules was observed for all annealing temperatures with the side chains standing on the substrates. Comparison of the (100) diffraction at different temperatures shows that the peak position does not change with Tc, which suggests that crystals with an identical unit cell were obtained. We observed that the intensity of the (100) diffraction (I100) continuously increases with Tc in the growth-limited regime. Conversely, in the nucleation-limited regime, I100 decreased with Tc. Interestingly, fluctuation of the diffraction intensity in the nucleation-limited regime correlated with the large variations in crystal size close to Tm (cf. Figure 3e). Overall, GIWAXS as well as UV–vis spectroscopy confirm that the highest degree of crystalline order is reached at Tc ≈ 50 °C. It is noticed that, even with similar crystallinity suggested by maximum diffraction and absorption intensities (such as for Tc ≈ 40 and 60 °C) in growth- and nucleation-limited regimes, the density and sizes of birefringent domains can differ significantly. Evidently, the here presented structural characterization highlights the pronounced influence of the crystallization kinetics on microstructure formation in P3EHT, with the occurrence of growth- and nucleation-limited regimes separated by the maximum rate of crystallization.

Conclusions

In this work, we found that the isothermal crystallization behavior of the conjugated polymer P3EHT could be evaluated using classical techniques such as DSC. The key parameters describing nucleation and crystal growth were extracted through Avrami analysis of DSC isotherms. We deduced an Avrami coefficient of about 3 for two batches of P3EHT that differed in molecular weight. This result suggests a three-dimensional crystal growth mode, which agrees with the spherulitic structure obtained for this class of materials at low nucleation rates. Despite the fact that the absolute values of the crystallization kinetic parameters can shift dramatically when translated into thin film structures, optical microscopy, GIWAXS, and UV–vis spectroscopy of thin films of the higher molecular-weight material reveal nucleation or growth limited microstructures that are consistent with the crystallization behavior deduced by DSC. This work demonstrates that solidification of conjugated polymers is not fundamentally different from that of commodity polymers. We propose that classical nucleation and growth processes can provide a convincing rationale for the commonly observed influence of thermal annealing on the optoelectronic properties of semicrystalline conjugated polymers.

Acknowledgments

Financial support from the Swedish Research Council the Swedish Energy Agency, the Knut and Alice Wallenberg Foundation through a Wallenberg Academy Fellowship, and the European Research Council (ERC) under Grant Agreement No. 637624 is gratefully acknowledged. The authors thank Anders Mårtensson (Chalmers) for help with SEC measurements and CHESS (supported by the NSF & NIH/NIGMS via NSF Award DMR-1332208) for providing experimental time for GIWAXS measurements.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.chemmater.7b01393.

  • Identification of molecular weight of both materials with SEC; an example demonstrating all details on data processing for the DSC isotherms; identification of glass transition temperatures by DMA analysis; melting behavior of isothermal crystallized sample monitored by DSC; a photograph of a P3EHT thin film isothermal crystallized on a hot bench with a temperature gradient; UV–vis absorption of thin films isothermally crystallized at various temperatures. (PDF)

The authors declare no competing financial interest.

Supplementary Material

cm7b01393_si_001.pdf (879.3KB, pdf)

References

  1. Chang J. F.; Clark J.; Zhao N.; Sirringhaus H.; Breiby D. W.; Andreasen J. W.; Nielsen M. M.; Giles M.; Heeney M.; McCulloch I. Molecular-Weight Dependence of Interchain Polaron Delocalization and Exciton Bandwidth in High-Mobility Conjugated Polymers. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 1–12. 10.1103/PhysRevB.74.115318. [DOI] [Google Scholar]
  2. Gomez E. D.; Barteau K. P.; Wang H.; Toney M. F.; Loo Y.-L. Correlating the Scattered Intensities of P3HT and PCBM to the Current Densities of Polymer Solar Cells. Chem. Commun. 2011, 47, 436–438. 10.1039/C0CC02927K. [DOI] [PubMed] [Google Scholar]
  3. Jimison L. H.; Toney M. F.; McCulloch I.; Heeney M.; Salleo A. Charge-Transport Anisotropy due to Grain Boundaries in Directionally Crystallized Thin Films of Regioregular Poly(3-hexylthiophene). Adv. Mater. 2009, 21, 1568–1572. 10.1002/adma.200802722. [DOI] [Google Scholar]
  4. O’Connor B.; Kline R. J.; Conrad B. R.; Richter L. J.; Gundlach D.; Toney M. F.; DeLongchamp D. M. Anisotropic Structure and Charge Transport in Highly Strain-Aligned Regioregular Poly(3-hexylthiophene). Adv. Funct. Mater. 2011, 21, 3697–3705. 10.1002/adfm.201100904. [DOI] [Google Scholar]
  5. Sirringhaus H.; Brown P. J.; Friend R. H.; Nielsen M. M.; Bechgaard K.; Langeveld-Voss B. M. W.; Spiering A. J. H.; Janssen R. A. J.; Meijer E. W.; Herwig P.; de Leeuw D. M. Two-Dimensional Charge Transport in Self-Organized, High-Mobility Conjugated Polymers. Nature 1999, 401, 685–688. 10.1038/44359. [DOI] [Google Scholar]
  6. Yang H.; Shin T. J.; Yang L.; Cho K.; Ryu C. Y.; Bao Z. Effect of Mesoscale Crystalline Structure on the Field-Effect Mobility of Regioregular Poly(3-hexyl thiophene) in Thin-Film Transistors. Adv. Funct. Mater. 2005, 15, 671–676. 10.1002/adfm.200400297. [DOI] [Google Scholar]
  7. Snyder C. R.; Henry J. S.; Delongchamp D. M. Effect of Regioregularity on the Semicrystalline Structure of Poly(3-hexylthiophene). Macromolecules 2011, 44, 7088–7091. 10.1021/ma201604n. [DOI] [Google Scholar]
  8. Mauer R.; Kastler M.; Laquai F. The Impact of Polymer Regioregularity on Charge Transport and Efficiency of P3HT:PCBM Photovoltaic Devices. Adv. Funct. Mater. 2010, 20, 2085–2092. 10.1002/adfm.201000320. [DOI] [Google Scholar]
  9. Koch F. P. V.; Rivnay J.; Foster S.; Müller C.; Downing J. M.; Buchaca-Domingo E.; Westacott P.; Yu L.; Yuan M.; Baklar M.; Fei Z.; Luscombe C.; McLachlan M. A.; Heeney M.; Rumbles G.; Silva C.; Salleo A.; Nelson J.; Smith P.; Stingelin N. The Impact of Molecular Weight on Microstructure and Charge Transport in Semicrystalline Polymer Semiconductors-Poly(3-hexylthiophene), a Model Study. Prog. Polym. Sci. 2013, 38, 1978–1989. 10.1016/j.progpolymsci.2013.07.009. [DOI] [Google Scholar]
  10. Hu H.; Zhao K.; Fernandes N.; Boufflet P.; Bannock J. H.; Yu L.; de Mello J. C.; Stingelin N.; Heeney M.; Giannelis E. P.; Amassian A. Entanglements in Marginal Solutions: A Means of Tuning Pre-Aggregation of Conjugated Polymers with Positive Implications for Charge Transport. J. Mater. Chem. C 2015, 3, 7394–7404. 10.1039/C5TC01425E. [DOI] [Google Scholar]
  11. Li G.; Shrotriya V.; Huang J.; Yao Y.; Moriarty T.; Emery K.; Yang Y. High-Efficiency Solution Processable Polymer Photovoltaic Cells by Self-Organization of Polymer Blends. Nat. Mater. 2005, 4, 864–868. 10.1038/nmat1500. [DOI] [Google Scholar]
  12. Treat N. D.; Nekuda Malik J. A.; Reid O.; Yu L.; Shuttle C. G.; Rumbles G.; Hawker C. J.; Chabinyc M. L.; Smith P.; Stingelin N. Microstructure Formation in Molecular and Polymer Semiconductors Assisted by Nucleation Agents. Nat. Mater. 2013, 12, 628–633. 10.1038/nmat3655. [DOI] [PubMed] [Google Scholar]
  13. Crossland E. J. W.; Rahimi K.; Reiter G.; Steiner U.; Ludwigs S. Systematic Control of Nucleation Density in Poly(3-hexylthiophene) Thin Films. Adv. Funct. Mater. 2011, 21 (3), 518–524. 10.1002/adfm.201001682. [DOI] [Google Scholar]
  14. Müller C.; Zhigadlo N. D.; Kumar A.; Baklar M. A.; Karpinski J.; Smith P.; Kreouzis T.; Stingelin N. Enhanced Charge-Carrier Mobility in High-Pressure-Crystallized Poly(3-hexylthiophene). Macromolecules 2011, 44, 1221–1225. 10.1021/ma102529f. [DOI] [Google Scholar]
  15. Kim Y.; Cook S.; Kirkpatrick J.; Nelson J.; Durrant J. R.; Bradley D. D. C.; Giles M.; Heeney M.; Hamilton R.; McCulloch I. Effect of the End Group of Regioregular Poly(3-hexylthiophene) Polymers on the Performance of Polymer/fullerene Solar Cells. J. Phys. Chem. C 2007, 111, 8137–8141. 10.1021/jp072306z. [DOI] [Google Scholar]
  16. Callister W. D.; Rethwisch D. G.. Materials Science and Engineering: An Introduction; John Wiley & Sons, Inc.: New York, 2007. [Google Scholar]
  17. Cobbs W. H. Jr; Burton R. L. Crystallization of Polyethylene Terephthalate. J. Polym. Sci. 1953, 10, 275–290. 10.1002/pol.1953.120100302. [DOI] [Google Scholar]
  18. Baranov V. G.; Kenarov A. V.; Volkov T. I. Morphology and Kinetics Studies of Spherulitization of Polyethylene Terephthalate. J. Polym. Sci., Part C: Polym. Symp. 1970, 30, 271–281. 10.1002/polc.5070300130. [DOI] [Google Scholar]
  19. Morton-Jones D. H.Polymer Processing; Chapman and Hall: London, 1989. [Google Scholar]
  20. Kuei B.; Gomez E. D. Chain Conformations and Phase Behavior of Conjugated Polymers. Soft Matter 2017, 13, 49–67. 10.1039/C6SM00979D. [DOI] [PubMed] [Google Scholar]
  21. Lee H. M.; Moon H.; Kim H. S.; Kim Y. N.; Choi S. M.; Yoo S.; Cho S. O. Abrupt Heating-Induced High-Quality Crystalline Rubrene Thin Films for Organic Thin-Film Transistors. Org. Electron. 2011, 12, 1446–1453. 10.1016/j.orgel.2011.05.015. [DOI] [Google Scholar]
  22. Treat N. D.; Westacott P.; Stingelin N. The Power of Materials Science Tools for Gaining Insights into Organic Semiconductors. Annu. Rev. Mater. Res. 2015, 45, 459–490. 10.1146/annurev-matsci-070214-021113. [DOI] [Google Scholar]
  23. Yu L.; Niazi M. R.; Ndjawa G. O. N.; Li R.; Kirmani A. R.; Munir R.; Balawi A. H.; Laquai F.; Amassian A. Programmable and Coherent Crystallization of Semiconductors. Sci. Adv. 2017, 3, 1–10. 10.1126/sciadv.1602462. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Lindqvist C.; Sanz-Velasco A.; Wang E.; Bäcke O.; Gustafsson S.; Olsson E.; Andersson M. R.; Müller C. Nucleation-limited fullerene crystallisation in a polymer−fullerene bulk-heterojunction blend. J. Mater. Chem. A 2013, 1, 7174–7180. 10.1039/c3ta11018d. [DOI] [Google Scholar]
  25. Wang G.; Swensen J.; Moses D.; Heeger A. J. Increased Mobility from Regioregular Poly(3-hexylthiophene) Field-Effect Transistors. J. Appl. Phys. 2003, 93, 6137–6141. 10.1063/1.1568526. [DOI] [Google Scholar]
  26. Van den Brande N.; Van Assche G.; Van Mele B. Isothermal Structure Development in Submicron P3HT Layers Studied by Fast Scanning Chip Calorimetry. Polymer 2015, 57, 39–44. 10.1016/j.polymer.2014.12.015. [DOI] [Google Scholar]
  27. Zhao Y.; Yuan G.; Roche P.; Leclerc M. A Calorimetric Study of the Phase Transitions in Poly(3-hexylthiophene). Polymer 1995, 36, 2211–2214. 10.1016/0032-3861(95)95298-F. [DOI] [Google Scholar]
  28. Pal S.; Nandi A. K. Cocrystallization Mechanism of Poly (3-hexyl thiophenes) with Different Amount of Chain Regioregularity. J. Appl. Polym. Sci. 2006, 101, 3811–3820. 10.1002/app.24067. [DOI] [Google Scholar]
  29. Andersson M. R.; Thomas O.; Mammo W.; Svensson M.; Theander M.; Inganäs O. Substituted Polythiophenes Designed for Optoelectronic Devices and Conductors. J. Mater. Chem. 1999, 9, 1933–1940. 10.1039/a902859e. [DOI] [Google Scholar]
  30. Beckingham B. S.; Ho V.; Segalman R. A. Melting Behavior of Poly(3-(2 ′-ethyl)hexylthiophene). Macromolecules 2014, 47, 8305–8310. 10.1021/ma501915v. [DOI] [PubMed] [Google Scholar]
  31. Beckingham B. S.; Ho V.; Segalman R. A. Formation of a Rigid Amorphous Fraction in Poly(3-(2′-ethyl)hexylthiophene). ACS Macro Lett. 2014, 3, 684–688. 10.1021/mz500262d. [DOI] [PubMed] [Google Scholar]
  32. Boudouris B. W.; Ho V.; Jimison L. H.; Toney M. F.; Salleo A.; Segalman R. A. Real-Time Observation of Poly(3-alkylthiophene) Crystallization and Correlation with Transient Optoelectronic Properties. Macromolecules 2011, 44, 6653–6658. 10.1021/ma201316a. [DOI] [Google Scholar]
  33. Loewe R. S.; Khersonsky S. M.; McCullough R. D. A Simple Method to Prepare Head-to-Tail Coupled, Regioregular Poly(3-alkylthiophenes) Using Grignard Metathesis. Adv. Mater. 1999, 11, 250–253. . [DOI] [Google Scholar]
  34. Sharma A.; Pan X.; Campbell J.; Andersson M. R.; Lewis D. A. Unravelling the Thermomechanical Properties of Bulk Heterojunction Blends in Polymer Solar Cells. Macromolecules 2017, 50, 3347–3354. 10.1021/acs.macromol.7b00430. [DOI] [Google Scholar]
  35. Leo M.Crystallization of Polymers: Vol. 2, Kinetics and Mechanisms; Cambridge University Press: Cambridge, U.K., 2004. [Google Scholar]
  36. Snyder C. R.; Nieuwendaal R. C.; Delongchamp D. M.; Luscombe C. K.; Sista P.; Boyd S. D. Quantifying Crystallinity in High Molar Mass Poly(3-hexylthiophene). Macromolecules 2014, 47, 3942–3950. 10.1021/ma500136d. [DOI] [Google Scholar]
  37. Wunderlich B.Macromolecular Physics: 2. Crystal Nucleation, Growth, Annealing; Academic Press: New York, 1976. [Google Scholar]
  38. Avrami M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. 10.1063/1.1750380. [DOI] [Google Scholar]
  39. Christian J. W.The Theory of Transformations in Metals and Alloys, 3rd ed.; Pergamon: New York, 2002. [Google Scholar]
  40. Malik S.; Nandi A. K. Crystallization Mechanism of Regioregular Poly(3-alkyl thiophene)s. J. Polym. Sci., Part B: Polym. Phys. 2002, 40, 2073–2085. 10.1002/polb.10272. [DOI] [Google Scholar]
  41. Wu W. R.; Jeng U. S.; Su C. J.; Wei K. H.; Su M. S.; Chiu M. Y.; Chen C. Y.; Su W.; Su C. H.; Su A. C. Competition between Fullerene Aggregation and Poly(3-hexylthiophene) Crystallization upon Annealing of Bulk Heterojunction Solar Cells. ACS Nano 2011, 5, 6233–6243. 10.1021/nn2010816. [DOI] [PubMed] [Google Scholar]
  42. Duong D. T.; Ho V.; Shang Z.; Mollinger S.; Mannsfeld S. C. B.; Dacuña J.; Toney M. F.; Segalman R.; Salleo A. Mechanism of Crystallization and Implications for Charge Transport in Poly(3-ethylhexylthiophene) Thin Films. Adv. Funct. Mater. 2014, 24, 4515–4521. 10.1002/adfm.201304247. [DOI] [Google Scholar]
  43. Müller C.; Radano C. P.; Smith P.; Stingelin-Stutzmann N. Crystalline-Crystalline Poly(3-hexylthiophene)-Polyethylene Diblock Copolymers: Solidification from the Melt. Polymer 2008, 49, 3973–3978. 10.1016/j.polymer.2008.07.006. [DOI] [Google Scholar]
  44. Fischer F. S. U.; Trefz D.; Back J.; Kayunkid N.; Tornow B.; Albrecht S.; Yager K. G.; Singh G.; Karim A.; Neher D.; Brinkmann M.; Ludwigs S. Highly Crystalline Films of PCPDTBT with Branched Side Chains by Solvent Vapor Crystallization: Influence on Opto-Electronic Properties. Adv. Mater. 2015, 27, 1223–1228. 10.1002/adma.201403475. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cm7b01393_si_001.pdf (879.3KB, pdf)

Articles from Chemistry of Materials are provided here courtesy of American Chemical Society

RESOURCES