Scale-freeness of dominant and piecemeal perceptions during binocular rivalry

Abstract

When two eyes are simultaneously stimulated by two inconsistent images, the observer’s perception switches between the two images every few seconds such that only one image is perceived at a time. This phenomenon is named binocular rivalry (BR). However, sometimes the perceived image is a piecemeal mixed of two stimuli known as piecemeal perceptions. In this study, a BR task was designed in which orthogonal gratings are presented to the two eyes. The subjects were trained to report 3 states: dominant perceptions (two state matching to perceived grating orientation) and the piecemeal perceptions (third state). We explored the scale-freeness of the BR percept durations considering the two dominant monocular states as well as the piecemeal transition state using detrended fluctuation analysis. Our results reproduced the previous finding of memory in the perceptual switches between the monocular perception states. Moreover, we showed that such memory also exists in the transitory periods of dichoptic piecemeal perceptions. These results support our hypothesis that the pool of unstable piecemeal perceptions could be regarded as separate multiple low-depth basin in the perceptual state landscape. Likewise, the transitions from these piecemeal state basins and stable monocular state basins are faced with resistance. Therefore there is inertia and memory (i.e. positive serial correlation) for the piecemeal dichoptic perception states as well as the monocular states.

Introduction

Binocular rivalry (BR) is a phenomenon observed when two eyes are stimulated by two inconsistent images simultaneously. In this case, the observer’s perception switches between the two images every few seconds such that only one image is perceived at a time; however, sometimes the perceived image is a piecemeal mixture of the two stimuli. Considering that the perception alternates despite constant visual inputs, BR studies have been employed to gain insight about the relation between consciousness and brain functions during visual perception (Pitts et al. 2010; Blake 2001; Brascamp et al. 2005).

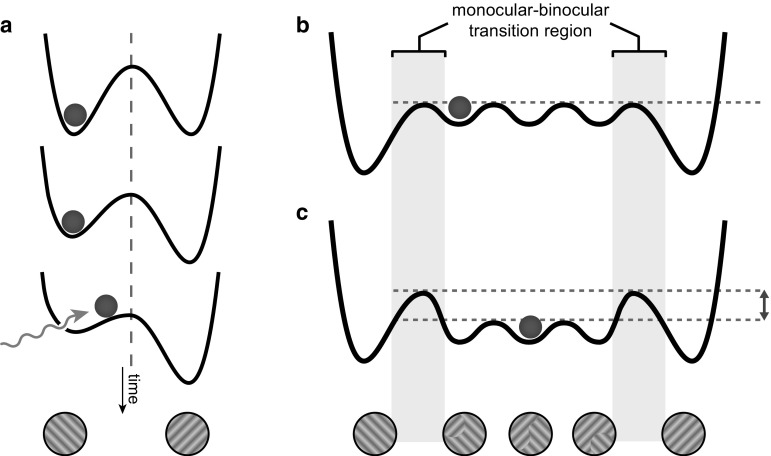
Different theoretic models have been proposed for describing BR and tried to describe the relation between different stimulus features (such as its strength and contrast) and the phenomenology of binocular rivalry (Brascamp et al. 2006, 2015). These models should explain two main aspects of this phenomenon, the mechanisms of selection and maintenance of alternative percepts, and the mechanisms underlying stochastic perceptual durations. The mainstream models of percept alternations during binocular rivalry are built upon the concept of mutual inhibition (Kang and Blake 2011). Mutual inhibition models propose that coalitions of neurons representing each perceptual state support the activity of their fellow neurons, while mutually inhibiting the activity of neurons representing alternative perceptual states. To account for stochastic percept change durations, models have included an adaptation component (Kalarickal and Marshall 2000; Laing and Chow 2002; Lankheet 2006). Simulation studies have successfully reproduced the stochastic percept duration series by introducing noise in either the mutual inhibition (Kim et al. 2006; Moreno-Bote et al. 2007) or adaptation modules (Van Ee 2009) of the model (Fig. 1a).

Fig. 1.

State space reinterpretation of perceptual change during binocular rivalry. a Noise and adaptation have been proposed as mechanisms underlying perceptual alternation during binocular rivalry. Adaptation mechanisms (shape changes presented during time) decrease the depth of the winning perceptual basin, eventually facilitating the jump to another perceptual basin. Energy impetuses produced by noise (wavy arrow) underlies the stochastic variations in percept durations. The height of the wall of a basin is the basis of positive serial correlation observed between perceptual duration time-series of each perceptual state. b, c Inclusion of piecemeal perceptions in the state landscape. b The piecemeal binocular perceptions during the transition from one monocular state to another could be conceptualized as multiple low-depth basins interleaving the stable monocular states. c The transition from a uniformly monocular perception to a mixed binocular perception might be inherently resisted by a monocular-binocular barrier (double-head arrow) in the energy landscape. This would impose inertia and memory specific to the period of piecemeal transitions as a whole

Most studies on perceptual switching time-series during binocular rivalry have ignored the transitory piecemeal perceptual periods, where the conscious perception is a dichoptic mixture of two monocular stimuli. In such studies certain measures have been taken to minimize the piecemeal formation (e.g. using experimental setups with small-sized stimuli). Furthermore, most studies did discard the time-course of piecemeal periods prior to applying mathematical correlation analyses. We propose that the piecemeal dichoptic perceptions during the transition from one monocular state to another could be conceptualized as multiple low-depth basins interleaving the stable monocular state basins (Fig. 1b). Such basins produce very little inertia and the inherent noise of neural activity might be sufficient for providing the energy for trespassing them. In the classic setup for binocular rivalry—that is two stationary monocular stimuli each exclusively presented to left or right eye—formation of a piecemeal percept means that the visual system has alternated from ignoring an eyes input altogether, to integrating the two eyes’ images. We conjecture that such a change from exclusively monocular consciousness to dichoptic piecemeal consciousness is faced with resistance, thus creating a barrier in the state landscape in between of a monocular and a piecemeal basin (Fig. 1c, double headed arrow; Kang and Blake 2011).

This hypothesis implies several predictions about the properties of piecemeal time courses during binocular rivalry. The basic implication is that there is inertia and memory (i.e. positive serial correlation) for the piecemeal dichoptic perception states as well as the monocular states. One of the ways of finding correlations and the memory of a system is studying the scale-freeness of that phenomenon. Scale-freeness of certain series of fluctuations means whether or not they have characteristic time scale (Gao et al. 2006) and can be assumed as self-affinity in fractal time series. Fractal time series are similar to geometric fractals. As self-similarity in geometric fractals, there is also a similar property called self-affinity in fractal time series which describes an anisotropic scaling for the time dimension (West 2010; Hardstone et al. 2012).

Distributions with characteristic scales can be appropriately described with measures of central tendency (e.g. mean, median) and dispersion (e.g. SD); however, for scale-free phenomena these statistical measures are insufficient. A better solution is to use exponent of a power-law function (Hardstone et al. 2012).

A method for examining the scale-freeness of a phenomenon is using the detrended fluctuation analysis (DFA). DFA characterizes the correlation structure of non-stationary time series and is an appropriate method for determining long range correlations and scaling properties in non-stationary time series (Gao et al. 2006; Hardstone et al. 2012; Stam and de Bruin 2004). This approach was used in diverse brain studies (Yuvaraj and Murugappan 2016; Bornas et al. 2015; Freeman and Zhai 2009). In a log–log plot of a power-law distribution of a time series the relationship between x-axis and y-axis becomes linear and its slope is independent of the scaling of the x-axis. In general, the slope of that line will be the DFA exponent, α, which is called scaling or self-similarity coefficient. Indeed, α shows the level of correlation between the signal and a power law function.

• If α is between 0 and 0.5 the system is anti-correlated and has memory.

• If α is between 0.5 and 1 the system is positive correlated and has memory.

• If α is 0.5 the system does not have memory and is identifiable from a random process.

• If α is between 1 and 2 the system is non stationary (Hardstone et al. 2012).

As an example, in a white noise signal which all the frequencies have similar amplitudes the result of DFA would be around 0.5 which confirms that a white noise signal is a random process; however, the result of DFA for 1/f signal which lower frequencies have higher amplitude is around 1 which shows that this signal is positively correlated.

Also in DFA, another coefficient is used called Hurst coefficient. If α is between 0 and 1 then Hurst coefficient is equal to α, and if α is between 1 and 2 then Hurst coefficient is α−1. Hurst coefficient is the dimensionless estimator of self-affinity. For a scale-free phenomenon, the statistical distribution of smaller part of the time series have the similar statistical distribution of the larger part, so, they can well define a self-affine process (Hardstone et al. 2012; Arita 2005; Barabási and Albert 1999). This method is used in a variety of fields like DNA sequences, cardiovascular dynamics, neuron spiking, solid state physics and even in economic and humanities such as ethnology (Peng et al. 1992; Kantelhardt et al. 2002). Neural activity is a substantial instance of physiological scale-free phenomena. Scale-freeness in brain connectivity has been proved by different studies based on EEG and fMRI signals. The results have shown that brain dynamics produced by scale-free synchronous cell assemblies (Stam and de Bruin 2004; Stam 2005; He et al. 2010; Minati et al. 2013; Freeman and Breakspear 2007) which means that brain could be considered as a complex self-organizing system (Ozaki et al. 2012; Feldman 2013; Yamaguti et al. 2014). In a previous study, Gao et al. indicated that BR fluctuations are also scale-free and can be considered as a 1/f process (Gao et al. 2006). They considered the two dominant states of BR, disregarding the piecemeal percept durations, and used DFA technique to study the time series of perception fluctuations.

In this study we aim to find out the scale-freeness of fluctuations in BR durations in order to test for evidence of memory in percept switch durations of both two dominant monocular states and the transitory piecemeal states using the DFA (Gao et al. 2006; Stam and de Bruin 2004). We used a classic binocular setup which was designed to facilitate vergence and binocular fusion while using stimuli size that allowed a satisfactory amount of piecemeal periods. If the transition between complete monocular perceptions and piecemeal dichoptic perceptions imposes any resistance to switching of consciousness, we expect to observe positive memory in the system, whether we include the piecemeal transitions periods or not. As Pearson and Brascamp (2008) suggested, studying the overlap between visual perception and memory will improve our understanding of these brain functions (Pearson and Brascamp 2008).

Materials and methods

Experimental design

In order to induce binocular rivalry, the stimuli were presented on a gamma-corrected CRT monitor (80 Hz refresh rate) and viewed through a customizable mirror stereoscope (Fig. 2). Chin and head rests were used to minimize head movements. They also fixed the eye to monitor distance at 50 cm, leading to an image viewing distance of ≃65 cm through mirror reflections. The rivaling stimuli (Fig. 2) consisted of two static oblique sine-wave gratings, oriented at +45° for the left and −45° for the right eye. Gratings had a spatial frequency of 6 cycles per visual degree and filled a circular patch (d = 0.7°) with a smooth edge boundary in which intensity dropped following a Gaussian kernel (FWHM = 0.1°) making a total stimulus span of one visual degree. The background was uniform gray (15 cd/m2) which matched the average luminance of gratings.

Fig. 2.

The binocular rivalry stimuli and mirror stereoscope setup. A vertical divider (thick black line) blocked image leaks to the contralateral eyes. Arrows represent mirror customizability. Gratings had a spatial frequency of 6 cycles per visual degree and filled a circular patch (d = 0.7°) with a smooth edge following a Gaussian kernel (FWHM = 0.1°). Dimensions are drawn arbitrarily for the sake of illustration

To assist perceptual superposition of gratings and facilitate binocular fusion, each stimulus was surrounded by a white alignment ring (d = 1.85°) with four nonius lines protruding 0.2° along cardinal axes. Moreover a binocular gray-scale natural pattern was used to backdrop the visual field afterward a 1.5° distance from gratings and onwards. The use of identical binocular elements and soft-edged stimuli turned out to be beneficial in enhancing stable vergence, while allowing both dominant monocular and piecemeal perceptions.

Data gathering

Data gathering was performed in a light and sound attenuated room. 12 subjects (7 males; age: 23-30) naïve to the purpose of study with normal or corrected-to-normal vision participated. Subjects were students of Amirkabir University of technology and participated in this test voluntary.

Preliminary to the experiment session, orientations of stereoscope’s mirrors were individually customized to yield best binocular fusion for each participant. Subjects were instructed to report rivalry dominances by pressing and holding either of left or right arrows on keyboard, corresponding to perceived grating orientation, or releasing all keys in case of a transition, piecemeal percept, or uncertainty; this is the special part of the experiment which considers the period of transitory mixed images as a third state. Each participant completed a 2-min training run followed by four experimental trials, each comprising 5 min of continuous viewing, with a mandatory 2-min resting period between trials. This resulted in 240 min time series of rivalry dominance durations. All Stimulus presentation and data gathering routines were performed using Psychtoolbox-3 (Brainard 1997; Pelli 1997; Kleiner et al. 2007), implemented in Matlab Mathworks.

Data analysis

Detrended fluctuation analysis (DFA)

The method which is followed here is DFA analysis which is applied to a discrete time series of every subject. These time series represent their state of perception. In our experiments we recorded the time interval of each state for every subject. Then, we changed these intervals to perception duration and finally, made a time series for each of them.

For using the DFA, in the first step, a cumulative sum of the time series was calculated in order to create a signal profile:

$$y\left(k\right)=\sum _{i=1}^k\left[x\left(i\right)-〈x〉\right]$$ 1

Then, a set of non-overlapping windows with specific sizes were applied to the signal profile. For each window, the linear trend was removed from the time series–preparing detrended signal—and then the SD was calculated:

$$F\left(n\right)=\sqrt{\frac{1}{N}\sum _{k=1}^N{\left[〈y〉-y_n\left(k\right)\right]}^2}$$ 2

where y was the mean of detrended signal in each window. Windows were applied to the data from beginning to the end and vice versa to cover all the data. After that, the fluctuation function was computed as the mean SD of all equal window sizes and finally, fluctuation function versus all window sizes would be plotted in logarithmic axis. By fitting a line on the given data and calculating its slope we found DFA exponent and Hurst coefficient. These values revealed the time scale of the fluctuations.

In this analysis we evaluated 3-states which included the transition state and two dominant percept states and all the states (right dominant, left dominant and piecemeal states) were considered as the same in DFA analysis.

In BR’s researches usually only the two dominant state data is studied. In a second analysis, we eliminated the transition periods from the time courses and analyzed the remaining data with DFA. Paired t test statistic was applied on the results of both analyzes to compare the outcomes. All analyses were performed with MATLAB R2014a.

Results

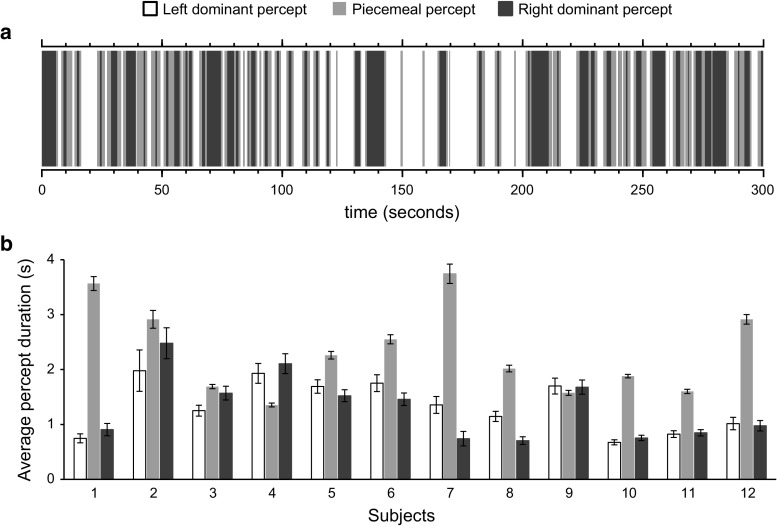
Figure 3a shows the BR fluctuations time series of an exemplary participant for three perceptual states. The average percept duration of subjects for left dominant and right dominant states was 1.34 ± 0.45 (mean ± SD) and 1.31 ± 0.56 respectively. Paired samples t-test showed that these values were statistically equal (t(11) = −0.29; p = 0.78). Piecemeal perception states had an average duration of 2.34 ± 0.80. Figure 3b shows the average percept duration of three perceptual states for each participants. It is apparent that participants showed varied amount of piecemeal percept durations, the average duration being larger in most cases but smaller in some others. Nevertheless, these transitory percept periods had larger durations in comparison with the two stable perceptual states (t(11) = −3.39; p = 0.006). The descriptive statistics evaluation of perception duration time series revealed that our experimental setup was effective in inducing binocular rivalry and also allowed for considerable periods of piecemeal perception.

Fig. 3.

Binocular rivalry time series. a Perceptual state fluctuations of a representative participant (subject number 4) during first 5 min of the experiment. Percept changes from a stable dominant state to another were mostly interleaved with a transitory piecemeal perception state. However, there are instances of direct jumps between stable perceptions and there are instances of returning to the same dominant perception after a piecemeal period. In this exemplary subject the average percept durations for left and right dominant states were close, 1.93 and 2.11 s respectively. The average piecemeal periods were shorter (1.35 s) in this subject. b Average duration of left dominant, piecemeal and right dominant perception periods across 12 subjects. Error bars represent ± standard error of mean

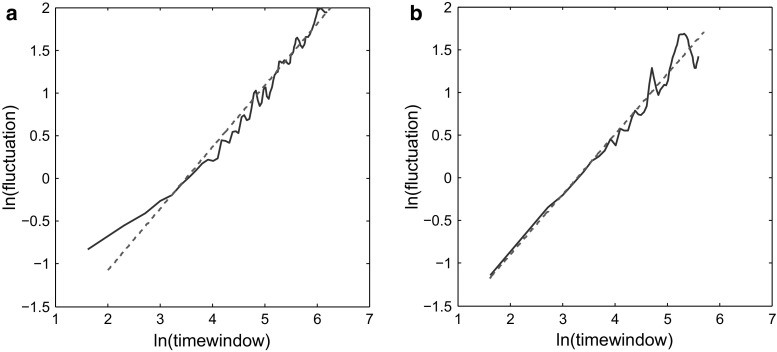
Now we will discuss the DFA results on these data. Figure 4 presents the fluctuation function versus time windows for the exemplary time series presented in Fig. 3a for double state rivalries (a) and triple state rivalries (b). Our results revealed that for this specific subject, the Hurst coefficient for perception time series including the piecemeal states (triple states) was 0.72 which is close to the Hurst coefficient value determined for double state time series (0.70).

Fig. 4.

Results of DFA analysis of a representative subject’s time series. a Considering triple states, including piecemeal periods as well as stable monocular perception periods. b Double states, excluding piecemeal periods

Table 1 contains the Hurst coefficient for all 12 subjects. The results reveal that the Hurst coefficients were in the range of 0.5 and1 implying that the system is positive correlated and has memory. Paired samples t-test comparison of Hurst coefficients calculated for the time series including (triple state) or excluding (double stat) the piecemeal periods did not show any significant difference (t(11) = −1.51; p = 0.16). Moreover, the Hurst coefficient for only piecemeal states were calculated to show that separate piecemeal states are also positive correlated and have memory (in the range of 0.5 and 1).

Table 1.

Hurst coefficient for all 12 subjects

Subject number	Hurst coefficient for triple state	Hurst coefficient for double state	Hurst coefficient for piecemeal states
1	0.68	0.73	0.77
2	0.85	0.91	0.83
3	0.64	0.67	0.86
4	0.63	0.61	0.89
5	0.82	0.84	0.63
6	0.67	0.71	0.66
7	0.55	0.65	0.59
8	0.71	0.83	0.58
9	0.69	0.66	0.82
10	0.72	0.70	0.75
11	0.72	0.70	0.80
12	0.70	0.65	0.78

Discussion

In this study, we investigated the scale-freeness of the BR percept durations considering the two dominant monocular states as well as the piecemeal transition state. Scale-freeness is a sign of existence of long memory in the process of BR switching. This memory implies that whenever a long switching time is detected, it is more expected for the next switching time to be long as well. Gao et al. (2006) suggested that, the long memory feature is in accordance with the “dynamic core hypothesis (DCH)” in the consciousness. Based on DCH, a transient coalition of neurons makes the content of our conscious perceptions. Therefore, perceptual switching relates to the exchange of one coalition of neurons by another. The memory and inertia is an index of the level of neuronal coalition stability. In a competition between neuronal coalitions, it takes longer time for replacement of a strong and stable coalition with another strong and stable one which results to a longer switching time (Gao et al. 2006).

A method for examining the scale-freeness of a phenomenon is using the DFA. Considering the two dominant monocular states as well as the piecemeal transition state, we showed that such memory also exists in the transitory periods of dichoptic piecemeal perceptions. In our study, we reinterpreted the inclusion of piecemeal perceptions based on the well model proposed by Kang and Blake (2011). Our results reproduced the previous finding of memory in the perceptual switches between the monocular perception states (Gao et al. 2006). Moreover, we showed that such memory also exists in the transitory periods of dichoptic piecemeal perceptions. In fact, we reinterpreted the inclusion of piecemeal perceptions based on the well model proposed by Kang and Blake (2011). Our results support our hypothesis that the transition between monocular and piecemeal perceptions is faced with resistance, and the pool of unstable piecemeal perceptions could be regarded as separate basin in the perceptual state landscape (see Fig. 1c). Our current reinterpretation of the transitional states as a set of shallow basins of perception is in line with epistemological view proposed by Hohwy et al. (2008). This view considers brain as engaged in probabilistic unconscious perceptual inference about the causes of its sensory input. Interpretations of ambiguous sensory inputs would have a higher chance of lingering in the consciousness when they explain a fair amount of prediction error signal and enjoy a high prior probability. The piecemeal perception entails the positive prior probability that it is resulted by fusing sensory inputs of both eyes.

The current reinterpretation of piecemeal states in the state landscape (Fig. 1c) also provides plausible explanations for the observation of perceptual waves of binocular rivalry (Wilson et al. 2001). This phenomenon refers to the highly ordered transitions in dominance as one monocular stimulus sweeps the other out of conscious awareness. These dominance waves are particularly prominent with larger rival stimuli subtending many degrees of visual angle, the same physical attributes that invokes the formation of piecemeal perceptions (Kang and Blake 2011; Wilson et al. 2001; Bressloff and Webber 2012; Kang and Blake 2008). In order to explain the alternations during BR, different hypotheses have been proposed. Our results are in line with one of the most prevailing hypotheses, i.e. neural adaptation. According to this theory, over time, adaptation mechanisms attenuate the dominant neural activities and hence, in the competition between two stimuli, the non-dominant stimulus will capture the conscious perception. There are three common types of neural adaptation theories (Tong 2001). Based on Levelt’s theory, BR is a competitive mechanism between monocular neurons in the primary visual cortex (V1) or in the lateral geniculate nucleus (LGN) of the thalamus which involves reciprocal inhibition between two eyes that one eye tries to inhibit the influence of the other eye (called intracellular competition; Levelt 1965). Unlike the first view, another theory by Logothetis et al. posits that a competition between inconsistent patterns emerging in higher level cortex causes BR rather than a low-level competition between eyes (Logothetis et al. 1996). However, in recent years, a hybrid view has been developed which assumes that both intracellular competition and pattern competition take part in BR (Tong et al. 2006).

The existence of piecemeal transient states and their effect on BR’s memory is in favour of the assumption that higher level cortex participates in BR fluctuations. A study by Knapen supports this view as well (Knapen et al. 2011). They evaluated brain functions during BR by considering both piecemeal and dominant states with fMRI and found that frontoparietal brain areas respond to BR transitions. Furthermore, they revealed that transition durations showed correlation with activation amplitude in frontal and parietal brain areas (Knapen et al. 2011).

In addition to adaptation theories, pioneer hypotheses have tried to explain BR fluctuation using quantum mechanics (Stapp 2007; Manousakis 2009a, b; Conte et al. 2009; Paraan et al. 2014). Some of these theories consider two quantum states for two dominance states of BR and try to achieve the observed probability distribution of dominance duration. Furthermore, they state that consciousness of each BR state correlates with actualization of its quantum state by collapsing its wave function through the Schrodinger equation (Manousakis 2009a, b). Also, there are other quantum studies that have considered both piecemeal and dominant perception states (Conte et al. 2009; Paraan et al. 2014). Some of them introduced the piecemeal transitions as a third quantum state which dominates consciousness randomly and should be considered in statistical calculations of quantum mechanics (Paraan et al. 2014). Our reinterpretation of piecemeal states in the state landscape is similar to quantum mechanics perspective on the importance of piecemeal percept durations in models of BR.

It should be noted that cognitive condition of subjects in BR experiments should be considered while discussing the results. Scocchia et al. discussed that intention, imagery and working memory can affect adaptation and perceptual dominance in bistable perceptions such as BR (Scocchia et al. 2014). In future studies of BR it can be considered whether or not intellectual bias affects judgments of the subjects about what they see during BR experiments. For example, if subjects are forced to report just two dominant states maybe, they will try to attribute the piecemeal states to one of the two dominant states, because their minds are biased that there are only two states.

In some psychiatric disorders, such as bipolar disorder and autism, patients exhibit slower rates of BR fluctuations in comparison with normal population (Vierck et al. 2013; Robertson et al. 2013). BR fluctuations’ rate could be conceived as a significant marker for diagnosing such disorders. Therefore, developing effective models of BR, which incorporates piecemeal periods as well, may help to define more precise diagnostic markers. Our results cannot exclusively justify all attributes of BR experiments. Analyzing the alternation dynamics of BR may be helpful in elucidating the responsible neural mechanisms producing BR.