Synchronization of generalized reaction-diffusion neural networks with time-varying delays based on general integral inequalities and sampled-data control approach

Abstract

This paper explores the problem of synchronization of a class of generalized reaction-diffusion neural networks with mixed time-varying delays. The mixed time-varying delays under consideration comprise of both discrete and distributed delays. Due to the development and merits of digital controllers, sampled-data control is a natural choice to establish synchronization in continuous-time systems. Using a newly introduced integral inequality, less conservative synchronization criteria that assure the global asymptotic synchronization of the considered generalized reaction-diffusion neural network and mixed delays are established in terms of linear matrix inequalities (LMIs). The obtained easy-to-test LMI-based synchronization criteria depends on the delay bounds in addition to the reaction-diffusion terms, which is more practicable. Upon solving these LMIs by using Matlab LMI control toolbox, a desired sampled-data controller gain can be acuqired without any difficulty. Finally, numerical examples are exploited to express the validity of the derived LMI-based synchronization criteria.

Introduction

Over the last few decades, neural networks have procured substantial intrigue for its applications in many practical areas including automatic control, image and signal processing, fault diagnosis, combinatorial optimization, associative memory, etc (Young et al. 1997; Atencia et al. 2005; Hopfield 1984; Diressche and Zou 1998). All such applications heavily depend on the qualitative properties of neural networks. Synchronization, one of the collective dynamical behavior and one of the most fascinating phenomena of neural networks has been widely explored in the literature, see for example He et al. (2017), Shen et al. (2017), Bao et al. (2015), Tong et al. (2015) and Prakash et al. (2016). Besides, based on the choice of neuron states (internal/external), neural networks can be classified as local field neural networks (LFNNs) and static neural networks (SNNs), but still these neural networks can be transfered from one to other under certain assumptions, which are not always practicable. Hence, independent analysis on their dynamical behaviors are acquired. To avoid this complication, an unified model that includes both LFNNs and SNNs has been constructed in Zhang and Han (2011) and investigated its stability. This model of generalized neural network has been applied in areas wherever different types of neural networks are used. This promoted researchers to analyze the dynamics of generalized neural networks, see for examples Zheng et al. (2015), Manivannan et al. (2016), Liu et al. (2015a), Rakkiyappan et al. (2016a, b) and Li and Cao (2016), which are yet far from complete. The stability analysis for the switched Hopfield neutral neural networks was conducted in Manivannan et al. (2016), and some delay dependent stability criteria were established by constructing a new Lyapunov–Krasovskii functional. The problem of stability and pinning synchronization of delayed inertial memristive neural networks was investigated by employing matrix measure and Halanay inequality (Rakkiyappan et al. 2016a). Some LMI-based criteria were presented to guarantee the stability of reaction-diffusion delayed memristor-based neural networks (Li and Cao 2016). Based on the Lyapunov theory and analytical techniques, the fixed-time synchronization for delayed memristive recurrent neural networks was studied in Cao and Li (2017).

Besides, owing to the finite switching speeds and traffic congestion in signal transmission processes, time delays may endure in various dynamical systems, which may be unfavorable to successful applications of neural networks. It is evident from the literature that most research work on delayed neural networks has been confined to simple cases of discrete delays. However, in reality, neural networks frequently exhibit a special nature due to the occurrence of multitude of parallel pathways with a variety of axon sizes and lengths and thus there is a distribution of conduction velocities along these pathways and a distribution of propagation delays. Therefore, to construct a realistic neural network model, it is indispensable to include both discrete and distributed delays. Thus, the qualitative analysis of different neural networks with discrete and distributed delays has been established in the literature, see Wang et al. (2006), Zheng and Cao (2014), Rakkiyappan and Dharani (2017), Lee et al. (2015), Zhang et al. (2009) and Yang et al. (2014), for instance. Robust stability analysis of generalized neural networks with discrete and distributed delays has been analyzed in Wang et al. (2006). Robust synchronization analysis for a class of coupled delayed neural networks has been examined in Zheng and Cao (2014). In addition, in most stability and synchronization analysis of delayed systems, integral inequalities are extensively employed since they exactly produce bounds for integral terms with respect to quadratic functions. Jensen’s inequality is the mainly used and has served as a dominant tool in the stability analysis of time delay systems. Recently, an auxiliary function-based integral inequality has been introduced in Park et al. (2015) and it has been proved that this class of integral inequality produce more tighter bounds than that of Jensen inequality. Over which, it is proved in Chen et al. (2016a) that there occurs a general inequality based on orthogonal polynomials which comprises of all existing inequalities such as the Bessel-Legendre inequality, Jensen inequality, the Wirtinger-based inequality and the auxiliary function-based inequality as its special cases. Motivated by this fact, this paper employs the general integral inequality based on orthogonal polynomials to derive new less conservative criteria for the synchronization of generalized reaction-diffusion neural networks with mixed time-varying delays.

As one of the main factors that bring bad performance to the system, diffusion phenomena is often encountered in neural networks and electric circuits once electrons move in a nonuniform electromagnetic field. This implies that the whole structure and dynamics of neural networks rely on the evolution time of each variable as well as intensively rely on its position status and thus, the reaction-diffusion system arises in response to the above mentioned phenomenon. Recently, neural networks with diffusion terms and Markovian jumping have been immensely investigated in the literature, see Wang et al. (2012a), Gan (2012), Yang et al. (2013), Zhou et al. (2007), Li et al. (2015) and references therein. The problem of exponential synchronization of reaction-diffusion Cohen-Grossberg neural networks and Hopfield neural networks with time-varying delays has been investigated in Gan (2012) and Wang et al. (2012a), respectively. To our knowledge, many phenomena such as time delay and diffusion effects may show the way to undesirable behaviors like oscillation and instability. Consequently, in order to make complete use of their advantages and restrain their disadvantages, some control techniques should be adopted to realize synchronization in generalized reaction-diffusion neural networks.

As far as we know, most of the benefications to nonlinear control theory are based on continuous-time control such as adaptive control, non-fragile control, feedback control and so on. The finite-time passivity problem was discussed by constructing a nonfragile state feedback controller (Rajavel et al. 2017). The problem of exponential $H_{\infty }$ filtering for discrete-time switched neural networks was investigated via the average dwell time approach and the piecewise Lyapunov function technique (Cao et al. 2016). The key point in implementing such continuous-time controllers is that the input signal should be continuous, which we cannot always ensure in real-time situations. Moreover, due to the expeditious furtherance in intelligent instrument and digital measurement, nowadays, continuous-time controllers are generally replaced by discrete-time controllers to embellish improved stability, precision and better performance. Further, in digital control method, namely, the sampled-data control approach, the response network accepts the signals from the drive system only in discrete times and the amount of information transferred decreases. This is very advantageous in implementation of controllers because of reduced control cost. Owing to this reason, sampled-data control theory has attracted appreciable notice from researchers and fruitful works have been done previously, few are Liu et al. (2015b), Liu and Zhou (2015), Lee and Park (2017), Rakkiyappan et al. (2015a, b), Su and Shen (2015) and Lee et al. (2014). In all such above mentioned works, only Jensen’s inequality has been utilized to handle integral terms that occur when deriving the synchronization criteria. Different from these works, in this paper, we suppose to derive the synchronization criteria for generalized neural networks with mixed delays using a general integral inequality that comprises Jensen’s inequality and many other existing inequalities as its special cases, which has not yet been established in the literature.

In response to the above discussion, it is worth noticing that both mixed delays and reaction-diffusion effects cannot be neglected when modeling neural networks since they have a potential influence on the dynamics of such networks and however, it is not that easy to handle all of them in a whole under a unified framework of generalized neural network model. Hence, it is of great interest to study this problem and still there is space for further improvement. The main goal of this paper is to explore the global asymptotic synchronization criteria for generalized reaction-diffusion neural networks with mixed delays based on a newly introduced general integral inequality which is derived based on the orthogonal polynomials and includes many existing inequalities such as Wirtinger-based inequality, Jensen’s inequality, the Bessel-Legendre inequality, etc. as its special cases. By constructing proper Lyapunov–Krasovskii functional with triple and four integral terms, new solvability criteria are derived in terms of LMIs which depends on the size of the delays, the sampling period as well as the diffusion terms. Finally, two numerical examples with simulation results are presented to exhibit the effectiveness of the derived theoretical results.

The structure of this paper is summarized as follows: In “Synchronization analysis problem” section, the problem under investigation is described and “Main results” section is devoted to establish some new synchronization criteria. “Numerical examples” section gives two numerical examples to demonstrate the effectiveness of our theoretical results. Finally, conclusion is presented in “Conclusions” section.

Notations and preliminaries Through the whole, $R^n$ represents the n-dimensional Euclidean space. For a matrix X,  $X>0(<0)$ refers to a positive (negative) definite symmetric matrix and $X^T,X^{-1}$ means the transpose and the inverse of a square matrix X,  respectively. The symbol $\star$ in a symmetric matrix indicates the elements that are induced by symmetry. The shorthand $diag\{·\}$ denotes a diagonal or block diagonal matrix. $S_n\text{and}{S}_n^{+}$ denotes the sets of symmetric and symmetric positive definite matrices of $R^{n\times n},$ respectively.

Before proceeding, we present some necessary lemmas which will be employed to derive the main results.

Lemma 1

(Lu 2008) Let $\mathit{\Gamma }$ be a cube $|x_k|<q_k(k=1,2,\dots ,m)$ and let w(x) be a real-valued function belonging to $C^1(\mathit{\Gamma })$ which satisfies ${w(x)|}_{\mathit{\partial }\mathit{\Gamma }}=0.$ Then

$${\int }_{\mathit{\Gamma }}{w}^2(x)\text{d}x\le q_k^2{\int }_{\mathit{\Gamma }}{\left|\frac{\mathit{\partial }w(x)}{\mathit{\partial }{x}_k}\right|}^2\text{d}x.$$

Lemma 2

(Chen et al. 2016a) Let $\dot{\mathit{\omega }}$ (s) be a multiple integrable function and $R\in S_n^{+}.$ The following integral inequalities hold:

$${\int }_a^b{\dot{\mathit{\omega }}}^T(s)R\dot{\mathit{\omega }}(s)\text{d}s\ge \frac{1}{b-a}{\dot{\mathit{\gamma }}}_0^{T}R{\dot{\mathit{\gamma }}}_0+\frac{3}{b-a}{\dot{\mathit{\gamma }}}_1^{T}R{\dot{\mathit{\gamma }}}_1+\frac{5}{b-a}{\dot{\mathit{\gamma }}}_2^{T}R{\dot{\mathit{\gamma }}}_2+\frac{7}{b-a}{\dot{\mathit{\gamma }}}_3^{T}R{\dot{\mathit{\gamma }}}_3+\frac{9}{b-a}{\dot{\mathit{\gamma }}}_4^{T}R{\dot{\mathit{\gamma }}}_4,$$ 1

$${\int }_a^b{\int }_c^b{\dot{\mathit{\omega }}}^T(s)R\dot{\mathit{\omega }}(s)\text{d}s\text{d}\mathit{\delta }\ge \frac{2}{{(b-a)}^2}{\dot{\mathit{\gamma }}}_{0^2}^{T}R{\dot{\mathit{\gamma }}}_{0^2}+\frac{16}{(b-a)2}{\dot{\mathit{\gamma }}}_{0,1}^{T}R{\dot{\mathit{\gamma }}}_{0,1}+\frac{54}{{(b-a)}^2}{\dot{\mathit{\gamma }}}_{0,2}^{T}R{\dot{\mathit{\gamma }}}_{0,2}+\frac{128}{{(b-a)}^2}{\dot{\mathit{\gamma }}}_{0,3}^{T}R{\dot{\mathit{\gamma }}}_{0,3},$$ 2

$${\int }_a^b{\int }_c^b{\int }_{\mathit{\delta }}^b{\dot{\mathit{\omega }}}^T(s)R\dot{\mathit{\omega }}(s)\text{d}s\text{d}\mathit{\delta }\text{d}\mathit{\delta }\ge \frac{6}{{(b-a)}^3}{\dot{\mathit{\gamma }}}_{0^3}^{T}R{\dot{\mathit{\gamma }}}_{0^3}+\frac{90}{{(b-a)}^3}{\dot{\mathit{\gamma }}}_{0^2,1}^{T}R{\dot{\mathit{\gamma }}}_{0^2,1}+\frac{504}{{(b-a)}^3}{\dot{\mathit{\gamma }}}_{0^2,2}^{T}R{\dot{\mathit{\gamma }}}_{0^2,2}$$ 3

where

$$\begin{array}{cc}\hfill {\dot{\mathit{\gamma }}}_0=& \mathit{\omega }(b)-\mathit{\omega }(a),{\dot{\mathit{\gamma }}}_{0^2}=(b-a)\mathit{\omega }(b)-{\mathit{\gamma }}_0,{\dot{\mathit{\gamma }}}_{0^3}=\frac{{(b-a)}^2}{2}\mathit{\omega }(b)-{\mathit{\gamma }}_{0^2},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_1=& \mathit{\omega }(b)+\mathit{\omega }(a)-\frac{2}{b-a}{\mathit{\gamma }}_0,{\dot{\mathit{\gamma }}}_2=\mathit{\omega }(b)-\mathit{\omega }(a)+\frac{6}{b-a}{\mathit{\gamma }}_0-\frac{12}{{(b-a)}^2}{\mathit{\gamma }}_{0^2},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_3=& \mathit{\omega }(b)+\mathit{\omega }(a)-\frac{12}{b-a}{\mathit{\gamma }}_0+\frac{60}{{(b-a)}^2}{\mathit{\gamma }}_{0^2}-\frac{120}{{(b-a)}^3}{\mathit{\gamma }}_{0^3},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_4=& \mathit{\omega }(b)-\mathit{\omega }(a)+\frac{20}{b-a}{\mathit{\gamma }}_0-\frac{180}{{(b-a)}^2}{\mathit{\gamma }}_{0^2}+\frac{840}{{(b-a)}^3}-\frac{1680}{{(b-a)}^4}{\mathit{\gamma }}_{0^4},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_{0,1}=& \frac{b-a}{2}\mathit{\omega }(b)+{\mathit{\gamma }}_0-\frac{3}{b-a}{\mathit{\gamma }}_{0^2},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_{0,2}=& \frac{b-a}{3}\mathit{\omega }(b)-{\mathit{\gamma }}_0+\frac{8}{b-a}{\mathit{\gamma }}_{0^2}-\frac{20}{{(b-a)}^2}{\mathit{\gamma }}_{0^3},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_{0,3}=& \frac{b-a}{4}\mathit{\omega }(b)+{\mathit{\gamma }}_0-\frac{15}{b-a}{\mathit{\gamma }}_{0^2}+\frac{90}{{(b-a)}^2}{\mathit{\gamma }}_{0^3}-\frac{210}{{(b-a)}^3}{\mathit{\gamma }}_{0^4},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_{0^2,1}=& \frac{{(b-a)}^2}{6}\mathit{\omega }(b)+{\mathit{\gamma }}_{0^2}-\frac{4}{b-a}{\mathit{\gamma }}_{0^3},\hfill \\ \hfill {\dot{\mathit{\gamma }}}_{0^2,2}=& \frac{{(b-a)}^2}{12}\mathit{\omega }(b)-{\mathit{\gamma }}_{0^2}+\frac{10}{b-a}{\mathit{\gamma }}_{0^3}-\frac{30}{{(b-a)}^2}{\mathit{\gamma }}_{0^4}.\hfill \end{array}$$

Lemma 3

(Gu et al. 2003) For any matrix $\mathit{\Phi }>0\in R^{n\times n}$ and a scalar $\mathit{\rho }>0,$ vector function $r:[0,\mathit{\nu }]\to R^n$ such that the following integrations are well defined, then

$${\left({\int }_0^{\mathit{\rho }}r(s)\text{d}s\right)}^T\mathit{\Phi }\left({\int }_0^{\mathit{\rho }}r(s)\text{d}s\right)\le \mathit{\rho }{\int }_0^{\mathit{\rho }}{r}^T(s)\mathit{\Phi }r(s)\text{d}s.$$

Lemma 4

(Park et al. 2011) For any vector $\mathit{\xi }\in R^m,$ matrices $R_1,R_2\in S_n^{+},S\in R^{n\times n},$ ${\mathit{\Theta }}_1,{\mathit{\Theta }}_2\in R^{n\times m},$ and real scalars $a\ge 0,b\ge 0$ satisfying $a+b=1,$ the following inequality holds:

$$\frac{1}{a}{\mathit{\xi }}^T{\mathit{\Theta }}_1^T{R}_1{\mathit{\Theta }}_1\mathit{\xi }+\frac{1}{b}{\mathit{\xi }}^T{\mathit{\Theta }}_2^T{R}_2{\mathit{\Theta }}_2\mathit{\xi }\ge {\mathit{\xi }}^T{\left[\begin{array}{c}{\mathit{\Theta }}_1\\ {\mathit{\Theta }}_2\end{array}\right]}^T\left[\begin{array}{cc}{R}_1& S\\ S^T& R_2\end{array}\right]\left[\begin{array}{c}{\mathit{\Theta }}_1\\ {\mathit{\Theta }}_2\end{array}\right]\mathit{\xi }$$

subject to $\left[\begin{array}{cc}{R}_1& S\\ S^T& R_2\end{array}\right]\ge 0.$

Synchronization analysis problem

Consider the generalized reaction-diffusion neural network model with mixed time-varying delay components as

$$\frac{\mathit{\partial }{y}_l(t,x)}{\mathit{\partial }t}=\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_{lk}\frac{\mathit{\partial }{y}_l(t,x)}{\mathit{\partial }{x}_k}\right)-c_l{y}_l(t,x)+\sum _{j=1}^n{a}_{lj}{f}_j(w_{lj}{y}_j(t,x))+\sum _{j=1}^n{b}_{lj}{f}_j(w_{lj}{y}_j(t-\mathit{\tau }(t),x))+\sum _{j=1}^n{d}_{lj}{\int }_{t-d(t)}^t{f}_j(w_{lj}{y}_j(s,x))\text{d}s,$$ 4

where $1\le l\le n$ and $x(t)={[x_1,x_2,\dots ,x_m]}^T\in \mathit{\Gamma }\subset R^m,$ with $\mathit{\Gamma }=\{x||x_k|\le {\mathit{\delta }}_k,k=1,2,\dots ,m\},$ where ${\mathit{\delta }}_k$ is a positive constant. $D_{lk}\ge 0$ is the transmission diffusion operator along the lth neuron, $y_l(t,x)$ is the state of the lth neuron, $c_l>0$ denotes the decay rate of the lth neuron, $a_{lj},b_{lj}$ and $d_{lj}$ are the connection strength, the time-varying delay connection weight, and the distributed time-varying delay connection strength of the jth neuron on the lth neuron, respectively. $w_{lj}$ is the value of the synaptic connectivity from neuron j to l. $f_j(y_j(t,x))$ represents the neuron activation function. ${\mathit{\tau }}_1\le \mathit{\tau }(t)\le {\mathit{\tau }}_2$ and $0\le d(t)\le d$ are the time-varying delay and distributed time-varying delay, where ${\mathit{\tau }}_1,{\mathit{\tau }}_2$ and d are positive constants. Also, $\mathit{\sigma }=max\{{\mathit{\tau }}_2,d\}.$ The initial and Dirichlet boundary conditions of system (4) are given by

$$y_l(s,x)={\mathit{\phi }}_l(s,x),(s,x)\in [-\mathit{\sigma },0]\times \mathit{\Gamma },$$ 5

and

$$y_l(t,x)=0,(t,x)\in [-\mathit{\sigma },+\infty ]\times \mathit{\partial }\mathit{\Gamma },$$ 6

respectively. $\mathit{\phi }(s,x)={({\mathit{\phi }}_1(s,x),{\mathit{\phi }}_2(s,x),\dots ,{\mathit{\phi }}_n(s,x))}^T\in C([-\mathit{\sigma },0]\times \mathit{\Gamma },R^n),$ where $C([-\mathit{\sigma },0]\times \mathit{\Gamma },R^n)$ is the Banach space of continuous functions from $[-\mathit{\sigma },0]\times \mathit{\Gamma }$ to $R^n$ with $\Vert \mathit{\phi }(s,x)\Vert ={\left[{\int }_{\mathit{\Gamma }}{\mathit{\phi }}^T(s,x)\mathit{\phi }(s,x)\text{d}x\right]}^{1/2}$.

Remark 1

It can be clearly seen that the model (4) is a generalized neural network model which incorporates some familiar neural networks as its particular cases. (i) Letting $a_{lj}=b_{lj}=d_{lj}=1,$ the model in (4) reduces to the reaction-diffusion static neural networks model and (ii) Letting $w_{lj}=1$, it reduces to a classic reaction-diffusion local field neural networks model.

For simplicity, we represent system (4) in a compact form as

$$\frac{\mathit{\partial }y(t,x)}{\mathit{\partial }t}=\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_k\frac{\mathit{\partial }y(t,x)}{\mathit{\partial }{x}_k}\right)-Cy(t,x)+Af(Wy(t,x))+Bf(Wy(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}f(Wy(s,x))\text{d}s,$$ 7

where $y(t,x)={(y_1(t,x),y_2(t,x),\dots ,y_n(t,x))}^T,D_k=diag\{d_{1k},d_{2k},\dots ,d_{nk}\}$, $f(y(t,x))={(f_1(y_1(t,x)),\dots ,f_n(y_n(t,x)))}^T,C=diag\{c_1,c_2,\dots ,c_n\},A={(a_{lj})}_{n\times n},B={(b_{lj})}_{n\times n},\text{and}D={(d_{lj})}_{n\times n}.$

Assumption 1

For any $u,v\in R,$ the neuron activation function $f_j(·)$ is continuously bounded and satisfy

$$l_j^{-}\le \frac{f_j(u)-f_j(v)}{u-v}\le l_j^{+},$$ 8

where $l_j^{-}$ and $l_j^{+}$ are some real constants and may be positive, zero or negative.

Remark 2

As it has been mentioned in Liu et al. (2013), the constants $l_j^{-}\text{and}{l}_j^{+}$ can be positive, negative or zero. Therefore, the resulting activation functions could be nonmonotonic and more general than the usual sigmoid functions. In addition, when using the Lyapunov stability theory to analyze the stability of dynamic systems, such a description is particularly suitable since it quantifies the lower and upper bounds of the activation functions that offer the possibility of reducing the induced conservatism.

To observe the synchronization of system (4), the slave system is designed as

$$\frac{\mathit{\partial }{v}_i(t,x)}{\mathit{\partial }t}=\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_k\frac{\mathit{\partial }{v}_i(t,x)}{\mathit{\partial }{x}_k}\right)-C{v}_i(t,x)+Af(W{v}_i(t,x))+Bf(W{v}_i(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}f(W{v}_i(s,x))\text{d}s+w_i(t,x),$$ 9

where $v_i(t,x)=(v_{i1}(t,x),v_{i2}(t,x),\dots ,v_{in}(t,x))\in R^n$ is the state vector and $w_i(t,x)$ is the sampled-data controller to be designed. The boundary and initial conditions for (9) are given by

$$v_i(t,x)=0,(t,x)\in [-\mathit{\sigma },+\infty ]\times \mathit{\partial }\mathit{\Gamma },$$ 10

$$v_i(s,x)=\mathit{\psi }(s,x),\mathit{\psi }(s,x)\in C([-\mathit{\sigma },0]\times \mathit{\Gamma },R^n).$$ 11

Define the error vector as $e_i(t,x)=v_i(t,x)-y(t,x).$ Subtracting (4) from (9), we arrive at the error system as follows:

$$\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }t}=\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_k\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }{x}_k}\right)-C{e}_i(t,x)+Ag(W{e}_i(t,x))+Bg(W{e}_i(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}g(W{e}_i(s,x))\text{d}s+w_i(t,x),$$ 12

where $g(W{e}_i(t,x))=f(W{v}_i(t,x))-f(Wy(t,x)).$

This paper adopts the following sampled-data controller:

$$w_i(t,x)=K{e}_i(t_k,x),t_k\le t\le t_{k+1},$$ 13

where $K_i\in R^{n\times n}$ is the gain matrix to be obtained, $t_k$ denotes the sampling instant and satisfies $0=t_0<t_1<\cdots <t_k<\cdots <{lim}_{k\to +\infty }{t}_k=+\infty .$

Using input delay approach, we have $t-t_k=h(t),t_k\le t<t_{k+1}$ and $0\le h(t)<h.$ Then the controller in (4a) becomes

$$w_i(t,x)=K{e}_i(t-h(t),x).$$ 14

Thus, (12) can be written as

$$\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }t}=\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_k\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }{x}_k}\right)-C{e}_i(t,x)+Ag(W{e}_i(t,x))+Bg(W{e}_i(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}g(W{e}_i(s,x))\text{d}s+K{e}_i(t-h(t),x).$$ 15

Main results

In this section, by constructing Lyapunov–Krasovskii functional and by utilizing advanced techniques, new criteria to ensure the global asymptotic synchronization of the concerned generalized neural networks with reaction-diffusion terms and mixed delays will be furnished. Eventually, a design method of the sampled-data controller for the considered generalized reaction-diffusion neural networks will be proposed.

Further, let us define

$$\begin{array}{cc}\hfill {\mathit{\zeta }}^T(t,x)& =[e_i^T(t,x),{\dot{e}}_i^T(t,x)e_i^T(t-{\mathit{\tau }}_1,x)e_i^T(t-\mathit{\tau }(t),x)e_i^T(t-{\mathit{\tau }}_2,x),\hfill \\ \hfill & {\dot{e}}_i^T(t-{\mathit{\tau }}_1,x)\frac{1}{{\mathit{\tau }}_1}{\int }_{t-{\mathit{\tau }}_1}^t{e}_i^T(s,x)\text{d}s\frac{1}{\mathit{\tau }(t)-{\mathit{\tau }}_1}{\int }_{t-\mathit{\tau }(t)}^{t-{\mathit{\tau }}_1}{e}_i^T(s,x)\text{d}s\hfill \\ \hfill & \frac{1}{{\mathit{\tau }}_2-\mathit{\tau }(t)}{\int }_{t-{\mathit{\tau }}_2}^{t-\mathit{\tau }(t)}{e}_i^T(s,x)\text{d}s\frac{2}{{\mathit{\tau }}_1^2}{\int }_{-{\mathit{\tau }}_1}^0{\int }_{t+\mathit{\theta }}^t{e}_i^T(s,x)\text{d}s\hfill \\ \hfill & \frac{2}{{\mathit{\tau }}_2^2}{\int }_{-{\mathit{\tau }}_2}^0{\int }_{t+\mathit{\theta }}^t{e}_i^T(s,x)\text{d}s\text{d}\mathit{\theta }\frac{2}{{(\mathit{\tau }(t)-{\mathit{\tau }}_1)}^2}{\int }_{-\mathit{\tau }(t)}^{-{\mathit{\tau }}_1}{\int }_{t+\mathit{\theta }}^{t-{\mathit{\tau }}_1}{e}_i^T(s,x)\text{d}s\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{2}{{({\mathit{\tau }}_2-\mathit{\tau }(t))}^2}{\int }_{-{\mathit{\tau }}_2}^{-\mathit{\tau }(t)}{\int }_{t+\mathit{\theta }}^{t-\mathit{\tau }(t)}{e}_i^T(s,x)\text{d}s\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{6}{{\mathit{\tau }}_1^3}{\int }_{-{\mathit{\tau }}_1}^0{\int }_{\mathit{\theta }}^0{\int }_{t+\mathit{\lambda }}^t{e}_i^T(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\frac{6}{{\mathit{\tau }}_2^3}{\int }_{-{\mathit{\tau }}_2}^0{\int }_{\mathit{\theta }}^0{\int }_{t+\mathit{\lambda }}^t{e}_i^T(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{6}{{(\mathit{\tau }(t)-{\mathit{\tau }}_1)}^3}{\int }_{-\mathit{\tau }(t)}^{-{\mathit{\tau }}_1}{\int }_{\mathit{\theta }}^{-{\mathit{\tau }}_1}{\int }_{t+\mathit{\lambda }}^{t-{\mathit{\tau }}_1}{e}_i^T(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{6}{{({\mathit{\tau }}_2-\mathit{\tau }(t))}^3}{\int }_{-{\mathit{\tau }}_2}^{-\mathit{\tau }(t)}{\int }_{\mathit{\theta }}^{-\mathit{\tau }(t)}{\int }_{t+\mathit{\lambda }}^{t-\mathit{\tau }(t)}{e}_i^T(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{24}{{\mathit{\tau }}_1^4}{\int }_{-{\mathit{\tau }}_1}^0{\int }_{\mathit{\theta }}^0{\int }_{\mathit{\lambda }}^0{\int }_{t+\mathit{\kappa }}^t{e}_i^T(s,x)\text{d}s\text{d}\mathit{\kappa }\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{24}{{\mathit{\tau }}_2^4}{\int }_{-{\mathit{\tau }}_2}^0{\int }_{\mathit{\theta }}^0{\int }_{\mathit{\lambda }}^0{\int }_{t+\mathit{\kappa }}^t{e}_i^T(s,x)\text{d}s\text{d}\mathit{\kappa }\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{24}{{(\mathit{\tau }(t)-{\mathit{\tau }}_1)}^4}{\int }_{-\mathit{\tau }(t)}^{-{\mathit{\tau }}_1}{\int }_{\mathit{\theta }}^{-{\mathit{\tau }}_1}{\int }_{\mathit{\lambda }}^{-{\mathit{\tau }}_1}{\int }_{t+\mathit{\kappa }}^{t-{\mathit{\tau }}_1}{e}_i^T(s,x)\text{d}s\mathit{\kappa }\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\hfill \\ \hfill & \frac{24}{{({\mathit{\tau }}_2-\mathit{\tau }(t))}^4}{\int }_{-{\mathit{\tau }}_2}^{-\mathit{\tau }(t)}{\int }_{\mathit{\theta }}^{-\mathit{\tau }(t)}{\int }_{\mathit{\lambda }}^{-\mathit{\tau }(t)}{\int }_{t+\mathit{\kappa }}^{t-\mathit{\tau }(t)}{e}_i^T(s,x)\text{d}s\text{d}\mathit{\kappa }\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\hfill \\ \hfill & e_i^T(t-h(t),x)e_i^T(t-h,x)g(W{e}_i(t,x))g(W{e}_i(t-{\mathit{\tau }}_1,x))\hfill \\ \hfill & g(W{e}_i(t-\mathit{\tau }(t),x))g(W{e}_i(t-{\mathit{\tau }}_2,x)){\int }_{t-d(t)}^{t}g(W{e}_i(s,x))\text{d}s]\hfill \\ \hfill r_1& =[I0\dots 0],r_2=[0I\dots 0],\dots ,r_{28}=[0\dots 0I],\hfill \\ \hfill \mathit{\alpha }& =\frac{\mathit{\tau }(t)-{\mathit{\tau }}_1}{{\mathit{\tau }}_{12}}\text{and}\mathit{\beta }=\frac{{\mathit{\tau }}_2-\mathit{\tau }(t)}{{\mathit{\tau }}_{12}}\mathit{\Lambda }={\left[\begin{array}{c}{\mathit{\Sigma }}_2\\ {\mathit{\Sigma }}_3\end{array}\right]}^T\left[\begin{array}{cc}{\tilde{U}}_2& L\\ L^T& {\tilde{U}}_2\end{array}\right]\left[\begin{array}{c}{\mathit{\Sigma }}_2\\ {\mathit{\Sigma }}_3\end{array}\right],\hfill \\ \hfill H_1=& diag\{l_1^{-}{l}_1^{+},l_2^{-}{l}_2^{+},\dots ,l_n^{-}{l}_n^{+}\},H_2=diag\left\{\frac{l_1^{-}+l_1^{+}}{2},\frac{l_2^{-}+l_2^{+}}{2},\dots ,\frac{l_n^{-}+l_n^{+}}{2}\right\}\hfill \\ \hfill {\mathit{\Sigma }}_1& =\left[\begin{array}{c}{(r_1-r_3)}^T\\ {(r_1+r_3-2r_7)}^T\\ {(r_1-r_3+6r_7-6r_{10})}^T\\ {(r_1+r_3-12r_7+30r_{10}-20r_{13})}^T\\ {(r_1-r_3+20r_7-90r_{10}+140r_{13}-70r_{16})}^T\end{array}\right],\hfill \\ \hfill {\mathit{\Sigma }}_2& =\left[\begin{array}{c}{(r_4-r_5)}^T\\ {(r_4+r_5-2r_9)}^T\\ {(r_4-r_5+6r_9-6r_{12})}^T\\ {(r_4+r_5-12r_9+30r_{12}-20r_{15})}^T\\ {(r_4-r_5+20r_9-90r_{12}+140r_{15}-70r_{18})}^T\end{array}\right],\hfill \\ \hfill {\mathit{\Sigma }}_3& =\left[\begin{array}{c}{(r_3-r_4)}^T\\ {(r_3+r_4-2r_8)}^T\\ {(r_3-r_4+6r_8-6r_{11})}^T\\ {(r_3+r_4-12r_8+30r_{11}-20r_{14})}^T\\ {(r_3-r_4+20r_8-90r_{11}+140r_{14}-70r_{17})}^T\end{array}\right],\hfill \\ \hfill {\mathit{\Sigma }}_4& =\left[\begin{array}{c}{(r_1-r_7)}^T\\ {(r_1+r_7-2r_{10})}^T\\ {(r_1-r_7+6r_{10}-6r_{13})}^T\\ {(r_1+r_7-12r_{10}+30r_{13}-20r_{16})}^T\end{array}\right],\hfill \\ \hfill {\mathit{\Sigma }}_5& =\left[\begin{array}{c}{(r_4-r_9)}^T\\ {(r_4+2r_9-3r_{12})}^T\\ {(r_4-3r_9+12r_{12}-10r_{15})}^T\\ {(r_4+4r_9-30r_{12}+45r_{15}-140r_{18})}^T\end{array}\right],\hfill \\ \hfill {\mathit{\Sigma }}_6& =\left[\begin{array}{c}{(r_3-r_8)}^T\\ {(r_3+2r_8-3r_{11})}^T\\ {(r_3-3r_8+12r_{11}-10r_{14})}^T\\ {(r_3+4r_8-30r_{11}+45r_{14}-35r_{17})}^T\end{array}\right],\hfill \\ \hfill {\mathit{\Sigma }}_7& =\left[\begin{array}{c}{(r_1-r_{10})}^T\\ {(r_1+3r_{10}-4r_{13})}^T\\ {(r_1-6r_{10}+20r_{13}-15r_{16})}^T\end{array}\right],{\mathit{\Sigma }}_8=\left[\begin{array}{c}{(r_1-r_{11})}^T\\ {(r_1+3r_{11}-4r_{15})}^T\\ {(r_1-6r_{11}+20r_{15}-15r_{19})}^T\end{array}\right],\hfill \\ \hfill {\mathit{\Sigma }}_9& =\left[\begin{array}{c}{(r_1-r_{19})}^T\\ {(r_1+r_{19}-2r_{20})}^T\\ {(r_1-r_{19}+6r_{20}-6r_{21})}^T\end{array}\right],\hfill \\ \hfill {\tilde{U}}_1& =diag\{U_1,3U_1,5U_1,7U_1,9U_1\},{\tilde{U}}_2=diag\{U_2,3U_2,5U_2,7U_2,9U_2\},\hfill \\ \hfill {\tilde{S}}_2& =diag\{S_2,3S_2,5S_2,7S_2,9S_2\},{\overline{S}}_1=diag\{2S_1,4S_1,6S_1,8S_1\},\hfill \\ \hfill {\overline{S}}_2=& diag\{2S_2,4S_2,6S_2,8S_2\},{\overline{S}}_3=diag\{2S_3,4S_3,6S_3\},\hfill \\ \hfill {\overline{T}}_1=& diag\{3T_1,5T_1,7T_1\},{\overline{T}}_2=diag\{3T_2,5T_2,7T_2\}.\hfill \end{array}$$

Theorem 1

The generalized neural networks with reaction-diffusion terms and mixed time-varying delays can be globally asymptotically synchronized under a sampled-data controller, if there exist matrices $0<P,0<G,0<Q_{\mathit{\nu }},(\mathit{\nu }=1,2,3),0<U_{\tilde{\mathit{\nu }}},0<S_{\tilde{\mathit{\nu }}},0<T_{\tilde{\mathit{\nu }}},0<X_{\tilde{\mathit{\nu }}},(\tilde{\mathit{\nu }}=1,2),0<W_1$ such that the following LMIs hold:

$$\begin{array}{cc}& \left[\begin{array}{cc}{\tilde{U}}_2+{\tilde{S}}_2& L\\ L^T& {\tilde{U}}_2\end{array}\right]\ge 0,\hfill \end{array}$$ 16

$$\begin{array}{cc}& \mathit{\Phi }<0,\hfill \\ \hfill \text{where}\\ \hfill \mathit{\Phi }=& r_2^{T}P{r}_1-r_1^{T}G{r}_2-r_1^{T}G\tilde{D}{r}_1-r_1^{T}GC{r}_1+r_1^{T}GA{r}_{24}+r_{1}GB{r}_{26}+r_1^{T}GD{r}_{28}\hfill \\ \hfill & +r_1^T{F}_i{r}_{22}-r_2^{T}G{r}_2+r_2^{T}GC{r}_1+r_2^{T}GA{r}_{24}+r_2^{T}GB{r}_{26}+r_2^{T}GD{r}_{28}\hfill \\ \hfill & +r_2^T{F}_i{r}_{22}+r_1^T(Q_1+Q_2)r_1+r_3^T(Q_3-Q_1)r_3-(1-\mathit{\mu })r_4^T{Q}_2{r}_4-r_5^T{Q}_3{r}_5\hfill \\ \hfill & +{\mathit{\tau }}_1^2{r}_2^T{U}_1{r}_2-{\mathit{\tau }}_{12}^2{r}_6^T{U}_2{r}_6+({\mathit{\tau }}_1^2/2)r_2^T{S}_1{r}_2+r_6^T{S}_2{r}_6+({\mathit{\tau }}_1^3/6)r_2^T{T}_1{r}_2\hfill \\ \hfill & +({\mathit{\tau }}_2^3/6)r_2^T{T}_2{r}_2+d^2{r}_{24}^T{W}_1{r}_{24}+r_1^T{X}_1{r}_1+r_{23}^T{X}_1{r}_{23}+h^2{r}_2^T{X}_2{r}_2\hfill \\ \hfill & -r_{28}^T{W}_1{r}_{28}-{(r_{22}-r_{23})}^T{X}_2(r_{22}-r_{23})-{(r_1-r_{22})}^T{X}_2(r_1-r_{22})\hfill \\ \hfill & -{\mathit{\Sigma }}_1^T{\tilde{U}}_1{\mathit{\Sigma }}_1-{\mathit{\Sigma }}_4^T{\overline{S}}_1{\mathit{\Sigma }}_4-{\mathit{\Sigma }}_5^T{\overline{S}}_2{\mathit{\Sigma }}_5-{\mathit{\Sigma }}_6^T{\overline{S}}_2{\mathit{\Sigma }}_6-{\mathit{\Sigma }}_8^T{\overline{T}}_1{\mathit{\Sigma }}_8-{\mathit{\Sigma }}_9^T{\overline{T}}_2{\mathit{\Sigma }}_9\hfill \\ \hfill & -r_1^T{H}_1{\mathit{\Omega }}_1{r}_1+2r_1^T{H}_2{\mathit{\Omega }}_1{r}_{24}-r_{24}^T{\mathit{\Omega }}_1{r}_{24}-r_4^T{H}_1{\mathit{\Omega }}_2{r}_4+2r_4^T{H}_2{\mathit{\Omega }}_2{r}_{26}\hfill \\ \hfill & -r_{26}^T{\mathit{\Omega }}_2{r}_{26}-r_3^T{H}_1{\mathit{\Omega }}_3{r}_3+2r_3^T{H}_2{\mathit{\Omega }}_3{r}_{25}-r_{25}^T{\mathit{\Omega }}_3{r}_{25}-r_5^T{H}_1{\mathit{\Omega }}_4{r}_5\hfill \\ \hfill & +2r_5^T{H}_2{\mathit{\Omega }}_4{r}_{27}-r_{27}^T{\mathit{\Omega }}_4{r}_{27}-\mathit{\Lambda }\hfill \end{array}$$ 17

with $F=GK.$

Proof

Consider the Lyapunov–Krasovskii Candidate

$$V(t,x)=\sum _{\mathit{\kappa }=1}^9{V}_{\mathit{\kappa }}(t,x)$$ 18

where

$$\begin{array}{cc}\hfill V_1(t,x)& ={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\left\{e_i^T(t,x)P{e}_i(t,x)+\sum _{k=1}^m{D}_k{\left(\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }{x}_k}\right)}^{T}G\left(\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }{x}_k}\right)\right\}\text{d}x,\hfill \\ \hfill V_2(t,x)& ={\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{t-{\mathit{\tau }}_1}^t{e}_i^T(s,x)Q_1{e}_i(s,x)\text{d}s\text{d}x+{\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{t-\mathit{\tau }(t)}^t{e}_i^T(s,x)Q_2{e}_i(s,x)\text{d}s\text{d}x\hfill \\ \hfill & +{\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{t-{\mathit{\tau }}_2}^{t-{\mathit{\tau }}_1}{e}_i^T(s,x)Q_3{e}_i(s,x)\text{d}s\text{d}x,\hfill \\ \hfill V_3(t,x)& ={\mathit{\tau }}_1{\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-{\mathit{\tau }}_1}^0{\int }_{t+\mathit{\theta }}^t{\dot{e}}_i^T(s,x)U_1{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\text{d}x\hfill \\ \hfill & +{\mathit{\tau }}_{12}{\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-{\mathit{\tau }}_2}^{-{\mathit{\tau }}_1}{\int }_{t+\mathit{\theta }}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)U_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\text{d}x,\hfill \\ \hfill V_4(t,x)& ={\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-{\mathit{\tau }}_1}^0{\int }_{\mathit{\theta }}^0{\int }_{t+\mathit{\lambda }}^t{\dot{e}}_i^T(s,x)S_1{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\text{d}x,\hfill \\ \hfill V_5(t,x)& ={\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-{\mathit{\tau }}_2}^{-{\mathit{\tau }}_1}{\int }_{\mathit{\theta }}^{-{\mathit{\tau }}_1}{\int }_{t+\mathit{\lambda }}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)S_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\text{d}x,\hfill \\ \hfill V_6(t,x)& ={\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-{\mathit{\tau }}_1}^0{\int }_{\mathit{\theta }}^0{\int }_{\mathit{\lambda }}^0{\int }_{t+\mathit{\kappa }}^t{\dot{e}}_i^T(s,x)T_1{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\kappa }\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\text{d}x,\hfill \\ \hfill V_7(t,x)& ={\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-{\mathit{\tau }}_2}^0{\int }_{\mathit{\theta }}^0{\int }_{\mathit{\lambda }}^0{\int }_{t+\mathit{\kappa }}^t{\dot{e}}_i^T(s,x)T_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\kappa }\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\text{d}x,\hfill \\ \hfill V_8(t,x)& =d{\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-d}^0{\int }_{t+\mathit{\theta }}^t{g}^T(W{e}_i(s,x))W_{1}g(W{e}_i(s,x))\text{d}s\text{d}\mathit{\theta }\text{d}x,\hfill \\ \hfill V_9(t,x)& ={\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{t-h}^t{e}_i^T(s,x)X_1{e}_i(s,x)\text{d}s\text{d}x\hfill \\ \hfill & +h{\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\int }_{-h}^0{\int }_{t+\mathit{\theta }}^t{\dot{e}}_i^T(s,x)X_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\text{d}x.\hfill \end{array}$$

The time derivative of V(t, x) is computed as follows:

$${\dot{V}}_1(t,x)=2{\int }_{\mathit{\Gamma }}\sum _{i=1}^n\left\{{\dot{e}}_i^T(t,x)P{e}_i(t,x)+\sum _{k=1}^m{D}_k{\left(\frac{\mathit{\partial }{\dot{e}}_i(t,x)}{\mathit{\partial }{x}_k}\right)}^{T}G\left(\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }{x}_k}\right)\right\}\text{d}x,$$ 19

$${\dot{V}}_2(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n{\mathit{\zeta }}^T(t,x)\{r_1^T(Q_1+Q_2)r_1+r_3^T(Q_3-Q_1)r_3-(1-\mathit{\mu })r_4^T{Q}_2{r}_4-r_5^T{Q}_3{r}_5\}\mathit{\zeta }(t,x)\text{d}x,$$ 20

$${\dot{V}}_3(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\{{\mathit{\zeta }}^T(t,x)\{{\mathit{\tau }}_1^2{r}_2^T{U}_1{r}_2-{\mathit{\tau }}_{12}^2{r}_6^T{U}_2{r}_6\}\mathit{\zeta }(t,x)-{\mathit{\tau }}_1{\int }_{t-{\mathit{\tau }}_1}^t{\dot{e}}_i^T(s,x)U_1{\dot{e}}_i(s,x)\text{d}s-{\mathit{\tau }}_{12}{\int }_{t-{\mathit{\tau }}_2}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)U_2{\dot{e}}_i(s,x)\text{d}s\}\text{d}x,$$ 21

$${\dot{V}}_4(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\{{\mathit{\zeta }}^T(t,x)\{({\mathit{\tau }}_1^2/2)r_2^T{S}_1{r}_2\}\mathit{\zeta }(t,x)-{\int }_{{\mathit{\tau }}_1}^0{\int }_{t+\mathit{\theta }}^t{\dot{e}}_i^T(s,x)S_1{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\}\text{d}x,$$ 22

$${\dot{V}}_5(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\{{\mathit{\zeta }}^T(t,x)r_6^T{S}_2{r}_6\mathit{\zeta }(t,x)-{\int }_{-{\mathit{\tau }}_2}^{-\mathit{\tau }(t)}{\int }_{t+\mathit{\theta }}^{t-\mathit{\tau }(t)}{\dot{e}}_i^T(s,x)S_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }-({\mathit{\tau }}_2-\mathit{\tau }(t)){\int }_{t-\mathit{\tau }(t)}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)S_2{\dot{e}}_i(s,x)\text{d}s-{\int }_{-\mathit{\tau }(t)}^{-{\mathit{\tau }}_1}{\int }_{t+\mathit{\theta }}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)S_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\}\text{d}x,$$ 23

$${\dot{V}}_6(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\{{\mathit{\zeta }}^T(t,x)({\mathit{\tau }}_1^3/6)r_2^T{T}_1{r}_2\mathit{\zeta }(t,x)-{\int }_{-{\mathit{\tau }}_1}^0{\int }_{\mathit{\theta }}^0{\int }_{t+\mathit{\lambda }}^t{\dot{e}}_i^T(s,x)T_1{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\}\text{d}x,$$ 24

$${\dot{V}}_7(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\{{\mathit{\zeta }}^T(t,x)({\mathit{\tau }}_2^3/6)r_2^T{T}_2{r}_2\mathit{\zeta }(t,x)-{\int }_{-{\mathit{\tau }}_2}^0{\int }_{\mathit{\theta }}^0{\int }_{t+\mathit{\lambda }}^t{\dot{e}}_i^T(s,x)T_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\}\text{d}x,$$ 25

$${\dot{V}}_8(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\{{\mathit{\zeta }}^T(t,x)d^2{r}_{24}^T{W}_1{r}_{24}\mathit{\zeta }(t,x)-d{\int }_{t-d}^t{g}^T(W{e}_i(s,x))W_{1}g(W{e}_i(s,x))\text{d}s\}\text{d}x,$$ 26

$${\dot{V}}_9(t,x)={\int }_{\mathit{\Gamma }}\sum _{i=1}^n\{{\mathit{\zeta }}^T(t,x)\{r_1^T{X}_1{r}_1-r_{23}^T{X}_1{r}_{23}+h^2{r}_2^T{X}_2{r}_2\}\mathit{\zeta }(t,x)-h{\int }_{t-h}^t{\dot{e}}_i^T(s,x)X_2{\dot{e}}_i(s,x)\text{d}s\}\text{d}x.$$ 27

Now by employing Lemma 2 to the integral terms in (21)–(25), we arrive at

$$-{\mathit{\tau }}_1{\int }_{t-{\mathit{\tau }}_1}^t{\dot{e}}_i^T(s,x)U_1{\dot{e}}_i(s,x)\text{d}s\le -{\mathit{\zeta }}^T(t,x)\{{(r_1-r_3)}^T{U}_1(r_1-r_3)+3{(r_1+r_3-2r_7)}^T{U}_1(r_1+r_3-2r_7)+5{(r_1-r_3+6r_7-6r_{10})}^T{U}_1(r_1-r_3+6r_7-6r_{10})+7{(r_1+r_3-12r_7+30r_{10}-20r_{14})}^T{U}_1\times (r_1+r_3-12r_7+30r_{10}-20r_{14})+9{(r_1-r_3+20r_7-90r_{10}+140r_{13}-70r_{18})}^T{U}_1(r_1-r_3+20r_7-90r_{10}+140r_{13}-70r_{18})\}\mathit{\zeta }(t,x)=-{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_1^T{\tilde{U}}_1{\mathit{\Sigma }}_1\mathit{\zeta }(t,x),$$ 28

$$-{\mathit{\tau }}_{12}{\int }_{t-\mathit{\tau }(t)}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)U_2{\dot{e}}_i(s,x)\text{d}s\le -\frac{{\mathit{\tau }}_{12}}{\mathit{\tau }(t)-{\mathit{\tau }}_1}{\mathit{\zeta }}^T(t,x)\{{(r_3-r_4)}^T{U}_2(r_3-r_4)+3{(r_3+r_4-2r_8)}^T{U}_2(r_3+r_4-2r_8)+5{(r_3-r_4+6r_8-6r_{12})}^T{U}_2(r_3-r_4+6r_8-6r_{12})+7{(r_3+r_4-12r_8+30r_{12}-20r_{16})}^T\times U_2(r_3+r_4-12r_8+30r_{12}-20r_{16})+9{(r_3-r_4+20r_8-90r_{12}+140r_{16}-70r_{20})}^T{U}_2(r_3-r_4+20r_8-90r_{12}+140r_{16}-70r_{20})\}\mathit{\zeta }(t,x)=-\frac{1}{\mathit{\alpha }}{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_2^T{\tilde{U}}_2{\mathit{\Sigma }}_2\mathit{\zeta }(t,x),$$ 29

$$-{\mathit{\tau }}_{12}{\int }_{t-{\mathit{\tau }}_2}^{t-\mathit{\tau }(t)}{\dot{e}}_i^T(s,x)U_2{\dot{e}}_i(s,x)\text{d}s\le -\frac{{\mathit{\tau }}_{12}}{{\mathit{\tau }}_2-\mathit{\tau }(t)}{\mathit{\zeta }}^T(t,x)\{{(r_4-r_5)}^T{U}_2(r_4-r_5)+3{(r_4+r_5-2r_9)}^T{U}_2(r_4+r_5-2r_9)+5{(r_4-r_5+6r_9-6r_{13})}^T{U}_2(r_4-r_5+6r_9-6r_{13})+7{(r_4+r_5-12r_9+30r_{13}-20r_{17})}^T{U}_2(r_4+r_5-12r_9+30r_{13}-20r_{17})+9{(r_4-r_5+20r_9-90r_{13}+140r_{17}-70r_{21})}^T{U}_2(r_4-r_5+20r_9-90r_{13}+140r_{17}-70r_{21})\}\mathit{\zeta }(t,x)=-\frac{1}{\mathit{\beta }}{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_3^T{\tilde{U}}_2{\mathit{\Sigma }}_3\mathit{\zeta }(t,x),$$ 30

$$-{\int }_{{\mathit{\tau }}_1}^0{\int }_{t+\mathit{\theta }}^t{\dot{e}}_i^T(s,x)S_1{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\le -{\mathit{\zeta }}^T(t,x)\{2{(r_1-r_7)}^T{S}_1(r_1-r_7)+4{(r_1+2r_7-4r_{10})}^T{S}_1(r_1+2r_7-4r_{10})+6{(r_1-3r_7+12r_{10}-10r_{14})}^T{S}_1(r_1-3r_7+12r_{10}-10r_{14})+8{(r_1+32r_7-30r_{10}+60r_{14}-35r_{18})}^T{S}_1(r_1+32r_7-30r_{10}+60r_{14}-35r_{18})\}\mathit{\zeta }(t,x)=-{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_4^T{\overline{S}}_1{\mathit{\Sigma }}_4\mathit{\zeta }(t,x),$$ 31

$$-{\int }_{-{\mathit{\tau }}_2}^{-\mathit{\tau }(t)}{\int }_{t+\mathit{\theta }}^{t-\mathit{\tau }(t)}{\dot{e}}_i^T(s,x)S_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\le -{\mathit{\zeta }}^T(t,x)\{2{(r_4-r_9)}^T{S}_1(r_4-r_9)+4{(r_4+2r_9-3r_{13})}^T{S}_1(r_4+2r_9-3r_{13})+6{(r_4-3r_9+12r_{13}-10r_{17})}^T{S}_1(r_4-3r_9+12r_{13}-10r_{17})+8{(r_4+4r_9-30r_{13}+45r_{17}-140r_{21})}^T{S}_1(r_4+4r_9-30r_{13}+45r_{17}-140r_{21})\}\mathit{\zeta }(t,x)=-{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_5^T{\overline{S}}_2{\mathit{\Sigma }}_5\mathit{\zeta }(t,x)$$ 32

$$\begin{array}{cc}& -({\mathit{\tau }}_2-\mathit{\tau }(t)){\int }_{t-\mathit{\tau }(t)}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)S_2{\dot{e}}_i(s,x)\text{d}s\le -\left(\frac{{\mathit{\tau }}_{12}}{\mathit{\tau }(t)-{\mathit{\tau }}_1}-1\right){\mathit{\zeta }}^T(t,x)\{{(r_3-r_4)}^T{S}_2(r_3-r_4)+3{(r_3+r_4-2r_8)}^T{S}_2(r_3+r_4-2r_8)+5{(r_3-r_4+6r_8-6r_{12})}^T{S}_2(r_3-r_4+6r_8-6r_{12})+7{(r_3+r_4-12r_8+30r_{12}-20r_{16})}^T{S}_2(r_3+r_4-12r_8+30r_{12}-20r_{16})+9{(r_3-r_4+20r_8-90r_{12}+140r_{16}-70r_{20})}^T{S}_2(r_3-r_4+20r_8-90r_{12}+140r_{16}-70r_{20})\}\mathit{\zeta }(t,x),\hfill \\ \hfill & =-\left(\frac{1}{\mathit{\alpha }}-1\right){\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_2^T{\tilde{S}}_2{\mathit{\Sigma }}_2\mathit{\zeta }(t,x),\hfill \end{array}$$ 33

$$-{\int }_{-\mathit{\tau }(t)}^{-{\mathit{\tau }}_1}{\int }_{t+\mathit{\theta }}^{t-{\mathit{\tau }}_1}{\dot{e}}_i^T(s,x)S_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\theta }\le -{\mathit{\zeta }}^T(t,x)\{2{(r_3-r_8)}^T{S}_2(r_3-r_8)+4{(r_3+2r_8-3r_{12})}^T{S}_2(r_3+2r_8-3r_{12})+6{(r_3-3r_8+12r_{12}-10r_{16})}^T{S}_2(r_3-3r_8+12r_{12}-10r_{16})+8{(r_3+4r_8-30r_{12}+45r_{16}-35r_{20})}^T{S}_2(r_3+4r_8-30r_{12}+45r_{16}-35r_{20})\}\mathit{\zeta }(t,x)=-{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_6^T{\overline{S}}_2{\mathit{\Sigma }}_6\mathit{\zeta }(t,x),$$ 34

$$-{\int }_{-{\mathit{\tau }}_1}^0{\int }_{\mathit{\theta }}^0{\int }_{t+\mathit{\lambda }}^t{\dot{e}}_i^T(s,x)T_1{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\le -{\mathit{\zeta }}^T(t,x)\{3({\mathit{\tau }}_1/2){(r_1-r_{10})}^T{T}_1(r_1-r_{10})+5({\mathit{\tau }}_1/2){(r_1+3r_{10}-4r_{14})}^T{T}_1(r_1+3r_{10}-4r_{14})+7({\mathit{\tau }}_1/2){(r_1-6r_{10}+20r_{14}-15r_{18})}^T{T}_1(r_1-6r_{10}+20r_{14}-15r_{18})\}\mathit{\zeta }(t,x)=-{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_7^T{\overline{T}}_1{\mathit{\Sigma }}_7\mathit{\zeta }(t,x),$$ 35

$$-{\int }_{-{\mathit{\tau }}_2}^0{\int }_{\mathit{\theta }}^0{\int }_{t+\mathit{\lambda }}^t{\dot{e}}_i^T(s,x)T_2{\dot{e}}_i(s,x)\text{d}s\text{d}\mathit{\lambda }\text{d}\mathit{\theta }\le {\mathit{\zeta }}^T(t,x)\{3({\mathit{\tau }}_2/2){(r_1-r_{11})}^T{T}_2(r_1-r_{11})+5({\mathit{\tau }}_2/2){(r_1+3r_{11}-4r_{15})}^T{T}_2(r_1+3r_{11}-4r_{15})+7({\mathit{\tau }}_2/2){(r_1-6r_{11}+20r_{15}-15r_{19})}^T{T}_2(r_1-6r_{11}+20r_{15}-15r_{19})\}\mathit{\zeta }(t,x)=-{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_8^T{\overline{T}}_2{\mathit{\Sigma }}_8\mathit{\zeta }(t,x).$$ 36

Further,

$$-d{\int }_{t-d}^t{g}^T(W{e}_i(s,x))W_{1}g(W{e}_i(s,x))\text{d}s\le -d(t){\int }_{t-d(t)}^t{g}^T(W{e}_i(s,x))W_{1}g(W{e}_i(s,x))\text{d}s\le -{\mathit{\zeta }}^T(t,x)r_{28}^T{W}_1{r}_{28}\mathit{\zeta }(t,x),$$ 37

$$-h{\int }_{t-h}^t{\dot{e}}_i^T(s,x)X_2{\dot{e}}_i(s,x)\text{d}s=-h{\int }_{t-h}^{t-h(t)}{\dot{e}}_i^T(s,x)X_2{\dot{e}}_i(s,x)\text{d}s-h{\int }_{t-h(t)}^t{\dot{e}}_i^T(s,x)X_2{\dot{e}}_i(s,x)\text{d}s\le -{\mathit{\zeta }}^T(t,x)\{{(r_{22}-r_{23})}^T{X}_2(r_{22}-r_{23})+{(r_1-r_{22})}^T{X}_2(r_1-r_{22})\}\mathit{\zeta }(t,x).$$ 38

According to the error system (15), we can have

$$0={\int }_{\mathit{\Gamma }}\sum _{i=1}^{N}2[e_i^T(t,x)G+{\dot{e}}_i^T(t,x)G]\left[-{\dot{e}}_i(t,x)+\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_k\frac{\mathit{\partial }{e}_i(t,x)}{\mathit{\partial }{x}_k}\right)-C{e}_i(t,x)+Ag(W{e}_i(t,x))+Bg(W{e}_i(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}g(W{e}_i(s,x))\text{d}s\right.\left.+K{e}_i(t-h(t),x)\right]\text{d}x$$ 39

Then, by using Green’s formula, Dirichlet boundary condition and Lemma 1 on (39) and adding upon to ${\dot{V}}_1(t,x)$ results in

$${\dot{V}}_1(t,x)\le 2{\int }_{\mathit{\Gamma }}{\mathit{\zeta }}^T(t,x)\{r_2^{T}P{r}_1-r_1^{T}G{r}_2-r_1^{T}G\tilde{D}{r}_1-r_1^{T}GC{r}_1+r_1^{T}GA{r}_{24}+r_1^{T}GB{r}_{26}+r_1^{T}GD{r}_{28}+r_1^{T}GK{r}_{22}-r_2^{T}G{r}_2+r_2^{T}GC{r}_1+r_2^{T}GA{r}_{24}+r_2^{T}GB{r}_{26}+r_2^{T}GD{r}_{28}+r_2^{T}GK{r}_{22}\}\mathit{\zeta }(t,x)\text{d}x$$ 40

Moreover, for positive diagonal matrices ${\mathit{\Omega }}_1,{\mathit{\Omega }}_2,{\mathit{\Omega }}_3\text{and}{\mathit{\Omega }}_4,$ we have from Assumption 1 that

$$\begin{array}{c}\hfill {\left[\begin{array}{c}{e}_i(t,x)\\ g(W{e}_i(t,x))\end{array}\right]}^T\left[\begin{array}{cc}{H}_1{\mathit{\Omega }}_1& -H_2{\mathit{\Omega }}_1\\ \star & {\mathit{\Omega }}_1\end{array}\right]\left[\begin{array}{c}{e}_i(t,x)\\ g(W{e}_i(t,x))\end{array}\right]\le 0,\end{array}$$ 41

$$\begin{array}{c}\hfill {\left[\begin{array}{c}{e}_i(t-\mathit{\tau }(t),x)\\ g(W{e}_i(t-\mathit{\tau }(t),x))\end{array}\right]}^T\left[\begin{array}{cc}{H}_1{\mathit{\Omega }}_2& -H_2{\mathit{\Omega }}_2\\ \star & {\mathit{\Omega }}_2\end{array}\right]\left[\begin{array}{c}{e}_i(t-\mathit{\tau }(t),x)\\ g(W{e}_i(t-\mathit{\tau }(t),x))\end{array}\right]\le 0,\end{array}$$ 42

$$\begin{array}{c}\hfill {\left[\begin{array}{c}{e}_i(t-{\mathit{\tau }}_1,x)\\ g(W{e}_i(t-{\mathit{\tau }}_1,x))\end{array}\right]}^T\left[\begin{array}{cc}{H}_1{\mathit{\Omega }}_3& -H_2{\mathit{\Omega }}_3\\ \star & {\mathit{\Omega }}_3\end{array}\right]\left[\begin{array}{c}{e}_i(t-{\mathit{\tau }}_1,x)\\ g(W{e}_i(t-{\mathit{\tau }}_1,x))\end{array}\right]\le 0,\end{array}$$ 43

$$\begin{array}{c}\hfill {\left[\begin{array}{c}{e}_i(t-{\mathit{\tau }}_2,x)\\ g(W{e}_i(t-{\mathit{\tau }}_2,x))\end{array}\right]}^T\left[\begin{array}{cc}{H}_1{\mathit{\Omega }}_4& -H_2{\mathit{\Omega }}_4\\ \star & {\mathit{\Omega }}_4\end{array}\right]\left[\begin{array}{c}{e}_i(t-{\mathit{\tau }}_2,x)\\ g(W{e}_i(t-{\mathit{\tau }}_2,x))\end{array}\right]\le 0,\end{array}$$ 44

Now, by employing Lemma 4 to (29), (30) and (33), we obtain

$$\frac{1}{\mathit{\alpha }}{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_2^T{\tilde{U}}_2{\mathit{\Sigma }}_2\mathit{\zeta }(t,x)+\frac{1}{\mathit{\beta }}{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_3^T{\tilde{U}}_2{\mathit{\Sigma }}_3\mathit{\zeta }(t,x)+\left(\frac{1}{\mathit{\alpha }}-1\right){\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_2^T{\tilde{S}}_2{\mathit{\Sigma }}_2\mathit{\zeta }(t,x)=\frac{1}{\mathit{\alpha }}{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_2^T\left({\tilde{U}}_2+{\tilde{S}}_2\right){\mathit{\Sigma }}_2\mathit{\zeta }(t,x)+\frac{1}{\mathit{\beta }}{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_3^T{\tilde{U}}_2{\mathit{\Sigma }}_3\mathit{\zeta }(t,x)-{\mathit{\zeta }}^T(t,x){\mathit{\Sigma }}_2^T{\tilde{S}}_2{\mathit{\Sigma }}_2\mathit{\zeta }(t,x)\ge {\mathit{\zeta }}^T(t,x)\mathit{\Lambda }\mathit{\zeta }(t,x).$$ 45

Upon adding all ${\dot{V}}_i(t),i=1,2,\dots ,9$ along with (41)–(44), we have

$$\dot{V}(t,x)\le {\mathit{\zeta }}^T(t,x)\mathit{\Phi }\mathit{\zeta }(t,x)<0$$ 46

where $\mathit{\Phi }$ is given in (17). This proves that the considered generalized delayed reaction-diffusion neural network model with time-varying delays is globally asymptotically stable under the sampled-data controller. $\square$

Remark 3

Lemma 1 is utilized to deal with the reaction-diffusion terms. It can be witnessed in the literature that in the problems on qualitative inspection of reaction-diffusion neural networks, see for example Wang et al. (2012b), Liu (2010), Wang and Zhang (2010) and Lv et al. (2008), the impact of diffusion terms have been expunged. However, the results derived in this paper also includes the effect of diffusion terms, which is worth mentioning. Moreover, the results presented here are generic and no limitation is urged on the time-varying delay.

Remark 4

It is to be noticed that Theorem 1 furnishes a synchronization scheme for generalized delayed reaction-diffusion neural networks in the framework of input delay approach. The results are revealed in the form of LMIs. An advantage of LMI approach is that the LMI condition can be verified easily and effectively by employing the available softwares which are meant to solve LMIs.

If the effects of diffusion are ignored, then following result will be obtained.

Theorem 2

The generalized neural networks with mixed time-varying delays is globally asymptotically synchronized under a sampled-data controller, if there exist matrices $0<P,0<Q_{\mathit{\nu }},(\mathit{\nu }=1,2,3),0<U_{\tilde{\mathit{\nu }}},0<S_{\tilde{\mathit{\nu }}},0<T_{\tilde{\mathit{\nu }}},0<X_{\tilde{\mathit{\nu }}},(\tilde{\mathit{\nu }}=1,2),0<W_1$ such that (16) and the following LMI hold:

$$\mathit{\Psi }<0,$$ 47

with

$$\mathit{\Psi }=r_2^{T}P{r}_1-r_1^{T}G{r}_2-r_1^{T}GC{r}_1+r_1^{T}GA{r}_{24}+r_{1}GB{r}_{26}+r_1^{T}GD{r}_{28}+r_1^T{F}_i{r}_{22}-r_2^{T}G{r}_2+r_2^{T}GC{r}_1+r_2^{T}GA{r}_{24}+r_2^{T}GB{r}_{26}+r_2^{T}GD{r}_{28}+r_2^T{F}_i{r}_{22}+r_1^T(Q_1+Q_2)r_1+r_3^T(Q_3-Q_1)r_3-(1-\mathit{\mu })r_4^T{Q}_2{r}_4-r_5^T{Q}_3{r}_5+{\mathit{\tau }}_1^2{r}_2^T{U}_1{r}_2-{\mathit{\tau }}_{12}^2{r}_6^T{U}_2{r}_6+({\mathit{\tau }}_1^2/2)r_2^T{S}_1{r}_2+r_6^T{S}_2{r}_6+({\mathit{\tau }}_1^3/6)r_2^T{T}_1{r}_2+({\mathit{\tau }}_2^3/6)r_2^T{T}_2{r}_2+d^2{r}_{24}^T{W}_1{r}_{24}+r_1^T{X}_1{r}_1+r_{23}^T{X}_1{r}_{23}+h^2{r}_2^T{X}_2{r}_2-r_{28}^T{W}_1{r}_{28}-{(r_{22}-r_{23})}^T{X}_2(r_{22}-r_{23})-{(r_1-r_{22})}^T{X}_2(r_1-r_{22})-{\mathit{\Sigma }}_1^T{\tilde{U}}_1{\mathit{\Sigma }}_1-{\mathit{\Sigma }}_4^T{\overline{S}}_1{\mathit{\Sigma }}_4-{\mathit{\Sigma }}_5^T{\overline{S}}_2{\mathit{\Sigma }}_5-{\mathit{\Sigma }}_6^T{\overline{S}}_2{\mathit{\Sigma }}_6-{\mathit{\Sigma }}_7^T{\overline{T}}_1{\mathit{\Sigma }}_7-{\mathit{\Sigma }}_8^T{\overline{T}}_2{\mathit{\Sigma }}_8-r_1^T{H}_1{\mathit{\Omega }}_1{r}_1+2r_1^T{H}_2{\mathit{\Omega }}_1{r}_{24}-r_{24}^T{\mathit{\Omega }}_1{r}_{24}-r_4^T{H}_1{\mathit{\Omega }}_2{r}_4+2r_4^T{H}_2{\mathit{\Omega }}_2{r}_{26}-r_{26}^T{\mathit{\Omega }}_2{r}_{26}-r_3^T{H}_1{\mathit{\Omega }}_3{r}_3+2r_3^T{H}_2{\mathit{\Omega }}_3{r}_{25}-r_{25}^T{\mathit{\Omega }}_3{r}_{25}-r_5^T{H}_1{\mathit{\Omega }}_4{r}_5+2r_5^T{H}_2{\mathit{\Omega }}_4{r}_{27}-r_{27}^T{\mathit{\Omega }}_4{r}_{27}-\mathit{\Lambda }$$

where $F=GK.$

Proof

The proof follows from Theorem 1 with the second term of $V_1(t,x)$ in (18) being neglected. $\square$

Remark 5

In general, computational complexity will be a big issue based on how large are the LMIs and how more are the decision variables. The results in Theorem 1 are derived based on the construction of proper Lyapunov–Krasovskii functional with triple and four integral terms and by using a newly introduced integral inequality technique which produces tighter bounds than what the existing ones such as the Wirtinger-based inequality, Jensen’s inequality and the auxiliary function-based integral inequalities produce. It should be mentioned that the derived synchronization criteria for the considered neural networks with reaction-diffusion terms and time-varying delays is less conservative than the other conditions in the literature, which will be proved in the next section. Meanwhile, it should also be noticed that the relaxation of the derived results is acquired at the cost of more number of decision variables. As far the results to be efficient enough it is more comfortable to have larger maximum allowable upper bounds but still in order to reduce computational burden and time consumption, our future work will be focused on reducing the number of decision variables.

Remark 6

It is worth to mention that, in the existing literature only few works that concerns with the qualitative analysis of generalized neural networks has been published (Zheng et al. 2015; Liu et al. 2015a; Rakkiyappan et al. 2016b). In Zheng et al. (2015) and Liu et al. (2015a), the stability analysis for a class of generalized neural networks with time-varying delays has been carried out based on a free-matrix-based inequality and an improved inequality, respectively. By constructing augmented Lyapunov–Krasovskii functional with more information on activation functions, improved delay-dependent stability criteria for generalized neural networks with additive time-varying delays has been presented in Rakkiyappan et al. (2016b). However, all these existing works does not include diffusion phenomena in the neural network model, which cannot be ignored when electrons are moving in a nonuniform electromagnetic field. Therefore, to manufacture high quality neural networks, it is must to consider the activations to vary in space as well as in time and in this case the model should be expressed by partial differential equations. In the existing literature there were only a very few works that investigate the synchronization of generalized reaction-diffusion neural networks with time-varying delays, namely Gan (2012) and Gan et al. (2016). Different from the existing literature, the present paper focuses on the synchronization behavior of generalized reaction-diffusion neural networks with mixed time-varying delays. Here, to realize synchronization, discrete controller, namely the sampled-data controller has been employed. Moreover, by using a new class of integral inequalities for quadratic functions, from which almost all of the existing integral inequalities can be obtained, such as Jensen inequality, the Wirtinger-based inequality, the Bessel-Legendre inequality, the Wirtinger-based double integral inequality, and the auxiliary function-based integral inequalities, less conservative synchronization criteria that depends on the information of delays as well as reaction-diffusion terms has been derived. The obtained results are formulated in the form of LMIs which can be efficiently solved via Matlab LMI control toolbox.

Numerical examples

This section offers two numerical examples with simulations to verify the validity of the proposed theoretical results acquired in this paper.

Example 1

Consider the drive-response generalized neural network model (7) and (9)

$$\frac{\mathit{\partial }y(t,x)}{\mathit{\partial }t}=\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_k\frac{\mathit{\partial }y(t,x)}{\mathit{\partial }{x}_k}\right)-Cy(t,x)+Af(Wy(t,x))+Bf(Wy(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}f(Wy(s,x))\text{d}s,y(t,x)=0,(t,x)\in [-\mathit{\sigma },+\infty ]\times \mathit{\partial }\mathit{\Gamma },\mathit{\varphi }(s,x)=0.7sin(\mathit{\pi }x)$$ 48

and

$$\frac{\mathit{\partial }{v}_i(t,x)}{\mathit{\partial }t}=\sum _{k=1}^m\frac{\mathit{\partial }}{\mathit{\partial }{x}_k}\left(D_k\frac{\mathit{\partial }{v}_i(t,x)}{\mathit{\partial }{x}_k}\right)-C{v}_i(t,x)+Af(W{v}_i(t,x))+Bf(W{v}_i(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}f(W{v}_i(s,x))\text{d}s+w_i(t,x),v_i(t,x)=0,(t,x)\in [-\mathit{\sigma },+\infty ]\times \mathit{\partial }\mathit{\Gamma },\mathit{\psi }(s,x)=0.3sin(\mathit{\pi }x)$$ 49

with the parameters

$$\begin{array}{c}\hfill C=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],A=\left[\begin{array}{cc}0.2& 2\\ -0.5& -0.2\end{array}\right],B=\left[\begin{array}{cc}1& 0.8\\ -0.1& 1.8\end{array}\right],D=\left[\begin{array}{cc}0.8& 0.3\\ -0.5& -0.1\end{array}\right],\end{array}$$

$D_k=diag\{0.01,0.01\},\text{and}W=diag\{1,1\}.$ We let $\mathit{\tau }(t)=0.1+0.4sin(t)$ and $d(t)=0.9+0.1cos(t).$ Moreover, the activation function is considered to be $f(y(s,x))=0.25tanh(y(s,x))-0.25.$ Through simple calculation, we arrive at ${\mathit{\tau }}_1=0,{\mathit{\tau }}_2=0.5,\mathit{\mu }=0.4,\mathit{\sigma }=1,l_j^{-}=-0.5,l_j^{+}=0.$ The sampling period is taken as $h=0.3.$

Next, by using Matlab LMI toolbox, the sufficient conditions in Theorem 1 are verified under the above chosen parameters and were found to be feasible with the control gain matrix

$$\begin{array}{c}\hfill K=\left[\begin{array}{cc}-2.5830& -3.0801\\ -2.9871& 1.5342\end{array}\right].\end{array}$$

Thus, we conclude that the generalized neural network model with mixed delays under a sampled-data controller is globally asymptotically synchronized.

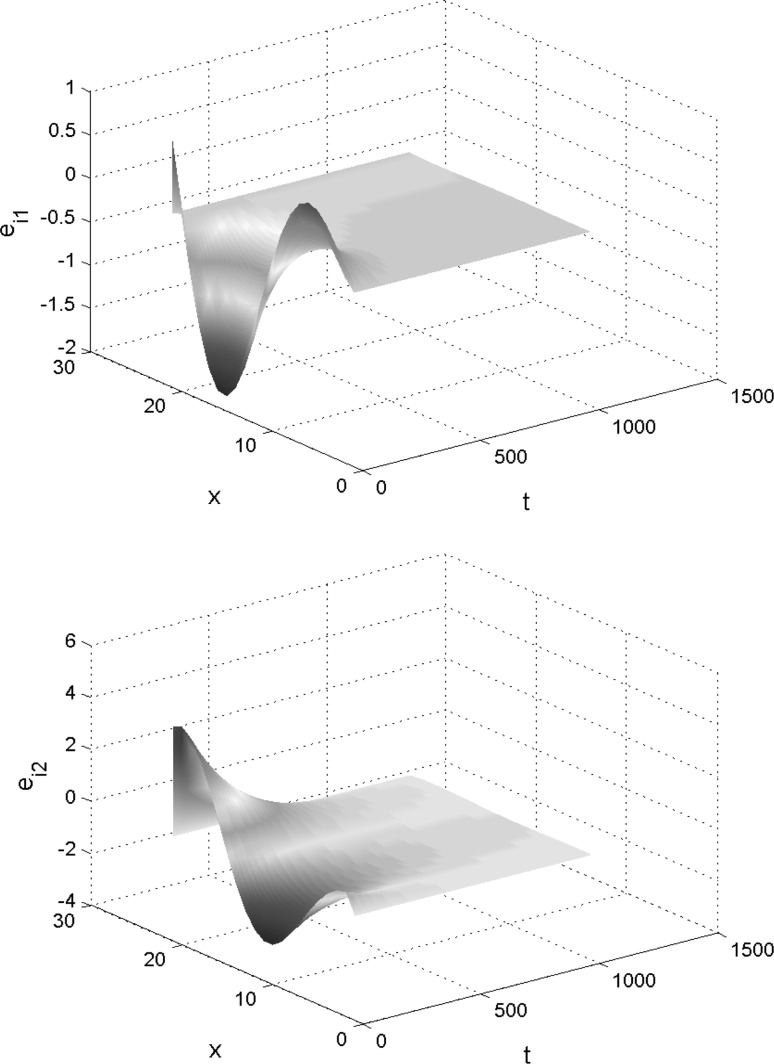
From Fig. 1 one can read that under the designed controller, the error dynamics of the generalized reaction-diffusion neural networks converges to zero. The simulation results clearly clarify the effectiveness of the controller to the asymptotical synchronization of generalized reaction-diffusion neural networks with mixed delays.

Fig. 1.

Dynamical behavior of the error states $e_{i1}(t,x)$ and $e_{i2}(t,x)$

Moreover, this paper utilizes novel integral inequalities in order to derive the bound for some cross terms that arises when deriving the time derivative of the Lyapunov–Krasovskii functional. To show the effectiveness of such novel integral inequalities, the maximum allowable upper bounds are calculated, which is presented in Table 1.

Table 1.

The maximum allowable upper bounds ${\mathit{\tau }}_2$ for different ${\mathit{\tau }}_1$

${\mathit{\tau }}_1$	0.2	0.4	0.6	0.8
${\mathit{\tau }}_2$	0.9024	0.8842	0.8005	0.6522

Example 2

Consider the generalized neural network model in Example 1 without diffusion term as

$$\frac{\mathit{\partial }y(t,x)}{\mathit{\partial }t}=-Cy(t,x)+Af(Wy(t,x))+Bf(Wy(t-\mathit{\tau }(t),x))+D{\int }_{t-d(t)}^{t}f(Wy(s,x))\text{d}s,$$ 50

where we take

$$\begin{array}{c}\hfill C=\left[\begin{array}{cc}1.2& 0\\ 0& 0.1\end{array}\right],A=\left[\begin{array}{cc}0.2& 0.5\\ 0.3& 0.1\end{array}\right],B=\left[\begin{array}{cc}0.2& 0.1\\ -0.2& -0.1\end{array}\right],D=\left[\begin{array}{cc}0.4& 1\\ -0.5& 0.1\end{array}\right]\end{array}$$

and the activation function is chosen to be $f(y(s,x))=\frac{1}{2}\left(|y(s,x)+1|-|y(s,x)-1|\right)$ and let $\mathit{\tau }(t)=0.6+0.5sin(t),d(t)=0.8+0.4sin(t).$ A straight forward calculation yields $l_i^{-}=0,l_i^{+}=1,{\mathit{\tau }}_2=1.1\text{and}\mathit{\mu }=0.5.$ The sampling period is chosen as $h=0.5.$ Verifying the results provided in Theorem 2 using Matlab LMI toolbox, it is proved that the LMIs presented are feasible and the controller gain is calculated as

$$\begin{array}{c}\hfill K=\left[\begin{array}{cc}-1.7841& -3.6279\\ -2.2487& -1.7690\end{array}\right]\end{array}$$

Table 2 lists the maximum allowable upper bound ${\mathit{\tau }}_2$ for different ${\mathit{\tau }}_1.$

Table 2.

The maximum allowable upper bounds ${\mathit{\tau }}_2$ for different ${\mathit{\tau }}_1$

${\mathit{\tau }}_1$	0.2	0.4	0.6	0.8
Theorem 1 (Chen et al. 2016b)	1.1139	0.9137	0.7135	0.5096
Theorem 2	1.1314	0.9421	0.7540	0.5201

It can be witnessed from Table 2 that Theorem 2 achieves larger allowable upper bounds than those obtained in Chen et al. (2016b), which implies that Theorem 2 has less conservative results, which is obtained by using the newly introduced general integral inequality lemma.

Conclusions

Over the past few years, the problem of synchronization of reaction-diffusion neural networks has become a hot area of research. However, only a few works on the synchronization problem for generalized reaction-diffusion neural networks have been established. This paper focuses on the synchronization of generalized reaction-diffusion neural network with mixed time-varying delay components under a sampled-data controller. In virtue of a general integral inequality based on orthogonal polynomials and Lyapunov–Krasovskii functionals with triple and four integral terms, new less conservative synchronization criterion has been derived in terms of LMIs. The acquired LMIs are solved numerically through MATLAB LMI toolbox. Finally, numerical simulations are established to illustrate the validity of the proposed theoretical results.

In practical sampled-data systems, the control packet can be lost because of several factors and this may induce undesirable behavior of the system under control. Therefore, it is worth to consider the problem of synchronization of generalized reaction-diffusion neural networks using sampled-data control with control packet loss, which will be one of our future topics.