Does the intercept of the heat–stress relation provide an accurate estimate of cardiac activation heat?

Abstract

Key points

• The heat of activation of cardiac muscle reflects the metabolic cost of restoring ionic homeostasis following a contraction. The accuracy of its measurement depends critically on the abolition of crossbridge cycling.

• We abolished crossbridge activity in isolated rat ventricular trabeculae by use of blebbistatin, an agent that selectively inhibits myosin II ATPase.

• We found cardiac activation heat to be muscle length independent and to account for 15–20% of total heat production at body temperature.

• We conclude that it can be accurately estimated at minimal muscle length.

Abstract

Activation heat arises from two sources during the contraction of striated muscle. It reflects the metabolic expenditure associated with Ca²⁺ pumping by the sarcoplasmic reticular Ca²⁺‐ATPase and Ca²⁺ translocation by the Na⁺/Ca²⁺ exchanger coupled to the Na⁺,K⁺‐ATPase. In cardiac preparations, investigators are constrained in estimating its magnitude by reducing muscle length to the point where macroscopic twitch force vanishes. But this experimental protocol has been criticised since, at zero force, the observed heat may be contaminated by residual crossbridge cycling activity. To eliminate this concern, the putative thermal contribution from crossbridge cycling activity must be abolished, at least at minimal muscle length. We achieved this using blebbistatin, a selective inhibitor of myosin II ATPase. Using a microcalorimeter, we measured the force production and heat output, as functions of muscle length, of isolated rat trabeculae from both ventricles contracting isometrically at 5 Hz and at 37°C. In the presence of blebbistatin (15 μmol l⁻¹), active force was zero but heat output remained constant, at all muscle lengths. Activation heat measured in the presence of blebbistatin was not different from that estimated from the intercept of the heat–stress relation in its absence. We thus reached two conclusions. First, activation heat is independent of muscle length. Second, residual crossbridge heat is negligible at zero active force; hence, the intercept of the cardiac heat–force relation provides an estimate of activation heat uncontaminated by crossbridge cycling. Both results resolve long‐standing disputes in the literature.

Key points

• The heat of activation of cardiac muscle reflects the metabolic cost of restoring ionic homeostasis following a contraction. The accuracy of its measurement depends critically on the abolition of crossbridge cycling.

• We abolished crossbridge activity in isolated rat ventricular trabeculae by use of blebbistatin, an agent that selectively inhibits myosin II ATPase.

• We found cardiac activation heat to be muscle length independent and to account for 15–20% of total heat production at body temperature.

• We conclude that it can be accurately estimated at minimal muscle length.

Abbreviations

BBS

blebbistatin

BDM

2,3‐butanedione monoxime

LV

left ventricle

RV

right ventricle

SR

sarcoplasmic reticulum

Introduction

In order for the heart to generate the next beat in a sequence, it must first be roused from its interbeat diastolic slumber. This is achieved by a ‘double‐triggering’ sequence, the first step of which is the spread of the cardiac action potential that, via depolarisation of transverse tubular sarcolemmal membranes, mediates the inflow of Ca²⁺ from the extracellular space and the sarcoplasmic reticulum in a process known as Ca²⁺‐induced Ca²⁺ release. It is the resulting spike in intracellular calcium concentration ([Ca²⁺]_i) that, in turn, activates contractile proteins and contraction of the heart. In order to terminate the resulting ‘active state’ (Hill, 1950a; Brady, 1968), thereby re‐achieving diastole, [Ca²⁺]_i must be decreased to its diastolic level and electrical equilibrium re‐established. The latter is achieved by the sarcolemmal Na⁺,K⁺‐ATPase, the former by the combined efforts of the sarcolemmal Ca²⁺‐ATPase and Na⁺/Ca²⁺ exchanger, and the sarcoplasmic reticular Ca²⁺‐ATPase (SERCA). Each of these membrane ion transporters directly or indirectly consumes ATP. It is the summed thermal outputs of this ATP consumption, plus ATP replenishment by mitochondrial oxidative phosphorylation, that is known collectively as ‘activation heat’.

The conceptual formulation of activation heat in skeletal muscle, well before its ionic basis was understood, is attributable to A. V. Hill (1949, 1950b), while its formulation in cardiac muscle is credited to Chapman & Gibbs (1972). Its method of measurement in skeletal muscle exploits the (inverse) linear dependence of active force on sarcomere length throughout the complete descending limb of the force–length relation (Gordon et al. 1966). Selected skeletal muscles can be reversibly stretched beyond optimal length to the point where active force development is negligible. Thus any heat at such a muscle length may unambiguously be attributed to the ‘activation’ processes detailed above (Homsher et al. 1972; Smith, 1972). The luxury of mimicking this experimental protocol does not extend to cardiac muscle since its sarcomere length cannot be increased beyond approximately 2.4 μm (ter Keurs et al. 1980) without risk of irreversible damage. Hence, any ‘pre‐shortening’ protocol must necessarily be applied on the ascending limb. Under this protocol, an isolated cardiac muscle preparation (papillary muscles, Ricchiuti & Gibbs, 1965; or trabeculae carneae, Han et al. 2010; Johnston et al. 2015) can readily be shortened to the point where no macroscopic active force appears in response to an applied stimulus. The resulting heat production, above that of basal heat, has been labelled ‘activation heat’. Nevertheless, there remains unease regarding the possible contribution of actively cycling crossbridges on any myosin filaments abutting the z‐lines, in the absence of macroscopic active force development; that is, the pre‐shortening procedure may consistently over‐estimate the value of activation heat in cardiac muscle.

We have circumvented this risk by using blebbistatin, a selective inhibitor of myosin II ATPase (Allingham et al. 2005). It acts by preferentially binding to the ATPase active site, while ADP and P_i are still bound, thereby greatly inhibiting phosphate release (Kovács et al. 2004). Blebbistatin has been shown to inhibit crossbridge cycling in slow‐twitch skeletal muscle (Barclay, 2012; Lewis & Barclay, 2014) and in murine papillary muscles and myocytes (Dou et al. 2007), as well as in rabbit psoas myofibrils, intact and skinned rat cardiac trabeculae and myocytes (Farman et al. 2008). Blebbistatin has no effect on either the Ca²⁺‐sensitivity of the contractile filaments (Dou et al. 2007) or excitation–contraction coupling (Farman et al. 2008).

The specific aims of our study were (i) to measure cardiac activation heat uncontaminated by crossbridge cycling, (ii) to determine whether activation heat is ventricle independent at body temperature, and (iii) to determine whether activation heat is muscle length dependent. We achieved these aims by use of blebbistatin.

Methods

Muscle preparation

Male Wistar rats (n = 8; age: 8–10 weeks, weight: 250–350 g) were deeply anaesthetised with isoflurane, followed by cervical dislocation, thoracotomy and cardiectomy. The heart was rapidly excised and Langendorff‐perfused (at room temperature) with oxygenated Tyrode dissection solution containing (in mmol l⁻¹): 130 NaCl, 6 KCl, 1 MgCl₂, 0.5 NaH₂PO₄, 0.3 CaCl₂, 10 Hepes, 10 glucose, 20 2,3‐butanedione monoxime (BDM) (pH adjusted to 7.4 using Tris). Experiments were conducted in accordance with protocols approved by the University of Auckland Animal Ethics Committee.

Unbranched and geometrically uniform trabeculae were dissected from the endocardial surfaces of both the left and right ventricles. A suitable trabecula was transferred to the mounting chamber of a calorimeter (Han et al. 2010; Taberner et al. 2011). The muscle was superfused with the same oxygenated Tyrode solution but in the absence of BDM and with [Ca²⁺]_o increased to 1.5 mmol l⁻¹. The superfusate flow rate through the measurement chamber was electronically maintained at 0.5 μl s⁻¹; this flow rate provides adequate oxygenation while maximising the thermal signal‐to‐noise ratio (Han et al. 2011). The use of isolated cardiac trabeculae (with a typical radius less than 150 μm) obviates any concerns regarding the intrinsic complexity of the ventricle and the adequacy of oxygen supply by diffusion, even under high rates of metabolic demand (ter Keurs et al. 1980; Han et al. 2011).

Flow‐through microcalorimeter and infusion system

Force and heat measurements were simultaneously recorded using a muscle calorimeter as previously described (Taberner et al. 2011; Johnston et al. 2015). The muscle was held between two platinum hooks connected to a custom‐built force transducer at one end and a linear motor at the other. The Tyrode superfusate flowed over the muscle. The rate of muscle heat production was calculated from the flow rate‐dependent temperature sensitivity and the difference in temperature measured between up‐stream and down‐stream thermopile arrays. Muscle force was monitored using a custom laser interferometer‐based force transducer, as described previously (Taberner et al. 2011). A mirror was located at 45 deg to the axis of the measurement chamber to allow muscle diameter to be measured in two orthogonal views. All software was written in the LabVIEW programming environment (National Instruments, Austin, TX, USA). During experiments, the calorimeter was located inside an optically isolated and thermally insulated enclosure to ensure that experimental temperature was maintained at 37°C.

A computer‐controllable syringe pump was used to infuse concentrated solution containing dimethyl sulfoxide (DMSO) or blebbistatin (dissolved in DMSO) into the flowing oxygenated Tyrode solution (Fig. 1). The final concentration of DMSO/blebbistatin (0.4% and 15 μmol l⁻¹, respectively) in the measurement chamber of the calorimeter was readily achieved by adjusting the flow rates from the syringe pump and the oxygenated Tyrode reservoir (Taberner et al. 2017). By ensuring that the infusate joined the superfusate well upstream of the point‐of‐entry to the measurement chamber (Fig. 1), the heat of mixing had dissipated before the mixture encountered the upstream thermopile.

Figure 1. Schematic diagram (not to scale) of the calorimeter (located in an isolated enclosure) coupled to the infusion system (syringe pump).

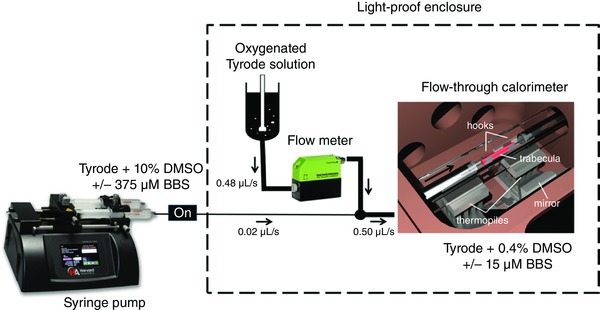
The arrow indicates the direction of superfusate flow. Note the 4:100 dilution of drugs in the superfusate. BBS, blebbistatin. [Color figure can be viewed at wileyonlinelibrary.com]

Experimental protocols

A trabecula was electrically stimulated to contract at 3 Hz at slack length until reaching steady‐states of force and heat and was then gradually stretched to the length (L _o) that maximised active force production. It was then required to undergo isometric contraction at 5 Hz while muscle length was progressively reduced, in 5 steps from L _o to L _min (the length at which developed force was zero) using the length‐control motor. At each step, steady‐state force and heat were simultaneously recorded over a period of 2 min. The muscle was then re‐lengthened back to L _o where steady‐state force and heat were re‐measured prior to the next intervention.

The muscle remained quiescent between interventions, thereby providing baselines of zero force and zero heat. The second and third interventions repeated the above length changes but in the presence of 0.4% DMSO or 15 μmol l⁻¹ blebbistatin (dissolved in 0.4% DMSO), respectively. DMSO (a polar aprotic molecule) was used as the solvent for blebbistatin; therefore the second intervention was carried out to test the effect of solvent (DMSO) per se on muscle performance. At the completion of each intervention, the muscle was re‐lengthened back to L _o, thereby providing a test of recovery from the length‐change intervention. No force recovery was observed following treatment with blebbistatin. (Para‐nitroblebbistatin (a generous gift from Prof. A. Málnási‐Csizmadia) was used to test for force recovery because of its reported reversibility in zebra‐fish embryo in vivo (Képiró et al. 2014); however we observed that its action too was irreversible in cardiac muscle despite lengthy periods of ‘wash‐out’.) The heat artifact resulting from electrical stimulation at 5 Hz was quantified at the end of each experiment in the absence of a muscle. The rate of muscle heat production by each trabecula was corrected retrospectively for the stimulus heat.

Normalisations and definitions

Trabeculae were assumed to have elliptical cross sections. Cross‐sectional area was calculated from measurements of muscle major and minor diameters in two orthogonal planes. Trabecula dimensions did not differ significantly between left ventricle (LV) and right ventricle (RV) in either cross‐sectional area (0.036 ± 0.007 mm² and 0.030 ± 0.005 mm², respectively) or length (3.28 ± 0.26 mm and 2.81 ± 0.36 mm, respectively). Results were obtained from four trabeculae from each ventricle.

Twitch force was converted to stress by dividing by muscle cross‐sectional area. Active stress was defined as the peak stress developed above the diastolic level (kPa). Heat per twitch (kJ m⁻³) was calculated by dividing the steady state rate of heat production (kW m⁻³) by the stimulus frequency (5 Hz) and normalizing by muscle volume. Normalised muscle length was expressed relative to optimal muscle length (L/L _o).

Data analysis

Data were acquired using LabView software (National Instruments) and analysed offline using a custom‐written MATLAB (MathWorks, Natick, MA, USA) program. Active stress development and muscle heat production were regressed against relative muscle length for each muscle. The resulting individual regression lines were averaged within groups (i.e. ventricles) using the random coefficient model within PROC MIXED of the SAS software package (SAS Institute Inc., Cary, NC, USA). Analysis of covariance (ANCOVA) was applied to test the main effect of ‘ventricle’ (i.e. ‘RV ‘versus ‘LV’) and the interaction between ‘ventricle’ and ‘intervention’ (i.e. ‘Control’, ‘DMSO’ and ‘blebbistatin + DMSO’ on the average intercepts and the average slopes. Values are expressed as means ± SEM and P < 0.05 was considered to be statistically significant.

Results

Effects of muscle length on active stress and heat

Figure 2 shows the effects of muscle length on stress production and heat output in the absence or presence of either 0.4% DMSO or 15 μmol l⁻¹ blebbistatin (dissolved in 0.4% DMSO). The reduction of muscle length below L _o resulted in a decrease of both stress production and heat output. The stress production of the same muscle decreased approximately 30% in the presence of 0.4% DMSO (in accord with observations reported by Dou et al. 2007), thereby giving a lower heat output. Blebbistatin inhibited muscle contraction to near zero level of stress at L _o, and heat production remained constant, independent of muscle length.

Figure 2. Typical experimental records of stress production and heat output of a representative trabecula at various muscle lengths (b–f) below its optimal length (a), at 5 Hz stimulation.

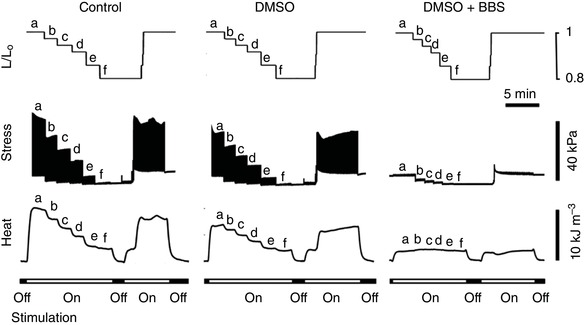
The muscle was returned to optimal length (a) before performing the next two interventions: DMSO and DMSO + blebbistatin (BBS), in that order. Trabecula dimensions: length, 2.82 mm; cross‐sectional area, 0.0347 mm². Its rate of heat production at L _o under control conditions was 4.91 μW. Note that the latter value exceeds the thermal resolution of the microcalorimeter by some 500‐fold.

Stress–length and heat–length relationships

As muscle length was reduced below L _o, both steady‐state isometric stress and steady‐state heat per twitch decreased whether in the absence or in the presence of DMSO. However, heat output remained constant while active stress was absent in the presence of blebbistatin. Values of active stress and resulting heat output were plotted as functions of relative muscle length (L/L _o) and fitted using quadratic regression (Fig. 3 A and D). The relations describing the dependence of stress and heat on relative muscle length for the four trabeculae from each ventricle were averaged and are plotted in Fig. 3.

Figure 3. Active stress and heat per twitch as functions of muscle length from a single trabecula.

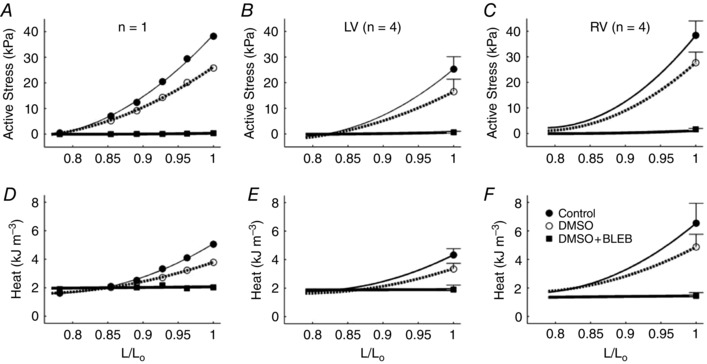
A and D, active stress (A) and heat per twitch (D) as functions of muscle length from a single representative trabecula. B, C, E and F, stress–length and heat–length regression relations describing individual muscles from the different interventions were averaged within the LV group (B and E) and the RV group (C and F). Mean ± SEM values at optimal length were superimposed appropriately in panels B, C, E and F.

Heat–stress relationships

Figure 4 shows the relation between active heat and active stress for a single trabecula (Fig. 4 A) and for the average of the four trabeculae from either ventricle (Fig. 4 B and C). Heat–stress relations were fitted using linear regression, as no statistically significant improvement was achieved when fitting with a quadratic function. The average heat‐intercept (an index of activation heat) was not significantly different among experimental interventions or between LV and RV preparations (Fig. 4 D).

Figure 4. Twitch heat as functions of active stress.

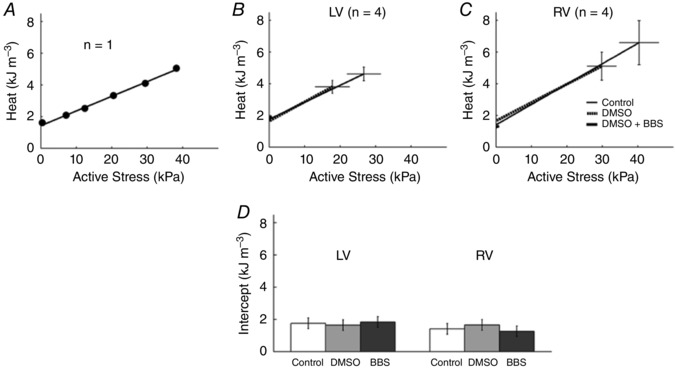
A–C, linear regression of active heat–stress relations arising from a single trabecula under control conditions (A) and from the averages of n = 4 trabeculae from each of LV (B) and RV (C) undergoing isometric contractions at various muscle lengths for all three experimental interventions. D, the average heat intercepts for all three treatments in trabeculae from both ventricles.

Discussion

This study is the first to have employed blebbistatin for the study of cardiac energetics. The rationale for its use was to exploit its ability to inhibit crossbridge cycling in order to partition crossbridge heat from activation heat. Activation heat is defined as the supra‐basal heat produced during the restoration of sarcolemmal and sarcoplasmic reticular ion gradients associated with relaxation following a twitch. In cardiac muscle, it has commonly been assessed using the ‘pre‐shortening’ protocol in which a preparation undergoing isometric contractions is progressively shortened until observed macroscopic force development is zero. Whatever heat is observed at this point, the intercept of the heat–stress relation is attributed to the activation process. But this attribution immediately poses the question: Does the absence of macroscopic force at this short muscle length belie the continued cycling of crossbridges, thereby inflating the estimate of activation heat?

In order to answer this question, we have adopted a modification of the above protocol by repeating the pre‐shortening procedure in the presence of blebbistatin (BBS), an agent shown to be an excitation–contraction uncoupler in rat and rabbit hearts (Fedorov et al. 2007), and an inhibitor of crossbridge cycling in a variety of murine cardiac tissues (Dou et al. 2007) and rat papillary muscle without diminishing the magnitude of the Ca²⁺ transient (Dou et al. 2007; Farman et al. 2008). Because of blebbistatin's insolubility in Tyrode solution, we required three interventions: ‘Control’ (Tyrode solution), ‘DMSO’ and ‘DMSO + BBS’ (Fig. 2). As can be seen in Fig. 2, progressive pre‐shortening progressively diminished active twitch stress from its maximum at L/L _o = 1.0 to its minimum at L/L _o = 0.77 under both Control and DMSO conditions. In the presence of DMSO + BBS, active force was zero at any length, thereby proving the effectiveness of blebbistatin in inhibiting crossbridge cycling. In the absence of active stress development, heat continued to be liberated. We attribute this thermal output (Fig. 3) to ‘activation heat’. Our confidence in this attribution is bolstered by the results shown in Fig. 4 where the same estimates of activation heat arise from all three interventions in both LV and RV trabeculae. These results clearly demonstrate the absence of thermal contamination from crossbridge cycling.

Furthermore, our finding of constant heat output, independent of muscle length, in the presence of blebbistatin (Figs 2 and 3), demonstrates that the energy cost of activation processes is length independent. Combining the results from Figs 3 and 4, we infer that activation heat is also stress independent. This inference has support from the results of experiments specifically designed to increase the heat of activation of contraction. Thus Gibbs et al. (1967), using adrenaline, Gibbs & Vaughan (1968), by lowering temperature, and Han et al. (2010), by elevating extracellular Ca²⁺ concentration, each showed an increase of activation heat with no change in slope of the heat–stress relation.

The results summarised in Fig. 4 are also fully consistent with those of Sathish et al. (2006), who showed identical peak values of Ca²⁺ transients elicited from myocytes harvested from right‐ and left‐ventricular rat myocardium, albeit at room temperature. Since it is the amount of Ca²⁺ released from the sarcoplasmic reticulum (SR) that determines the amount to be sequestered by the SR Ca²⁺‐ATPase, the correspondence of our thermal results with the aforementioned ionic results is unsurprising.

Also shown in the paper by Sathish et al. (2006) was a 50% greater extent of unloaded shortening of myocytes originating from the LV. This result provides a possible explanation for the higher rate of ‘activation heat’ observed (at room temperature) in LV than in RV trabeculae, reported earlier by our group (Han et al. 2013). In those experiments, we estimated activation heat using a protocol that allowed the muscles to shorten actively under zero load. Since it has long been recognised that active shortening of striated muscle is exothermic (Fenn, 1923; Hill, 1938; Gibbs et al. 1967), then it is again unsurprising that the heat estimated from minimally afterloaded isotonic contractions should be higher in LV than in RV trabeculae. Since these two conceptually distinct sources of heat (‘activation’ and ‘shortening’) cannot be distinguished macroscopically, we may have unwittingly over‐estimated LV activation heat in our earlier publication (Han et al. 2013). Be that as it may, our current findings show that activation heat accounts for some 15–20% of the total heat produced in an isometric contraction at optimal length, under conditions chosen to approximate those occurring in vivo: 5 Hz frequency of contraction at 37°C.

Comparison with other techniques

In addition to studies using pre‐shortening protocols, two other techniques are worthy of discussion. In the first of these, Alpert et al. (1989) measured ‘tension‐independent heat’ in rabbit papillary muscles at 21°C, finding it to be length dependent. Tension‐dependent heat was eliminated by use of 5 mm 2,3‐butanedione monoxime (BDM) and mannitol, to increase osmolality to as high as 2.5‐fold its normal value. We are hesitant to consider further the results of this study because subsequent investigations have demonstrated that the chemical phosphatase BDM reduces the open probability of the L‐type Ca²⁺ channels in guinea‐pig ventricular myocytes (Allen & Chapman, 1995), while abbreviating the duration of the action potential and reducing the Ca²⁺ current at any membrane potential (Gwathmey et al. 1991). The latter study also showed that BDM reduces maximum Ca²⁺‐activated force by upwards of 30% in ferret papillary muscles. Of further concern to any thermal study, BDM has been show to diminish the activity of the mitochondrial ATP–ADP translocase (Mojon et al. 1993) while hyperosmolality is now known to potentiate the rate of heat production of quiescent rat cardiac trabeculae (Loiselle et al. 1996).

A less contentious technique, ‘latency release’, was developed by Gibbs et al. (1988) in an attempt to obviate the risks of time‐ and length‐dependent de‐activation (Allen & Kurihara, 1982). Using this protocol, the length of a papillary muscle was rapidly reduced from optimal to minimal muscle length during the brief latent period between delivery of the stimulus and the onset of twitch force. Since the pre‐shortened length prevented the development of macroscopic force, it was presumed to quantify activation heat. But, at that time, it was not clear that the absence of macroscopic force development precludes the cycling of crossbridges.

The results of the present study strongly suggest that previous studies, in which heat–stress relations were extrapolated to zero stress, likewise produced accurate estimates of activation heat. Thus, for example, we can be confident that activation heat is lower in the rat than in either the cat or the guinea‐pig (Loiselle & Gibbs, 1979).

Limitations of the study

With only four muscles examined from each ventricle, statistical power is low. Whereas this is correct, it is readily countered. Since all eight trabeculae reported identical effects of blebbistatin (Figs 2, 3, 4), ethical considerations precluded the use of additional rats.

The order of presentation of treatments (‘Control’, ‘DMSO’, ‘DMSO + BBS’) was not randomised. This objection is again correct, but a randomised order of presentation was precluded by the inability to wash blebbistatin out of the tissues. Constraints inherent in the design of our microcalorimeter preclude the use of optical means (illumination of tissue using light in the blue region of the spectrum) to inactivate blebbistatin (Sakamoto et al. 2005), thereby allowing reversibility of its inhibitory action on force development. Irreversibility did not, however, prevent application of a ‘repeated‐measures’ ANOVA.

No correction was made for the change of osmolality by addition of DMSO or DMSO + blebbistatin. However, correction is unnecessary since the membrane permeability of DMSO is extremely high (some 50‐fold that of urea; Yu & Quinn, 1994) presumably reflecting its polar nature. Whereas tonicity may have increased marginally, osmolality did not.

Finally, in the interest of completeness, we consider the possibility that, at minimal muscle length, there remains residual crossbridge heat which is below the detection threshold of our microcalorimeter. But, in fact, the thermal resolution of the microcalorimeter (10 nW; Taberner et al. 2015) is three orders of magnitude below the rate of activation heat production of any trabecula use in this study.

Summary

We conclude that use of the crossbridge inhibitor blebbistatin, despite its irreversibility in our hands, is a suitable agent for isolating a component of total cardiac heat production that can unambiguously be attributed to thermal consequence of activating contraction. Using this agent, we demonstrate that activation heat is muscle‐length independent, thereby resolving a long‐standing dispute in the cardiac energetics literature. But, most importantly, with the respect to the question posed in the title, the intercept of the linear heat–stress relation provides an accurate estimate of cardiac activation heat.

Additional information

Competing interests

We declare no competing interests.

Author contributions

Experiments were performed at the Auckland Bioengineering Institute, The University of Auckland, New Zealand. T.P. contributed to the conception and design of the work, performed the experiments, and was central to the acquisition, analysis and interpretation of data. K.T. contributed to the conception and design of the work, writing of Matlab code, and analysis and interpretation of data. K.M. contributed to the conception and design of the work and interpretation of data. A.H. contributed to the interpretation of data. A.P. contributed to the interpretation of data. M.W. contributed to the interpretation of data. A.T. led the design, construction, programming and maintenance of the experimental apparatus, and contributed to the analysis and interpretation of data. J.‐C.H. contributed to the conception and design of the work, and the acquisition, analysis and interpretation of data. D.L. contributed to the conception and design of the work, and the acquisition, analysis and interpretation of data. All authors approved the final version of the manuscript and agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved, and all persons designated as authors qualify for authorship, while all those who qualify for authorship are listed.

Funding

This work was made possible by generous support from the National Heart Foundation of New Zealand: Project Grant 1601 (D.L.), Post‐Doctoral Fellowships (J.‐C.H. and K.T.) and a PhD Scholarship (TP). J.‐C.H. is the recipient of a Fast‐Start grant from the Marsden Fund, from Government funding, administered by the Royal Society of New Zealand.