Analysis on the Association Among Stunting, Wasting and Underweight in Malawi: An Application of a Log-Linear Model for the Three-Way Table

Abstract

Childhood undernutrition is an important public health problem. Many studies have investigated the factors of childhood undernutrition, but not the association between the undernutrition indicators. This study aimed at investigating the association between the childhood undernutrition indicators. A loglinear model of cell counts of a three way table of stunting, wasting, and underweight was fitted based on the 2010 Malawi demographic health survey data. Interaction terms in the model depicted deviations from independence. A multiple correspondence analysis of undernutrition indicators was also plotted to have a visual impression of association of the undernutrition variables. A loglinear model showed that underweight was associated with both stunting (P<0.001), and wasting (P<0.001). There was no association between stunting and wasting (P=1). Furthermore there was no three way association of stunting, wasting and underweight (P=1). Lack of three way interaction of stunting, wasting and underweight means that childhood undernutrition multidimensional nature is still valid, and no each indicator can represent the other.

Competing interest statement

Conflict of interest: the authors declare no potential conflict of interest.

Introduction

The indicators of childhood undernutrition are stunting (height-for-age below –2 Z-score), wasting (weight-for-height below –2 Z-score) and underweight (weight-forage below –2 Z-score).¹ Stunting is a result of chronic food shortages/malnutrition, and wasting is a short term effect of malnutrition and is termed as acute malnutrition. Underweight is a reflection of the two (stunting and/or wasting). Globally, an estimated 165 million children under-five years of age, or 26%, are stunted, 101 million children under-five years of age, or 16%, are underweight and 52 million children under-five years of age, or 8%, are wasted.² High prevalence levels of stunting among children under-five years of age are in Africa (36%) and secondly in Asia (27%), and this remains a public health problem.² Malawi which is part of the sub-Saharan Africa has 47% childhood stunting, 13% childhood wasting and 4% childhood underweight.³

The effects of childhood undernutrition are substantial. Globally, malnutrition (mild to severe) is associated with about 60 percent of all childhood deaths.⁴ Poor nutrition during childhood also causes severe cognitive and physical damage. Moreover, poor nutrition and health among children contribute to the general inefficiency of education systems worldwide. Studies have shown that improved nutrition and health lead to better performance, fewer repeated classes and reduced dropout cases.⁵

Many studies have focused on association of childhood undernutrition indicators with their predictors,^6-12 and have neglected the association of the indicators themselves. A few studies though have looked at relationship between the indicators,^13-15 and the studies have looked at pairwise relationship neglecting the three dimension association. The importance of looking at the three dimension association is that it helps to judge as to whether childhood undernutrition indicators are separate (main effects) or can be taken as one (interaction effect). This study aimed at investigating the association of childhood undernutrition indicator variables by using Poison modeling approach so as to investigate various association structures of undernutrition indicators. The deviations from independence would be represented by interaction terms.^16,17

The paper is organised as follows: first, methods in terms of study population, area, data and statistical analysis is presented. This is followed by results, discussion and conclusion.

Materials and Methods

Study area and data

The study focused on under five children in Malawi and used the standard and nationally representative 2010 MDHS data. The 2010 MDHS was conducted from June to November in 2010. Data were downloaded from the DHS web site (www.dhsprogram.com/data/dataset_admin) after being granted permission. Parents of the children whose weight and height were measured signed informed consent. The Malawi Health Research Committee saw that ethical approval was not deemed necessary in this study considering the fact that the study used data from a research study already approved by an ethical research committee. According to the 2010 MDHS report,³ the 2010 MDHS study was ethically approved by Malawi Health Research Committee, Institutional Review Board of ICF Macro, Centre for Disease and Control (CDC) in Atlanta, GA, USA. The sampling design according to 2010 MDHS report was a two stage cluster design with stratification.³ The primary sampling units were the enumeration areas (EAs) and the secondary sampling units were the households. EAs were stratified in terms of rural and urban. A total of 849 EAs were sampled with 158 in urban areas and 691 in rural areas. A total representative sample of 27,307 households was selected and 25,311 households were considered to be occupied in the 2010 MDHS. Data collection was by questionnaires. There were three types of questionnaires, woman, man and household questionnaire through face-to-face interviews. Households that were successfully interviewed were 24,825, yielding a response rate of 98%. Eligible women were 23,748 and 23,020 were successfully interviewed, yielding a response rate of 97%. For men 7783 were eligible and those that were successfully interviewed were 7175, yielding a response rate of 92%. The data set used in the analysis was child record data set which was based on woman and household questionnaires. All children under five years in the sampled households were considered as candidates for the weight, height and age data to be collected.

The analysis was based on children with complete anthropometric and valid age data. The overall number of child records with complete anthropometric and valid age data was 4861. Data management in terms of extracting and generation of variables from child record data set was done in STATA version 12 a software developed by StataCorp in Texas. The variables of interest generated were: stunting (HAZ<-2/HAZ≥-2), wasting (WHZ<-2/WHZ≥-2), and underweight (WAZ<-2/WAZ≥-2). These were indicator variables based on categorization of anthropometric indicators, height for age z-score (HAZ), weight for height z-score (WHZ) and weight for age z-score (WAZ) respectively. The methodology for computing the indicators was based on the 2006 WHO Child Growth Standards.¹

Statistical analysis

First, multiple correspondence analysis was used to have a descriptive analysis of association of the three undernutrition variables. Loglinear models were then fitted to see the significant associations. The loglinear models were fitted based on a cross table that was created based on the study design defined by the survey command from survey package in R. Loglinear models are interpreted as generalized linear models (GLM) which treat the cells counts as independent observations from the Poisson distribution with corresponding means equal to the expected cell counts. They are useful when all the three factors can be treated as response,^16,17 as it is the case in this study for underweight, stunting and wasting, and the focus is on their structure of association. Since there are three factors, 2³+1 (9) loglinear models are possible. Let µ_i,j,k be the mean cell count in the three way table for underweight, stunting and wasting, then the following are the nine loglinear models of the mean cell count:

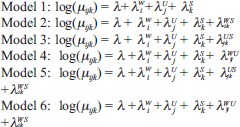where W, U and S represent wasting, underweight and stunting respectively. Model 1 means that there is mutual or complete independence among stunting, wasting and underweight, that is, they are pairwise independent. Model 2, 3, and 4 means partial independence (independence of one factor) leading to a loglinear model with one possible nonzero interaction parameter. Precisely, underweight is partially independent of stunting and wasting (Model 2), wasting is partially independent of stunting and underweight (Model 3) and stunting is partially independent of wasting and underweight (Model 4). Model 5, 6 and 7 represent conditional independence of two factors given the other factor. This results in a loglinear model with two possible nonzero interactions parameters. Specifically, wasting and underweight are conditionally independent of stunting (Model 5), stunting and underweight are conditionally independent of wasting (Model 6) and stunting and wasting are conditionally independent of underweight (Model 7). Model 8 depicts homogenous associations, that is, every factor interacts with each other factor, but there is no interaction between all three factors. The last model (Model 9), is the saturated model containing the three factors being analyzed and all possible relationships between the factors. Multiple correspondence analysis and fitting of loglinear models was done in R version 2.15.1.¹⁸

Results

Table 1 presents cross tabulation of stunting, wasting and underweight. There were 47.75% stunted children, 4.94% wasted children and 13.7% of all children were underweight. Figure 1 shows the multiple correspondecne analysis of stunting, wasting and underweight. There is no association between wasting and stunting as they are in different quadrants (first and fourth). Underweight is associated with the both stunting and wasting as it is on boundary line.

Table 1.

Cross classification of stunting, wasting and underweight.

Stunting	Wasting	Underweight		Total
		Yes	No
Yes	Yes	69	0	69
	No	491	1761	2252
No	Yes	71	100	171
	No	35	2334	2369
Total		666	4195	4861

Figure 1.

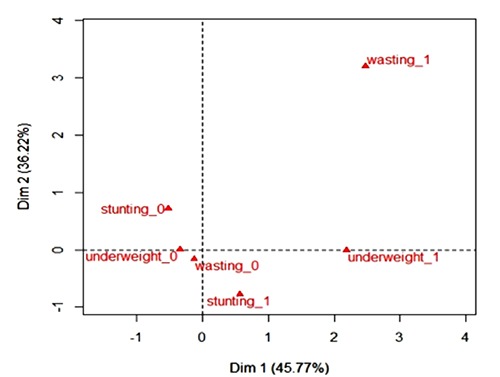
Multiple correspondence analysis of stunting, wasting and underweight. 0 means no and 1 means yes.

Table 2 shows goodness of fit tests for loglinear models of raw data from Table 1 that incorporated different terms for associations. The fit statistics basically compare the observed and fitted cell counts. Under the null hypothesis, the model fits the data well, that is, there is no difference between the observed and the fitted cell counts. The alternative hypothesis is that the model does not fit well the data, that is, there is a difference between the observed and the fitted cell counts. A small P-value for the fit statistics means stronger evidence against the null hypothesis and vice versa. Models 1 to 8 do not fit the data well because the P-values for the fit statistics are less than 0.05, while model 9 fits the data well as the p-values for the fit statistics are all more than 0.05. Thus, results of the saturated model (model 9) are presented and interpreted.

Table 2.

Goodness-of-fits tests for loglinear models relating stunting (S), wasting (W) and underweight (U).

Model	Loglinear model symbol	G2 (LR-Chi-square)	X2 (Pearson)	df	p
					G2	X2
1	(S,W,U)	940.3699	911.9636	4	<0.001	<0.001
2	(U,SW)	934.6622	947.5914	3	<0.001	<0.001
3	(W,SU)	353.5966	637.2217	3	<0.001	<0.001
4	(S,WU)	705.0068	661.4044	3	<0.001	<0.001
5	(SW,SU)	347.8889	589.5052	2	<0.001	<0.001
6	(SW,WU)	699.2991	657.9755	2	<0.001	<0.001
7	(SU,WU)	118.2335	114.8761	2	<0.001	<0.001
8	(SU,SW,UW)	8.176991	4.530044	1	0.004	0.033
9	(SWU)	0	0	0	1	1

Table 3 presents results of model 9. There is high significant association between underweight and stunting (P<0.001), and between underweight and wasting (P<0.001), but no interaction between stunting and wasting (P=1). Furthermore, the saturated loglinear model shows lack of three factor association among stunting, wasting and underweight (P=1).

Table 3.

Estimates for the saturated loglinear model for stunting, wasting and underweight.

Coefficient	Estimate	Standard error	Z-value	P-value
Intercept	7.79	0.27	385.201	<0.001
Stunting	-2.46	0.47	-19.240	<0.001
Wasting	-3.78	0.49	-27.905	<0.001
Underweight	-3.19	0.37	-31.357	<0.001
Stunting*wasting	-6.98	230.68	-0.001	1.000
Stunting*underweight	2.41	0.42	21.282	<0.001
Wasting*underweight	3.31	0.77	15.733	<0.001
Stunting*wasting*underweight	6.48	230.68	0.001	1.000

Discussion

This study employs the use of loglinear models for the three way table in assessing association among the undernutrition variables. The advantage of loglinear models according to Bishop et al ¹⁹ is that in addition to analysis of relationship between the response and the predictors, they allow an investigation of the relationship among the response variables, as it is the case in this study for the undernutrition variables. The association of the variables is depicted by the interaction terms.^16,17 In addition to the usual analysis of pairwise association, loglinear models give an additional insight on the three-way interaction.

The associations observed among nutrition variables in the saturated model (Table 3) are in agreement with those displayed in the multiple correspondence analysis. The fitted saturated loglinear model shows a significant interaction between stunting and underweight (P<0.001) and between underweight and wasting (P<0.001). This means the effect of underweight on expected cell counts vary by stunting level and vice versa, and also the effect of underweight on cell counts vary by wasting level and vice versa. These findings are consistent with Tsaguel and Dapi.¹⁴ In addition, this is in agreement with the knowledge that underweight reflect stunting and/or wasting; or a composite measure of both; thus inability to distinguish between both.^20,21 There is no association between stunting and wasting (P=0.999). This finding is consistent with Tsague1 and Dapi, and Victora.^14,15 Interestingly though Victora,¹⁵ found no association between stunting and wasting in Africa and Latin America, but she found an association of the two in Asia and Eastern Mediterranean. It was argued that an observed association of the two may be due to the fact that both of them are driven by energy deficiency and infections, and lack of association between them means that they be driven by different causes which are yet to be investigated. There is lack of a three way interaction among stunting, wasting and underweight (P=1). This means childhood undernutrition is statistically valid as multidimensional, that is, the three childhood undernutrition indicators cannot be considered as one, and that they are not redundant of each other.

The observed associations of child undernutrition indicators do not mean that the associated variables cause each other as no such conclusion can be made since data was from cross sectional survey. Such conclusion could be made if data was from prospective or retrospective cohort study. Future studies therefore can look at relationship of child undernutrition indicator variables by using data from prospective/retrospective cohort studies so as to establish temporal linkages between the variables.

Conclusions

The study finds an association between stunting and underweight and between underweight and wasting. It further reveals that there is no association between stunting and wasting and let alone among the three undernutrition indicators: stunting, wasting and underweight. Lack of association among the three undernutrition indicators implies that the three indicators are still separate and cannot be considered as redundant of each other. The choice of each of the indicator in addressing child undernutrition therefore should depend on government policy.