Hybrid Statistical and Mechanistic Mathematical Model Guides Mobile Health Intervention for Chronic Pain

Abstract

Nearly a quarter of visits to the emergency department are for conditions that could have been managed via outpatient treatment; improvements that allow patients to quickly recognize and receive appropriate treatment are crucial. The growing popularity of mobile technology creates new opportunities for real-time adaptive medical intervention, and the simultaneous growth of “big data” sources allows for preparation of personalized recommendations. Here we focus on the reduction of chronic suffering in the sickle cell disease (SCD) community. SCD is a chronic blood disorder in which pain is the most frequent complication. There currently is no standard algorithm or analytical method for real-time adaptive treatment recommendations for pain. Furthermore, current state-of-the-art methods have difficulty in handling continuous-time decision optimization using big data. Facing these challenges, in this study, we aim to develop new mathematical tools for incorporating mobile technology into personalized treatment plans for pain. We present a new hybrid model for the dynamics of subjective pain that consists of a dynamical systems approach using differential equations to predict future pain levels, as well as a statistical approach tying system parameters to patient data (both personal characteristics and medication response history). Pilot testing of our approach suggests that it has significant potential to well predict pain dynamics, given patients reported pain levels and medication usages. With more abundant data, our hybrid approach should allow physicians to make personalized, data-driven recommendations for treating chronic pain.

1. Introduction

In the fields of physics, chemistry, and engineering, models are often derived from mechanistic fundamental laws expressed in the form of differential equations. Resulting “dynamical systems” models can be used both to gain intuition into the expected behavior of the system and to make specific predictions about results of experiments (e.g., see Strogatz, 2014). In fields such as social sciences, bioinformatics, and medicine, models are often constructed from data via statistical inference, without direct derivation from fundamental principles (e.g., see Freedman, 2009). The mechanistic and statistical approaches to mathematical modeling have different advantages. The former allows prior knowledge to be introduced and validated or rejected based on the success of the model. The latter requires almost no a priori information about how the system is expected to behave.

In this article, we present a hybrid approach to mathematical modeling that incorporates both mechanistic and statistical elements, with the goal of gaining a deeper understanding of the human experience of subjective pain. Specifically, we hope to predict how patient-reported pain levels vary over time based on medication dosage information and other patient characteristics.

1.1. Application to pain

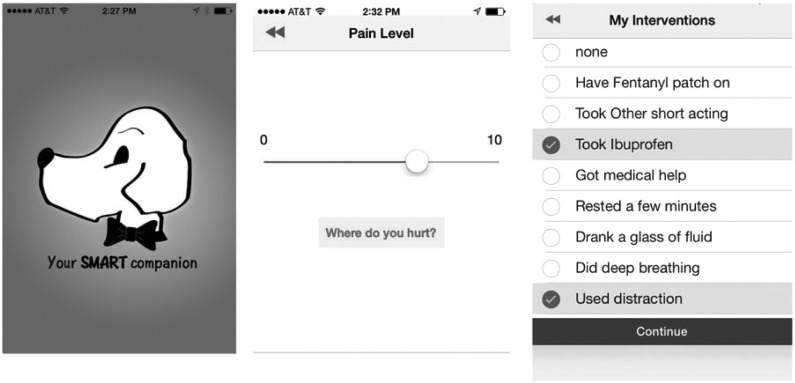
Sickle cell disease (SCD) is a chronic illness associated with frequent medical complications and hospitalizations. Approximately 90% of acute care visits are for pain events, and 30-day hospital reutilization rates are alarmingly high (Platt et al., 1991). While factors influencing these high reutilization rates are poorly understood, close follow-up and continued use of pain medications have been shown to decrease rehospitalization rates. Mobile technology has become an integral part of healthcare management, and our recently self-developed mobile application (Sickle cell Mobile Application to Record symptoms via Technology, or SMART app—see Fig. 1) for SCD assists with documentation and intervention of pain.

FIG. 1.

Smartphone app. Sample images of SMART app for iPhone/Android smartphone devices.

Pain in particular is difficult to quantify and has never before been monitored at the temporal scale we report here across so many patients. It is known that subjective pain, although indeed subjective, is correlated with objective measurable stimulus qualities in experiments (see, e.g., Stevens et al., 1958; Hughes et al., 2002; Granovsky et al., 2008). Thus, there is reason to believe that subjective pain may follow understandable dynamics in time, especially when mitigated by opioid or nonopioid drugs. Our approach to the problem is motivated by the hope that a reasonable model for pain dynamics will yield some level of predictive power, despite the clear expectation that there will also be significant noise within and across patients. We can attribute the stochastic variation to sources such as patient mood, temporal changes in patient state, and weather. In contrast, we hope that patient attributes such as age, gender, and SCD type will remain roughly constant on the time scale of the experiment and allow us to explore possible correlation of these attributes with model parameters.

1.2. Data source: mobile health app

We seek to understand the temporal dynamics of chronic pain as experienced by SCD patients. To that end, we have developed a mobile phone app that allows patients to record medication usage and subjective pain levels (measured on a 0–10 scale) in real time (Shah et al., 2014; Jonassaint et al., 2015).

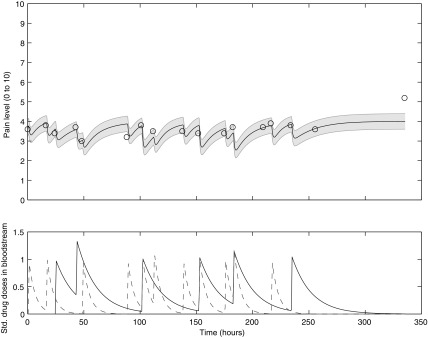
Figure 1 shows several images of the app interface, while Figure 2 shows a typical data set resulting from a single patient's use of the app over the course of several weeks.

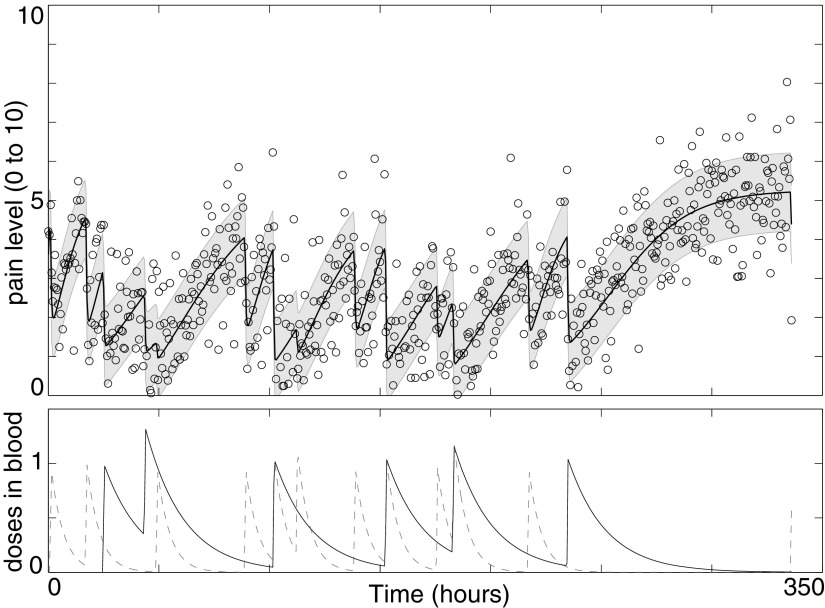
FIG. 2.

Sample pain and medication data from a single patient. Upper panel: patient-reported pain (circles) and model fit (thick solid line); shading indicates model fit ± one standard deviation. Lower panel: long-acting methadone (solid line) and short-acting oxycodone (dashed line) medication concentrations in patient bloodstream as inferred from medication usage reported via the SMART application.

2. Methods

2.1. Data

As of October 2016, data were available from 47 patients using the SMART app. Data sets from eight of those patients were excluded because of excessive sparsity based on the following criteria: (1) total number of reports 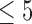or (2) pain reports never exceeded zero during the period under consideration. See Table 1 for demographic details of included patients. We denote the sample size .

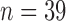Table 1.

Patient Demographic Information and the Number of Pain Reports Supplied by Patients Across the Entire Study

Demographic characteristics
Institution, N (%)
A	14 (35.9)
B	17 (43.6)
C	8 (20.5)
Gender, N (%)
Male	16 (41.0)
Female	23 (59.0)
Age at baseline (years), N (%)
18–34	24 (61.5)
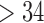
	15 (38.5)
SCD type, N (%)
Hemoglobin SC	8 (20.5)
Hemoglobin SS	22 (56.4)
Hemoglobin SB (Beta) Thalassemia	5 (12.8)
Beta-Zero Thalassemia	3 (7.7)
SOArab	1 (2.6)
Hydroxyurea user, N (%)	27 (69.2)
Folic acid vitamin user, N (%)	26 (66.7)
Long-acting opioid user, N (%)	29 (74.4)
Short-acting opioid user, N (%)	35 (89.7)
Nonopioid user, N (%)	29 (74.4)

	Mean	SD	(Min, Max)
Number of pain reports	67.2	60.4	(9.0, 257.0)
Days of pain reports	164.6	109.6	(10.3, 435.1)
Within-patient average VAS score	4.7	2.1	(0.3, 9.4)

	Mean	SD	(Min, Max)
Number of pain reports (first 2 weeks)	13.2	9.6	(2.0, 45.0)
Number of long-acting opioid doses (first 2 weeks)	6.0	8.4	(0.0, 35.0)
Number of short-acting opioid doses (first 2 weeks)	7.2	7.5	(0.0, 35.0)
Number of nonopioid doses (first 2 weeks)	2.1	3.1	(0.0, 12.0)

SCD, sickle cell disease; VAS, visual analog scale.

2.2. Predictive model

To develop a hybrid model that incorporates both a mechanistic a priori knowledge-driven component and a statistical data-driven component, we divide tasks into two disjoint sets that fit these two categories (see Section 4 for more context). We begin with a “dynamical systems” model for subjective pain motivated by the hypothesis that human sensory systems function on a roughly “return to set point” basis (McRuer and Krendel, 1974; Fors et al., 1988; Britton et al., 1995; Stepan, 2009). Any model of human pain response, however, will inevitably require specification of a variety of parameters determining the time scale(s) and degree of severity of the response. The statistical modeling tasks use patient data to infer parameters (1) from patient characteristics and population distributions and (2) from patient-specific pain and medication response history.

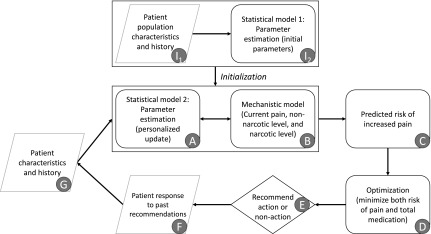
To make this more concrete, in Figure 3 we present a flow chart summarizing our approach to the hybrid modeling problem. Steps I₂ and A comprise the statistical modeling component; steps B and C comprise the mechanistic modeling component. A further optimization step D builds on the predictions of the hybrid model to allow for a balance between competing demands of pain reduction and medication usage minimization. This article details steps I₁, I₂, A, and B. We leave the remaining steps for future work.

FIG. 3.

Schematic flowchart showing model framework. Rounded rectangles represent modeling or computation steps, rhombuses represent data inputs or outputs, and diamond represents decision step. Items I₁ and I₂ are only necessary for initialization of the model. Items A and B are the focus of this article.

2.2.1. Mechanistic component (for every patient)

We propose and evaluate two related mechanistic models based on a set of coupled ordinary differential equations (ODEs), either (1) deterministic or (2) stochastic. The stochastic differential equation model comprises a Langevin equation, which can be converted into a Fokker–Planck partial differential equation for the evolution of the probability distribution for pain 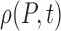(Gardiner et al., 1985). This allows for prediction of both the expected pain level for a patient at any point in the future and an assessment of the confidence in (and a confidence interval for) that prediction.

Mathematically, the deterministic mechanistic model we propose is the following, for a single patient:

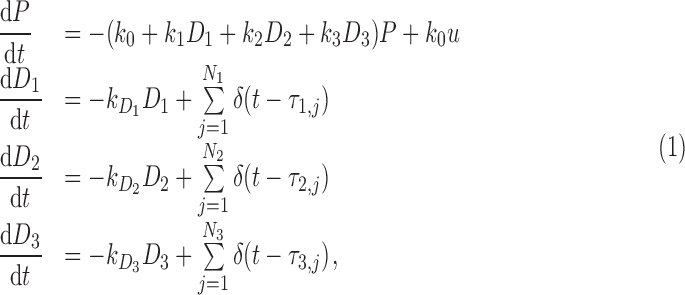where P is the patient pain level (on a scale of 1–10), k₀ is the pain relaxation rate without drugs, k_i is the marginal effect on the pain relaxation rate due to drug i (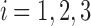), u is the unmitigated pain level (i.e., without drug intervention), D_i is the amount of standard drug i doses within the patient, 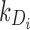is the elimination rate of drug i within the patient, 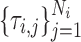are the drug i dosage times, and N_i is the number of doses of drug i taken. 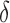represents the Dirac delta function. Note that the parameters and variables will in general need to be indexed with distinct values for each patient in a population, although we omit those indices here for clarity. For convenience and clarity, we also here omit “hatted” notation (e.g., 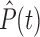) sometimes used for model predictions. Tables 2 and 3 summarize the meanings of model variables and parameters, respectively.

Table 2.

Variables in Mechanistic Models

Variable	Meaning	Units
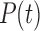	Instantaneous pain level on 0–10 scale	Pain
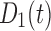	Concentration of drug 1 (long-acting opioid) in the body	Standard doses
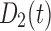	Concentration of drug 2 (short-acting opioid) in the body	Standard doses
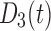	Concentration of drug 3 (nonopioid) in the body	Standard doses
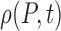	Instantaneous probability distribution of pain level P	Probability

Table 3.

Parameters in Mechanistic Models

Parameter	Meaning	Units
u	Unmitigated pain level	Pain
k0	Rate of decrease of pain in the absence of drugs or disease/sources of pain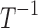
k1	Effect of drug 1 (long-acting opioid) on pain relaxation rate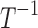
k2	Effect of drug 2 (short-acting opioid) on pain relaxation rate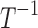
k3	Effect of drug 3 (nonopioid) on pain relaxation rate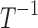
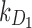	Rate of decay of drug 1 (long-acting opioid) in body due to metabolism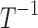
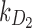	Rate of decay of drug 2 (short-acting opioid) in body due to metabolism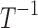
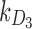	Rate of decay of drug 3 (nonopioid) in body due to metabolism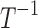
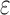	Amplitude of intrinsic noise (variability) in human subjective pain reports	T1/2
Ni	Number of standard drug i doses taken	Count
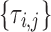	Drug i dose times (indexed by j)	T

In this very simple model for pain dynamics (1), pain is expected to relax at rate k₀ to unmitigated level u set by aggravating factors (such as SCD) in the absence of intervention through opioids (drugs 1 and 2) or nonopioids (drug 3). When drugs are present in the patient's body, pain drops at a faster rate and the short-term equilibrium pain level (not the unmitigated pain level u) is reduced. Note that we treat all parameters as constant over the time period of interest, which we take to be 2 weeks (based on clinical heuristic experience).

In the model for drug concentrations, medication in the body is assumed to be metabolized at a constant rate. Rates can be determined from existing substantiated pharmacokinetic models (e.g., Poulin and Theil, 2002; Yang et al., 2006); Dirac delta function onset of medication serum concentration is a good approximation to the fast rise typical of the medications under consideration. See Figure 2 for a sample deterministic model output.

Note that we deliberately chose to use an extremely simple conceptual model for pain dynamics. More sophisticated versions might be developed to incorporate higher order dynamics for P, or to include nonlinear or nonautonomous effects (e.g., allowing for explicit parameter variation with time of day or year), but currently available data are insufficient to constrain a model of greater complexity.

The stochastic differential (Langevin) equation version of our mechanistic model is as follows:

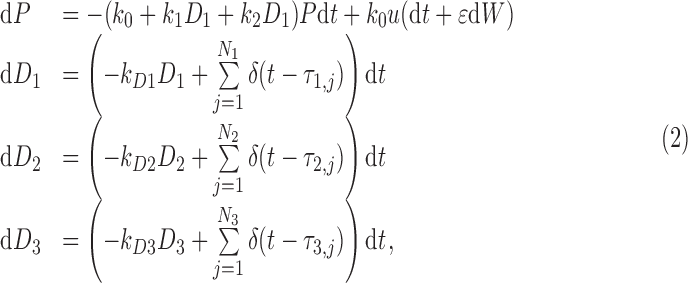where a hypothesis of uncorrelated additive white noise has been made. From this we derive the Fokker–Planck equation for the probability distribution of pain over time :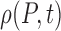

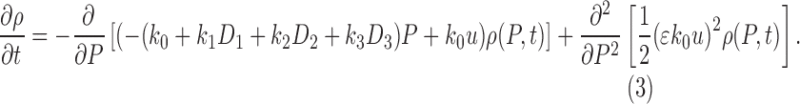Absent any pain medication, this Fokker–Planck equation implies the steady-state pain distribution

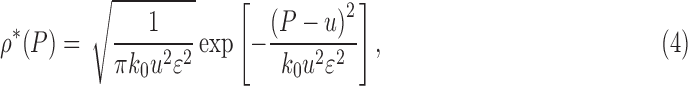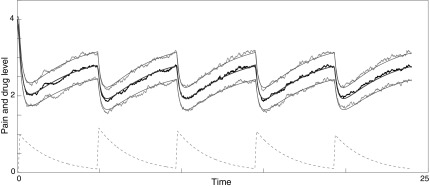
a Gaussian distribution with mean u and standard deviation 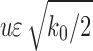. See Figure 4 for a sample stochastic model output.

FIG. 4.

Sample output from stochastic differential equation model (2). Middle smooth line: theoretical mean pain; upper and lower smooth lines: ±one theoretical standard deviation; middle noisy black line: mean of pain distribution in ensemble of 100 stochastic simulations; upper and lower noisy gray lines: ±one standard deviation in ensemble of 100 stochastic simulations; bottom dashed line: drug 1 dose in bloodstream. Spikes occur when patient takes recommended dosage.

2.2.2. Statistical component (for all patients)

To account for the variation among patients and improve prediction of the unmitigated pain level, we associate patient characteristics and history with the unmitigated pain level u (an n-dimensional vector with u_j corresponding to the j-th patient's unmitigated pain level) using a linear model. Let X be an 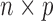design matrix containing the covariates of patients (i.e., patient characteristics). We write 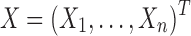, with X_j corresponding to the p-dimensional covariates of patient j. Then, we formulate the relationship between u and the p predictors as follows:

where 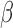is a p-dimensional coefficient vector, and 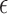is an n-dimensional vector of zero-mean random errors. When p is small, the estimate for 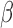is obtained using the ordinary least squares procedure: 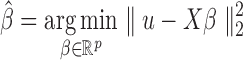, where 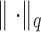denotes the 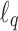norm. Then, the unmitigated pain level u_j is updated by , .

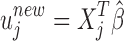Since the unmitigated pain levels are not observable from patient pain reports, the initial u_j's are independently sampled from a uniform distribution between 0 and 10, that is, 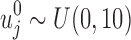. After using 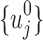as initial values to fit the mechanistic model, the resulting estimated 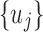will be updated by the linear model (5) as 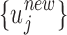, which will then be used as initial values in the next round of fitting of the mechanistic model. See Section 2.3 for more details on the hybridization of the statistical component with the mechanistic component.

Given a high-dimensional set of patient characteristics, we need to select a subset of patient characteristics that are significantly associated with u by minimizing the penalized loss function. In this study, we select patient characteristics using the Least Absolute Shrinkage and Selection Operator (LASSO) (Tibshirani, 1996), by minimizing the penalized loss function 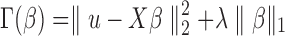with respect to 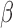. The penalty parameter 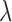is determined using a fivefold cross-validation. The selected p features are then used to fit the linear model (5) by ordinary least squares.

If time-varying unmitigated pain levels and time-varying covariates are present, the regression model (5) can be extended to the linear mixed model (Diggle, 2002; Fitzmaurice et al., 2012): 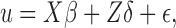where 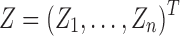is an 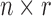design matrix for r random effect factors and 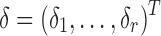is a vector of random effects. Patient characteristics can be selected by maximizing the penalized log likelihood: 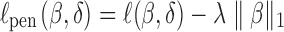(Groll and Tutz, 2014) where ℓ is the log likelihood function. Such an extension of the proposed hybrid model to allow for time-varying unmitigated pain levels and covariates will be considered in a future study with more data available.

2.3. Model fitting

We fit our model to real patient data by minimizing the residual sum of squares between model predictions and patient reports provided within the first two weeks of reporting. We expect that the assumption of constant model parameters breaks down after ∼2 weeks (clinical heuristics). Minimization over parameters u, k₁, k₂, and k₃ was done via the Nelder–Mead simplex algorithm (Nelder and Mead, 1965). Parameter k₀ was fixed at 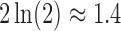corresponding to a pain equilibration half-life time scale of 30 minutes in the absence of medication. If a patient did not take all three classes of drugs, the model and fitting only included the consumed drugs.

We initialize the parameter optimization in n mechanistic models (one per patient) with random values during a first iteration, and then, we feed the optimization output into the statistical model (for all patients). Once the statistical model is run, it results in a new set of parameter estimates that can then be used as initial parameter seeds for a second round of optimization in n mechanistic models (to minimize the residual sum of squares). Proceeding iteratively in this manner (Fig. 3), we find convergence to a consistent set of parameters for each patient (details below).

2.4. Method verification

Before applying our hybrid model to real-world patient data, we verify the soundness of the approach with synthetic data constructed to resemble real-world data, but generated by the model itself with high sampling frequency. The synthetic data used for verification of the method are generated directly from the mechanistic model with an assumed parameter set generated in the following way: unmitigated pain 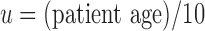, initial pain level 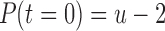, and drug parameters 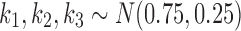. Each patient reports pain every 1/2 hour for 336 hours (2 weeks). At each report time, the probability of the patient taking a particular drug (among three drug classes) is 1/16; in other words, the patients took each drug on average every 8 hours. White noise of magnitude 1 is added to each pain report.

As an illustration using real patient drug times (specifically those of Patient A3), we create synthetic data generated using 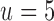, , 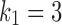and 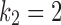(Fig. 5). When the initial parameter search is seeded with random parameter values, the mechanistic model fit can lead to convergence to either the “true” optimum 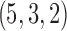or to other “spurious” optima with incorrect values of u, k₁, and k₂. In this illustrative example, the method converges to 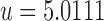, , 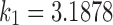and 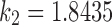. The relevant root-mean-square (RMS) error is 1.0133; this is close to the lowest possible expected error, given the unit magnitude noise added to the synthetic data. This numerical experiment shows that the mechanistic model fitting method can converge even in the presence of significant amounts of noise. However, with only the mechanistic model it can be quite difficult to find a good set of initial parameter seeds^*: that is one motivation for introducing the statistical model.

FIG. 5.

Model fitting demonstration for densely reported noisy synthetic data. Upper panel: hypothetical densely reported patient pain (circles) and model fit (solid line); shading indicates model fit ± one standard deviation. Lower panel: long-acting opioid (solid line) and short-acting opioid (dashed line) medication concentration in patient bloodstream.

To test our hybrid method using both the mechanistic model for fitting and the statistical model for parameter estimation, we create a synthetic patient database of 39 patients as described above. We then iterate rounds of fitting between mechanistic and statistical models, starting with uniform random guesses for all patient parameters . Figure 6 demonstrates how the parameter u converges to a value with small error after just a few iteration steps, even in the presence of significant noise. To evaluate the performance of the model on new data, we use the hold-out validation method by splitting the data set into a training set (first week) and a test set (second week). Model fit error and hold-out validation error, as well as other parameter values, converge similarly (Fig. 7).

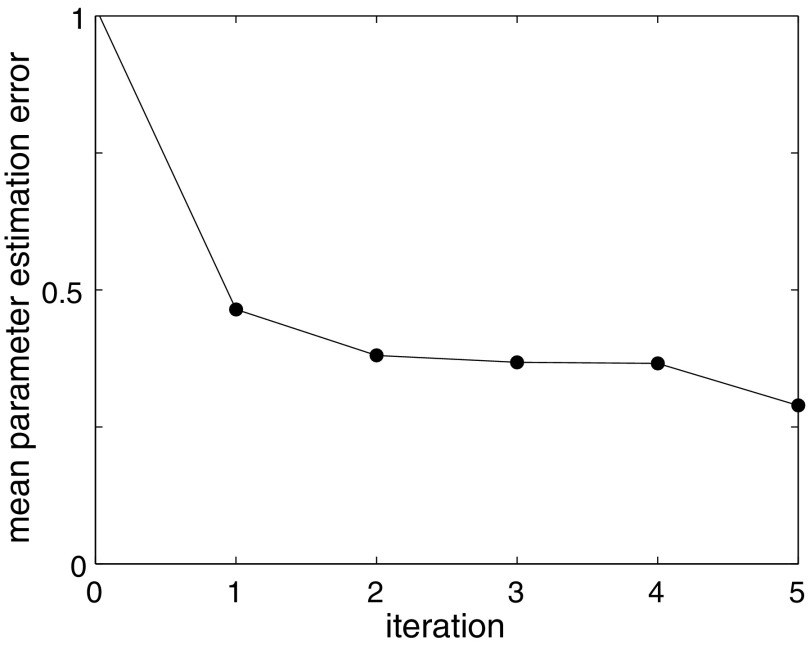
FIG. 6.

Hybrid model fitting demonstration for ensemble of densely reported noisy synthetic data. For an ensemble of 39 synthetic patient data sets, the average absolute error in u gradually decreases. Iteration 0 indicates one fit to the mechanistic model alone. Subsequent iterations indicate the number of hybrid model (statistical+mechanistic) fits.

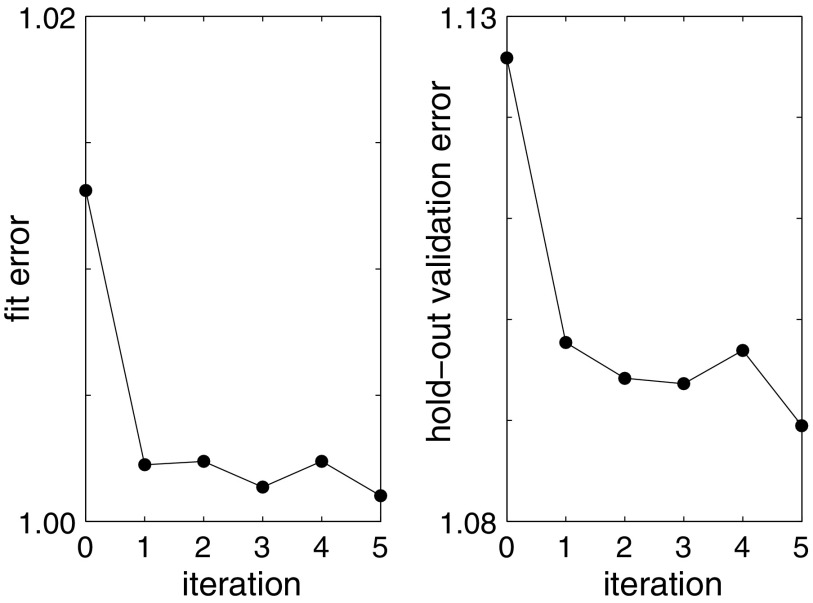
FIG. 7.

Hybrid model fitting demonstration for ensemble of densely reported noisy synthetic data. For an ensemble of 39 synthetic patient data sets, the average RMS error in patient pain levels gradually decreases. Iteration 0 indicates one fit to the mechanistic model alone. Subsequent iterations indicate the number of hybrid model (statistical+mechanistic) fits. Training error (or fit error) is on the left; test error (or validation error) is on the right. Due to the additive white noise of magnitude 1, the smallest testing or training error we could expect is 1. RMS, root-mean-square.

3. Results

3.1. General results

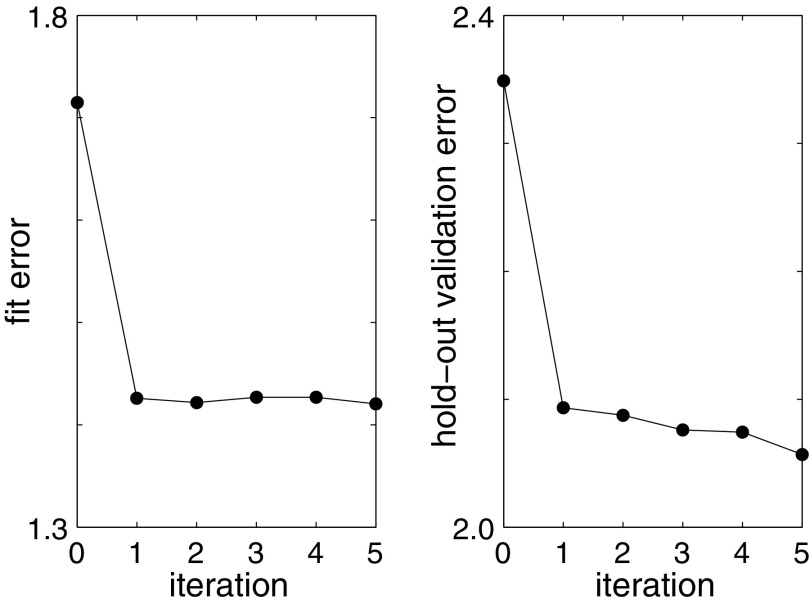
One key result is that our model for chronic pain does indeed have some predictive value (Fig. 8). This is an improvement over the current state-of-the-art, since no other predictive model exists of which we are aware. Furthermore, fitted parameter values correlate significantly with patient characteristics, suggesting that meaningful information is captured by this minimal plausible model. It may be possible to motivate new clinical insight on the basis of the observed correlations, perhaps leading to differential treatment of SCD sufferers with differing characteristics.

FIG. 8.

Hybrid model fitting on real patient data. For an ensemble of 39 real patient data sets, the average RMS error in patient pain levels gradually decreases. Iteration 0 indicates one fit to the mechanistic model alone. Subsequent iterations indicate the number of hybrid model (statistical+mechanistic) fits. Training error (or fit error) is on the left; test error (or validation error) is on the right.

3.2. Statistical results

We use the following baseline patient characteristics to predict the unmitigated pain levels in the statistical modeling step: age, gender, SCD type, hydroxyurea use, folic acid vitamin use, long-acting opioid use, short-acting opioid use, and nonopioid use. We explore the marginal effects of these characteristics and their possible pairwise two-way interactions using the LASSO. The model (5) can be extended to include time-varying covariates such as temperature, weather, patient's walking/social activities, and patient's mood at time t, once these data become available in a future study.

The statistical model that resulted from the LASSO variable selection is given by

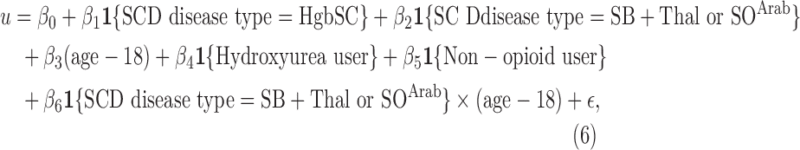where 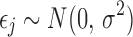, , 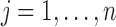and 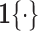is the indicator function.

Table 4 summarizes the results from one round of fitting of the regression model (6). Adjusting for the effect of other terms in the regression model, SCD type of SBThal or SO^Arab (with coefficient 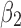), nonopioid use (with coefficient 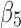), and the interaction term between SCD type of SBThal or SO^Arab and age (with coefficient 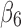) are important predictors of the unmitigated pain levels at the significant level of 0.05. Using nonopioid medication is associated with decreased unmitigated pain levels. Unmitigated pain levels increase with patients' age for SBThal or SO^Arab patients.

Table 4.

Result of the Prediction Model of Unmitigated Pain Using the Linear Regression Model

Variable	Estimate	Std Err	T	p
Intercept	7.646	1.228	6.228	0.000***
HgbSC	−1.566	0.890	−1.761	0.088
SB+Thal or SOArab	−5.479	2.332	−2.349	0.025*
Age at baseline−18	0.001	0.034	0.290	0.773
Hydroxyurea user	−1.205	0.839	−1.437	0.160
Nonopioid user	−2.523	0.842	−2.995	0.005**
SB+Thal or SOArab × (age at baseline −18)	0.241	0.010	2.419	0.021*

^*, ^**, and ^*** respectively denote levels .05, .01, and .001 of statistical significance.

4. Discussion and Limitations

4.1. Reflection on hybrid modeling

Statistical models and mechanistic models have both been successfully applied to various aspects of human behavior. The inference of “black box” statistical models from empirical data has the advantage that it obviates the need for a priori knowledge of system dynamics. However, mechanistic models (sometimes referred to as “white box” or “clear box”) can easily incorporate such knowledge when available.

Perhaps because of the often distinct educational background of practitioners or distinct typical applications, statistical and mechanistic approaches are not frequently combined in addressing a single problem. Compared with our work, the most similar hybrid modeling idea was developed by Sheiner and colleagues in the field of pharmacokinetics, where they proposed models to estimate population characteristics of pharmacokinetic parameters (Sheiner et al., 1977; Sheiner and Beal, 1980; Mandema et al., 1992). In their work, the pharmacokinetic models (i.e., mechanistic models) are well established, and the novelty and focus was the introduction of statistical models for pharmacokinetic parameter estimation. On the contrary, in our study, the mechanistic model is not known before but developed by us based on clinical knowledge and reasonable assumptions, and our focus is the prediction of pain levels rather than parameter estimation.

Other majority of attempts based on the hybrid modeling idea in the scientific literature have appeared in the context of neural networks (e.g., Psichogios and Ungar, 1992; Thompson and Kramer, 1994; Su et al., 2014) and chemical engineering (e.g., Schubert et al., 1994; Thompson and Kramer, 1994; Duarte and Saraiva, 2003), where they largely played a computational rather than analytical role. Some attempts have also been made with medical applications: Rosenberg et al. (2007) and Adams et al. (2007) developed a model by combining a dynamical systems approach with a statistical model to predict a patient's CD4 cell counts and HIV viral load over time in an HIV study. Timms et al. (2014) proposed a dynamical systems approach using ODEs to improve self-regulation in a smoking cessation study. Reinforcement learning techniques such as Q-learning (e.g., Jaimes et al., 2014) also share some commonalities with the hybrid approach.

In this work, we make our own attempt at a novel incorporation of statistical inference together with mechanistic dynamical systems modeling to produce a hybrid mathematical model for predicting and explaining human behavior. We apply the new approach specifically to the problem of predicting the dynamics of subjective pain in a population of individuals suffering from SCD. The rationale behind our method development is that we have prior knowledge of pain trajectories with medication, making the problem suitable for mechanistic modeling; meanwhile, we do not know the relationship between patient health characteristics and pain levels, so we would like to investigate this using a statistical model.

4.2. Limitations

The hybrid dynamical systems/statistical approach appear to have great potential. The low frequency of pain reporting currently limits its usefulness, but future addition of high-frequency pain correlates such as blood pressure, heart rate, and activity level via wearable medical devices (e.g., the “Fitbit”) may drastically improve on that. Furthermore, application of similar methods to more data-rich forecasting problems (e.g., insulin levels) may also expand the utility of our work.

Another important limitation to our current model lies in the mechanistic component. We presented here what we considered to be the simplest plausible model: pain fluctuates about an “unmitigated” equilibrium u, and medication reduces pain below that level, but pain returns as medication is metabolized and removed from the bloodstream. This simple model cannot capture long-term changes in the unmitigated pain level, and hence, its forecast validity is likely limited to short time scales (days to weeks).

Perhaps the most significant limitation lies in a potentially unmodeled bias in our data set. Patients typically reported pain levels when taking medication, but many of them only take medication when pain levels rise. Thus, there may be a selection bias of unknown significance, causing higher pain levels to be reported at a disproportionately high rate. This could be alleviated in future data collection efforts if pain estimates were based on automatically reported correlates or if patients' pain reports were requested at random times distinct from medication times.

Society is clearly moving in the direction of an overwhelming amount of medical data. It is imperative that we learn to take advantage of this information to improve patient treatments beyond the traditional standard of care. The approach we report here not only addresses the specific challenge of chronic pain mitigation in SCD patients but also provides a test bed for new ways of dealing with big, ever-growing data sets in real time.

5. Conclusions

A key goal of the modeling of human pain dynamics is to develop predictions that allow optimized treatment: both pain and medication use should be minimized. Excess medication carries particular long-term risks for chronic pain sufferers (Bannwarth, 1999; Savage, 1999; Brookoff, 2000; Gatchel, 2001), but pain mitigation is also a primary goal of SCD treatment. How can these contradictory objectives be balanced?

Our model allows us to forecast the probability distribution of pain for a patient at a point in the near future, given past data. We believe that this information will be useful to a physician, allowing him or her to make an optimized, data-driven decision balancing medication and pain for the patient. Real-time implementation of such a scheme remains the subject of ongoing work.

We have successfully demonstrated the hybrid application of statistical and mechanistic mathematical modeling with application to understanding the dynamics of subjective human pain. Our model explains real-world data on human pain and can generate predictions of future pain dynamics.

We expect that similar methods could be used to incorporate disease-specific knowledge and modeling with statistical inference in a variety of medical applications. Given the coming deluge of data from wearables (including clinical trial NCT02895841 already underway) and mobile health applications, there is a clear need for new mathematical methods to take advantage of the opportunity for personalizable, data-driven medical treatments.

Acknowledgment

The authors gratefully acknowledge NSF support through grants No. DMS-1557727 and No. DGE-1324585.

Author Disclosure Statement

No competing financial interests exist.