In vivo imaging of dentate gyrus mossy cells in behaving mice

Summary

Mossy cells in the hilus of the dentate gyrus constitute a major excitatory principal cell type in the mammalian hippocampus, however, it remains unknown how these cells behave in vivo. Here, we have used two-photon Ca²⁺ imaging to monitor the activity of mossy cells in awake, behaving mice. We find that mossy cells are significantly more active than dentate granule cells in vivo, exhibit spatial tuning during head-fixed spatial navigation, and undergo robust remapping of their spatial representations in response to contextual manipulation. Our results provide the first characterization of mossy cells in the behaving animal and demonstrate their active participation in spatial coding and contextual representation.

Graphical abstract

Danielson et al. monitored the activity of hippocampal mossy cells in vivo. They show that as a population, mossy cells are an active place coding population engaged in contextual encoding.

Introduction

The mammalian hippocampus supports spatial information processing and episodic memory by routing information through its canonical trisynaptic circuit: from the dentate gyrus (DG) input node, to area CA3, and finally to the CA1 output node, with each subfield carrying out specialized computational operations (Eichenbaum, 2000; Knierim and Neunuebel, 2016; Treves and Rolls, 1994). In particular, the DG has been widely implicated in pattern separation, a computational process of segregating and storing similar events in a non-overlapping fashion. This decorrelation function of the DG is commonly attributed to granule cells (GCs) (Knierim and Neunuebel, 2016; Treves and Rolls, 1994) – the most numerous principal excitatory cell type in the hippocampus. The polymorphic hilar region of the DG, however, also contains another major glutamatergic principal cell type: mossy cells (MCs) (Amaral, 1978; Scharfman, 2016), which receive their major excitatory input from a small number of GCs via massive synaptic boutons onto large spine complexes along their proximal dendrites (Amaral, 1978; Frotscher et al., 1991; Ribak et al., 1985). MCs provide widespread feedback monosynaptic excitatory and disynaptic inhibitory inputs to GCs (Scharfman, 1995, 2016), and therefore may play an important role in pattern separation (Jinde et al., 2012; Scharfman, 2016). However, at present there are no in vivo data available on the firing patterns of MCs in behaving animals, and thus physiological support for this hypothesized role of MCs in behavioral pattern separation is lacking. Two-photon (2p) Ca²⁺ imaging has recently become available for optical recordings of the DG in vivo, including its hilar region, during head-fixed behaviors in mice (Danielson et al., 2016a). In this study we therefore employed this approach to monitor Ca²⁺ activity in MCs, providing the first functional characterization of this enigmatic cell type during spatial navigation and behavior.

Results

In vivo imaging of identified mossy cells

We first sought to selectively label MCs with the genetically-encoded Ca²⁺ indicator GCaMP6f by taking advantage of two characteristic anatomical features: MCs are immunoreactive for glutamate receptor type 2 or 3 (GluR2/3) (Ratzliff et al., 2004); and MCs comprise the predominant hilar cell population projecting to the contralateral DG (Frotscher et al., 1991; Ribak et al., 1985) (Fig. 1). Therefore, we used a retrograde variant of recombinant adeno associated virus (rAAV2-retro) (Tervo et al., 2016) expressing Cre-recombinase injected into the contralateral DG, in combination with a Cre-dependent rAAV expressing GCaMP6f injected ipsilaterally into the hilar imaging site, to label contralaterally-projecting hilar neurons (Fig. 1A-B). This strategy labeled hilar but not CA3 neurons (Fig 1B), and in agreement with previous reports (Ratzliff et al., 2004), the vast majority of the retrogradely-labeled hilar neurons were immunopositive for GluR2/3; we therefore identified them as GluR2/3+, contralaterally projecting MCs (Fig. 1B, identified MCs hereinafter denoted as iMCs).

Figure 1. Optical imaging of identified mossy cells.

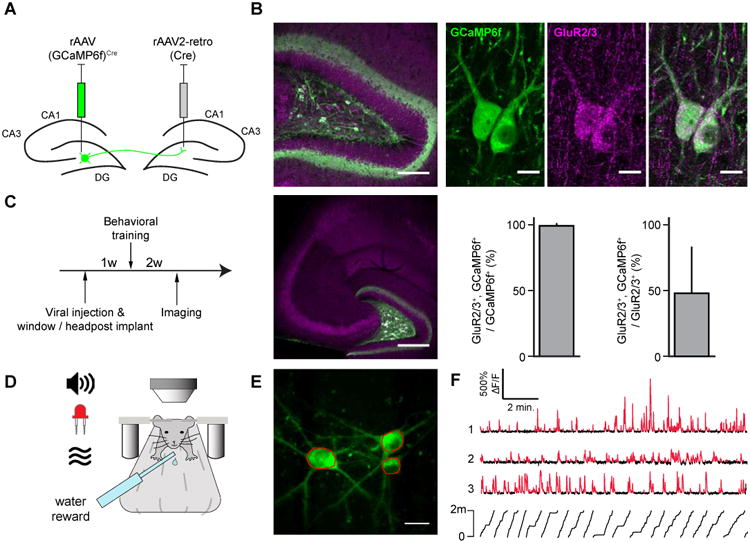
(A) Viral labeling strategy for mossy cells.

(B) (top) Confocal image of a horizontal section through the hilus of the dorsal DG. GCaMP6f-expressing and GluR2/3-expressing cells are labeled green, and magenta, respectively. The area indicated is shown at high resolution at right. (bottom, left) Low magnification image through the hilus shows the lack of CA3 pyramidal cell labeling. (bottom, right) Nearly all GCaMP6f+ cells were also GluR2/3+ (99.2%±0.2%, mean±std., n=11 slices from 3 mice), and approximately half of MCs were labeled with GCaMP6f (48%±35%, mean±std., n=11 slices from 3 mice).

(C) Experimental timeline.

(D) Schematic of the experimental apparatus. Head-fixed mice explored multisensory contexts comprised of the treadmill belt and other sensory stimuli (light, odor, sound).

(E) Max Z-projection image of a volume acquired in vivo of 3 GCaMP6f-expressing MCs. Example regions of interest in red.

(F) ΔF/F traces of three simultaneously recorded MCs. Significant transients in red (p<0.05).The mouse's position on the treadmill is indicated below.

Following viral injection, mice were implanted with a chronic imaging window above the dorsal DG to provide the optical access necessary for visualizing the hilus (Fig. 1C). To record Ca²⁺ activity from iMCs, we performed head-fixed 2p imaging as the animals (n=6) performed a random foraging task by running for water rewards on a treadmill across 3 sessions in different linear environments (Fig 1D-F; see STAR Methods, (Danielson et al., 2016a-b). In total we recorded from 57 iMCs in 6 animals (n=10±4 cells per mouse, mean±std.). Correction of motion artifacts was performed using a 2D Hidden Markov Model (Dombeck et al., 2007) implemented in the SIMA package (Kaifosh et al., 2014). Regions of interest (ROIs) were drawn over MC somata, and registration of ROIs across imaging sessions was performed using the ROI Buddy GUI. Signals were extracted from the resulting binary masks, and significant Ca²⁺ transients were identified as described in the STAR Methods.

Mossy cells are more active than GCs in vivo

We first quantified the activity of iMCs during head-fixed navigation by measuring the rate of area under significant Ca²⁺ transients (AUC rate, Fig. 2). In each session, nearly every cell fired at least one transient (and most fired many more), resulting in a high non-silent fraction (Fig 2B) across both recordings and behavioral states (running and non-running). Within this active population, the frequency of transients across all frames was 1.6±1.2 transients/min., (mean±std., n=57 cells) and of large amplitude (79%±46% ΔF/F, mean±std., n=57 cells; Fig S2), resulting in a high AUC rate within the non-silent population (Fig 2C). This finding was in stark contrast to the activity levels we previously reported for GCs in our recent study (identical behavioral paradigm, Danielson et al., 2016a), and we therefore directly compared the activity of iMCs and GCs (pooling our adult-born and mature recordings). GCs fired transients at a very low frequency (0.08±0.14 transients/min, mean±std., n=8,396 cells), and iMCs were thus considerably more active than GCs (Fig. 2B-C). To estimate activity in both populations in a manner independent of our transient detection procedure, we also estimated the spike trains underlying the fluorescence signals (Deneux et al., 2016). This analysis further supported a highly significant difference in spiking activity between iMCs and GCs (Fig S1). In summary, iMCs are more active than GCs at both the population and single-cell levels.

Figure 2. Mossy cells are more active than GCs in vivo.

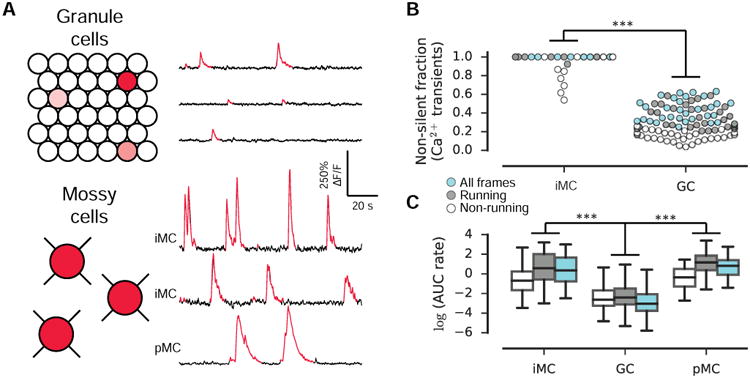
(A) Schematic of GC and MC activity. Only a small fraction of GCs are active (red shading) relative to MCs, and active MCs exhibit a significantly higher rate of Ca²⁺ activity than active GCs. (right) Ca²⁺ traces from 3 example active GCs (top) and 3 example MCs. Significant Ca²⁺ transients (p<0.05) are red.

(B) Activity was assessed by the rate of area under significant transients. The fraction of cells exhibiting non-zero activity is shown. Each circle represents a single recording session (with a minimum of 3 recorded cells) and is colored by the frames included in the analysis (non-running, running, and all frames). iMCs were significantly more active than GCs (F_{(1, 144)}=1,510, p<0.001, two-way ANOVA). pMCs were not included in this analysis.

(C) The activity of non-silent cells within each condition (non-running, running, all) is shown. Non-silent iMCs were significantly more active than non-silent GCs (F_{(1, 12,588)}=740, p<0.001, two-way ANOVA). Similarly, the activity of pMCs was significantly higher than GCs (F_{(1, 12,453)} = 345, p < 0.001, two-way ANOVA).

Because our GC and iMC recordings were acquired in different animals, we attempted to control for any possible differences between preparations by retrospectively analyzing our previous DG imaging dataset (Danielson et al., 2016a) to look for the presence of putative MCs (pMCs) in our imaging dataset. The high spatial resolution of 2p imaging allows for the unambiguous separation of GCs from hilar cells based on their location and distinct morphology. In our previous imaging study, GCaMP6f imaging was performed with broad labeling of all neuron types in the DG. In four of our fields-of-views, (n=4 animals), we could identify large, multipolar cells in the hilus (Figure S1 in Danielson et al., 2016a), and were therefore excluded from the original GC imaging dataset. In a subset of these hilar cells (n=11 out of 20) we were able to detect large amplitude transients with fast onset and exponential decay similar to the pattern observed in iMCs (Fig. 2A, bottom). When we directly compared the activity rates between these simultaneously recorded hilar pMCs and non-silent GCs, we again found a highly significant difference in activity between these populations (Fig. 2B-C).

Mossy cells exhibit more diffuse spatial tuning profiles compared to granule cells

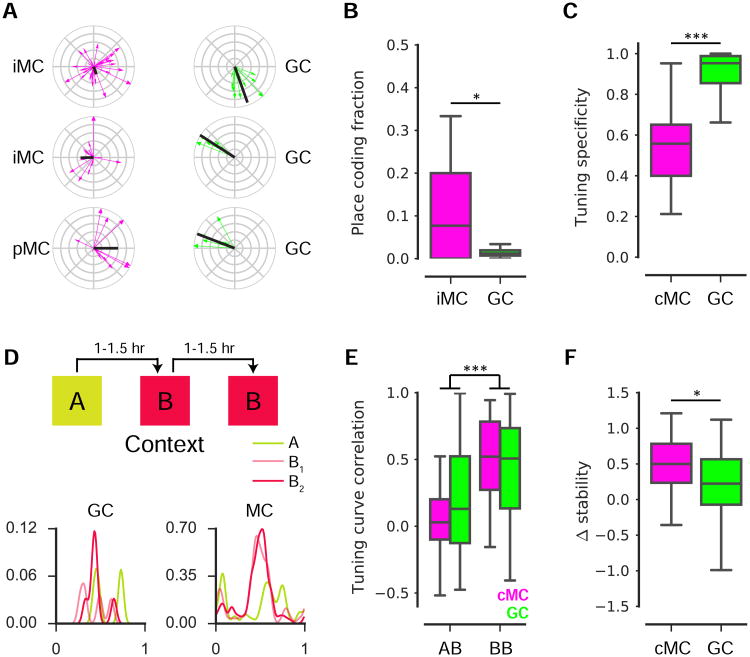
Because principal cells throughout the hippocampus are known to exhibit spatially selective, ‘place cell’ firing (Hartley et al., 2014), we next sought to determine whether this feature extends to MCs. Thus, for each MC we calculated a spatial firing rate map and identified those cells whose distribution of Ca²⁺ transients contained statistically significant spatial information (Skaggs et al., 1993); see STAR Methods, Fig 3A). In contrast to the very low place cell fraction among GCs (1.4±1.0%, mean±std., n=32 recording sessions), we found a significant spatial coding population among MCs: 16%±20% (mean±std., n=18 recording sessions, Fig 3B) of our iMCs were classified as spatially-tuned.

Figure 3. Spatial coding features of mossy cells.

(A) Spatial tuning plots for 3 example GCs and MCs identified as spatially-tuned. Each running-related transient is represented as a vector (direction, position at onset; magnitude, inverse of occupancy), and the complex sum of these vectors forms the tuning vector (black).

(B) The fraction of cells identified as spatially-tuned (≥4 Ca²⁺ transients, spatial information p-value < 0.05) within GC and iMC recording sessions. A higher fraction of MCs were spatially-tuned than of GCs across recording sessions (U₍₄₈₎=183, p=0.017, Mann Whitney U).

(C) Among cells identified as spatially-tuned, cMCs exhibited a significantly lower tuning specificity than GCs (U₍₂₈₂₎=836, p<0.001, Mann Whitney U).

(D) (top) Experimental schematic. Mice ran on a treadmill for randomly administered water rewards during three 12 min sessions in multisensory contexts ‘A’ and ‘B’. Contexts differed in auditory, visual, olfactory, and tactile cues, and sessions were separated by 60–90 min. (bottom) Spatial tuning curves are shown for an example GC and MC.

(E) The 1D correlation in spatial rate maps for GCs and cMCs were correlated in the ‘A-B’ and‘B-B’ conditions. For a cell to be included, it was required to be active and spatially-tuned in at least one of the two sessions being compared. Both populations exhibited a higher correlationin ‘B-B’ than ‘A-B’ (F_{(1, 355)}=40.3, p<0.001, two-way ANOVA).

(F) To calculate the Δstability, we examined the subset of cells satisfying the inclusion criterion for both conditions. The Δstability was significantly higher for cMCs than GCs (U₍₈₈₎=211, p=0.016, Mann Whitney U).

Previous extracellular electrophysiological recordings suggested that GCs (Leutgeb et al., 2007), perhaps with preference toward adult-born GCs located closer to the hilar border (Neunuebel and Knierim, 2012), exhibit multiple firing fields. While the sparse activity in our imaging dataset precluded precise quantification of the number of place fields, we attempted to address this question by comparing the tuning specificity (Danielson et al., 2016a-b) between the subpopulations of spatially-tuned GCs and combined MCs (cMCs), in which we pooled the spatially-tuned iMCs and pMCs to increase our statistical power. Finding both significant spatial information and low tuning specificity would indicate the presence of multiple firing fields. We found that the tuning specificity for spatially-tuned cMCs was significantly lower than for spatially-tuned GCs (Fig 3C). To guard against any biases resulting from our selection criteria, we expanded the analysis to include all cells firing at least four transients, and again we found that MCs exhibited a lower tuning specificity than GCs (data not shown, n=1,203 active GC recordings, n=195 active cMC recordings, p<0.001). These results indicate that although MCs are more likely to exhibit spatially-tuned firing than GCs, MCs exhibit more distributed spatial firing patterns than GCs.

Mossy cells robustly discriminate contexts

GCs in the hippocampus are thought to implement a “pattern separation” computation by remapping their firing fields in response to a contextual manipulation (Knierim and Neunuebel, 2016; Leutgeb et al., 2007). We asked whether this feature is unique to GCs or whether we could find evidence for pattern separation within MCs as well. To this end, we compared the similarity of single cell spatial tuning profiles between two sequential exposures to either different (‘A-B’, sessions 1 and 2) or identical (‘B-B’, sessions 2 and 3) multisensory contexts (Fig. 3D). To quantify remapping in each of the two conditions (‘A-B’ and ‘B-B’), we required that the cell be spatially tuned in at least one of the two sessions being compared. This was the same paradigm used in Danielson et al., 2016a, and therefore we could directly compare the remapping of cMCs with that of GCs.

For both cMCs and GCs, we found that place maps were more stable in the ‘B-B’ than in the ‘A-B’ conditions, as assessed by the tuning curve correlation (Fig. 3E). By looking at the subset of cells included in both comparisons, we calculated Δstability as the difference in stability between the ‘B-B’ and ‘A-B’ conditions (Fig. 3F). We found that cMCs had a significantly higher Δstability than GCs. These data indicate that MCs robustly discriminate contexts on the basis of their spatial tuning profiles.

Local dentate network model: MCs contribute to sparseness in GC coding

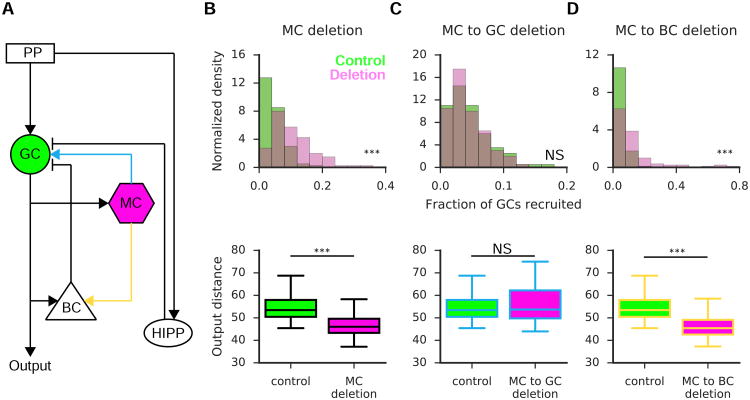
The efficacy of pattern separation is thought to depend on the sparseness of the GC representation (Alme et al., 2010; Treves and Rolls, 1994). To investigate whether and how MCs might shape the sparseness, and thus pattern separation efficacy, of GCs, we developed a simple, yet biologically relevant, computational model of the DG (Fig 4A) as per Chavlis et al. (2016) albeit with GCs modeled as point neurons. The model was calibrated to reflect an approximate control sparseness of ∼5% (Fig 4B-D top, green), reflecting the fraction of GCs we found to reliably code for an environment by regularly firing transients. We then simulated the effect on GC sparseness resulting from the deletion of MCs (Fig 4B). Deletion of MCs resulted in the recruitment of significantly more GCs in response to simulated entorhinal input (Fig 4B top, purple), and this in turn led to a reduction in the pattern separation efficacy of GCs (Fig 4B bottom), as measured by the distance between GC populations responding to two overlapping input patterns (see STAR Methods). To investigate whether this effect was primarily mediated through the direct excitatory or indirect inhibitory pathways between MCs and GCs, we deleted each of these connections individually. While deletion of the direct excitatory connection had little effect on GC excitability and pattern separation (Fig 4C), we found that deletion of the MC-basket cell connection significantly increased GC excitability at the expense of pattern separation performance (Fig 4D).

Figure 4. The role of mossy cells in pattern separation: a computational approach.

(A) Schematic of the DG computational model. Granule cells (GC, green) receive excitatory input from the perforant path (PP) and mossy cells (MC) in addition to feed-forward inhibition from hilar perforant path-associated (HIPP) cells and feedback inhibition from basket cells (BC). MCs also provide excitation to BCs.

(B-D, top): the fraction of recruited GCs in response to PP input. Green denotes the model under control conditions, while purple reflects the fraction of active GCs under various deletion conditions: complete MC deletion (B), deletion of the direct excitatory (C) or deletion of the disynaptic inhibition (D). Deletion of MCs (B) increased the fraction of GCs recruited (KS Stat=0.49, n=100 control, 100 deletion simulations, p<0.001, 2-sample KS Test). This effect was mediated by disynaptic inhibition (D; KS Stat=0.45, n=100 control, 100 deletion simulations, p<0.001, 2-sample KS Test). (bottom): pattern separation efficiency is measured as the output distance between the GC populations responding to two highly overlapping PP inputs for the three aforementioned cases. MC deletion (B) results in a reduction in pattern separation efficiency (U₍₉₈₎=395, p<0.001, Mann Whitney U), and this effect again was mediated by the disynaptic inhibitory pathway (D; U₍₉₈₎=349, p<0.001, Mann Whitney U).

Discussion

In summary, we performed cellular-resolution 2p Ca²⁺ imaging of MCs during head-fixed navigation in addition to computational modeling of the local DG network. We characterized the in vivo activity levels, spatial coding fractions, context specificity, and remapping dynamics of MCs, and we identified prominent differences in these properties between MCs and GCs. We found that MCs were more active and more likely to have detected place fields than GCs, and therefore, MCs represent an active population of spatially-tuned hippocampal principal neurons during behavior. In addition to exhibiting a higher place coding fraction, our results also suggest that these cells are more likely to exhibit multiple firing fields than GCs. While we cannot exclude the possibility that in vivo GCaMP Ca²⁺ imaging is biased toward the detection of burst events over single spikes in GCs, burst spiking is thought to be the most efficient mode of transmission from granule cells to their downstream targets (Bischofberger et al., 2006; Henze et al., 2002), and our most active GCs fired transients at a rate of 1-2/min., comparable to the burst rate reported in a previous in vivo intracellular recording study of GCs (Pernia-Andrade and Jonas, 2014). Moreover, although we cannot completely exclude the possibility that differences in intracellular Ca²⁺ buffering contributed to the observed differences in activity between GCs and MCs, the highly significant differences in activity, as reflected by both the transient AUC rate and the frequency of sharply peaked transients, suggest that differences in Ca²⁺ buffer protein expression are unlikely to fully explain our results.

Because the primary excitatory inputs onto MCs originate from large, ‘detonator’ mossy terminal synapses from the mossy fibers of GCs (Amaral, 1978; Henze et al., 2002; Scharfman, 2016), it is possible that the spatially-tuned firing pattern of MCs we observed is conveyed to MCs by GCs. However, given both the very sparse firing of GCs (Danielson et al., 2016a) and the low convergence of GCs to MCs (Amaral, 1978; Frotscher et al., 1991; Ribak et al., 1985; Scharfman, 2016), our results suggest that GC activity alone is unlikely to fully account for the high activity level and distributed spatially-tuning of MCs we observed. Relatedly, it is possible that MCs are preferentially innervated by young adult-born GCs, which exhibit higher activity and more diffuse firing compared to their mature counterparts (Danielson et al., 2016a). Excitation from entorhinal inputs (Scharfman, 1991), backprojecting CA3 pyramidal cells (Ishizuka et al., 1990), or various subcortical neuromodulatory inputs (Scharfman, 2016) might also contribute to the activity and tuning profiles of MCs. We also found that MCs exhibit strong remapping of their firing fields during random foraging in distinct contexts, suggesting that MCs may contribute to pattern separation on the behavioral level. Our computational model also suggests MCs contribute to the sparseness of GC representations and may thus support pattern separation in this manner as well. Furthermore we found that this effect is primarily mediated through disynaptic inhibition, in agreement with previously published experimental data (Jinde et al., 2012; Scharfman, 1995, 2016). Indeed, an active role for MCs in pattern separation and a disinhibitory influence of MCs on GCs are supported by previous experiments in which MC loss caused transient GC hyperexcitability and impaired contextual fear learning (Jinde et al., 2012). The enhanced remapping of firing fields in MCs compared to GCs we observed also suggests that context-specific inputs by sources other than GCs are conveyed to MCs. Taken together, our results support a view of hippocampal DG function in which pattern separation is implemented by the joint action of both MCs and GCs. Future in vivo studies combining recording with cell-type specific manipulations will help to delineate the precise mechanisms by which granule cells, mossy cells and other excitatory and inhibitory cell types of the dentate gyrus (Hosp et al., 2014; Williams et al., 2007) interact to support hippocampal-dependent behaviors.

Here we describe in brief the procedures pertaining to experiments with retrogradely-labeled MCs. Experimental procedures for simultaneous imaging of putative MCs and GCs are described in (Danielson et al., 2016a). All experiments were conducted in accordance with the US National Institutes of Health guidelines and with the approval of the Columbia University Institute Institutional Animal Care and Use Committees.

Contact For Reagent and Resource Sharing

Attila Losonczy (al2856@cumc.columbia.edu)

Experimental Model and Subject Details

Six 4-month-old wild-type male and female C57Bl6 mice were used for mossy cell imaging experiments. Mice were kept in the vivarium on a reversed 12-h light/dark cycle and were housed 3-5 mice in each cage. Experiments were performed during the dark portion of the cycle.

Method Details

Stereotactic viral injection and imaging window implant

For experiments with retrogradely-labelled mossy cells, a retrograde variant of recombinant adeno associated virus (rAAV2-retro, Tervo et al., 2016; gift from Dr. A. Karpova, Janelia Research Campus), expressing Cre-recombinase (rAAV2-retro.CAG.Cre.WPRE.SV40) with titer of 4×10¹² was stereotactically injected into the right dorsal dentate gyrus using a Nanoject syringe with injection coordinates -2.1, -2.3, -2.5 mm AP, -1.5 ML, and -1.7 DV; 60 nL of virus was injected per location in 20 nL increments. We also stereotactically injected Cre-dependent rAAV carrying the GCaMP6f with titer of 2-4×10¹² (rAAV1.Syn.Flex.GCaMP6f.WPRE.SV40, Penn Vector Core) into the left dorsal dentate gyrus with the same injection coordinates and 80 nL of virus per DV location in 20 nL increments.

Mice were surgically implanted with an imaging window over the left dorsal dentate gyrus and implanted with a stainless-steel headpost for head fixation during imaging experiments. Imaging cannulas were constructed by adhering (Norland optical adhesive) a 1.5 mm glass coverslip (Tower Optical Corporation) to a cylindrical steel cannula (1.5-mm diameter × 2.3-mm height). We used a headpost in which the posterior bar was thinned to accommodate the full 3.5mm working distance of the objective. The imaging window was implanted 100-200 μm above the hippocampal fissure, providing optical access to the dorsal blade of the DG and the hilus below. Following induction of anesthesia (Isoflurane: 3% induction, 1.5 - 2.0% maintenance; 1.0 L/min O₂) and administration of analgesia (buprenorphine 0.05-0.1mg/kg), the scalp was removed, and a 1.5 mm diameter craniotomy was performed with a fine-tipped dental drill (V00033, Henry-Schein). The dura and the underlying cortex were aspirated to reveal the capsular fibers. Following this, a 30g blunt syringe (B30-50, SAI) was used to gently aspirate CA1 directly superior to the dentate until the loose fibers and vasculature of stratum moleculare were visible. Bleeding was controlled with a collagen gel sponge (A00063, Avitene) and continuous irrigation with sterile aCSF. We then gently fit the cannula into the craniotomy and affixed the headpost to the skull using dental cement (675572, Dentsply). Mice were active within 15 minutes of surgery, and analgesia was continued for three days post-operatively.

Histology and Immunohistochemistry

Following the last imaging session, mice were deeply anaesthetized with isoflurane and transcardially perfused with 4% paraformaldehyde solution (in 0.1 mM PBS). The brains were removed from the skull, left in the fixative for overnight post-fixation, and sliced with a vibratome in horizontal or coronal planes. The slices were incubated for two days in a cocktail of the following primary antibodies: 1:1000 dilution of chicken anti-GFP (Abcam, ab6556) and 1:100 dilution of rabbit anti-GluR2/3 antibody (EMD Millipore, AB1506). Following several washes in PBS, the slices were incubated for two days in the secondary antibody cocktail: alexa488 conjugated anti-chicken IgY and Dylight649 conjugated anti-rabbit IgG (Jackson Immunoresearch Laboratories;1:250 dilution) and mounted on microscope slides. Two channel confocal image stacks were captured with a Leica SP5 microscope (Leica Microsystems) with the suitable excitation and emission filter sets. The single and double labeled cells in the hilus were quantified by two investigators independently.

In vivo 2-photon imaging

We used the same imaging system as described previously (Kaifosh et al., 2013; Lovett-Barron et al., 2014) with an 8kHz resonant galvanometer (Bruker). Approximately 150-250 mW of laser power was used during imaging (measured under the objective), with adjustments in power levels to accommodate varying window clarity. To optimize light transmission, we adjusted the angle of the mouse's head using two goniometers (Edmund Optics, ±10 degree range) such that the imaging window was parallel to the objective. All images were acquired with a Nikon 40× NIR water-immersion objective (0.8 NA, 3.5 mm WD). Green (GCaMP6f) fluorescence was acquired using an emission cube set (green, HQ525/70m-2p; red, HQ607/45m-2p; 575dcxr, Chroma Technology) taking images (512 × 512 pixels) at ∼30 Hz covering 160 μm × 160 μm area. The emitted photons were captured with a photomultiplier tube (GaAsP PMT, Hamamatsu Model 7422P-40), and a dual stage preamp (1.4 × 10⁵ dB, Bruker) was used to amplify signals prior to digitization.

Training

Mice were water-restricted (>90% pre-deprivation weight) and trained to run on a cue-deplete burlap treadmill belt for water rewards over the course of 1-2 weeks. We applied a progressively restrictive water reward schedule, with mice initially receiving 20-25 randomly placed rewards per lap and ultimately receiving 3 randomly placed rewards per lap. Mice were trained for 20 minutes daily until they regularly ran at least one lap per minute. Mice were also habituated to the optical instrumentation (presence of objective, laser, shutter sounds) prior to imaging experiments.

Contexts

As in our previous work (Danielson et al., 2016a-b; Kaifosh et al., 2013), each context (A and B) consisted of the same treadmill belt (the same sequence of 3 joined fabric ribbons), but distinct in their visual, auditory, tactile, and olfactory stimuli. During imaging sessions, mice received three randomly placed water rewards per lap, with reward positions changing randomly each lap. To allow for comparison of activity between similar contexts, the same three fabrics were used in the same order, but the locations of all of the tactile cues were shuffled around between the two belts.

Stimulus presentation and behavioral readout

Visual, auditory, and olfactory stimuli were presented and behavioral data were recorded as described previously (Danielson et al., 2016a-b; Kaifosh et al., 2013; Lovett-Barron et al., 2014). In order to reliably track the position of the treadmill belt, we established registration anchors at known positions along the belts and interpolated between them using a quadrature encoded movement signal tied to the rotation of the treadmill wheels. Registration anchors were marked by radio-frequency identification (RFID) buttons (16mm, 125kHz, SparkFun Electronics) at evenly spaced positions along the belt, and were read off as they passed over a fixed RFID reader (ID-12LA, SparkFun). The rotational quadrature signal was produced by marking treadmill wheels with offset tick marks, and this signal was encoded by a pair of photodiodes (SEN-0024, SparkFun) aligned to the wheels (<0.5cm resolution).

Calcium data processing

All imaging data were analyzed using the SIMA software package (Kaifosh et al., 2014). Motion correction was performed using a 2D Hidden Markov Model (Dombeck et al., 2010; Kaifosh et al., 2013), with modifications to accommodate the specific features of data acquired with resonant galvanometers. In cases where motion artifacts were not adequately corrected, the affected data was discarded from further analysis. We used the SIMA project's ROI Buddy graphical user interface (Kaifosh et al., 2014) to draw regions of interest (ROIs) over MC somata visible in the time-averaged image of the motion-corrected green/GCaMP6f channel. We also used this software to determine the correspondence of ROIs across datasets from different trials in which the same FOV was imaged.

Dynamic GCaMP6f fluorescence signals were extracted from ROIs using SIMA (Kaifosh et al., 2014) then converted to relative fluorescence changes (ΔF/F) as described in Jia et al. (2011), with uniform smoothing window t₁ = 3 sec and baseline size t₂ = 60 sec. After performing Ca²⁺ transient detection (see below), we recomputed the baseline excluding detected transients, after which we recomputed ΔF/F. This iterative procedure was repeated three times and effectively removed the transient contamination from the calculated baseline.

Calcium transient detection

In order to identify significant Ca²⁺ transients, we implemented an approach first described by Dombeck et al. (2007). This technique has been used in a number of subsequent hippocampal in vivo Ca²⁺ imaging publications from both our lab (Danielson et al., 2016a-b; Lovett-Barron et al., 2014) and others (Dombeck et al., 2010; Rajasethupathy et al., 2015; Sheffield and Dombeck, 2015). There are two primary assumptions underlying this algorithm: 1. All negative deflections in the ΔF/F trace are attributable to motion out of the focal plane; 2. Motion-induced deflections in the ΔF/F trace occur with equal likelihood in the positive and negative directions.

Combining these assumptions, for each positive deflection of the ΔF/F trace, we can estimate the probability that the observed event was motion-induced rather than activity-related by calculating the ratio of negative- to positive-going events. Because the signal-to-noise ratio can vary across cells, ΔF/F is expressed in units of σ (the standard deviation of the baseline fluorescence). Event onsets are defined as the frame at which fluorescence exceeds 2σ, and offset is defined as the frame at which it falls below 0.5σ. For an event of a given magnitude, this technique thus allows us to determine the minimum duration necessary to claim with confidence that the event was not attributable to motion. Put another way, this technique allows us to determine a duration threshold beyond which we can reject the null hypothesis that the deflection was not attributable to neuronal activity. In contrast to simple threshold-based techniques, this approach has the important advantage of being able to assign a statistical confidence level to each event.

One minor difference between our implementation of the algorithm and that described in Dombeck et al., (2007) concerns the definition of σ. Dombeck et al. “…manually selected regions of the fluorescence time series that did not contain large transients.” In order automate this procedure, which was necessary given the large number of recordings we obtained (> 20,000), we performed an iterative process in which σ was initially estimated as the standard deviation of the entire ΔF/F trace. This is certainly an overestimate of σ (though not an unreasonable one in sparsely firing cells), but it allowed us to conservatively identify transients at a p < 0.01 threshold. We then re-calculated σ after excluding these epochs and re-identified transients at a p < 0.01 threshold. After re-estimating σ a third and final time, we obtained our final identified transients. Empirically we have found that running the algorithm for additional iterations has little effect.

Spike estimation

We used the ML spike package (Deneux et al., 2016) to perform a maximum likelihood estimation of the spike trains underlying each fluorescence trace in our iMC, pMC, and GC datasets. We used the default GCaMP6f nonlinearity parameter ([0.85, -0.006]) and drift parameter (0.015, multiplicative). The only parameter we varied between GCs and MCs was the ‘spike-rate’ parameter. Deneux, et al. empirically recommend a default value of 1, which performed well for our MCs. However, this value led to a number of visually apparent false positives for our GCs; setting this value to 0.01 resulted in satisfactory performance for our GCs. Auto-calibration was performed for all remaining parameters.

Spatial tuning vectors

When evaluating the spatial tuning of MCs, we restricted our analysis to running-related epochs, defined as consecutive frames of forward locomotion (defined as an imaging frame in which at least one forward pair of beam breaks occurred on the quadrant reader) at least 1 sec in duration and with a minimum peak speed of 5 cm/sec. Consecutive epochs separated by < 0.5 seconds were merged. Running-related transients were defined as those that were initiated during a running-related epoch. Transient start was defined as the first imaging frame with mean fluorescence >= 2σ, with σ equal to the standard deviation of the baseline frames. Offset was defined as the first frame with mean fluorescence <= 0.5σ (Dombeck et al., 2010). The spatial tuning vector was calculated as ${\sum }_{\mathrm{j}}\frac{e^{i{\theta }_j}}{o({\theta }_j)}$, where θ_j is the position of the mouse at the onset time of the j-th running-related transient, and o_j is the fraction of running frames acquired at position θ_j.

Spatial information p-value analysis (place cell classification)

For each cell we first computed the spatial information content (Skaggs et al., 1993) as $I_N={\sum }_{i=1}^N{\lambda }_{i}ln\frac{{\lambda }_i}{\lambda }{p}_i$ where λ_i and p_i are the transient rate and fraction of time spent in the ith bin, λ is the overall firing rate, and N is the number of bins. We computed I_N for multiple values of N = 2, 4, 5, 8, 10, 20, 25, and 100. We then created 100,000 random reassignments of the transient onset times within the running-related epochs and recomputed the values of $I_N^s$, where s is the index of the shuffle. In calculated spatial information using binned data, it is important to note that this measure is biased by both the number of bins chosen and by the number of events fired by the cell. Performing shuffles on a per-cell basis addresses the latter bias. To roughly correct from the bias associated with binning, we subtracted the mean of this null distribution from all estimates to obtain values ${\widehat{I}}_N=I_N-\frac{1}{100,000}{\sum }_{s=1}^{100,000}{I}_N^s$. Finally, we computed a single estimate of the information content for the true transient onset times, Î = max_NÎ_N, and for the shuffles, ${\widehat{I}}_s={max}_N{\widehat{I}}_N^s$. Note that by maximizing ${\widehat{I}}_N^s$ over bin sizes we have allowed each iteration of the shuffle to maximize its value across bin sizes (an alternate less conservative choice would have been to enforce that each shuffle be calculated using the same bin size as was optimal for Î). The spatial tuning p-value was taken as the fraction of values of s for which Î exceeded Î_s.

Remapping analysis

Rate maps were formed by dividing the number of transients starting in each bin by the occupancy of that bin. We calculated rate maps with 100 position bins and smoothed with a Gaussian kernel σ=3 bins). The tuning curve correlation for each cell was defined as the Pearson correlation coefficient between tuning curves for a cell in the two sequential context exposures.

Computational modeling

The model was inspired by the structure and connectivity features described by Myers and Scharfman (Myers and Scharfman, 2009) and was derived from a more detailed DG network model detailed in (Chavlis et al., 2016). All simulations were performed using the BRIAN (BRIAN v1.4.3) spiking network simulator (Brette and Goodman, 2011; Goodman and Brette, 2009) running on a High-Performance Computing Cluster (HPCC) with 312 cores under a 64-bit CentOS 6.8 Linux operating system. The network model consists of 2000 simulated granule cells (GCs), a scale that represents 1/500 of the one million GCs found in the rat brain (West et al., 1991); the remaining neuronal cell types in the model are scaled down proportionally. The model population of GCs was organized into non-overlapping clusters, with each cluster containing 20 GCs; this organization roughly corresponds to the lamellar organization along the septotemporal extent of the DG (Sloviter and Lomo, 2012). Apart from the excitatory GCs and MCs, the model included two types of inhibitory interneurons: basket cells (BCs), which provide GCs with feedback inhibition; and the HIPP cells, which receive perforant path (PP) input, thus delivering feed-forward inhibition to GCs.

We included one BC per cluster of GCs, which in turn corresponds to 100 simulated BCs in the model. This is a form of “winner-take-all” competition (Coultrip et al., 1992), in which all but the most strongly activated GCs in a cluster are silenced. Given 100 clusters in the model, approximately 5% of GCs were active for a given stimulus under control conditions; this is in agreement with the theoretical and experimental estimates of ∼5% regular activity in the substrate (Danielson et al., 2016a; Treves et al., 2008). All cells included in the network were simulated as adaptive exponential integrate-and-fire models (Brette and Gerstner, 2005). External input to the network model was provided by 400 afferents representing the major input the DG receives from Entorhinal Cortex (EC) Layer II cells via the PP. For simplicity, the input cells were simulated as independent Poisson spike trains with a frequency of 45 Hz. The simulations reported here assumed that a given stimulus is represented by 10% of the PP afferents, which is in line with experimental evidence (McNaughton et al., 1991). Connectivity matrices were constructed randomly (uniform random distribution) before the start of the simulations and remained fixed across all simulations (no rewiring).

A GC model cell was considered active if it fired at least one spike during stimulus presentation. In order to quantify pattern separation efficiency, we used a metric f (“population distance”):

$$f=\frac{\text{HD}}{2(1-\mathrm{s})\mathrm{N}}$$

where s denotes the sparsity (i.e., the ratio of silent neurons to all neurons), N the number of neurons, and HD is the hamming distance between two binary patterns (Hamming, 1950). The factor of 2 in the denominator is used to limit the metric at zero. Our network is said to perform pattern separation if the input distance is smaller than the output distance, i.e., when f_(input) < f_(output).

For each simulation experiment, we constructed two overlapping input patterns. Each input pattern consisted of 40 PP afferents, 16 of which were common to both inputs, corresponding to f_(input) = 0.2. The distance of the input remained constant across all trials and different conditions. For each condition we performed 50 trials, using a new pair of inputs each time, and for each trial the network was simulated for 1310 ms. PP inputs were delivered at 300 ms and lasted for 1000ms. The first 300 ms and the final 10 ms were excluded from the analysis to assess the network during stimulus presentation. The time step for all simulations was set to 0.1 ms.

Quantification and Statistical Analysis

All statistical tests are described in the corresponding figure legends and in Tables S1 and S2. All comparisons were two sided. Non-parametric Mann-Whitney U Test or ANOVA were used throughout; two-sample KS Test was used in Fig. 4B-D to compare distributions. Summary data are presented in box plots, where horizontal line is the median, boxes are 25^th-75^th percentiles, and whiskers are 1.5*IQR (interquartile range).

Data and Software Availability

The SIMA package for Ca²⁺ imaging analysis is freely available online (www.losonczylab.org/sima). The computational model is available for download from ModelDB (accession #: 206397) and the Poirazi lab web site: http://www.dendrites.gr.

Additional Resources

None

Highlights.

• Ca²⁺ imaging indicates that MCs are significantly more active than GCs in vivo

• MCs exhibit spatially organized firing during navigation

• Spatially-tuned MCs strongly remap in response to contextual manipulation