A Model for Adult Organ Resizing Demonstrates Stem Cell Scaling through a Tunable Commitment Rate

Abstract

Many adult organs grow or shrink to accommodate different physiological demands. Often, as total cell number changes, stem cell number changes proportionally in a phenomenon called “stem cell scaling”. The cellular behaviors that give rise to scaling are unknown. Here we study two complementary theoretical models of the adult Drosophila midgut, a stem cell-based organ with known resizing dynamics. First, we derive a differential equations model of midgut resizing and show that the in vivo kinetics of growth can be recapitulated if the rate of fate commitment depends on the tissue’s stem cell proportion. Second, we develop a 2D simulation of the midgut and find that proportion-dependent commitment rate and stem cell scaling can arise phenomenologically from the stem cells’ exploration of physical tissue space during its lifetime. Together, these models provide a biophysical understanding of how stem cell scaling is maintained during organ growth and shrinkage.

Introduction

Mature organs contain both differentiated cells that execute physiological function and stem cells that generate new differentiated cells. In organ homeostasis, stem cells divide to replace differentiated cells that are lost, and numbers of stem and differentiated cells are constant. Increased functional demand can induce adaptive growth, a transient, nonhomeostatic state in which stem cells divide to generate excess differentiated cells (1, 2, 3, 4). Similarly, decreased demand leads to adaptive shrinkage, in which differentiated cells are reduced in part because stem cells cease to divide (5, 6). Adaptive resizing enables mature organs to maintain physiological fitness in the face of changing environmental conditions (1, 7, 8, 9).

Intriguingly, many organs exhibit altered numbers of stem cells in response to major physiological adaptation or resizing; examples of these include altered numbers of satellite stem cells in muscles after exercise or induced hypertrophy (10, 11, 12), altered numbers of mammary gland stem cells during pregnancy (13, 14), and altered numbers of intestinal stem cells after feeding (15). In particular, O’Brien et al. (15) found that stem cells scale with the size of the organ, that is, stem cells adjust their numbers during resizing to remain a similar proportion of total cells in the organ. Because of scaling, the cellular replacement burden of an individual stem cell stays constant irrespective of organ size. Physiologically, the constant replacement burden may be advantageous because it allows the organ to respond exponentially quickly (at least initially) to environmental changes. This is because the rate of change of the size of the system would typically be proportional to the number of stem cells and therefore proportional to the size of the system, leading to exponential response. In the adult Drosophila midgut, a simple epithelial organ functionally equivalent to the vertebrate small intestine, this scaling behavior is extraordinarily precise; a fourfold increase in differentiated cells, induced by increased dietary load, is matched by a fourfold increase in stem cells (15). Importantly, for stem cell scaling to occur, there must be populationwide coordination between symmetric and asymmetric fate outcomes after cell division (15, 16, 17). Although we know that at the individual cell level, fate outcomes are determined through Delta-Notch signaling, we do not know what mechanisms coordinate stem cell scaling at the population level.

Some prior models of the midgut (16, 18) and of other self-renewing organs (18, 19, 20, 21, 22, 23, 24, 25, 26, 27) have considered homeostasis without adaptive resizing. Some of these as well as other models have considered embryonic development (17, 18, 28, 29) or cancer (19, 24, 27, 30, 31, 32), two growth states that do not exhibit stem cell scaling. To shed light on scaling mechanisms, we develop a set of nonspatial differential equations as well as a 2D simulation of cell dynamics in the Drosophila midgut. Here we find that the physiological kinetics of stem cell scaling during midgut adaptive growth can be recapitulated by a set of ordinary differential equations. The ability of these equations to recapitulate physiological kinetics depends strongly on the inclusion of feedback. Specifically, physiological dynamics of cell populations are captured if the rate at which new cells commit to differentiation depends on the existing proportion of stem cells. Next, we develop a 2D simulation of the midgut and show that this tunable commitment rate can be explained by the concept of a stem cell territory—the physical space that a stem cell explores during its lifetime. We show that territory size is determined by cell-cell adhesion, stochastic motility, and Delta-Notch signaling. We find that stem cell scaling requires a threshold territory size and that systems within this regime fit our differential equations.

Methods

Nonspatial model

Description of nonspatial model. We propose a mathematical description of the midgut that considers the midgut’s three major cell types: stem cells, enteroblasts, and enterocytes, each of which exhibits a distinct cellular behavior (Fig. 1). Stem cells, s, are the only cells in the midgut that typically divide (33). In our model, all stem cell divisions generate two daughters that are equipotent stem cells (16); this division rate is denoted a. Some stem cells become enteroblasts, u. Enteroblasts are postmitotic and committed to differentiate into enterocytes, but still lack the morphological features of differentiation. The rate that stem cells commit to terminal fate is denoted b. Enterocytes, U, are fully mature epithelial cells that comprise most of the cells in the midgut epithelium. Enteroblasts differentiate into enterocytes at a rate λ. Enterocytes die, or are otherwise lost, at a rate Λ.

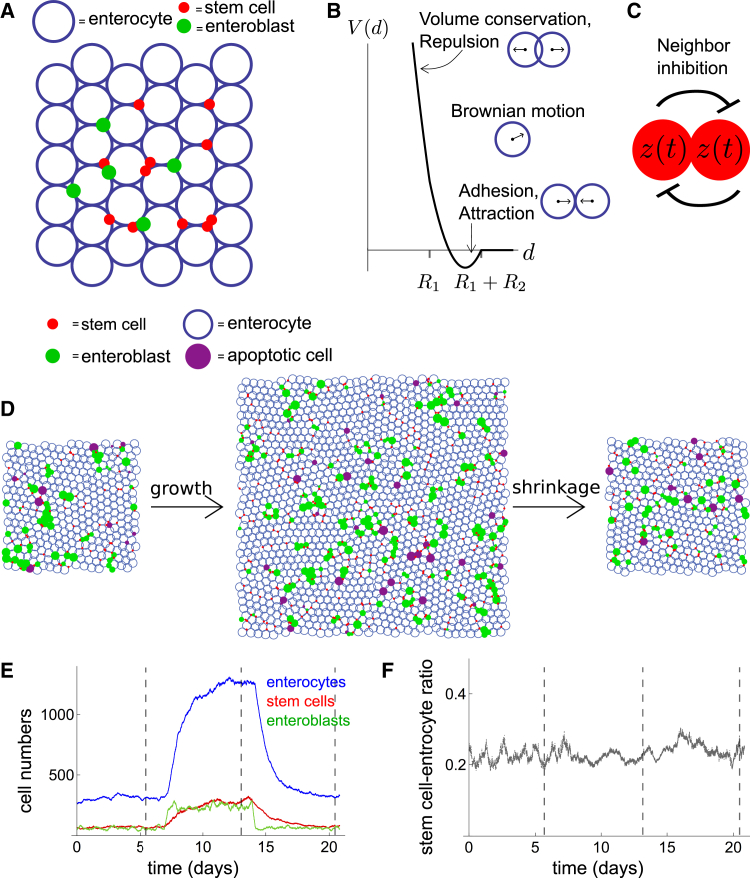
Figure 1.

Stem cells in the Drosophila midgut regulate growth and homeostasis. (A) Given here is a schematic of the Drosophila midgut (yellow). (B) Given here is a schematic of midgut epithelium with stem cells (red) and enteroblasts (green) situated among enterocytes (blue). (C) Cellular processes are taken into account by the model in Eq. 1. To see this figure in color, go online.

These cellular relationships lead to a simple mathematical description for numbers of stem cells, enteroblasts, and enterocytes as functions of time s(t), u(t), and U(t), with the following form:

$$\begin{array}{l}\dot{s}=as-bs,\hfill \\ \dot{u}=bs-\lambda u,\hfill \\ \dot{U}=\lambda u-\text{Λ}U.\hfill \end{array}$$ (1)

For the system to have a nonzero, finite steady state, either rates of division and commitment must always be equal (b = a), which would imply highly precise regulation of these two processes, or else some rates as given in Fig. 1 and Eq. 1 must depend on cell numbers. We assume the latter case because highly precise regulation is unlikely in a noisy tissue system.

To account for nutrient-driven adaptive growth and shrinkage (15), we propose that cell numbers depend on ingested nutrients, and that the system contains feedback. We denote the total energy of ingested nutrients as E_in and define the energy density, E_d, as follows:

$$E_d=\frac{E_{\text{in}}}{A_{1}s+A_{2}u+A_{3}U}\equiv \frac{E_{\text{in}}}{A},$$ (2)

in which A ≡ A₁s + A₂u + A₃U is the total tissue consumption of E_in, and A₁, A₂, and A₃ denote the cell-type specific consumption per cell.

Physiologically, we assume that cells most likely can access only the local value of nutrients, namely the energy density. Therefore, we designate rates of cell division a and cell loss Λ to depend on E_d. In fact, in vivo analysis of the midgut has shown that high levels of nutrients promote divisions and suppress death, whereas low levels of nutrients have the opposite effect, as reflected by levels of insulin signaling (15). Accounting for these observations, denoting a_m and Λ_m as maximal rates of division and death, respectively, nondimensionalizing E_d, and choosing Hill functions to represent generic sigmoidal functions, we arrive at nutrient-dependent expressions for division and death rates, as follows:

$$a=a_m\frac{E_d^2}{1+E_d^2},\text{Λ}={\text{Λ}}_m\frac{1}{1+E_d^2}.$$ (3)

Note that although we chose second-order Hill functions to represent the sigmoidal dependence of cell division and loss rates on nutrient density, other Hill functions do not significantly alter the results, as detailed in the Supporting Material. Model equations for s, u, and U taking into account nutrient-dependent division and death rates are therefore, as follows:

$$\begin{array}{l}\dot{s}=a_m\frac{E_d^2}{1+E_d^2}s-bs,\hfill \\ \dot{u}=bs-\lambda u,\hfill \\ \dot{U}=\lambda u-{\text{Λ}}_m\frac{1}{1+E_d^2}U.\hfill \end{array}$$ (4)

Importantly, the steady states of Eq. 4 satisfy scaling because $\left\{E_{\text{in}},s,u,U\right\}\to \left\{\alpha E_{\text{in}},\alpha s,\alpha u,\alpha U\right\}$ leaves the steady-state equations for Eq. 4 invariant. Below, we explore feedback and regulation in this model.

Although it is known that stem cell-to-enteroblast commitment is controlled by the dynamics of Delta-Notch signaling (33, 34, 35, 36), regulation of the differentiation program by which enteroblasts become enterocytes is less understood, and its kinetics had not been measured. Because the source of regulation for differentiation rate λ is unknown, in this article, we take λ to be constant, that is, independent of s, u, or U. An extended model with a regulated differentiation rate is suggested in the Supporting Material.

Given that differentiation rate λ is kept constant, a simplified model with similar dynamics to Eq. 4 could be considered, in which enteroblasts u and enterocytes U are combined into a single population of differentiated cells W = u + U. In this case, the model would be as follows:

$$\begin{array}{l}\dot{s}=a_m\frac{E_{\text{dW}}^2}{1+E_{\text{dW}}^2}s-bs,\hfill \\ \dot{W}=bs-{\text{Λ}}_m\frac{1}{1+E_{\text{dW}}^2}W,\hfill \end{array}$$ (5)

where E_dW would be analogous to E_d in Eq. 2, as follows:

$$E_{\text{dW}}=\frac{E_{\text{in}}}{A_{1}s+A_{4}W}.$$ (6)

We explored this model in the Supporting Material, and we found that it gives the same qualitative results as the model in Eq. 4. Given that this simplified model has one fewer equation, one might prefer this model for further analysis. However, to better adhere to biological convention and to provide convenient comparison to experimental data and literature, including our simulation results in the second-half of the article, we proceed for the rest of this article with the model in Eq. 4.

Results

Nonspatial model analysis

Constant versus stem cell proportion-dependent commitment rate: compatibility with empirical measurements

We next sought to compare the solutions of Eq. 4 to the known dynamics of the midgut in vivo. Solving Eq. 4 under steady-state conditions, we find for steady-state stem cell number ratios s₀/u₀, s₀/U₀, and s₀/(s₀ + u₀ + U₀), as follows:

$$s_0/u_0=\frac{\lambda }{b},$$ (7)

$$s_0/U_0={\text{Λ}}_m\left(\frac{1}{b}-\frac{1}{a_m}\right),$$ (8)

$$\frac{s_0}{s_0+u_0+U_0}=\frac{1}{1+\frac{\lambda }{b}+{\text{Λ}}_m\left(\frac{1}{b}-\frac{1}{a_m}\right)}.$$ (9)

Full steady-state solutions to Eq. 4 are in the Supporting Material. Note that in this general form, we assume that b may have functional dependence on s₀, u₀, or U₀, and that b cannot surpass a_m in value.

Important to the discussion of empirical measurements in the midgut is the definition of symmetric and asymmetric fate outcomes. Because, as a first approximation, stem cells are the only cells in the midgut capable of dividing (33), we designate fate outcomes as symmetric-stem if both daughter cells divide before either daughter becomes a committed enteroblast. Using similar logic, we designate fates as symmetric-terminal if both daughters become committed enteroblasts before either divides, and as asymmetric if one daughter becomes a committed enteroblast while the other divides (15).

Because we model division and commitment as Markov processes (uncorrelated) with rates a and b, the probability that a given stem cell undergoes division before commitment is a/(a + b). The frequency of symmetric-stem fate outcomes is therefore as follows:

$$P\left(\text{sym}\right)={\left(\frac{a}{a+b}\right)}^2,$$ (10)

where a and b can have any functional dependence. Note that, in steady state, similar to the results in Hannezo et al. (18), we have P(sym) = 1/4 because a = b in steady state. The maximum symmetric-stem division rate, often achieved during growth, is P_max(sym) = (a_m/(a_m + b))².

Constant rate of commitment is incompatible with empirical measurements

Other models of tissue homeostasis have assumed that commitment rate is constant (16, 22). We thus asked whether a constant commitment rate is compatible with growth. Solving Eq. 4 for b = B₀ = constant and a 4× increase in food, we find that the key features of midgut growth in vivo are indeed recapitulated: the cell numbers increase, the frequency of symmetric-stem fates increases transiently, and the stem cell number scales (Supporting Material). Here, the value of 4× food increase was chosen to generate a 4× increase in cell numbers so as to best compare to the experimentally measured 4× increase in cell numbers when the gut undergoes feeding (15). As noted, the cell number ratios s₀/U₀ and s₀/u₀ and are independent of food input or absolute cell number, so stem cell scaling arises naturally. Thus, in principle, a constant commitment rate is compatible with resizing.

However, the validity of a constant commitment rate model breaks down when we compare the theoretical parameter space with the biologically observed parameter space. Although commitment rates have not been experimentally measured, it is known that in steady state, s₀/u₀ ≈ 1 and s₀/U₀ ≈ 0.2 during midgut homeostasis (15, 16); specifically, the numbers of stem cells, enteroblasts and enterocytes are ∼700 ± 200, 500 ± 200, and 2800 ± 800, respectively (15). Using these values in Eqs. 7 and 8, and replacing commitment rate b with the constant B₀, we obtain

$$1=\frac{\lambda }{B_0},0.2=\frac{s_0}{U_0}={\text{Λ}}_m\left(\frac{1}{B_0}-\frac{1}{a_m}\right).$$ (11)

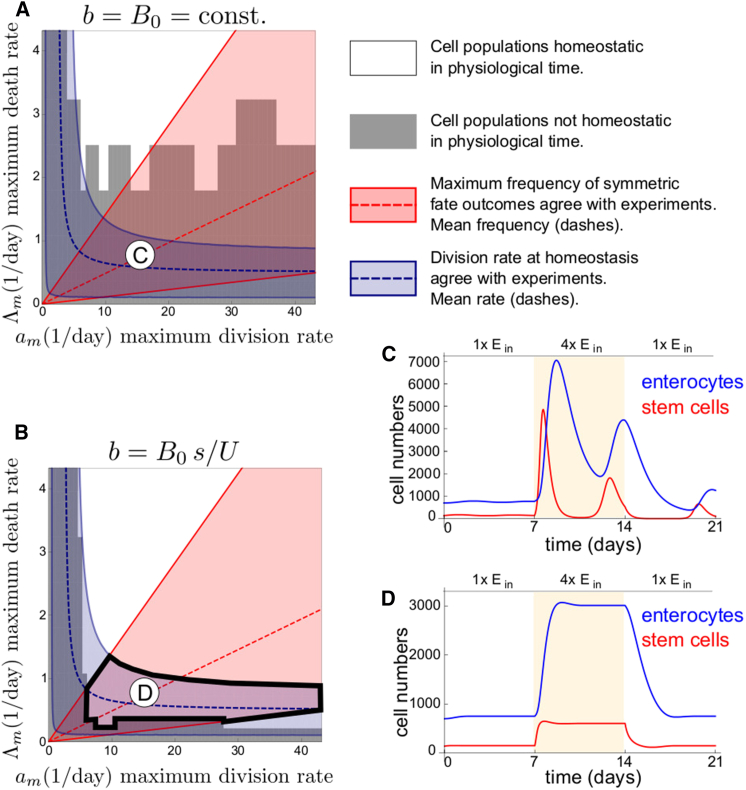
Using these relationships to deduce λ and B₀ from a_m and Λ_m, we solve Eq. 4 for various values of a_m and Λ_m. To focus our parameter range, we apply three criteria. First, homeostatic stem cell division rates a₀ vary from 0.5 to 4 times per day (15, 16). Given that division and commitment must be equal at homeostasis (a₀ = B₀), this biologically relevant range of a₀ is obtained from a_m and Λ_m using Eq. 11 (Fig. 2 A, blue shading). Second, the maximum reported rate of symmetric-stem fates under physiological conditions is 0.7, which is transiently observed during growth (15). We thus set P_max(sym) = (a_m/(a_m + b))² ≈ 0.7 (with b = B₀) and included a margin of error such that 0.5 ≤ P_max(sym) ≤ 0.9 (Fig. 2 A, red shading), where the margin of error is estimated from data in O’Brien et al. (15) (see Supporting Material). Third, the time required for the growth phase to reach completion is ∼3.5 days (15), after which homeostasis is reestablished at the organ’s new, larger size. Therefore, only values of a_m and Λ_m for which solutions to Eq. 4 approach steady state by t = 3.5 days give rise to steady states with in vivo kinetics (Fig. 2 A, white region). Conditions used to determine whether Eq. 4 has reached approximate equilibrium are in the Supporting Material.

Figure 2.

Stem cell proportion-dependent commitment rate b = B₀s/U model satisfies experimental observations whereas constant commitment rate b = B₀ model does not. (A and B) For b = B₀ (A) and b = B₀s/U (B), regions of parameter space (a_m, Λ_m) are given that satisfy: homeostatic division rate 0.5/day ≤ a₀ ≤ 4.0/day (blue), maximum frequency of symmetric-stem fate outcomes 0.5 < P_max(sym) < 0.9 (red), and homeostasis within t = 3.5 days (white). Averages a₀ = 2.5/day and P_max(sym) = 0.7 are indicated by dashed lines. Parameter values satisfying all experimental measurements do not exist for the b = B₀ model (A), whereas they exist for the b = B₀s/U model (B) (solid black outline). Circled letters indicate parameters corresponding to solutions in (C) and (D). (C) Solutions of b = B₀ model are highly oscillatory in parameter regimes that satisfy experimental values of division rate and maximum frequency of symmetric-stem fate outcomes. (D) Solutions of b = B₀s/U model respond quickly to food changes without large oscillations in parameter regimes that satisfy all experimental measurements. To see this figure in color, go online.

Applying these criteria, we observe that when commitment rate is constant (b = B₀), no regions of the theoretical parameter space satisfy all three biological measurements; i.e., there is no region in which blue, red, and white shading all overlap (Fig. 2 A). Specifically, solutions to Eq. 4 with constant b = B₀ show strong behaviors of ringing (see Fig. 2 C and Supporting Material), which prevents solutions from approaching steady state within physiological time. This ringing in solutions approaching a new steady state determined by E_in is present for all fold-changes of E_in. Thus, although constant commitment rate is theoretically compatible with midgut adaptive growth, it is incompatible when biologically relevant measurements are applied.

A rate of commitment that depends on stem cell proportion is compatible with scaling and empirical measurements

Because the model with constant commitment rate does not fit experimental measurements, we examine a second possibility, in which commitment rate varies depending on how many stem cells and enterocytes are present in the tissue. Such a relationship can give rise to more realistic dynamics by allowing cell numbers to feed-back into the commitment rate. In the midgut, commitment to enteroblast fate is known to occur through Delta-Notch signaling between stem cells (33, 34, 35, 36). This biological phenomenology suggests that it is reasonable to model the signaling frequency, and consequently commitment rate, such that it depends on the number ratio of stem cells in the tissue s/U. We therefore explore the effects of this additional feedback to our model in Eq. 4.

We find that a commitment rate proportional to stem cell-enterocyte ratio recapitulates midgut resizing within timescales that are biologically relevant. Specifically, we modify three elements: Eq. 4 such that b = B₀ s/U, Eq. 11 such that B₀ is replaced by B₀s₀/U₀, and the P_max calculation such that b = B₀ s₀/U₀. Incorporating these modifications, we solve Eq. 4 for various values of a_m and Λ_m. The resulting values define a theoretical parameter space that is compatible with the known biological measurements; i.e., the region in which blue, red, and white shading overlap (Fig. 2 B). In addition, stem cell scaling is maintained due to the form of b = B₀ s/U. Importantly, the large oscillations and ringing behaviors in the b = B₀ model (Fig. 2 C) that delays the approach to steady state are suppressed in the b = B₀ s/U model (Fig. 2 D). This result is confirmed by linear stability analysis, detailed in the Supporting Material. Moreover, the parameter region in which oscillations are significant is smaller in the b = B₀ s/U compared to the b = B₀ model, also detailed in the Supporting Material. We conclude that the known kinetics of midgut resizing can be accounted for by introducing an additional feedback term to Eq. 4, in particular, one that tunes the rate of enteroblast commitment to the existing proportion of stem cells.

Therefore, from these results, we propose that our model equations be modified as

$$\begin{array}{l}\dot{s}=a_m\frac{E_d^2}{1+E_d^2}s-B_0{s}^2/U,\hfill \\ \dot{u}=B_0{s}^2/U-\lambda u,\hfill \\ \dot{U}=\lambda u-{\text{Λ}}_m\frac{1}{1+E_d^2}U.\hfill \end{array}$$ (12)

Equation 12 captures stem cell scaling and in vivo resizing dynamics of the midgut. The steady-state solutions to Eq. 12 are presented in the Supporting Material. We note that the feedback through stem cell number ratio s/U does not uniquely allow the resizing model in Eq. 4 to capture realistic dynamics in the midgut; however, proportionality of commitment rate to s/U is one of the simplest forms for feedback that both represents biological phenomenology and captures realistic dynamics. Alternative models for feedback are suggested and explored in the Supporting Material.

2D model

2D model description. Although our nonspatial model implies that a tunable commitment rate b is needed for midgut resizing that fits experimental measurements, it does not provide insight into the cellular mechanisms that underlie this tunability. To explore these potential mechanisms, we develop a 2D model of the midgut that builds upon our nonspatial model. Many mathematical approaches have been used to model 2D epithelia including vertex models (37, 38, 39, 40), cellular automata (41, 42, 43), cellular Potts models (44, 45), and cell-centered models (46, 47, 48). Our 2D model is a cell-centered model based on overlapping spheres (49, 50, 51), where we represent cells as 2D spheres (disks) that are specified by the positions of their centers and that interact physically via forces such as cell-cell adhesion, volume exclusion, and stochastic motion (Fig. 3, A and B). We chose a cell-centered model, among others, because it describes the midgut system at the length scale of cells, which is the length scale of the phenomenology in which we are interested. As shown, in vivo (35, 52), contact-mediated, Delta-Notch signaling between individual stem cells serves to define commitment to terminal fate (Fig. 3 C). Thus, in the 2D model, commitment rate becomes a property that emerges from the fate decisions of individual stem cells, in contrast to the nonspatial model, in which commitment rate is explicitly defined with respect to the tissue-wide ratio of stem cells to enterocytes.

Figure 3.

2D model accounts for spatial tissue dynamics. Midgut cells are represented by physically interacting, soft pseudo-spheres that signal to each other via Delta-Notch interactions. (A) Given here is a schematic: stem cells, enteroblasts, and enterocytes in a 2D domain. (B) Attractive and repulsive forces from neighbor cells and stochastic motility are taken into account. Given here is trapping potential V(d) from neighbor interactions with preferred distance d₀ between cells of radii R₁ and R₂. (C) Given here is a schematic of Delta-Notch lateral inhibition from protein dynamics z(t). (D) Here we have frames from 2D simulation (Movie S1) of the feed-fast cycle: E_in is increased fourfold, then decreased to original value. (E and F) Given here are cell numbers (E) and stem cell-enterocyte ratio (F) as functions of time for the simulation in (D) with timeframes indicated (vertical dotted lines). To see this figure in color, go online.

Physical cell-cell forces. Assuming that the system is highly damped, we set the inertial term to 0 so that external forces are balanced by viscous drag: dx/dt = ηf, where the quantity f is the external force acting on a cell, the quantity x is the position of the cell center, and η is the mobility:

$$\frac{d\mathbf{x}}{dt}=\eta \left(\sum _{n\in \text{n}.\text{n}}\left({\rho }_n+{\gamma }_n\right)\widehat{{\mathbf{d}}_n}+\sigma \mathbf{X}\left(t\right)\right).$$ (13)

Here, the sum on n∈n.n indicates summing over nearest neighboring cells; if the cell centered at x has radius R₁ and another cell has radius R₂, the two cells are nearest neighbors if their cell centers are separated by less than R₁ + R₂. The quantities ρ_n and γ_n are magnitudes of repulsion and adhesion forces from neighbor cells, known to be important in epithelial cells, and $\widehat{{\mathbf{d}}_n}$ is a unit vector toward the neighbor cell. The self-generated random force is provided by X(t), which has components sampled from a normal distribution N(0,1); here σ indicates an amplitude factor for X. We refer to σX as an intrinsic stochastic motility. Cell motility has recently been shown to occur in enteroblasts (53), and labeled clones have been shown to split (15, 16). The latter may be due to stochastic motility or random cell shuffling, both of which are captured by the term σX. Forces are indicated in Fig. 3 B. Details are given in the Supporting Material.

Delta-Notch signaling. In the midgut, asymmetric fate outcomes arise through activation of Notch receptor on the surface of one stem cell by Delta ligand on an adjacent stem cell (33, 34, 35, 36, 52, 54). Activation of Notch marks a cell’s commitment to differentiate (52), and is the defining feature of enteroblast identity. Many mathematical models of Delta-Notch interactions separately describe Delta and Notch populations (54, 55, 56, 57), or distinguish between membrane-bound and intracellular Notch (56, 57). To model lateral inhibition signaling, we employed a fictitious protein with values z(t) indicating the “stemness” of a given cell. Delta-Notch interactions between neighboring cells are modeled with the dynamics of z through a delay differential equation. Delta-Notch signaling have been modeled to contain time delays to account for signal transduction (58), and a delayed model of lateral inhibition has been shown to reduce errors in patterning (59).

For each cell (stem cells and enteroblasts) expressing z, we assume that z is produced within the cell in a nonlinear fashion with saturating effects at level p, and z decays exponentially with rate β. To take into account the effects of nearest neighboring cells, we assume that neighbor cells’ protein levels z_n decreases z production in a given cell with time delay t_n, taking into account protein transport times, see Fig. 3 C. Choosing a sigmoidal Hill function of order m > 1 for the production term, we have for the dynamics of nondimensionalized z:

$$\frac{dz}{dt}=p\left(\frac{z^m}{1+z^m\left(t\right)}\right)\cdot \left(\frac{1}{1+{\left({\sum }_{n\in \text{n}.\text{n}}{z}_n\left(t-t_n\right)/g_n\right)}^k}\right)-\beta z,$$ (14)

where g_n denotes the switch point for neighbor interactions, and m and k are Hill exponents. Given that m > 1, Eq. 14 gives bistable steady states of z with stable fixed points at z^∗ = 0 and z^∗ ≠ 0 and an unstable fixed point in between that we denote by z_u^∗. The nonzero stable fixed point z^∗ ≠ 0 is interpreted as the stem cell state, and the trivial stable fixed point z^∗ = 0 is interpreted as the enteroblast state. A stem cell (that has z > z_u^∗) is defined to have permanently committed to terminal fate and become an enteroblast when its z value falls below the value of the unstable fixed point (z becomes z < z_u^∗). Inhibitory signaling from nearest neighbors cause a stem cell’s z value to be suppressed below z_u^∗, causing commitment. Therefore, in the 2D model, commitment kinetics and commitment rate are determined by dynamics that drive z below a threshold value. An enteroblast has a small value of z compared to stem cells and therefore signals weakly compared to stem cells; it undergoes growth in size to eventually reach the size of an enterocyte; at this point, the enteroblast is converted into an enterocyte, and its z value is set identically to 0. Note that commitment is still an uncorrelated Markov process, and therefore, the fraction of symmetric fate outcomes in steady state is still P(sym) = 1/4. See Supporting Material for details of implementation of the 2D model.

2D model analysis

Simulations with this 2D model successfully recapitulate essential features of the in vivo fly midgut with respect to growth, shrinking, scaling with food, and the presence of stem cells in every part of the epithelium (Fig. 3, D–F; Movie S1). Additionally, cell populations behave qualitatively similar to the nonspatial b = B₀ s/U model in that they are nonoscillatory (similar to Fig. 2 D instead of to Fig. 2 C).

Note that unlike the nonspatial model, the commitment rate b for the 2D model is not defined as a function of cell populations. Rather, for each individual cell, commitment rate arises from the duration and strength of contact-based cell-cell signaling. This dependence implies that global quantities such as stem cell ratios are determined by local dynamics.

Stem cell ratio depends on cells’ physical properties

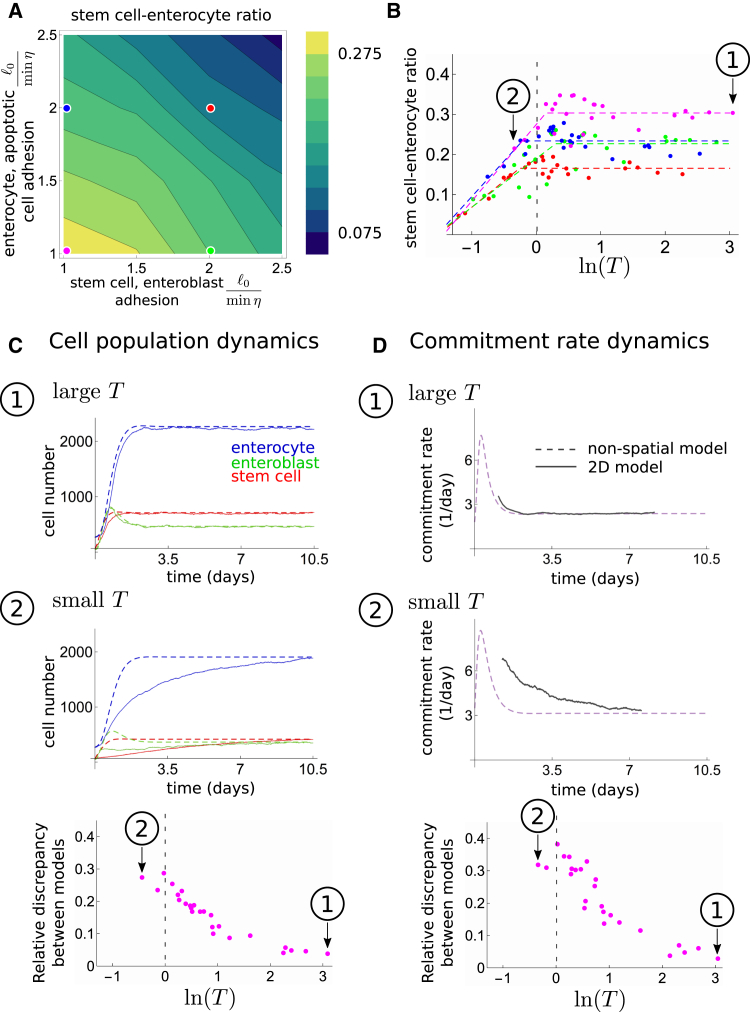
With the 2D model, we can explicitly examine the effects of local dynamics on population-level quantities by changing physical parameters. Specifically, the force magnitudes adhesion γ and motility σ in Eq. 13 determine how fast stem cells move in the tissue. In particular, stochastic motility specifies diffusive motion absent of other interactions. Additionally, these parameters affect the amount of time stem cells are in signaling contact with each other, ultimately affecting the stem cell ratio. Specifically, we found that the stem cell ratio is sensitive to adhesion values (see Fig. 4 A). Here the motilities σ_sc,eb for stem cells and enteroblasts and σ_EC for enterocytes were kept constant whereas adhesions were varied. Forces are expressed in units of ${\ell }_0$/(minη), where ${\ell }_0$ is the enterocyte diameter without adhesive or repulsive interactions, and η is the inverse viscosity. Note that we use minutes as the unit of time to employ the relevant values of a_m and Λ_m that were deduced from nonspatial model (Fig. 2 B) to compare to physiological timescales found in experiments.

Figure 4.

Local physical interactions define a critical territory above which stem cells can sense their density. (A) Given here is a stem cell-enterocyte ratio as a function of adhesion between stem cells and enteroblasts (x axis) and adhesion between enterocytes and apoptotic cells (y axis) for motility σ = 0.2${\ell }_0$/minη for all cells. Colored dots indicate the adhesion values used in (B). (B) Given here is the stem cell-enterocyte ratio as a function of natural log of stem cell territory ln(T) for various adhesion values. The onset of saturating values for stem cell ratios (dotted line T ≈ 1) corresponds to the lower threshold of T that enables stem cell scaling. (C and D) Given here is a comparison of the 2D model (solid lines, average of six replicate simulations) and the nonspatial b = B₀s/U model (dashed lines) using time courses of cell population dynamics (C) and commitment rate dynamics (D). Plots correspond to the magenta parameter set in (B). Circled numbers indicate large versus small T simulations: large T simulations (1) fit well to the b = B₀s/U model, whereas small T simulations (2) do not. Calculations of relative discrepancy between models are given in the Supporting Material. To see this figure in color, go online.

Stem cell territory determines whether system scales

In these simulations, we noted that values for adhesion and motility influenced the physical space that a stem cell explores during its lifetime. We denote this space as a “stem cell territory”, T. To gain insight into the relationship between territories and stem cell interactions, we define T as

$$T=\frac{1}{b}D/{\ell }^2.$$ (15)

Here, 1/b is the average lifetime of a stem cell, i.e., the time between the birth of a stem cell and its commitment to terminal fate; the quantity D is a diffusion constant fitted to simulated stem cell tracks (see Supporting Material); and $\ell$ is the average enterocyte diameter. Hence, T is the dimensionless area (number of enterocyte areas) over which a stem cell may influence or respond to other stem cells. Note that Eq. 15 can be generalized for nondiffusive motion.

Investigating resulting stem cell ratios as a function of T (Fig. 4 B), we find a transition from increasing stem cell ratios at lower T toward saturation for larger T. Here, the quantity T was varied via adhesion γ and stochastic motility σ. As expected, larger σ and lower γ lead to larger territories T. Note that this transition occurs around T ≈ 1, i.e., when stem cells start to explore a territory larger than the area of a single enterocyte. For T > 1, different stem cells can come in contact with each other via overlapping territories. The saturation for large T also indicates that additional interactions do not change global behavior. Moreover, the resulting stem cell ratio for large T depends on the intrinsic parameters (adhesion γ); this dependence suggests that the tissue can flexibly regulate its stem cell ratio.

It is insightful to compare the 2D simulations to the nonspatial model (Fig. 4, and see Eq. 12). We find that for large stem cell territories T, the population dynamics of the two models agree (simulation 1) in Fig. 4, C and D. This suggests that when T is large, stem cells can sense their density within the tissue, and hence their commitment rate can contain density feedback through s/U, as in the nonspatial model. When T is small, the two models differ (simulation 2) in Fig. 4, C and D, because the nonspatial model cannot account for the effect, in 2D, that stem cells with small territories do not obtain density knowledge. Additionally, we note that in the latter case, when T is small, the approximate time to reach new homeostatic cell numbers during resizing is longer than observed physiologically (∼7 days instead of 3.5 days (15)); this supports the notion that stem cells in the biological system may display motility to increase their territories.

Finally, we explored how stem cell territory T relates to stem-cell scaling. We performed numerical experiments for different values of food input E_in for various T (Fig. S4). We found that the regime for which stem cell scaling is enabled approximately coincides with the regime for which stem cell ratios saturate: at T ≥ 1 (dotted vertical line in Fig. 4 B). Therefore, when stem cells explore a large enough area to escape the inhibition signaling of its immediate sibling stem cell, stem cell scaling is enabled.

Discussion

Proportional scaling of stem cells to total cells during adaptive growth ensures that the organ has enough stem cells to support its new size after growth is complete. We have shown that the basic features of adaptive organ resizing can be captured by simple mathematical descriptions of the Drosophila midgut in which rates of stem cell division and enterocyte death depend on nutrient density. Importantly, we find that a nonconstant rate of commitment to terminal fate, specifically, a rate tuned to stem cell proportion, reproduces the in vivo kinetics of division and growth.

What biological mechanisms might enable cells to monitor stem cell proportions and tune their commitment rates appropriately? The models presented here show that a mechanism involving stochastic motility is compatible with in vivo measurements. Motility permits stem cells to explore a local tissue area and engage in signaling interactions with other, potentially nonsibling, stem cells. We define this local area as the stem cell’s territory and explore its parameter space by varying cell motility and adhesion.

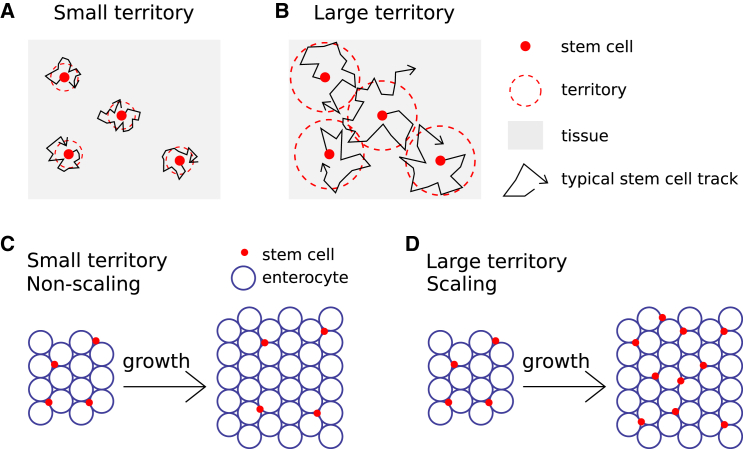
Intriguingly, proportion-dependent commitment and scaling occur only above a threshold territory size. This threshold size can be understood by its impact on commitment rate (i.e., rate of Notch activation), which occurs through cell-cell signaling (Notch-Delta interactions) between pairs of stem cells. Essentially, there are two scenarios: 1) When stem cells are constrained within small territories, two newborn sibling cells contact each other frequently, and their Notch-Delta interactions increase to the point of a near-certain asymmetric outcome. In this case, the total number of stem cells in the tissue remains nearly constant during growth, whereas the number of enterocytes increases, and scaling does not occur (Fig. 5, A and C). 2) When stem cells range in large territories, sibling cells often separate fast enough without Notch-Delta interaction having a differentiating effect, which promotes symmetric fate outcomes, i.e., the total number of stem cells in the tissue can increase. Importantly, the stem cell ratio does not increase beyond a certain value because pairs of nonsibling stem cells come into contact sufficiently frequently for Notch-Delta interactions to induce differentiation. In this case, both stem cells and enterocytes increase in proportion, and scaling does occur (Fig. 5, B and D).

Figure 5.

Scaling occurs when stem cell territories are above a critical threshold. (A and B) Cartoons of small (A) versus large (B) stem cell territory (red dotted line) are as defined by spatial range of physical cell motion (black line). (C) For territories below a threshold size, there is no stem cell scaling. (D) For territories larger than a threshold size, there is stem cell scaling. To see this figure in color, go online.

We make the following suggestions for future experimental tests. The core importance of a tunable commitment rate in these models contrasts with the scant empirical knowledge of commitment rates in vivo. Experimental measurements of commitment rate are currently impractical in many systems. However, the availability of fluorescent Notch reporters (60, 61) may provide a means to measure kinetics of fate commitment in systems such as the midgut in which Notch activation is the committing step. For the midgut in particular, the models here generate specific, testable predictions: 1) If newborn stem cells inherit unequal levels of the Delta ligand or Notch receptor, then because of the delayed nature of Eq. 14, commitment should occur more rapidly in sibling pairs than in pairs of stem cells that come into contact by chance. 2) The stem cell population should undershoot when a tissue undergoes shrinkage (Fig. 2 D). 3) Stem cell scaling should be disrupted by experimental perturbation of stochastic motility, adhesive force, or Delta-Notch signaling (Fig. 4 B). 4) The territory size of individual stem cells should be larger than one enterocyte area. In particular, for the last point (4), methods such as cell tracking in vivo to measure diffusion coefficients of cell motion, or clone-induction methods such as twin-spot mosaic analysis (15) to measure spatial dispersal of cells from a common division, can provide measurements and estimations of the stem cell territory in the midgut.

In summary, we have developed mathematical descriptions of a stem cell-based organ that undergoes adaptive resizing in response to external input. To realistically describe an in vivo system, the Drosophila midgut, we found that the stem cell commitment rate should depend on organwide stem cell proportion. To elucidate this dependence, we suggested local, spatially motivated, cell-level mechanisms such as cell motility, adhesion, and signaling, by which stem cells can detect their density and therefore tune their commitment rate. Importantly, these models naturally give rise to stem cell scaling, and we identify physical regimes in which scaling occurs.

Author Contributions

X.D., L.E.O., and I.R.-K. designed research, performed research, contributed analytic tools, analyzed data, and wrote the manuscript.

Editor: Mark Alber.