Structure and Dynamics of DNA and RNA Double Helices of CAG and GAC Trinucleotide Repeats

Abstract

CAG trinucleotide repeats are known to cause 10 late-onset progressive neurodegenerative disorders as the repeats expand beyond a threshold, whereas GAC repeats are associated with skeletal dysplasias and expand from the normal five to a maximum of seven repeats. The TR secondary structure is believed to play a role in CAG expansions. We have carried out free energy and molecular dynamics studies to determine the preferred conformations of the A-A noncanonical pairs in (CAG)_n and (GAC)_n trinucleotide repeats (n = 1, 4) and the consequent changes in the overall structure of the RNA and DNA duplexes. We find that the global free energy minimum corresponds to A-A pairs stacked inside the core of the helix with anti-anti conformations in RNA and (high-anti)-(high-anti) conformations in DNA. The next minimum corresponds to anti-syn conformations, whereas syn-syn conformations are higher in energy. Transition rates of the A-A conformations are higher for RNA than DNA. Mechanisms for these various transitions are identified. Additional structural and dynamical aspects of the helical conformations are explored, with a focus on contrasting CAG and GAC duplexes. The neutralizing ion distribution around the noncanonical pairs is described.

Introduction

Trinucleotide repeats (TRs) belong to the family of simple sequence repeats (SSRs), that comprises all sequences with core motifs of one to six (and even 12) nucleotides that are repeated up to 30 times (and more for pathological cases) (1). SSRs exhibit dynamic mutations that do not follow Mendelian inheritance (which asserts that mutations in a single gene are stably transmitted between generations). In the 1990s, scientists discovered that inherited neurological disorders known as “anticipation diseases”, where the age of the onset of the disease decreased and its severity increased, were caused by the intergenerational expansion of SSRs (2, 3, 4, 5). After a certain threshold in the length of the repeated sequence, the probability of further expansion and the severity of the disease increases with the length of the repeat. To date, ∼30 DNA expandable SSR diseases have been identified and the list is expected to grow (6, 7). In particular, the dynamic mutations in human genes associated with TRs cause severe neurodegenerative and neuromuscular disorders, known as trinucleotide (or triplet) repeat expansion diseases (TREDs) (3, 8, 9, 10). The expansion is believed to be primarily caused by some sort of slippage during DNA replication, repair, recombination, or transcription (5, 6, 7, 11, 12, 13, 14, 15). Cell toxicity and death have been linked to the atypical conformation and functional changes of the transcripts and, when TRs are present in exons, of the translated proteins (6, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25).

Of all the TRs, CAG repeats give rise to the largest group of neurodegenerative diseases. CAG repeats in the 5′-UTR of the gene PPP2R2B cause spinocerebellar ataxia type 12, whereas CAG repeats in the exon part of various genes cause another nine late-onset, progressive neurodegenerative disorders, including Huntington’s disease, dentatorubral-pallidoluysian atrophy, spinal and bulbar muscular atrophy, and several spinocerebellar ataxias. These disorders are also known as polyglutamine (polyQ) diseases (26), because although CAG repeats could likely encode three different amino acid repeats depending on the reading frame (codons CAG, AGC, and GCA would code for polyQ, polyS, and polyA, respectively), the CAG expansions in these genes only lead to polyQ expansions. These polyQ diseases, like other TREDs, are caused by expansions greater than a given threshold (26). For instance, in Huntington’s disease, the normal polyQ (or CAG repeat) length is 10–34 repeats, and pathological lengths are 36–250 repeats. Although each disease has a different pathology, they all share a common feature: the formation of polyQ aggregates (27), where the mature fibrils display cross-β conformations (28, 29, 30, 31, 32, 33, 34); and the eventual neuronal death.

Interestingly, after the discovery of the CAG repeats and their relation to neurological disease, it was found that the GAC trinucleotide is also involved in a completely different class of diseases from the known TREDs. These diseases are caused by a very small change in the repeat number, and therefore do not qualify as TREDs. In particular, the human gene for cartilage oligomeric matrix protein exhibits a (GAC)₅ repeat. Expansion by one repeat causes multiple epiphyseal dysplasia, whereas expansion by two repeats or, alternatively, deletion by one repeat, causes pseudoachondroplasia (35). The structure of the various duplexes seems to strongly depend on the pH of the solution and the ionic strength (36). Whereas the CAG trinucleotide leads to expansion, the GAC trinucleotide does not (except for, at most, two extra repeats).

Although the mechanisms underlying TREDs are believed to be extremely complex, simple and robust trends beyond the repeat threshold have been identified, such as the correlation between the repeat length and the probability of further expansion and increased severity of the disease. Another important breakthrough has been the recognition that stable atypical DNA secondary structure in the expanded repeats is “a common and causative factor for expansion in human disease” (37). In addition, mutant transcripts also contribute to the pathogenesis of TREDs through toxic RNA gain-of-function (6, 16, 17, 18, 19, 20, 21). In this mechanism, the RNA TRs sequester proteins that are generally involved in pre-mRNA splicing and regulation. Thus, a first step toward the understanding of these diseases involves the structural characterization of the atypical DNA and RNA structures. Because there is experimental consensus that the most typical DNA and RNA TR secondary structures, at least in the initial stages of expansion, are hairpins whose stem lengths can wildly vary (21, 38, 39, 40), a characterization of the mismatched helical duplexes forming the stems provides a foundation toward a structural understanding of the TR atypical secondary structures.

At present, little is known about the atomic structure and associated dynamics of trinucleotide CAG and GAC repeats. To date, experimental investigations have only considered CAG repeats in RNA; there are no experimental studies with atomic resolution of GAC repeats for DNA or RNA; and, perhaps most importantly, there are no experimental atomic resolution experiments of CAG repeats in DNA. Given that the expansions that characterize TRs originate at the DNA level, a structural understanding of these repeats at the atomic level in DNA is particularly important. Also, as described above, GAC repeats and CAG repeats behave in radically different ways in a biological context, and teasing out the structural differences between these two repeats both in the RNA and DNA context may help in the elucidation of their different behaviors with respect to expansion diseases.

Here we briefly review the experimental results for CAG repeats in RNA. The x-ray RNA-CAG duplex crystal structures include the following sequences: the sequence r(5′-GG-(CAG)₂-CC)₂ (41), and the sequence r(5′-UUGGGC-(CAG)₃-GUCC)₂ (42, 43). This last sequence was also analyzed via NMR (43). The first study found that the duplexes favor the A-RNA form and that the A-A noncanonical pairs are in the anti-anti conformation. In the second sequence, both anti-anti and syn-anti A-A conformations were observed: the A-A pairs in the internal CAG always displayed the anti-anti conformation, whereas one (43) or two (42) of the terminal A-A pairs displayed the anti-syn conformation. These results are in general agreement with the complementary molecular dynamics (MD) simulations (42). Thus, whereas the anti-anti conformation (with fluctuations) for an internal A-A pair in a TR is common to the three studies, the nature of the anti-syn conformations is not clearly established. This is because these conformations occur in the terminal A-A pairs of r(5′-UUGGGC-(CAG)₃-GUCC)₂, where the A-A pairs are flanked by CC/GG steps. Using high-level ab initio calculations, it has been shown that CC/GG steps are the least stable of the 10 dinucleotide steps, with well-separated energies (44) from the other dinucleotide steps. Because these steps are never present in a genuine (CAG)_n TR (which only exhibits GpC steps), it is clear that their presence could bias the conformation of the adjacent A-A pairs.

In addition to these RNA-CAG studies, there is one molecular dynamics study for CAG repeats in DNA (45). This study uses a sequence that is more relevant to the expanded disease, mainly d(CAG)₆. According to the conclusions of this study, the A-A mismatch in DNA behaves in exactly the opposite way than its RNA counterpart: it disfavors the anti-anti and the anti-(+syn) conformations and adopts the (−syn)-(−syn) conformations, resulting in a local Z-form around the mismatch (45). These results are intriguing and raise questions as to the true nature of the A-A mismatches in DNA-CAG.

In this work, we present a unified and comparative description of the nucleic acid duplexes for both DNA and RNA for both CAG and GAC trinucleotide repeats based on MD simulations and free energy calculations. A review of the field of MD simulations of nucleic acids is beyond the scope of this work, and the reader is referred to the authoritative reviews presented in the literature (46, 47, 48). Out of the four possible DNA/RNA CAG/GAC cases, there is experimental data only for RNA-CAG. We therefore begin by making the connection with this experimental data through an explicit investigation of a specific sequence employed in these studies and then move on to a four-trinucleotide repeat duplex. After that, we consider the other three cases—specifically RNA-GAC, DNA-CAG, and DNA-GAC. In particular, we present results corresponding to both free energy calculations and regular 1 μs MD simulations of single mismatch duplexes (5′-CCG-CAG-CGG-3′)₂ and (5′-GGC-GAC-GCC-3′)₂ both for RNA and DNA, and for regular 1-μs MD simulations of four-trinucleotide repeat duplexes (5′-(CAG)₄-3′)₂ and (5′-(GAC)₄-3′)₂. For each of the four duplexes, the free energy calculations involve two maps, each computed with a different pair of collective variables. The eight resulting free energy maps allow us to identify and rank the minima corresponding to the different A-A mismatch conformations. We also identify mechanisms of transition of the A-A mismatches toward the global free energy minimum, and link these mechanisms to paths over the free energy maps. We complete the work with a characterization of the neutralizing Na⁺ ion distributions around the mismatches. Strictly speaking, the noncanonical A-A pairs in RNA are not “mismatches”, because RNA is not necessarily self-complementary. However, because we are considering both DNA and RNA in their duplex form, we will call these noncanonical basepairs “mismatches” for simplicity.

Materials and Methods

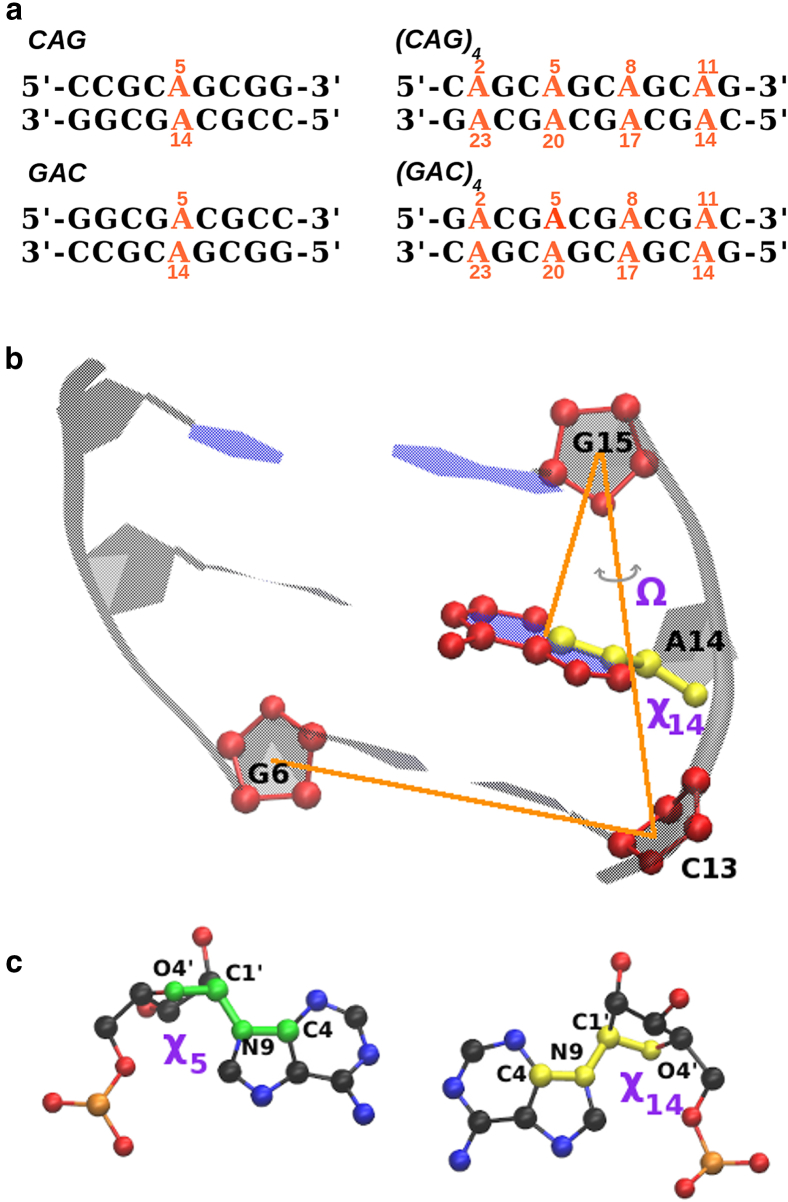
The sequences we investigated are shown in Fig. 1. For both DNA and RNA, we ran regular MD simulations for the four sequences (with various combinations of χ-angles for the mismatches) up to 1 μm. We used the sequences with a single mismatch, (5′-CCG-CAG-CGG)₂ (“CAG” for short), and the complementary sequence (5′-GGC-GAC-GCC)₂ (“GAC” for short) to determine the most favorable A-A mismatch conformation via the computation of free energy maps is described below. The initial conformations for the regular 1 μs MD simulations for the trinucleotide repeats (5′-(CAG)₄-3′)₂ (short-hand notation (CAG)₄) and (5′-(GAC)₄-3′)₂ (short-hand notation (GAC)₄) made use of the four possible combinations of A-A conformations, as described below.

Figure 1.

(a) Shown here are the sequences considered in this study (for both DNA and RNA). (b) Shown here is the schematic view of the center-of-mass pseudodihedral angle Ω (for A14 in CAG) and χ₁₄. (c) Given here is the view of χ₅ and χ₁₄. To see this figure in color, go online.

The simulations were carried out using the PMEMD module of the AMBER v.14 (49) software package with the ff12SB force field with parameters ff99BSC0 (50) for DNA and ff99BSC0+Yildirim’s χ-modification (51) for RNA. The TIP3P model (52) was used for the water molecules, along with the standard parameters for ions as in the AMBER force fields (53). The long-range Coulomb interaction was evaluated by means of the particle-mesh Ewald method (54) with a 9 Å cutoff and an Ewald coefficient of 0.30768. Similarly, the van der Waals interactions were calculated by means of a 9 Å atom-based nonbonded list, with a continuous correction applied to the long-range part of the interaction. The production runs were generated using the leap-frog algorithm with a 1 fs timestep with Langevin dynamics, and a collision frequency of 1 ps⁻¹. Conformations were saved every picosecond of the simulation. The SHAKE algorithm was applied to all bonds involving hydrogen atoms. We also emphasize here that our study is based on classical MD, and quantum effects are not accounted for. For instance, recent quantum chemistry investigations point to a possible transition of the A-base into a rare imino tautomeric form based on a double proton transfer giving rise to local wobbling between hydrogen bonds, which in turn can influence the dissociation rate of the mismatch (55, 56).

To calculate the free energy maps, we made use of the adaptively biased molecular dynamics (ABMD) method (57, 58), which has been implemented for PMEMD in AMBER v.16 (59). ABMD is a proven, elegant, nonequilibrium MD method that belongs to the general category of umbrella sampling methods with a history-dependent biasing potential, a method that, in the long-time limit, reproduces the negative of free energy. The free energy—or potential of mean force—is calculated as a function of one or more collective variables, which must be carefully chosen to reflect the underlying physics of the problem. ABMD has been implemented with multiple walkers (both noninteracting (60) and interacting walkers, with the latter interacting by means of selection algorithm (61)), replica exchange molecular dynamics (62), and well-tempered extensions (63). It is now a mature method that has been applied to a variety of biomolecular systems including small peptides (57, 58), sugar puckering (64), polyproline systems (65, 66, 67, 68, 69), polyglutamine systems (70), DNA systems (71), and others.

We computed free energy maps for a single mismatch in the CAG and GAC sequences for both DNA and RNA. The free energy of these mismatches was calculated as function of three main collective variables, chosen to reflect the structure of the mismatches and to make direct contact with a previous study of RNA-CAG (42). We define 1): Ω as the center-of-mass pseudodihedral angle, which is defined using the centers-of-mass of four atom groups: G6(C1′, C2′, C3′, C4′, O4′), C13(C1′, C2′, C3′, C4′, O4′), G15(C1′, C2′, C3′, C4′, O4′), and A14(N1, C2, N3, C4, C5, C6, N6, N7, C8, N9). This variable describes the base unstacking of A with respect to the helical axis 2); χ₅ as the glycosyl torsion angle χ of A5, namely the dihedral angle O4′-C1′-N9-C4; and 3) χ₁₄, which represents the χ-angle of A14. A schematic view of these collective variables is shown in Fig. 1. With these variables, we constructed two phase diagrams, (Ω, χ₁₄) and (χ₅, χ₁₄). For the first diagram, we found that if we choose χ₅ in the anti range, A5 stays in its anti conformation for all calculations, so the first diagram explores anti-anti and anti-syn conformations, and also whether they are stacked inside the helical core. By construction, therefore, the first diagram cannot explore syn-syn conformations. The (χ₅, χ₁₄) diagram, on the other hand, can explore all options of χ (anti-anti, anti-syn, syn-anti, and syn-syn) but is degenerate with respect to Ω, i.e., it cannot tell whether the bases are inside the helix or have flipped out. A given free energy landscape was deemed to have converged when both the position and differences in the free energy values of the minima remain approximately constant as further ABMD cycles are performed. For the RNA (DNA), ∼150 ns (180 ns) are required for each of the (χ₅, χ₁₄) maps; the DNA (Ω, χ₁₄) are much harder to converge, and results are shown simply after ∼220 ns.

Initial conformations for both MD and free energy calculations were obtained as follows. We first solvated the initial structures and then followed this up with a sequence of ABMD runs of ever finer resolution. The details are as follows. First, we created the duplexes with the four possible combinations of χ-angle for the A-A mismatch: anti-anti, anti-syn, syn-anti, and syn-syn. These were then solvated in an octahedral box with 16 neutralizing Na⁺ ions as in previous work (72), with a distance of at least 10 Å between the duplexes and walls of the box. The box was then filled with a suitable number of waters. The system was then minimized: first keeping the nucleic acid and ions fixed; then, allowing them to move. Subsequently, the temperature was gradually raised using constant volume simulations from 0 to 300 K over 50 ps, followed by a further 50 ps run. Then a 100 ps run at constant volume was used to gradually reduce the restraining harmonic constants for nucleic acids and ions. This was followed by a 1.0 ns constant pressure run, with the χ-angles of A5 and A14 slightly restrained so that these retain their initial anti- or syn- conformation. We took random conformations from the last 200 ps of these runs as the initial conformations for both the ABMD and MD runs. In particular, for the (Ω, χ₁₄) phase diagrams (where the collective variables are angles associated with A14), we picked four structures from A5(anti)-A14(anti) and four from A5(anti)–A14(syn), because the point of this calculation was to assess the anti-syn flipping of A14 (which is completely equivalent to A5). Because DNA is less stable than RNA, a small restraint was applied to χ₅ for the (Ω, χ₁₄) phase diagram. For the (χ₅, χ₁₄) phase diagrams, we picked two structures from each of the four runs (anti-anti, anti-syn, syn-anti, and syn-syn).

Multiple walker ABMD runs at constant volume and 300 K were carried out with eight replicas. The first ABMD simulation was for 20.0 ns with parameters τ_F = 1 ps and 4Δξ = 0.5 radians. This simulation provided for a rough estimate of the free energy landscape over the relevant parameter space. We then followed this up with a finer 100-ns well-tempered ABMD simulation (parameters τ_F = 1 ps, 4Δξ = 0.2 radians, pseudo-temperature 10,000 K). For these runs, the total number of hydrogen bonds in neighboring CG Watson-Crick basepairs were slightly restrained to be six using a 1.0 kcal/mol harmonic constraint. This was used to avoid the large-scale twisting of the whole structure during the long simulations. This constraint, however, was chosen to be flexible enough so as to readily allow for the relevant anti-syn transitions. Finally, a slower and smoother flooding to refine the landscapes was carried out with parameters τ_F = 5 ps, 4Δξ = 0.2 radians, and pseudo-temperature 10,000 K.

Although the above protocol was sufficient for RNA, the DNA duplexes proved to be much more flexible and the A-A mismatches readily became entangled with nucleotide backbone or formed short-lived stacking structures. To avoid these conformations, all the heavy atoms in the DNA duplex, except for the A-A mismatch and neighboring Watson-Crick pairs, were restrained using a very small harmonic constraint of 0.1 kcal/mol for the initial equilibration. For DNA, this constraint was large enough as to preserve the general shape of the structure, although readily allowing for transitions within the A-A mismatch. This small constraint was eliminated for the production runs. We also added a small plane-plane distance restraint between the A-A mismatch and the neighboring CG pairs, which prevents A-A stacking.

Results

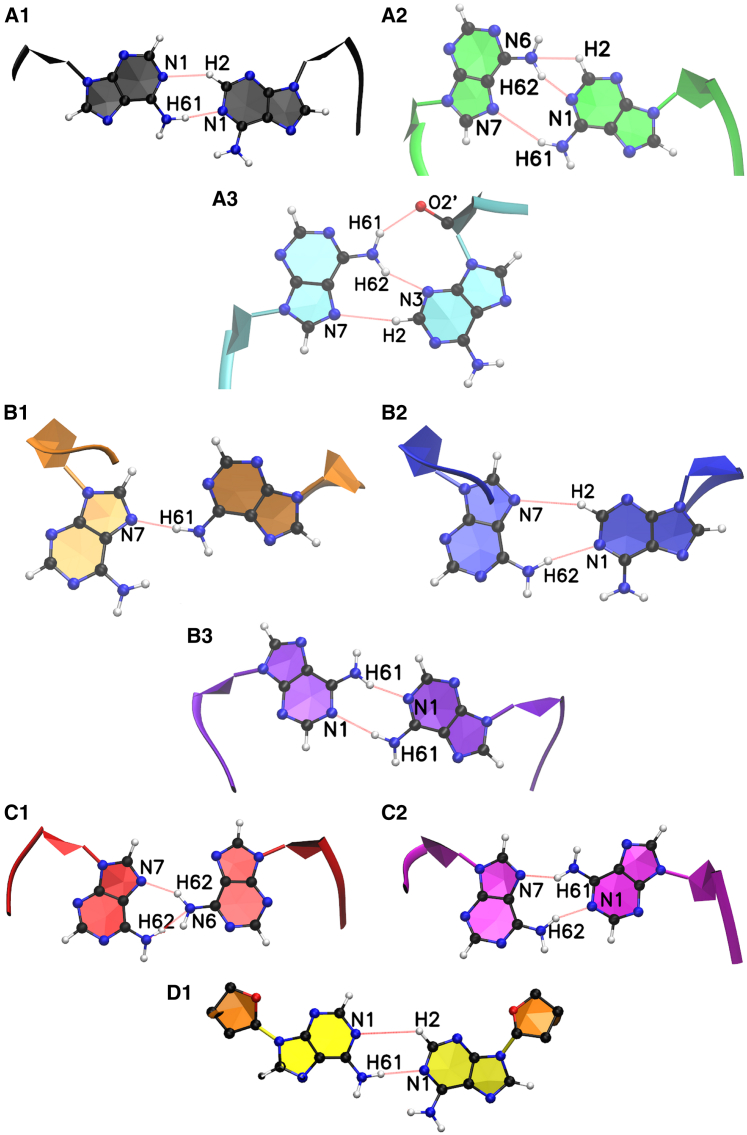
The sequences we investigated are shown in Fig. 1. We begin our discussion with a consideration of the single-mismatch sequence CAG and GAC. For each model CAG/GAC and RNA/DNA, we computed two free energy landscapes: one asymmetric map using the variables Ω and χ₁₄ for A14 (although A5 stays in the anti conformation; see Materials and Methods), and one symmetric map using the variables χ₅ for A5 and χ₁₄ for A14. Positive values of Ω represent well-stacked bases inside the helix core whereas negative values of Ω represent bases that had flipped out of the helix core. Values of χ between 90° and 270° (or, equivalently, between 90° and 180° and between −${180}^{\circ }$ and −${90}^{\circ }$) are considered anti conformations; the other half ranges –90° –90° (or, equivalently 270°–360° and 0°–90°), which corresponds to syn conformations. These free energy landscapes display several stable minima. We have set the deepest minimum in each free energy map as the zero level of the free energy. On the diagrams, we have labeled the more prominent minima with letters that correspond to conformations shown in Fig. 2. For these structures, we have marked the most important hydrogen bonds. These are in good agreement with those obtained from quantum chemistry calculations of unsolvated DNA bases (73, 74). The location and values of these minima are given in Table 1.

Figure 2.

Given here are the A-A mismatch conformations for the main minima associated with the free energy landscapes. The letters denote different conformations: A, anti-anti; B, syn-anti; and C, syn-syn. Here D1 is a special case, because the χ-angle corresponds to syn-syn, but the base conformation looks like anti-anti due to the twisting of the sugar rings that become parallel to the bases. Note also that the hydrogen bonds associated with each of the conformations are also marked. To see this figure in color, go online.

Table 1.

Main Minima for All the Free Energy Maps

Local Minimum		A1	A2	A3	B1	B2	B3	C1	C2	D1
A-A Form		Anti-Anti			Anti-Syn			Syn-Syn
Main H-Bond		N1-H2, H61-N1	N7-H61, H62-N1	N3-H62	N7-H61	N7-H2, H62-N1	H61-N1, N1-H61	N7-H62, N6-H61	N7-H61, H62-N1	N1-H2, H61-N1
RNA-CAG	approximate location (Ω, χ14)	(75,195)	(−35, 190)	—	(50,45)	—	(−35, 60)	—	—	—
	relative free energy (kcal/mol)	0	3.5 ± 0.1	—	1.2 ± 0.2	—	5.4 ± 0.4	—	—	—
	approximate location (χ5, χ14)	(−168, −168)			(−165, 55) for B, (58, −165) for B′			(55,55)		—
	relative free energy (kcal/mol)	0			2.7 ± 0.2			10.3 ± 0.3		—
DNA-CAG	approximate location (Ω, χ14)	(40, 250)	—	—	(61,40)	(23,43)	—	—	—	—
	relative free energy (kcal/mol)	0	—	—	0.2 ± 0.3	2.9 ± 0.3	—	—	—	—
	approximate location (χ5, χ14)	(−110, −110)	—	—	(−100, 40) for B, (45,−100) for B′	—	—	(45,45)	—	(−50, −50)
	relative free energy (kcal/mol)	0	—	—	2.0 ± 1.0	—	—	2.2 ± 0.5	—	5.4 ± 0.6
RNA-GAC	approximate location (Ω, χ14)	(70, 195)	(−35, 190)	—	(78,50)	(50,40)	(−3, 52)	—	—	—
	relative free energy (kcal/mol)	0	5.9 ± 0.1	—	5.6 ± 0.1	5.5 ± 0.1	5.9 ± 0.1	—	—	—
	approximate location (χ5, χ14)	(−163, −163)	—	—	(−165, 46) for B, (44, −162) for B′			(44,78)		—
	relative free energy (kcal/mol)	0	—	—	4.7 ± 0.2			9.8 ± 0.1		—
DNA-GAC	approximate location (Ω, χ14)	(40, 255)	—	—	(78,43)	(61,52)	—	—	—	—
	relative free energy (kcal/mol)	0	—	—	0.6 ± 0.4	0.2 ± 0.2	—	—	—	—
	approximate location (χ5, χ14)	(−101, −101)	—	—	(−140,50) for B, (50, −140) for B′		—	(50,50)	—	(−46, −46)
	relative free energy (kcal/mol)	0	—	—	0.9 ± 0.5		—	0.9 ± 0.2	—	2.4 ± 0.1

The mirror images of B(B1,B2,B3), B′(B1′,B2′,B3′), are not shown. The free energy values in the B columns are the average of B and B′. All the values and errors are calculated based on the last 20 ns of the ABMD simulations.

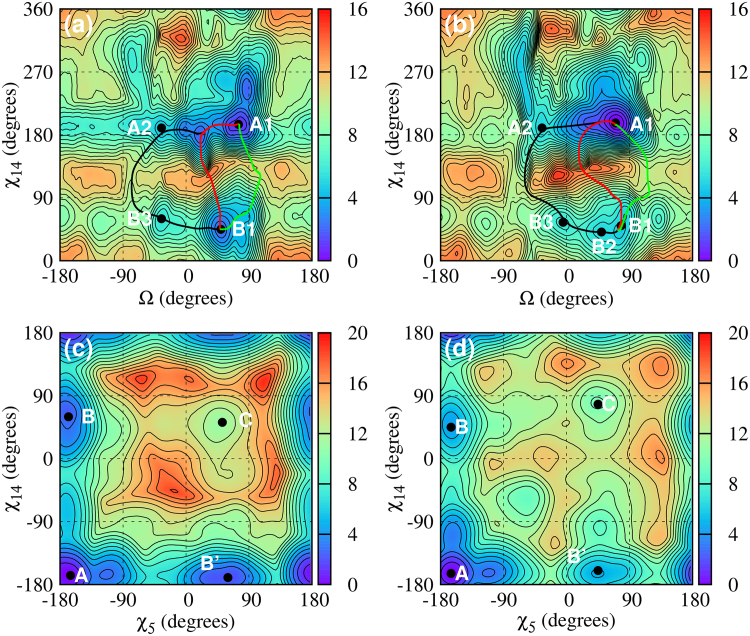
Fig. 3, a and b, shows the (Ω, χ₁₄) free energy maps for RNA-CAG and RNA-GAC. These figures share some general features: 1) the deeper minima with Ω > 0 correspond to well-stacked bases inside the helix core; 2) the shallower minima with Ω < 0 correspond to bases that have approximately flipped out of the helix core; and 3) the deepest minimum A1 corresponds to anti-anti conformation (because A5 is in anti conformation). The differences in free energies between the absolute minimum in A1 (stacked bases, anti-anti) and the next minimum in B1 or B2 (stacked bases, anti-syn) is ∼1.2 kcal/mol for RNA-CAG, but it is 5.6 kcal/mol in RNA-GAC. We have computed least free energy paths on the (Ω, χ₁₄) free energy landscapes in Fig. 3, and examined the corresponding profiles. Sample free energies along these paths are presented in Fig. S3. The paths are relatively similar for the different maps with barriers in the 5–11 kcal/mol range for the B → A transition. The lowest values correspond to RNA-GAC, which therefore exhibits a larger transition rate for the B → A reaction.

Figure 3.

Free energy maps for single mismatches in RNA-CAG (r(5′-CCG-CAG-CGG)₂) and RNA-GAC (r(5′-GGC-GAC-GCC)₂). (a) (Ω, χ₁₄) map for RNA-CAG; (b) (Ω, χ₁₄) map for RNA-GAC; (c) (χ₅, χ₁₄) map for RNA-CAG; and (d) (χ₅, χ₁₄) map for RNA-GAC. The letters represent the local minima, with associated structures as shown in Fig. 2 and free energy values given in Table 1. The primed letters represent minima that are mirror images of minima labeled with the corresponding unprimed letters. The solid lines (black, red and green) describe three possible transition paths from B1 to A1. To see this figure in color, go online.

Fig. 3, c and d, shows the (χ₅, χ₁₄) free energy maps for RNA-CAG and RNA-GAC. Because the two A-bases of the mismatch are completely equivalent, one can expect the free energy maps to show mirror symmetry across the diagonal, a feature that can generally be observed in these phase diagrams. The deepest minimum A1 is at (−168, −168) in RNA-CAG and ∼(−163, −163) in RNA-GAC, corresponding in both cases to anti-anti conformations. In these maps, primed letters indicate minima related by mirror symmetry (e.g., B indicating anti-syn and B′ indicating syn-anti). These minima are degenerate with respect to the base-stacking parameter Ω. In RNA-CAG, the three anti-anti minima A1, A2, and A3 are degenerate in the phase diagram, all ending in the same position (the same happens with the B and B′ minima, and C minima in RNA-CAG and RNA-GAC; see Fig. 1).

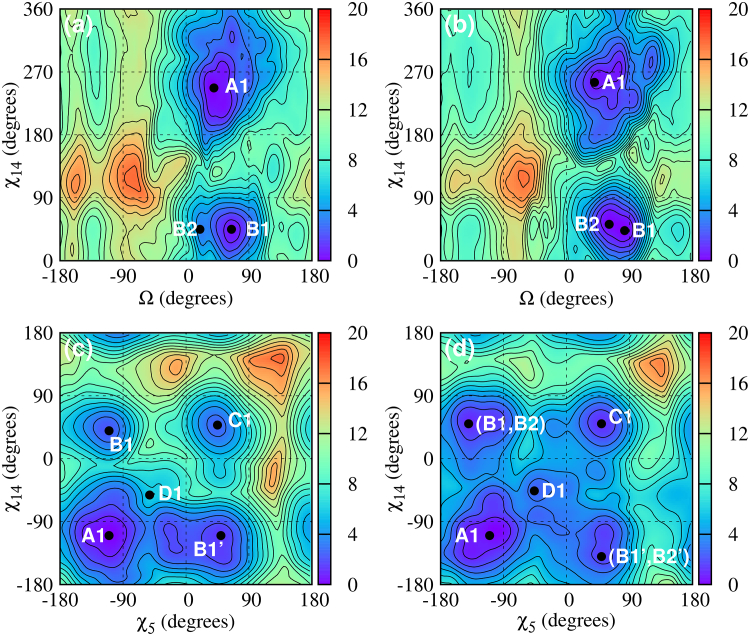
Fig. 4 shows the free energy maps for DNA-CAG, and DNA-GAC. Although there are clear similarities between these free energy maps and their RNA counterparts, differences arise because of the greater flexibility of the DNA sugar ring, which slows down the convergence of the DNA free energy maps. For instance, consider the conformation in Fig. 2 D1. Here, both sugar rings are twisted to lie in the same plane as the A-A mismatch, leading to a (−syn)-(−syn) combination that shows a marked similarity with that in Fig. 2 A1). The (Ω, χ₁₄) free energies are the landscapes most affected by this convergence issue. On these maps, the anti-anti and the anti-syn DNA minima are 0.5 kcal/mol apart, which is within the error of the calculation. Thus the (Ω, χ₁₄) maps cannot truly distinguish the free energy difference between these two minima. This issue, however, is resolved by the (χ₅, χ₁₄) free energy maps, which clearly identify the anti-anti conformation as the global minimum structure. Because the (χ₅, χ₁₄) maps are degenerate with respect to the stacking variable Ω, we inspected all the conformations corresponding to this minimum and found that in all cases the bases are stacked inside the helical core.

Figure 4.

Given here are free energy maps for single mismatches in DNA-CAG (d(5′-CCG-CAG-CGG)₂) and DNA-GAC (d(5′-GGC-GAC-GCC)₂). (a) Shown here are: (Ω, χ₁₄) map for DNA-CAG; (b) (Ω, χ₁₄) map for DNA-GAC; (c) (χ₅, χ₁₄) map for DNA-CAG; and (d) (χ₅, χ₁₄) map for DNA-GAC. The letters represent the local minima, with associated structures as shown in Fig. 2 and free energy values given in Table 1. The primed letters represent minima that are mirror images of minima labeled with the corresponding unprimed letters. To see this figure in color, go online.

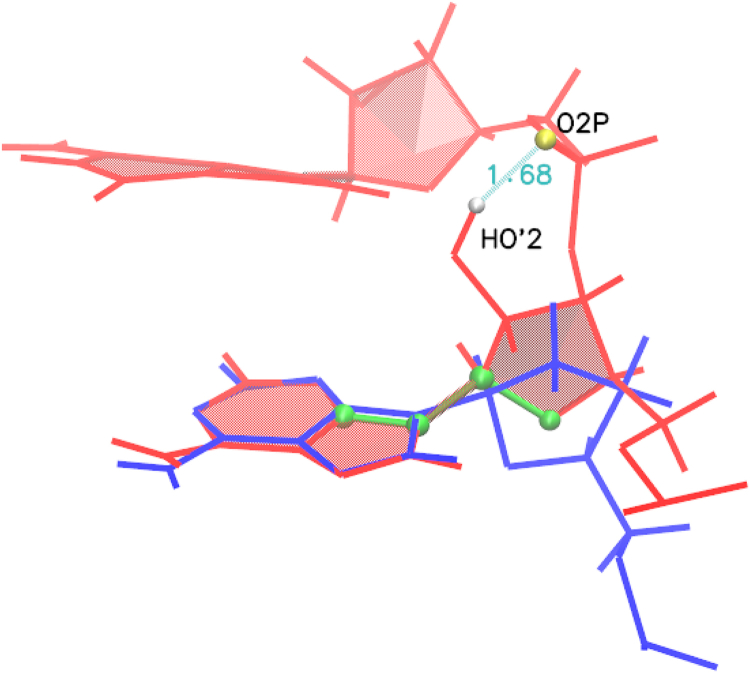
Finally we note that the values of χ for RNA in anti conformation correspond to ∼180–200°, which is properly anti, whereas the equivalent values for DNA correspond to ∼230–260°, which corresponds to high anti. This difference can be explained by the presence of the hydroxyl group at the 2′ position in the sugar ring of RNA, as shown in Fig. 5. This hydroxyl interacts with the RNA backbone, especially the phosphate oxygens (or the other bases) pulling the sugar ring at one end and causing a twist at the other end, which results in an overall decrease of the χ-angle.

Figure 5.

For the anti-anti conformations, the value of χ for DNA corresponds to high anti (230–260°) whereas for RNA, its value corresponds to just anti (180–200°). This difference is caused by the hydroxyl group at the 2′ position in the RNA sugar, which interacts with the backbone or other bases. (Blue lines) DNA; (red lines) RNA. The χ-torsion angle is indicated by green atoms. There is a strong direct interaction between the HO′2 atom and the O2P atom. To see this figure in color, go online.

To gain further insight into the single A-A mismatches, we have followed up these calculations with regular, 1-μs MD simulations. Initial conformations for these single mismatch runs were chosen to be anti-anti, anti-syn, and syn-syn, respectively. The RMSD of the A-A mismatches with respect to the initial A-A conformations is shown in Fig. S2. A summary of these results is as follows. RNA-CAG was found to be stable in the initial anti-anti conformation (global minimum), making occasional excursions from anti-anti A1 to anti-anti A2/A3 (Fig. 2). However, when started in the anti-syn conformation B1, it did not find the global minimum in the 1-μs simulation. On the other hand, when RNA-CAG was started in the initial syn-syn conformation, it quickly transitioned to the anti-syn B1 conformation using the mechanism depicted in Fig. 9 a. RNA-GAC, which starts its trajectory in either anti-anti or anti-syn conformations, transitioned readily to its global minimum conformation A1. However, when it was started in the syn-syn conformation, it did not find its way back to the global minimum in the 1-μs timescale. With respect to DNA there is no major change in the symmetry of the χ-angle for either CAG and GAC sequences and all the runs explored only neighboring minima (e.g., runs that start in the anti-anti A1 conformation transitioned to the A2/A3 conformations, runs that start in the anti-syn B1 conformation transitioned to the B2 conformation, etc.)

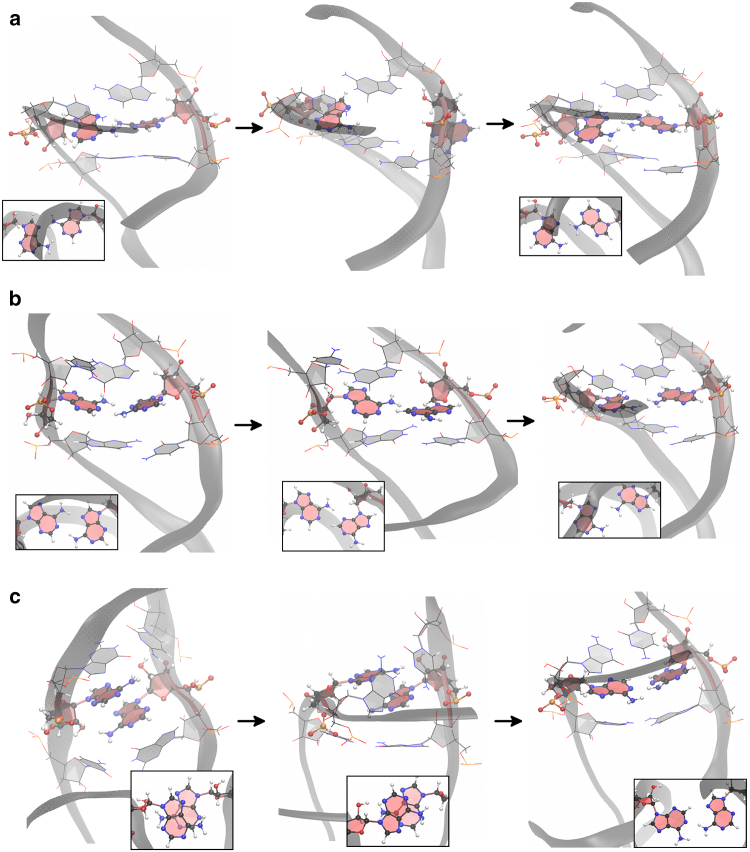
Figure 9.

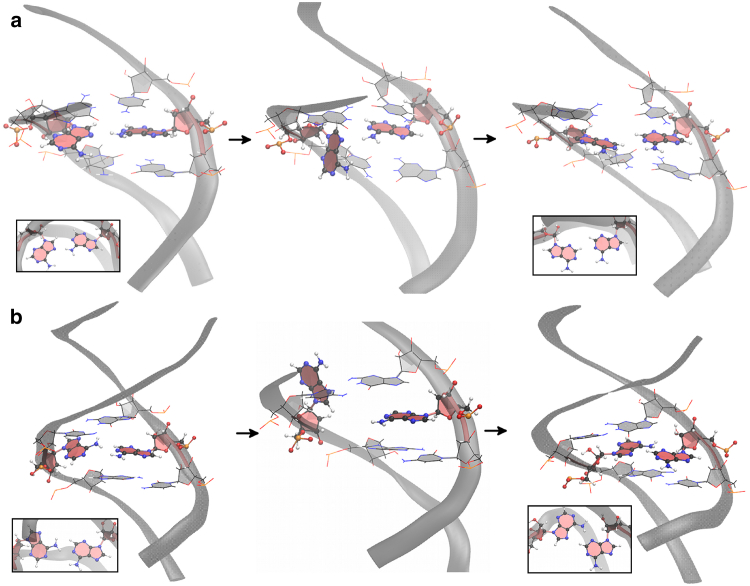
Three mechanisms associated with the transition from the syn-syn conformation to the anti-syn conformation. (a) The transition occurs through base flipping in the minor groove, following a path C1 → C2 → B1. (b) Shown here is the transition that occurs through base flipping in the major groove. (c) The two syn bases first stack on each other, one of them rotates while stacked, and then they become unstacked adopting anti-syn conformations. The insets show the A-A conformation in the vertical direction. See detailed descriptions in the text. To see this figure in color, go online.

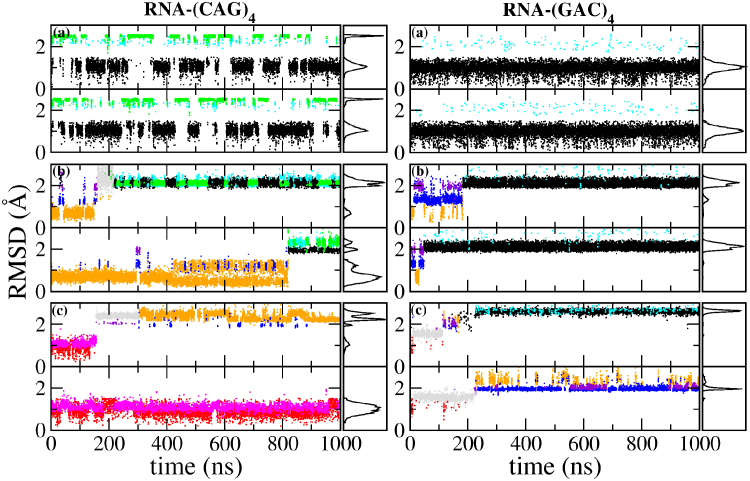
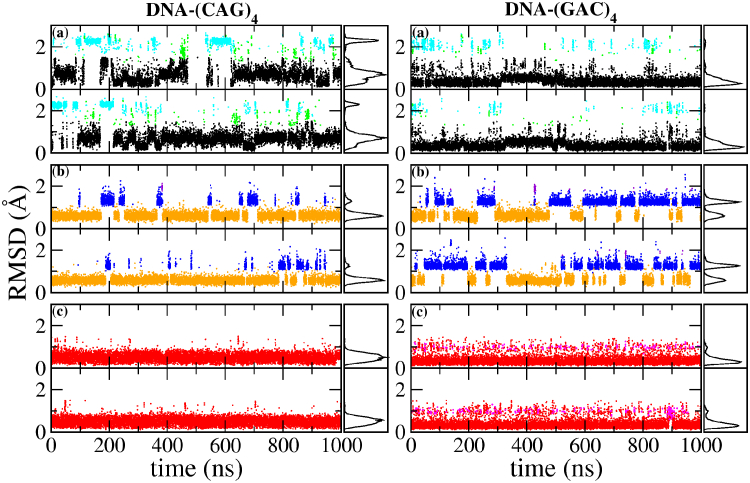
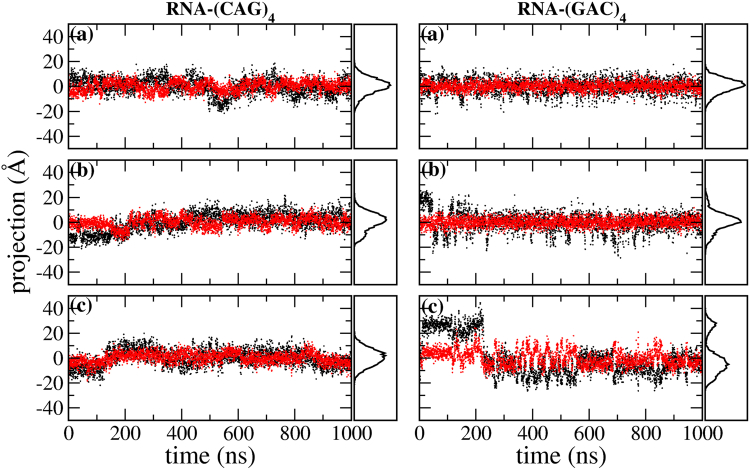
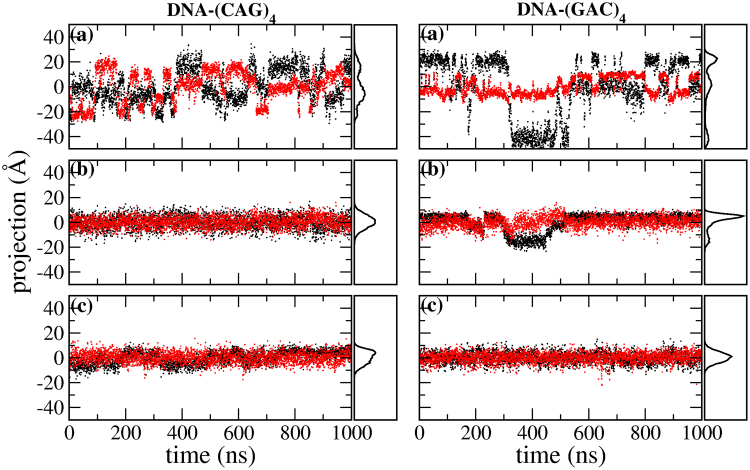
We also ran 1-μs simulations of the TRs (CAG)₄ and (GAC)₄. Figs. 6 and 7 show the RMSD of the inner mismatches A₅–A₂₀ and A₈–A₁₇ as a function of time. RNA duplexes starting in the anti-anti A1 global minimum conformation (Fig. 6) were observed to occasionally transition to the anti-anti A2/A3 conformations in RNA-(CAG)₄, but not in RNA-(GAC)₄, where they remain locked in the global minimum position. RNA duplexes that started in the anti-syn B1 conformation first sampled a few intermediate conformations like B2 and B3, before transitioning to the global minimum conformation A1 (with some A2/A3 in RNA-(CAG)₄ and almost none in RNA-(GAC)₄). Notice that the transition to the global minimum was not observed for the single-mismatch sequence RNA-(CAG). Presumably, this is because the adjacent Watson-Crick pairs in the single mismatch sequence constrain the motion of the mismatched bases. Correspondingly, the extra mismatches in RNA-(CAG)₄ seem to loosen the double helix, allowing for the rotations that lead to the minimum free energy. Also, our calculated free energy barrier in the B → A transition is smaller by 1.7 kcal/mol in RNA-GAC than in RNA-CAG, which helps account for the faster transition of the mismatch in RNA-(GAC)₄ over RNA-(CAG)₄. These simulations also allowed us to identify two different transition mechanisms (to be described below) from the major groove in RNA-(CAG)₄ (see Fig. 8), whereas only a single mechanism was observed from the major groove (see Fig. 8 a) for RNA-(GAC)₄. The corresponding increase in the entropy of the transition for RNA-(CAG)₄ may be the cause of the slightly higher free energy barrier in RNA-(CAG)₄. Finally, simulations in the initial syn-syn conformation were initially observed to oscillate between C1 and C2. In RNA-(CAG)₄ one of the internal mismatches managed to transition to anti-syn B1 using the mechanism depicted in Fig. 9 b, whereas the other remained trapped in the syn-syn conformation. In RNA-(GAC)₄, one of the mismatches transitions to the global minimum A1 (with some mixed A3), whereas the other transitions to the anti-syn conformations B1/B2, both according to the mechanism depicted in Fig. 9 c with a typical stacking conformation. DNA duplexes (Fig. 7), on the other hand, stayed in their initial geometry without major transitions over the 1 μs timescale. Thus, anti-anti conformations were observed to remain in A1, with a few transitions to A2/A3. Anti-syn conformations B1 stay anti-syn, with a few transitions to anti-syn B2, and syn-syn conformations stay syn-syn, with a few transitions from C1 to C2.

Figure 6.

Given here is the RMSD for the internal mismatches in RNA-(CAG)₄ and RNA-(GAC)₄ as obtained from 1-μs MD simulations. In each panel, the upper row shows the RMSD for A₅–A₂₀ and the lower row for A₈–A₁₇. Conformations are color-coded to agree with the mismatch conformations in Fig. 2. Initial conformations for each of the three panels in a column are as follows: (top) anti-anti (conformation A1 in Fig. 2); (middle) anti-syn (B1); and (bottom) syn-syn (C1). (Right panels) Shown here is the distribution of the observed conformations. (Gray) Here we show irregular structures observed during the transition. To see this figure in color, go online.

Figure 7.

Given here is the RMSD for the internal mismatches in DNA-(CAG)₄ and DNA-(GAC)₄ as obtained from 1-μs MD simulations. In each panel, the upper row shows the RMSD for A₅–A₂₀ and the lower row for A₈–A₁₇. Conformations are color-coded to agree with the mismatch conformations in Fig. 2. Initial conformations for each of the three panels in a column are as follows: (top) anti-anti (conformation A1 in Fig. 2); (middle) anti-syn (B1); and (bottom) syn-syn (C1). (Right panels) Shown here is the distribution of the observed conformations. To see this figure in color, go online.

Figure 8.

Two mechanisms associated with the transition from the anti-syn conformation to the anti-anti conformation. (a) The transition occurs through base flipping in the major groove. The structure goes from B1 to A3 to A1. (b) The transition occurs through base flipping in the minor groove. The insets show the A-A conformation in the vertical direction. See detailed descriptions in the text. To see this figure in color, go online.

The slower transition rate of DNA with respect to RNA as exemplified by these MD simulations may be qualitatively understood as follows. A χ-rotation of an A-base can be clockwise or counterclockwise. Clockwise rotations (that would take the A-base along the path 50° → 0° → −110°) are hindered both for RNA and DNA due to steric clashes with neighboring bases. Fig. S4 shows how this clash would occur when the transition is attempted from the major groove in a clockwise rotation. Counterclockwise rotations (50° → 180° → −165°) are free from these clashes. For an RNA A-base, which is in an anti conformation, the counterclockwise rotation is also the shorter path to achieve a B → A (anti-syn to anti-anti) transition. However, for the DNA A-base that is in a high anti conformation, the shorter path is the clockwise rotation, which is strongly hindered. Thus the DNA-A mismatch is forced to rotate through a considerably longer path than the RNA mismatch, presumably resulting in a higher free energy barrier. In addition, both the bending and the hollow core that accompany A-RNA give more breathing space for the base to rotate as compared to B-DNA.

Now we consider the atomic mechanisms involved in various transitions. Fig. 8 shows two different mechanisms involved in an anti-syn to anti-anti conformational transition. In the top row the transition occurs through syn-to-anti base flipping in the major groove. The initial mismatch is in the B1 form. Then one of the A-bases rotates toward the major groove, breaking the N7-H61 hydrogen bond in the process. Its glycosyl angle χ twists and eventually rotates to anti, bringing the conformation to the A3 form, which can easily transition to A1. This corresponds to the green path in Fig. 3. The bottom row illustrates another mechanism where the transition occurs through the minor groove. In this case, one of the mismatched bases in syn conformation rotates toward the minor groove, allowing a transition from B1 to B2 and then B3. At this point the base may rotate back to the B1 form or interact with the backbone or neighboring bases, forming an irregular structure. This is shown as gray shading in Fig. 6 for A5–A10 in RNA-(CAG)₄. The irregular structure may last ∼10 ns. In all cases, the transition is completed when the rotated base flips to the anti form, going to conformation A3 and then A1. This mechanism corresponds to the black path in Fig. 3.

Fig. 9 shows three mechanisms involved in syn-syn to anti-syn conformation. Fig. 9 a shows the transition path through the minor groove. First one mismatched base rotates toward the minor groove side, leading to a C2 form. Then it flips out, generally interacting with the backbone, and then it quickly flips back and changes to the anti B1 form. Fig. 9 b shows the transition path through the major groove. One A-base starts the transition by rotating from C1 to C2. Then the two A-bases separate and one of the bases flips to anti. This results in an unstacked anti-syn mismatch (not often observed in the simulations), as shown in the second graph of Fig. 9 b. The presence of hydrogen bonds in this uncommon anti-syn form makes it relatively stable, and the conformation lasts for ∼100 ns, after which it finally transitions to the B1 form where it remains. Finally Fig. 9 c shows a relatively rare mechanism where the two syn A-bases first become stacked and then one base changes to anti. After this, the bases become unstacked and transition to conformation B1 and then B2.

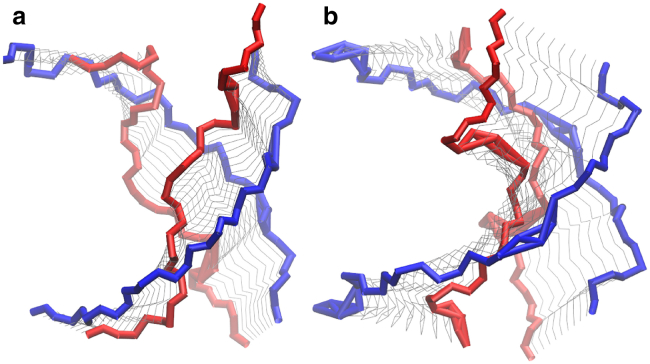
To elucidate to what extent the mismatches distort the initial A-RNA and B-DNA forms, we have carried out a principal component analysis (75) (PCA) on the backbone of the duplexes. Figs. 10 and 11 show the time evolution of the first and second eigenvalues as well as the distribution of conformations projected onto the first principal component for the backbone of (CAG)₄ and (GAC)₄ for RNA and DNA. Only considered for this analysis are the internal residues that encompass internal mismatches, mainly residues 4–9 on one strand and 16–21 on the other. For RNA the eigenvalues stay relatively constant, and the projection of the conformations onto the first principal component results in a stable Gaussian distribution. The only exception is the RNA-(GAC)₄ duplex that starts in a syn-syn conformation, where a transition in the backbone conformation takes place at ∼200 ns, after which the backbone remains stable. On the other hand, the DNA duplexes are stable when they start in anti-syn and syn-syn conformations, but they undergo considerable reaccommodation when they start in anti-anti conformations, both in the (CAG)₄ and (GAC)₄ forms. Conformational fluctuations along the direction of the first PCA eigenvector in the DNA-(CAG)₄, and DNA-(GAC)₄ duplexes with initial anti-anti conformations are shown in Fig. 12. This figure shows that the first eigenvector corresponds to the simultaneous coupling of unbending and unwinding modes.

Figure 10.

Given here are time plots of the PCA first- and second eigenvalues and distribution of the projections of the conformations onto the first principal component axis for the backbone corresponding to internal mismatches in RNA. Considered here are the residues 4–9 on one strand and the complementary residues 16–21 on the other. (Left column) DNA-(CAG)₄; (right column) DNA-(GAC)₄. (Black) First eigenvalue; (red) second eigenvalue. Initial conformations for the MD runs are (a) anti-anti, (b) anti-syn, and (c) syn-syn. To see this figure in color, go online.

Figure 11.

Given here are time plots of the PCA first- and second eigenvalues and distribution of the projections of the conformations onto the first principal component axis for the backbone corresponding to internal mismatches in DNA. Considered here are the residues 4–9 on one strand and the complementary residues 16–21 on the other. (Left column) DNA-(CAG)₄; (right column) DNA-(GAC)₄. (Black) First eigenvalue; (red) second eigenvalue. Initial conformations for the MD runs are as follows: (a) anti-anti, (b) anti-syn, and (c) syn-syn. To see this figure in color, go online.

Figure 12.

Shown here are fluctuations of duplex conformations around the first eigenvector direction, based on the PCA analysis of the backbone. (a) DNA-(CAG)₄; (b) DNA-(GAC)₄. Both duplexes have an initial anti-anti conformation. (Blue line) Most bending conformation; (red line) most unwinding conformation. To see this figure in color, go online.

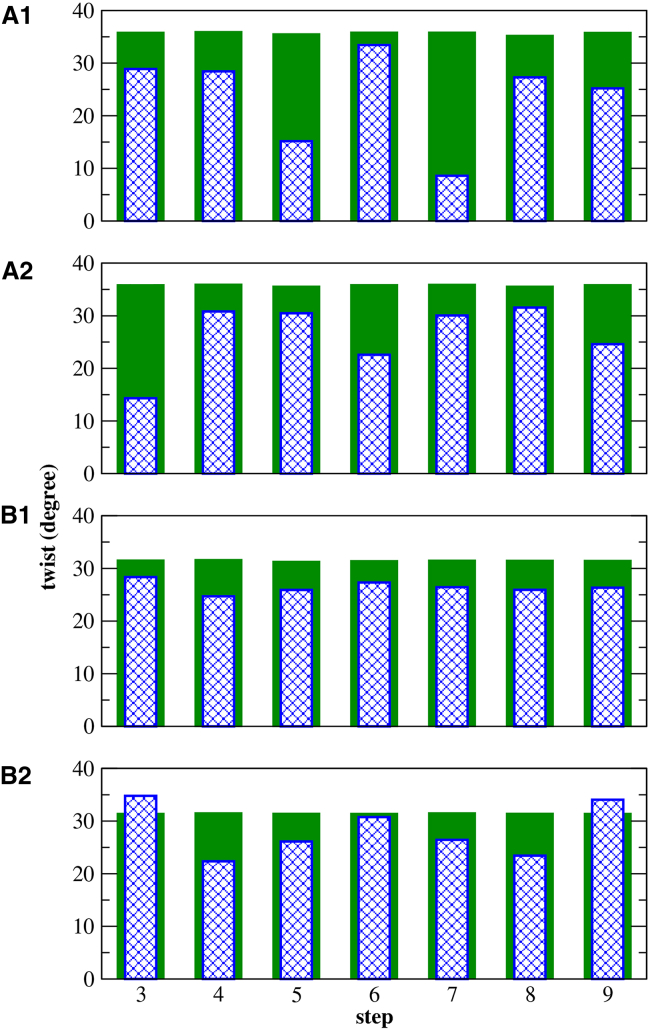
To further quantify this unwinding, we show the simple twist based on C1′ atoms (see definition in the Supporting Material) in Fig. 13 for the middle eight steps for DNA and RNA with initial mismatches in anti-anti conformation. The green bars show the initial, constant twist corresponding to ideal B-DNA with a value of 36°, and ideal A-RNA with a value of 31.5°. Immediately after equilibration, the twist has already acquired sequence-dependent values (data not shown). The blue bars in the figure show the average value of twist for the last 200 ns of the 1 μs simulations. Notice that the final conformations display a mirror symmetry around the central step (step 6) that reflects the inversion symmetry of the sequences. Both DNA and RNA experience some degree of unwinding, but this is considerably more marked for DNA. Although both CAG and GAC sequences show a general decrease of twist, they do not share the same pattern of twist decrease. We take the general definition of Watson-Crick steps as GpC = GC/GC and CpG = CG/CG. In addition, we define steps containing mismatches as m₁ = AG/CA = CA/AG and m₂ = AC/GA = GA/AC. Thus, the pattern of steps for (CAG)₄ is m₁m₁-GpC-m₁m₁-GpC-m₁m₁-GpC-m₁m₁, and for (GAC)₄ it is m₂m₂-CpG-m₂m₂-CpG-m₂m₂-CpG-m₂m₂. Fig. 13 shows that DNA-(CAG)₄ experiences most unwinding in the m₁ steps surrounding the central GpC step (with a considerable decrease of twist) whereas DNA-(GAC)₄ experiences most unwinding at the CpG steps. The twist of RNA-(CAG)₄ barely decreases and it is not much affected by the sequence, the structure staying quite close to ideal A-RNA. The twist of RNA-(GAC)₄ decays at the mismatches, and stays almost the same or even increases at the CpG steps. We also considered the twist for the duplexes starting in initial mismatch conformations other than anti-anti. The RNA duplexes are evolving toward the global minimum with transitions taking place at different times (Fig. 6), and therefore it is enough to consider the anti-anti mismatch conformations, as done in Fig. 13. The DNA duplexes, on the other hand, get stuck in their initial mismatch conformations (Fig. 7). While in these nonequilibrium conformations, DNA does not experience unwinding (see Fig. S5). The unwinding of the anti-anti DNA duplexes can also be illustrated using the concept of handedness, defined in the Supporting Material and shown in Figs. S6–S8. In these figures, positive values of handedness mean a right-handed helix, zero stands for a duplex with no helicity, and negative values of handedness represent a left-handed helix. On Figs. S6 and S8, we see a clear decay of the positive, right-handed values for DNA sequences starting in the anti-anti mismatch conformation. Temporarily, different local turns can show zero or negative handedness for both sequences. The total handedness for the middle basepairs exhibits an oscillatory nature in DNA-(CAG)₄ (with a cycle of ∼200 ns), whereas in addition DNA-(CAG)₄ experiences sudden zero handedness (parallel strands) for ∼200 ns, and then it also recovers suddenly, reinitiating the smoothly oscillatory behavior. Naturally, when the helix unwinds, its radius of gyration increases, as shown in Fig. S9. This is in agreement with the PCA analysis, where the first mode is seen as a coupling of (un)winding and (un)bending. As shown, on average the helix stays slightly unwound but still right-handed, even at the local level (Fig. S8). By contrast, the RNA handedness stays constant throughout the simulation (Fig. S7). This analysis indicates that the global minimum A1 (anti-anti) corresponds to a fairly stable helix in RNA (with relatively small fluctuations), and a very dynamical helix for DNA (with rather large fluctuations). For RNA, in contrast to DNA, it is therefore possible to select from the simulation data a helix that is close to the free energy minimum as being representative of these structures. The duplexes corresponding to RNA-(CAG)₄ and RNA-(CAG)₄ are shown in Fig. S10. The widths of the major and minor grooves, and the inclination angles, are given in Table S1 for the duplexes close to the global minimum A1 and for the duplexes close to the next minimum (anti-syn). Results for anti-anti RNA-(CAG)₄ are in general agreement with those observed previously (43): there is a wider major groove and a substantial decrease of the inclination angle with respect to the canonical A-RNA form. Notably, the next minimum (anti-syn) is quite close to the canonical A-RNA form, with a narrower major groove and larger inclination angles compared to A1. Our results indicate that the RNA-(GAC)₄ structures follow similar trends.

Figure 13.

Shown here is a simple twist based on the C1′ atoms for the middle eight basepairs of the duplexes starting in anti-anti mismatch conformations. (A1) DNA-(CAG)₄; (A2) DNA-(GAC)₄; (B1) RNA-(CAG)₄; and (B2) RNA-(GAC)₄. Green bars show the initial value of ideal B-DNA (36°) and ideal A-RNA (31.5°). Blue bars show the final average values taken from the final 200 ns of the 1 μs simulations. To see this figure in color, go online.

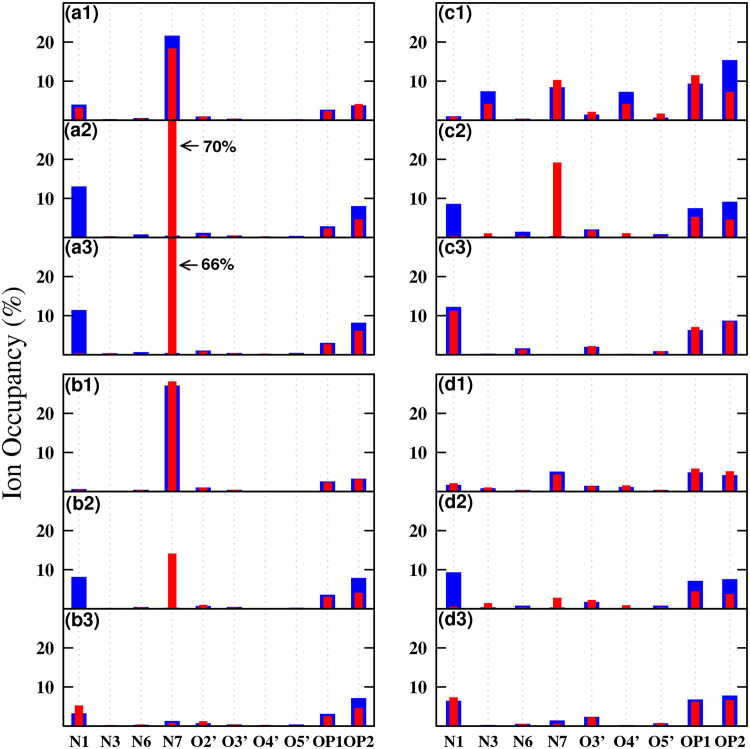
Now we consider the distribution of the neutralizing Na⁺ ions. Fig. S11 shows the distance between Na⁺ ions to the center of mass of the A-A single mismatch in RNA and DNA. Different colors represent different ions to show the single-ion binding time for separate ions. Ions within a distance of 5 Å always have direct interactions with the bases in the mismatch. From the figures we see that the binding time for any single ion in RNA-(GAC) is very short. Both DNA duplexes have slightly longer (and comparable) binding times. RNA-(CAG), on the other hand, has the longest binding times, especially for initial anti-syn and syn-syn conformations. Fig. 14 shows the (any) ion occupancy of the A-A single mismatch in RNA and DNA. If the A-A mismatches stayed in the initial anti-anti or syn-syn conformations, ion distributions around A5 (red) should be the same as ion distribution around A14 (blue) due to the inversion symmetry of the single-mismatch duplexes (which is not present in the initial anti-syn conformations). Both DNA duplexes display this symmetry for initial anti-anti and syn-syn conformations. RNA-(CAG) with initial syn-syn conformation does not show this symmetry because it transitions to anti-syn. For the anti-syn conformations there is a large peak of ion occupation at atom N7 in base A5, which is in the anti conformation.

Figure 14.

Given here is the ion occupancy around a single A-A mismatch in RNA and DNA. (Red) Base A5; (blue) base A14. RNA-CAG: (a1) anti-anti; (a2) anti-syn; and (a3) syn-syn. RNA-GAC: (b1) anti-anti; (b2) anti-syn; and (b3) syn-syn. DNA-CAG: (c1) anti-anti; (c2) anti-syn; and (c3) syn-syn. DNA-GAC: (d1) anti-anti; (d2) anti-syn; and (d3) syn-syn. To see this figure in color, go online.

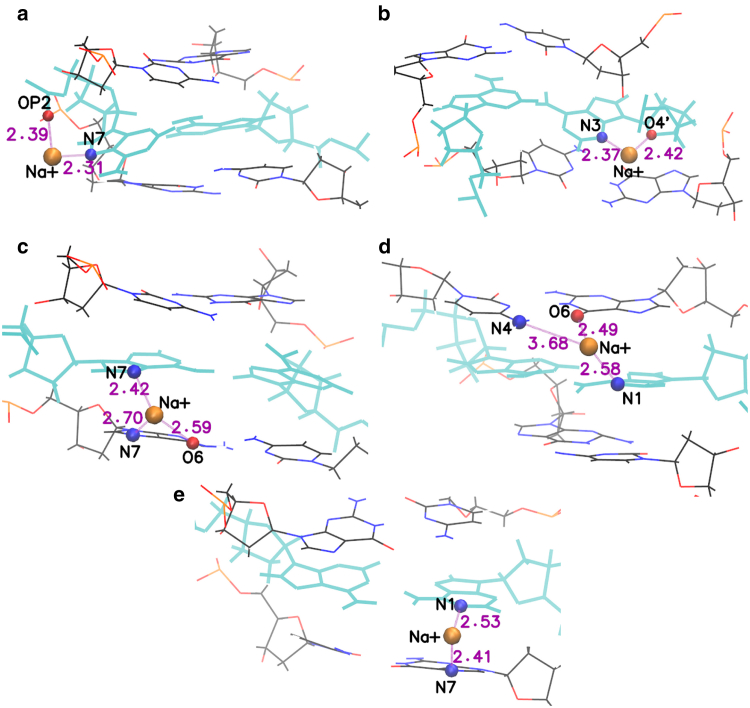
Some typical Na⁺ ion binding conformations are shown in Fig. 15. In an anti-anti conformation, a typical binding site involves the A-N7 atoms (Fig. 15 a). In DNA the ion may also interact directly with the OP2 atom in the backbone, but not in RNA, where distances between bases and backbone are increased by the duplex bending (in this case, the ion interacts through intermediate waters with A-N6 or OP2). However, the ion occupancy of N7 is higher in RNA than in DNA. Fig. 15 b shows binding of Na⁺ by A-N3 and A-O4′ in the minor groove. This binding site has only been observed in DNA-CAG. For anti-syn conformations, a strong ion bridge is observed where the Na⁺ ion forms a bridge between the A-N7 (A in anti conformation) and the G-N7 and G-O6 atoms in the neighboring G-base in the major groove (Fig. 15 c). This ion bridge has highest occupancy and binding time for RNA-CAG (Fig. 14). A similar ion bridge was observed in Gacy et al. (39). For other structures, this bridge is also observed but not as strong as in RNA-CAG. In particular, in GAC sequences the A-mismatch in anti conformation has a weaker stacking with the neighboring G-base, increasing the distances of the atoms that would contribute to trapping the Na⁺ ion. Ion binding in the minor groove can also connect the A-N1 atom (A in syn conformation) and atoms in a C-G Watson-Crick basepair: C-N4 and G-O6 in CAG sequences (Fig. 15 d), and C-N4 and G-N7 in GAC sequences (Fig. 15 e). Finally ion binding to syn-syn mismatches also exhibits a large peak in A-N7 in RNA-CAG, but not in the three other sequences. Other than this, the next important binding site in the bases is A-N1, which engages in binding similar to that described in Fig. 15, d and e.

Figure 15.

Given here are some typical Na⁺ ion binding sites. A-A mismatches are highlighted in cyan and Na⁺ ions are represented by orange spheres. (a) In an anti-anti conformation, a typical binding site involves the A-N7 atoms. In DNA, the ion may also interact with the OP2 atom in the backbone, but not in RNA. (b) Shown here is the ion binding by A-N3 and A-O4′ in the minor groove. This binding site has only been observed in DNA-CAG. (c) For anti-syn conformations, a strong ion bridge is observed where the Na⁺ ion forms a bridge between the A-N7 (A in anti conformation) and the G-N7 and G-O6 atoms in the neighboring G-base in the major groove. (d) Shown here is the ion binding in the minor groove involving the A-N1 atom (A in syn conformation) and G-O6 and C-N4 in neighboring bases, as it occurs in CAG sequences. (e) Shown here is the ion binding in the minor groove involving A-N1 (A in syn conformation) and C-N4 and G-N7 in neighboring bases, as it occurs in GAC sequences. To see this figure in color, go online.

Discussion

Although the mechanisms underlying TREDs are believed to be extremely complex, an important breakthrough has been the recognition that stable atypical DNA secondary structure in the expanded repeats is “a common and causative factor for expansion in human disease” (37). In addition, mutant transcripts also contribute to the pathogenesis of TREDs through toxic RNA gain-of-function (6, 16, 17, 18, 19, 20, 21). Thus, a first step toward the understanding of these diseases involves the structural characterization of the atypical DNA and RNA structures.

As stated in the Introduction, experimental investigations with atomic resolution have only considered CAG repeats in RNA; there are no experimental studies with atomic resolution of GAC repeats—not for DNA or RNA; and, perhaps most importantly, there are no experimental atomic resolution experiments of CAG repeats in DNA. The x-ray RNA-CAG duplex crystal structures include the following sequences: the sequence r(5′-GG-(CAG)₂-CC)₂ (41), and the sequence r(5′-UUGGGC-(CAG)₃-GUCC)₂ (42, 43), which was also analyzed via NMR (43). The first study found that the duplexes favor the A-RNA form and that the A-A noncanonical pairs are in the anti-anti conformation. In the second sequence, both anti-anti and syn-anti A-A conformations were observed: the A-A pairs in the internal CAG always displayed the anti-anti conformation, whereas one (43) or two (42) of the terminal A-A pairs displayed the anti-syn conformation. These results are in general agreement with the complementary MD simulations (42). In this work, the authors computed an (Ω, χ₁₄) phase diagram for r(5′-CCG-CAG-CGG)₂; i.e., for RNA-CAG (the existence of this phase diagram is why we chose the sequences for the single mismatches). Our results for the (Ω, χ₁₄) RNA-CAG phase diagram are in very good agreement with these previous results, identifying the same set of minima with very similar free energy differences (∼1 kcal/mol between the second minimum anti-syn at B1 and the deepest minimum anti-anti at A1). This in turn gives us confidence about the results obtained for the other seven free energy maps not previously investigated.

The other study is for DNA (45) and uses a sequence with a single CAG mismatch inserted in the middle of an otherwise complementary CAG$\cdot$ CTG B-DNA, and a sequence that is more relevant to the expanded disease, mainly d(CAG)₆. According to the conclusions of this study, the A-A mismatch in DNA behaves in exactly the opposite way than its RNA counterpart: it disfavors the anti-anti and the anti-(+syn) conformations and adopts the (−syn)-(−syn) conformations, resulting in a local Z-form around the mismatch (45). Our results, which are based on careful free energy calculations, contradict these conclusions. First, the (Ω, χ₁₄) RNA-CAG free energy map precludes the exploration of syn-syn conformations because one of the mismatched bases always remains in an anti conformation. However, the (χ₅, χ₁₄) landscapes do probe these conformations. Our results are unequivocal: the global minimum for all possible combinations of CAG/GAC RNA/DNA is always anti-anti, followed by anti-syn. We speculate that the observed difference in the previous study may well be due to convergence issues (the lack of convergence of the simulations can be observed, for instance, in the figures that show twist; see Figs. S8 and S15 in the Supporting Information of (40)), which certainly do not reflect the inversion symmetry of the sequences) because the study only reports on 300-ns DNA simulations (45). Having said this, we also notice that difference between “high anti” in our case (250−255°) and the “−syn” reported previously in Khan et al. (45) (270−300°) may not be so large.

In this work, we have carried out free energy calculations and MD studies to determine the preferred conformations of the A-A mismatches in (CAG)_n and (GAC)_n trinucleotide repeats (n = 1 or 4) and the way in which these mismatch conformations affect the overall structure of RNA and DNA duplexes. Our main findings are the following.

• 1)The global minimum (A1) of the various free energy maps corresponds to A-A mismatches stacked inside the core of the helix with anti-anti conformations in the RNA sequences and (high-anti)-(high-anti) conformations in the DNA sequences. In terms of the free energy, the next higher minimum corresponds to anti-syn conformations, whereas syn-syn conformations are even higher.
• 2)DNA helices near the global minimum are very dynamic, exhibiting large fluctuations. RNA helices still fluctuate, but with considerably lesser amplitude than DNA. Fluctuations of the DNA helix around the first eigenvector direction in the PCA of the backbone shows a coupling of bending and unwinding modes. On the other hand, the anti-anti RNA helices close to the global free energy minimum are very stable. They exhibit a wider major groove and a substantial decrease of the inclination angle with respect to the canonical A-RNA form. RNA helices close to the next anti-syn minimum, on the other hand, are quite close to the canonical A-RNA form.
• 3)Free energy barriers between minima corresponding to different states of the glycosyl torsion angle χ are rather high, which results in low transition rates during regular MD. The systems can readily transition between conformations within the same χ-range (say, A1, A2, and A3 for anti-anti; B1, B2, and B3 for anti-syn; and C1 and C2 for syn-syn (see Fig. 2)) because these categories represent minima that are quite close in phase space. However, transitions between different χ categories are much slower.
• 4)Rates of MD transitions of the A-mismatches between different χ-categories are higher for RNA than DNA. The i2′ hydroxyl group in the sugar ring of RNA interacts with the backbone, keeping the corresponding value at a lower χ-value (just anti) with respect to DNA, whose sugar ring adopts a high anti conformation. This results in a shorter path for the RNA ring to rotate from syn to anti, as compared to that for DNA. This, in addition to the hollow core and bending of the A form in RNA, results in a higher transition rate for the syn → anti χ-rotation in RNA. In the 1-μs RNA-(CAG)₄ and RNA-(GAC)₄ simulations, initial conformations starting in anti-anti and in anti-syn all end up in the global minimum, whereas all mismatches except one in RNA-(CAG)₄ manage to transition from syn-syn to anti-syn. Instead, the DNA sequences remain in the initial conformations during the 1-μs simulations (except for transitions to neighboring local minima).
• 5)Several mechanisms for the transitions anti-syn → anti-anti and syn-syn → anti-syn have been identified both through the major and minor grooves. These are identified in Figs. 8 and 9, and all involve intermediate conformations (a transition from syn-syn → anti-anti is achieved through intermediate transitions steps: syn-syn → anti-syn and anti-syn → anti-anti). These transitions involve local distortions of the helical duplexes in the regions surrounding the mismatch. We note that quantum chemistry calculations for the anti-syn → anti-anti transition for isolated A$\cdot$A mismatched bases (without the sugar ring) have recently been published (76).
• 6)DNA-(CAG)₄ and DNA-(GAC)₄ duplexes in anti-anti conformations experience some degree of unwinding. DNA-(CAG)₄ unwinds at the mismatches surrounding the GpC steps and DNA-(GAC)₄ unwinds at the CpG steps. Except for some instantaneous local oscillations, none of the sequences becomes left-handed, and there is no local Z-DNA structure (in addition, the mismatches remain in anti-anti conformations). We notice that the duplex structure seems to strongly depend on the pH of the solution and the ionic strength (36). In particular, CD and UV absorption spectroscopy experiments reveal the presence of GAC (but not CAG) Z-DNA under conditions of low alkaline pH, high NaCl salt, and various divalent ions.
• 7)Under conditions of neutral pH and only neutralizing ions, the main distinctions between CAG and GAC RNA sequences is given by the difference in free energy between the second minimum anti-syn B1 and the first minimum anti-anti A1. This difference is ∼1 kcal/mol for RNA-CAG but ∼5 kcal/mol for RNA-GAC in the (Ω, χ₁₄) map. In addition, the transition rates B1 → A1 are higher for RNA-GAC than RNA-CAG. Taken together, this means that given the proper environment, the mismatches in CAG-rich RNA can easily adopt, and remain relatively stable in, the anti-syn conformation with long lifetimes, whereas those in GAC-rich RNA are less stable in the anti-syn conformation and would evolve more readily toward the global anti-anti minimum.
• 8)Under conditions of neutral pH and only neutralizing ions, the main distinctions between CAG and GAC DNA sequences are given by 1) the difference in the pattern of unwinding described in point 5 above; and 2) the presence of a unique minimum D1 in DNA-GAC that corresponds to a (−syn)-(−syn) conformation quite similar to the anti-anti A1 conformation due to twisting of the sugar rings. D1 is also present in CAG-rich DNA but at higher free energies, and is absent in RNA. On the (χ₅, χ₁₄) phase diagram the situation is inverted as compared to RNA: the differences between the second and first minima are 2.2 kcal/mol for DNA-CAG and 1.1 kcal/mol for DNA-GAC.
• 9)We have characterized the neutralizing Na⁺ ion distribution around the A-A mismatches. The mismatches in RNA-CAG and RNA-GAC have the longest and shortest single-ion binding times, respectively. A-N7 represents a major binding site for all three RNA-CAG geometries, for RNA-GAC anti-anti, and to a lesser extent in RNA-GAC anti-syn and DNA-CAG anti-syn. The other important binding site is A-N1, which contributes to important ion bridges between the A-mismatches and adjacent G-C pairs.

We finish with two more comments. First, a comparison between the two homopurine mismatches A-A in trinucleotide repeats (CAG)_n and (GAC)_n and the G-G mismatches in trinucleotide repeats (GGC)_n and hexanucleotide repeats (GGGGCC)_n shows that they prefer different conformations: A-A favor anti-anti whereas G-G favors anti-syn (77, 78, 79). Second, as stated in the Introduction, CAG expansions cause late-onset, progressive neurodegenerative disorders after the expansions become greater than a given threshold (26). In diseases like Huntington’s disease they can reach up to 250 repeats. GAC repeats, on the other hand, lead to rare skeletal dysplasias but do not expand by more than two repeats (from five normal repeats to a maximum of seven pathological repeats), therefore GAC diseases do not belong to the family of TREDs. Although the duplexes formed by GAC repeats seem to strongly depend on pH and ionic strength, it is interesting to check whether these results (under neutral pH and only neutralizing ions) reflect some differences between the two sequences. The main differences are summarized in points 6 and 7 above. We hope that our future studies under different pH and ionic conditions will help elucidate further differences between the CAG and GAC secondary structures.

Author Contributions

Designed research: all authors. Performed research: F.P. and V.H.M. Analyzed data: F.P. and V.H.M. Wrote paper: all authors.

Editor: Wilma Olson.

Supporting Citations

References (80, 81) appear in the Supporting Material.