BinomiRare: a robust test of the association of a rare-variant with a disease for pooled and meta-analysis, with application to the HCHS/SOL

Abstract

Most regression-based tests of the association between a low-count variant and a binary outcome do not protect type 1 error, especially when tests are rejected based on a very low significance threshold. Noted exception is the Firth test. However, it was recently shown that in meta-analyzing multiple studies all asymptotic, regression-based tests, including the Firth, may not control type 1 error in some settings, and the Firth test may suffer a substantial loss of power. The problem is exacerbated when the case-control proportions differ between studies. We propose the BinomiRare exact test that circumvents the calibration problems of regression-based estimators. We quantify the strength of association between the variant and the disease outcome based on the departure of the number of diseased individuals carrying the variant from the expected distribution of disease probability, under the null hypothesis of no association between the disease outcome and the rare variant. We provide a meta-analytic strategy to combine tests across multiple cohorts that requires that each cohort provides the disease probabilities of all carriers of the variant in question, and the number of diseased individuals among the carriers. We show that BinomiRare controls type 1 error in meta-analysis even when the case-control proportions differ between the studies, and does not lose power compared to pooled analysis. We demonstrate the test in studying the association of rare variants with asthma in the Hispanic Community Health Study/Study of Latinos.

Introduction

With whole-exome and whole-genome sequencing studies becoming increasingly common, low-count variants are frequently observed. Regression-based association tests such as the Wald, Score, and likelihood ratio tests, are known to be poorly calibrated for rare variants, i.e. they often do not protect type 1 error rates. An exception is the Firth test (Firth, 1993) in which a penalized likelihood is used to correct for the asymptotic bias of the parameter estimates. The Firth test has better type 1 error performance, but, as Ma et al. (2013) showed, in meta-analyzing test statistics from multiple studies, even the Firth test may not always protect type 1 error and may lose power compared to the pooled test.

In this work we propose a novel test for the association of low-count variants with an outcome, that works well in both pooled- and meta-analysis. To test a given variant, we first estimate the within-sample disease probability model using the entire sample. We account for potential confounding bias by estimating this probability in a regression model, adjusting for covariates. Under the null hypothesis of no association between the genetic variant and disease status, we use this model to obtain disease probabilities for each of the carriers. Under the null hypothesis the number of diseased carriers is distributed as a random variable sampled from Poisson-Binomial distribution with these probabilities, and p-values are readily obtained. For meta-analysis, each cohort provides the estimated disease probabilities of the carriers, and the total number of diseased carriers.

BinomiRare does not suffer from the same asymptotic calibration problems as the traditional regression-based tests, as it only requires estimation of a probability model based on the entire sample. Therefore, as we show, it controls type 1 error in both pooled- and meta-analysis. It is extremely quick and efficient: it requires fitting a simple regression model to all observations once, and then calculating Poisson-Binomial probabilities based on the probabilities of disease in the carriers and the number diseased carriers, to obtain p-values. In what follows, we first provide a detailed description of the BinomiRare approach, followed by demonstration in simulations and in studying the association of rare variants with asthma in the HCHS/SOL. Asthma is a particularly interesting trait, since its prevalence widely differs between the HCHS/SOL ethnic groups.

Methods

We begin by describing the BinomiRare approach for the simple case of no covariates, and then generalize it to accommodate adjusting variables. Consider a study sample of N individuals. For the i = 1, . . . , N individual, let D_i ∈ {0, 1} denote disease status, and g_i ∈ {0, 1, 2} denote the allele count at the variant of interest. In practice, since the variants of interest are rare, usually g_i ∈ {0, 1}. We say that individual i is a “carrier” if g_i > 0, and a “non-carrier” otherwise. Let $n_c={\sum }_{i=1}^N{1}_{(g_i>0)}$ denote the number of carriers in the study, and $n_{c,d}={\sum }_{i=1}^N{1}_{(g_i>0)}{D}_i$ denote the number of diseased carriers.

Single study, no covariates

Under the null hypothesis, g ⊥ D, where ⊥ denotes independence, and we can estimate the within-sample disease probability in the study as the proportion

$${\widehat{p}}_d=\widehat{Pr}(D_i=1)=\frac{{\sum }_{i=1}^N{D}_i}{N}.$$ (1)

Here note that even if the variant is associated with the disease status, since the variant is assumed rare, the disease probability will likely not change much if calculated based only using non-carriers, say, or using the entire sample. Under the null hypothesis the following holds:

$$\widehat{Pr}(D_i=1\mid g_i>0)=\widehat{Pr}(D_i=1)={\widehat{p}}_d.$$ (2)

Therefore, the disease status in any carrier i could be treated as a random draw from a Bernoulli distribution with probability p̂_d, and the total number of diseased carriers is a draw from a Binomial(n_c, p̂_d) distribution. We calculate the p-value for testing the association of the genetic variant with the disease using the binomial probability function, as the probability of obtaining the observed number of diseased individuals within the carriers n_c, plus the probability of a less likely number of individuals. Since the Binomial distribution is asymmetric, a “more extreme number of individuals” is defined as the number of individuals with probability lower than the probability of the observed number of individuals. In practice, we use the so-called mid p-value. The mid p-value was first proposed by Lancaster (1961) and lately shown to be beneficial in exact tests for Hardy-Weinberg equilibrium when the variant’s minor allele frequency is low (Graffelman and Moreno, 2013). Specifically:

Let X ~ binomial(n_c, p̂_d). Define p̂_d(k) = p(X = k|p̂_d, n_c). The mid p-value is given by:

$$\frac{1}{2}{\widehat{p}}_d(n_{c,d})+\sum _{\begin{array}{c}k=1\\ k\ne n_{c,d}\end{array}}^{n_c}{\widehat{p}}_d(k)1_{[{\widehat{p}}_d(k)\le {\widehat{p}}_d(n_{c,d})]},$$ (3)

and this is the p-value of the test of association between variant g and the disease.

Adjustment for covariates

Adjustment for confounders is often important, most notably in avoiding population stratification by adjusting for principal components of the genetic data (Astle and Balding, 2009). If carriers are enriched for diseased individuals, solely due to to the association of both the disease and the genetic variant with ancestry, a test that does not adjust for ancestry may wrongly reject the null hypothesis. We handle confounders by estimating their effect on the probability of disease in the whole sample, and accounting for them in estimating disease probabilities that are allowed to vary between study individuals. Let h(·) be a link function, e.g. the logistic function h(u) = log[u/(1−u)], or the identity function h(u) = u, and let x_i be the vector of adjusting covariates of individual i = 1, . . . , N. Consider the model

$$h[Pr(D_i=1\mid {\mathit{x}}_i)]=\alpha +{\mathit{x}}_i^T\mathit{\beta }.$$ (4)

We fit the model to obtain maximum likelihood estimates α̂, β̂. Assuming no genotype-covariates interaction on the effect on disease, under the null hypothesis

$${\widehat{p}}_{d,i}=\widehat{Pr}(D_i=1\mid {\mathit{x}}_i,g_i)=h^{-1}\left(\widehat{\alpha }+{\mathit{x}}_i^T\widehat{\mathit{\beta }}\right).$$ (5)

As in the simpler case of no covariates, the disease status in a carrier i can be treated as a random draw from a Bernoulli distribution with probability p̂_d,i. However, since the disease statuses of the different carriers are not identically distributed (potentially p̂_d,i ≠ p̂_d,j for i ≠ j), the total number of diseased carriers is now a draw from a Poisson-Binomial distribution.

The Poisson Binomial distribution

A Poisson-Binomial random variable is a sum of independent Bernoulli random variables with different probabilities of success. Here, the number of diseased carriers n_c,d is distributed as a Poisson-Binomial random variable with a parameter vector p̂ = (p̂_d,k1, . . . p̂_d,knc )^T, where k₁, . . . , k_nc is the vector of indices of the carriers of the genetic variant. Although the computation of the Poisson-Binomial distribution is not straightforward, Hong (2013) developed a computationally efficient algorithm that is implemented in a public R package “poibin” (Hong, 2011). To compute p-values, we take a similar approach to the mid p-value described before. Define D^pb(p̂) to be the Poisson-Binomial random variable with parameter vector p̂. Then the BinomiRare p-value for a variant-trait association is calculated by:

$$\begin{gathered} \frac{1}{2}Pr[D^{pb}(\widehat{\mathbf{p}})=n_{c,d}]+\sum _{\begin{array}{c}k=1\\ k\ne n_{c,d}\end{array}}^{n_c} \\ Pr[D^{pb}(\widehat{\mathbf{p}})=k]1_{(Pr[D^{pb}(\widehat{\mathbf{p}})=k]\le Pr[D^{pb}(\widehat{\mathbf{p}})=n_{c,d}])}. \end{gathered}$$ (6)

Meta-analysis

Suppose now that there are s = 1, . . . , S studies to combine the evidence from in meta-analysis. Suppose the sth study has N^s individuals, $n_c^s$ carriers, and $n_{c,d}^s$ diseased carriers, and study level covariates are allowed to differ between studies. Consider the model

$$h_s[Pr(D_i=1\mid {\mathit{x}}_i,\text{study}s)]={\alpha }_s+{\mathit{x}}_i^T{\mathit{\beta }}_s,s=1\dots ,S.$$ (7)

We fit the model in each individual study to obtain maximum likelihood estimates α̂_s, β̂_s from (7), and obtain disease probabilities for each individual in the study population. Let ${\widehat{\mathbf{p}}}_s={({\widehat{p}}_{d,k_1}^s,\dots {\widehat{p}}_{d,k_{n_c^s}}^s)}^T$ be the vector of estimated disease probabilities in the carriers of the sth study, s = 1, . . . , S. Denote the vector of length $n_c^1+\dots +n_c^S=n_c$ of disease probabilities across all carriers in the combined set of studies by $\widehat{\mathbf{p}}={({\widehat{\mathbf{p}}}_1^T,\dots ,{\widehat{\mathbf{p}}}_S^T)}^T$. The BinomiRare test for a single (pooled) study readily generalizes to meta-analysis. Each variant is tested using the mid p-value based on the Poisson-Binomial random variable D^pb(p̂) $n_{c,d}=n_{c,d}^1+\dots +n_{c,d}^S$ diseased carriers. We summarize the proposed approach to testing the associations between rare variants and a disease outcome using BinomiRare in the following procedure:

Procedure for meta-analysis

1. Each study fits a disease probability model on all study individuals. The probability models do not include the tested variants. Estimated disease probabilities are assigned for each of the study participants.

2. For each variant, each study s = 1, . . . , S identifies the set of carriers and provides

   • The vector ${\widehat{\mathbf{p}}}^s=\{{\widehat{p}}_{k_1}^s,\dots ,{\widehat{p}}_{k_{n_c^s}}^s\}$ of their estimated disease probabilities.

   • $n_{c,d}^s$, the number of diseased individuals among them.

3. The meta-analysis site calculates the BinomiRare p-value for each of the variants based on the combined vector of estimated disease probabilities $\widehat{\mathbf{p}}={({\widehat{\mathbf{p}}}_1^T,\dots ,{\widehat{\mathbf{p}}}_S^T)}^T$, the total number of diseased individuals carrying this variant $n_{c,d}^1+\dots +n_{c,d}^S$, and the Poisson-Binomial distribution with parameter vector p̂.

In the Supplementary Material, we show how one can calculate power for the Binomi-Rare test for a given study based on the number of cases and controls, the number of carriers, and the effect size of the variant.

Simulation studies

We studied the size and power of the BinomiRare test and compared it to other existing tests in various simulation scenarios. In all simulations we generated 10,000 individuals. We considered pooled analyses, in which all data are available to the investigators and are analyzed together, mimicking a single study, and meta-analyses of 5 studies, each with 2,000 individuals. For meta-analysis, we considered both the settings in which all studies have the same case-control proportions, and the settings in which the studies have different case-control proportions.

We sampled disease status according to the logistic model

$$\text{logit}\{p(D=1\mid x,g)\}={\alpha }_s+20x+\beta g,s=1,\dots ,5,$$

with x a confounder, simulated as associated with both the genotype g and the disease status D, as explained henceforth. When studying pooled and meta-analysis with the same case-control proportions, we set α₁ = . . . = α₅ = −2.6, so there are about 7% diseased individuals among non-carriers with x = 0. When studying meta-analysis with different case-control proportions between studies, we set α₁ = −2.6, α₂ = −2.4, . . . , α₅ = −1.6. The confounder x was generated by first sampling a random variable from a normal distribution $x~N(0,{\sigma }_x^2)$, with σ_x ∈ {0.02, 0.01, 0.005, 0.0025}, depending on the scenario, then thresholding at 0. After thresholding x_i ∈ [0, 1). Then, each variant count g_i was sampled from a Binomial distribution with probabilities x_i, i = 1, . . . , n. Thus, x_i was associated with both the outcome and the variant, satisfying the definition of a confounder. Lower σ_x yielded lower counts of the variant. We ran 10⁷ simulations from each scenario to evaluate type 1 error, and 10⁴ simulations to evaluate power.

To glean into the effect of model misspecification in pooled and meta-analysis on the performance of the various estimators, we simulated an additional scenario in which the disease status was sampled according to a linear disease risk model:

$$p(D=1\mid x,g)={\alpha }_s+20x+\beta g,s=1,\dots ,5,$$

with now α_s = 0.02, 0.04, . . . , 0.1. We applied both pooled and meta-analysis.

The compared tests were the BinomiRare, Firth (implemented using the “logistf” package (Heinze et al., 2013)), Wald, Score, and Likelihood Ratio test (LRT). When studying meta-analysis, we applied inverse-variance weighted fixed-effect meta-analysis for the Firth and Wald tests, summed the score test statistics from each study to obtain a test statistic distributed as N(0, f) in meta-analyzing the Score test, and for the LRT, we summed the study-specific LRT statistics to obtain a χ² distribution with f degrees of freedom, where f is the number of meta-analyzed studies, and the distributions are under the null. When there were no carriers in one of the studies, it did not contribute to the meta-analysis.

The HCHS/SOL

The HCHS/SOL (LaVange et al., 2010; Sorlie et al., 2010) is a community based cohort study, following self-identified Hispanic individuals from four field centers (Chicago, IL; Miami, FL; Bronx, NY; and San Diego, CA). The study was approved by the institutional review boards at each field center, where all participants gave written informed consent. Individuals were sampled via a two-stage sampling scheme, in which census block units were sampled in the first stage, and households were sampled from the block units at the second stage. The sampling was preferential towards Hispanics/Latinos. Almost 13,000 study participants consented for genotyping. Of these, 11,222 study individuals are available with genotyping data and self reported doctor diagnosis of current asthma status. We removed at random correlated individuals, defined as relatives of first, second, or third degree, and individuals living in the same household as other participants. 7,175 eligible individuals remained.

Genotyping and quality control are described in Conomos et al. (2016) which also defined the construction of the Genetic Analysis Groups, a classification of individuals based on both their self-reported ethnicity and their genetic makeup, into six groups: Central American, Cuban, Dominican, Mexican, Puerto Rican, and South American. Table 1 provides the number of eligible individuals belonging to each of the genetic analysis groups, and the number of participants with current asthma, of those. The observed proportions of asthmatic individuals differ among the genetic analysis groups: while about 4% of the individuals in the South American, Central American, and Mexican genetic analysis groups reported current asthma, about 10% of the Cuban and the Dominican genetic analysis groups reported current asthma, and 26% of the individuals in the Puerto Rican genetic analysis group. It is easy to show, based on the strategy for power calculation provided in the Supplementary Material, that for a variant that has the same frequency and the same effect in all genetic analysis groups, the BinomiRare has the highest power to detect associations in the Puerto Rican group (and much higher power if all groups are combined).

Table 1.

The number of analysis participants by genetic analysis groups, and the number of participants with current asthma (as percentage of their group in parentheses).

Group	Participants	Current asthma
CentralAmerican	773	29 (3.8%)
SouthAmerican	499	22 (4.4%)
Mexican	2688	119 (4.4%)
PuertoRican	1298	339 (26.1%)
Cuban	1234	136 (11%)
Dominican	670	70 (10.4%)
All combined	7162	715 (10%)

We analyzed 601,914 genotyped SNPs with a minor allele count of up to 250 on the entire HCHS/SOL together. We compared the Firth and the BinomiRare tests when pooling all individual level data together, and in meta-analyzing results applied on each geneticanalysis group separately. For Firth, we used the small sample approximation implemented in the SKAT R package (Lee et al., 2015) when the groups had less than 2,000 individuals, and use a fixed-effects inverse-variance weighted meta-analysis. Distributions of p-values are compared by scatter plots, and genomic inflation factor λ_gc (Devlin and Roeder, 1999) for each of the analyses were calculated based on transforming the median p-values into ${\chi }_{(1)}^2$ random variables, since BinomiRare does not have a test statistic. Specifically, we had

$${\lambda }_{gc}(\mathbf{p})=\frac{F_{{\chi }_{(1)}^2}^{-1}[\text{median}(\mathbf{p})]}{F_{{\chi }_{(1)}^2}^{-1}[0.5]}$$

where p is a vector of p-values and $F_{{\chi }_{(1)}^2}$ is the distribution function of a chi-square random variable with one degree of freedom. We also report the top results from all analyses, as all variants with p-value < 10⁻⁶.

Results

Simulation studies

Table 2 provides type 1 error and power estimates obtained from various simulation studies, and focusing on the BinomiRare and the Firth tests. To save space, the type 1 error is scaled by the p-value threshold (α), so that the desired number is 1 (conversely, the type 1 error is the written number, multiplied by α). In all settings, we do not provide power when the corresponding type 1 error was inflated. One can see that in all these simulations, the BinomiRare controlled the type 1 error. Although it is always slightly less powerful than the Firth test in the pooled scenario, it is almost as powerful when the allele count is very low, and it controls type 1 error in meta-analysis, while in these simulations the Firth test does not. Additional simulation results are provided in the Supplementary Material. In brief, these results show that the Wald test, Score test, and LRT usually do not protect the type 1 error when testing rare variants, while the LRT sometimes becomes very conservative. When considering sensitivity to model misspecification of using a logistic model when the data were simulated from a linear model, both BinomiRare and the Firth tests performed well in a pooled analysis, but Firth has increased inflation in meta-analysis.

Table 2.

Results from simulation studies, focusing on the BinomiRare (BR) and Firth tests, by levels of α for declaring significance. σ_x ∈ {0.02, 0.01, 0.005, 0.0025}, corresponding to average number of {160, 80, 40, 20} carriers in the simulations. Meta-analysis had either the same or different case proportions across studies. Top: type 1 error estimates given in terms of the proportion of rejected tests at the given α level, divided by α, calculated from 1× 10⁷ simulations. Bottom: power, computed as the proportion of rejected tests at the given α level, computed from 1 × 10⁴ simulations. The power is not provided when tests did not control the type 1 error.

	pooled analyses								meta-analyses - case proportion
									same		diff		same
Scaled type 1 error, βg = 0 (multiply by α)
	σx = 0.02		σx = 0.01		σx = 0.005		σx = 0.0025		σx = 0.02				σx = 0.01
α	BR	Firth	BR	Firth	BR	Firth	BR	Firth	BR	Firth	BR	Firth	BR	Firth
1 × 10−2	0.80	0.97	0.88	0.93	0.86	0.69	0.81	0.76	0.80	2.84	0.81	1.37	0.88	5.61
1 × 10−3	0.69	0.95	0.80	0.86	0.80	0.73	0.74	0.80	0.69	4.38	0.71	1.47	0.79	10.20
1 × 10−4	0.63	0.94	0.65	0.62	0.70	0.73	0.72	0.86	0.61	6.49	0.62	1.44	0.65	16.96
1 × 10−5	0.61	0.94	0.60	0.68	0.72	0.76	0.70	0.88	0.53	9.23	0.56	1.24	0.64	26.62
Power, βg = 1
1 × 10−2	0.97	0.98	0.72	0.73	0.42	0.40	0.01	0.01	0.98	–	1.00	–	0.73	–
1 × 10−3	0.90	0.91	0.47	0.49	0.19	0.18	0.00	0.00	0.91	–	0.98	–	0.48	–
1 × 10−4	0.76	0.79	0.28	0.29	0.07	0.08	0.00	0.00	0.78	–	0.93	–	0.29	–
1 × 10−5	0.58	0.62	0.15	0.15	0.03	0.03	0.00	0.00	0.61	–	0.83	–	0.15	–

Association of rare variants with current asthma in the HCHS/SOL Analyses of the entire HCHS/SOL cohort

Table 3 reports results from the compared analyses as λ_gc, p-values of two variants with p-value < 10⁻⁶, and the correlation between the p-value obtained using all tests and the Firth pooled. Figure 1 displays scatter plots comparing the distribution of p-values of the same tests to p-values of Firth pooled. There were two adjacent variants reported, and all analyses gave similar p-values. rs13401266 had 71 carriers and rs13421020 had 72 carriers, and 25 of the carriers of both variants self reported current asthma diagnosis.

Table 3.

Comparison of the Firth and BinomiRare tests performed on the HCHS/SOL cohort of uncorrelated individuals, in pooled analysis of all individuals, and in meta-analyzing the six genetic analysis groups. λ_gc is the inflation factor, “cor W Firth pooled” is the correlation between the p-values in the Firth analysis on the pooled data set and the test in question, and rs13401266 (chr2:143070709, 71 carriers, 25 diseased) and rs13421020 (chr2:143074067, 72 carriers, 25 diseased) pval are the p-values of these variants in each of the analyses.

Test	λgc	cor w Firth pooled	rs13401266 pval	rs13421020 pval
Firth pooled	1.00	–	6.05×10−7	9.94×10−7
Firth meta	0.65	0.37	4.17×10−6	6.12 ×10−6
BR pooled	0.91	0.94	2.38×10−7	2.70×10−7
BR meta	0.91	0.94	2.38×10−7	2.70×10−7

Figure 1.

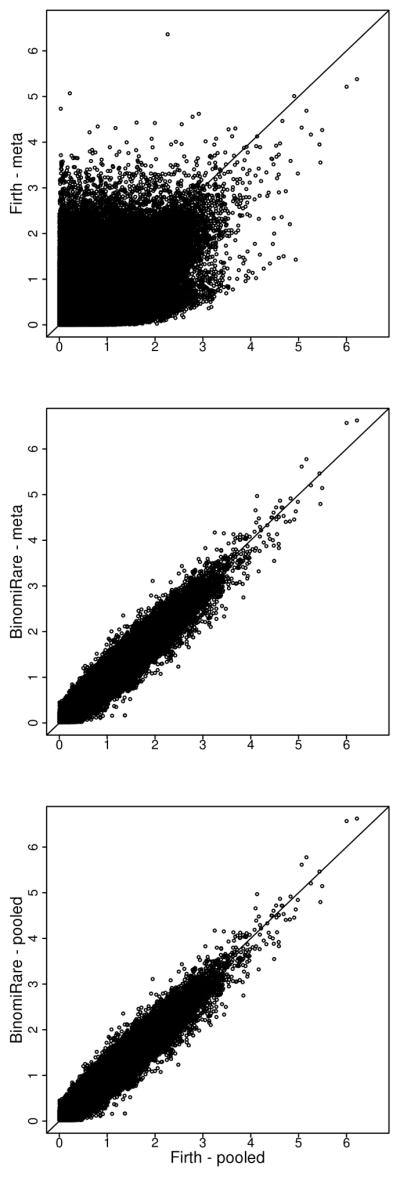
Scatter plots comparing p-values (with −log(p, 10) transformation) from Firth pooled test to Firth meta, BinomiRare pooled, and BinomiRare meta, on variants with 1–250 carriers in the HCHS/SOL current asthma analysis.

While genomic inflation is well controlled by the Firth pooled test, the meta-analyzed Firth is significantly deflated (λ_gc = 0.65)). Yet, as seen in Figure 1, there are many variants with low p-value in the Firth pooled analysis, and very low p-value in the Firth meta, reminiscent of the inflation observed in simulations. This inconsistent scatter pattern of Firth meta results compared to Firth pooled results is in agreement with the findings of Ma et al. (2013), where meta-analysis of Firth tests may lead to either poor power or poor type 1 error control, depending on the settings. The pooled and meta-analyzed BinomiRare are also somewhat deflated, but the deflation is not as bad (λ_gc = 0.91). Moreover, the pvalue of the top SNPs are slightly smaller for the BinomiRare. The BinomiRare p-values are almost identical in the pooled- and meta-analysis, since the estimated disease probabilities were similar in the two analyses. Finally, one can see that the p-values obtained by the BinomiRare tests are highly correlated with the p-values of the Firth pooled test, while the same does not hold for the meta-analyzed Firth.

From a computational perspective, testing 900 rare variants on chromosome 22 using BinomiRare (pooled) took about 6 minutes, while testing the same variants using Firth took more than an hour and a half (in both the logistf and the SKAT R packages), on the same computer.

Group-specific analyses

We also considered the results from the analysis of each of the groups. In the Supplementary Material, we provide figures with the number of variants with 1–50 carriers, 51–100 carriers, etc, in each of the genetic analysis groups, and λ_gc for each of the BinomiRare and Firth analyses for these categories of variants. We also compare the p-values from both tests. Table 4 provides details of 3 variants overall with p-values < 10⁻⁶ in the various analyses. For these, the BinomiRare p-values are similar but slightly larger than the Firth p-values. This is in agreement with Figure 10 in the Supplementary Material, showing that BinomiRare tends to be more conservative than the Firth in the group-specific analyses.

Table 4.

All SNPs with p-value < 10⁻⁶ in one of the analyses restricted to a single genetic analysis group. A1 and A2 are the minor major alleles, respecitvely, the number of carriers of the minor allele is given in the column Carrier and Diseased is the number of diseased carriers. BR and Firth pval are the p-values of BinomiRare and Firth tests, respectively.

group	rsID	chrom	A1	A2	Carriers	Diseased	BR pval	Firth pval
CentralAmerican	rs116491009	2	T	C	5	4	2.35 × 10−6	7.93 × 10−7
PuertoRican	rs113050298	16	T	C	83	41	4.54 × 10−7	1.07 × 10−7
PuertoRican	rs117787335	19	A	C	57	32	9.88 × 10−7	6.79 × 10−7

Discussion

We propose the BinomiRare test for the association of a low-count variant with a disease outcome. The BinomiRare fills an important gap in the existing methodology: it is useful for meta-analyzing association results from multiple studies, even when the case-control proportions differ between them. In such settings, the Firth test, which is the gold standard for testing rare-variants in general cohorts, performs poorly. For a single study, BinomiRare is slightly conservative compared to the Firth test. Of note, it takes less then 10% of the computation time that the Firth test requires.

Other tests that do not rely on problematic asymptotic approximations to the rarevariant effect exist. For instance, tabulation of the disease status against carrier status leads to tests based on conditional or exact inferences (or both). However, such methods are generally inappropriate for population-based wide-scale association studies. First, adjustment for covariates is difficult, if at all possible. Second, they usually require consideration of various instantiations of the data under the specific model (e.g. permutations under fixed margins of the table, as in Fisher’s exact test), and are therefore too time consuming when considering millions of variants. Can the BinomiRare test be viewed as a generalization of a conditional or an exact test? If the probabilities of disease were known (rather than estimated), it would have been an exact test. Marginal tests provide means to test associations by conditioning on sufficient statistics of nuisance variables (Agresti, 2001), e.g. the four margins of 2×2 tables. However, existing marginal tests usually focus on comparing rates or odds between two groups (carriers and non-carriers, in our settings), and do not condition on the proportion of diseased individuals in the study, as the Binomi- Rare does. It would be interesting to study whether the BinomiRare test can be obtained using sufficiency arguments.

The BinomiRare test does not account for variability in the estimation of the disease probability. This is somewhat similar the controversial habit of fixing table margins in the context of significance tests for 2×2 tables. To alleviate this shortcoming, one can follow the recommendation of Berger and Boos (1994) and calculate maximal possible p-values over the range of plausible values of disease probabilities. However, since our test controlled type 1 error in simulations, and the order of magnitude of the confidence intervals for marginal disease probabilities are $O(1/\sqrt{n})$ (giving, e.g., 0.015 maximum increase/decrease in probability for n = 1, 000, $\widehat{p_d}=0.5$, and 95% confidence intervals), we do not pursue this approach.

The BinomiRare test is not recommended for high-count variants because it would be too conservative, as it assumes only a dominant model and cannot accommodate an additive inheritance model. Therefore, for minor allele count 250 and higher, we recommend using one of the traditional regression-based tests. The BinomiRare test uses estimated disease probabilities under the null hypothesis of no disease-variant association. We emphasize a few aspects of disease probability estimation. First, the computed probabilities are calculated from the case-control study, and are not population quantities. Still, using the Poisson-Binomial distribution we are able to combine probabilities from different samples with different case-control proportion, while controlling type 1 error. Second, the disease probability model could be general. We used logistic regression, but any model is appropriate. In contrast to other regression-based estimators, our disease model does not pose any assumptions on the from of association between the variant and the disease. However, implicitly, BinomiRare will be more powerful with an additive change on the disease risk scale, while other tests that model the variant in a logistic regression, become more powerful with a change in the odds ratio. Third, better disease probability estimates may improve BinomiRare. In unreported simulation results, we tested the use of an “oracle” BinomiRare test, that is based on known disease probabilities. The oracle BinomiRare is, as expected, more powerful than the BinomiRare test that estimates disease probabilities. However, in trying to estimate a better disease probability model under the null hypothesis, one should be wary of overfitting. We recommend assessing model fit using previously described methods (e.g. Harrell (2015)).

In the present study, we only discussed testing genotyped variants. Rare variants may also be imputed. BinomiRare could be applied to imputed dosages only when the imputation quality is good enough to produce actual count data (natural numbers rather then values such as 0.8, that are sometimes produced in imputation), i.e. when the distinction between a carrier and a non-carrier is clear.

This work can be extended in a few ways. First, it is of interest to extend the Binomi- Rare to studies with related individuals and with shared environment. This is challenging because the predicted disease probabilities are not independent of each other. Other avenues are the adaptation of the approach for continuous and secondary outcomes. While developing BinomiRare for these settings is challenging, it is likely more feasible than adapting the Firth test.

Software

An R package implementing the BinomiRare test for both pooled and meta-analysis can be installed using the R commands

library(devtools)
install_github(“tamartsi/BinomiRare”)

and the manual can be viewed in https://github.com/tamartsi/BinomiRare/blob/master/BinomiRare-manual.pdf.