Synthetic and Computational Studies on the Rhodium-Catalyzed Hydroamination of Aminoalkenes

Abstract

The influence of ligand structure on rhodium-catalyzed hydroamination has been evaluated for a series of phosphinoarene ligands. These catalysts have been evaluated in a set of catalytic intramolecular Markovnikov hydroamination reactions. The mechanism of hydroamination catalyzed by the rhodium(I) complexes in this study was examined computationally, and the turnover-limiting step was elucidated. These computational studies were extended to a series of theoretical hydroamination catalysts to compare the electronic effects of the ancillary ligand substituents. The relative energies of intermediates and transition states were compared to those of intermediates in the reaction catalyzed by the unsubstituted catalyst. The experimental difference in the reactivities of electron-rich and electron-poor catalysts was compared to the computational results, and it was found that the activity for the electron-poor catalysts predicted from the reaction barriers was overestimated. Thus, the analysis of the catalysts in this study was expanded to include the binding preference of each ligand, in comparison to that of the unsubstituted ligand. This information accounts for the disparity between observed reactivity and the calculated overall reaction barrier for electron-poor ligands. The ligand-binding preferences for new ligand structures were calculated, and ligands that were predicted to bind strongly to rhodium generated catalysts for the experimental catalytic reactions that were more reactive than those predicted to bind more weakly.

Graphical Abstract

INTRODUCTION

Hydroamination is defined as the addition of an N–H bond across an alkene or alkyne. Catalysts are required for this transformation because the transition state for a concerted, uncatalyzed [2s+2p] reaction is thermally disallowed by the Woodward–Hoffmann rules¹ and the stepwise reaction requires the interaction of two electron-rich components.^2–4 Although the first hydroamination reactions were reported as early as the 1950s,^2,3 the development of improved catalysts for the hydroamination of unactivated alkenes has been slow. Catalysts based on lanthanides and early transition metals have been developed for hydroamination, but catalysts based on late transition metals offer many advantages, such as improved functional group tolerance and greater stability toward air and water. Despite more than 40 years of research in the field of late-transition-metal-catalyzed hydroamination, there are few additions of the N–H bonds of amines across alkenes that are suitable for practical applications.^4–6

Because both reactants in hydroamination reactions are electron-rich, either the amine or alkene can be rendered more reactive for the addition process by modification with electron-withdrawing groups. Reagents containing activated N–H bonds include amides and sulfonamides,⁷ ureas,^8,9 carbamates,¹⁰ and indole-type heterocycles.¹¹ The N–H bonds in these nucleophiles are more acidic than those of unactivated alkylamines and arylamines, and the proposed mechanisms for hydroamination with these nucleophiles often involve cleavage of the N–H bond by the metal center to form a bond between the metal and an X-type nitrogen ligand.

Early reports of hydroamination of alkenes were limited to reactions with high temperature and pressures, harsh reaction conditions, and limited substrates, such as ethylene and styrene.^2,3 Other alkenes that have been activated for hydroamination include those possessing substituents that enable a stepwise pathway. Examples of such alkenes include Michael acceptors, alkenes bearing directing groups,^12–14 and alkenes that react to form allyl or benzyl complexes, such as dienes,^15–17 allenes, and vinylarenes.^18–26 Likewise, strained bicyclic alkenes^27,28 undergo migratory insertion steps more quickly than unstrained alkenes and form alkyl intermediates that do not undergo β-hydrogen elimination to form oxidized products. Intermolecular hydroamination of unactivated alkenes with unactivated amines has been limited to lanthanide-catalyzed examples that require long reaction times and elevated temperatures.^29–31

Although rhodium catalysts were among the first systems reported for alkene hydroamination,⁵ improved rhodium catalysts were not identified until much later. In 2003, our group reported the intermolecular, anti-Markovnikov addition of amines to vinylarenes, ^2,5 and the origin of selectivity in this system has been studied computationally.³² Hull recently showed this combination of cationic rhodium precursor and DPEPhos catalyzes the reaction of amines with N-allyl imines with Markovnikov selectivity¹² and reactions of homoallyl amines with anti-Markovnikov selectivity.¹³ Rhodium catalysts for intermolecular hydroamination of dienes also have been reported.¹⁵ The intramolecular additions of unactivated amines to unactivated alkenes are also limited. Prior to the work by our research group (vide infra), the addition of unactivated alkylamines to unactivated alkenes have been limited to those catalyzed by lanthanide and electrophilic group IV metal systems.

In 2008 and 2010 our group reported rhodium catalysts for intramolecular cyclization reactions of primary and secondary aminoalkenes to form five- or six-membered rings. Amino-alkenes containing one or more substituents on the tether between the amine and the alkene reacted more quickly at lower temperatures than aminoalkenes lacking substituents on the tether (a manifestation of the Thorpe–Ingold effect).³³ In 2008, the authors’ laboratory reported a catalyst for the hydroamination of primary and secondary aminoalkenes generated from a cationic rhodium(I) precursor and biaryl phosphine ligand.³⁴ An enantioselective version of this process was then reported by Shen and Buchwald with a catalyst containing chiral binaphthyl monophosphine ligands.³⁵ The scope of these methods catalyzed by rhodium complexes ligated by phosphines containing biaryl and binaphthyl scaffolds is limited to secondary aminoalkenes and to primary aminoalkenes possessing geminal substitution. The enantioselective reactions reported by Shen and Buchwald require N-benzyl substitution for aminoalkenes that lack geminal substituents, and these catalysts react with only moderate enantioselectivity.

In 2010, our group reported a rhodium(I) catalyst containing a derivative of Xantphos bearing diethylamino groups at phosphorus. This catalyst was more reactive for additions of primary amines; even primary aminoalkenes lacking geminal disubstitution underwent cyclization in the presence of this catalyst under mild conditions.³⁶ Although the mechanism of hydroamination with this catalyst was studied extensively, efforts to modify the catalyst to expand the scope did not lead to intermolecular reactions, and studies on catalysts bearing phosphorus ligands derived from chiral diamines reacted with modest enantioselectivities.

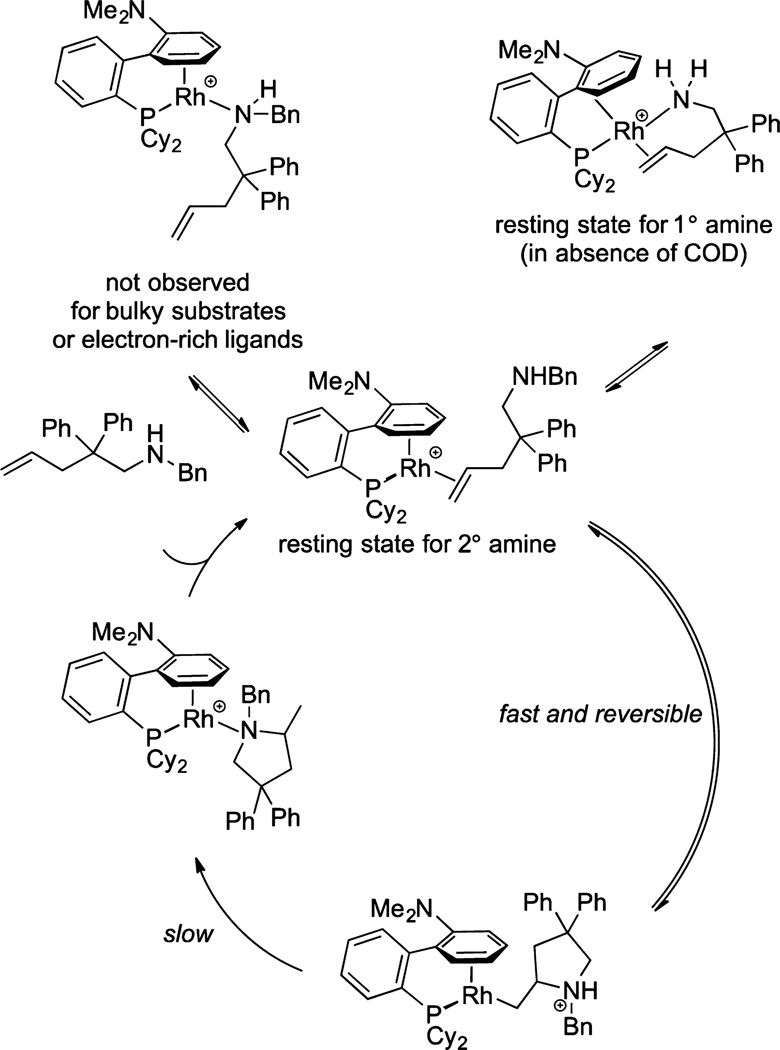
The structure of the active catalyst in the system developed by Liu and Hartwig and the mechanism by which it reacts have been reported.³⁷ The active catalyst was found to be the complex in Figure 1, containing a biarylphosphine in which one arene ring and the phosphorus atom are bound to rhodium in an η⁶,κ¹ binding mode. The experimental data from this study are consistent with the catalytic cycle shown in Figure 1. In this pathway, the amine reversibly bonds to the coordinated alkene, and intramolecular, rate-limiting protonolysis of the rhodium alkyl intermediate subsequently occurs. Importantly, the active catalyst has only one available coordination site; the absence of a second site was proposed to suppress undesired side reactions, such as β-hydrogen elimination. The structure of the resting state for the hydroamination reactions of secondary aminoalkenes was determined by 1D and 2D NMR spectroscopy and X-ray crystallographic analysis to be a complex bound to the alkene unit of the aminoalkene with one arene of the biaryl phosphine ligand bound in an η⁶ fashion. The structure of the resting state for hydroamination reactions of primary aminoalkenes was determined by the same methods to be the four-coordinate, η²,κ¹ complex in Figure 1, in which the alkene and amine of the aminoalkene are both bound to rhodium. Primary aminoalkenes lacking geminal substituents do not undergo hydroamination reactions in the presence of this catalyst.

Figure 1.

Mechanism of hydroamination with (L1a)Rh⁺ as catalyst.

We sought to evaluate the effect of the steric and electronic properties of the ancillary ligand on the overall rate, the relative rates of individual steps of the catalytic cycle, and the reactivity of primary aminoalkenes and unbiased substrates. Our approach included both experimental and computational studies. We studied a series of ligands with modified arene and phosphine substituents and modified tethers between the arene and phosphine. These studies showed that changes to the tether led to greater increases in reactivity than did changes to the arene or phosphine substituents. To help reveal how subtle changes in the structure of the catalyst resulted in vastly different reactivity, we studied the system computationally. Through computational analysis we gained insight into (1) the mechanism of the turnover-limiting protonolysis step, (2) the origin of the effect of structural changes on the reactivity of different substrates, and (3) the influence of the relative binding affinity of altered ligands on reactivity. With this information, we developed a computational model to evaluate new ligands for rhodium-catalyzed hydroamination of aminoalkenes. In addition, these computational studies suggest that differences in stabilities of the most stable form of the catalyst give rise to the common Thorpe–Ingold effect on cyclization of aminoalkenes in these reactions and explain the different reactivities of primary and secondary aminoalkenes. Upon establishing steric and electronic requirements for catalyst activity in the computational study, we prepared catalysts for the hydroamination reactions of aminoalkenes that react to form product in yields that are higher than those of reactions catalyzed by the previously reported rhodium catalyst ligated by a biarylphosphine in an η⁶,κ¹ fashion.^34,37

RESULTS AND DISCUSSION

Reactivity of Catalysts Bound by a Series of Modular Phosphino Arene Ligands

To examine the influence of each component of the ligand on catalyst activity, a series of systematically varied ligands that would be bound to the metal through a phosphino group and a pendant arene were synthesized. The structures of the ligands are shown in Scheme 1. Ligands containing one, two, and three ether or amine substituents on the arene, as well as ligands containing ethyl or amino groups, were varied while the biphenyl structure was maintained. Ligands L2a,b and L3 possessed different substituents on the arene but contained the same dicyclohexylphosphine group; ligands L1b,c possessed different substituents at phosphorus but contained the same dimethylamino group on the aryl ring distal from phosphorus. The catalysts for the hydroamination of a set of aminoalkenes were generated by combining these ligands with [Rh(COD)₂]BF₄ (Scheme 1).

Scheme 1.

Evaluation of Ligands with Varied Substituents on Phosphorus and on the Tethered Arene for Hydroamination of Primary and Secondary Aminoalkenesa

^aConditions: 0.040 mmol of substrate, 5 mol % of [Rh(COD)₂]BF₄, 10 mol % of ligand, 0.1 mL of 1,4-dioxane, 70 °C. Yields were determined by GC analysis and measured at 2 and 18 h. Yields shown are at 18 h.

The two catalysts formed from L1a or L2c and the cationic rhodium precursor were used as benchmarks. Ligand L1a had previously been shown to form an active catalyst and thus was chosen as one benchmark to compare with catalysts bearing the new ligands. Ligand L2c was chosen as a second benchmark to compare with catalysts bearing ligands that lack electron-donating groups on the bound arene. By comparison of the activity of catalysts containing these ligands to those containing L2c, the influences of the structure of the tether and the dimethylamino group can be assessed separately. The influences of the tether, the arene, and the substituents on the phosphorus atom were examined by comparison of the reactivity of the catalyst formed from each ligand.

The yields of reactions catalyzed by complexes of the various ligands are shown in Scheme 1. Catalysts containing ligands bearing diethylamino and ethyl groups at phosphorus were inactive (L1b,c). This result, combined with the results of prior studies on binaphthyl-based ligands, in which ligands containing phenyl and tert-butyl substituents on phosphorus generated catalysts that were less active than those from ligands containing cyclohexyl groups on phosphorus,³⁵ indicates that modification of the cyclohexyl group leads to less active catalysts. The activities of the catalysts generated from ligands possessing more than one electron-donating group on the coordinated aryl ring were similar to that of the benchmark catalyst formed from L1a (e.g., L2a,b and L3) for cyclization of the more reactive secondary aminoalkene substrate 2s but were lower for cyclization of primary aminoalkene 1s and monosubstituted secondary aminoalkene 3s. The results from this set of ligands show that the catalyst is sensitive to the steric and electronic parameters of the components of the catalyst that are bound directly to the metal. Further variations of the ligand focused on the remaining component of the ligand, the tether between the bound arene, and the phosphino group (Scheme 2).

Scheme 2.

Evaluation of Modified Ancillary Ligands with Different Scaffolds for Hydroamination of Primary and Secondary Aminoalkenesa

^aConditions: 0.040 mmol of substrate, 5 mol % of [Rh(COD)₂]BF₄, 10 mol % of ligand, 0.1 mL of 1,4-dioxane, 70 °C, 2–18 h. Yields were determined by GC analysis, and conversion was measured at 2 and 18 h. Yields shown are at 18 h.

The previously reported structure of the rhodium–-ethylene complex in which L1a is bound in an η⁶,κ¹ fashion served as a guideline for designing new ligands (Scheme 2). We hypothesized that the arene may slip from η⁶ to η² to relieve strain induced by binding to the metal, because this slipped complex was isolated from the reaction of the primary aminoalkene 1s, characterized by X-ray crystallography and determined to be the resting state of the reaction of this aminoalkene by NMR spectroscopy (Figure 1). We proposed that the η⁶-arene binding mode would be favored for complexes containing a longer tether between the phosphorus and the pendant arene. The C–C bond lengths of a two-carbon alkyl tether would be longer than those of the phenylene linker in the parent ligand. Thus, L5 was synthesized as an analogue of L2c containing an alkyl tether. An analogue containing a vinyl linker (L4) also was synthesized, because the steric properties of this ligand would be similar to those of L5 and the electronic properties and bond lengths would be similar to those of L2c. Both L4 and L5, in combination with a cationic rhodium precursor, catalyzed the cyclization of 2s to form 2p in low yield. The catalyst containing the more rigid KitPhos ligand L6 was no more active for hydroamination of 2s than was that containing L2c.

To determine if these ligands bind to the metal to form complexes with structures that are similar to those of the active catalyst in Figure 1, the rhodium–ethylene complexes ligated by the various phosphines were synthesized and characterized by X-ray diffraction. Single crystals suitable for X-ray diffraction were obtained for ethylene adducts of cationic rhodium bound to the ligands linked by alkyl, vinyl, and phenylene units (Figure 2). Polycyclic ligand L6 formed a rhodium complex with a structure that is similar to that of the rhodium complexes formed by the other ligands, but the quality of the data was only suitable for a structural assignment. All of these ligands formed rhodium complexes having similar structural parameters, despite the marked difference in reactivities of the corresponding catalysts: namely, Rh–P bond lengths, C–C bond lengths in ethylene, and the angles between the tether carbon, ipso carbon, and distal carbon of the bound arene varied less than 0.1 Å or 1°. Therefore, we conclude that changes in reactivity are not controlled by the most stable structures of the of the alkene complexes.

Figure 2.

ORTEP representations of rhodium(ethylene) complexes ligated by L4, L5, and L2c. The complex formed from L6 yielded poor-quality crystals, but a structural assignment was made that matches the structure of the other complexes in this series.

In these preliminary studies with a range of ligands, the substituents at phosphorus and the identity of the tether had the largest effects on the yields of desired product in the catalytic reaction. Further studies focused on ligands with cyclohexyl groups on phosphorus, and structural variation focused on evaluating a wider range of tethers. Although ligands, such as L7a–d containing indole linkers formed less reactive hydroamination catalysts, the yield from the reaction catalyzed by rhodium and L8 containing a cyclopropyl tether was only slightly lower than that of the benchmark reaction catalyzed by rhodium and phenylene-linked L2c. The activities of catalysts generated from commercially available ligands L9a,b containing alkene linkers both were higher than that of the catalyst generated from ligand L2c, and the activity of the catalyst generated from ligand L9b was higher for all substrates than that for the catalyst generated from ligand L1a, despite the absence of an electron-donating substituent on the η⁶-arene (Scheme 2). This result indicates that the structure of the backbone in L9b (Scheme 2) is more favorable than that of the starting biaryl backbone in L1a and L2c. However, the catalyst bound by the ligand containing an alkene tether lacking substituents (L4) was found to be much less active. Ligand L9a was synthesized to evaluate the effect of the methyl substituent in L9b on catalyst activity. The catalyst containing ligand L9a was much less reactive than that containing ligand L9b, indicating that substitution at the ipso carbon to phosphorus leads to a more active catalyst.

Computational Study of Rhodium-Catalyzed Hydroamination

To help elucidate how subtle structural changes in the ancillary ligand of the rhodium catalyst affect the reactivity of the catalyst toward hydroamination, we studied the effect of the structure on the individual steps of the catalytic cycle by DFT calculations with the M06 functional (see Computational Details). With these DFT calculations, we hoped to accomplish three goals. First, we sought to determine the mechanism of the turnover-limiting protonolysis step³⁸ and to use this information to design ligands that would reduce the barrier to this step. Second, we sought to elucidate the origin of the higher reactivity of substrates bearing geminal disubstitution that biases the substrate toward cyclization. This reactivity could not be explained by the traditional kinetic origin of the Thorpe–Ingold effect because the cyclization step is fast and reversible (Scheme 1). Third, we hoped to determine the effects of steric and electronic perturbation of the ancillary ligand by varying the components of the structure and computing the effect of these changes on individual steps of the catalytic cycle. Although the previous experimental data on the hydro-amination of secondary aminoalkenes catalyzed by rhodium and L1a were collected with the N-benzyl substrate in Figure 1, the simplified secondary aminoalkene A was used for the initial computations of potential mechanistic pathways for the reaction catalyzed by the rhodium complex of L1a (Figure 3).

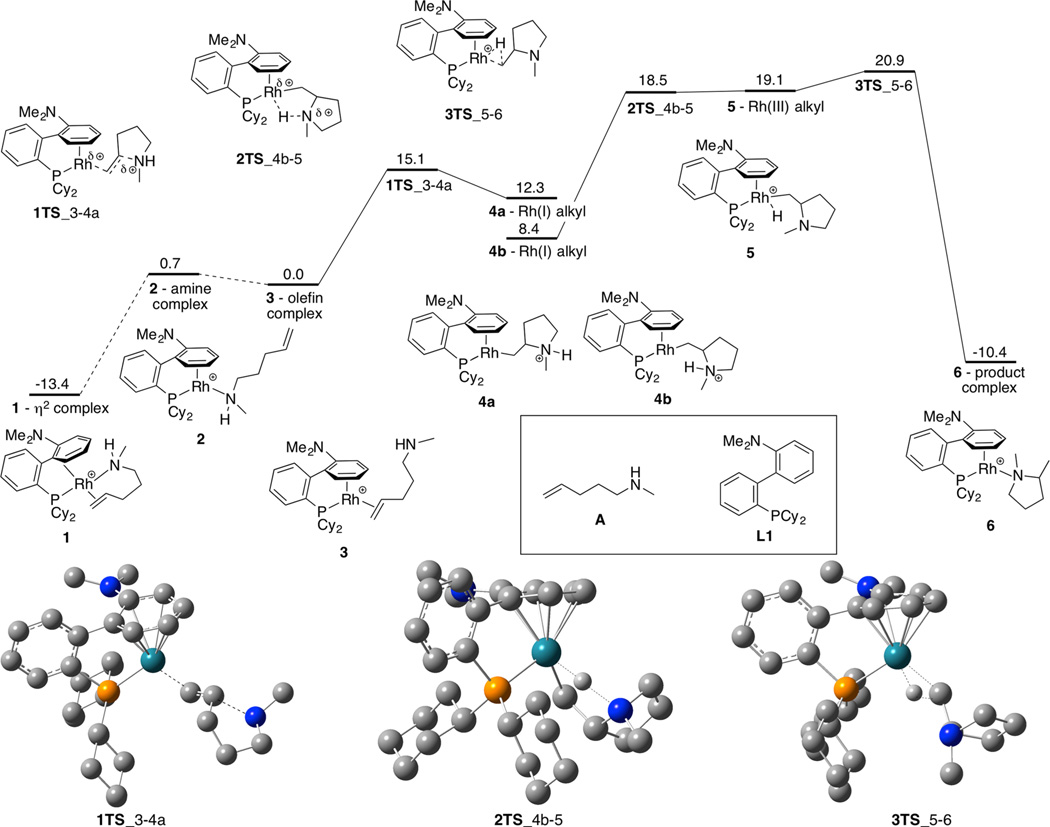
Figure 3.

Calculated mechanism of hydroamination of secondary aminoalkenes catalyzed by (L1a)rhodium(I). Energies given are ΔG values with solvent correction in kcal/mol. Protons are omitted from calculated transition state structures, except when they participate in bond-forming or bond-cleaving events.

We compared the energies of various resting states in which the aminoalkene was bound to the metal through the amine (complex 2) or alkene (complex 3), and the ancillary phosphinoarene ligand was bound in an η⁶,κ¹ fashion. We compared the energies of these η⁶,κ¹ complexes to the energy of complex 1, containing the amino alkene bound in a bidentate fashion and the ancillary ligand bound in an η²,κ¹ fashion. The energy of the alkene complex was found to be lower than the energy of the amine complex, but the difference in energy was small (0.7 kcal/mol). From experiment, the alkene complex was observed as the resting state for reactions of sterically hindered secondary aminoalkenes (Figure 1). The computation indicated that nucleophilic attack of the amine on the bound alkene is uphill with a low barrier to reversion to the alkene complex. Calculation of an alternative initial step, oxidative addition of the amine N–H bond, indicated that the thermodynamics for this step are prohibitively unfavorable (~45 kcal/mol uphill to form a rhodium(III) intermediate).

We explored both the stepwise and concerted pathways for the turnover-limiting proton transfer from the nitrogen atom to the rhodium-bound carbon atom. Prior experimental studies by our group showed that proton transfer from nitrogen to the metal–carbon bond of the intermediate formed by nucleophilic attack on the bound olefin was turnover-limiting. Subsequent kinetic studies by Stradiotto and Tobisch on the mechanism of hydroamination catalyzed by (cod)IrCl (cod = cycloocta-1,5-diene) were consistent with rate-limiting proton transfer; further studies on this system by DFT suggested that the proton transfer occurs by formation of a hydridoiridium(III) alkyl intermediate, which undergoes reductive elimination to form the C–H bond in the product.³⁷ The rhodium and iridium systems are similar because the mechanism involves nucleophilic attack and protonolysis of the metal–carbon bond. However, the difference in basicities of the metal center in the two systems and the numbers of available coordination sites could lead to different pathways for proton transfer by the two aminoalkyl intermediates.

The barrier to proton transfer from the nitrogen atom to the neutral rhodium(I) center in 4b to form a rhodium(III) hydride intermediate 5, followed by reductive elimination, was computed to be 12.5 kcal/mol, with an overall barrier of 20.9 kcal/mol (Figure 3). The calculated kinetic isotope effect (KIE) of 4.2 for this proton transfer to the metal was consistent with the primary KIE of 2.6 measured experimentally.³⁷ Two rhodium(I)–alkyl intermediates were found upon relaxing 1TS toward products (4a) and 2TS toward reactants (4b). These minima are separated by a low-barrier rotation around the Rh–C bond.³⁹ We were unable to find a transition state for a concerted intramolecular protonolysis of the rhodium–carbon bond.

A mechanism for the catalytic cycle that is consistent with these computational results and previous experimental evidence thus comprises the following: (1) initial, reversible nucleophilic attack of the amine on the bound alkene to form a rhodium(I) alkyl intermediate, which can rotate to facilitate proton transfer to the metal center; (2) proton transfer from the nitrogen atom to the metal center to form an alkylrhodium(III) hydride complex that undergoes C–H bond-forming reductive elimination to form the tertiary amine product; (3) displacement of the product from the metal by an aminoalkene reactant to complete the catalytic cycle.

Effects of the Aminoalkene Substitutents at Nitrogen on the Energetics of the Catalytic Cycle

From this mechanistic study, we identified nine stationary points: three saddle points (transition states) with a single imaginary frequency and six minima (intermediates) with only real frequencies. To compare the energies of these stationary points for the reactions of different aminoalkenes, the corresponding nine stationary points generated from reactants B–D in Figure 4 were optimized. These substrates vary in the presence or absence of geminal disubstitution and include primary and secondary amino groups. We also examined the energetics of the intermolecular reactions of ethylene and 2-methyl-1-propene with dimethylamine.⁴⁰

Figure 4.

Relative energies of key intermediates and transition states for different substrates. Energies given are ΔG values with solvent correction in kcal/mol.

For all of the substrates A–D the structure computed to be most stable is that containing an η² arene and the aminoalkene bound through both the alkene and the amino groups. According to these computations, the difference in energy between the η² arene complex 1 and the alkene complex 3 is larger for primary aminoalkenes and for substrates lacking geminal disubstitution than it is for secondary aminoalkenes and geminally disubstituted primary aminoalkenes. Although the computed energy of the η²-arene complex was lower than that of the η⁶-arene complex with the aminoalkene bound solely through the alkene (complex 3), the resting state of the catalyst was observed by experiment to be the η⁶-arene complex 3 for reactions of secondary aminoalkenes and the η²-arene complex 1 for reactions of primary aminoalkenes (vide supra, Figure 1). The difference between the most stable species determined by computation and the experimentally observed resting states is proposed to result from kinetic barriers that prohibit formation of the η²-arene complex 1 from the η⁶-arene complexes containing a bound olefin or amine (2 or 3). However, we were unable to quantify this barrier because we were unable to find a transition state for the reorganization required to interconvert these structures.

The computed difference in energy between the highest-energy transition state and the experimental resting states explains the relative reactivity of the different alkenes (Figure 5) and offers a strategy for the development of more active catalysts. Comparing the experimental relative rates of a set of aminoalkenes containing different substituents with the computed activation energies for complexes that lie on and off the catalytic cycle provides the true overall reaction barrier (Figure 5). For example, the computed barrier for reaction of the unsubstituted aminoalkene D is 20.6 kcal/mol starting from the alkene complex, but this substrate forms a lower energy, off-cycle complex by chelating the metal center. The barrier for reaction from this more stable complex is 15.2 kcal/mol higher than that from the alkene complex. These data suggest that the barriers to cyclization of primary aminoalkenes could be as much as 15 kcal/mol lower if the resting state of the catalyst during reactions of these substrates were the higher-energy η⁶-arene complexes 2 and 3 that lie on the catalytic cycle, instead of the η²-arene complex 1 that lies off the catalytic cycle.

Figure 5.

Relative stabilities and reactivities of bidentate η² complex 1 and olefin-bound η⁶ complex 3.

Effects of the Aminoalkene Backbone Composition on Hydroamination Reactions

The kinetic data show that the nucleophilic attack forming the C–N bond is fast and reversible. Thus, we sought to determine if the origin of the effect of the two geminal substituents in the tether linking the alkene and the amine on the rate is different from that in uncatalyzed or base-catalyzed cyclizations. For the rhodium-catalyzed process described here, the effect of the geminal substituents could result from destabilization of the off-cycle resting state of the catalyst or it could result from an effect on the events occurring within the catalytic cycle (Figure 4).

The barrier to nucleophilic attack during reaction of the unsubstituted primary aminoalkene D is 0.9 kcal/mol lower than the barrier to nucleophilic attack during reaction of the substituted primary aminoalkene C. However, the off-cycle η²-arene complex 1 containing the chelating aminoalkene is 5.8 kcal/mol more stable when it is generated from D than when it is generated from C. This greater stability of the off-cycle complex 1 generated from the unsubstituted primary amino-alkene D causes the overall calculated barrier for the reaction of D to be 35.8 kcal/mol. This high barrier is consistent with the lack of reactivity of unsubstituted primary aminoalkenes, such as D in hydroamination reactions catalyzed by the combination of L1a and rhodium.

We propose that the greater stability of complex 1 containing the unsubstituted aminoalkene in comparison to that of complex 1 containing the gem-disubstituted aminoalkene is due to steric crowding between the ancillary ligand and substrate. This effect is consistent with the experimental and computational data on the mechanism of hydroamination. Because the nucleophilic attack is fast and reversible, the substituent effect arises from the thermodynamics for the reversible binding of the aminoalkene within the coordination sphere of the metal, rather than an effect on the barrier to cyclization.

To test our hypothesis about the origin of the decreased reactivity of primary aminoalkenes, a competition reaction between primary and secondary aminoalkenes 1s and 2s was performed (Figure 6). The resting states of the catalyst during the reaction of these substrates are different from each other (vide supra). The alkene-bound (on-cycle) complex 3 of the primary aminoalkene containing methyl backbone substituents is 9.4 kcal/mol higher in energy than the (off-cycle) complex 1, which is the experimentally observed resting state. However, the experimentally observed resting state during reaction of the secondary aminoalkene in Figure 6 is the alkene complex 3. The two alkene complexes formed from the two aminoalkenes can be assumed to have the same relative energies because the distal amines should not affect the strength of the bond between the alkene and the metal. Therefore, the lower-energy resting state 1 is presumed to be the predominant species in the competition reaction.

Figure 6.

Competition of primary and secondary aminoalkenes. At 12 h the primary amine has reacted before the secondary amine. At 48 h both substrates have reached full conversion.

The computed barriers for cyclization of secondary amino-alkene 2s starting from the alkene complex is 21.4 kcal/mol, and the barrier for cyclization of the primary aminoalkene is a similar 23.6 kcal/mol (normalized to 0.0 kcal/mol for both aminoalkene complexes with methyl substituents on the backbone). Figure 6 shows the results from the reactions of each substrate alone catalyzed by the rhodium(I) precursor and L1a and the reaction of both substrates together. The conversion of the secondary aminoalkene alone is higher than that of the primary aminoalkene after 2 h in side-by-side reactions. However, in the reaction of the two amines together, all of the primary aminoalkene had converted to the cyclized product after 12 h, whereas only 5% of the secondary aminoalkene had reacted. The high yields of both products in separate reactions after 48 h show that the catalyst does not decompose in the presence of the primary amine. Instead, these results are consistent with stronger binding of the primary aminoalkene in comparison to that of the secondary amino-alkene to the rhodium and either a larger difference in binding energies than in barriers for reaction of the two amines or, less likely, slower displacement of the primary aminoalkene by the secondary aminoalkene than that in reaction of the bound primary aminoalkene. We favor the former explanation because the version of complex 3 containing the secondary aminoalkene was shown in a previous study to react with primary aminoalkene to form exclusively the primary aminoalkene complex 1.³⁷

Barriers to Hydroamination Catalyzed by Complexes of Different Ligands

The effect of the ligand on the barriers to reaction of secondary aminoalkene A was computed by DFT. Electronic effects were evaluated by varying substituents on the bound arene and the aryl linker of the ancillary ligand for each of the same nine stationary points as studied for substrates A–D. The results of these computations are summarized in Figure 7. For more electron rich ligands, the olefin complex 3 is lower in energy than the amine-bound complex 2, but for more electron poor ligands, the amine-bound complex 2 is lower in energy than the olefin complex 3. Thus, the transition state energies reported in Figure 7 for proton transfer and reductive elimination are given relative to both the alkene complex 3 and the amine complex 2. The barriers for reaction of the more electron rich catalysts were generally lower than those for reaction of the more electron poor catalysts, but competing ground and transition state effects attenuate the electronic influence.

Figure 7.

Overall computed barriers for hydroamination of A catalyzed by complexes with electronically varied ancillary ligands, starting from amine-bound (2) and olefin-bound (3) complexes. Each bar represents the energy difference between the transition state for proton transfer or reductive elimination and either the alkene-bound or amine-bound intermediate. The highest bar for each ligand represents the predicted highest barrier to hydroamination.

In addition to the electronic properties of the ancillary ligand, the structure of the unit connecting the bound arene and phosphino group was varied. These data are summarized in Figure 8. The ligands that generate the most reactive catalysts experimentally do not lead to the lowest computed overall barriers for cyclization of A by the phosphine-ligated Rh(I) complexes. For example, the catalyst generated from ligand L2c is predicted to be less reactive than the catalyst generated from ligand L9a, and the catalyst generated from ligand L9b is predicted to be less reactive than the catalyst generated from ligand L2c (Figure 8). Thus, we hypothesized that competitive binding of the substrate and the ligand to rhodium could lead to different concentrations of the active catalyst and, therefore, activities different from those predicted by computations that include only the phosphine-ligated species.

Figure 8.

Overall computed barriers for hydroamination of A catalyzed by complexes with ancillary ligands with varied tether structures, starting from amine-bound (2) and olefin-bound (3) complexes. Each bar represents the energy difference between the transition state for proton transfer or reductive elimination and either the alkene-bound or amine-bound intermediate. The highest bar for each ligand represents the predicted highest barrier to hydroamination.

Computed Relative Binding Energies of the Ancillary Ligands

The relative free energies for binding of the phosphine ligands to rhodium were determined by computing the energetics of the isodesmic reaction in Figure 9. The relative free energies and enthalpies were calculated, and it was found that the ligands containing more electron-donating substituents bind much more strongly to the rhodium center than those containing more electron-poor substituents. Substituents on the arene (Y; Figure 9) affected the binding energy more strongly than did substituents on the phosphine (X; Figure 9). On the basis of the data in Figure 9, the substituent effects on the binding enthalpies are approximately additive. These data show that there is a ~12 kcal/mol difference in the relative binding energies of ligands possessing different electronic properties. These calculations indicate that electron-poor ligands may not form active catalysts for hydroamination, even though the computed barriers to the reaction of aminoalkenes from these bound complexes are similar to the barriers to hydroamination from complexes ligated by electron-rich ligands because the more electron poor ligands binds more weakly.

Figure 9.

Isodesmic equation comparing relative binding energies of different ligands. ΔH and ΔG values are given in kcal/mol.

The relative binding affinities of the ligands correlate more strongly with the activity of the corresponding catalysts than do the computed reaction barriers from the phosphine-ligated species. For example, catalysts generated from ligands with particularly large binding affinities (L1a and L9b) are more reactive than those generated from ligands with particularly small binding affinities (L5 and L9a, vide supra). This correlation suggests that identification of ligands with high binding enthalpies could lead to the discovery of improved catalysts for hydroamination.

The relative binding affinity of the ligand containing the tether with longer bonds, L5, was compared computationally to that of a ligand containing even longer C-Si bonds, L5-Si. Ligand L5-Si is predicted to bind even more weakly than the electron-poor ligand in Figure 9 bearing two trifluoromethyl substituents. The catalyst generated from rigid ligand L13a, however, is computed to have a large binding energy and a low overall reaction barrier (Figures 8 and 10). On the basis of this prediction, a series of dihydronaphthyl-based ligands were synthesized, and catalysts generated from them were tested for hydroamination.

Figure 10.

Influence of ligand scaffold structure on ligand binding.

Synthetic Studies Based on Computational Models

Ligands containing varied structures based on those of L9b and L13a (Scheme 3) were synthesized. Ligands L9a and L9c,d, which are variants of ligand L9b containing a series of substituents in place of the methyl group in L9b, generated complexes that catalyzed the reactions of aminoalkene 3s with reactivity similar to or lower than that of the catalyst formed from L9b (Scheme 3). On the basis of the previous experimental results (Scheme 1) and the analysis of the binding energies of the ligands, electron-rich variants of L9b should form more active catalysts for the hydroaminations than electron-neutral ligands. However, the reactivity of the catalyst generated from the electron-rich ligand L9e was similar to that of ligand L9b. Ligand L9e is more sterically congested at the proposed η⁶,κ¹ binding pocket, and for this ligand to bind to the metal the two aryl groups must be configured with the coordinating aryl group perpendicular to the plane of the vinyl tether. Thus, to favor the desired conformation, we synthesized variants of ligand L13a that have a more defined conformation of the backbone. The reaction of 3s catalyzed by the complex generated from L13a formed the product in quantitative yield. The related ligand L12 is less rigid, and the catalyst formed from this ligand formed the product from cyclization of 2s in lower yield than did the catalysts formed from the more rigid ligand L13a. The reactivity of the catalyst formed from aromatic naphthyl-bridged ligand L11 was similar to that of the catalyst formed from ligand L13a.

Scheme 3.

Evaluation of Rigid Ligands in Catalytic Hydroamination Reactionsa

^aConditions: 0.040 mmol of substrate, 5 mol % of Rh(COD)₂BF₄, 10 mol % of ligand, 0.1 mL of 1,4-dioxane, 70 °C. Yields were determined by GC analysis and measured at 2 and 18 h. Yields shown are those measured after 18 h.

Derivatives of ligand L13a containing electron-donating and electron-withdrawing groups on the bound arene were synthesized to evaluate the computational prediction that ligands containing pendant electron-poor arenes would form less active catalysts. The complexes of L13a and of the electron-rich ligand L13b were more active catalysts for cyclization of 3s than those of the electron-poor ligand L13c. Most generally, the results in Scheme 3 show that the complexes with the lowest predicted activation barriers for hydroamination are not necessarily the most active catalysts and that incorporating the ligand binding energies into the design of new catalysts is advantageous. Calculation of the relative ligand binding energy is a simple approximation of the efficacy of these catalysts for hydroamination, without the need for calculation of multiple resting states, intermediates, and transition states.

Reactions of Primary and Secondary Aminoalkenes with a Rhodium Ethylene Precatalyst

During our evaluation of ligand L9e (Scheme 4), we found that the yields of reactions catalyzed by the rhodium COD precursor and L9e after 18 h were comparable to those of reactions with the benchmark catalyst formed from rhodium COD and L1a, but the yield after 2 h was variable (5–15%) and lower for the reaction of 1s (Scheme 4, entry 9). We hypothesized that the formation of the active catalyst from the rhodium COD precursor and L9e might be slow and that a rhodium species that is smaller or more labile than [Rh(COD)₂]BF₄ could form the active catalyst more rapidly under the catalytic conditions. Therefore, a solution of the cationic ethylene complex [Rh(ethylene)₂(1,4-dioxane)₂]BF₄ was prepared and added to the reaction mixture as a solution in 1,4-dioxane (see the Supporting Information). As shown in Scheme 4, the yield at 2 h was higher for the reaction catalyzed by the rhodium ethylene complex and L9e or L9b (entries 1–4) in comparison to that for the reaction catalyzed by the rhodium COD complex with these ligands. Reactions of primary aminoalkene 1s were also run with the ethylene complex precursor to test if the faster rates with this precursor were observed for reactions of primary aminoalkenes. Entry 10 shows that the yield of the reaction initiated with this precursor was higher after 2 h than that of the reactions with the rhodium COD precursor, indicating that the active catalysts formed more quickly from the ethylene complex than from the COD complex and that the rate of formation of the active catalyst influenced the apparent catalyst activity.

Scheme 4.

Evaluation of Rhodium Precatalyst in Hydroamination Reactions of Primary and Secondary Aminoalkenesa

^aConditions: 0.040 mmol of substrate, 5 mol % of rhodium, 10 mol % of ligand, 0.1 mL of 1,4-dioxane, 70 °C, 2–18 h. Yields were determined by GC analysis, and conversion was measured after 2 and 18 h.

However, in contrast to the yields of reactions of secondary aminoalkenes, the yields for reactions of primary aminoalkenes were lower in general when the reactions were initiated with the ethylene complex than when they were initiated with the COD complex. This result might be due to catalyst stabilization by COD in reactions of primary aminoalkenes. Thus, the hindered and electron-rich ligand L9e forms an active catalyst more rapidly with a rhodium ethylene precursor, but reactions of primary aminoalkenes occur in lower yield when they were initiated with this catalyst precursor due to catalyst deactivation.

CONCLUSIONS

We report a systematic study of cationic rhodium hydro-amination catalysts, with modified substituents at phosphorus, substituents on the arene, and structure linking the phosphino group to the arene. Initial findings indicated that the backbone of the ancillary ligand could be modified to improve catalyst activity, and this change in reactivity was evaluated computationally. Our computational study suggests that the mechanism of the turnover-limiting protonolysis is a stepwise proton transfer to rhodium, followed by reductive elimination.

Computational analysis of the energetics of the reaction with different substrates and catalysts containing a series of ancillary ligands showed that changes in catalyst structure did not have a large effect on the overall reaction barriers starting from the phosphine-ligated complexes. Instead, these calculations showed that the relative binding energies of the ligand to rhodium correlate with catalyst activity. These calculations showed that rigid, electron-rich ligands bind favorably to rhodium. These binding energies were combined with calculations of the overall reaction barriers to predict catalyst structures that would result in improved activity. Following the development of a computational model to evaluate new ligand structures on the basis of ligand binding affinity, we applied the model to the development of improved modular catalyst structures for hydroamination. Additionally, our computations suggest that the experimentally observed faster cyclization of gem-disubstituted aminoalkenes resulted from destabilization of an off-cycle complex, rather than an enhancement of the rate of nucleophilic attack. Although reactions of primary amino-alkenes are slower than reactions of secondary aminoalkenes, the primary aminoalkenes react more quickly than the secondary aminoalkenes when the two substrates are present in the same vessel. A catalyst precursor with ligands more labile than COD was found to form the active catalyst with hindered ancillary ligands rapidly and reliably, but yields were found to be higher for reactions of primary aminoalkenes when the rhodium COD precursor was used, presumably due to inhibition of catalyst decomposition pathways by the presence of COD.

EXPERIMENTAL SECTION

Unless noted otherwise, all manipulations were performed using standard Schlenk techniques or in a nitrogen-filled glovebox. Glassware was dried at 130 °C overnight before use. Pentane, Et₂O, THF, benzene, and toluene were collected from a solvent purification system containing a 0.33 m column of activated alumina under nitrogen. All other solvents and reagents were purchased from commercial suppliers, stored in the glovebox, and used as received. The authors thank Johnson Matthey for a gift of [Rh(COD)₂]BF₄. Substrates 1s–3s were synthesized through literature procedures.³⁶ Ligands L1a, L2a–c, L3, L7a, L7c,d, L8, and L9b were purchased from Aldrich or Strem.

Computational Details

Calculations were conducted by density functional theory (DFT) with the M06^41,42 set of functionals using the Gaussian09 program at the CTCC (Center for Theoretical and Computational Chemistry) at the University of Oslo, Oslo, Norway, and at the MCGF (Molecular Graphics and Computation Facility) at the University of California, Berkeley, CA, with assistance from Dr. Kathleen Durkin at UC Berkeley. Two basis sets, BS-1 and BS-2, were used. With BS-1 (M06), all elements were described with the full-electron double-ζ 6-31G** basis set, except the heaviest elements (Rh and P), which were described with the small-core LANL2DZ(d,f) ECP-adapted basis set. Geometries were fully optimized with BS-1 without any geometry or symmetry constraint. BS-1 was also used in the analytical calculation of frequencies, which identified each stationary point as either a minimum (reactants, intermediates and products) or a saddle point (transition state). The identity of the transition states was further confirmed by intrinsic reaction coordinate (IRC) calculations. The frequency calculations were also used to estimate the thermochemistry corrections as the difference between the Gibbs (G) and potential (E) energies, G – E. With BS-2, all elements were described with a triple-ζ basis set including the LANL2TZ(d,f) for Rh and P and 6-311+ +G** for all other elements. BS-2 (SMD-M06) was used to compute the energy in solution (E_sol) of all stationary points by modeling solvent effects at the DFT/M06/SMD level. The energy profiles were constructed by using the Gibbs energy in solution (G_sol), which was calculated by adding the thermochemistry corrections (G – E) to the energy in solution (E_sol).

Representative Procedure for Catalytic Reactions with [Rh(COD)₂]BF₄

In a N₂-filled glovebox, a 1 dram vial was charged with a stir bar and the substrate (0.040 mmol). A solution of [Rh(COD)₂]BF₄ (0.70 mg, 0.0020 mmol) in 40 µL of 1,4-dioxane was added, and a solution of ligand L1a (1.6 mg, 0.0040 mmol) in 40 µL of 1,4-dioxane was added. The vial was sealed with a Teflon-lined cap and removed from the glovebox. The reaction mixture was heated to 70 °C in an aluminum heating block, and aliquots at 2 and 18 h were analyzed by GC.

Representative Procedure for Catalytic Reactions with [Rh(ethylene)₂(1,4-dioxane)₂]BF₄

(1) A stock solution of the [Rh(ethylene)₂(1,4-dioxane)₂]BF₄ was prepared according to the literature procedure.

In a N₂-filled glovebox in the dark, a 1 dram vial was charged with a stir bar, [rhodium(ethylene)₂Cl]₂, AgBF₄, and 1 mL of methylene chloride, and the vial was capped. The solution was stirred in the dark at room temperature in the glovebox for 1 h. The solution was filtered through Celite, and the filtrate was concentrated under high vacuum. The resulting orange solid was dissolved in 1,4-dioxane (1 mL).

(2) A 1 dram vial was charged with a stir bar and the ligand L1a as a solution in 40 µL of 1,4-dioxane (0.0040 mmol). A solution of Rh(ethylene)₂(1,4-dioxane)₂]BF₄ was added (40 µL, 0.0020 mmol), and the substrate (0.040 mmol) was added to the mixture of rhodium and ligand. The vial was sealed with a Teflon-lined cap and removed from the glovebox. The reaction mixture was heated to 70 °C in an aluminum heating block, and aliquots at 2 and 18 h were analyzed by GC.

Representative Procedure for Synthesis of Dihydronaphthyl-Based Ligands

1-(2-Methoxyphenyl)-2-tetra-lone

In a N₂-filled glovebox, a 1 dram vial was charged with a stir bar, NaOtBu (264 mg, 2.75 mmol), (dtbpf)PdCl₂ (dtbpf = 1,1’-bis(di-tert-butylphosphino)ferrocene; 32.9 mg, 2 mol %), 2-methoxychlorobenzene (317 µL, 2.50 mmol), and β-tetralone (330 µL, 2.50 mmol). 1,4-Dioxane (2.0 mL) was added, and the vial was sealed with a Teflon-lined cap, shaken to dissolve the solid reagents, removed from the glovebox, and heated to 80 °C in an aluminum heating block Reaction progress was monitored by GC analysis, and the reaction mixture was cooled to 25 °C when the aryl chloride was consumed (after 24 h). The reaction mixture was diluted with hexane and filtered through silica, washing with 1/1 hexane/EtOAc. The filtrate was concentrated in vacuo and used without further purification. ¹H NMR (400 MHz, CDCl₃): δ 7.38–7.28 (m, 1H), 7.26 (d, J = 8.3 Hz, 1H), 7.22–7.06 (m, 3H), 7.04–6.96 (m, 1H), 6.91 (d, J = 8.2 Hz, 1H), 6.79 (d, J = 7.6 Hz, 1H), 4.80 (s, 1H), 3.66 (s, 3H), 3.29–3.11 (m, 2H), 2.89–2.65 (m, 2H).

1-(2-Methoxyphenyl)-3,4-dihydronaphthalen-2-yl Trifluoromethanesulfonate

To a solution of KHMDS (293 mg, 1.47 mmol) in THF at −78 °C was added a solution of 1-(2-methoxyphenyl)-2-tetralone (237 mg, 1.34 mmol) in 10 mL of THF in two portions. The reaction was stirred at 30 min at −78 °C, warmed to 25 °C, and stirred for 1 h at 25 °C. The reaction mixture was cooled to −78 °C, and PhN(Tf)₂ (525 mg, 1.47 mmol) was added in one portion. The reaction mixture was warmed to 25 °C and stirred overnight. The reaction mixture was concentrated, and the PhNHTf byproduct was recrystallized from cold pentane to yield a more concentrated solution of the desired product. The resulting solution was concentrated and purified by silica gel chromatography, with 99/1 hexanes/EtOAc as eluent, to yield 256 mg of white solid (50% yield). Note: the isolated yield reflects pure product obtained from one column; higher yields could be obtained by additional purification of the remaining solid. ¹H NMR (400 MHz, CDCl₃): δ 7.51–7.43 (m, 1H), 7.30–7.19 (m, 3H), 7.18–7.00 (m, 3H), 6.81 (d, J = 7.7 Hz, 1H), 3.80 (s, 3H), 3.21 (t, J = 8.2 Hz, 2H), 3.05–2.78 (m, 2H). ¹⁹F NMR (376 MHz, CDCl₃): δ −74.3 (s).

1-(2-Methoxyphenyl)-2-(dicyclohexylphosphino)-3,4-dihydronaphthalene (L13b)

In a N₂-filled glovebox, a 1 dram vial was charged with a stir bar, the enol triflate (256 mg, 0.667 mmol), Pd(OAc)₂ (16.3 mg, 10 mol %), DPPB (1,4-bis(diphenylphosphino)butane; 28.4 mg, 10 mol %), DIPEA (N,N-diisopropylethylamine; 174 µL, 1.00 mmol), and toluene (5 mL). Dicyclohexylphosphine (202 µL, 1.00 mmol) was added, and the vial was sealed with a Teflon-lined cap. The reaction mixture was removed from the glovebox and heated to 120 °C in an aluminum heating block. The reaction was monitored by ³¹P NMR spectroscopy, and the mixture was cooled to 25 °C when dicyclohexylphosphine was consumed. The reaction mixture was diluted with toluene in the glovebox, filtered through silica, and concentrated in vacuo. The crude reaction mixture was purified by column chromatography in the glovebox, with toluene as eluent, to yield 214 mg of white solid (74% yield). ¹H NMR (400 MHz, C₆D₆): δ 7.31–7.23 (m, 3H), 7.11 (m, 2H), 7.04 (m, 2H), 6.70 (d, J = 8.1 Hz, 1H), 3.35 (s, 3H), 2.92–2.73 (m, 2H), 2.49 (m, 2H), 1.95–1.69 (m, 12H), 1.41–1.16 (m, 10H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 157.1, 146.2 (d, J = 4.1 Hz), 136.4, 135.3, 132.3, 132.2, 129.8, 128.5, 127.09, 126.99, 126.3, 126.0, 119.9, 110.1, 55.0, 34.3 (d, J = 14.5 Hz), 33.8 (d, J = 2.8 Hz), 33.7 (d, J = 4.7 Hz), 31.4 (d, J = 19.0 Hz), 30.6 (d, J = 5.8 Hz), 30.5 (d, J = 4.8 Hz), 28.7, 27.6 (d, J = 6.7 Hz), 27.5 (d, J = 9.1 Hz), 27.4, 27.3, 26.6 (d, J = 9.7 Hz), 26.3, 26.0. ³¹P{¹H} NMR (202 MHz, CDCl₃): δ −3.47. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₉H₃₈OP, 433.2660; found, 433.2646.

1-(2-Trifluoromethylphenyl)-2-(dicyclohexylphosphi-no)-3,4-dihydronaphthalene (L13c)

The title compound was prepared from 2-bromobenzotrifluoride by the representative procedure above. ¹H NMR (600 MHz, CDCl₃): δ 7.70 (d, J = 7.7 Hz, 1H), 7.55 (d, J = 7.0 Hz, 2H), 7.50–7.44 (m, 1H), 7.22 (d, J = 7.2 Hz, 1H), 7.18 (d, J = 7.2 Hz, 1H), 7.13 (t, J = 7.0 Hz, 1H), 7.02 (t, J = 7.2 Hz, 1H), 6.40 (d, J = 7.5 Hz, 1H), 3.00–2.80 (m, 2H), 2.63 (dd, J = 9.9, 5.5 Hz, 1H), 2.56–2.38 (m, 1H), 1.95–1.56 (m, 12H), 1.33–1.01 (m, 10H). ¹³C{¹H} NMR (151 MHz, CDCl₃): δ 148.0, 147.8, 138.9, 136.41, 136.35, 136.1, 136.0, 135.8, 133.74, 133.72, 133.0, 132.2, 131.6, 131.3, 130.9, 130.64, 130.61, 129.2, 129.1, 129.0, 128.7, 128.0, 127.54, 127.45, 127.3, 127.2, 126.91, 126.88, 126.73, 126.69, 126.66, 126.63, 126.5, 126.2, 126.1, 125.2, 123.2, 35.4, 35.3, 34.2, 34.1, 31.5, 31.4, 31.11, 31.09, 31.04, 31.02, 30.9, 30.38, 30.33, 30.31, 28.4, 27.8, 27.71, 27.66, 27.54, 27.48, 27.41, 27.3, 27.2, 26.4, 26.42, 26.35, 26.27, 23.35 (complexity due to C–P and C–F splitting). ³¹P{¹H} NMR (243 MHz, CDCl₃): δ −5.5. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₉H₃₅F₃P, 471.2429; found, 471.2414.

1-Phenyl-2-(dicyclohexylphosphino)cyclohex-1-ene (L12)

The title compound was prepared from 2-phenyl-cyclohexanone by the representative procedure above. ¹H NMR (500 MHz, CDCl₃): δ 7.35–7.26 (m, 2H), 7.26–7.19 (m, 1H), 7.06 (d, J = 7.1 Hz, 2H), 2.42–2.31 (m, 2H), 2.24 (m, 2H), 1.85–1.58 (m, 16H), 1.33–1.03 (m, 10H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 152.6 (d, J = 30.8 Hz), 145.6 (d, J = 11.3 Hz), 130.0 (d, J = 17.5 Hz), 128.9 (d, J = 2.8 Hz), 127.6, 126.1, 35.0 (d, J = 6.8 Hz), 34.0 (d, J = 13.5 Hz), 31.4 (d, J = 18.8 Hz), 30.5 (d, J = 9.8 Hz), 27.6 (d, J = 7.8 Hz), 27.3 (d, J = 11.7 Hz), 26.7 (d, J = 4.6 Hz), 23.4 (d, J = 21.8 Hz). ³¹P{¹H} NMR (202 MHz, CDCl₃): δ −7.8. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₄H₃₆P, 355.2555; found, 355.2543.

(2-Phenethyl)dicyclohexylphosphine, Fluoroboric Acid Salt (L5)

To a solution of dicyclohexylphosphine in THF at −78 °C was added n-BuLi (2.6 M solution in hexane) dropwise over 5 min. The mixture was stirred at −78 °C for 1 h, and 2-phenethyl bromide was added dropwise over 10 min. The reaction mixture was warmed to room temperature, and after it was stirred at room temperature for 30 min, it was cooled to 0 °C and excess HBF₄(aq) was added. The reaction mixture was transferred to a round-bottomed flask and concentrated in vacuo. The crude solid was washed with pentane and purified by recrystallization from a mixture of pentane and ether to yield 200 mg of white solid (70% yield). ¹H NMR (400 MHz, CD₂Cl₂): δ 7.46–7.03 (m, 5H), 2.90–2.57 (m, 1H), 1.96–1.62 (m, 12H), 1.55 (s, 2H), 1.25 (d, J = 6.4 Hz, 10H). ¹³C{¹H} NMR (151 MHz, CD₂Cl₂): δ 145.70 (d, J = 0.8 Hz), 130.11, 129.92, 127.54, 36.72 (d, J = 22.4 Hz), 35.33 (d, J = 13.4 Hz), 32.31 (d, J = 14.7 Hz), 31.54, 30.99 (d, J = 8.8 Hz), 29.28 (d, J = 12.3 Hz), 29.21 (d, J = 7.9 Hz), 25.66 (d, J = 18.3 Hz), 1.44. ³¹P{¹H} NMR (162 MHz, CD₂Cl₂): δ −2.04. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₀H₃₂P, 303.2242; found, 303.2233.

(Z)-Phenyl(dicyclohexylphosphino)ethene (L4)

To a solution of 2-(dicyclohexylphosphino)-1-phenylethyne (1.00 mmol, 298 mg) at −78 °C was added dropwise a solution of diisobutylaluminum hydride (1.50 mmol, 0.750 mL, 2.0 M in ether). The reaction mixture was warmed to room temperature and was stirred for 2 h at room temperature. The mixture was cooled to 0 °C, and excess saturated, degassed NH₄Cl(aq) was added. The organic phase was transferred via cannula to a flask containing dry MgSO₄, under nitrogen. To the remaining aqueous liquid was added 10 mL of dry, degassed ether, and the organic phase was transferred into the receiving flask via cannula. The organic phase was concentrated to approximately 2 mL in vacuo, and the flask was moved into the glovebox. The organic phase was concentrated in vacuo, and the crude solid was purified by recrystallization from cold pentane to yield 276 mg of white solid in 92% yield. ¹H NMR (400 MHz, C₆D₆): δ 8.05 (d, J = 7.5 Hz, 1H), 7.27 (t, J = 5.7 Hz, 2H), 7.11 (t, J = 7.4 Hz, 1H), 6.10 (dd, J = 13.0, 5.9 Hz, 1H), 2.04–1.57 (m, 12H), 1.57–1.12 (m, 11H). ¹³C{¹H} NMR (101 MHz, C₆D₆): δ 145.3 (d, J = 16.3 Hz), 138.1, 130.2 (d, J = 10.9 Hz), 129.8, 129.5, 128.3, 35.0 (d, J = 11.6 Hz), 30.4 (d, J = 15.9 Hz), 28.8 (d, J = 8.0 Hz), 27.3 (d, J = 3.9 Hz), 27.2, 26.6. ³¹P{¹H} NMR (162 MHz, CDCl₃): δ −6.35. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₀H₃₀P, 301.2085; found, 301.2074.

2-(Diethylphosphino)-2′-(N,N-dimethylamino)-biphenyl (L1c)

To a solution of 2-bromo-2′-(N,N-dimethylamino)biphenyl (250 mg, 0.905 mmol) at −78 °C was added n-BuLi (1.6 M solution in hexane, 0.566 mL, 0.905 mmol) dropwise over 10 min, and the reaction mixture was stirred for 30 min. Diethylchlorophosphine (110 µL, 0.905 mmol) was added in one portion, and the reaction mixture was stirred for an additional 30 min at −78 °C. The reaction mixture was warmed to room temperature, and the solvent was evaporated under high vacuum. The crude mixture was transferred into the glovebox and was filtered through 0.5 mL of silica. The silica was rinsed with toluene, and the mixture was concentrated under high vacuum. The filtered solid was dissolved in pentane and filtered again through 0.5 mL of silica to yield 168 mg of the title compound as a white solid after concentration in vacuo (63%). ¹H NMR (300 MHz, CDCl₃): δ 7.64–7.50 (m, 1H), 7.44–7.26 (m, 4H), 7.14–6.89 (m, 3H), 2.46 (s, 3H), 1.66 (q, J = 7.7 Hz, 1H), 1.47 (q, J = 7.4 Hz, 1H), 1.01 (dt, J = 15.5, 7.7 Hz, 2H), 0.75 (dt, J = 14.9, 7.6 Hz, 1H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 151.6, 148.6 (d, J = 30.5 Hz), 137.8 (d, J = 16.0 Hz), 135.5 (d, J = 5.2 Hz), 131.9, 130.4 (d, J = 3.5 Hz), 123.0 (d, J = 5.8 Hz), 128.7, 128.3, 126.8, 121.1, 117.4, 43.2, 22.3 (d, J = 12.3 Hz), 21.0 (d, J = 12.2 Hz), 10.4 (d, J = 17.1 Hz), 10.0 (d, J = 13.9 Hz).³¹P{¹H} NMR (CDCl₃): δ −27.6 ppm. HRMS-ESI (m/z): [M + H]⁺ calcd for C₁₈H₂₅NP, 286.1725; found, 286.1714.

2-Bis(N,N-diethylamino)phosphino-2′-(N,N-dimethylamino)biphenyl (L1b)

To a solution of 2-bromo-2′-(N,N-dimethylamino)biphenyl (250 mg, 0.905 mmol) at −78 °C was added n-BuLi (1.6 M solution in hexane, 0.566 mL, 0.905 mmol) dropwise over 10 min, and the reaction mixture was stirred for 30 min. Bis(N,N-diethylamino)chlorophosphine (191 µL, 0.905 mmol) was added in one portion, and the mixture was stirred for an additional 30 min at −78 °C. The reaction mixture was warmed to room temperature, and the solvent was evaporated under high vacuum. The crude solid was transferred to the glovebox and recrystallized from pentane at −35 °C to yield 212 mg of white waxy solid (63% yield). ¹H NMR (600 MHz, CDCl₃): δ 7.81–7.65 (m, 1H), 7.40–7.17 (m, 4H), 7.03–6.78 (m, 3H), 3.01–2.78 (m, 4H), 2.76–2.58 (m, 4H), 2.50 (s, 6H), 1.15–0.94 (m, 6H), 0.89–0.62 (m, 6H). ¹³C{¹H} NMR (151 MHz, CDCl₃): δ 151.0 (d, J = 3.2 Hz), 145.1, 141.2, 134.8, 131.8, 131.0, 130.5, 127.7, 125.9, 120.2, 117.5, 43.4 (d, J = 19.4 Hz), 43.0, 41.9 (d, J = 18.2 Hz), 14.5, 14.2. ³¹P{¹H} NMR (243 MHz, CDCl₃): δ 95.4. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₂H₃₄N₃P, 371.2490; found, 371.2414.

1,1-diphenyl-2-(dicyclohexylphosphino)ethene (L9a)

To a solution of 1,1-diphenyl-2-bromoethene (1.00 g, 3.86 mmol) in THF (10 mL) at −78 °C was added n-BuLi (1.6 M solution in hexane, 2.41 mL, 3.86 mmol) dropwise over 10 min, and the reaction mixture was stirred for 30 min. Dicyclohexylchlorophosphine (0.852 mL, 3.86 mmol) was added in one portion, and the mixture was stirred for an additional 30 min at −78 °C. The reaction mixture was warmed to room temperature, and the mixture was evaporated under high vacuum. The crude mixture was transferred into the glovebox and was filtered through 0.5 mL of silica, washed with toluene, and concentrated under high vacuum to yield 1.08 g of off-white solid (75% yield). ¹H NMR (600 MHz, CDCl₃): δ 7.34 (d, J = 6.6 Hz, 3H), 7.29 (m, 5H), 7.22 (d, J = 6.9 Hz, 2H), 6.51 (d, J = 5.7 Hz, 1H), 1.89–1.55 (m, 12H), 1.21 (dd, J = 27.1, 11.8 Hz, 10H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 141.1 (d, J = 6.3 Hz), 130.5 (d, J = 3.0 Hz), 131.6, 128.2, 127.9, 127.7, 127.6, 127.5, 127.3, 100.0, 34.5 (d, J = 10.5 Hz), 30.3 (d, J = 15.9 Hz), 29.0 (d, J = 7.1 Hz), 27.4 (d, J = 5.5 Hz). ³¹P{¹H} NMR (243 MHz, CDCl₃): δ −18.7. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₆H₃₄P 377.2398; found, 377.2386.

Representative Procedure for Synthesis of Vinyl-Bridged Ligands

1,1-Diphenylbut-1-ene

To a solution of methyl butyrate (1.70 mL, 15.0 mmol) in THF (60 mL) at 0 °C was added PhMgBr (1.0 M in THF). The reaction mixture was warmed to room temperature and stirred overnight. The mixture was cooled to 0 °C and quenched with saturated NH₄Cl(aq). The mixture was transferred into a separatory funnel and was diluted with EtOAc. The organic phase was separated, and the aqueous phase was extracted three times with EtOAc (10 mL). The combined organic phases were dried (MgSO₄) and concentrated in vacuo. The crude mixture was added to a solution of pyridium p-toluenesulfonate mono-hydrate that had been dried at reflux with a Dean–Stark apparatus and cooled to room temperature. The mixture was heated to reflux with a Dean–Stark apparatus and refluxed overnight. The mixture was cooled to 25 °C and concentrated in vacuo. The crude mixture was diluted with hexanes, filtered through silica, concentrated in vacuo, and used without purification in the next reaction.

1,1-Diphenyl-2-bromobut-1-ene

To a solution of 1,1-diphenylbut-1-ene (2.81 g, 13.5 mmol) in 1,2-DCE (10 mL) at 0 °C was added a solution of bromine (695 µL, 13.5 mmol) in 1,2-DCE (5 mL) dropwise. The mixture was stirred at 0 °C for 30 min, and pyridine (4.35 mL, 54.0 mmol) was added dropwise. The mixture was heated to reflux and stirred overnight. The mixture was cooled to 0 °C and quenched with saturated Na₂S₂O₄(aq). The mixture was transferred to a separatory funnel, the organic layer was separated, and the aqueous layer was extracted with CH₂Cl₂ (2 × 20 mL). The organic layer was concentrated, and the crude solid was recrystallized from hot MeOH.

1,1-Diphenyl-2-(dicyclohexylphosphino)but-1-ene (L9d)

To a solution of 1,1-diphenyl-2-bromobut-1-ene (718 mg, 2.50 mmol) in THF (10 mL) at −78 °C was added n-BuLi (1.6 M solution in hexane) dropwise over 10 min, and the mixture was stirred for 2 h. Dicyclohexylchlorophosphine (552 µL, 2.50 mmol) was added in one portion, and the mixture was stirred for an additional 30 min at −78 °C. The reaction mixture was warmed to room temperature, and the solvent was evaporated under high vacuum. The crude mixture was transferred into the glovebox and was filtered through 0.5 mL of silica, washed with pentane, and concentrated under high vacuum to yield 819 mg of white solid (81% yield). ¹H NMR (500 MHz, CDCl₃): δ 7.37–7.02 (m, 10H), 2.50–2.32 (m, 2H), 1.96–1.60 (m, 12H), 1.42–1.08 (m, 10H), 0.83 (m, 3H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 144.5 (d, J = 12.2 Hz), 138.6 (d, J = 23.5 Hz), 129.8 (2C), 129.8 (2C), 128.3 (2C), 127.6, 126.4 (d, J = 10.6 Hz), 34.8 (d, J = 15.1 Hz), 31.3 (d, J = 18.1 Hz), 31.1 (d, J = 11.2 Hz), 27.4 (d, J = 8.6 Hz), 27.3 (d, J = 11.7 Hz), 14.5. ³¹P{¹H} NMR (202 MHz, CDCl₃): δ 1.5. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₈H₃₄P, 405.2711; found, 405.2696.

1,1-Diphenyl-2-(dicyclohexylphosphino)-3-methyl-prop-1-ene (L9c)

The title compound was prepared from methyl isobutyrate by the representative procedure above. ¹H NMR (600 MHz, CDCl₃): δ 7.29–7.22 (m, 4H), 7.22–7.15 (m, 4H), 7.13 (d, J = 7.4 Hz, 2H), 2.84–2.70 (m, 1H), 2.06–1.96 (m, 2H), 1.85–1.76 (m, 2H), 1.72–1.62 (m, 6H), 1.52–1.41 (m, 2H), 1.31–1.10 (m, 10H), 1.03 (d, J = 6.9 Hz, 6H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 145.1 (d, J = 3.6 Hz), 144.5 (d, J = 6.9 Hz), 141.7, 141.5, 128.3, 128.1, 128.0, 127.7, 126.4, 126.3, 35.4 (d, J = 14.1 Hz), 33.3 (d, J = 16.9 Hz), 32.4 (d, J = 20.0 Hz), 31.7 (d, J = 11.2 Hz), 27.4 (d, J = 8.7 Hz), 27.3 (d, J = 12.6 Hz), 26.5, 23.3 (d, J = 7.6 Hz). ³¹P{¹H} NMR (243 MHz, CDCl₃): δ −2.6. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₉H₄₀P, 419.2868; found, 419.2853.

1,1-(2-Methoxyphenyl)-2-(dicyclohexylphosphino)-prop-1-ene (L9e)

The title compound was prepared from methyl propionate by the representative procedure above. ¹H NMR (600 MHz, CDCl₃): δ 7.25–7.01 (m, 4H), 6.95–6.78 (m, 3H), 6.77 (d, J = 7.7 Hz, 1H), 3.80 (br s, 6H), 1.91–1.56 (m, 15H), 1.31–1.11 (m, 10H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 156.24–154.68 (m), 146.9 (d, J = 32.3 Hz), 134.84–133.85 (m), 133.65–132.94 (m), 133.23–132.17 (m), 131.82–130.84 (m), 129.7, 127.8, 127.7, 120.4, 119.5, 111.59–110.33 (m), 110.33–109.49 (m), 36.10–34.64 (m), 55.4, 54.9, 34.2 (dd, J = 15.9, 5.0 Hz), 32.08–31.17 (m), 31.24–30.58 (m), 30.66–29.99 (m), 28.33–27.58 (m), 27.70–27.22 (m), 26.8, 17.0 (d, J = 1.9 Hz). ³¹P{¹H} NMR (243 MHz, CDCl₃): δ −5.1. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₉H₄₀O₂P, 451.2766; found, 451.2760.

1-Methyl-2-phenyl-3-(dicyclohexylphosphino)indole (L7b)

¹H NMR (500 MHz, CDCl₃): δ 7.92 (d, J = 7.8 Hz, 1H), 7.54–7.46 (m, 3H), 7.40 (dd, J = 16.4, 7.3 Hz, 3H), 7.31 (d, J = 7.6 Hz, 1H), 7.22 (t, J = 7.2 Hz, 1H), 3.57 (s, 3H), 2.32 (s, 2H), 1.82 (dd, J = 47.3, 11.3 Hz, 5H), 1.63 (d, J = 6.4 Hz, 5H), 1.43–0.95 (m, 15H). ¹³C{¹H} NMR (126 MHz, CDCl₃): δ 138.1, 132.7 (d, J = 3.1 Hz), 131.5, 131.5, 130.7, 128.4, 127.9, 121.9, 121.6, 119.8, 109.7, 104.1 (d, J = 13.1 Hz), 34.2 (d, J = 8.1 Hz), 32.0 (d, J = 20.3 Hz), 31.2, 30.5 (d, J = 8.1 Hz), 27.3 (d, J = 7.8 Hz), 27.2, 26.5. ³¹P{¹H} NMR (202 MHz, CDCl₃): δ −17.6. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₇H₃₅NP, 404.2507; found, 404.2493.

1-Phenyl-2-(dicyclohexylphosphino)naphthalene (L11)

To a solution of 1-phenyl-2-iodonaphthalene (419 mg, 1.27 mmol) in THF (10 mL) at −78 °C was added n-BuLi (1.6 M solution in hexane, 0.794 mL, 1.27 mmol) dropwise over 10 min, and the mixture was stirred for 30 min. Dicyclohexylchlorophosphine (0.280 mL, 1.27 mmol) was added in one portion, and the mixture was stirred for an additional 30 min at −78 °C. The reaction mixture was warmed to room temperature, and the solvent was evaporated under high vacuum. The crude mixture was transferred into the glovebox and was filtered through 0.5 mL alumina, washed with CH₂Cl₂, and concentrated under high vacuum to yield 437 mg of off-white solid (86% yield). HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₈H₃₄P, 401.2398; found, 401.2384.

1-Phenyl-2-(dicyclohexylphosphino)-3,4-dihydro-naphthalene (L13a)

To a solution of 1-phenyl-2-iodo-3,4-dihydronaphthalene (200 mg, 0.602 mmol) in THF (10 mL) at −78 °C was added n-BuLi (1.6 M solution in hexane, 0.376 mL, 0.602 mmol) dropwise over 10 min, and the mixture was stirred for 30 min. Dicyclohexylchlorophosphine (0.133 mL, 0.602 mmol) was added in one portion, and the mixture was stirred for an additional 30 min at −78 °C. The reaction mixture was warmed to room temperature, and the solvent was evaporated under high vacuum. The crude mixture was transferred into the glovebox and was filtered through 0.5 mL alumina, washed with CH₂Cl₂, and concentrated under high vacuum to yield 204 mg of off-white solid (84% yield). ¹H NMR (300 MHz, CDCl₃): δ 7.48–7.27 (m, 4H), 7.21–6.94 (m, 4H), 6.60 (d, J = 7.8 Hz, 1H), 2.92–2.80 (m, 2H), 2.59–2.47 (m, 2H), 1.68 (m, 12H), 1.32–1.07 (m, 10H).¹³C{¹H} NMR (126 MHz, CDCl₃): δ 136.6 (d, J = 34.4 Hz), 130.9 (d, J = 1.9 Hz), 131.6, 128.8, 128.2, 127.8, 127.3, 127.0, 126.9, 126.7, 126.3, 125.5, 34.2 (d, J = 13.9 Hz), 31.1 (d, J = 19.2 Hz), 30.6 (d, J = 9.3 Hz), 28.7, 27.5 (d, J = 7.6 Hz), 27.3 (d, J = 12.3 Hz), 26.5, 26.0 (d, J = 5.5 Hz). ³¹P{¹H} NMR (CDCl₃): δ −5.6 ppm. HRMS-ESI (m/z): [M + H]⁺ calcd for C₂₈H₃₆P, 403.2555; found, 403.2541.