Fluorinated h-BN as a magnetic semiconductor

A strategic approach toward functionalization can change properties: effect of the “oxidizer of oxygen” on hexagonal boron nitride.

Abstract

We report the fluorination of electrically insulating hexagonal boron nitride (h-BN) and the subsequent modification of its electronic band structure to a wide bandgap semiconductor via introduction of defect levels. The electrophilic nature of fluorine causes changes in the charge distribution around neighboring nitrogen atoms in h-BN, leading to room temperature weak ferromagnetism. The observations are further supported by theoretical calculations considering various possible configurations of fluorinated h-BN structure and their energy states. This unconventional magnetic semiconductor material could spur studies of stable two-dimensional magnetic semiconductors. Although the high thermal and chemical stability of h-BN have found a variety of uses, this chemical functionalization approach expands its functionality to electronic and magnetic devices.

INTRODUCTION

There has recently been strong interest in developing new semiconductor magnetic materials to realize devices such as magnetic bipolar transistors and magnetic storage media (1). The pursuit for magnetic semiconductors has led to a class of materials called dilute magnetic semiconductors (DMS) (2). Many DMS materials have been reported, although the low Curie temperature still continues to be a major impediment (2). In contrast to the reported ferromagnetic (FM) semiconductors, such as tellurides and oxides (2), we report a new possibility for a stable two-dimensional (2D) wide bandgap insulator to be chemically and structurally modified into a magnetic semiconductor. The realm of 2D materials has emerged as a promising new set of low-dimensional materials for semiconductor electronic devices (3). Chemical functionalization has been a known strategy to modulate and change the electronic properties of 2D materials (4–9). Here, we demonstrate a new approach to modify a 2D layered material, namely, hexagonal boron nitride (h-BN, “white graphene”), known for its structural, chemical, and thermal stability, to create fluorinated h-BN (F-BN), which modifies the bandgap and electronic structure, leading to an unconventional semiconductor magnet. h-BN, a layered ceramic, is an electrical insulator, but theoretical studies have shown a reduction in the bandgap of h-BN on functionalization with -H, -F, -OH, and -NH₂ (10, 11). In our current study, we explore the band structure transformation of h-BN to a wide bandgap semiconductor on functionalization with fluorine. Using optical spectroscopy, structural characterization, and density functional theory (DFT) calculations, we decipher the structure, defects and defect levels, and their influence on the band structure and the surprisingly emergent magnetic properties of F-BN. Our experimental observations show room temperature ferromagnetism in F-BN, and temperature-dependent ac magnetic measurements reveal signatures of frustrated magnetism that can include coexistence of FM and antiferromagnetic (AFM) interactions or spin-glass type of behavior (12). Our study constitutes the first observation of these phenomena in this high-temperature ceramic material and opens up possibilities of finding new 2D atomic layer–based magnetic semiconductors.

RESULTS

In the current method of fluorination, Nafion, a perfluorinated polymer, was used as the fluorinating agent. Bulk h-BN (supplied by Sigma-Aldrich) dispersed in N,N´-dimethylformamide (DMF) and Nafion was taken in a solvothermal reactor for fluorination. Figure 1A lays out a schematic of the synthesis. The polymer undergoes degradation at the synthesis temperature of 200°C to give fluorine (F) radicals and polymer fragments (13). The F radicals interact with the B-N bonds, whereas the polymer fragments remain in solution and can be easily separated. After the reaction, the supernatant containing the polymer fragments are separated, and the F-BN sheets, which settle to the bottom, are washed with acetone. More details of the synthesis are given in section S1A.

Fig. 1. Synthesis and characterization of fluorinated boron nitride.

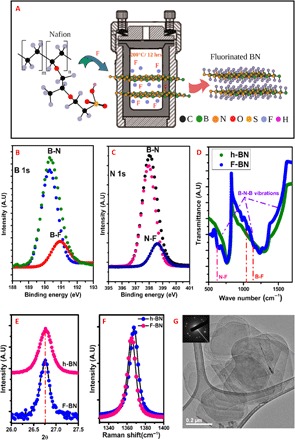
(A) The schematic of the method used for the fluorination of h-BN is outlined. The bulk h-BN is dispersed in DMF, and Nafion is added to it. The mixture is heated in an autoclave at 200°C for 12 hours. (B) The deconvoluted XPS spectrum of B 1s peak shows two peaks, one corresponding to B-N bonding in h-BN and the other low intensity peak at higher energy corresponds to B-F bonding. (C) Deconvoluted XPS spectrum of N 1s peak also shows two peaks corresponding to N-B and N-F. (D) The IR spectra showing the broad B-N-B bending vibrations in h-BN and F-BN. In F-BN, the F-B peaks can be clearly seen interspersed with the broad B-N peak. (E) XRD showing the most intense peaks in h-BN and F-BN. (F) Raman spectra shows the E_2g peak in h-BN and the shifted peak, which appears in F-BN. (G) Low-magnification bright-field TEM image of the thin F-BN sheets and the diffraction pattern of 001 orientation (inset) confirms the hexagonal structure.

The deconvoluted x-ray photoelectron spectroscopy (XPS) spectra evidently shows B-N, B-F, and N-F bonding (Fig. 1, B and C). The peaks ascribed to B-N bond are seen at 190.3 and 398 eV of the B 1s and N 1s spectrum, respectively (14). It is reasonable to assign the higher energy peaks seen in the spectrum to B-F and N-F bonding. The increased columbic interaction due to the high electronegativity of F, compared to B and N, account for the occurrence of the peaks at a higher binding energy. It is explicit at higher concentrations of fluorine and is further affirmed by direct gas fluorination of h-BN at high concentrations (section S1B). High-resolution infrared (IR) spectra (Fig. 1D) show a number of bands overlapping with the broad B-N TO (transverse optical) mode at ~1380 cm⁻¹ (14). The additional bands arise from the F-bonded B and N. The bands at 1053 and 1235 cm⁻¹ are ascribed to primary vibrational modes in covalent B-F bonding (15). N-F bond vibrations at 633 cm⁻¹ overlap with the B-N-B out-of-plane bending vibrations (16). Preliminary fluorine-19 magic angle spinning nuclear magnetic resonance (MAS ¹⁹F NMR) spectra do not allow a definitive interpretation of the signals (section S2).

The high-temperature fluorination leads to the introduction of defect sites in the lattice. X-ray diffraction (XRD) and electron microscopy studies were performed to explore these defects and their effects on the layered structure. From the XRD pattern shown in Fig. 1E, the plane spacing in pure h-BN and F-BN are not significantly different, except for broadening of the peaks, which can be due to strain induced by defects in the lattice. In the Raman spectra (Fig. 1F), a red shift of the E_2g peak of F-BN when compared with h-BN suggests the influence of strain due to doping in the lattice (17, 18). The above results confirm that fluorination creates local defects. The detailed scanning electron microscope (SEM) and transmission electron microscope (TEM) images are acquired to understand the effect of fluorination on the morphology of the sheet. The low-magnification bright-field TEM image shown in Fig. 1G confirms the circular morphology, and the selected-area electron diffraction (SAED) covering these sheets reveals hexagonal 0001 plane of F-BN. These thin sheets are found to be single or bilayers, with defects introduced by the fluorination. A detailed TEM characterization of the material is given in section S3.

h-BN has a high exciton binding energy of 700 meV and strong exciton-phonon interactions (19). Consequently, determination of the bandgap by absorption or photoluminescence (PL) measurements is challenging. Therefore, here, we use a combination of absorbance and PL spectroscopy to aid the study of band structure and defect states created in h-BN on fluorination. The determined absorption bandgap of h-BN has a value 5.86 eV (section S4), which has been observed previously for excitonic transitions (20). Figure 2A shows the variation of bandgap in absorbance spectroscopy as we increase the doping with fluorine, starting from the pristine sample. At the lowest doping concentration of 3.2%, a sharp decrease from 5.86 (h-BN) to 5.5 eV is observed. However, with consequent increase in the fluorination, an increase in the bandgap is observed up to 10.6% of doping, following which it starts decreasing again. The apparent decrease in bandgap observed in the previous study may be due to low doping concentration or the introduction of defect levels (8). The defect levels are further probed by PL spectroscopy. The broad emission spectra observed in PL (section S5) could be deconvoluted into three peaks. On deconvolution, each spectrum could be resolved into three peaks, which are designated as A, B, and C, in order from the lowest peak to the highest peak in each spectra (Fig. 2B). Recent experimental evidence has shown that these emissions take place from the impurity or defect states in h-BN (21). A discussion of the origin of various peaks is given in section S5. Phonon interactions at 3.2 and 10.6% doping are observed from the calculation of energy gap between the three peaks at these doping levels, which eliminate the possibility of a defect state. At the intermediate doping of 8.1%, the PL peaks cannot be ascribed to known phonon modes in h-BN; therefore, a defect state introduced by the doping between the valence and conduction band might be contributing to the observed emission. The role of dopant on the actual electronic properties of h-BN was understood by electrical conductivity measurements.

Fig. 2. Electronic properties and band structure of fluorinated boron nitride.

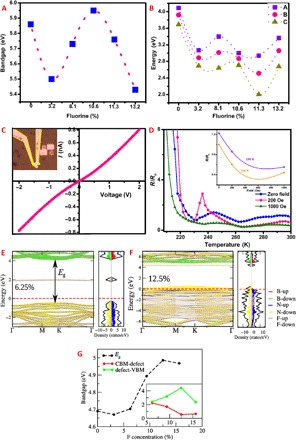
(A) Variation of bandgap calculated from the UV-vis absorption measurements with the percentage of fluorine doping. The bandgap was calculated from the absorbance measurements using Tauc plot. (B) Variation of deconvoluted PL spectra according to the percentage of fluorine doping. Each PL spectrum was deconvoluted into three peaks, namely, A, B, and C. (C) I-V curve obtained from two-probe measurements conducted on a device fabricated on fluorinated boron nitride (F-BN) on a silicon substrate with SiO₂ coating. The inset shows an optical image of the device. (D) Magnetotransport measurements as a function of temperature at zero field, low field, and at high field. The inset shows the negative magnetoresistance at two different temperatures. (E and F) Band structures and density of states with atomic contribution obtained by spin-polarized calculations for F-BN sheets having (E) 6.25% and (F) 12.5% F concentrations. (G) Change in bandgap (E_g) as a function of F concentrations calculated from DFT calculations. Inset shows variation in defect level and valence band maximum (VBM) and conduction band minimum (CBM) from doping above 5%, where defect level is seen.

The I-V (current-voltage curve) characteristics of an exfoliated h-BN flake with 13.2% fluorination is shown in Fig. 2C. The nonlinear behavior suggests current conduction via tunneling through defect states. A more affirmative evidence of the semiconducting nature is obtained from the decrease in resistance with increasing temperature (Fig. 2D). The resistance increases several times below ~230 K, a marked change is not seen above this temperature. This behavior could be due to the limited amount of charge carries available for thermal excitation (22, 23). h-BN is an intrinsically insulating material, and the charge carriers are contributed mainly by the dopant F atoms. The small amount of dopant limits the number of charge carriers available for thermal excitation. Magnetotransport measurements performed with respect to temperature reveals negative magnetoresistance (Fig. 2D), which suggests the presence of localized moments in the F-BN system, where the negative magnetoresistance is due to the suppression of thermodynamic spin fluctuations on application of magnetic field (24). As more spins align, the spin scattering decreases, thereby leading to reduction in resistance.

The effect of fluorination on the electronic band structure of h-BN is investigated by calculating spin-polarized electronic band structures for low-energy structures. The structural details of the simulation and their formation energies are given in section S7. The h-BN sheet is functionalized with F atoms up to 15.625% doping by considering various symmetrically nonequivalent positions. In the case of h-BN, B and N atoms are sp²-hybridized, and they show a notably large fundamental bandgap (E_g) of 4.69 eV at Γ point due to significant electronegativity difference between B and N, shown in fig. S10A. The calculated E_g value is underestimated compared to the experimental value of 5.56 eV (optical bandgap) (25). This is a well-known problem of Perdew, Burke, and Ernzerhof (PBE) functional, which entails the self-interaction error and lack of an integer discontinuity in the exchange-correlation energy as the number of electrons change (26, 27). However, the calculated E_g is in well agreement with previous reported theoretical results (25, 28). On introducing the first F (3.125%), the bandgap decreases by 0.02 eV. A defect level between the VBM and CBM is not observed below 5% F doping, and there is an actual decrease in the fundamental bandgap. In the PL studies at the lowest doping of fluorine, the calculated phonon energy is close to the phonon energies of h-BN at the Γ point, and the decrease is the bandgap observed in absorption measurements in tone with the calculated band structure. Introduction of the second F introduces a dispersionless defect level (shown in brown colored line in Fig. 2E) between the band positions of h-BN. This defect level continues to appear between the band positions at higher doping levels as well (Fig. 2F). Thus, on increasing the doping above 5%, the effect of defect level is seen in the experiment and calculations. In Fig. 2G, the plot of change in bandgap as a function of fluorine content (E_g, difference between CBM and VBM), E_g, first decreases and then increases as a function of F concentration until 12.5%. Further enhancement in F concentration reduces the gap, a trend similar to the bandgap variation (Fig. 2A) estimated from an ultraviolet-visible spectroscopy (UV-vis) absorption measurement. This nonlinear behavior of bandgap with F concentration has been explained on the basis of the alignment of band edges with respect to vacuum level and the band-decomposed charge density as shown in fig. S10. The energy difference between CBM and the defect level as well as the defect level and VBM are plotted as a function of F concentration in the inset of Fig. 2G. The energy difference between CBM and defect level decreases as F concentration increases. This trend matches the experimentally observed change in peak C of the deconvoluted PL spectrum with F concentration (Fig. 2B) except for 13.2%, where peak C increases unlike theoretical findings.

The electronic states of an h-BN sheet in fig. S11A, within −2.0 eV from VBM, are mainly contributed by N-p states. When F atoms attach at the B sites of h-BN, the bonding states of F-B are located far below the VBM (fig. S11B). Because of the low energy of F-B states compared to VBM, the electrons from nearest N atoms move toward the F-B bonding states, as shown by charge accumulation and depletion in fig. S12A. This gives rise to the unpaired electron in the nearest N-p states. On the other hand, the F-N bonding state is located close to or above the Fermi energy (fig. S11C). This indicates that the N-F bond electrons move toward the N atoms, as a result of which charge accumulates in N atom (fig. S12B), and the amount of charge accumulated in F atom in this case is less compared to F atom in B-F bond (fig. S12A). Therefore, the number of F atoms attached at the B and N sites in h-BN sheet will determine the number of unpaired electrons in the system, thereby the magnetism of the F-BN sheet. Completely fluorinated h-BN sheet (fig. S11D) and 6.25% F concentration having two F atoms attached to B and nearest N atoms on opposite sides show no magnetic moment due to absence of unpaired electron, whereas 9.375, 12.5, and 15.625% can show magnetic ground state (fig. S9F, where the spin-polarized state is energetically more favorable). In light of this understanding, we look at the magnetic property of the next highest fluorine doping (8.1%).

The room temperature hysteresis measurement of 8.1% F-doped h-BN (Fig. 3A) shows FM ordering with a saturation magnetism of 0.018 emu (electromagnetic units)/g. The temperature-dependent magnetization measured at 500 Oe (Fig. 3B) is fitted according to the Curie’s law. The details of the fitting parameters are given in section S6. The negative Néel temperature obtained from the fitting is suggestive of AFM behavior contrasting the observed room temperature hysteresis. The susceptibility against temperature plot (Fig. 3C) starts diverging at around room temperature, and it starts increasing below a particular temperature, as opposed to the decrease/saturation in ferromagnets. These are the characteristic behavior of frustrated magnetism (12). A frustrated system might arise either when two types of magnetic behavior compete to coexist in the lattice or when the spins align at an angle as seen in spin glass. It has been reported that graphene samples having two to seven layers, prepared by different methods, show coexistence of FM features along with AFM, leading to frustrated magnetization (12, 29). A recent report suggests that upon fluorination in MoS₂ (30), there is competition between FM and AFM ordering, leading to frustrated magnetization. Spin-glass type of magnetism has never been reported on 2D materials. This anomalous magnetic behavior was first observed in Au_1-xFe_x and Cu_1-xMn_x alloys, in which the alternating signs of coupling constants between the host and the impurity lead to a frustrated state. The signature of spin-glass behavior is its frequency dependence of the spin-freezing temperature, which is not observed in any other magnetic system (31, 32). This frequency dependence of magnetism is the best tool for differentiating between these two possible scenarios of frustrated magnetism.

Fig. 3. Unconventional magnetic properties of fluorinated boron nitride.

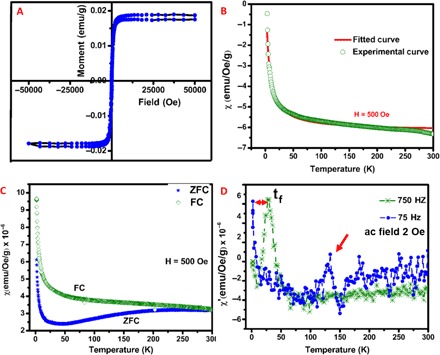
(A) The room temperature hysteresis curve of F-BN with 8.1% fluorine. (B) The experimentally observed temperature-dependent susceptibility fitted with the Curie’s law. The measurement was performed at an applied dc field of 500 Oe. (C) The susceptibility variation with temperature obtained on zero field cooling (ZFC) and field cooling (FC) after subtracting the diamagnetic background. (D) The real part of the ac susceptibility against temperature for measurements at 75 and 750 Hz at an ac field of 2 Oe. The freezing temperature (T_f) is marked.

The measurement conditions for ac susceptibility are outlined in section S6. The plot between the real part of the susceptibility and temperature (Fig. 3D) shows a shifted maximum around low temperatures (~25 K). The higher frequency curve shows a peak at around the same temperature, as expected from the dc measurements. This is regarded as the freezing temperature (T_f), at which the randomly oriented spins are frozen without any long-range order. At lower frequency, this is shifted to much lower temperatures, which is expected because the spins can follow the external perturbation to much lower temperatures. At low frequency, we observe another peak at ~125 K higher than T_f. Such a change is intriguing, and previous observations in TbAuIn have been attributed to a phase change on freezing (33). However, in this case, because we do not see the same change in the higher frequency, it cannot be regarded as a phase change. The existence of the peak at this lower frequency is confirmed by repeating the measurement at 79 Hz (fig. S8). At 79 Hz, the peak is shifted to a slightly higher temperature closer to 150 K. This can only be attributed to a spin glass–related transition. According to the Heisenberg model for spin glasses, there can be successive transitions in the presence of magnetic field. The freezing of spin components that are transverse to the magnetic field, called the Gabay-Toulouse transitions, is followed by further freezing of the components longitudinal to the field, called the Almeida-Toulouse transitions (34). This high temperature peak may be corresponding to these transitions occurring before the actual freezing of the spins at T_f. The imaginary part of susceptibility (fig. S8B) reflects the energy loss in the process of transition and is usually seen to be positive. Some exceptions to this are observed in SiGe systems, where the thermodynamic potential changes can lead to a negative change in susceptibility at the transition temperature (35). Theoretical simulations of the possible structures and energy configurations aid further understanding of the magnetic behavior.

The magnetization in F-BN originates because of the difference between up and down spin states of N atoms. The partial density of states of different atoms (Fig. 2, D and E) for different F concentrations relates this difference. At 6.25% F concentrations, both spin states are equivalent, leading to zero magnetization. Subsequently, as F concentration increases, the difference between the two spin states increases, resulting in an enhanced net magnetization. The corresponding values of magnetization are 0.83, 1.92, and 2.95 μ_B for 9.375, 12.5, and 15.625% F concentration (plotted by orange diamonds in Fig. 4A), respectively, and are nearly equal to the number of unpaired electrons present in the F-BN sheet.

Fig. 4. DFT calculations of the magnetic moment for various configurations.

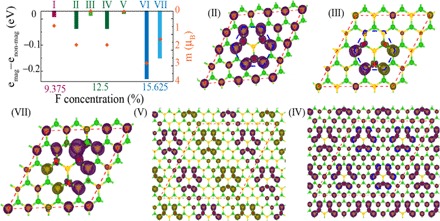
The energy difference between different magnetic solutions marked by I to VII for different F concentrations and their corresponding nonmagnetic states. I, II, IV, and VI; III and V; and VII are FM, AFM, and ferrimagnetic solutions, respectively. The total magnetic moment [M(μ_B)] for different magnetic states is also shown in the same plot by orange diamonds, whereas axis is marked on the right side. The spin-up and spin-down densities are colored purple and yellow, respectively. The isosurface value of 0.002 e/A³ is fixed for spin-density plots. The magnetic moment is localized to the nearest six N atoms of the region, where three F atoms (red color sphere) are attached to three B atoms, and one F atom is attached in the opposite site with N atom in the middle of hexagon (as shown by dotted blue line). II (IV) and III (V) are FM and AFM solutions of the 4 × 4 × 1 (8 × 8 × 1) supercell (shown in orange dotted line) corresponding to 12.5% F concentration. VII is the FM solution of the 4 × 4 × 1 supercell corresponding to 15.625%. I and VI are not displayed because these have the same structure as II but with 9.375 and 12.5% F.

To understand the distribution of these magnetic moments in the system, we have considered different spin configurations of N atoms in F-BN sheets having 12.5 and 15.625% F concentration. In the case of 9.375% F concentration having only one unpaired electron, FM ordering is the only possible magnetic state for this particular choice of unit cell of h-BN sheet. In the other F concentrations, the energy difference between magnetic and nonmagnetic states, along with the magnetization values for these magnetic solutions represented in Fig. 4A, reveals the lower energy of magnetic states as opposed to the nonmagnetic states. Moreover, the energy values of the FM solution are more negative compared to the other magnetic solutions indicating that FM state is energetically more favorable. Increasing the F concentration increases the saturation magnetism in all the possible concentrations considered. The spin densities are mainly located at the nearest-neighbor N atoms to those B atoms, which are attached to F atoms, as shown in Fig. 4 for different representative magnetic structures marked by II to VII. The spins on N atoms of F-BN sheet is arranged in triangular fashion, which can cause frustrated magnetization due to conflicting interatomic forces, a well-known phenomenon for triangular lattices (35). This frustrated magnetization can occur for different magnetic ordering in the F-BN sheet. Because of these conflicting interatomic forces, the exact AFM solution is not found using self-consistent DFT calculations. However, the formation energy values calculated for different magnetic solutions denote the possibility of coexistence of these magnetic states with FM states, which explains our experimental observation. An interesting observation is the hexagonal magnetic cluster formed by the six nearest-neighbor N atoms of the region where three F atoms are attached on three B atoms (marked by a blue dotted line in Fig. 4, structures II and III), and these atoms mainly generate the magnetic moment of the system. To evaluate the interaction between these magnetic clusters having different ordering, we have considered an 8 × 8 × 1 supercell of F-BN sheets having 12.5% F concentration (structures IV and V in Fig. 4). The energy for the 8 × 8 × 1 supercell with two hexagonal clusters having FM ordering is only 0.35 meV lower than that of the single unit cell, as shown in configuration II in Fig. 4, denoting that interaction between the clusters is independent of supercell size. The small spin-charge density between the two magnetic clusters (structures IV and V in Fig. 4) affirms this weak interaction. When consecutive arrays of magnetic clusters have alternative spin-up and spin-down ordering, the energy increases by ~51.40 meV with respect to FM states, indicating that FM ordering is the most stable. From these two configurations (IV and V), considering each magnetic cluster as one unit (either +J or –J, depending on the spin arrangement, where J is the exchange interaction between two magnetic clusters), we found that according to the Heisenberg model, the interaction energy between two magnetic clusters in the 8 × 8 × 1 supercell of F-BN having 12.5% F concentration is 12.85 meV. This low interaction energy is due to the weak FM interaction between the magnetic clusters. Considering the magnetic clusters as one unit, in the region between the spin-up and spin-down magnetic clusters, the absence of magnetic moment is due to the competition between up and down spin arrangement. This indicates that frustrated magnetization can occur due to the equal probability of spin-up and spin-down states in N atoms depending on the nearest-neighbor spin orientation.

DISCUSSION

In summary, we have introduced a simple and scalable method of fluorination for h-BN. This generic approach can potentially be applied for the fluorination of other 2D materials. Fluorination is found to be a reliable method of reducing the bandgap of h-BN, making it a wide bandgap semiconductor. High thermal conductivity and thermal and chemical stability are the distinguishing characteristics of h-BN, and the transformation of h-BN to semiconducting F-BN can expand the scope of the material for high-power electronic devices and sensors. Besides changes in the electronic properties, fluorine causes significant changes in the charge density of nitrogen atoms; fluorine bonded to boron induces a partial charge in the neighboring three nitrogen atoms resulting in FM ordering from room temperature magnetic measurements, whereas the temperature-dependent magnetic measurements reveal a frustrated ground state. This is the first report of a spin-glass behavior in layered materials making an extremely interesting 2D magnetic semiconductor.

MATERIALS AND METHODS

Analytical tools

The structural characterizations were performed using PHI Quantera XPS, Nicolet Fourier transform infrared spectrometer, Rigaku D/Max Ultima II XRD, and Renishaw Raman spectrometer. TEM images and SAED were obtained on JEOL 2100F 200-kV field emission electron microscope. SEM images were acquired with FEI Quanta high-resolution microscope. PL spectra were recorded on a Horiba NanoLog spectrofluorometer. The emission spectra were recorded through a 5-nm slit width with an excitation wavelength of 280 nm passing through a 5-nm slit width. UV-vis absorption measurements were performed on a Shimadzu 2450 UV-vis spectrophotometer in the range of 190 to 800 nm. The four-lead resistivity measurements were performed on the 9T Quantum Design Physical Property Measurement System. The magnetic measurements were performed using the 7T Quantum Design Magnetic Property Measurement System (MPMS3). The samples in powder form were sealed in gelatin capsules in a glove box under argon atmosphere to eliminate any possibility of oxygen in the samples. The gelatin capsule was mounted on the MPMS3 probe in a straw. The details of experimental parameters are given in the Supplementary Materials.

Computational tools

Theoretical calculations were performed using first-principles–based DFT as implemented in Vienna ab initio simulation package. Electron-ion interactions were described using all-electron projector augmented wave pseudopotentials, and Perdew-Burke-Ernzerhof generalized gradient approximation was used to approximate electronic exchange and correlation. The Brillouin zone had been sampled using a well-converged Monkhorst-Pack scheme. The spin-charge density has been plotted using the visualization software VESTA.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/7/e1700842/DC1

section S1. Synthesis

section S2. ¹⁹F NMR analysis

section S3. Structural characterizations

section S4. Bandgap calculations

section S5. Photoluminescence spectra

section S6. Magnetic measurements

section S7. Computational methodology

fig. S1. Structural characterizations of plasma-fluorinated boron nitride.

fig. S2. XPS spectrum of highly fluorinated boron nitride.

fig. S3. ¹⁹F MAS spectra (376.3-MHz) of F-BN with MAS rate of 12 and 10 kHz.

fig. S4. Electron microscope images of the fluorinated boron nitride sheets.

fig. S5. Tauc plot for the various doping of h-BN sheets.

fig. S6. Emission spectra for the different doping concentrations of the fluorine in boron nitride nanosheets on excitation at 280 nm.

fig. S7. Control measurements of the blank cuvette.

fig. S8. ac magnetic measurements.

fig. S9. Structures of fluorinated BN sheets.

fig. S10. Alignment of band edges and band-decomposed charge density.

fig. S11. Band structure and density of states of F-BN.

fig. S12. Charge accumulation and depletion of F-BN.

table S1. Literature of ¹⁹F chemical shifts of B-F and N-F.

table S2. Literature of ¹⁹F chemical shifts of FNXY and F₂NXY.

table S3. Literature of ¹⁹F chemical shifts of FBXY and F₂BXY.

References (36–57)