Abstract
Gamma band rhythms may synchronize distributed cell assemblies to facilitate information transfer within and across brain areas, yet their underlying mechanisms remain hotly debated. Most circuit models pose that soma-targeting parvalbumin (PV) positive GABAergic neurons are the essential inhibitory neuron subtype necessary for gamma rhythms. Using cell-type specific optogenetic manipulations in behaving animals, we show that dendrite-targeting somatostatin (SOM) interneurons are critical for a visually induced, context-dependent gamma rhythm in the visual cortex (V1). A novel computational model independently predicts that context-dependent gamma rhythms depend critically on SOM interneurons. Further in vivo experiments show that SOM neurons are required for long distance coherence across V1. Taken together, these data establish a new mechanism for synchronizing distributed networks in the visual cortex. By operating through dendritic and not just somatic inhibition, SOM-mediated oscillations may expand the computational power of gamma rhythms for optimizing the synthesis and storage of visual perceptions.
Introduction
Rhythmic activity is a commonly observed feature of neuronal activity, from insects to primates, across a wide array of brain regions1–4. Although oscillatory synchronization, particularly in the gamma band, is thought to facilitate communication between phase-locked ensembles of excitatory neurons, its exact role, particularly in the cerebral cortex, remains a matter of debate5–7. Nevertheless, the underlying circuits that mediate gamma rhythmic entrainment are thought to depend on the reciprocal connection between excitatory neurons and local, soma-targeting PV inhibitory interneurons8–11.
Gamma band rhythms in primary visual cortex have been particularly well studied in the context of visual processing4, yet direct evidence for the circuits that mediate these rhythms is mostly lacking. For this reason, we leveraged optogenetic manipulations in awake, behaving mice, and computational modeling, to address the cell-types and circuit mechanisms of visually-induced synchrony in the gamma band. We found that SOM neurons are intimately involved in a context-dependent visually induced gamma rhythm around 30Hz, with their activity required for the phase locking of cortical neurons to the ongoing oscillation. Importantly, and consistent with their specific role in long range horizontal circuits in V112, SOM neuron activity critically contributes to gamma coherence between coactive ensembles that encode widely separated regions of visual space. As SOM neurons primarily target the dendrites of cortical excitatory neurons, this implies that rhythmic dendritic inhibition represents an alternative mechanism for the generation or maintenance of gamma rhythms in the visual cortex.
Results
We first explored cortical rhythmicity using multi-electrode array recordings in Layer 2/3 (L2/3) in the primary visual cortex (V1) of awake, head-fixed, but freely locomoting mice and collected both local field potentials (LFPs) and isolated single units. We presented full contrast drifting gratings of multiple sizes and quantified power in different frequency bands of the LFP. As we increased the size of the visual stimulus we observed a large, nearly monotonic increase in power in a narrow band of the low gamma range (peak frequency at 21 degrees: 32±1 Hz, n = 32 mice; significant effect of stimulus size on gamma power p < 0.001, Kruskal-Wallis ANOVA, Fig. 1a–c). Importantly, many L2/3 units showed significant phase locking to this visually induced oscillation (69/130 regular spiking (RS) units, 55.1%; 37/54 fast spiking (FS) 68.5%; stimulus size = 60°). At the same time, in most animals (25/30) we also observed a higher frequency narrow gamma band peak in the LFP (peak frequency: 60.7±0.6Hz, n = 32 mice; range: 53–66 Hz), which increased with the luminance of a uniform screen, but was suppressed by drifting gratings of increasing size or contrast, and was strongly modulated by behavioral state, consistent with prior studies (Suppl. Fig. 1a–g)13,14. We focus here exclusively on the size-dependent gamma oscillations typically found around 30 Hz.
Figure 1. Visually induced gamma rhythms in V1 of the awake, running mouse are stimulus dependent. a).

Top: Experimental schematic of a head-fixed mouse on a running wheel facing a screen for visual stimulation. Bottom left: schematic of visual stimuli. Bottom right: Example LFP traces in L2/3 of V1 while presenting drifting gratings of varying sizes. b) Representative power spectra of the LFP for gratings of increasing size. Thickness of line denotes mean ± standard error. c) Plot of normalized peak gamma power (peak frequency: 28±1 Hz, n = 32 mice) versus stimulus size (p < 0.001, Kruskal-Wallis ANOVA). d) Left: schematic of iso-oriented and cross-oriented visual gratings. Right: Example LFP traces for iso- and cross-oriented gratings. e) Representative power spectra of the LFP to iso- and cross-orientated gratings. Inset: plot of peak gamma power between iso- and cross-oriented gratings (n = 16 mice, p = 0.0004, Wilcoxon signed rank test). f) Top: example voltage-clamped inhibitory current recorded in a L2/3 neuron during presentation of a 58° drifting grating. Bottom: plot of gamma power (30–40 Hz) versus stimulus size (n = 17 cells, p < 0.001, Kruskal-Wallis-ANOVA). Inset: example PSD of IPSCs at four increasing sizes (gray to black). Error bars in c) and f) are s.e.m.
Importantly, we note that the size-dependent increase in gamma synchronization in mouse V1 is also a reported feature of induced activity in awake, behaving monkeys15,16 and humans17, suggesting that it represents a fundamental and conserved feature of stimulus-driven V1 activity, even if the underlying center frequency varies between species. Furthermore, as in primates, in some mice (13/32) the peak frequency of gamma also decreased monotonically with stimulus size (significant effect of size on peak frequency p = 0.014, Suppl. Fig. 1h,i). While the visually induced gamma we observed in mice is found in the lower end of the ‘typical’ gamma spectrum9,11,18, owing to its strong similarity to conventional visually induced gamma rhythms in alert primates, we call it ‘gamma’ and not ‘beta’, a 15–25 Hz rhythm often associated with movement control. Moreover, since the peak frequency of visually induced gamma in primates spans a wide range depending on the size, contrast, and the attention paid to the stimulus (~20 to greater than 60 Hz)15,19,20, the gamma rhythm we observed in mice falls within the gamma spectrum delineated by many other studies.
Gamma rhythms have been linked to processing stimulus features that extend across large regions of the visual field21. Consistent with this notion, and with prior reports in cats22, the strength of the visually induced gamma rhythm depended on the match between stimulus features within and outside the classical receptive field (CRF) of the recording sites. If we rotated the orientation of the stimulus outside the CRF or offset its spatial phase relative to the stimulus presented inside the CRF, gamma power was substantially reduced (Fig. 1d,e, rotated surround: n = 16 mice; 49±3% reduction, p < 0.001, signed rank test; phase offset surround: n = 11 mice; 33±3% reduction, p < 0.001, signed rank test). This indicates that these gamma rhythms depend not only on the size, but more generally on the spatial context of the visual stimuli that induce them. We thus refer to these visually induced oscillations as ‘context-dependent gamma rhythms’.
What circuits mediate this visually induced, context-dependent gamma band synchronization? Gamma oscillations in other brain areas are thought to be mediated by rhythmic inhibition to principal cells8,9, and gamma in V1 correlates with subthreshold oscillations in the membrane potential23,24. To address whether inhibitory currents might underlie the visually induced gamma, we made intracellular patch clamp recordings from V1 neurons in L2/3 in awake mice. We found prominent inhibitory currents with similar frequency and stimulus size-dependence in some of the recorded neurons (Fig. 1f, n = 17 cells). This indicates that the oscillations observed with extracellular recordings correlate well with gamma-paced inhibitory synaptic activity.
Next, we sought to dissect the differential contributions of cortical interneuron subtypes in generating the context-dependent gamma rhythm. Prevailing models of gamma rhythm generation in the cortex implicate the action of soma-targeting PV neurons, yet to our knowledge none rely on the action of dendrite-targeting SOM neurons. However, the size-dependence of the visually induced gamma power mirrors the size-dependent increase in SOM neurons’ firings rates previously reported12, suggesting that SOM cells could be important. First we quantified how well the firing of PV and SOM neurons (identified optogenetically, see Methods) correlated with the visually induced gamma power. We found that PV and SOM cells phase-locked to the gamma rhythm equally well (pairwise phase consistency (PPC), an unbiased metric of oscillatory phase-locking: PV: 0.10±0.04, n = 11 cells; SOM: 0.09±0.04, n = 11 cells, p = 0.47, rank sum test), albeit to slightly different phases (see Suppl. Fig 2). On a trial-by-trial basis, however, PV neurons’ firing rates were anti-correlated with spectral power in the context-dependent gamma band (−0.1±0.02), and instead correlated more broadly with frequencies above 40 Hz (Fig. 2a). In contrast, SOM neurons’ firing rates correlated strongly and specifically with the visually induced context-dependent rhythm around 30 Hz (0.2±0.1, significantly different from PV, p = 0.002, rank sum test, Fig. 2a). These findings, together with the size-dependent firing of SOM neurons, led us to hypothesize that SOM neurons may be critical for this lower-frequency, visually induced gamma oscillation.
Figure 2. Cortical somatostatin interneurons are essential for visually induced gamma rhythms. a).
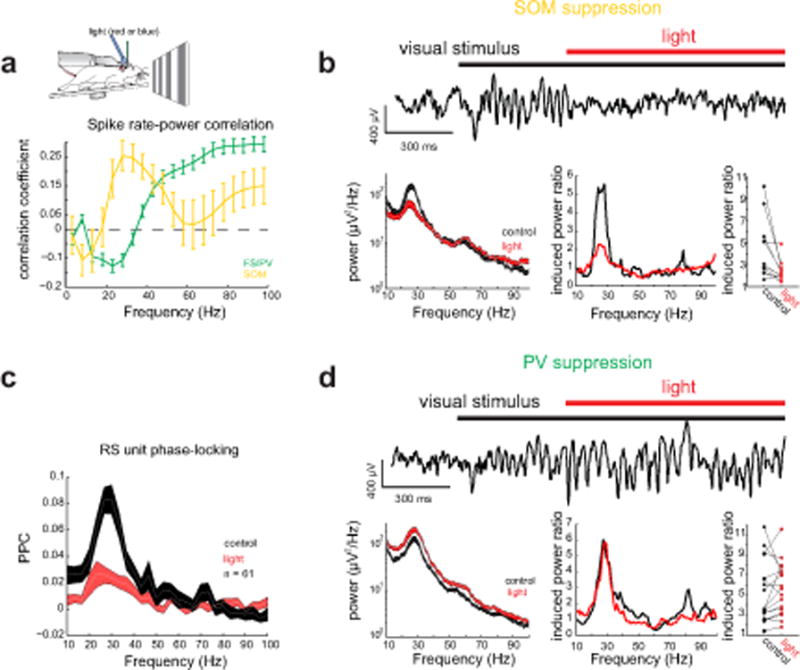
Top: Schematic of a head-fixed mouse on a running wheel with an optic fiber placed close to the recording location. Bottom: Average correlation between firing rate with spectral power for FS/PV (green) and SOM (yellow) units. Error bars denote s.e.m. b) Top: example LFP trace from V1 of a SOM-Cre mouse during photo-suppression of cortical SOM neurons. Left: Representative power spectrum from V1 during visual stimulation with a large grating in the absence (black) and presence of red light (red) to suppress SOM neurons (Thickness of line denotes mean ± standard error). Middle: visually induced (ratio of spectral response to grating compared to grey screen) power spectrum for the same conditions. Right: plot of the impact of light in SOM-Cre mice on induced gamma power (n = 11 mice, p = 0.024, Wilcoxon signed rank test). c) Average pairwise phase consistency spectrum for all L2/3 RS units in SOM-Cre mice in the absence (black) and presence (red) of light n = 61 cells; thickness of line denotes mean ± standard error. d) As in b) but for PV-Cre mice (n = 18 mice, p = 0.17, Wilcoxon signed rank test).
To test this hypothesis, we suppressed SOM neurons with the optogenetic silencer eNpHR3.0, expressed using standard viral approaches (see Methods, Suppl. Fig. 3a). Under our conditions 89±2% of SOM neurons in L2/3 expressed eNpHR3.0, and of 7 units we identified as putative SOM neurons (see Methods, Suppl. Fig. 3c), we observed a 67±8% reduction in their firing rate during illumination at the largest stimulus size. Surprisingly, we found that even this partial suppression of SOM neurons strongly reduced gamma power induced by large gratings in all 14 mice tested (Fig. 2b; induced gamma power (for calculation see Methods) control: 4.5±0.8, light: 2.3±0.3, n = 11 mice, p = 0.003, signed rank test; for similar analyses see Suppl. Fig. 3b). The reduction in spectral power was also largely specific to the visually induced context-dependent gamma band (Suppl. Fig. 3d), with a tight correlation between the center frequency of the visual gamma peak and the center frequency of the reduction in spectral power (r = 0.78, p < 0.001; Suppl. Fig. 3e). At the same time, SOM suppression nearly abolished the phase-locking of L2/3 RS units as measured by the pairwise phase consistency (Fig. 2c; n = 21/61 significantly locked units, PPC control: 0.26±0.03, PPC light: 0.06±0.02, p < 0.001, signed rank test). Importantly, optogenetic suppression of SOM neurons also potently reduced the phase locking of FS units to the gamma rhythm (Suppl. Fig. 3f, n = 17 locked units, PPC control: 0.16±0.03, PPC light: 0.05±0.01, p < 0.001, signed rank test). Since FS units often correspond to PV neurons, this demonstrates that SOM neuron activity is also crucial for the entrainment of putative PV neurons to the context-dependent gamma rhythm. Finally, we also tested whether suppressing SOM neurons even before the onset of the grating stimulus would reduce context-dependent gamma power, and also found this to be the case (Suppl. Fig. 3b; mean reduction light after vis stim: 42.3±7.4%, mean reduction light before vis stim 29.9±6.1%, p = 0.1, n = 7 mice signed rank test).
These findings demonstrate that SOM neurons are critical for the context-dependent gamma rhythm in V1 of awake mice. But what might the role of PV neurons be? To probe a causal relationship between PV neuron activity and context-dependent gamma oscillations, we optogenetically suppressed PV neurons (partial inactivation to avoid epileptiform activity, see Methods, Suppl. Fig. 4a) and quantified the resulting effects on gamma power in response to large gratings. Of 11 FS units we could identify as putative opsin-expressing PV neurons through their strong suppression to light, we observed a net 66±6% decrease in their firing rate (see Suppl. Fig. 4d). Post-hoc histology indicated that 88±4% of PV neurons expressed the silencing opsin in L2/3 of V1. We found that suppressing PV neurons had no significant impact on the induced power in the context-dependent gamma band (control: 5.2±0.7; light: 5.5±0.6; n = 18 mice; p = 0.17, signed rank test, Fig. 2d), and actually increased absolute spectral power across a broad frequency range (Suppl. Fig. 4b absolute gamma power control: 170±40 μV2/Hz, absolute gamma power light: 460±130 μV2/Hz, p <0.001 signed rank test), even when optogenetic suppression preceded the visual stimulus (Suppl. Fig. 4b). PV suppression also slightly increased the phase-locking of L2/3 RS units to the context-dependent gamma band as measured by the spike-PPC (47/105 significantly locked L2/3 RS cells; PPC control: 0.23±0.03, PPC light: 0.3±0.04, n = 47 cells; p = 0.01 signed rank test; Suppl. Fig. 4c). At the same time, we observed an increase in the mean firing rate of most isolated units, including some FS units that presumably did not express the opsin, consistent with broad network disinhibition during PV neuron inactivation (RS: 134±20% increase n = 145 cells, non-suppressed FS: 78±21% increase, n = 32 cells, for optogenetic modulation index see Suppl. Fig. 4f).
To test how varying levels of optogenetic suppression of PV or SOM neurons influenced gamma power, we measured the impact of suppression on context-dependent gamma oscillations across a range of light intensities. While SOM suppression reduced gamma power at all levels of illumination, increasing light levels in PV-Cre mice drove further increases in total spectra power, consistent with the notion that PV neurons generally control cortical gain (Suppl. Fig. 4g,h). In a subset of animals we tested even higher levels of PV neuron suppression, but this often resulted in uncontrolled network activity, evidenced by ictal like events in the LFP, precluding further quantitative analysis (Suppl. Fig. 4j,k). As a control for our optogenetic experiments, illumination of V1 in mice either un-injected with any virus or injected with a virus driving only YFP expression had no effect on gamma power (Suppl. Fig. 4i).
To gain better mechanistic insight into the cortical generation of context-dependent gamma rhythms, we developed a novel computational model of upper layer V1 dynamics. This model builds on previous PING (Pyramidal Interneuron Network for Gamma)9 models of oscillations in Wilson-Cowan networks25–27 that describe, using a single inhibitory cell-type, the stimulus-size dependence of spectral gamma power in the visual cortex, as observed in primates15 and here in mice. In a PING model, excitatory neurons drive inhibitory neurons, which provide recurrent inhibition back onto the excitatory population, thus driving an oscillation. Most PING models involve a single class of inhibitory neuron. Our new model features two distinct inhibitory neuronal populations solely constrained by the connectivity motifs of SOM and PV in the upper layer of V1 in mice28 and their physiological responses to visual stimuli12. The two cell types in the model critically differ in terms of connectivity from outside the network: SOM neurons specifically integrate larger regions of visual space, through L2/3 horizontal projections, as compared to PV neurons, which are preferentially driven by ascending projections from L4 (Fig. 3a,b, and see Methods). In this model, the power of size-dependent gamma critically depends on the size-dependent E/I balance at pyramidal cells. Because SOM cells are the interneuron subtype that is preferentially driven as stimulus size increases, SOM cells would be predicted to control the size-dependent change in E/I balance, and not PV cells (see below). The model was not constrained by the experimental data presented above, to independently test if its predictions would be confirmed by physiological data.
Figure 3. A computational model of visually induced gamma oscillations including both PV type and SOM type inhibitory neurons. a).
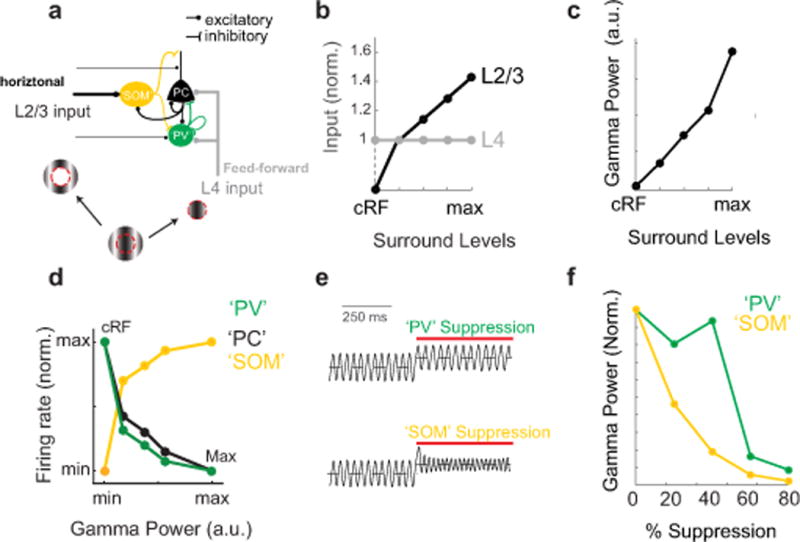
Schematic of the connectivity diagram for the computational model (see Suppl. Fig. 5 for additional details). b) Diagram of the total input to L2/3 PCs in the model from L4 and L2/3 as a function of increasing surround levels of input, analogous to visual stimuli of increasing size. The levels were varied from 1 to 4 to simulate increasing size of visual surround. c) Plot of the gamma power of L2/3 PC activity as a function of surround levels. d) Model prediction for the firing rate of PCs (black), PVs (green) and SOMs (yellow) as a function of total gamma power in the model. e) Modeled plot of oscillatory firing rates of excitatory neurons during stimulation with large gratings during suppression of ‘PV’ (green) and ‘SOM’ (yellow) type inhibitory neurons. f) Model prediction for gamma power as a function of % silencing of ‘PV’ (green) and ‘SOM’ (yellow) type inhibitory neurons.
We found that the model predicted many of the core experimental findings. First, we asked if this model would recapitulate size-dependent gamma oscillations, and indeed, we found this to be the case (Fig. 3c). Next we plotted the relationship the model predicts for the firing rate of the various neuronal subtypes with context-dependent gamma power. Consistent with the physiological data (Fig. 2a), the model predicted that SOM firing increases with gamma power, while that of PCs and PVs decreases (Fig. 3d). Finally, we addressed how suppressing PV-type or SOM-type inhibitory neurons in the model influenced context-dependent gamma power. The model predicted that suppression of SOM-type interneurons would dramatically reduce gamma power, even for low levels of inactivation (Fig. 3e,f). This implies that SOM neurons are a crucial component of the inhibitory network for gamma generation in this PING model. In contrast, moderate suppression of PV-type interneurons (20–40%) had little to no effect on gamma power (Fig 3e,f). Higher levels of inactivation of PV neurons, resulted in a dramatic increase of excitatory neuron activity (Suppl. Fig. 5b) and a drastic reduction in gamma power (Fig. 3f), suggesting that network stabilization via PV neurons is essential for gamma band oscillations, a prediction consistent with our physiological data in which strong PV inactivation resulted in epileptic-like activity (see above, Suppl. Fig. 4j,k).
Importantly, the model also predicted that SOM suppression would enhance both PC and PV firing rates, even as it potently reduced context-dependent gamma power (Suppl. Fig 5a,b). This prediction was consistent with our physiological data; during SOM suppression, both L2/3 RS and FS cells significantly increased their firing rates (RS: 240±50% increase, n = 82 cells; FS: 100±30% increase, n = 33 cells, for optogenetic modulation index see Suppl. Fig. 5c,d). The increase in PV activity did not result in increases in gamma power, as might be assumed, because what drives gamma power in this model is not the increase in inhibition per se, but the net E/I balance at PCs, which is under control of both SOMs and PVs. The increase in the activity of PV cells in the model during SOM suppression was not due to direct disinhibition of PV cells, as it persisted when the inhibitory connection from SOM to PV in the model is set to zero (see Suppl. Fig. 5e,f). Instead, it can be explained by the increase of PC activity, which, in turn, increases PV neurons firing rates (a typical consequence of the inhibition stabilized network, see Methods). Broadly consistent with the extracellular data and the model, intracellular patch clamp recording revealed that optogenetic SOM suppression also significantly reduced the relative gamma power of IPSCs (n = 7 cells, Friedman test: significant effect of light p = 0.022, Suppl. Fig. 5g,h). Thus, even though this model was developed entirely independently of the physiological data presented above, it qualitatively predicted many of the physiological impacts of PV and SOM suppression on V1 dynamics. Taken together, the data and the model support the notion that SOM neurons are critical for these context-dependent gamma rhythms.
While these experiments indicate that SOM neuron activity is essential for context-dependent gamma band power, previous work has suggested that elevation of PV neuron activity, through optogenetic photo-stimulation, is sufficient to enhance gamma rhythms11. Our model predicts that gamma power correlates with the E/I balance in pyramidal cells. This means that photo-activating either interneuron subtype could, in principle, increase gamma power, so long as the net effect of the increase in their activity is a reduced E/I balance in pyramidal cells. Therefore we tested whether SOM neuron photo-stimulation could also enhance gamma band power. Using SOM-Cre and PV-Cre mice crossed to the Cre-dependent ChR2 reporter mouse, Ai32, we asked how photo-stimulation of each interneuron subclass at different frequencies influenced spectral power in different bands, similar to a previous approach11. We used glass electrodes to minimize photo-electric artifacts. Under these conditions, we found that driving both PV and SOM neurons was sufficient to increase spectral power, preferentially around 24–32 Hz, similar to the frequency of the context-dependent gamma rhythms (Fig. 4a,b; SOM-ChR2: 11±2 fold increase, n = 7 mice; significant effect of stimulation frequency on fold-increase p < 0.001, Kruskal-Wallis ANOVA; PV-ChR2: 28±6 fold increase, n = 6 recordings in 4 mice; significant effect of stimulation frequency on fold-increase p = 0.013, Kruskal-Wallis ANOVA). These data are consistent with model predictions and support the notion that activation of either inhibitory neuron subtypes in V1 is sufficient to enhance gamma band oscillations. It should be noted that the peak frequency of these light-induced rhythms in awake mice is lower than previously reported under anesthetized conditions in S111. The difference in peak frequency is due to anesthesia (and not a difference in brain area) as repeating the same experiments in S1 or V1 of anesthetized mice revealed a peak at ~48 Hz as previously reported (Suppl. Fig 6a).
Figure 4. SOM neuron photo-stimulation can entrain gamma rhythmicity in vivo and in vitro. a).
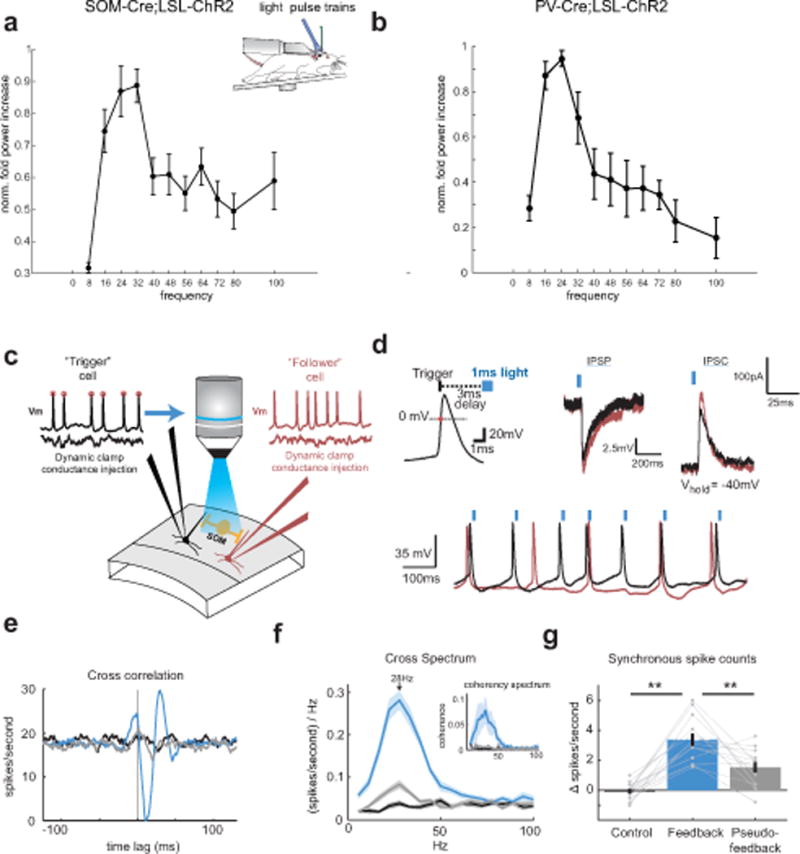
Plot of the normalized fold increase in spectral power in different bands as a function of photo-stimulating SOM neurons at those frequencies (SOM: n = 7 cells; significant effect of stimulation frequency on fold-increase p < 0.001, Kruskal-Wallis ANOVA, error bars denote mean ± s.e.m.). b) As in a) but for PV neurons. n = 6 cells; significant effect of stimulation frequency on fold-increase p = 0.013, Kruskal-Wallis ANOVA c) Experimental schematic: Two L2/3 pyramidal neurons are patched in a slice from a mouse expressing ChR2 specifically in SOM neurons. The pyramidal neurons are injected with random and independent barrages of simulated excitatory conductances via a dynamic clamp. A custom fast feedback circuit detects rising 0 mV crossings of the membrane potential in the trigger cells, and drives blue light stimulation of nearby SOM-ChR2 neurons with a pulse of blue light. d) Top left: schematic of the spike-triggered optical feedback scheme. Top middle: Example membrane potential traces of the IPSP recorded in a pair of pyramidal cells to a flash of blue light (peak IPSP amplitude population mean = 8.0 ± 0.9mV). Current was injected to bring membrane potentials to −50mV. Top right: Voltage-clamp recording from the same Pyramidal neurons to the same light stimulus. −40mV holding potential (peak IPSC amplitude population mean = 210±40 pA). Bottom: example traces of action potentials in the recorded pair while optical feedback was engaged. Blue ticks indicated triggered flashes of blue light to the action potentials in the black trace. e) Example cross correlation between a recorded pair of pyramidal cells under control conditions (black), feedback (blue), and pseudo-feedback (grey). f) Average cross spectrum between the two recorded neurons’ spiking, (mean values between 22–39Hz: control= 0.033 (sp/s)/Hz, feedback= 0.242 (sp/s)/Hz, pseudo-feedback= 0.065 (sp/s)/Hz; p<0.001, Kruskal-Wallis ANOVA). Inset: Average coherence spectrum. g) Average change in synchronous spike probability for the recorded pairs of neurons under control, feedback, and pseudo-feedback conditions (mean values: control= −0.001, feedback= 0.034, pseudo-feedback= 0.015; n=13 pairs; p < 0.001, Kruskal-Wallis ANOVA). All error bars are s.e.m.
In many models of gamma rhythm generation, feedback inhibition from local interneurons is critical for pacing excitatory neuron activity. Previously, it was shown that photo-stimulation of PV neurons in response to the activity of a single pyramidal cell was sufficient to generate gamma rhythms10. Therefore, using a similar approach, we asked if photo-stimulating SOM neurons could also generate gamma rhythms. We built a feedback circuit where the action potentials of a single pyramidal cell triggered the photo-stimulation of ChR2-expressing SOM cells (Fig. 4c,d). We also patched a second pyramidal cell to allow for coherence measurements between the two nearby excitatory neurons (<50μm separation). Both pyramidal cells were driven to spike with random and independent barrages of excitatory conductances (see Methods). When optical feedback was triggered off one cell’s action potentials, we observed a dramatic and significant increase in the coherence, specifically in the gamma band, between the two recorded neurons’ spiking (see Methods, Fig. 4e,f, p < 0.001, Kruskal-Wallis ANOVA, n=13), as well as a significant increase in synchronous spikes (see Methods, p < 0.001, Kruskal-Wallis ANOVA, n=13). As a control, we switched off the optical feedback, and instead photo-stimulated SOM neurons with a light pulse train derived from randomly selected previous trials where feedback was engaged (‘pseudo-feedback’). Despite the photo-stimulation of SOM neurons at essentially the same frequency, in the absence of true optical feedback, no increases in coherence or gamma rhythmicity were observed (Fig. 4e–g). These experiments indicate the SOM inhibition, in a recurrent circuit with excitatory neurons, is sufficient to generate and entrain gamma band rhythms and coherence between excitatory neurons.
What role might SOM-dependent gamma oscillations play in the spatial coding of visual stimuli? PCs in superficial cortical layers are well known to project long-range axons across the retinotopic map29, which have been hypothesized to contribute to long range synchronization21. To test this hypothesis we presented different types of drifting gratings to awake mice, covering the CRF of two distinct V1 locations (~600μm separation) targeted with independently movable laminar multi-electrode arrays (Fig. 5a). By recording two sites in V1 simultaneously we could measure both gamma power (as in Fig. 1), and the coherence of the gamma oscillations between the two distal sites. When the visual stimuli covering both receptive fields shared the same orientation and direction of motion, we observed a prominent peak in the LFP coherence in the context-dependent gamma band (Fig. 5b,c n = 10 mice, iso-oriented: 0.56±0.07; cross-oriented: 0.39±0.05, p = 0.002, signed rank test). We obtained identical results if we offset the center and surround in spatial phase, or if we used side-by-side gratings of different orientations (data not shown). Optogenetic suppression of SOM neurons significantly reduced the LFP-LFP coherence between the two recording locations (Fig. 5d,e, control: 0.56±0.7, light: 0.36±0.06, p = 0.002, n = 10 mice). These data demonstrate that SOM neurons are essential for the long-range synchronization observed in the visual cortex during contextual stimulation.
Figure 5. SOM interneurons synchronize distal ensembles in V1 of awake, behaving mice. a).
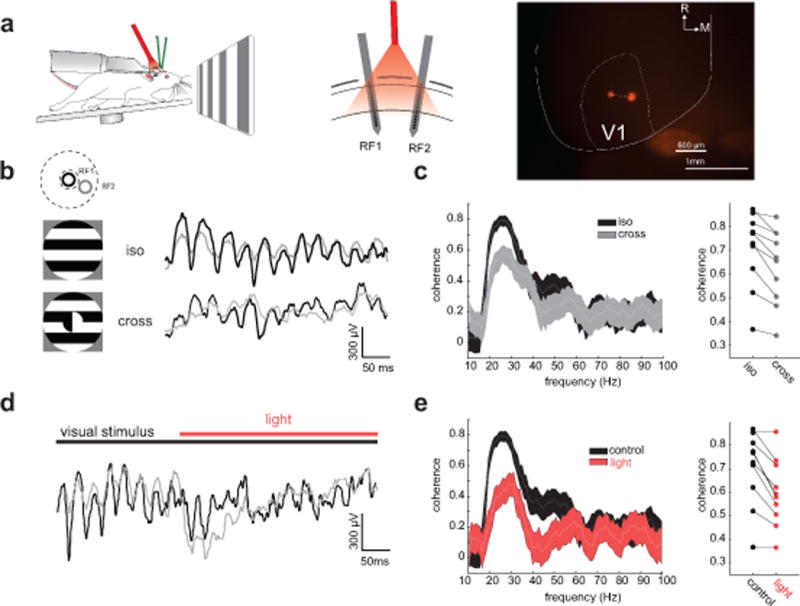
Left: recording schematic in awake, head-fixed SOM-Cre mice. Middle: Schematic of the multi-electrode array recording configuration with two laminar arrays in distant sites (610±90 μm apart (histology from n = 5 mice), 18±2 degrees of visual angle, n = 10 mice). Right: example image from the brain of a SOM-Cre mouse showing two electrode tracks in V1. White lines show approximate outline of V1 in the left hemisphere. R: rostral; M: medial. b) Left: Schematic of the receptive fields’ locations of the two laminar probes (top) and the large drifting gratings used to drive neural activity (bottom). Right: Example simultaneously recorded LFP traces from the two electrodes during presentation of an iso-oriented surround grating (top) and a cross-oriented surround grating (bottom). c) Left: example coherence spectra for simultaneously recorded LFP traces from the two laminar probes during iso-oriented (black) and cross-oriented gratings (gray). Thickness of line denotes 95% confidence intervals. Right: plot of the peak gamma coherence for iso- and cross-oriented gratings (n = 10 mice, p =0.002, Wilcoxon signed rank test). d) Example LFP traces from two simultaneously recorded sites in V1 during photo-suppression of SOM neurons during the iso-oriented grating. e) Left: Example coherence spectra between the two recorded sites for control (black) and SOM photo-suppression (red) conditions. Thickness of line denotes 95% confidence intervals. Right: plot of peak gamma coherence between pairs of recording sites under control (black) and SOM photo-suppression (red) conditions, n = 10 mice, p = 0.002, Wilcoxon signed rank test).
Discussion
This study demonstrates for the first time that a type of gamma rhythm critically depends on SOM interneurons. Although gamma frequency oscillations in other cortical areas and brain regions8–11, such as the hippocampus, and in higher spectral bands, may depend primarily on PV neurons, context-dependent, visually induced gamma activity in mouse V1 requires SOM neurons. PV neurons probably also contribute to these rhythms in V1, although our data more directly imply that they are necessary for stabilizing the cortical network and controlling cortical gain, consistent with prior findings30,31. Thus, one interpretation is that PV neurons provide the basis upon which SOM-mediated inhibition can then entrain gamma oscillations for large visual stimuli. Importantly, a novel computational model, built independently of this data, predicted many of the key physiological findings in this study. This model provides quantitative insight and a future testing ground for further hypotheses concerning V1 gamma oscillations.
Previous studies using optogenetic manipulation of PV neurons10,11 have demonstrated that altering their activity can influence or induce oscillations in the gamma range. We found that photo-stimulation of either inhibitory neuronal subtype was sufficient to enhance activity around 30Hz in V1 of the awake mouse. This implies that there could be multiple circuit mechanisms for entraining gamma oscillations, which is potentially consistent with the heterogeneity of gamma oscillations observed in different cortical areas, brain states, and frequency bands. A single brain area can exhibit distinct gamma rhythms32 which might differentially depend on different neuronal sources of inhibition. In V1, we also observed a second prominent narrowband gamma rhythm around 55–65 Hz that was enhanced by luminance but suppressed by stimuli of increasing size and contrast, modulated by brain state, and not reliant on SOM cell activity. Since this rhythm does not depend on contrast in the visual stimulus14 and may arise in the retina33–35, it is not clear what its specific role is in cortical processing. We do note that while locomotion and brain state are known to have profound effects on V1 activity13,36, we did not observe any difference of the impact of SOM or PV suppression on gamma power between quiescent and running conditions (Suppl. Fig. 6b,c).
A key finding in our data is that SOM-dependent oscillations specifically synchronize ensembles in V1 that are processing matched stimulus features. This is consistent with a potential role for these long-range rhythms in linking disparate pieces of a sensory stimulus into a complete perception. However, several studies have called into question whether gamma rhythms do indeed contribute to feature binding37–39. Although our data do not resolve this question directly, by having revealed circuitry critically involved in long-range gamma synchronization, future studies could devise appropriate means to address this controversy.
What is the importance of gamma oscillations that depend on SOM neurons? By operating through dendritic inhibition, SOM-dependent gamma rhythms could provide much greater flexibility for influencing cortical computation and synaptic plasticity by interacting with specific dendritic compartments, perhaps on a gamma cycle by gamma cycle basis. A wealth of evidence indicates that dendrites can act as independent computational units by virtue of their ability to generate local spikes40. In V1 these local dendritic spikes have been implicated in improving feature coding41, as well as compartmentalizing information storage through dendrite-specific synaptic plasticity42. Since dendrite-targeting inhibitory neurons powerfully gate dendritic spiking and backpropagating action potentials43, SOM-dependent gamma rhythms may enforce coordinated time windows for synaptic integration and spike timing dependent plasticity. Rhythmic inhibition of pyramidal cell dendrites may thus provide a flexible means for binding distributed cell assembles in time to optimize information processing and storage. Indeed a recent paper showed that dendrite targeting Martinotti cells in L5 could effectively synchronize thick-tufted L5 pyramidal neurons in a frequency-dependent manner. Since evidence suggests that SOM cells are involved in many aspects of V1 processing12,31, their role in gating dendritic activation appears to be fundamental to sensory computation.
While our experiments have addressed SOM neurons’ involvement in long-range gamma oscillations within the primary visual cortex, they also may play a key role in inter-areal gamma synchronization involved in higher cognitive processes. This is consistent with the fact that V1 SOM neurons have been shown to be among the targets of long-range, top-down input from higher cortical areas44. SOM neurons might also contribute to local gamma oscillations in other brain regions. For example, the neuropeptide somatostatin, itself, has been shown to be involved in gamma rhythms in the olfactory bulb45. Lastly, since some brain disorders have been linked to impaired gamma oscillations, such as schizophrenia46, it might be fruitful to explore whether defects in SOM cells, and not just PV neurons, might be relevant for the etiology of these diseases47,48. If SOM neurons are broadly involved in gamma rhythms beyond V1, future experiments may help explain why reductions in somatostatin and SOM interneurons are frequently associated with a host of neuropsychiatric diseases49.
Online Methods
Transgenic mice
All experiments were performed in accordance with the guidelines and regulations of the ACUC of the University of California, Berkeley. Mice for the in vivo experiments were housed in groups of five or less with a 12:12h light:dark cycle. Both female and male mice were used. Experiments in vivo were performed on animals aged between 7–20 weeks during their subjective night. In vitro experiments were performed on animals aged P19–P23. We used PV-Cre (JAX stock 008069), SOM-IRES-Cre (JAX stock 013044), AI32 (JAX stock 012569) and Rosa-LSL-tdTomato (JAX stock 007909) mice. Mice were out-crossed for one generation to the ICR white strain (Charles River). Number of animals used was not predetermined for a specified effect size.
Viral infection
Neonatal SOM and PV-Cre mice (P3–6) were briefly cryo-anesthetized and placed in a head mold. Transcranial injection of ~45nl of undiluted AAV9-EF1a-DIO-eNpHR3.0-YFP or AAV9-DIO-ChR2 (UPenn Vector Core, SOM-cre: 20 animals; PV-Cre: 12 animals, ChR2: SOM-Cre: 3 animals; PV-Cre: 3 animals) was performed using a Drummond Nanoject injector at three locations in V1 using a glass pipette beveled to fine tip (~30–60μm). With respect to the lambda suture coordinates for V1 were 0.0 mm AP, 2.2 mm L and injection was as superficial as possible under the skull. AAV-EF1a-DIO-eArch3.0-YFP (UNC vector core, 7 animals) injections were performed on PV-Cre animals 3–6 weeks old. Mice were anesthetized with isoflurane (2.5% vapor concentration) and ~500nl of undiluted virus was injected through a burr hole 3mm lateral of lambda, ~400–600 μm deep.
Preparation for in vivo recording
Mice were anesthetized with isoflurane (2.5% vapor concentration). The scalp was removed, the fascia retracted, and the skull lightly etched with a 27 gauge needle. Following application of Vetbond to the skull surface, a custom stainless steel headplate was fixed to the skull with dental cement (Metabond). Mice were allowed to recover from surgery for at least 2 days. Then mice were habituated for 2–10 days to head-fixation on a free-spinning circular treadmill. On the day of recording mice were briefly anesthetized with isoflurane (2%), the skull over V1 was thinned, and one or two (spacing 400–1000μm) small (<250 μm) craniotomies were opened over V1 with a fine needle.
Visual stimulation
Visual stimuli were generated with Psychophysics Toolbox50 running on an Apple Mac Mini and were presented on a gamma corrected 23-inch Eizo FORIS FS2333 LCD display with a 60-Hz refresh rate. At the beginning of each recording session the receptive fields of MUA recorded at each cortical location was mapped with sparse noise to be able to precisely position the grating stimuli. The stimulus was centered on a location where a small grating, movable by hand, elicited a clear response. Sparse noise consisted of black and white squares (2 visual degrees, 80 ms) on a 20×20 visual degree grid flashed onto a gray background of intermediate luminance. To improve receptive field estimation the same stimulus grid was offset by 1 degree and the resulting maps were averaged. MUA average receptive fields were calculated online by reverse correlation. Visual stimuli consisted of full contrast drifting square-wave gratings at 0.04 cycles per degree and 2 cycles per second centered on the average MUA receptive field. Gratings were presented in two different configurations: 1) Square-wave gratings of eight different directions (0–315° in steps of 45°) and five different sizes (8, 13, 21, 36, and, if possible, 60 visual degrees – if the RF was not perfectly centered on the monitor, the effective largest size was slightly smaller; see Fig. 1a); 2) Square-wave gratings with a circular aperture of 12 visual degrees diameter, centered on the MUA receptive field of one of the two simultaneously recorded cortical locations, that was surrounded by a 60 degree grating of either the same orientation, a grating of the orthogonal orientation, or a grating of the same orientation but offset by 180° of phase. For the coherence analysis we only analyzed cases in which the second receptive field was covered entirely and exclusively by the surround-stimulus (see Fig. 1d and 4b). For the contrast dependence of the high gamma rhythm we also presented small (12˚) gratings centered on the MUA receptive field at varying contrasts levels (0, 0.1, 0.18, 0.32, 0.56, 1.0 Michelson contrast). Temporal and spatial frequencies, as well as presentation time, were the same as above. In a subset of animals we also showed an iso-luminant screen without contrast and varied the luminance in 5 steps between 0 and 1.
Optogenetic stimulation in vivo
For optogenetic stimulation of eNpHR3.0 in vivo we used red (center wavelength: 640 nm, 3–30 mW for the dose response curve in Suppl. Fig. 4f,g), for stimulation of eArch3.0 we used green light (center wavelength: 550nm, 0.3–12mW) from the end of a 1-mm diameter multimode optical fiber coupled to a solid state source (Lumencor Spectra X), for stimulation of ChR2 we used blue light (center wavelength: 455nm, 0.5–3mW) from a fiber coupled LED (Thorlabs) both controlled by digital outputs (NI PCIe-6353). The fiber was placed as close to the craniotomy as possible (<3 mm). The illumination area was set to illuminate a wide area including all of V1. Light levels were tested in increasing intensities at the beginning of the experiment and were kept at the lowest possible level that still evoked observable change in ongoing activity for the remainder of the recording. In the eArch3.0 injected PV-Cre mice very low intensities of light (~0.3mW) already evoked substantial changes in ongoing activity and if the light intensity was increased beyond 5–12 mW ictal/epileptiform activity was typically observed. In these cases, the light was kept at a level that did not induce epileptiform activity, and, if necessary, the optic fiber was moved slightly farther from the craniotomy. We only used viral injections into V1, and did not attempt to use an Arch or eNphR transgenic reporter line to avoid off-target expression of the opsin and non-specific optogenetic suppression of subcortical nuclei (such as the thalamic reticular nucleus) that are also labeled in the PV-Cre line.
Gratings drifted for 2 seconds with 1-second inter-trial intervals with the red or green LED switched on for 1 s starting 0.5 s after start of the visual stimulus in 50% of the trials. The period of light was chosen to influence the stable steady-state of the response to the grating and all analysis was performed during this time window. For a subset of animals (n = 7 for SOM mice and n = 8 for PV mice) we ran a separate experiment where only large, full contrast gratings were presented and the light was turned on 500 ms before the onset of the 2s grating in 50% of the trials. In this case analysis was performed on a 1 s window immediately after grating onset. For optogenetic identification of SOM cells the cortex was illuminated by low intensity blue light ramps, or pulse-trains during the same light window for the same stimulus set as for the eNpHR experiments.
In vivo extracellular multi-electrode electrophysiology
One or two 16-channel linear electrodes with 25 micron spacing (NeuroNexus, A1x16-5mm-25-177-A16) were guided into the brain using micromanipulators (Sensapex) and a stereomicroscope (Leica). Electrical activity was amplified and digitized at 30 kHz (Spike Gadgets), and stored on a computer hard drive. The cortical depth of each electrical contact was determined by zeroing the bottom contact to the surface of the brain. Electrodes were inserted close to perpendicular to the brain’s surface for single electrode recordings and ~25 degrees from vertical for the two electrode experiments. After each recording a laminar probe coated with the lipophilic dye DiI was used to mark each electrode track to quantitatively assess insertion angle and depth with post-hoc histologic reconstructions. The laminar depth of recorded units was corrected for the insertion angle and the local curvature of the neocortex.
Analysis of local field potential data
All analysis was performed using custom written code or openly available packages in Matlab (Mathworks). Local field potentials were extracted by low pass filtering the raw signal, sampled at 30 kHz, below 200 Hz and subsequent down-sampling to 1 kHz. For LFP-only analysis we always analyzed the LFP from the electrode contact closest to a cortical depth of ~330 μm (in cortical layer 3). For spike locking to the LFP we used the LFP from an electrode contact 50 μm away from the contact with the largest spike-waveform amplitude to reduce contamination of the LFP.
The power spectrum was computed in a 800 ms analysis window starting 200 ms after light onset (to exclude any photo-electric artifacts sometimes present in the first ~150 ms after light onset) using multi-taper estimation in Matlab with the Chronux package (http://chronux.org/)51 using 3 tapers. All analysis was performed on the power at the peak of each animal’s specific gamma oscillation. Peaks were identified as local maxima on the smoothed spectrum between 20 and 40Hz for the low gamma peak and 50 and 70Hz for the high gamma peak that were preceded by local minima in the 15Hz preceding the peak. For the high gamma peak two animals were excluded because of visible line noise in the recording that would have precluded proper analysis. 25/30 animals thus had a distinguishable high gamma peak for the smallest stimulus size and all 32/32 animals had a visual gamma peak for the largest stimulus size. Visually induced spectra were calculated by dividing the spectrum for the largest grating size by the spectrum for a plain gray screen. Relative gamma power was calculated as the peak gamma power divided by the average spectral power between 10 and 100Hz. The peak/trough ratio was estimated as power at the peak divided by the power of the preceding trough.
For calculation of coherence, bipolar derivatives of the LFP were calculated by subtracting the electrode channel immediately above the channel of interest, to remove the common recording reference and to enhance spatial specificity of the signal. Coherence between the sites was determined using the chronux package with the same number of tapers as the power analysis. All spectral plots show mean±s.e.m, the coherence spectra show jack-knifed 95% confidence intervals. In 7 SOM Ai32 mice – 7 sites total – and 4 PV Ai32 mice – 6 sites total – we stimulated V1 in the awake condition with 3s bouts of 11 different frequencies of blue light pulses (3ms pulse duration) from 8 to 100Hz ([8,16,24,32,40,48,56,64,72,80,100] and under control conditions (no stimulation), similar to a previous study in anesthetized barrel cortex11. 30 repetitions per stimulation frequency were recorded for 2–4 different light intensities between 0.1 and 4.1mW for each animal. For these experiments, the local field potential was recorded with low resistance borosilicate pipettes to avoid a direct opto-electric artifact from the stimulating light on the silicon electrodes. Resulting LFP traces were mean subtracted, frequency transformed (as above), and the resulting spectra averaged over the 30 trials for each frequency. For analysis we chose the lowest light intensity for each animal that produced reliable peaks higher than the control spectrum for all stimulation frequencies. For each stimulation frequency we calculated the ratio of the power at the stimulation frequency compared to the power at the same frequency under control conditions. We repeated this experiment in PV-Cre mice injected in adult mice with AAV9-DIO-ChR2-YFP in V1 (n = 4 mice) and S1 (n = 3 mice) and anesthetized with Isoflurane (2.5% vapor concentration).
Analysis of spiking data
Spiking activity was extracted by filtering the raw signal between 800 and 7000 Hz. Spike detection was performed using the UltraMega Sort package52. Detected spike waveforms were sorted using the MClust package (http://redishlab.neuroscience.umn.edu/MClust/MClust.html). Waveforms were first clustered automatically using KlustaKwik and then manually corrected to meet criteria for further analysis. With the exception of two burst firing units, included units had no more than 1.5% of their individual waveforms violating a refractory period of 2 ms. Individual units were classified as either fast-spiking or regular spiking using a k-means cluster analysis of spike waveform components. Since the best separation criterion was the trough-to-peak latency of the large negative going deflection and clustering is non-deterministic, we defined all units with latencies shorter than 0.36 ms as fast spiking and all units with latencies larger than 0.38ms as regular spiking. Cells with intermediate latencies were excluded from further analysis. Putative eNpHR3.0 or eArch3.0-expressing cells were identified by significantly reduced firing rates during the red light illumination period. Putative ChR2-expressing cells were identified by dramatic increases in spike rates to blue light stimulation. For PV cells, the spike waveform had to be additionally classified as FS as described above. For SOM cells, three additional criteria suggested they were in fact SOM cells: all waveforms were of intermediate spike width (0.37–0.44 ms)53, preferred either the largest or second to largest size stimulus12, and often exhibited a rebound spike after light offset consistent with their known physiological properties54. Data from PV-Cre mice injected with either eNpHR3.0 or eArch3.0 were not significantly different and so were combined (fold power change Halo: 2.19±0.19, fold power change eArch: 2.22±0.30, p = 0.97 (Wilcoxon rank sum test). Identified PV and SOM neurons were grouped with the eNpHR3.0-identified neurons for the analysis of phase locking and gamma power correlation. Because there was no difference between the identified PV cell group and the FS group these were merged for these analyses as well.
The depth of each unit was assigned based on the calculated depth of the electrode on the array that exhibited its largest amplitude sorted waveform. Layer boundaries were determined following a previously established approach55. Firing rates were computed from counting spikes in a 1 second window starting 500 ms after the onset of the visual stimulus, which coincided with the onset of the LED during optogenetic suppression trials. Unless otherwise stated, we only analyzed trials when the animal was moving (at least 1cm/s) and not accelerating or decelerating abruptly (not more than 1.5 s.d. deviation from the animal’s mean running speed). However, we observed the same effects of SOM and PV neuron suppression when the animal was not running (Suppl. Fig. 6 b,c). Average running speed across the population was 41±25cm/s (n = 20 animals). 2 animals were excluded because they ran fewer than 15% of total trials.
For the correlation of spike rate and LFP power the LFP was filtered into 20 non-overlapping narrow frequency bands (5Hz each) and the power in each trial was estimated using the Hilbert transform. The average power in each band was then correlated with the spike rate of the neuron on a trial by trial basis using Spearman’s rank correlation.
To quantify locking of spiking activity to the gamma band we bandpass filtered the LFP in a 20 Hz band around the peak and extracted the oscillation’s instantaneous phase by using the imaginary part of the analytical signal using the Hilbert transform. Each spike is thus assigned an exact phase in the gamma oscillation. Phase locking magnitude is determined for each unit by the pairwise phase consistency (PPC), a measure of synchrony that is not biased by the number of spikes56 but results were similar when quantifying phase locking strength by the resultant vector length (phase locking value, data not shown). Significance of locking is determined by the Rayleigh test for non-uniformity on the distribution of spike-phases. All units with p<0.05 are considered to be significantly locked. We only included units that fired more than 10 spikes total in response to the largest grating size in the control condition. PPC-spectra were calculated from the spike triggered LFP spectrum for each unit using the FieldTrip Matlab package57.
Optogenetic modulation index (OMI) was calculated as where is the average firing rate of the neuron in the light period and is the average firing rate of the neuron in the control condition.
In vivo intracellular recording and analysis
Mice were prepared identically as for extracellular recording. To make blind whole cell patch clamp recordings a glass borosilicate pipette (Sutter) was pulled to a long taper and a low resistance (3–5 Megaohms) and inserted axially through the dura mater under high positive pressure. Electrode solution was the same as for brain slice recording for voltage clamp (see below, containing cesium, QX-314, and TEA). Signals were amplified with an Axopatch 200B (Molecular Devices), filtered at 2 kHz, and digitized with a National Instruments DAQ device (PCIe-6323). The depth of the electrode was set to zero when the pipette encountered the dural surface, which was easily identified electrically by a large, transient increase in pipette resistance. The pipette was then advanced to L2/3 (~100–350 μm below the dura, mean cell depth: 250±20 μm) under high pressure (~180 mbar). The pipette was advanced in 2 micron steps and following a sudden and transient increase in pipette resistance the positive pressure was released. Following gigaseal formation brief suction ruptured the membrane providing whole cell access. The cell was dialyzed 5–10 minutes prior to voltage clamping to the reversal potential of synaptic excitation to isolate inhibitory conductances. Gamma power (25–40 Hz) was measured in power spectra of the averages of IPSCs recorded across different stimulus sizes. Relative gamma power was computed as the ratio between power from 25–40 Hz to that between 50–70 Hz.
Brain slice preparation
Cortical slices containing primary visual cortex were cut in the coronal plane (400 μm thick) were prepared from mice aged P19–P23 using a DSK Microslicer in a reduced sodium solution containing (in mM) NaCl 83, KCl 2.5, MgSO4 3.3, NaH2PO4 1, glucose 22, sucrose 72, CaCl2 0.5, and stored submerged at 34 °C for 30 min, then at room temperature for 1–5 h in the same solution before being transferred to a submerged recording chamber maintained at 31–32 °C by inline heating in a solution containing (in mM) NaCl 119, KCl 2.5, MgSO4 1.3, NaH2PO4 1.3, glucose 20, NaHCO3 26, CaCl2 2.5. Before the beginning of the recordings, all slices were inspected with epifluorescence to ascertain the location and quality of transfection.
Whole cell recordings in vitro
Whole cell recordings were performed using glass micropipettes (2–3MΩ resistance) pulled on a Sutter P-1000 Micropipette Puller. For voltage clamp recordings, pipettes were filled with a Cs+− based internal (CsMeSO4 135 mM, NaCl 8 mM, HEPES 10 mM, Na3GTP 0.3 mM, MgATP 4 mM, EGTA 0.3 mM, QX-314-Cl 5 mM, TEA-Cl 5mM). For current clamp recordings, pipettes were filled with a potassium-gluconate based internal (K-gluconate 135 mM, NaCl 8 mM, HEPES 10 mM, Na3GTP 0.3 mM, MgATP 4 mM, EGTA 0.3 mM). Voltage recordings were not corrected for the liquid junction potential. Series resistance was not compensated, yet monitored continuously with negative voltage steps. Data were analyzed from recordings in which series resistance was below 25MΩ and did not change by more than 30% during the course of the experiment. Data were acquired and filtered at 2 kHz using a Multiclamp 700B Amplifier (Axon Instruments) and digitized at 20 kHz (National Instruments). All data were acquired using custom written MATLAB (Mathworks) software. Excitatory and inhibitory currents were isolated by voltage clamping the neuron at the reversal potential for synaptic inhibition and excitation respectively. For cell-attached experiments, only cells that exhibited at least one spike to a brief, high intensity pulse of blue light were included for analysis.
Optogenetic stimulation in vitro
Photo-stimulation of ChR2-expressing neurons was triggered by an Arduino UNO that sampled the membrane potential of the “trigger” neuron in real time (10 kHz sampling). The threshold for spike detection was 0mV. The blue light was generated using a multicolor LED light engine (Lumencor Spectra X) controlled by digital outputs (NI PCIe-6353) and was then routed via a liquid light guide before being focused onto the slice chamber using a 40× objective lens. Light intensity was titrated to induce a single action potential in ChR2+ SOM neurons to a 1ms pulse of light. To impose simulated excitatory conductances (sEPSGs), a custom analogue dynamic clamp was used58. The sEPSG waveforms were generated by convolving an EPSG-shaped template with a binary Poisson train.
Analysis of in vitro experiments
All analysis was performed using custom written code or openly available packages (Chronux, chronux.org59 in Matlab). Power spectra as well as phase locking were calculated as described for the in vivo data with 4 leading tapers and a time bandwidth product of 2. Charge was calculated as the integral of the EPSC/IPSC during photostimulation. Average values are expressed as mean ± s.e.m. Cells that exhibited peak gamma power lower than 25 pA2/Hz were excluded from analysis. Spike-spike coherence was computed as the power spectrum of a 300 ms window, centered at zero, of the cross correlation between the spike trains of the recorded neurons. Spike-coupling, a metric of spike-synchrony, was computed as the increase in spiking probability during a 5ms window surrounding a zero time lag between spikes. Inter-spike interval (ISI) histograms were computed with a 4 ms time bin. Cross-spectra were computed as the spectral power of the cross correlation between −100 and 100 ms lag times, giving a 6 Hz bin. Coherence was computed using a 250ms Welch window. Synchronous spike counts were calculated as the number of spikes in the ‘follower’ cell during a 10 ms window surround a trigger cell spike.
Statistics
We used only non-parametric statistical tests (Kruskal-Wallis ANOVA, Wilcoxon signed rank, rank sum and Friedman test) to determine significance except in Suppl. Fig. 6a, where a 2-factor design with interaction was needed. For this, the distribution was assumed to be normal but this was not formally tested. No statistical methods were used to pre-determine sample sizes. Visual stimulus presentation was randomized as outlined above. Data collection and analysis were not performed blind to the conditions of the experiments.
Computational Modeling
The model consists of an excitatory population (E) and two inhibitory populations (PV & SOM) that capture the functional connectivity between pyramidal neurons, PV inhibitory neurons and SOM inhibitory neurons in the local network of Layer 2/3 of the mouse visual cortex. The model defines the local network to be a group of neurons that code the same visual space and have similar tuning properties. The simplified firing rate model (Equations 1–5) describes the temporal evolution of excitatory ( ) and inhibitory ( and ) population firing rates of Layer 2/3 neurons as a function of two types of external inputs ( and ) to both the E and I populations. is the input from excitatory population in L4; it is held constant during all the simulations included in this study to mimic the presence of an unchanging visual stimulus in the receptive field, that is, the visual space coded by the local network (Fig. 3b). is the input from the excitatory population of other local networks in L2/3 that code the visual space in the surround and project their output through lateral connections. , and indicate the rate at which the populations approach their steady state firing rates.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
, and are the population response functions: they map the firing rates of the three neural populations in the local network as a function of their net inputs39,86. and are described by threshold-linear functions, while is described by a supra-linear function of weighted inputs to the respective sub-network, as described in Equations 6 and 7. The parameters and describe the threshold input and rate of the response functions, respectively. Their values for the excitatory, PV and SOM populations in our model are defined in Suppl. Table 1.
| (6) |
| (7) |
Previous work has shown that this choice of response functions results in network oscillations whose strength is positively correlated with the suppression of excitatory activity41. In the two-population model, this choice of response functions ensures an increase in the strength of oscillations either by increase in excitation to the I population or decrease in excitation to E population40,41. When extended to the current model, this choice of response functions predicts an increase in strength of oscillations in response to either withdrawal of excitation to the E population, or an increase in excitation to PV or SOM populations. reflects the net response of the L2/3 excitatory populations that code for the surround visual space. In our model, this response is modeled as a linear function of the size of the surround visual stimulus (Equation 5 & Fig. 3b), with the parameters as defined in Suppl. Table 1. For the results shown in Fig. 3 and Supp. Fig. 5, we varied the parameter from 1 to 4, in integer steps, to simulate increasing sizes of the visual surround. The steady-state firing rate of each population is determined by the weighted sum of individual population firing rates and the external input. All the weights ( : from population Y to population X) are positive numbers representing strength of connections (see Suppl. Table 1). For example, represents the product of the average number of recurrent excitatory contacts per cell and the average postsynaptic current arising from one pre-synaptic action potential. The two inhibitory subpopulations are differentiated as SOM and PV based on the connections they form with each other and the excitatory population, and also the relative strength of inputs from L4 and L2/3 to each inhibitory population. Connectivity between the excitatory and PV inhibitory populations was tuned to keep the E-PV sub-network in an inhibition-stabilized network (ISN) regime87. Previous modeling work has shown that the presence of surround facilitation in SOM neurons84 is compatible with the E-PV loop being in the ISN regime70. reflects the evidence for weak connectivity between SOM neurons88. was set to zero since the net effect of L2/3 lateral input in this model is inhibitory 84, through its action on mainly SOM neurons. Non-zero values of did not change the qualitative results as long as the net effect of lateral input was inhibitory in the local network. The steady-state network behavior is determined by the intersection of the , and curves in the -hyperplane.
Suppl. Table 1 shows the parameter values used for generating the simulation data. Given the values of time constants, the connection weights were chosen such that the frequency of the oscillations in the model was in the gamma, more specifically in the 20–30 Hz, range. The model network was simulated using Matlab 2014b (Mathworks, Natick, MA). The power spectral density (PSD) of the average activity signal was estimated non-parametrically by calculating the discrete-time Fourier Transform of the signal. Gamma power was reported as the peak power at the center frequency of narrowband peak in the PSD in the 20–30 Hz range.
Supplementary Material
Acknowledgments
The authors thank D. Taylor for technical assistance, K. Chesnov and D. Abdelhalim for help with histology, J. Isaacson, M. Feller, D. Feldman, Y. Dan, and B. Atallah, for comments on the manuscript. This work was supported by NEI grant R01EY023756-01. H.A. is a New York Stem Cell Foundation Roberston Investigator. J.V. was supported by grants from the Swiss National Foundation (P300PA_164719 and P2FRP3_155172). M.P.J. was supported by NEI grant 5K99EY025026-02 and Howard Hughes Medical Institute (HHMI). T.J.S. was supported by HHMI.
Footnotes
Data availability
All relevant data for the experimental and theoretical work can be made available by the authors upon reasonable request.
Author Contributions
H.A., J.V., and M.P.J. conceived of the study. J.V. performed all in vivo extracellular experiments, H.A. performed the in vivo patch clamp experiments, and R.H. performed all brain slice experiments. M. P.J conceived of the computational model and carried out all simulations. T.J.S. provided guidance to the computational study.
Competing financial interests
The authors declare no competing financial interests.
Code availability
All analysis and modelling code can be made available by the authors upon reasonable request.
References and notes
- 1.Singer W, Gray CM. Visual Feature Integration and the Temporal Correlation Hypothesis. Annual review of neuroscience. 1995;18:555–586. doi: 10.1146/annurev.neuro.18.1.555. [DOI] [PubMed] [Google Scholar]
- 2.Buzsaki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- 3.Traub RD, Whittington MA. Cortical oscillations in health and disease. Oxford University Press; 2010. [Google Scholar]
- 4.Fries P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annual review of neuroscience. 2009;32:209–224. doi: 10.1146/annurev.neuro.051508.135603. [DOI] [PubMed] [Google Scholar]
- 5.Whittington MA, Cunningham MO, LeBeau FEN, Racca C, Traub RD. Multiple Origins of the Cortical Gamma Rhythm. Developmental neurobiology. 2011;71:92–106. doi: 10.1002/dneu.20814. [DOI] [PubMed] [Google Scholar]
- 6.Fries P, Nikolic D, Singer W. The gamma cycle. Trends in neurosciences. 2007;30:309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
- 7.Womelsdorf T, et al. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- 8.Bartos M, Vida I, Jonas P. Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. Nature reviews Neuroscience. 2007;8:45–56. doi: 10.1038/nrn2044. [DOI] [PubMed] [Google Scholar]
- 9.Buzsaki G, Wang XJ. Mechanisms of gamma oscillations. Annual review of neuroscience. 2012;35:203–225. doi: 10.1146/annurev-neuro-062111-150444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sohal VS, Zhang F, Yizhar O, Deisseroth K. Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature. 2009;459:698–702. doi: 10.1038/nature07991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cardin JA, et al. Driving fast-spiking cells induces gamma rhythm and controls sensory responses. Nature. 2009;459:663–U663. doi: 10.1038/nature08002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Adesnik H, Bruns W, Taniguchi H, Huang ZJ, Scanziani M. A neural circuit for spatial summation in visual cortex. Nature. 2012;490:226–231. doi: 10.1038/Nature11526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Niell CM, Stryker MP. Modulation of visual responses by behavioral state in mouse visual cortex. Neuron. 2010;65:472–479. doi: 10.1016/j.neuron.2010.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Saleem A, et al. On the Origin and Modulation of Narrow-Band Gamma Oscillations in Mouse Primary Visual Cortex. Perception. 2016;45:702–702. [Google Scholar]
- 15.Gieselmann MA, Thiele A. Comparison of spatial integration and surround suppression characteristics in spiking activity and the local field potential in macaque V1. European Journal of Neuroscience. 2008;28:447–459. doi: 10.1111/j.1460-9568.2008.06358.x. [DOI] [PubMed] [Google Scholar]
- 16.Jia XX, Smith MA, Kohn A. Stimulus Selectivity and Spatial Coherence of Gamma Components of the Local Field Potential. Journal of Neuroscience. 2011;31:9390–9403. doi: 10.1523/Jneurosci.0645-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Perry G, Hamandi K, Brindley LM, Muthukumaraswamy SD, Singh KD. The properties of induced gamma oscillations in human visual cortex show individual variability in their dependence on stimulus size. NeuroImage. 2013;68:83–92. doi: 10.1016/j.neuroimage.2012.11.043. [DOI] [PubMed] [Google Scholar]
- 18.Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bosman CA, et al. Attentional Stimulus Selection through Selective Synchronization between Monkey Visual Areas. Neuron. 2012;75:875–888. doi: 10.1016/j.neuron.2012.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jia XX, Xing DJ, Kohn A. No Consistent Relationship between Gamma Power and Peak Frequency in Macaque Primary Visual Cortex. Journal of Neuroscience. 2013;33:17–U421. doi: 10.1523/Jneurosci.1687-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gray CM, Konig P, Engel AK, Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338:334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- 22.Biederlack J, et al. Brightness induction: Rate enhancement and neuronal synchronization as complementary codes. Neuron. 2006;52:1073–1083. doi: 10.1016/j.neuron.2006.11.012. [DOI] [PubMed] [Google Scholar]
- 23.Perrenoud Q, Pennartz CMA, Gentet LJ. Membrane Potential Dynamics of Spontaneous and Visually Evoked Gamma Activity in V1 of Awake Mice. PLoS biology. 2016;14 doi: 10.1371/journal.pbio.1002383. ARTN e100238310.1371/journal.pbio.1002383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jagadeesh B, Gray CM, Ferster D. Visually Evoked Oscillations of Membrane-Potential in Cells of Cat Visual-Cortex. Science. 1992;257:552–554. doi: 10.1126/science.1636094. [DOI] [PubMed] [Google Scholar]
- 25.Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical journal. 1972;12:1–24. doi: 10.1016/S0006-3495(72)86068-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jadi MP, Sejnowski TJ. Cortical oscillations arise from contextual interactions that regulate sparse coding. Proceedings of the National Academy of Sciences of the United States of America. 2014;111:6780–6785. doi: 10.1073/pnas.1405300111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jadi MP, Sejnowski TJ. Regulating Cortical Oscillations in an Inhibition-Stabilized Network. Proc IEEE Inst Electr Electron Eng. 2014;102 doi: 10.1109/JPROC.2014.2313113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pfeffer CK, Xue MS, He M, Huang ZJ, Scanziani M. Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nature neuroscience. 2013;16:1068–U1130. doi: 10.1038/nn.3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gilbert CD, Wiesel TN. Columnar specificity of intrinsic horizontal and corticocortical connections in cat visual cortex. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1989;9:2432–2442. doi: 10.1523/JNEUROSCI.09-07-02432.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Atallah BV, Bruns W, Carandini M, Scanziani M. Parvalbumin-expressing interneurons linearly transform cortical responses to visual stimuli. Neuron. 2012;73:159–170. doi: 10.1016/j.neuron.2011.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wilson NR, Runyan CA, Wang FL, Sur M. Division and subtraction by distinct cortical inhibitory networks in vivo. Nature. 2012;488:343–348. doi: 10.1038/nature11347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Colgin LL, et al. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–U119. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- 33.Neuenschwander S, Singer W. Long-range synchronization of oscillatory light responses in the cat retina and lateral geniculate nucleus. Nature. 1996;379:728–733. doi: 10.1038/379728a0. [DOI] [PubMed] [Google Scholar]
- 34.Koepsell K, et al. Retinal oscillations carry visual information to cortex. Frontiers in systems neuroscience. 2009;3:4. doi: 10.3389/neuro.06.004.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Storchi R, et al. Modulation of Fast Narrowband Oscillations in the Mouse Retina and dLGN According to Background Light Intensity. Neuron. 2017;93:299–307. doi: 10.1016/j.neuron.2016.12.027. [DOI] [PubMed] [Google Scholar]
- 36.Vinck M, Batista-Brito R, Knoblich U, Cardin JA. Arousal and Locomotion Make Distinct Contributions to Cortical Activity Patterns and Visual Encoding. Neuron. 2015;86:740–754. doi: 10.1016/j.neuron.2015.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ray S, Maunsell JHR. Differences in Gamma Frequencies across Visual Cortex Restrict Their Possible Use in Computation. Neuron. 2010;67:885–896. doi: 10.1016/j.neuron.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Thiele A, Stoner G. Neuronal synchrony does not correlate with motion coherence in cortical area MT. Nature. 2003;421:366–370. doi: 10.1038/nature01285. [DOI] [PubMed] [Google Scholar]
- 39.Shadlen MN, Movshon JA. Synchrony unbound: A critical evaluation of the temporal binding hypothesis. Neuron. 1999;24:67–77. doi: 10.1016/S0896-6273(00)80822-3. [DOI] [PubMed] [Google Scholar]
- 40.Larkum ME, Nevian T, Sandler M, Polsky A, Schiller J. Synaptic integration in tuft dendrites of layer 5 pyramidal neurons: a new unifying principle. Science. 2009;325:756–760. doi: 10.1126/science.1171958. [DOI] [PubMed] [Google Scholar]
- 41.Smith SL, Smith IT, Branco T, Hausser M. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature. 2013;503:115–+. doi: 10.1038/nature12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Losonczy A, Makara JK, Magee JC. Compartmentalized dendritic plasticity and input feature storage in neurons. Nature. 2008;452:436–441. doi: 10.1038/nature06725. [DOI] [PubMed] [Google Scholar]
- 43.Murayama M, et al. Dendritic encoding of sensory stimuli controlled by deep cortical interneurons. Nature. 2009;457:1137–U1195. doi: 10.1038/Nature07663. [DOI] [PubMed] [Google Scholar]
- 44.Zhang SY, et al. Long-range and local circuits for top-down modulation of visual cortex processing. Science. 2014;345:660–665. doi: 10.1126/science.1254126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lepousez G, Mouret A, Loudes C, Epelbaum J, Viollet C. Somatostatin Contributes to In Vivo Gamma Oscillation Modulation and Odor Discrimination in the Olfactory Bulb. Journal of Neuroscience. 2010;30:870–875. doi: 10.1523/Jneurosci.4958-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Uhlhaas PJ, Singer W. Abnormal neural oscillations and synchrony in schizophrenia. Nature Reviews Neuroscience. 2010;11:100–113. doi: 10.1038/nrn2774. [DOI] [PubMed] [Google Scholar]
- 47.Jadi MP, Behrens MM, Sejnowski TJ. Abnormal Gamma Oscillations in N-Methyl-D-Aspartate Receptor Hypofunction Models of Schizophrenia. Biol Psychiatry. 2016;79:716–726. doi: 10.1016/j.biopsych.2015.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Hamm JP, Yuste R. Somatostatin Interneurons Control a Key Component of Mismatch Negativity in Mouse Visual Cortex. Cell Rep. 2016;16:597–604. doi: 10.1016/j.celrep.2016.06.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lin LC, Sibille E. Reduced brain somatostatin in mood disorders: a common pathophysiological substrate and drug target? Frontiers in pharmacology. 2013;4:110. doi: 10.3389/fphar.2013.00110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. doi: 10.1163/156856897x00357. [DOI] [PubMed] [Google Scholar]
- 51.Mitra P, Bokil H. Observed brain dynamics. Oxford University Press; 2008. [Google Scholar]
- 52.Hill DN, Mehta SB, Kleinfeld D. Quality Metrics to Accompany Spike Sorting of Extracellular Signals. Journal of Neuroscience. 2011;31:8699–8705. doi: 10.1523/Jneurosci.0971-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Munoz W, Tremblay R, Rudy B. Channelrhodopsin-Assisted Patching: In Vivo Recording of Genetically and Morphologically Identified Neurons throughout the Brain. Cell Rep. 2014;9:2304–2316. doi: 10.1016/j.celrep.2014.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ma YY, Hu H, Berrebi AS, Mathers PH, Agmon A. Distinct subtypes of somatostatin-containing neocortical interneurons revealed in transgenic mice. Journal of Neuroscience. 2006;26:5069–5082. doi: 10.1523/Jneurosci.0661-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Pluta S, et al. A direct translaminar inhibitory circuit tunes cortical output. Nature neuroscience. 2015;18:1631–1640. doi: 10.1038/nn.4123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Vinck M, van Wingerden M, Womelsdorf T, Fries P, Pennartz CM. The pairwise phase consistency: a bias-free measure of rhythmic neuronal synchronization. NeuroImage. 2010;51:112–122. doi: 10.1016/j.neuroimage.2010.01.073. [DOI] [PubMed] [Google Scholar]
- 57.Oostenveld R, Fries P, Maris E, Schoffelen JM. FieldTrip: Open Source Software for Advanced Analysis of MEG, EEG, and Invasive Electrophysiological Data. Comput Intel Neurosc. 2011 doi: 10.1155/2011/156869. doi: Artn 15686910.1155/2011/156869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Adesnik H, Scanziani M. Lateral competition for cortical space by layer-specific horizontal circuits. Nature. 2010;464:1155–1160. doi: 10.1038/nature08935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bokil H, Andrews P, Kulkarni JE, Mehta S, Mitra PP. Chronux: A platform for analyzing neural signals. Journal of neuroscience methods. 2010;192:146–151. doi: 10.1016/j.jneumeth.2010.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ozeki H, Finn IM, Schaffer ES, Miller KD, Ferster D. Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron. 2009;62:578–592. doi: 10.1016/j.neuron.2009.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL. Paradoxical effects of external modulation of inhibitory interneurons. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1997;17:4382–4388. doi: 10.1523/JNEUROSCI.17-11-04382.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Litwin-Kumar A, Rosenbaum R, Doiron B. Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes. Journal of neurophysiology. 2016;115:1399–1409. doi: 10.1152/jn.00732.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pfeffer CK, Xue M, He M, Huang ZJ, Scanziani M. Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nat Neurosci. 2013;16:1068–1076. doi: 10.1038/nn.3446. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


