Strength of onset and ongoing cues in judgments of lateral position

Abstract

This study describes the contributions to auditory image position of an interaural time delay (ITD) cue at onset relative to subsequent ITDs during the ongoing part of a stimulus. Test stimuli were trains of 1-ms binaural noise bursts; lateral position was measured with a wideband acoustic pointer that subjects adjusted to match the intracranial position of test stimuli. In different conditions the ongoing part of the stimulus (the bursts following the first one) either had a consistent ITD (the same ITD on each ongoing burst), or had alternating leading and lagging components with ITDs that opposed one another. As duration of the ongoing part was increased from 4 to 250 ms, with the initial ITD fixed, lateral position changed from being dominated by the onset ITD to being dominated by the ongoing consistent or leading ITD. With alternating ongoing ITDs equal contributions from onset and ongoing parts were obtained at an ongoing duration of about 40 ms; with consistent ongoing ITDs equal contributions were obtained at about 15 ms. The results point up the increased dominance of onset cues when ongoing cues are ambiguous, as they often are in real-world settings.

I. INTRODUCTION

There are many real-world conditions, especially in rooms with reflections, in which the interaural cues used to localize sounds are different during the later, or ongoing, part of the sound than they are at onset. The relative importance of onset and ongoing cues in determining where a sound is heard has been studied frequently. The consistent outcome of those studies has indicated that spatial cues delivered at an abrupt stimulus onset are strongly influential, and may even dominate later-arriving cues. This general result is associated with well-known spatial effects such as the precedence effect (Wallach et al., 1949) and the Franssen (1962) effect.

The strong influence of onsets in spatial hearing has been demonstrated with a variety of experimental methods. Onset dominance is seen in the weights attached to onset sounds in paradigms that estimate the influence of individual pulses in a train (Hafter et al., 1988; Saberi, 1996; Brown and Stecker, 2010), and in techniques that probe the influence of various temporal manipulations of interaural cues in white noise (Zurek, 1980; Houtgast and Aoki, 1994; Akeroyd and Bernstein, 2001). In terms that are relevant to functioning in everyday acoustic environments, Rakerd and Hartmann (1986) showed that abrupt onsets greatly facilitate accurate sound localization in reverberant spaces.

Onset dominance is subject to limitations, and some of those limitations are better understood than others. Various studies have documented the dependence of onset dominance on parameters such as rise time (Kunov and Abel, 1981) and inter-click interval (Hafter and Dye, 1983; Saberi and Perrott, 1995; Brown and Stecker, 2010), with results that are generally as expected from an onset-sensitive mechanism. Other factors, such as the detailed characteristics of both the onset and ongoing sounds that weaken or enhance onset dominance, are still being studied. One factor is the type of onset delay—whether the onset sound is presented with a gating delay or a whole-waveform delay can lead to vastly different estimates of onset dominance (Tobias and Schubert, 1959; Buell et al., 1991; Zurek, 1993).

Differences in onset dominance are also observed when stimuli differ in ambiguity of ongoing cues (Freyman et al., 1997) or in the spectral sparseness of the ongoing part of the stimulus (Hartmann, 1983; Hartmann and Rakerd, 1989; Freyman et al., 1997). A well-known example of the dependence of onset dominance on characteristics of the ongoing part is observed with the Franssen effect. In that phenomenon, a sine tone presented in a room is divided into an onset transient from one loudspeaker and an ongoing tone from another. The sound is localized at the transient loudspeaker long after the signal from that location has been turned off. But the Franssen effect fails if the sine tone is presented in an anechoic room, or if the stimulus is random noise rather than a tone (Hartmann and Rakerd, 1989). So, while onset cues can be strongly dominant in many stimulus conditions, there is still an incomplete understanding of the factors that control the extent of onset dominance and the mechanism(s) that underlie the phenomena.

The present report describes our attempt to characterize the transition from dominance of lateral position by an onset cue to that by the ongoing cues as stimulus duration is varied. In the present experiments, discrete and easily manipulated noise bursts were used to create stimuli consisting of an initial noise burst (the “onset”), with one interaural cue, followed by a train of bursts (the “ongoing” part of the stimulus), with a different set of interaural cues. Lateral position of this composite stimulus was measured as a function of the duration of the ongoing part.

A secondary interest in this study was to compare onset dominance with two types of ongoing stimuli. One of these had a single unambiguous interaural delay while the other had two conflicting interaural delays. The former is typical of ongoing stimuli that have been used in past studies. The latter type of ongoing stimulus was composed of a lead sound, with one interaural delay, and a delayed repetition, a lag sound, with a different interaural delay. We used this simple simulation of a direct sound plus reflection as a step toward the complex cues that are present in rooms. Several studies have used such lead/lag stimuli to explore the “ongoing precedence effect” (Zurek, 1980; Braasch et al., 2003; Dizon and Colburn, 2006; Freyman et al., 2010; Donovan et al., 2012). Using stimulus durations of 100 ms and longer, and usually with a slow rise to eliminate abrupt onsets, these studies have found that the interaural differences in the leading component have much more influence on image position than those in the lagging component, similar to the precedence effect with transients (e.g., Wallach et al., 1949; Yost and Soderquist, 1984).

Aside from increasing our understanding of how the binaural auditory system uses interaural cues, the present study may have implications for sound localization in everyday environments. In common acoustic scenarios, multiple sources produce complex sequences of steady sounds, rapid transitions, and wideband transients. The duration of consonant sounds in speech, for example, ranges between a few and a few hundred milliseconds. By examining onset dominance over the relevant range of stimulus durations we might shed some light on the spatial perception of sound in real-world settings.

II. METHOD

A. Subjects

Three normal-hearing female listeners with audiometric thresholds ≤20 dB Hearing Level at octave frequencies between 500 and 8000 Hz participated in this study. Their ages ranged between 22 and 28 years old. Subjects were graduate student research assistants in the Communication Disorders department at the University of Massachusetts, Amherst.

B. Stimuli

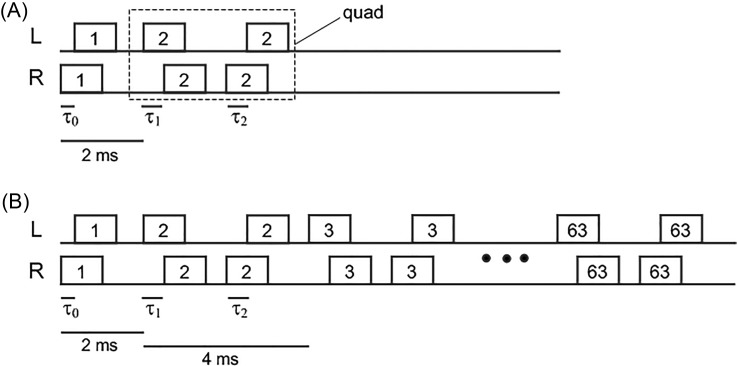
The target stimuli were variable-length trains of 1-ms binaural noise bursts, with the temporal structure illustrated in Fig. 1. The first burst in a train, the onset burst, had an ITD of τ₀ while the remainder of the train, the ongoing part, had bursts with ITDs that alternated between τ₁ and τ₂. ITDs less than zero indicate a lead to the left.

FIG. 1.

Schematic showing the temporal structure of the target stimuli. Each rectangle represents a 1-ms noise burst. The number inside each rectangle identifies the noise token. Sets of two binaural bursts with the same token are called “quads.” The figure shows an onset burst (token 1) followed by either one quad (A) or 62 quads (B). A quad consists of a lead component with ITD τ₁ and a lag component with ITD τ₂. The diagram illustrates the conditions where τ₂ = −τ₁. In other conditions, τ₁ and τ₂ were equal, resulting in a consistent interaural delay throughout the ongoing part of the signal.

Fresh tokens of noise were used for the onset burst and for every two binaural bursts in the ongoing part (the number in each burst in Fig. 1 identifies a noise token). Two binaural bursts with the same token are called a “quad.” Thus, each quad contained a leading burst with an ITD of τ₁ and a lagging burst with an ITD of τ₂. The interval from the onset of one burst pair to the next in the train was fixed at 2 ms, and the interval from one quad to the next was 4 ms. These stimuli were substantially the same as those employed in the “unfrozen” noise burst conditions from Freyman et al. (2010) to create the ongoing precedence effect, in which the leading burst in each quad strongly influences the perceived lateral position of the sound. All the sounds in that study were approximately 250 ms in duration, whereas duration was manipulated in the current study. Further descriptions of the stimuli used in experiments 1 and 2 are given below.

Stimuli were generated on a personal computer with a 24-bit sound card, low-pass filtered at 8.5 kHz, attenuated (TDT PA4), and delivered through Etymotic ER2 insert earphones via a headphone amplifier (TDT HB5) and a passive attenuator at a level of 50 dBA for a 250 ms train. No adjustments to the attenuator settings were made for stimuli of shorter durations. The level was estimated using the procedures of Bernstein and Trahiotis (2002) by measuring the level of the same stimulus as produced by TDH-39 headphone in a 6 cm³ coupler and measuring the attenuation necessary for a centered image for a high-frequency (2 kHz) narrowband noise with the headphone on one ear and the insert in the other.

The test stimuli were generated and presented at a 20 kHz digital-to-analog D/A conversion rate. Lateral position was measured through subjects' adjustment of the ITD of an acoustic pointer, a 50-ms burst of white noise with a linear 5-ms rise and fall. The pointer was presented at a 40 kHz D/A conversion rate, permitting a resolution of 25 μs in the pointer's whole-waveform ITD. The maximum pointer ITD was ±800 μs, and its initial value prior to subjects' adjustment was roved randomly through a range of ±500 μs. The level of the pointer was 5 dB lower than the 250 ms target.

C. Procedure

Subjects were seated behind a desk in a double-walled sound-treated booth (IAC 1640) with a keyboard on the desk. They were asked to use the keyboard to adjust the ITD of the acoustic pointer until its intracranial position matched that of a target stimulus, with no time limit imposed. The keys “M” and “N” increased the pointer ITD by 125 and 25 μs, respectively, which moved the image of the pointer toward the right, while the keys “V” and “B” decreased it by 125 and 25 μs, respectively, moving the pointer image toward the left. Target and pointer stimuli alternated continuously during a trial with an onset-to-onset period of 1 s. The “X” key entered the subject's final match. A new trial began immediately after the preceding one ended.

III. EXPERIMENT 1

In this experiment, the ITD of the onset burst was equal to that of each lag burst in the ongoing part, and equal in magnitude but opposite in sign to the ITD of the lead burst (i.e., τ₀ = τ₂ = −τ₁). The number of quads in the stimulus train ranged from 1 to 62, resulting in stimulus durations from approximately 6 to 250 ms, while τ₀ (and consequently τ₁ and τ₂) was varied from −500 (left) to 500 μs (right) in 100 μs steps. Within a run of 11 trials the ongoing train length was held constant and each value of τ₀ was presented once in random order. Subjects completed six such runs at a given ongoing length before testing with a new length.

A. Results

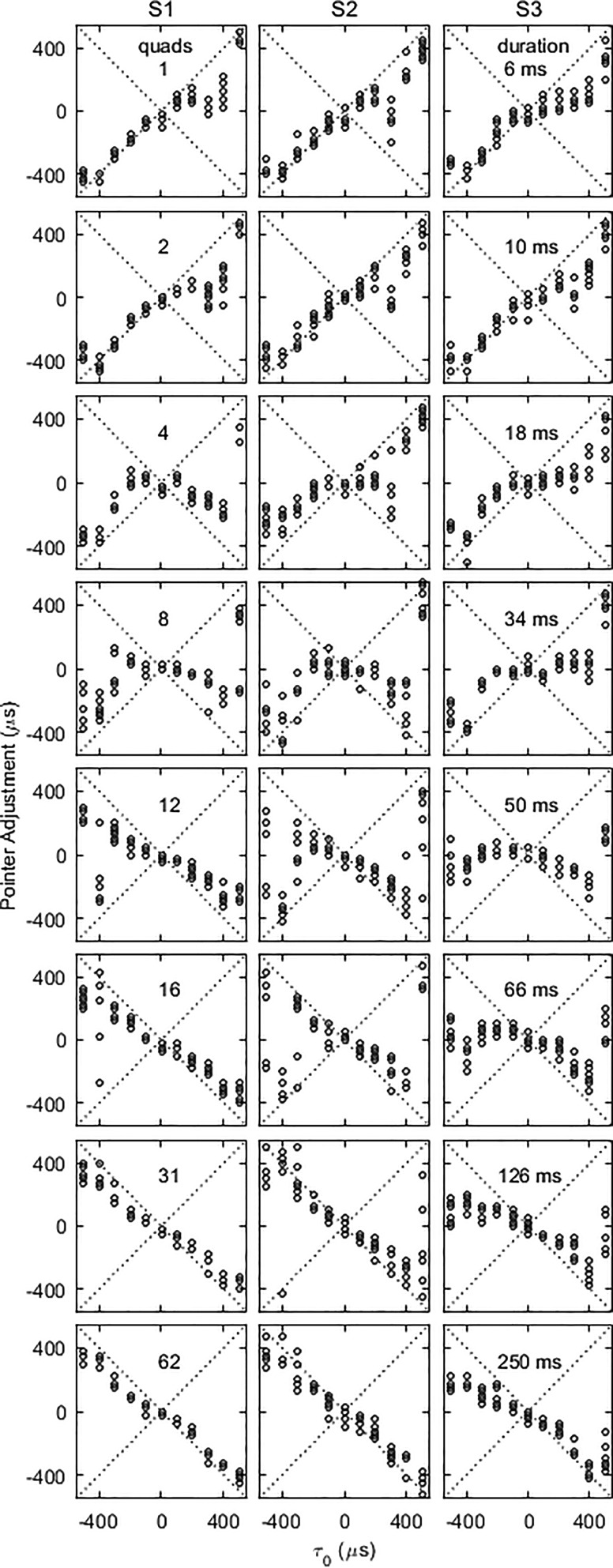
The effects of ongoing train duration and τ₀ on lateral position are shown for the three listeners in Fig. 2. Each pointer adjustment is shown as a separate symbol. For the shortest signals (one quad), and for τ₀ < 0, lateralization was largely determined by τ₀ (=τ₂), the onset (=lag) ITD, as opposed to the lead ITD in the quad, −τ₀. For the symmetrically opposite stimuli, with τ₀ > 0, however, all three subjects adjusted to much more central positions than with τ₀ < 0. Only when τ₀ reached its largest value of 500 μs did pointer adjustments increase abruptly to be nearly equal to the onset ITD.

FIG. 2.

Pointer adjustments as a function of τ₀ and stimulus duration. Data from the three subjects are given in the three columns. Rows present data with various numbers of quads (1,2,…,62) following the onset burst. Each symbol represents a single pointer adjustment.

As the number of quads was increased, lateral position became more variable, but the overall trend was for the influence of the initial ITD to decline. By 125 ms (31 quads), lateralization responses became less variable again and largely followed the ongoing lead ITD, τ₁ (=−τ₀). At long durations, the leftward asymmetry seen at short durations was observed again for S3, with more central adjustments with τ₀ < 0 than with τ₀ > 0. The results at 250 ms for S1 and S2 were fairly left/right symmetric and are similar to those from an identical condition in Freyman et al. (2010) (their Fig. 7).

Although one is tempted to think about integration of cues into a single image, this was not necessarily the case under all conditions. Subjects were not asked about their subjective impressions while participating in the experiment, but two were contacted afterward (one who listened to the stimuli again) and indicated that they based their matches on the dominant image. The authors also listened to the stimuli and heard movement under some conditions—where there were large differences between τ₁ and τ₂ at intermediate values of duration—and were also able to identify a dominant image amidst some sensations of movement over the course of the stimulus. The relative stability of the results suggests that listeners were not confused by multiple images.

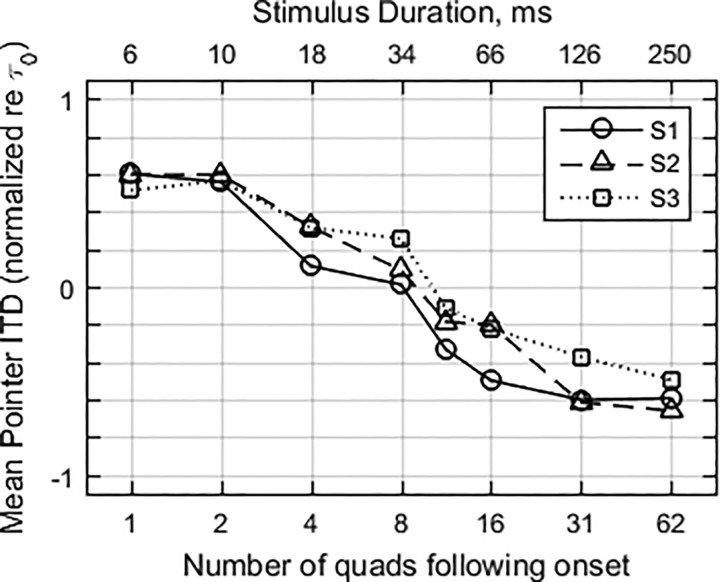
Notwithstanding the asymmetries in the raw data, the strong overall trend is for pointer adjustments to follow the onset ITD at short durations, and to change over to follow the lead ongoing ITD at long durations. To quantify that trend, a summary measure of the relative influence of the onset was obtained by first normalizing (dividing) each pointer adjustment by the value of τ₀ (excluding τ₀ = 0), and then averaging normalized adjustments over τ₀ and repetitions. Figure 3 shows this measure for the three subjects plotted as a function of the number of quads in the ongoing part of the stimulus. The subjects showed a very similar trend as a function of stimulus duration. With one quad following the onset burst, pointer adjustments were on average equal to about 60% of the value of τ₀. Similarly, with 62 quads (250-ms ongoing duration), pointer adjustments were approximately 60% of the ongoing lead ITD, τ₁. Approximately equal contribution from the conflicting ITDs was achieved with an ongoing duration estimated to be about 10 quads, or 40 ms.

FIG. 3.

Pointer adjustments from Fig. 2, normalized and averaged over repetitions, as a function of ongoing stimulus duration (in terms of number of post-onset quads), for the three subjects.

IV. EXPERIMENT 2

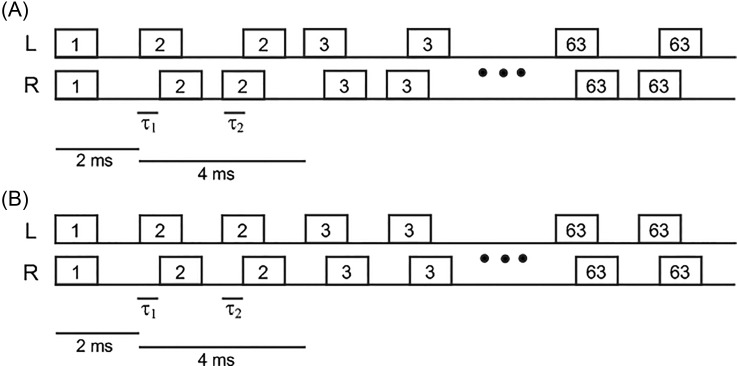
In experiment 1, the onset ITD matched the ongoing lag ITD exactly (τ₀ = τ₂). This represents a potential confound in the sense that the influence of the onset ITD is not separated from that of the ITDs in the ongoing part. In this experiment, this confound was removed by fixing the initial ITD at 0 and the ongoing ITDs at ±500 μs while varying the number of quads. Figure 4(A) shows a schematic diagram of an example with 62 quads. Each block consisted of 16 trials, with τ₁ = +500 or −500 μs and τ₂ = −τ₁ with the eight different numbers of quads used in experiment 1. As before, the blocks were repeated six times with an individual random order of conditions for each block.

FIG. 4.

Schematic showing the temporal structure of the target stimuli for experiment 2. (A) Onset burst with τ₀ = 0 followed by an ongoing train of quads with τ₁ = −τ₂. (B) Onset burst with τ₀ = 0 followed by an ongoing train of quads with equal ITDs (i.e., τ₁ = τ₂).

For comparison, another condition was run with ongoing trains of bursts that had consistent ITDs fixed at either +500 or −500 μs. The structure of the noise samples was the same, with the sample changing after every two bursts [Fig. 4(B)].

Control conditions (stimuli not shown) were run to measure the strength of the ongoing precedence effect alone, with no onset burst. For this purpose, six matches were obtained with the 62-quad stimuli with a 125-ms linear rise-fall envelope for both τ₁ = +500 and τ₁ = −500 μs, with τ₂ = −τ₁, and no added onset burst. This condition was run in one block of 12 trials with τ₁ = +500 and τ₁ = −500 μs conditions randomly interspersed. In a second control condition a similar train of slow-onset bursts was tested with τ₂ = τ₁ (i.e., a consistent interaural delay in an ongoing train). As additional references, these two control conditions were also tested with no rise-fall envelope.

A. Results

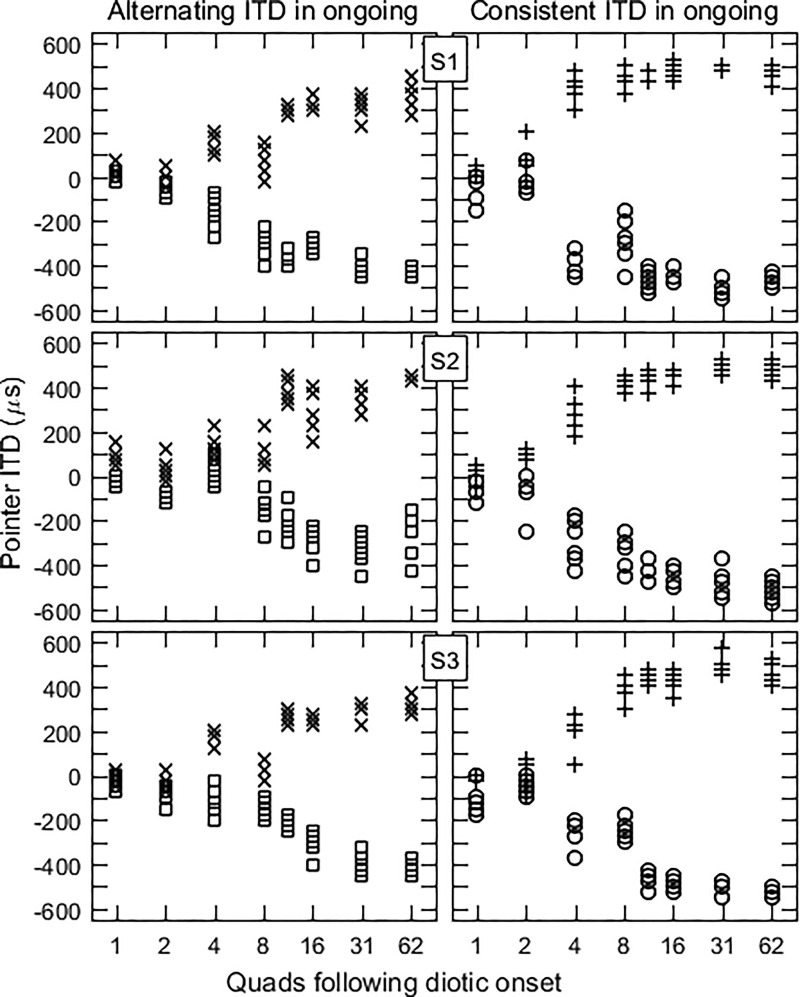
The individual results are shown in Fig. 5 and mean results in Fig. 6. In Fig. 5, the left panels display the data for the alternating ongoing ITD condition. With one quad, pointer adjustments were near zero, the value of the onset ITD. As the number of quads increased, pointer adjustments increased in magnitude, reaching 60%–90% of the value of the ongoing lead ITD, depending on the subject and the sign of τ₁. The matches reached the halfway points (±250 μs) between the initial ITD (0 μs) and the ongoing lead ITD (±500 μs) between 8 and 12 quads (32 and 48 ms) across subjects as the number of quads increased. This result is qualitatively consistent with that found in experiment 1 (see Figs. 2 and 3), and suggests that the influence of the initial ITD depends little, if at all, on whether it matches the lag ITD in the ongoing train. The data for the consistent ITD condition show similar trends, but with the influence of the ongoing lead ITD seen at shorter ongoing durations.

FIG. 5.

Pointer adjustments for experiment 2 with τ = ±500 μs. Results in the left column were obtained with alternating ITDs in the ongoing train of quads (×: +500; ◻: −500). For the right column the ITDs in the ongoing train were all consistent (+: +500; ○: −500).

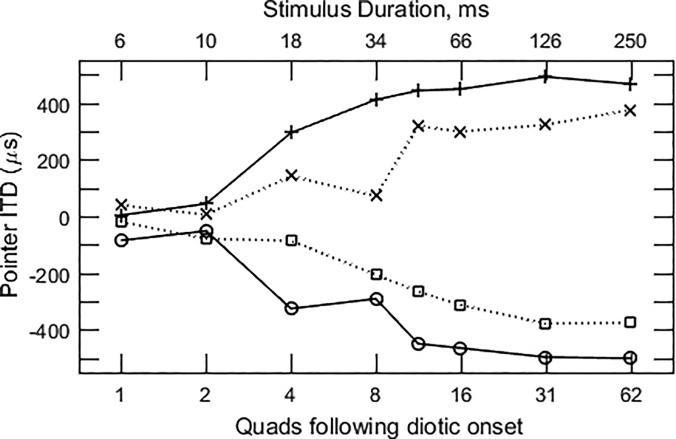
FIG. 6.

Averages of the data in Fig. 5 over repetitions and subjects. Consistent ongoing ITDs with τ₁ = +500 (+) or −500 μs (○) and τ₂ = τ₁. Alternating ITDs with τ₁ = 500 (×) or −500 μs (◻).

There is a possible confounding factor in this comparison, which is that for a given number of quads there were twice as many binaural pairs with a delay of τ₁ in the consistent condition than in the alternating conditions. This factor can be evaluated first by noting that pointer matches with 31 quads of consistent ITDs are not equal to those with 62 quads of alternating ITDs (Fig. 6). At shorter durations, however, the equivalent comparison (e.g., comparing 8 quads of consistent ITDs with 16 quads of inconsistent ITDs) yields similar pointer matches and more comparable crossover durations for the two conditions. The difference in these comparisons makes is difficult to tease apart the role of consistency per se versus number of quads with a given ITD.

Results of the control conditions with no onset burst are shown in Table I. Adjustments made in the alternating condition, which measures the ongoing precedence effect, were 80%–85% of the lead ITD for two of the subjects. S3's adjustments, on the other hand, were equal to or slightly larger than the lead ITD. There may also be a small effect of the slow rise yielding less lateral adjustments than an abrupt rise. The difference in matches for abrupt versus gradual gating was confirmed statistically for the data as a whole [F(1,33) = 14.368, p < 0.001], although subject 3 individually did not exhibit this trend (p = 0.643). Adjustments with a consistent ITD in the train were essentially equal to that ITD, as expected, with no clear difference between slow and abrupt rise.

TABLE I.

Mean pointer adjustments (in microseconds) for the control conditions in experiment 2, in which the stimuli consisted of 62 quads only, with no onset burst. The stimuli were gated on and off either abruptly (no rise-fall) or with a 125-ms rise-fall, and the ITDs within a quad (±500 μs) were alternated or were consistent throughout the train. Table entries are the means of absolute values with τ₁ = 500 μs and with τ₁ = −500 μs. The right-most column presents the model parameter $c_1$, explained in Sec. V.

	Consistent		Alternating
	Rise-fall	No rise-fall	Rise-fall	No rise-fall	c1
S1	495	504	418	448	0.918
S2	516	502	429	485	0.929
S3	540	540	533	540	1.033

V. WEIGHTING MEASURES

Shinn-Cunningham et al. (1993) described a measure, called c, that quantifies the influence of a leading ITD relative to a trailing ITD. The measure is based on the assumption that the lateral position, α, of a sound containing leading and trailing components is the weighted sum of the leading and trailing ITDs, d₁ and d₂,

$$\propto =c{d}_1+(1-c)d_2,$$ (1)

which defines the onset weight c to be

$$c=\frac{\propto -\hspace{0.17em}{d}_2}{d_1-d_2}.$$ (2)

Here, we extend this measure to represent both onset dominance and the ongoing precedence effect. This extension is premised on the assumption that the lateral position α of one of the present experimental stimuli is the following function of the three ITDs, τ₀, τ₁, and τ₂, and two weights, c₀ and c₁,

$$\propto =c_0{\tau }_0+(1-c_0)\hspace{0.17em}\left[(c_1{\tau }_1)+(1-c_1)\hspace{0.17em}{\tau }_2\hspace{0.17em}\right],$$ (3)

where $\propto$ = ITD of pointer matched to the lateral position of the target, ${\tau }_0$ = onset ITD, ${\tau }_1$ = ongoing lead ITD, ${\tau }_2$ = ongoing lag ITD, $c_0$ = weighting of onset ITD re the effective ITD of the ongoing part, and $c_1$ = weighting of ongoing lead ITD re the ongoing lag ITD.

The first weight, $c_0,\hspace{0.17em}$ expresses the influence of the onset ITD relative to the ongoing stimulus, while $c_1$ weights the ongoing lead ITD relative to the ongoing lag ITD. To compute $c_1$, the results from the control condition of experiment 2 were used (slow-onset 62 quads, with alternating ITDs, given in Table I). This condition is assumed to represent the “pure” ongoing precedence effect (i.e., $c_0$ = 0), which from Eq. (3) leads to

$$c_1=\frac{\propto -\hspace{0.17em}{\tau }_2}{{\tau }_1-{\tau }_2},$$ (4)

where mean pointer adjustments are used as estimates of the lateral position $\propto$.

The value of $c_0$ was then estimated using those values of $c_1$ and pointer adjustments from experiments using both onset and ongoing components

$$c_0=\frac{\propto -b}{{\tau }_0-b}$$ (5)

with

$$b=\left[(c_1{\tau }_1)+(1-c_1)\hspace{0.17em}{\tau }_2\hspace{0.17em}\right].$$

Using the subject-dependent values of $c_1$ from Table I, we examined the consistency of $c_0$ estimates from the conditions of experiments 1 and 2.

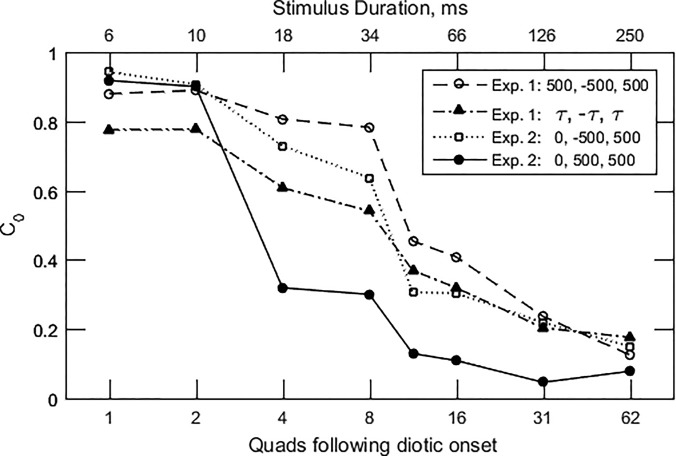
Figure 7 shows subject-averaged values of $c_0$ for four sets of data. Let us consider first the two sets for which τ₁ and τ₂ alternated between ±500 μs in the ongoing part of the stimulus, those labeled “Exp. 1: 500, −500, 500” (open circles), and “Exp. 2: 0, −500, 500” (open squares). As discussed earlier, this pair of conditions contrasts an onset ITD equal to the ongoing lag ITD with an onset ITD midway between the lead and lag ITDs. Their $c_0$ functions follow similar courses, beginning at about 0.9 at short durations, declining to 0.1 at 250 ms duration, and crossing the $c_0$ = 0.5 threshold at roughly 40 ms. This similarity suggests that, for a given ongoing stimulus, onset dominance is not strongly dependent on the magnitude of the onset ITD.

FIG. 7.

Onset-weighting parameter $c_0$ as a function of the number of quads in the ongoing part of the stimulus. The numbers in the legend indicate the values of τ₀, τ₁, and τ₂ (and their opposite signs) for the data summarized.

Next consider the set of data labeled “Exp. 2: 0, 500, 500” (filled circles), which had an ongoing part with a consistent ITD. That function begins and ends at approximately the same points as the functions for alternating ongoing ITDs, but it crosses $c_0$ = 0.5 at about 15 ms. This difference suggests a stronger contribution from the ongoing part, presumably due to the consistency of its ITDs.

The fourth set of $c_0$ estimates are based on all the data of experiment 1. This function, “Exp 1: τ, −τ, τ” (filled triangles), is a transformation of the average of the normalized lateral position data in Fig. 3, along with $c_1$.¹ This set is similar to the others that are based on alternating ongoing ITDs, but with clearly lower values at short durations. These lower values can be traced to the left/right asymmetry in the data at short durations, with more central adjustments with τ₀ > 0.

Overall, the three $c_0$ functions that are based on alternating ongoing ITDs are similar enough (discounting the low values at short durations for the fourth set) to conclude tentatively that, for alternating-ITD ongoing stimuli, onset dominance does not depend strongly on the relation between onset ITD and lead or lag ITD, or on the magnitude of the ITDs. In comparison, the function based on stimuli with consistent ongoing ITDs exhibits a transition duration (at $c_0\hspace{0.17em}$ = 0.5) that is clearly smaller than those for the other three. This difference suggests that the consistent ongoing ITD is a stronger counterweight to the onset than is the alternating ongoing ITD.

VI. DISCUSSION

The purpose of this study was to determine the relative contributions of onset and ongoing interaural cues to the lateralization of sounds of varying duration presented via headphones. Specifically, this study investigated the contribution of the ITD of a single binaural noise burst at the beginning of a noise-burst train in relation to the ITDs of the bursts in the ongoing signal that ranged in duration between 4 and 250 ms. For ongoing stimuli with alternating ITDs, the point at which the onset and ongoing ITDs contributed equally was between 32 and 64 ms, across subjects and conditions. The strength of onset dominance was largely independent of whether the initial ITD matched the ITDs of the ongoing signals, although it may well be dependent on a variety of other stimulus parameters not manipulated in this study, including, for example, the number and delay of “reflections” simulated by the lagging noise tokens. For ongoing stimuli with a fixed, consistent, ITD, the duration for equal contributions was about 15 ms, indicating a stronger ongoing influence than that for stimuli with alternating ITDs.

One noteworthy aspect of the raw data for stimuli with alternating ongoing ITDs (Fig. 2) is the asymmetric pattern of pointer adjustments with durations up to 34 ms. With onset ITDs leading to the right (positive τ₀) pointer adjustments for all three subjects were more central than when the stimulus was swapped left/right (negative τ₀). This held true until τ₀ was between 400 and 500 μs, where it quickly rose to be close to τ₀. Such asymmetries are not unexpected given previous results with stimuli that evoke the precedence effect (Yost and Soderquist, 1984; Clifton and Freyman, 1989; Shinn-Cunningham et al., 1993; Grantham, 1996). We can offer no explanation for left/right asymmetries, but do note that they tend to be observed with stimuli that carry conflicting cues.

Several other studies have examined the relative contributions of onset and ongoing parts to the lateralization of sounds and they, along with the present study, point to several factors that affect the trade. The primary factor studied here, the duration of the ongoing part, is a clear determinant of its contribution to lateralization in relation to the onset and has been the subject of study for a variety of stimulus types and conditions (e.g., Tobias and Schubert, 1959; Perrott and Baars, 1974; Abel and Kunov, 1983; Rakerd and Hartmann, 1986; Houtgast and Aoki, 1994; Saberi, 1996; Buell et al., 2008; Donovan et al., 2012; Stecker and Bibee, 2014). As mentioned previously, another factor evident in the current results is the consistency of the ongoing ITD, with consistent-ITD ongoing stimuli contributing more to lateralization (at shorter durations) than stimuli with alternating ongoing ITDs.

For stimuli with inconsistent ongoing ITDs, an additional factor affecting the contribution of the ongoing part is the delay between lead/lag components. Using 250-ms trains of quads, but with no opposing initial ITD [like the stimuli in Fig. 4(A) with the onset burst absent], Freyman et al. (2010) found that presenting the stimulus with an abrupt onset compared to a slow rise had a much stronger effect with a 10-ms lag than with a 2-ms lag. Thus, in the condition where ongoing precedence was weaker (10-ms lag delay), the contribution from the onset ITD was stronger.

Periodicity of the ongoing stimulus also appears to be an important factor. In contrast to what was observed here with ongoing aperiodic stimuli, where onset influences are rather small for the longer durations, there is evidence of overwhelming onset dominance for longer-duration periodic click trains and frozen noise burst trains, even when the ongoing delays are consistent (Saberi and Perrott, 1995; Freyman et al., 1997; Freyman et al., 2010; Balakrishnan and Freyman, 2002). In some conditions, the lateralization of an entire ongoing stimulus of, say, 250 ms, is almost completely controlled by the very first ITD even if the ITD of the rest of the signal is consistently opposite the initial ITD. These phenomena observed under headphones are likely related to the well-known Franssen effect in the sound field, mentioned earlier, in which the spatial location of an initial transient controls the localization of a much longer periodic sound (Franssen, 1962; Hartmann and Rakerd, 1989; Yost et al., 1997; Dent et al., 2004; Dent et al., 2007).

Several factors within ongoing periodic stimuli are important determinants of onset dominance. Using measurement methods that estimate the effective weights associated with each click in a click train (not lead/lag pairs), previous research has shown a clear dependence on inter-click interval (ICI) (Saberi, 1996; Brown and Stecker, 2010, 2011; Stecker et al., 2013). They find a strong weight attached to the initial click with a 1–2 ms inter-click interval, with decreasing initial weight at longer intervals. Consistent results showing weaker onset influence with longer inter-stimulus intervals have been seen in other lateralization paradigms (e.g., Saberi and Perrott, 1995; Freyman et al., 1997). One possible explanation for the effect of ICI is that at longer ICI's each click is processed more like an onset click, whereas at short ICI's successive clicks are subject to binaural adaptation (Hafter et al., 1988). Hartmann (1983) and Hartmann and Rakerd (1989) suggested that the relative sparseness or density of a periodic sound's spectrum, particularly in relation to broad spectrum onset transients, affects its resistance to onset dominance, with sparser spectra being more vulnerable. Because longer inter-click intervals create denser spectra, it is difficult to untangle temporal from spectral interpretations of the effect of click rate. Both types of explanations may be in play. Freyman et al. (1997) showed greater onset dominance for a spectrally sparse quasi-periodic complex tone than a spectrally dense tone, consistent with the spectral density hypothesis of Hartmann and Rakerd.

Less thoroughly studied are variations in perception that occur across different periodic stimuli with the same interclick interval but different values of the consistent ongoing ITD. For example, Freyman et al. (2010) observed much weaker onset dominance for periodic trains of bursts with a 0-μs ITD than with a 500-μs ITD. They speculated that even though both stimuli have clear spatial percepts without an abrupt onset, the short inter-burst interval of 2 ms employed in the study may have created a subtle ambiguity at the level of binaural processing for the stimuli with 500-μs ITD. This idea arises from the fact that the 0-μs ITD creates a central cross-correlation peak while the 500-μs ITD creates laterally opposing peaks at +500 μs and −1500 μs. Freyman et al. (2010) proposed that this centrality difference (Stern et al., 1988) may cause the 500-μs ITD signal to be more vulnerable to onset dominance.

However, this notion of ambiguity must be interpreted carefully. For example, Freyman et al. (1997) observed that an uncorrelated noise of 250-ms duration appears uninfluenced by a brief initial coherent noise burst. One instead hears a lateralized initial transient followed by an extended diffuse image. Perhaps this is because, while the perception of an uncorrelated noise is far from punctate, it is not fragile or ambiguous in the sense that it could be perceived in two or more different ways. This result, along with the present results and previous reports (Buell et al., 1991; Freyman et al., 2010), reinforces an important distinction—that ongoing stimuli with ambiguous or “fragile” intracranial images may be vulnerable to onset dominance, while those with diffuse but robust percepts (such as uncorrelated noise) are less likely to be vulnerable.

The factors discussed so far have been those that affect the strength of the ongoing part of the stimulus. But there can also be differences in how onsets are created that likely affect their potency. The relation between data from Tobias and Schubert (1959) and the current results illustrates this difference. Tobias and Schubert (1959) measured the relative effect of onset and ongoing cues for wideband noise as a function of duration. They imposed an ongoing delay in the waveform to one ear, but gated the delayed channel on before the ongoing lead stimulus, placing the gating and ongoing delays in opposition. Results showed a very weak onset effect, with the gating delay needing to be seven times larger than the ongoing delay to offset its effect when the stimulus was only 30 ms in duration. Figure 7 of the current study suggests that the ratio of ongoing to onset contribution is only about two to one ($c_0$ ≈ 0.33) for stimuli that are most comparable to those of Tobias and Schubert (8 quads, 34 ms, with a consistent ongoing ITD). This difference, seven to one versus two to one, is likely due in part to the difference in how the onset delay was imposed—a gating delay only in their case, and a whole-waveform delay (envelope and fine structure delayed equally) in the current paper. Zurek (1993) and Buell et al. (2008), among others, have stressed the importance of how the onset is configured and defined. Zurek (1993) suggested that many of the differences observed across studies in the strength of onset capture can be interpreted by assuming that whole waveform delays are more potent than either a gating delay alone or a fine structure delay alone.

Additional, if less direct, evidence of the importance of onsets relative to ongoing parts of sounds comes from studies that have measured ITD or ILD sensitivity. These studies have shown less than expected improvement as a function of stimulus duration, suggesting that the earliest part of the signal contributes more information than later parts (e.g., Houtgast and Plomp, 1968; Hafter and Dye, 1983). Other studies have used time varying ITDs and ILDs and have obtained discrimination results supporting greater sensitivity to these cues near signal onset (Stecker and Brown, 2012; Stecker and Bibee, 2014; Diedesch and Stecker, 2015). Yost (2016), using a localization paradigm, recently showed no improvement in accuracy as duration increasing from 25 to 450 ms. Other studies have directly probed ITD or ILD sensitivity using temporal segments embedded within a longer noise and have found best sensitivity at onset, followed by a period of very poor sensitivity, followed by gradual improvement in sensitivity tens of ms after onset (Zurek, 1980; Akeroyd and Bernstein, 2001). It is not yet certain whether these measurements of sensitivity reflect the same processes as lateralization and localization measures of onset dominance. Nor is it clear how they relate to a well-known benefit of binaural hearing—spatial unmasking. Balakrishnan and Freyman (2002) found that a pulse train with alternating ITDs that was lateralized by its onset pulse to a position different from the masker's was detected no better than a train whose onset lateralized it at the position of the masker.

What is clear is that onsets are expected to be important for the accurate localization of sounds under realistic conditions. Given the ubiquity and strength of reflections and masking sounds in our environments, there will almost always be inconsistency between onset and ongoing spatial cues. Determining how the auditory system combines those cues should lead to a better understanding of localization performance in real world settings.