A review on neuroimaging-based classification studies and associated feature extraction methods for Alzheimer’s disease and its prodromal stages

Abstract

Neuroimaging has made it possible to measure pathological brain changes associated with Alzheimer’s disease (AD) in vivo. Over the past decade, these measures have been increasingly integrated into imaging signatures of AD by means of classification frameworks, offering promising tools for individualized diagnosis and prognosis. We reviewed neuroimaging-based studies for AD classification and mild cognitive impairment, selected after online database searches in Google Scholar and PubMed (January, 1985 to June, 2016). We categorized these studies based on the following neuroimaging modalities (and sub-categorized based on features extracted as a post-processing step from these modalities): i) structural magnetic resonance imaging [MRI] (tissue density, cortical surface, and hippocampal measurements), ii) functional MRI (functional coherence of different brain regions, and the strength of the functional connectivity), iii) diffusion tensor imaging (patterns along the white matter fibers), iv) fluorodeoxyglucose positron emission tomography (metabolic rate of cerebral glucose), and v) amyloid-PET (amyloid burden). The studies reviewed indicate that the classification frameworks formulated on the basis of these features show promise for individualized diagnosis and prediction of clinical progression. Finally, we provided a detailed account of AD classification challenges and address some future research directions.

1. Introduction

Alzheimer’s disease (AD), the most prevalent form of dementia, is expected to affect 1 out of 85 people in the world by the year 2050 (Brookmeyer et al., 2007). The pathophysiology of AD is increasingly becoming clearer. The brain of an AD patient accumulates abnormal proteins (Aβ and tau) in the form of amyloid plaques and neurofibrillary tangles, eventually resulting in loss of neurons (Frisoni et al., 2010; Jagust, 2013). Brain changes due to AD occur even before amnestic symptoms appear (Buckner, 2004), and occur in a pattern that typically includes the temporal lobe and hippocampus (Braak, Braak, 1991). It has been suggested that this inevitable atrophy can be a valuable marker of neurodegeneration (Frisoni et al., 2010), as measured with structural magnetic resonance imaging (sMRI). Further alterations in function, connectivity and metabolism can be detected using functional MRI (fMRI) (Agosta et al., 2012; Binnewijzend et al., 2012; Dennis, Thompson, 2014; Fan et al., 2011; Fox, Raichle, 2007), and fluorodeoxyglucose positron-emission tomography (FDG-PET) (Gray et al., 2012; Padilla et al., 2012; Pagani et al., 2015; Teipel et al., 2015; Toussaint et al., 2012). However, the subtleties of the changes in early AD stages make it difficult to distinguish patterns easily by conventional radiologic readings or even by quantitative analysis. Thus, it remains challenging to establish reliable markers for diagnosing and monitoring disease progression in the early stages and on an individual basis.

Numerous neuroimaging studies have used region of interest (ROI)-types of analyses to investigate subtle changes associated with AD (Chetelat, Baron, 2003; Lerch et al., 2008). Such studies rely solely on prior knowledge to guide the selection of ROIs and features, thus ignoring brain changes outside the studied region(s) and failing to discover new knowledge. Machine learning offers a systematic approach in developing sophisticated, automatic, and objective classification frameworks for analyzing high-dimensional data and can learn complex and subtle patterns of change across various imaging modalities (Sajda, 2006). Typically, a classification framework includes at-least feature extraction and classification algorithm to build predictive models that facilitate the automation of medical decision support (Chiang, Pao, 2016) and provide increased objectivity in these decisions. Furthermore, classification frameworks can be used to develop imaging markers or indices (Davatzikos et al., 2008) with high sensitivity and specificity in individuals (Sajda, 2006) that can summarize the imaging profile of a subject into a single meaningful value (Habes et al., 2016b). This creates a more individualized, patient-tailored approach (Ithapu et al., 2015), which is imperative in the current age of personalized medicine because it allows further consideration of genetic or life-style risks, by utilizing advanced computational power (Habes et al., 2016a; Habes et al., 2016b; Habes et al., 2016c).

In recent years, a large body of research has been published on neuroimaging-based computer-aided classification of AD and its prodromal stage, mild cognitive impairment (MCI). Motivated by this rapid proliferation of AD/MCI classification studies and the lack of literature summarizing different AD-related features as extracted from neuroimaging data and classification algorithms, we present an overview of pertinent advances in this field. We summarize key representative studies on neuroimaging-based classification of AD/MCI and provide a brief account of the main aspects of these studies, such as study population, type of features, the adopted classification algorithm, and the reported classification success rates. Furthermore, we highlight several bottlenecks (i.e. limited sample size and variability in data settings across the different studies) and discuss the generalizability and reproducibility of existing AD classification studies, as well as the important and largely unexplored issue of heterogeneity in AD.

Recent review papers (Arbabshirani et al., 2017; Falahati et al., 2014) reported studies on MRI-based classification of AD and MCI, limiting AD classification to MRI only. Pathological brain changes related to AD can be captured via various imaging modalities, such as FDG-PET and amyloid-PET, therefore, a comprehensive review on AD classification should not be limited to MRI only. This review is further unique in that it focuses exclusively on those studies that have extensively leveraged cross-validation strategies to estimate the performance of their classification frameworks. Cross-validation is generally designed to achieve independent training and test data for a classification algorithm and defined as split the data once (split-in-train-test) or several times (k-fold cross-validation) to obtain an unbiased estimate of the classification performance of the algorithm and avoid over fitting (Arlot, Celisse, 2010; Kohavi, 1995). In the split-in-train-test, data is randomly divided into independent training and test subsets, optimally with matched demographic characteristics. The training subset is used solely for the learning procedure of the classification algorithm and the test subset is used to estimate the performance of the trained classification algorithm. In k-fold, data is divided into k-folds and a classification algorithm is tested on k^th fold after being trained on k-1 folds in k^th iteration. Furthermore, we provide in-depth detail about AD-related feature extraction methods from various neuroimaging modalities, important information that is mostly lacking in existing review papers.

2. Selection criteria

We searched in PubMed and Google Scholar, from January 1985 to June 2016, and identified 409 studies based on the given search criteria. We included original peer-reviewed research studies that exclusively used cross-validation strategies to estimate the performance of their classification frameworks. In addition, studies conducted for method comparisons and studies not focusing primarily on AD classification were excluded from this review. Finally, this criterion resulted in 81 studies that were reviewed and presented here. A more thorough explanation of the search and screening process, and databases generated from the search in Google Scholar and PubMed are provided in the Supplementary Material.

3. Classification frameworks for Alzheimer’s disease and its prodromal stages

Over the past decade, classification frameworks have been used successfully to analyze complex patterns in neuroimaging data with a view to the classification of AD and MCI subjects. A classification framework is comprised of four major components: feature extraction, feature selection, dimensionality reduction, and feature-based classification algorithm. Feature extraction and classification algorithm are the minimally required components, as shown in Figure 1, whereas other components can be applied as needed. The studies having minimal required components of classification framework were considered potential candidates for inclusion in the paper provided meeting other criteria. In the feature-extraction process, AD-related features from various neuroimaging modalities, such as structural MRI, functional MRI, diffusion tensor imaging (DTI), amyloid-PET, and FDG-PET, are extracted from the training subjects. The term ‘features’ refers to the post-processing applied on raw medical imaging data to derive more informative measures. The examples of such derived measures include regional tissue densities, regional cortical thickness, etc. These derived measures can vary from millions (when all the voxels are used as features) to a few (when a few representative measures are extracted from the brain). The features extracted from various modalities can be used in isolation or combined to make use of the complementary information provided by several modalities. A classification algorithm (predictive model) is then trained on the extracted features to provide diagnostic support in predicting cognitively normal (CN) and diseased subjects.

Figure 1.

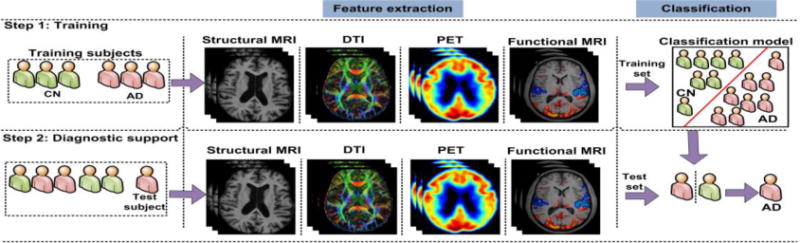
A top-level layout of neuroimaging-based classification framework for AD classification

In the aforementioned classification framework, the selection of an appropriate modality for obtaining imaging data and accurate feature extraction for AD classification is often more important than the selection of the underlying classification algorithms in order to achieve higher prediction rates (Sabuncu, Konukoglu, 2015). Therefore, we provided more details on feature extraction for the included studies in this review. Overall, the paper is divided into various sections, where each section focuses on features extracted from one particular imaging modality, such as structural MRI, functional MRI, DTI, and PET. A section on multimodal AD/MCI classification studies, which describes how features extracted from various imaging modalities are combined to utilize their complementary information, is included at the end.

3.1. Structural MRI-based studies

Cerebral neurodegeneration is characterized by early damage to synapses, followed by degeneration of axons and ultimately, atrophy of the dendritic tree and perikaryon (Serrano-Pozo et al., 1101). This neurodegeneration process is more severe in certain parts of the brain, such as the right and left hippocampus, temporal and cingulate gyri, and precuneus (Baron et al., 2001; Busatto et al., 2003; Frisoni et al., 2002; Ishii et al., 2005). The inevitable atrophy, caused by neurodegeneration, is generally measured using structural MRI, and serves as a valuable marker of the stage and aggressiveness of the neurodegenerative aspect of the AD pathology in the individual (Frisoni et al., 2010; Vemuri, Jack, 2010). The atrophic process in these regions leads to profound structural changes in the brain, such as thinning of the cortical surface, structural variation in several brain regions and variation in the regional tissue densities, and have been demonstrated in several neuroimaging-based studies of AD classification. A top-level breakdown of these studies is shown in Figure 2. Three main feature extraction methods for assessing structural variation are considered: i) density maps, ii) cortical surface, and iii) pre-defined regions-based methods.

Figure 2.

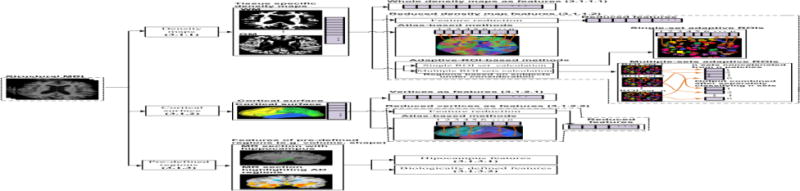
A top-level breakdown of structural MRI-based classification studies for AD classification

3.1.1. Density map-based methods

Density map-based methods quantify patterns of atrophy by utilizing density maps of white matter (WM), grey matter (GM), and cerebrospinal fluid (CSF), which are generated by methods such as voxel-based morphometry (VBM) (Ashburner, Friston, 2000) or regional analysis of volumes examined in normalized space (RAVENS) maps (Davatzikos et al., 2001). Depending on how the density maps are used, these methods can be further divided into two categories: i) whole density maps as features (DMAF), and ii) reduced density map features. The studies that fall within these categories are listed in Table 1.

Table 1.

A brief description of the datasets used for the validation of density map-based AD classification frameworks

Study	Subjects					Type	Classification algorithm	Database	Classification accuracy
	AD	MCI	pMCI	sMCI	CN				AD/CN	MCI/CN	sMCI/pMCI
(Kloppel et al., 2008)	20	—	—	—	20	DMAF	SVM	RM	95.00	—	—
(Kloppel et al., 2008)	14	—	—	—	14	DMAF	SVM	DRCUCL	92.90	—	—
(Kloppel et al., 2008)	33	—	—	—	57	DMAF	SVM	RM	81.10	—	—
(Casanova et al., 2011)	49	—	—	—	49	DMAF	LSR	ADNI	85.70	—	—
(Hinrichs et al., 2009)	89	—	—	—	94	DMAF	LPBM	ADNI	82.00	—	—
(Termenon, Graña, 2012)	49	—	—	—	49	DMAF	RVM,SVM	OASIS	83.00	—	—
(Adaszewski et al., 2013)	108	—	142	61	137	DMAF	SVM	ADNI	—	—	62.00
(Plant et al., 2010)	32	—	9	15	18	DMAF	SVM,BS,VFI	CPLMU	92.00	—	75.00
(Moller et al., 2016)	84	—	—	—	94	DMAF	SVM	ACVUMC+ACEUMC	88.00	—	—
(Liu et al., 2013)	86	—	97	93	137	SUFR	RLR,SVM,LDA	ADNI	90.00	—	68.00
(Salvatore et al., 2015)	137	—	76	134	162	SUFR	SVM	ADNI	76.00	72.001	66.00
(Beheshti, Demirel, 2015)	130	—	—	—	130	SUFR	SVM	ADNI	89.65	—	—
(Magnin et al., 2009)	16	–	—	—	22	Atlas	SVM	Internal	94.50	—	—
(Fan et al., 2008a)	56	88	—	—	66	S-ROI	SVM	ADNI	94.30	—	—
(Davatzikos et al., 2008)	—	15	—	—	15	S-ROI	SVM	BLSA	—	90.00	—
(Misra et al., 2009)	56	—	27	76	66	S-ROI	SVM	ADNI	—	—	81.50
(Min et al., 2014)	97	—	117	117	128	M-ROI	SVM	ADNI	91.64	—	72.41
(Liu et al., 2015)	97	—	117	117	128	M-ROI	SVM	ADNI	92.51	–	78.88

SUFR = Supervised/unsupervised feature reduction

S(M)-ROI = Single(Multiple)-set adaptive ROIs

LSR = Large scale regularization

VFI = Voting feature intervals

BS = Bayes statistics

OASIS = Open access series of imaging initiative (Chan et al., 2003)

RM = Rochester, Minnesota, USA

DRCUCL = Dementia research center, University College London

CPLMU = Clinic of psychiatry at the Ludwig Maximilian university, of Munich

ACVUMC = Alzheimer center of the VU university medical center

ACEUMC = Alzheimer center of the Erasmus university medical center

¹= cMCI/CN

In all the tables, blank entry (–) means information was not provided by the authors or is irrelevant.

3.1.1.1. Whole density maps as features (DMAF)-based methods

This method is centered on the construction of a feature vector by utilizing the density maps for WM, GM, or both for classification.

In an earlier study, the GM density map of the entire brain together with a support vector machine (SVM) achieved promising AD classification (Kloppel et al., 2008). In that study, relatively lower GM density was found in the hippocampus of AD subjects, which was a strong indicator of hippocampal atrophy, consistent with previous research (Frisoni et al., 2002). In addition, GM maps have been used for AD classification, by employing a large-scale regularization approach (Casanova et al., 2011) and spatially augmented linear programming boosting method (LPBM) (Hinrichs et al., 2009), and to predict conversion from MCI to AD, by using SVM (Adaszewski et al., 2013). Termenon et al., used GM density maps to develop feature vectors for AD classification (Termenon, Graña, 2012) by employing a two-stage classification framework, wherein a relevance vector machine classifier (Tipping, 2001) was used in the first stage. The subjects that fell into the low confidence interval of the classifier were used as the input for the second classifier in the prediction. SVM, nearest neighbor, relevance vector machine, and learning vector quantization were used as second-stage classifiers, however, SVM was better. Recently, Moller et al. also used GM density map for SVM-based AD classification (Moller et al., 2016).

Furthermore, the Jacobian determinants, calculated from these density maps, have been used as features for predicting conversion from MCI to AD by using SVM, Bayes statistics, and voting feature interval classifiers (Plant et al., 2010).

These methods achieved a ≥ 81% accuracy in AD classification, and a ≥ 62% accuracy in prediction of AD conversion. Furthermore, the two-stage framework proposed by Termenon et al. demonstrated superior classification accuracy (from 77% to 87%) than its single-stage-based counterpart (Termenon, Graña, 2012).

3.1.1.2. Reduced density map feature-based methods

DMAF-based methods suffer the drawback of dimensionality, as the numbers of features are typically larger than, or comparable to, the number of the available subjects. When the number of features is high relative to the number of subjects in the training set, it is possible that classification rules yielding high accuracy on the training set were originated only by chance. This can lead many classification algorithms to select classification rules that could fail to generalize to new data (Vapnik, 1999). Consequently, features have been reduced using supervised or unsupervised feature-reduction methods, or they have been extracted from pre-defined atlases and adaptive regions in order to reduce dimensionality.

• Supervised/unsupervised feature-reduction-based methods

These methods essentially focus on distilling large-sized density maps to fewer, meaningful features in a supervised or unsupervised fashion. Among the unsupervised methods, Salvatore et al. used principal component analysis (PCA) to reduce the dimensions of WM and GM density maps. The reduced density maps were used for SVM-based AD classification and prediction of conversion from MCI to AD (Salvatore et al., 2015). In addition, Liu et al. used local linear embedding method to transform multivariate regional brain volume and cortical thickness MRI data to a locally linear space, with fewer dimensions, while also utilizing the global nonlinear data structure (Liu et al., 2013). The embedded brain features were then used to train classification algorithms such as regularized logistic regression (RLR), SVM, and linear discriminant analysis (LDA).

On the other hand, Beheshti et al. proposed reduction of the dimensions of GM maps in a supervised fashion (Beheshti, Demirel, 2015). They used the intensity distribution of voxels of GM maps, rather than using the intensities of all the voxels of GM maps, as features. The optimal number of bins in the intensity distribution was selected based on the Fisher criterion maximization between AD and CN subjects, and the resultant intensity distribution-based features were used for SVM-based AD classification.

• Atlas-based methods

These methods rely on parcellation of brain image into several anatomical regions based on pre-defined anatomically labeled atlases (such as automated anatomical labeling (AAL) atlas (Tzourio-Mazoyer et al., 2002) and laboratory of neuroimaging (LONI) atlas (Shattuck et al., 2008)), followed by extraction of features from those particular regions. For example, Magnin et al., used AAL to parcellate the brain image into 116 regions, and then used the relative weight of the GM, compared to that of the WM and CSF, for each parcellated region to develop a feature vector for SVM-based AD classification (Magnin et al., 2009).

• Adaptive-ROI-based methods

Traditionally, atlas-based methods are used to obtain regional measurement of anatomical features and to investigate abnormal tissue structures in disease conditions. However, in practice, prior knowledge of abnormal regions is not always available. Even when a prior hypothesis can be made about specific ROIs, a region demonstrating abnormality might be part of a single ROI, or span multiple ROIs, thereby potentially reducing the significance of further analysis. Therefore, adaptive ROIs have been calculated to reduce the dimensions of density maps and to resolve this issue. Furthermore, depending on the number of sets of adaptive ROIs that are calculated, these methods can be divided into two categories: i) single-set adaptive ROIs, and ii) multiple-set adaptive ROIs.

1. Single-set adaptive ROIs

In this method, subjects are registered to one particular atlas, and adaptive ROIs and corresponding regional volumetric measures are calculated in that atlas space. In earlier work, Davatzikos et al. calculated RAVENS density maps and used a watershed clustering algorithm-based method (Fan et al., 2007) to calculate an adaptive set of ROIs for SVM-based AD classification, using the multi-centric ADNI (Alzheimer’s disease neuroimaging initiative (Weiner et al., 2015)) dataset. They reported a high cross-validated classification accuracy of 94.30%, with a pattern involving many temporal lobe GM regions, peri-hippocampal WM, and CSF (Fan et al., 2008a). The trained SVM in this study was used to determine the spatial pattern of abnormality for recognition of early AD (SPARE-AD) index, which was later tested independently in CN and MCI subjects of the Baltimore longitudinal study of aging (BLSA) (Davatzikos et al., 2011) dataset. In subsequent studies, the same classification framework was used for MCI classification (Davatzikos et al., 2008) and prediction of conversion from MCI to AD (Misra et al., 2009).

2. Multiple-set adaptive ROIs

In this method, subjects are registered to multiple atlases, and adaptive ROIs and corresponding regional volumetric measures are calculated in each atlas space to overcome the inherent bias associated with one atlas. For example, Min et al. derived multiple atlases from the non-overlapping clusters of subjects (Min et al., 2014), obtained using affinity propagation (Frey, Dueck, 2007). They registered subjects to the atlases and adaptively calculated a set of ROIs and volumetric features in each atlas space. The top-most K discriminating features calculated from each atlas space were combined for SVM-based classification. Subsequently, Liu et al. argued that the features extracted from K sets of adaptive ROIs are different representations of the same subject (Liu et al., 2015), and should not be concatenated, as in a previous study (Min et al., 2014). To resolve this, Liu et al. registered subjects to different selected atlases and extracted features from adaptive regions of each atlas-registered image, viewing that image as the main source, and all other atlas registered-images as adjunctive sources (Liu et al., 2015). SVM was separately trained on features extracted from each set and the results of multiple sets were combined using majority voting.

The multiple-set adaptive ROIs-based methods were quite effective, and improved AD/CN classification from 84.18% to 92.51% (Liu et al., 2015) and progressive MCI (pMCI)/stable MCI (sMCI) classification from 70.06% to 78.88% (Liu et al., 2015) compared to single-set adaptive ROIs-based methods.

3.1.2. Surface-based methods

AD patients generally show changes in temporal and parietal regions of the cortical surface (Bakkour et al., 2009; Dickerson et al., 2009; Dickerson et al., 2011). Although these changes are not easily visible or measureable in the early stages of AD, classification frameworks have been able to detect subtle changes in the cortical surface by analysis of complex cortical surface data, in a way that is complementary to regional volumetric maps extracted in a voxel-wise manner. Cortical surface measures are extracted from all the vertices of a surface. These measures are either used directly or are reduced by applying feature reduction methods, thereby leading to two main categories: i) vertices as features-based methods, and ii) reduced vertices as features-based methods. The studies of AD diagnosis support employing cortical surface-based features are listed in Table 2.

Table 2.

A brief description of the datasets used for the validation of cortical thickness-based AD classification frameworks

Study	Subjects					Type	Classification algorithm	Database	Classification accuracy
	AD	MCI	pMCI	sMCI	CN				AD/CN	AD/MCI	MCI/CN	sMCI/pMCI
(Li et al., 2014b)	—	24	—	—	26	VAF	SVM	XWH	—	—	80.00	—
(Cho et al., 2012)	128	—	72	131	160	RV	LDA	ADNI	88.33	—	—	71.21
(Park et al., 2012)	25	25	—	—	50	RV	SVM	OASIS	90.00	90.00	86.00	—
(Park et al., 2013)	—	30	12	—	30	RV	SVM	ADNI	—	83.001	90.00	—
(Desikan et al., 2009)	65	57	—	—	94	Atlas	LR	ADNI	95.00	—	95.00	—
(McEvoy et al., 2009)	84	175	—	—	139	Atlas	LDA	ADNI	89.00	—	—	—
(Oliveira et al., 2010)	14	—	—	—	20	Atlas	SVM	DPUSP	88.20	—	—	—
(Eskildsen et al., 2013)	194	—	340	134	226	Atlas	LDA	ADNI	86.70	—	—	71.10
(Eskildsen et al., 2013)	—	—	29 (36)	134	–	Atlas	LDA	ADNI	—	—	—	77.30
(Eskildsen et al., 2013)	—	—	61 (24)	134	—	Atlas	LDA	ADNI	—	—	—	73.00
(Eskildsen et al., 2013)	—	—	128 (12)	134	—	Atlas	LDA	ADNI	—	—	—	74.50
(Eskildsen et al., 2013)	—	—	122 (06)	134	—	Atlas	LDA	ADNI	—	—	—	80.90
(Wee et al., 2013)	198	—	89	111	200	Atlas	Multi-kernel SVM	ADNI	92.35	79.24	83.75	75.05
(Lillemark et al., 2014)	114	240	—	—	170	Atlas	LDA	ADNI	87.70*	76.60*	78.40*	—

RV = Reduced vertex-wise

XWH = Xuan Wu Hospital, Beijing, China

D Department of s chiatr, niversit of ao aulo, ao aulo, razil

¹= prediction of conversion from MCI to AD

^*shows AUC.

The first entry for (Eskildsen et al., 2013) shows the classification accuracy by using all the sMCIs and pMCIs. The remaining entries show the classification between sMCI and different sets of pMCI subjects, divided according to their time of conversion from sMCI to pMCI. Numbers of months are shown in parenthesis against pMCI subjects.

3.1.2.1. Vertices as features-based methods

This family of AD classification frameworks solely relies on the features calculated from all the vertices of a cortical surface. For instance, Li et al. calculated a variety of morphological features, including volumetric (cortical thickness, surface area, and GM volume) and geometric (sulcal depth, metric distortion, and mean curvature) measures, at each vertex on the pial surface (Li et al., 2014b), which were used for SVM-based MCI classification.

3.1.2.2. Reduced vertices as features-based methods

The use of cortical surface features of all the vertices suffers from the same dimensionality drawback, for reasons similar to those mentioned in Section 3.1.1.2. Consequently, these features have either been reduced by means of feature-reduction methods, or extracted from regions of pre-defined atlases.

• Supervised/unsupervised feature-reduction-based methods

In these methods, the dimensions of long feature vector comprising features of all the vertices of the brain are reduced by applying supervised or unsupervised feature reduction methods. For example, Cho et al. converted thickness data to a frequency domain and achieved lower dimensionality by filtering out high-frequency (noise) components (Cho et al., 2012). They employed an incremental learning-based LDA for reduced dataset-based AD classification. Park et al. addressed this issue by modeling the cortical surface using three-dimensional (3D) meshes and extracted cortical thickness parameterized by these meshes (Park et al., 2012) for SVM-based AD and MCI classification. Later, Park et al. applied this classification framework to longitudinal data for the early detection of AD (Park et al., 2013). They trained SVM on MCI and CN subjects, and tested it on the subjects who converted to AD, using the images of the subjects taken one time-point before the actual conversion. They achieved promising early prediction of conversion (83%) from MCI to AD.

• Atlas-based methods

In these methods, the original brain images are registered to certain standardized stereotaxic spaces (Fischl et al., 1999), and cortical maps/features are computed (Fischl, Dale, 2000; Jones et al., 2000; MacDonald et al., 2000) and tessellated into various regions using existing atlas templates (Desikan et al., 2006). Unlike the structural templates discussed in Section 3.1.1.2, which are used in the volume space, these atlas templates are used in the surface space. The features of the tessellated regions are used in feature vector development, which then is used in classification.

Desikan et al. used average cortical thickness of all the tessellated regions for MCI and AD classification (Desikan et al., 2009) using logistic regression (LR). The cortical thickness in the entorhinal cortex and supramarginal gyrus proved to be a better predictor of MCI than the cortical thickness of other regions. Similarly, Oliveira et al. used regional thickness measures and the average thickness of the entire brain for AD classification by means of SVM (Oliveira et al., 2010). They found that the average cortical thickness of the entire brain was a better predictor of AD than the regional thickness features. Wee et al. used regional thickness measures, cerebral cortical GM and associated WM volumes, and correlative features, which were obtained based on the similarity of cortical thickness between pairs of brain regions (Wee et al., 2013). Features were first selected using t-tests, and later using minimum-redundancy and maximum-relevance (mRMR) (Peng et al., 2005) in conjunction with SVM recursive-feature elimination (SVM-RFE). Multi-kernel SVM was used for classification. McEvoy et al. also used average regional cortical thickness and volumetric measures for LDA-based AD classification and prediction of conversion from MCI to AD (McEvoy et al., 2009). Lillemark et al. used the proximity between the center of mass and percentage surface connectivity of different brain regions as features for LDA-based AD and MCI classification (Lillemark et al., 2014).

Recently, Eskildson et al. investigated the prediction of AD conversion by measuring regional thickness at various stages of MCI conversion to AD (Eskildsen et al., 2013). To this end, pMCI subjects were categorized based on time to conversion to AD (6, 12, 24, or 36 months), and each category was classified against sMCI subjects. Features were reduced using mRMR, and LDA was used to determine the classification accuracy. The classification based on stage-specific categories of pMCI subjects demonstrated better accuracy than the overall classification of pMCI and sMCI subjects.

In addition, the efficacy of regional thickness measures was investigated using orthogonal partial least-squares of the latent structures for AD classification in two independent cohorts (ADNI and AddNeuroMed (Lovestone et al., 2009; Lovestone et al., 2007)) and a pool of these cohorts (ADNI + AddNeuroMed) (Westman et al., 2011). Results demonstrated similar patterns of atrophy in two individual cohorts, showing that the key regions involved in AD classification were similar in both cohorts. They further proved similarity in the patterns of atrophy through training the classification algorithm on one cohort and testing it on the other. For example, AD classification derived from training on the AddNeuroMed cohort and testing on the ADNI cohort, and vice versa, led to accuracies of 86.0% and 83.40%, respectively. The individual and pooled cohorts were further used to predict the conversion from MCI to AD. For instance, the classification algorithm trained on the combined cohort classified 71% of the pMCI as AD-like and 60% of the sMCI as CN-like.

The reduced vertices as features-based methods demonstrated better classification accuracy than raw vertices as feature-based methods as shown by improvement of 10–13% for different subject groups (Park et al., 2012). Moreover, the supervised/unsupervised feature reduction-based methods offered better classification accuracy than atlas-based methods. An overall improvement of 2–8% over atlas-based methods was seen for different subject groups (86.67%–88.33% for AD/CN (Cho et al., 2012) and 65.22%–71.21% for pMCI/sMCI (Cho et al., 2012)).

3.1.3. Pre-defined regions-based methods

These methods are based on the prior knowledge of the magnitude and spatial pattern of AD that were acquired by studies previously conducted on histological or imaging data (Baron et al., 2001; Frisoni et al., 2002). Generally, features of some of the important regions that have shown to contain discriminatory AD-related information are extracted and used for classification. The datasets and classification accuracies of the studies using these methods are listed in Table 3.

Table 3.

A brief description of the datasets used for the validation of pre-defined regions-based AD classification frameworks

Study	Subjects					Type	Classification algorithm	Database	Classification accuracy
	AD	MCI	pMCI	sMCI	CN				AD/CN	MCI/CN	sMCI/pMCI
(Wang et al., 2007b)	18	—	—	—	26	Hippocampus	LR	ADRC	81.10	—	—
(Li et al., 2007)	19	—	—	—	20	Hippocampus	SVM	Internal	94.90	—	—
(Gerardin et al., 2009)	23	23	—	—	25	Hippocampus	SVM	HCUDC	94.00	83.00	—
(Shen et al., 2012)	99	—	—	—	138	Hippocampus	Bagged SVM	ADNI	88.30	—	—
(Costafreda et al., 2011)	71	—	22	81	88	Hippocampus	SVM	AddNeuroMed	—	—	80.00
(Sorensen et al., 2016)	101	233	93	140	169	Hippocampus	SVM	ADNI	91.20*	76.40*	74.20*
(Chincarini et al., 2011)	144	—	136	166	189	BSR	SVM	ADNI	97.00*	92.001,*	74.00*
(Tang et al., 2015)	175	—	135	87	210	BSR	LDA	ADNI	—	—	74.77

BSR = Biologically selected regions

ADRC = Alzheimer disease research center, Washington University School of Medicine, St. Louis, Missouri.

HCUDC = Hospital center University De Caen, Caen, France.

¹= cMCI versus CN

^*shows AUC.

3.1.3.1. Hippocampal features

The hippocampus is amongst the few structures of the medial temporal lobe that undergo severe structural changes in AD (Braak, Braak, 1991). The structural variation between the hippocampus of AD and healthy individuals has been studied intensively (Killiany et al., 2002; Wisse et al., 2014). The geometric properties of the hippocampus have been exploited as useful biomarkers in a few AD and MCI classification studies. For example, the shape of the hippocampus, quantified by spherical harmonics (Gerardin et al., 2009), surface-based anatomic mesh modeling (Li et al., 2007), statistical shape modeling (Shen et al., 2012), and large-deformation diffeomorphic metric mapping and PCA (Wang et al., 2007b), has been shown to be an effective biomarker for AD and MCI classification. The shape and volumetric features of the hippocampus have also been combined for SVM-based AD conversion prediction (Costafreda et al., 2011). Interestingly, a study demonstrated superiority of hippocampal texture over reduction in its volume for SVM-based prediction of conversion from MCI to AD (Sorensen et al., 2016).

3.1.3.2. Biologically selected features

AD affects brain regions well beyond the hippocampus, such as atrophy of the entorhinal cortex (Dickerson et al., 2001), expansion of the ventricles (Ridha et al., 2008), and volumetric changes in other subcortical nuclei (amygdala, putamen, caudate, and thalamus) (Madsen et al., 1312; Visser et al., 1999). The analysis of structures beyond the hippocampus may not only improve understanding of the spatial pattern of AD, but may also lead to a more precise diagnosis. Therefore, features of these biologically selected regions are sometimes used directly for classification of subjects into normal and diseased classes. For example, Chincarini et al. used the statistical and textural features of the entorhinal cortex, perirhinal cortex, hippocampus, and parahippocampal gyri (Chincarini et al., 2011). The features of each region were analyzed with a random forest classifier to extract the relevant ones, which were subsequently processed with SVM for prediction of AD conversion. Recently, Tang et al. used shape diffeomorphometry of the left and right amygdala, hippocampus, thalamus, caudate, putamen, globus pallidus, and lateral ventricle for prediction of AD conversion using LDA (Tang et al., 2015).

3.2. Functional MRI-based studies

The neurodegenerative process of AD induces changes in functional connectivity between various regions of the brain (Fransson, 2005; Wang et al., 2007a). These alterations are generally measured while the patient is at rest, using resting-state functional MRI (rs-fMRI). Rs-fMRI, in principle, measures the brain activity by quantifying the blood oxygen level-dependent signal, whereby an increased oxygen level is observed in activated regions of the brain due to increased blood flow. Various rs-fMRI studies have reported the existence of resting-state networks, which are characterized by spatially coherent, spontaneous fluctuations in the blood ox gen level-dependent signal and are made up of regional patterns that are commonly involved in brain functions, such as attention, sensory, or default mode processing (Fox, Raichle, 2007; Seeley et al., 2007). A network that is related to AD and has increasingly received attention is the default mode network (DMN) (Greicius et al., 2003; Greicius et al., 2004) also called the ‘task-negative’ network (anti-correlated to ‘task positive’ network) (Fox et al., 2005; Fransson, 2005), since its activity increases in the absence of a task. AD compromises primary brain targets, such as the DMN, by disrupting their functional activity (He et al., 2007; Li et al., 2002), as well as the functional connectivity between primary targets and the remaining parts of the brain (Wang et al., 2007a; Wang et al., 2006). Some studies have reported that functional changes appear well before the changes in structural MRI become evident (Pievani et al., 2011; Teipel et al., 2015). However, those studies are rare, and additional studies should be conducted to test whether functional MRI changes can appear before structural MRI.

The preliminary evidence of disrupted functional connectivity (Li et al., 2002; Wang et al., 2007a; Wang et al., 2006), and its association with AD have led researchers to hypothesize that proper quantification of the functional connectivity across different brain regions can capture the global distribution of the abnormalities present in AD, and can further aid in AD classification (Chen et al., 2011; Jie et al., 2014). Such quantification involves spatial parcellation of fMRI data according to a structural brain template, and calculation of pair-wise connectivity between the activation in all pairs of regions. The connectivity information, generally defined as the correlation, covariance, or the mutual information between the fMRI time series of the two regions, is stored in an n × n matrix for each subject, where n is the number of brain regions obtained by parcellation. The connectivity information is then used as input for classification. For example, Chen et al. used Pearson correlation coefficient as connectivity metric for Fisher LDA-based AD and MCI classification (Chen et al., 2011). In addition, Challis et al. used covariance as a connectivity metric for Gaussian-process, logistic regression model-based AD and MCI classification (Challis et al., 2015). They showed that the connectivity strength between the medial structures and temporal and sub-cortical regions best classified MCI, and that the connectivity strength between the frontal areas and the rest of the brain best classified AD. It has also been suggested to develop graphs on connectivity matrcies and compute network measures from the graph instead of using raw connectivity matrices. For example, Jie et al., proposed to extract global topology and local connectivity based features from the graph. The least absolute shrinkage and selection operator was used for feature selection, while multi-kernel SVM was used for MCI classification (Jie et al., 2014). Similarly, Khazaee et al. computed integration and segregation measures from the graph, and used Fisher score for feature selection and SVM for AD classification (Khazaee et al., 2015).

Overall, the functional connectivity-based methods demonstrated good classification results (97.00% for AD/MCI (Challis et al., 2015) and 91.90% for MCI/CN (Jie et al., 2014)).

3.3. Diffusion tensor imaging (DTI)-based studies

AD is associated with loss of brain barriers that restrict water motion, thereby compromising the integrity of WM, and leading to abnormal diffusivity patterns (Xie et al., 2006). DTI is used to analyze water diffusion at the microstructural level of the brain for determining the abnormal diffusion pattern of AD. Voxel-based studies showed that AD and MCI subjects have reduced fractional anisotropy (FA) in multiple posterior WM regions (Medina et al., 2006) and increased mean diffusivity (MD) in the posterior occipital–parietal cortex, and right parietal supramarginal gyrus (Rose et al., 2006). ROI-based studies demonstrated higher MD and/or lower FA in the hippocampus (Fellgiebel et al., 2006; Kantarci et al., 2001; Muller et al., 2005; Muller et al., 2007) and posterior cingulate (Choo et al., 2010; Fellgiebel et al., 2005). Interestingly, a previous study suggested that diffusivity measures of the hippocampus are better predictors of MCI conversion than volume (Fellgiebel et al., 2006). Evidence of abnormal and complex diffusivity patterns has led to the hypothesis that these biomarkers can be used for AD classification using advanced classification framework (Selnes et al., 2013). The studies using DTI-based features, summarized in Table 5, can be further divided into three categories, depending on how features are extracted: i) tractography, ii) connectivity network measures, and iii) discriminative voxel selection.

Table 5.

A brief description of the datasets used for the validation of DTI based AD classification frameworks

Study	Subjects					Type	Classification algorithm	Database	Accuracy
	AD	MCI	pMCI	sMCI	CN				AD/CN	MCI/CN	sMCI/pMCI
(Nir et al., 2015)	37	113	—	—	50	Tractography	SVM	ADNI	80.60	68.30	—
(Wee et al., 2011)	—	10	—	—	17	Network	SVM	BIAC	—	88.90	—
(Prasad et al., 2015)	38	—	38	74	50	Network	SVM	ADNI	78.20	62.801, 59.202	63.40
(Dyrba et al., 2013)	137	—	—	—	143	DVS	SVM	EDSD	83.00	—	—
(Dyrba et al., 2015a)	—	—	35	35	25	DVS	SVM	EDSD	—	77.00	68.00

DVS = Discriminative voxel selection

EDSD = European DTI study on Dementia

BIAC = Brain imaging and analysis center, Duke University, North Carolina, USA

For (Dyrba et al., 2015a), pMCI = amyloid+, sMCI = amyloid-

For (Prasad et al., 2015), pMCI = late MCI, sMCI = early MCI

¹_{= CN}/late MCIs

²= CN/early MCIs

3.3.1. Tractography-based methods

In this method, the fibers located by means of tractography are clustered into various fiber bundles, based on an anatomical atlas. The located fibers are reduced to a compact, low-dimensional representation, from which diffusivity measures are calculated for classification. For example, Nir et al. used tractography to locate fibers, then clustered them into 18 fiber bundles based on the 18 regions defined in Johns Hopkins University probabilistic WM tract atlas (Nir et al., 2015). They computed density maps to quantify the number of fibers passing through each voxel, and used the shortest path graph search to reduce fiber bundles to a compact, low-dimensional representation, based on the maximum density path (MDP). These MDPs were registered across subjects, and diffusivity measures of FA and MD, computed along all the MDPs, were used as features for SVM-based AD and MCI classification.

3.3.2. Connectivity network measure-based methods

In this method, DTI images are parcellated into anatomical regions, and several features are calculated from the fibers within these regions. Connectivity networks are developed based on these regions (i.e., features) and a collection of network measures are derived for classification. In this context, Wee et al. parcellated the brain into anatomical regions, and developed connectivity networks based on the regional features of fiber count, averages of on-fiber FA, MD, and three principal diffusivities (Wee et al., 2011). Clustering coefficients of all the regions, computed for all the networks, were used as features. The feature set was reduced by determining the Pearson correlation coefficient, and SVM-RFE was used for MCI classification. Recently, Prasad et al. adopted the same methodology, and developed two connectivity networks based on regional features of fiber count, and flow along the fibers (Prasad et al., 2015). Raw connectivity matrices and various other network measures, such as global efficiency, transitivity, path-length, modularity, radius, and diameter were used for SVM-based classification of early and late MCI subjects.

3.3.3. Discriminative voxel selection-based methods

In this method, discriminative voxels are selected to reduce the dimensionality of DTI data, and diffusion measures of selected voxels are used as features for classification. Dyrba et al. adopted this approach in two of their studies. In the first study, they used PCA and an entropy-based information gain criterion for selecting discriminative voxels, and used diffusion measures of the FA, MD and mode of anisotropy of the selected voxels as features for SVM-based AD classification (Dyrba et al., 2013). In the subsequent study (Dyrba et al., 2015a), they used the same classification framework for classifying MCI subjects, stratified by their positive or negative amyloid burden.

3.4. Positron-emission tomography (PET)-based studies

The characteristic patterns of glucose metabolism on brain FDG-PET and of amyloid deposition on amyloid PET can help in differentiating AD from healthy individuals. An association between AD and hypometabolism was found in several brain regions, such as the parieto–`temporal and posterior cingulate cortices (Mosconi et al., 2008), and hippocampus (Mosconi et al., 2005). Similarly, AD subjects compared to healthy individuals have shown higher amyloid burden in overall cortex and all cortical regions (precuneus, anterior and posterior cingulate, and frontal median, temporal, parietal and occipital cortex) (Camus et al., 2012). These evidences of the association of hypometabolism and amyloid burden with AD encouraged the use of FDG-PET and amyloid PET as a suitable biomarker for AD classification.

3.4.1. FDG-PET

Recently, there has been a growing interest in using the cerebral glucose metabolism rate for AD classification and prediction of conversion from MCI to AD (Gray et al., 2012; Toussaint et al., 2012). Four main methods that utilize the cerebral glucose metabolism rate are considered here: voxels as feature (VAF)-based, discriminative voxel selection-based, atlas-based, and projection-based methods. Table 6 lists the studies using these methods, and their datasets and corresponding classification performance.

Table 6.

A brief description of the datasets used for the validation of FDG-PET and amyloid-PET based AD classification frameworks

Study	Subjects					Type	Classification algorithm	Database	Classification accuracy
	AD	MCI	pMCI	sMCI	CN				AD/CN	MCI/CN	AD/MCI	sMCI/pMCI
(Hinrichs et al., 2009)	89	–	–	–	94	VAF	LPBM	ADNI	84.00	—	—	—
(Vandenberghe et al., 2013)	27	20	—	—	25	VAF	SVM	Internal	88.46	—	—	100.00
(Cabral et al., 2015)	—	—	44	56	—	DVS	SVM+GNB	ADNI	—	—	—	85.00
(Cabral et al., 2015)	—	—	26 (6)	56	—	DVS	SVM+GNB	ADNI	—	—	—	86.00
(Cabral et al., 2015)	—	—	41 (12)	56	—	DVS	SVM+GNB	ADNI	—	—	—	82.00
(Cabral et al., 2015)	—	—	33 (18)	56	—	DVS	SVM+GNB	ADNI	—		—	75.00
(Cabral et al., 2015)	—	—	25 (24)	56	—	DVS	SVM+GNB	ADNI	—		—	74.00
(Gray et al., 2012)	50	—	53	64	54	Atlas	SVM	ADNI	88.00	81.302	83.501	63.10
(Pagani et al., 2015)	–	—	62	–	109	Atlas	SVM	EADC	—	91.002	—	—
(Padilla et al., 2012)	53	114	—	—	52	PRO	SVM	ADNI	86.59	—	—	—

PRO = Projection based techniques

DVS = Discriminative voxel selection

EADC = European Alzheimer’s disease consortium GNB = Gaussian naive bayes

¹= AD/sMCI

¹= CN/pMCI

The first entry for (Cabral et al., 2015) shows the classification accuracy by using all the sMCIs and pMCIs. The remaining entries show the classification between sMCI and different sets of pMCI subjects, divided according to their time of conversion from sMCI to pMCI. Numbers of months are shown in parenthesis against pMCI subjects.

3.4.1.1. VAF-based methods

This set of methods, similar to those discussed for structural MRI in section 3.1, utilizes the intensity value of all the voxels of an input PET scan. Hinrichs et al. adopted this approach for AD classification using LPBM (Hinrichs et al., 2009).

3.4.1.2. Discriminative voxel selection-based methods

The prominent goal of these methods is to simultaneously select the informative voxels (features) used in VAF-based methods. For example, Cabral et al. used this method to investigate the prediction of AD conversion based on FDG-PET images at various time-points (Cabral et al., 2015). Discriminative voxels of the images were selected using mutual information criterion, and SVM and Gaussian naive bayes were used for classification. The classification based on stage-specific categories of pMCIs demonstrated better predictive accuracy than did the overall classification of pMCI and sMCI, a result also demonstrated earlier by (Eskildsen et al., 2013).

3.4.1.3. Atlas-based methods

Several FDG-PET based AD classification studies are based on parcellation of PET images into different anatomical regions, utilizing pre-defined structural atlases. Pagani et al. used the average regional intensity and inter-hemispheric symmetry between the parcellated regions as features for SVM-based classification (Pagani et al., 2015). Similarly, Gray et al. used the average regional intensities of baseline and 12-months follow-up scans, and the difference of intensity between these two time-points as features for SVM-based classification (Gray et al., 2012). Accuracy increased by a factor of 1–2% when using both the longitudinal and cross-sectional features in this study.

3.4.1.4. Projection-based methods

Projection-based methods reduce the dimensionality of features by projecting the higher-dimensional feature space into a lower-dimensional space, where the significance of each feature, with respect to the problem at hand, can be measured in terms of its variance. Thus, a subset of features with relatively larger variance may be selected for further inspection. In this context, Padilla et al. applied non-negative matrix factorization projections to input images (Padilla et al., 2012). They then selected several subsets of these projections, and classified those using SVM. Ultimately, the classification results obtained from several projections were combined to obtain a final prediction. The authors showed that this method achieved a 17% improvement in classification accuracy as compared to a VAF-based method for the same dataset.

3.4.2. Amyloid-PET

In vivo measurements of the cerebral am loid burden (β-amyloid) may be clinically useful in the management of patients with cognitive impairment who are being evaluated for possible AD. Several radioligands are used for measuring amyloid burden, such as the ¹¹C-Pittsburgh Compound B (¹¹C-PIB), and ¹⁸F-labelled amyloid-PET tracers, including florbetapir, flutemetamol, and florbetaben. Some group analysis-based studies have revealed differences in amyloid burden in various brain regions in different subject groups; higher amyloid burden has been found in MCI (Klunk et al., 2004) and AD subjects (Camus et al., 2012) than in healthy individuals, and in subjects with pMCI than in those with sMCI (Koivunen et al., 2011; Okello et al., 2009). However, very little attention has been paid to quantification of plaque levels in different brain regions and its use in AD classification. Vandenberghe et al. proposed one such classification framework in which they used the intensity values of all the voxels of ¹⁸F-flutemetamol PET scans as features for SVM-based classification of AD versus healthy individuals, and pMCI versus sMCI subjects (Vandenberghe et al., 2013).

3.5. Multimodal studies

Several biomarkers have shown association with AD, including proteins measured in the CSF (Melah et al., 2016), brain atrophy, particularly in the hippocampus (Frisoni et al., 2002) and posterior cingulate gyrus (Baron et al., 2001), measured through structural MRI, and hypometabolism, associated with AD in the temporal and parietal lobe, as well as in the posterior cingulate cortex, measured via functional imaging (Herholz et al., 2002; Langbaum et al., 2009). In addition, AD brains demonstrate the formation of insoluble β amyloid plaques and neurofibrillary tangles (Jagust, 2013), and it has been suggested that the quantity of β am loid can be related to the disease stage (Murpy, LeVine III, 2010).

These biomarkers yield complementary information, i.e., different modalities capture disease information from different perspectives, thereby improving understanding of the disease pattern over that presented by one modality. Classification frameworks facilitate exploitation of the complementary information obtained from multiple modalities. A top-level breakdown of two classification frameworks, straightforward feature concatenation and specialized fusion frameworks, used to exploit multimodal data for AD classification is shown in Figure 3. The terms F₁, F₂, …, F_n−1, F_n are the feature sets extracted from 1, 2, …, n−1, n modalities or other biomarkers, respectively. The symbols C₁, C₂,…, C_n−1, C_n represent the classification algorithms trained on feature sets 1, 2, …n−1, n, respectively. Table 7 summarizes the results and the corresponding datasets for the studies using these frameworks.

Figure 3.

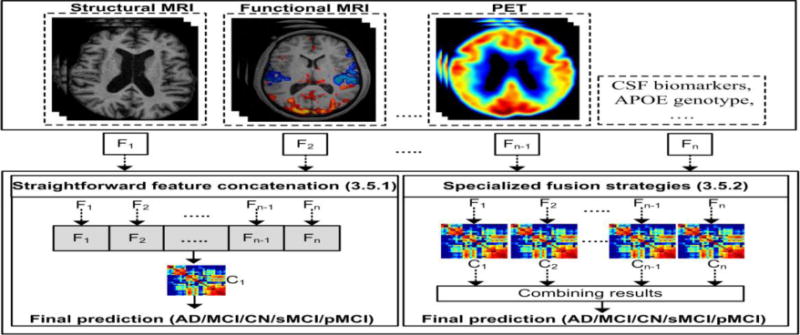
A top-level breakdown of multimodality-based classification studies for AD classification

Table 7.

A brief description of the datasets used for the validation of various multimodality based AD classification frameworks

	Subjects					Type	Classification algorithm	Database	Classification accuracy
	AD	MCI	pMCI	sMCI	CN				AD/CN	MCI/CN	AD/MCI	sMCI/pMCI
(Fan et al., 2008b)	—	15	—	—	15	SFC	SVM	BLSA	—	90.00	—	—
(Vemuri et al., 2008)	190	—	—	—	190	SFC	SVM	ADNI	89.30	—	—	—
(Kohannim et al., 2010)	158	264	—	—	213	SFC	SVM	ADNI	93.81	75.49	—	—
(Davatzikos et al., 2011)	—	—	69	170	—	SFC	SVM	ADNI	—	—	—	61.70
(Dukart et al., 2011a)	21	—	—	—	13	SFC	SVM	Leipzig	100.00	—	—	—
(Cui et al., 2011)	96	—	56	87	111	SFC	SVM	ADNI	—	—	—	67.13
(Cui et al., 2012)	—	79	—	—	204	SFC	SVM	SMAS	—	71.09	—	—
(Dukart et al., 2013)	49	—	—	—	41	SFC	SVM	ANDI+Leipzig	90.001	—	—	—
(Zhang et al., 2014)	24	57	—	—	97	SFC	Kernel SVM decision-tree	OASIS	96.00	85.00	88.00	—
(Zhu et al., 2014)	51	99	—	—	52	SFC	SVM	ADNI	95.90	82.00	—	—
(Li et al., 2014a)	21	—	—	—	15	SFC	SVM	TH	94.30	—	—	—
(Apostolova et al., 2014)	95	182	—	—	111	SFC	SVM	ADNI	85.00	79.00	70.00	—
(Moradi et al., 2015)	200	—	164	100	231	SFC	LDS,Random forest	ADNI	—	—	—	81.72
(Zheng et al., 2015)	163	—	104	94	189	SFC	SVM	ADNI	92.11	—	—	79.37
(Tang et al., 2016)	29	—	—	—	23	SFC	LDA+SVM	TH	94.60	—	—	—
(Schouten et al., 2016)	77	—	—	—	173	SFC	Elastic net classifier	PRODEM	93.00	—	—	—
(Clark et al., 2016)	—	24	—	—	—	SFS	Ensemble classifier	ADRC	—	—	87.202	—
(Hinrichs et al., 2011)	48	119	—	—	66	SFS	Multi-kernel SVM	ADNI	92.40	—	—	—
(Zhang et al., 2011)	51	99	—	—	52	SFS	Multi-kernel SVM	ADNI	93.20	76.40	—	—
(Dai et al., 2012)	16	—	—	—	22	SFS	Ensemble of MU-LDA	XWH	89.47	—	—	—
(Zhang, Shen, 2012)	45	91	—	—	50	SFS	Multi-kernel SVM	ADNI	93.33	83.20	—	—
(Young et al., 2013)	63	—	47	96	73	SFS	Gaussian process classifier	ADNI	—	—	—	74.00
(Gray et al., 2013)	37	—	34	41	35	SFS	Random forest	ADNI	89.00	74.60	—	58.00
(Casanova et al., 2013)	171	—	153	182	188	SFS	RLR	ADNI	87.10	—	—	63.00
(Liu et al., 2014)	50	—	—	—	70	SFS	Multi-kernel SVM	ADNI	87.12	—	—	—
(Xu et al., 2015)	113	—	27	83	117	SFS	SRC	ADNI	94.80	74.50	—	77.80
(Zu et al., 2015)	51	—	43	56	52	SFS	Multi-kernel SVM	ADNI	95.95	80.26	—	69.78
(Cheng et al., 2015b)	51	—	43	56	52	SFS	Domain transfer SVM	ADNI	—	86.40	82.70	79.40
(Cheng et al., 2015a)	51	—	43	56	52	SFS	M2TL	ADNI	—	—	—	80.10
(Dyrba et al., 2015b)	28	—	—	—	25	SFS	Multi-kernel SVM	EDSD	85.00	—	—	—
(Korolev et al., 2016)	—	—	139	120	—	SFS	Probabilistic multi-kernel	ADNI	—	—	—	80.00
(Yu et al., 2016)	50	97	—	—	52	SFS	Multi-task learning	ADNI	92.60	80.00	—	—

SFC = Straightforward feature concatenation

SFS = Specialized fusion strategies LDS = Low density separation

SRC = Sparse representation-based classification

MU-LDA = Maximum uncertainty-linear discriminant analysis

M2TL = Multimodal manifold-regularized transfer learning

TH = Tongji hospital, Wuhan, China

SMAS = Sydney memory and aging study

XWH = Xuan wu hospital, Beijing, China

PRODEM = Prospective registry on dementia in Austria

ADRC = Alzheimer disease research center, Washington University school of medicine, St. Louis, Missouri

¹= Accuracy for the combined ADNI+Leipzig cohort

²= Prediction of conversion from MCI to AD (AUC)

3.5.1. Straightforward feature concatenation

The simplest method for exploiting the complementary information provided by multiple modalities is concatenation of the features of these modalities into a single feature vector and training a classifier on that vector.

Structural MRI is a key component of these studies, and its features are combined with features extracted from various other modalities to improve classification. In this context, various authors have combined structural MRI-based features with the features calculated from DTI and functional MRI. In earlier studies, the regional volumetric measures, calculated from structural MRI, and FA, calculated from WM tracts, have been combined for SVM-based MCI and AD classification (Cui et al., 2012; Li et al., 2014a). Among recent studies, Tang et al. used volumetric, shape, and diffusion features of the hippocampus and amygdala for AD classification (Tang et al., 2016). They used PCA and tudent’s t-test for reducing the feature set, and LDA and SVM for classification. Similarly, Schouten et al. combined regional volumetric measures, diffusion measures, and correlation measures amongst all brain regions calculated from functional MRI (Schouten et al., 2016). They employed logistic elastic net (Zou, Hastie, 2005) for classification.

The combination of structural MRI with demographics, cognitive tests, and genetic data has also been explored in a few studies. For instance, Vemuri et al. combined GM, WM, and CSF density maps with age, gender, and APOE genotype for SVM-based AD classification (Vemuri et al., 2008). Zhang et al. used GM density maps, intracranial volume, atlas-scaling factor, normalized whole brain volume, and age as features for AD and MCI classification (Zhang et al., 2014). The feature set was classified by using a kernel SVM decision-tree (a variant of the SVM decision-tree). Recently, Moradi et al. used GM density maps, age, and cognitive tests as features, and employed classification algorithms such as low-density separation and random forest for AD conversion prediction (Moradi et al., 2015).

The combination of structural MRI features with PET and CSF biomarkers is another dimension. In earlier studies, Fan et al. combined regional volumetric measures, and regional cerebral blood flow for MCI classification using SVM (Fan et al., 2008b). In addition to this, the SPARE-AD index (Davatzikos et al., 2009) was combined with CSF biomarkers (Davatzikos et al., 2011) to predict conversion from MCI to AD using SVM. Further, Dukart et al. first used FDG-PET and GM density values of all the voxels of selected ROIs (Dukart et al., 2011a) and later the average of all the voxels of selected ROIs for SVM-based AD classification (Dukart et al., 2013). In recent studies, Zhu et al. combined regional GM volume, regional average PET intensity, and CSF biomarkers as features, and proposed a matrix-similarity-based loss function for better classification using SVM (Zhu et al., 2014). Similarly, Zheng et al. used regional thickness measures, regional correlative measures (calculated from thickness measures) and APOE genotype for SVM-based AD classification, and AD prediction conversion (Zheng et al., 2015). Apostolova et al. used hippocampal volume and CSF biomarkers for SVM-based AD and MCI classification (Apostolova et al., 2014).

The combination of structural MRI, PET, and CSF biomarkers together with genetic data and neuropsychological status exam scores has also been common. For example, SPARE-AD was combined with cognitive scores, APOE genotype, and CSF biomarkers (Da et al., 2014) to predict conversion from MCI to AD. Similarly, Kohannim et al. combined hippocampal, ventricular, and temporal lobe volumes, FDG-PET numeric summary, CSF biomarkers, APOE genotype, age, sex, and body mass index for SVM-based AD and MCI classification (Kohannim et al., 2010). In addition, Cui et al. combined average regional cortical thickness, standard deviation of thickness, average regional surface area and cortical volume from structural MRI with CSF biomarkers and neuropsychological status exam scores (Cui et al., 2011). Features were reduced using mRMR, and SVM was used for classification.

3.5.2. Specialized fusion strategies

While the simplicity of straightforward concatenation may be considered desirable, the method suffers from a major pitfall: because it treats all features as equivalent, it provides no way to account for the different natures of features extracted from different modalities (Hinrichs et al., 2011; Liu et al., 2014). For instance, where one modality has many more features than another (or has variation on a much larger scale), classification algorithms trained on concatenated features may produce prediction models that effectively ignore the other modalities. Specialized fusion strategies can be used to ensure that the complementary information found across all modalities is still used. These strategies may either combine the results of classification rules trained on the individual modalities (Dai et al., 2012) or use special combination rules to combine features before training (Dyrba et al., 2015b; Zhang, Shen, 2012; Zhang et al., 2011).

These strategies were employed to utilize the complementary information of features extracted from structural MRI, rs-fMRI, and DTI for AD classification. Dai et al. used regional GM volumetric measures, and functional measures (amplitude of low-frequenc fluctuations, regional homogeneit, and regional functional connectivity strength) as features (Dai et al., 2012). They trained separate maximum uncertainty LDA classifiers on the structural and functional measures, and combined the output of the classifiers via weighted voting. Recently, Dyrba et al. used regional GM volumetric measures, average tract intensity for FA, MD, and mode of anisotropy, and network measures of weighted local clustering coefficient and the shortest weighted path-length calculated from rs-fMRI as features (Dyrba et al., 2015b). They adopted multi-kernel SVM for AD classification.

In addition, the features extracted from structural MRI and PET images, as well as CSF biomarkers were also fused using these strategies. In this context, regional GM volume, regional average FDG-PET intensity, and CSF biomarkers were used as features for AD and MCI classification along with multi-kernel learning (Zhang, Shen, 2012; Zhang et al., 2011) and multi-task learning (Yu et al., 2016). The same features were also used for prediction of conversion from MCI to AD by using domain transfer learning (Cheng et al., 2015b) and semi-supervised multimodal manifold-regularized transfer learning (Cheng et al., 2015a). Recently, Liu et al. used CSF biomarkers, and shape measures of hippocampus and GM volume in atlas-defined ROIs for AD classification using multi-kernel SVM (Liu et al., 2014). Xu et al. proposed using the GM volume, regional average intensity from FDG-PET and Florbetapir images as features (Xu et al., 2015). They assigned different weights to the features of different modalities for classification of AD versus MCI subjects, and pMCI versus sMCI subjects using a sparse representation-based classification method. Zu et al. used regional GM volume, and the regional average FDG-PET intensity for AD and MCI classification, and used multi-kernel SVM for classification (Zu et al., 2015).

Furthermore, these strategies were also used to exploit the features of structural MRI, PET, and CSF biomarkers together with genetic data and neuropsychological status exam scores. In earlier studies, Hinrichs et al. used structural MRI-based density maps, FDG-PET intensities, CSF biomarkers, APOE genotype, and neuropsychological status exam scores as features for multi-kernel SVM-based AD classification, and AD conversion prediction (Hinrichs et al., 2011). Young et al. used regional GM volume, regional average FDG-PET intensity, and CSF biomarkers along with APOE genotype, and employed Gaussian process classifier to train multiple kernels on AD and CN subjects, and test on pMCI and sMCI subjects (Young et al., 2013). Also, Gray et al. trained random forest classifiers on regional GM volumetric measures, CSF biomarkers, voxel-based FDG-PET intensities, and APOE genotype for AD and MCI classification (Gray et al., 2013). Casanova et al. combined SPARE-AD index with GM, WM and CSF density maps, total hippocampal volume, regional volumetric and cortical thickness measures, and cognitive scores for AD classification and prediction of conversion from MCI to AD using large-scale RLR (Casanova et al., 2013). In recent studies, Korolev et al. used cortical and subcortical volumes, mean cortical thickness, surface area, and curvature from structural MRI, clinical measures and plasma measures for AD conversion prediction. They used mutual information criterion for feature selection and probabilistic multi-kernel learning for classification (Korolev et al., 2016). Similarly, Clark et al. used cognitive scores, cortical thickness measures, hippocampal and ventricular volume along with age, sex, and education. They selected features using random forest, and used an ensemble of random forests of conditional trees, SVM, naive Bayes, and multilayer perceptrons for classification. (Clark et al., 2016).

Overall, the multimodal techniques under this category have demonstrated varied improvement over single modalities, ranging from 1 to 7%. Almost all the methods demonstrated some improvement (Dyrba et al., 2015b), however, no improvement was observed using multimodality data as compared to DTI measures alone.

4. Discussion

Recent advances in neuroimaging research suggest that AD pathology can be detected preclinically (Perrin et al., 2009). Consequently, an important body of research has been devoted to the neuroimaging-based AD/MCI classification and AD conversion prediction using various neuroimaging modalities, such as structural MRI, functional MRI, DTI, and PET. In this review, we presented only those studies that used appropriate cross-validation strategies to assess the performance of their classification frameworks. Among the various neuroimaging modalities, structural MRI was the most frequently used, likely due to its widespread availability. The second most common method was the combination of features from one or more modalities with data levels such as genetic data, cognitive scores, and CSF biomarkers. Research based on features extracted from FDG-PET, amyloid-PET, DTI, and functional MRI were less common. The main objective in most of the studies reviewed here was the production and selection of AD-related inherent features from high-dimensional raw neuroimaging data. Therefore, we grouped the classification studies appertaining to each modality according to feature extraction methods. Brain atrophy was most often quantified via tissue density maps (Casanova et al., 2011; Kloppel et al., 2008), cortical/subcortical thickness measurements (Desikan et al., 2009; Wee et al., 2013), and geometric measures of hippocampus (Costafreda et al., 2011; Gerardin et al., 2009) from structural MRI. Connectivity networks developed on top of the functional strength (Chen et al., 2011; Koch et al., 2012) and diffusion measures (Prasad et al., 2015; Wee et al., 2011) of parcellated brain regions were the most common feature extraction methods in functional MRI and DTI, respectively. Similarly, the cerebral glucose metabolic rate measured in parcellated brain regions was common in FDG-PET (Gray et al., 2012; Pagani et al., 2015). These automated feature extraction methods generate a high-dimensional data for further analysis. A wide variety of sophisticated and well-established supervised classification algorithms such as SVM and LDA have been applied on extracted neuroimaging features for AD/MCI classification or AD prediction conversion in different studies.

The main advantage of applying classification algorithms on neuroimaging data is the potential use for detecting AD at the prodromal stages, well even before clinical manifestation (Misra et al., 2009; Park et al., 2013), demonstrating the probable use in routine clinical settings in the future. Among the wide range of classification algorithms, SVM was the most frequent for AD classification (Apostolova et al., 2014; Cui et al., 2012; Kohannim et al., 2010; Padilla et al., 2012). Multi-kernel learning, which are an extension of ordinary kernel-based classification algorithms, were also increasingly used in AD classification (Dyrba et al., 2015b; Liu et al., 2014; Zu et al., 2015). Other less common classification algorithms used in AD research were LDA (Lillemark et al., 2014; Tang et al., 2015), orthogonal partial least square regression (Westman et al., 2011), random forest (Moradi et al., 2015), regularization-based methods (Casanova et al., 2011), voting-based ensemble methods (Liu et al., 2015), kernel SVM decision-tree (Zhang et al., 2014), and LPBM (Hinrichs et al., 2009). While SVM could have the advantage of achieving high classification accuracy with small training sample size compared to other classification algorithms such as neural networks (Shao, Lunetta, 2012), they might have the disadvantage of the need for parameter tuning (Chapelle et al., 2002). For neuroimaging AD classification it remains important to conduct studies comparing between diverse classification algorithms thoroughly, as only limited number of studies have been conducted so far (Khondoker et al., 2016; Lehmann et al., 2007).

The feature extraction methods summarized here are influenced by several factors that vary across studies. One factor is spatial smoothing of structural MRI and FDG-PET, which is generally performed to account for noise (i.e. registration errors). Usually, Gaussian smoothing of full-width half-max is used for denoising. It is important to note that too small kernel size might lead to missing the many regions that might present group differences. Conversely, too large kernel may blur image features in regions that display group differences from the rest of the regions. An optimal solution has yet to be achieved as the kernel size is chosen either ad hoc or empirically. A majority of the reviewed studies used a Gaussian kernel of 8 mm for both structural MRI (Misra et al., 2009; Moradi et al., 2015) and FDG-PET (Gray et al., 2013; Pagani et al., 2015; Zhang et al., 2011; Zhu et al., 2014). However, kernels of other sizes, such as 10 mm for structural MRI (Dai et al., 2012; Plant et al., 2010) and 15 mm for FDG-PET (Fan et al., 2008b), were rarely used. An additional factor that influences the atlas-based methods is the selection of the atlas itself. Atlas-based parcellation using a pre-defined anatomical brain atlas is a methodologically simple and computationally tractable feature extraction method, with general versatility (Ota et al., 2015; Zhang et al., 2011). However, the choice of atlas will have an effect on classification performance. It has been shown that features extracted based on different anatomical parcellations lead to differences in classification performance under similar experimental conditions (Ota et al., 2014, 2015). These differences in classification performances may be associated with changes in parcellation between atlases, for example, the cerebellum region. The LONI probabilistic brain atlas considers the cerebellum as one single region, whereas the AAL atlas finely parcellates the cerebellum into 26 smaller regions.

In addition to feature extraction and classification, feature selection is also important for identifying distinguishing features. Selection of appropriate features not only removes the non-informative signal, but also reduces the computational time involved in classification. Two widely adopted methods for feature selection are biologically informed and automated feature selection. The former relies on prior biological knowledge about the discriminating ability of certain regions, generally obtained from existing literature, whereas the latter selects features based on general data characteristics, without prior knowledge. Among the automated methods, various ranking-based methods, such as t-tests (Tang et al., 2016; Wee et al., 2013) and earson’s correlation coefficient test (Davatzikos et al., 2008; Wee et al., 2011), wrapper-based methods, a combination of ranking and wrapper-based methods, such as mRMR (Wee et al., 2013), and embedded methods, such as elastic net regression, were used in the reviewed studies, and improved the classification performance. It is feasible that variations in feature-selection methods will lead to differences in AD classification performance. It has been suggested that automated feature selection will not improve classification accuracy as compared to biologically informed feature selection, driven by prior biological knowledge of regions typically affected by AD, such as the hippocampus, amygdala, thalamus, and caudate (Chu et al., 2012). Similar results were observed in the Pittsburgh Brain Activity Interpretation Competition, wherein the team applying prior biological knowledge for feature selection (Chu et al., 2011) outperformed the teams using automated feature selection. In addition, the winning method (Sørensen et al., 2014) in the recent CADDementia 2015 challenge (Bron et al., 2015) was also based on biologically informed feature selection.

4.1. AD classification studies comparison

The key components of each classification study, such as prediction accuracy, study population, and feature types were summarized in table format in this review. It should be emphasized that these tables are meant to provide a glance to each individual study and not for comparative purposes. Frequently throughout reviewing these studies, authors stated that their proposed classification framework was superior to existing ones solely on the basis of the achieved accuracy. However, we believe that considering the number of factors involved in each study, summarized below, it is difficult to compare these studies directly and therefore to draw general conclusions about the state of the field as a whole.

Length of follow-up period

The length of the follow-up period for defining MCI conversion also varied from a minimum of 6 months to a maximum of 36 months across different studies. It is well-known that the level of neurodegeneration, and hence, the rate of AD prediction increases as the MCI subjects progress on a continuum from the CN state to the AD state (Cabral et al., 2015; Eskildsen et al., 2013). Therefore, we believe that the prediction performance of various studies cannot be compared directly, considering the different lengths of the follow-up periods.

Study population

Baseline characteristics of the study population, such as gender, age, genotype (APOE), and education are considered to be confounding factors in AD classification. These factors may have a profound effect on key features extracted from the neuroimaging modalities and therefore on the resultant classification accuracies. AD classification studies in general differ in how they deal with the confounding factors, i.e., the number of confounding factors that need to be considered, and how they are considered, etc. In the past, confounding factors have mainly been dealt with by matching the subjects in different groups according to the factors or by using confounding factors as covariates in a statistical model, in order to remove their effect from the model. However, increasing attention has been given to this issue in recent years, and several automated methods have now been proposed to control for the effects of confounding factors (Dukart et al., 2011b; Li et al., 2011).

Degree of impairment

An objective, final diagnosis of AD can only be made through autopsy and therefore is rarely used (Kloppel et al., 2008). Even then, the disease stage at autopsy can be very different from the disease stage determined by scanning. Alternatively, clinical diagnostic criteria for AD (McKhann et al., 2011) and MCI (Petersen, 2004) are used in practice as a reference standard for evaluation. The MCI diagnosis based on these criteria leads to a clinically heterogeneous mix of more and less impaired patients, where each patient presents a disease stage on a continuum from CN to AD (Misra et al., 2009). A more severely impaired MCI group, when MCI is used as one diagnostic entity, may show larger structural differences from healthy individuals, leading to potentially higher classification accuracies.

Evaluation metrics

Classification performance in some of the studies reviewed here was only reported in terms of classification accuracy. The measure of classification accuracy by itself could be uninformative in unbalanced datasets and cannot be used for comparison. For instance, a 90% classification accuracy in a dataset of 90 diseased and 10 healthy individuals does not convey any information, since a biased classification algorithm that classifies all the subjects as diseased can also lead to a 90% classification accuracy. Therefore, we believe that balanced accuracy; sensitivity/specificity or precision/recall, along with the area under a receiver-operating-characteristic curve should be reported for direct comparison of results.

Factors affecting the performance of classification algorithms

The expected performance of a classification algorithm is defined by two factors. The first is the number of subjects in the training set and the second is the relative proportion of subjects from each class present in the test set. Mostly the first factor is determined by the sample size available for training, and by the cross-validation strategy used in the experiment. The larger the number of subjects in the training set, the better the generalizability of the classification algorithm. The second factor could affect the classification accuracy as depending on class relative proportion, the sensitivity and specificity of a classification algorithm could differ. This factor can be easier to fix, as stratification is becoming increasingly common, and subjects of different classes are selected based on matched demographic characteristics.

The choice of the split-in-train-test or k-fold cross-validation strategies, adopted in the classification framework, influences the statistical significance of the classification accuracy (Mendelson et al., 2014), which can be calculated via binomial or permutation tests (Noirhomme et al., 2014). The split-in-train-test assumes independence between the training and test sets, which is the key to binomial tests. However, the split-in-train-test can generally be limited in some medical applications where classification algorithms are trained on small number of subjects. Consequently, k-fold cross-validation is more commonly applied. K-fold cross-validation does not hold the independence assumption, as the training subjects in different iterations could overlap; therefore, permutation tests are feasible for evaluating the statistical significance of k-fold cross-validation strategies (Noirhomme et al., 2014). It has been suggested that 10-fold or 5-fold cross-validation should be used to establish a trade-off between bias and variance (Lemm et al., 2011). Furthermore, it has been suggested that permutation tests should be used along with cross-validation, especially when dealing with a small sample size (Noirhomme et al., 2014).

4.2. Challenges with AD classification studies

Generalization ability

A critical challenge underlying the clinical use of AD classification frameworks is the ability of predictive models that allow good generalization to new patient data. Ideally, the models should be able to perform well regardless of the variability of imaging protocols, scanners (Abdulkadir et al., 2011) and demographics, and should be free of double-dipping, a phenomenon very common in older studies. The term double-dipping, or circular analysis, refers to the use of test subjects in any part of the training process, such as selection of features and training of classification algorithm, and may lead to over-fitted classification (Kriegeskorte et al., 2009). To conduct a fair validation, one should avoid double-dipping by excluding the test subjects used in the subsequent validation of the classification algorithms from the process of feature selection and training of the classification algorithm. Double-dipping was quite common in feature selection in older studies (Querbes et al., 2009; Wolz et al., 2011); however, it has become less common as its effects became clearer. In order to encourage the development of classification frameworks that are generalizable to new datasets, the neuroimaging community has organized more AD classification challenges, in which different researchers attempt to solve the classification problem by leveraging the current state-of-the-art techniques on publicly available datasets.

For example, the purpose of CADDementia 2015 challenge (Bron et al., 2015) was to measure the generalizability of structural MRI-based classification studies on unseen subjects, where the best performing study yielded an area under the receiver-operating-characteristic curve of 78.8%. Similarly, the main aim of the DREAM 2016 challenge (Allen et al., 2016) was to identify accurate biomarkers of cognitive decline for advancing early diagnosis. These challenges not only help to determine the generalizability of any study, but also enable fair performance comparison of different studies on the same dataset, which would otherwise not be possible due to different experimental conditions across distinct studies. Furthermore, efforts have been made to standardize comparison of various studies on the same dataset, such as in the study of Cuingnet et al., in which the authors evaluated the performances of 10 studies using the ADNI dataset (Cuingnet et al., 2011).

Sample size

It is generally believed that smaller datasets do not capture the full spectrum of heterogeneity among different classes and therefore, may be less generalizable on unseen patient data, whereas opposite is true for larger datasets. Nonetheless, quite different results were seen in CADDementia 2015 challenge (Bron et al., 2015), where the studies training classification algorithms on larger training sets (Abdulkadir et al., 2014; Eskildsen et al., 2014) did not perform better than the studies training classification algorithms on relatively smaller datasets. Therefore, the minimum sample size required for training a generalizable classification model remains debatable.

Reproducibility

Disregard of the appropriate packaging of classification frameworks, where numerical solutions could lead to different experimentation conditions, and the use of local datasets or a subset of a larger public dataset without providing detailed subject level identification, are the main factors hindering the reproducibility of existing results and comparison between study findings. We highly encourage reporting the results derived from public datasets, and appropriate listing of the subjects, as had been done in a few studies (Moradi et al., 2015; Zhang et al., 2011). We also recommend that authors attend to the proper packaging and availability of their code, particularly in cases where sophisticated feature extraction and classification algorithms have been used, as this can markedly improve reproducibility.

AD heterogeneity

The heterogeneity of AD necessitates a definition of distinct clinicopathological subtypes of AD. While AD has been stereotypically defined using the Braak stages, atypical AD cases do not fit into this scheme. For example, a recent study has shown that hippocampal sparing and limbic-predominant AD subtypes might account for about 25% of AD cases (Murray et al., 2011). Simplistic measures, such as the ratio of hippocampal to cortical volumes, showed a high discrimination ability between the subtypes (Whitwell et al., 2012). Other studies used clustering-based approaches for defining the AD pattern; a recent study made use of cortical thickness clustering and showed that AD in the earlier stages can be categorized into various anatomical subtypes, with distinct clinical features (Noh et al., 2014). By including additional biomarkers, such as cerebrospinal fluid and serum biomarkers, four clusters emerged with distinct biomarker patterns, the first of which was biologically similar to healthy individuals and which rarely converted to AD (Nettiksimmons et al., 2014). We believe that the heterogeneity of AD patterns has been widely ignored in the existing AD classification studies, and more attention should be paid to this line of research in future. The development of tools that can deal with heterogeneous imaging patterns is important and should become an area of focus (Dong et al., 2016a; Dong et al., 2016b; Varol et al., 2017). It is likely that systematic quantification of heterogeneity is critical for developing effective personalized diagnostic and predictive tools using machine learning.

4.3. Conclusion and future directions

Neuroimaging-based classification of AD and MCI has increasingly been reported in the literature over the past decade, as a means to derive individual biomarkers of these conditions. The ultimate goal of AD classification is to generate an individual diagnosis using a single MRI scan by applying classification models already trained on a large pool of diseased and healthy individuals, and to predict future progression at earlier disease stages. Several neuroimaging modalities, as discussed in this review, including structural and functional MRI, DTI, FDG-PET, and amyloid-PET, have shown characteristic alterations in the brains of AD and MCI patients that can help rule-in the pathophysiological process of AD. No single neuroimaging modality can be sufficient, as each has complementary merits and limitations. Combining information from multiple modalities has improved the classification performance of AD/MCI and AD conversion prediction. In addition, the combination of features extracted from neuroimaging modalities with demographics, cognitive test scores, CSF biomarkers, and genetic data were also effective in achieving accurate classification. However, there is a great need for validation of these markers in clinical settings, along with their validation in databases comprising highly preselected subjects, which significantly differ from that seen in the clinic. Some challenges faced by the researchers in the field of AD classification, such as high dimensions of raw neuroimaging data, smaller sample sizes, generalizability, and heterogeneity in AD, make it difficult to derive a more precise classification. However, the use of neuroimaging for AD classification remains highly promising, as many of the aforementioned challenges can be addressed.

The potential consideration of classification frameworks in clinical practice has largely driven the development of machine-learning tools that can integrate several imaging features and make predictions on an individual basis. This line of research is likely to become a focus-point in the upcoming decade. In addition, multimodal approaches that seek to find patterns of neurodegeneration across different types of images that form distinctive imaging signatures of the stages of AD, and consensus-based approaches, which tend to improve classification by combining the output of multiple classification algorithms, are also gaining increasing attention. Biologically informed feature selection, and characterization of heterogeneity of AD are also important lines of research that are likely to be emphasized in future studies.

Table 4.

A brief description of the datasets used for the validation of functional MRI based AD classification frameworks

Study	Subjects			Type	Classification algorithm	Database	Classification accuracy
	AD	MCI	CN				AD/CN	MCI/CN	AD/MCI
(Chen et al., 2011)	20	15	20	Connectivity	Fisher LDA	MDC	82.001	91.00
(Challis et al., 2015)	27	50	39	Connectivity	GP-LR	Internal	—	75.00	97. 00
(Jie et al., 2014)	—	12	25	Graph measures	Multi-kernel SVM	BIAC	—	91.90
(Khazaee et al., 2015)	20	—	20	Graph measures	SVM	ADNI	100.00	—	—

GP-LR = Gaussian-process logistic regression

MDC = Memory disorders clinic, Medical College of Wisconsin

BIAC = Brain imaging and analysis center, Duke university, North Carolina, USA

¹= AD/(MCI+CN)

Abbreviations (Acronym Abbreviation)

AAL

Automated anatomical labeling

AD

Alzheimer’s disease

ADNI

Alzheimer’s disease neuroimage initiative

AUC

Area under a receiver-operating-characteristic curve

CN

Cognitively normal

CSF

Cerebrospinal fluid

DMAF

Density maps as features

DMN

Default mode network

DTI

Diffusion tensor imaging

FDG-PET

Fluorodeoxyglucose positron emission tomography

fMRI

Functional magnetic resonance imaging

GM

Gray matter

LDA

Linear discriminant analysis

LPBM

Linear program boosting method

LR

Logistic regression

MCI

Mild cognitive impairment

MRI

Magnetic resonance imaging

mRMR

Minimum-redundancy and maximum-relevance

OASIS

Open access series of imaging initiatives

pMCI

Progressive mild cognitive impairment

RAVENS

Regional analysis of volumes examined in normalized space

ROI

Region of interest

RLR

Regularized logistic regression

RVM

Relevance vector machines

rs-fMRI

Resting state functional magnetic resonance imaging

sMCI

Stable mild cognitive impairment

sMRI

Structural magnetic resonance imaging

SPARE-AD

Spatial pattern of abnormality for recognition of early Alzheimer’s disease

SVM

Support vector machines

SVM-RFE

Support vector machines-recursive feature elimination

VAF

Voxels as features

VBM

Voxel based morphometry

WM

White matter