Simultaneous Time Interleaved MultiSlice (STIMS) for Rapid Susceptibility Weighted Acquisition

Abstract

T₂* weighted 3D Gradient Echo (GRE) acquisition is the main sequence used for Susceptibility Weighted Imaging (SWI) and Quantitative Susceptibility Mapping (QSM). These applications require a long echo time (TE) to build up phase contrast, requiring a long repetition time (TR), and leading to excessively lengthy scans. The long TE acquisition creates a significant amount of unused time within each TR, which can be utilized for either multi-echo sampling or additional image encoding with the echo-shift technique. The latter leads to significant saving in acquisition time while retaining the desired phase and T₂* contrast.

In this work, we introduce the Simultaneous Time Interleaved MultiSlice (STIMS) echo-shift technique, which mitigates slab boundary artifacts by interleaving comb-shaped slice groups with Simultaneous MultiSlice (SMS) excitation. This enjoys the same SNR benefit of 3D signal averaging as previously introduced multi-slab version, where each slab group is sub-resolved with kz phase encoding. Further, we combine SMS echo-shift with Compressed Sensing (CS) Wave acceleration, which enhances Wave-CAIPI acquisition/reconstruction with random undersampling and sparsity prior. STIMS and CS-Wave combination thus yields up to 45-fold acceleration over conventional full encoding, allowing a 15 sec full-brain acquisition with 1.5 mm isotropic resolution at long TE of 39 ms at 3T. In addition to utilizing empty sequence time due to long TE, STIMS is a general concept that could exploit gaps due to e.g. inversion modules in magnetization-prepared rapid gradient- echo (MPRAGE) and fluid attenuated inversion recovery (FLAIR) sequences.

Graphical abstract

1. Introduction

3D Gradient Echo (GRE) is the workhorse sequence for Susceptibility Weighted Imaging (SWI) (Haacke et al., 2004), Quantitative Susceptibility Mapping (QSM) (de Rochefort et al., 2009; Li et al., 2011; Schweser et al., 2011; Shmueli et al., 2009), Susceptibility Tensor Imaging (STI) (Liu, 2010) and phase imaging in general (Duyn et al., 2007; Wharton and Bowtell, 2012). These applications exploit the phase contrast mechanism, which reaches its optimum signal-to-noise ratio (SNR) when the echo time (TE) is equal to the T₂* relaxation time of the tissue (Wu et al., 2012a). At 3 Tesla, T₂* ranges between 38 (white matter) to 45 ms (gray matter) (Wu et al., 2012a), whereas this value drops to ∼32 ms (cortex) at 7 Tesla due to faster spin dephasing (Cohen-Adad et al., 2012). Imaging with optimal phase SNR thus necessitates late TEs, which in turn constrain the repetition time (TR) to be long and lead to excessively lengthy scans.

Parallel imaging (Griswold et al., 2002; Pruessmann et al., 1999; Sodickson and Manning, 1997) allows faster acquisition by undersampling the k-space and reconstructing the data using the encoding capability provided by multi-channel receiver arrays. While this typically allows up to R=3-fold acceleration along one k-space direction, both of the phase encoding axes in 3D GRE acquisition can be utilized to achieve even higher undersampling rates, typically up to 6 fold (3×2) with 32 channel brain arrays. Controlled aliasing in volumetric parallel imaging (2D-CAIPI) is a sampling technique that capitalizes on this and evenly distributes the undersampling between the two axes (Breuer et al., 2006). This strategy provides high quality reconstruction at R=6-fold acceleration with much lower g-factor noise penalty (Brenner et al., 2014). Controlled aliasing is also applicable to Simultaneous MultiSlice (SMS) acquisition, where multiple imaging slices are excited at the same, then unaliased using coil sensitivity encoding (Breuer et al., 2005; Larkman et al., 2001; Setsompop et al., 2012; Weaver, 1988). CAIPI sampling in SMS acquisition also exploits sensitivity variations in two dimensions, since such acceleration can be viewed as undersampling in 3D k-space (Zahneisen et al., 2014). Bunched Phase Encoding (BPE) is an alternative strategy that plays sinusoidal or zigzag gradients on the Gy axis during data sampling, thus spreading the aliasing also in the readout axis to improve parallel imaging reconstruction (Breuer et al., 2008; Moriguchi and Duerk, 2006). Wave-CAIPI is a more recent encoding technique that combines 2D-CAIPI and BPE strategies to distribute aliasing in all three directions, thus allowing an order of magnitude acceleration (Bilgic et al., 2015). It involves playing sinusoidal gradient waveforms on both Gy and Gz axes during the readout, so that a corkscrew trajectory is traced out around each line in k-space. This strategy is applicable to both 3D (Bilgic et al., 2015) and SMS (Gagoski et al., 2015) acquisitions.

Utilizing the unused sequence time prior to the late TE in susceptibility weighted acquisitions is another method to improve efficiency in a sequence. This can be done using an echo-shift technique, where additional gradients are used to shift the gradient echo to a later TR (Duyn et al., 1994; Liu et al., 1993b; Moonen et al., 1992). The effective TE is thus longer than the TR, i.e. a short TR acquisition with desired T₂* and phase contrast becomes possible. Echo-shift is known as PRESTO in functional imaging (Liu et al., 1993a), and has been combined with parallel imaging and SMS for faster temporal sampling (Boyacioğlu et al., 2016; Golay et al., 2000). This has also allowed improved slice coverage in 2D GRE imaging at ultra high field while preserving the SNR and contrast (Ehses et al., 2015).

Application of echo-shift to SWI with 3D GRE acquisition was recently proposed (Ma et al., 2016), where the field of view (FOV) was divided into contiguous slabs with selective excitation. This technique used an interleaved multi-slab acquisition so that a single slab was excited and encoded in each TR. Since the encoded FOV is small in the partition direction for each of the slabs, the number of required kz phase encodes, hence the scan time, was reduced while preserving the T₂* contrast. However, multi-slab echo-shift suffers from a couple of disadvantages, namely (i) slab boundary artifacts due to imperfect selective excitation, (ii) reduced slab FOV which makes parallel imaging more difficult along kz axis.

In this work, we propose the Simultaneous Time Interleaved MultiSlice (STIMS) technique to eliminate both issues. Instead of using multiple slabs, this interleaves comb-shaped slice groups using MultiBand (MB) excitation (Fig1). As such, there are no slab boundary artifacts between the interleaved volumes. Because each simultaneously excited slice group spans the entire FOV in the slice direction, parallel imaging has full power to unalias them. It is important to emphasize that STIMS uses phase encoding in the slice direction just like conventional multi-slab 3D GRE, except that the “slabs” are comb-shaped slice groups rather than contiguous slices. This SMS echo-shift approach allows faster acquisition because the slice thickness that needs to be resolved is equal to the gap between the simultaneously excited slices. This divides the maximum kz that needs to be encoded by the echo-shift factor, thus reducing the total number of kz steps.

Fig1.

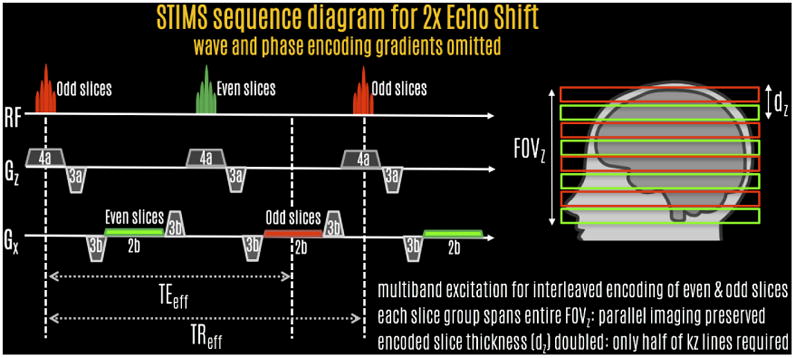
STIMS pulse sequence diagram for 2-fold echo-shift acceleration. The first MultiBand pulse excites odd slices, and the readout is shifted to the second TR. The second RF excites the even slices, with signal readout at the third TR. This allows effective TE to be long, thereby providing increased phase and T₂* contrast. STIMS allows half of the imaging volume to be excited simultaneously, which provides the SNR benefit of volumetric signal averaging. Because the slice thickness that needs to be resolved is doubled for each slice group, the number of kz phase encodes is reduced by half, providing 2-fold acceleration.

For additional efficiency gain, we combine 2-fold STIMS acceleration with Wave-CAIPI acquisition for R=18-fold total speed-up at 3T (R_stims=2, R_wave-caipi=9) and R=24-fold acceleration at 7T (R_stims=2, R_wave-caipi=12). Further, we simultaneously exploit Wave encoding, sparsity prior and random k-space sampling in Compressed Sensing (CS) Wave (Bilgic et al., 2016c; Curtis et al., 2015), and combine this with STIMS to achieve R=30-fold total acceleration (R_stims=2, R_cs-wave=15). Finally, the echo-shift factor is increased to 3-fold to obtain R=45-fold acceleration (R_stims=3, R_cs-wave=15). This permits a 15 sec whole-brain acquisition with 1.5 mm isotropic resolution at 3T, while keeping the effective TE and TR unchanged necessitates doubling the readout bandwidth.

We combine such fast acquisition with a regularized QSM algorithm that estimates the tissue susceptibility distribution from the acquired GRE phase data. The phase image is related to the underlying susceptibility map through an ill-posed linear system, whose solution benefits from prior information in the form of wavelet and gradient sparsity (Wu et al., 2012b). This facilitates the inversion of the linear system while successfully mitigating potential streaking artifacts.

STIMS acquisition with CS-Wave could facilitate the fast acquisition of SWI and QSM contrasts without compromising image resolution or slice coverage. This could find important applications in imaging vulnerable populations e.g. pediatric, while avoiding negative side effects of sedation (Flick et al., 2011; Ing et al., 2012). Rapid acquisition would also permit collecting multiple averages to boost SNR, with the ability to reject motion-corrupted volumes. For neuroscientific studies, STIMS could be impactful in accelerating encoding-intensive techniques that prohibit in vivo human exams, such as COSMOS (Liu et al., 2009) and Susceptibility Tensor Imaging (STI) (Liu, 2010) that require data acquisition at multiple head orientations relative to the main field. By limiting the spatial resolution to 3 mm isotropic, STIMS could also allow undistorted functional MRI acquisition with a sampling rate of 3 sec.

While STIMS exploits the long TE in GRE acquisition for extra image encoding, it is possible to extend it to applications with empty sequence time, such as MP-RAGE (Mugler and Brookeman, 1990), FLAIR (De Coene et al., 1992), VISTA (Oh et al., 2013) and 3D Double Inversion Recovery (DIR) (Geurts et al., 2005) imaging that involve inversion modules.

2. Material and Methods

2.1. Pulse sequence and RF excitation design

Fig1 shows the STIMS sequence with echo-shift gradients applied on both Gx and Gz axes with SMS echo-shift factor of 2 (echo is shifted into the next TR period). In this sequence, the first RF excites the odd slices of the pseudo-3D imaging volume with the signal readout echo-shifted to the second TR, while the second RF excites the even slices with the readout shifted to the third TR. The use of SMS echo-shift enables a comb of slices to be excited simultaneously, allowing desirable volumetric noise averaging while avoiding slice edge profile issues of multi-slab acquisitions. The labels under the gradients indicate their area, which have been designed to spoil the signal coming from the unwanted slice group. For instance, at time TE_eff, the net Gx gradient area odd slices have experienced is equal to zero (−3b + 2b + 3b − 3b + 2b/2 = 0). On the other hand, following the excitation of the even slices, they have experienced a net Gx gradient area of −2b (−3b + 2b/2), effectively spoiling their contribution during readout of the odd slice group.

MultiBand (MB) RF pulses for 2-fold echo-shift acceleration were designed to span 144 mm in the head-foot direction with 1.5 mm slice thickness, corresponding to 96 imaging slices. As such, MB factor 48 was used to excite even and odd slice groups in an interleaved fashion. RF duration was 7.2 ms, Time-Bandwidth Product (TBP) was 4 and the nominal flip angle was 8 degrees.

For 3-fold STIMS acceleration, the head-foot coverage was 135 mm with 1.5 mm slice thickness, this time corresponding to 90 imaging slices. MB factor 30 was used to excite each of the 3 slice groups, with RF duration of 3.2 ms, TBP of 3 and nominal flip angle of 16 degrees. Reducing the TBP and the RF duration permitted a shorter TE, so that three slice groups could interleaved while keeping the effective TE within the range required for optimal susceptibility contrast.

2.2. Sensitivity estimation, coil compression and Wave trajectory estimation

Coil sensitivities for Wave parallel imaging reconstruction were estimated using ESPIRiT (Uecker et al., 2014), as implement in the BART library (Uecker et al., 2015). The estimation was based on low-resolution 3D-GRE data with 64×64×36 matrix size (smallest size achievable with the product sequence) with short TE/TR = 2.3/4.9 ms at bandwidth = 710 Hz/pixel and acquisition time of 11.3 sec. Only the center 16×16×16 points were used in ESPIRiT calibration (corresponding to a 1.3 sec calibration scan). Effect of calibration size is explored in section 2.5. Singular Value Decomposition (SVD) coil compression (Buehrer et al., 2007; Huang et al., 2008) down to 24 channels was applied to speed-up ESPIRiT calibration and Wave reconstruction. 24 channels were selected to ensure that the RMSE (root-mean-squared error) due to compression remained below 1% for the low-resolution calibration data. At 3T, the dominant channel in SVD compression acts as a virtual body coil with smooth phase, allowing high quality coil combination without phase singularities (Chatnuntawech et al., 2016). While SVD compression is a heuristic approach to coil combination, it performs similarly as the Roemer combination (Roemer et al., 1990) that uses an actual body coil acquisition (at 3T, less than 3% difference between virtual- and actual-body coil reference (Bilgic et al., 2016b)).

As demonstrated in (Bilgic et al., 2016a), the assumption that the dominant SVD channel includes a smooth, body-coil like phase breaks down at 7T because the wavelength corresponding to the Larmor frequency is shorter then the size of the head. This leads to increased interaction between the subject and the receive coil, creating receive profiles that vary rapidly across the FOV. As such, a simple SVD becomes insufficient to get a smooth, singularity-free phase. Due to this, an additional low-resolution calibration acquisition was performed with the birdcage reception mode of our custom 7T head array (Keil et al., 2010), as the Siemens Magnetom 7T system lacks a physical body coil. The birdcage image served as a reference with smooth phase in ESPIRiT sensitivity estimation.

Because the actual Wave gradient waveforms played out can differ from the theoretical sinusoidal curves due to system imperfections, the trajectory was estimated from the undersampled data without additional calibration scans using a joint-reconstruction method which estimates the trajectory errors (Cauley et al., 2016). This was done by representing the waveforms as a superposition of 4 complex harmonics, thus requiring the estimation of 16 coefficients (4 real + 4 imaginary numbers each for the Gy and Gz axes). These coefficients were estimated using binary search, where the optimization objective for Wave reconstruction was the data consistency in the SENSE model.

2.3. STIMS Wave-CAIPI acquisition at 3T: (R_stims=2, R_wave-caipi=9)

A healthy male volunteer of age 35 was imaged with a Siemens Tim Trio 3T scanner in compliance with Institutional Review Board (IRB) protocol. Imaging FOV was 216×216×144 mm³, with 144×144×96 matrix size and 1.5 mm isotropic resolution. With these parameters and TE_eff/TR_eff = 35/47 ms, prospectively accelerated Wave-CAIPI acquisition took 36 sec (2-fold echo-shift, 9-fold parallel imaging acceleration using 32 channel product head coil). The readout bandwidth was 90 Hz/pixel, and Wave corkscrew gradients were generated due to maximum gradient strength = 6 mT/m, maximum slew = 30 mT/m/s, and number of sinusoidal cycles = 5. No FOV shift was applied during acquisition. Results from the protocol will be shown in Fig2.

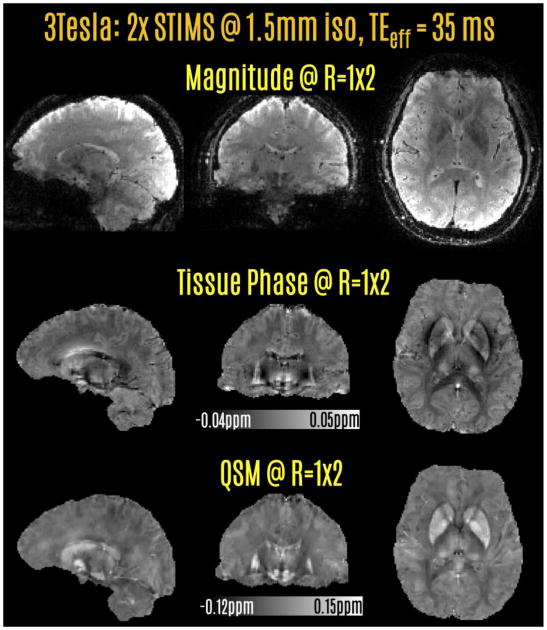
Fig2.

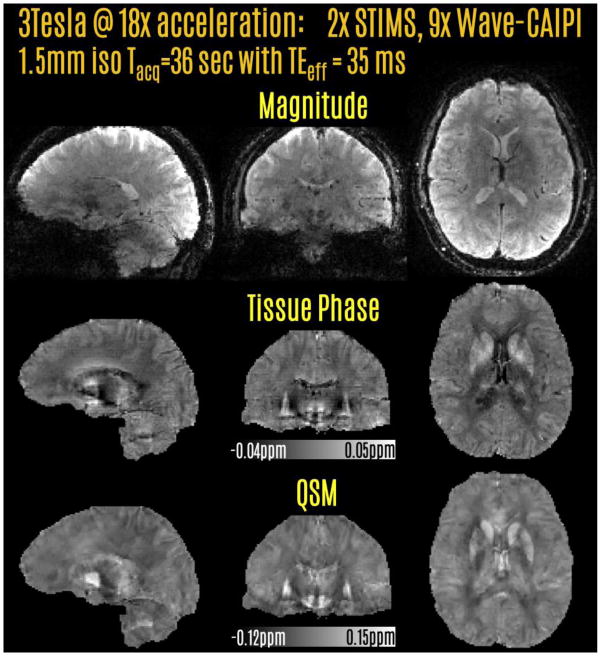
Prospectively accelerated acquisition at 3T using 2-fold SMS echo-shift and 9-fold Wave-CAIPI acceleration. This allowed a 36 sec acquisition with whole-brain coverage and 1.5 mm isotropic resolution. Tissue phase and QSM reconstructions were obtained from this rapid acquisition.

2.4. STIMS Wave-CAIPI acquisition at 7T: (R_stims=2, R_wave-caipi=12)

A healthy male volunteer, age 26, was scanned at the Siemens Magnetom 7T scanner. Salient parameters were, FOV = 240×240×144 mm³, with 160×160×96 matrix size and 1.5 mm isotropic resolution. To allow the TE to be closer to the 20-25 ms range for optimal phase SNR at 7T, the bandwidth was increased to 180 Hz/pixel. This way, TE_eff/TR_eff = 25.5/34 ms was achieved. The prospectively accelerated acquisition took 22 sec using 2-fold echo-shift and 12-fold Wave-CAIPI acceleration with 32 channel custom head array (Keil et al., 2010). Since the readout duration is halved, there is less time to play out the Wave sinusoidal gradients. As such, the parameters were relaxed to max gradient = 9 mT/m, and max slew = 45 mT/m/s to trace a corkscrew with large diameter. No FOV shift was applied during acquisition. Results from this acqusition are shown in Fig3.

Fig3.

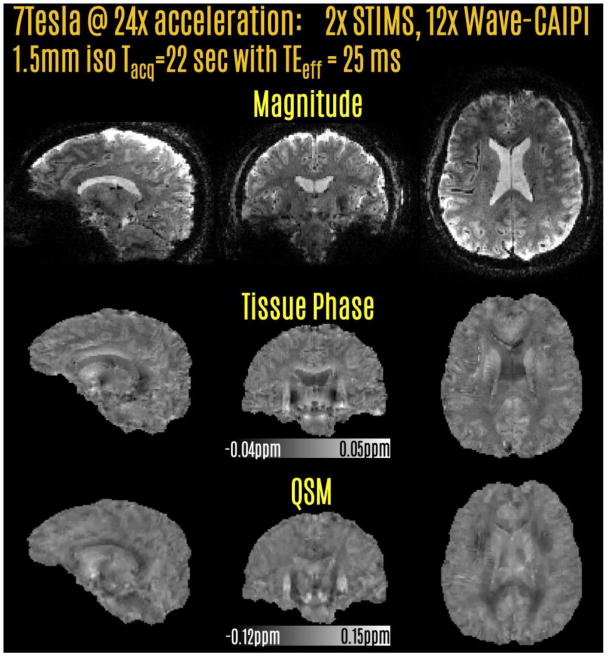
Prospective acceleration at 7T using 2-fold SMS echo-shift and 12-fold Wave-CAIPI. The acquisition time was 22 sec at 1.5 mm isotropic resolution. Tissue phase and QSM contrasts were derived from the raw phase of this reconstruction.

2.5. STIMS CS-Wave acquisition at 3T using 2-fold echo-shift: (R_stims=2, R_cs-wave=15)

To allow random undersampling for CS-Wave reconstruction, fully sampled STIMS data at 2-fold echo-shift factor were collected at 3T. The FOV and matrix size were 240×240×144 mm³ and 160×160×96, while the rest of the parameters were the same as the acquisition in 2.3. The scan time of the fully sampled acquisition was 6 min, and Wave gradients were turned on during the readout. The data were retrospectively subsampled using a variable density Poisson mask (using the poisson routine in BART (Uecker et al., 2015)) for 15-fold CS-Wave acceleration. Reconstruction was performed by solving:

$${\mathit{\text{min}}}_{\rho }{\Vert \mathbf{M}{\mathbf{F}}_{\mathit{y}\mathit{z}}\mathbf{P}{\mathbf{F}}_{\mathit{x}}\mathbf{C}\rho -k\Vert }_2^2+{\lambda }_{\mathrm{g}}{\Vert \mathbf{G}\rho \Vert }_1+{\lambda }_{\mathrm{w}}{\Vert \mathbf{W}\rho \Vert }_1$$

where ρ is the unknown image, M is the undersampling mask, F_yz denotes discrete Fourier transform (DFT) along ky and kz, and P is the point spread function (PSF) that explains the voxel spreading in the readout direction due to Wave trajectory (Bilgic et al., 2015). F_x computes the DFT along kx, C are the coil sensitivity maps, k are undersampled Wave k-space data, and G and W denote 3D image gradient and Haar wavelet transforms. To simplify parameter selection, the regularization parameters λ_g and λ_w were set equal to each other, λ = λ_g = λ_w. Optimization was performed by nonlinear conjugate gradient (Lustig et al., 2007), for details please refer to the accompanying Matlab code and data available at: bit.ly/2iAJ7tS which will also be made available at martinos.org/∼berkin/software

The regularization parameter λ was selected to minimize RMSE relative to the fully-sampled STIMS data with 2-fold echo-shift speed-up, and was found to be λ = 3·10⁻¹⁴. For comparison, Wave-CAIPI reconstruction at uniform R=4×3 acceleration was also performed without CS regularization. This included FOV/3 slice shifting which was selected to minimize RMSE. While the CS-Wave experiment corresponded to a scan time of 24 sec (R_stims=2, R_cs-wave=15), acquisition of a corresponding Wave-CAIPI scan with (R_stims=2, R_wave-caipi=12) would take 30 sec.

The effect of ESPIRiT calibration region on parallel imaging reconstruction has also been quantified using the RMSE metric relative to the fully sampled reconstruction. Calibration sizes of 16×16×16 and 24×24×24 have been compared using 12-fold accelerated Wave-CAIPI reconstruction.

To facilitate QSM reconstruction from multiple head orientations with the COSMOS technique (Liu et al., 2009), two additional fully-sampled acquisitions were made where the subject was asked to move their head to left and right. Such three orientation acquisition would require 3×24=72 sec using 30-fold accelerated STIMS acquisition, ignoring time spent on shimming and coil sensitivity calibration for each head position. Fig4 depicts the resulting reconstructions. Finally, to better judge the quality of CS-Wave reconstructions, magnitude, phase and QSM images from the fully sampled acquisition are also depicted in Fig7.

Fig4.

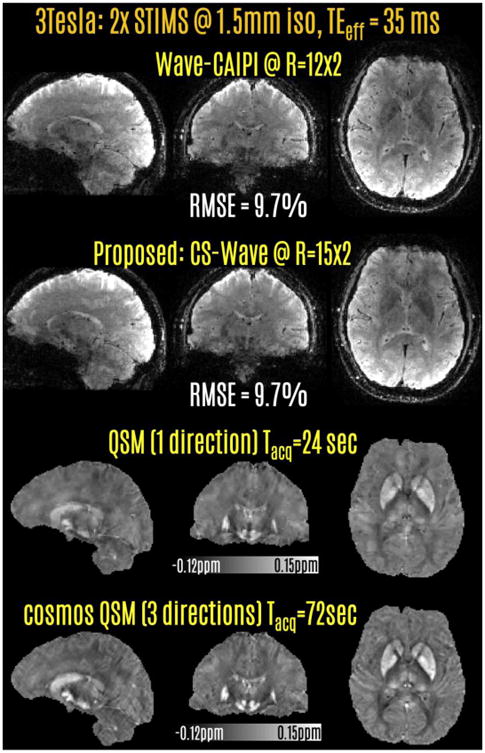
Retrospective acceleration at 3T using 2-fold SMS echo-shift. 12-fold Wave-CAIPI acceleration had similar quality as 15-fold CS-Wave reconstruction. Combination of STIMS and CS-Wave led to a 24 sec acquisition, which yielded the QSM images on the 3^rd row. Merging phase data from 2 additional head orientations further improved the gray/white contrast in QSM, corresponding to a 72 sec acquisition.

Fig7.

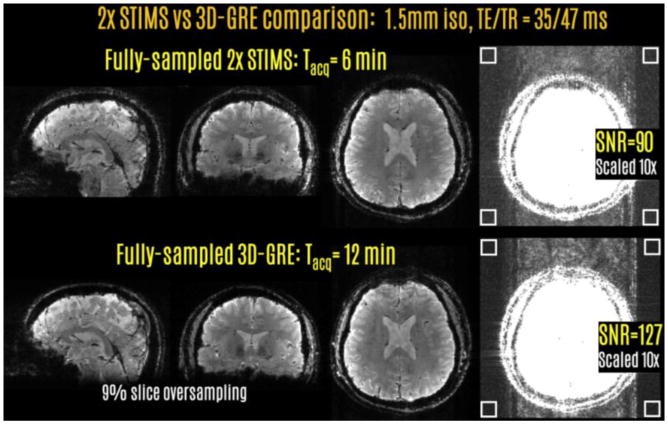
In vivo SNR comparison between the full-sampled STIMS and conventional 3DGRE acquisitions revealed a factor of 1.41 difference. The four white boxes indicate the ROIs of size 12×12 voxels for noise measurement.

2.6. STIMS CS-Wave acquisition at 3T using 3-fold echo-shift: (R_stims=3, R_cs-wave=15)

A final fully-sampled acquisition was performed on the same subject in section 2.5, this time with echo-shift factor 3. In this setting, the first pulse RF excited slices {1,4,…,88} and the echo was shifted to the 3^rd TR. The second MB pulse excited slices {2,5,…,89} was read out during the 4^th TR, and the echo for the third slice group comprising slices {3,6,…,90} was shifted to the 5^th TR. To reduce the effective TE, shorter RF pulses and higher readout bandwidth (200 Hz/pixel) were utilized. These changes led to TE_eff/TR_eff = 38.8/47 ms. FOV and matrix size were 240×240×135 mm³ and 160×160×90. To allow large Wave corkscrew diameter at the higher readout bandwidth, sinusoidal gradient parameters were relaxed to max gradient = 16 mT/m, max slew = 90 mT/m/s using 7 cycles.

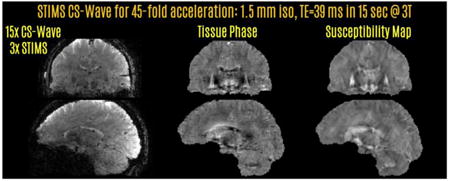
The data were retrospectively undersampled using variable density Poisson pattern to allow 45-fold total acceleration (R_stims=3, R_cs-wave=15) corresponding to a 15 sec scan. The regularization parameter was again λ = 3·10⁻¹⁴. For comparison, Wave-CAIPI reconstruction at the lower acceleration factor of 36 (R_stims=3, R_wave-caipi=12) was also performed. This included FOV/2 slice shift, which yielded the optimal RMSE performance. Fig5 presents the results from this protocol.

Fig5.

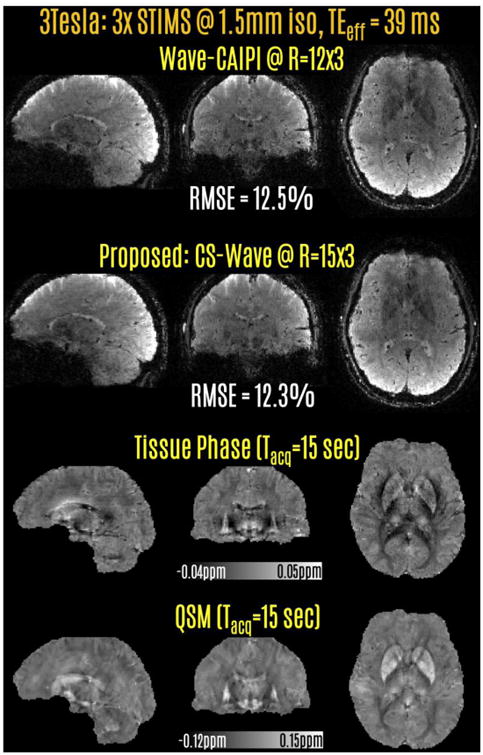
Retrospective acceleration at 3T with 3-fold SMS echo-shift. 15-fold CS-Wave acceleration had slightly better RMSE performance than 12-fold Wave-CAIPI reconstruction. The STIMS CS-Wave at 45-fold acceleration yielded the phase and QSM contrasts on the last two rows from a 15 sec acquisition at 1.5 mm isotropic resolution.

2.7. STIMS and 3D-GRE: phantom comparison at 3T

To provide additional validation, STIMS acquisition with 2-fold echo-shift factor was compared against conventional 3D-GRE. The acquisitions were performed on a spherical water phantom using the same parameter setting as in 2.3, except that both data were collected with fully sampled k-space. To prevent slice aliasing due to the slab selective excitation in the 3D GRE acquisition, 9% slice oversampling was employed. The middle slice was selected for SNR measurement. The images were coil combined using root-sum-of-squares, which allowed noise estimation from the standard deviation of a 24×24 box outside of the phantom. The signal component was taken to be the mean inside the phantom. Rayleigh noise bias was corrected due to (Gudbjartsson and Patz, 1995) to estimate the Gaussian noise standard deviation from the magnitude images. Fig6 shows the results from this comparison.

Fig6.

SNR comparison between the full-sampled STIMS and conventional 3D-GRE acquisitions revealed a factor of 1.43 difference, close to the theoretical √2 difference. The white boxes indicate the ROIs of size 24×24 voxels for noise measurement.

2.8. STIMS and 3D-GRE: in vivo comparison at 3T

A healthy male volunteer, age 26, was scanned following the same protocol in 2.7 to compare the two acquisition methods in vivo. SNR measurements were again performed on the middle slice of the volume. Noise component was estimated from the standard deviation of four 12×12 boxes at the corners of the field of view, so that subtle ghost artifacts could be avoided (Fig7). Signal was taken to be the mean within the brain mask, which was computed using BET (Smith, 2002).

2.9. Phase processing and QSM reconstruction

Reconstructed complex volumes were further processed to produce tissue phase and QSM contrasts. Magnitude images were used to create brain masks with BET (Smith, 2002). Phase images were unwrapped with Laplacian unwrapping (Li et al., 2011; Schofield and Zhu, 2003) and background removal was performed with V-SHARP filtering (Wu et al., 2012b) using a kernel radius of 25 voxels to obtain tissue phase images Φ. These are related to the underlying susceptibility map χ via the ill-posed dipole relation (Marques and Bowtell, 2005) DFχ = FΦ, where D is the dipole kernel and F is the 3D DFT operator. Dipole inversion was performed using the CS compensated formulation in (Wu et al., 2012b), for which the reconstruction parameters were chosen to optimize the RMSE in the 2016 QSM Reconstruction Challenge dataset: qsm.rocks

For the dataset in 2.5, an additional COSMOS reconstruction was performed to fuse the phase data at three different head orientations. This obviated the need for regularization parameter selection, and followed the same phase processing pipeline. For the registration of individual volumes, rigid body transformation matrices were computed based on the magnitude images using FLIRT (Smith et al., 2004), which were then applied to the tissue phase data.

Because the contribution of B₁⁺ transmit profile to the phase images is higher at ultra high field than 3T, an additional phase processing step was applied for the 7T dataset in 2.4. Transmit phase offset presents itself as a dark minimum in the center of the FOV (F Schweser et al., 2011), which was corrected by fitting a 3D polynomial of 4^th order to the V-SHARP tissue phase. The fitted component was then subtracted to yield the final tissue phase, which was processed by QSM dipole inversion.

All computations were performed in Matlab using a workstation with 64 Intel Xeon CPUs and 256 GB memory

3. Results

Common computation times for the following results at 1.5 mm isotropic resolution were 2.4 min for PSF auto-calibration and 2.6 min for Wave-CAIPI reconstruction. Phase and QSM processing were done on a 2-fold zero-padded grid, and required 0.6 min for V-SHARP and 33 min for CS-compensated dipole inversion.

CS-Wave reconstruction time in sections 3.3 and 3.4 was 7.0 minutes, which was a factor of ∼3 longer than the Wave-CAIPI computation time.

3.1. STIMS Wave-CAIPI acquisition at 3T: (R_stims=2, R_wave-caipi=9)

Acquisition with 18-fold prospective acceleration and auto-calibrated Wave-CAIPI reconstruction yielded an image volume with good quality (Fig.2). The raw phase data were processed to provide tissue phase images. QSM images reconstructed with CS-compensated dipole inversion were largely free of streaking or over-smoothing artifacts. The scan time was 36 sec at the long TE_eff of 35 ms.

3.2. STIMS Wave-CAIPI acquisition at 7T: (R_stims=2, R_wave-caipi=12)

Fig.3 depicts the prospectively 24-fold accelerated acquisition at 7T. Successful reconstructions were obtained for magnitude, tissue phase and QSM contrasts. The acquisition time was 22 sec, with a long TE_eff of 25 ms that provided high T₂* and phase contrast.

3.3. STIMS CS-Wave acquisition at 3T using 2-fold echo-shift: (R_stims=2, R_cs-wave=15)

Fig.4 presents the results of the retrospective acceleration experiments using 2-fold echo-shift. Wave-CAIPI at 24-fold undersampling rate had similar RMSE (9.7%) as the CS-Wave reconstruction at the higher acceleration rate of 30-fold. Wave-CAIPI accelerated acquisition corresponded to a scan time of 30 sec, whereas this was 24 sec with CS-Wave acceleration. Fully-sampled data were taken as the reference in RMSE computation.

Last two rows demonstrate QSM results using the CS-Wave reconstructions from a single head orientation with CS-compensated inversion, and from 3 orientations with COSMOS processing. While the single-orientation QSM image from the 24 sec acquisition does not suffer from streaking artifacts, COSMOS reconstruction computed from the 72 sec acquisition appears to provide higher gray/white matter contrast due to the lack of regularization.

While the RMSEs in Fig.4 reflect the reconstruction performance using a calibration region of size 16×16×16, the larger calibration region of 24×24×24 samples led to the same 6.7% RMSE in Wave-CAIPI reconstruction.

3.4. STIMS CS-Wave acquisition at 3T using 3-fold echo-shift: (R_stims=3, R_cs-wave=15)

Reconstructions with 3-fold echo-shift and retrospective undersampling are presented in Fig.5. In this setting, 45-fold accelerated CS-Wave had slightly better RMSE performance (12.1%) than Wave-CAIPI at the lower rate of 36-fold (12.3%). CS-Wave reconstruction corresponded to a 15 sec acquisition, whereas the scan time for Wave-CAIPI would have been 19 sec. The last two rows depict tissue phase and QSM images obtained using the 15 sec CS-Wave data.

3.5. STIMS and 3D-GRE: phantom comparison at 3T

Fig.6 compares the STIMS and 3D-GRE acquisitions with full k-space encoding. The scan time for STIMS with 2-fold echo-shift was 6 min, whereas this was 12 min for 3D-GRE. Measurements on the middle slice revealed that the SNR levels were 359 and 514 for the two acquisitions. This leads to an SNR ratio of 1.43, which is close to the theoretical √2 factor due to the reduced encoding and scan time in STIMS.

3.6. STIMS and 3D-GRE: in vivo comparison at 3T

In vivo STIMS versus 3D-GRE comparison is presented in Fig.7. Estimated SNR levels were 90 and 127 for the two acquisitions, leading to an SNR ratio of 1.41.

3.7. Reconstructions from fully sampled STIMS acquisition at 3T using 2-fold echo-shift

Magnitude, tissue phase and QSM reconstructions from the fully-sampled, 6 min STIMS acquisition are depicted in Fig.8.

Fig8.

Magnitude, phase and QSM reconstructions from the fully-sampled STIMS acquisition with 2-fold echo-shift speed-up.

4. Discussion

The combination of STIMS and CS-Wave techniques allowed up to 45-fold acceleration in long TE acquisitions. While CS-Wave exploits coil sensitivity encoding, random undersampling and transform sparsity, STIMS utilizes the unused sequence time in susceptibility weighted acquisitions for additional spatial encoding. As such, the efficiency gain provided by the two techniques combines multiplicatively. Since SMS echo-shift divides the imaging volume into smaller comb-shaped slice groups, the SNR benefit of 3D noise averaging is diminished by the square root of echo-shift factor. This square root SNR penalty is also present in parallel imaging acceleration, which is further impacted by the g-factor noise amplification. The contribution of STIMS is to provide an additional 2-3 fold efficiency gain multiplicative with parallel imaging, but without the g-factor penalty. This is made possible by the comb-shaped excitation that spans the entire slice FOV, which preserves the coil sensitivity variation in this dimension. An additional benefit of the proposed SMS echo-shift is to avoid slab boundary artifacts present in multi-slab approaches.

CS reconstruction has been found most useful in applications where there are extra dimensions such as time (Jung et al., 2009), b-value (Menzel et al., 2011) or frequency (Chatnuntawech et al., 2015) that facilitate more sparse/compact representation. In GRE neuroimaging with tight FOV and image phase information, sparsity in either wavelet or gradient transforms is compromised and may lead to decreased return from the CS prior. In this work, retrospectively undersampled experiments demonstrated the benefit of CS-Wave in allowing higher acceleration rates than Wave-CAIPI. This made it possible to attain 15-fold undersampling with similar or slightly better RMSE performance than Wave-CAIPI at 12-fold acceleration. STIMS CS-Wave can thus allow rapid acquisition of the clinically important, but time consuming SWI contrast, as well as tissue phase and QSM images that yield quantitative and high-CNR information. It would also enable efficient acquisition of encoding intensive multi-orientation methods such as COSMOS and STI, and facilitate the clinical translation of these promising techniques that are currently limited to research studies and ex vivo specimens. For instance, the 15 sec STIMS CS-Wave acquisition would allow a 5 min STI exam with 12 orientations at 1.5 mm isotropic resolution, including time spent for repositioning and calibration (15 sec × 12 = 180 sec = 3 min, plus an extra 2 min for preparation).

Below, we discuss potential limitations of STIMS and how these can be mitigated, as well as future directions for extending its application.

Even though STIMS CS-Wave allows dramatic acceleration rates in 3D imaging, this comes at the cost of intrinsic √R penalty on image SNR. This √R penalty is not specific to STIMS acquisition, but instead an inherent loss common to all undersampled acquisition schemes. E.g. R=45-fold total acceleration would have an intrinsic ∼6.7-fold SNR penalty relative to the fully sampled acquisition, due to (i) dividing the image volume into multiple slice groups in echo-shift (less volumetric averaging), and (ii) k-space undersampling due to parallel imaging acceleration.. Such penalty would limit the achievable voxel sizes with clinically desirable SNR levels. While the presented results were at the isotropic resolution of 1.5 mm, reducing the voxel size to 1 mm isotropic would require ∼11 signal averages to achieve similar SNR.

We think that there are a few ways to address the intrinsic SNR problem. First is going to higher field strength, which we discuss in more detail below. A second way is to acquire multiple averages very rapidly, then register the individual volumes with the ability to reject motion-corrupted volumes. Scaling the scan time of the 15 sec acquisition at 1.5 mm resolution to 1 mm isotropic voxel size, we would get a 35 sec acquisition per average, which would help mitigate patient motion especially in vulnerable populations (e.g. pediatric, elderly). A third strategy is to exploit the inherent signal averaging in multi-orientation QSM imaging. Using 3 acquisitions at different head orientations, COSMOS technique both mitigates the dipole streaking artifacts in QSM reconstruction, and boosts the SNR by merging multiple measurements. Similarly, STI technique combines at least 6 head orientations to estimate susceptibility anisotropy, which would enjoy similar signal averaging during reconstruction.

Susceptibility weighted acquisitions at ultra high field benefit both from increased SNR and reduction in required TE for optimal phase contrast. Achieving such shorter TE poses a couple of constraints in echo-shift imaging. For our experiments at 7T, we limited the echo-shift factor to 2 and increased the readout bandwidth to shorten the effective TE. Going to 3-fold STIMS acceleration while remaining in the 20-25 ms effective TE range would require a large increase in the bandwidth, which would negatively impact the image SNR. An alternative direction could be to shorten the RF duration while keeping to within the system peak voltage limit by using pulse design techniques such as VERSE (Conolly et al., 1988) and optimized phase scheme (Wong, 2012). Shortening the RF duration would normally exacerbate the RF heating and SAR problems, but this is unlikely to be an issue for T₂* weighted imaging that uses low flip angles. Although 3-fold echo-shift factor may not be easily achieved at ultra high field, the reduction in optimal TE permits shorter TRs, and lead to shorter scans. An additional benefit is the increased spatial variation in coil sensitivities, permitting higher parallel imaging acceleration rates than 3T (Wiesinger et al., 2004). Combination of these two factors allowed 24-fold prospective acceleration at 7T, with TE_eff of 25 ms and scan time of 22 sec (Fig.3).

Another consideration is the effect of the slice profile on the susceptibility maps, which require 3D processing due to the nature of the dipole deconvolution. Increasing the TBP of the MultiBand pulses would mitigate this concern, with the usual trade-offs involving increased pulse duration and/or SAR. Recent algorithmic developments have also enabled slice-by-slice processing of phase and QSM from 2D acquisitions while retaining the fidelity relative to their 3D counterparts (Kaaouana et al., 2015; Sun and Wilman, 2015; Wei et al., 2017). Using SMS excitation with a large MB factor have prevented us from achieving the Ernst angle for the 2-fold echo-shift acquisitions. This was due to the peak voltage limitation, which constrained us to use an 8-degree flip angle rather than the Ernst angle of 16 degrees (assuming an average brain T₁ of 1.2 sec and TR of 47 ms). Despite the two-fold difference between the two flip angles, the signal level (1−E)·sinα/(1−E·cosα) in the Ernst angle acquisition would have been only 25% larger, where α is the flip angle and E = e^−TR/T1. This 25% SNR loss could be recovered by reducing the peak voltage using VERSE (Conolly et al., 1988) and phase scrambling (Wong, 2012).

While increasing the readout bandwidth to achieve a shorter TE at 7T, we have also opted to increase the Wave gradient and slew rate parameters (max gradient = 9 mT/m, and max slew = 45 mT/m/s instead of 6 mT/m and 30 mT/m/s). The rationale behind this selection was that employing shorter readouts with the same parameters could limit the attained g-factor benefit. Our recent work analyzed the dependence of g-factor performance on the wave parameters (Polak et al., 2017). This analysis indicated that increasing gradient amplitude results in improved g-factor, which is largely independent of the number of cycles. Meanwhile, increasing the number of cycles necessitates larger gradient slew rates to achieve the same maximum gradient amplitude. For most readout bandwidths employed in spin-warp imaging, there are many parameter combinations that would yield similar g-factor performance. For instance, at BW=200 Hz/pixel, the number of cycles can be chosen arbitrarily between 3 to 15, and maximum gradient amplitude of 10 mT/m provides very similar g-factor performance (Polak et al., 2017) (supporting Figure 1). The parameter selection is more important in applications such as EPI, where BWs as high as 2000 Hz/pixel are used. Slew rate becomes the limiting factor in this scenario, preventing large maximum gradient amplitude to be realized. In such cases, using as few as 1-2 cycles would allow this limitation to be mitigated.

CS-Wave provided higher acceleration rates than Wave-CAIPI with similar image quality (Figs.4&5), but this came at the cost of ∼3-fold longer reconstruction time. Another drawback of CS reconstruction is the selection of the regularization parameter. In both datasets, the same parameter (λ = 3·10⁻⁴) provided the best RMSE performance. So it is likely that the same parameter value could generalize to other acquisitions, provided similar data scaling, matrix size and contrast. To simplify this selection, we set both wavelet and total variation (TV) parameters to the same value, which might have led to slightly sub-optimal RMSE performance in CS-Wave reconstruction. While this work employed RMSE as a measure of image quality, this does not always reflect visual image quality as experienced by human readers. Other metrics such as structural similarity (SSIM) (Wang et al., 2004) aim to amend this issue, and have been mainly used in image processing literature.

Functional MRI (fMRI) acquisitions dominantly rely on echo planar imaging (EPI) readout. SMS (Feinberg and Setsompop, 2013; Uğurbil et al., 2013) and 3D EPI techniques (Narsude et al., 2016; Poser et al., 2013) allow high acceleration rates that can be traded off between faster temporal sampling (high MB or Rz) and reduced geometric distortion (high Ry). An alternative way to minimize geometric distortion could be using spin-warp fMRI with STIMS acceleration. Reducing the spatial resolution of 45-fold accelerated STIMS CS-Wave acquisition to 3 mm isotropic would allow the temporal sampling rate to be under 3 sec (e.g. FOV=222×222×126 mm³, matrix=74×74×42, TR=44 ms). STIMS fMRI could help investigate frontal regions such as the orbitofrontal cortex, which are otherwise heavily impacted by the distortion in EPI readout.

3D EPI is also a prime candidate for fast structural imaging, allowing SWI and QSM acquisition at 1 mm isotropic resolution with whole-brain coverage in just 10 sec (Langkammer et al., 2015). To boost SNR, several repetitions of this acquisition can be registered and averaged as well. The main drawbacks of 3D EPI are the T₂* blurring due to the long echo-train readout, and the geometric distortion due to the B0 inhomogeneity. While deploying 2DCAIPI in 3D EPI have allowed 10-fold reduction in distortion (Narsude et al., 2016; Poser et al., 2013), this has come at the cost of ∼30% average SNR penalty due to g-factor noise amplification. Segmented 3D EPI is another effective way to mitigate distortion, allowing efficient and high resolution imaging (Sati et al., 2014). This leads to some reduction in acquisition speed, making it comparable to Wave-CAIPI acquisition (0.55 mm isotropic in 4 min in (Sati et al., 2014) versus 0.5 mm isotropic in 5 min in (Bilgic et al., 2016)). STIMS with CS-Wave addresses the T₂* blurring, geometric distortion and g-factor amplification shortcomings of 3D EPI. The trade-offs are that 3D EPI enjoys faster acquisition speed, reduced motion sensitivity and higher SNR-efficiency because of the long data-sampling period per excitation.

In addition to using the empty sequence time in long TE acquisitions, it could also be possible to utilize the inversion time in sequences such as MPRAGE (Mugler and Brookeman, 1990), FLAIR (De Coene et al., 1992) and VISTA (Oh et al., 2013) for extra image encoding. MPRAGE is a 3D sequence that provides excellent gray/white matter contrast, and is routinely used as anatomical reference. FLAIR is a 2D spin echo acquisition with inversion preparation to null the CSF signal, and has found widespread application in clinical protocols. VISTA is a more recent 2D sequence that isolates the signal from myelin water. Because it includes double inversion recovery preparation, acquisition for this encoding intensive technique takes 2-3 min per imaging slice. Deploying STIMS with CS-Wave in these sequences could simultaneously utilize parallel imaging and empty sequence time due to inversion modules to permit >20-fold acceleration.

Recent advances in image reconstruction such as LORAKS (Haldar, 2014; Haldar and Zhuo, 2016; Kim et al., 2016) exploit low rank, spatial support and phase constraints. Making use of these constraints in STIMS reconstruction could allow even higher acceleration rates than CS-Wave, which currently exploits only sparsity priors in wavelet and TV domains. LORAKS is also successful in leveraging partial-Fourier type sampling patterns, which would be more applicable to MPRAGE, VISTA (short TE) and FLAIR (spin echo) acquisitions where conjugate symmetry assumptions are more valid than SWI at long TE.

5. Conclusions

This work introduced the STIMS echo-shift technique, which was combined with CS-Wave to allow dramatic acceleration rates. While CS-Wave harnesses coil sensitivity encoding, incoherent sampling and image sparsity, SMS echo-shift utilizes empty sequence time in long TE acquisitions for extra spatial encoding. The comb shaped slice groups that are excited in an interleaved fashion avoid slab boundary artifacts present in conventional multi-slab echo-shift acquisition, and does not decrease the parallel imaging capability. The efficiency gain provided by the two techniques combines multiplicatively, allowing up to 45-fold speed-up using 15-fold CS-Wave and 3-fold STIMS acceleration. This permits a 15 sec acquisition with whole brain coverage at 1.5 mm isotropic resolution and long TE required for SWI, QSM and STI applications. Future extensions include spin-warp fMRI and faster MPRAGE, FLAIR and VISTA acquisitions.

Highlights.

• STIMS exploits unused time in long TE scans for extra encoding using SMS echo-shift

• Compressed Sensing (CS) Wave harnesses sensitivity encoding and sparsity

• Combination of STIMS with CS-Wave allows 45-fold accelerated 3D-GRE

• STIMS is a general concept that could improve efficiency in e.g. MP-RAGE and FLAIR