A Method to Predict the 3D Structure of an RNA Scaffold

Abstract

The ever increasing discoveries of noncoding RNA functions draw a strong demand for RNA structure determination from the sequence. In recently years, computational studies for RNA structures, at both the two-dimensional and the three-dimensional levels, led to several highly promising new developments. In this chapter, we describe a recently developed RNA structure prediction method based on the virtual bond-based coarse-grained folding model (Vfold). The main emphasis in the Vfold method is placed on the loop entropy calculations, the treatment of noncanonical (mismatch) interactions and the 3D structure assembly from motif-based template library. As case studies, we use the glycine riboswitch and the G310-U376 domain of MLV RNA to illustrate the Vfold-based prediction of RNA 3D structures from the sequences.

1 Introduction

To perform crucial cellular functions, RNA molecules fold up to form compact three-dimensional (3D) structures [1–5]. The RNA structure determination by experiments alone cannot keep up the pace with the ever increasing number of RNA sequences and new functions. The gap between the number of known RNA 3D structures and the number of biologically significant RNA sequences underscores more than ever the request for accurate computational models for RNA structure prediction.

An RNA structure can be described at the two-dimensional (2D) and three-dimensional (3D) levels. A 2D structure is defined as the sum of all the base-base pairs in the structure, including long-range base pairs in tertiary folds. Computational prediction of RNA 2D structures falls into two categories [6–10]: sequence comparison (alignment) analysis and free energy-based modeling. In general, sequence comparison-based methods can give more reliable predictions than free energy-based methods, but it depends on the availability of homologous sequences and often cannot directly provide information about the alternative structures. For the free energy-based modeling, a key problem is to determine the helix stabilities and loop free energies. The free energy parameters for a helix stem can be calculated from the Turner experimental data [11], but the loop free energy requires a model.

The recently developed Vfold model is a statistical mechanics-based RNA folding model. The model relies on a coarse-grained (virtual bond) representation of RNA structures [12–14]. Compared with other free energy-based RNA 2D structure prediction models, such as Mfold [15] and RNAstructure [16], the Vfold model computes loop entropy parameters from explicit conformational sampling. Furthermore, by enumerating all the possible (sequence-dependent) intra-loop mismatches, the Vfold model partially accounts for the sequence-dependence of the loop free energy. Through application to a broad range of experimental and biological problems, the Vfold-based predictions have shown to be able to provide novel insights for RNA mechanisms, such as pseudoknot-involved conformational switch between bistable secondary structures [17], microRNA–gene target interactions [18], and RNA–RNA kissing dimerization in viral replication [19, 20].

Knowing RNA 2D structures alone is often not sufficient to understand RNA function. We also need RNA 3D structure information in order to understand the interactions between RNA and other molecules and RNA functions [21–24]. One way to predict RNA 3D structure is to combine a coarse-grained RNA structure model with the knowledge-based force field and fold the RNA through discrete molecular dynamics (DMD) simulations [25–28]. Due to the limitation of conformational sampling, this method would be most suitable for short RNAs or large RNAs with auxiliary constraints from experimental data. Based on the assumption that 3D structure is more conserved and can be recognized by the alignment of sequences and structure motifs, (3D structure) template-based modeling has become a promising method in RNA 3D structure predictions [29–31]. The template-based methods build RNA 3D structures using known structures ranging from fragments of 1–3 nucleotides to larger structural motifs. One of the common limitations for the template (structure assembly) approaches is the completeness of the fragment library. The lack of reliable structural motifs for many loops and junctions greatly hampers the success of accurate 3D structure prediction.

For a given 2D structure, the Vfold-based 3D structure prediction method searches for the appropriate template for each loop/junction in the structure, and assembles the 3D template structures into a scaffold for further structure refinement. In comparison with other template-based (structure assembly) methods such as FARNA/FARFAR [29] and MC-Sym [31], which sample structures from small fragments of known RNA structures, the Vfold-based method uses motif-based instead of fragment-based templates.

2 Algorithms

2.1 RNA Motif-Based Loop Entropy

Using two virtual bonds per nucleotide to represent the backbone conformation, the Vfold model samples fluctuations of loops/ junction conformations in 3D space through conformational enumeration (see Fig. 1). By calculating the probability of loop formation, it gives the conformational entropy parameters for the formation of the different types of loops such as hairpin, bulge, internal, pseudoknot loops. The model has the advantage of accounting for chain connectivity, exclude volume and the completeness of conformational ensemble.

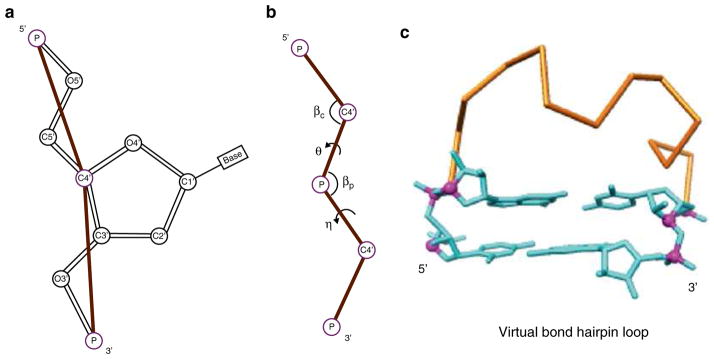
Fig. 1.

Vfold computes loop entropies by sampling virtual bond conformations in 3D space. (a) Virtual bond representation: two bonds (P-C4′ and C4′-P) per nucleotide. (b) The bond angles (β_c, β_p) and the torsional angles (θ, η) for the virtual bonds. Vfold enumerates RNA backbone conformations on a diamond lattice with bond length of 3.9 Å, bond angle of ~109.5° and three equiprobable torsional angles (60°, 180°, 300°). (c) A virtual bond backbone conformation of a hairpin loop, with two ends fitted to the base pair structure in an A-form helix

1. Enumerate all the possible virtual bond backbone conformations for a given chain length (see Note 1) and count the total number Ω_coil of the conformations.

2. From the conformational ensemble above, identify the loop conformations according to the loop closure condition. For example, for hairpin loops, the two ends of a loop conformation should be fitted to an A-form base pair. Count the total number Ω_loop of loop conformations.

3. Calculate the loop entropy ΔS_loop = k_B 1n (Ω_loop / Ω_coil). Here, k_b is the Boltzmann constant.

4. Vfold computations lead to pre-tabulated entropy parameters for hairpin loops [12], internal/bulge loops [12], H-type pseudoknots with/without inter-helix junction [32, 33] and hairpin-hairpin kissing motifs [19].

2.2 RNA Motif-Based Template Library

The (3D structure) template library was built from 2,621 PDB structures (see Note 2), including RNA-involved complexes. It contains 3D templates for hairpin loops, internal/bulge loops, H-type pseudoknots, and multibranched junctions.

1. For a given RNA 3D structure, extract the A-form helices. From the information of helices and base pairs, the corresponding 2D structure is determined.

2. Identify all the non-helix 2D structure motifs for the given 3D structure.

3. Remove the redundant templates for those with root mean square deviation (RMSD) ≤1.5 Å for the same motif, same size, and identical sequence.

4. Collect all the nonredundant motif structures to construct a template library. Table 1 shows the statistics for the current template library.

Table 1.

RNA motif-based template library

Motif name	Number of templates
Hairpin loops	2,366
Internal/bulge loops	3,260
3-way junctions	820
4-way junctions	506
5-way junctions	222
6-way junctions	49
7-way junctions	61
H-type pseudoknots	56

3 Methods

To predict RNA 3D structures, Vfold first predicts the 2D structures from the sequence. Using the 2D structures as constraint, the model then predicts the corresponding 3D structures.

3.1 RNA 2D Structure Prediction from the Sequence

The key of the free energy-based RNA 2D structure prediction is the enthalpy and entropy parameters used to evaluate the stability of sampled structures. The enthalpy and entropy for the canonical and mismatched base stacks are calculated from Turner’s experimental data. The loop entropies are from the Vfold pre-tabulated parameters.

1. Enumerate all the possible base pair arrangements (2D structures), including H-type pseudoknots with/without inter-helix loops and non-pseudoknotted secondary structures, for a given RNA sequence (see Note 3).

2. For each helix, calculate its free energy ΔG_helix (see Note 4) as a sum of the free energy ΔG_stack of each constituent base stack: $\mathrm{\Delta }{G}_{\text{helix}}={\displaystyle \sum _{\text{stack}}}\mathrm{\Delta }{G}_{\text{stack}}$ based on the nearest-neighbor model, where ΔG_stack is determined from Turner’s experimental parameters¹¹ (see Note 5).

3. Enumerate all the possible intra-loop mismatches and compute the loop free energy for each given set of intra-loop mismatches (see Note 6) (see Fig. 2 for a hairpin loop for illustration). The loop free energy ΔG_loop is calculated (see Note 4) from the loop partition function Q_loop , the Boltzmann sum over all the possible arrangements of intra-loop mismatched base stacks:

   $$\mathrm{\Delta }{G}_{\text{loop}}=-k_{\mathrm{B}}Tln{Q}_{\text{loop}},Q_{\text{loop}}=\sum _{\text{mismatches}}{\mathrm{e}}^{-\left(\mathrm{\Delta }{G}_{\text{mm}}-T\mathrm{\Delta }{S}_{\text{loop}}\right)/k_{\mathrm{B}}T}$$

   Here ΔG_mm is total free energies of the mismatched base stacks and ΔS_loop is the loop entropy for the given intra-loop mismatch constraints.

4. Assign the free energy for each sampled 2D structure: ΔG_s = ΔG_helix + ΔG_loop.

5. Calculate the total partition function as the sum over all the possible (2D) structures:

   $$Q_{\text{tot}}=\sum _{\text{structures}}{\mathrm{e}}^{-\mathrm{\Delta }{G}_{\mathrm{s}}/k_{\mathrm{B}}T}$$

6. Following the similar procedure as above for the total partition function, compute the conditional partition function Q_ij for all the 2D structures with nucleotides i and j base paired.

7. Calculate the probability of forming the (i, j) base pair: p_ij = Q_ij / Q_tot.

8. From the base pairing probability for all the possible (i, j) pairs, extract the predicted most probable (see Note 7) as well as alternative structures.

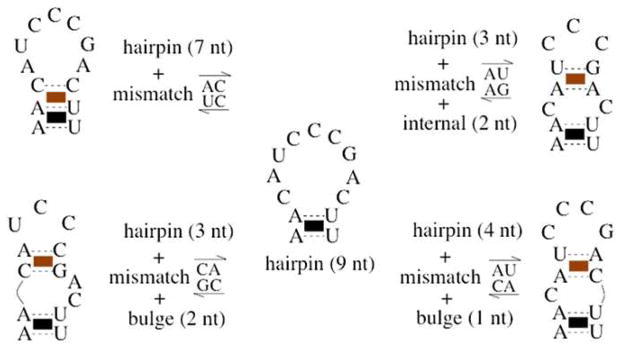
Fig. 2.

Ensemble of a 9-nt hairpin loop closed by an A–U base pair, containing five different arrangements of mismatched base stacks within the loop

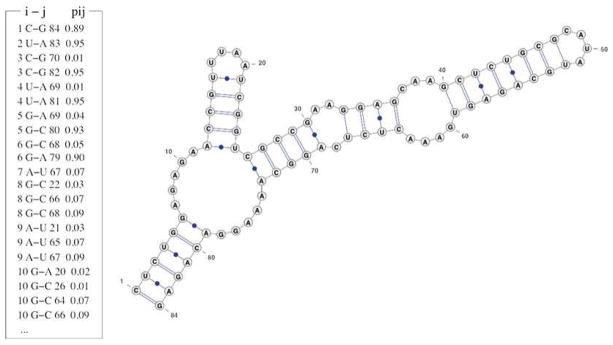
We use the glycine riboswitch (PDB: 3owi) as an example to show how Vfold predicts the 2D structure. Given the 84-nt RNA sequence of the glycine riboswitch (see Note 8), Vfold calculates the base pairing probabilities pij for all the possible base pairs. The predicted most probable 2D structure (see Note 7) can be predicted from pij, as shown in Fig. 3. It should be noted that depending on the sequence, the Vfold model predicts all the stable structures, including the most probable (most stable) structure as well as the alternative (metastable) structures. Therefore, it is recommended to also find out the possible alternative structures from the base pairing probabilities.

Fig. 3.

Left: Partial list for the predicted base pairing probabilities for the glycine riboswitch. The first two columns are the position and the nucleotide type of residue i; the fourth and fifth columns are the nucleotide type and position for residue j; the last column is the probability of forming the i, j base pair. Right: predicted most probable 2D structure derived from the base pairs with probability p_ij around 0.90 (e.g., 0.89, 0.95)

3.2 RNA 3D Structure Prediction for a Given 2D Structure

The Vfold model predicts the 3D structure from a 2D structure by assembling motif-specific structural templates. Currently, due to the limited structural template database, Vfold can only predict the 3D structures with hairpin loops, internal/bulge loops, multi-branched junctions and pseudoknots.

1. Identify the structure motifs (such as hairpin loop, internal loop, pseudoknot loop, and three-way junction) from the given 2D structure.

2. Build the virtual bond 3D structure for helices according to the A-form helix template.

3. For each non-helix motif, search for the best templates from the template library. The search criteria are based on the size (first) and sequence (second) matches (see Note 9).

4. From the (all-atom) templates found in the previous step (see Notes 10 and 11), build the virtual bond 3D structures of each motifs.

5. Assemble the virtual bond 3D structure of the motifs to construct the 3D scaffold of the whole RNA.

6. Add bases to the virtual bond backbone according to the templates for base configurations (see Note 12).

7. Refine the 3D structure by AMBER energy minimization (see Note 13).

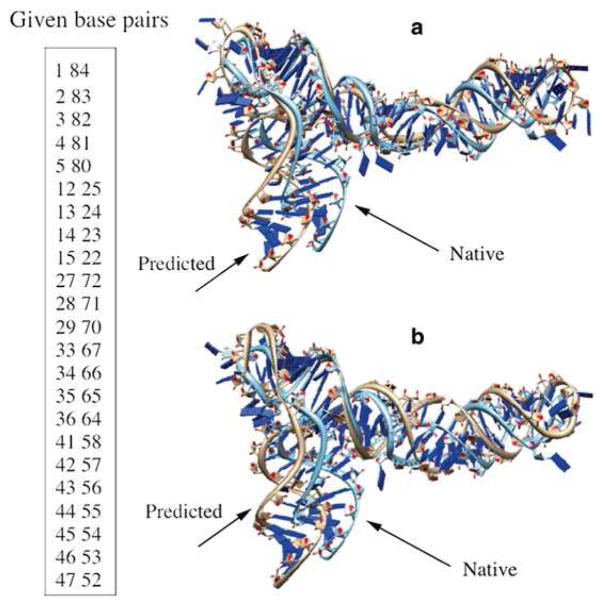
We use the glycine riboswitch (PDB: 3owi) case for the illustration of the 3D structure prediction. For the purpose of 3D structure prediction, we list only the canonical base pairs in the 2D structure and treat noncanonical base pairs as part of the loop/ junction structure (see Fig. 3). The predicted 2D structure shows a three-way junction, two internal loops, two hairpin loops and five helices. If the motif structure in the glycine riboswitch is included in the template library, as shown in Fig. 4a, the RMSD between the predicted structure and the experimentally determined structure is 6.3 Å. This RMSD is smaller than the previous prediction of 7.24 Å, shown in Fig. 4b, which excluded the native templates in the template library.

Fig. 4.

Given the base pairs shown in the left, the predicted 3D structures (a) with and (b) without including templates from the native structure in the template library, respectively, and the comparisons with the PDB structures (PDB: 3owi) for the glycine riboswitch. The RMSDs are (a) 6.3 Å and (b) 7.2 Å , respectively

It should be noted that even with the native templates included in the template library, the predicted structure still shows a non-zero RMSD with the PDB structure. The small difference between the A-form helix and the real (slightly distorted) RNA helix (see Note 14) could results in a notable structural difference in the global fold.

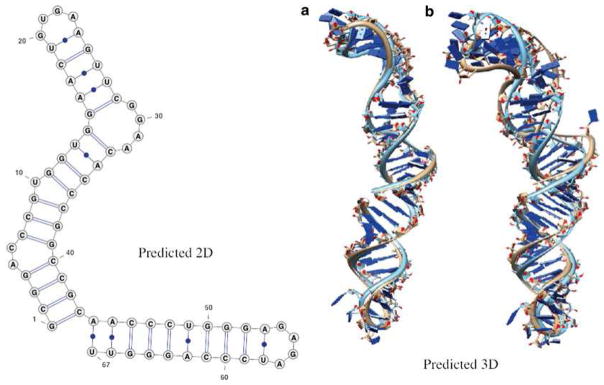
As another example, we predict the 3D structure for the G310-U376 domain of MLV RNA (see Note 15). Vfold correctly predicts the 2D structure (see Note 16) (see Fig. 5). If the native motif structure (PDB: 1s9s) is not included in the template library, we find a larger RMSD between the predicted and the PDB structure.

Fig. 5.

The prediction of the G310-U376 domain of MLV RNA. The RMSDs between the predictions (a) with and (b) without templates from the native structure and the experimentally determined all-atom structure (PDB: 1s9s) are 3.1 Å and 7.0 Å, respectively. Vfold correctly predicts its 2D structure, shown in the left

Because the template-based 3D structure prediction algorithm relies on the knowledge of the known structures, we can realistically expect continuous improvements in the quality of the structure prediction as more and more structures are solved.