Discrimination of Native-like States of Membrane Proteins with Implicit Membrane-Based Scoring Functions

Abstract

A scoring protocol based on implicit membrane-based scoring functions and a new protocol for optimizing the positioning of proteins inside the membrane was evaluated for its capacity to discriminate native-like states from misfolded decoys. A decoy set previously established by the Baker lab (Proteins (2006), 62, 1010–1025) was used along with a second set that was generated to cover higher resolution models. The Implicit Membrane Model 1 (IMM1), IMM1 model with CHARMM 36 parameters (IMM1-p36), generalized Born with simple switching (GBSW), heterogeneous dielectric generalized Born version 2 (HDGBv2) and 3 (HDGBv3) were tested along with the new HDGB van der Waals (HDGBvdW) model that adds implicit van der Waals contributions to the solvation free energy. For comparison, scores were also calculated with the distance-scaled finite ideal-gas reference (DFIRE) scoring function. Z-scores for native state discrimination, energy vs. root mean square deviation (RMSD) correlations, and the ability to select the most native-like structures as top-scoring decoys were evaluated to assess the performance of the scoring functions. Ranking of the decoys in the Baker set that were relatively far from the native state was challenging and dominated largely by packing interactions that was captured best by DFIRE with less benefit of the implicit membrane-based models. Accounting for the membrane environment was much more important in the second decoy set where especially the HDGB-based scoring functions performed very well in ranking decoys and providing significant correlations between scores and RMSD that show promise for improving membrane protein structure prediction and refinement applications. The new membrane structure scoring protocol was implemented in the MEMScore web server (http://feiglab.org/memscore).

TOC image

INTRODUCTION

Membrane proteins play important roles in many cellular processes, ranging from intercellular signal transduction to the transport of small molecules across cell membranes.¹ Membrane proteins are also targeted by more than half of the currently approved drugs on the market.² Information about the three-dimensional structure of membrane proteins is crucial in understanding their function and assisting structure-based drug design. At the same time, experimental structure determination of membrane proteins continues to be difficult. The rate of new membrane structures that are being solved remains low and structures of membrane proteins constitute only around 1% of all available structures in the Protein Data Bank (PDB)³.

Computational structure prediction is a powerful alternative that can compensate for the experimental challenges. Structure prediction methods are generally classified into two main categories: 1) template based methods,^4–8 which utilize a structure from a related sequence as the template for structure prediction, and, 2) ab initio methods,^9–14 that do not rely on known structures and employ extensive sampling to optimize conformations according to an energy function. Modern prediction algorithms often use a hybrid protocol where partial template-based structure fragments are combined via sampling. For membrane protein structures, the lack of known structures generally limits simple homology modeling.^15–18 Instead, a hybrid assembly protocol⁹ is often most successful where the presence and location of transmembrane helices is initially predicted,^19–23 the overall topology of the protein is determined,^{19, 24} and helices are then assembled to form tertiary structure candidates.^{15–17, 25–27} The crucial final step following the generation of models is the application of a scoring function to find the structure presumed to be closest to the true native structure according to the most favorable score. Protein structure scoring functions are also important for computational protein design^28–29 and during protein structure refinement of template-based models.^30–32

Protein structure scoring functions can also be categorized into two general categories: 1) physics-based functions that use optimized force fields and solvation models and, 2) knowledge-based functions that rely on statistical information derived from known structures.³³ As a result of extensive optimization and an effective reduction of noise, knowledge-based scoring functions are often more successful when evaluating models of aqueous solvent proteins.^{7, 34–39} Knowledge-based scoring functions for membrane proteins have not been developed as extensively, in part, again, because of more limited available structures, but also because the membrane environment provides a complex physicochemical environment that is more difficult to capture with a simple statistical approach. The careful application of physics-based energy ranking can also provide significant discrimination of native-like structures in aqueous solution.^{33, 40} For membrane proteins, physics-based scoring functions may offer advantages by more competently capturing the balance between different interactions in aqueous solvent and in the membrane interior faced by membrane proteins.

A common approach in physics-based scoring functions is to combine an atomistic force field with an implicit solvent or membrane model so that the solvent degrees of freedom can be accounted for instantaneously. This idea has been applied to water soluble proteins^40–43 and more recently also to membrane protein structures by Yuzlenko and Lazaridis⁴⁴. In the latter study, physics-based scoring using implicit membrane models was used to evaluate decoys from five transmembrane protein test sets provided by the Baker laboratory¹⁷ (bacteriorhodopsin (BRD7), rhodopsin (RHOD), V-ATPase (VATP), fumarate reductase (fmr5), and lactose permease (ltpA)). The study compared the Implicit Membrane Model 1 (IMM1),⁴⁵ the Generalized Born with simple SWitching (GBSW)⁴⁶ and an early version of the Heterogeneous Dielectric Generalized Born (HDGB)⁴⁷ model, all of which resulted in good native-state discrimination relative to the energies of the decoys as measured by Z-scores. However, a relative ranking of decoys and identification of the most native-like decoy, which is more important in practical applications where the native structure is not known, was problematic due to poor correlation between the scores and RMSD values. This suggests a need for improvement for the scoring protocol. While improvements in the actual scoring energy function may be possible, an effective protocol for optimizing the position and orientation of a given decoy within the membrane is also critical since scoring of protein structures depends on how they are placed within the membrane. Finally, another issue is the choice of decoys. If the decoys are not sufficiently native-like for scoring functions to be able to reliably distinguish more native-like from less native-like structures, the performance of any scoring function would be expected to be poor. Therefore, decoy sets with additional structures closer to the native state could offer further insights into how well membrane protein scoring functions can perform.

In this study, we are revisiting the scoring of membrane protein structures using physics-based scoring function with implicit membrane models. In particular, we tested a recently improved version of the HDGB implicit membrane model including a van der Waals term that better describes amino acid interactions within the membrane (HDGBvdW)⁴⁸ but results are also compared with IMM1⁴⁵, GBSW⁴⁶, and previous versions of the HDGB model.^48–50 We also developed a refined protocol for the optimization of the position and orientation of the structure decoys with respect to the membrane. In terms of the decoy set, we revisited the five-protein Baker decoy set mentioned above to compare with the previous study by Yuzlenko and Lazaridis,⁴⁴ but also generated additional models closer to the native structures to test whether the performance of the scoring functions improves for the closer decoys. Finally, encouraged by a good performance of the methods tested here, we developed the new MEMScore (http://feiglab.org/memscore) web service to provide our scoring protocol to the broader community.

METHODS

Test Systems and Decoy Sets

Five transmembrane proteins, BRD7 (Bacteriorhodopsin), fmr5 (fumarate reductase), ltpA (Lactose permease), RHOD (Rhodopsin), and VATP (V-ATPase) were considered here with the native structures taken from the Protein Data Bank (PDB) from PDB codes 1PY6⁵¹ (BRD7), 1QLA⁵² (fmr5), 1PV6⁵³ (ltpA), 1U19⁵⁴ (RHOD), and 2BL2⁵⁵ (VATP).

Two decoy sets were considered. The first decoy set (set 1) was provided by the Baker group.¹⁷ Set 1 consisted of 100 decoys for BRD7, fmr5, ltpA, and VATP and 50 decoys for RHOD with RMSD values with respect to the native structures ranging from 3 to 25 Å. A second set of decoys (set 2) was prepared for each system by generating additional structures closer to the native structures. This was done by initially selecting five decoy structures of set 1 with the lowest RMSD values. Using a C_α-based representation, trajectories were generated where the decoys were pulled towards the native and, vice versa, the native structure was pulled towards the decoys during 200 ps of molecular dynamics (MD) using a harmonic restraint with a force constant of 10 kcal/mol/Ų that was applied with respect to the target structures. In these simulations, transmembrane helix segments were restrained separately, and contacts between C_α-atoms that were initially less than 8 Å distance from each other were weakly restrained using a flat-bottom potential (1 Å) with a weak force constant of 0.1 kcal/mol/Ų to maintain contacts where possible via the CONS NOE command in CHARMM.^56–57 From the pulling simulations, frames were selected more frequently at the beginning of each simulation and less frequently towards the end as the target structure was approached. The selected frames were subsequently reconstructed to all-atom detail and energy minimized over 1,000 steps using the IMM1 model. From the 130 models generated in this manner, only the ones with final energies lower than 0.8 times of the minimum energy of all structures were subsequently included in the decoy set 2. For each selected decoy structure in set 2, another short 20-ps MD simulation was performed followed by 100 steps of minimizations using the IMM1 model, during which C_α atoms were restrained with a 0.10 kcal/mol/Ų force constant to yield the final decoy structures. Set 2 consists of 75 decoys for BRD7, 83 decoys for fmr5, 72 decoys for ltpA, 90 decoys for RHOD and 118 decoys for VATP covering an RMSD range between 1 and 13 Å.

Scoring Protocol

All of the decoy structures were subjected to the protocol illustrated in Fig. 1. In brief, initial models were optimized first in aqueous solvent before being inserted into the membrane. After finding an optimal orientation in the membrane, further minimization and MD was carried out before scoring the final models. The details of this protocol are described in the following.

Figure 1.

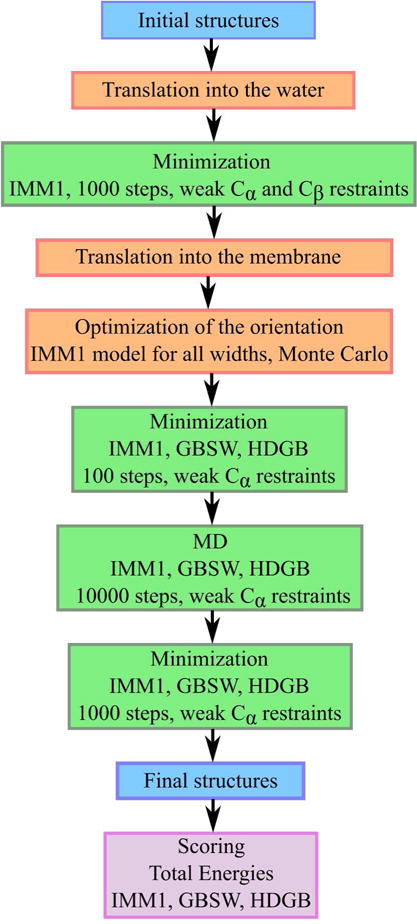
Scoring protocol applied to protein decoys in set 1 and set 2.

Initial Minimization in Aqueous Solvent

Initial models were first completed by adding hydrogens using the CHARMM HBUILD module. Initial relaxation was then carried out with IMM1. Because the degree of membrane insertion for a given structure is not assumed to be known a priori each model was translated so that the center of mass is located at z=100 Å (with z being the membrane normal), which corresponds to the bulk water phase in the IMM1 model. Minimizations were performed using the steepest descent (SD) algorithm over 50 steps and followed by the adopted-basis Newton-Raphson algorithm (ABNR) over 1,000 steps. During minimization, C_α and C_β atoms were restrained by a force constant of 0.10 kcal/mol/Ų to prevent large deviations from the initial models.

Optimization of Membrane Orientation

The minimized structures were transferred to the membrane by placing the center of mass at z=0 and orienting each molecule with the first principal axis aligned parallel to the membrane normal. The position and orientation was then further optimized with a Monte Carlo protocol where random rigid body translations along the z axis between -12 and 12 Å and random rotations around the x and y axes between −60° and 60° were explored to find an optimal orientation according to the minimum solvation energy. Monte Carlo sampling was carried out for 500 steps which was generally sufficient to reach convergence. The orientation with the minimum energy was then used as the starting point for further optimization.

Minimization in Membrane Environment

Optimally oriented models were minimized initially over 50 steps with SD and over 100 steps with the ABNR algorithms using the implicit membrane model that was later used for scoring. C_α positions were restrained by a force constant of 0.10 kcal/mol/Ų during the minimization process. After minimization, 20 ps of MD simulations were performed using the velocity Verlet integrator using a 2 fs time step. Long-range electrostatics and van der Waals interactions were switched to zero between 20 and 24 Å for GB models and between 7 and 9 Å for the IMM1 implicit membrane model. The SHAKE⁵⁸ algorithm was applied to constrain bond lengths involving H atoms. The temperature was coupled to a bath at 298 K using a Nosé-Hoover thermostat.^59–60 C_α atoms were again restrained with a force constant of 0.10 kcal/mol/Ų. The final structures at the end of the MD run were further minimized for 50 steps using SD algorithm and 1,000 steps using the ABNR algorithm with a weak C_α restraint by a force constant of 0.10 kcal/mol/Ų.

Scoring of Decoys

The oriented and minimized models were scored using total energies that are consist of bonded and non-bonded interaction energies as well as the solvation energies calculated with a variety of energy functions. The implicit membrane models IMM1,⁴⁵ IMM1-p36,⁴⁴ GBSW⁴⁶ and HDGB⁴⁷ (HDGBv2,⁵⁰ HDGBv3⁴⁹ and HDGBvdW⁴⁸) were used with five different membrane widths of 23.1, 25.4, 27.0, 28.5, and 30.4 Å. Long-range electrostatic and van der Waals interactions were cut-off with a switching function applied between 20 and 24 Å for GB models and 7 and 9Å for the IMM1 models. The implicit membrane models are described in more detail below. For comparison, the distance-scaled, finite ideal-gas reference (DFIRE)³⁸ potential was also applied to test the performance of a popular knowledge-based scoring function that has not been optimized for membrane environments. In the case of DFIRE, the models optimized with HDGBvdW were used.

Implicit Membrane Models

Three major types of implicit membrane models were used in this study: IMM1, GBSW and HDGB.

The IMM1 model employs an empirical Gaussian function to describe the solvation free energy term along with a distance-dependent dielectric term; both terms vary along the membrane normal to describe the effect of the membrane environment. The IMM1 method is an extension of the Effective Energy Function (EEF1) model for soluble proteins^61–62 and is based originally on the CHARMM19 polar force field.⁶³ In addition, the IMM1-p36 model,^{44, 64} which is an extension of IMM1 for the all-atom CHARMM36 force field, was used as well for the comparison.

The GBSW model is a two-dielectric heterogeneous implicit solvent model,⁶⁵ where the electrostatic solvation free energy is calculated via a generalized Born (GB) formalism and the non-polar contribution of the solvation free energy is approximated by a solvent accessible surface area (SASA) model.^66–67 The CHARMM36 force field⁶⁸ was used for the proteins during the GBSW model calculations.

The HDGB model is also a GB-based formalism that implements a dielectric profile along the z-axis instead of a simple two-dielectric representation. The dielectric profile was initially motivated by solving the Poisson equation for ionic spheres in a dielectric layer system⁴⁷ but subsequently optimized against free energies of insertion of amino acid side chain analogs.⁵⁰ More recent additional optimizations of the original dielectric profile in HDGB⁴⁷ led to update models HDGBv2⁵⁰ and HDGBv3.⁴⁹ Recently, the HDGB model was further extended with an implicit van der Waals term (HDGBvdW)⁴⁸ to improve the description of non-polar interactions within the membrane where electrostatic interactions are less important. For all of the HDGB models, the CHARMM36 protein force field⁶⁸ was used again.

While the membrane width is a simple parameter in the IMM1 and GBSW models, HDGB requires a scaling of the dielectric and non-polar profiles that were initially optimized for a membrane with a hydrophobic thickness of 28.5 Å.⁵⁰ For the HDGBvdW model, we also scaled atom type density profiles that vary as a function of z⁴⁸ when modeling different membrane widths.

Software

All the simulations were performed using CHARMM⁶⁹ version c40a2 or c41a1 (for the HDGB models) where the implicit membrane models are implemented. The Multiscale Modeling Tools for Structural Biology (MMTSB) tool set⁷⁰ was used to simplify the scoring protocol.

MEMScore web server

The membrane protein scoring protocol was implemented in the MEMScore web server (http://feiglab.org/memscore). The server allows the submission of a set of structures, optimizes their orientation within the membrane, and returns scores using either of HDGBvdW, HDGBv3, GBSW and IMM1 implicit membrane models. Typical turnaround times for a set of 100 models are within a few hours.

Analysis

The performance of the scoring functions was evaluated in a number of different ways. First, native state discrimination was analyzed based on z-scores^{44, 71} for the difference between native state and decoy scores:

$$Z=\frac{<E_{dc}>-E_{\mathit{nat}}}{S{D}_{dc}}$$ (1)

where <E_dc>, E_nat, and SD_dc are the average energy calculated for the structures of decoys, the energy of the native protein structure, and the standard deviation of the energies for the decoy structures, respectively. Native state scores were obtained by subjecting the experimental structures to the same protocol as the decoys.

Second, Spearman’s rank correlation between scores and RMSD were calculated based on regression analysis. To obtain RMSD values, two different protocols were followed: 1) Models after the initial minimization in aqueous solvent were superimposed onto the native structures based on a least squares fit before calculating C_α RMSD values. 2) Models after orientation and optimization within the membrane were compared with the membrane-optimized native structures. In this case, the least-squares fit to the native structures allowed only translation in x-and y-directions and rotation around the z-axis to preserve the z positions and relative orientations within the membrane. The first RMSD metric (RMSD₁) only considers differences in the internal structure while the second metric (RMSD₂) also emphasizes the orientation within the membrane.

Third, we also evaluated how close top-scoring decoys were with respect to the native structure (in terms of RMSD). In practice, this is the most important property because scoring functions would be tasked to select one or more top-scoring decoys from a set of models. We analyzed the average RMSD for the top 1 (top-1) and top 10 (top-10) decoys.

RESULTS

We tested the scoring of membrane protein structure decoys for five systems with mostly GB-based implicit membrane models in the scoring protocol shown in Fig. 1. We tested a range of implicit models (IMM1, IMM1-p36, GBSW, HDGB (HDGBv2 and HDGBv3), HDGBvdW) as well as DFIRE. The protocol involved initial relaxation, optimization of the membrane orientation of each decoy, and further optimization via minimization and MD before energy scores were finally calculated.

Two decoy sets were studied, for which results are presented separately in the following. The first set was examined already earlier⁴⁴ and we primarily focused here on comparing improvements in the scoring protocol to the previous work. The second set extends structures closer to the native structure and was studied to evaluate how different scoring functions perform at different distances from the native.

Scoring of Decoy Set 1

The scoring protocol was applied to decoy set 1, generated originally by the Baker lab and studied before by Yuzlenko and Lazaridis.⁴⁴ Fig. 2 shows the distribution of scores relative to the energy of the native structure as a function of RMSD₂ (which includes differences in membrane orientation, see Methods) with respect to the native structure. It can be seen that all of the scoring functions generally discriminated decoys from the native and provided some degree of correlation between the scores and RMSD in qualitative agreement with the previous analysis by Yuzlenko and Lazaridis.⁴⁴ The results were analyzed quantitatively via z-scores to assess native state discrimination, Spearman’s rank correlation coefficients to describe the correlation between scores and RMSD, and the RMSD values of the top-scoring decoys.

Figure. 2.

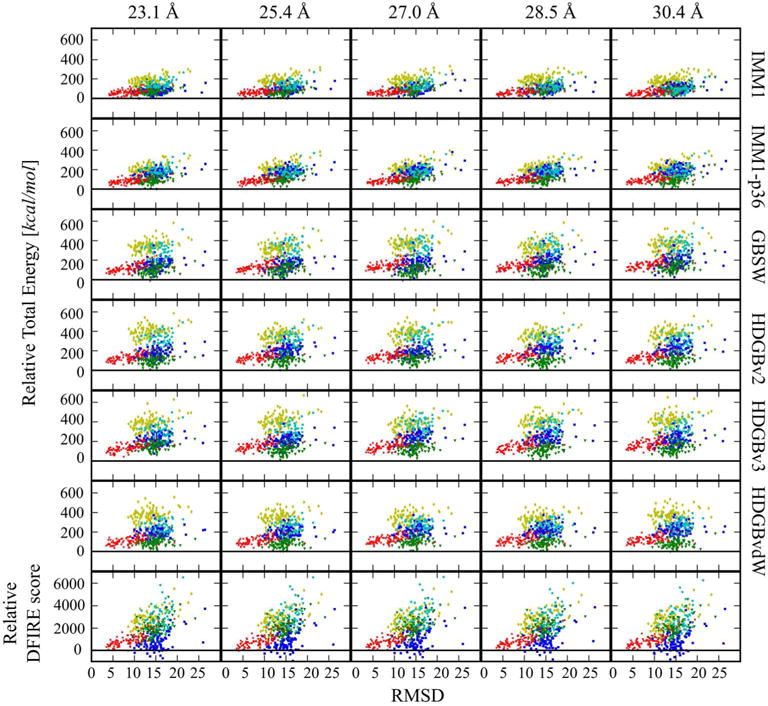
Relative energy vs. RMSD₂ for decoy set1 for each protein. RMSD₂ values were calculated for C_α atoms at the optimized positions along the membrane. Energies were taken relative to the native state energies. Columns are corresponding to different membrane widths, rows are corresponding to the different models. Color codes are as follow: BRD7: yellow diamonds; fmr5: blue squares; ltpA: green triangles; RHOD: cyan circles; VATP: red crosses. Relative DFIRE scores are shown in the last row for the structures optimized by HDGBvdW simulations.

Detailed z-score results are given in Table S1 and summarized in Table 1. The results vary only moderately as a function of membrane width, but widths between 27.0 and 28.5 Å give best overall results for the systems studied here (see below). To facilitate comparisons with the previous work by Yuzlenko and Lazaridis we focus initially on the results for a membrane width of 28.5 Å which corresponds to a dipalmitoyl-phosphatidylcholine (DPPC) bilayer. We found good native state discrimination with z-scores ranging from just below 3 with IMM1 to more than 4 with the HDGB models when the full protocol was applied. With DFIRE, the z-score was around 2.4 and DFIRE failed to fully discriminate the native structures for fmr5 and VATP from the decoys (see Fig. 2). This is still remarkable, however, considering that this knowledge-based potential was not optimized for membrane proteins. To examine the effect of optimizing membrane placement, we also calculated scores from a protocol variant where that step was omitted. Without optimizing membrane positioning, the z-scores were reduced by about one unit for all scoring functions except DFIRE, for which the z-score remained essentially unaltered as may be expected since DFIRE does not consider the membrane environment. The results without optimizing the membrane placement were similar to the results reported previously by Yuzlenko and Lazaridis,⁴⁴ where an extensive optimization of the membrane orientation was not carried out. This suggests that careful placement and orientation of protein structures in the membrane is an important factor in discriminating decoys from native states.

Table 1.

Z-scores for native state discrimination in decoy set 1.

Scoring function	Full protocol	w/o optimization of membrane orientation	w/o MD	Yuzlenko and Lazaridis38
IMM1	2.97 (0.8)	2.10 (0.7)	2.25 (1.3)	1.9
IMM1-p36	3.74 (0.9)	2.79 (0.8)	2.99 (1.5)	2.5
GBSW	3.85 (1.3)	2.71 (0.9)	3.12 (1.6)	2.9
HDGBv2	4.22 (1.4)	3.33 (1.0)	3.57 (1.8)	2.8*
HDGBv3	4.27 (1.3)	3.23 (0.9)	3.30 (1.3)	–
HDGBvdW	4.03 (1.3)	2.97 (0.9)	2.98 (1.2)	–
DFIRE	2.35 (0.9)	2.38 (1.0)	2.06 (0.9)	–

Average z-scores over proteins for a membrane width of 28.5 Å (not applicable for DFIRE). Results are compared between scores calculated for the full protocol, without optimization of the membrane orientation, and without the MD step. Results reported previously by Yuzlenko and Lazaridis³⁸ are also shown for comparison. Values given in parentheses indicate standard deviations with respect to variations between different proteins.

^*using the older HDGBv1 dielectric and non-polar profiles

Correlation coefficients between the scores and RMSD are given in detail in Table S2 and summarized in Table 2. Two different RMSD metrics were considered here: RMSD₁ compares with the native structure after a simple least-squares fit (neglecting any difference in membrane orientation) whereas RMSD₂ preserves differences in membrane orientation (see Methods for details). Again, there was little difference as a function of membrane width (Table S2). The optimization of the membrane placement improved correlation coefficients with respect to RMSD₂ for some scoring functions. However, the correlation with respect to RMSD₁ for all scores except DFIRE (Table 2) deteriorated when the membrane placement was optimized for reasons that are not entirely clear. Correlation coefficients with the full protocol were higher with respect to RMSD₂ than RMSD₁ but, overall, correlation coefficients remained quite low, and never exceeded 0.5. This suggests that the relative ranking of the models in decoy set 1 is challenging with any of the scoring functions tested here. Moreover, the GB-based scores led to worse correlation than the IMM1 and DFIRE scores, contrary to the z-score results, whereas DFIRE had the highest correlation coefficients, especially when using the RMSD₁ metric that ignores differences in membrane orientation. This suggests that accurate modeling of the membrane environment is not the most important feature for ranking models in decoys set 1. Since DFIRE is known to do well with distinguish better-packed structures models from less optimal conformations^{38, 72} the good performance with DFIRE suggests that differences in packing may be the main distinguishing factor in the models of this decoy set. This is further corroborated by a detailed analysis of how individual energy components in the implicit membrane-based models contribute to the correlation between scores and RMSD (see Table S3). The main finding is that the van der Waals contributions to the total energy and, to a lesser extent, the cavity-based non-polar solvation term are most strongly correlated with RMSD. Electrostatic and solvation interactions that are much more sensitive to the membrane environment, on the other hand, were more weakly correlated with the RMSD values (Table S3).

Table 2.

Correlation between scores and RMSD in decoy set 1.

	Correlation with RMSD1			Correlation with RMSD2
Scoring function	Full protocol	w/o optimization of membrane orientation	w/o MD	Full protocol	w/o optimization of membrane orientation	w/o MD
IMM1	0.28 (0.1)	0.35 (0.1)	0.24 (0.1)	0.38 (0.1)	0.35 (0.1)	0.31 (0.1)
IMM1-p36	0.29 (0.2)	0.35 (0.1)	0.24 (0.2)	0.40 (0.1)	0.35 (0.1)	0.34 (0.1)
GBSW	0.26 (0.2)	0.32 (0.1)	0.22 (0.2)	0.36 (0.2)	0.32 (0.1)	0.32 (0.2)
HDGBv2	0.23 (0.2)	0.26 (0.1)	0.16 (0.2)	0.31 (0.2)	0.26 (0.1)	0.23 (0.1)
HDGBv3	0.23 (0.2)	0.26 (0.1)	0.17 (0.2)	0.32 (0.2)	0.26 (0.1)	0.25 (0.2)
HDGBvdW	0.15 (0.2)	0.23 (0.1)	0.12 (0.1)	0.24 (0.2)	0.23 (0.1)	0.19 (0.1)
DFIRE	0.35 (0.2)	0.37 (0.2)	0.36 (0.2)	0.38 (0.2)	0.37 (0.2)	0.39 (0.2)

Average Spearman’s rank correlation coefficients between scores and RMSD1 (without consideration of different orientations) and RMSD2 (considering different orientations) for a membrane width of 28.5 Å (not applicable for DFIRE). Results are compared between scores calculated for the full protocol, without optimization of the membrane orientation, and without the MD step. Values given in parentheses indicate standard deviations with respect to variations between different proteins.

What matters most in real structure prediction applications is the ability to select one or few native-like models from a set of decoys. Table 3 shows average RMSD₁ and RMSD₂ values for the top 1 and top 10 best-scoring models (details are shown in Table S4). In all cases, the RMSD values of the selected models are significantly larger than what would be the optimal selections based on the lowest RMSD values. There is relatively little variation between scoring functions although IMM1 may perform slightly better than other functions in picking the single best model while HDGBvdW does somewhat worse than all of the other soring functions. These results highlight again the challenges of reliably selecting native-like models from decoy set 1.

Table 3.

Top-scoring models selected from decoy set 1.

Scoring function	RMSD1 [Å]		RMSD2 [Å]
	top-1	top-10	top-1	top-10
IMM1	11.10 (3.3)	11.86 (3.3)	11.33 (3.1)	12.22 (3.2)
IMM1-p36	11.50 (4.2)	11.90 (3.7)	11.83 (4.0)	12.29 (3.4)
GBSW	12.59 (3.7)	11.80 (3.6)	12.94 (3.7)	12.09 (3.6)
HDGBv2	11.18 (4.3)	11.80 (4.0)	12.15 (4.4)	12.20 (4.0)
HDGBv3	11.48 (4.2)	11.73 (3.9)	11.97 (4.1)	12.07 (3.9)
HDGBvdW	12.79 (3.4)	12.26 (3.5)	13.16 (3.5)	12.61 (3.5)
DFIRE	12.24 (5.2)	11.78 (4.0)	12.64 (4.8)	12.16 (4.0)
optimal	8.16 (2.7)	9.31 (3.3)	8.23 (2.7)	9.64 (3.3)

Average RMSD₁ and RMSD₂ values for top-scoring models (best, top-1, and average over best 10, top-10) with different scores for a membrane width of 28.5 Å (not applicable for DFIRE) using the full scoring protocol. Theoretically optimal values based on selecting the best models using RMSD instead of a scoring function are shown for reference. The optimal values vary slightly for different scoring functions because of different optimization and the given values are averaged over all scoring functions. Values given in parentheses indicate standard deviations with respect to variations between different proteins.

Scoring of Decoy Set 2

The decoy set 1 generated by the Baker lab consists of models that deviate significantly from the native structures with RMSD values as high as 25 Å. As discussed above, ranking these models is difficult and apparently driven mostly by distinguishing optimal packing interactions. This gives little opportunity for membrane-focused scoring functions to show their potential. The decoy set 2 was generated to cover the conformational space between the best decoys in set 1 and the native structures and reassess how membrane-focused scoring functions perform on such models.

Fig. 3 shows the scores as a function of RMSD₂ for decoy set 2. In all cases, there is, again, good native state discrimination. In addition, it is immediately apparent that the correlation between the scores and RMSD is better than for set 1 with the scores following a funnel-shaped decline towards the native state. The average decoy scores are slightly higher in set 2 compared to set 1 as a result of different degrees of relaxation of the models.

Figure. 3.

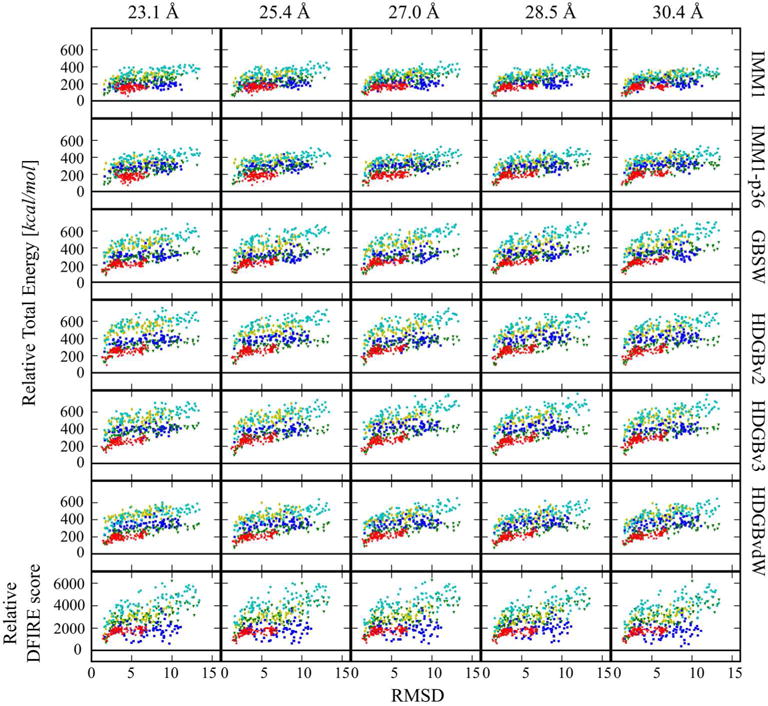
Relative energy vs. RMSD₂ distributions for decoy set 2 for each protein and scoring function as in Fig. 2.

Tables S5–S7 provide a detailed quantitative analysis while Table 4 summarizes the results. Large z-scores confirm good native state discrimination even as the native state is approached more closely. Z-scores are higher again for the HDGB-based models and lower for DFIRE. Correlation coefficients of scores vs. RMSD increased significantly over the results for set 1 indicating a much better ability to provide relative ranking when models come closer to the native state. Interestingly, correlations were now highest for the GB-based models suggesting that the membrane environment is a more critical factor for scoring the decoys in set 2. This is further illustrated by the much larger correlations of the electrostatic terms in the implicit membrane models with RMSD when soring the decoys in set 2 (see Table S8) compared to the almost entirely absent correlation when scoring decoys in set 1 (see Table S3). The GB-based scoring functions also do well with selecting the top-scoring models close to the native. Especially the HDGB-based scoring function did well in selecting the top 10 structures close to the native. As an example, Fig. 4 shows the decoys that were selected by the HDGBvdW-scoring function for each of the proteins. It is readily apparent that all of the models are very close to the native structures While IMM1 still performs similarly compared to the GB-based models, DFIRE cannot match the performance of the implicit-membrane based models when scoring the models in set 2.

Table 4.

Scoring of decoy set 2.

Scoring function	Z-score	Score correlation vs.		RMSD1 [Å]		RMSD2 [Å]
		RMSD1	RSMD2	top-1	top-10	top-1	top-10
IMM1	5.48 (1.3)	0.53 (0.3)	0.53 (0.3)	1.79 (0.7)	2.93 (1.9)	1.94 (0.6)	3.10 (1.9)
IMM1-p36	5.96 (1.7)	0.56 (0.2)	0.55 (0.2)	1.77 (0.7)	2.89 (1.4)	1.97 (0.6)	3.05 (1.3)
GBSW	5.62 (1.0)	0.59 (0.3)	0.61 (0.3)	1.48 (0.1)	2.87 (2.0)	1.64 (0.1)	3.00 (1.9)
HDGBv2	6.47 (1.6)	0.61 (0.2)	0.61 (0.2)	1.55 (0.2)	2.72 (1.3)	1.76 (0.1)	2.88 (1.3)
HDGBv3	6.44 (1.6)	0.61 (0.2)	0.62 (0.2)	2.39 (2.0)	2.68 (1.3)	2.60 (2.0)	2.84 (1.3)
HDGBvdW	5.80 (1.2)	0.60 (0.2)	0.64 (0.2)	1.48 (0.1)	2.74 (1.1)	1.68 (0.1)	2.93 (1.1)
DFIRE	4.50 (1.3)	0.52 (0.3)	0.51 (0.3)	2.97 (3.3)	3.37 (2.2)	3.15 (3.1)	3.61 (2.0)
optimal	–	–	–	1.45 (0.1)	2.02 (0.4)	1.54 (0.1)	2.17 (0.4)

Z-scores, correlation coefficients between scores and RMSD1 and RMSD2, and top-1 and average top-10 RMSD1 and RMSD2 values as in Tables 1–4 but for decoy set 2. Values are shown for a membrane width of 28.5 Å and standard deviations are given in parentheses.

Figure 4.

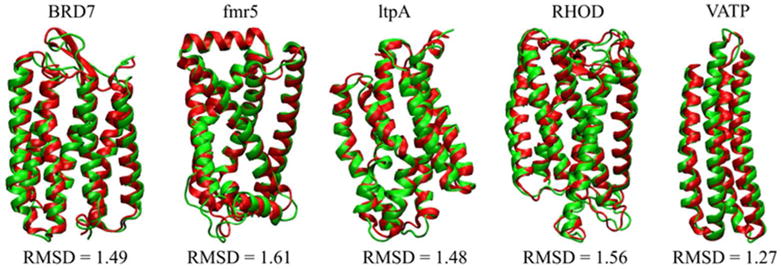
Native structures (red) of the proteins and the decoy structures (green) with the lowest energies obtained by the HDGBvdW model using a 28.5 Å membrane width.

Finally, we examined in more detail the question of how to choose the best membrane width. Generally, hydrophobic mismatch between a protein and a given membrane model would be expected to either lead to membrane deformations and/or lipid raft formation so that the effective membrane width in the local vicinity should match the hydrophobic profile of a given membrane protein structure. This, in turn, suggests that scoring performance may be improved when the most likely membrane width is estimated for a given structure and the corresponding width is then used for the implicit membrane model when scoring decoys. The optimal membrane width for a given structure essentially depends on the hydropathy profile of a given structure along the membrane normal after finding the optimal membrane positioning. We obtained estimates of the width of the hydrophobic region for the five systems studied from the Orientations of Proteins in Membranes (OPM) database⁷³ (see Table 5). In the implicit membrane models, we would expect that this measure should approximately match the energetic midpoint between the polar head-group and solvent environment and the membrane interior. In the HDGB models, this may correspond to the point where the dielectric profile reaches about half of the bulk solvent value, which is roughly between the position of the glycerol and phosphate groups in phospholipid bilayers. This point is about 2 Å further away from the membrane center than the end of the hydrocarbon acyl chain region that commonly defines what is meant by membrane width in the implicit membrane models. Therefore, we assumed that an optimal implicit membrane model should use a width that is about 4 Å less than the hydrophobic region predicted by OPM. Accordingly, we analyzed for the HDGB-based models whether selecting the results corresponding to the closest membrane width to the estimated hydrophobic width for each of the five protein systems would improve the overall performance. The results are shown in Table 5. Essentially, we find that choosing the optimal width for each structure leads to good results but is not significantly better than just selecting the overall best-performing implicit membrane widths (27–28.5Å). This may be due to challenges in accurately estimating the optimal membrane width for a given system and/or simply reflect that uncertainties in our scoring protocol are still large enough for the subtleties of choosing slightly non-optimal membrane widths not to matter.

Table 5.

Scoring of decoy set 2 for each protein with different membrane widths.

		BRD7	fmr5	ltpA	RHOD	VATP	Average
Hydrophobic width from OPM [Å]		29.6	31.4	31.8	31.2	35.6
Correlation score vs. RMSD2	23.1	0.61	0.36	0.78	0.73	0.51	0.60
	25.4	0.61	0.32	0.76	0.77	0.57	0.61
	27.0	0.66	0.31	0.76	0.79	0.63	0.63
	28.5	0.61	0.33	0.75	0.77	0.65	0.62
	30.4	0.60	0.31	0.74	0.76	0.65	0.61
		Average correlation at the optimal widths					0.62
Top-1 RMSD2	23.1	1.68	1.64	1.56	1.73	1.89	1.70
	25.4	1.66	2.08	1.55	1.85	1.81	1.79
	27.0	1.69	1.62	1.69	1.60	1.82	1.68
	28.5	1.67	3.14	1.70	1.73	1.84	2.02
	30.4	1.80	3.00	1.56	1.62	1.78	1.95
		Average RMSD at the optimal widths					1.67
Top-10 RMSD2	23.1	3.40	5.33	2.29	2.58	1.92	3.10
	25.4	3.46	5.32	2.38	2.50	1.91	3.11
	27.0	3.40	5.15	2.33	2.26	1.88	3.00
	28.5	3.33	4.77	2.22	2.22	1.86	2.88
	30.4	3.73	4.83	2.54	2.36	1.91	3.07
		Average RMSD at the optimal widths					3.00

Average correlation scores, top-1 and top-10 lowest energy RMSD₂ values. Results from HDGBv2, HDGBv3 and HDGBvdW were averaged for different membrane widths. The hydrophobic width of the proteins along the membrane normal was obtained from the OPM database. The shaded area indicates the values for the optimal membrane widths (hydrophobic widths from OPM – 4 Å, see text).

DISCUSSION and CONCLUSIONS

The main goal of the present work was to test how new GB-based implicit membrane models and an improved optimization protocol for positioning decoys in the membrane can perform with protein structure prediction and refinement applications in mind. The previous study by Yuzlenko and Lazaridis.⁴⁴ established that implicit membrane-based models may be applicable for the scoring of membrane proteins. Here, we show that extensive optimization of the orientation and placement of a given decoy in the membrane appears to be important in improving scoring performance. Furthermore, we found that the real benefit of such scoring functions only comes into play when decoys come sufficiently close to the native structure. In decoy sets that involve structures far away from the native state, such as the Baker set used previously and again here, the main factor for distinguishing better models appears to be mostly related to packing and much less to the presence of the membrane environment. Hence, the practical insight from this study is that the initial sampling and scoring of membrane protein structures could very well be driven by knowledge-based functions such as DFIRE but as conformations closer to the native state are explored, for example during protein structure refinement, the use of scoring functions that accurately represent the membrane environment becomes essential. The GB-based models, GBSW and HDGB and in particular our recent HDGBvdW model, perform very well, especially for decoy set 2 involving models close to the native state. This suggests that this protocol would be especially well-suited for future applications in the refinement of membrane protein structures.

While the scoring of decoys close to the native state is quite good, further improvements could be gained by improved force fields or further improvements in the implicit membrane models, e.g. by allowing the dynamic deformation of membranes.⁷⁴ The development of specific knowledge-based scoring functions for membrane proteins could avoid some of the inherent problems with force-field based scoring such as noise, but another possibility is the application of general statistical methods to reduce noise in scoring functions that exhibit funnel-shape characteristics^75–76. When scoring decoys very close to the experimental structures, an accurate representation of the conditions under which the structure was determined, e.g. crystallization in the presence of detergent, becomes important. Future efforts may focus on this aspect as well, although it is not clear that exactly targeting a crystal structure obtained under non-biological conditions would result in the most useful predictions.³⁰

The membrane-protein scoring protocol presented here is available via CHARMM⁵⁶ and the MMTSB Tool Set⁷⁰ but the protocol was also implemented in form of a web server available at http://feiglab.org/memscore to provide broader community access.

ABBREVIATIONS

ABNR

adopted-basis Newton-Raphson

BRD7

bacteriorhodopsin 7

CHARMM

Chemistry at Harvard Molecular Mechanics

DFIRE

distance-scaled finite ideal-gas reference state score

fmr5

fumarate reductase 5

DPPC

dipalmitoyl-phosphatidylcholine

EEF1

effective energy function 1

GB

generalized Born

GBSW

generalized Born with simple switching

HDGB

heterogeneous dielectric generalized Born

HDGBvdW

heterogeneous dielectric generalized Born with van der Waals terms

IMM1

implicit membrane model 1

ltpA

lactose permease A

MD

molecular dynamics

MMTSB

Multiscale Modeling Tools in Structural Biology

OPM

orientations of proteins in membranes

PDB

Protein Data Bank

RHOD

rhodopsin

RMSD

root mean square deviation

RMSD₁

RMSD based on least-squares fit without considering differences in orientation

RMSD₂

RMSD based on least-squares fit that preserves orientation and position within the membrane

SASA

solvent-accessible surface area

SD

steepest descent

VATP

V-ATPase