Abstract
As one of the most important hypotheses on biogeographical distribution, Rapoport's rule has attracted attention around the world. However, it is unclear whether the applicability of the elevational Rapoport's Rule differs between organisms from different biogeographical regions. We used Stevens’ method, which uses species diversity and the averaged range sizes of all species within each (100 m) elevational band to explore diversity‐elevation, range‐elevation, and diversity‐range relationships. We compared support for the elevational Rapoport's rule between tropical and temperate species of seed plants in Nepal. Neither tropical nor temperate species supported the predictions of the elevational Rapoport's rule along the elevation gradient of 100–6,000 m a.s.l. for any of the studied relationships. However, along the smaller 1,000–5,000 m a.s.l. gradient (4,300 m a.s.l. for range‐elevation relationships) which is thought to be less influenced by boundary effects, we observed consistent support for the rule by tropical species, although temperate species did not show consistent support. The degree of support for the elevational Rapoport's rule may not only be influenced by hard boundary effects, but also by the biogeographical affinities of the focal taxa. With ongoing global warming and increasing variability of temperature in high‐elevation regions, tropical taxa may shift upward into higher elevations and expand their elevational ranges, causing the loss of temperate taxa diversity. Relevant studies on the elevational Rapoport's rule with regard to biogeographical affinities may be a promising avenue to further our understanding of this rule.
Keywords: biogeographical affinities, elevational gradient, elevational range size, hard boundary effects, Nepal, species diversity, the elevational Rapoport's rule
1. Introduction
Biodiversity patterns are among the hottest topics in ecology and biogeography. However, spatial patterns of species’ range sizes along geographical gradients, which to a certain extent underlie the biodiversity patterns, have received much attention in the past decades (Connolly, 2009; Gaston & Chown, 1999; Sizling, Storch, & Keil, 2009; Taylor & Gaines, 1999; Tomasovych, Jablonski, Berke, Krug, & Valentine, 2015; Tomasovych et al., 2016; Vazquez & Stevens, 2004), compared with those on biodiversity patterns it seems to attract less attention (McCain & Knight, 2013). The elevational Rapoport's rule (ERR), which predicts trends of increased elevational ranges with the increase in elevation (Stevens, 1992), has received much attention in recent decades (e.g., Bhattarai & Vetaas, 2006; Fu, Wu, Wang, Lei, & Chen, 2004; McCain & Knight, 2013; Patterson, Pacheco, & Solari, 1996; Sanders, 2002) and is still catching attention from ecologists and biogeographers around the world (e.g., Garcia‐Rosello et al., 2015; Rohner et al., 2015; Sheldon, Leache, & Cruz, 2015; Tomasovych et al., 2015). Two issues may be responsible for this attention. First, considerable controversies about ERR remain, as there is a high degree of variability in support for this hypothesis. For example, some studies found strong support for ERR (e.g., Chatzaki, Lymberakis, Markakis, & Mylonas, 2005; Fleishman, Austin, & Weiss, 1998; Gaston & Chown, 1999; Hausdorf, 2006; Patterson et al., 1996; Ribas & Schoereder, 2006; Sanders, 2002), whereas others found little or no support (Bhattarai & Vetaas, 2006; Fu et al., 2004; Nathan & Werner, 1999; Patterson et al., 1996; Rahbek, 1997; Ribas & Schoereder, 2006). Second, elevational range shift caused by global climate change may increase the risk of extinction for small‐ranged species (La Sorte & Jetz, 2010; McCain & Colwell, 2011; Sekercioglu, Schneider, Fay, & Loarie, 2008). Thus, more studies on ERR may not only help to deepen our understanding of ERR, but also be helpful to conserve biodiversity, especially in small‐ranged species.
The core prediction of ERR is a positive relationship between range size and elevation (Stevens, 1992). However, the patterns of elevational range size may be taxon‐specific (McCain & Knight, 2013), which suggests that range‐elevation relationships may depend on the adaptation of ecophysiological traits to climatic or environmental factors along elevation gradients. Due to strong associations between ecophysiological traits of taxa and their biogeographical affinities (e.g., compared with tropical species, temperate species may be more resistant to cold weather) (Wilson, 1975), biogeographical affinities may be linked with elevational range sizes and their elevational trends (e.g., compared with tropical taxa, temperate taxa show broader elevational range sizes, as the latter may have experienced higher variability of environmental factors in their evolutionary or biogeographical history) (Oommen & Shanker, 2005; Wang, Tang, & Fang, 2007). However, little attention has been paid to range‐elevation relationships with regard to the influence of biogeographical affinities.
Another prediction of ERR is that species diversity decreases with increasing elevation. However, this has not been consistently observed. Elevational trends in diversity other than monotonic decreasing ones, that is, unimodal trends, have also been observed worldwide, suggesting that further investigations of this hypothesis are needed. There are strong linkages between ecophysiological traits and biogeographical affinities (e.g., taxa with tropical affinities may be prone to inhabit warm climates) (Wilson, 1975), which may imply that taxa with different biogeographical affinities may show differentiated adaptation to environmental factors, including elevation. Species with different biogeographical affinities may show different elevational patterns of richness, resulting in varying support for the richness–elevation hypothesis of ERR. To date, few studies have tested this assumption (e.g., Li & Feng, 2015; Oommen & Shanker, 2005).
The third prediction of ERR is an inverse relationship between species richness and elevational range (Stevens, 1989, 1992). This hypothesis has not been tested extensively. However, when predictors of climatic variability or source–sink dynamics show weaker influences than expected, the hypothesis remains in question (Kerr, 1999; Ribas & Schoereder, 2006).
The hypothesis of hard boundary effects predicts that the unimodal patterns of species diversity on elevational gradients are caused by the increasing overlapping of species ranges toward the centers of the elevational gradient, as species range is bounded by upper and lower limits (boundaries) of the elevational gradient (Colwell & Hurtt, 1994). This hypothesis also predicts that species range increases toward the centers of the elevational gradient. Overall, this hypothesis contradicts the ERR. Since 1994, when this hypothesis was proposed, it has remained controversial (Colwell, Rahbek, & Gotelli, 2005; Hawkins, Diniz‐Filho, & Weis, 2005; Herzog, Kessler, & Bach, 2013; Kluge, Kessler, & Dunn, 2006).
Using an online dataset of seed plants in Nepal, this study tested the following hypotheses: (1) the range‐elevation, diversity‐elevation, and range‐diversity relationships vary with biogeographical affinities and (2) reduction in hard boundary effects may enhance support for ERR, which may also depend on the biogeographical affinities.
2. Materials and Methods
2.1. Area description
Our study area was the whole country of Nepal (80°04′–88°12′E, 26°22′–30°27′N), with a total area of 147,181 km2. Topographically, Nepal is characterized by extreme elevational variation; for example, in some locations, elevation changes from about 60 to 8,848 m a.s.l. in just 150 km of horizontal distance (Hagen, 1969; Manandhar, 1999). The area at each elevation decreases until around 3,750 m a.s.l. and then shows a slight increasing trend. Mean monthly precipitation has two peaks along the elevational gradient, at about 300–400 and 1,600–1,700 m a.s.l., and decreases with further increases in elevation; Mean annual temperature linearly decreases with elevation, from 24.1°C around 100 m a.s.l and declining by 0.55°C per 100 m elevation (Fig. 1). Temperature seasonality, annual temperature range, and precipitation seasonality decrease and then increase along the elevational gradient from 100 to 6,000 m a.s.l as well as within the smaller range of 1,000–5,000 m a.s.l., showing open‐upward‐parabola patterns (Fig. 1). Annual precipitation range (precipitation of the wettest month precipitation of the driest month) on elevation showed patterns similar to that of mean monthly precipitation (Fig. 1). Cloud formation is mostly around 2,000 m a.s.l. (Bhattarai & Vetaas, 2003) in the lesser Himalayas, whereas in the greater Himalayas, it is normally between 2,500 and 3,200 m a.s.l. (Bhattarai & Vetaas, 2003; Dobremez, 1976). Consistent with the elevational climatic patterns, with the increase of elevation one can observe tropical/subtropical, temperate, subalpine, and alpine vegetation zones, respectively (Bhattarai & Vetaas, 2003; Dobremez, 1976).
Figure 1.
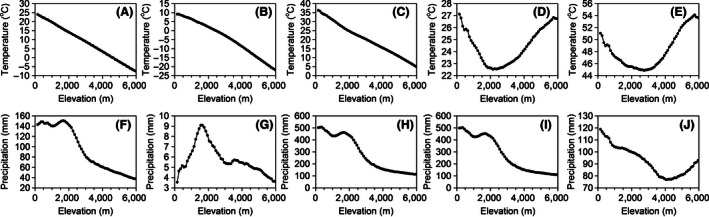
Temperature seasonality‐elevation (A), min temperature of the coldest month‐elevation (B), max temperature of the warmest month‐elevation (C), annual temperature range‐elevation (D), annual mean temperature‐elevation (E), precipitation seasonality‐elevation (F), precipitation of the driest month‐elevation (G), precipitation of the wettest month‐elevation (H), annual precipitation range‐elevation (I), and mean monthly precipitation‐elevation (J). All of the data were downloaded from the Worldclim (http://www.worldclim.org/) (Hijmans, Cameron, Parra, Jones, & Jarvis, 2005)
2.2. Plant data sources
We obtained plant information from the online version of the Annotated Checklist of the Flowering Plants of Nepal (http://www.efloras.org/, accessed on 1 December 2014). This dataset gave us family, genus, and species identified across the country, and the minimum and maximum elevations of each. We considered a small number of varieties and subspecies as separate species for this study. In all, there were 4,914 species, representing 222 families and 1,426 genera.
2.3. Subdivision of the study area into elevational bands
We divided the study area into 59 elevational bands, each with 100 m altitude change, from 100 to 6,000 m a.s.l. (100–200 m a.s.l., 200–300 m a.s.l., and so on). Grytnes and Vetaas (2002) suggested that the interpolation method, used in the present study, may underestimate species diversity at the gradient extremes. In addition, hard boundary effects may significantly reduce ranges and species diversity around gradient extremes (Colwell & Hurtt, 1994). Hard boundary effects on plant diversity in Nepal are mostly observed below 1,000 m a.s.l. and above 5,000 m a.s.l. (Grytnes & Vetaas, 2002). As both of these biases may reduce the support for ERR, we focused our attention on the elevational gradient from 1,000 to 5,000 m a.s.l., which we assumed strongly reduced hard boundary effects. This method was adopted by Vetaas and Grytnes (2002) and led to robust conclusions. We surmised that compared with the support for the ERR observed on the full elevational gradient from 100 to 6,000 m a.s.l., the support within the smaller elevational gradient would be stronger.
2.4. Biogeographical affinities
Following Harrison and Grace (2007) and Wang, Fang, Tang, and Lin (2011), we assigned each species within a genus the same biogeographical affinity, using a classification system of biogeographical affinities (Wu, 1991). This system determines biogeographical affinity of species according to their biogeographical history, fossil records, and modern distribution, especially the modern distribution centers of the species (Wu, 1991). The distribution centers located in pantropic regions, including tropical Asia and tropical America, old world tropic regions, tropical Asia to tropical Australia, tropical Asia to tropical Africa, and tropical Asia were all considered tropical species. Those from north temperate regions, including east and north Asia, America, old world temperate regions, temperate Asia, Mediterranean, west to central Asia, central Asia, and east Asia were considered temperate species. Species and genera that span from tropics to temperate regions and have no obvious distribution centers were considered cosmopolitan species or genera. This method was adopted in a variety of study cases (e.g., Li & Feng, 2015; Qian, 1998; Qian et al., 2006; Wang, You, & Feng, 2015; Zhu, 2012). We assigned biogeographical affinities to 4,699 species, including 1,972 tropical species (40.5%), 2,142 temperate species (44.0%), and 585 cosmopolitan species (12.0%). Subsequent analyses considered only tropical and temperate species.
2.5. Variables considered
We focused on elevational patterns of the following variables: (1) elevational range sizes of tropical species (ERTRS); (2) elevational range sizes of temperate species (ERTES); (3) tropical species diversity (TRSD); and (4) temperate species diversity (TESD). To correct for the influence of area on elevational patterns of plant diversity, we used area‐adjusted species diversity (species density) instead of species richness, as follows:
where D is the species density for each elevational band, S is the number of species in the elevational band, and A is the area of the elevational band.
2.6. Diversity‐elevation and biogeographical affinities
We counted the number of species which occurred in each elevational band and generated the elevational patterns of species diversity (TRSD and TESD), for two ranges, 100–6,000 and 1,000–5,000 m a.s.l. In consideration of unimodal patterns of species density along elevational gradients, we used general additive models (GAM) with Gaussian function of variance to determine the trends of the response curve instead of using linear correlation analysis. In this method, a cubic smooth spline (Hastie & Tibshirani, 1990) was used to evaluate the significance of specific trend for diversity‐elevation relationships, as well as for range‐elevation and diversity‐range relationships. These analyses were carried out using R (https://www.r-project.org/).
2.7. Range‐elevation and biogeographical affinities
We used Stevens’ (1992) method and GAM to investigate elevational patterns of ERTRS and ERTES within 100–6,000 and 1,000–5,000 m a.s.l.
2.8. Diversity‐range and biogeographical affinities
We used Stevens’ method and GAM to explore diversity‐range relationships for both tropical and temperate species within both elevational ranges, 100–6,000 and 1,000–5,000 m a.s.l. It must be noted that the three approaches used to test the three predictions are not really independent tests, and diversity‐range relationships follow from diversity‐elevation and range‐elevation relationships.
3. Results
3.1. Range‐elevation and biogeographical affinities
General additive models showed that with increased elevation from 100 to 6,000 m a.s.l., ERTRS significantly increased to about 4,300 m a.s.l., decreased until about 5,500 m a.s.l., and then showed a slightly increasing trend. From 1,000 to 5,000 m a.s.l., ERTRS had a unimodal pattern, with maximum diversity at about 4,300 m a.s.l. (Figs 2 and 3). The GAM models also showed that with increased elevation from 100 to 6,000 m a.s.l., ERTES increased with elevation until 1,150 m a.s.l., decreased until about 4,150 m a.s.l., increased again until about 5,450 m a.s.l., and then decreased. (p < .001) (Fig. 2). From 1,000 to 5,000 m a.s.l., ERTES decreased until about 4,150 m a.s.l. and then increased (Fig. 3).
Figure 2.
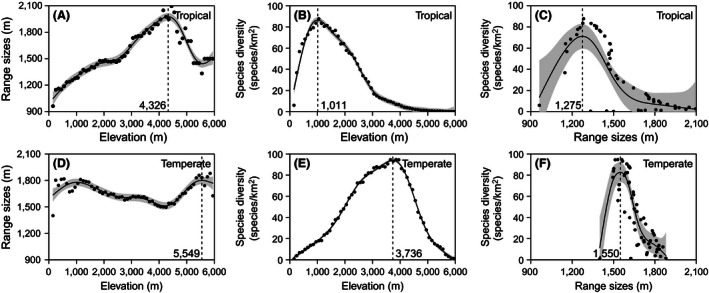
Range size‐elevation (A), species diversity‐elevation (B), and diversity‐range sizes (C) relationships for tropical and temperate species from 100 to 6,000 m a.s.l
Figure 3.
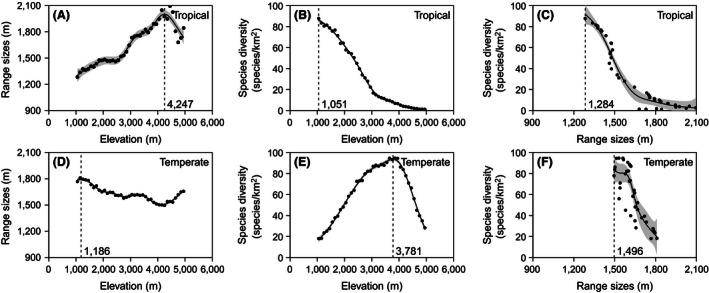
Range size‐elevation (A), species diversity‐elevation (B), and diversity‐range sizes (C) relationships for tropical and temperate species from 1,000 to 5,000 m a.s.l
3.2. Diversity‐elevation patterns and biogeographical affinities
General additive models showed that with the increase of elevation from 100 to 6,000 m a.s.l., both TRSD and TESD increased to some point and then decreased. TRSD peaked at about 1,000 m a.s.l., while the maximum TESD was at about 3,750 m a.sl. (Fig. 2). GAM models also showed within the range 1,000 to 5,000 m a.s.l., TRSD consistently decreased with increasing elevation but TESD still showed a unimodal pattern (Fig. 3).
3.3. Diversity‐range and biogeographical affinities
GAM models showed that from 100 to 6,000 m a.s.l., there were no linear negative relationships between species density and range sizes for either tropical or temperate species (Fig. 2). However, from 1,000 to 5,000 m a.s.l., there were negative relationships between species density and range size for both tropical and temperate species (Fig. 3).
4. Discussion
We observed strong support for the range‐elevation relationships predicted by ERR in tropical species from 1,000 to 4,300 m a.s.l., where their elevational ranges linearly increased. However, from 4,300 to 5,000 m a.s.l., there was a trend of decreasing ERTRS, which may imply that although we truncated the higher end of the elevational gradient by 1,000 m, it was not enough to eliminate boundary effects such as environmental or climatic conditions. These effects may strongly constrain the distribution of tropical species and thus reduce their elevational ranges, as tropical species may not have strong resistance to the harsh climate at very high elevations (Wilson, 1975). It may imply that if boundary effects are eliminated, the elevational patterns of the tropical ranges may support the range‐elevation relationship predicted by ERR. However, there was a decreasing trend of ERTES in most of the elevational gradient from 1,000 to 4,300 or 5,000 m a.s.l. In this case, the reduction or even the elimination of boundary effects did not result in obvious support for the range‐elevation relationship predicted by ERR.
McCain (2009) observed that bats, mostly observed in subtropical or tropical regions, showed a stronger positive trend of elevational range sizes across latitudes than rodents, numerous in arctic regions, and possessing wider adaptability. This is somewhat analogous to the varying support for the range‐elevation relationship predicted by ERR by tropical and temperate species when hard boundary effects were accounted for in the present study. Compared with temperate taxa, tropical taxa may be more responsive to climatic variability and thus increase their elevational range sizes to adapt to an increase in climatic variability (McCain, 2009). In contrast, temperate taxa may have experienced wider adaptability to climatic variability in their evolutionary history and may therefore be less responsive to the increasing variability at higher elevations, contradicting the ERR. It must be noted that none of annual variability of climatic factors (e.g., temperature seasonality, precipitation seasonality, annual temperature range, and annual precipitation range) shows consistently increasing trends with the increase of elevation (Fig. 1). Therefore, we propose that increasing variability of daily variation in temperatures with elevation (e.g., Ghalambor, Huey, Martin, Tewksbury, & Wang, 2006; Porter, Sabo, Tracy, Reichman, & Ramankutty, 2002) may cause the increasing trends in ERTRS, although we were unable to test this due to a lack of reliable datasets. It may be that when hard boundary effects are accounted for, the support for the range‐elevation relationship predicted by ERR may primarily depend on biogeographical affinities of the focal taxa.
Our results showed that from 100 to 6,000 m a.s.l., both TRSD and TESD showed unimodal patterns, suggesting that hard boundary effects may strongly shape the elevational patterns of species density (Colwell et al., 2005; Grytnes & Vetaas, 2002; Lee, Chun, Song, & Cho, 2013). This may have reduced the strength of the support for the diversity‐elevation relationship predicted by ERR. However, from 1,000 to 5,000 m a.s.l., there was a consistent decrease in TRSD and unimodal patterns of TESD along the elevation gradient. This may be due to strong rescue effects in tropical species and weak rescue effects in temperate species. However, we cannot deny that decreases in water‐related variables with increased elevation may strongly shape elevational diversity patterns of tropical taxa, or that decreasing energy availability with elevation mainly influences diversity patterns of temperate taxa in quadratic terms (Li & Feng, 2015). Taken together, we can reasonably infer that the support for the diversity‐elevation relationship predicted by ERR may be modified not only by hard boundary effects but also by the biogeographical affinities of the taxa. It therefore may, to some extent, explain why even when the hard boundary effects were reduced, the diversity‐elevation relationships predicted by the ERR were not supported (Vetaas & Grytnes, 2002).
In the present study, for both tropical and temperate species, we did not observe consistent support for the three relationships predicted by ERR over the broad range from 100 to 6,000 m a.s.l. However, when hard boundary effects were accounted for, we observed consistent support for all three predicted relationships by tropical species. Temperate species did not show consistent support for the predicted relationships. This may suggest that when hard boundary effects are accounted for, support for ERR may be primarily biogeographical‐affinity specific. In sum, studies on the elevational form of Rapoport's rule with regard to biogeographical affinities may be a promising avenue to further our understanding of this rule, as suggested by McCain and Knight (2013), although the influence of hard boundary effects cannot be overlooked.
Since c. 1901 and 1961, the increasing trends of the rise of annual mean temperature with elevation have been observed in most of regional groups of meteorological stations around the world (Ohmura, 2012). With global warming, there is an increasing rate of warming with altitude, propelled by a rapid increase in daily minimum temperature (Diaz & Bradley, 1997), which may result in strong trends of upward shifting of tropical taxa from lower elevational or latitudinal regions (Anderson, Storlie, Shoo, Pearson, & Williams, 2013; Freeman & Freeman, 2014; Hickler et al., 2012; Thuiller, Lavorel, Araujo, Sykes, & Prentice, 2005; Vegas‐Vilarrubia, Nogue, & Rull, 2012). The present study suggests that tropical species seem to be sensitive to climatic variability on an elevational gradient, showing wider elevational range sizes with the increase of climatic variability (Chen et al., 2011) when hard boundary effects were reduced. These findings together may suggest that with ongoing global climate change, tropical taxa in lower elevational regions may shift upward and expand their elevational ranges into higher elevational regions already occupied by temperate taxa, causing temperate taxa contract habitats or lose habitats entirely, and hence cause the loss of temperate taxa diversity (Franco et al., 2006; Vegas‐Vilarrubia et al., 2012). This may pose a tough challenge to biodiversity conservation, especially for temperate taxa in higher elevational regions.
Conflict of Interest
None declared.
Acknowledgments
We thank anonymous reviewers for their constructive comments on this article. This study was supported by the National Natural Scientific Foundation of China (Nos. 31360143 and 31560178) to Jianmeng Feng.
References
- Anderson, A. S. , Storlie, C. J. , Shoo, L. P. , Pearson, R. G. , & Williams, S. E. (2013). Current analogues of future climate indicate the likely response of a sensitive montane tropical avifauna to a warming world. PLoS ONE, 8, e69393.1 – e69393.12. doi:10.1371/journal.pone.0069393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattarai, K. R. , & Vetaas, O. R. (2003). Variation in plant species richness of different life forms along a subtropical elevation gradient in the Himalayas, east Nepal. Global Ecology and Biogeography, 12, 327–340. [Google Scholar]
- Bhattarai, K. R. , & Vetaas, O. R. (2006). Can Rapoport's rule explain tree richness along the Himalayan elevation gradient, Nepal? Diversity and Distributions, 12, 373–378. [Google Scholar]
- Chatzaki, M. , Lymberakis, P. , Markakis, G. , & Mylonas, M. (2005). The distribution of ground spiders (Araneae, Gnaphosidae) along the altitudinal gradient of Crete, Greece: Richness, activity, and altitudinal range. Journal of Biogeography, 32, 813–831. [Google Scholar]
- Chen, I. C. , Hill, J. K. , Shiu, H. J. , Holloway, J. D. , Benedick, S. , Chey, V. K. , … & Thomas, C. D. (2011). Asymmetric boundary shifts of tropical montane Lepidoptera over four decades of climate warming. Global Ecology and Biogeography, 20, 34–45. [Google Scholar]
- Colwell, R. K. , & Hurtt, G. C. (1994). Nonbiological gradients in richness and a spurious Rapoport effect. The American Naturalist, 144, 570–595. [Google Scholar]
- Colwell, R. K. , Rahbek, C. , & Gotelli, N. J. (2005). The mid‐domain effect: There's a baby in the bathwater. The American Naturalist, 166, E149–E154. [Google Scholar]
- Connolly, S. R. (2009). Macroecological theory and the analysis of species richness gradients In Witman J. D. & Roy K. (Eds.), Marine macroecology (pp. 279–309). Chicago: University Of Chicago. [Google Scholar]
- Diaz, H. F. , & Bradley, R. S. (1997). Temperature variations during the last century at high elevation sites. Climate Change, 36, 253–279. [Google Scholar]
- Dobremez, J. F. (1976). Le Népal, écologie et biogéographie. Paris: Centre National de la Rechereche Scientifique. [Google Scholar]
- Fleishman, E. , Austin, G. T. , & Weiss, A. D. (1998). An empirical test of Rapoport's rule: Elevational gradients in montane butterfly communities. Ecology, 79, 2482–2493. [Google Scholar]
- Franco, A. M. A. , Hill, J. K. , Kitschke, C. , Collingham, Y. C. , Roy, D. B. , Fox, R. , … & Thomas, C. D. (2006). Impacts of climate warming and habitat loss on extinctions at species’ low‐latitude range boundaries. Global Change Biology, 12, 1545–1553. [Google Scholar]
- Freeman, B. G. , & Freeman, A. M. C. (2014). Rapid upslope shifts in New Guinean birds illustrate strong distributional responses of tropical montane species to global warming. Proceedings of the National Academy of Sciences of the United States of America, 111, 4490–4494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu, C. , Wu, J. , Wang, X. , Lei, G. , & Chen, J. (2004). Patterns of diversity, altitudinal range and body size among freshwater fishes in the Yangtze River basin, China. Global Ecology and Biogeography, 13, 543–552. [Google Scholar]
- Garcia‐Rosello, E. , Guisande, C. , Manjarres‐Hernandez, A. , Gonzalez‐Dacosta, J. , Heine, J. , Pelayo‐Villamil, P. , … & Lobo, J. M. (2015). Can we derive macroecological patterns from primary Global Biodiversity Information Facility data? Global Ecology and Biogeography, 24, 335–347. [Google Scholar]
- Gaston, K. J. , & Chown, S. L. (1999). Elevation and climatic tolerance: A test using dung beetles. Oikos, 86, 584–590. [Google Scholar]
- Ghalambor, C. K. , Huey, R. B. , Martin, P. R. , Tewksbury, J. J. , & Wang, G. (2006). Are mountain passes higher in the tropics? Janzen's hypothesis revisited. Integrative and Comparative Biology, 46, 5–17. [DOI] [PubMed] [Google Scholar]
- Grytnes, J. A. , & Vetaas, O. R. (2002). Species richness and altitude: A comparison between null models and interpolated plant species richness along the Himalayan altitudinal gradient, Nepal. The American Naturalist, 159, 294–304. [DOI] [PubMed] [Google Scholar]
- Hagen, T. (1969). Report on the Geological survey of Nepal. Denckschrift derschweizerischen Naturforschenden Gesellschaft, 86, 1–160. [Google Scholar]
- Harrison, S. , & Grace, J. (2007). Biogeographic affinity helps explain productivity‐diversity relationships at regional and local scales. The American Naturalist, 170, S5–S15. [DOI] [PubMed] [Google Scholar]
- Hastie, T. J. , & Tibshirani, R. J. (1990). Generalized additive models. London: Chapman & Hall. [DOI] [PubMed] [Google Scholar]
- Hausdorf, B. (2006). Latitudinal and altitudinal diversity patterns and Rapoport effects in north‐west European land snails and their causes. Biological Journal of the Linnean Society, 87, 309–323. [Google Scholar]
- Hawkins, B. A. , Diniz‐Filho, J. A. F. , & Weis, A. E. (2005). The mid‐domain effect and diversity gradients: Is there anything to learn. The American Naturalist, 166, E140–E143. [DOI] [PubMed] [Google Scholar]
- Herzog, S. K. , Hamel‐Leigue, A. C. , Larsen, T. H. , Mann, D. J. , Soria‐Auza, R. W. , Gill, B. D. , … & Spector, S. (2013). Elevational distribution and conservation biogeography of Phanaeine dung beetles (Coleoptera: Scarabaeinae) in Bolivia. PLoS ONE, 8, 0064963.1–0064963.11. doi:10.1371/journal.pone.0064963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickler, T. , Vohland, K. , Feehan, J. , Miller, P. A. , Smith, B. , Costa, L. , … & Sykes, M. T. (2012). Projecting the future distribution of European potential natural vegetation zones with a generalized, tree species‐based dynamic vegetation model. Global Ecology and Biogeography, 21, 50–63. [Google Scholar]
- Hijmans, R. J. , Cameron, S. E. , Parra, J. L. , Jones, P. G. , & Jarvis, A. (2005). Very high resolution interpolated climate surfaces for global land areas. International Journal of Climatology, 25, 1965–1978. [Google Scholar]
- Kerr, J. T. (1999). Weak links: ‘Rapoport's rule’ and large‐scale richness patterns. Global Ecology and Biogeography, 8, 47–54. [Google Scholar]
- Kluge, J. , Kessler, M. , & Dunn, R. R. (2006). What drives elevational patterns of diversity? A test of geometric constraints, climate and species pool effects for pteridophytes on an elevational gradient in Costa Rica. Global Ecology and Biogeography, 15, 358–371. [Google Scholar]
- La Sorte, F. A. , & Jetz, W. (2010). Projected range contractions of montane biodiversity under global warming. Proceedings of the Royal Society B: Biological Sciences, 277, 3401–3410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, C. B. , Chun, J. H. , Song, H. K. , & Cho, H. J. (2013). Altitudinal patterns of plant species richness on the Baekdudaegan Mountains, South Korea: Mid‐domain effect, area, climate, and Rapoport's rule. Ecological Research, 28, 67–79. [Google Scholar]
- Li, M. , & Feng, J. M. (2015). Biogeographical interpretation of elevational patterns of genus diversity of seed plants in Nepal. PLoS ONE, 10, e0140992.1– e0140992.16. doi:10.1371/journal.pone.0140992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manandhar, M. S. (1999). Evolution of the Himalaya Majupuria TC (pp. 13–17). Majupuria RK. Nepalnature's paradise. Kathmandu: Hillside Press Ltd. [Google Scholar]
- McCain, C. M. (2009). Vertebrate range sizes indicate that mountains may be ‘higher’ in the tropics. Ecology Letters, 12, 550–560. [DOI] [PubMed] [Google Scholar]
- McCain, C. M. , & Colwell, R. K. (2011). Assessing the threat to montane biodiversity from discordant shifts in temperature and precipitation in a changing climate. Ecology Letters, 14, 1236–1245. [DOI] [PubMed] [Google Scholar]
- McCain, C. M. , & Knight, K. B. (2013). Elevational Rapoport's rule is not pervasive on mountains. Global Ecology and Biogeography, 22, 750–759. [Google Scholar]
- Nathan, R. , & Werner, Y. L. (1999). Reptiles and breeding birds on Mt. Hermon: Patterns of altitudinal distribution and diversity species density. Israel Journal of Zoology, 45, 1–33. [Google Scholar]
- Ohmura, A. (2012). Enhanced temperature variability in high‐altitude climate change. Theoretical and Applied Climatology, 110, 499–508. [Google Scholar]
- Oommen, M. A. , & Shanker, K. (2005). Elevational species diversity patterns emerge from multiple local mechanisms in Himalayan woody plants. Ecology, 86, 3039–3047. [Google Scholar]
- Patterson, B. D. , Pacheco, V. , & Solari, S. (1996). Distributions of bats along an elevational gradient in the Andes of south‐eastern Peru. Journal of Zoology, London, 240, 637–658. [Google Scholar]
- Porter, W. P. , Sabo, J. L. , Tracy, C. R. , Reichman, O. J. , & Ramankutty, N. (2002). Physiology on a landscape scale: Plant–animal interactions. Integrative and Comparative Biology, 42, 431–453. [DOI] [PubMed] [Google Scholar]
- Qian, H. (1998). Large‐scale biogeographic patterns of vascular plant diversity in North America: An analysis at the genera level. Journal of Biogeography, 25, 829–836. [Google Scholar]
- Qian, H. , Wang, S. L. , He, J. S. , Zhang, J. L. , Wang, L. S. , Wang, X. L. , & Guo, K. (2006). Phytogeographical analysis of seed plant genera in China. Annals of Botany, 98, 1073–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahbek, C. (1997). The relationship among area, elevation, and regional richness in Neotropical birds. The American Naturalist, 149, 875–902. [DOI] [PubMed] [Google Scholar]
- Ribas, C. R. , & Schoereder, J. H. (2006). Is the Rapoport effect widespread? Null models revisited. Global Ecology and Biogeography, 15, 614–624. [Google Scholar]
- Rohner, P. T. , Bachli, G. , Paltrinieri, L. P. , Duelli, P. , Obrist, M. K. , Jochmann, R. , & Blanckenhorn, W. U. (2015). Distribution, diversity gradients and Rapoport's elevational rule in the black scavenger flies of the Swiss Alps (Diptera: Sepsidae). Insect Conservation and Diversity, 8, 367–376. [Google Scholar]
- Sanders, N. J. (2002). Elevational gradients in ant richness: Area, geometry, and Rapoport's rule. Ecography, 25, 25–32. [Google Scholar]
- Sekercioglu, C. H. , Schneider, S. H. , Fay, J. P. , & Loarie, S. R. (2008). Climate change, elevational range shifts, and bird extinctions. Conservation Biology, 22, 140–150. [DOI] [PubMed] [Google Scholar]
- Sheldon, K. S. , Leache, A. D. , & Cruz, F. B. (2015). The influence of temperature seasonality on elevational range size across latitude: A test using Liolaemus lizards. Global Ecology and Biogeography, 24, 632–641. [Google Scholar]
- Sizling, A. L. , Storch, D. , & Keil, P. (2009). Rapoport's rule, species tolerances, and the latitudinal diversity gradient: Geometric considerations. Ecology, 90, 3575–3586. [DOI] [PubMed] [Google Scholar]
- Stevens, G. C. (1989). The latitudinal gradient in geographical range: How so many species coexist in the tropics. The American Naturalist, 133, 240–256. [Google Scholar]
- Stevens, G. C. (1992). The elevational gradient in altitudinal range: An extension of Rapoport's latitudinal rule to altitude. The American Naturalist, 140, 893–911. [DOI] [PubMed] [Google Scholar]
- Taylor, P. H. , & Gaines, S. D. (1999). Can Rapoport's rule be rescued? Modeling causes of the latitudinal gradient in species richness. Ecology, 80, 2474–2482. [Google Scholar]
- Thuiller, W. , Lavorel, S. , Araujo, M. B. , Sykes, M. T. , & Prentice, I. C. (2005). Climate change threats to plant diversity in Europe. Proceedings of the National Academy of Sciences of the United States of America, 102, 8245–8250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasovych, A. , Jablonski, D. , Berke, S. K. , Krug, A. Z. , & Valentine, J. W. (2015). Nonlinear thermal gradients shape broad‐scale patterns in geographic range size and can reverse Rapoport's rule. Global Ecology and Biogeography, 24, 157–167. [Google Scholar]
- Tomasovych, A. , Kennedy, J. D. , Betzner, T. J. , Kuehnle, N. B. , Edie, S. , Kim, S. , … & Jablonski, D. (2016). Unifying latitudinal gradients in range size and richness across marine and terrestrial systems. Proceedings of the Royal Society B‐Biological Sciences, 283, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez, D. P. , & Stevens, R. D. (2004). The latitudinal gradient in niche breadth: Concepts and evidence. American Naturalist, 164, E1–E19. [DOI] [PubMed] [Google Scholar]
- Vegas‐Vilarrubia, T. , Nogue, S. , & Rull, V. (2012). Global warming, habitat shifts and potential refugia for biodiversity conservation in the neotropical Guayana Highlands. Biological Conservation, 152, 159–168. [Google Scholar]
- Vetaas, O. R. , & Grytnes, J. A. (2002). Distribution of vascular plant species richness and endemic richness along the Himalayan elevation gradient in Nepal. Global Ecology and Biogeography, 11, 291–301. [Google Scholar]
- Wang, Z. H. , Fang, J. Y. , Tang, Z. Y. , & Lin, X. (2011). Patterns, determinants and models of woody plant diversity in China. Proceedings of the Royal Society B‐Biological Sciences, 278, 2122–2132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Z. H. , Tang, Z. Y. , & Fang, J. Y. (2007). Elevational patterns of seed plant diversity in the Gaoligong Mountains, south‐east Tibet, China. Diversity & Distributions, 13, 845–854. [Google Scholar]
- Wang, Y. M. , You, J. E. , & Feng, J. M. (2015). A comparative study on fl oras in Nepal and Southern Tibet. Palaeogeography, Palaeoclimatology, Palaeoecology, 417, 1–5. [Google Scholar]
- Wilson, E. O. (1975). Sociobiology (pp. 1–498). Cambridge: The New Synthesis. Harvard University Press. [Google Scholar]
- Wu, C. Y. (1991). The areal‐types of Chinese genera of seed plants. Acta Botanical Yunnanica, 4, 1–139. [Google Scholar]
- Zhu, H. (2012). Biogeographical divergence of the flora of Yunnan, southwestern China initiated by the uplift of Himalaya and extrusion of Indochina. PLoS ONE, 7, e45601.1–e45601.9. doi:10.1371/journal.pone.0045601 [DOI] [PMC free article] [PubMed] [Google Scholar]


